Train-Induced Building Vibration and Radiated Noise by Considering Soil Properties

Abstract

Constructing buildings above subway tracks exploits urban-area space intensively by adopting the three-dimensional overlapping development mode, which is one of the important measures for solving the contradictions among urban population increase, land resource shortage, and environmental protection. However, the vibration generated by the frequent train operations is transmitted to the upper buildings through the track structure and ground soil, which can cause structural vibrations and radiated noise and bring physical and mental side effects to occupants within the buildings. Subway projects are often located in geologically sensitive areas, while the influences of the encountered geological problems on the generation and propagation of structural vibration and structure-radiated noise within the buildings are not yet clear. Hence, this paper presents a method of studying the train-induced vibration transmission from the ground up into the buildings and the structure-radiated noise within the building. The method consists of a train-track model, track-soil-building model, and structure-radiated noise simulation. The impact of soil properties on the building vibration and structure-radiated noise is analyzed and ground-improvement measures are proposed in order to mitigate vibration and structure-radiated noise within buildings. The results show that the interaction between soil and structure has a great impact on vibration transmission from the ground into the building. Good foundations reduce vibration transmission from ground soil up into the building and lead to a lower level of structure-radiated noise. Ground improvements increase the impedance of ground soil, thereby weakening the vibration transmission and lowering the structure-radiated noise.

1. Introduction

In the process of urban development and expansion, a city should adopt efficient, energy-saving, and environmentally friendly urban transportation systems and intensive development strategies against traffic congestion, environmental deterioration, and encroachment on arable land. With the continuous urban development, the contradiction between population increase and land shortage will become more serious [1]. Therefore, the three-dimensional overlapping development of urban space gains its importance. The construction of buildings above subway tracks is a mode of three-dimensional overlapping development of urban space [2]. This mode not only provides the subway system’s operation with the financial support from property development, but also makes comprehensive utilization of urban land [3], improving both the social and economic benefits.

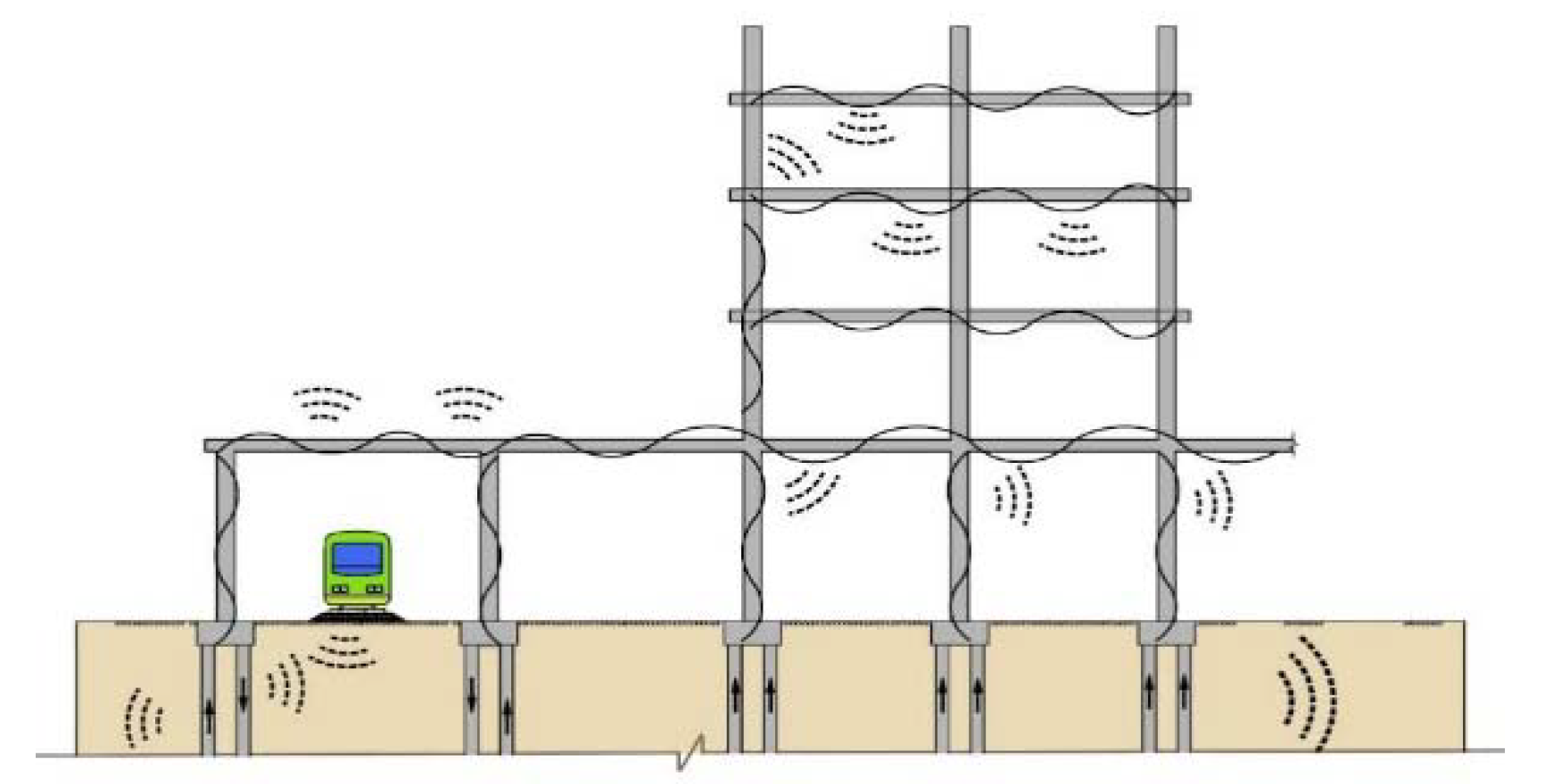
However, train-induced vibrations will transmit into the buildings and cause radiated noise from indoor structures or furniture [4,5]. The energy, in the form of vibration waves, transmits from the ground soil to the foundation of the building through the interaction between them and results in building vibrations and structure-radiated noise, which may affect people’s normal lives and work within the building [6], as shown in Figure 1. Therefore, effectively estimating and reducing the environmental problems caused by vibration and radiated noise has become a key factor in the three-dimensional overlapping development of urban space.

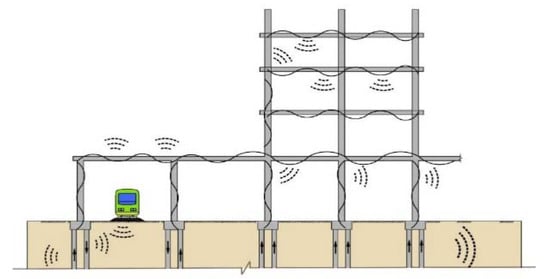
Figure 1. Building vibration and structure-radiated noise.

At present, the impact evaluation of environmental vibration caused by train operations was primarily based on empirical methods, experimental methods, numerical methods, or the combination of comprehensive methods during the preliminary design and the construction stage, as well as the operation stage [7,8,9,10,11]. The empirical methods are based on theoretical researches and a large number of field test data. The impact factors accounting for the distance between the vibration receiver and the vibration source, wheel-rail contact force, train speed, and vibration attenuation are taken into consideration, and then empirical formulas are formed to guide vibration assessment [12,13]. The experimental methods usually use transfer functions to predict the vibration responses in a building. By applying excitation to the track, the excitation force and the vibration response of the surrounding buildings can be recorded in the frequency domain, from which the transfer function between the vibration source and the receiver can be calculated [14]. Although the experimental methods result in good accuracy, they need a large number of field measurements to find out the vibration wave transmission characteristics of a specific site, thus requiring a long prediction period and high cost.

The numerical method is a relatively mature method, including the finite difference method, finite element method, infinite element method, and boundary element method [15,16,17,18,19]. The finite element method is most commonly used, and its main advantage is that objects with complex geometries and boundary conditions can be simulated [20,21,22]. To reduce calculation time and eliminate the impact of artificial boundaries, the finite and infinite element methods can be combined, forming a 2.5-dimensional (2.5D) finite element model to simulate the ground vibration responses induced by moving loads [23]. Lopes et al. [24] used the 2.5D finite element model to simulate train-track-foundation soil, and used the 3D finite element model to simulate the building structure and predict the vibration caused by train operation. Nagy et al. [25] and Fiala et al. [26] used finite element and boundary element models to predict the vibration propagation and structure-radiated noise in the buildings.

For the structure-radiated noise, it is generally believed that the influencing factors include the vibration velocity of the building structure, the geometric size of the room, the setting of doors and windows, and the sound-absorbing properties of the room surface [27,28]. Urban areas affected by noise typically include schools, residence, office buildings, markets, airports, and subway stations [29,30,31,32,33]. To predict the structure-radiated noise, methods such as numerical methods, empirical formulas, or experimental methods can be adopted [34,35]. The empirical formula method is widely used because of its convenience and low cost [36].

However, there is little research on the impact of ground soil properties on train-induced building vibrations and structure-radiated noise. The engineering environment of subway construction is complex, and it is often referred to as a geologically sensitive area which has many geological engineering problems. For example, the water-rich soft silt stratum has a high natural water content, larger pore ratio and compressibility, and low bearing capacity, which makes it easy to cause the settlement of the track and building structures. The water-rich sand layer has large pores and a loose structure, which also makes it easy to cause ground and building settlement. However, the influences of these geological problems on the propagation of vibration and structure-radiated noise within the buildings are not clear. Hence, it is necessary to study the train-induced building vibration and radiated noise under different geological conditions.

The purpose of this study is to explore the train-induced vibration transmission from the ground up into the building and the structure-radiated noise within the building. A method which consists of a train-track model, track-soil-building model, and structure-radiated noise simulation is presented and verified by measurements. The impact of soil properties on the building vibration and structure-radiated noise is analyzed and ground improvement is proposed as a measure to mitigate vibration and structure-radiated noise within buildings.

2. Methods

2.1. Overview

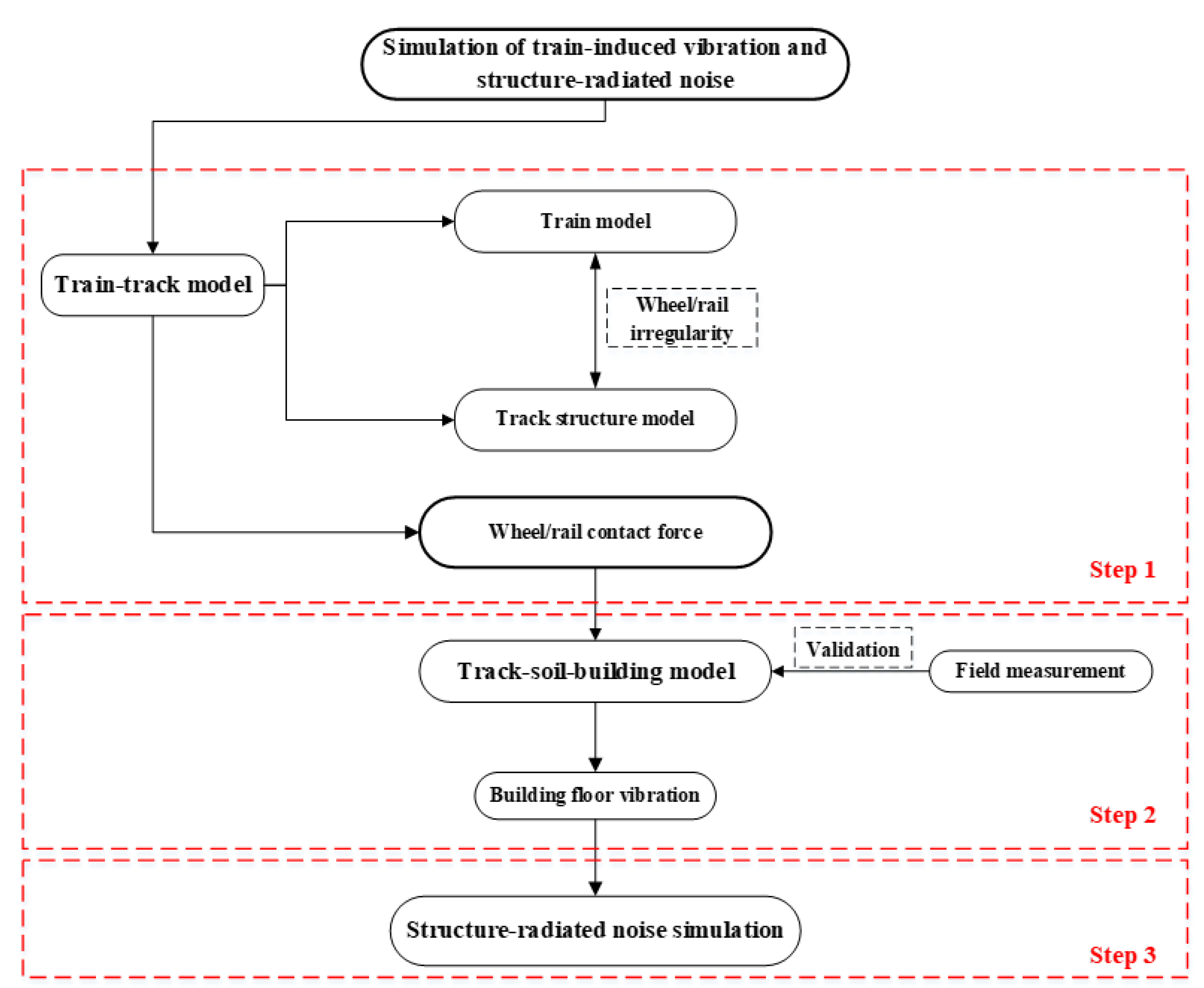
As shown in the Figure 2, the simulation of train-induced vibration and structure-radiated noise within buildings can be divided into three steps, which are the train-track vibration generation simulation, track-soil-building vibration transmission simulation, and structure-radiated noise calculation.

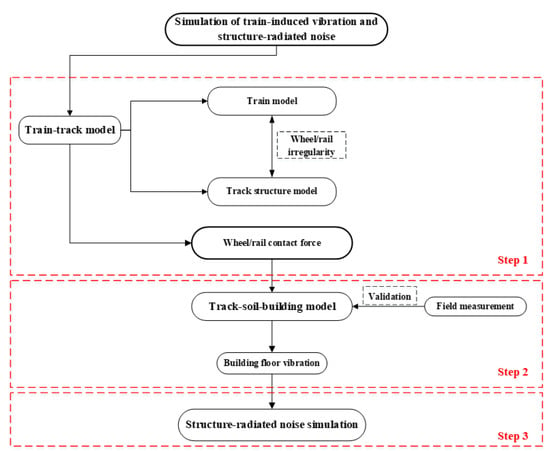
Figure 2. Overview of the simulating procedure of train-induced vibration and structure-radiated noise.

The simulating procedure can be described as:

• Train-track coupling dynamic model is established, including a train model and track structure model. Based on the displacement compatibility and force balance coordination between the wheel and rail, the train and track structure dynamics equations are solved using the simple and fast explicit integration method developed by Zhai [37]. Considering wheel and rail irregularity, the time-variant contact force between the wheel and rail can be obtained.
• The track-soil-building finite element model is established using the ABAQUS package. By compiling the moving load subroutine and using the wheel and rail contact force as the moving load for the model, the ground and building floor vibrations can be obtained and then verified by field measurements.
• Based on the calculated vibration level, the structure-radiated noise level is deduced according to the FTA standard.

2.2. Train-Track Model

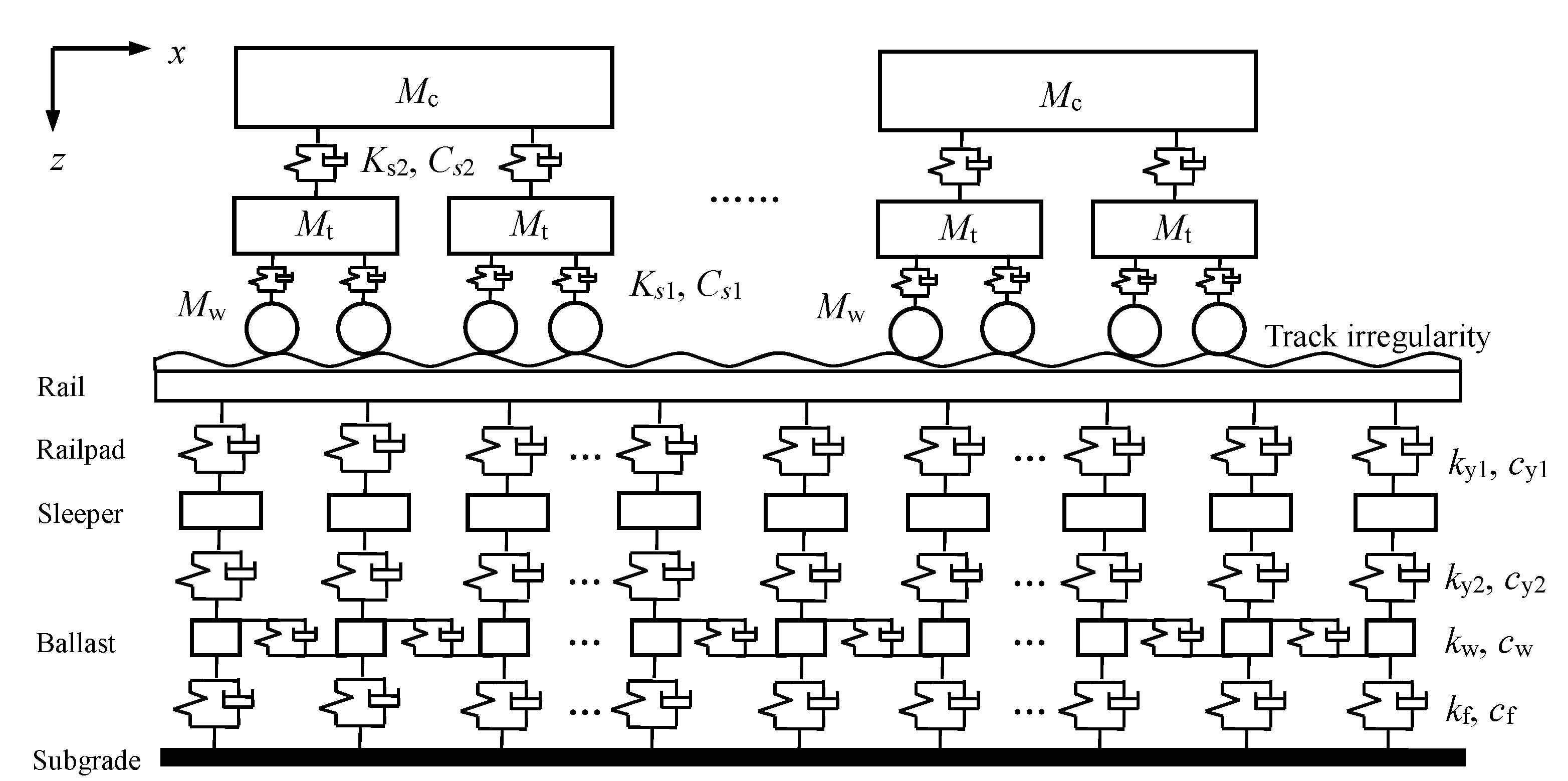
In a subway system, the dynamic interaction between the train and track structure generates vibrations which are transmitted to the surrounding soil and then to the surrounding buildings, resulting in building vibrations and structure-radiated noise. Given this, the vibration source model usually includes two parts, namely the train model and the track structure model.

The train model is a vibration system with 10 degrees of freedom, which is composed of the vehicle body, bogies, and wheelsets. The vehicle body, bogies, and wheelsets are all considered as rigid bodies, connected to each other by the primary and secondary suspensions, which are both modeled using spring-dampers, as shown in Figure 3.

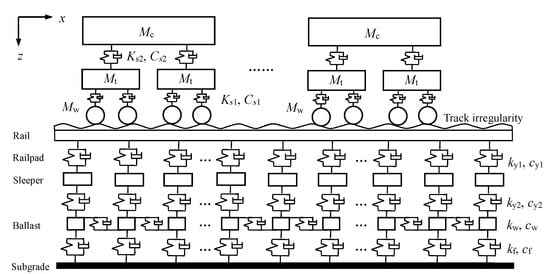
Figure 3. Train-track model.

The train is assumed to be traveling along the track at a constant speed, so the relative displacement between cars can be ignored. The dynamic equation of the train model is [38]:

$${\left[\mathrm{M}\right]}_{\mathrm{c}}{\left\{\ddot{\mathrm{q}}\right\}}_{\mathrm{c}}+{\left[\mathrm{C}\right]}_{\mathrm{c}}{\left\{\dot{\mathrm{q}}\right\}}_{\mathrm{c}}+{\left[\mathrm{K}\right]}_{\mathrm{c}}{\left\{\mathrm{q}\right\}}_{\mathrm{c}}={\left\{\mathrm{F}\right\}}_{\mathrm{rail}/\mathrm{wheel}}\hspace{0.17em}\hspace{0.17em}(\mathrm{c}=1,2\dots ,6)$$

(1)

where ${\left\{\ddot{\mathrm{q}}\right\}}_{\mathrm{c}}$, ${\left\{\dot{\mathrm{q}}\right\}}_{\mathrm{c}}$ and ${\left\{\mathrm{q}\right\}}_{\mathrm{c}}$ represent the acceleration, velocity and displacement vectors of the train, respectively. ${\left[\mathrm{M}\right]}_{\mathrm{c}}$, ${\left[\mathrm{C}\right]}_{\mathrm{c}}$ and ${\left[\mathrm{K}\right]}_{\mathrm{c}}$ are the mass, damping and stiffness matrices of the train. ${\left\{\mathrm{F}\right\}}_{\mathrm{rail}/\mathrm{wheel}}$ is the vertical wheel/rail contact force vector deduced from the displacement and track irregularity of the train and track. The dynamic parameters of a metro train with 6 cars are listed in Table 1.

Table 1. Dynamic parameters of the metro train.

Name	Value
Car length	19,520 mm
Car body mass	42,600 kg
Inertia moment of car body	1,262,000 kg·m2
Bogie mass	2550 kg
Inertia moment of bogie	2410 kg·m2
Distance between two bogie centers	12,600 mm
Distance between two axles of a bogie	2300 mm
Primary suspension stiffness	1.5 kN/mm
Primary suspension damping	5 kN∙s/m
Secondary suspension stiffness	0.48 kN/mm
Secondary suspension damping	60 kN∙s/m
Wheelset mass	1760 kg

The simulated track structure in this research is a ballast track, which is modeled as a three-layer structure, including the rail, sleepers, and ballast [38]. The degrees of freedom of the track system are set in the same plane as the degrees of freedom of the train model. The rail is modeled as an Euler beam, ignoring the influence of shear force and moment of inertia. The elastic and damping characteristics of the rail fasteners, ballast, and foundation are expressed by equivalent stiffness coefficients (${\mathrm{k}}_{\mathrm{y}1}$, ${\mathrm{k}}_{\mathrm{y}2}$, ${\mathrm{k}}_{\mathrm{f}}$) and damping coefficient (${\mathrm{c}}_{\mathrm{y}1}$, ${\mathrm{c}}_{\mathrm{y}2}$, ${\mathrm{c}}_{\mathrm{f}}$), respectively.

The dynamic equation of the track model is [39]:

$${\left[\mathrm{M}\right]}_{\mathrm{r}}{\left\{\ddot{\mathrm{q}}\right\}}_{\mathrm{r}}+{\left[\mathrm{C}\right]}_{\mathrm{r}}{\left\{\dot{\mathrm{q}}\right\}}_{\mathrm{r}}+{\left[\mathrm{K}\right]}_{\mathrm{r}}{\left\{\mathrm{q}\right\}}_{\mathrm{r}}={\left\{\mathrm{F}\right\}}_{\mathrm{rail}/\mathrm{wheel}}$$

(2)

where ${\left\{\ddot{\mathrm{q}}\right\}}_{\mathrm{r}}$, ${\left\{\dot{\mathrm{q}}\right\}}_{\mathrm{r}}$ and ${\left\{\mathrm{q}\right\}}_{\mathrm{r}}$ represent the acceleration, velocity and displacement vectors of the track, respectively. ${\left[\mathrm{M}\right]}_{\mathrm{r}}$,${\left[\mathrm{C}\right]}_{\mathrm{r}}$ and ${\left[\mathrm{K}\right]}_{\mathrm{r}}$ are the mass, damping and stiffness matrices of the track. The dynamic parameters of track model are listed in Table 2.

Table 2. Dynamic parameters of the track model.

Name	Unit	Value	Name	Unit	Value
Elastic modulus of rail	N/m2	2.06 × 1011	Rail mass per unit length	kg/m	60.64
Area of rail cross-section	m2	7.745 × 10−3	Area moment of rail cross-section	m4	3.217 × 10−5
Rail density	kg/m3	7830	Rail pad damping	N∙s/m	5 × 104
Rail pad stiffness	N/m	1.0 × 108	Mass of sleeper	kg	251
Sleeper spacing	m	0.6	Ballast stiffness	N/m	0.8 × 108
Ballast density	kg/m3	1750	Subgrade modulus	Pa/m	1.3 × 108
Ballast Damping	N∙s/m	1.6 × 105	Subgrade damping	N∙s/m	6.32 × 104
Ballast shear stiffness	N/m	7.8×107	Ballast shear damping	N∙s/m	8.0 × 104

The selection of the rail length and elements’ sizes should take the computing efficiency and accuracy of the model into consideration, which has been studied by many scholars. Popp et al. [40] proposed that at least 10 sleepers should be modeled in the model, and the number of sleepers should increase with the increase of train speed. In fact, when the calculated length of the rail is long enough, the influence of the boundary conditions at both ends of the rail can be ignored. To consider the situation where all six of the vehicles are running on the rail, the rail length is set to be more than 2.5 times the total length of the train.

The wheel-rail contact force F_rain/wheel is calculated based on the nonlinear Hertz contact theory:

$${\mathrm{F}}_{\mathrm{rail}/\mathrm{wheel}}=\{\begin{array}{ll}{\left[\frac{1}{\mathrm{G}}{(\mathrm{q}}_{\mathrm{w}}{-\mathrm{q}}_{\mathrm{r}}-\mathrm{h})\right]}^{\frac{3}{2}}\hfill & {\mathrm{q}}_{\mathrm{w}}{-\mathrm{q}}_{\mathrm{r}}-\mathrm{h}\ge 0\hfill \\ 0\hfill & {\mathrm{q}}_{\mathrm{w}}{-\mathrm{q}}_{\mathrm{r}}-\mathrm{h}<0\hfill \end{array}$$

(3)

where ${\mathrm{q}}_{\mathrm{wi}}$ and ${\mathrm{q}}_{\mathrm{ri}}$ are vertical displacements of the wheelset and the rail at wheel–rail contact points, respectively, and $\mathrm{h}$ is the amplitude of the track irregularity. $\mathrm{G}$ is a geometric and material parameter which is defined as:

$$\mathrm{G}=3.86{\mathrm{R}}^{-0.115}\times {10}^{-8}{(\mathrm{m}/\mathrm{N}}^{2/3})$$

(4)

where R is the wheel radius of 0.4575 m. The simulation of rail irregularity is based on the railway track of line grade six in the American Railway Standard [41]. The simple and fast explicit integration method developed by Zhai [37] is used to solve the system dynamic equations.

The train-track model is closely related to the train vibration properties, rail smoothness and condition, train speed, and load combination, which reflects: (1) The influence factors of the vehicle itself, including axle weight and suspensions; (2) the influence of track irregularity, which is considered as the main factor that causes the dynamic load of vehicles and rails; (3) the influence of train speed; (4) the moving train load and the transfer and dispersion effects of the rail and sleeper on load are considered.

2.3. Track-Soil-Building Model

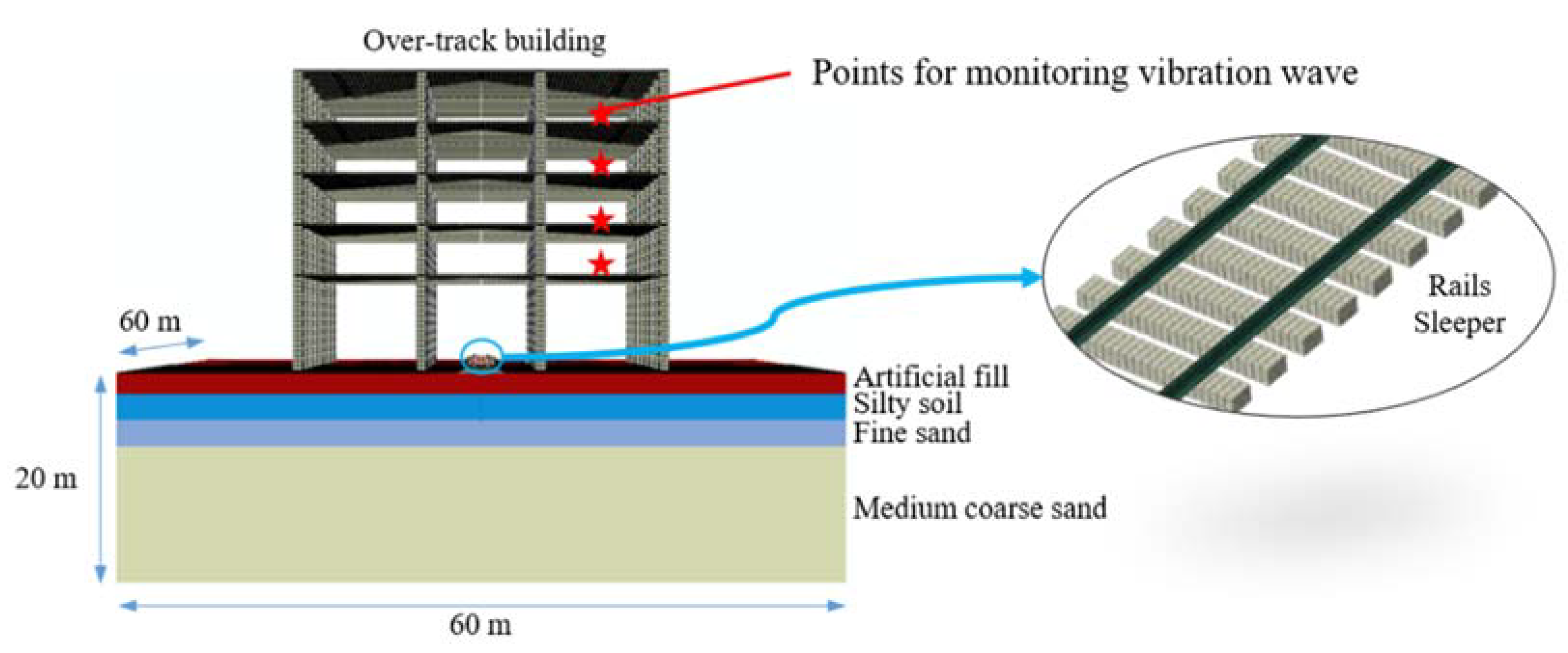
The track-soil-building model consists of the track structure, soil, and building structure, and is constructed with the finite element method, as shown in Figure 4.

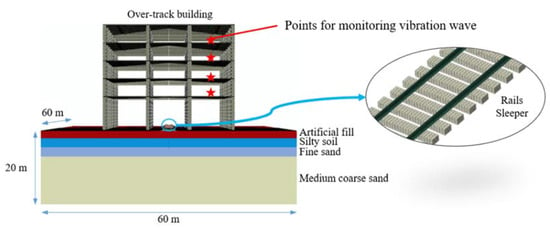
Figure 4. Track-soil-building finite element model.

The finite element model of the track structure is composed of rails, sleepers, and the ballast. The seamless rail is 60 kg/m, U75V hot-rolled with 1435 mm gauge. The number of sleepers is 1680/km. The ballast has a gravel structure with a thickness of 0.45 m, and the thickness of its surface layer and subballast are 0.25 m and 0.20 m, respectively. The top width of the ballast is 3.3 m, and the slope ratio is 1:1.75. The mechanical properties of the track structure are shown in Table 3.

Table 3. Mechanical properties of the track structure.

Material	Elastic Modulus (MPa)	Poisson’s Ratio	Density (kg/m3)
Rail	210,000	0.25	7850
Sleeper	30,000	0.2	2400
Ballast	300	0.35	1800
Subballast	300	0.35	2200

Since the train-induced vibration mainly propagates through the ground surface and its impact on the soil is mainly within the elastic range, the soil model can be simplified as homogeneous and linearly elastic. The soil model is discretized to obtain a number of eight-node solid elements in the local coordinate system. After the mass matrix, stiffness matrix, damping matrix, and equivalent nodal force matrix of each element are established, the system matrix can be constructed, and then the displacement, velocity, and acceleration of the structure can be obtained based on the explicit central difference method.

According to geological drilling data, the soil under the track is simplified into four layers. From the soil surface to the bottom, they are artificial fill, silty soil, fine sand, and medium coarse sand. The mechanical properties of the soil are shown in Table 4. The dimensions of the soil are 60 × 60 × 20 m (length × width × height). The element size is set to be less than one sixth of the minimum shear wavelength, which is selected as 0.3 m.

Table 4. Mechanical properties of the soil.

Soil	Thickness (m)	Density (g/cm3)	Dynamic Elastic Modulus E (MPa)	Poisson’s Ratio	Shear Wave Velocity (m/s)	Compression Wave Velocity (m/s)	Damping Ratio
Artificial fill	2.0	1.98	205	0.31	198.7	378.7	0.03
Silty soil	2.5	1.53	120	0.35	170.3	354.5	0.03
Fine sand	2.5	1.74	220	0.23	225.4	380.6	0.03
Medium coarse sand	13.0	1.96	280	0.25	240.2	416	0.03

When a finite size model is used to simulate infinite ground, the biggest problem is the artificially truncated boundary, which will cause the wave reflections and the vibration energy to transmit back to the analysis area from the boundary, resulting in distortion of the simulation. One solution is to use infinite elements [42,43] at the boundaries of the soil. The vibration energy is attenuated outward by introducing the attenuation formula of the infinite element at the boundary.

A five-story building model is generated to study the vibration transmission within it and the structure-radiated noise. The building is built over the track using a load-bearing concrete frame structure. The bottoms of the ground columns are located 1.5 m below the ground surface, and the interactions between the soil and the columns are simulated by spring and damper elements. The height of the first floor is 9.5 m, which leaves enough space for the train’s operation. To meet the height needs of the relevant equipment, other floors are set to 5.0 m. The cross-sectional dimensions of the building beams and columns are 0.5 × 0.5 m² and 1.0 × 1.0 m², respectively. The floor thickness is 0.2 m. The elastic modulus of the concrete material for beams, columns, and floors is 30 GPa, and its density is 2500 kg/m³. The structural damping is assumed as 0.02 for reinforced concrete structures.

In the ABAQUS finite element package, the application of moving loads requires the establishment of subroutine VDLOAD, which can simulate the train moving on the rail at a certain speed by defining the relationship between wheel-rail contact forces and positions, as shown in Figure 5. The wheel-track contact forces can be obtained through the train-track model as described in Section 2.2, and the acting locations of the forces on the rail change as the train runs.

Figure 5. Schematic diagram of moving train loads.

2.4. Structure-Radiated Noise Simulation

The structure-radiated noise caused by train operation affects people in the frequency range of 16–250 Hz, which is generated because the vibration excites the floor slabs, walls, columns, or other household devices in the room [44]. Structure-radiated noise can be derived from the velocity level of structural vibrations. In general, the A-weighted sound pressure level of structure-radiated noise is related to room volume, surface area, and reverberation time, whose relationship can be expressed as [45]:

$${\mathrm{L}}_{\mathrm{A}}{=\mathrm{L}}_{\mathrm{v}}{+\mathrm{A}+\mathrm{K}}_{A-wt}$$

(5)

where L_v is the velocity level (dB, re 2.54 × 10⁻⁸ m/s); A is the coefficient related to room volume, surface area, air density, and wave speed; K_A−wt is the A-weighted network value in the 1/3 frequency octave band.

For a typical residential room, the value of coefficient A is assumed to be equal to −5 dB when the decibel reference value for L_v is 2.54 × 10⁻⁸ m/s. The value of K_A−wt can be found in the Federal Transit Administration (FTA) standard [45].

3. Validation of the Methods

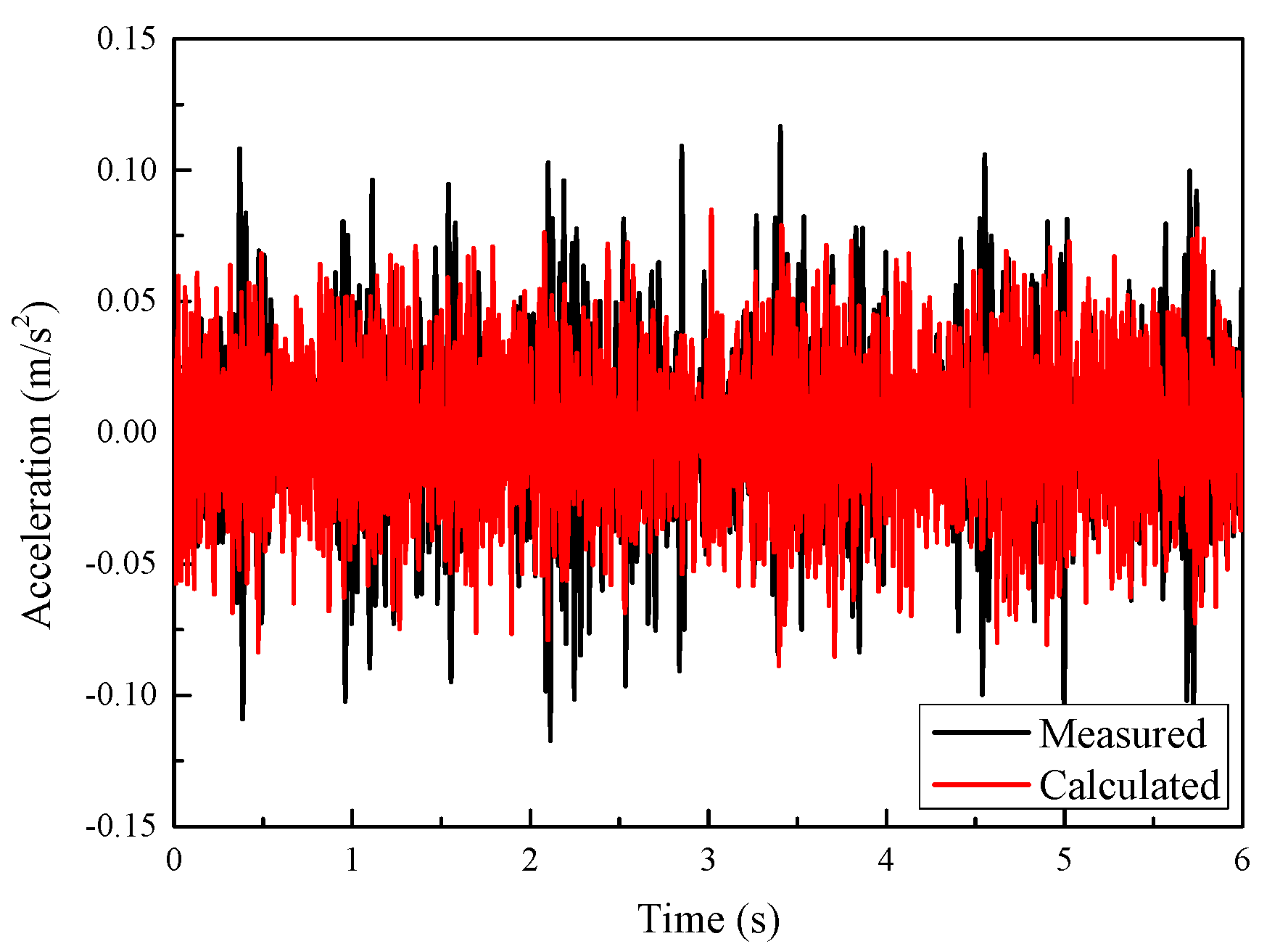
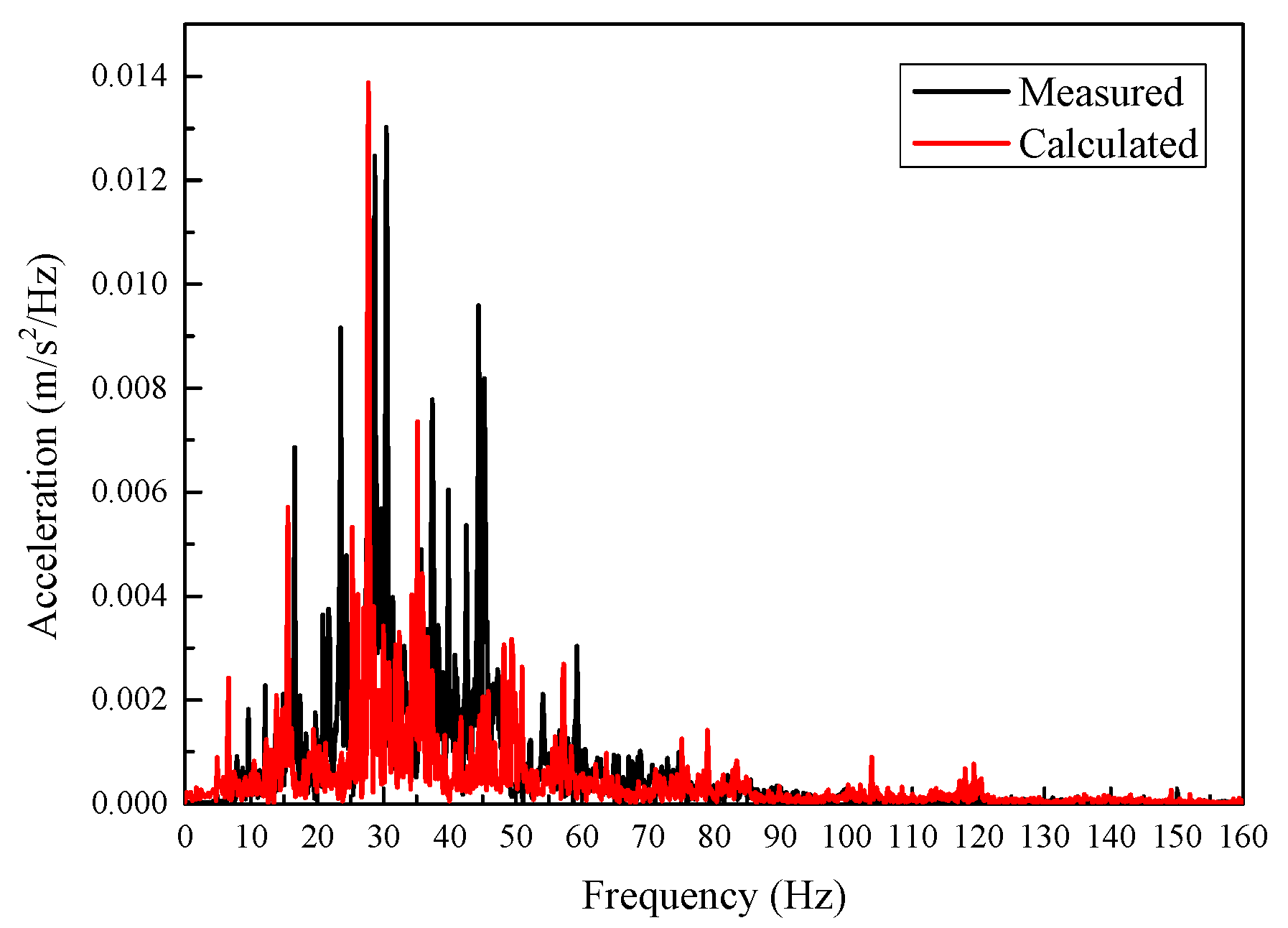
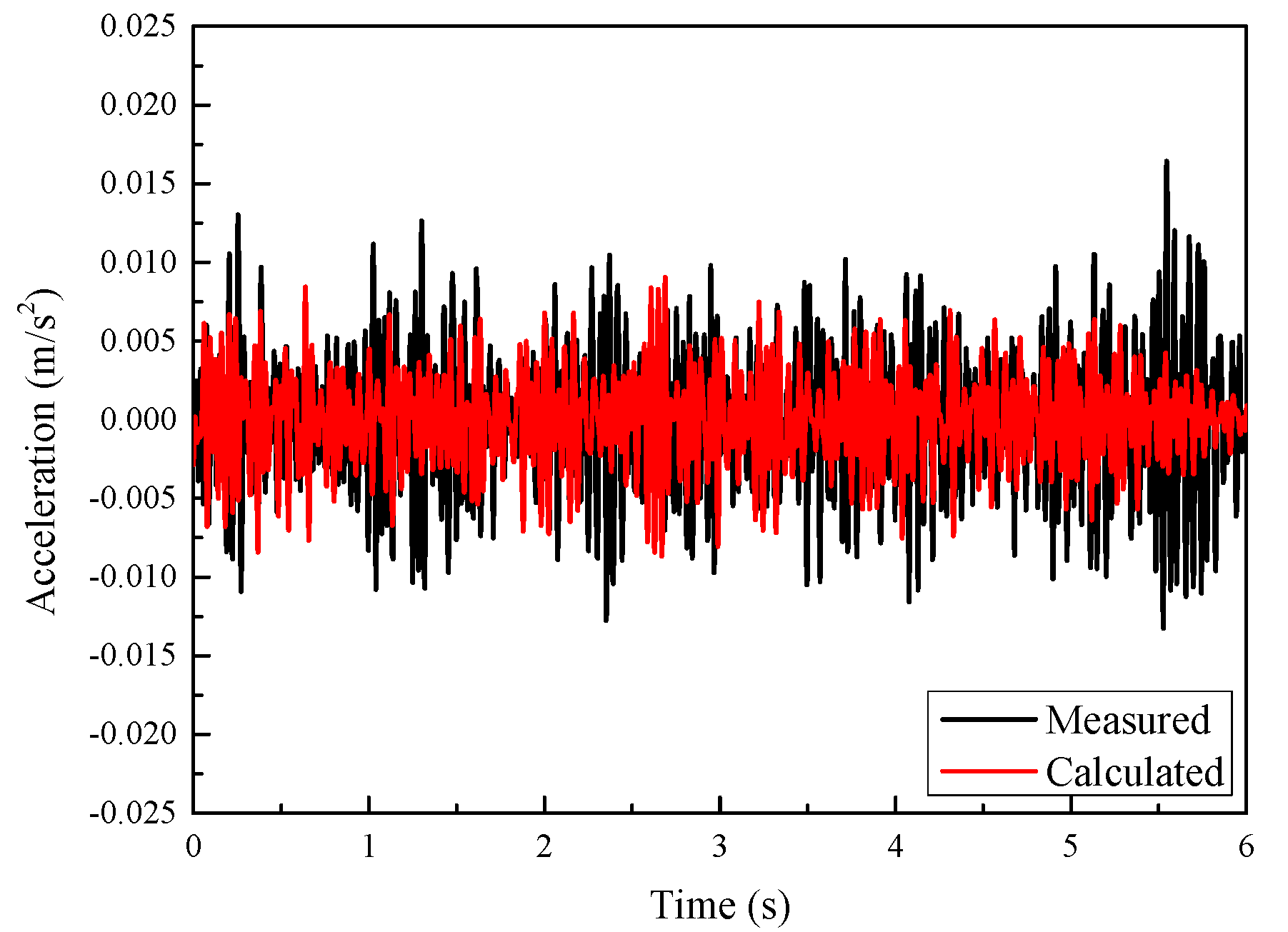
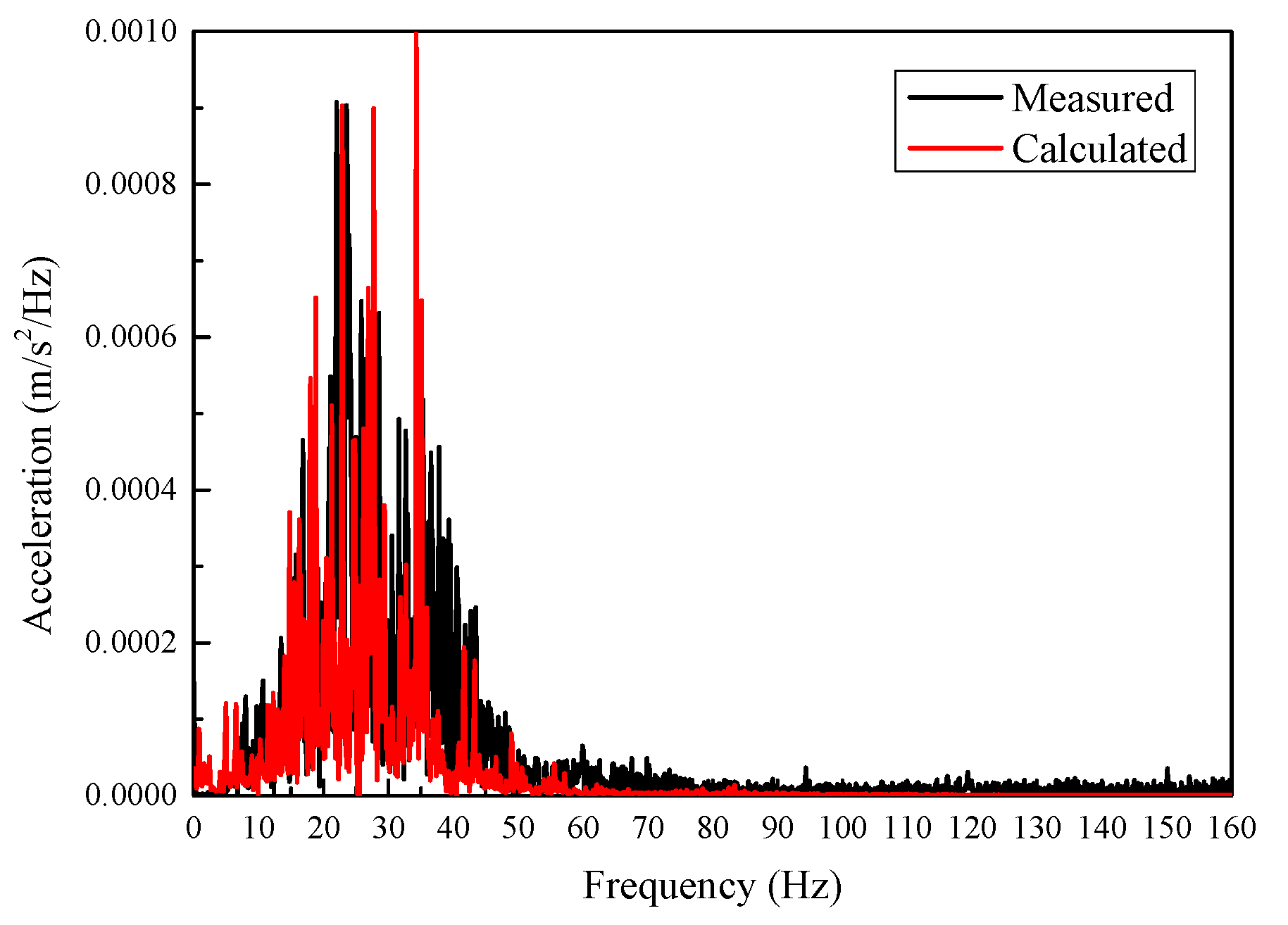
To verify the correctness of the proposed method, the track-soil-building finite element model is calculated using moving train loads as inputs, which are obtained from the train-track model. The soil parameters are selected based on the field geological drilling data. Through the repeated comparison between the calculated data and the measured data, the optimal value of each material parameter is determined within the field geological drilling data range. Both the time and frequency domain of the ground and building floor vibration are obtained. At the ground and on the 3rd floor, the calculated vibrations are compared with the measurements obtained by Zou et al. [5]. The compared results are shown in Figure 6, Figure 7, Figure 8 and Figure 9.

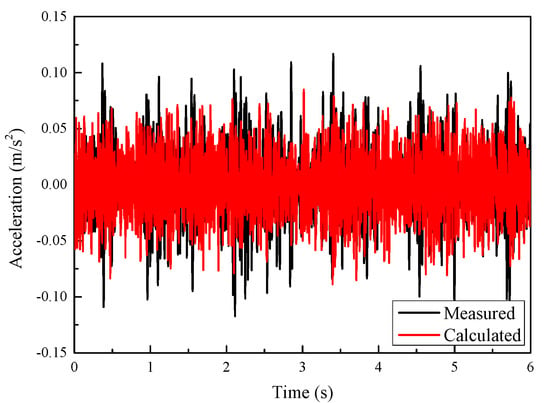
Figure 6. Comparison of measured and calculated acceleration time histories at the ground 12 m away from the track centerline.

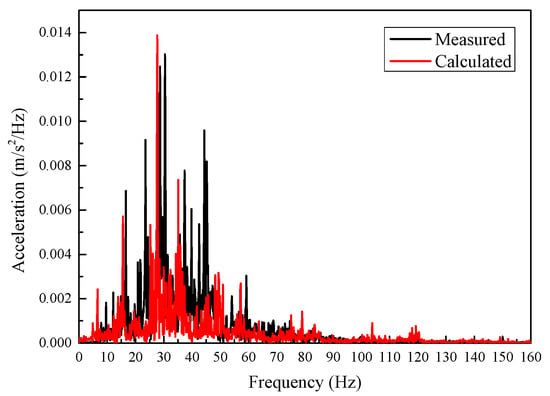
Figure 7. Comparison of measured and calculated acceleration frequency spectra at the ground 12 m away from the track centerline.

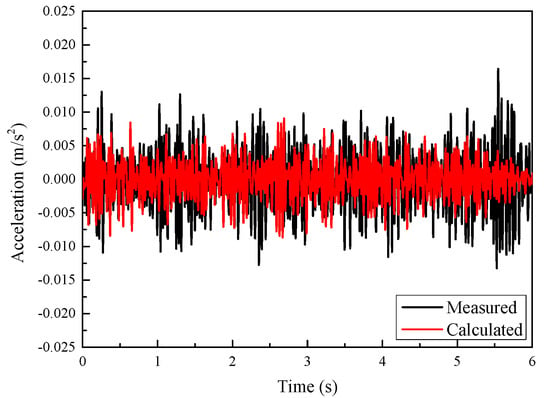
Figure 8. Comparison of measured and calculated acceleration time histories on the 3rd floor of the building.

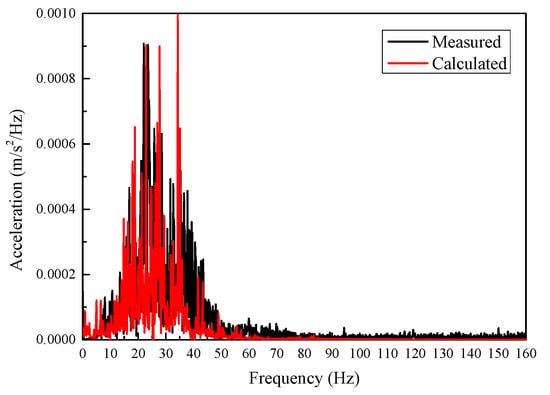
Figure 9. Comparison of measured and calculated acceleration frequency spectra on the 3rd floor of the building.

Figure 6 shows the calculated and measured vibrations in the time domain on the ground 12 m away from the track centerline. The calculated acceleration is close to the measured in terms of waveform and overall trend, both of which can reflect the train passing process. In addition, the calculated acceleration amplitude is also close to the measured. By converting the time histories into spectra using the Fast Fourier transform algorithm (FFT), the acceleration amplitudes in the frequency domain are obtained, as shown in Figure 7. As seen in the measured vibrations, the dominant frequency range of soil vibration is below 50 Hz, and the peak frequency is around 30 Hz. The frequency range is only shown up to 160 Hz because train-induced building vibration components above 160 Hz are almost negligible. The dominant frequency range and peak frequency of the calculated vibration are close to the measured. On the whole, the established method can simulate the train-induced vibration on the ground near the track structure.

Figure 8 and Figure 9 compare the calculated and measured acceleration on the 3rd floor of a nearby three-story building in time history and frequency domain, respectively [5]. The changing tendency of the calculated acceleration is in good agreement with the measured. The measured and calculated spectra consistently show that the dominant frequency range of building vibrations caused by train operation is below 50 Hz. The calculated and measured peak frequencies are also close. Hence, the established method can simulate the vibration transmission either from the ground into the building or within the building.

4. Impact of Soil Properties on the Building Vibrations and Structure-Radiated Noise

According to the Code for seismic design of urban rail transit structures (GB50909-2014) [46], rock and soil can be divided into five categories, which are rock, hard soil, medium-hard soil, medium-soft soil, and soft soil. Their corresponding shear wave velocity ranges are shown in Table 5.

Table 5. Rock and soil classifications and corresponding shear wave velocity ranges [46].

Type	Shear Wave Velocity vs (m/s)
Rock	vs > 800
Hard soil	800 ≥ vs > 500
Medium-hard soil	500 ≥ vs > 250
Medium-soft soil	250≥ vs > 150
Soft soil	vs ≤ 150

To explore the impact of soil properties on the train-induced vibrations and structure-radiated noise, four soil types—the hard soil, medium-hard soil, medium-soft soil, and soft soil—are chosen for calculations and comparisons. The mechanical properties of each layer of the medium soft soil are the same as in Table 4. Through replacing the values of shear wave velocity and dynamic elastic modulus, the mechanical properties of each layer of the other three soil types are designed based on parameters in Table 4. The mechanical properties of each layer of different soil types are shown in Table 6.

Table 6. Mechanical properties of different soil types.

Soil	Hard Soil		Medium-Hard Soil		Medium-Soft Soil		Soft Soil
	E (MPa)	vs (m/s)	E (MPa)	vs (m/s)	E (MPa)	vs (m/s)	E (MPa)	vs (m/s)
Layer 1	1868	600	830	400	205	199	52	100
Layer 2	1117	520	423	320	120	170	15	60
Layer 3	1645	620	755	420	220	225	62	120
Layer 4	2266	680	1129	480	280	240	110	150

4.1. Train-Induced Vibrations

Based on the established model, the maximum vibration accelerations on the ground and at different floors induced by train operation are compared, as shown in Table 7.

Table 7. Maximum vibration accelerations at different locations.

Soil Type	Ground	1st Floor	3rd Floor
Hard soil (m/s2)	0.088	0.017	0.017
Medium-hard soil (m/s2)	0.104	0.026	0.029
Medium-soft soil (m/s2)	0.109	0.042	0.033
Soft soil (m/s2)	0.097	0.059	0.034

As shown in Table 7, the train-induced maximum accelerations are different for different soil types. For building vibrations, the value of maximum acceleration increases with soil type, ranging from hard to soft soil. Comparing the maximum accelerations on the ground and at the 1st floor within the building, it can be found that the interaction between soil and building foundations leads to a rapid attenuation of the maximum acceleration. In addition, the attenuation speed for the soft soil is the lowest.

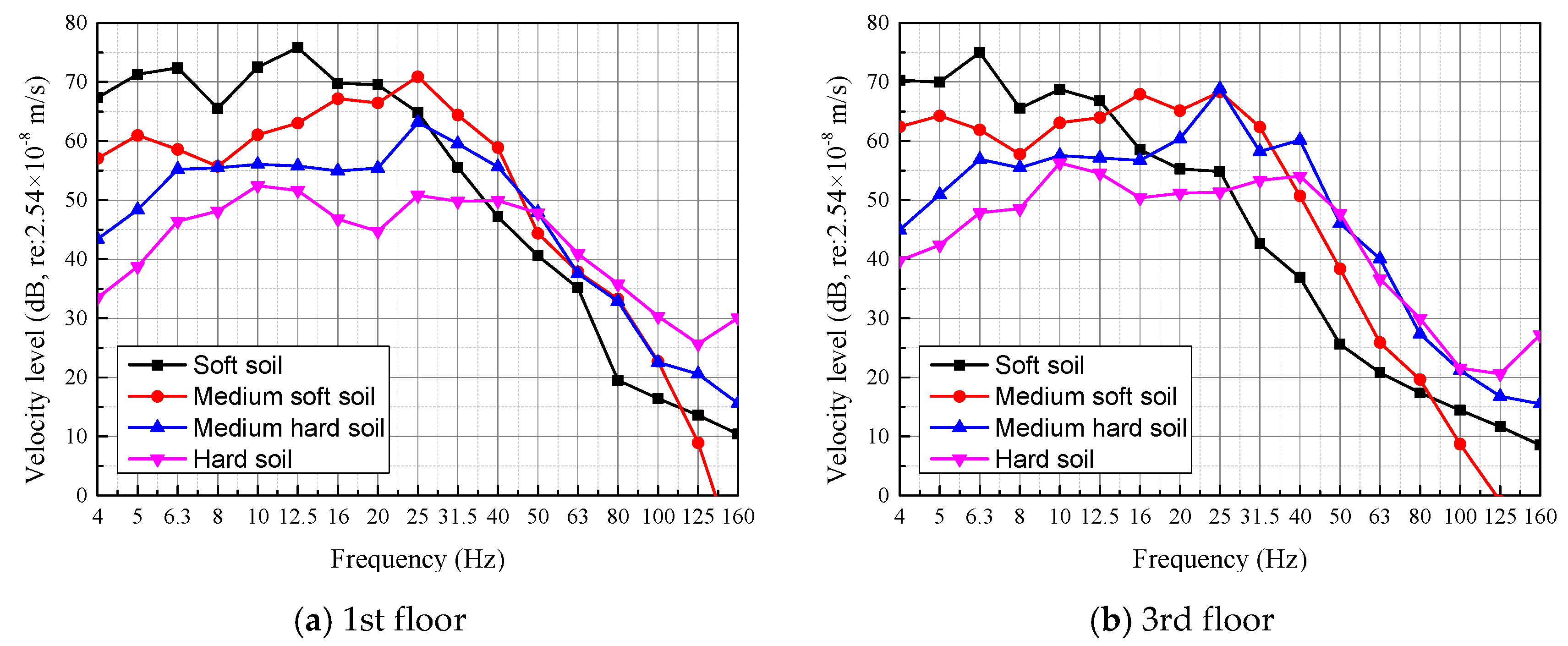
By converting the acceleration to velocity and transforming it into a frequency domain, the 1/3 octave band velocity spectra at the 1st and 3rd floors within the building under different soil type configurations are compared, as shown in Figure 10. This shows that the dominant vibration frequency ranges of the four different soil types are all between 10 and 40 Hz; they gradually move towards lower frequencies with the floor increase. The peak frequency also generally becomes lower as soil type ranges from hard to soft. At frequencies below 20 Hz, building vibration amplitudes of softer soil are larger. However, at frequencies above 40 Hz, building vibration amplitudes of harder soil become larger. The coupling losses of vibration energy vary with building type and soil characteristics, which is the main reason for the different performances of building vibrations on different soil types.

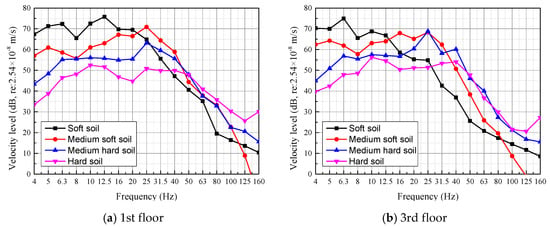
Figure 10. Vibration spectra at the 1st and 3rd floors for different soil types.

Lopes et al. [24] used the finite element model to simulate the dynamic response characteristics of a two-story building and fully considered the interaction between the soil and structure. They found that the vibration peak frequency was related to the interaction between the soil and structure. The lower the soil stiffness and shear wave velocity, the lower the peak vibration frequency. The calculated vibrations agree with the conclusion of Lopes et al. [24].

4.2. Structure-Radiated Noise

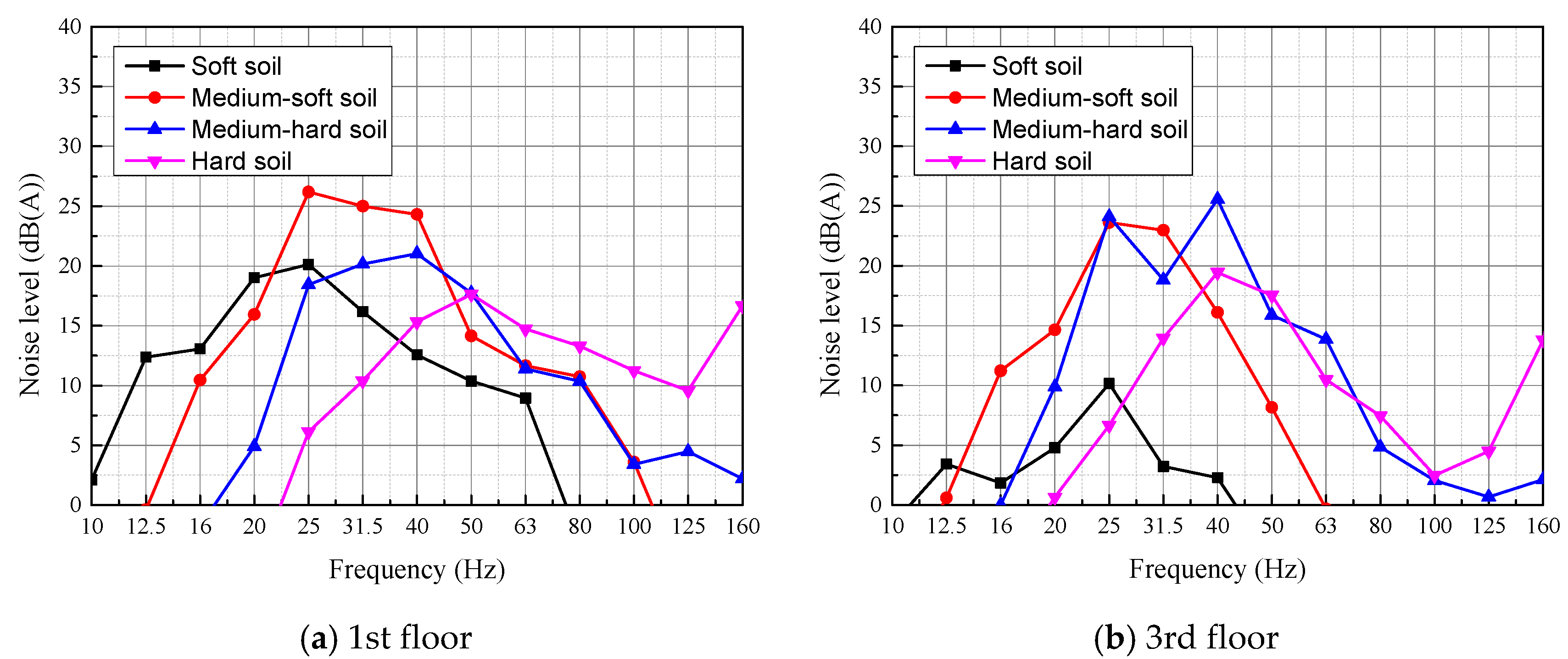
Figure 11 shows the structure-radiated noise within the building calculated based on FTA (2018) [45]. As shown in Figure 11, the structure-radiated noise levels are within the standard limit of 35 dB(A). The dominant noise frequency is between 25 and 40 Hz for all the soil types. Different from the building vibrations, the noise levels are higher when the building is built on medium-soft soil and medium-hard soil. The A-weighting adjustment drops rapidly at low frequencies, reflecting the relative insensitivity of human hearing to low frequencies. That is the reason for why the noise levels of the buildings built on soft soil are so small. Therefore, the train-induced structure-radiated noise within buildings built on the medium-soft soil or medium-hard soil has more impact. The hard soil can effectively reduce vibration impacts and the soft soil can shift peak vibration frequencies to lower ones; thus, both of them result in lower structure-radiated noise levels.

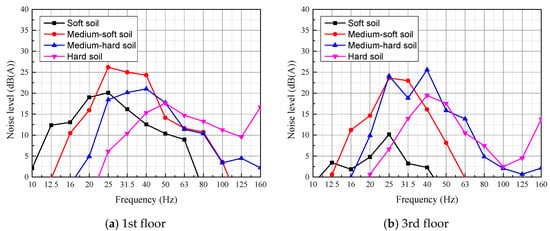
Figure 11. Structure-radiated noise at the 1st and 3rd floors for different soil types.

5. Ground Improvement for Reducing Vibration Transmission and Structure-Radiated Noise

It is shown that the dynamic interaction between soil and building foundations has a great impact on the vibration transmission from the ground to the building and that the maximum acceleration decreases with the soil shear wave velocity increase [47].

Therefore, increasing the stiffness of the soil surrounding the building foundation may help to reduce the vibration transmission into the building and result in lower structure-radiated noise. One practical method is mixing binder (such as cement, lime, slag, fly ash, etc.) into the soil to improve its stiffness. This method is widely used in road engineering. It can reduce the settlement of the embankment and pavement by increasing the subgrade stiffness. By mixing the soil and the binder, the elastic modulus of the mixture can be effectively improved, and thus, the stiffness of the mixture is increased.

This research studied the effect of ground improvement on reducing train-induced vibrations and structure-radiated noise by increasing the soil stiffness surrounding the building foundations within a depth of 2 m. Three cases with reinforced soil mixtures with elastic moduli of 1.0, 5.0, and 10.0 Gpa are presented; other parameters are kept unchanged. The finite element model after ground improvement is shown in Figure 12, where the ground improvement area is depicted in dark blue.

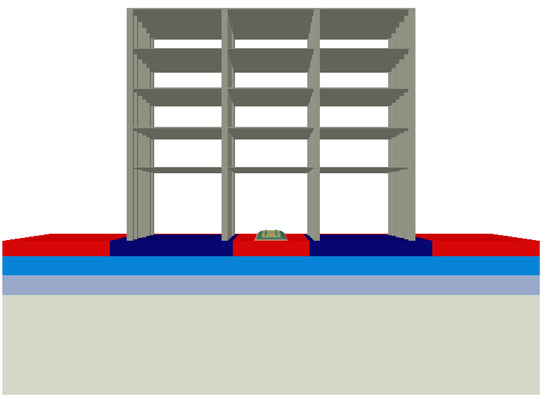
Figure 12. Finite element model with ground improvement.

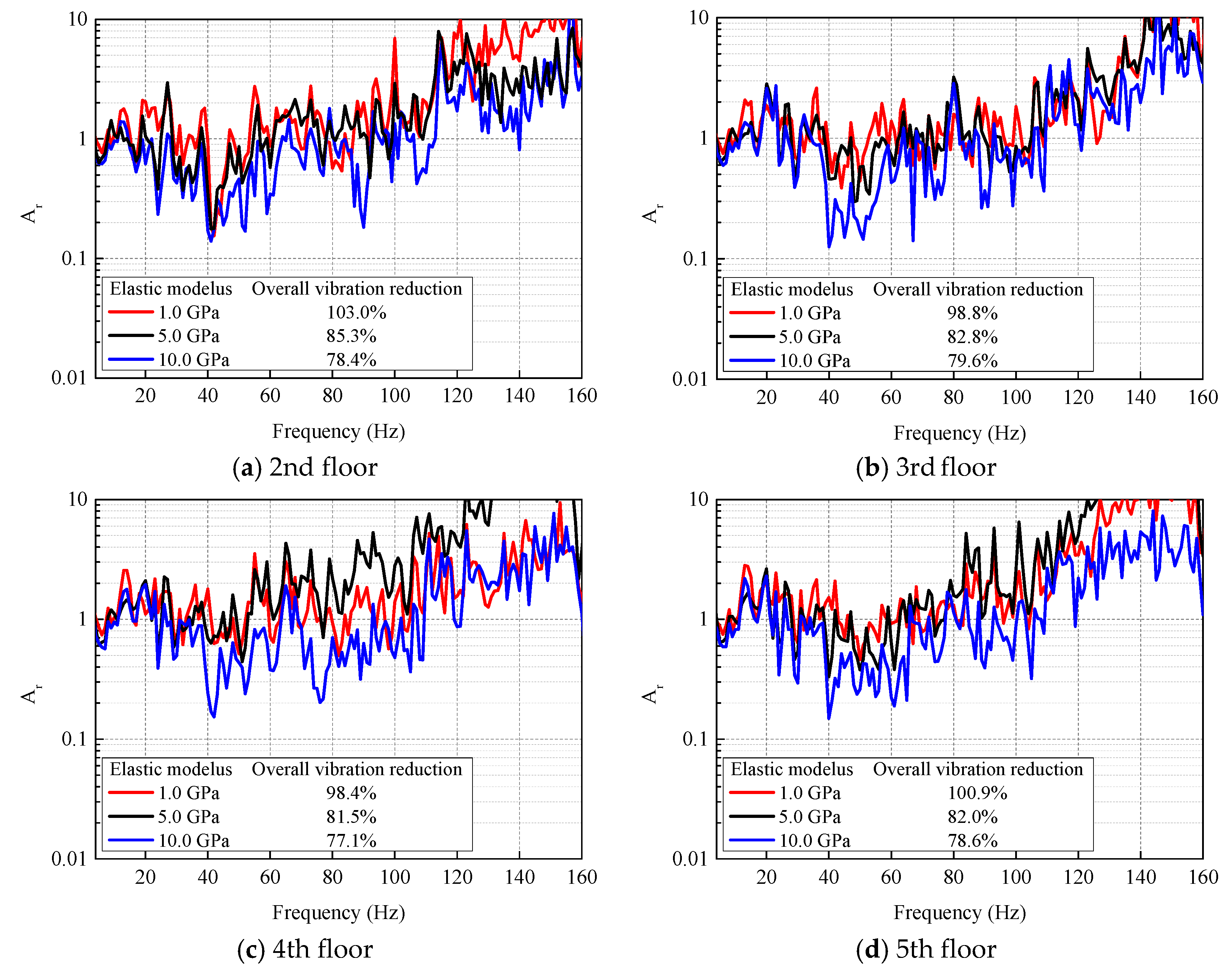
Figure 13 shows the vibration attenuation coefficients (A_r) of the 2nd to 5th building floors after ground improvement. The vibration attenuation coefficient is the velocity level ratio between the after- and before-improvement configurations. When A_r is zero, the vibration energy is completely isolated. When A_r is 1, it implies that the ground improvement has no effect on vibration isolation.

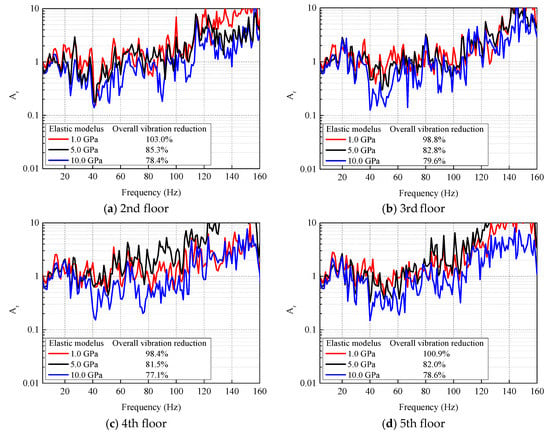
Figure 13. Vibration attenuation within the building with ground improvement.

The overall vibration reduction is described by the ratio of the root-mean-square velocity with ground improvement to that without ground improvement. When the soil elastic modulus is 1 GPa, the vibration isolation effect is barely shown. However, with the increase of elastic modulus, the vibration isolation effect of ground improvement becomes more obvious. The averaged overall vibration reduction of mixing binder into the soil is around 78%, which does not look very effective when compared to other more expensive ground improvement measures. As shown in Figure 13, the increase of the soil elastic modulus has a significant effect on the building vibration attenuation on each floor, especially in the range of 40–80 Hz. The reason is that with the increase of the soil elastic modulus, the soil impedance increased, also making the impedance differences increase between the improved and original soil. When the vibrations transmit from the original soil to the improved, vibration waves will partly reflect at the mutual edge due to the soil impedance mismatches, thus also weakening vibration transmission into the building. However, when the soil elastic modulus is 1 or 5 GPa, the vibrations of each floor are amplified to a certain extent above 60 Hz. This is possibly attributed to resonances. Therefore, in order to obtain a good vibration attenuation effect, it is necessary to ensure that the soil elastic modulus after improvement is greater than 5 GPa. This soil improvement can be conducted along with the construction of the building foundation or the construction of the basement. In addition, this specific conclusion is only valid for the example case used in this research. In future work, researches of other cases need to be done to determine their specific values.

It can be concluded that the ground improvement is helpful for reducing the vibration transmission into the building, and increasing the soil impedance difference has a significant effect on the building’s vibration isolation.

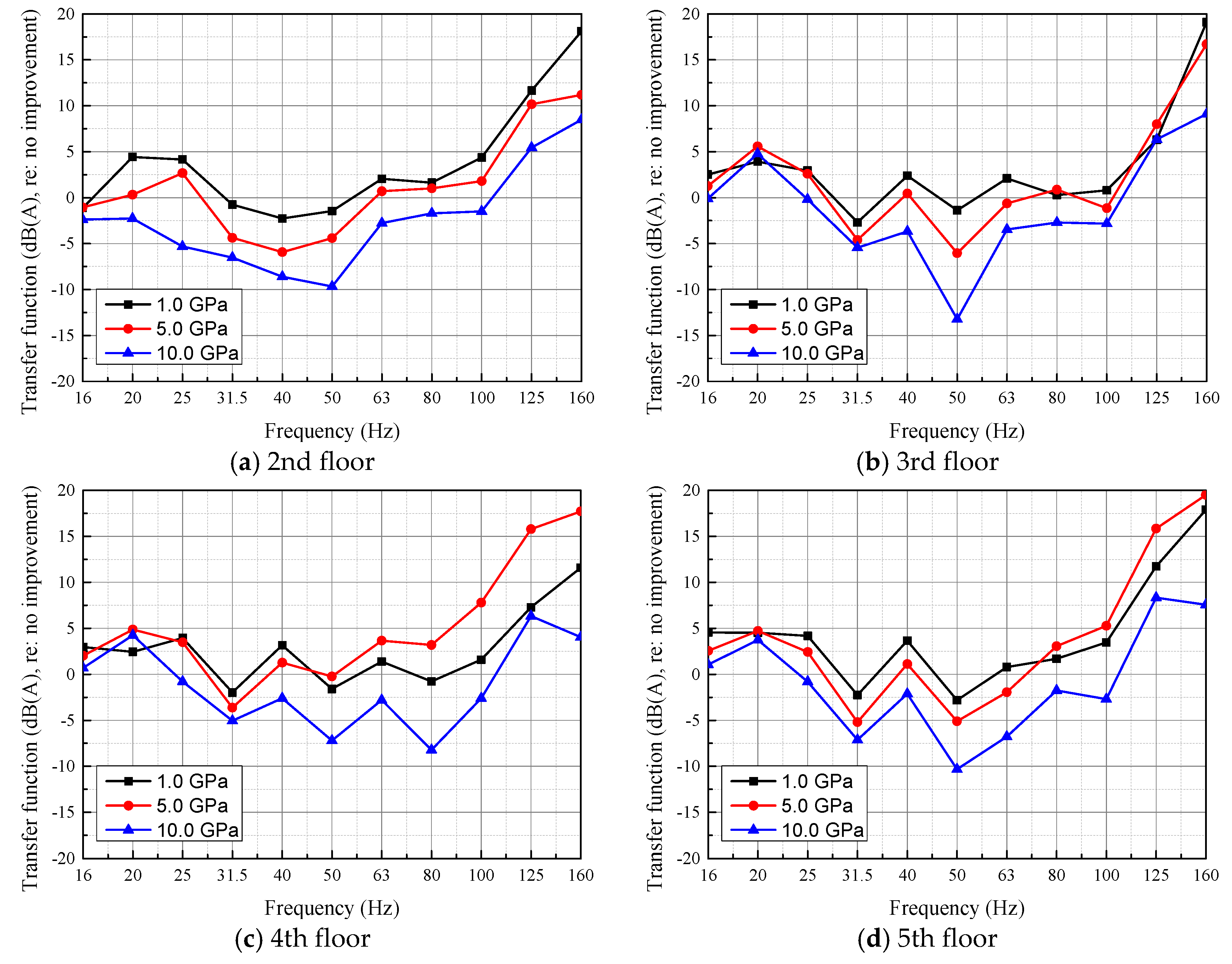
Figure 14 shows the structure-radiated noise transfer function at each floor between after- and before-improvement configurations. On the whole, the increase of the soil elastic modulus is conducive to the reduction of structure-radiated noise within 100 Hz. The reduction effect arrives best at around 50 Hz. However, when the improved soil elastic modulus is 1.0 or 5.0 Gpa, the transfer function is greater than 0 for most frequencies, which means that the ground improvement will lead to the amplification of structure-radiated noise. For the improved soil elastic modulus of 10.0 Gpa, the structure-radiated noise levels between 25 and 100 Hz are reduced. For the frequencies above 100 Hz, ground improvement will lead to structure-radiated noise amplification. Since the sensitive frequency range of the human ear to the structure-radiated noise is 16–250 Hz, the elastic modulus of strengthened soil should be guaranteed to be higher than 5.0 Gpa to achieve an acceptable structure-radiated noise reduction effect.

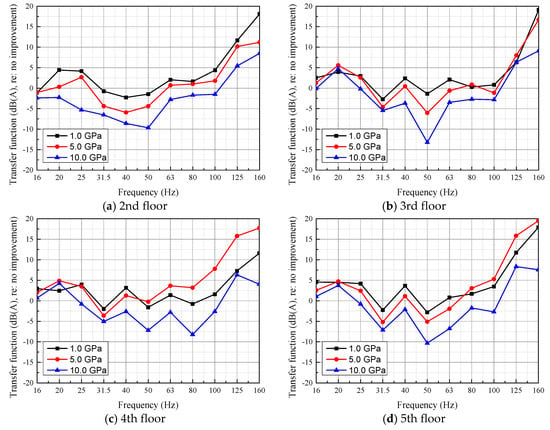
Figure 14. Structure-radiated noise transfer functions between after- and before-improvement configurations.

6. Conclusions

A prediction method for building vibration and structure-radiated noise caused by train operation is proposed in this paper. The method consists of three steps: (1) Building the train-track model; (2) building the track-soil-building model; (3) structure-radiated noise simulation. By comparing the calculated results with the field measurements, it is confirmed that the established method has the ability to predict the train-induced building vibrations and structure-radiated noise.

The impact of different soil properties on train-induced vibration transmission from the ground up into the building and structure-radiated noise generation within the building were analyzed by the established method. The results show that the interaction between soil and structure has a great influence on vibration transmission from the ground into the building. With the increase of shear wave velocity, the maximum acceleration of structural vibration decreases. However, for some soil Rayleigh wavelengths, a higher shear wave velocity may result in vibration amplification due to resonances of the stabilized soil. The amplification may lead to vibration and noise levels that exceed the standard limit and cause people to be uncomfortable from the perspective of public health, especially with such high frequencies. In conclusion, buildings constructed on good foundations help to reduce vibration transmission from ground soil up into the building and lead to lower structure-radiated noise.

The attenuation law of building vibration and structure-radiated noise by ground improvement was also discussed. Ground improvement is helpful for increasing the impedance of the strengthened soil so as to weaken the propagation of vibration into the building and reduce the structure-radiated noise. The greater the elastic modulus of strengthened soil, the more obvious the attenuation effect of building vibration and structure-radiated noise. However, the impact of ground improvement on the seismic resistance and settlement characteristics of buildings is not considered, as it is not within the scope of this paper. The seismic performance of the building after ground improvement should be done during the design stage to maintain safety, and the foundation settlement issues should be considered to avoid cracks. Moreover, the ground improvement can be combined with the construction of the building foundation and the basement.