Core Competitiveness Evaluation of Clean Energy Incubators Based on Matter-Element Extension Combined with TOPSIS and KPCA-NSGA-II-LSSVM

Abstract

Scientific and accurate core competitiveness evaluation of clean energy incubators is of great significance for improving their burgeoning development. Hence, this paper proposes a hybrid model on the basis of matter-element extension integrated with TOPSIS and KPCA-NSGA-II-LSSVM. The core competitiveness evaluation index system of clean energy incubators is established from five aspects, namely strategic positioning ability, seed selection ability, intelligent transplantation ability, growth catalytic ability and service value-added ability. Then matter-element extension and TOPSIS based on entropy weight is applied to index weighting and comprehensive evaluation. For the purpose of feature dimension reduction, kernel principal component analysis (KPCA) is used to extract momentous information among variables as the input. The evaluation results can be obtained by least squares support vector machine (LSSVM) optimized by NSGA-II. The experiment study validates the precision and applicability of this novel approach, which is conducive to comprehensive evaluation of the core competitiveness for clean energy incubators and decision-making for more reasonable operation.

1. Introduction

Clean energy plays an important role in reducing carbon emissions, so more and more countries vigorously develop clean energy [1]. As a promotion agency of clean energy industrialization, clean energy incubator has become a crucial part of innovation system. With the burgeoning development of clean energy incubators in recent years, governments all over the world are introducing policies to actively encourage their establishment [2]. Whereas, these incubators are faced with the problems of valuing quantity and neglecting quality. Some incubators still stay in the stage of property leasing and simple incubation service, but still enjoy the preferential policies of the government and waste public resources [3]. In addition, the planning of many clean energy business incubators is mainly oriented towards the layout of hardware and space, and ignores the planning of soft capabilities such as incubation ability [4]. In order to further play the role of incubators and realize their sustainable development, it is necessary to make the factors clear which affect the core competitiveness and propose a feasible evaluation model. The research on the core competitiveness evaluation of clean energy incubator can help managers find out the deficiencies, and then help managers to improve these deficiencies. Thus this study can provide suggestions for enhancing competitiveness of clean energy incubators.

In 1990, C.K. Prahalad and Gary Hamel, professors of Michigan University and London Business School, respectively, formally raised the concept of “core competitiveness” for the first time. They pointed out that core competitiveness was the ability to coordinate different production skills as well as organically combine various technological schools [5]. Literature [6] discussed how to integrate technological innovation into the core competitiveness of enterprises. The research held that it was of great theoretical and practical significance to put the core competitiveness evaluation into force for sustainable development. Reference [7] considered that environmental adaptability was an important component of the core competitiveness in photovoltaic module supply enterprises. Thereby, it provided suggestion in business decision-making. Thirteen influential factors of core competitiveness were selected in modern circulation industry from market expansion, innovation, circulation efficiency, sustainable development and circulation effect in reference [8]. The evaluation was achieved through study on both independent and synergistic effect of the factors. Hence, it becomes a good entry point to analyze the key resources and capabilities demanded by the sustainable development of enterprises.

At present, scholars have published their significant work on core competitiveness evaluation of incubators, but few focus on the clean energy enterprise. There are some similarities among these research subjects, such as the content and components of kernel competence. Thus the existing study also can provide reference for the research. Reference [9] developed Principal component analysis (PCA) and SPSS based model to evaluate scientific enterprise incubators of nine cities in Pearl River Delta. The results showed the ranking and classification of incubators and put forward development plan accordingly. Literature [10] conducted a questionnaire survey on six chain incubators. The relationship between quantitative performance and importance was revealed through IPA in competitiveness evaluation. Reference [11] outlined the assessment approach of enterprise incubator based on PCA and DEA from the perspective of service and operation efficiency. A comprehensive technique that integrates questionnaire survey with grey correlation assesses the national incubators regarding knowledge service capability in [12]. Reference [13] paid close attention to social benefits in core competitiveness assessment of incubators. The evaluation is executed from five aspects, that is, public service, innovation and development, social education, labor employment and enterprise cultivation.

Evaluation methods can be separated into two categories: traditional assessment technique and modern intelligent algorithm. The former needs complex calculation despite its mature development and accurate results, such as fuzzy comprehensive evaluation method [14] matter-element extension assessment [15] and TOPSIS [16]. Reference [14] developed an approach to reveal the relationship between exposure, sensitivity and adaptive capacity for better flood vulnerability assessment, based on the fuzzy comprehensive evaluation method. Reference [15] utilized the improved fuzzy matter-element extension assessment model to evaluate urban water ecosystem health effectively. Reference [16] used the improved TOPSIS model to evaluate the sustainability of power grid construction projects. Modern intelligent approaches chiefly consist of back propagation neural network [17], extreme learning machine [18], support vector machine [19], least squares support vector machine (LSSVM) [20]. Thereby, this paper intends to combine the traditional evaluation model and intelligent algorithm to assess the core competitiveness of clean energy incubators. Concretely, matter-element extension assessment is first applied to obtain the results. Then, LSSVM is employed for intelligent evaluation. However, owing to blind selection of penalty and kernel coefficients, it’s essential to use an appropriate method for optimization [21]. NSGA-II is a multi-objective model based on the first generation of non dominated sorting genetic algorithm with the advantage of excellent performance and high efficiency [22]. For example, reference [23] used the NSGA-II algorithm to obtain the multi-objective optimisation of an interactive buildings-vehicles energy sharing network with high energy flexibility, which achieved good optimization results. To this end, this paper exploits NSGA-II to automatically decide the appropriate values in LSSVM.

It is worth noting that there exist many influencing factors on the core competitiveness of clean energy incubators. Dimension reduction is critical for accuracy on account of strong coupling, nonlinearity and redundancy in the indicators [24]. PCA, as a multivariate statistical approach, has the advantage over dealing with indexes with strong linear relationship [25]. Nevertheless, the relationship among the core competitiveness indicators of clean energy incubators is mostly nonlinear. PCA is not able to acquire high-order features which ignores the nonlinear information while reducing the dimension [26]. As a result, kernel principal component analysis (KPCA) is used in this paper to map the initial input variables to high-dimensional feature space through nonlinear transformation so that the input dimension can be reduced on the premise of retaining nonlinear information among variables [27].

Therefore, this paper establishes the core competitiveness index system of clean energy incubator and proposes a hybrid model integrated matter-element extension assessment and KPCA-NSGA-II-LSSVM for evaluation. The rest of paper is organized as follows: Section 2 designs the indicator system including strategic positioning ability, seed selection ability, intelligent transplantation ability, growth catalytic ability as well as service value-added ability, and introduces the preprocessing method. Section 3 presents a brief description of the proposed evaluation technique. In Section 4, a case study is carried out to validate the established model. Section 5 concludes the paper.

2. Establishment of Evaluation Index System for Core Competitiveness of Clean Energy Incubator

2.1. Selection of Evaluation Index

The kernel function of clean energy incubator is to cultivate corresponding enterprises. Whether incubator owns core competitiveness resolves its survival rate and growth. The main workflow includes seed business selection, related incubation service and tracking. Thus, specific conditions can be employed for judgement whether incubated enterprises are able to graduate or be obsoleted. These links are closely relevant and interact with each other. The core competitiveness is dependent on the crucial resource and capabilities required by these parts.

It is obvious that the seed quality is significant. Clean energy incubators must make a choice subjected to the resource. Furthermore, incubated service is an interactive process limited both by the ability of incubator and enterprise itself. Enterprises with no development potential can hardly survive or grow slowly even if they devote quantities of resources. Consequently, the quality of incubated seed is quite important which is principally determined by strategic positioning ability and seed selection ability [4].

The service provided by clean energy incubator aims at making the enterprises realize burgeoning development. Entrepreneurs are mostly confronted with lack resource and systematic knowledge, weak management capability as well as experience. Service with core competitiveness can be measured by the following conditions: An entrepreneurial team can become an independent and growing enterprise after incubation. It means incubator should possess the ability to transfer or graft the pivotal resource needed by entrepreneurs. In particular, it mainly refers to intelligent transplantation ability, growth catalytic ability, and service value-added ability.

In brief, the core competitiveness of clean energy incubator is chiefly decided by: strategic positioning ability, seed selection ability, intelligent transplantation ability, growth catalytic ability, service value-added ability. Figure 1 shows the established index system.

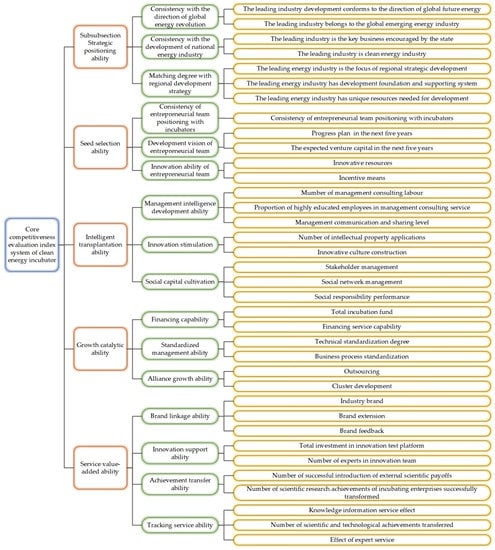
Figure 1. Core competitiveness evaluation index system of clean energy incubator.

2.1.1. Subsubsection Strategic Positioning Ability

Strategic positioning ability refers to the location capability of clean energy incubators in industries, regions and entrepreneurial groups. Incubators should first make strategic positioning for the target enterprises or customers. The more technology opportunities and better development prospects the incubators face, the more they match the regional progress. Additionally, strategic positioning ability displays the positive change with the potential the entrepreneurial group.

(1)

Consistency with the direction of global energy revolution: judge whether the leading business development conforms to the direction of global future energy and whether it belongs to the global emerging energy industry via the literature on key progress of clean energy assembled from the United States, the United Kingdom, the European Union, Japan and other developed countries.

(2)

Consistency with the development of national energy industry: considering national economic planning and policy, identify the key development of clean energy industry in China. Determine whether the leading industry of the incubator is the key business encouraged by the state.

(3)

Matching degree with regional development strategy: provincial and regional energy planning as well as relevant materials can be used as the foundation to distinguish strategic development. Thus, matching degree is able to be estimated from the perspective of supporting system and unique resources through enterprise research and expert interview.

2.1.2. Seed Selection Ability

Seed selection ability represents the capability of incubator to identify the prospects of clean energy enterprises. If the seed is identical with incubator positioning, development as well as innovation ability, it declares the seed selection capability is strong.

(1)

Consistency of entrepreneurial team positioning with incubators.

(2)

Development vision of entrepreneurial team: progress plan and the expected venture capital in the next five years.

(3)

Innovation ability of entrepreneurial team: innovative resources and incentive means.

2.1.3. Intelligent Transplantation Ability

Intelligent transplantation ability stands for the capability to improve intellectual capital of incubated enterprises including management intelligence development, innovation stimulation and social capital cultivation.

(1)

Management intelligence development ability: number of management consulting labour, proportion of highly educated employees in management consulting service, management communication and sharing level.

(2)

Innovation stimulation: number of intellectual property applications, innovative culture construction.

(3)

Social capital cultivation: stakeholder management, social network management, social responsibility performance.

2.1.4. Growth Catalytic Ability

Growth catalytic ability can judge whether the incubated enterprises grow rapidly and expand well which includes financing capability, standardized management ability as well as alliance development ability.

(1)

Financing capability: total incubation fund, financing service capability.

(2)

Standardized management ability: technical standardization degree, business process standardization.

(3)

Alliance growth ability: outsourcing, cluster development.

2.1.5. Service Value-Added Ability

Service value-added ability reflects the increase of value that incubator brings itself and enterprises, including brand linkage ability, innovation support ability, achievement transfer ability and tracking service ability.

(1)

Brand linkage ability: industry brand, brand extension, brand feedback.

(2)

Innovation support ability: total investment in innovation test platform, number of experts in innovation team.

(3)

Achievement transfer ability: number of successful introduction of external scientific payoffs, number of scientific research achievements of incubating enterprises successfully transformed.

(4)

Tracking service ability: knowledge information service effect, number of scientific and technological achievements transferred, effect of expert service.

2.2. Preprocessing of Evaluation Index

There mainly exist three kinds in the indicator system, namely extremely large, extremely small and interval indexes. For example, extremely large indicators change in accordance with core competitiveness. In order to make comparison with schemes and obtain the valuation results, normalization processing should be implemented. In this paper, all the indicators are assigned into extremely large indexes.

Due to distinguished attribute and quantity level of original data, it is essential to make the indicators dimensionless as Equation (1):

$$x_{ij}^{*}=\frac{x_{ij}}{\sqrt{{\sum }_{i=1}^m{x}_{ij}{}^2}},i=1,2,\cdots ,m;j=1,2,\cdots ,n$$

(1)

where $m$ and n represent the number of incubators and indexes, respectively.

3. Methodology

3.1. Entropy Weight Method

As a common approach in objective weight calculation, the principle of entropy weight method derives from thermodynamics. Entropy is a measure of the system uncertainty. The greater entropy means more chaotic system and less information [28]. Suppose the system locates in $n$ states, the probability of each state is set as $P_i(i=1\to n)$. The entropy of the system is described as Equation (2)

$$E=-{\displaystyle \sum _{i=1}^n{P}_i\ln p_i}$$

(2)

where $P_i(i=1\to n)$ satisfies: $0\le P_i\le 1$, ${\displaystyle \sum _{i=1}^n{P}_i}=1$.

The following procedures are listed:

(1) Establishment of standardized judgment matrix

In accordance with standardized data obtained from Equation (1), the standardized judgment matrix is acquired.

(2) Calculate the information entropy of each index

$$H_j=-k{\displaystyle \sum _{i=1}^m}{f}_{ij}\ln f_{ij}$$

(3)

$$f_{ij}=\frac{x_{ij}^{*}}{{\sum }_{i=1}^m{x}_{ij}^{*}}$$

(4)

$$k=\frac{1}{\ln m}$$

(5)

(3) Index weighting

$$w_j=\frac{1-H_j}{{\sum }_{j=1}^n\left(1-H_j\right)}$$

(6)

where $0\le w_j\le 1,{\sum }_{j=1}^n{w}_j=1$.

3.2. Evaluation Model Integrated Matter-Element Extension with TOPSIS

TOPSIS, also known as approximate ideal solution, firstly draws up two schemes. One of the scheme presents the best attribute values, called positive ideal solution, while the attributes of the other plan are all the worst, named negative ideal solution. Then, compare each scheme with the positive as well as negative ideal solutions, respectively. The optimal programme is selected which is close to the positive ideal solution and far away from the negative one simultaneously [29]. Hence, this best scheme shows the highest core competitiveness. Whereas, TOPSIS can not judge the competitiveness level of each plan, that is, it can’t be decided whether the level belongs to very high, high, general or low [30].

Matter-element extension evaluation method combined matter-element theory, extension set with correlation degree for quantitative evaluation. This model divides the data interval of the evaluated target into several orders and determine their levels. Correlation degree is calculated between each plan and the grade. The larger the correlation degree is, the higher the membership extent present. The level of the evaluated target depends on the grade of data interval with the highest membership degree [31].

Thus, this paper integrates matter-element extension model with TOPSIS for core competitiveness assessment. TOPSIS is firstly used to determine the positive and negative ideal solutions and divide the interval into several grades by equal distance. Each grade corresponds to the given level of core competitiveness. Then calculate the correlation degree between each scheme and the grades. Hence, the core competitiveness level of the plan can be accordingly judged.

The main measures can be described as follows:

(1) Establishment of standardized index matrix

Suppose the scheme set including $n$ evaluation indicators is $M=\left(M_1,M_2,\cdot \cdot \cdot ,M_m\right)$. The assessment indexes are presented as $D=\left(D_1,D_2,\cdot \cdot \cdot ,D_n\right)$. The standardized index matrix $C$ is derived from consistent and dimensionless processing as Equation (7)

$$C={\left(c_{ij}\right)}_{m\times n}=\left[\begin{array}{cccc}{c}_{11}& c_{12}& \cdots & c_{1n}\\ c_{21}& c_{22}& \cdots & c_{2n}\\ \cdots & \cdots & \cdots & \cdots \\ c_{m1}& c_{m2}& \cdots & c_{mn}\end{array}\right]$$

(7)

where $c_{ij}=\left(i=1,2,\cdot \cdot \cdot ,m;j=1,2,\cdot \cdot \cdot ,n\right)$ is the standardized indicator of $D_i$ in scheme $M_i$.

(2) Establishment of weighted standardized matrix

The entropy weight method is applied to calculate the weight of indexes $w_j$. The weighted standardized matrix is shown as Equation (8)

$$X={\left(x_{ij}\right)}_{m\times n}=\left[\begin{array}{cccc}{w}_1{c}_{11}& w_2{c}_{12}& \cdots & w_n{c}_{1n}\\ w_1{c}_{21}& w_2{c}_{22}& \cdots & w_n{c}_{2n}\\ \cdots & \cdots & \cdots & \cdots \\ w_1{c}_{m1}& w_2{c}_{m2}& \cdots & w_n{c}_{mn}\end{array}\right]$$

(8)

(3) Determine positive and negative ideal solutions of each scheme

The positive ideal solution is:

$$X^{+}=\left\{\underset{1\le i\le m}{\max }{x}_i(j)|j\in J^{+},\underset{1\le i\le m}{\min }{x}_i(j)|j\in J^{-}\right\}$$

(9)

The negative ideal solution is:

$$X^{-}=\left\{\underset{1\le i\le m}{\min }{x}_i(j)|j\in J^{+},\underset{1\le i\le m}{\max }{x}_i(j)|j\in J^{-}\right\}$$

(10)

(4) Division of extremum interval and calculation of closeness degree

The extremum interval composed of negative positive ideal solutions is divided into $N$ layers. namely, $H_{it}=(h_{it}^1,h_{it}^2),i=1,2,\cdots ,n;t=1,2,\cdots ,N$, $x_i^{-}\le h_{it}^1\le x_i^{+},x_i^{-}\le h_{it}^2\le x_i^{+}$, $[x_i^{-},x_i^{+}]$ consists of $h_{it}^1$ and $h_{it}^2$.

The closeness degree between each index and evaluation interval in standardized decision matrix can be obtained according to Equation (11):

$$E(N_i)=\left|x_{ij}-\frac{h_{jt}^1+h_{jt}^2}{2}\right|$$

(11)

Thus, the weighted closeness degree of each evaluation plan can be further derived:

$$Q_j(N_i)=1-{\displaystyle \sum _{j=1}^n{w}_{j}E(N_i)}$$

(12)

(5) Determine the grade of each scheme

The level that the maximum of $Q_j(N_i)$ belongs to can be regarded as the evaluation grade of the scheme.

3.3. KPCA

PCA is able to merge the original features and reduce the dimension to simplify computation, especially aiming at strong linear indicators. However PCA is difficult to grab high-order features, so it ignores nonlinear information during dimension reduction. With consideration of nonlinearity in core competitiveness of clean energy incubators, kernel principal component analysis (KPCA) is taken advantage of to extract key factors in this study [32].

This approach can validly reduce the dimension of the input in condition of retaining main nonlinear information. It is achieved by using nonlinear transformation to map initial input into high-dimensional feature space. Apparently, KPCA is able to compress the information contained in a large number of indexes into some comprehensive indicators. The basic steps are presented as follows:

Set a random vector $X={\left\{x_1,x_2,\dots ,x_{\mathrm{n}}\right\}}^T$, $x_k\in R^N(k=1,2,\dots ,m)$, m is the number of input, namely the original input can be expressed as $M={[a_1,a_2,\dots \dots ,a_{\mathrm{n}}]}^T=[b_1,b_2,\dots \dots ,b_m]$. The dataset is projected into the space F via nonlinear mapping Φ, $M=[\varphi (b_1),\varphi (b_2),\dots \dots ,\varphi (b_m)]$, ${\displaystyle \sum _{k=1}^m\tilde{\varphi }(b_i)=0}$.

The covariance matrix is shown as follows:

$$C^F=\left[\begin{array}{l}{C}_{11},C_{12},\dots ,C_{1\mathrm{n}}\\ \dots \dots \\ C_{n1},C_{n2},\dots ,C_{nn}\end{array}\right]$$

(13)

$$C=\frac{1}{m}{\displaystyle \sum _i^m\varphi (b_i)}\varphi {(b_i)}^T$$

(14)

The eigenvalue and eigenvector can be obtained as Equation (15)

$${\mathit{C}}^F{\mathit{W}}^F={\lambda }^F{\mathit{W}}^F$$

(15)

where ${\lambda }^F$ is the eigenvalue, ${\mathit{W}}^F={\displaystyle \sum _{k=1}^M{\alpha }_k\tilde{\varphi }(x_k)}$ represents the corresponding eigenvector. The symmetric matrix K is shown in Equation (16):

$$\mathbf{K}(x_k,x_j)=(\varphi (x_k)\cdot \varphi (x_j))$$

(16)

$\tilde{\mathbf{K}}$ can be acquired via matrix centralization:

$$\tilde{\mathbf{K}}=\mathbf{K}-{\mathbf{I}}_n\mathbf{K}-\mathbf{K}{\mathbf{I}}_n+{\mathbf{I}}_n\mathbf{K}{\mathbf{I}}_n$$

(17)

where I_n is n × n matrix, I_i,j = 1/n, Equation (15) can be simplified as:

$$m{\lambda }^{F}M=\tilde{\mathbf{K}}M$$

(18)

Thus the kernel principal component can be calculated with reference to extraction technique of traditional PCA.

3.4. NGSA-II

NSGA-II optimization algorithm is a novel genetic algorithm on the foundation of NSGA. Despite Pareto optimum can be derived from individual classification in accordance with non dominated sorting via NSGA, it needs complicated calculation and given shared radius value. Therefore, fast non-dominated sorting technique, crowding degree and elite strategy are introduced into NSGA, namely NSGA-II, to promote the robustness and operation speed [33].

The specific procedures of NSGA-II are described as follows:

(1)

Generate initial population P_t and achieve non-dominated sorting as well as given Pareto optimum. The genetic operation P_t is carried out to form the offspring Q_t.

(2)

Aamalgamate P_t with Q_t to generate the new species R_t. Implement non-dominated ranking on R_t and calculate the crowding degree d_i of r_i.

(3)

A new generation P_t+1 comes into being in line with non-dominated ranking and crowding degree d_i.

(4)

If t does not reach the maximum number of iteration t_max, $t=t+1$. Otherwise, the calculation will be terminated and the output will be obtained.

The crowding degree (d_i.) refers to the density of other individuals around each personality in the population. The individual crowding degree at the boundary is defined as infinite, the crowding degree at other positions can be calculated as follows:

$$d_i={\displaystyle \sum _{j=1}^m\frac{\left|f_{j,i+1}-f_{j,i-1}\right|}{f_{j\max }-f_{j\min }}}$$

(19)

where d_i. represents the crowding degree of i, $m$ equals the number of objective functions, f_jmax, f_jmin are the maximum and minimum of j-th objective function.

3.5. LSSVM

LSSVM is an extension of SVM. This method makes use of equality constraints to replace the inequality constraints and employs kernel functions to transform prediction into equation problems, which contributes to the improvement of evaluation accuracy and speed [34].

In LSSVM, the sample is set as $T={\left\{\left(x_i,y_i\right)\right\}}_{i=1}^N$, $N$ is the number of samples. The regression model can be established as Equation (20)

$$y\left(x\right)={\mathit{w}}^T·\phi \left(x\right)+b$$

(20)

where $\phi (\ast )$ maps the training samples into a highly dimensional space. $\mathit{w}$ and $b$ are the weight vector and bias, partly.

The converted optimization problem is shown as follows:

$$\min \frac{1}{2}{\mathit{w}}^T\mathit{w}+\frac{1}{2}\gamma {\displaystyle \sum _{i=1}^N{\mathit{\xi }}_i^2}$$

(21)

$$y_i={\mathit{w}}^T\varphi (x_i)+b+{\xi }_i,i=1,2,3,\dots N$$

(22)

where $\gamma$ equal the regularization parameter applicable to balance the complexity and accuracy in LSSVM. ξ_i is the error.

The Lagrange function is defined to address the problem:

$$L\left(\mathit{w},b,{\xi }_i,{\alpha }_i\right)=\frac{1}{2}{\mathit{w}}^T\mathit{w}+\frac{1}{2}\gamma {\displaystyle \sum _{i=1}^N{\mathit{\xi }}_i^2}-{\displaystyle \sum _{i=1}^N{\alpha }_i}\left[{\mathit{w}}^T\phi (x_i)+b+{\mathit{\xi }}_i-y_i\right]$$

(23)

where ${\mathit{\alpha }}_i$ is Lagrange multipliers. In the light of the Karush-Kuhn-Tucker (KKT) conditions, Equation (24) is derived:

$$\{\begin{array}{l}\frac{\partial L}{\partial \mathit{w}}=0\to \mathit{w}={\displaystyle \sum _{i=1}^N{\alpha }_i\phi (x_i)}\\ \frac{\partial L}{\partial b}=0\to {\displaystyle \sum _{i=1}^N{\alpha }_i=0}\\ \frac{\partial L}{\partial \mathit{\xi }}=0\to {\alpha }_i=\gamma {\mathit{\xi }}_i\\ \frac{\partial L}{\partial \alpha }=0\to {\mathit{w}}^T+b+{\mathit{\xi }}_i-y_i=0\end{array}$$

(24)

The optimization problem is converted into the following matter through eliminating the variables of $\mathit{w}$ and ξ_i:

$$\left[\begin{array}{cc}0& {\mathit{e}}_n^T\\ {\mathit{e}}_n& \mathit{\Omega }+{\gamma }^{-1}\cdot I\end{array}\right]\cdot \left[\begin{array}{c}b\\ a\end{array}\right]=\left[\begin{array}{c}0\\ y\end{array}\right]$$

(25)

where

$$\mathit{\Omega }={\phi }^T\left(x_i\right)\phi \left(x_i\right)$$

(26)

$${\mathit{e}}_n={\left[1,1,\dots ,1\right]}^T$$

(27)

$$\alpha =\left[{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right]$$

(28)

$$y={\left[y_1,y_2,\dots ,y_n\right]}^T$$

(29)

The final form of LSSVM is displayed in Equation (30):

$$y\left(x\right)={\displaystyle \sum _{i=1}^N{\alpha }_{i}K\left({\mathit{x}}_{\mathit{i}},\mathit{x}\right)}+b$$

(30)

where K(x_i, x) equals the kernel function that satisfies Mercer’s condition. The paper selects radial basis function (RBF) as the kernel function of LSSVM on account of its wide convergence range and application, as described in Equation (31):

$$K\left({\mathit{x}}_{\mathit{i}},\mathit{x}\right)=\exp \left\{-{\Vert x-x_i\Vert }^2/2{\sigma }^2\right\}$$

(31)

where ${\sigma }^2$ is the width of the kernel width.

Evidently, the performance of LSSVM is chiefly decided by two parameters: kernel parameter $\gamma$ and regularization parameter σ².

3.6. Approaches of Matter-Element Extension Combined with TOPSIS and KPCA-NSGA-II-LSSVM

Based on the approach that combines matter-element extension, the core competitiveness evaluation model incorporating KPCA, NSGA-II, and LSSVM is constructed for clean energy incubators where KPCA is utilized for the determination of input and NSGA-II is exploited for parameter optimization in LSSVM. The flowchart of the novel evaluation technique is illustrated in Figure 2.

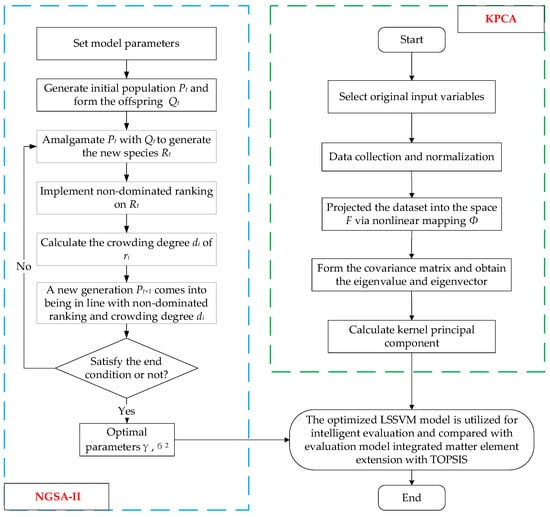
Figure 2. The flowchart of the proposed model.

Step 1: Parameters initialization and data preprocessing. Suppose the input $X=\left\{x_i,i=1,2,\cdots ,n\right\}$ consists of the aforementioned core competitiveness evaluation indexes of clean energy incubators, as Table 1 shows. Consistency and standardized processing are implemented on the original input x_i.

Table 1. The input of evaluation model.

Input	Index	Input	Index
x1	Leading industry is in line with the global future energy development direction	x19	Social network management
x2	Leading industry belongs to the global emerging energy industry	x20	Social responsibility performance
x3	Leading industry is attributed to key industries encouraged by the state	x21	Total incubation fund
x4	Leading industry is ascribed to clean energy industry	x22	Financing service capability
x5	Leading energy industry is the focus of regional strategic progress	x23	Technical standardization degree
x6	Leading energy industry possesses growth foundation and supporting system	x24	Business process standardization
x7	Leading energy industry owns unique resources	x25	Outsourcing
x8	Positioning consistency between entrepreneurial team and incubator	x26	Cluster development
x9	Future five-year plan	x27	Industry brand
x10	Future five-year expected venture capital investment	x28	Brand extension
x11	Innovation resources	x29	Brand feedback
x12	Innovative incentives	x30	Total investment in innovation test platform
x13	Number of management consulting labour	x31	Number of experts in innovation team
x14	Proportion of highly educated employees in management consulting service	x32	Number of successful introduction of external scientific payoffs
x15	Management communication and sharing level	x33	Number of scientific research achievements of incubating enterprises successfully transformed
x16	Number of intellectual property applications	x34	Knowledge information service effect
x17	Innovative culture construction	x35	Number of scientific and technological achievements transferred
x18	Stakeholder management	x36	Effect of expert service

Step 2: Weight Determination. The entropy weight method is used here. Besides, evaluation results can be obtained based on matter-element extension integrated with TOPSIS.

Step 3: Input selection. Crucial factors in original input $X$ are extracted via KPCA. Gaussian kernel function is selected for nonlinear mapping as shown in Equation (32). The kernel principal components whose cumulative variance contribution is higher than 95% form the new input matrix.

$$k(x,y)=\exp \left\{-\frac{{\Vert x-y\Vert }^2}{2{\sigma }^2}\right\}$$

(32)

Step 4: Parameter optimization. Initialize the parameters in LSSVM and NSGA-II. Due to the influence of parameters on training and learning ability in LSSVM, this paper applies NSGA-II to optimize the two parameters, that is, $\gamma$ and ${\sigma }^2$. Circulation ends at the maximum number of iteration $t_{\max }$, thus the optimal parameters can be substituted into LSSVM. Through continuous retraining and testing, the two parameters are adjusted again and the optimal core competitiveness evaluation model for clean energy incubator is established.

Step 5: Output the evaluation results. According to the characteristics of the core competitiveness level of clean energy incubators, the category labels are set as 1, 2, 3 and 4, that corresponds to the grades of core competitiveness, namely very high, high, general and low, respectively.

4. Experiment Study

4.1. Input Selection and Preprocessing

In order to verify the performance of the established approach, this paper conducts a study on core competitiveness evaluation base on 20 clean energy incubators. The type and representative quantitative index data of 20 incubators are shown in Table 2.

Table 2. The type and representative quantitative index data of 20 incubators.

Clean Energy Incubator	Type	Future Five-Year Expected Venture Capital Investment (Million Chinese Yuan)	Proportion of Highly Educated Employees in Management Consulting Service (%)	Total Incubation Fund (Million Chinese Yuan)
A	Solar, hydro, biomass	59	91	111
B	Solar	79	61	98
C	Wind, solar, biomass	73	49	68
D	Wind, solar, hydro, biomass	88	95	92
E	Solar	87	64	83
F	Biomass	71	69	105
G	Hydro	46	47	70
H	Wind, Solar, biomass	58	84	86
I	Solar, biomass	81	89	77
J	Wind, solar, hydro	49	72	87
K	Wind, biomass	71	63	74
L	Wind, solar, hydro, biomass	80	72	103
M	Wind, solar, biomass	120	42	98
N	Wind, solar, hydro, biomass	56	73	84
O	Wind, solar	59	79	96
P	Wind, solar	84	54	101
Q	Wind, biomass	79	80	69
R	Wind, solar, hydro, biomass	58	96	94
S	Wind, hydro	165	79	94
T	Wind, solar, hydro, biomass	69	57	156

According to the evaluation index system for the core competitiveness of clean energy incubator, Table 3 shows the indicator properties and attributes. Through field investigation and data collection, the relevant data are assembled and sorted out. Simultaneously, 15 experts are invited to score the qualitative indexes in [0, 100]. The corresponding mean value can be considered as the stationary criteria.

Table 3. Evaluation index properties for core competitiveness of clean energy incubator.

Index	Index Properties
Leading industry is in line with the global future energy development direction	qualitative indicator
Leading industry belongs to the global emerging energy industry	qualitative indicator
Leading industry is attributed to key industries encouraged by the state	qualitative indicator
Leading industry is ascribed to clean energy industry	qualitative indicator
Leading energy industry is the focus of regional strategic progress	qualitative indicator
Leading energy industry possesses growth foundation and supporting system	qualitative indicator
Leading energy industry owns unique resources	qualitative indicator
Positioning consistency between entrepreneurial team and incubator	qualitative indicator
Future five-year plan	qualitative indicator
Future five-year expected venture capital investment	quantitative indicator
Innovation resources	qualitative indicator
Innovative incentives	qualitative indicator
Number of management consulting labour	quantitative indicator
Proportion of highly educated employees in management consulting service	quantitative indicator
Management communication and sharing level	qualitative indicator
Number of intellectual property applications	quantitative indicator
Innovative culture construction	qualitative indicator
Stakeholder management	qualitative indicator
Social network management	qualitative indicator
Social responsibility performance	qualitative indicator
Total incubation fund	quantitative indicator
Financing service capability	qualitative indicator
Technical standardization degree	qualitative indicator
Business process standardization	qualitative indicator
Outsourcing	qualitative indicator
Cluster development	qualitative indicator
Industry brand	qualitative indicator
Brand extension	qualitative indicator
Brand feedback	qualitative indicator
Total investment in innovation test platform	quantitative indicator
Number of experts in innovation team	quantitative indicator
Number of successful introduction of external scientific payoffs	quantitative indicator
Number of scientific research achievements of incubating enterprises successfully transformed	quantitative indicator
Knowledge information service effect	qualitative indicator
Number of scientific and technological achievements transferred	quantitative indicator
Effect of expert service	qualitative indicator

In the light of above-mentioned data preprocessing method, the standardized results of the 20 samples are derived as listed in Table 4 and Table 5.

Table 4. Data processing results of core competitiveness evaluation indexes for clean energy incubator (A–J).

Index	Clean Energy Incubator
	A	B	C	D	E	F	G	H	I	J
x1	0.1759	0.1699	0.2176	0.2653	0.1580	0.1699	0.1550	0.2176	0.1669	0.2116
x2	0.2106	0.2106	0.2244	0.2494	0.2411	0.2217	0.1690	0.2549	0.2522	0.1607
x3	0.1946	0.1828	0.2270	0.2830	0.2329	0.2299	0.2329	0.2299	0.1533	0.2005
x4	0.1611	0.1845	0.2577	0.2109	0.2314	0.1669	0.1992	0.2577	0.1845	0.1962
x5	0.2542	0.1636	0.1928	0.2571	0.1461	0.1870	0.2308	0.2717	0.2747	0.1636
x6	0.2367	0.2033	0.2200	0.2144	0.1392	0.1922	0.1810	0.1782	0.2367	0.2646
x7	0.1713	0.2156	0.1624	0.1565	0.1477	0.2805	0.2126	0.1595	0.2599	0.1624
x8	0.1923	0.2358	0.2203	0.2637	0.1830	0.1954	0.2575	0.2854	0.2078	0.2296
x9	0.2744	0.1547	0.2481	0.2568	0.1693	0.2043	0.1868	0.2481	0.1780	0.1985
x10	0.1580	0.2534	0.2117	0.2653	0.2743	0.2295	0.1520	0.1818	0.2236	0.1580
x11	0.1849	0.2333	0.1992	0.2561	0.1451	0.2162	0.2134	0.2703	0.2532	0.2504
x12	0.2156	0.1983	0.2529	0.2616	0.1696	0.2414	0.2299	0.1955	0.2443	0.2817
x13	0.1532	0.1763	0.2746	0.2659	0.1705	0.2544	0.2804	0.2341	0.2544	0.1445
x14	0.2644	0.1968	0.1783	0.2829	0.2060	0.1906	0.1568	0.2460	0.2644	0.2306
x15	0.1948	0.1791	0.2765	0.1948	0.1885	0.2137	0.1760	0.2168	0.2639	0.1571
x16	0.2401	0.2075	0.2579	0.2519	0.1838	0.1838	0.1512	0.2312	0.2579	0.2579
x17	0.1985	0.1496	0.1438	0.2761	0.1668	0.2617	0.2013	0.2128	0.1841	0.2646
x18	0.2753	0.1639	0.2227	0.2691	0.1639	0.1547	0.1639	0.1949	0.2011	0.2815
x19	0.2199	0.1789	0.2785	0.2140	0.1554	0.2375	0.2610	0.2140	0.2698	0.2170
x20	0.1850	0.1577	0.2395	0.2426	0.1910	0.2335	0.1941	0.1546	0.2426	0.2880
x21	0.2783	0.2416	0.1529	0.2294	0.1927	0.2661	0.1591	0.2111	0.1743	0.2111
x22	0.1675	0.1764	0.1645	0.2871	0.1884	0.1615	0.2183	0.2422	0.2392	0.1884
x23	0.1934	0.1876	0.1817	0.2726	0.1671	0.1700	0.2579	0.1817	0.2608	0.2491
x24	0.1527	0.2363	0.2392	0.2709	0.2248	0.2162	0.2796	0.1787	0.2248	0.1643
x25	0.1630	0.2673	0.2804	0.2413	0.1924	0.1728	0.2869	0.1663	0.1695	0.2739
x26	0.2383	0.2085	0.1519	0.2234	0.1758	0.1847	0.2800	0.2949	0.1639	0.1609
x27	0.2686	0.1618	0.2773	0.2195	0.2571	0.2282	0.2369	0.2109	0.1878	0.2253
x28	0.1572	0.1659	0.1688	0.2678	0.1717	0.2853	0.1979	0.2445	0.2125	0.2649
x29	0.2057	0.2299	0.2541	0.2814	0.2420	0.2511	0.1694	0.2602	0.2965	0.1634
x30	0.2547	0.2179	0.2009	0.2122	0.1641	0.1472	0.1953	0.2405	0.2377	0.2377
x31	0.1662	0.1543	0.1484	0.2463	0.1721	0.2018	0.2967	0.2077	0.2166	0.2196
x32	0.2060	0.1752	0.2060	0.2367	0.1537	0.1722	0.2336	0.1906	0.2582	0.2859
x33	0.2935	0.1585	0.1585	0.2641	0.1761	0.1819	0.1790	0.1643	0.2406	0.2524
x34	0.2185	0.1742	0.2805	0.2923	0.2067	0.1801	0.1506	0.1978	0.1713	0.2244
x35	0.2219	0.1849	0.1941	0.2435	0.2712	0.1602	0.2496	0.2219	0.2157	0.1849
x36	0.2709	0.1777	0.1602	0.2855	0.2564	0.2156	0.2069	0.2797	0.2535	0.2709

Table 5. Data processing results of core competitiveness evaluation indexes for clean energy incubator (K–T).

Index	Clean energy Incubator
	K	L	M	N	O	P	Q	R	S	T
x1	0.1908	0.2832	0.2534	0.2623	0.2414	0.2414	0.2265	0.2891	0.1997	0.2891
x2	0.1746	0.2328	0.2716	0.2383	0.2078	0.1773	0.2106	0.2688	0.2189	0.2328
x3	0.2801	0.2948	0.1739	0.1533	0.2299	0.1651	0.1946	0.2859	0.2211	0.2270
x4	0.1464	0.2929	0.1581	0.1523	0.2460	0.2753	0.2665	0.2812	0.2197	0.2812
x5	0.2600	0.2308	0.2425	0.2484	0.1753	0.1812	0.1899	0.2659	0.2338	0.2308
x6	0.2116	0.2673	0.2590	0.1671	0.1894	0.2701	0.2172	0.2089	0.2701	0.2785
x7	0.2510	0.2599	0.2451	0.2185	0.2835	0.2392	0.2303	0.2776	0.2717	0.1683
x8	0.2327	0.1923	0.2047	0.1861	0.1861	0.2078	0.2482	0.1706	0.2761	0.2482
x9	0.2860	0.2919	0.2131	0.2247	0.1722	0.2919	0.1868	0.1605	0.2423	0.1956
x10	0.2146	0.2534	0.2862	0.1848	0.1878	0.2534	0.2206	0.1789	0.2921	0.2117
x11	0.1679	0.2418	0.2731	0.2361	0.1536	0.1849	0.1792	0.2731	0.1878	0.2760
x12	0.2328	0.2472	0.2070	0.2213	0.1667	0.1437	0.1725	0.2817	0.2414	0.2041
x13	0.2544	0.2197	0.2833	0.2601	0.1532	0.1503	0.2457	0.2486	0.1792	0.1590
x14	0.1753	0.2306	0.1599	0.2029	0.2460	0.1753	0.2737	0.2952	0.2491	0.1630
x15	0.1791	0.2828	0.2074	0.1791	0.2168	0.2671	0.2734	0.2514	0.2357	0.2514
x16	0.2193	0.2549	0.1838	0.1719	0.1778	0.1927	0.2342	0.1541	0.2964	0.2845
x17	0.1956	0.2531	0.1639	0.2560	0.2100	0.2704	0.2330	0.1783	0.2819	0.2790
x18	0.2103	0.3062	0.2475	0.2073	0.1980	0.1918	0.1732	0.3093	0.2506	0.1825
x19	0.2082	0.2199	0.1965	0.2698	0.2404	0.1613	0.2639	0.1701	0.1730	0.2580
x20	0.2304	0.2971	0.1607	0.1789	0.1789	0.2850	0.2213	0.2850	0.2426	0.1698
x21	0.1743	0.2600	0.2478	0.1958	0.2386	0.2569	0.1560	0.2355	0.2325	0.2845
x22	0.2452	0.2093	0.1525	0.2452	0.2452	0.2692	0.2063	0.2632	0.2303	0.2931
x23	0.2638	0.2520	0.1465	0.2052	0.2579	0.2403	0.2550	0.2110	0.2257	0.2286
x24	0.1556	0.1989	0.2248	0.2709	0.2767	0.1441	0.1787	0.2680	0.1960	0.2796
x25	0.2641	0.2999	0.1858	0.2282	0.2250	0.1826	0.2152	0.2021	0.1663	0.1989
x26	0.1490	0.2234	0.2443	0.2830	0.2115	0.2443	0.1996	0.2800	0.1966	0.2651
x27	0.2455	0.2744	0.1618	0.1820	0.1762	0.2658	0.2484	0.2195	0.1733	0.1878
x28	0.2009	0.1892	0.2387	0.2212	0.2678	0.1921	0.2503	0.2212	0.2824	0.2009
x29	0.2481	0.2299	0.1967	0.1785	0.1573	0.1815	0.2693	0.2299	0.1936	0.1513
x30	0.2660	0.2660	0.2462	0.1783	0.2717	0.2462	0.2009	0.2151	0.2405	0.1783
x31	0.1721	0.2285	0.2819	0.2819	0.2404	0.1899	0.2522	0.2255	0.2344	0.2552
x32	0.2859	0.2675	0.2183	0.1906	0.1937	0.2798	0.1875	0.2336	0.1845	0.2429
x33	0.1614	0.2348	0.2377	0.1878	0.2817	0.2582	0.2758	0.2612	0.2465	0.1585
x34	0.2510	0.2658	0.1742	0.1919	0.1536	0.2599	0.2923	0.2628	0.2303	0.2038
x35	0.1664	0.2928	0.2589	0.2003	0.2619	0.2280	0.2157	0.2743	0.1695	0.1911
x36	0.1632	0.2185	0.1894	0.2156	0.2098	0.1777	0.2331	0.2506	0.1748	0.1923

4.2. Evaluation and Analysis of Core Competitiveness of Clean Energy Incubator Based on Matter-Element Extension Model Integrated with TOPSIS

Table 6 presents the indicator weights derived from Equations (2)–(5).

Table 6. Indicator weights.

Index	Weight	Index	Weight
x1	0.0306	x19	0.0230
x2	0.0156	x20	0.0327
x3	0.0278	x21	0.0262
x4	0.0364	x22	0.0278
x5	0.0256	x23	0.0229
x6	0.0236	x24	0.0327
x7	0.0353	x25	0.0312
x8	0.0165	x26	0.0327
x9	0.0306	x27	0.0224
x10	0.0285	x28	0.0246
x11	0.0273	x29	0.0290
x12	0.0223	x30	0.0195
x13	0.0401	x31	0.0283
x14	0.0295	x32	0.0241
x15	0.0232	x33	0.0354
x16	0.0280	x34	0.0314
x17	0.0326	x35	0.0226
x18	0.0358	x36	0.0243

The weighted standardized matrix $X$ can be further obtained as Equation (33):

$$X=\left[\begin{array}{ccccc}0.0058& 0.0087& 0.0078& \cdots & 0.0088\\ 0.0027& 0.0036& 0.0042& \cdots & 0.0036\\ 0.0078& 0.0082& 0.0048& \cdots & 0.0063\\ ⋮& ⋮& ⋮& \cdots & ⋮\\ 0.0040& 0.0053& 0.0046& \cdots & 0.0047\end{array}\right]$$

(33)

Table 7 manifests the positive ideal solution $Z^{+}$ as well as the negative one calculated from Equations (9) and (10). The extremum interval composed of the above results is divided into four levels, namely low, general, high and very high. Here, x₁ is taken as an example, the corresponding positive and negative ideal solutions are 0.0088 and 0.0047, respectively. The interval can be expressed as Equation (34). This technique is applicable for other indexes.

$$\begin{array}{l}{H}_{11}=[0.0047,0.0058]\\ H_{12}=[0.0058,0.0068]\\ H_{13}=[0.0068,0.0078]\\ H_{14}=[0.0078,0.0088]\end{array}$$

(34)

Table 7. Positive and negative ideal solutions.

Index	Positive Ideal Solution	Negative Ideal Solution	Index	Positive Ideal Solution	Negative Ideal Solution
x1	0.0088	0.0047	x19	0.0064	0.0036
x2	0.0042	0.0025	x20	0.0097	0.0051
x3	0.0082	0.0043	x21	0.0075	0.0040
x4	0.0107	0.0053	x22	0.0081	0.0042
x5	0.0070	0.0037	x23	0.0062	0.0034
x6	0.0066	0.0033	x24	0.0091	0.0047
x7	0.0100	0.0052	x25	0.0094	0.0051
x8	0.0047	0.0028	x26	0.0096	0.0049
x9	0.0089	0.0047	x27	0.0062	0.0036
x10	0.0083	0.0043	x28	0.0070	0.0039
x11	0.0075	0.0040	x29	0.0086	0.0044
x12	0.0063	0.0032	x30	0.0053	0.0029
x13	0.0114	0.0058	x31	0.0084	0.0042
x14	0.0087	0.0046	x32	0.0069	0.0037
x15	0.0066	0.0036	x33	0.0104	0.0056
x16	0.0083	0.0042	x34	0.0092	0.0047
x17	0.0092	0.0047	x35	0.0066	0.0036
x18	0.0111	0.0055	x36	0.0069	0.0039

Furthermore, the closeness degree E(N_i) between each index in standardized decision matrix and four evaluation intervals is computed as Equations (35)–(38).

$$E(N_1)=\left[\begin{array}{l}\begin{array}{ccccc}0.0001& 0.0001& 0.0014& \cdots & 0.0036\\ 0.0006& 0.0006& 0.0008& \cdots & 0.0009\\ 0.0007& 0.0003& 0.0016& \cdots & 0.0016\\ ⋮& ⋮& ⋮& \cdots & ⋮\end{array}\\ \begin{array}{ccccc}0.0023& 0.0000& 0.0004& \cdots & 0.0004\end{array}\end{array}\right]$$

(35)

$$E(N_2)=\left[\begin{array}{l}\begin{array}{ccccc}0.0009& 0.0011& 0.0004& \cdots & 0.0026\\ 0.0001& 0.0001& 0.0003& \cdots & 0.0005\\ 0.0003& 0.0007& 0.0006& \cdots & 0.0006\\ ⋮& ⋮& ⋮& \cdots & ⋮\end{array}\\ \begin{array}{ccccc}0.0015& 0.0007& 0.0011& \cdots & 0.0004\end{array}\end{array}\right]$$

(36)

$$E(N_3)=\left[\begin{array}{l}\begin{array}{ccccc}0.0019& 0.0021& 0.0006& \cdots & 0.0015\\ 0.0003& 0.0003& 0.0001& \cdots & 0.0000\\ 0.0013& 0.0016& 0.0004& \cdots & 0.0004\\ ⋮& ⋮& ⋮& \cdots & ⋮\end{array}\\ \begin{array}{ccccc}0.0008& 0.0015& 0.0019& \cdots & 0.0011\end{array}\end{array}\right]$$

(37)

$$E(N_4)=\left[\begin{array}{l}\begin{array}{ccccc}0.0030& 0.0031& 0.0017& \cdots & 0.0005\\ 0.0007& 0.0007& 0.0005& \cdots & 0.0004\\ 0.0023& 0.0026& 0.0014& \cdots & 0.0014\\ ⋮& ⋮& ⋮& \cdots & ⋮\end{array}\\ \begin{array}{ccccc}0.0000& 0.0022& 0.0027& \cdots & 0.0019\end{array}\end{array}\right]$$

(38)

Figure 3 and Table 8 illustrate the weighted closeness degree of each evaluation scheme. The level of the maximum of Q_j(N_i) can be determined as the level of the evaluation object.

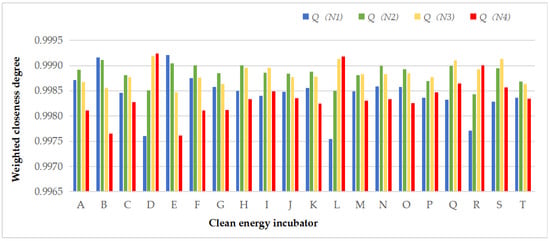
Figure 3. The weighted closeness degree of each evaluation scheme.

Table 8. The weighted closeness degree and valuation level of each evaluation scheme.

Clean Energy Incubator	Q(N1)	Q(N2)	Q(N3)	Q(N4)	Max Value	Valuation Level
A	0.9987	0.9989	0.9987	0.9981	0.9989	general
B	0.9992	0.9991	0.9986	0.9977	0.9992	low
C	0.9985	0.9988	0.9988	0.9983	0.9988	general
D	0.9976	0.9985	0.9992	0.9992	0.9992	very high
E	0.9992	0.9990	0.9985	0.9976	0.9992	low
F	0.9988	0.9990	0.9988	0.9981	0.9990	general
G	0.9986	0.9988	0.9986	0.9981	0.9988	general
H	0.9985	0.9990	0.9990	0.9983	0.9990	general
I	0.9984	0.9989	0.9990	0.9985	0.9990	high
J	0.9985	0.9988	0.9988	0.9984	0.9988	general
K	0.9986	0.9989	0.9988	0.9983	0.9989	general
L	0.9975	0.9985	0.9991	0.9992	0.9992	very high
M	0.9985	0.9988	0.9988	0.9983	0.9988	high
N	0.9986	0.9990	0.9988	0.9983	0.9990	general
O	0.9986	0.9989	0.9988	0.9983	0.9989	general
P	0.9984	0.9987	0.9988	0.9985	0.9988	high
Q	0.9983	0.9990	0.9991	0.9986	0.9991	high
R	0.9977	0.9984	0.9989	0.9990	0.9990	very high
S	0.9983	0.9990	0.9991	0.9986	0.9991	high
T	0.9984	0.9987	0.9986	0.9983	0.9987	general

4.3. Evaluation and Analysis of Core Competitiveness of Clean Energy Incubator Based on KPCA-NSGA-II-LSSVM

Exact though it is, the aforementioned techniques are not suitable to address massive data for their weakness of complex calculation and low efficiency. Thus, the intelligent evaluation model is proposed in this paper.

4.3.1. Growth Catalytic Ability

In this part, the above 20 clean energy incubators are taken as training sample, and the other 20 incubators are used as testing samples. PCA and KPCA are applied to 36 indicators to attain the variance contribution rates and cumulative variance contribution rate, as shown in Table 9 and Table 10. Figure 4 and Figure 5 exhibit the results more intuitively.

Table 9. Variance contribution rates and cumulative variance contribution rate of PCA.

Component	Variance Contribution Rate/%	Cumulative Variance Contribution Rate/%
1	25.68	25.68
2	16.67	42.35
3	8.66	51.01
4	8.56	59.57
5	6.56	66.13
6	6.02	72.15
7	5.22	77.37
8	3.65	81.02
9	3.02	84.04
10	2.66	86.7
11	2.56	89.26
12	2.36	91.62
13	1.88	93.5
14	1.83	95.33
15	1.16	96.49
16	0.96	97.45
17	0.88	98.33
18	0.52	98.85
19	0.38	99.23
20	0.22	99.45
21	0.18	99.63
22	0.16	99.79
23	0.09	99.88
24	0.06	99.94
25	0.03	99.97
26	0.01	99.98
27	0.01	99.99
28	0.01	100
29	0	100
30	0	100
31	0	100
32	0	100
33	0	100
34	0	100
35	0	100
36	0	100

Table 10. Variance contribution rates and cumulative variance contribution rate of KPCA.

Component	Variance Contribution Rate/%	Cumulative Variance Contribution Rate/%
1	69.56	69.56
2	18.58	88.14
3	7.56	95.7
4	2.82	98.52
5	0.99	99.51
6	0.26	99.77
7	0.18	99.95
8	0.03	99.98
9	0.02	100
10	0	100
11	0	100
12	0	100
13	0	100
14	0	100
15	0	100
16	0	100
17	0	100
18	0	100
19	0	100
20	0	100
21	0	100
22	0	100
23	0	100
24	0	100
25	0	100
26	0	100
27	0	100
28	0	100
29	0	100
30	0	100
31	0	100
32	0	100
33	0	100
34	0	100
35	0	100
36	0	100

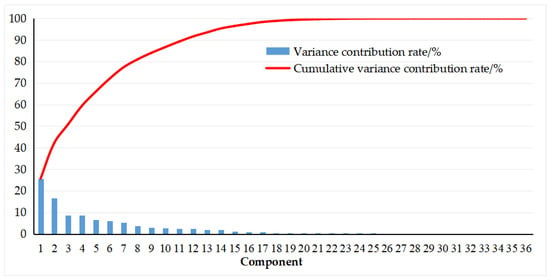
Figure 4. Total variance of PCA.

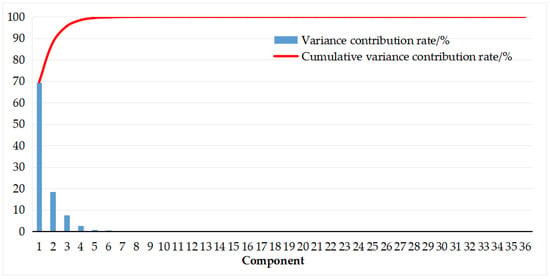
Figure 5. Total variance of KPCA.

From Table 9 and Table 10, Figure 4 and Figure 5, it can be seen that the first principal component of KPCA explains 69.56% of the factors, while the contribution rate of the first principal component in PCA is only 25.68%. In addition, it needs to extract 14 principal components in PCA or 3 principal components in KPCA to ensure cumulative contribution rate more than 95%, which can retain enough original data information. Therefore, the dimension reduction and simplification of KPCA is superior to PCA.

The selected principal components coefficients are acquired through dividing the principal component load vectors by the arithmetic square root of the eigenvalues. The output component matrix is presented in Table 11.

Table 11. Component matrix of KPCA.

Factor	Component
	1	2	3
x1	−0.903	−0.933	0.598
x2	0.267	−0.452	0.948
x3	0.471	0.700	0.352
x4	0.862	−0.548	0.821
x5	−0.060	0.708	0.861
x6	0.673	−0.721	0.440
x7	0.443	−0.199	−0.368
x8	0.227	−0.669	−0.607
x9	0.174	−0.645	0.547
x10	−0.399	0.181	0.487
x11	−0.508	−0.852	0.475
x12	−0.167	0.401	0.438
x13	−0.690	0.548	0.379
x14	−0.385	0.568	−0.053
x15	0.750	−0.054	−0.055
x16	−0.125	−0.007	−0.809
x17	−0.475	0.350	0.336
x18	0.958	0.696	0.610
x19	0.901	−0.248	0.948
x20	0.066	−0.182	0.663
x21	0.033	0.991	0.125
x22	0.144	0.006	−0.919
x23	0.378	0.491	0.527
x24	0.518	0.784	0.144
x25	−0.561	0.964	0.333
x26	−0.960	−0.256	−0.828
x27	0.659	0.961	−0.572
x28	−0.814	0.307	0.110
x29	0.717	0.876	0.236
x30	−0.295	−0.077	−0.607
x31	0.600	0.987	−0.400
x32	0.029	0.147	−0.289
x33	0.227	−0.445	0.886
x34	0.867	0.105	0.006
x35	−0.025	−0.826	−0.299
x36	0.546	−0.771	−0.841

4.3.2. Result Analysis

This paper performs on Matlab R2014a with Intel Core i5-6300U, 4G memory and 500G hard disk. It should be noted that important parameters of the proposed model are obtained by NSGA algorithm to guarantee the precision. In NSGA-II, the population size is 300, the maximum iteration number equals 200 and crossover and mutation probability is set as 2. In this way, the optimized parameters of LSSVM are $\gamma =36.6786$ and ${\sigma }^2=16.1816$.

The experiment selects several techniques to make comparison so as to examine the performance of the proposed method. The involved approaches include NSGA-II-LSSVM, GA-LSSVM, LSSVM and SVM. In LSSVM, γ and σ² equal 9.8568 and 16.2657 by cross validation, partly. In SVM, penalty parameter c is 8.659, kernel function parameter g equals 0.299 and loss function parameter p is 2.869.

The three principal components extracted by KPCA are exploited as input samples. The results of the test samples are displayed in Table 12 and Figure 6. In order to show the results clearly, the samples are divided into four groups, which are shown in (a–d) of Figure 6. Here, the relative errors in Table 12 are the results of the test samples and the number 1, 2, 3, 4 in Figure 6 represent the level of very high, high, general and low, respectively. In addition, the accuracy of 5 models is shown in Figure 7.

Table 12. Results of 5 models in core competitiveness valuation of clean energy incubators.

Clean Energy Incubator	Valuation Level	KPCA-NSGA-II-LSSVM	NSGA-II-LSSVM	GA-LSSVM	LSSVM	SVM
A	general	general	very high	general	low	general
B	low	low	low	low	low	general
C	general	general	general	low	general	general
D	very high	very high	very high	very high	general	very high
E	low	low	low	general	low	low
F	general	high	general	general	general	general
G	general	general	low	general	high	general
H	general	general	general	general	general	general
I	high	high	high	high	high	low
J	general	general	general	general	general	general
K	general	general	general	general	general	low
L	very high	very high	very high	very high	general	very high
M	high	high	high	high	high	general
N	general	general	general	general	general	high
O	general	general	general	general	general	general
P	high	high	high	high	high	high
Q	high	high	high	very high	high	high
R	very high	very high	very high	very high	very high	very high
S	high	high	high	high	very high	high
T	general	general	general	general	general	high
Relative error	-	5%	10%	15%	25%	30%

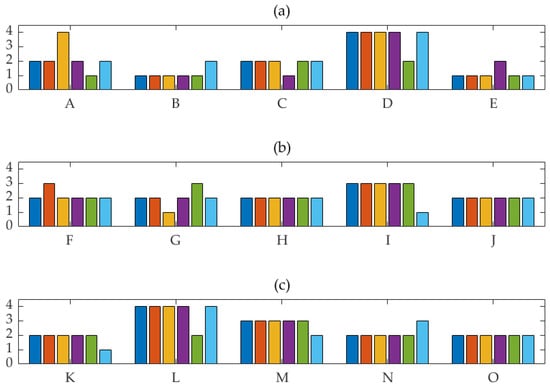
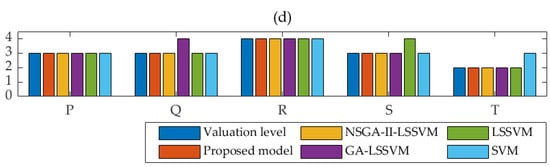
Figure 6. Results of 5 models in core competitiveness valuation of clean energy incubators. Note: (a) shows the results from sample A to E; (b) shows the results from sample F to J; (c) shows the results from sample K to O; (d) shows the results from sample P to T.

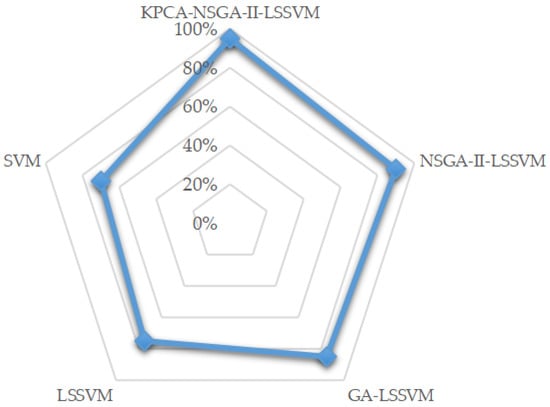
Figure 7. The accuracy of the proposed model and the comparison models.

In terms of method performance, the relative error is minimum, only 5% between KPCA-NSGA-II-LSSVM and matter-element extension model combined with TOPSIS. That is, only one of the 20 clean energy incubators presents diverse level. Whereas, the relative errors of NSGA-II-LSSVM, GA-LSSVM, LSSVM and SVM. In LSSVM are 10%, 20%, 25% and 30%, respectively. As a consequence, the established model in this paper outperforms other approaches with reference to relative error as well as classification accuracy. Compared with NSGA-II-LSSVM, KPCA overcomes the adverse effects of redundant factors on LSSVM training. The GA optimization part is inferior to NSGA-II of the parameters’ setting in LSSVM in aspect of improving its generalization ability and classification precision. In comparison with SVM, the categorization accuracy is enhanced due to the transformation of forecasting problems into equations through kernel function. Overall, the evaluation performance can be ranked from superior to inferior as follows: KPCA-NSGA-II-LSSVM, NSGA-II-LSSVM, GA-LSSVM, LSSVM, SVM. What’s more, we can also observe the advantages of the proposed model through Figure 7, where the accuracy of the proposed model is the highest.

Hence, KPCA-NSGA-II-LSSVM is able to be utilized in the field of core competitiveness of clean energy incubators scientifically and effectively. On the foundation of extension matter-element model integrated with TOPSIS, the introduction of auxiliary intelligent algorithm can achieve fast calculation and support the decision-making of relevant investors.

5. Conclusions

This paper designs an evaluation index system for core competitiveness of clean energy incubators and puts forward an assessment approach based on matter-element extension model integrated with TOPSIS as well as KPCA-NSGA-II-LSSVM. The indicator system is built from five aspects, that is strategic positioning ability, seed selection ability, intelligent transplantation ability, growth catalytic ability and service value-added ability to respect its core competitiveness. The paper takes advantage of extension matter-element model and TOPSIS to weight the selected evaluation indexes objectively and acquires the result from the perspective of traditional approaches. KPCA is manipulated in response to feature dimension so as to extract important information. Then LSSVM optimized by NSGA-II outputs the evaluation level concerning modern intelligence. The case study demonstrates the scientificity and accuracy of the proposed model in this paper, thereinto the traditional technique is able to obtain exact results while the intelligent evaluation methods can achieve fast calculation and decision-making support. Research on the evaluation of the core competitiveness of clean energy incubator will help managers to understand the level and deficiency of their core competitiveness, and then help managers to carry out more targeted work. To sum up, this research is expected to provide decision-making basis for more reasonable operation mode of clean energy incubators. However, more sample data is needed for verification. At the same time, using more intelligent models to evaluate the core competitiveness of clean energy incubators is also our next work.