Abstract
Most traditional AC/AC power converters suffer from power quality problems and multi-stage power conversion losses. The rectifier and inverter-based AC/AC converter topology not only increases multi-stage power conversion losses, but also increases the volume, weight, and cost, and decreases the longevity of the converter due to the DC-link capacitor, line filter and electromagnetic interference (EMI) filter. High-frequency (about 10 kHz) switching advanced pulse width modulation techniques are generally used in order to compensate the power quality problems, which increase the switching losses and introduce the EMI problems. In this paper, a new generalized step-down single-stage line-frequency switching AC/AC power converter topology is proposed. The proposed converter uses line-frequency switching, and does not require any pulse width modulation techniques. The proposed topology offers promising performances in terms of lower order harmonics, total harmonic distortion, the elimination of DC-link capacitors and EMI filters, and switching losses. The circuit was designed and simulated in a MATLAB/Simulink environment. A scaled-down laboratory prototype of the proposed topology was developed in order to validate the feasibility. The experimental and simulation results reveal the feasibility of the proposed generalized step-down single-stage converter topology, and its excellent features.
1. Introduction
The utility grid generally provides fixed frequency and voltage power to consumers. However, some industrial loads—for example, electric traction, induction heating, voltage regulation and controlled rectifier—require variable frequency power supply [1,2]. Therefore, AC/AC power electronic converters are used to convert the one frequency AC power to another frequency AC power [3]. This can be achieved by adjusting the input–output relation in such a way that the effective output voltage value refers to a certain required output voltage [4]. Thyristors enable the commercial development of static AC/AC converters. With the advent of massive rated thyristors and the development of microprocessor-based switching and control, thyristor-controlled AC/AC converters are widely used in manufacturing industries for applications in electrical traction [5], rolling steel mills [6], semi-autogenous grinding (SAG) mill drives [7,8,9], and grinding mill drives in mining [10,11].
For the ever-increasing demand from industrial applications, variable frequency generation has now become important. AC/AC variable frequency conversion can be acheived in two ways. One is a rectifier and inverter-based converter, which performs two-stage of power conversion, AC/DC and DC/AC. Nowadays, the variable frequency drive (VFD) has become very popular in industries for motor drive applications; it utilizes rectifier and inverter-based converters. However, it suffers from various problems. It uses two-stage power conversion, which significantly reduces the system’s efficiency, and enhances the control difficulty and the size of the converter. Large size filters are required in the rectifier and inverter sides of the VFD in order to compensate the power quality problems. A bulky multi-pulse phase-shifting transformer is used in VFD for the rectification, which introduces harmonics to the grid [12,13]. As a result, the input power factor of the line is reduced significantly, which degrades the power quality. A cycloconverter provides direct AC/AC power conversion, which may overcome the issues related to rectifier and inverter-based converter. However, traditional a single-stage AC/AC converter (e.g., cycloconverter) has the following limitations:
- It cannot perform generalized/multi frequency power conversion;
- The output voltage waveform suffers from high total harmonic distortion (THD) problem;
- It adds lower-order harmonic and inter-harmonic contents to the output power for the inductive load.
Due to these limitations, industries prefer to use two-stage converters instead of the single-stage AC/AC converter (e.g., the cycloconverter).
Moreover, the harmonic components, i.e., the total harmonic distortions, of AC/AC converters should be low in order to use AC/AC converters in variable speed drive applications. It is known to all that the output voltage of an AC/AC power converter is not purely sinusoidal, and its Fourier series involves harmonics which include a) higher-order harmonics and [14] b) nonstandard harmonics. A single-phase AC/AC power converter with a constant gate pulse provides a high harmonic content in its output voltage [15]. High-frequency (about 10 kHz) switching advanced modulation techniques can be used to generate gate pulses in order to reduce the harmonics. However, the high-frequency switching advanced modulation techniques increase switching losses and introduce electromagnetic interference (EMI) problems. Recent articles have highlighted different operational parameters for AC/AC converters. Advanced modulation techniques [16,17,18,19,20,21,22,23] and the standard filter scheme [24] were considered for the reduction of harmonic distortion. Different modulation techniques—such as pulse width modulation (PWM) [18], sinusoidal PWM [19], space vector modulation, delta modulation [17], discrete amplitude modulation, and pulse density modulation (PDM) [16]—were used to improve the quality of the output power. Most of the presented AC/AC power converters used complex topology with a large number of switches, as well as the complex modulation technique. PWM and sinusoidal PWM methods reduce the THD of the output voltage, but a complex gate drive pulse generation circuit is required for this. In space vector modulation, a large number of switches are used with the complex switching technique. Delta modulation is another technique that is used for the removal of the harmonics of the AC/AC power converter output voltage. However, an extra controller circuit is used to control the output voltage as required, which makes the topology costly and bulky. Discrete amplitude modulation needs an extra circuit topology to produce carrier wave for amplitude modulation (AM) and pulse density modulated (PDM) needs an extra delta-sigma analog to digital converter [17]. Therefore, traditional techniques with advanced modulation are not really attractive because the techniques increase circuit complexity and cost.
The output voltage filtering is another technique to compensate for the harmonic problem of the AC/AC power converter without using the modulation technique. Different type of passive, comb and hybrid filters are available to reduce the output voltage and input current harmonics. However, it is very difficult to reduce the inter-harmonic components using classical passive filters tuned at the dominant harmonics. Moreover, due to the parallel resonance between the passive filter and the source impedance, the current magnification of the inter-harmonics can be created. The use of a large number of inductors [24] in the filtering process may reduce the power factor. In [25], comb filtering was proposed, which uses the phase shift technique. However, the phase shift technique needs an extra circuit topology to shift the phase. The hybrid filter is very effective for the reduction of the harmonic problem of the output voltage because it is a combination of active and passive filters. However, the circuit topology of the hybrid filter is very complex, in relative terms [26]. Controller circuits are used in most of hybrid filters, which need an extra controller board with a sensing mechanism and a large number of other parallel filter components [27]. In [28], a complex filtering technique was used with a large number of inductors, as well as a transformer for the galvanic isolation. However the large number of inductors decrease the power factor and increase the cost. There are some available techniques to improve the power factor problem, but they need extra power switches and passive components [29]. The series–parallel hybrid filter is another technique used in an AC/AC converter, which needs a complex synchronous reference frame (SRF) harmonic detection circuit [30]. In [31], a new topology was proposed for current harmonics removal, but the topology uses a large number of phase converted switches with a galvanic isolated transformer.
Therefore, it is highly desirable to develop a new generalized single-stage AC/AC power converter topology with the capability to overcome the problems of the conventional single-stage AC/AC power converter (e.g., a cycloconverter), which will then be a good choice the industrial community to replace the multi-stage AC/AC power converters used in different variable frequency applications.
In this paper, a new generalized step-down single-stage line frequency switching AC/AC power converter topology is proposed, which significantly reduces the harmonic distortion of the output voltage without using any pulse width modulation techniques in the switching circuit. The proposed alternative solution does not require any complex firing angle modulation or EMI filters. The proposed topology offers promising performances in terms of lower order harmonics, total harmonic distortion, the elimination of DC-link capacitors and EMI filters, and switching losses.
The major contributions of this article are:
- A new single-stage line-frequency switching AC/AC power converter is proposed;
- The proposed converter can be used to convert any frequency without changing the hardware circuit;
- The proposed topology does not require any high-frequency switching pulse width modulation technique.
The organization of the paper is as follows: the theoretical background and the mathematical analysis of the conventional AC/AC power converter is introduced in Section 2. The generalized configuration and the operating principle of the proposed AC/AC power converter are described in Section 3. The simulation-based performances of the proposed converter are demonstrated in Section 4. The mathematical analysis of the proposed converter is described in Section 5. The experimental results of the proposed AC/AC power converter are evaluated in Section 6. The comparison of the proposed topology is shown in Section 7. Finally, the paper is concluded in Section 8.
2. Theoretical Background
The output voltage waveforms of the conventional step-down AC/AC power converter are shown in Figure 1a, for 3:1 (m = 3) or 16.67 Hz, and in Figure 1b, for the 15:1 (m = 15) conversion of a 50 Hz input frequency. As the half-cycle amplitude of the conventional AC/AC power converter output is the same, the output voltage tracks the square wave shape by increasing the frequency order, which is clearly observed in Figure 1b, for the m = 15 frequency conversion. This is the main reason for the high THD of conventional AC/AC power converters. If the frequency conversion order (m) increases, the THD of a conventional AC/AC power converter also increases, and significant lower-order harmonic contents present in the output voltage. Therefore, it is clear that conventional AC/AC power converters suffer from high THD problems. Basically, AC/AC power converters are affected by two types of harmonics: characteristic harmonics and circuit-dependent harmonics.
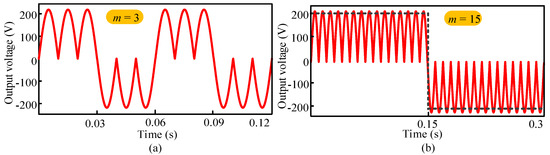
Figure 1.
Simulated output voltage waveform of the conventional: (a) 3:1 (m = 3) and (b) 15:1 (m = 15) frequency conversions of a 50 Hz input frequency.
For a conventional AC/AC power converter, the characteristic harmonic frequencies can be calculated as:
where fi and f0 are the input and output voltage frequency, respectively, and n = 1, 2, 3… For a six pulse bridge converter, the harmonic frequencies can be calculated as:
where P = 1, 2, 3…. and n = 0, 1, 2, 3…. The combination of (1) and (2) can be written as follows:
where q = 1, 5, 7, 11… (for an m = 3 conversion). When q = 1; n = 1, 2, 3 …, otherwise n = 0, 1, 2, 3 … From (3), it is clear that the output of the AC/AC power converter is affected by the DC component or the low frequencies component when 2nf0 equals or very close to qfi.
fch = fi ± 2nf0
fch = (6P ± 1) fi ± 2nf0
fh = qfi ± 2nf0
3. Proposed AC/AC Power Converter
The topology of the proposed step-down AC/AC power converter is described in this section. The generalized circuit topology and the working principle of the proposed topology are explained here.
3.1. Generalized Configuration of Proposed AC/AC Power Converter
The generalized structure of the proposed step-down AC/AC power converter topology is shown in Figure 2. The proposed topology uses a multi-winding center tapped transformer, pre-rectified diodes, and silicon controlled rectifiers (SCRs). The multi-winding transformer is used here to create a different voltage level according to the desired frequency conversion, with a lower THD. The frequency conversion, m, can be divided into odd frequency conversion, mo, and even frequency conversion, me.
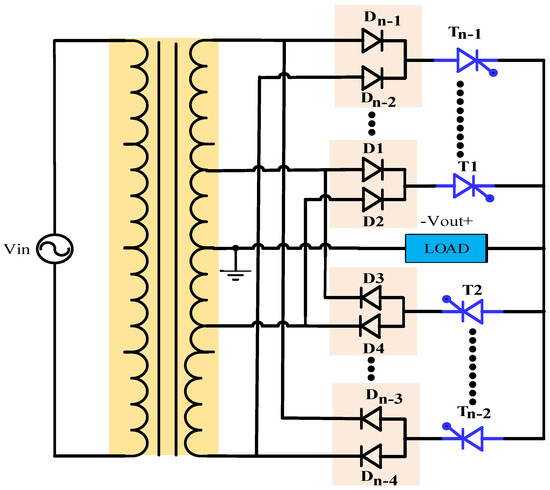
Figure 2.
Generalized configuration of the proposed step-down AC/AC power converter topology.
Hence, the required number of windings for mo can be calculated as:
Nwo = mo + 1
Similarly, the required number of windings for me can be calculated as:
Nwe = me
The required number of power diodes for mo can be calculated as:
NDo = 2(mo + 1)
The required number of power diodes for me can be calculated as:
NDe = 2me
The required number of switches (SCRs) for mo can be calculated as:
NSo = mo + 1
For an even frequency conversion (me), the required number of switches is equal to the number of even frequency conversions (me).
NSe = me
3.2. Operating Principle of the Proposed Topology
The operating principle of the proposed AC/AC power converter topology is described here with the help of 3:1 (m = 3) and 4:1 (m = 4) frequency conversions. By connecting the multi-winding center tapped transformer with the AC voltage source, the input AC voltage is divided into small AC voltage levels in the different section of the winding. Power diodes are used as a pre-rectifier, which rectifies both the positive cycle and the negative cycle for each section of the winding. Hence, only one unidirectional switch is required for each winding to pass the corresponding positive cycle and the negative cycle. The odd numbering switches work as the positive converter, and the even numbering switches work as the negative converter. There are eight operating modes, as shown in Figure 3, which describe the working principle of the 3:1 (m = 3) and 4:1 (m = 4) frequency conversions. The explanation of the eight operating modes also helps us to understand other frequency conversions. The eight operating modes are explained as follows:
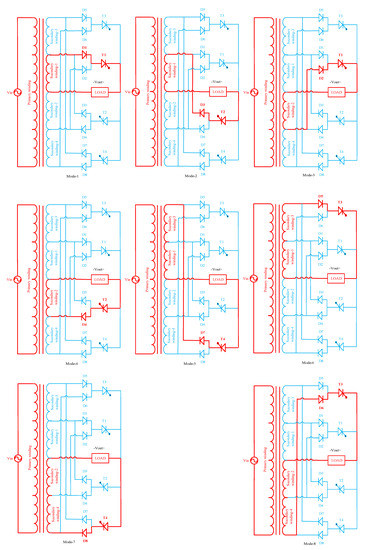
Figure 3.
Eight operating modes for the 3:1 (m = 3) and 4:1 (m = 4) frequency conversions of a 50 Hz fundamental frequency.
Mode-1: in this mode, the first winding of the secondary side, diode D1 and switch T1, create a conduction path for the flow of the load current, as shown in Figure 3 (Mode-1). Only the positive cycle can pass, and the polarity of the input–output voltage remains the same. Thus, the output voltage expression of this mode can be written as follows:
Vout = Vm/2
Mode-2: in Figure 3 (Mode-2), the first winding, diode D3 and switch T2 allow the flow of the load current through this conduction path. Only the negative cycle can pass in this conduction path. The polarity of the input–output voltage remains unchanged. Thus, the output voltage expression of this mode can be written as follows:
Vout = −Vm/2
Mode-3: in this mode, the second winding of the secondary side, diode D2 and switch T1, create a conduction path to allow the flow of the load current, as shown in Figure 3 (Mode-3). Only the positive cycle can pass, and the polarity of the input–output voltage is changed by 180°. Thus, the output voltage expression of this mode can be written as follows:
Vout = Vm/2
Mode-4: the second winding, diode D4 and switch T2, create a conduction path to allow the flow of the load current, as shown in Figure 3 (Mode-4). Only the negative cycle can pass, and the polarity of the input–output voltage is changed by 180°. Thus, the output voltage expression of this mode can be written as follows:
Vout = −Vm/2
Mode-5: in this mode, the first and third winding of the secondary side, diode D7 and switch T4, create a conduction path to allow the flow of the load current, as shown in Figure 3 (Mode-5). Only the negative cycle can pass, and the polarity of the input–output voltage is unchanged. Thus, the output voltage expression of this mode can be written as follows:
Vout = −Vm
Mode-6: the first and third winding of the secondary side, diode D5 and switch T3, create a conduction path to allow the flow of the load current, as shown in Figure 3 (Mode-6). Only the positive cycle can pass, and the polarity of the input–output voltage is unchanged. Thus, the output voltage expression of this mode can be written as follows:
Vout = Vm
Mode-7: in this mode, the second and fourth winding of the secondary side, diode D8 and switch T4, create a conduction path to allow the flow of the load current, as shown in Figure 3 (Mode-7). Only the negative cycle can pass, and the polarity of the input–output voltage is changed by 180°. Thus, the output voltage expression of this mode can be written as follows:
Vout = −Vm
Mode-8: The second and fourth winding of the secondary side, diode D6 and switch T3, create a conduction path to allow the flow of the load current, as shown in Figure 3 (Mode-8). Only the positive cycle can pass, and the polarity of the input–output voltage is changed by 180°. Thus, the output voltage expression of this mode can be written as follows:
Vout = Vm
Table 1 shows a summary of the individual output voltage levels with the corresponding switching state. Table 1 clearly shows the entire operation of the 3:1 (m = 3) and 4:1 (m = 4) frequency conversions of the proposed AC/AC power converter.

Table 1.
Switching states with the corresponding frequency conversions.
For a 3:1 (m = 3) frequency conversion, four operating modes are required, including mode-1, mode-2, mode-7 and mode-8. There are three states that occur during the positive half cycle, and another three states that occur during the negative half cycle of the output voltage. Operating mode-1 and mode-2 repeat two times, as shown in Figure 4a. Hence, the output voltage equation of the corresponding six states are shown as follows:
Vout = 0.5*Vm*sinα; 0 ≤ α ≤ π
Vout = −Vm*sinα; π ≤ α ≤ 2π
Vout = 0.5*Vm*sinα; 2π ≤ α ≤ 3π
Vout = 0.5*Vm*sinα; 3π ≤ α ≤ 4π
Vout = −Vm*sinα; 4π ≤ α ≤ 5π
Vout = 0.5*Vm*sinα; 5π ≤ α ≤ 6π
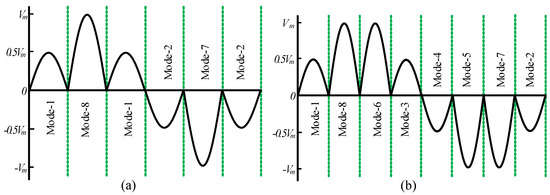
Figure 4.
Active operating mode for the (a) 3:1 (m = 3) and (b) 4:1 (m = 4) frequency conversions of a 50 Hz fundamental frequency.
For the 4:1 (m = 4) frequency conversion, all eight operating modes are required. There are four states that occur during the positive half cycle and another four states that occur during the negative half cycle of the output voltage shown in Figure 4b. Hence, the output voltage equations of the corresponding eight states can be shown as follows:
Vout = 0.5*Vm*sinα; 0 ≤ α ≤ π
Vout = −Vm*sinα; π ≤ α ≤ 2π
Vout = Vm*sinα; 2π ≤ α ≤ 3π
Vout = −0.5*Vm*sinα; 3π ≤ α ≤ 4π
Vout = −0.5*Vm*sinα; 4π ≤ α ≤ 5π
Vout = Vm*sinα; 5π ≤ α ≤ 6π
Vout = −Vm*sinα; 6π ≤ α ≤ 7π
Vout = 0.5*Vm*sinα; 7π ≤ α ≤ 8π
4. Performance Analysis of the Proposed AC/AC Power Converter
In order to analyze the performances of the proposed AC/AC power converter, two different frequency conversion, including 3:1 (m = 3) and 4:1 (m = 4), were simulated in a MATLAB/Simulink software environment. The value of the AC voltage source is considered to be 220 V, 50 Hz, and a 1:4 multi-winding center tapped transformer is used. Figure 5a shows the secondary four winding transformer voltage waveforms. By connecting the full-wave pre-rectified diode, the ac voltage is rectified in each winding before the SCRs switches; the rectified voltage is shown in Figure 5b. The switching pulses of the proposed 3:1 (m = 3) frequency conversion are shown in Figure 5c. The converted output voltage of the proposed 3:1 (m = 3) is presented in Figure 5d.
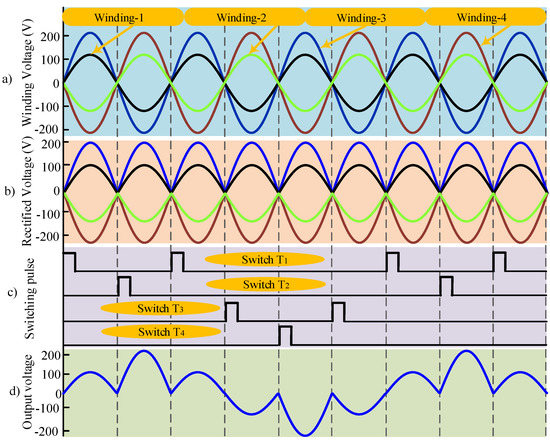
Figure 5.
(a) Winding voltage, (b) Rectified voltage, (c) Switching pulses, and (d) Output voltage for 3:1 (m = 3) of a 50 Hz frequency conversion.
For the 4:1 (m = 4) frequency conversion of the proposed topology, the winding voltage and the rectified voltage are unchanged, as shown in Figure 6a,b, respectively. Here, the gate drive pulses are different, as shown in Figure 6c. The converted output voltage of the 4:1 frequency conversion is shown in Figure 6d. Here, the converted output voltage of the proposed AC/AC power converter is more sinusoidal compared to the conventional output voltage shown in Figure 1. Figure 7a,b shows the current waveform of the proposed AC/AC power converter for the 3:1 (m = 3) and 4:1 (m = 4) frequency conversions, respectively.
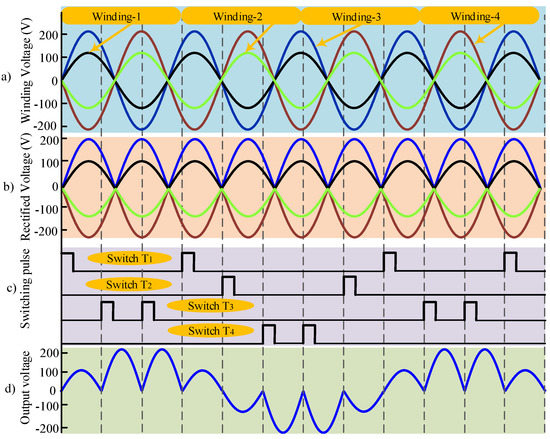
Figure 6.
(a) Winding voltage, (b) Rectified voltage, (c) Switching pulses, and (d) Output voltage for 4:1 (m = 4) of a 50 Hz frequency conversion.
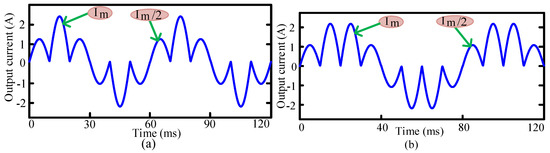
Figure 7.
Simulated current waveform for (a) 3:1 (m = 3) and (b) 4:1 (m = 4) of a 50 Hz frequency conversion.
From the output voltage and the current waveform, it can be clearly seen that the output voltage and the current waveform of the proposed topology are more sinusoidal compared with conventional AC/AC power converter’s output waveform. Here, the output voltage and current are presented for the resistive load only. The harmonic spectrums of the output voltage and output current for the proposed 3:1 (m = 3) are shown in Figure 8a,b, respectively.
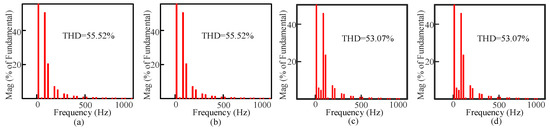
Figure 8.
The harmonic spectrums of the: (a) output voltage, (b) output current for the proposed 3:1 (m = 3) and 4:1 (m = 4) conversions, harmonic spectrums of the (c) output voltage, and (d) output current.
For the proposed 4:1 (m = 4) conversion, the harmonic spectrums of the output voltage and output current are shown in Figure 8c,d respectively. From these figures, it is obvious that the conversion order (m) increases, the value of the THD decreases. The harmonic spectrums also show that the lower order harmonic contents are significantly reduced for the proposed converter. The stress voltages of the transformer’s secondary side are shown in Figure 5b. For the proposed 3:1 (m = 3) and 4:1 (m = 4) frequency conversions, the stress voltage of the winding-1 and winding-2 is 110 V. For winding-3 and winding-4, the stress voltage is 220 V, where the primary winding voltage is 220 V. The voltage stress on the switching devices also depends on the winding voltage of the transformer’s secondary side. The switch T1 and T2 pass the winding-1 and winding-2 voltage, and switch T3 and T4 pass the winding-3 and winding-4 voltage. Therefore, the possible voltage stress for switches T1 and T2 is 110 V, and the possible voltage stress for switches T3 and T4 is 220 V.
5. Harmonics Analysis of the Proposed AC/AC Power Converter
In this section, the total harmonic distortion is analyzed for the 3:1 (m = 3) frequency conversion. The Fourier series of the AC/AC power converter output wave-form can be written as follows:
where m = the conversion ratio. The Fourier coefficients of a0 and an are always zero, and bn exists. For the bn coefficient, all of the even terms are zero; only odd harmonic terms exist. The output wave-form of the conventional AC/AC converter is always half-wave symmetry. Hence, using the technique of the half-cycle pairs method [26], the Fourier series expression of the conventional 3:1 frequency conversion output voltage can be written as follows:
where the first term is the third harmonic component and the second term represents harmonic components other than the 3rd order. The symbols ‘m’ and ‘n’ represent the frequency conversion ratio and harmonic order, respectively. The fundamental component can be calculated by inputting n = 1 in (34),
whith the frequency conversion ratio m = 3. The harmonic distortion of the proposed 3:1 (m = 3) AC/AC power converter output voltage can also be calculated using the half-cycle pair method. The primary distinction between the conventional and the proposed AC/AC power converter is the half-cycle amplitude of the output voltage waveform. The conventional 3:1 (m = 3) has a total of six half-cycle portions in the output waveform, and the amplitude of all six half cycles is Vm. However, in the proposed AC/AC converter, the amplitude of all of the half cycles is not the same. The amplitude of the second half cycle and the fifth half cycle is Vm, but the first, third, fourth, and sixth half cycles are Vm/2 as shown in Figure 3. Therefore, the Fourier series expression of the proposed AC/AC power converter (e.g., 3:1 conversion) can be rewritten as follows:
The fundamental component of the output waveform is found by putting n = 1 in (36):
Equation (35) shows that the third order harmonic component is completely removed for the proposed 3:1 (m = 3) conversion of a 50 Hz fundamental frequency. Therefore, the proposed AC/AC power converter is much better than the conventional AC/AC converter in terms of THD and lower order harmonic components.
Thus, for any order frequency conversion of 50 Hz fundamnetal, the Fourier series expression of the output waveform can be calculated using the half-cycle pair method according to their conventional half-cycle pair formula.
6. Hardware Implementation
In order to verify the proposed AC/AC power converter topology, a prototype circuit was built and tested in the laboratory. The whole circuit can be divided into three parts, including: (i) the zero-cross detection (ZCD), (ii) the pulse generator and (iii) the switching (SCRs).
A half wave rectifier with 4n35 IC was used for the zero-cross detection. Figure 9 depicts the zero-crossing waveform for the input supply. ZCD is used to synchronize the firing of SCRs with the input supply. An Arduino Uno (ATmega328) processor board was used to generate the gate drive pulses, and a MOC3021 opto-coupler IC was used to isolate the DC signal from the AC supply. TYN612 SCRs were used to control the phase of the sinusoid. A 1N4007 diode was connected in series with the SCR. The gate drive signals for the m = 3 and m = 4 frequency conversions of each switch are shown in Figure 10a,b, respectively.
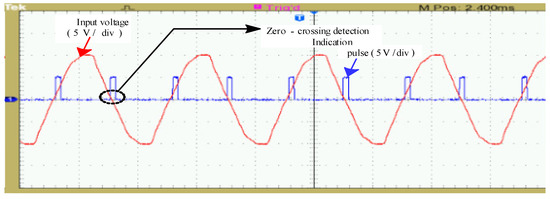
Figure 9.
Experimental zero crossing detection waveforms.
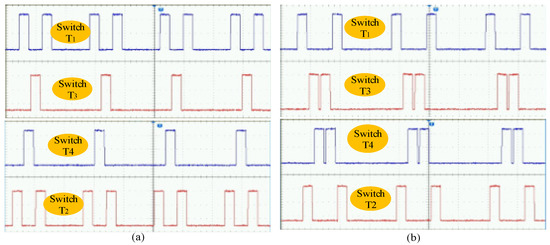
Figure 10.
Experimental gate drive signals (5V/div) for the (a) 3:1 (m = 3) and (b) 4:1 (m = 4) frequency conversions of a 50 Hz fundamental frequency.
Table 2 depicts the list of the equipment used in the experimental testing. Figure 11a,b shows the output voltage and current waveforms for the 3:1 (m = 3) and 4:1 (m = 4) conversions, respectively. The dynamic frequency change response of the output voltage of the proposed converter is depicted in Figure 12. From the datasheet of the diode and SCR used in the implemented converter, the reverse recovery time of the 1N4007 diode and the TYN 612 SCR was found to be 30 µs and 26 µs, respectively. The difference is very low, which cannot demerit the dynamic response of the converter significantly, as shown in Figure 12. From Figure 13, the experimental voltage THDs for the m = 3 and m = 4 frequency conversions were found to be 59.32% and 55.77%, respectively, which are slightly higher than the simulation values.

Table 2.
Specifications of the implemented AC/AC power converter.
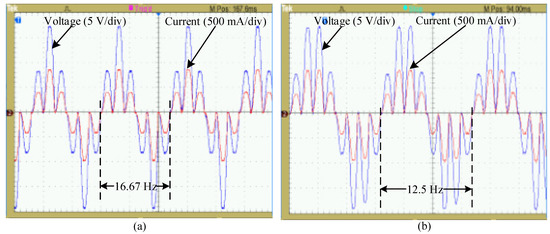
Figure 11.
Experimental output voltage and current waveform for the (a) 3:1 (m = 3) and (b) 4:1 (m = 4) frequency conversions of a 50 Hz fundamental frequency.
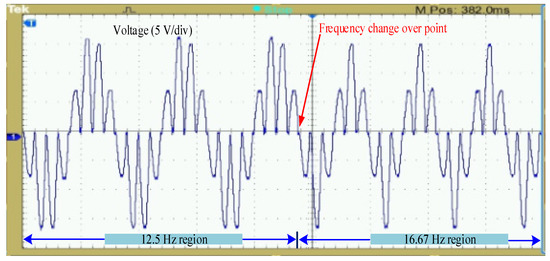
Figure 12.
Experimental dynamic frequency change response of the output voltage of the proposed AC/AC converter.
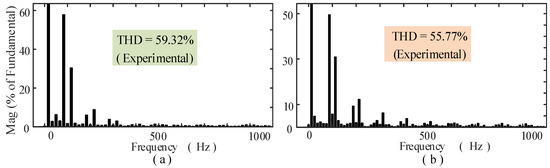
Figure 13.
Experimental frequency spectra of the output voltage for the (a) 3:1 (m = 3) and (b) 4:1 (m = 4) frequency conversions.
7. Result Analysis and Comparison
The comparison between the conventional and the proposed AC/AC power converter is described here with the help of a 3:1 (m = 3) frequency conversion for resistive load and motor load. The output voltage and output current waveforms of the proposed AC/AC power converter are shown in Figure 5d and Figure 7a for resistive load, where it can be seen that the output voltage and output current waveforms are more sinusoidal compared with the conventional output voltage waveform shown in Figure 1. For the motor load, the output voltage and load current waveforms of the proposed AC/AC power converter are shown in Figure 14a,b, respectively, for the 3:1 (m = 3) frequency conversion. Figure 15a,b shows the output voltage and load current waveforms of the conventional AC/AC power converter for the motor load, respectively. The output voltage of the proposed topology is still tracked by the sinusoidal waveform, with a little distortion for motor load. However, the output voltage of the conventional topology is not tracked by the sinusoidal waveform with more distortion for the motor load.
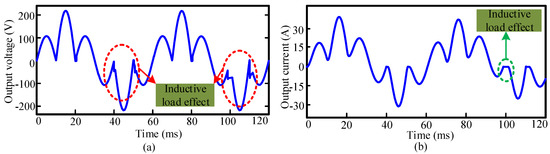
Figure 14.
Simulated output (a) voltage waveform and (b) current waveform of the 3:1 (m = 3) frequency conversion for the motor load of the proposed topology.
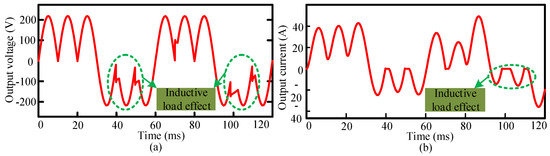
Figure 15.
Simulated output (a) voltage waveform and (b) current waveform of the 3:1 (m = 3) frequency conversion for the motor load of the conventional topology.
The motor load current of the proposed topology is very similar to the resistive load current, with a little change of its wave-shape, as shown in Figure 14b. However, the motor load current of the conventional topology is slowly changed in its wave-shape, as shown in Figure 15b. The total harmonic distortion of the output voltage and output current for the motor load of conventional and proposed 3:1 (m = 3) frequency conversion is shown in Figure 16. The output voltage THD of the conventional 3:1 (m = 3) converter was found to be 60.4% for the motor load shown in Figure 16a, while 51.76% of THD was found for the proposed 3:1 (m = 3) converter for the motor load shown in Figure 16b. The output current THD was found to be 91.39% and 58.16% of the conventional and proposed converter, respectively, as shown in Figure 16c,d. As such, the output voltage THD reduction of 8.64% and the output current THD reduction of 33.23% were achieved for proposed 3:1 (m = 3) frequency conversion for the motor load. For the resistive load, the output voltage THDs of conventional m = 3 and m = 4 converters are 68.42% and 70.31%, respectively, whereas the proposed AC/AC converter is 55.52% and 53.07%, respectively, as shown in Figure 17 and Figure 18. Therefore, the output voltage THD reduction of the proposed m = 3 and m = 4 were found to be 12.90% and 17.24%, respectively, for the resistive load. It was also noticed that the conventional output voltage has a large amount of lower order harmonics content for the 3:1 (m = 3) and 4:1 (m = 4) frequency conversions shown in Figure 17a and Figure 18a, respectively.
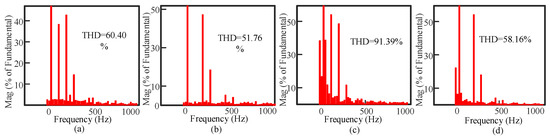
Figure 16.
Simulated total harmonic distortion of: (a) the conventional output voltage, (b) the proposed output voltage, (c) the conventional output current, and (d) the proposed output current of the 3:1 (m = 3) frequency conversion for the motor load.
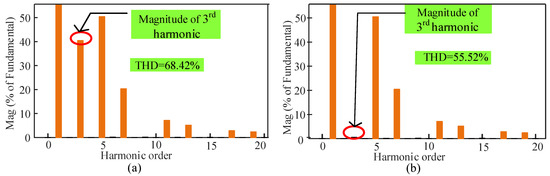
Figure 17.
Simulated harmonic spectra of the (a) conventional and (b) proposed 3:1 (m = 3) AC/AC power converters for the resistive load.

Figure 18.
Simulated harmonic spectra of the (a) conventional and (b) proposed 4:1 (m = 4) AC/AC power converters for the resistive load.
It is known that the lower-order harmonics content (especially the third harmonic) is more harmful to variable frequency drive applications. For the 3:1 (m = 3) and 4:1 (m = 4) frequency conversions, the lower order harmonic content is reduced significantly in the proposed topology. The third harmonic content is totally removed for the proposed 3:1 (m = 3) conversion shown in Figure 17b, which is also verified by the mathematical equation mentioned in (35). For the 4:1 (m = 4) conversion of the proposed AC/AC converter, the third and fifth harmonics content is very much lower, or close to zero, as shown in Figure 18b.
Table 3 shows the entire summarization of the harmonic distortion profiles of the conventional and proposed AC/AC power converter for the resistive load and motor load. The third harmonic content was found to be 40.39% in the output voltage for the resistive load, and 58.35% in the load current of the motor for the conventional AC/AC power converter. However, in the proposed topology, the third harmonic content was found to be 0.00% in the output voltage for the resistive load, and 03.22% in the load current of the motor. Therefore, the achieved reduction of the third harmonic was 40.39% and 55.13% for the resistive load voltage and the motor load current, respectively. In the proposed AC/AC power converter, the THD was gradually decreased when the conversion order was increased. However, it was totally reversed in the conventional topology. It is highly desirable to change the supply frequency in order to vary the motor speed for drive applications. The continuous frequency change response of the AC/AC power converter should be smooth for the ripple-free speed response which has to be offered by the AC/AC power converter.

Table 3.
Comparison of the proposed and conventional 3:1 (m = 3) AC/AC power converter.
The dynamic frequency change response of the proposed AC/AC power converter is depicted in Figure 19a. From Figure 19a, it is clear that there is a sharp transition of the output voltage from one state to another. The THDs of the output voltage for the proposed and conventional converters is shown in Figure 19b. The experimental voltage THDs of the proposed AC/AC power converter for 3:1 (m = 3) and 4:1 (m = 4) were found to be 59.32% and 55.77%, respectively. There is a difference of 3.82% and 2.74% between the simulation and the experimental THDs for the 3:1 (m = 3) and 4:1 (m = 4) frequency conversions.
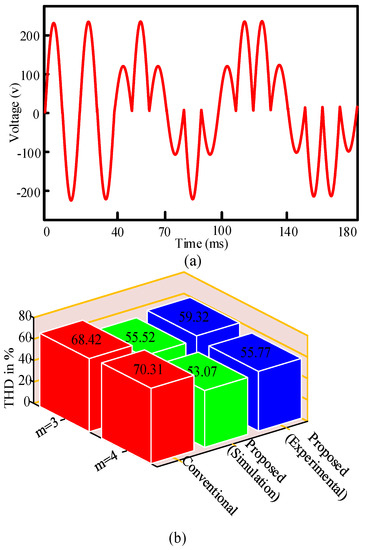
Figure 19.
(a) Simulated dynamic frequency change response and (b) a comparison of the output voltage THDs between the conventional and proposed AC/AC converter.
However, the scheme still encounters harmonics and subharmonics in the output voltage and output current, because the proposed technique can remove only the lower order harmonic content but has no effect on the higher order harmonic content. However, it is known to all that, in drive applications, the higher order harmonic content has very little effect on the motor. The lower order content has a high effect on the drive application, such as high speed ripples, vibrations, and unwanted heat generation. Therefore, the reduction of the lower order harmonic content is highly desirable, and it can be significantly minimized by the proposed topology. However, in order to reduce the overall THD, the higher order harmonic should also be reduced. For this purpose, the voltage level can be increased, or a line filter can be used.
The role of the AC/AC power converter in induction motor speed control is to vary the frequency of the supply which, in effect, changes the motor speed. The relationship between the speed and frequency of the induction motor can be written as follows:
where f is the supply frequency, p is the number of magnetic poles, and Ns is the speed of the machine. The proposed series-connected diode SCR-controlled AC/AC power converter drive operates on the variable frequency drive principle; when the frequency is changed, the speed is changed as well. Figure 20 depicts the dynamic speed change response of the single phase induction motor using the conventional and proposed AC/AC power converters. There is a significant speed ripple in the dynamic response of conventional converter drive. The power quality problems are responsible for this phenomena. The rated and variable frequency operations were also noted in Figure 20. In the rated frequency operating region, there is no difference between the speeds of the conventional and proposed AC/AC power converters.
Ns = 120f/p
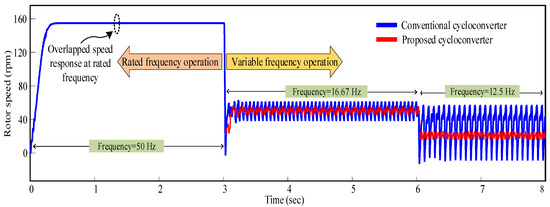
Figure 20.
Simulated dynamic speed change response of a single phase induction motor using the conventional and proposed AC/AC power converter.
However, while changing the operating region from the rated to the variable frequency region, the promising performance of the proposed AC/AC power converter can be observed. In the frequency transition region from 16.67 Hz to 12.5 Hz, the speed ripples of the conventional AC/AC power converter are significantly increased. However, at this transition, the speed ripples of the proposed AC/AC power converter are decreased greatly. The proposed converter can perform any order frequency conversion of fundamental 50 Hz input. Thus, the proposed AC/AC power converter offers a reduced speed ripple compared to a conventional AC/AC power converter due to its improved power quality, which is highly preferable for drive applications. The above-mentioned analysis regarding motor drive purpose proves the excellency of the proposed AC/AC power converter.
The proposed transformer-based harmonic reduction technique of the AC/AC converter is more suitable than PWM/dela modulation or filtering technique because of the following reasons.
- The PWM/delta modulation technique uses a complex gate driving technique with high frequency switching. However, every modulation technique needs a line filtering method for harmonic removal. As a result, the modulation technique is very complex, in relative terms.
- The line filtering technique needs a massive number of passive components. The passive components, i.e., the inductor, reduce the power factor, and the tuning of the filtering parameter is difficult at the dominant harmonics.
- The proposed transformer based harmonic reduction technique can easily remove the lower order harmonic content, as well as reducing the overall THD without using any line filtering technique. The lower order harmonic content removal is highly desirable for motor drive applications, in order to reduce the speed ripple. Most of the industry uses a transformer-based AC/AC converter topology because it provides galvanic isolation for the converter as well as the motor load. As such, the proposed transformer-based harmonic reduction technique proves its excellency as an AC/AC converter in variable frequency drive applications.
8. Conclusions
In order to improve the power quality of the existing AC/AC power converter, the proposed step down AC/AC power converter can be a good solution for different variable frequency applications. The output voltage THD was reduced by 12.90% for a 3:1 (m = 3) frequency conversion, and 17.24% for a 4:1 (m = 4) frequency conversion for the resistive load. The output voltage and current THD was reduced by 8.64% and 33.23%, respectively, for a 3:1 (m = 3) frequency conversion of the motor load. The performance comparison between the conventional and proposed AC/AC power converter was conducted on the basis of THD, the percentage of lower-order harmonic content in the output voltage, and the current for both the resistive load and motor load, as well as the condition of the rotor speed. From the results, it is evident that the lower-order harmonic contents of the proposed AC/AC power converter are very small compared to a conventional AC/AC power converter, and the speed ripple of the proposed AC/AC power converter-fed induction motor is very low, which is desirable for variable speed drive applications. Therefore, it can be concluded that the proposed AC/AC power converter is an attractive solution for the industrial community for different variable frequency applications.
Although the proposed topology reduces the lower-order harmonic content as well as the overall THD, it has some limitations, which may be mitigated in future research. One such limitation is the fact that increasing the frequency conversion order also increases the number of switches. For example, a 15:1 or (m = 15) order frequency conversion needs 16 SCR switches.
Author Contributions
Idea and conceptualization, M.S.U., S.P.B. and M.R.I.; design and simulation, M.S.U., M.S.A. and M.A.P.M.; prototyping, M.S.U., S.P.B. and M.R.I.; writing and drawing, M.S.U., S.P.B., M.S.A. and M.A.P.M.; revision and correction, M.R.I. and A.Z.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| SAG | Semi-autogenous grinding |
| THD | Total harmonic distortion |
| PDM | Pulse density modulation |
| VFD | Variable frequency drive |
| PWM | Pulse width modulation |
| AM | Amplitude modulation. |
References
- Surapaneni, R.K.; Yelaverthi, D.B.; Rathore, A.K. Cycloconverter-based double-ended microinverter topologies for solar photovoltaic ac module. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 1354–1361. [Google Scholar] [CrossRef]
- Xu, D.; Zhong, S.; Xu, J. Bipolar Phase Shift Modulation Single-Stage Audio Amplifier Employing a Full Bridge Active Clamp for High Efficiency Low Distortion. IEEE Trans. Ind. Electron. 2020. [Google Scholar] [CrossRef]
- Branko, L.; Branko, B. Power Electronics: Converters and Regulators; Springer: New York, NY, USA, 2015. [Google Scholar]
- Rashid, M.H. Power Electronics: Circuits, Devices, and Applications; Prentice Hall: Upper Saddle River, NJ, USA, 1993. [Google Scholar]
- Jacovides, L.J.; Matouka, M.F.; Shimer, D.W. A cycloconverter-synchronous motor drive for traction applications. IEEE Trans. Ind. Electron. 1981, IA-17, 407–418. [Google Scholar] [CrossRef]
- Wu, B.; Pontt, J.; Rodríguez, J.; Bernet, S.; Kouro, S. Current-source converter and cycloconverter topologies for industrial medium-voltage drives. IEEE Trans. Ind. Electron. 2008, 55, 2786–2797. [Google Scholar]
- Palavicino, P.C.; Valenzuela, M.A. Modeling and evaluation of cycloconverter-fed two-stator-winding SAG mill drive—Part I: Modeling options. IEEE Trans. Ind. Appl. 2015, 51, 2574–2581. [Google Scholar]
- Palavicino, P.C.; Valenzuela, M.A. Modeling and evaluation of cycloconverter-fed two-stator-winding SAG mill drive—Part II: Starting evaluation. IEEE Trans. Ind. Appl. 2015, 51, 2582–2589. [Google Scholar] [CrossRef]
- Greer, S.A. Selection criteria for SAG mill drive systems. IEEE Trans. Ind. Appl. 1990, 26, 901–908. [Google Scholar] [CrossRef]
- Rodríguez, J.R.; Pontt, J.; Newman, P.; Musalem, R.; Delpino, H.A.M.; Moran, L.; Alzamora, G. Technical evaluation and practical experience of high-power grinding mill drives in mining applications. IEEE Trans. Ind. Appl. 2005, 41, 866–874. [Google Scholar] [CrossRef]
- Pontt, J.; Rodriguez, J.; Rebolledo, J.; Martin, L.S.; Cid, E.; Figueroa, G. High-power LCI grinding mill drive under faulty conditions. In Proceedings of the 2005 Fourtieth IAS Annual Meeting. Conference Record of the 2005 Industry Applications Conference, Kowloon, Hong Kong, China, 2–6 October 2005; pp. 670–673. [Google Scholar]
- Kant, P.; Singh, B.; Chandra, A.; Al-haddad, K. Twenty pulse AC-DC converter fed 3-level inverter based vector controlled induction motor drive. In Proceedings of the 43rd Annual Conference IEEE Industry Applications Society Annual Meeting, Beijing, China, 29 October–1 November 2017; pp. 2225–2230. [Google Scholar]
- Singh, B.; Kant, P. A 54-pulse AC-DC converter fed 15-level inverter based vector controlled induction motor drive. In Proceedings of the 2017 IEEE Industry Applications Society Annual Meeting, Cincinnati, OH, USA, 1–5 October 2017; pp. 1–7. [Google Scholar]
- Liu, Y.; Heydt, G.T.; Chu, R.F. The power quality impact of cycloconverter control strategies. IEEE Trans. Power Deliv. 2005, 20, 1711–1718. [Google Scholar] [CrossRef]
- Slonim, M.A.; Biringer, P.; Slonim, M.A.; Biringer, P.P. Harmonics of Cycloconverter Voltage Waveform (New Method of Analysis). IEEE Trans. Ind. Electron. Control Instrum. 1980, IECI-27, 53–56. [Google Scholar] [CrossRef]
- Taufik, T.; Adamson, J.; Prabuwono, A.S. Pulse density modulated soft-switching single-phase cycloconverter. In Proceedings of the 2011 IEEE Applied Power Electronics Colloquium (IAPEC), Johor Bahru, Malaysia, 18–19 April 2011; pp. 189–194. [Google Scholar]
- Agarwal, V.; Agarwal, A. FPGA based delta modulated cyclo-converter. In Proceedings of the 2011 5th International Power Engineering and Optimization Conference, Shah Alam, Selangor, Malaysia, 6–7 June 2011; pp. 301–305. [Google Scholar]
- Babaei, E.; Heris, A.A. PWM-based control strategy for forced commutated cycloconverters. In Proceedings of the 2009 IEEE Symposium on Industrial Electronics & Applications, Kuala Lumpur, Kuala Lumpur, Malaysia, 4–6 October 2009; pp. 669–674. [Google Scholar]
- Agarwal, A.; Agarwal, V. Design of Delta-Modulated Generalized Frequency Converter. IEEE Trans. Ind. Electron. 2010, 57, 3724–3729. [Google Scholar] [CrossRef]
- Idris, Z.; Hamzah, M.K.; Hamzah, N.R. Modelling & Simulation of a new Single-phase to Single-phase Cycloconverter based on Single-phase Matrix Converter Topology with Sinusoidal Pulse Width Modulation Using MATLAB/Simulink. In Proceedings of the 2005 International Conference on Power Electronics and Drives Systems, Kuala Lumpur, Malaysia, 28 November–1 December 2005; pp. 1557–1562. [Google Scholar]
- Yan, Z.; Xu, S.; Han, X.; Sun, X.; Li, J. A novel de-re-couple modulation strategy for full-wave mode single-phase high-frequency link inverter. In Proceedings of the 2014 IEEE Transportation Electrification Conference & Expo Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 31 August–3 September 2014; pp. 1–4. [Google Scholar]
- Meier, S.; Norrga, S.; Nee, H. Modulation strategies for a mutually commutated converter system in wind farms. In Proceedings of the 2007 European Conference on Power Electronics and Applications, Aalborg, Denmark, 2–5 September 2007; pp. 1–10. [Google Scholar]
- Nayanasiri, D.R.; Vilathgamuwa, D.M.; Maskell, D.L. Half-Wave Cycloconverter-Based Photovoltaic Microinverter Topology With Phase-Shift Power Modulation. IEEE Trans. Ind. Appl. 2013, 28, 2700–2710. [Google Scholar] [CrossRef]
- Basic, D.; Ramsden, V.S.; Muttik, P.K. Selective compensation of cycloconverter harmonics and interharmonics by using a hybrid power filter system. In Proceedings of the 2000 IEEE 31st Annual Power Electronics Specialists Conference, Galway, Ireland, 23–23 June 2000; pp. 1137–1142. [Google Scholar]
- Olivares, C.; Astudillo, P.; Moran, L.; Dixon, J. Interaction between Passive Filter and High Power Cycloconverter Drive. In Proceedings of the 2009 IEEE Industry Applications Society Annual Meeting, Houston, TX, USA, 4–8 October 2009; pp. 1–5. [Google Scholar]
- Ashraf, N.; Hanif, A.; Farooq, U.; Asad, M.U.; Rafiq, F. Half cycle pairs method for harmonic analysis of cycloconverter voltage waveform. In Proceedings of the 2013 International Conference on Open Source Systems and Technologies, Lahore, Pakistan, 16–18 December 2013; pp. 97–102. [Google Scholar]
- Bessadet, I.; Tedjini, H. The Performances of Hybrid Filter in Elimination of AC-AC Converters Harmonics Pollution. In Proceedings of the 2018 6th International Renewable and Sustainable Energy Conference (IRSEC), Rabat, Morocco, 5–8 December 2018; pp. 1–6. [Google Scholar]
- Frangopol, G.; Dache, C.R. A Solution for Reducing Harmonic Regime and Reactive Power Absorbed by a Cycloconverter. In Proceedings of the 2019 6th International Symposium on Electrical and Electronics Engineering (ISEEE), Galati, Romania, 18–20 October 2019; pp. 1–6. [Google Scholar]
- Kornilov, A.; Reznikov, S.B. Hybrid Direct Frequency Cycloconverter with Power Factor Correction for Use in Single and Multi-Phase Electric Power Systems. In Proceedings of the 2019 IEEE International Symposium on Electromagnetic Compatibility, Signal and Power Integrity (EMC+SIPI), New Orleans, LA, USA, 22–26 July 2019; pp. 13–17. [Google Scholar]
- Antunes, H.M.A.; Pires, I.A.; Silva, S.M. Evaluation of Series and Parallel Hybrid Filters Applied to Hot Strip Mills with Cycloconverters. IEEE Trans. Ind. Appl. 2019, 55, 6643–6651. [Google Scholar] [CrossRef]
- Thompkins, T.M.; Kim, D.; Stone, P.; Shin, Y. Rolling Mill Cycloconverter Condition Assessment by Harmonic Current via Time–Frequency Signature. IEEE Trans. Ind. Inform. 2018, 14, 4376–4384. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).