Abstract
Aiming at the stability of a medium-voltage DC network based on a modular multilevel converter (MMC), this paper proposes an admittance stability criterion considering the influence of current-limiting inductors at the medium voltage side, which prevents the complex products and matrix calculations of traditional criteria. The DC admittance model DC transformers (DCTs) under different working modes are then established based on Thevenin/Norton equivalent circuit methods to analyze the stability of the DC system based on the proposed admittance stability criterion, which proves that the voltage resonance problem at the medium voltage side can be improved by adding active damping control strategies on DCTs also proves the effectiveness of the proposed stability criterion. The time-domain simulation and the hardware-in-loop simulation are then built in PLECS and RT Box to further verify the correctness of the system stability analysis and the effectiveness of the proposed admittance criterion, which provides a theoretical basis and technical reserve for the stable operation of the DC distribution power system.
1. Introduction
With a high proportion of renewable energy and new DC loads interfaced with the power grid, more and more sources and loads in the new power system show DC characteristics, which can provide flexible access to the distributed power and DC loads and improve the operation of the system [1,2]. The high-voltage DC (HVDC) power grid [3] and low-voltage DC (LVDC) microgrid [4] have been gradually promoted and applied, and at present, scholars are making developments in the field of medium voltage DC (MVDC) power distribution systems [5,6,7].
However, the converters for the MVDC distribution power system (DPS) are mostly customized by different suppliers, which makes the system have the characteristics of low damping, weak inertia, and complex structure. Therefore, the potential stability problem is one of the major challenges for the development of an MVDC DPS, and an effective and simple small signal stability criterion is desperately needed.
Firstly, small signal stability criteria are mainly focused on the stability of two cascaded converters [8], and some scholars have successively proposed impedance criteria with different stability regions, such as the Gain Margin Phase Margin (GMPM) criterion [9], the Opposing Argument (OA) criterion [10], the Energy Source Analysis Consortium (ESAC) criterion [11], etc. However, these criteria divided converters into load converters and source converters [12]. The admittance criterion for current source converters and the impedance criterion for voltage source converters are not equivalent and cannot be directly applied to the analysis of multiple converters connected to the common bus. On this basis, Sun [13] proposed a general criterion for both voltage-source and current-source converters for grid-connected converters and unified the admittance and impedance criteria. The criteria above first adopted the Nyquist criterion for impedance stability but only focused on the cascaded converters system; these criteria have clear physical meaning and simple methods but are not applicable to the DC system with multiple converters in parallel.
Zhang [14] then divided the converter into bus voltage-controlled converters (BVCCs) or bus current-controlled converters (BCCCs) and obtained the equivalent impedance ratio of the DC system through the loop analysis. The system stability could then be evaluated through the Nyquist criterion, which realized the stability analysis of multiple converters connected to the common DC bus. Pan et al. [15,16] further extended the BVCC and BCCC concepts to the multi-voltage DC system and carried out loop analysis to obtain the overall stability impedance ratio criterion of the system. According to Zhang et al. [14,15,16], the converter is regarded as directly connected to the DC bus. But for the MVDC DPS, both the output sides of the voltage source converter (VSC) and the DC transformer (DCT) are equipped with a current-limiting inductor due to the low damping characteristics of the system [17,18], and the inductor impedance and line impedance have a certain impact on the loop analysis of criteria based on the concepts of BVCC and BCCC. Therefore, this type of criteria has great scalability and simplicity but ignores the influence of current-limiting inductors and line impedance and is not applicable to the MVDC DPS.
Therefore, Li [19] developed a stability analysis for the multi-terminal DC power grid composed of four modular multilevel converters (MMCs). The voltage stability of each port is analyzed respectively based on the method of node reduction. This method has clear ideas and high accuracy, but it is more complex for a system with more nodes. He [20] puts forward the node admittance criterion method to evaluate the system stability by calculating the node determinant, but it is difficult to obtain the determinant of the admittance matrix when the impedance expression is complex.
Compared with the criteria above, the proposed admittance criterion takes full consideration of line impedance and current-limiting inductors. This criterion has good scalability and clear physical meaning. The stability can be evaluated by the equivalent admittance ratio through this proposed criterion so the evaluation process is simpler, which prevents the complex product and matrix calculation and is convenient and suitable for the stability evaluation of the MVDC DPS.
In this paper, an admittance stability criterion of the DPS considering the influence of current-limiting inductors is proposed. Then, the DCT admittance models under different working modes are established, which shows the potential instability risk of the MVDC DPS through the proposed criterion. Afterwards, active damping strategies are proposed to improve the phase margin and system stability. Finally, the simulation model of the corresponding DC system is built in PLECS, which proves the accuracy of the stability analysis and the effectiveness of the proposed criterion, and RT Box hardware-in-loop simulation is also used to further verify the correctness of the PLECS simulation.
2. Structure of MVDC DPS
The grid structure of the MVDC DPS is shown in Figure 1. The MVDC voltage is ±10 kV. Two MMCs are used in this system as the interface with the AC side to provide reliable power supply, and several photovoltaic DCTs (PVDCTs) are interfaced to provide renewable power for the DC system. Other DCTs interfaced in this system include DC charging piles and MVDC to LVDC microgrid DCTs, and they can be treated as the load-type DCT (LTDCT) in this system. The LVDC side of DCT is 750 V.
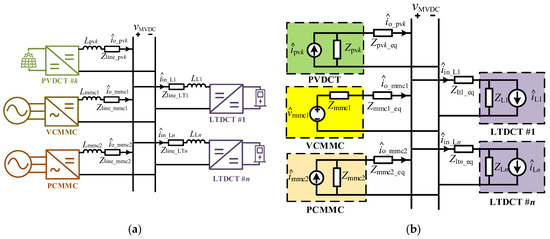
Figure 1.
Structure of the MVDC DPS. (a) Topology; (b) Small-signal impedance network.
Among the converters, one MMC adopts DC voltage control and the other MMC adopts power control. The PVDCTs work under the (Maximum Power Point Tracking) MPPT mode, and the LTDCTs work under the DC voltage control mode to control the LVDC side voltage. In Figure 1, Lmmc1 is the current-limiting inductor at the output side of the voltage-controlled MMC (VCMMC). Lmmc2 is the current-limiting inductor at the output side of the power-controlled MMC (PCMMC). Lpvk is the current-limiting inductor at the output side of the kth PVDCT. LLTm is the current-limiting inductor at the input side of the mth LTDCT. By analogy, Zline_mmc1, Zline_mmc1, Zline_pvk, Zline_ltm are the line impedances of the corresponding converters, and immc1, immc1, iPVk, iltm are the currents of the corresponding converters.
3. Admittance Criterion for MVDC DPS
According to the Thevenin/Norton equivalence theorem, the VCMMC controls its output voltage, so it can be equivalent to a voltage source series with the output impedance, which is in the form of Thevenin equivalent circuits. The other converter controls its input/output current, so they are equivalent to the current source resistance parallel with the input/output impedance. The small-signal impedance network of the MVDC DPS is shown in Figure 1b. The equivalent series impedance in Figure 1b is the sum of the inductor and line impedance, which is written as (1). Suppose that the system has n PVDCTs and m LTDCTs. The input impedance of PCMMC is Z1, the output impedance of the 1st to the nth PVDCT is Z2 to Zn+1, the input impedance of the 1st to the mth LTDCT is Zn+2 to Zm+n+1, the corresponding current source and the equivalent impedance are also numbered according to this law, and the current flowing into the converter is positive. So, the impedance and current of the converters can be expressed as below:
Then, the output current of the VCMMC can be expressed as (4). is the equivalent admittance of the kth converter considering the effect of current-limiting inductors and line impedance, and Zout_k is the impedance of the kth converter at the MVDC side.
Then, the latter part of o_mmc1 can be simplified as (5), and o_mmc1 can be rewritten as (6). At last, dc_mmc1 can be simplified as (7).
It can be known from Figure 1b that VCMMC controls its output voltage, so it is stably loaded by an ideal current source, which means that vmmc(s) and are stable. Other converters in this system control their output current, so they are stable loaded by an ideal voltage source, which means that ik(s) and Zk/(ZLk + Zk) are stable. Then, the stability of the system can be evaluated by applying the Nyquist criterion to Tm as shown below:
4. DC Impedance Modelling of System Converters
The topologies of the converters in this system are shown in Figure 2. The topology of MMC is shown in Figure 2a; vga, vgb, and vgc are the AC voltages of MMC, and vdc is the DC voltage of MMC. Each arm of MMC contains K series sub-modules (SMs) and an arm inductor. In Figure 2, iau is the current of the upper arm in phase a, and ial is the current of the lower arm in phase A, and so on.
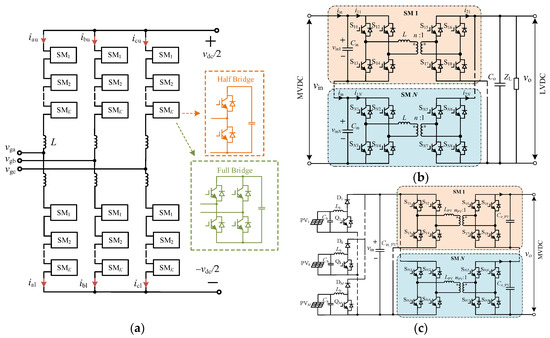
Figure 2.
Topology of converters. (a) MMC; (b) LTDCT; (c) PVDCT.
Due to the voltage restrictions of semiconductor devices, the input-series output-parallel (ISOP) topology is adopted for the DCT, and dual active bridge (DAB) topology is selected as the submodule of the DCT. For the LTDCT, vin is the input voltage of DCT, vo is the output voltage of DCT, iin is the input voltage of DCT, i1k is the input current of the kth SM, i2k is the output current of the kth SM, k = 1, 2,…, N, and N is the number of SMs. ZL is the load impedance, and Co is the output capacitance. Cin, L, n are the input capacitance, transfer inductor, and transformer ratio of the SM, respectively.
For the PVDCT, Cb is the capacitance of the boost converter, and Lb is the inductor. Cin_PV is the capacitance of the DCT at the LVDC side, and Co_PV is the capacitance of the DCT at the MVDC side. LPV is the inductor of each DAB SM, and nPV is the transform ratio of each DAB SM.
The corresponding control strategies are shown in Figure 3; the circulating current control is adopted at both VCMMC and PCMMC. For the LTDCT, it adopts a dual loop control to control its output current and voltage, and the voltage balance control of each module is also implemented. For the PVDCT, the MPPT control is used for boost converters to track the maximum power of PV arrays, and the input voltage control of DAB converters is used to control the voltage of the LVDC system.
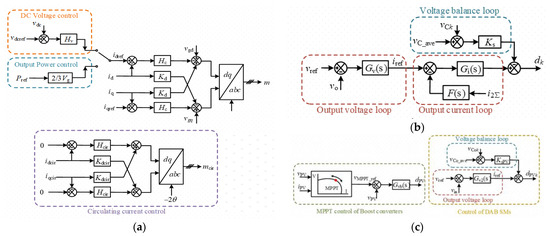
Figure 3.
Control strategies of converters (a) MMC; (b) LTDCT; (c) PVDCT.
Li [19] proves that the DC impedance of MMC can be built based on harmonic linearization. To simplify the modeling process, the effect of PLL is ignored, and the specific modeling process is not repeated in this paper.
Zhang et al. [21,22] proves that the voltage balancing control does not affect the impedance characteristics of the ISOP DCT. Thus, the small-signal model of DCTs can be equivalent to a single module shown as in Figure 4, and the corresponding control diagrams are shown as Figure 5. The parameter with a hat “^” means that it is a small-signal parameter.

Figure 4.
Equivalent small-signal models of DCTs. (a) LTDCT; (b) PVDCT.

Figure 5.
Equivalent control diagrams of DCTs. (a) LTDCT; (b) PVDCT.
In Figure 5, the coefficient terms are derived as (8). For LTDCT, fs is the switching frequency of the DAB modules, and D, Vin, and Vo are the phase shift, input voltage, and output voltage of the DAB SM under steady state, respectively. For PVDCT, fs2 is the switching frequency of the DAB SM, and D2, Vin_PV, and Vo_PV are the phase shift, input voltage, and output voltage of the DAB SM under steady state, respectively.
Through Mason’s gain formula, the DC admittance of the DCT can be obtained as (9) and (10).
The corresponding frequency-sweep simulation is established to verify the impedance model. The parameters of LTDCT#1 are listed in Table 1, and the parameters of PVDCT#1 are listed in Table 2. The simulation result in Figure 6 shows that the impedance model is of great accuracy with the simulation result. The LTDCT shows negative input impedance at low frequencies, while the PVDCT shows positive input impedance at low frequencies.

Table 1.
Simulation parameters of LTDCTs.

Table 2.
Simulation parameters of PVDCTs.
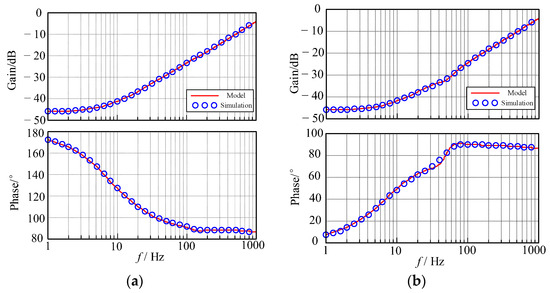
Figure 6.
Admittance of DCTs at MVDC side. (a) LTDCT; (b) PVDCT.
5. Stability Analysis of the DC System
The stability analysis for the DC system shown in Figure 1 is carried out. The parameters of the VCMMC and PCMMC are shown in Table 3. Suppose that the system includes 2 PVDCTs and 6 LTDCTs; the corresponding parameters are shown in Table 1 and Table 2, and the line impedance is listed in Table 4. DCTs all work under rated state, and the PCMMC outputs 3 MW active power. The admittance characteristics of the system are shown in Figure 7a; it can be seen that the resonance occurs at 130 Hz and 178 Hz in the bode plot of due to the impact of the DCT’s capacitors and its corresponding current limiting inductor. At the same time, the admittance characteristics of PVDCT #2 and LTDCT #4/#5/#6 transfer from inductance to capacitance at 130 Hz, and parallel resonance is generated with PVDCT#1 and LTDCT#1/#2/#3, which are still inductive. Thus, has resonance peaks at 130 Hz and 178 Hz and a resonance valley at 151 Hz. The resonance problem may lead to oscillation of the capacitor voltage of the DCT. Moreover, the resonance may lead to the oscillation of the grid voltage.

Table 3.
Simulation parameters of MMC.

Table 4.
Line impedance.
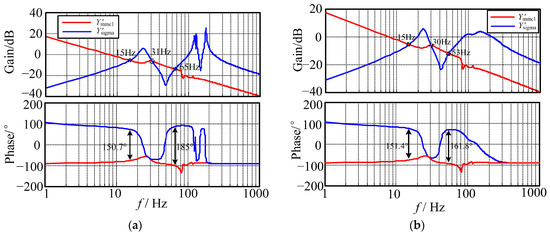
Figure 7.
Stability analysis bode plots of the system under different conditions. (a) Without the active damping loop. (b) With the active damping loop.
As shown in Figure 7a, overlaps with at 15 Hz, 31 Hz, and 65 Hz. The phase difference at 15 Hz is 150.7°, and the phase difference at 31 Hz is 3.4°, which all meet the stability requirements. Meanwhile, the phase difference at 65 Hz is 185°, which means that the phase margin is −5°, and the system is unstable. It can be seen that at 65 Hz, shows capacitance, while shows negative resistance and inductance. The lack of damping leads to system instability.
To solve the instability problem, the LC resonance at the medium voltage side of the DCT can be weakened by adding active damping, which can effectively enhance the stability at the input side of the DCT.
5.1. Active Damping Control Strategies for DCTs
It can be known from the previous analysis that the resonant peak and valley of are mainly caused by the influence of the capacitor and current-limiting inductor at the medium voltage side of DCTs. Therefore, active damping control strategies can be implemented to increase the equivalent resistance at the resonant frequency to improve the system stability. The active damping loops are implemented in Figure 8:

Figure 8.
Active damping control strategies of DCTs. (a) LTDCT; (b) PVDCT.
With the active damping loops above, the admittance of the LTDCT and PVDCT are reshaped as (11) and (12). Comparing (9) with (11) and (10) with (12), it can be known that the active damping control is equivalent to parallel virtual impedance at the medium voltage side of DCTs.
Let Gsh1(s), Gsh2(s) satisfy the relationship in (13) and (14) respectively, where BFl(s), BFPV(s) are the band-pass filters (BFs) for LT DCTs and PV DCTs. The center frequency of the filter is its corresponding DCT’s LC resonant frequency. The expression of the BF is written as (15); Q is the quality factor, which is 1 in this article, and fp is the center frequency of the filter. In (13), Rvd is the virtual resistance of the LTDCT. In (14), RvPV is the virtual resistance of the PVDCT.
According to the system parameters in Table 1 and Table 2, set Rvd and RvPV as 25 Ω. For LTDCT#1/#2/#3 and PVDCT#1, the central frequency for their BFs is 130 Hz. For LTDCT#4/#5/#6 and PVDCT#2, the central frequency for their BFs is 178 Hz. With the active damping loop, the bode plot of system admittance is shown in Figure 7b. The admittance overlapping frequencies are 15 Hz, 30 Hz, and 53 Hz. The phase difference is 151.4° at 11 Hz and 4.5° at 30 Hz, which all meet the stability requirements. At 53 Hz, the phase difference is decreased to 161.8°, which means that the phase margin increases to 18.2° and the system stability is effectively improved.
5.2. PLECS Simulation Verification
To verify the stability analysis above, the corresponding system simulation is built in PLECS. The system adopts the parameters in Table 1, Table 2, Table 3 and Table 4. The system reaches the rated operating point before 2 s. At 2 s, the active damping control methods are cancelled. Then, the active damping control loops are implemented at 3 s. The voltage waveform of the DC system is shown as Figure 9a.
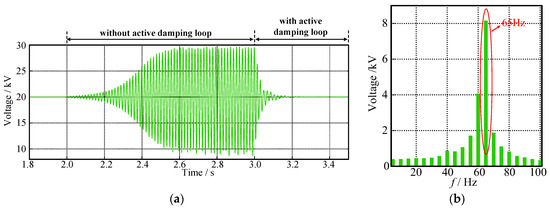
Figure 9.
Voltage waveforms of the DC system. (a) With or without the active damping loop; (b) Frequency spectrum of the oscillation.
In Figure 7a, the impedance amplitude of and intersects at 65 Hz without the active damping loop, the phase angle difference is 185°, and the phase margin is −5°, which means that the system is unstable. The corresponding DC voltage waveform in Figure 9a is 2–3 s, and the DC voltage fluctuates up to 10 kV. The corresponding Fourier analysis spectrum is shown in Figure 9b. It shows that the oscillation frequency is 65 Hz, indicating that the instability phenomenon is consistent with the theoretical analysis. With the active damping loop implemented, Figure 7b shows that the impedance amplitude of and intersects at 53 Hz with the active damping loop implemented. The phase difference is 161.8°, and the phase margin increases to 18.2°. The system can operate stably, and the corresponding waveform shown in Figure 9a is after 3 s. The bus voltage is maintained at 20 kV, which is consistent with the theoretical analysis in Figure 7b.
To verify the voltage resonance results from the current-limiting inductors, the corresponding system simulations were repeated while both inductors of the PCMMC and VCMMC at the medium voltage side were removed. As shown in Figure 10, the system remains stable, and the corresponding DC voltage fluctuates slightly and quickly stabilizes to 20 kV at 2 s and 3 s when the loop control is withdrawn or added.
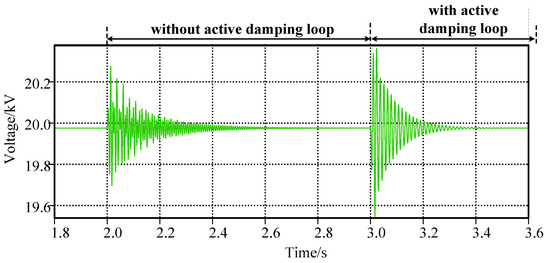
Figure 10.
Voltage waveforms of the DC system without current-limiting inductors.
In Figure 6, the LTDCT shows negative input impedance at low frequencies, while the PVDCT shows positive input impedance at low frequencies. Therefore, the PVDCT can provide damping for the system and be conducive to system stability, and the LTDCT has the opposite effect. The corresponding system simulation verifies the characteristics through setting differently rated power ratios of the LTDCT and PVDCT. As shown in Figure 11, a disturbance is added at 2 s and withdrawn at 2.5 s, and the corresponding voltage can stabilize to 20 kV in both conditions. However, the voltage fluctuation in the high ratio condition (LTDCT:PVDCT = 1:2) is less than 0.1 kV and much smaller than the low ratio condition (LTDCT:PVDCT = 1:5), which is over 4.0 kV at 2.5 s. The result verifies the analysis above, and it is recommended to moderately increase the rated power of the LTDCT in the DC system.
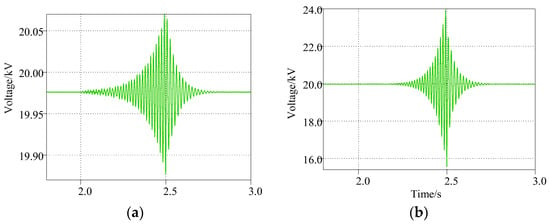
Figure 11.
Voltage waveforms of the DC system with differently rated power ratios of LTDCT and PVDCT. (a) LTDCT:PVDCT = 1:2; (b) LTDCT:PVDCT = 1:5.
5.3. RT Box Hardware-in-Loop Simulation Verification
Hardware-in-loop simulation is highly recommended to further verify the correctness of the theoretical analysis and simulation results, and the RT Box semi-physical simulator of PLECS is designed for power electronics applications with rich digital and analog interfaces. It can effectively simulate the actual performance of converters while avoiding device damage caused by real experiments of the 20 kV system. As shown in Figure 12a, connecting two RT Boxes back-to-back allows for complete system testing; one simulates the system, and the other simulates the controller.
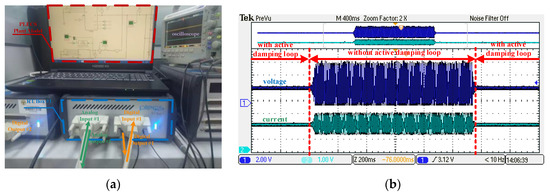
Figure 12.
RT Box hardware-in-loop simulation. (a) Voltage waveforms of the oscilloscope; (b) Back-to-back experiment platform.
6. Conclusions
- A new admittance stability criterion is proposed in this paper. The overall stability of the system can be determined only by the equivalent admittance ratio Tm in Equation (3). This criterion has clear physical meaning and concise evaluation expression. In practical engineering, the corresponding impedance sum can be obtained with frequency-sweeping impedance measurement, and the impedance stability can be determined.
- The output impedance of the PVDCT shows positive resistance characteristics in the bandwidth range, which can provide damping for the system and be conducive to system stability, while the input impedance of the LTDCT shows negative resistance characteristics in the bandwidth range, which is not conducive to system stability.
- The current-limiting inductors are equipped in DCTs and have resonance with the capacitors of DCTs. Due to the negative input impedance characteristic of the LTDCT, resonance between the inductor and capacitor easily causes the instability of the system. The active damping control methods adopted in this paper can provide virtual resistance for DCTs to suppress resonance. The active damping methods can be generally configured in DCTs connected with the DC DPS to improve the stability of the DC system.
Author Contributions
Conceptualization, J.Y. and J.W.; methodology, J.W.; software, S.L.; writing—review and editing, X.J.; validation, X.X.; resources, Z.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science and Technology Project of State Grid Corporation of China (5400-202255160A-1-1-ZN).
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rodriguez, E.; Vasquez, J.C.; Guerrero, J.M. Intelligent DC Homes in Future Sustainable Energy Systems: When efficiency and intelligence work together. IEEE Consum. Electron. Mag. 2016, 5, 74–80. [Google Scholar] [CrossRef]
- Dragičević, T.; Lu, X.; Vasquez, J.C.; Guerrero, J. DC Microgrids—Part II: A Review of Power Architectures, Applications, and Standardization Issues. IEEE Trans. Power Electron. 2016, 31, 3528–3549. [Google Scholar] [CrossRef]
- Rao, H. Architecture of Nan’ao multi-terminal VSC-HVDC system and its multi-functional control. CSEE J. Power Energy Syst. 2015, 1, 9–18. [Google Scholar] [CrossRef]
- Gabderakhmanova, T.; Engelhardt, J.; Zepter, J.M.; Sørensen, T.M.; Boesgaard, K.; Ipsen, H.H.; Marinelli, M. Demonstrations of DC Microgrid and Virtual Power Plant Technologies on the Danish Island of Bornholm. In Proceedings of the 2020 55th International Universities Power Engineering Conference (UPEC), Torino, Italy, 1–4 September 2020. [Google Scholar]
- Stieneker, M.; Butz, J.; Rabiee, S.; Doncker, R.W.D. Medium-Voltage DC Research Grid Aachen. In Proceedings of the International ETG Congress 2015, Die Energiewende—Blueprints for the New Energy Age, Bonn, Germany, 17–18 September 2015. [Google Scholar]
- Li, W.; Yu, S.; Wei, T.; Li, Y.; Chen, J.; Liu, Y.; Xu, S. State of the Art of Researches and Applications of MVDC Distribution Systems in Power Grid. In Proceedings of the IECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019. [Google Scholar]
- Zheng, J.; Chen, J.; Liu, Y.; Qu, L.; Yu, Z.; Song, Q.; Yuan, Z.; Zhao, B.; Zeng, R. Urban Energy Internet Based on Flexible DC Distribution Network. South. Power Syst. Technol. 2021, 15, 25–32. [Google Scholar] [CrossRef]
- Middlebrook, R.D. Input-filter considerations in design and application of switching regulators. In Proceedings of the 1976 IEEE Industy Applications Society Annual Conference, Chicago, IL, USA, 11–14 October 1976. [Google Scholar]
- Wildrick, C.M.; Lee, F.C.; Cho, B.H.; Choi, B. A method of defining the load impedance specification for a stable distributed power system. IEEE Trans. Power Electron. 1995, 10, 280–285. [Google Scholar] [CrossRef]
- Feng, X.; Ye, Z.; Xing, K.; Lee, F.C.; Borojevic, D. Impedance specification and impedance improvement for dc distributed power system. In Proceedings of the 30th Annual IEEE Power Electronics Specialists Conference, Charleston, SC, USA, 1 July 1999. [Google Scholar]
- Sudhoff, S.D.; Glover, S.F.; Lamm, P.T.; Schmucker, D.H.; Delisle, D.E. Admittance space stability analysis of power electronic systems. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 965–973. [Google Scholar] [CrossRef]
- Fang, J.; Shuai, Z.; Li, Y.; Wang, Z.; Wu, X.; Shen, X.; Shen, Z.J. Stability investigation and improvement for DC cascade systems with simplified impedance-based stability criterion. CSEE J. Power Energy Syst. 2023, 1–9. Available online: https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=9770518 (accessed on 16 April 2023).
- Sun, J. Impedance-Based Stability Criterion for Grid-Connected Inverters. IEEE Trans. Power Electron. 2011, 26, 3075–3078. [Google Scholar] [CrossRef]
- Zhang, X.; Ruan, X.; Chi, K.T. Impedance-based local stability criterion for DC distributed power systems. IEEE Trans. Circuits Syst. I Regul. Pap. 2015, 62, 916–925. [Google Scholar] [CrossRef]
- Pan, P.; Chen, W.; Shu, L.; Mu, h.; Zhang, K.; Zhu, M.; Deng, F. An Impedance-Based Stability Assessment Methodology for DC Distribution Power System With Multivoltage Levels. IEEE Trans. Power Electron. 2020, 35, 4033–4047. [Google Scholar] [CrossRef]
- Mu, H.; Zhang, Y.; Tong, X.; Chen, W.; He, B.; Shu, L.; Ruan, X.; Zhang, X.; Gao, F.; Cao, W.; et al. Impedance-Based Stability Analysis Methods for DC Distribution Power System With Multivoltage Levels. IEEE Trans. Power Electron. 2021, 36, 9193–9208. [Google Scholar] [CrossRef]
- Li, B.; He, J.; Li, Y.; Li, B.; Wen, W. High-speed directional pilot protection for MVDC distribution systems. Int. J. Electr. Power Energy Syst. 2020, 121, 106141. [Google Scholar] [CrossRef]
- Liu, R.; Yang, J.; Jia, Y.; Liu, Y.; Yuan, Y.; Xiao, X. Engineering Applications of DC Transformer in Medium-voltage DC Distribution Network. Autom. Electr. Power Syst. 2019, 43, 131–140. [Google Scholar] [CrossRef]
- Li, Z.; Wang, Z.; Wang, Y.; Yin, T.; Mei, N.; Yue, B.; Lei, W. Accurate Impedance Modeling and Control Strategy for Improving the Stability of DC System in Multiterminal MMC-Based DC Grid. IEEE Trans. Power Electron. 2020, 35, 10026–10049. [Google Scholar] [CrossRef]
- He, B.; Chen, W.; Ruan, X.; Zhang, X.; Zou, Z.; Cao, W. A Generic Small-Signal Stability Criterion of DC Distribution Power System: Bus Node Impedance Criterion (BNIC). IEEE Trans. Power Electron. 2022, 37, 6116–6131. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, X.; Li, M.; Yu, F.; Yu, D. Input-series-output-parallel DC transformer impedance modeling and phase reshaping for rapid stabilization of MVDC distribution systems. Electronics 2022, 10, 3163. [Google Scholar] [CrossRef]
- Li, S.; Wang, J.; Li, X.; Xiao, X. Impedance Characteristics and Stability Analysis of Input-series Output-parallel Medium-voltage DC Transformer. High Volt. Eng. 2022, 48, 210–219. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).