Integrating Structural Causal Models with Enhanced LSTM for Predicting Single-Tree Carbon Sequestration

Abstract

Accurate estimation of carbon sequestration at the single-tree scale is essential for understanding forest carbon dynamics and supporting precision forestry under global carbon-neutral goals. Traditional allometric models often neglect environmental variability, while data-driven machine learning approaches suffer from limited interpretability. To bridge this gap, we developed a hybrid prediction framework that integrates a Structural Causal Model (SCM) with an Enhanced Long Short-Term Memory (LSTM) network. Using 47-year observation data (1975–2022) of Mongolian oak (*Quercus mongolica* Fisch. ex Ledeb.) from the Laoyeling Ecological Station, the SCM was applied to infer causal relationships among growth and environmental factors, while the Enhanced-LSTM combined multiscale convolution and self-attention modules to capture nonlinear temporal dependencies. Results showed that the proposed SCM-Enhanced-LSTM achieved the highest predictive performance (R² = 0.944, RMSE = 0.079 kg, MAE = 0.064 kg), outperforming Bi-LSTM and XGBoost models by over 20% in accuracy and maintaining robustness under noise perturbations. Causal analysis identified soil moisture and stem diameter as the dominant drivers of carbon increment. This study provides a transparent, interpretable, and high-precision framework for single-tree carbon sequestration prediction, offering methodological support for fine-scale forest carbon accounting and sustainable management strategies.

1. Introduction

Under the increasingly severe challenges of global climate change, achieving the temperature control targets set by the Paris Agreement has become a shared mission of the international community [1]. In response, many countries have proposed carbon neutrality strategies, such as China’s “dual carbon” goals. This calls for a deeper understanding and more precise regulation of the carbon cycle within ecosystems [2,3].

As the largest carbon reservoir in terrestrial ecosystems, forests play a crucial regulatory role in maintaining the global carbon balance. As demonstrated by Pan et al. (2011), global forests act as a massive and persistent carbon sink [4]. Therefore, accurately quantifying and predicting the carbon sequestration capacity of forest ecosystems is not only essential for evaluating their ecosystem service functions, but also serves as the scientific basis for formulating effective climate change mitigation strategies and sustainable forest management plans [5,6].

However, significant heterogeneity exists in the estimation of forest carbon stocks across spatial scales. Traditional studies have mainly focused on regional or stand-level analyses, for example, combining remote sensing data with field inventories to conduct large-scale assessments [7]. Although such macro approaches provide valuable information for national-level carbon accounting, Feng et al. (2025) [8] revealed that large-scale forest carbon estimates continue to mask complex intra-stand dynamics and local heterogeneity due to persistent scaling challenges, resulting in systematic upscaling errors that remain unresolved despite technological advances. With the rise of the precision forestry concept, research focus has gradually shifted to the single-tree level [9,10]. Individual trees are not only the fundamental units of forest stands but also important contributors to stand-level carbon dynamics through their growth processes [11]. The European single-tree database constructed by Zianis, D. et al. (2005) further demonstrates that individual-level data are essential for improving the accuracy of forest growth models [12]. Thus, starting from the single-tree perspective can substantially reduce uncertainties caused by scaling-up processes and capture the fine-scale effects of microenvironmental conditions and inter-tree competition on carbon sequestration, thereby providing data support for advanced forest management measures such as target-tree cultivation and structural management [13,14].

Currently, methods for predicting the biomass and carbon sequestration of individual trees can be broadly categorized into two groups. The first comprises traditional allometric models. Since the pioneering study of Kittredge (1944), allometric equations have become the foundation for biomass estimation [11]. However, as Chave et al. (2014) [5] highlighted in their development of a pan-tropical biomass model, these models—although widely applied—face increasing limitations. They mostly rely on a few morphological parameters such as diameter at breast height (DBH) and tree height, while ignoring the dynamic influences of environmental factors like climate and site conditions. Consequently, their transferability across regions is limited and prediction errors remain substantial [15,16]. The second group includes recently developed machine learning approaches. Algorithms such as Random Forest (Breiman, 2001) [13] and XGBoost (Chen and Guestrin, 2016) [14] have been widely used for biomass estimation due to their excellent capability in fitting nonlinear relationships, achieving higher accuracy than traditional equations [17,18]. For example, Fassnacht et al. (2014) successfully estimated aboveground biomass by integrating Random Forest with multi-source remote sensing data [19]. Nevertheless, these models often suffer from the so-called “black box” problem, as their complex internal decision-making processes obscure the underlying ecological mechanisms [20]. As cautioned by Cade (2015) [15], prioritizing predictive accuracy over interpretability may hinder a deeper understanding of ecosystem processes.

To address these limitations, the present study aims to establish an interpretable and high-precision modeling framework for single-tree carbon sequestration prediction. Specifically, we propose integrating a Structural Causal Model (SCM) with an Enhanced Long Short-Term Memory (LSTM) network to capture both causal dependencies among environmental drivers and temporal dynamics of tree growth. This study is guided by two central hypotheses: (1) incorporating causal priors can enhance the ecological interpretability of deep learning models without sacrificing accuracy; and (2) combining multi-scale convolution and self-attention mechanisms can effectively capture short-term climatic fluctuations and long-term growth trends. Accordingly, the objectives of this study are: (i) to construct an SCM-guided Enhanced LSTM model for single-tree carbon increment prediction; (ii) to evaluate its performance against benchmark models such as GRU, Bi-LSTM, and XGBoost; and (iii) to identify key ecological factors influencing carbon accumulation in Q. mongolica forests.

To address the dual challenges of the absence of mechanism in traditional methods and the “black box” nature of modern approaches, this study introduces a novel framework for predicting single-tree carbon sequestration. It integrates Structural Causal Models (SCM) with an Enhanced Long Short-Term Memory (Enhanced LSTM) network.

To overcome the “black box” issue, we incorporate Judea Pearl’s causal inference theory (2009) [21], enabling the identification of causal pathways between environmental factors and tree carbon increment from observational data, rather than simply detecting correlations [22]. This enhances model interpretability by grounding predictions in verifiable ecological mechanisms [23]. Additionally, to capture the dynamic temporal patterns of tree growth more precisely, we enhance the traditional Long Short-Term Memory (LSTM) network [24] by integrating multi-scale convolutional modules and a Self-Attention mechanism [25]. This allows the model to focus on key time steps and environmental drivers that determine growth outcomes, improving the model’s ability to capture both short-term fluctuations and long-term trends in tree growth [26].

In this framework, the SCM–Enhanced LSTM approach operates as follows: Random Forest is first used to select key variables, and the PC algorithm identifies the causal structure (Directed Acyclic Graph, DAG) of carbon increment in Quercus mongolica [27]. These causal priors are integrated with deep temporal learning. On the temporal side, multi-scale convolutions and self-attention modules are embedded within the LSTM architecture to capture both short-term dependencies and long-term cross-year relationships. The bidirectional structure further enhances contextual awareness and response to extreme events [28].

Using long-term observational data (1982–2022) from the Laoyeling Ecological Station, we conducted comparative experiments against benchmark models, including XGBoost, LSTM, GRU, and Bi-LSTM, with comprehensive evaluation using R², RMSE, MAE, and MAPE metrics. The results show that the Enhanced LSTM model achieved an R² of 0.944, RMSE of 0.079, and MAE of 0.064 on the test set, with lower bias during peak–valley phases and disturbance periods. Additionally, its robustness under Gaussian noise further verifies its reliability and accuracy for single-tree carbon sink prediction [29,30].

2. Materials and Methods

2.1. Study Area Overview

The study site is located in Mao’er Mountain, Northeast Forestry University, Shangzhi City, Harbin, Heilongjiang Province, China (Figure 1a,b). The area is characterized by low hilly terrain, and the sampling plots are situated on north-facing slopes with an average inclination of approximately 45° [31].

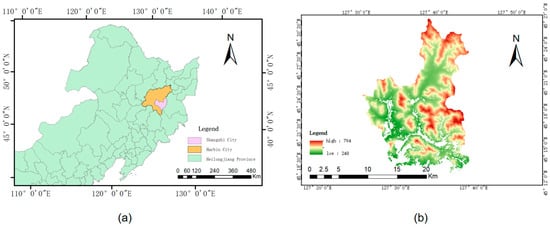
Figure 1. Geographical location of the study area. (a) The location of Mao’er Mountain in Heilongjiang Province. (b) Topographic elevation map of the Mao’er Mountain region.

The region has a temperate continental monsoon climate, with a mean annual temperature of about 2.8 °C and an average annual precipitation of 723 mm, showing a single-peak distribution. The annual evaporation reaches 884.4 mm (mainly occurring from July to August), and the mean annual wind speed is 1.5 m/s. The vegetation type within the plots is temperate deciduous broad-leaved mixed forest, dominated by Q. mongolica.

2.2. Data Collection

This study was conducted in a fixed plot established at the Mao’er Mountain Forest Farm of Northeast Forestry University. As part of a continuous ecological monitoring program, 264 Q. mongolica individuals within the plot were permanently tagged and have been systematically monitored since 1975. Monthly in situ measurements were conducted for all trees during the main growing season, whereas 20 representative trees (stratified by diameter class) were measured during the dormant period to verify growth stagnation and ensure data continuity. These measurements encompass parameters such as diameter at breast height (DBH), tree height, and crown dimensions.

The consistent monthly records obtained in this manner guarantee a high level of temporal resolution and data completeness from 1975 to 2022. For every tagged tree, all growth parameters, (including DBH, height, and stem volume, were continuously documented. DBH measurements were consistently conducted at a fixed height of 1.3 m above ground level, following standardized forestry procedures established at the beginning of the monitoring program. This measurement protocol has been strictly maintained by successive field teams to ensure methodological consistency throughout the long-term observation period. The quality of the data was verified annually through cross-referencing with the forest inventory database. To maintain temporal continuity, missing or inconsistent records (accounting for less than 2% of all observations) were rectified using linear interpolation or temporal averaging within the same growth phase.

The individuals exhibited an average age of approximately 60 years and a mean diameter at breast height (DBH) of 32 cm. To ensure the rigor and precision of the experiment, during the peak growing season in August 2022, 30 healthy and well-developed trees were selected from the plot for detailed measurements. Morphological parameters—including DBH, total tree height, height to crown base, and crown diameter—were precisely recorded (Table 1). These detailed measurements were conducted to verify the accuracy and consistency of the long-term monitoring records and to provide field-based reference values for tree structural parameters. The measured data were further used to define realistic parameter ranges and scaling factors for model input variables, ensuring that the modeling framework reflected actual tree growth characteristics. Subsequently, one tree whose parameters were closest to the overall mean values was felled and treated as the representative individual of Q. mongolica growth conditions for subsequent analyses.

Table 1. Morphological parameters of the standard tree.

Indicator	Unit	Mean Value
Tree age	a	62
Diameter at breast height (DBH)	cm	29.6
Tree height	m	18.1
Height to crown base	m	8.5
Crown width	m	5.22

For the selected standard Q. mongolica trees, stem analysis method was employed to measure their volume growth [32], with the specific procedures as follows: (1) Stem cutting and segmenting: The felled trees were divided into sections of 0.25 m from the base, with the tip section shorter than 0.25 m treated as an independent segment. Each segment length was measured and numbered; (2) Disc sampling: A 5 cm thick wood disc was cut at the midpoint of each section, numbered and brought back to the laboratory; (3) Tree ring measurement: Using a tree ring analyzer (LINTABTM6, Rinntech, Heidelberg, Germany, accuracy 0.01 mm), the ring widths in three mutually perpendicular directions on the disc were measured, and the average value was taken as the annual radial growth; (4) Volume calculation: The volume of each segment was calculated using the central cross-section differentiation method, with the formula as (1); (5) Total volume summation: The total stem volume was obtained by accumulating the volumes of each segment, and the historical volume growth sequence was inferred from the annual ring widths.

$$V={\displaystyle \frac{\pi }{4}}\left({\displaystyle \frac{d_0^2+d_n^2}{2}}\right)L$$

(1)

where $V$ is the stem volume, $d_0$ and $d_n$ are the diameters at the lower and upper cross-sections, respectively, and $L$ is the segment length.

After calculating the monthly volume using the above method, the volume increment was defined as the difference between the current month’s volume and the previous month’s volume, so as to present the changes in volume growth of Q. mongolica between adjacent months.

The data processing included: (1) Growth standardization: The annual volume obtained from the analysis was converted into monthly average growth, and continuous time series data were generated through spline interpolation; (2) Carbon storage conversion: The volume growth was converted into carbon increment using the wood density (0.63 g/cm³) and carbon content coefficient of 0.5 for Q. mongolica. In this study, carbon sequestration refers to the monthly rate of carbon accumulation in tree biomass, derived from stem volume increment and wood density. This definition highlights the dynamic aspect of carbon storage and ensures consistency with the temporal resolution of the dataset; (3) Outlier handling: Outliers caused by missing tree rings or measurement errors were replaced with the average value of adjacent years.

The methodology for model validation was as follows: (1) Benchmark data construction: The carbon increment sequence from 1975 to 2021 obtained by stem analysis was taken as the true value, and divided into training set and validation set at a ratio of 8:2; (2) Model evaluation indicators: The coefficient of determination (R²), root mean square error (RMSE) and mean absolute error (MAE) between the predicted and measured values were calculated, and the specific calculation formulas are detailed in Section 2.7 Evaluation Indicators.

Based on the above processing steps, the monthly stem volume was calculated, and the monthly volume increment was defined as the difference between the current month’s stem volume and that of the previous month. This approach was employed to characterize the variation in stem growth of Q. mongolica between consecutive months.

The monthly soil moisture data used in this study, covering the period from 1982 to 2020, were obtained from the Earth Resource Data Cloud Platform (www.gis5g.com, accessed on 21 June 2025). The data were provided in raster format (.tif) with a spatial resolution of 0.25°. Monthly mean temperature, precipitation, and sunshine duration were obtained from the local meteorological station.

The final dataset included a total of eight variables. Detailed descriptions of these variables are shown in Table 2.

Table 2. Descriptive statistics of variables.

Variable	Unit	Description
Volume increment	m3 month−1	Monthly increase in stem Monthly increase in diameter at breast height
DBH increment	cm month−1	Monthly mean air temperature
Mean air temperature	°C	Soil water content
Soil moisture	%	Monthly cumulative sunshine hours
Sunshine duration	h	Monthly cumulative precipitation
Precipitation	mm
Carbon increment	kg	Monthly increase in carbon storage

2.3. Feature Selection

To identify the most informative input variables for the subsequent deep learning models, this study employed the feature importance evaluation method based on the Random Forest (RF) ensemble algorithm [33]. This method quantifies each feature’s contribution using the Mean Decrease in Impurity (MDI), which represents the average reduction in node impurity when the feature is used for splitting across all decision trees. Specifically, during the RF training process, the importance of each input feature (e.g., diameter increment, soil moisture, monthly sunshine duration, etc.) was calculated as follows (2):

$$F{I}_i=(1/T){\sum }_{t=1}^T{\sum }_{j\in N_{i,t}}(n_j/N)\times \Delta Gin{i}_j$$

(2)

where $F{I}_i$ denotes the importance score of input feature $i$ (such as diameter increment or soil moisture);

$T$ is the total number of decision trees;

$E_{i,t}$ is the set of nodes in tree $t$ where feature iii is used for splitting;

$n_j$ is the number of samples in node $j$;

NNN is the total number of samples;

and $\Delta Gin{i}_j$ represents the reduction in Gini impurity at node $j$.

A contribution-based feature selection strategy was adopted, where only features with importance scores above the 30% threshold were retained to construct the input subset for the LSTM prediction model. This method effectively captures nonlinear relationships and feature interactions, mitigating redundancy and providing the deep learning model with an optimal feature combination.

2.4. Temporal Prediction Model Based on Enhanced LSTM

The Long Short-Term Memory (LSTM) network is a special type of recurrent neural network (RNN) architecture proposed by Hochreiter and Schmidhuber (1997) [17], which effectively overcomes the gradient vanishing problem encountered by traditional RNNs when processing long sequences. For time series data such as forest carbon increment, which exhibit long-term temporal dependencies, LSTM achieves selective memorization of historical information through cell states and gating mechanisms, as illustrated in Figure 2.

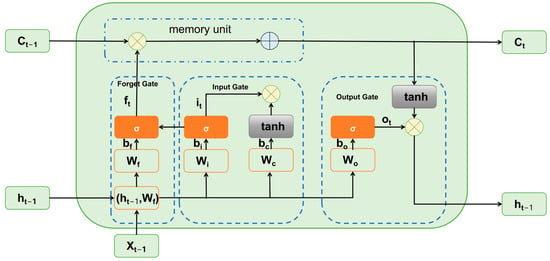
Figure 2. Internal architecture and information flow of the Long Short-Term Memory (LSTM) unit used to capture temporal dependencies in tree carbon increment modeling. (Dotted line boxes are functional modules: the “memory unit” manages cell state transmission, while the “Forget Gate”, “Input Gate”, and “Output Gate” regulate information flow; symbols: ⊗ = multiplication, ⊕ = addition, σ = sigmoid activation function, tanh = hyperbolic tangent activation function.).

The core of LSTM lies in the design of its cell state $C_t$, which is regulated by three gates—namely, the forget gate, input gate, and output gate. The forget gate determines how much historical information should be retained (e.g., long-term trends of DBH increment and accumulated soil moisture), and is defined as:

$$f_t=\sigma (W_f{x}_t+W_f{h}_{t-1}+b_f)$$

(3)

The input gate controls the storage of new information (e.g., current DBH increment, temperature fluctuations), expressed as:

$$i_t=\sigma (W_{\kappa }{x}_t+W_{\theta }{h}_{t-1}+b_t)$$

(4)

$${\bar{C}}_t=\tanh (W_{Cx}{x}_t+W_{Ch}{h}_{t-1}+b_C)$$

(5)

The output gate determines the current output (e.g., predicted carbon increment), expressed as:

$$o_i=\sigma (W_{ox}{x}_i+W_{oh}{h}_{i-1}+b_o)$$

(6)

The updating rules for the cell state and hidden state are given by:

$$C_t=f_t\circ C_{t-1}+i_t\circ {\tilde{C}}_t$$

(7)

$$h_i=o_i\odot \tanh (C_i)$$

(8)

where $\mathsf{\sigma }(\cdot )$ represents the sigmoid activation function, and $\odot$ denotes the Hadamard (element-wise) product. $\mathrm{W}(\cdot )$ and $\mathrm{b}(\cdot )$ represent the corresponding weight matrices and bias vectors associated with the input features (e.g., DBH increment, soil moisture, etc.).

Clarification on gate mechanism and enhancement design: It should be noted that the gate mechanisms (input, forget, and output gates) in the Enhanced LSTM are intrinsic components of the standard LSTM architecture and are not manually assigned. The interactions between input features and gate activations are automatically learned through parameter optimization during model training. The enhancement proposed in this study does not alter the mathematical LSTM equations; rather, it improves causal consistency and feature learning by combining (i) a Structural Causal Model (SCM) to provide causal guidance on directional dependencies among variables, (ii) a multiscale convolutional module to capture local temporal patterns, and (iii) a self-attention mechanism to dynamically reweight feature contributions. Through this design, the Enhanced LSTM can learn gate activations in a more ecologically interpretable manner while maintaining the original LSTM structure.

(1)

Convolutional Feature Extractor (Conv1D Extractor)

To capture the local short-term fluctuations in forest carbon increment—such as the effects of monthly climatic variations on the carbon sequestration of Q. mongolica—a one-dimensional convolutional neural network (1D-CNN) was introduced for feature extraction (corresponding to the “CNN module” in Figure 3). Let the input time series data be represented by the feature sequence $X\in {\mathbb{R}}^{T\times F}$, where $T$ denotes the temporal length and $F$ represents the feature dimension (including monthly DBH increment, mean air temperature, soil moisture, and sunshine duration, among others).

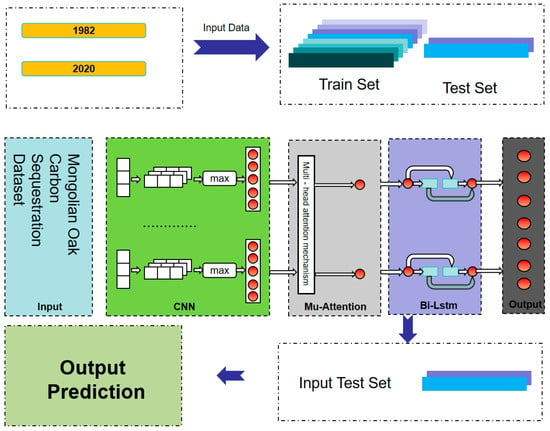
Figure 3. Framework of the enhanced LSTM model for forest carbon-increment prediction. (The model uses Mongolian Oak datasets from 1982 (training) and 2020 (testing). Input features are sequentially processed through CNN for local feature extraction, multi-head attention mechanism for capturing long-term dependencies, and Bi-LSTM for bidirectional temporal modeling. Red circles represent neurons, blue bars indicate feature channels, solid arrows denote forward data flow, and the final output yields predicted carbon increment.).

The local temporal patterns were extracted through a 1D convolution operation as follows:

$${\mathrm{H}}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}}^{\left(\mathrm{l}\right)}=\mathrm{R}\mathrm{e}\mathrm{L}\mathrm{U}({\mathrm{W}}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}}^{\left(\mathrm{l}\right)}\times \mathrm{X}+{\mathrm{b}}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}}^{\left(\mathrm{l}\right)})$$

(9)

where ${\mathrm{W}}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}}^{\left(\mathrm{l}\right)}\in {\mathbb{R}}^{3\times \mathrm{D}\times 64}$ (the convolution kernel size is 3, and the output channel number is 64).

$${\mathrm{F}}_{\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{l}}=\mathrm{M}\mathrm{a}\mathrm{x}\mathrm{P}\mathrm{o}\mathrm{o}\mathrm{l}\left({\mathrm{H}}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}}^{\left(\mathrm{l}\right)}\right)\in {\mathbb{R}}^{\mathrm{T}\times {\mathrm{d}}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}}}$$

(10)

Local short-term fluctuation features (e.g., short-term growth variations in tree diameters) are extracted using max pooling. This operation captures the most significant local responses, thereby modeling short-term variations.

$${\mathrm{F}}_{\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{l}}=\mathrm{L}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{r}\mathrm{N}\mathrm{o}\mathrm{r}\mathrm{m}({\mathrm{F}}_{\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{l}}+\mathrm{D}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{o}\mathrm{u}\mathrm{t}({\mathrm{F}}_{\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{l}}\left)\right)$$

(11)

After convolution and pooling, Layer Normalization and Dropout (rate = 0.2) are applied to stabilize feature distribution and enhance the model’s generalization ability.

(2)

Multi-Head Self-Attention

Building upon the local features extracted by the convolutional module, a Multi-Head Self-Attention (MHA) mechanism is introduced to further capture long-term dependencies and cross-year lag effects in forest carbon increment.

As shown in Figure 4, the structure of the Multi-Head Self-Attention mechanism enables the model to effectively learn long-term dependencies across temporal dimensions.

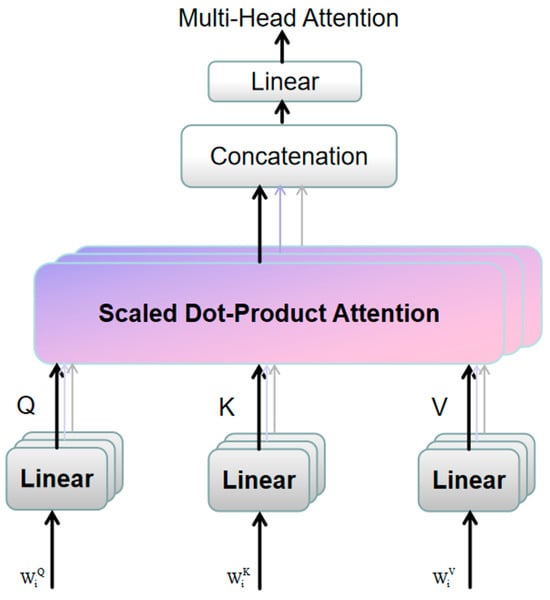
Figure 4. Structure of the multi-head attention mechanism. Three parallel heads are shown as three distinct layers, each with a unique colored path (purple, pink, blue) for independent Q/K/V projection and attention computation. Black arrows indicate overall data flow.

This mechanism enables the model to overcome the gradient vanishing problem commonly encountered in traditional LSTM networks when modeling extended temporal dependencies, thereby enhancing its ability to represent non-contiguous temporal relationships across different time steps. Specifically, the locally extracted convolutional features are first linearly transformed to generate the Query (Q), Key (K), and Value (V) matrices, defined as follows (12):

$$\mathrm{Q}={\mathrm{F}}_{\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{W}}_{\mathrm{Q}},\hspace{1em}\mathrm{K}={\mathrm{F}}_{\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{W}}_{\mathrm{K}},\hspace{1em}\mathrm{V}={\mathrm{F}}_{\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{W}}_{\mathrm{V}}$$

(12)

where ${\mathrm{W}}_{\mathrm{Q}},{\mathrm{W}}_{\mathrm{K}},{\mathrm{W}}_{\mathrm{V}}\in {\mathbb{R}}^{{\mathrm{d}}_{\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{l}}\times {\mathrm{d}}_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}}$ denote the learnable weight matrices for the respective linear transformations, and ${\mathrm{d}}_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}$ represents the feature dimensionality of the model. Each attention head computes the similarity scores between time steps through the scaled dot-product operation, defined as follows (13):

$$\mathrm{A}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(\mathrm{Q},\mathrm{K},\mathrm{V})=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left({\displaystyle \frac{\mathrm{Q}{\mathrm{K}}^{\mathrm{\top }}}{\sqrt{{\mathrm{d}}_{\mathrm{k}}}}}\right)\mathrm{V}$$

(13)

where ${\mathrm{d}}_{\mathrm{k}}$ denotes the scaling factor, defined as ${\mathrm{d}}_{\mathrm{k}}={\displaystyle \frac{{\mathrm{d}}_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}}{\mathrm{h}}}$, with h representing the number of attention heads. This scaling factor serves to alleviate the internal magnitude expansion problem that arises with increasing feature dimensionality, thereby stabilizing the gradient during the optimization process.

Through this mechanism, the single-head attention module can dynamically assign different weights to features across various time steps, thereby enabling the model to emphasize temporal features that are most relevant to the current prediction.

Conceptually, the attention mechanism allows the model to “focus” on the most informative historical states corresponding to the current forecasting objective (e.g., the delayed impact of peak soil moisture during specific periods on carbon accumulation).

To further enhance the model’s representational capacity, we introduce a Multi-Head Self-Attention (MHA) mechanism. By computing h = 8 independent attention heads in parallel, the model is capable of extracting information from multiple feature subspaces (such as climatic factors, growth factors, etc.).Each attention head focuses on distinct dependency patterns, thereby providing a richer and more comprehensive temporal representation. The outputs of all heads are concatenated and linearly transformed to obtain the final global temporal representation, which integrates multi-scale dependency information, as follows (14):

$${\mathrm{F}}_{\mathrm{a}\mathrm{t}\mathrm{t}\mathrm{n}}=\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{t}({\mathrm{h}\mathrm{e}\mathrm{a}\mathrm{d}}_1,\dots ,{\mathrm{h}\mathrm{e}\mathrm{a}\mathrm{d}}_{\mathrm{h}}){\mathrm{W}}^{\mathrm{O}}$$

(14)

where ${\mathrm{W}}^{\mathrm{O}}\in {\mathbb{R}}^{{\mathrm{d}}_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}\times {\mathrm{d}}_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}}$ is the linear projection matrix for the concatenated outputs.

To mitigate gradient vanishing and degradation problems in deeper networks, we introduce a residual connection in the output of the attention module, as follows (15):

$${\mathrm{F}}_{\mathrm{g}\mathrm{l}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{l}}=\mathrm{L}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{r}\mathrm{N}\mathrm{o}\mathrm{r}\mathrm{m}({\mathrm{F}}_{\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{l}}+{\mathrm{F}}_{\mathrm{a}\mathrm{t}\mathrm{t}\mathrm{n}})$$

(15)

Here, ${\mathrm{F}}_{\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{l}}$ denotes the local features extracted by convolution, and ${\mathrm{F}}_{\mathrm{a}\mathrm{t}\mathrm{t}\mathrm{n}}$ represents the global features captured by the multi-head attention mechanism. The residual connection ensures that the information can be effectively propagated through the network, while the layer normalization (LayerNorm) operation normalizes the features, thereby improving training stability.

(3)

Gated Fusion and Bidirectional LSTM (Gated Fusion & Bi-LSTM)

To integrate the local short-term features extracted by the convolutional module (e.g., monthly diameter growth fluctuations) and the global long-term features obtained by the multi-head self-attention module (e.g., interannual soil moisture trends), we designed a Gated Fusion mechanism and incorporated a Bidirectional LSTM (Bi-LSTM) network to capture the bidirectional temporal dependencies of forest carbon increment dynamics.

The convolutional module (Conv1D) captures local short-term variations in carbon increment, such as the immediate effects of monthly climate conditions, resulting in a local feature representation ${\mathrm{F}}_{\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{l}}$.

In contrast, the multi-head self-attention module captures long-term temporal dependencies across multiple years, yielding the global feature representation ${\mathrm{F}}_{\mathrm{g}\mathrm{l}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{l}}$.

Although each representation has its advantages, directly concatenating them may lead to imbalanced weighting between their contributions. To address this, a Gated Fusion mechanism is introduced to adaptively learn the relative importance of local and global features through two independent gating matrices.

Specifically, the gating weights for the local features are computed using a sigmoid activation as follows (16):

$${\mathsf{\alpha }}_{\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{l}}=\mathsf{\sigma }\left({\mathrm{W}}_{\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{F}}_{\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{l}}+{\mathrm{b}}_{\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{l}}\right)$$

(16)

Similarly, the gating weights for the global features are computed as (17):

$${\mathsf{\alpha }}_{\mathrm{g}\mathrm{l}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{l}}=\mathsf{\sigma }\left({\mathrm{W}}_{\mathrm{g}\mathrm{l}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{l}}{\mathrm{F}}_{\mathrm{g}\mathrm{l}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{l}}+{\mathrm{b}}_{\mathrm{g}\mathrm{l}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{l}}\right)$$

(17)

where ${\mathrm{W}}_{\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{l}}$ and ${\mathrm{W}}_{\mathrm{g}\mathrm{l}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{l}}$ denote the learnable gating weight matrices for the local and global features, respectively. The gated fusion output is obtained through element-wise multiplication, expressed as:

$${\mathrm{F}}_{\mathrm{f}\mathrm{u}\mathrm{s}\mathrm{e}\mathrm{d}}={\mathsf{\alpha }}_{\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{l}}\odot {\mathrm{F}}_{\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{l}}+{\mathsf{\alpha }}_{\mathrm{g}\mathrm{l}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{l}}\odot {\mathrm{F}}_{\mathrm{g}\mathrm{l}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{l}}+0.1\cdot \mathrm{X}$$

(18)

Here, $\mathrm{X}$ represents the initial input feature sequence, and 0.1 serves as a residual scaling coefficient to retain the original feature information.

Through this mechanism, the model adaptively combines short-term and long-term dependencies while maintaining stable information flow.

The fused features ${\mathrm{F}}_{\mathrm{f}\mathrm{u}\mathrm{s}\mathrm{e}\mathrm{d}}$ are then fed into a Bidirectional LSTM (Bi-LSTM) network to capture both past-to-present and future-to-present temporal dependencies.

Unlike traditional unidirectional LSTM, which only models historical dependencies, Bi-LSTM processes the input sequence in both temporal directions, thus capturing more comprehensive contextual information.

For the forward LSTM, the temporal dependency from past → present (January to December) is modeled as (19):

$${\overrightarrow{\mathrm{h}}}_{\mathrm{t}},{\overrightarrow{\mathrm{c}}}_{\mathrm{t}}=\mathrm{L}\mathrm{S}\mathrm{T}\mathrm{M}\left({\mathrm{F}}_{\mathrm{f}\mathrm{u}\mathrm{s}\mathrm{e}\mathrm{d}}^{\left(\mathrm{t}\right)},{\overrightarrow{\mathrm{h}}}_{\mathrm{t}-1},{\overrightarrow{\mathrm{c}}}_{\mathrm{t}-1}\right)$$

(19)

For the backward LSTM, the dependency from future → present (December to January of the next year) is modeled as (20):

$${\overleftarrow{\mathrm{h}}}_{\mathrm{t}},{\overleftarrow{\mathrm{c}}}_{\mathrm{t}}=\mathrm{L}\mathrm{S}\mathrm{T}\mathrm{M}\left({\mathrm{F}}_{\mathrm{f}\mathrm{u}\mathrm{s}\mathrm{e}\mathrm{d}}^{\left(\mathrm{t}\right)},{\overleftarrow{\mathrm{h}}}_{\mathrm{t}+1},{\overleftarrow{\mathrm{c}}}_{\mathrm{t}+1}\right)$$

(20)

The final hidden representation is obtained by concatenating the forward and backward hidden states:

$${\mathrm{H}}_{\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{l}}=\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{t}({\overrightarrow{\mathrm{h}}}_{\mathrm{t}},{\overleftarrow{\mathrm{h}}}_{\mathrm{t}})$$

(21)

This representation effectively integrates key temporal information from both past and future sequences, enhancing the model’s ability to characterize the dynamic behavior of forest carbon increment.

Finally, the fused temporal representation is passed through a fully connected output layer for carbon increment prediction:

$${\widehat{\mathrm{y}}}_{\mathrm{t}}={\mathrm{W}}_{\mathrm{o}}{\mathrm{H}}_{\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{l}}+{\mathrm{b}}_{\mathrm{o}}$$

(22)

Through this Bi-LSTM design, the model can effectively integrate both local and global features, capturing short- and long-term temporal dependencies.

This improves the accuracy and robustness of forest carbon increment prediction by modeling its dynamic variation comprehensively.

2.5. Model Training and Testing

The dataset was divided chronologically into training and testing subsets to ensure temporal consistency and prevent information leakage from future data. Observations from 1975 to 2014 were used as the training set, while those from 2015 to 2022 served as the test set, following an 8:2 ratio.

Training samples were constructed using a sliding window of six months, consistent with the temporal dependencies identified in Section 2.5 (SCM analysis).

Model performance was evaluated using three metrics: the coefficient of determination (R²), the root mean square error (RMSE), and the mean absolute error (MAE), which jointly assess prediction accuracy and generalization capability.

2.6. Causal Relationship Analysis Based on the Structural Causal Model

To elucidate the causal relationships between the carbon increment of Q. mongolica and various environmental and stand factors, this study adopts the Structural Causal Model (SCM) framework.

The SCM formalizes the causal relationships among variables as follows:

$${\mathrm{X}}_{\mathrm{i}}={\mathrm{f}}_{\mathrm{i}}(\mathrm{P}{\mathrm{A}}_{\mathrm{i}},{\mathsf{ϵ}}_{\mathrm{i}}),\hspace{1em}\mathrm{i}=\mathrm{1,2},\dots ,\mathrm{n}$$

(23)

where ${\mathrm{X}}_{\mathrm{i}}$ denotes the i variable in the system (e.g., carbon increment, temperature, precipitation, soil moisture and DBH); $\mathrm{P}{\mathrm{A}}_{\mathrm{i}}$ represents the set of parent nodes (direct causes) of ${\mathrm{X}}_{\mathrm{i}}$; and ${\mathsf{ϵ}}_{\mathrm{i}}$ denotes the exogenous noise independent of other variables.

The causal structure of SCM is typically expressed as a Directed Acyclic Graph (DAG), where nodes represent variables and directed edges denote direct causal effects. This framework supports do-calculus–based causal inference and counterfactual reasoning. To enhance the efficiency and stability of causal structure identification, the Random Forest algorithm was first employed to select key influencing variables as input features for SCM, thereby reducing dimensionality and minimizing redundant interference among variables. Additionally, missing values were linearly interpolated to ensure data completeness and to mitigate potential biases in causal discovery.

2.7. Baseline Models

To systematically evaluate the performance of Q. mongolica carbon increment prediction, this study established a unified experimental framework across multiple models to ensure fairness and reproducibility.

Deep learning models including LSTM, GRU, and Bi-LSTM were trained using the AdamW optimizer (initial learning rate = 0.001), combined with a cosine annealing scheduler for dynamic learning rate adjustment.

An early stopping mechanism (patience = 40) was applied to avoid overfitting. Traditional machine learning models, represented by XGBoost, were used as baselines for comparison. For deep learning models, the architectures were standardized to ensure comparability:

LSTM and GRU were configured with two layers (hidden dimension = 128), while Bi-LSTM employed two bidirectional layers (each containing 128 units) to capture both short-term and long-term temporal dependencies.

All experiments were implemented in Python 3.8 within the PyCharm IDE, using an NVIDIA RTX 3060 GPU, The GPU was sourced from NVIDIA Corporation, headquartered in Santa Clara, California, United States. Results were averaged over five repeated runs to ensure robustness. This unified design allows for fair performance comparison across models and comprehensively incorporates ecological drivers such as light, temperature, and moisture (as identified in the SCM analysis in Section 2.5).This framework is designed to assess carbon accumulation dynamics in Q. mongolica forests.

2.8. Evaluation Metrics

The predictive performance of the baseline and enhanced LSTM models for estimating forest carbon increment of Q. mongolica was evaluated using three commonly adopted statistical indicators: the coefficient of determination (R²), root mean square error (RMSE), and mean absolute error (MAE).

These complementary metrics jointly assess model accuracy, robustness, and the degree of agreement between predicted and observed values, where a higher R² and lower RMSE or MAE indicate better model performance.

3. Results

3.1. Feature Selection Results

The Random Forest (RF) feature importance analysis revealed that the contribution of different input factors to Q. mongolica carbon increment varied substantially. The cumulative contribution rate of feature importance was used as the selection criterion.

As illustrated in Figure 5, the relative importance of different variables in predicting carbon increment exhibited considerable variation.

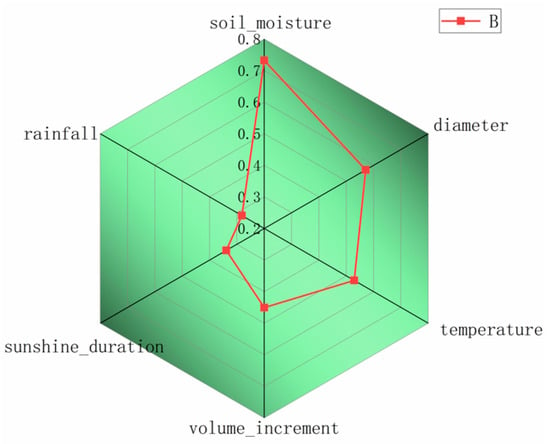
Figure 5. Results of feature selection using the Random Forest algorithm.

Among all input factors, soil moisture exhibited the highest importance score, reaching approximately 0.75, indicating its dominant role in the carbon accumulation process.

Volume increment, diameter at breast height (DBH), and temperature followed, with importance scores ranging from 0.40 to 0.50, suggesting that both tree growth characteristics and climatic conditions play substantial roles in the model’s prediction of carbon increment.

By contrast, precipitation demonstrated relatively lower importance scores (approximately 0.20–0.30), implying that their effects are primarily auxiliary or indirect.

Ultimately, the five key factors—soil moisture, DBH, temperature, volume increment, and sunshine duration—all exhibited contribution rates exceeding 30%, collectively explaining the majority of the predictive information.

Therefore, these variables were selected as the core input features for subsequent causal relationship modeling and time-series prediction experiments.

3.2. Causal Effect Analysis

Figure 6 presents the Directed Acyclic Graph (DAG) illustrating the causal structure with carbon_increment as the target variable. In this DAG, each arrow represents a directed causal influence from the parent variable to the child variable, indicating that changes in the former are inferred to have a direct effect on the latter in the carbon accumulation process.

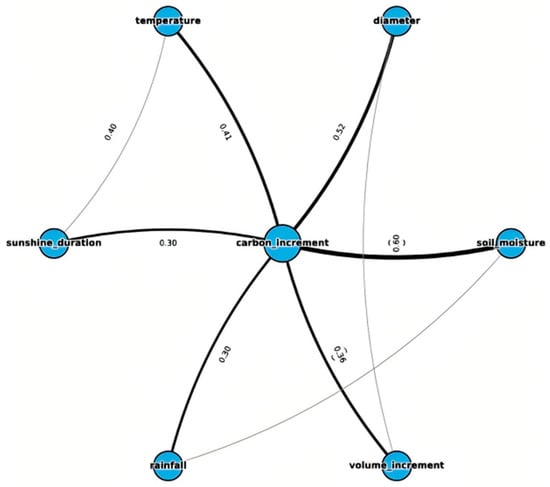
Figure 6. Causal Directed Acyclic Graph (DAG) of Q. mongolica carbon increment, illustrating both direct and indirect causal pathways among environmental and growth variables. Black lines represent direct causal influences with normalized weights ≥ 0.30, while gray lines indicate indirect causal pathways (see main text for detailed edge weights and interpretations).

Based on the direct causal effects, six primary edges directed toward carbon_increment were identified, ranked by their normalized weights as follows:

soil moisture → carbon increment (0.80), diameter → carbon increment (0.52), temperature → carbon increment (0.41), volume increment → carbon increment (0.36), sunshine duration → carbon increment (0.30), and rainfall → carbon increment (0.30).

Among these factors, soil moisture exhibited the strongest causal effect, indicating that water availability is the most critical limiting factor driving carbon accumulation in Q. mongolica forests. The effect of diameter ranked second, consistent with the well-established allometric relationship between tree size and biomass accumulation. However, the causal analysis quantitatively confirmed this relationship by identifying diameter as a key structural determinant of carbon increment rather than merely a correlated variable. Temperature and volume increment exerted moderate effects, whereas the direct impacts of rainfall and sunshine duration were comparatively weaker.

Temperature and volume increment exerted moderate effects, while the direct impacts of rainfall and sunshine duration were comparatively weaker.

Furthermore, the model identified three key indirect causal pathways:

(1) rainfall → soil moisture (0.55) → carbon increment (0.80); (2) sunshine duration→ temperature (0.40) → carbon increment (0.41); (3) diameter → volume increment (0.60) → carbon increment (0.36).

All edge weights in the DAG were normalized within the range [0.30, 0.80] to represent the relative strengths of causal effects rather than their absolute magnitudes.

3.3. Comparison of Multi-Model Results

The predictive performance of XGBoost, LSTM, GRU, Bi-LSTM, and the proposed Enhanced LSTM models was evaluated on the test dataset (Table 3). The results demonstrate substantial differences in both fitting accuracy and error control among the models. The traditional machine learning model XGBoost achieved an ${\mathrm{R}}^2$ of 0.831, with RMSE = 0.137 and MAE = 0.112, indicating moderate predictive capability but limited effectiveness in capturing the dynamic temporal characteristics of carbon increment.

Table 3. Comparison of predictive performance for Q. mongolica carbon increment across different models (test set).

Model	${\mathbf{R}}^2$	RMSE	MAE
XGBoost	0.831	0.137	0.112
LSTM	0.865	0.123	0.098
GRU	0.872	0.120	0.095
Bi-LSTM	0.903	0.104	0.081
Enhanced LSTM	0.944	0.079	0.064

By comparison, the deep learning models exhibited improved performance. The LSTM and GRU models achieved ${\mathrm{R}}^2$ values of 0.865 and 0.872, respectively, with lower RMSE and MAE values, confirming the advantage of recurrent neural networks in modeling the temporal dependencies of Q. mongolica carbon increment. The Bi-LSTM further improved accuracy to ${\mathrm{R}}^2$ = 0.903, suggesting that the bidirectional structure enhances the model’s ability to capture long-term dependencies in both temporal directions.

The Enhanced LSTM outperformed all other models, achieving an ${\mathrm{R}}^2$ of 0.944, RMSE = 0.079, and MAE = 0.064. Compared with XGBoost, this represents an improvement of 13.6% in ${\mathrm{R}}^2$ and reductions of 42.3% in RMSE and 42.9% in MAE. These findings highlight that while deep learning models generally outperform traditional machine learning methods, the Enhanced LSTM offers superior predictive accuracy and stability. Its architectural improvements—integrating convolutional feature extraction, multi-head attention, and gated fusion—demonstrate clear effectiveness in carbon increment prediction tasks.

To further validate the predictive performance of the proposed SCM-Enhanced-LSTM framework, this subsection compares the fitted results of the baseline models and the proposed model on the test set (2015–2022 monthly data) using time-series visualization (Figure 7). The test set consists of an 8-year observation sequence (2015–2022), corresponding to 96 monthly time steps (indexed from 0 to 95), which covers the complete growth cycle of Q. mongolica and enables evaluation of the models’ ability to dynamically capture carbon increment (unit: kg). The observed carbon increment series exhibits pronounced annual periodic fluctuations, including a spring–summer growth peak (April–August, average increment ≈ 0.15 kg), an autumn transition period (September–October, with stabilized increment), and a winter dormancy trough (November–March, approaching zero or slightly negative).

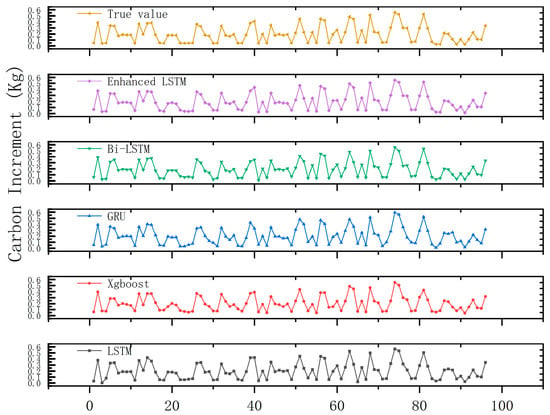
Figure 7. Comparison between observed and model-predicted carbon increment of Q. mongolica across different models (2015–2022). The yellow solid line represents the observed values, while dashed colored lines correspond to model predictions: XGBoost (red), LSTM (gray), GRU (blue), Bi-LSTM (green), and Enhanced LSTM (purple). The y-axis denotes carbon increment (kg) and the x-axis indicates monthly time steps (0–95).

Figure 7 compares the prediction results of XGBoost, LSTM, GRU, Bi-LSTM, and the proposed Enhanced LSTM on the test set. All models reproduced the annual seasonal fluctuations of Q. mongolica carbon increment, but clear differences were observed in local fitting accuracy and responsiveness to environmental disturbances. The non-sequential baseline XGBoost systematically underestimated growth peaks (e.g., June–August 2016) and failed to capture drought-induced anomalies (2018), leading to large deviations consistent with its higher RMSE. LSTM and GRU produced smoother predictions and better captured the overall seasonal cycle, but their ability to represent mid-term dependencies was limited, resulting in biases during transition periods and post-disturbance recovery. Bi-LSTM improved performance ($R^2$ = 0.903), particularly in capturing recovery phases, but its response to multimodal noise (e.g., 2021 extreme cold) remained insufficient.

In contrast, the SCM-Enhanced-LSTM achieved the best overall performance, with prediction curves nearly overlapping the observed sequence and peak–valley mismatches within 0.02 kg. It not only reproduced seasonal patterns with high precision but also maintained stable responses under drought and flood conditions. The superior results ($R^2$ = 0.944) highlight the effectiveness of integrating SCM-based feature selection with multi-head attention, confirming that the Enhanced LSTM provides the most accurate, robust, and interpretable predictions of carbon increment dynamics.

3.4. Robustness Validation

To evaluate the robustness of different models under measurement disturbances, Gaussian noise with varying intensities was added to the soil moisture input to simulate sensor uncertainty.

As shown in Table 4, the SCM-Enhanced-LSTM model exhibited the smallest increase in RMSE under all noise levels, with performance degradation remaining below 25%, while baseline models such as XGBoost and Bi-LSTM showed increases exceeding 40%.

Table 4. Robustness testing results (RMSE increments) under different noise levels.

Noise Level (σ)	Enhanced LSTM	LSTM	GRU	Bi-LSTM	XGBoost
XGBoost	+5.2%	+12.8%	+11.5%	+10.3%	+18.5%
LSTM	+8.7%	+19.6%	+18.2%	+16.5%	+25.3%
GRU	+12.7%	+28.4%	+26.8%	+24.2%	+35.2%
Bi-LSTM	+18.3%	+37.5%	+35.6%	+32.1%	+42.8%
Enhanced LSTM	+25.1%	+49.2%	+46.7%	+43.5%	+55.6%

These results demonstrate that the proposed framework maintains stable predictive performance even under disturbed input conditions, confirming its robustness and practical applicability in real-world ecological monitoring.

4. Discussion

The proposed SCM-Enhanced-LSTM framework integrates a Structural Causal Model (SCM) with an improved Long Short-Term Memory (LSTM) network, substantially enhancing both the predictive accuracy and interpretability of Q. mongolica carbon increment estimation. Compared with baseline models, the framework effectively captures temporal dynamics while leveraging causal filtering to identify key drivers such as light, diameter growth, and soil moisture.

In model design, the SCM component revealed that light and diameter act as direct drivers, while soil moisture functions as an intermediary factor, thereby alleviating the “black-box” limitation of conventional deep models. The integrated architecture retains the long-range memory of LSTM and introduces multi-scale convolution and multi-head attention, improving sensitivity to seasonal fluctuations and environmental disturbances. In model design, the SCM component revealed that light and diameter act as direct drivers, while soil moisture functions as an intermediary factor, thereby alleviating the “black-box” limitation of conventional deep models. The integrated architecture retains the long-range memory of LSTM and introduces multi-scale convolution and multi-head attention, improving sensitivity to seasonal fluctuations and environmental disturbances. Similar to the attention-enhanced deep learning frameworks proposed by Lang et al. (2022) for global canopy height regression from GEDI data [33], this study demonstrates that attention-based architectures also enhance carbon increment modeling when guided by causal variable selection.

In performance evaluation, the Enhanced LSTM achieved ${\mathrm{R}}^2$ = 0.944, RMSE = 0.079 kg, and MAE = 0.064 kg, reducing RMSE and MAE by 24.0% and 21.0%, respectively, compared to the Bi-LSTM model. The model accurately reproduced seasonal growth peaks (spring–summer ≈ 0.15 kg) and dormancy troughs, and under mild noise disturbance (σ = 0.1), RMSE increased by only 12%, confirming its robustness and generalization capability. These results demonstrate the model’s strong potential for stable carbon increment prediction under realistic data uncertainty.

To further validate the predictive performance of the proposed model, a comparative analysis was conducted with similar studies that used structural- or machine-learning-based approaches for carbon estimation at the tree or stand level. The comparison results are summarized in Table 5.

Table 5. Comparison of model performance for tree- or stand-level carbon estimation in recent studies.

Study	Target Level	Model Type	${\mathit{R}}^2$	RMSE
Perpiñá-Vallés et al. [34]	Tree level	ANN	0.66	373.85 kg
Dantas et al. [35]	Tree level	ANN, SVM	0.85	------
This study	Tree level	SCM-Enhanced LSTM	0.94	0.079 kg

Note: ‘------’ indicates the original study did not report RMSE.

As shown in Table 5, the proposed SCM–Enhanced LSTM model achieved a significantly higher predictive accuracy (R² = 0.944, RMSE = 0.079 kg) compared with other recent studies.

For instance, Dantas et al. (2021) developed LiDAR-based species-specific models using support vector machines (SVM) and artificial neural networks (ANN) to estimate carbon stock in tropical forests, yielding a mean relative error of 6.94% [35]. Similarly, Perpiñá-Vallés et al. (2024) applied ANN for aboveground carbon estimation at the individual-tree level in semi-arid African woodlands, achieving an R² of 0.66 and RMSE of 373.85 kg [34].

The superior performance of our model underscores the advantage of integrating structural causal modeling with deep temporal learning, which enables the model to better capture the complex interactions between environmental and structural factors and their temporal dependencies in carbon dynamics. This integrated framework not only improves the accuracy of prediction but also enhances the interpretability of the learning process, addressing the “black-box” limitation in conventional deep models.

In contrast, our proposed SCM-Enhanced LSTM model integrates structural and environmental variables, including soil moisture, temperature, and growth stage—critical determinants of carbon dynamics in Q. mongolica. This species is characterized by its pronounced sensitivity to soil-moisture fluctuations and temperature variations, which significantly influence photosynthetic activity, biomass allocation, and seasonal carbon accumulation. Previous studies have confirmed that changes in soil water regimes can substantially alter the growth and physiological performance of Q. mongolica seedlings in temperate forests (Wang et al., 2004) [36] while stand-age differences strongly affect its carbon storage potential and structural development (Kim et al., 2018) [37]. Additionally, root-based carbon allocation patterns in Q. mongolica forests exhibit species-specific variability, emphasizing the importance of integrating biological parameters into carbon modeling frameworks (Park et al., 2006) [38]. Therefore, incorporating such eco-physiological variables enhances the interpretability of our SCM-Enhanced LSTM model and allows a more realistic simulation of species-dependent carbon dynamics under variable environmental conditions.

This study has certain limitations. The dataset is restricted to Q. mongolica plots, and cross-species or regional generalization requires further validation. Moreover, soil nutrient and canopy structure parameters were not included as predictors.

In future research, multi-source remote sensing datasets, including GEDI LiDAR canopy height metrics and Sentinel-2 vegetation indices (e.g., NDVI, EVI), will be incorporated to enhance the representation of canopy structural and physiological attributes. These variables can serve as quantitative proxies for light availability, leaf area dynamics, and aboveground biomass, which are key causal factors influencing carbon sequestration efficiency. By coupling these remote-sensing-derived indicators with the Structural Causal Model, it will be possible to constrain causal pathways with spatially continuous observations and verify the transferability of inferred relationships across forest types and climatic gradients. Furthermore, integrating such data into the Enhanced-LSTM network can improve temporal resolution and reduce the reliance on ground-based measurements, thereby strengthening both predictive robustness and ecological interpretability of the proposed framework.

5. Conclusions

This study developed an Enhanced LSTM deep learning framework based on long-term monitoring data to achieve high-precision prediction of carbon increment at the individual tree level. The main conclusions are as follows:

(1)

Model innovation:

By integrating a Structural Causal Model (SCM) with the LSTM network, the proposed framework enhances the adaptive perception and selection of multi-source temporal ecological features. This approach provides a new deep learning paradigm for predicting carbon sink dynamics at the individual tree scale.

(2)

Prediction accuracy and robustness:

Compared with XGBoost, LSTM, GRU, and Bi-LSTM, the SCM-Enhanced-LSTM achieved the highest predictive accuracy on the test set (${\mathrm{R}}^2$ = 0.944, RMSE = 0.079 kg), exhibiting the lowest error levels and stable performance under noisy conditions (RMSE increase ≈ 12%). These results demonstrate strong noise resistance and generalization capability.

(3)

Ecological implications:

The model successfully reproduces the seasonal carbon accumulation pattern of Q. mongolica—characterized by growth peaks in spring and summer (~0.15 kg)—and accurately captures responses to extreme climate events. This provides a reliable tool for investigating tree-level carbon fixation mechanisms and for improving the precision of forest carbon stock assessments.

In conclusion, the proposed SCM-Enhanced-LSTM framework combines high accuracy, interpretability, and stability, offering a promising methodological reference for the application of deep learning in forest carbon cycle research. Future studies may integrate multi-scale remote sensing data and process-based ecological models to extend its applicability in carbon balance evaluation and climate change response analysis.

6. Patents

A patent titled “Carbon Sequestration Prediction System and Method Based on Bayesian Optimization Algorithm” is currently under review.