A Method for Estimating Tree Age Based on the Tree Trunk Diameter and the Average Radial Growth Rate in Recent Years
Abstract
1. Introduction
2. Materials and Methods
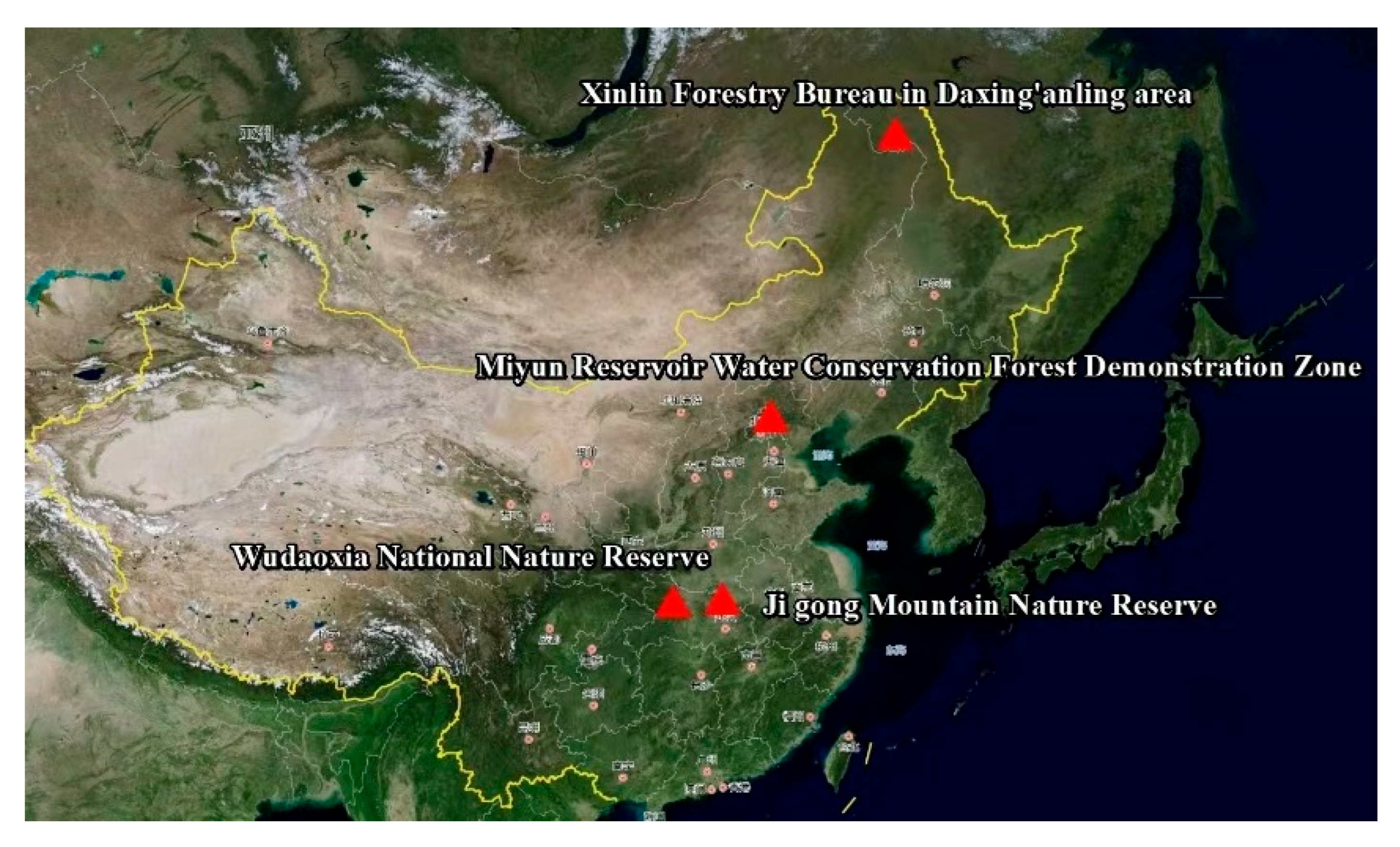
2.1. Overview of the Research Area and Tree Species
- (1)
- Wudaoxia National Nature Reserve
- (2)
- Ji Gong Mountain Nature Reserve
- (3)
- Miyun Reservoir Water Conservation Forest Demonstration Zone
- (2)
- Xinlin Forestry Bureau in Daxing’anling area
2.2. Disk Sampling and Processing
2.3. Data Processing
2.4. Modeling Method
2.5. Model Evaluation Method
3. Results and Analysis
3.1. Modeling Results
3.1.1. The Results of Alternative Mathematical Model Forms
3.1.2. The Results of Selected Model Form from the Alternative Mathematical Model Forms
3.1.3. Modeling Results
3.2. Test Results
4. Discussion
5. Conclusions
6. Patents
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dieler, J.; Uhl, E.; Biber, P.; Müller, J.; Rötzer, T.; Pretzsch, H. Effect of forest stand management on species composition, structural diversity, and productivity in the temperate zone of Europe. Eur. J. For. Res. 2017, 136, 739–766. [Google Scholar] [CrossRef]
- Ling, R.; Xie, C.; Qiu, C. Study on Forest Management Plan Based on Forecast of the Carbon Sequestration and Comprehensive Value. In Proceedings of the 4th International Conference on Business, Economics, Management Science (BEMS 2022); International College, Xiamen University, Ed.; International College, Xiamen University: Xiamen, China, 2022; pp. 452–464. [Google Scholar]
- Nath, C.D.; Boura, A.; De Franceschi, D.; Pélissier, R.J.T. Assessing the utility of direct and indirect methods for estimating tropical tree age in the Western Ghats, India. Trees-Struct. Funct. 2012, 26, 1017–1029. [Google Scholar] [CrossRef]
- Schall, P.; Ammer, C. How to quantify forest management intensity in Central European forests. Eur. J. For. Res. 2013, 132, 379–396. [Google Scholar] [CrossRef]
- Tian, H.; Zhu, J.; Lei, X.; Jian, Z.; Chen, X.; Zeng, L.; Huang, G.; Liu, C.; Xiao, W. Models considering the theoretical stand age will underestimate the future forest carbon sequestration potential. For. Ecol. Manag. 2024, 562, 121982. [Google Scholar] [CrossRef]
- Barry, D. Refining Dendrochronology to Evaluate the Relationship Between Age and Diameter for Dominant Riparian Trees in the Redwood Creek Watershed. Master’s Thesis, The University of San Francisco, San Francisco, CA, USA, 2014. [Google Scholar]
- Ricker, M.; Gutiérrez-García, G.; Juárez-Guerrero, D.; Evans, M.E. Statistical age determination of tree rings. PLoS ONE 2020, 15, e0239052. [Google Scholar] [CrossRef]
- Garet, J.; Raulier, F.; Pothier, D.; Cumming, S.G. Forest age class structures as indicators of sustainability in boreal forest: Are we measuring them correctly? Ecol. Indic. 2012, 23, 202–210. [Google Scholar] [CrossRef]
- Reyes-Palomeque, G.; Dupuy, J.; Portillo-Quintero, C.; Andrade, J.; Tun-Dzul, F.; Hernández-Stefanoni, J. Mapping forest age and characterizing vegetation structure and species composition in tropical dry forests. Ecol. Indic. 2021, 120, 106955. [Google Scholar] [CrossRef]
- Martin, M.; Fenton, N.; Morin, H. Structural diversity and dynamics of boreal old-growth forests case study in Eastern Canada. For. Ecol. Manag. 2018, 422, 125–136. [Google Scholar] [CrossRef]
- Bonou, W.; Kakaï, R.G.; Assogbadjo, A.; Fonton, H.; Sinsin, B. Characterisation of Afzelia africana Sm. habitat in the Lama forest reserve of Benin. For. Ecol. Manag. 2009, 258, 1084–1092. [Google Scholar] [CrossRef]
- Zhang, H.; Lei, X.; Zhang, C.; Zhao, X.; Hu, X. Research on theory and technology of forest quality evaluation and precision improvement. J. Beijing For. Univ. 2019, 41, 1–18. [Google Scholar] [CrossRef]
- Michel, A.K.; Winter, S. Tree microhabitat structures as indicators of biodiversity in Douglas-fir forests of different stand ages and management histories in the Pacific Northwest, USA. For. Ecol. Manag. 2008, 257, 1453–1464. [Google Scholar] [CrossRef]
- Winter, S. Forest naturalness assessment as a component of biodiversity monitoring and conservation management. Forestry 2012, 85, 293–304. [Google Scholar] [CrossRef]
- Moussaoui, L.; Leduc, A.; Girona, M.M.; Bélisle, A.C.; Lafleur, B.; Fenton, N.J.; Bergeron, Y. Success factors for experimental partial harvesting in unmanaged boreal forest: 10-year stand yield results. Forests 2020, 11, 1199. [Google Scholar] [CrossRef]
- Wilhelmsson, P.; Wallerman, J.; Lämås, T.; Öhman, K. Dynamic treatment units in forest planning improves economic performance over stand-based planning. Eur. J. For. Res. 2024, 144, 163–177. [Google Scholar] [CrossRef]
- Ashraf, M.I.; Meng, F.-R.; Bourque, C.P.-A.; MacLean, D.A. A novel modelling approach for predicting forest growth and yield under climate change. PLoS ONE 2015, 10, e0132066. [Google Scholar] [CrossRef]
- Wen, Z. Research on Forest Utility for Maximizing Forest Value. In Proceedings of the 3rd International Symposium on Frontiers of Economics and Management Science (FEMS 2022), Macao, China, 29–30 April 2022; p. 9. [Google Scholar]
- Forrester, D.I.; Tachauer, I.H.H.; Annighoefer, P.; Barbeito, I.; Pretzsch, H.; Ruiz-Peinado, R.; Stark, H.; Vacchiano, G.; Zlatanov, T.; Chakraborty, T. Generalized biomass and leaf area allometric equations for European tree species incorporating stand structure, tree age and climate. For. Ecol. Manag. 2017, 396, 160–175. [Google Scholar] [CrossRef]
- Yao, N.; Gu, C.; Qi, J.; Shen, S.; Nan, B.; Wang, H. Protecting Rural Large Old Trees with Multi-Scale Strategies: Integrating Spatial Analysis and the Contingent Valuation Method (CVM) for Socio-Cultural Value Assessment. Forests 2023, 15, 18. [Google Scholar] [CrossRef]
- Diallo, A.; Agbangba, E.C.; Ndiaye, O.; Guisse, A. Ecological structure and prediction equations for estimating tree age, and dendometric parameters of acacia senegal in the senegalese semi-arid zone—Ferlo. Am. J. Plant Sci. 2013, 4, 1046–1053. [Google Scholar] [CrossRef]
- Lei, X.; Peng, C.; Wang, H.; Zhou, X. Individual height–diameter models for young black spruce (Picea mariana) and jack pine (Pinus banksiana) plantations in New Brunswick, Canada. For. Chron. 2009, 85, 43–56. [Google Scholar] [CrossRef]
- Kang, H. Juvenile selection in tree breeding: Some mathematical models. Silvae Genet. 1985, 34, 75–84. [Google Scholar]
- Zhou, H.; Feng, R.; Huang, H.-H.; Lin, E.-P.; Yu, J.-L. Method of tree-ring image analysis for dendrochronology. Opt. Eng. 2012, 51, 077202. [Google Scholar] [CrossRef]
- Duncan, R. An evaluation of errors in tree age estimates based on increment cores in kahikatea (Dacrycarpus dacrydioides). N. Z. Nat. Sci. 1989, 16, 31–37. [Google Scholar]
- Norton, D.A.; Palmer, J.G.; Ogden, J. Dendroecological studies in New Zealand 1. An evaluation of tree age estimates based on increment cores. N. Z. J. Bot. 1987, 25, 373–383. [Google Scholar] [CrossRef]
- Altman, J.; Doležal, J.; Čížek, L. Age estimation of large trees: New method based on partial increment core tested on an example of veteran oaks. For. Ecol. Manag. 2016, 380, 82–89. [Google Scholar] [CrossRef]
- Fraver, S.; Bradford, J.B.; Palik, B.J. Improving tree age estimates derived from increment cores: A case study of red pine. Forest Sci. 2011, 57, 164–170. [Google Scholar] [CrossRef]
- Yao, J.F.; Zhao, Y.D.; Zhang, H.R.; Song, X.Y.; Lei, X.D.; Tang, S.Z. Drill resistance expression method of tree micro drill instrument. Trans. Chin. Soc. Agric. Mach. 2021, 52, 271–277, 286. [Google Scholar]
- Downes, G.M.; Lausberg, M.; Potts, B.; Pilbeam, D.; Bird, M.; Bradshaw, B. Application of the IML Resistograph to the infield assessment of basic density in plantation eucalypts. Aust. For. 2018, 81, 177–185. [Google Scholar] [CrossRef]
- Sharma, R.P.; Vacek, Z.; Vacek, S.; Jansa, V.; Kučera, M. Modelling individual tree diameter growth for Norway spruce in the Czech Republic using a generalized algebraic difference approach. J. For. Sci. 2017, 64, 227–238. [Google Scholar] [CrossRef]
- Loewenstein, E.F.; Johnson, P.S.; Garrett, H.E. Age and diameter structure of a managed uneven-aged oak forest. Can. J. For. Res. 2000, 30, 1060–1070. [Google Scholar] [CrossRef]
- Wang, M.; Borders, B.E.; Zhao, D. An empirical comparison of two subject-specific approaches to dominant heights modeling: The dummy variable method and the mixed model method. For. Ecol. Manag. 2008, 255, 2659–2669. [Google Scholar] [CrossRef]
- Hu, Y.Y.; Kang, X.G.; Zhao, J.H. Variable relationship between tree age and diameter at breast height for natural forests in Changbai Mountains. J. Northeast For. Univ. 2009, 37, 38–42. [Google Scholar]
- Divya, K.; Kaur, S. A Study on Tree Rings: Dendrochronology using Image Processing. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1022, 012115. [Google Scholar] [CrossRef]
- Wu, W.N.; Wan, T. Progress of dating methods of tree age. J. Green Sci. Technol. 2013, 7, 152–155. [Google Scholar]
- Villalba, R.; Veblen, T.T. Improving estimates of total tree ages based on increment core samples. Ecoscience 1997, 4, 534–542. [Google Scholar] [CrossRef]
- Wang, H.; Sun, J.; Duan, A.; Zhu, A.; Wu, H.; Zhang, J. Dendroclimatological analysis of chinese fir using a long-term provenance trial in Southern China. Forests 2022, 13, 1348. [Google Scholar] [CrossRef]
- Oh, J.-A.; Seo, J.-W.; Kim, B.-R. Verifying the possibility of investigating tree ages using resistograph. J. Korean Wood Sci. Technol. 2019, 47, 90–100. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, H.; Zhang, X.; Lei, Y.; Huang, J.; Liu, X. An Approach to Estimate Individual Tree Ages Based on Time Series Diameter Data—A Test Case for Three Subtropical Tree Species in China. Forests 2022, 13, 614. [Google Scholar] [CrossRef]
- Gao, S.; Wang, X.; Wiemann, M.C.; Brashaw, B.K.; Ross, R.J. A critical analysis of methods for rapid and nondestructive determination of wood density in standing trees. Ann. For. Sci. 2017, 74, 27. [Google Scholar] [CrossRef]
- Yao, J.f.; Lu, J.; Fu, L. Micro drill resistance instrument measurements at different feed speeds: Novel conversion algorithm for enhanced accuracy. J. Nondestruct. Eval. 2023, 42, 56. [Google Scholar] [CrossRef]
- Pan, H.; Lu, J.; Guo, X.Z.; Tang, S.Z.; Gao, R.D.; Xu, J.J. Algorithm for Determining Tree Age Using Acupuncture Instrument Based on Spectrum Analysis. For. Res. 2021, 34, 19–25. [Google Scholar] [CrossRef]
- Orozco-Aguilar, L.; Nitschke, C.R.; Livesley, S.J.; Brack, C.; Johnstone, D. Testing the accuracy of resistance drilling to assess tree growth rate and the relationship to past climatic conditions. Urban For. Urban Green. 2018, 36, 1–12. [Google Scholar] [CrossRef]
- Yao, J.F.; Wang, F.H.; Zhao, C.C.; Gao, C.; Hu, X.F. Study on Mathematical Model of Camellia oleifera Tree Age. J. Xinyang Norm. Univ. (Nat. Sci. Ed.) 2025, 38, 402–407. [Google Scholar]
- Khan, M. Advanced estimation of orange tree age using fuzzy inference and linear regression models. Int. J. Knowl. Innov. Stud. 2024, 2, 119–129. [Google Scholar] [CrossRef]
- Chen, J.J.; Du, H.Q.; Mao, F.J.; Huang, Z.H.; Chen, C.; Hu, M.C.; Li, X.J. Improving forest age prediction performance using ensemble learning algorithms base on satellite remote sensing data. Ecol. Indic. 2024, 166, 112327. [Google Scholar] [CrossRef]
- Melesse, S.F.; Zewotir, T. Additive mixed models to study the effect of tree age and climatic factors on stem radial growth of Eucalyptus trees. J. For. Res. 2020, 31, 463–473. [Google Scholar] [CrossRef]
- Iqbal, J.; Ahmed, M.; Siddiqui, M.F.; Khan, A. Tree ring studies from some conifers and present condition of forest of Shangla district of Khyber Pukhtunkhwa Pakistan. Pak. J. Bot. 2020, 52, 653–662. [Google Scholar] [CrossRef]
- Xiong, B.; Wang, Z.; Li, Z.; Zhang, E.; Tian, K.; Li, T.; Li, Z.; Song, C. Study on the correlation between age, diameter at breast height, and tree height of Chinese fir in the Seven Sisters Mountain Nature Reserve. Res. For. Grass Resour. 2016, 41. [Google Scholar] [CrossRef]
- Matsushita, M.; Takata, K.; Hitsuma, G.; Yagihashi, T.; Noguchi, M.; Shibata, M.; Masaki, T. A novel growth model evaluating age–size effect on long--term trends in tree growth. Funct. Ecol. 2015, 29, 1250–1259. [Google Scholar] [CrossRef]
- Abrams, M.D. Age-diameter relationships of Quercus species in relation to edaphic factors in gallery forests in northeast Kansas. For. Ecol. Manag. 1985, 13, 181–193. [Google Scholar] [CrossRef]
- Kalliovirta, J.; Tokola, T. Functions for estimating stem diameter and tree age using tree height, crown width and existing stand database information. Silva Fenn. 2005, 39, 227–248. [Google Scholar] [CrossRef]
- Chen, J.; Yang, H.; Man, R.; Wang, W.; Sharma, M.; Peng, C.; Parton, J.; Zhu, H.; Deng, Z. Using machine learning to synthesize spatiotemporal data for modelling DBH-height and DBH-height-age relationships in boreal forests. For. Ecol. Manag. 2020, 466, 118104. [Google Scholar] [CrossRef]
- Rohner, B.; Bugmann, H.; Bigler, C. Towards non-destructive estimation of tree age. For. Ecol. Manag. 2013, 304, 286–295. [Google Scholar] [CrossRef]
- Rohner, B.; Bugmann, H.; Bigler, C. Estimating the age–diameter relationship of oak species in Switzerland using nonlinear mixed-effects models. Eur. J. For. Res. 2013, 132, 751–764. [Google Scholar] [CrossRef]
- Lu, J.; Huang, C.; Schleeweis, K.; Zou, Z.; Gong, W. Tree age estimation across the US using forest inventory and analysis database. For. Ecol. Manag. 2025, 584, 122603. [Google Scholar] [CrossRef]
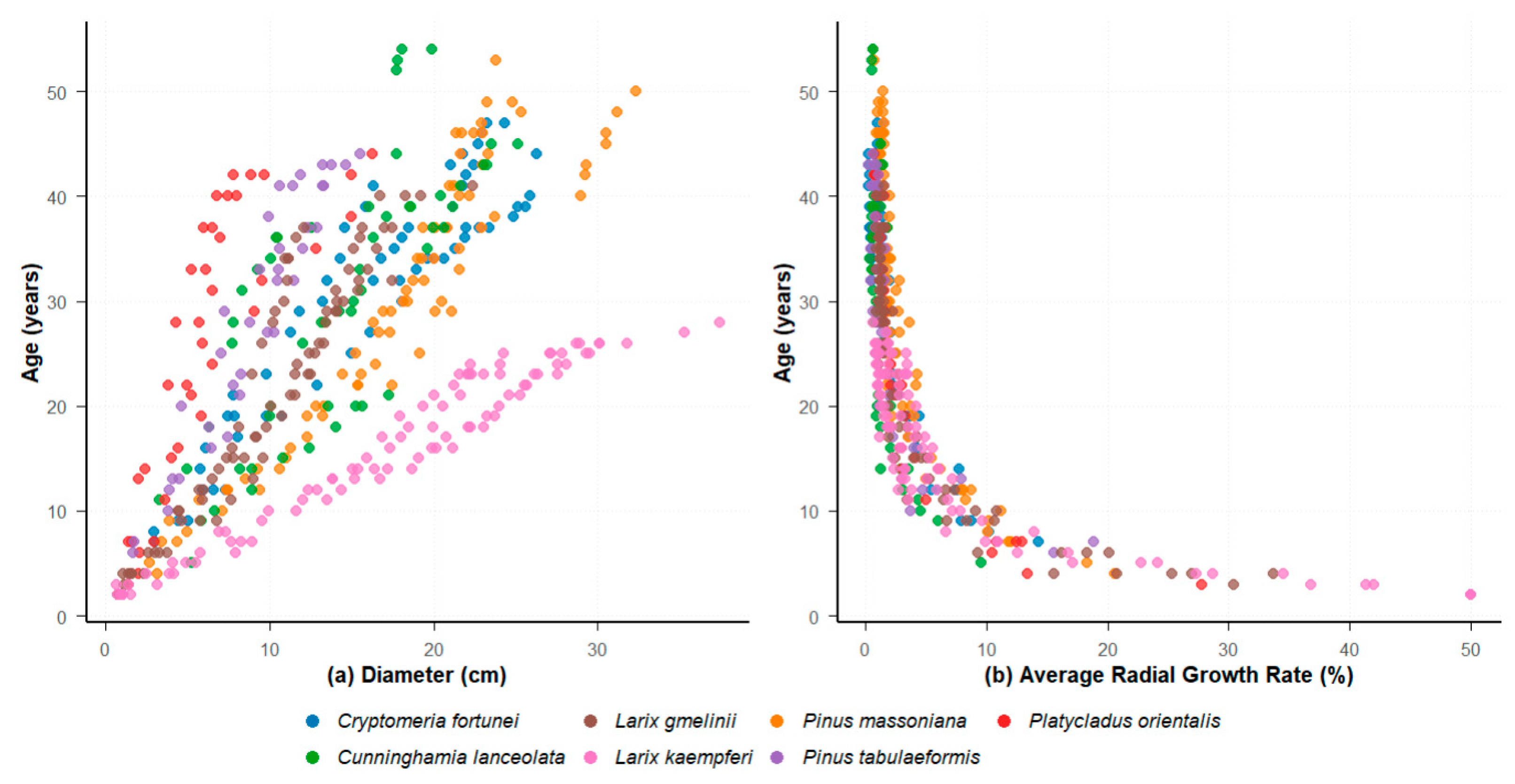
| Tree Species | Tree Height Range/m | Diameter at Breast Height (DBH) Range/cm | Tree Age Range/yr | Area |
|---|---|---|---|---|
| Cryptomeria fortunei | 11~17 | 15~26 | 37~48 | Ji Gong Mountain Nature Reserve |
| Pinus massoniana | 15~19 | 18~31 | 39~53 | Ji Gong Mountain Nature Reserve |
| Cunninghamia lanceolata | 14~18 | 10~25 | 37~54 | Ji Gong Mountain Nature Reserve |
| Pinus tabuliformis | 10~12 | 10~14 | 42~46 | Miyun Reservoir Water Conservation Forest Demonstration Zone |
| Platycladus orientalis | 8.5~10.3 | 6~15 | 42~44 | Miyun Reservoir Water Conservation Forest Demonstration Zone |
| Larix kaempferi | 15~22 | 17~30 | 24~28 | Wudaoxia National Nature Reserve |
| Larix gmelinii | 14~17 | 11~17 | 31~41 | Xinlin Forestry Bureau in Daxing’anling area |
| Total | 8.5~22 | 6~31 | 24~54 | - |
| Tree Species | Disk Number | Range of Tree Ring/A Numbers | Diameter Range/cm |
|---|---|---|---|
| Cryptomeria fortunei | 93 | 7~48 | 2~27 |
| Pinus massoniana | 109 | 4~53 | 2~33 |
| Cunninghamia lanceolata | 86 | 5~54 | 3~28 |
| Pinus tabulaeformis | 54 | 6~46 | 1~16 |
| Platycladus orientalis | 55 | 2~44 | 0.8 ~17 |
| Larix kaempferi | 131 | 2~28 | 0.6~38 |
| Larix gmelinii | 118 | 2~41 | 0.7~23 |
| Total | 646 | 2~54 | 0.6~38 |
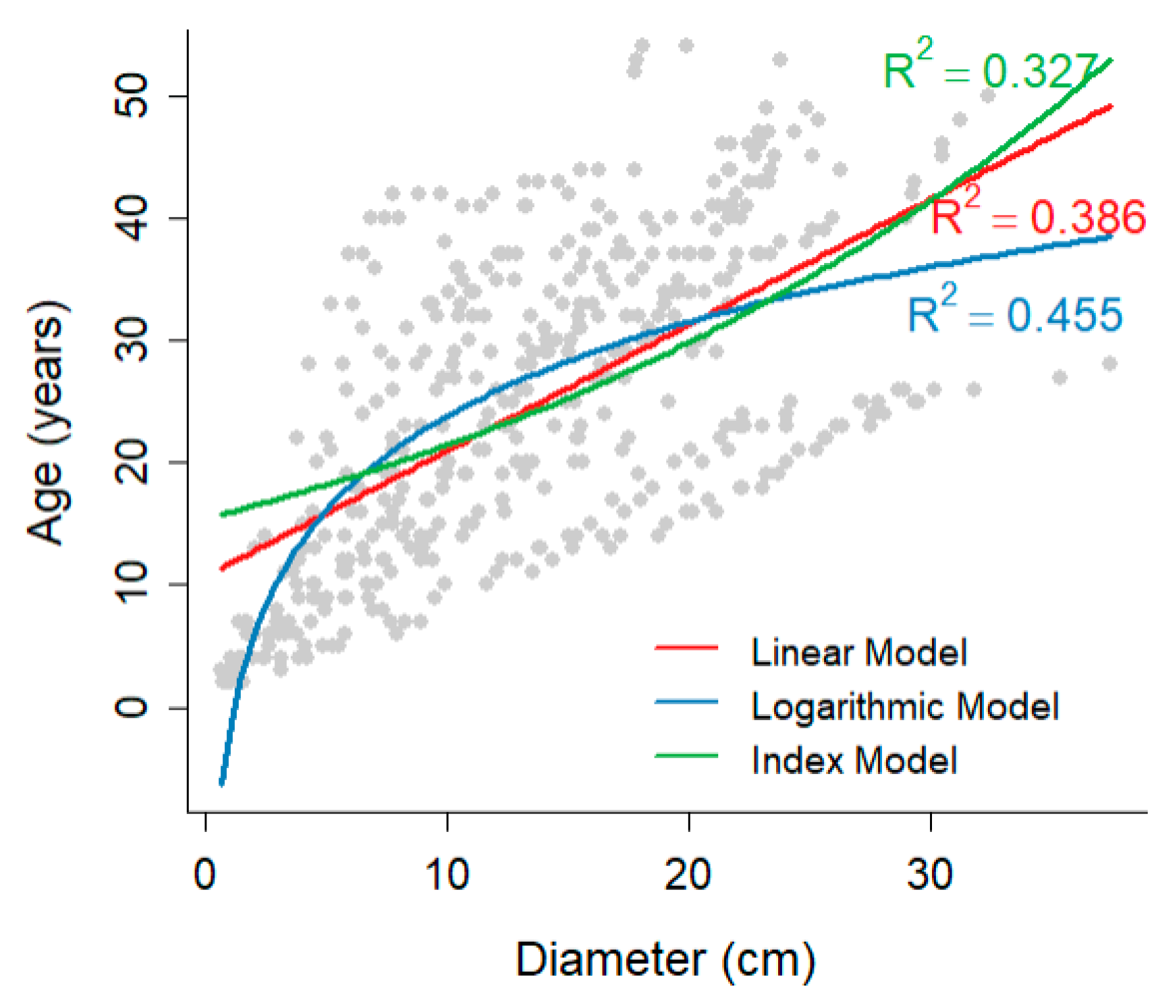
| Model Type | Formula | |
|---|---|---|
| Linear model | 0.386 | |
| Index model | 0.327 | |
| Logarithmic model | 0.455 |
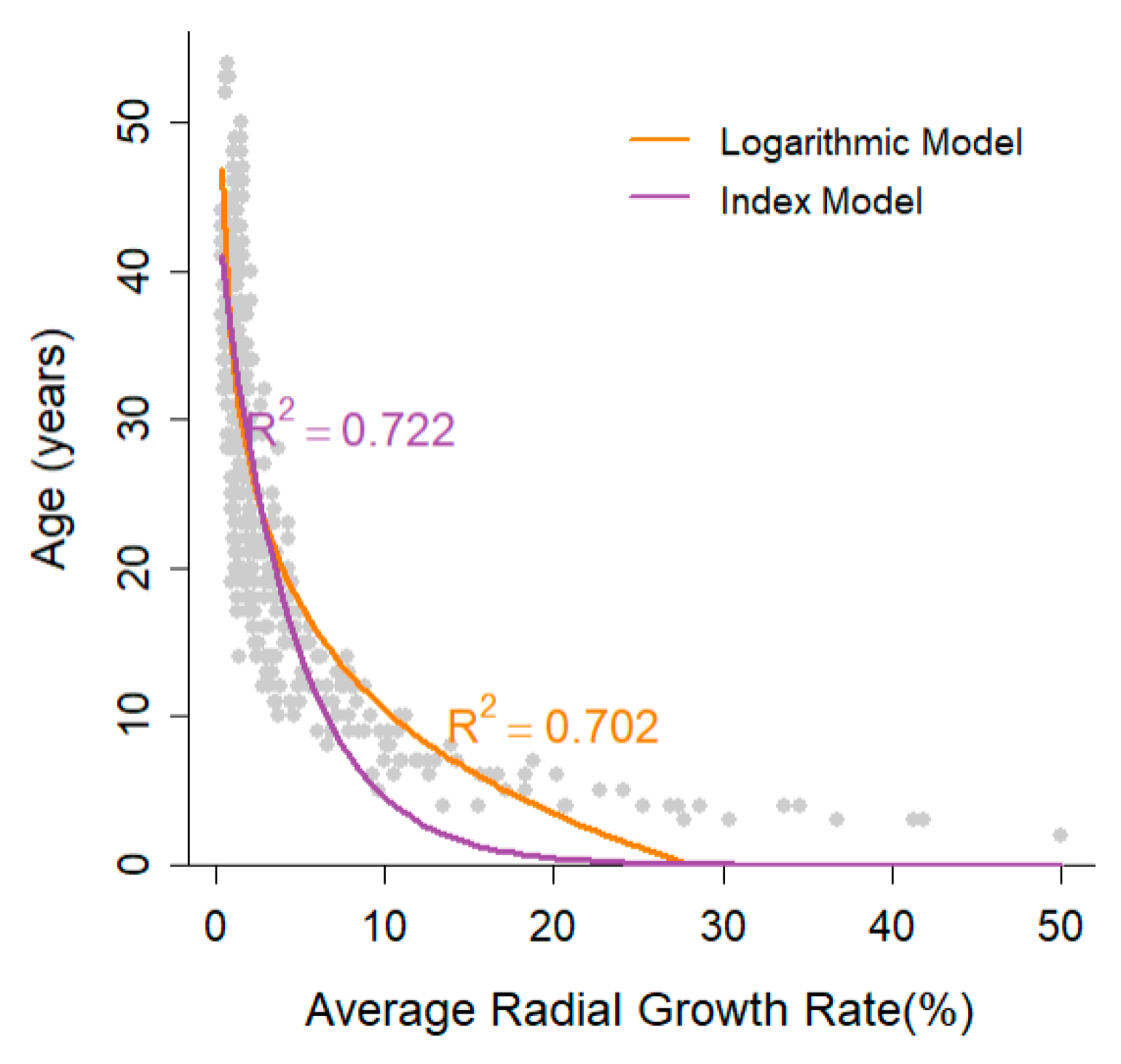
| Model Type | Formula | |
|---|---|---|
| Index model | 0.722 | |
| Logarithmic model | 0.702 |
| Tree Species | Equation | |
|---|---|---|
| Cryptomeria fortunei | 0.878 | |
| 0.829 | ||
| 0.901 | ||
| Pinus massoniana | 0.795 | |
| 0.835 | ||
| 0.924 | ||
| Cunninghamia lanceolata | 0.571 | |
| 0.542 | ||
| 0.778 | ||
| Pinus tabulaeformis | 0.824 | |
| 0.717 | ||
| 0.890 | ||
| Platycladus orientalis | 0.795 | |
| 0.912 | ||
| 0.944 | ||
| Larix kaempferi | 0.788 | |
| 0.829 | ||
| 0.888 | ||
| Larix gmelinii | 0.751 | |
| 0.854 | ||
| 0.923 | ||
| Total | 0.455 | |
| 0.722 | ||
| 0.762 |
| Model | Equation |
|---|---|
| M1: between age and diameter | |
| M2: between the age and average radial growth rate of the outermost layer | |
| M3: between the age and diameter, and average radial growth rate of the outermost layer |
| Model | Accuracy/% | RMSE/a | MAE/a | AIC | BIC | SD/a | |
|---|---|---|---|---|---|---|---|
| M1 | 50.76 | 8.571 | 7.263 | 1547.096 | 1557.222 | 74.153 | 8.611 |
| M2 | 73.01 | 5.761 | 4.657 | 1375.460 | 1385.586 | 33.499 | 5.788 |
| M3 | 80.29 | 5.006 | 3.859 | 1318.735 | 1335.611 | 25.528 | 5.053 |
| Tested Models | t-Value | p-Value |
|---|---|---|
| Between M1 and M2 | 6.627 | <0.001 |
| Between M1 and M3 | 8.887 | <0.001 |
| Between M2 and M3 | 2.606 | <0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, J.; Yang, M.; Li, Z.; Ha, D.; Gao, W.; He, X.; Hu, X.; Song, X. A Method for Estimating Tree Age Based on the Tree Trunk Diameter and the Average Radial Growth Rate in Recent Years. Forests 2025, 16, 1725. https://doi.org/10.3390/f16111725
Yao J, Yang M, Li Z, Ha D, Gao W, He X, Hu X, Song X. A Method for Estimating Tree Age Based on the Tree Trunk Diameter and the Average Radial Growth Rate in Recent Years. Forests. 2025; 16(11):1725. https://doi.org/10.3390/f16111725
Chicago/Turabian StyleYao, Jianfeng, Mengmeng Yang, Zhuofan Li, Denglong Ha, Wenqiang Gao, Xiao He, Xuefan Hu, and Xinyu Song. 2025. "A Method for Estimating Tree Age Based on the Tree Trunk Diameter and the Average Radial Growth Rate in Recent Years" Forests 16, no. 11: 1725. https://doi.org/10.3390/f16111725
APA StyleYao, J., Yang, M., Li, Z., Ha, D., Gao, W., He, X., Hu, X., & Song, X. (2025). A Method for Estimating Tree Age Based on the Tree Trunk Diameter and the Average Radial Growth Rate in Recent Years. Forests, 16(11), 1725. https://doi.org/10.3390/f16111725








