Optimized Low-Carbon Economic Dispatch of Island Microgrids via an Improved Sine–Cosine Algorithm

Abstract

Under the environment of globalized energy restructuring and achieving the goal of “peak carbon and carbon neutrality”, this paper proposes an optimal scheduling method based on the improved cosine algorithm for island microgrids, which relies on diesel generators, resulting in high carbon emissions and high operating costs. First, an optimal scheduling model for island microgrids is established with the objective of minimizing the system operating cost, which comprehensively considers the carbon emission penalty, power balance constraints, equipment operation constraints, and the volatility of renewable energy sources. Secondly, the traditional sine–cosine algorithm is improved by introducing an adaptive adjustment factor, elite retention strategy and chaotic mapping initialization population in order to solve its shortcomings of falling into local optimums and insufficient convergence accuracy when solving high-dimensional complex problems. Finally, the effectiveness of the proposed method is verified by simulation experiments. The results show that the method in this paper reduces the total system cost to 2994.2 yuan (6.5% lower than the baseline scenario), reduces the carbon emission to 968.8 kg (55.1% lower), and improves the wind and light consumption rate to 98.84%, which is an obvious advantage and provides a theoretical basis and technical support for the realization of the low-carbon and economic operation of island microgrids.

1. Introduction

With the continuous growth of global energy demand and the intensifying challenges brought by climate change, the global energy structure is shifting toward low-carbon development, becoming a common objective for the international community. The heavy dependence on conventional fossil fuels has considerably increased greenhouse gas emissions, posing severe risks to ecological balance and hindering sustainable societal progress [1,2]. In this context, renewable resources—particularly wind and solar energy—have become crucial forces driving the ongoing energy transition, thanks to their environmental friendliness and sustainability. In recent decades, as renewable technologies such as photovoltaic and wind power have rapidly advanced, the realization of low-carbon operation for island microgrids has become increasingly achievable. Nevertheless, the stochastic nature of renewable generation and the volatility of load demand continue to present obstacles to achieving an optimal balance between economic efficiency and environmental performance under traditional scheduling strategies [3,4,5].

Microgrid optimization scheduling is a complex, high-dimensional, nonlinear problem [6], and traditional mathematical methods often fail to provide accurate solutions. Intelligent optimization algorithms [7], due to their powerful global search capabilities and adaptability, have been widely applied in this field. Common optimization algorithms include particle swarm optimization [8], bird flock optimization [9], whale optimization [10], and bat algorithm [11]. Literature [12] considers desalination benefits and improves the gray wolf algorithm using multiple strategies, significantly reducing the scheduling cost of island microgrids. Literature [13] employs a dynamic mutation differential evolution algorithm based on mixed-integer fuzzy membership to solve the multi-objective optimization model for microgrids, achieving a higher fuzzy rank optimal trade-off solution. Literature [14] proposes an improved bat algorithm based on a horizontal crossover strategy, bidirectional learning mechanism, and conversion regulation mechanism to solve microgrid optimization scheduling models, effectively reducing microgrid scheduling costs. Literature [15] presents an improved particle swarm optimization algorithm for multi-objective optimization scheduling of microgrids, with verification demonstrating its effectiveness in reducing electricity costs, minimizing environmental pollution, and enhancing the operational efficiency of microgrids. However, the aforementioned algorithms still face challenges such as slow optimization speeds and a tendency to become trapped in local optima. Furthermore, most of these approaches focus solely on algorithm improvements and overlook the integration with carbon emission reduction strategies, thereby failing to fully unleash the potential of low-carbon economic scheduling in microgrids. Recently, scholars both domestically and internationally have begun attempting to incorporate carbon emission costs into dispatch models as endogenous variables. By introducing carbon penalty mechanisms or carbon trading systems, they aim to harmonize economic performance with low-carbon development objectives. For instance, Liu et al. [16] developed an economic scheduling framework oriented toward low-carbon operation, which integrates carbon trading into the dispatch process of isolated microgrids and illustrates how carbon price signals can guide cleaner energy allocation. Similarly, Chen et al. [17] applied a tiered carbon-trading mechanism within park-scale integrated energy systems, realizing progressive low-carbon optimization across multiple planning stages.

To address the coexistence of high carbon emissions and high operational costs in island microgrids, this study establishes an optimized low-carbon scheduling framework based on the Enhanced Sine–Cosine Algorithm (ISCA). Building upon the traditional Sine–Cosine Algorithm (SCA), this algorithm integrates adaptive adjustment factors, an elite retention mechanism, and chaotic mapping for population initialization to balance global search and local exploration capabilities. By embedding a carbon penalty component, a dispatch model tailored for low-carbon economic operation of island microgrids is thereby formulated, effectively incorporating carbon cost considerations.

The main research content and innovations of this paper are as follows:

(1) Establishing a low-carbon economic dispatch model for island microgrids incorporating carbon penalties, comprehensively considering both system operating costs and carbon emission costs;

(2) Proposes the Improved Sine–Cosine Algorithm (ISCA), enhancing global and local optimization capabilities through adaptive and chaotic strategies;

(3) Validates the model and algorithm through multi-scenario simulations, comparing economic and low-carbon performance metrics across different algorithms and carbon penalty mechanisms.

The structure of this paper is organized as follows:

Section 1 introduces the background, research motivation, and literature review on low-carbon economic scheduling of island microgrids. Section 2 introduces the modeling framework of the low-carbon economic dispatch problem and introduces the proposed Improved Sine–Cosine Algorithm (ISCA). Section 3 details the case study setup and analyzes the simulation results under various scenarios. Finally, Section 4 offers a discussion on the conclusions and suggests directions for future research.

2. Microgrid Model Incorporating Carbon Penalties

2.1. Microgrids and Their Structure

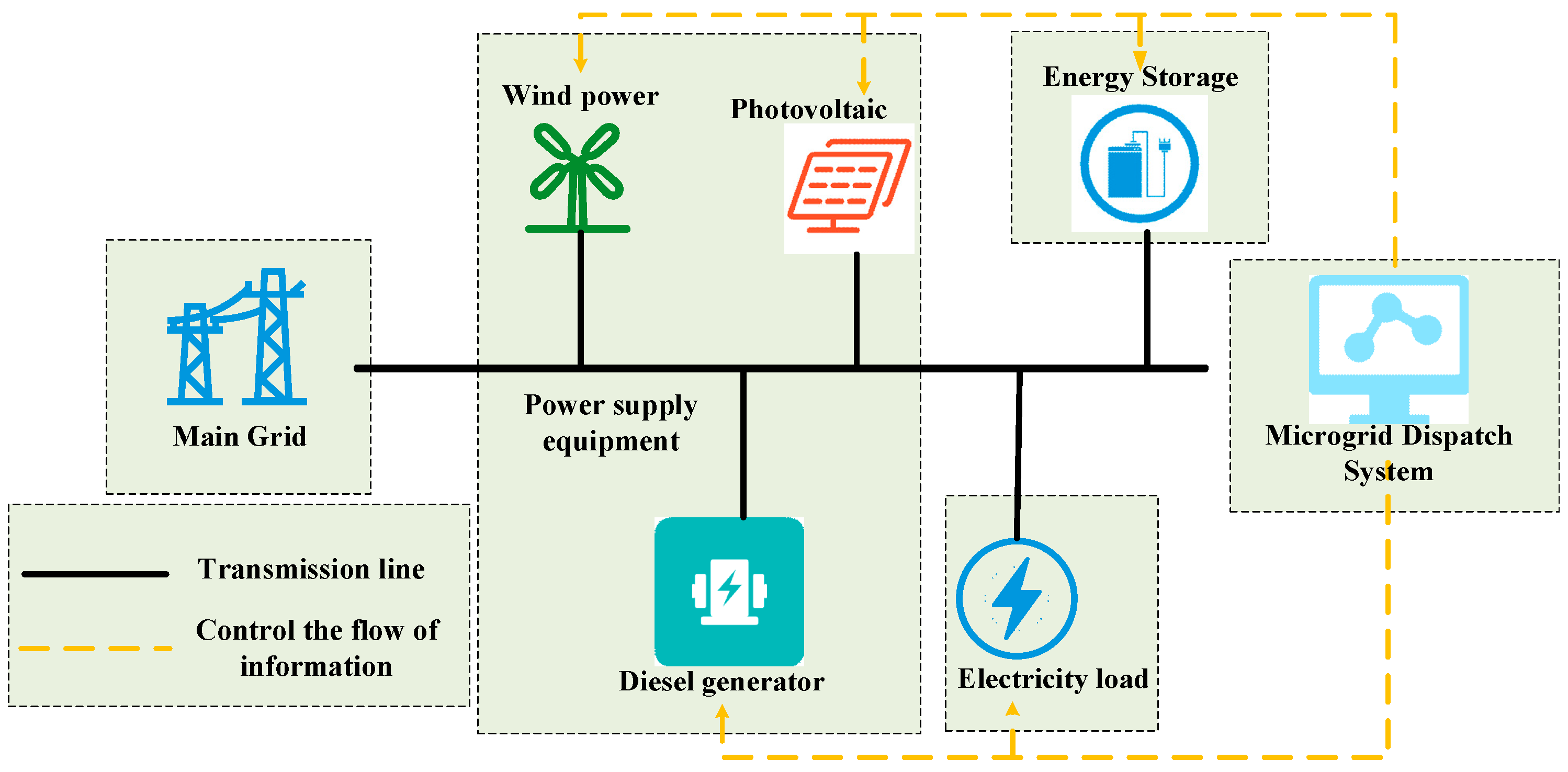
A microgrid is a small-scale, distributed energy system that integrates various energy sources such as wind turbines (WTs), photovoltaic (PV) cells, energy storage batteries, and diesel generators (DEs), along with loads, monitoring, and protection devices, to form a controllable, independent power system [18]. The microgrid constructed in this paper consists of several power generation units, including wind turbines (WTs), photovoltaic cells (PV), and diesel generators (DEs), as well as a battery storage system and electrical loads. Additionally, it can exchange electrical energy with the main grid through a common connection point. The configuration of the microgrid is shown in the figure below (Figure 1).

Figure 1. Schematic diagram of a simple model of a microgrid.

2.2. Microgrid Power Supply and Energy Storage Model

(1)

Wind Turbine (WT) Model

As a common form of renewable energy, wind turbine output mainly depends on wind velocity and the characteristics of the generation equipment. If the wind is below the cut-in threshold or surpasses the cut-out limit, the turbine cannot start and will not produce electricity. When wind speeds fall between the cut-in and rated speeds, the turbine operates normally, with the output power increasing as the wind speed rises. If the wind exceeds the rated speed but remains below the cut-out speed, the turbine maintains its rated power output. The relationship between wind speed and power generation for the WT is shown in the following formula:

$$P_{\mathrm{wd}}=\left\{\begin{array}{cc}0& v<v_{ci}, v>v_{co}\\ P_N{\displaystyle \frac{v^2-v_{ci}^2}{v_n^2-v_{ci}^2}}& v_{ci}\le v\le v_n\\ P_N& v_n<v\le v_{co}\end{array}\right.$$

(1)

In the formula, $P_{wd}$ represents the output power of the wind turbine unit; $v$ is the operating wind speed of the wind turbine; $v_n$ is the rated wind speed; $v_{ci}$ is the rated wind speed; $v_{co}$ is the cut-out wind speed; $P_N$ denotes the rated output power of the wind turbine unit.

(2)

Photovoltaic (PV) Generation Model

The power output of a photovoltaic (PV) generation unit is mainly influenced by solar irradiance, temperature, and the parameters of the solar panels. The model for the PV power output can be expressed as:

$$P_{pv}={\xi }_{pv}{P}_{pve}{G}_{dq}[1+{\xi }_u(T_u-T_{stc})]/G_{stc}$$

(2)

In the formula, $P_{pv}$ denotes the power generated by the photovoltaic unit; ${\xi }_{pv}$ is the photovoltaic power coefficient; $P_{pve}$ is the unit’s rated power; $G_{dq}$ represents the current irradiance received by the photovoltaic unit; $G_{stc}$ is the rated irradiance intensity for the photovoltaic unit; ${\xi }_u$ is the temperature coefficient for the photovoltaic unit; $T_u$ is the working temperature of the photovoltaic unit; $T_{stc}$ is the temperature of the photovoltaic unit under rated working conditions.

(3)

Diesel Generator Model

Diesel generators have a simple structure and are easy to use, making them commonly employed as power generation devices in microgrid systems. The simplified model established in this paper is as follows:

$$\left\{\begin{array}{l}{P}_{DE}(t)={\eta }_{DE}{P}_{rated}(t)\\ E_{DE}(t)={\eta }_E{P}_{DE}(t)\\ P_{DE,\min }\le P_{DE}(t)\le P_{DE,\max }\\ \mathsf{\Delta }{P}_{DE,\min }\le P_{DE}(t)-P_{DE}(t-1)\le \mathsf{\Delta }{P}_{DE,\max }\end{array}\right.$$

(3)

In the formula: $P_{DE}(t)$ represents the electrical power produced by the diesel generator at time t; ${\eta }_{DE}$ is the energy conversion coefficient of the diesel generator; $P_{rated}(t)$ is the rated power output of the diesel generator; $E_{DE}(t)$ is the carbon emission from the diesel generator during time period t; $P_{DE,\min }$ and $P_{DE,\max }$ are the minimum and maximum ramp limits of the generator’s output, respectively; $\mathsf{\Delta }{P}_{DE,\min }$ and $\mathsf{\Delta }{P}_{DE,\max }$ are the minimum and maximum ramp rates of the diesel generator’s power output, respectively. The ramping constraint is set at 30%.

(4)

Energy Storage Model

$$\left\{\begin{array}{l}{E}_S(t)=E_S(t-1)+{\displaystyle \frac{P_S(t)\cdot \mathsf{\Delta }t}{{\eta }_{ch}}}\cdot {\mathbb{I}}_{ch}-{\displaystyle \frac{P_S(t)\cdot \mathsf{\Delta }t}{{\eta }_{dis}}}\cdot {\mathbb{I}}_{dis}\\ E_{\min }\le E_S(t)\le E_{\max }\\ -P_{ch,\max }\le P_S(t)\le P_{dis,\max }\end{array}\right.$$

(4)

In the formula, $E_S(t)$ and $P_S(t)$ denote the state of charge (SOC) and the charging/discharging power at time t (negative for charging, positive for discharging), respectively; ${\eta }_{ch}$/${\eta }_{dis}$ represents the charging/discharging efficiency; ${\mathbb{I}}_{ch}$ and ${\mathbb{I}}_{dis}$ are indicator functions, showing whether the unit is charging or discharging; $P_{ch,\max }$ and $P_{dis,\max }$ are the maximum charging and discharging power, respectively; $E_{\min }$ and $E_{\max }$ represent the minimum and maximum state of charge, respectively.

2.3. Carbon Penalty Model

To improve the carbon emissions from the microgrid and encourage low-carbon operation, a price penalty range is defined for the carbon dioxide emissions produced by the system. The greater the carbon emissions, the larger the penalty coefficient, thus encouraging enterprises, factories, and other entities to reduce carbon emissions and improve energy efficiency. This paper primarily considers the carbon emissions from diesel generators, and the mathematical model for carbon emission penalties is as follows:

$$f_{C{O}_2}=\left\{\begin{array}{l}{\lambda }_{C}E,\hspace{1em}E\le l\\ {\lambda }_{C}E+{\lambda }_C(1+\delta )(E-l), l<E\le 2l\\ {\lambda }_C(2+\delta )l+{\lambda }_C(1+2\delta )(E-2l), 2l<E\le 3l\\ {\lambda }_C(3+3\delta )l+{\lambda }_C(1+3\delta )(E-3l), 3l\le E\end{array}\right.$$

(5)

In the formula, $f_{CET}$ denotes the penalty cost associated with carbon emissions for the system; $E$ is the carbon emission of the system; $l$ is the duration of each carbon emission interval; $\delta$ indicates the increment of the penalty coefficient for each emission interval; ${\lambda }_C$ is the base value of the carbon emission penalty coefficient.

2.4. Objective Function

This study proposes a model that minimizes the overall operating cost of the power grid, with the objective function expressed as follows:

$$F=\min (f_{DE}+f_{grid}+f_{op}+f_{C{O}_2}+f_{wd}+f_{pv})$$

(6)

In the formula, F represents the total scheduling cost of the microgrid system; $f_{DE}$ is the generation cost of the diesel generator; $f_{grid}$ refers to the cost associated with electricity transactions between the microgrid and the main grid; $f_{op}$ indicates the operation and maintenance expenses of the microgrid equipment; $f_{C{O}_2}$ is the carbon emission penalty cost; $f_{wd}$ and $f_{pv}$ correspond to the penalty costs for curtailment of wind and solar power, respectively.

(1) The formula for calculating the power generation cost of a diesel generator is:

$$f_{DE}=a{\left[{\displaystyle \sum _{t=1}^{24}{P}_{DE}(t)}\right]}^2+b{\displaystyle \sum _{t=1}^{24}{P}_{DE}(t)}+c$$

(7)

In the formula, $a,b,c$ is the fuel cost coefficient of the diesel generator; $P_{DE}(t)$ is the electrical power output of the diesel generator during time period t. In this paper, the three coefficients are set to the following values: 0.0002, 0.2, 1.

(2) The cost of electricity transactions between the microgrid and the main grid is the difference between the cost of purchasing electricity from the main grid and the revenue from selling electricity.

$$f_{grid}={\displaystyle \sum _{t=1}^{24}\left[{\lambda }_{buy}(t)P_{buy}(t)-{\lambda }_{sell}(t)P_{sell}(t)\right]}$$

(8)

In the formula, $P_{buy}(t)$ and $P_{sell}(t)$ represent the amounts of electricity purchased from and sold to the main grid by the microgrid during time period t, respectively; $f_{buy}(t)$ and $f_{sell}(t)$ denote the corresponding purchase and selling prices for the same period.

(3) The formulas for calculating the operation, maintenance, and depreciation costs for each piece of equipment are presented as follows:

$$f_{op}={\displaystyle \sum _{t=1}^{24}\left\{{\lambda }_{DE}{P}_{DE}(t)+{\lambda }_{wd}{P}_{wd}(t)+{\lambda }_{pv}{P}_{pv}(t)+{\lambda }_S\left[P_{ch}(t)+P_{dis}(t)\right]\right\}}$$

(9)

In the formula, ${\lambda }_{DE}$, ${\lambda }_{wd}$, ${\lambda }_{pv}$, ${\lambda }_S$ are the operation and maintenance and depreciation cost coefficients for the diesel generator, wind turbine, photovoltaic system, and energy storage device, respectively.

(4) Carbon Emission Penalty Cost is given by Equation (5).

(5) Wind and Solar Curtailment Penalty is shown as follows:

$$\left\{\begin{array}{l}{f}_{wd}={\displaystyle \sum _{t=1}^T{\lambda }_{wd}^{\prime }{P}_{wd}^{\prime }(t)}\\ f_{pv}={\displaystyle \sum _{t=1}^T{\lambda }_{pv}^{\prime }{P}_{pv}^{\prime }(t)}\end{array}\right.$$

(10)

In the formula, ${\lambda }_{wd}^{\prime }, {\lambda }_{pv}^{\prime }$ are the penalty coefficient for wind and solar curtailment; $P_{wd}^{\prime }\left(\mathrm{t}\right), P_{pv}^{\prime }\left(\mathrm{t}\right)$ represent the redundant wind and solar power during time period t.

2.5. Constraint

The constraint conditions in the microgrid operation scheduling process mainly include the output and ramping constraints of each generation unit, energy storage device constraints, system power balance constraints, and interaction power constraints with the main grid.

(1) The constraints for the diesel generator and energy storage devices are given by Equations (3) and (4).

(2) The output constraints for renewable energy sources are as follows:

$$\left\{\begin{array}{c}0\le P_{wd}(t)\le p_{wd,ref}(t)\\ 0\le P_{pv}(t)\le p_{pv,ref}(t)\end{array}\right.$$

(11)

In the formula, $p_{wd,ref}(t)$ and $p_{pv,ref}(t)$ are the forecasted power outputs of the wind turbine and photovoltaic system during time period t, respectively.

(3) System Electrical Power Balance Constraint

$$\left\{\begin{array}{l}{\displaystyle \sum _{t=1}^{24}\left[P_{DE}(t)+P_{wd}(t)+P_{pv}(t)+P_{ch}(t)+P_{dis}(t)+P_{grid}(t)\right]}={\displaystyle \sum _{t=1}^{24}{P}_{load}(t)}\\ P_{grid}(t)=P_{buy}(t)-P_{sell}(t)\end{array}\right.$$

(12)

In the formula, $P_{grid}(t)$ is the interaction power between the microgrid and the main grid during time period t.

(4) Power Interaction Constraints

$$\left\{\begin{array}{c}0\le P_{buy}(t)\le P_{grid,\max }\\ 0\le P_{sell}(t)\le P_{grid,\max }\end{array}\right.$$

(13)

In the formula, $P_{grid,\max }$ is the maximum interaction power between the microgrid and the main grid.

(5) RES inverter output constraints are represented in the model through the following optional constraints to reflect the maximum grid-connected output ratio of the inverter:

$$P^{\prime }(t)\le {\alpha }^{\prime }{S}^{\max }, 0<{\alpha }^{\prime }<1$$

(14)

In the formula, ${\alpha }^{\prime }$ is the maximum Grid-Connected Output Ratio Coefficient of the Inverter. Considering the dual-mode operation (grid-connected and islanded) of the studied microgrid, the inverter output upper limit is set to 90% of the rated power to ensure safe operation during grid switching and transient conditions. Although certain inverters can temporarily operate in overload mode (e.g., up to 120% [19]), the sustained overload capability is rarely recommended in practical dispatch scheduling.

3. Model Solving

Microgrid optimization scheduling is a highly representative optimization problem in the field of power systems, characterized by high dimensions, nonlinearity, and multiple constraints. The Sine–Cosine Algorithm (SCA) is widely favored for its simple structure, fast convergence speed, and powerful global search capability, making it particularly suitable for solving complex optimization problems. Therefore, the microgrid optimization model proposed in this paper is solved using an improved Sine–Cosine Algorithm.

3.1. Traditional Trigonometric Algorithms

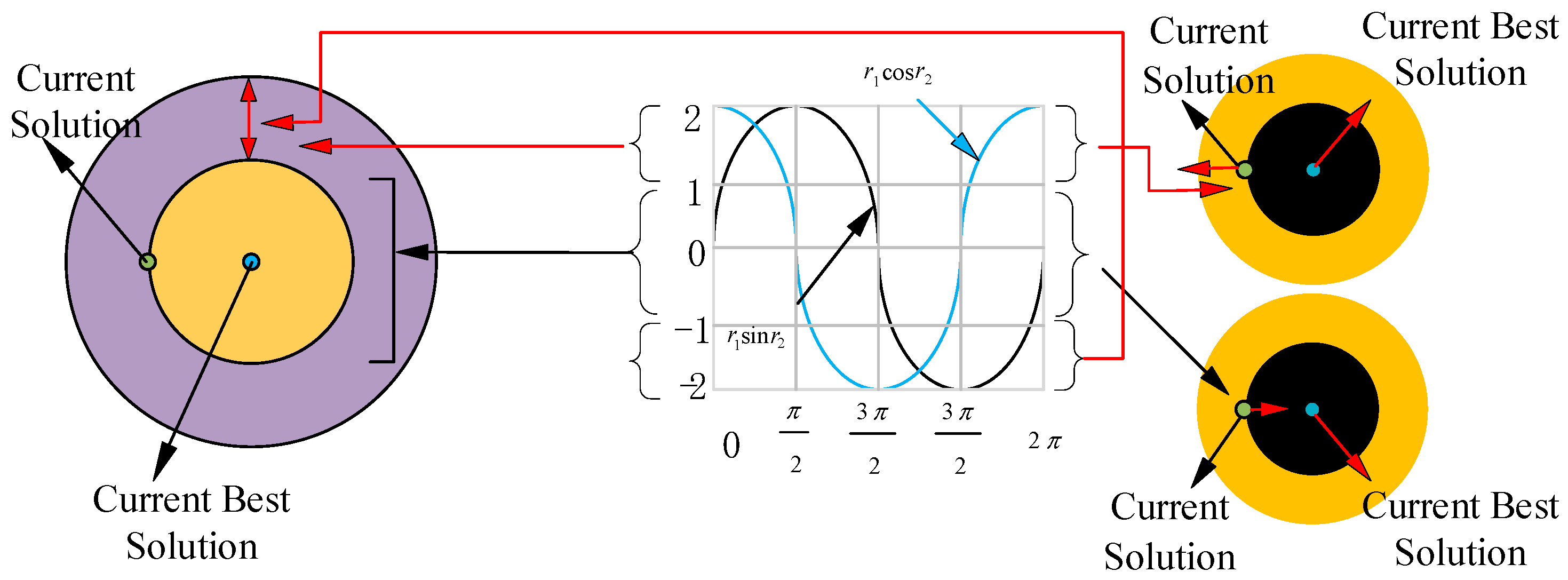
The Sine–Cosine Algorithm (SCA) is a swarm intelligence optimization method that leverages the mathematical properties of sine and cosine functions. It updates the population’s positions by simulating the oscillatory behavior of these functions, enabling the algorithm to balance global exploration and local exploitation.

The fundamental principle of SCA lies in adjusting the positions of individuals dynamically by exploiting the periodic oscillations of sine and cosine functions. During each iteration, the algorithm randomly chooses either the sine or cosine function to update an individual’s position, which facilitates broad exploration of the search space while maintaining fine-grained local search. The position update equation is defined as follows:

$$X_i^{t+1}=\left\{\begin{array}{l}{X}_i^t+r_1\times \sin (r_2)\times |r_3{X}_{best}^t-X_i^t|, \left(\mathrm{a}\right) \mathrm{if} r_4<0.5\\ X_i^t+r_1\times \cos (r_2)\times |r_3{X}_{best}^t-X_i^t|, \left(b\right) \mathrm{if} r_4\ge 0.5\end{array}\right.$$

(15)

In the formula, $X_i^t$ denotes the position of the i individual at the t iteration; $X_{best}^t$ denotes the global best solution found in the current iteration; $r_1,r_2,r_3,r_4$ are random number that control the search direction, step size, the effect of the best solution, and the switching between sine and cosine functions.

The parameter $r_1$ is a key parameter controlling the search range, and its value dynamically varies with the number of iterations, as expressed by the following equation:

$$r_1=a-t·{\displaystyle \frac{a}{T}}$$

(16)

In the formula, a is a constant (typically set to 2); t denotes the current iteration number; T indicates the maximum iteration limit.

In the early stages of the algorithm, the value of $r_1$ is relatively large, which facilitates extensive global exploration within the search space. As the iteration proceeds, $r_1$ gradually decreases, and the algorithm progressively shifts toward local exploitation, thereby enhancing the precision of the solution. A schematic diagram of the optimization process is shown below (Figure 2).

Figure 2. Schematic diagram of SCA seeking optimization.

3.2. Improved Sine and Cosine Algorithms

To overcome the limitations of the traditional Sine–Cosine Algorithm (SCA) in global exploration and local exploitation capabilities, this paper introduces an Improved Sine–Cosine Algorithm (ISCA). By incorporating adaptive adjustment factors, an elite retention strategy, and chaotic mapping for population initialization [20,21,22], ISCA significantly enhances ISCA significantly improves convergence speed and solution accuracy. It is particularly effective in solving complex optimization problems, such as those related to microgrid optimization.

3.2.1. Introduction of Adaptive Adjustment Factors

In traditional SCAs, the parameter r1 decreases linearly, which may cause premature convergence in the early stages or hinder fine-grained search in the later stages. To address this, ISCA introduces an adaptive adjustment factor that dynamically adjusts the search range and step size, balancing global exploration and local exploitation capabilities. The formula for the adaptive adjustment factor is as follows:

$$r_1=a·(1-{\displaystyle \frac{t}{T}}{)}^b$$

(17)

In the formula, a is the initial value (typically set to 2); t denotes the current iteration number; T represents the maximum number of iterations; b is a nonlinear adjustment coefficient (usually assigned a value of 2).

By nonlinearly adjusting r₁, the algorithm achieves more extensive global exploration in the early stages and more refined local exploitation in the later phases. Therefore, this mechanism aligns well with the main objective of this study—to enhance both global optimization capability and local convergence precision of the improved sine–cosine algorithm (ISCA) for achieving low-carbon economic scheduling of island microgrids. Similar nonlinear control mechanisms have been demonstrated to be effective in other swarm intelligence algorithms, such as PSO with nonlinear inertia weight and WOA with exponential decay control [23].

3.2.2. Implement an Elite Retention Strategy

To prevent the loss of high-quality solutions during the iterative process, the ISCA incorporates an elite retention strategy. This strategy preserves the current best individual in each generation, ensuring that the optimal solution is not compromised by subsequent stochastic search operations. The elite retention strategy is mathematically described by the following equation:

$$X_{best}^{t+1}=\left\{\begin{array}{l}{\mathrm{X}}_{best}^t, \mathrm{if} f{(\mathrm{X}}_{best}^t)\le f{(\mathrm{X}}_{best}^{t+1})\\ {\mathrm{X}}_{best}^{t+1}, \mathrm{otherwise}\end{array}\right.$$

(18)

In the formula, $X_{best}^{t+1}$ denotes the global best solution in the t iteration; $f(X)$ represents the fitness value of an individual.

By employing the elite retention strategy, the algorithm effectively prevents the loss of high-quality solutions, thereby enhancing both the convergence speed and stability.

3.2.3. Initialize the Population Using a Chaotic Mapping

In the standard SCA, the initial population is usually generated through random sampling, which can result in suboptimal quality and limited diversity of the initial solutions. To overcome this limitation, the improved SCA (ISCA) employs chaotic mapping for population initialization. Chaotic maps provide initial solutions with enhanced randomness and ergodicity, thereby improving both the quality and diversity of the population. In this study, the Logistic map is adopted as the chaotic mapping method, and its formulation is given as follows:

$$z_{k+1}=\mu ·z_k·(1-z_k)$$

(19)

In the formula, $z_k$ is the chaotic variable at the k iteration; $\mu$ is the control parameter (typically set to 4).

The initial solutions generated via chaotic mapping exhibit a more uniform distribution, thereby helping the algorithm avoid premature convergence to local optima and enhancing its global exploration capability.

3.2.4. ISCA Flowchart

This paper assumes that the predicted data for system load and renewable energy output are known and accurate throughout the optimization cycle, disregarding the uncertainty of random fluctuations. The algorithm assumes that equipment states are continuously adjustable during the solution process, without considering start-stop constraints.

The limitations primarily include: (1) sensitivity to initial parameters and population size; (2) inability to strictly guarantee global optimality; (3) the need to further integrate prediction correction mechanisms in complex dynamic environments.

The number of iterations for this scenario is set to T = 200. The value of iteration count T is determined based on the complexity of the calculation example and the scale of the problem. Empirically, a range of 100–300 iterations ensures convergence stability. In this paper’s scenario, T = 200 was adopted, validated through multiple simulations as optimal in balancing computational accuracy and time efficiency. The flowchart for the improved sine–cosine algorithm is shown in Figure 3.

Figure 3. Flowchart of the improved sine–cosine algorithm for solving the problem.

4. Case Study Analysis

To validate the low-carbon and economic characteristics of the proposed microgrid optimization dispatch model, the microgrid system topology described in Figure 4 is adopted as the research subject. The system operates on a 24 h cycle with a time step of one hour. The simulation environment for the case study is MATLAB R2023a, employing an improved cosine algorithm to solve the established model.

Figure 4. Simplified Topology Diagram of Island Microgrid.

4.1. Basic Data for the Example

This system is a “wind-solar-storage-diesel complementary islanded microgrid,” comprising one diesel generator, two wind turbines, one photovoltaic array, and one energy storage unit. It connects to the main grid via a public connection point (PCC), enabling both islanded and grid-connected operating modes. Wind and solar power output forecasts are shown in Figure 5, while Figure 6 depicts time-of-use electricity pricing. Within the carbon emissions penalty model, the base penalty price is set at 0.1 (RMB/kg), with each tiered penalty price incrementing by 25%. Energy storage device parameter settings are detailed in Table 1.

Figure 5. Forecasted outputs of wind, PV, and power load.

Figure 6. Time-of-use tariffs.

Table 1. Parameter settings for energy storage devices.

Content	Maximum Energy Storage Capacity/(kW·h)	Charging and Discharging Restrictions/(kW·h−1)	Charging and Discharging Efficiency/%	Initial Energy Storage State/(kW·h)
numerical value	200	±30	90	50

The feasibility of the proposed low-carbon economic dispatch model for microgrids is evaluated through four case scenarios, with detailed settings provided in Table 2. Scenario 1 serves as the baseline, without considering carbon emission penalties and employing the conventional Sine–Cosine Algorithm (SCA) for optimization. Scenario 2 introduces carbon emission penalties based on the baseline scenario. Scenario 3 further applies the Ant Colony Optimization (ACO) algorithm to solve the model established in Scenario 2. Scenario 4 adopts the improved Sine–Cosine Algorithm (ISCA) in conjunction with the carbon penalty framework of Scenario 2, representing the method proposed in this study.

Table 2. Setting information for each scene.

Scene Number	Carbon Emissions Penalty	Traditional Trigonometric Algorithms	Ant Colony Optimization	Improved Sine and Cosine Algorithms
1	×	√	×	×
2	√	√	×	×
3	√	×	√	×
4	√	×	×	√

4.2. Analysis of Case Study Results

Based on the scenario settings in the paper, this section considers the optimization results of each scenario from three aspects: operational cost, carbon reduction capability, and the output of relevant units. Additionally, a comparative analysis of several algorithms is conducted to verify the superiority of the proposed method.

4.2.1. Operating Cost and Carbon Reduction Capability Analysis

The optimization scheduling results for each scenario are summarized in Table 3, and the corresponding carbon emissions are illustrated in Figure 7. In Scenario 2, a carbon emission penalty strategy is introduced. Although this results in a moderate increase in penalty costs, carbon emissions are considerably reduced, with only a slight rise in the total scheduling cost. Furthermore, the electricity purchase cost decreases by 205.6 yuan, and the utilization rate of wind and solar power reaches 97.92%. This improvement is attributed to the penalty mechanism, which discourages high carbon emissions, leading the system to lower diesel generator output while increasing reliance on wind and solar generation, thereby reducing electricity procurement costs.

Table 3. Optimized scheduling for each scenario.

	Scene 1	Scene 2	Scene 3	Scene 4
Total Cost/CNY	3037.09	3189.41	3246.5	2994.2
Carbon Emission Penalty Cost/CNY	0	430.88	516.32	401.2
Cost of purchasing and selling electricity	851.3	645.7	684.2	612.3
Wind Power Absorption Rate/%	93.65	97.92	97.48	98.84
Carbon emissions/kg	2154.4	1028.9	1209.2	968.8

Figure 7. Carbon Emissions by Scenario.

Scenario 4 adopts the enhanced Sine–Cosine Algorithm (ISCA), which lowers the total scheduling cost by 195.21 yuan relative to the conventional SCA and by 252.3 yuan compared to the Ant Colony Optimization Algorithm. ISCA also optimizes diesel generator output and the energy storage system’s charging and discharging strategy, effectively cutting carbon emissions and improving renewable energy utilization. As a result, the wind and solar utilization rate reaches 98.84%, and carbon emissions are reduced to 968.8 kg. These findings indicate that the improved SCA offers substantial advantages in both reducing microgrid operational costs and supporting low-carbon operation.

4.2.2. Comparison of Optimization Algorithms

To assess the effectiveness of the proposed Improved Sine–Cosine Algorithm (ISCA), this study compares the optimization performance of the traditional Sine–Cosine Algorithm (SCA), Ant Colony Optimization (ACO), and ISCA under identical test conditions. The iterative convergence curves of each algorithm are shown in Figure 8. It can be observed that ISCA converges to a stable optimal value after approximately 16 iterations, demonstrating significantly faster convergence speed compared to SCA (requiring about 28 iterations) and ACO (requiring about 22 iterations). Additionally, ISCA achieves a lower objective function value, with a total system scheduling cost of 2994.2 yuan—reducing costs by 195.21 yuan compared to traditional SCA and by 252.3 yuan compared to ACO. Under the same test case, the average computation time for ISCA was 7.83 s, compared to 11.26 s for traditional SCA and 13.14 s for the ant colony algorithm. This demonstrates that the proposed algorithm exhibits a significant computational efficiency advantage.

Figure 8. Iterative diagram for solving each algorithm.

To validate result stability, 10 independent simulations were conducted with identical parameters, calculating the mean and variance of each algorithm’s optimal outcomes. The results of multiple simulations are shown in Table 4. Results show ISCA achieved an average optimal value of 2995.1 yuan with a standard deviation of 14.8, while SCA and ACO exhibited standard deviations of 28.6 and 35.9, respectively. This demonstrates ISCA’s superior stability and convergence consistency across multiple runs. Furthermore, ISCA achieved the lowest carbon emissions (968.8 kg) and the highest wind-solar integration rate (98.84%), demonstrating its advantage in coordinating dual objectives of economic efficiency and low-carbon performance.

Table 4. The results of multiple simulations.

Algorithm	Average Total Cost/CNY	Standard Deviation	Average Carbon Emissions per Kilogram	Average Wind and Solar Power Absorption Rate
SCA	3189.8	28.6	1028.9	97.92
ACO	3246.5	35.9	1209.2	97.48
ISCA	2995.1	14.8	968.8	98.84

Comprehensive analysis reveals that ISCA effectively balances global search and local exploration capabilities through adaptive adjustment factors, elite retention, and chaotic initialization mechanisms. This avoids the pitfall of traditional algorithms becoming trapped in local optima, achieving dual optimization of system operating costs and carbon emissions while ensuring computational stability. This further validates the feasibility and superiority of the proposed improved algorithm for low-carbon economic operation scheduling in island microgrids.

4.2.3. Analysis of Relevant Unit Output

The wind and solar power outputs of each scenario are shown in Figure 9. The wind utilization rate in Scenarios 2, 3, and 4 is significantly higher than in Scenario 1. This is because the carbon emission penalty strategy motivates the system to lower the output of high-carbon diesel generators and boost the utilization of wind and solar power, which significantly reduces the wind curtailment rate in the microgrid. Scenario 4 utilizes the enhanced Sine–Cosine Algorithm, further improving optimization outcomes. The wind power output in this scenario is also the highest.

Figure 9. Actual wind power outputs in different scenarios.

The specific load optimization results and output conditions for Scenario 4 are shown in Figure 10.

Figure 10. Scene 4 specific load optimization results and output situation.

As shown in Figure 9, from 01:00 to 07:00, the load is relatively low, and the diesel generator maintains a low output to avoid shutdown. The system can sell the surplus electricity to the main grid, while the energy storage device is in charging mode during the first 5 h. From 08:00 to 12:00, the load gradually increases, marking the first electricity peak of the day. The energy storage device begins discharging, and to reduce the high electricity purchase costs, the diesel generator increases its output to maintain a higher output level during the peak period. After 12:00, following the first electricity peak, the photovoltaic system generates a large amount of power, and in the next 3 h, the energy storage device starts to charge again, with a slight reduction in diesel generator output. From 17:00 to 19:00, the microgrid faces the second electricity peak of the day. The energy storage device discharges at its maximum capacity, and since the electricity purchase price is high, the system maintains the diesel generator at maximum output to minimize purchasing electricity. From 20:00 to 24:00, the electricity demand gradually decreases, and the wind power output increases. At this time, the system has surplus electricity, and the diesel generator operates at its lowest output level. The microgrid starts selling electricity to the main grid at 21:00, and the energy storage device begins charging extensively afterward. The figure also shows that the energy storage system charges during low electricity demand periods and discharges during high electricity demand periods. This helps reduce electricity purchases from the main grid and, to some extent, “shaves the peaks and fills the valleys” of the load curve, which is more favorable for system scheduling.

5. Conclusions

To promote renewable energy utilization, reduce carbon emissions from Renewable Energy Integrated Systems (RIES), and minimize operational costs, a low-carbon economic scheduling model for microgrids based on the enhanced Sine–Cosine Algorithm (SCA) is proposed. The carbon emission penalty factor is introduced, and multiple scenario cases are analyzed. Key conclusions are summarized as follows:

(1)

By comparing the models before and after introducing the carbon emission penalty, it is found that incorporating the proposed strategy into the microgrid optimization scheduling effectively suppresses the growth of carbon emissions while positively contributing to the utilization of renewable energy.

(2)

The improved Sine–Cosine Algorithm proposed in this paper exhibits higher convergence accuracy compared to the traditional Sine–Cosine Algorithm and the Ant Colony Optimization Algorithm. Under the same conditions, it results in the lowest scheduling cost and demonstrates potential for engineering applications.

(3)

This study only investigates the optimization scheduling problem of a single microgrid. In scenarios involving interconnected microgrids, distributed collaborative optimization will become an important research direction in the future.

(4)

Future work may further draw upon hybrid optimization and model predictive control (MPC) methods to achieve coordination between intraday and real-time scheduling [24].

(5)

It should be noted that heuristic algorithms still have theoretical limitations in the convergence guarantee. Future studies may explore solver-based exact optimization or deep reinforcement learning (DRL)-based adaptive scheduling to achieve dynamic and long-term energy management. Furthermore, integrating hydrogen and battery hybrid systems within multi-energy microgrids could further enhance low-carbon, intelligent, and sustainable energy operation.