A Holistic Framework for Optimizing CO₂ Storage: Reviewing Multidimensional Constraints and Application of Automated Hierarchical Spatiotemporal Discretization Algorithm

Abstract

Climate change mitigation demands scalable, technologically mature solutions capable of addressing emissions from hard-to-abate sectors. Carbon Capture and Storage (CCS) offers one of the few ready pathways for deep decarbonization by capturing CO₂ at large point sources and securely storing it in deep geological formations. The long-term viability of CCS depends on well control strategies/injection schedules that maximize storage capacity, maintain containment integrity, ensure commercial deliverability and remain economically viable. However, current practice still relies heavily on manual, heuristic-based well scheduling, which struggles to optimize storage capacity while minimizing by-products such as CO₂ recycling within the high-dimensional space of interdependent technical, commercial, operational, economic and regulatory constraints. This study makes two contributions: (1) it systematically reviews, maps and characterizes these multidimensional constraints, framing them as an integrated decision space for CCS operations, and (2) it introduces an industry-ready optimization framework—Automated Optimization of Well control Strategies through Dynamic Time–Space Discretization—which couples reservoir simulation with constraint-embedded, hierarchical refinement in space and time. Using a modified genetic algorithm, injection schedules evolve from coarse to fine resolution, accelerating convergence while preserving robustness. Applied to a heterogeneous saline aquifer model, the method was tested under both engineering and financial objectives. Compared to an industry-standard manual schedule, optimal solutions increased net stored CO₂ by 14% and reduced recycling by 22%, raising retention efficiency to over 95%. Under financial objectives, the framework maintained these technical gains while increasing cumulative cash flow by 23%, achieved through leaner, smoother injection profiles that minimize costly by-products. The results confirm that the framework’s robustness, scalability and compatibility with commercial simulators make it a practical pathway to enhance CCS performance and accelerate deployment at scale.

1. Introduction

Climate change remains an existential challenge, with recent data indicating a troubling acceleration in global greenhouse gas emissions. According to the 2024 Global Carbon Budget presented at COP29, global CO₂ emissions reached an all-time high of 41.6 billion tonnes, up from 40.6 billion tonnes in 2023 [1]. Of this total, approximately 37.4 billion tonnes originated from fossil fuel combustion, while land-use changes such as deforestation contributed an additional 4.2 billion tonnes [1]. Despite record-breaking progress in renewable energy—highlighted by the installation of over 450,000 megawatts of new capacity in Asia alone in 2024, the deployment of low-carbon technologies continues to lag behind the accelerating pace of energy demand, urbanization and industrial activity [2]. This imbalance underscores a pivotal moment in climate strategy: renewables alone cannot bridge the emissions gap. Therefore, scalable and technologically mature solutions, such as Carbon Capture and Storage (CCS), are urgently required to complement the energy transition and address emissions from hard-to-abate sectors [3,4,5].

Among complementary solutions, CCS stands out as one of the few technologically ready options capable of delivering deep emissions reductions in sectors where decarbonization remains intrinsically challenging [6]. CCS involves capturing CO₂ directly at large point sources—such as fossil-fuel-based power plants and industrial facilities—and permanently storing it in deep geological formations, thereby preventing its release into the atmosphere. In the power sector, CCS enables significant reductions in carbon intensity without undermining system reliability, offering a pragmatic transitional pathway for regions that remain reliant on fossil fuels. More critically, CCS is indispensable for hard-to-abate industries such as cement, steel, and chemicals, where emissions arise not only from energy use but also from high-temperature reactions and molecular transformations inherent to production processes that cannot yet be addressed by electrification or renewable energy. As such, CCS forms a foundational component of any credible net-zero strategy [7].

The viability of any CCS project depends on the seamless integration of its three fundamental components: CO₂ capture, transportation, and geological storage [7]. These elements must function as a tightly coupled system to enable efficient capture, timely delivery and secure long-term containment of emissions. Among them, geological storage emerges as the critical bottleneck—and ultimately, the key determinant of project success [8]. This stage involves injecting CO₂ into deep subsurface formations such as saline aquifers or depleted hydrocarbon reservoirs, both of which offer substantial storage capacity and containment integrity. Deep saline aquifers alone present a globally significant storage potential, estimated between 400 and 10,000 gigatonnes of CO₂ [9]. However, geological storage is not solely a matter of volumetric capacity; it also governs the continuity of injection operations, the ability to provide reliable storage services to capture facilities, and the scalability of the entire CCS chain. Operational challenges such as injectivity decline [10], pressure buildup [9], or deviations from expected storage capacity can compromise the broader system, disrupt operational targets, and trigger cascading financial or contractual repercussions. Mitigating these risks requires rigorous, early-stage multiscale subsurface characterization to assess technical feasibility, commercial viability, long-term containment security, and compliance with regulatory standards [11]. This characterization process, as outlined in the European Union’s CCS legislative framework—the EU CCS Directive 2009/31/EC (Annex I) and its accompanying guidance documents—proceeds in two complementary phases: foundational characterization and advanced characterization [12].

The first characterization phase—foundational characterization—establishes the technical and geological viability of a storage site through comprehensive subsurface data acquisition and integrated modeling. This phase involves collecting a suite of geological, geophysical, hydrogeological, seismicity, geochemical, and geomechanical datasets to enable a multidimensional assessment of storage feasibility and containment risks. Particular emphasis is placed on identifying natural or anthropogenic features—such as faults, fractures, or legacy wells—that could compromise long-term integrity. The primary output is a high-resolution three-dimensional static geological model capturing critical subsurface features, including structural traps, stratigraphic discontinuities, pore connectivity and baseline fluid saturations. This static framework is then coupled with fluid flow modeling, culminating in dynamic reservoir simulations that forecast CO₂ plume migration, pressure evolution and reservoir response under various operational scenarios [13]. Together, these models form a digital twin of the subsurface storage complex—a strategic asset for estimating dynamic capacity, informing injection strategies, defining field development parameters, and setting monitoring thresholds. Crucially, this modeling workflow is iterative, evolving throughout the project lifecycle as new data become available, thereby serving as a living decision-support system.

The second phase—advanced characterization—focuses on operational readiness and proactive risk mitigation, building upon the integrated static–dynamic model foundation. At this stage, a site-specific field development plan is designed, with particular emphasis on well control strategies. These strategies are progressively refined to enhance field injectivity and storage capacity while maintaining pressures below geomechanical thresholds, ensuring safe and contained plume migration within the storage formation. Reactive transport modeling is incorporated to capture geochemical and geomechanical interactions that may affect caprock integrity or create potential vertical leakage pathways. This phase also integrates probabilistic and sensitivity analyses to quantify uncertainties, improve model robustness and guide the definition of resilient operational strategies. Based on these insights, a site-specific containment risk assessment framework is developed to evaluate potential failure modes, exposure pathways and long-term performance indicators. Collectively, these assessments inform the development of the project’s Monitoring, Measurement, and Verification (MMV) plan and Corrective Measures (CM) plan—two technical and regulatory pillars that ensure operational transparency, public confidence, and compliance across both injection and post-injection monitoring periods [13].

While workflows for site and reservoir characterization are becoming increasingly standardized, several persistent challenges continue to hinder their practical execution. In the foundational phase, three core issues dominate: limited availability of subsurface data, high uncertainty in key geological parameters, and the inherent complexity of heterogeneous formations. These challenges are particularly acute in saline aquifers, frontier basins, and offshore settings, where well log coverage and seismic resolution are often sparse or incomplete. Addressing these limitations requires integrating advanced geophysical acquisition methods, high-resolution inversion techniques, and probabilistic modeling frameworks to enhance data density, interpretability, and geological realism. Iterative model updating—where new field data and monitoring results are continuously assimilated—helps reduce epistemic uncertainty and improve model convergence over time. Complementary numerical tools, such as computational fluid dynamics and reactive transport simulations, further support the characterization process by providing insight into the coupled flow, transport, and geochemical processes that govern subsurface CO₂ behavior. Together, these methods help de-risk early-stage decisions and increase confidence in site selection and development strategies [9].

In the advanced characterization phase, well control strategies emerge as the operational backbone of the field development plan—and, by extension, the entire CCS deployment effort. These strategies dictate how, when, and where CO₂ is injected into the reservoir, directly influencing storage capacity, injection efficiency, containment security, and financial viability [14]. Despite their critical role, the development of well control strategies remains largely manual, relying on empirical heuristics, “rules of thumb,” and expert-led iterative reservoir simulations [15]. While these methods draw upon valuable field experience and historical precedent, they increasingly fall short when confronted with the full complexity of geological systems and the vastness of the potential design space.

The shortcomings of manual well control planning are not merely procedural but structural, rooted in a multidimensional landscape of interdependent constraints spanning five key domains: technical, commercial, operational, economic, and regulatory. These constraints do not act in isolation; rather, they are deeply interconnected, collectively defining a complex and evolving design space that challenges intuition-driven decision-making:

• Technical constraints encompass subsurface policies and engineering limits designed to safeguard storage integrity and security. For example, pressure buildup during injection can induce mechanical stress on the caprock or reactivate faults and fractures, posing significant containment risks [16,17]. To mitigate these risks, operators embed such constraints into injection strategy design—often adopting conservative measures such as limiting injection rates or wellhead pressures—which can underutilize pore space and reduce overall storage capacity [18].
• Commercial constraints arise from long-term contractual obligations mandating consistent CO₂ intake over project lifespans, often exceeding a decade. Storage operators commit to delivery agreements with capture facilities based on uninterrupted injection profiles that typically match the capture rate. Consequently, well control strategies—manual or otherwise—must align with these commercial commitments.
• Operational constraints stem from the physical and mechanical limitations of the injection infrastructure. Parameters such as surface facility capacity (e.g., brine or CO₂ treatment) in brownfield developments, offshore throughput limitations, tubing diameter, and wellbore integrity define strict operational envelopes that further complicate the design of optimal injection strategies [18].
• Economic constraints introduce trade-offs between pressure management and project cost. While strategies such as brine extraction can enhance injectivity by reducing formation pressure, they entail significant capital and operating expenditures [19]. Minimizing unintended CO₂ recycling is equally critical to maximize net storage and reduce costs, adding another layer of financial complexity.
• Regulatory constraints reflect the legal imperative to contain the CO₂ plume within the permitted storage site. Any migration beyond these boundaries—whether toward the broader storage complex or outside it—triggers compliance violations and costly corrective actions as stipulated in the CO₂ storage permit. Such outcomes can delay operations, increase financial burden, threaten permit revocation, and erode stakeholder confidence [12].

Taken together, these interdependent constraints reveal the fundamental limitations of manual, experience-based well control planning. As CCS projects scale in size and complexity, reliance on heuristic approaches becomes increasingly untenable. Navigating this high-dimensional, constraint-driven design space requires a paradigm shift toward systematic, optimization-based frameworks capable of balancing technical, operational, commercial, economic, and regulatory requirements in an integrated manner.

Building on these insights, this work makes a twofold contribution.

(1)

It systematically maps the multidimensional constraints—technical, commercial, operational, economic, and regulatory—that govern well control strategies in geological CO₂ storage projects, with particular attention to how these constraints interact across spatial and temporal scales.

(2)

It introduces a novel computational framework, titled Automated Optimization of Well Control Strategies Through Dynamic Time–Space Discretization. This framework integrates reservoir engineering fundamentals with advanced optimization techniques to automate the design of well control strategies. It is adaptable to site-specific complexities and is designed to co-optimize CO₂ storage capacity and overall field-scale performance. By enhancing injection efficiency under cost and commercial constraints, the framework enables operators to accommodate high-volume emitters and deliver economically viable, large-scale storage solutions.

Conceptually, the framework resembles the resilience and adaptability of offshore Tension-Leg Platforms (TLPs) [20], which maintain stability under shifting environmental loads through a balance of flexibility and anchoring. Similarly, the framework is engineered for optimization stability under evolving project conditions. At its core is a derivative-free Genetic Algorithm (GA) [21,22], modified for efficiency by reusing optimal solutions from earlier stages as initial guesses for subsequent stages, thereby accelerating convergence without sacrificing robustness. This core is supported by three foundational components/”anchors”:

• Automated and industry-ready integration: The framework automatically updates well control strategies in response to changing subsurface models, operational constraints or business priorities. Fully compatible with commercial reservoir simulators, it integrates seamlessly into existing industrial workflows, enabling deployment without disrupting established workflows.
• Dynamic adaptability to operational cadence: A hierarchical greedy optimization process runs over discretized time–space domains, accommodating any field management approach—from coarse, infrequent rate adjustments to fine, high-frequency well-by-well changes. This modular structure supports interruptible, resumable runs that align with actual operational decision cycles.
• Embedded, real-world constraints: Technical, operational, commercial, and economic limits are incorporated directly into the optimization logic, hard bounds, logical conditions, or penalized soft constraints—ensuring that every computed strategy is both computationally optimal and practically deployable.

Collectively, these components deliver a scalable, adaptable, and computationally efficient solution for optimizing well control strategies in CO₂ storage projects. By maximizing injection performance within real-world constraints, the framework offers a robust pathway to improve operational effectiveness, unlock greater storage potential, and reduce the economic barriers that currently limit the scalability of CCS.

The remainder of this paper is organized as follows. Section 2 defines the multidimensional constraints that shape well control strategy design in carbon storage projects, framing them as interdependent factors that necessitate a systematic approach. Section 3 introduces the proposed optimization framework, detailing its mathematical formulation, objective function, constraint integration and algorithmic structure. Section 4 demonstrates the application of the framework, evaluating its ability to optimize overall field performance from two distinct yet complementary perspectives—engineering and financial—under realistic site conditions. Finally, Section 5 concludes the manuscript by summarizing the key findings and outlining directions for future research.

2. Multidimensional Constraints in Well Control Strategies

This Section establishes the conceptual and technical foundation necessary to understand the multidimensional constraints governing well control strategies in CO₂ storage projects. We begin by outlining the essential physical and geological context—including storage formation types, subsurface dynamics and the governing mechanisms of CO₂ behavior—that inform the formulation of these constraints.

The range of constraints that define the feasible design space for well control strategies includes technical constraints such as pressure limits; commercial constraints encompassing delivery obligations and contractual agreements; operational constraints related to infrastructure capacity and well deliverability; economic constraints embedding trade-offs (e.g., brine production) that affect project viability; and regulatory constraints imposing limits on plume migration and conformance. The interaction of these constraints across spatial and temporal scales creates a complex, high-dimensional and strongly coupled optimization landscape, necessitating a balanced approach between localized reservoir behavior and broader system-wide objectives.

2.1. Geological Storage Principles

Geological CO₂ storage relies predominantly on two dedicated options, depleted oil and gas reservoirs [23] and deep saline aquifers [24], each offering distinct advantages and presenting unique challenges.

Depleted reservoirs are particularly attractive due to their well-characterized subsurface properties, established infrastructure, and demonstrated ability to retain hydrocarbons over geological timescales. The availability of existing wells and historical production data enhances reservoir modeling accuracy, reducing uncertainties related to storage capacity and injectivity [23]. Furthermore, the potential for CO₂-enhanced hydrocarbon recovery offers economic incentives, potentially improving project viability [25,26]. However, risks include the possibility of leakage through legacy wells, pressure-induced fault reactivation and infrastructure degradation, all of which necessitate rigorous integrity assessments before repurposing assets for CO₂ injection [27,28].

In contrast, deep saline aquifers offer greater storage capacity and are more geographically widespread, positioning them as the most scalable long-term solution [29]. These formations, typically composed of brine-saturated porous rocks, remain underexplored compared to hydrocarbon reservoirs, resulting in higher uncertainty in geological characterization [30]. Key challenges include the absence of baseline well data, high upfront infrastructure investment, and the time-intensive and computationally complex nature of dynamic reservoir modeling [31,32]. In addition, pressure management poses significant risks particularly in closed or semi-closed systems where brine displacement and induced seismicity can pose operational risks. These storage options and their variations—including hybrid approaches that combine carbon storage with enhanced hydrocarbon recovery—are conceptually depicted in Figure 1, which outlines the major categories of geological CO₂ storage.

Once injected, CO₂ is retained in geological formations through four principal mechanisms that evolve over varying timescales: structural/stratigraphic trapping, residual trapping, solubility trapping and mineral trapping [33]. In the short term, structural and stratigraphic trapping—relying on impermeable caprocks or sealing faults—prevent CO₂ migration and account for the majority of initial containment (60–80%). Solubility trapping provides a safe trapping mechanism because CO₂ dissolved in brine (or oil) is unlikely to abandon the solution unless a significant pressure drop occurs at the storage site. Furthermore, when CO₂ is dissolved in brine, the CO₂–brine solution density increases, resulting in convective mixing, which acts to prevent buoyant CO₂ flow toward the caprock [34,35]. Residual trapping follows by immobilizing CO₂ in pore spaces via capillary forces, contributing 10–20% sequestration depending on rock characteristics. Over longer periods, solubility trapping dissolves CO₂ into formation brine, reducing buoyancy and migration risks and contributing 10–30% to containment [36,37]. Mineral trapping, although slow to initiate, gradually converts dissolved CO₂ into stable carbonate minerals, securing storage over millennial timescales—especially in formations rich in reactive minerals such as basalts [38,39]. Figure 2 illustrates how the relative importance of each trapping mechanism shifts over time and collectively ensures long-term storage security.

The interplay of these trapping mechanisms is strongly influenced by reservoir lithology, injection strategy, and operational timescales. Acting in concert, they provide both immediate containment and long-term storage security, collectively forming the scientific and engineering basis for safe, scalable geological CO₂ sequestration.

2.2. Multidimensional Constraints in CO₂ Storage Well Control Strategies

The design and execution of well control strategies in CCS projects are governed by a complex set of multidimensional constraints. These constraints arise from the interplay of subsurface physics, operational envelopes, regulatory standards, and economic objectives—each imposing limits on feasible decisions and optimization potential. This Section categorizes and analyzes these constraints, explicitly linking each to its impact on well control design, particularly in defining permissible injection rates and pressures. Understanding their nature and interdependencies is essential for developing robust, safe, and scalable injection strategies.

2.2.1. Technical Constraints: Subsurface

Successful CO₂ storage depends not only on accurate modeling of reservoir behavior but also on strict adherence to subsurface engineering policies that ensure geomechanical stability and containment integrity. These technical policies define operational thresholds—such as maximum allowable pressure, injectivity limits and fault stability criteria—that establish the feasible domain for well control decisions. As such, they represent hard constraints that must be embedded within any optimization strategy, particularly under long-term liability and regulatory oversight.

Pressure Build-Up and Geomechanical Complications

Commercial-scale CO₂ storage requires injecting substantial volumes of CO₂ into deep subsurface formations, displacing native fluids and increasing pore pressure within the reservoir. The magnitude of this pressure build-up is primarily governed by the storage system’s boundary conditions—whether it is closed, semi-closed, or open [40]. These characteristic pressure responses are schematically illustrated in Figure 3.

In closed systems, such as depleted hydrocarbon reservoirs or confined saline aquifers, pressure dissipation is minimal due to the absence of fluid outflow pathways [40,41]. While this containment reduces the risk of unintended fluid migration, it imposes a stringent operational constraint: injection-induced pressure must remain below the formation’s fracture threshold. Exceeding this threshold risks compromising caprock integrity or reactivating faults, potentially leading to containment failure [42]. Unlike conventional hydrocarbon reservoirs—where pressure behavior is well-documented from decades of production experience—CO₂ injection into deep saline aquifers presents unique challenges. These formations are typically saturated with nearly incompressible brine, causing even modest CO₂ volumes to trigger rapid pressure escalation. If unmanaged, such pressure increases can create new flow pathways for CO₂ migration or displace brine into overlying formations, heightening the risk of groundwater contamination.

Semi-closed and open systems allow partial pressure relief through mechanisms such as brine migration into semi-permeable formations or lateral fluid flow [43]. Nonetheless, commercial-scale injection in these settings can still lead to significant pressure increases that limit effective storage capacity.

Previous research, including the work of Szulczewski et al. [44], has demonstrated that in the short term, maximum allowable reservoir pressure is the dominant constraint on injectivity and storage, while in the long term, pore volume availability becomes more limiting. Therefore, pressure build-up and associated geomechanical risks represent foundational constraints in well control strategy formulation, extending beyond injectivity management to influence the fundamental feasibility and safety of storage operations.

Geological Storage Security: Improving Residual and Solubility Trapping

At depths exceeding 800 m, CO₂ is injected in a supercritical state, where pressure and temperature favor its dense and mobile form. Long-term containment depends on effective trapping mechanisms, with residual trapping and solubility trapping being the most actively influenced by injection strategies, and therefore key constraints in well control design [33].

Residual trapping immobilizes CO₂ within pore spaces via capillary forces, while solubility trapping reduces buoyancy by dissolving CO₂ into formation brine, thus increasing its density. Both mechanisms provide more immediate risk reduction than mineral trapping, which occurs over geological timescales and is largely unalterable during a project’s operational lifespan. Optimizing injection parameters—such as rate, timing, and fluid composition—can enhance residual trapping by increasing the proportion of disconnected CO₂ ganglia and improve solubility trapping by promoting greater brine–CO₂ contact [45,46,47,48]. Techniques such as water-alternating-gas injection exemplify [49] these approaches. Well-designed injection schedules can significantly reduce reliance on structural trapping, thereby minimizing leakage risk and improving operational safety.

Maximizing residual and solubility trapping thus constitutes a critical design constraint for ensuring both short-term containment and long-term storage security, while meeting safety requirements and regulatory standards.

2.2.2. Commercial Constraint: Constant Field Intake

The constant field intake commitment represents a hybrid constraint in CCS projects—originating from commercial imperatives and ultimately acquiring legal enforceability—with direct implications for well control strategies and optimization planning [50,51]. It is fundamental to ensuring long-term project viability, aligning the interests of capture and storage entities, and securing financing across the CCS value chain [52].

At the business model level, this constraint reflects the essential service relationship between CO₂ storage operators and emitters, typically large industrial facilities or power plants. Storage operators must provide injection and containment services that are synchronized with the steady-state CO₂ output of capture facilities [53]. To ensure alignment, a predictable and continuous CO₂ intake must be guaranteed over a multi-year horizon—typically a minimum of ten to fifteen years—matching the emitter’s capture profile and investment lifecycle [50].

For example, a cement producer emitting 1.5 Mtpa of CO₂ would only proceed with a Final Investment Decision (FID) on a capture facility if it could secure sufficient storage capacity and injectivity to accommodate 1.5 Mtpa consistently over a contractual duration, such as 15 years. Similarly, a storage operator would only proceed with its own FID if it could secure predictable and sustained CO₂ intake commitments from multiple emitters. Consequently, the storage field development plan must be tailored to meet the forecasted delivery volumes from one or more clients, requiring well control strategies that support both subsurface constraints and commercial obligations [15].

This model parallels operational frameworks in natural gas pipeline systems, where flow and pressure must be maintained continuously to meet supply contracts [50]. However, CCS operations are subject to stricter constraints due to the requirement for permanent CO₂ containment, the complexity of reservoir behavior, and the absence of flexible surface storage. As a result, CO₂ injectivity must remain stable, and pressure regimes must be carefully managed throughout the project lifetime. These conditions place increased demands on well control strategies, which must ensure continuous injection performance that satisfies both technical and commercial standards [15]. Figure 4 illustrates the commercial interface between a CO₂ capture facility and a storage operator where well control strategies must therefore be robust enough to accommodate maximizing injection performance across the field to support multiple emitters and optimize revenue.

Before permitting, the operator typically conducts a non-binding market test—a structured process to assess interest from potential CO₂ suppliers and allocate available injection capacity. This is analogous to capacity auctions in electricity markets, where grid operators distribute transmission capacity to optimize usage. In the CCS context, the market test identifies CO₂ volumes from emitters—usually fixed annual quantities reflecting capture facility output—so that the operator can match and maximize the field intake, accordingly, thereby validating the project’s economic and technical feasibility [50,52,53].

Once market intelligence is collected and the injection plan is optimized for constant field intake, the operator submits it as part of the storage permit application to the competent authority. This submission includes comprehensive technical documentation—geological characterization, dynamic reservoir modeling, risk assessments, and environmental impact reports. Upon approval, the operator receives the legal right to inject CO₂ according to the permitted design and schedule [12,13].

Subsequently, the operator negotiates and finalizes binding agreements with emitters. These contracts define CO₂ volumes, delivery schedules, stream specifications, pricing structures, and penalty clauses for non-compliance. At this stage, what began as a business preference becomes a regulatory and contractual obligation, akin to a power purchase agreement (PPA) in the energy sector [50,51]. These agreements guarantee that emitters will deliver, and operators will receive and inject fixed volumes of CO₂ annually, ensuring the predictability needed to secure financing and maintain regulatory compliance.

2.2.3. Operational Constraint: Feasible Injection Rates and Well Control Adjustments

A key operational constraint in CCS project design is the feasible injection rate for each well, reflecting the mechanical thermal, and reservoir limits within which CO₂ can be injected safely and efficiently. These bounds (lower and upper) define the operating window and are influenced by wellbore design, formation pressure, temperature gradients, and surface infrastructure capacity [54,55].

Mechanically, the internal diameter of the injection tubing sets an upper limit on volumetric flow capacity. For instance, a typical 5.5-inch tubing can accommodate up to approximately 1500 metric tons of CO₂ per day under ideal conditions. However, thermal stresses—arising from large temperature differentials between the injected CO₂ and the surrounding formation—can reduce this limit significantly. A temperature difference of 100 °C, for example, may cause material fatigue, cement debonding, or stress relaxation near the wellbore and within the reservoir [56,57]. Such effects often necessitate derating the maximum injection rate to around 1000 metric tons per day, unless thermal mitigation measures (e.g., preheating the CO₂) are applied.

In addition, pressure constraints impose further operational boundaries. Injected CO₂ must not elevate reservoir pressure beyond critical thresholds, most notably the formation fracture pressure (FFP). Operating too close to this limit increases the risk of fracturing, caprock breach, or induced seismicity. For example, in a reservoir with an initial pressure of 2500 psi and a fracture pressure of 4000 psi, the feasible injection rate might start at 1200 metric tons per day but would need to be reduced to around 800 metric tons per day as reservoir pressure builds over time. These pressure-dependent limitations introduce a time-varying element to well control strategies, requiring continuous monitoring and adjustment [58]. Figure 5 illustrates the time-dependent interaction between mechanical, thermal and reservoir pressure constraints that define the evolving feasible injection envelope.

Ultimately, feasible injection rates represent a non-negotiable operational constraint. This constraint is typically implemented as an upper bound on injection rates at each well and time step. The challenge is to anticipate the dynamic nature of these bounds and embed this adaptability within automated control frameworks.

2.2.4. Economics Constraints

Economic constraints in CCS projects are critical for ensuring financial sustainability over the project lifecycle while maintaining operational feasibility and regulatory compliance. These constraints shape well control strategy design by introducing trade-offs between cost, injectivity, and storage efficiency. Two of the most impactful are:

(i)

balancing brine production to control costs while preserving injectivity and integrity;

(ii)

minimizing CO₂ recycling, which directly affects storage efficiency and operational expenditures.

Balanced Brine Production and Cost Optimization

Balanced brine production represents an important economic constraint influencing both reservoir performance and cost structure. The focus on balance—rather than minimization—reflects the dual role brine production plays: while it incurs treatment and disposal costs, it is often essential for managing reservoir pressure, especially in closed or semi-closed systems operating at commercial scale [59,60].

On one hand, brine extraction relieves pressure, reducing the risk of caprock fracturing, fault reactivation, or induced seismicity [60]. On the other hand, unnecessary or excessive brine production raises both capital expenditure (CAPEX)—due to handling infrastructure—and operational expenditure (OPEX) from pumping, transporting, treating and disposing of the fluid [60,61]. These costs are particularly significant offshore, where infrastructure is more complex and regulatory requirements are stricter.

Brine management strategies are highly context dependent. Closed systems may require active brine production to maintain injectivity, whereas open systems with natural pressure dissipation may need relatively minimal intervention. In all cases, optimal handling requires integrated planning—combining reservoir simulation, geomechanical modeling, and surface facility design—to size pumps, pipelines, and treatment units according to projected volumes and operational timelines [62].

Well control strategies are central to this balance. Embedding brine production constraints into optimization frameworks enables operators to maintain a “balance” on different project components such as injectivity, contain CAPEX and OPEX within viable limits and strengthen long-term project economics.

Minimizing CO₂ Recycling for Efficiency and Cost Reduction

Unlike brine production, which requires careful calibration, CO₂ recycling is a clear economic liability. Recycling occurs when injected CO₂ prematurely returns to the surface, typically due to reservoir heterogeneities, preferential flow paths, or suboptimal injection strategies [63]. Each recycling event reduces net storage capacity and imposes operational and financial burdens.

The economic impact is substantial. Recycled CO₂ must be reprocessed, recompressed, and reinjected, consuming energy, straining surface infrastructure, and increasing OPEX through higher power and maintenance costs [64]. Persistent recycling may even require expanded processing capacity, inflating CAPEX. In severe cases, it can undermine the business case for long-term storage.

Technically, CO₂ recycling signals poor sweep efficiency, uneven plume migration, and underutilized storage zones—issues common in stratified or low-permeability reservoirs. These inefficiencies not only lower storage utilization but can also increase overpressure risk and reduce the predictability of long-term containment [65].

Effective well control strategies must shift from reactive management to proactive optimization, forecasting potential breakthrough events, adjusting injection rates, refining well locations, and dynamically ultimately designing optimal injection schedules based on reservoir feedback. Embedding CO₂ recycling constraints into automated control workflows allows optimization algorithms to maintain stable plume distribution, maximize net storage efficiency, and minimize reinjection costs.

2.2.5. Regulatory Constraint: Ensuring CO₂ Containment Within Licensed Boundaries

A fundamental regulatory constraint in CCS projects is the requirement to ensure that injected CO₂ remains confined within the licensed storage site boundaries. This is particularly critical in open and semi-closed geological systems, where complex pressure regimes and lateral connectivity increase the likelihood of unintended plume migration beyond the permitted zone [66,67]. In fully closed systems, containment relies mainly on structural and stratigraphic barriers, whereas open formations often require active operational controls to prevent plume advance into unauthorized areas.

The licensed boundary is more than a legal perimeter—it is a dynamic design constraint with direct implications for storage security, environmental risk, and regulatory compliance [12]. Breaching it can result in permit violations, legal penalties, reputational damage and potentially severe environmental impacts. For this reason, plume confinement must be embedded as a core design objective within well control strategies. Figure 6 illustrates a top view of a storage site and complex, showing CO₂ plume migration beyond the licensed storage site into the broader complex and potentially beyond permitted limits.

Regulatory frameworks typically require predictive modeling, supported by site-specific dynamic reservoir simulations, to demonstrate that the CO₂ plume will remain within licensed limits throughout the project lifecycle [13]. From a well control perspective, these constraints influence injection rates, well placement, zonation strategies, and pressure management. Aggressive injection may boost short-term injectivity but can accelerate plume migration, increasing lateral escape risk. Mitigation options include brine extraction for pressure relief, staggered or cyclic injection to moderate plume advance and zonal injection control to restrict flow to targeted intervals.

In summary, regulatory CO₂ containment constraints are non-negotiable design boundaries that must be embedded within well control strategy architecture. Their significance is heightened in open and semi-closed systems, where containment cannot rely solely on static geological barriers.

2.2.6. Interconnection of Key Constraints in Well Control Strategies

In CO₂ storage, well control strategies are governed by a tightly coupled network of technical, operational, regulatory, commercial, and economic constraints. These factors interact dynamically across spatial and temporal scales, so an adjustment to meet one constraint often propagates through others, creating trade-offs and feedback loops.

For example, brine extraction—primarily an operational measure to maintain reservoir pressure below critical thresholds—also affects economic constraints by increasing the volume of brine that must be treated and disposed of. Likewise, minimizing CO₂ recycling improves storage efficiency and reduces energy penalties, but enforcing a strict no-breakthrough policy may limit additional storage capacity. In certain well configurations, allowing controlled breakthrough and recycling can enable higher injection volumes without violating containment boundaries.

These interactions highlight a central reality: no constraint can be addressed in isolation. Effective well control strategy design must integrate all constraints in a balanced manner, weighing

• Injectivity versus containment and economics (e.g., recycling);
• Short-term performance versus long-term commercial deliverability;
• Operational feasibility versus infrastructure limitations.

Adopting this system-level perspective reframes well control design from a sequential engineering task into a coordinated optimization challenge. It requires adaptive strategies that evolve with reservoir monitoring, dynamic system behavior and shifting regulatory or commercial conditions. Ultimately, embedding this interdependency-aware mindset into automated optimization workflows enables the development of strategies that are technically robust, economically viable, and legally compliant. This principle forms the conceptual bridge to the automated well control optimization methodology introduced in the next Section 3.

3. Methodology: Optimization Framework

The methodology developed in this work introduces a system-level optimization framework designed to tackle the optimal performance of CO₂ storage operations considering the intertwined technical, commercial, operational and economic constraints. Its central objective is to determine well control strategies that maximize in place CO₂ storage over the operational lifetime of a reservoir while minimizing undesirable byproducts and operational inefficiencies. This is achieved by systematically manipulating injection rates across both space—considering well groupings and individual injectors—and time, thereby increasing the degree of freedom for rate allocation along the wells, which ultimately enhances well control strategies to achieve ultimate storage efficiency and containment integrity while respecting the full suite of operational and physical constraints. The discussion in this Section begins by outlining the overall architecture of the methodology, explaining how it approaches the problem in a structured and systematic way. Next, the Section presents the objective functions adopted that guide optimization, highlighting their role in balancing operational performance and financial considerations. The core optimization algorithm is then introduced, providing an overview of how the adopted method becomes iteratively refined to navigate the competing demands of the system. Finally, the key components that anchor the methodology—including its automation, adaptability, and integration of constraints—are described, giving the reader a clear sense of the framework’s scope, flexibility and practical relevance.

3.1. Optimization Architecture

The framework employs an innovative approach/architecture centered on automated optimization coupled with a dynamic time-space discretization scheme. Instead of attempting to solve a single, computationally prohibitive, high-dimensional problem from the outset, the methodology follows a scenario-based iterative refinement process. It begins with a simplified, coarse representation of the control problem and systematically increases its complexity in a structured manner. This entire workflow is managed by a sophisticated Python-based [68] architecture that automates the generation of control schedules, executes full-physics reservoir simulations to evaluate their performance and seamlessly feeds the results back into a core optimization engine.

Let a CO₂ storage reservoir be operated by $N_I$ injectors and $N_P$ producers and let the injectors’ rate be described by a $q_{I,i}\left(t\right)$ function with $i\in I=\left\{1, \dots , N_i\right\}$. Similarly, let the producers brine and CO₂ production (CO₂ may be recycled at surface) be given by $q_{P,i}^b\left(t\right)$ and $q_{P,i}^{C{O}_2}\left(t\right)$ with $i\in P=\left\{1, \dots , N_P\right\}$. The target of the proposed method is to identify the injection rates $q_{I,i}\left(t\right)$ which optimize the reservoir storage capacity and overall performance, subject to all needed constraints. It is noted that typically the producers are automatically controlled by the reservoir simulator rather than by the optimizer. Productions rates $q_{P,i}^b\left(\mathrm{t}\right)$ and $q_{P,i}^{C{O}_2}\left(\mathrm{t}\right)$ are obtained by the simulator subject to specific bottom hole pressure (BHP) constraints satisfying technical constraints. In other words, the simulator through its decision process computes the production rates provided that the producing wells bottom hole pressure does not fall below the minimum required value which guarantees flow within the wellbore and arrival of the produced fluids at surface. Figure 7 illustrates the workflow diagram on the overall optimization architecture.

With the control variables being $\mathbf{x}=\left\{q_{I,i}\left(t\right)\right\}$, the algorithm starts by assuming that the injection rate is common for all injectors (all wells are clustered as one group), and it is constant throughout the injection period (e.g., simulation time), i.e., $q_{I,i}\left(t\right)=q_I$. Therefore, the optimizer only seeks a single value, i.e., ${\mathbf{x}}_{\mathrm{0,0}}=\left\{q_I\right\}$.

Once the ${\mathbf{x}}_{\mathrm{0,0}}$ value that optimizes the objective function is found, it is forwarded to the second optimization configuration step which now allows the injectors to be split into two groups, each allowed to have its own rate which now is equal over that group injectors and constant over time. Let $I_1$ and $I_2$ be the complementary sets containing the indices of the two injectors subsets, i.e., $I=\left\{I_1,I_2\right\}$. In that case, the optimizer seeks two values, i.e., ${\mathbf{x}}_{\mathrm{1,0}}=\{q_{I_1},q_{I_2}\}$. Importantly noted, the optimization configuration of this stage is initialized by the one found in the previous stage and is expected to arrive at a better optimum due to the increased flexibility and degrees of freedom.

Subsequently, the next stage evolves around time split/cut where each injectors group is allowed to have two different injection rates, each for the first or second half of the simulation period. Those injection rates are denoted by ${\mathbf{x}}_{\mathrm{1,1}}=\left\{q_{I_1,t_1},q_{I_1,t_2},q_{I_2,t_1},q_{I_2,t_2}\right\}$, where $t_1$ and $t_2$ denote the two time periods. ${\mathbf{x}}_{\mathrm{1,1}}$ denotes the set of variables to be optimized once the injectors have been split once in two groups and time has also been split once in two halves. Once again, the optimization is initialized using the previous solution ${\mathbf{x}}_{\mathrm{1,0}}=\{q_{I_1},q_{I_2}\}$ as a starting point. The process is continued repeatedly by alternating a cut in time and subsequently a cut in space. Therefore, the next scenarios contain more control variables denoted by ${\mathbf{x}}_{\mathrm{2,1}}$, ${\mathbf{x}}_{\mathrm{2,2}}$, ${\mathbf{x}}_{\mathrm{3,2}}$ and so on. Embedding the maximum allowed number of cuts or any similar rules (e.g., prohibiting the time cut to reduce to below 3 years as an example in accordance with case specific field operation guideline) is straightforward. For further information and examples on how optimization architecture works, readers are encouraged to consider the Table in the subsequent Section.

3.2. Objective Functions

The optimization problem is formally defined by an objective function, a set of decision variables $\mathbf{x}$ and a set of constraints. The primary objective function, $J$, adopted in this work is designed on engineering perspective addressing multiple goals simultaneously, reflecting both engineering and operational priorities. At its core, the function seeks to maximize the net CO₂ retained in the reservoir, often expressed as Field Gas (CO₂) In Place (FGIP) the difference between the cumulative gas injected (FGIT) and the field cumulative gas produced (FGPT) over the simulation period. The difference between FGIT and FGPT is chosen rather than directly attempting to optimize FGIP, as maximizing FGIP alone is insufficient if a large fraction of the injected CO₂ is subsequently recycled or produced; therefore, the objective function also emphasizes relative CO₂ retention, promoting higher injection efficiency. In parallel, it seeks to minimize CO₂ recycling volumes, which enhances sweep efficiency and reduces operational burdens associated with surface handling and reinjection of produced CO₂.

From these considerations, the primary engineering-focused objective function is expressed as

$$J=FGIT\left(t_{end}\right)-{\lambda }_0·FGPT\left(t_{end}\right)$$

(1)

Here, ${\lambda }_0$ is a tunable penalty factor applied to back-produced CO₂. This parameter allows project-specific priorities to be reflected: for example, offshore reservoirs with limited processing capacity may require a higher ${\lambda }_0$ to emphasize minimizing recycling, whereas onshore sites with more flexible infrastructure can tolerate higher recycling to maximize total injection volumes. Through sensitivity analysis, a value of ${\lambda }_0=2.5$ was found to provide a balanced trade-off between maximizing injected CO₂ and suppressing recycling under the studied reservoir case study defined in this work and operational conditions.

A more advanced version of the objective function incorporates financial considerations, integrating the overall engineering performance with project costs and revenues to produce a financially driven optimization perspective. This extended objective function accounts for FGIP, FGIT, FGPT, and fluid water production total/cumulative (FWPT), weighted by coefficients ${\lambda }_0$ through ${\lambda }_3$ that reflect tariffs, operational expenditure, and other economic parameters in euros per physical unit:

$$J={\lambda }_0·FGIP\left(t_{end}\right)-{\lambda }_1·FGIT\left(t_{end}\right)-{\lambda }_2·FGPT\left(t_{end}\right){- \lambda }_3·FWPT\left(t_{end}\right).$$

(2)

The adopted values for each coefficient ${\lambda }_0$ to ${\lambda }_3$ is discussed in detail in Section 4.

3.3. Core Optimization Algorithm: Modified Genetic Algorithm

The optimization engine at the core of this framework is a Genetic Algorithm (GA), a powerful and flexible evolutionary algorithm from the family of derivative-free methods [21,22]. For scenarios that evolve to have a very high number of decision variables, the framework is designed to seamlessly transition to the Covariance Matrix Adaptation Evolution Strategy (CMAES), an algorithm renowned for its performance on difficult continuous optimization problems [69]. In the present work, however, the GA serves as the primary workhorse due to its unique strengths in handling the complexities inherent to reservoir simulation, while the CMA-ES is retained as an optional alternative for cases involving highly continuous or high-dimensional control spaces. A systematic performance comparison between GA and CMA-ES, including convergence efficiency and scalability, will be addressed in future work dedicated to algorithmic benchmarking.

The selection of a Genetic Algorithm is deliberate, justified by several key advantages that make it exceptionally well-suited for this context. Firstly, its nature as a global search method provides a significant advantage over gradient-based optimizers, which are prone to becoming trapped in suboptimal local minima within the highly complex and multimodal search spaces typical of reservoir performance. This advantage is particularly pronounced in this work, where the optimization is performed sequentially. The process begins with a single decision variable, and once its optimal value has been determined, space and time cuts are introduced, substantially increasing the number of variables. This previously optimized solution is then used to “seed” the initial population for the new, higher-dimensional problem. A gradient-based method, if started at this previous optimum, would struggle to overcome the local nature of its starting point and would be less effective at exploring the newly enhanced search space. Secondly, the GA functions as a “black box” optimizer, meaning it does not require derivative or gradient information from the objective function. This is an essential characteristic, as the reservoir simulator provides only a performance output (the objective value) for a given set of inputs (the injection rates), with no accessible mathematical gradient. Finally, GAs exhibit considerable robustness to noisy or discontinuous objective functions, which can arise from the numerical methods employed within the reservoir simulator, ensuring stable and reliable progress toward an optimal solution [21].

Overall, the GA operates by mimicking the principles of natural selection, evolving a population of candidate solutions over a series of generations. Each “individual” in the population represents a complete well control strategy, encoded as a vector of injection rates for all well groups and time steps. The evolutionary process is driven by three primary operators. Selection ensures that individuals with higher fitness scores, i.e., those that yield greater net CO₂ storage capacity and perhaps better retention factor are more likely to be chosen as “parents” for the next generation. Crossover then combines the genetic material of two parent solutions to create one or more “offspring,” allowing for the propagation and combination of successful traits. Finally, mutation introduces small, random alterations into an offspring’s genetic code, providing a crucial mechanism for maintaining population diversity and preventing premature convergence to a single region of the search space.

Taken together, the pivotal innovation of this framework does not lie only in the fundamental modification of the core GA operators, but in its strategic deployment through a methodology we term scenario-based iterative refinement. As previously mentioned, rather than attempting to solve one massive, high-dimensional optimization problem from the start, our approach decomposes the problem into a sequence of more tractable, lower-dimensional stages. The optimal solution derived from a coarse-grained scenario (with fewer time steps and well groups) is not discarded. Instead, it is intelligently processed and used as a high-quality initial guess, or “seed,” for the initial population of the subsequent, more refined optimization stage. This “warm start” technique provides the GA with a highly evolved starting point, dramatically accelerating convergence at each level of refinement and ultimately making the exploration of highly complex and granular control strategies computationally feasible.

3.4. Constraints

The optimization process is governed by a multi-layered set of constraints that ensure the resulting strategies are both practical and physically realistic. The underlying reservoir simulator solves the coupled mass- and momentum-balance equations for multiphase flow of CO₂ and brine in porous media using a finite-volume formulation with implicit time stepping. Flow is governed by Darcy’s law and component conservation equations, and thermophysical properties are updated at each iteration through Black oil model EOS-based PVT module. This ensures full consistency between pressure, saturation, and compositional fields during optimization. At the most direct level, explicit box constraints define lower and upper limits on allowable injection rates for each well, i.e., $\mathbf{x}$, reflecting the operational constraints discussed in Section 2. Beyond these explicitly defined limits, the framework leverages the reservoir simulator to enforce a suite of implicit physical constraints. More specifically, each injector’s BHP is forced to stay below the $BH{P}_{I, i}^{max}$ limit, which is controlled by the reservoir geomechnical aspects therefore technical constraints discussed in the previous Section, i.e.,

$$BH{P}_{I,i}\left(t\right)\le BH{P}_{I, i}^{max}.$$

(3)

If such a constraint is activated at some timestep $t$ during the simulation for injector $i$, the simulator would force the implemented injection rate to stay below the required $q_{I,i}\left(t\right)$ value to avoid excessive pressure buildup in the injector’s bottom hole. Similarly, each producer’s BHP should be limited by the lowest pressure value allowed to ensure that the produced fluids arrive at surface being powered by the reservoir pressure rather than pumping solution (e.g., ESPs). This is defined by

$$BH{P}_{P,i}\left(t\right)\ge BH{P}_{P, i}^{min}.$$

(4)

If a candidate injection rate proposed by the optimization algorithm would violate this pressure limit, the simulator’s physics engine automatically curtails the rate. This elegant mechanism ensures that all evaluated strategies inherently adhere to the fundamental laws of fluid flow within the porous medium without requiring these complex physical interactions to be explicitly formulated as mathematical constraints in the optimization problem itself. This in turn enforces a complex and non-linear objective function response to the control variables chosen, strengthening the need for an efficient optimizer over the high-fidelity simulator.

In turn, commercial constraints are applied to maintain stable and economically viable field operations. Therefore, another crucial operational constraint is imposed to maintain a constant total injection rate across the field for all timesteps, ensuring a delivery viable injection profile to be serviced. The constraint is given by

$$q_{I,tot}\left(t\right)={\sum }_{i=1}^{i=N_I}{q}_{I,i}\left(t\right)=Q_{I,tot}$$

(5)

where $Q_{I,tot}$ is the design total injection rate.

A constant total injection rate is maintained across all time periods by using a hybrid of two sophisticated methods. One implementation employs a custom MyRepair operator [70], a function that algorithmically adjusts each new candidate solution to strictly satisfy the equality constraint before its evaluation. A second, more flexible implementation utilizes a penalty function within the objective evaluation itself, where any deviation from the target total rate adds a numerically significant penalty to the solution’s fitness score, mathematically guiding the optimizer toward the feasible region.

Finally, the simulator can enforce field-level production constraints—such as maximum daily water production (bbl/day) or maximum CO₂ recycling capacity—based on facility limits (both brownfield and greenfield surface infrastructure). These can also be applied at the producer level, ensuring compatibility with specific well design considerations.

3.5. Key Anchors of the Framework

The effectiveness of the optimization framework is anchored in three core technical principles: comprehensive automation, a strategy of dynamic discretization to manage complexity at any level required, and a multi-faceted approach to constraint handling. These pillars work in concert to make the complex task of well control optimization both computationally tractable and physically realistic.

3.5.1. Automation & Industry Ready Integration

A central pillar of the framework is its end-to-end automation, enabling the entire optimization cycle—from generating candidate control strategies to evaluating their performance—to run without manual intervention. The Python 3.13-based architecture acts as a high-level controller, dynamically constructing the SCHEDULE section of a standard ECLIPSE-format reservoir simulation input deck based on decision variables proposed by the optimization algorithm. It then calls the OPM Flow simulator [71] via a subprocess command, executes a full-physics simulation, and automatically parses the resulting summary files (e.g., SuMmary SPECification file, SMSPEC) using OPM’s I/O libraries to extract the objective function value [71]. This “black-box” coupling allows high-level optimization tools such as pymoo to steer the simulator without altering its underlying code.

This non-invasive, file-based communication protocol ensures compatibility with any reservoir simulator adhering to common industry standards, making the framework easy to integrate into existing CCS modeling workflows. Because it operates independently of the simulator’s internal code, the system can be deployed at any stage of a CCS project—particularly after history matching or model updates—allowing for repeated optimization as new data becomes available. This adaptability ensures its long-term relevance for operational decision-making.

The main challenge in simulation-based optimization is computational intensity: a single optimization campaign may require thousands of full-physics simulations. The framework addresses this through a multi-layered efficiency strategy. First, Dynamic Time–Space Discretization breaks the high-dimensional control problem into a sequence of smaller, lower-dimensional subproblems, avoiding the “curse of dimensionality” and accelerating early-stage optimization. Second, iterative refinement with solution seeding—implemented via the map_previous_solution function—uses the optimal strategy from a coarser stage as a “warm start” for the next refinement stage, drastically reducing the number of simulations needed for convergence.

To further reduce wall-clock time, the framework exploits high-performance computing capabilities: each objective function evaluation (i.e., one reservoir simulation) is run in parallel using mpirun [68], distributing the workload across multiple cores. Combined with advanced optimization algorithms such as Genetic Algorithms and CMA-ES from the pymoo library, the search process becomes both targeted and computationally feasible. All optimization runs were executed on a workstation-class laptop equipped with an Intel^® Core™ i5-8250U processor (4 cores, 1.8 GHz) and 8 GB RAM, running a 64-bit Windows operating system. Each reservoir-simulation call was executed sequentially through the mpirun interface within the OPM Flow framework to maintain consistency with parallelizable workflows. Under this configuration, a complete optimization campaign (Stages 0–2,4) required approximately 24 h of wall-clock time, confirming that the proposed workflow is computationally efficient and feasible even on standard engineering hardware.

Through this integration of automation, modular simulator coupling, problem decomposition, intelligent seeding, parallel computing, and advanced search algorithms, the framework transforms the inherently complex and computationally demanding task of optimizing long-term CCS well control strategies into an industry-ready, repeatable, and scalable process.

3.5.2. Dynamic Adaptability to Operational Cadence

Beyond its engineering and economic underpinnings, the optimization framework is designed to align closely with operator priorities and operational philosophies. In practice, different operators may have varying appetites for operational complexity. Some may prefer a simplified strategy—treating all injectors as a single unit and adjusting rates only infrequently—while others may seek highly granular control, splitting wells into multiple groups and updating rates at short operational intervals to capture more nuanced reservoir responses.

To accommodate this flexibility, the methodology avoids defining a fixed, high-resolution control problem from the outset, which would create an intractably large search space. Instead, it begins with a coarse representation and progressively refines it through the SplitManager class. Temporal refinement is governed by the time_split_level, which determines the number of discrete time intervals in the project schedule. At each refinement stage, the number of intervals is doubled, enabling progressively more frequent rate adjustments. Spatial refinement follows the space_split_level, which controls how injectors are grouped. Initially, all injectors may operate as one, but as refinement progresses, binary identifiers partition them into smaller, strategically distinct groups, allowing for differentiated injection patterns across the reservoir.

This staged increase in both temporal and spatial resolution enables operators to decide the level of complexity they are willing to manage—whether that means keeping operational changes minimal to reduce logistical burden or embracing finer-scale adjustments to maximize technical and economic performance. By embedding these refinements within the optimization process, the framework ensures that operational details are added only when it provides tangible value, keeping strategies aligned not only with subsurface performance goals but also with overarching business objectives.

3.5.3. Multidimensional Constraint: Matching Reality (Simulation to Field)

A third pillar of the framework is its robust capability to incorporate constraints across multiple domains in a way that ensures optimization results remain both feasible in practice and defensible in real-world decision-making. Whereas automation enables scale and adaptability ensures operations alignment, the embedding of constraints provides the necessary guardrails that anchor optimized strategies to the realities of subsurface physics, facility capacity, field economics and the commercial obligations faced by operators.

From a business case perspective, constraints are not simply limitations but essential enablers of trust in optimization results. No operator will adopt a mathematically “optimal” solution if it violates well integrity thresholds, overwhelms surface processing systems, or generates operating costs that undermine financial viability. Embedding these multidimensional constraints directly into the optimization loop bridges the gap between theoretical optima and operationally actionable strategies.

On the technical side, the framework leverages the simulator’s physics engine to enforce reservoir engineering principles and the reality of subsurface fluid flow. Bottomhole pressure limits align with well and reservoir safety requirements, reducing risks such as caprock breach, while production BHP thresholds ensure both safe injection and reliable fluid deliverability without reliance on artificial lift [72] systems not envisaged in the base case. Operational and commercial constraints extend this realism by enforcing field-wide conditions: for example, maintaining a constant total injection rate as committed to emitters/capturers, respecting CO₂ and brine handling capacities for brownfield reuse or new facility design. Economic constraints—such as penalties tied to excessive water production or surcharges for CO₂ recycling and reinjection energy—are embedded directly within the objective function, ensuring that the optimizer’s pursuit of technical efficiency is balanced against economic performance.

The strength of this approach lies in its multi-layered enforcement strategy. By embedding constraints not as external filters but as intrinsic components of the optimization loop, the framework ensures that every proposed strategy is evaluated within the bounds of what is physically, operationally, and commercially feasible. The outcome is a set of strategies that are not only mathematically sound but also credible, compliant, and implementable. For decision-makers, this multidimensional alignment transforms the optimization exercise from an abstract tool into a reliable decision-support system that balances technical feasibility with commercial reality—ensuring that optimized CO₂ storage strategies can transition seamlessly from simulation to the field.

4. Case Study: Implementation & Results

To evaluate the feasibility of applying the automated optimization approach for developing robust well control strategies in saline aquifer formations, we developed a three-dimensional Cartesian model incorporating industry-relevant characteristics from worldwide carbon storage projects. The algorithm was tested across two main perspectives with different objective functions: engineering and financial. This Section follows a structured approach, discussing the model setup, well configuration and operations, the application of optimization constraints, hierarchical refinement in space and time, and finally the results obtained using the different objective functions, concluding with a comparative analysis.

4.1. Model Setup

The 3D Cartesian reservoir model integrates representative subsurface characteristics from large-scale commercial CCS projects, encompassing a realistic range of geological and petrophysical parameters such as porosity, permeability, formation thickness, and depth.

The modeled reservoir extends 2100 m in both horizontal directions and has a vertical thickness of 250 m. Grid discretization is uniform, with 150-m spacing in the x and y directions and 5-m spacing in the z direction based on sensitivity analysis, resulting in a total grid configuration of 14 × 14 × 50 cells. This resolution balances computational efficiency with sufficient detail to resolve key vertical heterogeneities influencing CO₂ plume migration.

Petrophysical heterogeneity is represented by Beta-distributed porosity and log-normally distributed permeability fields. Base porosity values range from 13% to 37%, and permeability spans 5 to 450 millidarcies, consistent with global CCS reservoir analogs. These statistical distributions provide a geologically plausible representation of subsurface variability and create a robust testbed for the optimization framework.

To introduce spatial asymmetry and increase algorithmic challenge, the reservoir was divided into four quadrants, each assigned a distinct multiplier applied to the base porosity and permeability fields: 0.85 (top-left), 1.15 (top-right), 0.60 (bottom-left), and 0.40 (bottom-right). This heterogeneity generates variations in injectivity and sweep efficiency across the domain, increasing optimization complexity. Figure 8 illustrates the spatial distribution of these petrophysical properties across different quadrants.

Further complexity arises from the inclusion of three faults within the model. Each fault has a specific transmissibility [73] multiplier: 0.70 for Fault 1 (F1), 0.45 for Fault 2 (F2), and 0.60 for Fault 3 (F3). These faults act as internal baffles or partial barriers that influence local flow dynamics and CO₂ migration pathways. The combined spatial distribution of porosity and fault locations is shown in Figure 9.

The reservoir top is set at a depth of 1925 m, based on weighted averages from multiple case studies to ensure broad applicability. The system is modeled as horizontally layered and isothermal, with a constant temperature of 100 °C. The physical–mathematical representation of the storage process follows classical two-phase flow theory, assuming local thermodynamic equilibrium and negligible capillary diffusion across grid interfaces. CO₂ is treated as miscible in brine, compressible fluids and the density–pressure relationship is handled through black oil table provided as inputs from the selected equation of state offline the simulator. The geomechanical response is not explicitly coupled but is indirectly represented through pressure constraints embedded in the simulation. Due to limited consistent global salinity data, a representative brine salinity of 150,000 ppm was adopted, based on the Lower Tuscaloosa Sandstone Formation from the SECARB Mississippi Pilot project. The initial reservoir pressure at the top is set at 206 bar, indicating a nearly normally pressurized system.

Two-phase flow behavior is modeled using relative permeability curves, with a connate water saturation of 0.27 and residual CO₂ saturation of 0.20 uniformly applied throughout the model. The system is assumed to be closed, without external pressure relief. To manage pressure buildup during injection, brine production is incorporated, simulating a constrained, pressure-limited environment typical of commercial CCS projects. This setup offers a rigorous and realistic platform to assess the flexibility and robustness of the proposed optimization approach.

4.2. Well Configuration and Operation

The reservoir model contains four CO₂ injection wells positioned along one side of the domain and six brine production wells located on the opposite side. This arrangement is designed to maximize sweep efficiency, enhance storage capacity, and minimize the risk of early CO₂ breakthrough. The injector-to-producer ratio of 1:1.5 aligns with common industrial practice, where ratios between 1:1.5 and 1:2 are typically adopted to ensure effective pressure management and fluid displacement in closed systems.

The injection wells—designated I1, I2, I3, and I4—are positioned at grid coordinates (1,5), (1,9), (4,14), and (9,14), respectively. The production wells—P1 through P6—are located at (14,9), (14,5), (14,1), (10,1), (6,1), and (11,4), respectively. For visual reference, Figure 10 presents both a 3D perspective (Figure 10a) and a 2D top-down map (Figure 10b) of well locations.

Injection wells operate under rate control, while production wells are governed by bottom-hole pressure control, enabling active pressure regulation during the injection phase. All wells are completed in the lower half of the reservoir (layers 26–50). For injection wells, lower completions promote CO₂ dissolution and improved sweep efficiency through gravitational segregation, allowing denser brine to remain at depth while CO₂ migrates upward and laterally. For production wells, lower completions help reduce the likelihood of early CO₂ breakthrough and promote uniform water displacement.

The simulation covers a continuous 24-year injection period, representative of a typical operational phase for CCS projects.

4.3. Optimization Constraints

The constraints architecture is designed to safeguard reservoir integrity, ensure operational feasibility, and respect economic limits, while maximizing CO₂ storage capacity and overall field injectivity. Constraints are applied at two complementary levels:

• Within the reservoir simulator, acting directly on physical responses such as pressure and fluid flow;
• Within the optimization algorithm, shaping the evolution and selection of the control variables (i.e., injection rates).

This dual-layered approach maintains physical realism without sacrificing computational efficiency.

Table 1. Summary of Constraints in the Optimization Framework.

Constraint Category	Constraint Type	Description & Rationale	Enforcement Location	Value/Limit (Case-Specific)
Technical	Bottom-Hole Pressure	Limits BHP below fracture pressure to prevent reservoir and wellbore damage. Producer wells use BHP control to maintain reservoir pressure within safe limits. This indirectly limits pressure buildup in the reservoir below the BHP threshold set for injectors.	Reservoir Simulator	Max 6000 psi per injector Min 3000 psi per producer
Commercial	Constant Field Injection Rate	Enforces a fixed total CO2 injection volume over the project lifetime, reflecting contractual storage obligations and quota commitments. Implemented as a linear equality constraint.	Optimization Algorithm	Fixed total field intake/injection volume over 24 years
Operational	Feasible Injection Rate per Well	Ensures injection rates remain within mechanical and thermal limits related to tubing, well integrity, and operational safety.	Optimization Algorithm	Max 1.5 Mtpa per well
Economic	Field Brine Production	Limits brine production to surface facility capacity and disposal constraints, maintaining cost-effective voidage replacement and pressure management.	Reservoir Simulator	Max field production: 65,000 bbl./day.
Economic	Field CO2 Production (Breakthrough)	Penalizes CO2 recycling to reduce operational costs and improve storage efficiency; incorporated as a penalty term in the objective function.	Optimization Algorithm	Penalized through objective function
Regulatory	Plume Migration	Ensures the CO2 plume remains within licensed boundaries. Not explicitly enforced due to the closed-system model; in open systems, this would be actively constrained or penalized if the plume migrated beyond limits.	Implicit (Closed System)	Confined system; no out-of-bound migration

summarizes the constraints applied in the 3D Cartesian model, categorized by type, along with their enforcement mechanisms and limits. Physical, operational, and infrastructure constraints are implemented within the reservoir simulator, leaving only commercial and economic objectives incorporated into the optimization algorithm, thus greatly reducing the complexity of the optimization problem. Regulatory requirements, particularly plume containment—are inherently satisfied by the model’s closed-boundary configuration. Note that additional operational constraints, such as regular partial or full shutdowns, can be incorporated anytime in the model.

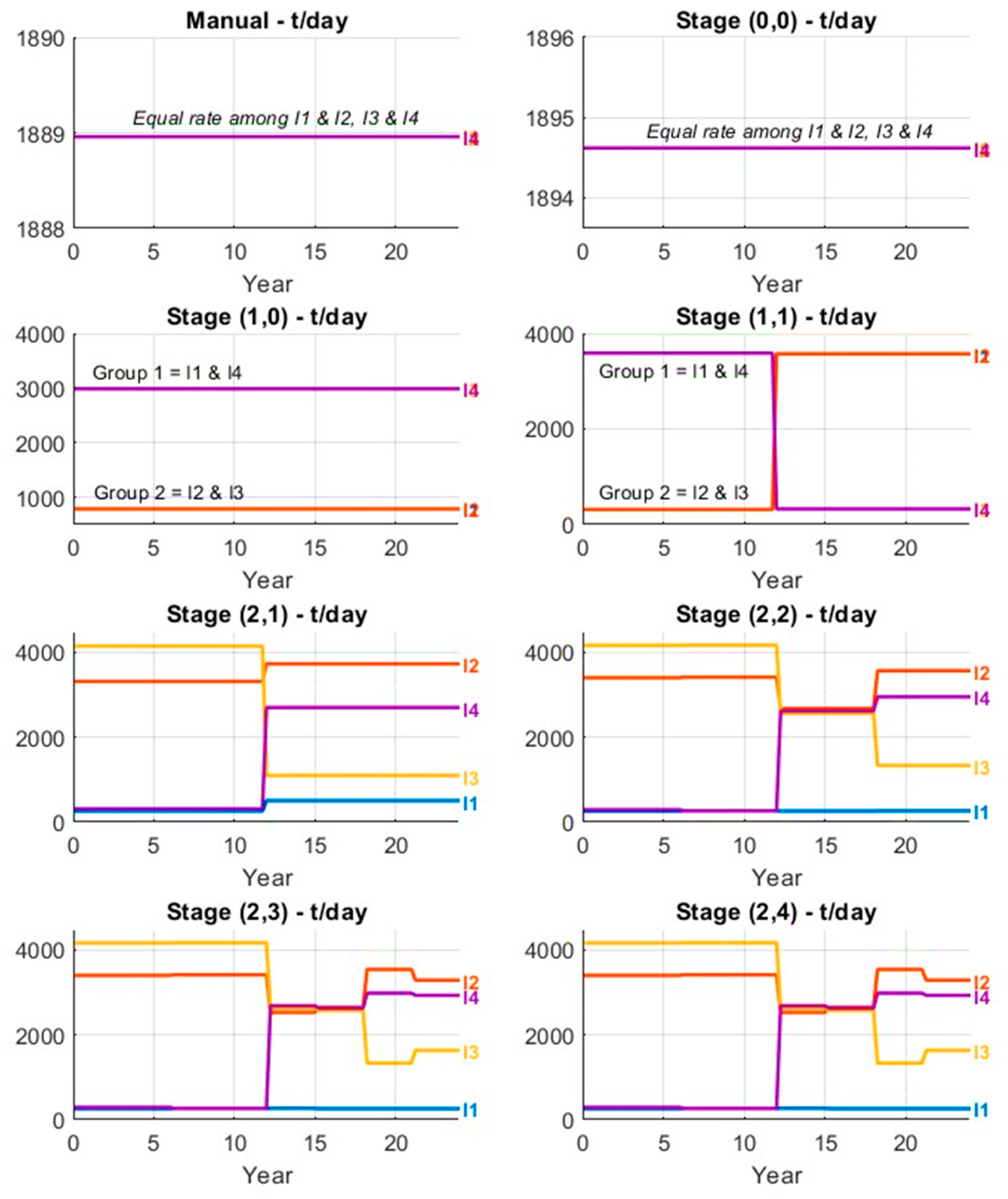
4.4. Hierarchical Refinement Strategy in Space and Time

The hierarchical refinement strategy discussed in Section 3 is employed to balance control granularity with optimization performance. This approach progressively increases the complexity of control variables by introducing discretized cuts in both space (injectors) and time (over the 24-year injection period):

• Spatial refinement is limited by the number of injectors, with a maximum of two spatial cuts allowing control at either the group or individual well level’
• Temporal refinement introduces up to four successive time cuts, each doubling the number of control intervals to enhance temporal resolution.

Each refinement stage builds upon the previous one, initializing with the optimal solution from the preceding stage.

Table 2. Summary of Hierarchical Refinement Stages in Space and Time.

Refinement Stage (Space Cuts, Time Cuts)	Space Cuts	Time Cuts	Time Intervals	Decision Variables	Description
Stage 0 (0,0)	0	0	1 (0–24 yrs)	1	Global control: all injectors follow a single shared injection schedule (industry standard)
Stage 1 (1,0)	1	0	1 (0–24 yrs)	2	Two-group control: Group 1 = I1 & I4; Group 2 = I2 & I3.
Stage 2 (1,1)	1	1	2 (0–12, 12–24 yrs)	4	Time-varying control per group with low temporal granularity
Stage 3 (2,1)	2	1	2 (0–12, 12–24 yrs)	8	Independent, time-varying control per well (I1–I4)
Stage 4 (2,2)	2	2	4 (6-year intervals)	16	Higher-frequency, well-level control.
Stage 5 (2,3)	2	3	8 (3-year intervals)	32	High-resolution control with well-level schedules segmented into 3-year intervals.
Stage 6 (2,4)	2	4	16 (1.5-year interval)	64	Maximum resolution: full spatiotemporal optimization per well and time segment

summarizes the refinement stages, including the number of decision variables, time intervals, and a brief description of each stage.

4.5. Results

The optimization framework is evaluated with two distinct yet complementary perspectives in mind: the purely engineering-driven approach, which focuses on maximizing CO₂ storage effectiveness and storage site performance, and the financial perspective, where the objective function factors all parameters into economic factors through Cash Flow (CF) optimization. This dual approach allows exploration of trade-offs between technical storage efficiency and financial viability, providing a comprehensive assessment of well control strategies discretization approach.

4.5.1. Engineering Perspective

The engineering-focused optimization problem is formulated around a field-level objective function that directly captures CCS performance:

$$Objective=FGIT-\lambda ·FGPT$$

(6)

where

• $FGIT$ (Field Gas Injection Total) represents the total CO₂ injected over the project life;

• $FGPT$ (Field Gas Production Total) represents the cumulative CO₂ produced back to surface, either via intentional brine producers or breakthrough.

$\lambda$ is a weighting factor that penalizes CO₂ production according to its operational and economic impact.

This objective function explicitly addresses three core engineering goals critical for commercial-scale CO₂ storage:

▪

Maximize Absolute CO₂ Retention ($\mathrm{F}\mathrm{G}\mathrm{I}\mathrm{P}$): $FGIP=FGIT-FGPT$; this represents the net CO₂ retained underground. Increasing FGIP improves storage capacity utilization and reservoir pore space efficiency, a primary technical performance indicator.

▪

Maximize Relative CO₂ Retention (Injection Efficiency): defined by $FGIP/FGIT$. This metric measures how effectively injected CO₂ is retained. Simply increasing FGIT is insufficient if accompanied by proportionally high FGPT. The objective rewards increased injection that is not offset by excessive recycling.

▪

Minimize CO₂ Recycling Volume: The penalty term $-\lambda ·FGPT$ discourages early and excessive CO₂ breakthrough, promoting sweep efficiency and reducing operational challenges associated with surface CO₂ handling and recycling.

The simplicity of the formulation is deliberate: it concentrates the competing technical drivers—storage maximization, relative retention/efficiency and recycling minimization—into a single scalar metric. The tunable $\lambda$ factor, typically considered as a system hyperparameter, allows project-specific priorities to be reflected: For instance, in offshore reservoirs with limited processing capacity, higher value places stronger emphasis on minimizing recycling. Conversely, onshore sites with more flexible infrastructure can accept higher recycling levels to maximize total injected volumes by using a lower $\lambda$. Through extensive tuning and sensitivity analysis, a value of $\lambda =2.5$ was found to provide an effective balance between maximizing injection volumes and suppressing CO₂ recycling for the considered reservoir and operational conditions. This choice reflects a moderate penalty on CO₂ recycling appropriate for the project’s processing capacity and commercial goals.

The evaluation presents the field performance metrics for each stage of hierarchical time–space discretization, providing direct insight into the evolution of FGIT, FGPT, and FGIP, alongside the optimization trajectory of storage gain versus produced CO₂. These raw metrics are then synthesized into the Field Performance Panel, which visualizes the impact of the discretization strategy across several integrated indicators:

• CO₂ Retention (% of Injected Mass): Defined as FGIP/FGIT, this metric quantifies the fraction of injected CO₂ that remains permanently stored. Higher retention reflects more efficient injection and improved sweep performance.
• Produced CO₂ Volume (Million Tonnes): Represented by FGPT, this measures the cumulative CO₂ recycled to the surface. Reducing this volume minimizes operational recycling costs and potential penalties, aligning with the objective function’s recycling penalty term.
• Storage Capacity Increase Over Manual (%): This is expressed relative to the baseline manual schedule results. The manual schedule serves as a practical engineering benchmark, balancing injectivity with acceptable recycling. This percentage indicates the proportional improvement in stored CO₂ mass.
• Additional Stored Mass Over Manual (Million Tonnes): Complementing the percentage increase, this absolute measure shows the net extra CO₂ stored due to optimization, highlighting tangible operational and commercial benefits.
• Field Gas Injection Rate (Mtpa): This constant rate, maintained over the project lifetime, represents the maximum sustainable injection capacity within reservoir and operational constraints, ensuring commercial feasibility.
• Actual Field Gas Injection Rate (Mtpa): After accounting for CO₂ recycling and re-injection, this reflects the net effective injection volume delivered to emitters or clients, directly influencing the economic value of storage operations.

By examining these metrics collectively, the performance evolution across the time–space discretization stages can be interpreted holistically. This approach highlights not only the incremental benefits of each refinement step but also the trade-offs between additional storage capacity, injection deliverability, and operational efficiency, ultimately identifying the stage where these competing objectives reach an optimal balance.

Figure 11 illustrates the results of the dynamic time–space discretization optimization. Figure 11a shows the evolution of key field metrics—FGIT, FGIP, and FGPT—across all optimization stages, including the Manual baseline. Figure 11b plots the corresponding optimization trajectory, showing storage gain (ΔFGIP) versus produced CO₂ change (ΔFGPT), both relative to the Manual scenario.

Together, these subfigures provide a dual view: the absolute progression of field performance and the trade-offs between storage maximization and CO₂ recycling control. Starting from the Manual baseline, each scenario can be compared in terms of both direct field metrics and its position along the optimization path, highlighting the impact of each discretization step on storage efficiency and operational balance.

The Manual schedule, designed for industry-standard operational (manual equal rate along all wells), delivers an FGIP of 60.325 Mt, corresponding to a CO₂ retention efficiency of 91.38%. While operationally stable, this baseline leaves a significant portion of the storage potential untapped due to its static well rates allocation.

Transitioning to Stage 0,0—where optimization is applied without temporal discretization and all wells share the same injection rate—already produces a notable improvement: FGIP rises to 62.77 Mt, a 2.44 Mt gain over the Manual case. FGPT increases from 5.69 Mt to 7.14 Mt (+1.45 Mt). The net effect is a positive storage–production balance of nearly +1 Mt, highlighting the optimizer’s early ability to enhance storage capacity.

Applying spatial discretization in Stage 1,0, with two groups of wells (Group 1 = I1 & I4; Group 2 = I2 & I3) each sharing equal injection rates, further improves performance. FGIT increases to 71.30 Mt and FGIP to 64.41 Mt (+1.64 Mt over Stage 0,0 and +4.08 Mt over Manual), while FGPT decreases slightly to 6.89 Mt (−0.25 Mt compared to Stage 0,0). Relative to the Manual baseline, FGPT remains higher (+1.2 Mt), but the net storage–production balance improves to +2.8 Mt. This stage marks the first tangible enhancement of the storage–recycling trade-off (Figure 11b): capacity continues to grow while recycling slightly decreases compared to Stage 0,0.

Stage 1, 1 introduces temporal discretization for the first time. FGIT slightly drops to 70.58 Mt, while FGIP holds at 64.24 Mt. Importantly, FGPT falls to 6.34 Mt, improving retention efficiency. The optimization begins to prioritize reducing recycling, even at the cost of a marginal reduction in gross storage, moving the trajectory toward the low-recycle quadrant in Figure 11b without sacrificing significant storage benefit.

The transition to Stage 2,1, where all wells are controlled independently, marks a decisive leap in performance. FGIT rises to 71.63 Mt, FGIP surges to 67.23 Mt (+6.9 Mt over Manual and +2.99 Mt over Stage 1,1), and FGPT drops sharply to 4.40 Mt (−22.7% from Manual and −30.6% from Stage 1,1). This stage represents the first point where both major objectives—maximizing storage and minimizing recycling—advance simultaneously, positioning the trajectory in the most desirable zone of Figure 11b.

Stage 2,2 targets maximum storage, achieving FGIT of 74.65 Mt and the highest FGIP of 69.22 Mt (+8.89 Mt over Manual and +1.99 Mt over Stage 2,1). However, this comes with a rebound in FGPT to 5.43 Mt, partially reversing the recycling advantage gained in Stage 2,1. The result highlights a key trade-off: pushing storage to its absolute limit tends to reintroduce higher recycling volumes.

Stage 2,3 resolves much of this tension. FGIP remains high at 68.25 Mt (~+8 Mt over Manual), while FGPT drops again to 4.69 Mt, recovering most of the low-recycle benefit of Stage 2,1 while retaining nearly all the capacity gains of Stage 2,2. On the optimization path, this stage represents a clean return toward the optimal quadrant—high retention and low recycling.

Stage 2,4 confirms this convergence. FGIP is 68.27 Mt and FGPT is 4.68 Mt, essentially unchanged from Stage 2,3, demonstrating solution stability. No further gains in storage or reductions in recycling are achievable within the existing injector configuration, completions and operational or reservoir constraints, indicating that the practical optimum has been reached.

Overall, the trajectory reflects a clear learning curve, leveraging additional spatial–temporal degrees of freedom at each successive stage. Early stages trade storage gains for increased recycling; mid-stages rebalance the equation; and final stages consolidate near an operational sweet spot. Among all configurations, Stage 2,3 and Stage 2,4 offer the most balanced solutions—retaining ~8 Mt more CO₂ than the Manual case while reducing recycling by ~1 Mt—maximizing both storage efficiency and operational feasibility compared to the industry-standard equal-injection-rate approach.

Figure 12 Integrated performance indicators summarizing the evolution from the Manual baseline through optimized scenarios (Stages 0,0 to 2,4). Unlike “black-box” optimization methods that may deliver performance gains without offering insight into the underlying trade-offs, the present approach emphasizes human interpretability of the results. Each of the six panels is not merely a numerical outcome but a structured representation of how storage, recycling, and deliverability evolve together. This explicit framing allows operators to understand why certain scenarios perform better, to trace the causal links between optimization choices and system responses, and to evaluate whether the resulting strategies align with operational priorities. Such interpretability is a critical advantage of the approach, as it supports informed decision-making and builds confidence in the optimized outcomes.

The top-left panel, Retention of CO₂ Injected Mass (%), measures the percentage of injected CO₂ permanently stored in the reservoir, serving as a direct indicator of injection efficiency. Retention Starts at 91.38% for the Manual baseline, retention dips in Stage 0,0 (89.79%) and Stage 1,0 (90.33%) as the optimizer prioritizes capacity gains at the expense of higher recycling—consistent with the FGPT increases observed in these scenarios. Stage 1,1 records a partial recovery to 91.02%, but the most notable improvement occurs in Stage 2,1, where retention rises to 93.86%. This corresponds to the point in Figure 11b where both major objectives—greater capacity and reduced recycling—advance together. However, Stage 2,1 does not push storage capacity to its absolute maximum. Stage 2,2 reaches that peak but at the cost of higher recycling and a slight reduction in retention. Stages 2,3 and 2,4 maintain retention above 92.7% with balanced recycling levels that do not significantly compromise storage gains, demonstrating that temporal discretization—by introducing additional degrees of freedom—enables the system to sustain high storage efficiency while moderating recycling rates.

The injection rate panels (bottom row) are of crucial operational importance, reinforcing the feasibility of the optimized scenarios. Gross injection capacity, representing the constant field injection rate maintained over the project lifetime, increases steadily from 2.75 Mtpa (Manual) to over 3.1 Mtpa in Stage 2,2, with a slight reduction to 3.04 Mtpa in Stages 2,3 and 2,4. More importantly, actual field injection rates—accounting for the CO₂ that must be re-injected—reflect the net effective annual injection capacity, which is the key metric for commercial delivery to CO₂ capture facilities. This net capacity rises from 2.28 Mtpa (Manual) to 2.66 Mtpa in the final stages. This improvement in deliverable CO₂, coupled with reduced recycling, directly enhances both the economic viability and environmental performance of the storage project.

Taken together, Figure 11 and Figure 12 demonstrate that the operator retains clear strategic flexibility. If the objective is to maximize storage at all costs, Stage 2,2 offers the largest additional stored mass (+8.89 Mt) but with higher recycling. If a more balanced outcome is preferred—maintaining high storage while minimizing recycling—Stages 2,3 and 2,4 deliver nearly the same storage gain (~+8 Mt) while avoiding roughly 1 Mt of additional recycling compared to Stage 2,2. Operational simplicity then becomes decisive: Stage 2,3 requires adjusting injection rates every three years, whereas Stage 2,4 demands adjustments every 1.5 years. From both performance and field-management perspectives, Stage 2,3 emerges as the practical “sweet spot,” combining high retention, low recycling, strong deliverability and reduced operational complexity.

For completeness, Figure 13 illustrates the evolution of well-level injection schedules from the Manual baseline through Stage 2,4. These eight subplots provide a visual record of how the optimized scenarios adjust individual well injection rates over time, complementing the field-scale indicators discussed above.

4.5.2. Financial Perspective

While the engineering perspective focuses on maximizing CO₂ storage performance in terms of injected and retained volumes, commercial-scale CCS projects must also satisfy financial viability criteria. From an operator’s standpoint, profitability depends not only on the amount of CO₂ retained underground but also on the balance between revenues from storage and the operational expenditures (OPEX) incurred for injection, recycling/re-injection, and brine handling.

To capture these trade-offs, the optimization problem is reformulated into a total cash-flow–based objective function:

$$Objective={\lambda }_0·FGIP-{\lambda }_1·FGIT-{\lambda }_2·FGPT{- \lambda }_3·FWPT$$

(7)

where

• $FGIP$—total CO₂ permanently retained/stored in the reservoir over the project lifetime (Field Gas In-Place);

• $FGIT$—total CO₂ injected regardless of retention (Field Gas Injected Total);

• $FGPT$—cumulative CO₂ produced back to surface for recycling/re-injection (Field Gas Produced Total);

• $FWPT$—cumulative brine production requiring treatment/disposal (Field Water Produced Total);

The coefficients ${\lambda }_0$ to ${- \lambda }_3$ represent the economic weighting associated with revenues and OPEX costs, expressed in euros per physical unit. Since the reservoir simulation outputs are given in Mscf for CO₂ and stock tank barrels (stbbl) for water,

Table 3. Economic coefficients used in the objective function.

Economic Elements	Value (€)	Unit	Source	Final Coefficient
CO2 Storage Tariff ${\lambda }_0$	50	€/tonne	Porthos Tariff and EU Benchmarks (Average)	2.61 €/Mscf
CO2 Injection Cost ${\lambda }_1$	15	€/tonne	Sleipner Project Injection Cost	0.783 €/Mscf
CO2 Recycling and Re-injection Cost ${\lambda }_2$	40	€/tonne	High-end CCS cost estimates	2.088 €/Mscf
Brine production & Treatment ${\lambda }_3$	5	€/m3	Industry average disposal cost	0.7949 €/bbl

represents the economic coefficients applied to express λ in simulation units in the objective functions:

This formulation directly rewards permanent CO₂ storage through the revenue term ${\lambda }_0·FGIP$, while penalizing operational costs associated with injection (${-\lambda }_1·FGIT$), CO₂ recycling and reinjection ${-\lambda }_2·FGPT$, and brine handling $({- \lambda }_3·FWPT)$.

Compared with an engineering-only objective, the economic formulation places stronger disincentives on scenarios with high CO₂ recycling, excessive brine production, or poor retention efficiency, thereby shifting the optimal strategy toward maximizing net retained CO₂ while minimizing costly by-products.

Figure 14 illustrates the progressive evolution of key financial and operational metrics through the successive stages of time–space discretization. The optimization process progressively enhances project profitability by balancing revenue from CO₂ retention (FGIP) against operating costs from injection (FGIT), recycling (FGPT), and brine handling (FWPT). Each stage’s cash-flow (CF) shift can be traced directly to variations in these four drivers, weighted by their respective economic coefficients.

The manual baseline establishes the reference point, delivering a total cash flow (CF) of 1.46 billion euro (B€). Revenue stems predominantly from storing 60.33 Mt of CO₂ (FGIP), while operating costs are dominated primarily by injection FGIT: ~990 million euro (M€) followed by brine production and treatment (FWPT: ~343.4 M€) and recycling (FGPT: ~228 M€). Injection-related OPEX from FGIT is significant with notable economic inefficiency reflecting 91.39% of injected CO₂ is permanently stored meaning a significant fraction of injection costs does not translate into revenue (85 M€ loss in injection cost with its corresponding recycling cost).

In Stage 0.0, uniform optimization at a global scale yields no net financial improvement over the manual case. A marginal FGIP increase (~0.12 Mt reflecting 6 M€ gain) is outweighed by a rise in FGIT (+0.20 Mt reflecting 3 M€ loss) and a small FGPT increase (+0.07 Mt reflecting ~2.8 M€ loss). The retention rate therefore remains essentially unchanged, neutralizing the minor engineering gains, leaving profitability flat.

The first true optimization jump occurs between Stage 0.0 and Stage 1.0, with CF rising by ~60 M€ (+4.55%) relative to the manual case. Here, modest but coordinated improvements drive the gains: FGIP rises by ~0.71 Mt, FGPT drops by ~0.82 Mt (reducing costly re-injection), and FGIT falls slightly, cutting injection expenses. Produced water increases marginally, but its impact is small. The result is a retention rate of 92.6%, with injector grouping enabling more CO₂ to be stored permanently at lower recycling cost.

At Stage 1.1, CF reaches 1.54 B€ (+6.04%). The introduction of time-varying control improves injection sequencing, aligning it more effectively with reservoir dynamics. FGIP grows further, producing incremental revenue, while water production again increases slightly but remains a minor cost contributor. Meanwhile, FGPT rebound with retention dips slightly to 92.08%, signaling untapped potential despite the financial benefit.

A pivotal leap occurs in Stage 2.1, when well-level control is combined with the first degree of temporal refinement. CF jumps to 1.78 B€ (+22.44%), driven by substantial FGIP gains (+6.56 Mt vs. Manual, worth ~328 M€) and a sharp FGPT reduction (−2.42 Mt, worth ~97 M€ in avoided costs). These improvements far outweigh the added FGIT cost (~62 M€) and increased brine handling (~36 M€). The optimizer effectively increases the retention rate to 95.32%, adding permanent storage without proportional increases in costly by-products.

From Stage 2.1 to Stage 2.2, CF edges up to ~1.79 B€ (+23.26% vs. Manual), a relatively modest ~1 M€ improvement. FGIP grows slightly (66.89 to 67.52 Mt), but FGPT also ticks upward (3.27 to 3.39 Mt) and water production rises further, eroding the net benefit. This stage represents diminishing returns: additional tonnes of stored CO₂ come at lower marginal contribution due to offsetting cost increases.

Beyond Stage 2.2, the CF curve flattens (Stages 2.3 and 2.4 remain ~1.79 B€). The marginal economic benefit of finer temporal refinement is negligible, while operational complexity rises with more frequent schedule changes. The highest monetized value is reached at Stage 2.2 (identical within plotting precision to Stages 2.3 and 2.4).

Overall, the financial uplift across stages is overwhelmingly driven by increased permanent storage (FGIP) and reduced CO₂ recycling (FGPT). The most significant economic step is the transition to well-level control with moderate temporal refinement (Stage 2.1), which captures ~95.32% of the total gain. Stage 2.2 offers a relatively small extra boost (~1–M€) but at the expense of slightly higher operational complexity. For practical deployment, Stage 2.2 or Stage 2.3, when a 3-year cadence is preferred and additional relatively small clients bid at relatively higher prices (2.65 to 2.67 Mtpa increase) than the major emitters, marks the financial sweet spot, while Stage 2.1 stands out as the efficiency-focused alternative with nearly maximum benefit at minimal operational overhead (fewer control intervals than the highest-resolution designs).

For completeness, Figure 15 illustrates the evolution of well-level injection schedules from the Manual baseline to Stage 2,4 based on the financial objective.

4.5.3. Comparative Analysis: Engineering vs. Financial

To establish a common ground of comparison, the two optimal cases with Stage 2,3 from each case are selected for comparison at both field- and well-level performance. Since solutions (engineering and financial) produce nearly identical field water production (FWPT), this parameter was excluded from the comparison to focus on more discriminating metrics. Furthermore, the cash flow of the optimal case under the engineering objective was also estimated for direct financial benchmarking.

Figure 16 directly contrasts the optimized outcomes obtained under both objectives for Stage 2,3. At the field scale, both formulations converge toward broadly similar solutions, reflecting the strong overlap between high technical performance and high economic return in this case study. The two approaches achieve comparable permanent storage volumes (FGIP of 68.26 Mt for engineering vs. 67.52 Mt for financial), indicating that the financial optimization does not sacrifice significant storage capacity despite its explicit cost penalties. However, the financial objective function attains this capacity with a notably lower gross injection total (FGIT: 70.91 Mt vs. 72.95 Mt), resulting in a substantially reduced recycled CO₂ volume (FGPT: 3.39 Mt vs. 4.69 Mt) and, consequently, a higher retention efficiency (95.22% vs. 93.57%). This outcome stems directly from the financial formulation’s explicit penalization of injection costs, which promotes leaner injection profiles that maximize net retained CO₂ per tonne injected.

From a revenue perspective, this leaner injection strategy translates into a higher cumulative cash flow: 1.79 B€ for the financial case versus 1.75 B€ for the engineering case when the latter’s FGIP and by-products are monetized using the same economic coefficients. This ~40 M€ uplift, though modest relative to total project value, is significant given the similarity in overall storage performance, and is primarily driven by the financial formulation’s ability to avoid costly excessive injection volumes without materially compromising retained mass. Both cases deliver nearly identical net effective field injection rates (2.65–2.67 Mtpa), underscoring that the operational deliverability to CO₂ suppliers is preserved in both optimization philosophies.

On the other hand, Figure 17 provides a well-level perspective, illustrating how the two objective functions arrive at their respective optima. The engineering formulation produces more dynamic, high-amplitude adjustments across the injection period—particularly for wells I1 and I2—resulting in periods of moderate injection followed by aggressive injection. This behavior stems from its prioritization of maximizing FGIP, even if that requires higher FGIT and tolerating more recycling. In contrast, the financial formulation yields smoother, more conservative injection patterns, particularly for I1 and I4, with fewer extreme rate shifts. For I2 and I3, the financial case maintains higher rates during intervals where retention is high and costs are low but curtails injection earlier when breakthrough risks rise. This reflects a more cost-conscious sequence that balances capacity gains against the marginal cost of additional tonnes stored.

Overall, both optimization philosophies identify practical sweet spot solutions that combine high storage, strong retention and stable deliverability. The key difference lies in the route to this solution: the engineering case extracts slightly more gross capacity at the expense of higher recycling, while the financial case achieves nearly the same retained mass with improved economic efficiency and smoother operational profiles. From an optimization standpoint, the convergence of both formulations to similar optimal solutions—despite fundamentally different objective functions—demonstrates the robustness of the spatio-temporal discretization approach and suggests that the global optimum has been reached for this case study. From an operator’s perspective, factoring in CAPEX requirements for injection and recycling infrastructure, the financial formulation presents a more attractive solution—delivering balanced technical performance and economic returns with lower infrastructure demands.

5. Discussion, Conclusions and Final Remarks

The results demonstrate that the proposed Dynamic Time–Space Discretization of well control strategies approach fundamentally changes how well control strategies can be developed for CO₂ storage operations. By explicitly mapping and embedding the full set of multidimensional constraints—technical, commercial, operational, economic, and regulatory—into the optimization logic, the framework ensures that resulting schedules are not only computationally optimal but also physically deployable within real-world project boundaries.

This study delivers two major advances for CCS well control optimization. First, it systematically maps and characterizes the multidimensional constraint space governing large-scale CO₂ storage—encompassing technical, operational, commercial, economic, and regulatory factors—and reframes it as an integrated decision space. This mapping ensures that optimization outcomes are not only computationally optimal but also physically, commercially, and legally deployable. Second, it demonstrates an automated, hierarchical time–space discretization framework that embeds these constraints directly into the optimization process, enabling schedules to evolve from coarse to fine resolution while accelerating convergence and preserving robustness.

From the engineering perspective, the methodology consistently outperformed the manual industry-standard equal-rate schedule. Gains of up to +14% in net retained CO₂, combined with a 22% reduction in recycling, indicate that the optimizer can exploit spatiotemporal flexibility to unlock previously inaccessible storage capacity while controlling operational inefficiencies. Importantly, the retention efficiency increases to 95% was achieved without sacrificing injection deliverability, confirming that higher technical performance can be obtained without jeopardizing supply obligations to CO₂ capture facilities.

From the financial perspective, the optimization reached comparable storage volumes but did so with leaner injection profiles and smoother well-level adjustments. This produced an estimated +23% cumulative cash flow improvement over the manual baseline, driven by reduced injection and recycling costs. Notably, the economic formulation converged to nearly the same retained mass as the engineering formulation but with fewer operational fluctuations, suggesting that cost-awareness in the objective function inherently smooths operational complexity.

A key outcome is the identification of practical “sweet spots” where storage gains and recycling control are jointly maximized under manageable operational schedules. These scenarios are particularly relevant for commercial operators, as they balance capacity expansion with cost efficiency and infrastructure constraints. The fact that both formulations independently converged to similar optimal solutions underscores the robustness of the discretization approach and suggests proximity to the global optimum for the given reservoir configuration.

When compared to current manual planning practices, the benefits are twofold:

• Constraint integration ensures that operational limits, safety margins, and commercial commitments are respected from the outset, reducing the risk of infeasible solutions emerging late in project planning.
• Hierarchical refinement allows the optimizer to progressively target the most sensitive control variables, achieving significant performance gains without the computational cost of full-resolution optimization from the start.

The framework’s scalability is evident: it can be applied to larger fields, varied reservoir types, or evolving operational priorities simply by modifying constraint sets and discretization parameters. Furthermore, its compatibility with commercial simulators facilitates adoption in existing industrial workflows.

Limitations remain. Results here are based on a closed-boundary saline aquifer; open systems with plume migration constraints may present different trade-offs. Economic parameters are project-specific, and different tariff structures or cost coefficients could shift optimal solutions. Future extensions of the framework should incorporate other boundary systems as well as sensitivity and uncertainty analysis of key financial parameters. Such probabilistic evaluation would enable a more robust assessment of economic performance under varying tariff structures, injection costs, and recycling penalties, thereby enhancing the decision-making value of the optimization outcomes.

The present study focused primarily on demonstrating the conceptual framework and engineering applicability of the proposed dynamic spatiotemporal discretization methodology. A subsequent study, currently under preparation, will extend this research to a broader range of geological contexts and to full-scale field models. That study will provide a detailed evaluation of the algorithm’s convergence characteristics, computational efficiency, and scalability, complementing the engineering-oriented validation presented herein. Finally, while the hierarchical approach effectively reduces computational burden, extremely large asset portfolios may still require parallelization or surrogate modeling for full-field applications.

Future research should explore extending the framework in three main directions. First, testing alternative optimization algorithms—such as Particle Swarm Optimization, Differential Evolution, or hybrid metaheuristics—could reveal whether further convergence speed or solution quality gains are possible relative to the modified Genetic Algorithm used here. Second, incorporating machine-learning-based surrogate models could allow rapid pre-screening of scenarios, enabling near-real-time operational adjustments in response to new geological data or market conditions. Third, applying the methodology to multi-reservoir portfolios, open-boundary systems, and formations with complex fault/plume dynamics would test its robustness under a wider range of geomechanical and regulatory constraints. Integrating uncertainty quantification into the optimization process, so that solutions are not only optimal under deterministic conditions but also resilient to parameter variability and geological risks, is also an important avenue for development. Together, these directions would further enhance the technique’s readiness for deployment in diverse CCS contexts worldwide.