Abstract
This study focuses on the stability of time-delay load frequency control (LFC) systems. Based on the Lyapunov–Krasovskii (L–K) functional method, a stability criterion with less conservatism and lower computational complexity is proposed. Unlike recent methods that decrease conservatism through enhancing the complexity of L–K functional, only the double integral is augmented in this paper. To estimate the L–K functional derivatives more precisely, an improved matrix-separation-based inequality is proposed, which introduces some delay-derivative-dependent matrices rather than the high-dimensional free matrices. By applying the augmented L–K functional and the improved matrix-separation-based inequality, the stability criterion is established. Case analysis demonstrates that the new stability criterion has less conservatism and lower computational complexity, thereby validating the correctness of the method presented.
1. Introduction
Frequency is a key indicator for measuring power quality, and fluctuations in frequency affect the reliable operation of the power system [1]. The power system must maintain the frequency within a narrow range around the nominal value, with an allowable deviation typically not exceeding ±0.2 to 0.5 Hz [2]. When the system is disturbed, improper frequency regulation can lead to large-scale power outages, severely affecting production and daily life. The LFC system responds to system disturbances by adjusting the output power, thereby maintaining system stability [3,4,5,6]. In practical applications, various time-delay phenomena occur in the LFC system, including signal transmission delays, dynamic response delays of the actuator, and calculation delays of the controller [7,8]. These time delays significantly impact the system stability and control performance, which is particularly dangerous in large-scale interconnected power grids [8,9,10]. Time delay effects must be considered in LFC system design and analysis to ensure system stability across various operating conditions. Therefore, investigating the influence of time delay on systems holds great significance for ensuring power system safety.
The stability analysis of time-delay systems aims to obtain the delay margin (for ease of understanding, the maximum delay at which an LFC system can maintain stability is considered the delay margin). The main research method is the L–K functional method. But this method provides only sufficient conditions for the stability criterion. To deal with this problem, many researchers have conducted in-depth studies in two areas: the improvement of L–K functionals and the estimation of functional derivatives. For the improvement of L–K functionals, approaches include augmented L–K functionals [11,12], delay-related L–K functionals [13], and multiple integral L–K functionals [14]. For the estimation of functional derivatives, there are Jensen inequality [15], Writinger inequality [16], auxiliary-function-based integral inequality [17], free matrix-based integral inequality [18], Bessel–Legendre integral inequalities [19], and different forms of reciprocally convex combination lemmas [20,21,22]. Many scholars have conducted relevant studies on the time-delay LFC systems. Jiang et al. conducted research on time-delay LFC systems using simple L–K functional. Although the computational complexity was low, the conservatism of the conclusion was too high [4]. Yang et al. obtained a stability criterion by applying an improved L–K functional containing triple integrals and estimating the integral term by applying the double integral inequality [17]. To simplify the calculation and obtain a stability criterion with relatively low conservatism, Ramakrishnan et al. estimated the integral term in the derivative by applying different inequalities according to the variation in the time delay [23]. By increasing the complexity of the L–K functional and applying an improved integral inequality, Yang et al. obtained a less conservative criterion, but they only considered the case of systems with constant delay [24]. Feng et al. reduced the conservatism of the criterion by augmenting the single integral L–K functional, but increased the computational complexity due to the introduction of matrices [25]. Sun et al. made fuller use of the information of system state variables to construct an augmented L–K functional. Although they obtained stability criteria with less conservatism, they ignored the issue of computational complexity [26]. Chen et al. adopted model reconstruction techniques to reduce conservatism, but made the calculation more complex [27].
In existing studies, researchers primarily focus on decreasing the conservatism of stability criterion. To achieve this, methods such as constructing complex L–K functionals and introducing free matrices have been adopted. However, these approaches have resulted in the increase in computational complexity. As the power system scale expands, the dimensions of the system matrix increase proportionally [4]. Excessively high computational complexity reduces the efficiency of solving the delay margin. Therefore, deriving a stability criterion with less conservatism and lower computational complexity has become the main challenge at present.
Based on existing research, the stability issues of the LFC system are further investigated. Zhang et al. proposed a matrix-separation-based inequality in the study of discrete-time systems [28]. Inspired by their work, the inequality is improved and applied to the LFC system in this paper. Unlike previous studies, complex L–K functionals are not constructed here; instead, only a double integral is augmented by more fully utilizing both the system state and its derivative information. To estimate the derivatives of the augmented L–K functional more precisely, an improved matrix-separation-based inequality is proposed, which introduces some delay-derivative-dependent matrices rather than the high-dimensional free matrices. By applying the augmented L–K functional and the improved inequality, a stability criterion is established. On this basis, the performance of the LFC system is studied. Through the analysis of delay margins under various delay types and control gains , the correctness of the method is validated. The results show that by using the improved matrix-separation-based inequality, a stability criterion with less conservatism and lower computational complexity can be obtained.
Notation 1.
The meanings of the relevant symbols are explained below. and indicate the -dimensional vector space and the matrix space, respectively. ( ) indicates the dimensional (positive definite) symmetric matrices. () indicates the transpose (inverse) of the matrix . () indicates that is a positive (negative) definite matrix. represents a block-diagonal matrix. . is the identity (zero) matrix. indicates the symmetry term in a symmetric matrix. denotes a column vector.
2. Problem Formulation
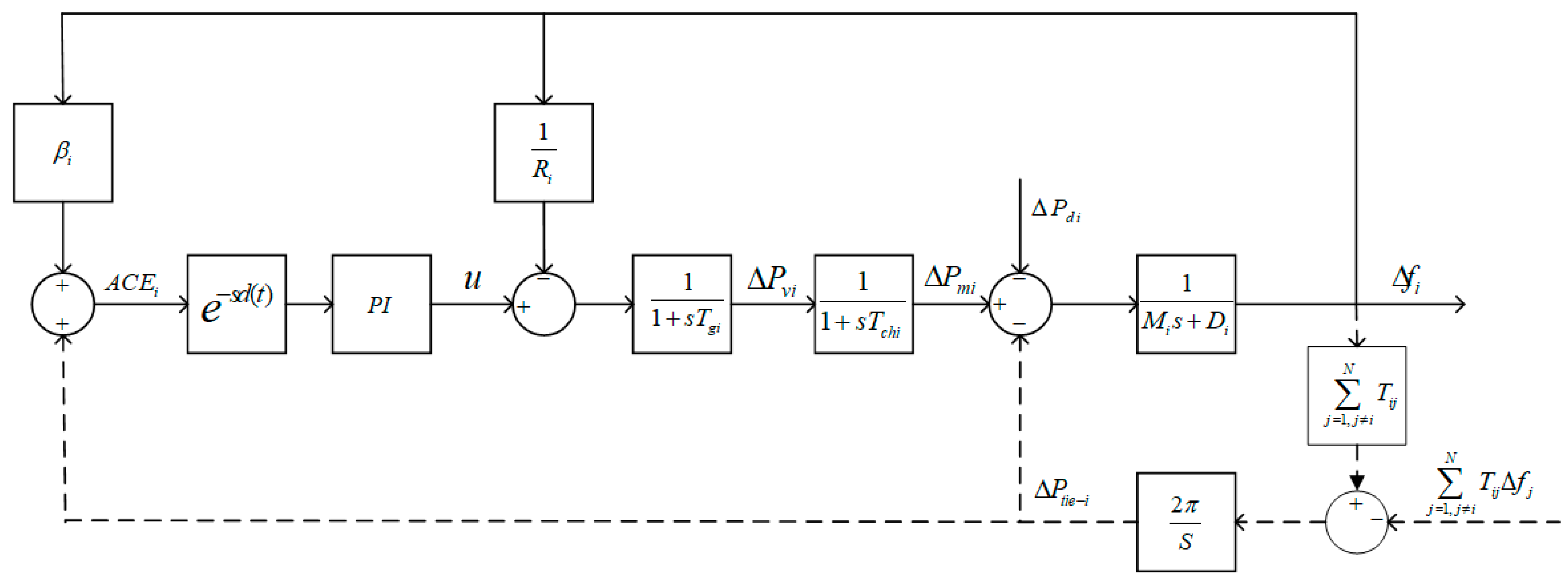
The actual power systems exhibit high-dimensional, nonlinear, and time-varying properties, making precise modeling extremely challenging [29]. For the convenience of analysis, a simplified LFC model is adopted in this paper. The system structure is shown in Figure 1 (for one-area LFC systems, there are no dotted line connections).
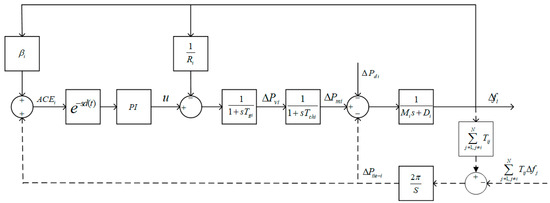
Figure 1.
The simplified diagram of the time-delay LFC system.
In Figure 1, the LFC model includes the generator-load model, the prime mover model, the speed regulation system model, and the LFC controller model. and are the control area numbers, indicates the synchronizing coefficient, and . is the deviation of the exchange power in area . represents the comprehensive impact of time-delay and is the time delay. is the frequency bias factor. , , , and are the frequency deviation, valve position deviation, the mechanical output deviation, and load deviation, respectively.
2.1. One-Area LFC Model
According to the LFC system structure block diagram, the model of a one-area LFC system is as follows:
where
, , , and are the moment of inertia, generator damping coefficient, area control error, and speed drop, respectively. () is the time constant of the turbine (governor). represents the total number of control areas.
The PI controller is:
To simplify the analysis, the following new vectors are defined:
Apply the PI controller described in Equation (2) to the system defined by Equation (1); the model is expressed as follows:
where
As external disturbances have no affect on stability of system at the equilibrium point, stability analysis can be performed without accounting for them. Equation (3) can be further transformed into the following:
where
Scalars and are the upper and lower bound of the time delay, respectively. The function is the initial state.
2.2. Multi-Area LFC Model
For ease of analysis, in the multi-area LFC model, all generation units within a region are aggregated into a single equivalent unit in multi-area LFC models. According to the LFC system structure block diagram, the model is expressed as follows:
where
For each area, the PI controller is designed as follows:
Combining Equations (5) and (6) yields the following:
where
In addition, it should be noted that the net tie-line power exchange among multiple control areas satisfies the following zero-sum property:
In a multi-region LFC system, multiple delays occur. For the convenience of calculation, assume that all delays are equal. Then, the following simple model is obtained:
where
Scalars and are the upper and lower bound of the time delay, respectively. The function is the initial state.
A two-area LFC system is used as a representative example to clarify the multi-area LFC model, with the corresponding system matrix provided in Appendix A.
3. Main Results
The stability criterion for system (10), together with key lemmas underpinning its derivation, are provided in this section.
3.1. Main Lemmas
Lemma 1 ([30]).
For a matrix , scalars and
with
, and a continuous function
:, the following inequality integral holds:
where
Lemma 2 ([16]).
For a matrix , scalars and
with
, and a continuous function
:, the following inequality integral holds:
where
Lemma 3 ([21]).
For a scalar , matririces
, if there exist a matrix
such that
, the following inequality integral holds:
Corollary 1.
For a given matrix and a matrix
, there exist a matrix
and a vector
of suitable dimensions such that the following equation holds for
:
Proof.
Refer to Appendix B. □
Corollary 2.
Consider a continuous function
and a matrix
with appropriate dimension. For
, and scalars
and
with
, if there exist symmetric matrices
, and
, such that
and the following inequality holds:
where
Proof.
Refer to Appendix C. □
Remark 1.
Inspired by references [28,31], a new matrix separation inequality that significantly improves upon existing matrix separation inequalities is proposed.
- In references [28,31], only the matrix was introduced in , which results in only a slight connection between and . On this basis, is further improved to in this paper. The delay derivative and its upper and lower bound information are introduced by this improved method. Its advantage lies in the fact that, for cases involving time-varying delays, this approach can further reduce the conservatism.
- Zhang et al. introduced high-dimensional free matrices to increase the coupling between different variables, which could further reduce conservatism. However, it resulted in increased computational complexity [28]. Xiong et al. estimated the derivative using a generalized free-weighting-matrix method and also introduced some free matrices [31]. The LFC system is taken as the research target of this paper, and the computational complexity must be taken into consideration. So, the Wirtinger inequality is used to estimate the derivative. This improved method reduces computational complexity under the condition of slightly increased conservatism, making it more suitable for application in power systems.
3.2. Stability Criterion
The stability criterion of System (10) are given in this section. To simplify the expression, the following symbol definitions are given:
Theorem 1.
For scalars
and
, if there exist matrices
,
,
,
,
, ,
, and
such that the following matrix inequalities hold for
and
, then the system (10) is asymptotically stable.
where
Proof.
Refer to Appendix D. □
Remark 2.
Compared to the double integral
in reference [13], is extended to in this paper, which is key to reducing the conservatism. Moreover, for the estimation of , the integration interval is split into and . Then, the improved matrix-separation inequality presented in this paper is applied for the estimation.
To demonstrate the advantages of the augmented functionals and the improved matrix-separation-based inequality, the in the double integral is deleted, and the derivatives of the functional are estimated using Lemmas 1 and 3. Theorem 2 can then be derived.
Theorem 2.
Given scalars ,
, the system (10) is asymptotically stable if there exist matrices
, , , and
such that the following matrix inequalities hold for
and
.
where
The definitions of the other symbols can be found in Theorem 1.
Proof.
Refer to Appendix E. □
3.3. Analysis of Performance
The performance of the system is analyzed in this section. Given a specified controller gain, the objective is to minimize the robust performance index to improve the system resistance to disturbances [8].
According to the LFC system modeling process in Section 1, the state feedback control system is adapted into a conventional static feedback control system. Subsequently, the equation is rewritten as follows:
Theorem 3.
For scalars
and
, disturbance performance index
, and controller gain
, if there exist matrices
,
,
,
,
,
,
, and
such that the following matrix inequalities hold for
and
, then the LFC system (21) with disturbance performance index is asymptotically stable.
where
The definitions of the other symbols can be found in Theorem 1.
Proof.
Refer to Appendix F. □
4. Case Studies
Conservatism comparisons and simulation verification are introduced in this section to demonstrate the superiority and correctness of the proposed method. The delay margins were calculated by using MATLAB 2023. Then, the corresponding models were established to verify the obtained results. Additionally, a robust performance evaluation was conducted. Table 1 presents the parameters of LFC systems [4].

Table 1.
Parameters of LFC systems.
In this paper, the computational complexity is not directly discussed but is reflected by introducing the Number of Decision Variables (NDVs). The more NDVs there are, the greater the computational complexity is, and the longer the time it takes to calculate the delay margin is. The NDVs of the relevant theorems are all given on the right side of the table.
4.1. One-Area LFC System
4.1.1. Conservatism Comparisons
When the system has a constant delay , the delay margins for various and are solved. The delay margin and the NDVs are presented in Table 2. The symbol “-” indicates that the result is not given in the reference, and n is the dimension of the system matrix. Both - and n retain these meanings in the subsequent table. For the sake of convenience, the abbreviation for Theorem 1 is defined as Th. 1. The abbreviations of the other theorems are the same as those used here.

Table 2.
The delay margin of one-area LFC system for .
Table 2 shows that the delay margins obtained using Th. 1 and Th. 2 are significantly better than the results in references [4,17]. Compared to references [25,26], the result of Th. 1 is the same as that of reference [26] and is slightly worse than that of reference [25]. However, the NDVs are significantly lower than in both references [25,26]. Compared with reference [27], the result obtained by using Th. 1 is greater, but the NDVs slightly increase. This demonstrates that the proposed method effectively reduces conservatism in stability criterion while maintaining lower computational complexity.
For one-area LFC systems with time-varying delays, two scenarios, and , are analyzed.
As shown in Table 3, the delay margin from Th. 1 significantly exceeds those of reference [32] and Th. 2, demonstrating the effectiveness of the method. Furthermore, compared to the case of , it is clear that in the LFC system with time-varying delay ( or ), the effectiveness of Theorem 1 in reducing conservatism is more pronounced.

Table 3.
The delay margin of one-area LFC system for and .
4.1.2. Simulation Verification
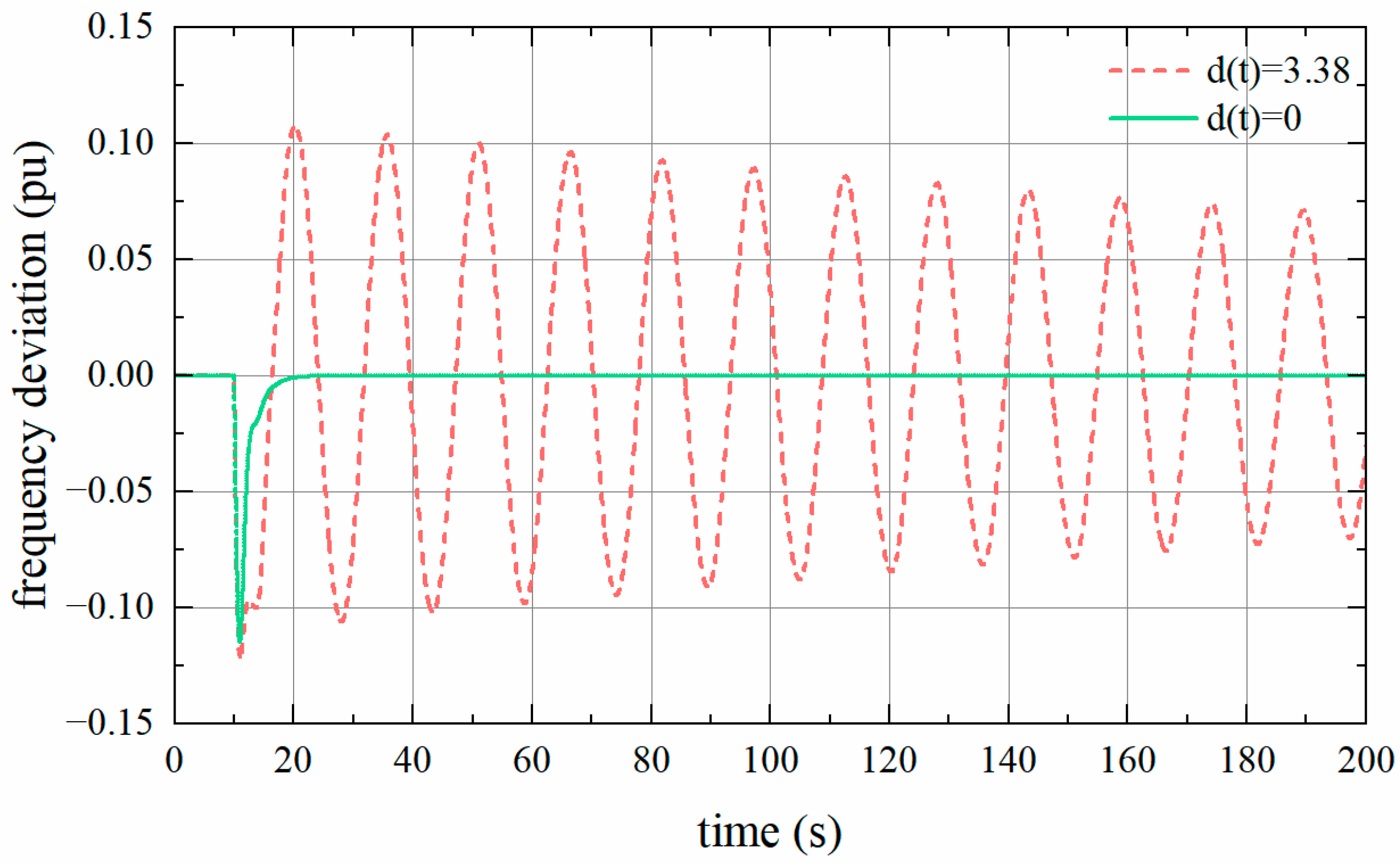
The correctness of the obtained time delay margin is verified through MATLAB R2023a simulations. Set and , and add a step load of 0.1 pu to the system at 10 s. The frequency deviation of the system is shown in Figure 2.
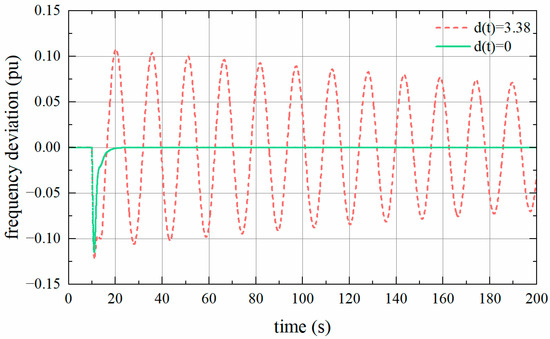
Figure 2.
Frequency deviation of one-area LFC system with .
Figure 2 shows the frequency responses of the one-area LFC system with . For and , the delay margin is 3.38 s. As observed in Figure 2, when the , the frequency deviation gradually decreases, and the system returns to stability.
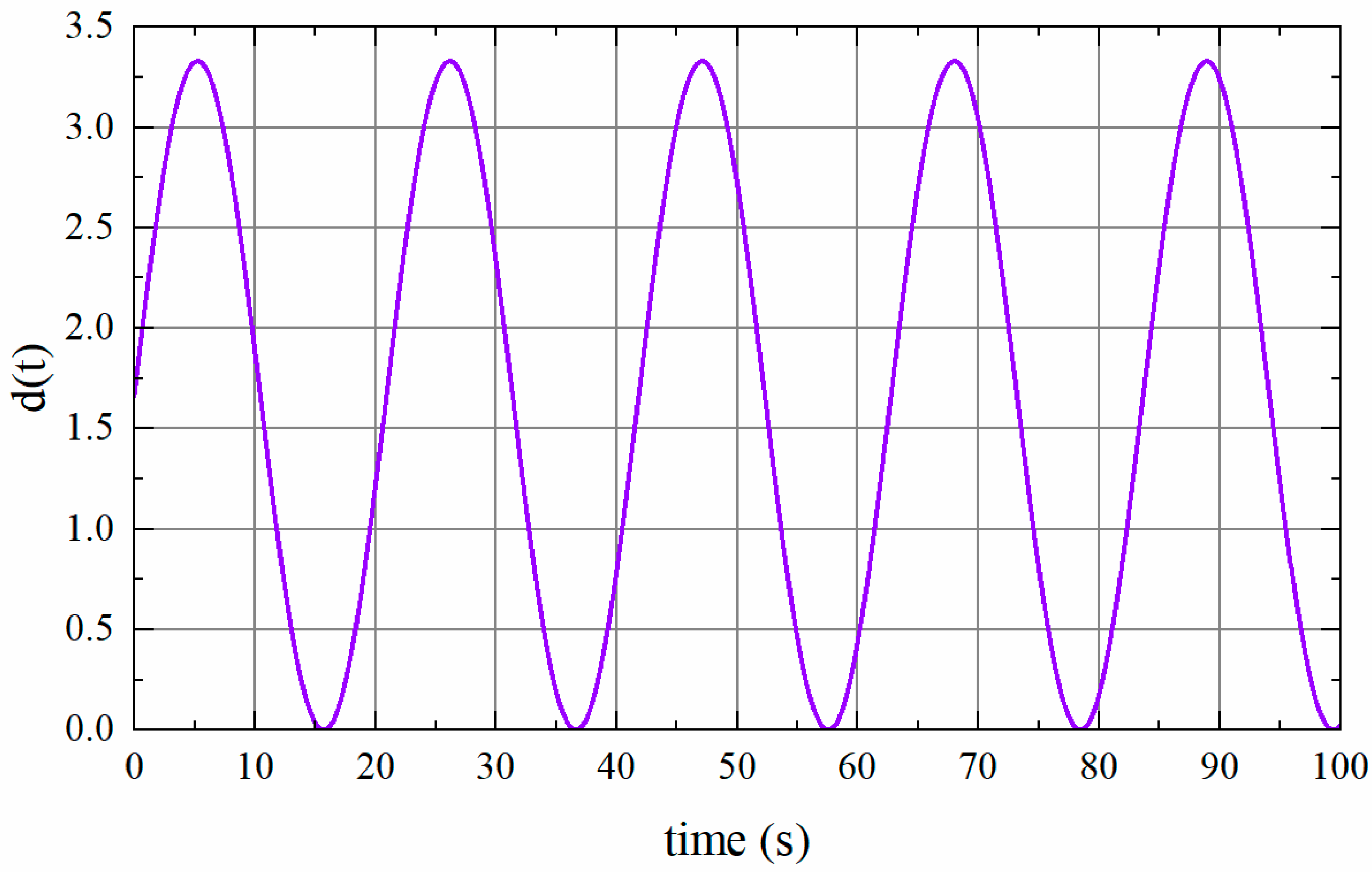
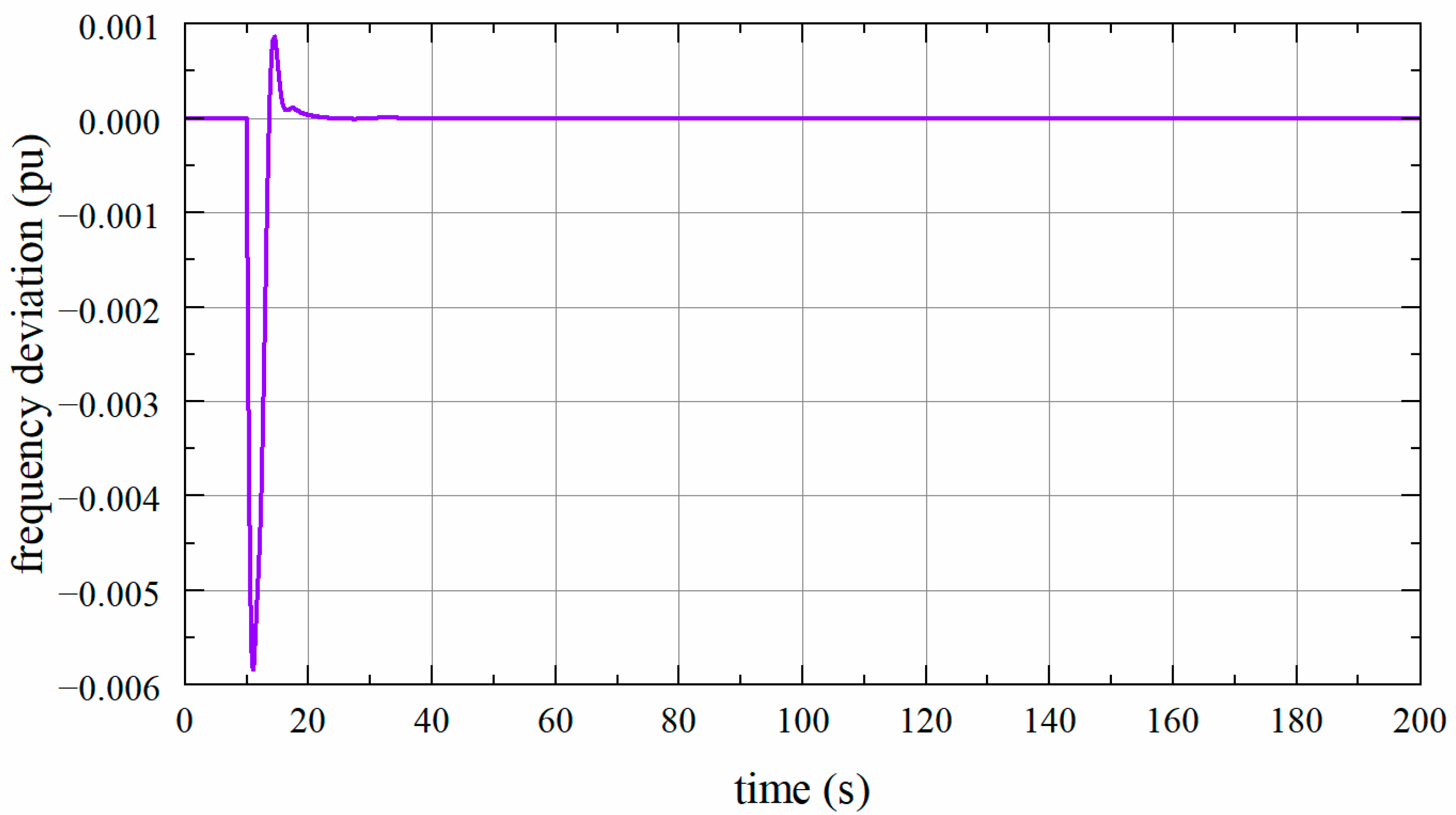
Based on the results obtained from Theorems 1, it is assumed that (see Figure 3) to verify the correctness of this method in the system with . The frequency deviation is shown in Figure 4. It can be observed that when and , the system is stable.
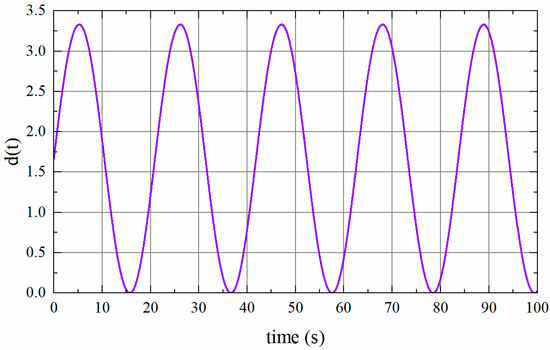
Figure 3.
Time-varying delay .
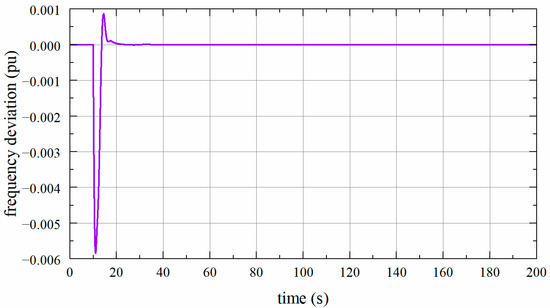
Figure 4.
Frequency deviation of one-area LFC system with .
4.2. Two-Area LFC System
4.2.1. Conservatism Comparisons
The delay margin of the two-area LFC system is calculated and compared with results from relevant literature in this section.
The delay margins and the NDVs are presented in Table 4. As shown, the delay margin reported here is less conservative than those in references [4,17,27]. Moreover, the delay margin exhibits a similar trend to that of the one-area system. The delay margin decreases as increases when is held constant.

Table 4.
The delay margin of two-area LFC system for .
The delay margin is presented in Table 5. It can be observed that, compared to reference [27], the results of this paper are significantly better.

Table 5.
The delay margin of two-area LFC system for and .
4.2.2. Simulation Verification
The method is the same as that described in Section 4.1.1.
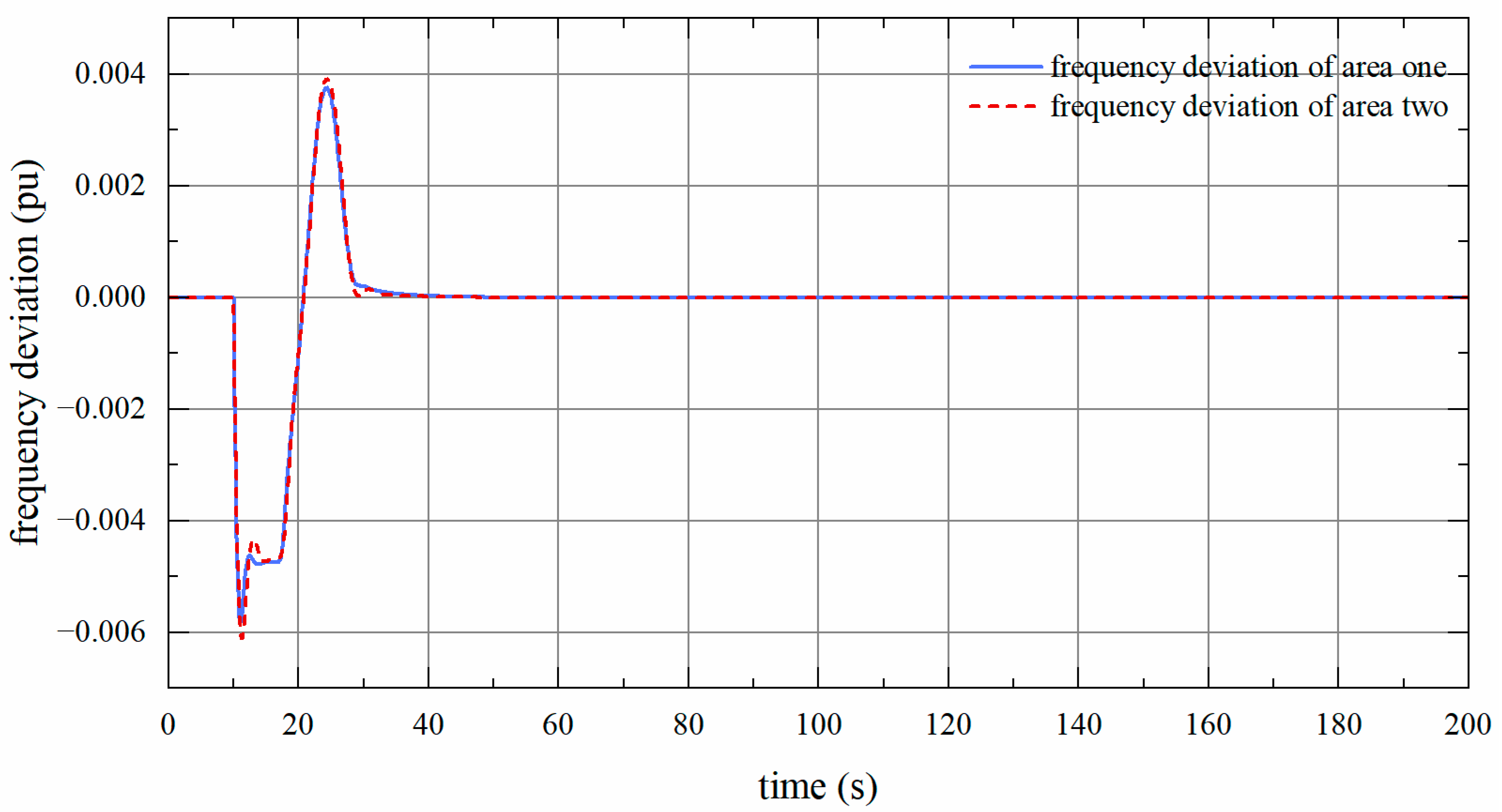
For , , the delay margin is 7.59 s according to Theorem 1. The frequency response is shown in Figure 5. As illustrated, the frequency deviations in both areas approach zero, indicating that the system is gradually returning to stability.
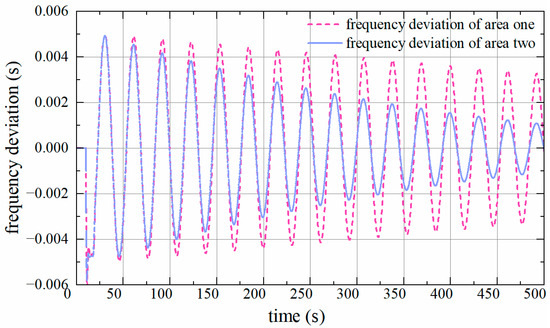
Figure 5.
Frequency deviation of two-area LFC system with constant time-delay.
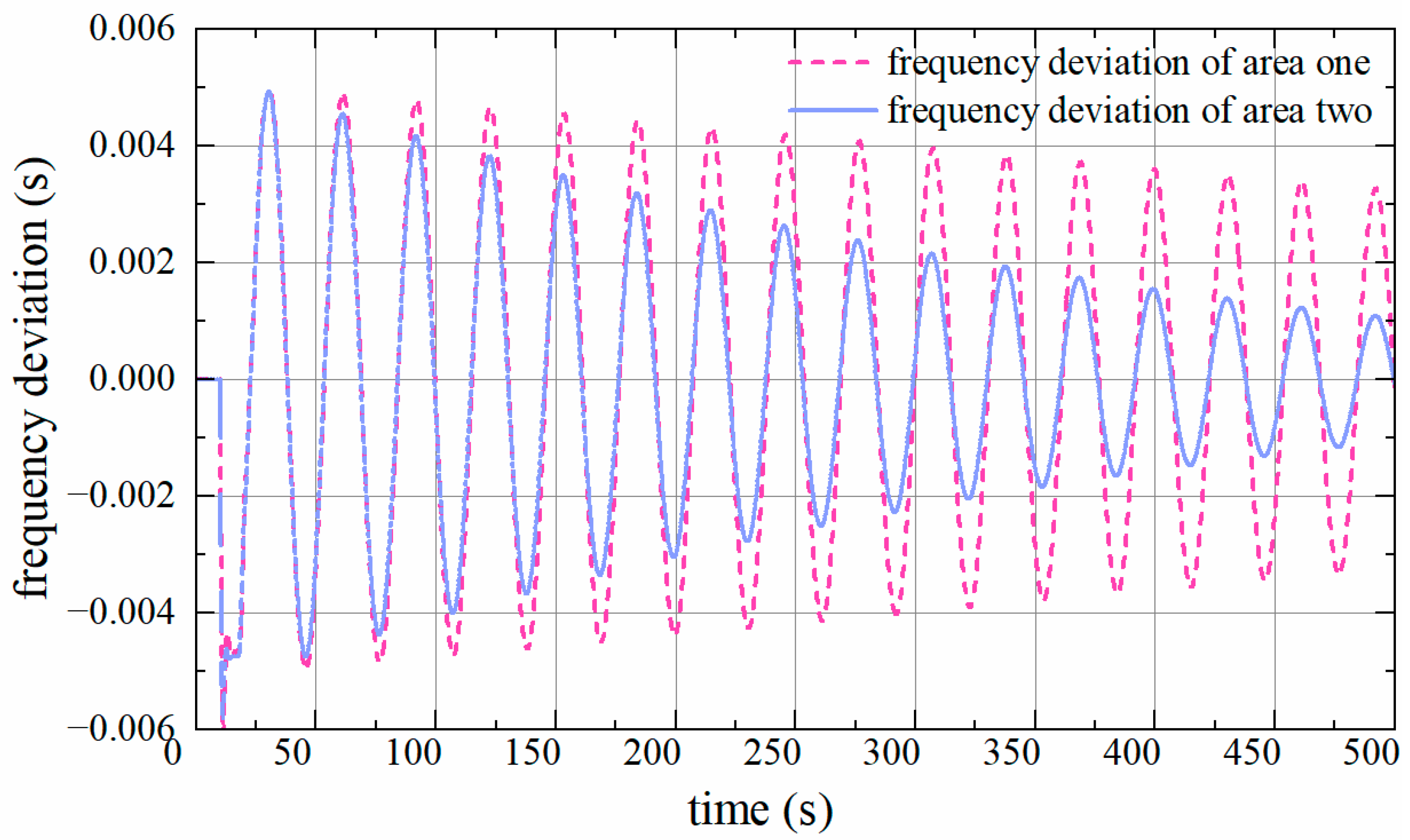
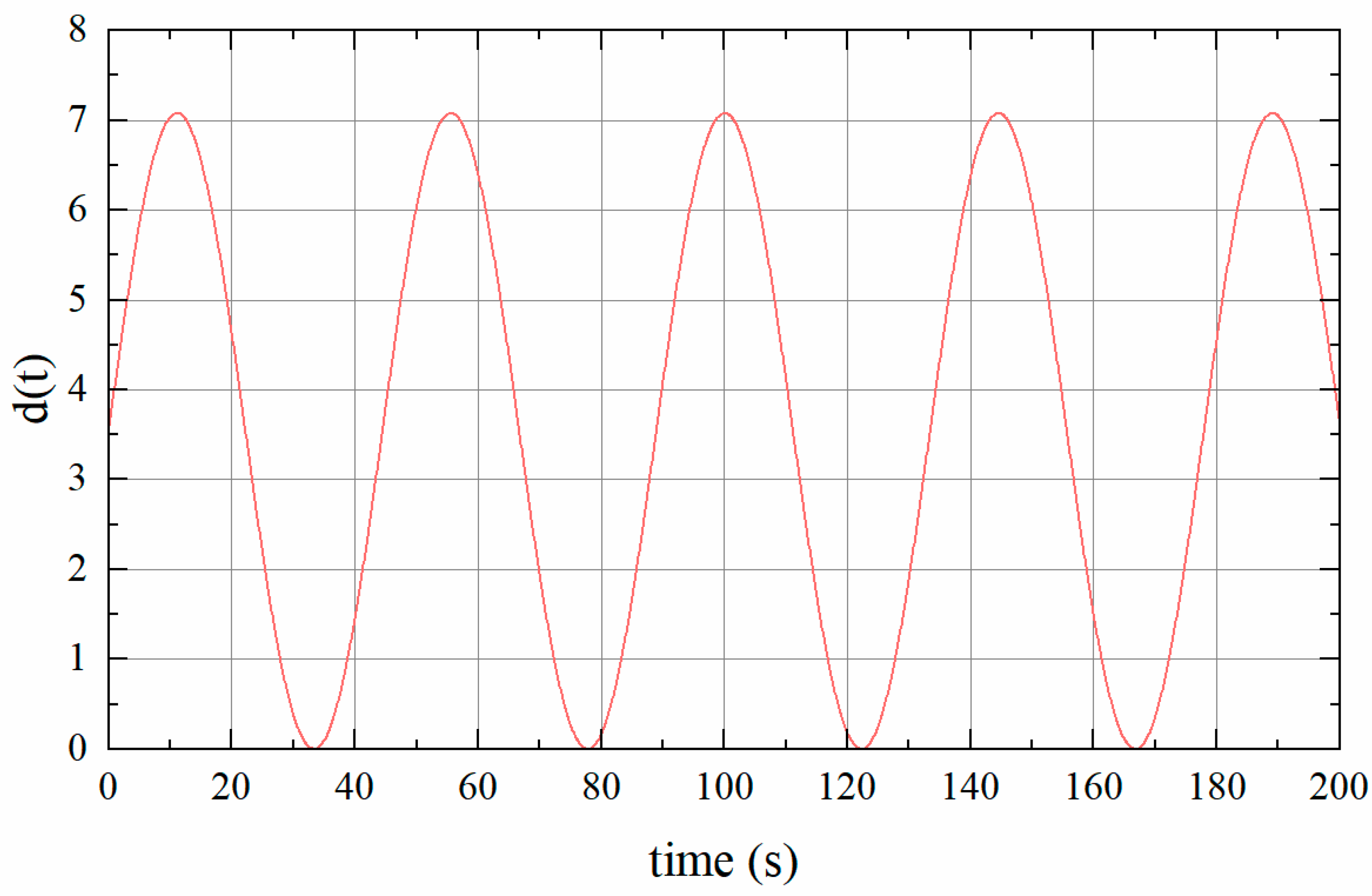
The time-varying delay is , as shown in Figure 6. According to the frequency deviation in Figure 7, it can be observed that when and , the system returns to stability in 40 s. This further confirms the accuracy of the method proposed.
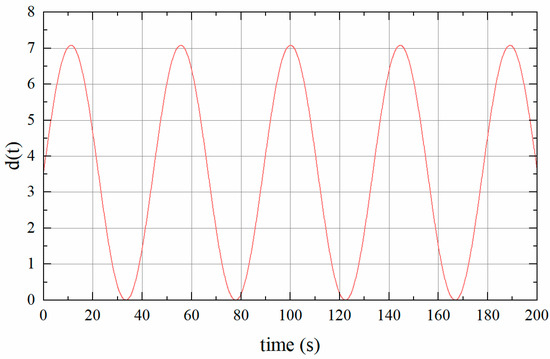
Figure 6.
Time-varying delay .
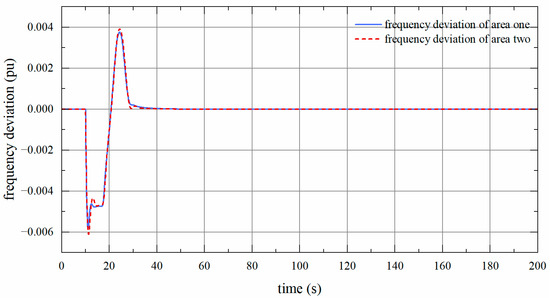
Figure 7.
Frequency deviation of two-area LFC system with time-varying delay for , .
4.3. Performance Analysis
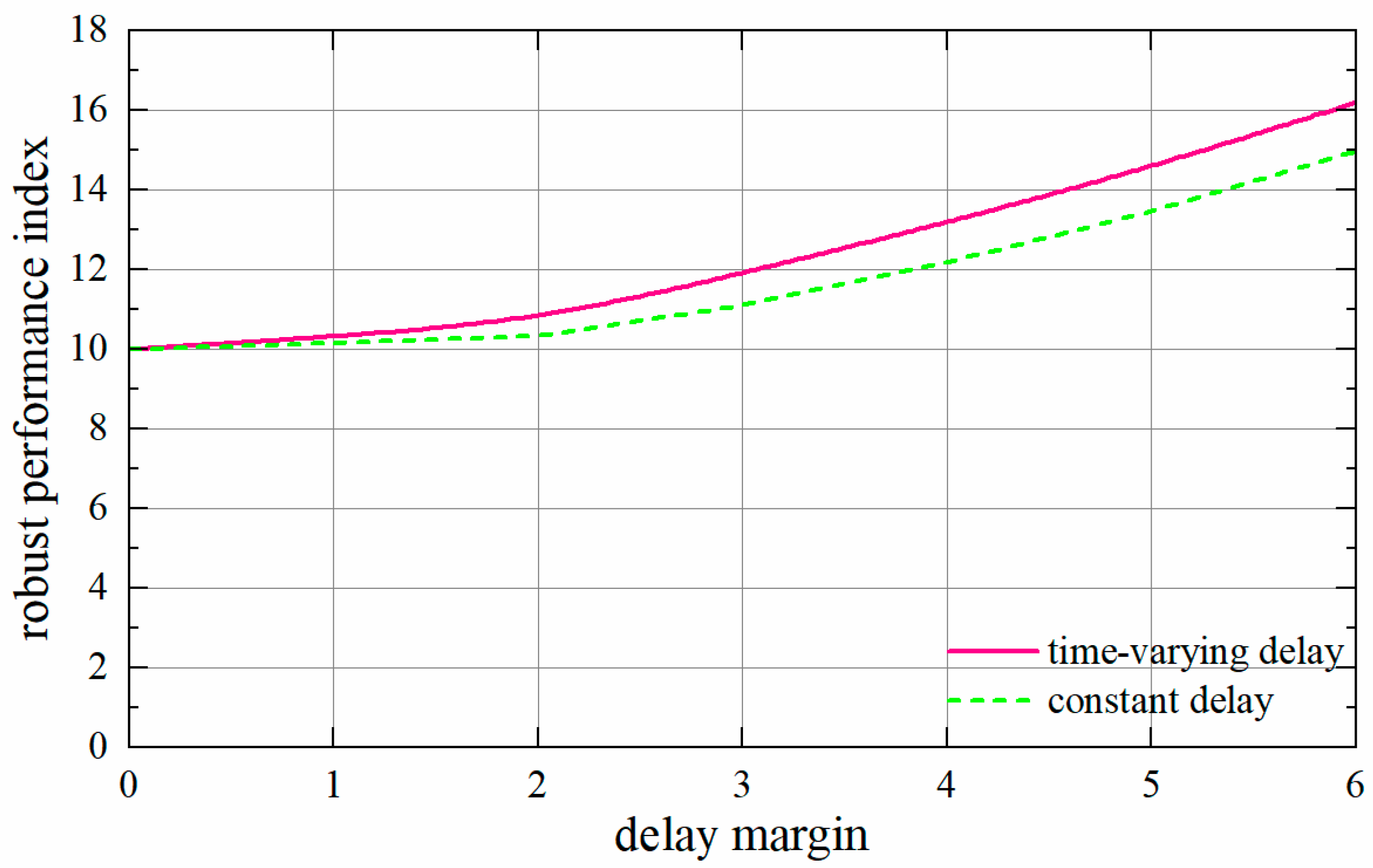
Given the and , the minimum robust performance index —representing the disturbance suppression level of systems—can be calculated for various delay margins. The details are shown in Figure 8.
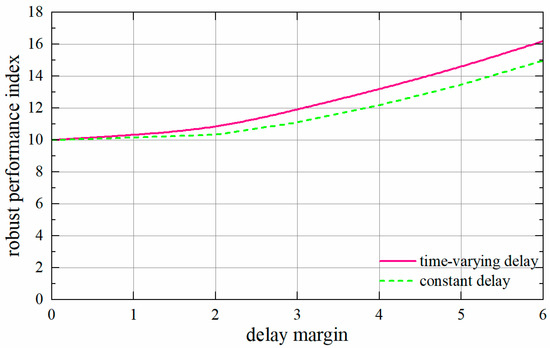
Figure 8.
The minimum robust performance index of different delay margins.
As can be seen from Figure 8, with the increase in delay margin, the minimum performance index also rises. This indicates that an increase in time delay decreases the robustness. Furthermore, for the same delay margin, the robust performance index under constant delay is higher than the corresponding value under time-varying delay. This indicates that time-varying delay also reduces the robustness of the system.
5. Conclusions
The stability of time-delay LFC systems is studied, and an innovative analysis method via an improved matrix-separation-based inequality is proposed to derive a stability criterion with less conservatism and lower computational complexity. By applying a double integral augmented L–K functional, a foundation is established for deriving a stability criterion with less conservatism. Meanwhile, the improved matrix-separation-based inequality is obtained by deleting the high-dimensional free matrices but introducing some delay-derivative-dependent matrices of lower dimensions, utilizing the information of delay more fully. By applying the augmented L–K functional and the improved inequality, the stability criterion is established. The numerical results of two examples demonstrate that this method reduces criterion conservatism with a lower computational complexity, particularly in the case of time-varying delays. The simulation results strongly validate the correctness of the stability analysis method. The method provides a theoretical basis and technical support for the design and optimization of the LFC schemes in the power system and helps to improve the stability and reliability.
The research findings presented in this paper can be extended to LFC systems with multiple time-delays, multiple areas, and uncertain parameters. Additionally, to further reduce the computational complexity, optimizing the modeling method of multi-area systems to lower the dimension of the system matrix is our next research direction.
Author Contributions
Methodology, F.L. and H.D.; software, F.L. and H.D.; validation, F.L., H.D. and M.L.; writing—original draft preparation, F.L., H.D. and M.L.; writing—review and editing, F.L., H.D. and M.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China under Grant 62303266, the 111 Project under Grant B17040, the Open and Innovation Fund of Hubei Three Gorges Laboratory under Grant SK240008, and the Hubei Provincial Natural Science Foundation Project under Grant 2024AFB472.
Data Availability Statement
The data is included in the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| LFC | Load frequency control |
| L–K | Lyapunov–Krasovskii |
| NDVs | Number of Decision Variables |
| Theorem 1 | Th. 1 |
| Theorem 2 | Th. 2 |
Appendix A
The system matrixs of two-area LFC system.
Appendix B
Proof of Corollary 1.
The following Equation (A1) can be obtained from [33]:
where
Let , and it can be obtained as follows:
Let and , and substitute them into Equation (A2) yields the following equation.
Equation (A3) is Corollary 1. Proof completed. □
Appendix C
Proof of Corollary 2.
Provide the following definitions:
where
For , applying the Lemma 2, is estimated as:
where
Then, applying the Corollary 1, the Equation (A4) is estimated as:
For , the calculation yields the following result:
For , applying the Lemma 1, is estimated as:
Summing Equations (A5)–(A7) leads to Corollary 2. □
Appendix D
Proof of Theorem 1.
Consider the following L–K functionals:
where
In Theorem 1, it has been required that matrixs , and be a positive definite matrix, so the functional holds.
Calculating the derivative of the yields:
where , , ,
Based on Lemma 1, with is estimated as:
Based on Corollary 2, and with are respectively estimated as:
where , .
and cause the derivative to be non-convex. Applying Lemma 3 to estimate and , we obtained:
It follows from Equations (A11)–(A15) that:
Combining Equations (A9), (A10) and (A16) leads to:
When , the following equation holds:
According to Shure Complement, it follows that Equation (A18) is equivalent to Equations (16) and (17).
Based on the above analysis, if LMIs (16), (17), and (18) hold, then the system (10) is asymptotically stable. □
Appendix E
Proof of Theorem 2.
Construct the following L–K functionals:
where
In Theorem 2, it has been required that matrixs , and be a positive definite matrix, so the functional holds.
Calculating the derivative of the yields:
where , , ,
The estimation method for is the same as in Theorem 1. Based on Lemma 1, and with are respectively estimated as:
Applying Lemma 3 to estimate Equations (A21) and (A22), we obtain:
Combining Equations (A9), (A10) and (A23) yields:
When , the following equation holds:
From the Schur complement, Equation (A25) is equivalent to Equation (19). When Equation (A25) holds, the system (10) is asymptotically stable. □
Appendix F
Proof of Theorem 3.
Construct the following L–K functionals:
In Theorem 3, it has been required that matrixs , and be a positive definite matrix, so the functional holds.
Calculating the derivative of the yields:
To reduce the impact of external load disturbances on the control output, the disturbance performance index are defined as follows:
If the Equation (A29) holds:
According to Equation (A27), the inequality holds:
When and , integrate Equation (A29) from to , it can be obtained:
Equation (A31) means For sufficiently small scalars , it follows that
By replacing Equation (A29) with and using Schur complement, the LMI criterion in Theorem 3 can be derived, thereby verifying the asymptotic stability of the system (21). This completes the proof. □
References
- Zhang, G.; Ren, J.; Zeng, Y.; Liu, F.; Wang, S.; Jia, H. Security assessment method for inertia and frequency stability of high proportional renewable energy system. Int. J. Electr. Power Energy Syst. 2023, 153, 109309. [Google Scholar] [CrossRef]
- Ducoin, E.A.; Gu, Y.; Chaudhuri, B.; Green, T.C. Analytical design of contributions of grid-forming and grid-following inverters to frequency stability. IEEE Trans. Power Syst. 2024, 39, 6345–6358. [Google Scholar] [CrossRef]
- Dokht Shakibjoo, A.; Moradzadeh, M.; Moussavi, S.Z.; Vandevelde, L. A novel technique for load frequency control of multi-area power systems. Energies 2020, 13, 2125. [Google Scholar] [CrossRef]
- Jiang, L.; Yao, W.; Wu, Q.; Wen, J.; Cheng, S. Delay-dependent stability for load frequency control with constant and time-varying delays. IEEE Trans. Power Syst. 2011, 27, 932–941. [Google Scholar] [CrossRef]
- Ramakrishnan, K.; Vijeswaran, D.; Manikandan, V. Stability analysis of networked micro-grid load frequency control system. J. Anal. 2019, 27, 567–581. [Google Scholar] [CrossRef]
- Grigsby, L.L. Power System Stability and Control; Taylor & Francis: Abingdon, UK, 2007. [Google Scholar]
- Hu, Z.; Liu, S.; Luo, W.; Wu, L. Resilient distributed fuzzy load frequency regulation for power systems under cross-layer random denial-of-service attacks. IEEE Trans. Cybern. 2020, 52, 2396–2406. [Google Scholar] [CrossRef]
- Peng, C.; Zhang, J.; Yan, H. Adaptive event-triggering H∞ load frequency control for network-based power systems. IEEE Trans. Ind. Electron. 2017, 65, 1685–1694. [Google Scholar] [CrossRef]
- Luo, H.; Hiskens, I.A.; Hu, Z. Stability analysis of load frequency control systems with sampling and transmission delay. IEEE Trans. Power Syst. 2020, 35, 3603–3615. [Google Scholar] [CrossRef]
- Milano, F.; Anghel, M. Impact of time delays on power system stability. IEEE Trans. Circuits Syst. I Regul. Pap. 2011, 59, 889–900. [Google Scholar] [CrossRef]
- Kwon, O.; Lee, S.-H.; Park, M.-J.; Lee, S.-M. Augmented zero equality approach to stability for linear systems with time-varying delay. Appl. Math. Comput. 2020, 381, 125329. [Google Scholar] [CrossRef]
- Zhang, X.-M.; Han, Q.-L.; Ge, X. The construction of augmented Lyapunov-Krasovskii functionals and the estimation of their derivatives in stability analysis of time-delay systems: A survey. Int. J. Syst. Sci. 2022, 53, 2480–2495. [Google Scholar] [CrossRef]
- Ren, W.; Xiong, J. Vector-Lyapunov-function-based input-to-state stability of stochastic impulsive switched time-delay systems. IEEE Trans. Autom. Control 2018, 64, 654–669. [Google Scholar] [CrossRef]
- Qian, W.; Xing, W.; Fei, S. H∞ state estimation for neural networks with general activation function and mixed time-varying delays. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 3909–3918. [Google Scholar] [CrossRef]
- Zhang, Z.-M.; He, Y.; Wu, M.; Wang, Q.-G. Exponential synchronization of neural networks with time-varying delays via dynamic intermittent output feedback control. IEEE Trans. Syst. Man Cybern. Syst. 2017, 49, 612–622. [Google Scholar] [CrossRef]
- Seuret, A.; Gouaisbaut, F. Wirtinger-based integral inequality: Application to time-delay systems. Automatica 2013, 49, 2860–2866. [Google Scholar] [CrossRef]
- Yang, F.; He, J.; Wang, J.; Wang, M. Auxiliary-function-based double integral inequality approach to stability analysis of load frequency control systems with interval time-varying delay. IET Control Theory Appl. 2018, 12, 601–612. [Google Scholar] [CrossRef]
- Zeng, H.-B.; He, Y.; Wu, M.; She, J. Free-matrix-based integral inequality for stability analysis of systems with time-varying delay. IEEE Trans. Autom. Control 2015, 60, 2768–2772. [Google Scholar] [CrossRef]
- Seuret, A.; Gouaisbaut, F. Stability of linear systems with time-varying delays using Bessel–Legendre inequalities. IEEE Trans. Autom. Control 2017, 63, 225–232. [Google Scholar] [CrossRef]
- Zeng, H.-B.; Lin, H.-C.; He, Y.; Teo, K.-L.; Wang, W. Hierarchical stability conditions for time-varying delay systems via an extended reciprocally convex quadratic inequality. J. Frankl. Inst. 2020, 357, 9930–9941. [Google Scholar] [CrossRef]
- Park, P.; Ko, J.W.; Jeong, C. Reciprocally convex approach to stability of systems with time-varying delays. Automatica 2011, 47, 235–238. [Google Scholar] [CrossRef]
- Seuret, A.; Gouaisbaut, F. Delay-Dependent Reciprocally Convex Combination Lemma. 2016. Available online: https://hal.science/hal-01257670/ (accessed on 6 August 2025).
- Ramakrishnan, K.; Ray, G. Stability criteria for nonlinearly perturbed load frequency systems with time-delay. IEEE J. Emerg. Sel. Top. Circuits Syst. 2015, 5, 383–392. [Google Scholar] [CrossRef]
- Yang, F.; He, J.; Pan, Q. Further improvement on delay-dependent load frequency control of power systems via truncated B–L inequality. IEEE Trans. Power Syst. 2018, 33, 5062–5071. [Google Scholar] [CrossRef]
- Feng, W.; Xie, Y.; Luo, F.; Zhang, X.; Duan, W. Enhanced stability criteria of network-based load frequency control of power systems with time-varying delays. Energies 2021, 14, 5820. [Google Scholar] [CrossRef]
- Sun, Y.; Bo, X.; Duan, W.; Lu, Q. Stability analysis of load frequency control for power systems with interval time-varying delays. Front. Energy Res. 2023, 10, 1008860. [Google Scholar] [CrossRef]
- Chen, C.; Fan, C.; Lian, H.; Zhou, S.; Huang, T. Delay-dependent stability analysis for load frequency control systems with time-varying delays. J. Frankl. Inst. 2024, 361, 106927. [Google Scholar] [CrossRef]
- Zhang, C.-K.; Chen, W.-H.; Zhu, C.; He, Y.; Wu, M. Stability analysis of discrete-time systems with time-varying delay via a delay-dependent matrix-separation-based inequality. Automatica 2023, 156, 111192. [Google Scholar] [CrossRef]
- Bevrani, H. Robust Power System Frequency Control; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Van Hien, L.; Trinh, H. Refined Jensen-based inequality approach to stability analysis of time-delay systems. IET Control Theory Appl. 2015, 9, 2188–2194. [Google Scholar] [CrossRef]
- Xiong, D.; Zhang, C.-K.; Wan, X.; He, Y. Stability and stabilization of T–S fuzzy systems under sampled-data control via a matrix-separation-based inequality. IEEE Trans. Fuzzy Syst. 2024, 32, 4312–4323. [Google Scholar] [CrossRef]
- Yang, F.; He, J.; Wang, D. New stability criteria of delayed load frequency control systems via infinite-series-based inequality. IEEE Trans. Ind. Inform. 2017, 14, 231–240. [Google Scholar] [CrossRef]
- Park, P. A delay-dependent stability criterion for systems with uncertain time-invariant delays. IEEE Trans. Autom. Control 1999, 44, 876–877. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).