Maximum Torque per Ampere Control of IPMSM Based on Current Angle Searching with Sliding-Mode Extremum Seeking
Abstract
1. Introduction
2. MTPA Model and Control of IPMSM Based on Current Angle Searching with SMES
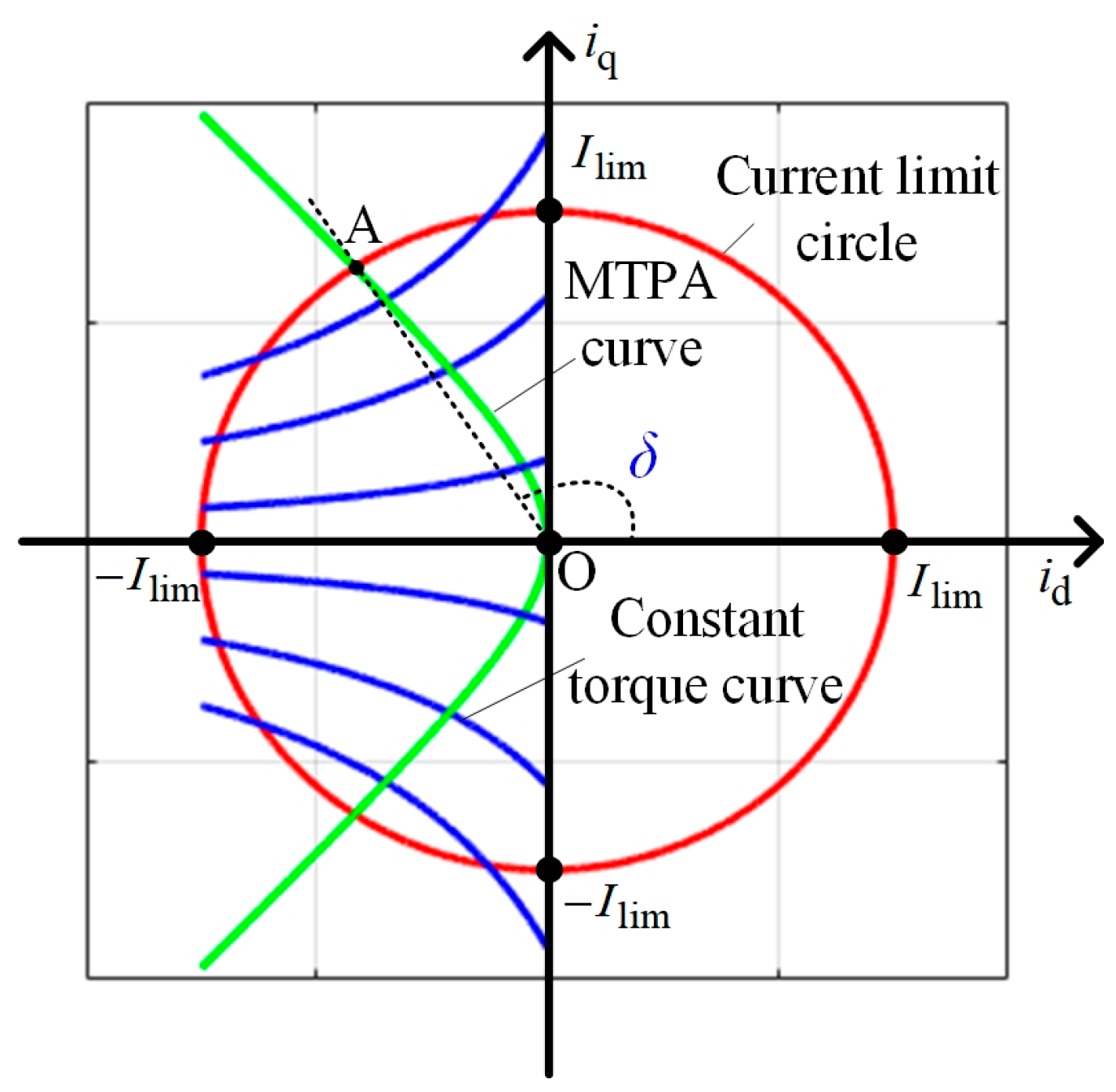
2.1. MTPA Model of IPMSM
2.2. MTPA Control of IPMSM Based on Current Angle Searching with SMES
3. Performance Analysis of the SMESC-MTPA Controller
3.1. Stability Proof
- ①
- When υ > 0, < 0;
- ②
- When υ < 0, > 0.
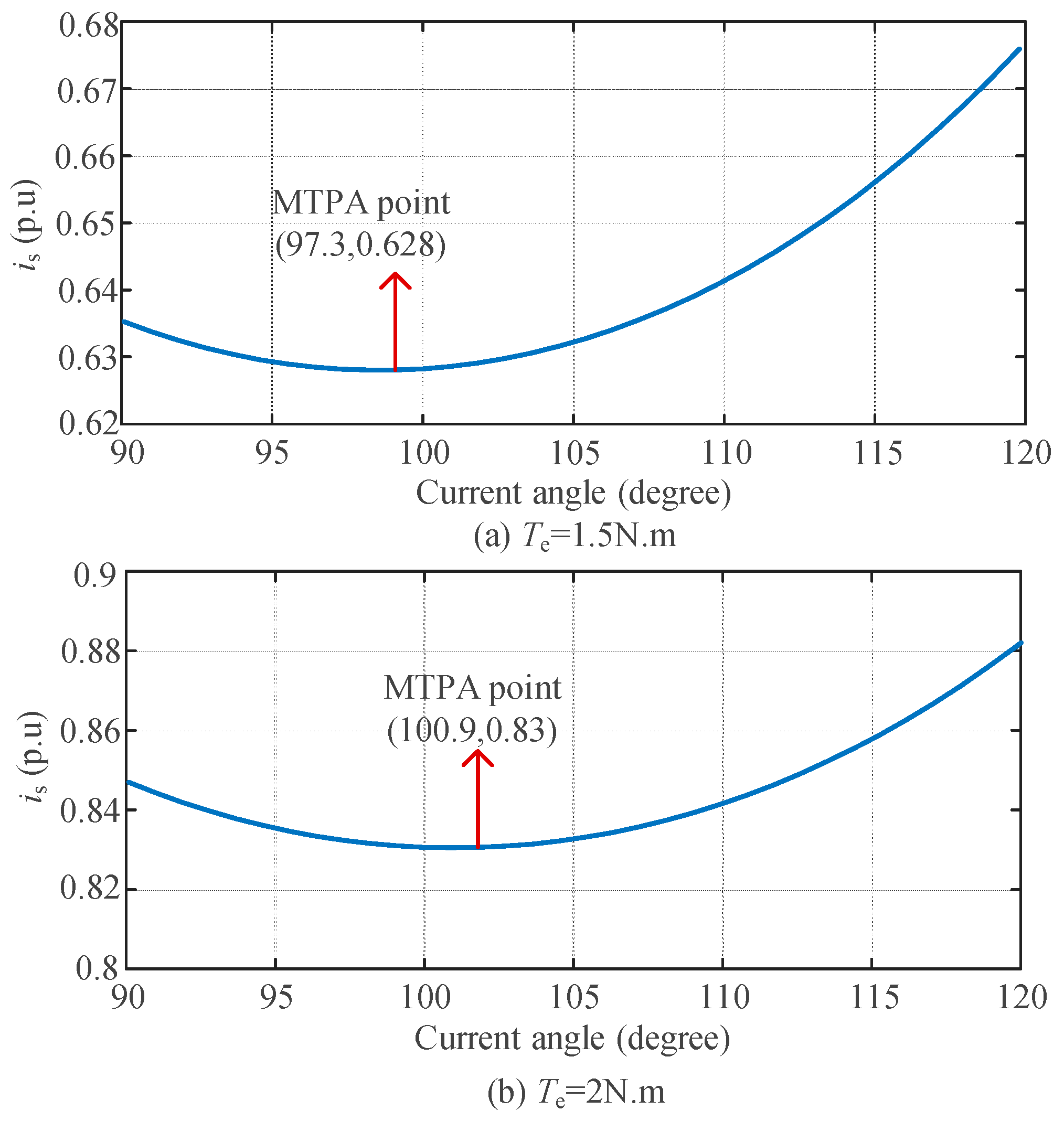
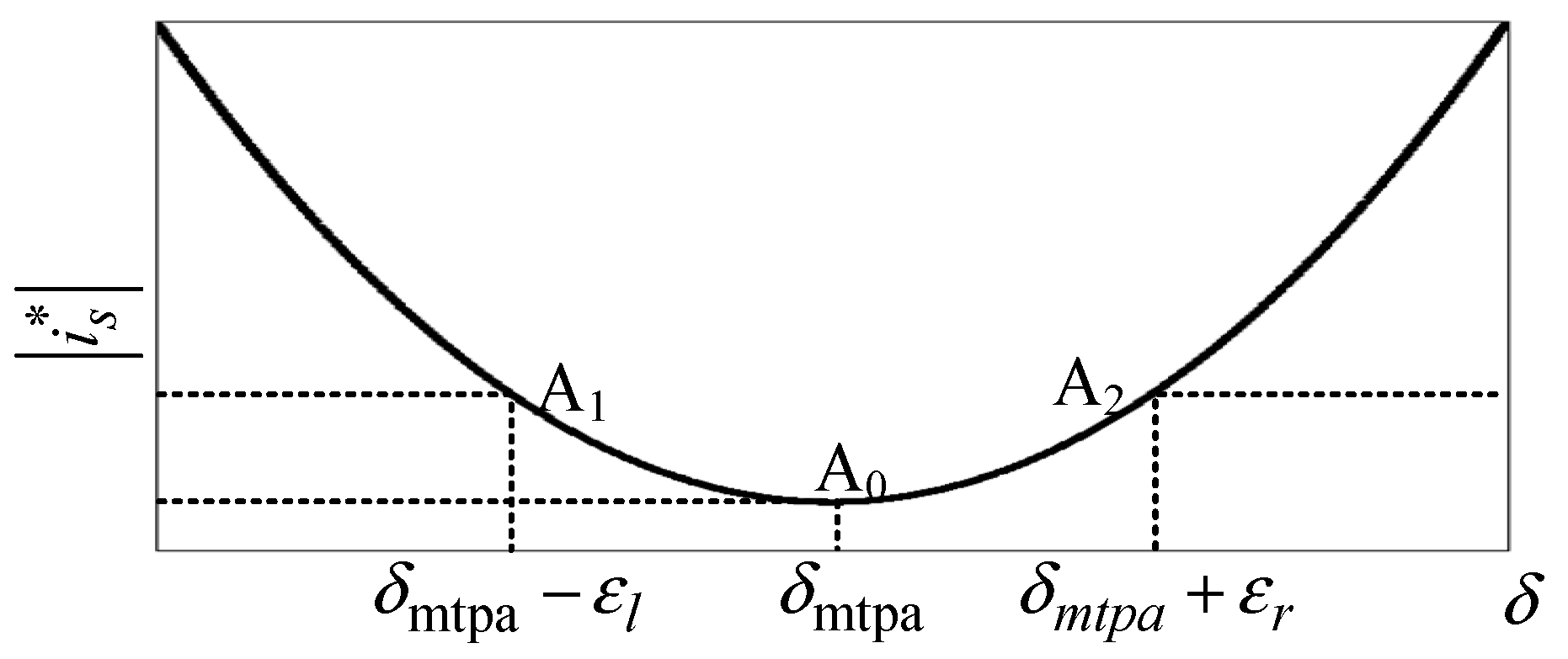
3.2. Convergence Processes and Control Accuracy
4. Simulation Analysis and Experimental Verification
4.1. Simulation Analysis
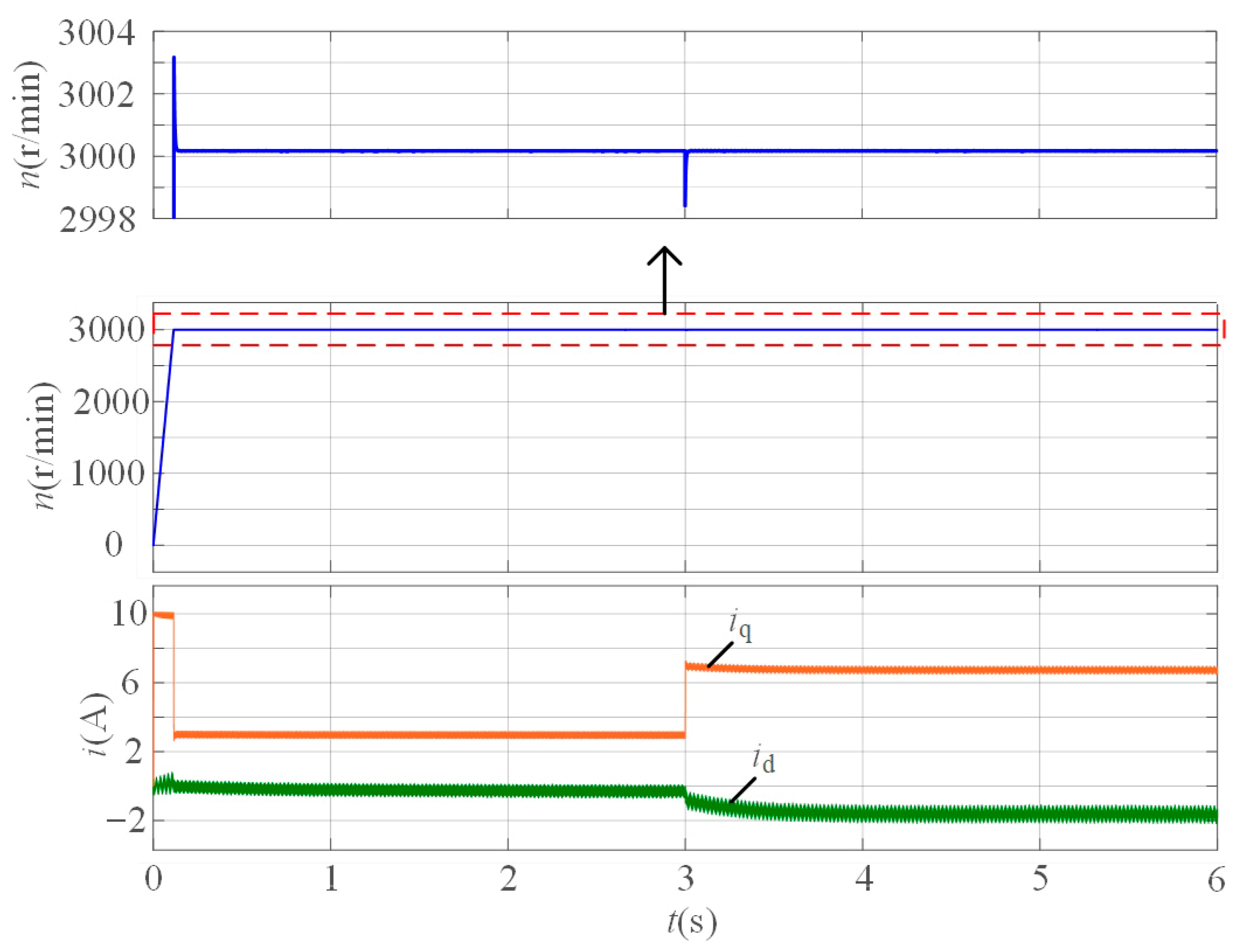
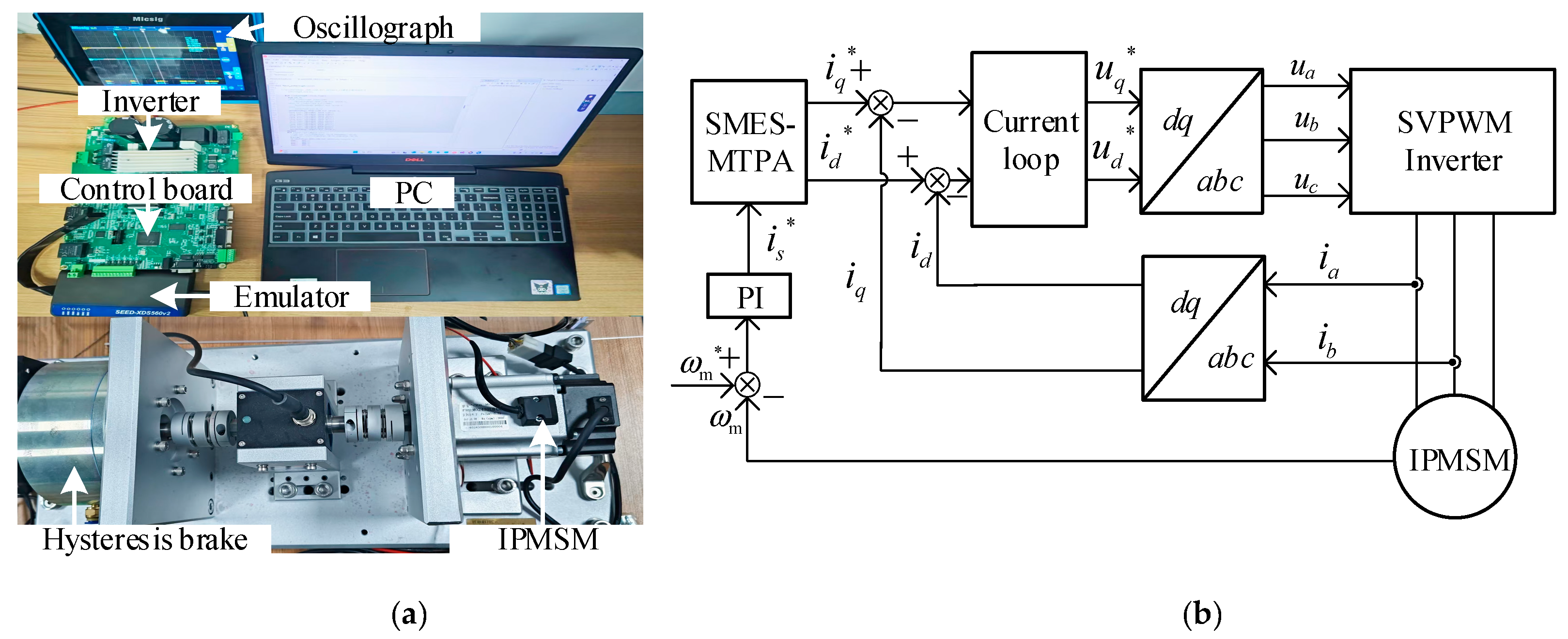
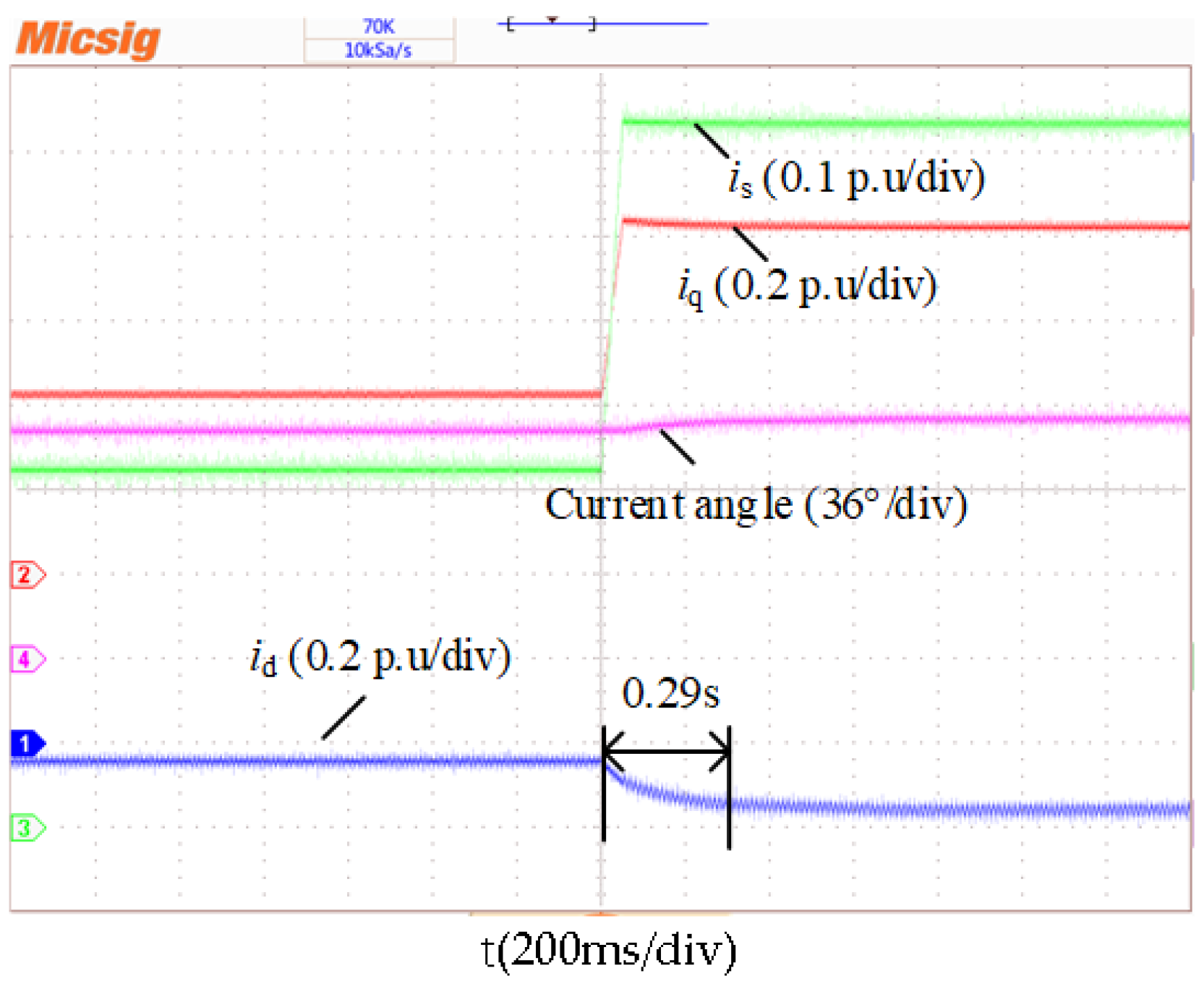
4.2. Experimental Verification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yu, Y.; Cong, L.; Tian, X.; Xie, R.; Lu, J. Stator Current Vector Orientation-Based Backstepping Predictive Control of Torque Ripple Minimization for PMSM with consideration of Electrical Loss. Math. Probl. Eng. 2020, 2020, 7319329. [Google Scholar] [CrossRef]
- Hu, D.; Xu, L. Characterizing the torque lookup table of an IPM machine for automotive application. In Proceedings of the 2014 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Xi’an, China, 31 August–3 September 2014; IEEE: New York, NY, USA, 2014; pp. 1–6. [Google Scholar]
- Miao, Y.; Ge, H.; Preindl, M.; Ye, J.; Cheng, B.; Emadi, A. MTPA fitting and torque estimation technique based on a new flux-linkage model for interior-permanent-magnet synchronous machines. IEEE Trans. Ind. Appl. 2017, 53, 5451–5460. [Google Scholar] [CrossRef]
- Pan, C.T.; Sue, S.M. A linear maximum torque per ampere control for IPMSM drives over full-speed range. IEEE Trans. Energy Convers. 2005, 20, 359–366. [Google Scholar] [CrossRef]
- Özçiflikçi, O.E.; Koç, M.; Bahçeci, S. Evaluation of Maximum Torque per Ampere Control Method for Interior Permanent Magnet Machine Drives on dSpace with Emphasis on Potential Practical Issues for High Energy Efficiency. Energies 2025, 18, 4118. [Google Scholar] [CrossRef]
- Dianov, A.; Tinazzi, F.; Calligaro, S.; Bolognani, S. Review and Classification of MTPA Control Algorithms for Synchronous Motors. IEEE Trans. Power Electron. 2022, 37, 3990–4007. [Google Scholar] [CrossRef]
- Rabiei, A.; Thiringer, T.; Alatalo, M.; Grunditz, E.A. Improved maximum-torque-per-ampere algorithm accounting for core saturation, cross-coupling effect, and temperature for a PMSM intended for vehicular applications. IEEE Trans. Transp. Electrif. 2016, 2, 150–159. [Google Scholar] [CrossRef]
- Jena, M.R.; Mohanty, K.B. MTPA Control of IPMSM with Self-Correction of Parameters Equivalent Base Current. IEEE Trans. Energy Convers. 2025, 40, 1750–1762. [Google Scholar] [CrossRef]
- Jung, H.-S.; Kim, H.; Sul, S.-K.; Berry, D.J. Temperature Estimation of IPMSM by Using Fundamental Reactive Energy Considering Variation of Inductances. IEEE Trans. Power Electron. 2021, 36, 5771–5783. [Google Scholar] [CrossRef]
- Hu, Z.; Zhan, J.; Li, Z.; Hou, X.; Fu, Z.; Yang, X. Enhanced Raccoon Optimization Algorithm for PMSM Electrical Parameter Identification. Energies 2025, 18, 869. [Google Scholar] [CrossRef]
- ZXia, Z.; Nalakath, S.; Tarvirdilu-Asl, R.; Sun, Y.; Wiseman, J.; Emadi, A. Online Optimal Tracking Method for Interior Permanent Magnet Machines with Improved MTPA and MTPV in Whole Speed and Torque Ranges. IEEE Trans. Power Electron. 2020, 35, 9753–9769. [Google Scholar] [CrossRef]
- Qiu, Z.-H.; Lai, Y.-S. New On-Line MTPA Angle Search and Control Methods Based on Digital Twins for IPM Synchronous Motor Drives Considering Motor Non-Linearity. IEEE Access 2023, 11, 146185–146193. [Google Scholar] [CrossRef]
- Kim, S.; Yoon, Y.D.; Sul, S.K.; Ide, K. Maximum torque per ampere (MTPA) control of an IPM machine based on signal injection considering inductance saturation. IEEE Trans. Power Electron. 2013, 28, 488–497. [Google Scholar] [CrossRef]
- Li, K.; Sun, T.; Liang, J.; Koc, M.; Zhou, Y. Automatic MTPA Control for IPMSM Drives Based on Pseudorandomly Reversed Fixed-Frequency Sinusoidal Signal Injection. IEEE Trans. Ind. Electron. 2024, 71, 6863–6874. [Google Scholar] [CrossRef]
- Chen, Z.; Yan, Y.; Shi, T.; Gu, X.; Wang, Z.; Xia, C. An Accurate Virtual Signal Injection Control for IPMSM with Improved Torque Output and Widen Speed Region. IEEE Trans. Power Electron. 2021, 36, 1941–1953. [Google Scholar] [CrossRef]
- Sun, T.; Long, L.; Yang, R.; Li, K.; Liang, J. Extended Virtual Signal Injection Control for MTPA Operation of IPMSM Drives with Online Derivative Term Estimation. IEEE Trans. Power Electron. 2021, 36, 10602–10611. [Google Scholar] [CrossRef]




| Parameter | Value | Parameter | Value |
|---|---|---|---|
| pole pairs (pn) | 5 | rotor flux (ψf) | 0.053 Wb |
| stator resistance (R) | 0.93 Ω | dc-link voltage (Udc) | 311 V |
| stator inductance (Ld/Lq) | 4.03/6.24 mH | switching frequency (fc) | 10 kHz |
| rated speed | 3000 r/min | rated power | 750 W |
| Load Torque/N.m | Theoretical Value/Degree | Searching Value/Degree | Error Value/% |
|---|---|---|---|
| 0.4 | 92.3 | 91.2 | 1.2 |
| 0.8 | 94.9 | 93.8 | 1.2 |
| 1.2 | 97.0 | 95.2 | 1.9 |
| 1.6 | 99.0 | 98.2 | 0.8 |
| 2.0 | 100.98 | 100.93 | 0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Wu, X.; Yang, B. Maximum Torque per Ampere Control of IPMSM Based on Current Angle Searching with Sliding-Mode Extremum Seeking. Energies 2025, 18, 5613. https://doi.org/10.3390/en18215613
Zhang Z, Wu X, Yang B. Maximum Torque per Ampere Control of IPMSM Based on Current Angle Searching with Sliding-Mode Extremum Seeking. Energies. 2025; 18(21):5613. https://doi.org/10.3390/en18215613
Chicago/Turabian StyleZhang, Ziqing, Xiang Wu, and Bo Yang. 2025. "Maximum Torque per Ampere Control of IPMSM Based on Current Angle Searching with Sliding-Mode Extremum Seeking" Energies 18, no. 21: 5613. https://doi.org/10.3390/en18215613
APA StyleZhang, Z., Wu, X., & Yang, B. (2025). Maximum Torque per Ampere Control of IPMSM Based on Current Angle Searching with Sliding-Mode Extremum Seeking. Energies, 18(21), 5613. https://doi.org/10.3390/en18215613





