Stability Analysis of a Time-Delay Load Frequency Control System via an Improved Matrix-Separation-Based Inequality
Abstract
1. Introduction
2. Problem Formulation
2.1. One-Area LFC Model
2.2. Multi-Area LFC Model
3. Main Results
3.1. Main Lemmas
- In references [28,31], only the matrix was introduced in , which results in only a slight connection between and . On this basis, is further improved to in this paper. The delay derivative and its upper and lower bound information are introduced by this improved method. Its advantage lies in the fact that, for cases involving time-varying delays, this approach can further reduce the conservatism.
- Zhang et al. introduced high-dimensional free matrices to increase the coupling between different variables, which could further reduce conservatism. However, it resulted in increased computational complexity [28]. Xiong et al. estimated the derivative using a generalized free-weighting-matrix method and also introduced some free matrices [31]. The LFC system is taken as the research target of this paper, and the computational complexity must be taken into consideration. So, the Wirtinger inequality is used to estimate the derivative. This improved method reduces computational complexity under the condition of slightly increased conservatism, making it more suitable for application in power systems.
3.2. Stability Criterion
3.3. Analysis of Performance
4. Case Studies
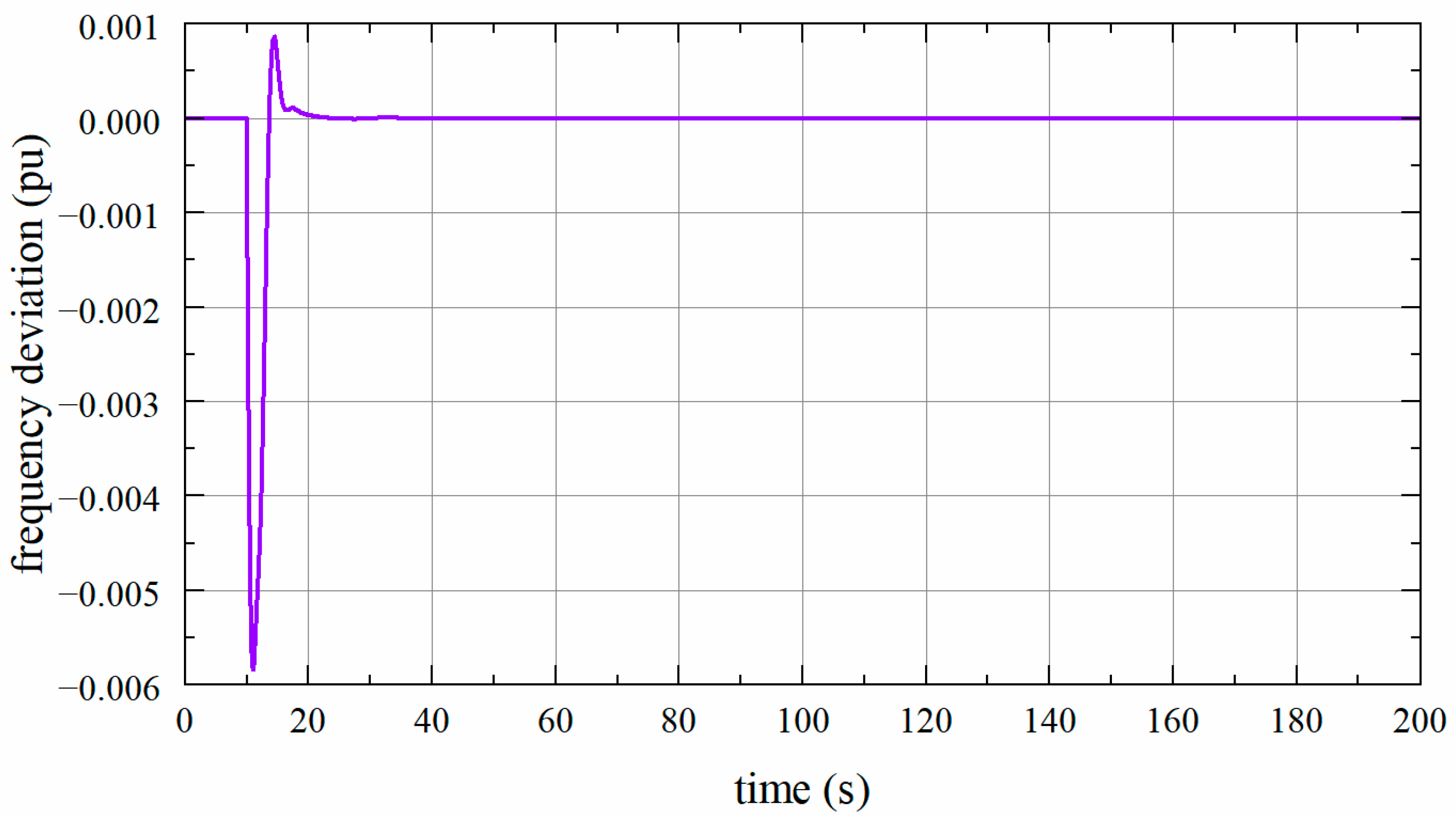
4.1. One-Area LFC System
4.1.1. Conservatism Comparisons
4.1.2. Simulation Verification
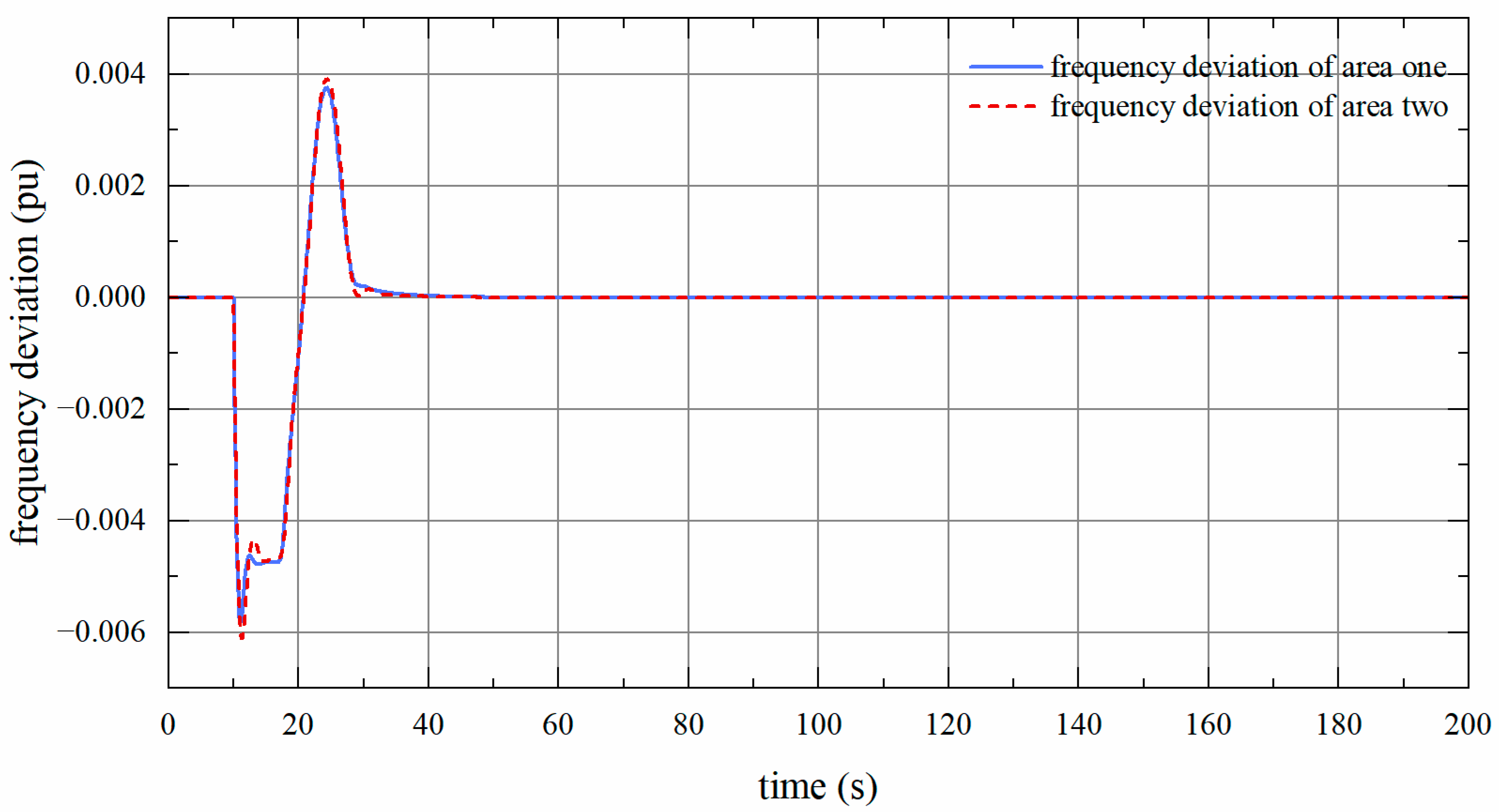
4.2. Two-Area LFC System
4.2.1. Conservatism Comparisons
4.2.2. Simulation Verification
4.3. Performance Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| LFC | Load frequency control |
| L–K | Lyapunov–Krasovskii |
| NDVs | Number of Decision Variables |
| Theorem 1 | Th. 1 |
| Theorem 2 | Th. 2 |
Appendix A
Appendix B
Appendix C
Appendix D
Appendix E
Appendix F
References
- Zhang, G.; Ren, J.; Zeng, Y.; Liu, F.; Wang, S.; Jia, H. Security assessment method for inertia and frequency stability of high proportional renewable energy system. Int. J. Electr. Power Energy Syst. 2023, 153, 109309. [Google Scholar] [CrossRef]
- Ducoin, E.A.; Gu, Y.; Chaudhuri, B.; Green, T.C. Analytical design of contributions of grid-forming and grid-following inverters to frequency stability. IEEE Trans. Power Syst. 2024, 39, 6345–6358. [Google Scholar] [CrossRef]
- Dokht Shakibjoo, A.; Moradzadeh, M.; Moussavi, S.Z.; Vandevelde, L. A novel technique for load frequency control of multi-area power systems. Energies 2020, 13, 2125. [Google Scholar] [CrossRef]
- Jiang, L.; Yao, W.; Wu, Q.; Wen, J.; Cheng, S. Delay-dependent stability for load frequency control with constant and time-varying delays. IEEE Trans. Power Syst. 2011, 27, 932–941. [Google Scholar] [CrossRef]
- Ramakrishnan, K.; Vijeswaran, D.; Manikandan, V. Stability analysis of networked micro-grid load frequency control system. J. Anal. 2019, 27, 567–581. [Google Scholar] [CrossRef]
- Grigsby, L.L. Power System Stability and Control; Taylor & Francis: Abingdon, UK, 2007. [Google Scholar]
- Hu, Z.; Liu, S.; Luo, W.; Wu, L. Resilient distributed fuzzy load frequency regulation for power systems under cross-layer random denial-of-service attacks. IEEE Trans. Cybern. 2020, 52, 2396–2406. [Google Scholar] [CrossRef]
- Peng, C.; Zhang, J.; Yan, H. Adaptive event-triggering H∞ load frequency control for network-based power systems. IEEE Trans. Ind. Electron. 2017, 65, 1685–1694. [Google Scholar] [CrossRef]
- Luo, H.; Hiskens, I.A.; Hu, Z. Stability analysis of load frequency control systems with sampling and transmission delay. IEEE Trans. Power Syst. 2020, 35, 3603–3615. [Google Scholar] [CrossRef]
- Milano, F.; Anghel, M. Impact of time delays on power system stability. IEEE Trans. Circuits Syst. I Regul. Pap. 2011, 59, 889–900. [Google Scholar] [CrossRef]
- Kwon, O.; Lee, S.-H.; Park, M.-J.; Lee, S.-M. Augmented zero equality approach to stability for linear systems with time-varying delay. Appl. Math. Comput. 2020, 381, 125329. [Google Scholar] [CrossRef]
- Zhang, X.-M.; Han, Q.-L.; Ge, X. The construction of augmented Lyapunov-Krasovskii functionals and the estimation of their derivatives in stability analysis of time-delay systems: A survey. Int. J. Syst. Sci. 2022, 53, 2480–2495. [Google Scholar] [CrossRef]
- Ren, W.; Xiong, J. Vector-Lyapunov-function-based input-to-state stability of stochastic impulsive switched time-delay systems. IEEE Trans. Autom. Control 2018, 64, 654–669. [Google Scholar] [CrossRef]
- Qian, W.; Xing, W.; Fei, S. H∞ state estimation for neural networks with general activation function and mixed time-varying delays. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 3909–3918. [Google Scholar] [CrossRef]
- Zhang, Z.-M.; He, Y.; Wu, M.; Wang, Q.-G. Exponential synchronization of neural networks with time-varying delays via dynamic intermittent output feedback control. IEEE Trans. Syst. Man Cybern. Syst. 2017, 49, 612–622. [Google Scholar] [CrossRef]
- Seuret, A.; Gouaisbaut, F. Wirtinger-based integral inequality: Application to time-delay systems. Automatica 2013, 49, 2860–2866. [Google Scholar] [CrossRef]
- Yang, F.; He, J.; Wang, J.; Wang, M. Auxiliary-function-based double integral inequality approach to stability analysis of load frequency control systems with interval time-varying delay. IET Control Theory Appl. 2018, 12, 601–612. [Google Scholar] [CrossRef]
- Zeng, H.-B.; He, Y.; Wu, M.; She, J. Free-matrix-based integral inequality for stability analysis of systems with time-varying delay. IEEE Trans. Autom. Control 2015, 60, 2768–2772. [Google Scholar] [CrossRef]
- Seuret, A.; Gouaisbaut, F. Stability of linear systems with time-varying delays using Bessel–Legendre inequalities. IEEE Trans. Autom. Control 2017, 63, 225–232. [Google Scholar] [CrossRef]
- Zeng, H.-B.; Lin, H.-C.; He, Y.; Teo, K.-L.; Wang, W. Hierarchical stability conditions for time-varying delay systems via an extended reciprocally convex quadratic inequality. J. Frankl. Inst. 2020, 357, 9930–9941. [Google Scholar] [CrossRef]
- Park, P.; Ko, J.W.; Jeong, C. Reciprocally convex approach to stability of systems with time-varying delays. Automatica 2011, 47, 235–238. [Google Scholar] [CrossRef]
- Seuret, A.; Gouaisbaut, F. Delay-Dependent Reciprocally Convex Combination Lemma. 2016. Available online: https://hal.science/hal-01257670/ (accessed on 6 August 2025).
- Ramakrishnan, K.; Ray, G. Stability criteria for nonlinearly perturbed load frequency systems with time-delay. IEEE J. Emerg. Sel. Top. Circuits Syst. 2015, 5, 383–392. [Google Scholar] [CrossRef]
- Yang, F.; He, J.; Pan, Q. Further improvement on delay-dependent load frequency control of power systems via truncated B–L inequality. IEEE Trans. Power Syst. 2018, 33, 5062–5071. [Google Scholar] [CrossRef]
- Feng, W.; Xie, Y.; Luo, F.; Zhang, X.; Duan, W. Enhanced stability criteria of network-based load frequency control of power systems with time-varying delays. Energies 2021, 14, 5820. [Google Scholar] [CrossRef]
- Sun, Y.; Bo, X.; Duan, W.; Lu, Q. Stability analysis of load frequency control for power systems with interval time-varying delays. Front. Energy Res. 2023, 10, 1008860. [Google Scholar] [CrossRef]
- Chen, C.; Fan, C.; Lian, H.; Zhou, S.; Huang, T. Delay-dependent stability analysis for load frequency control systems with time-varying delays. J. Frankl. Inst. 2024, 361, 106927. [Google Scholar] [CrossRef]
- Zhang, C.-K.; Chen, W.-H.; Zhu, C.; He, Y.; Wu, M. Stability analysis of discrete-time systems with time-varying delay via a delay-dependent matrix-separation-based inequality. Automatica 2023, 156, 111192. [Google Scholar] [CrossRef]
- Bevrani, H. Robust Power System Frequency Control; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Van Hien, L.; Trinh, H. Refined Jensen-based inequality approach to stability analysis of time-delay systems. IET Control Theory Appl. 2015, 9, 2188–2194. [Google Scholar] [CrossRef]
- Xiong, D.; Zhang, C.-K.; Wan, X.; He, Y. Stability and stabilization of T–S fuzzy systems under sampled-data control via a matrix-separation-based inequality. IEEE Trans. Fuzzy Syst. 2024, 32, 4312–4323. [Google Scholar] [CrossRef]
- Yang, F.; He, J.; Wang, D. New stability criteria of delayed load frequency control systems via infinite-series-based inequality. IEEE Trans. Ind. Inform. 2017, 14, 231–240. [Google Scholar] [CrossRef]
- Park, P. A delay-dependent stability criterion for systems with uncertain time-invariant delays. IEEE Trans. Autom. Control 1999, 44, 876–877. [Google Scholar] [CrossRef]






| Parameters | |||||||
|---|---|---|---|---|---|---|---|
| Area 1 | 10 | 1.0 | 21 | 0.1 | 0.3 | 0.05 | 0.1986 |
| Area 2 | 12 | 1.5 | 21.5 | 0.17 | 0.1 | 0.05 |
| 0 | 0 | 0 | 0 | 0 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | NDVs | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.05 | 0.1 | 0.2 | 0.4 | 0.6 | 0.05 | 0.1 | 0.2 | 0.4 | 0.6 | ||
| [4] | 27.92 | 13.77 | 6.69 | 3.12 | 1.91 | 27.03 | 13.68 | 6.94 | 3.29 | 2.02 | |
| [17] | 28.66 | 14.17 | 6.90 | 3.23 | 1.98 | 27.98 | 14.42 | 7.23 | 3.41 | 2.10 | |
| [25] | 30.79 | 15.15 | 7.33 | 3.38 | 2.03 | 32.73 | 16.08 | 7.81 | 3.62 | 2.19 | |
| [26] | - | - | 7.33 | 3.38 | 2.04 | - | - | 7.79 | 3.61 | 2.19 | |
| [27] | 30.30 | 14.96 | 7.26 | 3.36 | 2.03 | 29.49 | 15.15 | 7.79 | 3.61 | 2.19 | |
| Th. 1 | 30.78 | 15.15 | 7.33 | 3.38 | 2.04 | 29.97 | 16.01 | 7.79 | 3.61 | 2.19 | |
| Th. 2 | 30.32 | 15.04 | 7.32 | 3.37 | 2.04 | 29.68 | 15.43 | 7.77 | 3.60 | 2.19 |
| Th. 1 | Th. 2 | [32] | Th. 1 | Th. 2 | [32] | ||
|---|---|---|---|---|---|---|---|
| 0 | 0.2 | 7.17 | 6.41 | 6.45 | 7.13 | 6.33 | 6.43 |
| 0 | 0.4 | 3.33 | 2.94 | 2.94 | 3.37 | 2.91 | 2.91 |
| 0 | 0.6 | 2.02 | 1.74 | 1.75 | 2.02 | 1.71 | 1.71 |
| 0.1 | 0.2 | 7.56 | 6.68 | 6.80 | 7.51 | 6.37 | 6.59 |
| 0.1 | 0.4 | 3.53 | 3.12 | 3.13 | 3.52 | 3.07 | 3.11 |
| 0.1 | 0.6 | 2.16 | 1.87 | 1.88 | 2.16 | 1.84 | 1.84 |
| 0 | 0 | 0 | 0 | 0 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | NDVs | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.05 | 0.1 | 0.2 | 0.4 | 0.6 | 0.05 | 0.1 | 0.2 | 0.4 | 0.6 | ||
| [4] | 27.84 | 13.69 | 6.60 | 3.00 | 1.74 | 27.00 | 13.65 | 6.88 | 3.17 | 1.86 | |
| [17] | 28.86 | 14.31 | 6.94 | 3.15 | - | 28.29 | 14.70 | 7.27 | 3.34 | - | |
| [27] | 30.41 | 14.95 | 7.16 | 3.21 | 1.84 | 29.85 | 15.33 | 7.56 | 3.42 | 1.98 | |
| Th. 1 | 30.47 | 14.99 | 7.20 | 3.23 | 1.85 | 29.92 | 15.38 | 7.59 | 3.43 | 2.00 | |
| Th. 2 | 30.43 | 14.97 | 7.18 | 3.23 | 1.84 | 29.89 | 15.36 | 7.57 | 3.43 | 1.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Long, F.; Du, H.; Li, M. Stability Analysis of a Time-Delay Load Frequency Control System via an Improved Matrix-Separation-Based Inequality. Energies 2025, 18, 5614. https://doi.org/10.3390/en18215614
Long F, Du H, Li M. Stability Analysis of a Time-Delay Load Frequency Control System via an Improved Matrix-Separation-Based Inequality. Energies. 2025; 18(21):5614. https://doi.org/10.3390/en18215614
Chicago/Turabian StyleLong, Fei, Haojie Du, and Mo Li. 2025. "Stability Analysis of a Time-Delay Load Frequency Control System via an Improved Matrix-Separation-Based Inequality" Energies 18, no. 21: 5614. https://doi.org/10.3390/en18215614
APA StyleLong, F., Du, H., & Li, M. (2025). Stability Analysis of a Time-Delay Load Frequency Control System via an Improved Matrix-Separation-Based Inequality. Energies, 18(21), 5614. https://doi.org/10.3390/en18215614






