Abstract
The smart grid (SG) plays a seminal role in the modern energy landscape by integrating digital technologies, the Internet of Things (IoT), and Advanced Metering Infrastructure (AMI) to enable bidirectional energy flow, real-time monitoring, and enhanced operational efficiency. However, these advancements also introduce critical challenges related to data privacy, cybersecurity, and operational balance. This review critically evaluates SG systems, beginning with an analysis of data privacy vulnerabilities, including Man-in-the-Middle (MITM), Denial-of-Service (DoS), and replay attacks, as well as insider threats, exemplified by incidents such as the 2023 Hydro-Québec cyberattack and the 2024 blackout in Spain. The review further details the SG architecture and its key components, including smart meters (SMs), control centers (CCs), aggregators, smart appliances, and renewable energy sources (RESs), while emphasizing essential security requirements such as confidentiality, integrity, availability, secure storage, and scalability. Various privacy preservation techniques are discussed, including cryptographic tools like Homomorphic Encryption, Zero-Knowledge Proofs, and Secure Multiparty Computation, anonymization and aggregation methods such as differential privacy and k-Anonymity, as well as blockchain-based approaches and machine learning solutions. Additionally, the review examines pricing models and their resolution strategies, Demand–Supply Balance Programs (DSBPs) utilizing optimization, game-theoretic, and AI-based approaches, and energy storage systems (ESSs) encompassing lead–acid, lithium-ion, sodium-sulfur, and sodium-ion batteries, highlighting their respective advantages and limitations. By synthesizing these findings, the review identifies existing research gaps and provides guidance for future studies aimed at advancing secure, efficient, and sustainable smart grid implementations.
1. Introduction
The smart grid (SG) technology has sparked a revolutionary shift in the manner in which energy is produced, distributed, and consumed. These modernized grids are an enhancement of traditional grids, empowered by digital technologies, the Internet of Things (IoT), and Advanced Metering Infrastructure (AMI). This transformation has enabled them to bridge the gap between energy efficiency, sustainability, and resource reliability [1]. With the help of SGs, energy and electricity can flow in both directions, allowing consumers to interact with energy providers in real time. This interaction facilitates real-time monitoring of energy consumption, automatic billing, and demand-response systems [2,3].
Nonetheless, like every other digital transformation, the accompanying increase in data usage, communication, andautomation introduces issues of data privacy, security, and cyber threats. Examples of sensitive information circulating within SG networks include patterns of electricity consumption, supply/demand data, and price fluctuations [4]. If such data is intercepted or manipulated by malicious actors, it can reveal users’ personal information, potentially leading to identity theft, energy theft, and interruptions in energy services [5,6]. Therefore, to defend these systems against evolving cybersecurity threats, robust protection mechanisms and strong security measures must be established.
The primary distinction between SGs and traditional electrical grids lies in their bidirectional electricity flow, moving beyond the unidirectional model of the past. SGs integrate real-time data processing and two-way communication [7]. The inclusion of digital technologies allows for more efficient grid management, preventing real-time overloads or shortages in energy demand and supply. This results in improved energy efficiency, reduced operational costs, and enhanced reliability [8]. Furthermore, the penetration of renewable energy forms, such as solar and wind, becomes easier, fostering a more environmentally friendly energy ecosystem.
SGs also enable the development of more sophisticated consumer services. Using smart meters, consumers can make informed decisions regarding their electricity consumption in real time, based on their actual usage. Additionally, dynamic pricing models offer consumers the opportunity to optimize electricity usage when it is most cost-effective, thereby saving money on energy costs and conserving energy during peak hours [9].
Nevertheless, security risks emerge alongside these innovations. Because SGs gather and transmit sensitive consumer information and offer the functionality to operate or command power-related devices remotely, they present various attack vectors that can be exploited by cybercriminals [10]. Beyond information interception, SGs face challenges such as Denial-of-Service (DoS) attacks, among others [11].
IoT technologies have been central to the emergence of SGs. Integrating smart meters (SMs), grid sensors, smart appliances, and electric vehicles (EVs) with intelligent capabilities, IoT facilitates real-time data monitoring, collection, and control of grid operations. These devices capture data and transmit it to control centers (CCs) that analyze and interpret the information to predict demand, modify generation levels, and optimize energy distribution [12].
Advanced Metering Infrastructure (AMI) is a core element of SGs, implementing the use of smart meters to transmit and gather data regarding consumers’ electricity consumption and transfer that information to utility providers. The real-time transfer of this data enables utilities to understand demand fluctuations, energy consumption habits, and efficiency opportunities [13]. Moreover, the integration of renewable energy sources, such as solar panels and wind turbines, into SG systems is achievable with the help of highly advanced data communication and control systems. AMI systems also allow for automated billing, minimizing human error and ensuring accurate charge calculations [14].
Despite these advantages, the advent of IoT devices and AMI brings significant privacy concerns that cannot be neglected. Data stored in these devices, such as electricity usage habits over time, can be used to infer users’ activities, daily lifestyles, and even the presence of individuals in a household. Accessing such information by an unauthorized party can lead to identity theft, surveillance, or physical security breaches [15]. Furthermore, IoT devices are often susceptible to hacking due to their inherent vulnerabilities, exposing them to attackers who can tap into or modify data, leading to severe privacy and security implications.
Secure communication requires participants to share information such as energy demand, supply, prices, and the time of delivery or requirement with market operators [16]. Using this information, market operators can estimate the expected Demand and Supply Ratio, which helps determine the price of energy through uniform pricing or auctions by deploying several techniques such as optimization [17], game-theoretic models [18], and artificial intelligence models [19].
An effective price signal further assists the grid in maintaining a balanced state by distributing surplus energy among buyers. However, the stochastic nature of renewable energy sources creates challenging conditions for keeping the grid in a balanced state [20]. To overcome this problem, the Demand–Supply Balance Program (DSBP) provides further guidelines to participants by deploying several models such as optimization [21], game-theoretic [22], and artificial intelligence [23].
Energy storage systems (ESSs) further improve the grid’s balance by injecting surplus energy during times of high demand [24]. This energy is stored in batteries made from different chemical compositions, such as lead–acid [25], lithium-ion [26], sodium–sulfur [27], and sodium-ion [28].
In this review article, we have deeply explored all these important elements and discussed in detail the methods and techniques that have been extensively used in the past and are currently being deployed in the smart grid. Based on an intensive literature analysis, this review article further assists researchers by highlighting current research gaps and providing a clear path for future research directions.
The rest of this paper is organized as follows: Section 2 and its associated subsections discuss data privacy in the smart grid, along with vulnerabilities and entry points for possible cyberattacks. Furthermore, in this section, several techniques have been explored in detail to analyze their usage in the smart grid. Section 3 and its associated sections deeply analyze pricing models along with their solution techniques. Section 4 highlights the important factors that impact Demand–Supply Balance Programs and how different methods are used to solve them. Section 5 discusses energy storage systems in the smart grid by incorporating several types of batteries and their associated merits and challenges. Section 6 provides existing research gaps and highlights future research directions. Finally, Section 7 presents the conclusion of this work.
2. Data Privacy Threats in Smart Grids
Data privacy is a crucial concern for smart grid (SG) systems, primarily due to the vast amount of sensitive information exchanged across the network. The information gathered by smart meters (SMs) can be processed to reveal specific user behaviors, including their energy usage hours, the nature of appliances they use, and the time they spend at home. When this information becomes available to malicious actors, it can be used to infer an individual’s lifestyle or even anticipate their future actions [29]. Because SGs collect vast amounts of detailed energy consumption data, they create the potential for consumer profiling. Malicious or unauthorized parties could use this data to deduce sensitive information about individuals, such as their daily routines, presence or absence from home, and even the appliances they use [30]. For example, an attacker could infer when people are at home, what devices they are using, or predict their behavior based on consumption patterns.
Malicious entities may alter consumption data to lower electricity bills or access electricity without paying, a practice known as energy theft. Since SG systems rely on continuous data transmission, attackers can manipulate the data exchanged between smart meters and aggregators, leading to revenue loss for utility companies [31]. Additionally, with inadequate encryption or authentication, data being transmitted from SMs to central hubs can be intercepted, revealing confidential consumption patterns or allowing attackers to tamper with the data [32,33]. Furthermore, attackers can link data from different sources to reconstruct a user’s schedule, inferring when they are present, when they are absent, or even when they are engaged in certain activities based on their energy consumption profile [5].
As the collection of sensitive data grows, these privacy concerns become more significant. Without effective privacy-preserving solutions, users may lose confidence in SG systems, which could lead to a reluctance to adopt smart meters and smart appliances. Therefore, privacy preservation is a critical requirement for the successful implementation and widespread acceptance of SGs.
2.1. Overview of Smart Grid Systems
The smart grid (SG) is an advanced, bidirectional electrical power system that integrates traditional grid infrastructure with cutting-edge Information and Communication Technology (ICT). This integration enables SGs to dynamically manage and monitor the flow of energy, offering numerous advantages over traditional power grids. The SG system optimizes electricity generation, distribution, and consumption through the integration of smart meters, sensors, automated control systems, and renewable energy sources [34].
The SG is composed of a series of interrelated subsystems that contribute to the provision of sustainable, reliable, and efficient energy management. These subsystems are as follows:
Smart Management System: This system supports the balance of electricity demand and supply. It operates through control centers (CCs) where smart meters (SMs) and other devices relay information to be analyzed. This analysis helps anticipate demands, thereby enabling optimal control of grid operations. An intelligent management system also facilitates the integration of renewable energy sources into the power grid and the efficient distribution of available resources.
Smart Infrastructure System: This subsystem allows for the bidirectional flow of electricity and information between end-users and utilities. It incorporates smart meters (SMs) that monitor electricity consumption, smart appliances that can manage energy levels in buildings or businesses, and communication systems that facilitate the seamless flow of information among various entities within the grid.
Smart Protection System: This subsystem improves grid reliability by monitoring for faults and preventing permanent equipment damage. It has built-in automated units that can respond promptly to conditions like power failures or equipment malfunctions, thereby reducing repair time and ensuring uninterrupted service.
Smart Grid Communication Network: A communication network is a primary characteristic of the SG because it enables the interchange of information between all elements. The structure of communication systems in SGs is typically hierarchical, with information flowing from SMs to control centers via intermediate aggregators. This architecture allows for the optimization of data transmission, the minimization of delays, and ensures all components collaborate effectively. The communication framework of a smart grid generally consists of the following networks:
- Customer Premises Area Network (HAN/BAN): Data on electricity usage by individual devices is sent to SMs via the Home Area Network (HAN) and Building Area Network (BAN). The communication protocols used by these networks are low-power, such as ZigBee, Wi-Fi, and blacktooth [35,36]. The primary concerns in this layer are privacy and security because personal data regarding consumer actions is collected and distributed.
- Wide Area Network (WAN): The WAN links all regional networks and the CCs. It is responsible for long-distance data transfer, often spanning tens of kilometers. For this purpose, optical communication and cellular networks are widely applied because they facilitate fast data transfer. The WAN is vital for providing a reliable control linkage to the distributed smart grid and its control systems [37].
2.2. Key Components of the Smart Grid
The SG system consists of multiple important elements, which allow an enhanced performance of the grid and its intelligence, as shown in Figure 1.
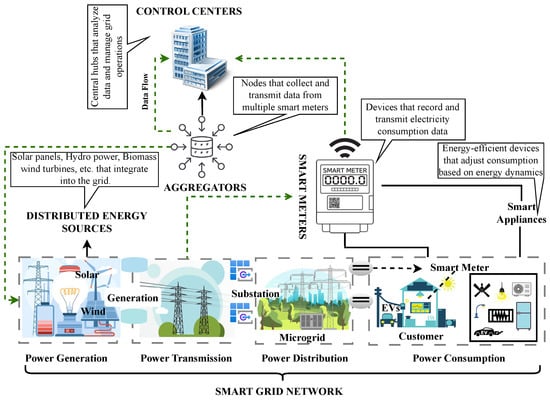
Figure 1.
Architecture of smart grid and key components.
From Figure 1, it can be seen that the smart grid consists of several components such as the smart meter (SM), control center (CC), aggregators, smart appliances, and renewable energy sources (RESs).
Smart meters are intelligent devices installed in residential areas and businesses to collect electricity usage data and transmit it back to the operations centers [38]. SMs enable real-time monitoring, a factor that is vital for optimizing demand-response programs and implementing dynamic pricing [39].
The CC is the central hub of the SG that receives, transmits, and analyzes data from SMs and other equipment to facilitate real-time decision-making regarding energy supply and demand. This information is used by the CC to optimize grid operation, identify possible failures, and react to unforeseen situations like power cuts or supply shortages [40,41].
Nodes that gather data from various SMs, known as aggregators, also serve as an intermediary between SMs and the CC. They collect usage data and send it to the CC for analysis [42].
Smart appliances are intelligent products that can regulate the amount of energy they use based on directions from the SG. Smart appliances are instrumental in demand-side management as they can reduce energy consumption during peak periods [43].
RESs are a means of energy generation. The SG promotes the inclusion of renewable energy sources such as solar panels and wind turbines. This integration helps in balancing supply and demand, in addition to reducing the carbon footprint of energy production [44].
2.3. Vulnerabilities and Entry Points for Data Leaks in the Smart Grid Network
While SGs offer numerous benefits in terms of efficiency and sustainability, they also present various vulnerabilities that can be exploited by attackers. One of the primary concerns is the reliance on cyber-physical systems, which combine computational systems with physical infrastructure like SMs, aggregators, and CCs. These devices and their interconnected communication channels present numerous points of vulnerability.
The SG system, while revolutionizing the energy sector, has introduced new cybersecurity vulnerabilities due to its reliance on digital communication and data exchange [45]. As shown in Figure 2, cyberattacks pose significant risks, as evidenced by several high-profile incidents that have affected energy infrastructures worldwide. These recent cyberattacks on SG and energy infrastructure highlight therapidly evolving threats and vulnerabilities.
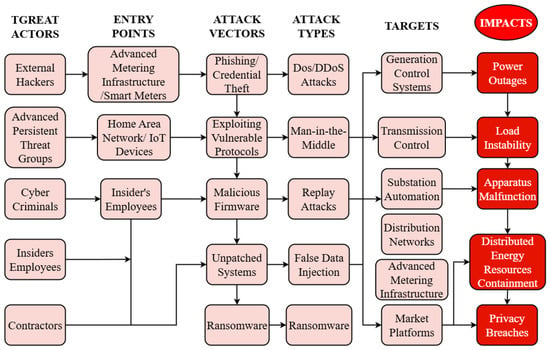
Figure 2.
Comprehensive mapping of smart grid cybersecurity threats, showing threat actors, attack entry points, vectors, types, targeted systems, and resulting operational impacts.
One of the major threats to the SG network is the Man-in-the-Middle (MITM) attack. During this attack, an intruder listens in on and intercepts a legitimate communication between two devices in a network (e.g., between an SM and an aggregator) [46]. This allows the culprit to intercept or manipulate information being exchanged, resulting in data loss, privacy breaches, and interruptions to the energy supply chain. Hackers can also forge data, such as inaccurate electricity usage measurements, to manipulate power distribution [5,47].
The Denial-of-Service (DoS) attack is another type of vulnerability where intruders flood the network with excessive data, thereby slowing down or blocking legitimate service requests [48]. Such attacks can cause a system failure, preventing users from accessing important services like real-time energy consumption details or the ability to adjust their energy usage during peak demand times. A Distributed Denial-of-Service (DDoS) attack is particularly harmful because it uses multiple sources of traffic, making it more difficult to mitigate [49].
Another significant issue in SG networks is the Replay attack. This involves the interception and retransmission of data communicated on the network, causing distorted information to be processed by the receiving system [50]. This can lead to improper load balancing, overcharging of users, and even blackouts if the corrupted data affects grid management decisions.
In SG networks, Theft of Resources and Insider attacks are also highly dangerous. Insider attacks occur when malicious individuals (including disgruntled employees or contractors) gain unauthorized access to system resources, including control systems, databases, or SMs. Such actions can result in the manipulation of data or physical assets, thereby disrupting grid operations and compromising customer privacy [51].
The major attacks and their historical impact are given as follows:
- In 2023, Hydro-Québec, a major grid operator in Canada, experienced a cyberattack that disrupted its outage verification app and website. This incident underscores the increasing cyber threats faced by energy utilities and the need for robust cybersecurity measures to protect critical infrastructure [52,53].
- In 2024, Spain’s National Cybersecurity Institute (Incibe) investigated a massive blackout that disrupted essential services. The focus was on smaller electricity generators, which may have lacked robust cyber defenses, making them potential vulnerabilities in the national power grid [54].
- In May 2023, a critical vulnerability in the MOVEit-managed file transfer software was exploited by the ransomware group CL0P, leading to unauthorized access to sensitive databases. The breach affected over 2,700 organizations across various sectors, including energy, highlighting the systemic risks inherent in the interconnected nature of digital supply chains [54,55].
- From December 2023 through to early 2024, Iranian hacker groups engaged in successful cyberattacks on various sectors, including the energy sector. Such attacks interrupted services and exposed weaknesses in critical infrastructure, pointing to the necessity of more efficient cybersecurity practices to defend against state-sponsored cyber threats [56].
2.4. Security and Privacy Requirements in the Smart Grid Network
The smart grid (SG) network involves a large number of interdependent devices and systems that regularly transfer sensitive information. To maintain an efficient and secure operational network, several key security and privacy requirements must be met. These needs include upholding confidentiality, data integrity, availability, and secure storage, as well as ensuring scalability.
Confidentiality is crucial in SG networks. It refers to the protection of sensitive information from unauthorized access. This is especially necessary in SG systems, where data specific to individuals, such as energy usage trends, is constantly uploaded from smart meters (SMs) to local aggregation nodes [57]. If this data is intercepted, attackers could learn about users’ consumption habits, leading to serious privacy invasions. Furthermore, businesses that optimize operations based on electricity consumption patterns may expose sensitive data like trade secrets or customer behavior analytics [58].
Integrity ensures that information transmitted through the SG network cannot be altered and remains trustworthy. When applied to SGs, a lack of integrity can be a significant issue [59]. For instance, if an attacker gains control over electricity usage data transmitted from a smart meter to the control center, the grid could over- or underestimate demand, which might cause blackouts or inefficient resource utilization. Threats to data integrity, such as Man-in-the-Middle (MITM) attacks and replay attacks, must be addressed and monitored constantly [60].
Availability is a safeguard that ensures services and data within the SG network are accessible when needed. Having real-time energy consumption information is critical for grid operators to make real-time decisions, which helps manage peak demand and implement curtailment strategies. In case of a loss of availability due to a Denial-of-Service (DoS) or Distributed Denial-of-Service (DDoS) attack, grid operators would be unable to control resource distribution, potentially causing widespread outages and operational inefficiencies [61].
The SG network is also affected by major issues in terms of secure storage. Because SG networks contain a large amount of sensitive data, the importance of keeping such data in a secure environment cannot be understated. Without proper encryption and data protection mechanisms, stored data is at risk of theft or manipulation [62]. The risk of data breaches escalates if hackers can access data centers or other storage facilities.
Scalability is another important concern in SG networks. Security solutions must be able to support an expanding network and adapt as more smart devices are deployed, thus handling the increasing data and communication traffic [63]. Traditional security procedures may not be adequate for larger, decentralized systems, necessitating more robust and dynamic security solutions.
To address these security and privacy needs, a layered security approach is essential. This includes features such as advanced encryption, multi-factor authentication, intrusion detection systems, and regular security audits. The SG network can only be safe and consistent by ensuring that all its aspects—confidentiality, integrity, availability, secure storage, and scalability—receive due attention.
2.5. Privacy Preservation Techniques in Smart Grid Network
Since SGs are becoming an essential part of modern-day energy systems, it is of utmost importance to ensure the privacy of highly sensitive data, including the energy consumption patterns of consumers. An SG connects energy producers, consumers, and utility providers, and facilitates real-time communication. Nevertheless, the constant flow of data exposes consumers to vulnerabilities, particularly concerning data confidentiality. Preserving privacy in SG networks is aimed at protecting sensitive information, such as the energy usage of individuals, preventing unauthorized access, and mitigating the potential risks of privacy disclosure that arise from sharing this sensitive information. Various methods have been introduced in the literature, all of which aim to address a particular aspect of privacy and the secure transfer of information via the grid, as shown in Figure 3.
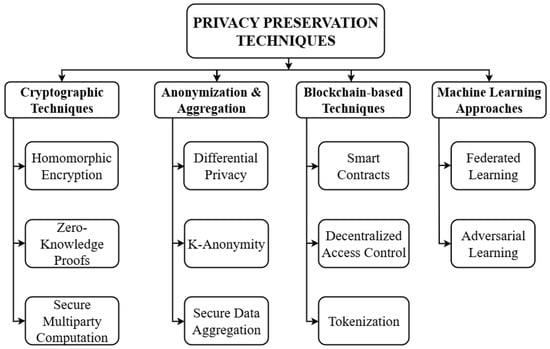
Figure 3.
Classification of privacy preservation techniques in smart grids, highlighting cryptographic, anonymization and aggregation, blockchain-based, and machine learning approaches.
2.5.1. Cryptographic Techniques
Cryptography is a major defense applied to establish the security of SG network data, whether in transit or at rest, and also ensures that sensitive information links are not hacked or altered. Within the dynamics of the smart grid, cryptographic methods are utilized to ensure the privacy and integrity of data while still preserving the functionality of the grid. Various cryptographic mechanisms have been suggested to ensure data privacy.
2.5.2. Homomorphic Encryption (HE)
HE is a cryptographic technique that enables computers to perform operations on encrypted data without first decrypting it. The subsequent output is also encrypted and can only be decoded by the authorized user, which means the data remains confidential throughout processing [64,65]. Such an approach is highly beneficial in SG systems because data is often consolidated and processed on third-party servers. In recent years, a number of researchers have suggested Homomorphic Encryption schemes to implement SG metering systems whose aggregation protocols can collect consumption data without interfering with the privacy of specific users [66,67]. Furthermore, HE can be utilized when collecting data to allow electricity companies to aggregate the information they obtain through smart meters (SMs) without revealing intimate user behaviors [68,69,70].
HE provides the dual advantage of preventing the disclosure of sensitive data while simultaneously enabling utilities to gain insights into energy consumption trends [71]. This is especially important for privacy in SGs, where exposing consumption patterns can lead to security threats or user profiling [72]. Nevertheless, HE is associated with a high computational cost due to its more complex operations on encrypted data compared to conventional encryption or plaintext processing [73]. Research has therefore focused on streamlining these methods to minimize overhead costs and ensure they are viable for handling large-scale SG networks, as can be summarized in Table 1.

Table 1.
Summary of Homomorphic Encryption for privacy preservation in Smart Grids.
2.5.3. Zero-Knowledge Proofs (ZKPs)
Zero-Knowledge Proofs (ZKPs) are a cryptographic protocol in which one party can prove the veracity of a claim to another party without revealing any information about the proof itself, other than whether the claim is true or not [79]. ZKPs are especially useful for authorization and identity verification in SG systems, where privacy is a primary concern [80]. Liang et al. [81] explained how blockchain-based ZKPs can enhance the privacy of transactions and smart contract predicates in SG systems. With ZKPs, SG participants can authenticate themselves without revealing sensitive data, such as consumption statistics or personal identifiers [80].
Works by [80,82] highlight that the primary advantage of ZKPs is that they preserve user privacy during the authentication process. For example, a smart meter can prove that it is in proper working order without revealing any specific information on the amount of energy it is consuming, as has been suggested in [83,84]. This capability is vital for addressing the rising concerns regarding individual privacy, as no external party can access data that could then be used to profile a user or perform other nefarious actions.
Moreover, ZKPs are increasingly employed in privacy-preserving applications where proving the correctness of data is required without revealing the underlying data. El-Hajj et al. [85] compared various ZKP protocols, including zk-SNARKs, for privacy-preserving authentication in blockchain-based systems and discussed their applications in billing verification and identity authentication. Similarly, Ref. [85] describes how ZKPs can guarantee that smart grid users receive accurate billing without exposing sensitive usage patterns. However, as pointed out by El-Hajj et al., while ZKPs provide strong security guarantees, they introduce significant computational complexity, making them unsuitable for real-time applications requiring rapid processing, such as fault detection or real-time load balancing [85,86].
One drawback of ZKPs is that they can be computationally intensive, particularly in real-time applications, which may limit their scalability in large SG networks, as shown in Table 2.

Table 2.
Summary of Zero-Knowledge Proof (ZKP) and blockchain-based privacy techniques.
2.5.4. Secure Multiparty Computation (SMPC)
SMPC is a cryptographic method that enables multiple parties to jointly compute a function over their private inputs while keeping those inputs confidential [93]. In SGs, SMPC can be used to enable energy consumers, utility companies, and third-party aggregators to collaborate on energy consumption analysis and demand-response programs without sharing sensitive consumption data [76]. Samuel et al. [75] discussed an SMPC framework for SGs that ensures users’ energy usage data remains private, even during collaborative optimization and demand-response computations. Furthermore, this technique ensures that each party can perform computations on their own encrypted data, with only the final aggregated result being revealed [94].
Additionally, SMPC has the advantage of allowing collaboration among multiple stakeholders in a smart grid without exposing confidential private data [95]. For example, a consumer may want to share their energy usage information with the utility to optimize energy pricing but not reveal detailed personal behavior. SMPC achieves this by ensuring that computations are conducted over encrypted data [96]. However, the main challenge with SMPC is its high computational complexity and communication overhead. Handling large datasets and ensuring that computations scale efficiently are key challenges that ongoing research is trying to address [97]. Recent work has focused on improving the efficiency and practicality of SMPC in real-time smart grid systems, as shown in Table 3.

Table 3.
Summary of Secure Multiparty Computation (SMPC) privacy-preserving techniques in smart grids.
2.5.5. Anonymization and Aggregation
Anonymization and aggregation are techniques used to protect personal identities by altering data in such a way that it cannot be traced back to an individual. These methods are often applied to aggregate datasets, which reduces the granularity of the information while maintaining its usefulness for grid management.
- Differential Privacy: The process of anonymization, particularly through differential privacy (DP), has gained significant attention in the smart grid sector for protecting individual data. Differential privacy guarantees that no individual’s data or the data collected on themsignificantly affects the response of a query [100]. Researchers Hu et al. [101] proposed a privacy-preserving data aggregation and management approach for smart grid architecture, highlighting the feasibility of using differential privacy in data aggregation in smart meters. As another example, Rai et al. [102] used differential privacy to provide privacy guarantees to energy consumption data and showed that, under this scheme, individual consumer privacy could be achieved without compromising the utility of the aggregate consumption statistics for optimizing a smart grid. Bourechak et al. [103] demonstrated that a smart grid model based on differential privacy could be constructed, in which noise is added to smart meter data in such a way that the privacy of individual consumers is guaranteed. Among the main benefits of DP is that it provides formal privacy guarantees and is, therefore, a powerful strategy to protect sensitive information in smart grids. The method ensures that no individual’s data can significantly influence query results, even if an adversary has access to auxiliary information [104]. However, a known trade-off of DP is that the addition of noise may slightly reduce the accuracy of aggregated results [105].Further research focuses on optimizing the amount of noise added to maintain a balance between privacy and data utility, ensuring that the SG can still function efficiently while maintaining strong privacy guarantees [106,107]. The following Table 4 provides a summary of a few works concerning the deployment of differential privacy in the smart grid.
 Table 4. Summary of differential privacy techniques in smart grids.Table 4. Summary of differential privacy techniques in smart grids.
Table 4. Summary of differential privacy techniques in smart grids.Table 4. Summary of differential privacy techniques in smart grids.Refs. System Model Goal Security Parameters Performances Limitations [108] General privacy-preserving model Provide privacy guarantees while sharing data from smart meters in smart grids Privacy, data perturbation, noise addition Provable privacy guarantees under differential privacy Increased noise can affect data utility [109] SG with individual consumer data Protect individual user data while enabling utility companies to aggregate energy consumption Data privacy, utility preservation, statistical analysis High privacy preservation with minimal data alteration Performance degradation in the aggregation of data due to noise [107] SG with multiple consumers and data aggregation points Enable privacy-preserving data aggregation for demand-response management Privacy, data aggregation, differential privacy Ensures that data leaks do not occur, and efficient aggregation is maintained Limited effectiveness for highly detailed data [109] SG with large-scale data collection Apply differential privacy to protect energy usage data for large-scale grids Data perturbation, confidentiality, utility maximization Enhances privacy without large overhead for large datasets Requires balancing between privacy and data quality - k-Anonymity, another widely studied anonymization technique, has been proposed [110] and applied to ensure that energy consumption data cannot be linked to fewer than k-1 other users. Sweeney et al. [111] initially introduced this concept, and it has been applied in various domains, including SGs. In the context of SGs, k-Anonymity helps obscure individual energy usage to prevent privacy violations. However, recent studies, such as the one proposed in [112], indicate that k-Anonymity is vulnerable to attacks when auxiliary information is available, which makes it insufficient for protecting against linkability attacks. Moreover, Sakthivel et al. [113] proposed a k-Anonymity-based model for anonymizing smart meter data, where they ensure that the consumption patterns are generalized so that no individual data point can be traced back to a particular consumer.Additionally, the advantage of k-Anonymity is that it is relatively simple to implement and can provide a basic level of privacy by masking individual consumption details [114]. The proposed studies make it a useful tool for SGs where data must be aggregated and shared, but individual privacy must be preserved [115]. However, k-Anonymity can lead to a loss of granularity in the data, which might diminish its usefulness for detailed grid analysis [116]. Additionally, the technique is vulnerable to attacks that use auxiliary data or background knowledge, such as the homogeneity attack or the background knowledge attack, where attackers may still infer sensitive information [117]. A summary of a few other studies based on k-Anonymity is presented in Table 5.
 Table 5. Summary of k-Anonymity and data anonymization techniques.Table 5. Summary of k-Anonymity and data anonymization techniques.
Table 5. Summary of k-Anonymity and data anonymization techniques.Table 5. Summary of k-Anonymity and data anonymization techniques.Refs. System Model Goal Security Parameters Performances Limitations [118] Residential SM data Protect consumers’ privacy by ensuring that energy consumption patterns are indistinguishable from other
consumersk-Anonymity, data generalization,
suppressionAchieves a high level of privacy with minimal loss of data quality Data utility significantly decreases when increasing k [119] SG with aggregated consumption data Preserve privacy of consumers’ energy usage data while allowing aggregation for demand response Data anonymization, k-Anonymity, data perturbation Effective at protecting privacy without large computational overhead Performance degradation in data analysis when large k is required [120] SG with individual consumption data from residential users Protect sensitive data while maintaining usability for grid management tasks k-Anonymity, noise injection, clustering Effective for privacy protection in real-time smart grid applications Increased noise can reduce the accuracy of demand
forecasting - Data aggregation models have also been extensively researched as an alternative to individual data storage. Zhan et al. [121] discussed how aggregation at the community level can maintain grid performance while ensuring that individual data is protected. The proposed research in [122] highlights the advantage of aggregating energy usage data, as it reduces the risk of sensitive data leakage while optimizing grid control. Privacy protection through aggregation, however, has limitations because it increases data generalization, which can limit its value for individualized services such as adaptive pricing or demand-response programs [123].However, a balance must be maintained between data aggregation and the loss of detail, as privacy protection should not undermine effective grid management [124]. Furthermore, Xu et al. [125] proposed a data aggregation framework for SG systems utilizing Secure Multiparty Computation (SMPC) to aggregate data from multiple smart meters while preserving the privacy of individual consumption information. This approach ensures that only aggregated consumption data is shared with the grid operator, thereby preventing the disclosure of sensitive user information.Data aggregation in the smart grid is essential as it enables operators to analyze overall consumption and develop an understanding of future requirements and efficient strategies for resource allocation. However, there are some limitations in achieving both privacy and utility because excessive noise added during the aggregation process may reduce its usefulness for grid optimization [126]. Researchers are working on developing models that aggregate data in a way that maintains privacy while providing accurate and useful insights for grid management. Table 6 presents a summary of a few studies with their limitations.
 Table 6. Summary of privacy-preserving data aggregation techniques.
Table 6. Summary of privacy-preserving data aggregation techniques.
2.5.6. Blockchain-Based Mechanism
Blockchain technology has gained popularity in the smart grid space for its ability to provide decentralized, secure, and transparent data management. By using a distributed ledger system, blockchain enables secure transactions without the need for a central authority [130].
Smart contracts, which are a key part of blockchain technology, are self-executing contracts with the terms of the agreement written directly into code. Saeed et al. [131] proposed using smart contracts in peer-to-peer energy trading platforms to automate transactions between consumers and producers of renewable energy. Moreover, smart contracts ensure transparency, security, and privacy while eliminating the need for intermediaries, thereby reducing the risk of data manipulation or privacy breaches [132]. As noted in the literature, however, blockchain scalability remains a major concern, particularly as the number of participants grows [133].
A privacy-preserving scheme based on blockchain was proposed in a study by Alsheavi et al. [134] to provide privacy in SGs by using blockchain and smart contracts that automate the sharing of energy consumption data only with authorized entities. Smart contracts eliminate the need for a central authority to implement privacy policies, which leads to greater transparency and trust for all participants. Furthermore, to enable all transactions to be registered and stored in the blockchain in an immutable and easily traceable manner, smart contracts can be used to automate important processes in SGs, such as releasing energy data, delivering payments for energy use, and implementing demand-response measures [135].
Nevertheless, blockchain’s slow transaction speed and the computational resources it requires can cause performance bottlenecks in large-scale smart grid applications, as depicted in Table 7.

Table 7.
Summary of smart contract applications in smart grids.
Decentralized access control has been suggested as a way to use blockchain-based systems to secure consumer information in smart grids (SGs) [140]. Hasan et al. [130] discussed the possibility of making access to energy consumption data decentralized with the help of blockchain, where consumers can control access to their data using cryptographic keys. This strategy provides enhanced privacy and security compared to conventional centralized approaches [141]. Researchers like Alsheavi et al. [134] also demonstrated that a well-structured decentralized access control system can be implemented in SGs to regulate access to sensitive information, including consumption statistics and pricing.
The distributed nature of decentralized access control effectively eliminates the threats of a single point of failure and a central authority being corrupted by an adversary. It achieves this by sharing access control decisions across the entire network. The advantage of blockchain-based decentralized access control is that it enhances transparency and accountability, making it easier to track who accessed what data and when [142]. This ensures that access is granted based on pre-defined permissions and that users can verify that their data is not being accessed without authorization [143]. However, one key challenge of using blockchain for access control is ensuring scalability, as the number of transactions in a large SG network can increase substantially, as shown by the comparative analysis of a few studies in Table 8.

Table 8.
Summary of access control mechanisms in smart grids.
Several consensus algorithms have been used in blockchain for deployment in the smart grid. Table 9 presents a comparative analysis of several consensus mechanisms for smart grid applications. From Table 9, it can be observed that among the various consensus mechanisms, PBFT and PoA are the most practically applicable to large-scale smart grid applications, as they offer low latency rates with high scalability.

Table 9.
Comparison of consensus mechanisms for smart grid applications.
2.5.7. Tokenization
Tokenization, another blockchain-based technique, involves replacing sensitive data with tokens that can be securely exchanged or traded. Tokenization has been proposed [154] and applied in energy systems to represent energy credits or trading rights, allowing consumers to engage in energy trading without revealing detailed consumption data. Taherdoost et al. [155] explored tokenization in decentralized energy markets and demonstrated how it can be leveraged to ensure privacy while allowing participants to trade energy efficiently. Moreover, Chen et al. [156] proposed a tokenization-based approach for protecting sensitive data in SGs, where energy usage information is replaced with anonymous tokens during billing processes, ensuring that users’ data cannot be easily traced or identified.
The primary advantage of tokenization is that it reduces the risks of data breaches because tokens cannot be reverse-engineered to rediscover the original data. This makes tokenization a viable solution for SGs whose transactions and sensitive data should be secured. However, managing the tokenization process requires careful design to ensure that tokens cannot be easily misused and that they do not introduce processing delays or errors in energy data handling [157]. As noted in their study, key management is a critical issue in tokenization systems. The security of tokenized data relies on the secure handling of encryption keys, which, if compromised, can expose sensitive information, as shown in Table 10.

Table 10.
Summary of tokenization applications in smart grids.
2.5.8. Machine Learning Approaches
Machine learning (ML) techniques can also be applied to privacy preservation in SGs. By learning patterns from data without directly accessing sensitive information, ML models can improve system efficiency while maintaining privacy, with methods like federated learning and adversarial learning gaining popularity.
Federated learning is a decentralized approach to training machine learning models where the data remains on local devices, such as SMs, and only the model updates are shared with a central server [160]. Su et al. [161] explored how federated learning could be applied in smart grid load forecasting, where data privacy is preserved by not transmitting sensitive consumer data to the central server. Furthermore, Alshehri et al. [162] discussed a federated learning framework for detecting energy theft in smart grids, where local models are trained at individual SMs and then aggregated to build a global model without revealing the sensitive energy consumption data of each user. The advantage of federated learning in SGs is that it provides a privacy-preserving way to train machine learning models without centralizing sensitive user data [163]. It enables the detection of anomalies in energy consumption patterns without compromising privacy.
However, federated learning requires efficient communication between devices to share model updates, and it can suffer from performance issues when there is significant data heterogeneity across devices [164]. While federated learning reduces the risk of data breaches, it faces challenges in terms of communication overhead and model convergence, especially when the data distribution across devices is heterogeneous, as shown in Table 11.

Table 11.
Summary of federated learning applications in smart grids.
Adversarial learning, in which synthetic data is generated to simulate real-world data without revealing sensitive information, has been applied to data augmentation in privacy-preserving machine learning models [107]. Adewole et al. [168] pioneered the use of adversarial learning with Generative Adversarial Networks (GANs), which have since been employed for privacy-preserving data generation in SGs. Takiddin et al. [169] applied adversarial learning to SGs for anomaly detection, training models to identify fraudulent activities, such as energy theft, even in the presence of malicious data tampering. By making the models robust to adversarial inputs, SG systems can become more resilient against data manipulation. While adversarial learning can effectively protect data privacy, it incurs computational costs, and ensuring the quality of synthetic data remains a key challenge, as shown in Table 12.

Table 12.
Summary of adversarial machine learning applications in smart grids.
The trade-offs of privacy preservation approaches in smart grids vary significantly. For instance, Homomorphic Encryption (HE) and Zero-Knowledge Proofs (ZKPs) provide strong privacy guarantees but entail high computational costs, limiting their scalability in real-time systems. Secure Multiparty Computation (SMPC) enables collaborative data analysis without sharing raw data but introduces substantial communication overhead. In contrast, anonymization and differential privacy (DP) offer lightweight and scalable solutions, albeit with reduced accuracy. Blockchain-based mechanisms provide tamper-proof data management; however, transaction speed and scalability remain concerns. Table 13 presents a comparative analysis of these privacy-preserving techniques, highlighting their key insights, computational intensity, and suitability for smart grid applications.

Table 13.
Comparison of privacy-preserving techniques for smart grids.
Noting the latency and computational scalability from Table 13, it can be observed that traditional privacy-preserving techniques such as Homomorphic Encryption (HE), Zero-Knowledge Proofs (ZKPs), and blockchain (BC) are still immature for deployment on resource-constrained IoT devices. Therefore, future research should focus on modifying these techniques to make them suitable for such devices. For instance, a lightweight privacy-preserving model has been proposed in [177], which is based on proxy re-encryption and asymmetric scalar product preserving encryption. In this model, the encryption process involves only addition and multiplication operations along with pairing operations rather than more computationally intensive individual operations, thus offering reduced computational overhead while maintaining the privacy of IoT devices.
Another approach addressing computational challenges in ZKPs was proposed in [178], where the authors utilized a Merkle tree architecture to aggregate user attributes and construct commitments for Zero-Knowledge Proof verification. This modification ensures that user attributes and access policies remain confidential while reducing computational overhead.
Regarding the computational intensity of blockchain, a scalable blockchain model has been proposed in [179]. In this model, the authors employed physically unclonable functions (PUFs), one-way hash functions, and bitwise XOR operations to achieve lightweight mutual authentication between smart meters and regional gateways, improving efficiency while maintaining security.
2.6. Trade-Offs Between Privacy Guarantees and Data Utility
Privacy-preserving mechanisms employed in smart grids span a spectrum from cryptographic techniques (Homomorphic Encryption (HE), Zero-Knowledge Proofs (ZKP), Secure Multiparty Computation (SMPC)) to statistical/anonymization approaches (differential privacy (DP), k-Anonymity, aggregation), blockchain/tokenization, and machine learning methods (federated and adversarial learning). Each class delivers a different point on the privacy–utility–performance frontier. Cryptographic tools provide very strong confidentiality; for example, HE enables computation over encrypted measurements but incurs substantial computation and latency that often makes it impractical for hard real-time use cases (high computation/latency, limited scalability). ZKPs provide strong verification without disclosure but add proof-generation latency and implementation complexity. SMPC offers collaborative analytics without revealing raw inputs but typically introduces large communication overheads and scaling difficulties. By contrast, DP and aggregation are lightweight and highly scalable and provide formal privacy guarantees, yet their injected noise or data generalization reduces accuracy for downstream tasks such as short-term load forecasting or fine-grained demand response. Blockchain and tokenization improve tamper resistance and auditability but suffer transaction speed and storage costs that reduce their applicability in very high-throughput measurement scenarios. Federated and adversarial learning keep raw data local and preserve privacy to varying degrees, but they face communication costs, data heterogeneity, and potential leakage through model updates. These qualitative trade-offs are summarized in Table 13.
To make these trade-offs concrete, systems researchers should move beyond qualitative statements and report a small set of standardized metrics for each use case:
- A privacy-level parameter (e.g., DP’s , key sizes or proof sizes for cryptographic techniques, attacker success rate/re-identification probability);
- Utility metrics tied to the application (e.g., RMSE/MAE for forecasting, billing error for billing tasks, detection F1/AUC for theft/anomaly detection);
- Operational costs (CPU cycles, latency, memory, communication bytes).
Reporting curves that sweep the privacy parameter and plot utility and cost (e.g., utility vs. , latency vs. message size, re-identification risk vs. k for k-Anonymity) reveals practical operating points. For instance, DP implementations require choosing to balance forecasting error and privacy: very small (strong privacy) implies larger injected noise and degraded forecasting/billing accuracy, while larger reduces noise but weakens formal guarantees. Similarly, HE/ZKP/SMPC variants differ in proof size/operation time and hence in feasibility for real-time grid control. The literature repeatedly emphasizes these trade-offs and the need to optimize noise/complexity for smart grid constraints, as shown in Table 9, Table 10, and Table 12.
Therefore, future research should focus on hybrid architectures: use lightweight DP or aggregation for continuous high-frequency monitoring (to preserve utility at scale), and reserve heavier cryptographic proofs (HE, ZKP, SMPC) for periodic audits, billing settlement, or offline analytics where latency is acceptable. Federated learning can complement this approach by keeping model training local and sharing only encrypted/DP-protected updates for centralized model aggregation. Such a mixed strategy leverages the strengths of each technique while controlling utility loss and performance overhead.
3. Pricing Mechanisms for Energy Trading in Smart Grid
Secure information motivates smart grid energy market participants to share their data with confidence, without fear of tampering. Such secure information enables regulatory authorities to determine fair energy trading prices. Market price determination also involves various pricing mechanisms, which depend on supply and demand, encouraging efficient use of energy resources and stabilizing the market.
Depending on the trading process, energy pricing in peer-to-peer (P2P) energy trading can be categorized into synchronous and asynchronous techniques, assuming P2P energy trading occurs within a two-sided market among multiple prosumers and consumers exchanging electrical energy [16]. This categorization provides a foundational understanding of energy prices by highlighting the trading process and the peculiarities of each approach.
A synchronous pricing mechanism is one where market players submit bids, and the energy price and trading volume are determined using market objectives, which may include optimizing social welfare or minimizing production costs. This system-centric approach to P2P energy trading resembles traditional wholesale electricity markets [17,180]. In this process, a forward energy trading market is initiated on a platform at a specified time. Prosumers and consumers submit sealed bids indicating the price and quantity of energy they wish to trade during this window. After the bidding period ends, the platform reveals the results and clears the market. The resulting energy price controls the welfare of all market participants.
Synchronous energy trading can enhance market efficiency compared to asynchronous pricing, particularly if trading partners directly manage transaction parameters. However, its effectiveness may diminish if a participant manipulates the merit order to exercise market power [180].
Figure 4 illustrates the types of synchronous and asynchronous pricing mechanisms.
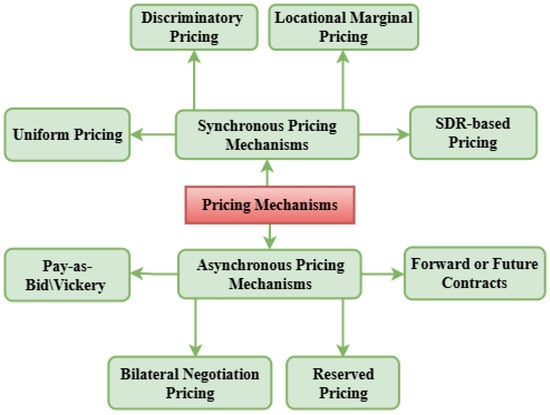
Figure 4.
Types of pricing mechanisms in P2P energy trading.
Different synchronous pricing models, as depicted in Figure 4, share a common objective function outlined in Table 14. While these models offer multiple advantages, they also present operational challenges, summarized in Table 15.

Table 14.
Objective functions for synchronous energy pricing mechanisms.
Asynchronous energy pricing enables numerous bilateral agreements between prosumers and consumers during the trading window, analogous to a flea market where participants negotiate energy prices that suit them individually. This methodology aims to achieve a collective agreement among market players in diverse situations. To facilitate optimal outcomes, distributed decision-making procedures have been proposed to support cooperation and coordination among participants [181].
In the asynchronous model, the market platform allows prosumers and consumers to negotiate energy prices and trading volumes directly. The consensus process varies depending on the framework employed. A key feature of asynchronous energy pricing is that trading is participant-driven, which reduces economic and political interventions typical in centralized markets. This decentralized approach allows market players to consider multiple factors, such as energy price, participant reputation, and preferences for renewable energy sources [182].
The objective functions, advantages, and operational challenges for asynchronous pricing models are summarized in Table 16 and Table 17.

Table 15.
Advantages, disadvantages, and challenges of synchronous pricing mechanisms in energy markets.
Table 15.
Advantages, disadvantages, and challenges of synchronous pricing mechanisms in energy markets.
| Type | Advantages | Disadvantages | Challenges | Refs. |
|---|---|---|---|---|
| Uniform Pricing | Simple, transparent, easy to implement. | Does not reflect grid constraints, inefficiencies in large markets. | May lead to price distortion, congestion handling issues. | [18,183,184,185,186] |
| Discriminatory Pricing | Aligns payment with bidder’s price, promotes competition. | Can lead to inefficiency and mark-ups, potential for strategic bidding. | Complexity in matching bids and price setting, potential for unfair market behavior. | [187,188,189,190,191] |
| Locational Marginal Pricing (LMP) | Reflects true cost of energy at different locations, efficient, encourages investment in grid capacity. | Computationally complex, exposes participants to locational price risk. | Requires accurate modeling of grid constraints, difficult for dynamic systems with high renewable penetration. | [192,193,194,195,196,197,198,199,200] |
| SDR-based Pricing | Simple to implement, encourages participation, promotes fairness. | Lack of grid constraint consideration, incentivization issues. | Requires accurate supply and demand data, challenges in fluctuating renewable energy markets. | [201,202,203,204,205,206,207] |

Table 16.
Advantages, disadvantages, and challenges for asynchronous pricing mechanisms in energy markets.
Table 16.
Advantages, disadvantages, and challenges for asynchronous pricing mechanisms in energy markets.
| Pricing Type | Advantages | Disadvantages | Challenges | Refs. |
|---|---|---|---|---|
| Pay-as-Bid/Vickrey Pricing | Predictable for sellers; transparency in price determination. | Can lead to market inefficiency; high risk for sellers if bids are too low. | Manipulation of bids; price uncertainty. | [208,209,210] |
| Bilateral Negotiation Mechanisms | Flexibility in terms; enables tailored agreements. | Lack of transparency; can lead to inefficiency if not well-negotiated. | Lack of market transparency; disagreement on terms. | [211,212,213,214,215] |
| Reserved Pricing | Provides a minimum price guarantee; protects sellers from low market prices. | Can prevent market clearing; prices may be set too high, reducing competition. | Determining an optimal reserve price; potential market inefficiency. | [216,217,218,219,220] |
| Forward and Futures Contracts | Price certainty for future transactions; mitigates price risk. | Not suitable for all markets; limited flexibility for customization. | Determining an appropriate contract price; market volatility risks. | [221] |

Table 17.
Objective functions for asynchronous pricing mechanisms.
Table 17.
Objective functions for asynchronous pricing mechanisms.
| Pricing Type | Objective Function (Mathematical Formulation) |
|---|---|
| Pay-as-Bid/Vickrey Pricing | Pay-as-Bid: Minimize total market cost, where each seller receives the price they bid.
|
| Bilateral Negotiation Mechanisms | Maximize the utility of the buyer and seller based on the negotiated price .
|
| Reserved Pricing | Maximize seller’s revenue subject to the reservation price being met.
|
| Forward and Futures Contracts | Maximize the expected profit from a future transaction based on the agreed price .
|
3.1. Uniform Pricing Mechanism
The uniform pricing rule is a synchronous market-clearing mechanism in which all matched trades—whether a prosumer’s sale or a consumer’s purchase—are settled at a common price. Typically, this price is determined by aggregating all buy and sell bids in the form of supply and demand curves. The intersection of these curves establishes the clearing price for all transactions, regardless of individual bid values submitted by participants [222,223].
Several researchers have developed models to identify uniform pricing in peer-to-peer (P2P) energy trading markets. For instance, optimization-based models aim to maximize objectives such as social welfare [224,225]. Alternatively, the price may be set through stakeholder agreement. Uniform pricing contributes to reducing voltage imbalances within the distribution network and promoting supply–demand equilibrium [226,227,228].
The market-surplus-maximizing energy price is generally defined as the highest bid at the intersection of the supply and demand curves [229]. In practice, however, market clearing often uses the second-highest bid instead of the absolute highest bid to promote fairness [229,230,231]. Studies such as [232,233] examine uniform pricing in P2P markets, demonstrating that a common clearing price can ensure fairness, even under grid constraints or in 100% renewable electricity markets.
Fair competition among sellers determines the single clearing price, typically selected via a heuristic search over submitted bids to maximize revenue or minimize costs [223,234]. While uniform pricing enhances transparency and provides a common price for all participants, it is susceptible to strategic bid shading, where bidders may inflate offers above their true willingness to pay [235].
3.2. Discriminatory Pricing Mechanism
The discriminatory pricing system settles each approved transaction at the specific price bid by the respective participant. In this mechanism, sellers post their quantity–price combinations, and bids are accepted until demand is fulfilled. Successful sellers are then paid their individual bid price rather than a single uniform price, and the traded quantity corresponds to the minimum of the bid and ask quantities [236,237].
Discriminatory pricing has also been employed in renewable energy markets to provide more accurate price signals and optimize distribution performance. For instance, Ref. [238] demonstrates that discriminatory pricing can enhance the integration of renewable energy sources while maintaining fairness and effectiveness. The mechanism better reflects actual energy costs by allowing prices to vary according to local generation capacity and fluctuations in demand [239].
Pricing strategies under discriminatory pricing are typically aligned with specific market objectives. For example, Ref. [240] links matching rules to pricing approaches that can achieve the Nash equilibrium in simultaneous games [241]. In [242], a distributed approach is proposed to maximize overall energy-user benefit, creating an envy-free and Pareto-optimal outcome. Similarly, a two-stage Stackelberg game model [243] allows small distributed energy sources to trade at higher payments by targeting users willing to pay more, thereby reducing controller costs while maximizing user utility. Overall, discriminatory pricing improves market efficiency by emphasizing price flexibility, while necessitating careful pairing and matching of trading partners.
3.3. Locational Marginal Pricing Mechanism
Building on discriminatory pricing, Locational Marginal Pricing (LMP) incorporates the physical characteristics of the energy network. Unlike standard discriminatory pricing, which relies solely on bid prices, LMP determines a price at each grid node that accounts not only for the energy cost but also for transmission congestion and line losses. This provides a more accurate and location-specific pricing signal, facilitating cost-effective energy delivery across large, complex networks [244].
LMP calculation typically involves three main components:
- The marginal cost of electricity generation at a specific power plant [245].
- Costs associated with failing to clear electricity flows in the transmission network, requiring additional dispatch of generation resources [246].
- Energy losses due to resistance in transmission lines [247].
Research by [248] approximates LMPs using AC and DC Optimal Power Flow (OPF) models, providing a detailed decomposition to understand the pricing mechanism in power markets. The study in [200] examines implementation challenges for LMP in transitioning power systems, emphasizing complexities introduced by decarbonization and heterogeneous participants. Other works, such as [197], highlight LMP’s role in grid optimization and transparent energy pricing, taking into account generation costs, delivery, and transmission constraints at different network locations.
3.4. SDR-Based Pricing Mechanism
Building on discriminatory and Locational Marginal Pricing, the SDR (Supply and Demand Ratio)-based method provides an alternative where the ratio of available energy supply to demand directly influences energy prices. Unlike LMP, which considers grid physical characteristics, SDR focuses on real-time supply versus demand, making it suitable for small or decentralized energy markets [207,249].
The SDR is calculated as the total energy provided divided by the total energy required. This ratio, combined with bidding information, is used to determine energy prices. Studies such as [250] have shown SDR to be effective in renewable energy markets with fluctuating supply. Community-based energy trading scenarios also benefit from SDR, as it promotes fairness and encourages market participation [225,251]. Price determination may involve a convex combination of local purchasing and grid-selling prices [252,253].
3.5. Pay-as-Bid (PAB) and Vickrey Pricing
Pay-as-bid (PAB) and Vickrey auctions are competitive bidding mechanisms for energy markets.
In a PAB auction, participants submit bids indicating their desired selling or buying price. The market clears by accepting bids starting from the most competitive until total demand is met. Each successful seller receives their submitted price, incentivizing competitive bidding to maximize returns [254,255,256,257,258].
Vickrey pricing modifies PAB by having the winning bidder pay the second-highest bid rather than their own. This promotes truth-telling, as bidders reveal their true valuation without overbidding or underbidding, enhancing efficiency [259,260,261,262]. Recent research explores repeated and multi-unit PAB auctions [263] and adaptive bidding strategies [264,265], optimizing utility and market performance.
3.6. Reserved Pricing Mechanism
Reserved pricing sets the minimum acceptable price for energy in an auction. Bids below this threshold are rejected, protecting sellers from losses and ensuring that auction outcomes reflect real market value [266,267].
Reserved pricing is commonly applied in pay-as-bid or Vickrey auctions, influencing bidding behavior and maintaining market stability, especially with high renewable penetration or variable demand [206,268,269]. Research has examined its effect on operating reserves, scarcity pricing, and market incentives [270,271,272,273,274,275].
3.7. Forward and Futures Contracts
Forward and futures contracts are asynchronous mechanisms where prices are agreed upon today for delivery at a future date.
A forward contract is privately negotiated and customizable between two parties, while a futures contract is standardized and traded on an exchange [276,277,278,279,280,281,282]. These contracts allow participants to hedge against price volatility or speculate on future prices.
Forward/futures contracts provide price stability, particularly important in markets with renewable generation or fluctuating supply–demand conditions [221,283,284,285,286]. They also inform price discovery and market decision-making while enabling small-scale generators to secure predictable revenue streams.
3.8. Game-Theoretic Techniques
Game theory is a branch of mathematics that studies strategic interactions among rational decision-makers, where the payoff of each participant depends on the actions of others [19]. In energy markets, game-theoretic methods are used to model interactions among market players—such as buyers, sellers, operators, and regulators—to establish optimal pricing, bidding strategies, and contract negotiations.
Nash equilibrium is a fundamental concept in game theory [19,287], representing a set of outcomes where no player can improve their payoff by unilaterally changing their strategy. In energy markets, Nash equilibrium helps predict participants’ behavior in competitive pricing environments, particularly during auctions.
Several studies have applied Nash equilibrium to optimize energy market prices:
- A Nash Stackelberg game model [288] was proposed to study strategic interactions between distributed energy resource (DER) aggregators and electricity retailers. This hierarchical model captures profit-maximizing behaviors of DER aggregators while accounting for retailers’ pricing strategies, providing insights into optimal bidding strategies in decentralized systems.
- A hybrid approach combining Mixed-Integer Linear Programming (MILP) with game theory [289] has been used to represent P2P energy market settlements.
- Nash equilibrium has been used to identify optimal trading strategies among prosumers in decentralized energy markets [290] and to maximize bids in bilateral electricity markets [291].
- Game-theoretic bargaining solutions have been applied to determine prices for Tradable Green Certificates (TGCs) and other auctioned energy products [292].
- Learning-based approaches, such as the no-regret algorithm, have been integrated with Nash equilibrium to model supplier bidding strategies in forward electricity markets [293].
Cooperative vs. Non-Cooperative Games [294] are also widely applied:
- Cooperative game theory analyzes coalition formation among prosumers in P2P networks and equitable profit distribution using concepts like the Shapley value or the core. For example, online coalitional games have been proposed to compute payoffs in real-time P2P markets [295], ensuring fairness and scalability.
- Distributed negotiation mechanisms facilitate stable bilateral contracts within coalitions, improving participation and user satisfaction [296].
- Hedonic games incorporate social preferences and community relationships, enabling coalition formation that maximizes total energy exchange [297].
Stackelberg models are used in non-cooperative scenarios, where grid operators or aggregators act as leaders, and DER prosumers are followers. These models optimize network costs and prosumer utilities simultaneously [298]. Hybrid models combining cooperative and Stackelberg frameworks balance self-interest with group stability [294,299].
Game theory provides diverse tools for modeling pricing in electricity markets, accommodating both market-like structures and P2P energy trading. Table 18 summarizes recent applications of game-theoretic methods in energy price determination.

Table 18.
Applications of game theory in energy pricing.
3.9. Optimization Techniques
Optimization methods are widely used for efficient and fair cost determination in energy markets, particularly in market-based electricity systems. These methods are crucial for forecasting prices and improving market mechanisms by considering multiple constraints, including supply–demand balance, transmission limits, and cost minimization. This section reviews recent applications of optimization in energy pricing.
Linear Programming (LP) is employed in centralized market clearing to determine optimal generation dispatch, transmission allocation, and price setting. The objective is typically to minimize total generation costs while satisfying demand and operational constraints. LP models are attractive for their simplicity and computational efficiency. For example, Ref. [312] proposes an LP model that accounts for generation and transmission line constraints to clear the electricity market in advance, minimizing costs and maximizing reliability. Similarly, Ref. [313] applied LP for renewable energy integration, optimizing market prices while ensuring that solar and wind generation meets demand.
Mixed-Integer Linear Programming (MILP) extends LP by incorporating both continuous and integer variables, enabling modeling of discrete decisions such as unit commitment, generation scheduling, and bidding strategies. MILP is particularly useful for markets requiring binary choices, e.g., turning generators on/off [314]. Studies like [315,316] use MILP to minimize operational costs while respecting environmental limits, ensuring generation flexibility, and optimizing contracts between market participants. MILP has also been applied in auction-based electricity markets [316,317,318] to optimize bidding strategies and long-term investment planning.
Convex Optimization has gained popularity in price forecasting and market equilibrium analysis due to its guarantee of global optimality for convex problems. These techniques are used to maximize social welfare or profit while minimizing costs under operational constraints. For instance, Ref. [319] uses convex optimization to forecast electricity prices under renewable energy uncertainty, whereas [320] incorporates demand response and DER integration to enhance price stability.
Stochastic Optimization is essential in markets with uncertain future conditions, such as real-time pricing, futures, and renewable integration. By modeling probabilistic variations in demand, generation, and market factors, stochastic optimization improves pricing under uncertainty. Applications include real-time pricing considering wind and solar forecasting errors [321] and modeling electricity price fluctuations under water supply–demand uncertainty and financial risk [322].
Metaheuristic Optimization Techniques such as Genetic algorithms (GAs), Particle Swarm Optimization (PSO), and Simulated Annealing (SA) are used to solve complex, non-linear problems in bidding strategies and market behavior [312]. These methods are particularly useful for dynamic, real-time price adjustments. For example, Ref. [323] applies GA to optimize bidding strategies considering competitor actions, Ref. [324] uses PSO for real-time auction pricing, and [325] employs SA for calculating real-time P2P energy prices.
Table 19 summarizes key studies that use optimization techniques for energy price determination.

Table 19.
Applications of optimization techniques in energy pricing.
3.10. Numerical Method-Based Techniques
Numerical methods play a critical role in energy pricing, particularly for complex, non-linear problems where analytical solutions are not feasible. They are widely applied in modeling market behavior, handling uncertainty, stochastic processes, price prediction, real-time pricing, and renewable energy integration.
Monte Carlo simulation (MCS) is extensively used to model uncertainty in pricing mechanisms, especially in stochastic environments such as forward contracts, futures markets, and renewable integration. It enables analysis of price variations and forecasts likely outcomes based on random variables. For instance, Ref. [340] investigates the impact of solar energy uncertainty on real-time electricity pricing using Monte Carlo simulation, while [341] uses it to project future prices in electricity futures markets.
Partial Differential Equations (PDEs) arising in price evolution and energy derivatives are often solved using Finite Difference Methods (FDMs). These methods approximate PDEs to simulate dynamic energy pricing, where prices depend on multiple factors such as demand, supply, and external conditions. For example, Ref. [22] models electricity price fluctuations in forward contracts using FDM, enhancing time-dependent price prediction accuracy. Other studies [342,343] apply FDM for non-linear pricing problems under market uncertainties.
Iterative Techniques are used for solving non-linear optimization problems and market-clearing algorithms, especially in decentralized energy markets. Iterative algorithms assist in balancing supply and demand to achieve market equilibrium [344,345].
The Newton–Raphson Method is an iterative approach for solving non-linear equations, often applied in real-time market clearing under complex price relationships [346,347]. Similarly, gradient descent is applied to optimize bidding and pricing strategies iteratively, particularly under competitive market conditions [348,349]. Stochastic gradient descent has been used for price modeling under renewable energy uncertainty and volatile markets [350,351].
3.11. AI-Based Techniques
AI-based approaches, including machine learning (ML), reinforcement learning (RL), and deep learning (DL), are increasingly applied to dynamic and complex pricing problems in energy markets, especially with the integration of renewable energy sources and smart grids.
Machine learning (ML) techniques predict energy prices using historical data, weather conditions, and market factors. Supervised learning models such as regression and ensemble methods (e.g., random forests) are widely used for real-time price forecasting [352,353]. Support Vector Machines (SVMs) have been employed for electricity futures pricing under renewable generation uncertainty [354,355].
Reinforcement learning (RL) is suitable for dynamic pricing, where agents learn optimal pricing strategies through interaction with market conditions. Q-learning has been applied to real-time pricing in smart grids [356,357], while Deep Reinforcement Learning (DRL) models optimize bidding strategies considering market states and competition [358,359].
Deep learning (DL) models, including neural networks (NN), LSTM, and CNN, are effective for complex pattern recognition in price forecasting. LSTM models capture long-range dependencies in electricity price data [360,361], while CNNs characterize price variability under uncertain renewable generation [362].
Hybrid AI Models integrate multiple techniques (e.g., DL, RL, ML) to optimize pricing comprehensively. Examples include CNN-LSTM models for spot price prediction [363], DRL-DL hybrids for dynamic smart grid pricing [364], and DNN-GA hybrids for P2P energy market bidding [365]. These hybrid approaches outperform conventional models in forecasting accuracy and market decision-making.
Table 20 summarizes the advantages, disadvantages, and challenges of the numerical and AI-based pricing techniques discussed.

Table 20.
Advantages and disadvantages of the techniques used for price determination.
4. Demand–Supply Balance Program (DSBP)
The integration of distributed energy resources (DERs) into smart grids is facilitated by effective pricing signals and energy conversion technologies. However, DER generation is inherently variable due to changing weather conditions, directly affecting generation capacity. This variability often causes a mismatch between supply and demand in the smart grid.
During periods of favorable weather, DERs, such as photovoltaic (PV) systems, operate near maximum capacity, potentially producing excess supply relative to demand. Conversely, during evenings or cloudy conditions, DER output declines, leading to a supply deficit relative to the energy demands of buyers.
To maintain demand–supply balance, the smart grid often relies on energy imports from or exports to the utility grid, which primarily consists of fossil-fuel-based generation. Such interactions not only increase CO2 emissions but also impose operational stress on the grid and participants. Importing energy from the utility grid is costlier than P2P energy, reducing potential savings for buyers, while exporting excess energy may reduce profitability for DER sellers.
The Demand–Supply Balance Program (DSBP) addresses these challenges by dynamically balancing generation and consumption while optimizing energy flows and prices. The DSBP can be formulated using various methodologies, including iterative methods, optimization models, game-theoretic frameworks, and AI-based approaches, as illustrated in Figure 5.
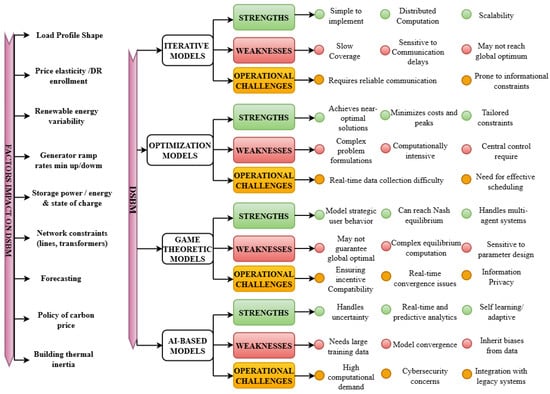
Figure 5.
Factors impacting the Demand–Supply Balance Program along with formulation techniques.
Each formulation approach in Figure 5 has unique merits and operational challenges. Table 21 provides a comparative overview of these models in terms of methodology, application, advantages, and limitations.

Table 21.
Comparative analysis of several models used to design DSBP.
4.1. Demand–Supply Balance Program Solving Models
Several researchers have proposed advanced methods to address the challenges of DSBP. This section explores notable approaches, highlighting their objectives and strengths.
4.1.1. Iterative Models
Iterative models rely on numerical formulations of the DSBP, updating system values repeatedly until a pre-defined convergence threshold is met. These models are widely used in smart grid management due to their simplicity and adaptability.
For instance, Ref. [20] introduced a Mixed-Integer Linear Programming (MILP)-based iterative model to manage real-time energy in an IEEE-33 AC-DC distribution network. Similarly, Ref. [366] proposed an iterative MILP model to optimize household energy consumption while respecting the operative supply envelope.
Another iterative approach using an inclined block tariff with real-time varying prices was developed in [367], enabling the adjustment of home appliances according to real-time energy costs. A demand-side management iterative sizing method was proposed in [368] to improve system efficiency.
Iterative weighting strategies have also been employed. In [369], different weights were assigned to household appliances, and appliance operating cycles were adjusted based on the Demand–Supply Ratio. Another iterative model [370] maintained the balance between requested demand and supply, achieving an average peak-hour load reduction of 52.8%, which is approximately 26.1% more efficient than comparable iterative methods. Additionally, this model demonstrated a 33.9% profit increase for aggregators by dynamically adjusting the demand–supply balance.
Table 22 presents a comparative analysis of several iterative DSBP models, summarizing their methodologies, objectives, and performance outcomes in maintaining demand–supply equilibrium in smart grids.

Table 22.
Summary of selected studies on DSBP based on iterative methods.
Although iterative models are scalable and easy to deploy in smart grids and perform effectively under pre-defined threshold conditions, the solutions they provide do not capture the strategic interactions among participants in DSBP programs.
Strategic interactions are crucial in DSBP design, as participants select their consumption based on private information, such as financial constraints, comfort preferences, and other individual factors. These interactions can be effectively modeled and analyzed using game-theoretic approaches.
4.1.2. Game-Theoretic Models
Game-theoretic models are an effective tool to capture and analyze the strategic behavior of participants by formulating their interactions as cooperative, non-cooperative, or evolutionary games.
In cooperative game models, participants form coalitions to determine optimal demand and supply values collectively. The achieved outcomes are then distributed among participants using allocation schemes such as Shapley values or other fair division models.
In non-cooperative game models, each participant independently selects their strategy, and outcomes are not shared with others. These models allow the analysis of individual optimization behavior in decentralized energy markets.
Several studies have utilized game-theoretic approaches to identify optimal strategies in DSBP programs. Table 23 provides a comparative summary of notable research using game-theoretic models for demand–supply balancing in smart grids.

Table 23.
Game theory applications in energy pricing and management.
4.1.3. Optimization Models
Although iterative models are highly scalable and game-theoretic models effectively capture participant interactions in DSBP design, both approaches often overlook critical system constraints, such as network operating capacity, available generation, and supply-to-demand ratios. To address these challenges, optimization models have been widely employed to design effective Demand–Supply Balance Programs in smart grids.
For instance, Zhao et al. [21] proposed a multi-objective optimization model to balance demand and supply while considering both economic and environmental impacts. This model utilized the AUGMECON2 optimization algorithm to obtain optimized solutions under multiple constraints.
An Ant Colony Optimization (ACO)-based model was introduced in [385] to determine optimized demand and supply values. The model was compared with other optimization approaches, such as Evolutionary Algorithm, Moth-Flame Optimization, and Bacterial Foraging Optimization, with simulation results demonstrating superior performance of the ACO model. Similarly, Nanibabu et al. [386] applied the Butterfly Optimization Algorithm, achieving an 18.4% cost reduction during peak hours through effective demand-side management strategies.
Optimization models have also been applied to control appliance operation and social welfare. For example, Ref. [367] employed Optimal Adaptive Wind-Driven Optimization to schedule appliance usage and balance supply and demand efficiently. Particle Swarm Optimization (PSO)-based models have been proposed in [387,388] to maximize social welfare and formulate the DSBP. Furthermore, a two-layered optimization model was introduced in, where the first layer manages appliance operation cycles, and the second layer optimizes consumption costs while maintaining consumer comfort levels.
These optimization models demonstrate the ability to integrate system constraints, operational flexibility, and economic objectives, making them a robust approach for designing effective DSBPs in smart grids.
A bi-level optimization model to maintain the balance between demand and supply in the smart grid was proposed in [389]. Additionally, a study in [390] introduced a model that considers multi-energy sources along with their planning and operational costs. This model employs a hybrid genetic algorithm (GA) and pattern search algorithm to balance energy generation and supply efficiently in the smart grid.
Beyond these studies, several other works deploying optimization models to maintain demand–supply balance are compared in Table 24.

Table 24.
Optimization techniques in energy pricing and management.
4.1.4. AI-Based Models
While optimization models provide highly accurate outputs for the present time horizon, their effectiveness can diminish for future horizons due to the need to analyze large volumes of historical data. As the dataset grows, computational time increases, which directly impacts the scalability of these models.
To overcome these limitations and capture the true dynamics of the system, artificial intelligence (AI) models are increasingly employed in designing DSBP programs. AI methods can learn important patterns and events from historical data, enabling better forecasting and adaptive demand–supply management in smart grids.
Table 25 summarizes several studies that applied AI models to determine optimized demand–supply values, highlighting the techniques, objectives, and key results.

Table 25.
AI models applied in DSBM and smart grid management.
4.2. AI-Driven Approaches in Pricing and Balance: Economic and Environmental Perspectives
The integration of artificial intelligence (AI) in smart grid (SG) systems, particularly through Demand–Supply Balance Programs (DSBPs) and pricing models, enhances operational efficiency and supports economic viability by leveraging real-time data from Advanced Metering Infrastructure (AMI) and Internet of Things (IoT) devices [2,12,13]. AI models facilitate demand prediction, supply optimization, and dynamic pricing, which contribute directly to reduced operational costs and improved resource reliability [8]. For instance, AI-driven DSBPs enable market operators to estimate demand–supply ratios using optimization and game-theoretic frameworks augmented by AI [17,18], allowing for uniform pricing or auction mechanisms that minimize energy waste during peak hours. This results in economic benefits such as lower electricity bills for consumers through informed usage decisions and dynamic pricing models that incentivize off-peak consumption, thereby conserving energy and reducing costs [9]. Utilities also benefit from automated billing and real-time monitoring, which reduce human error and enhance revenue management by preventing overages or undersupplies [14].
From a financial viability standpoint, AI deployment in SG pricing and balance programs offsets initial implementation costs, such as those for smart meters (SMs), control centers (CCs), and aggregators [38], through long-term gains in grid efficiency and scalability. By integrating renewable energy sources (RESs), such as solar panels and wind turbines, AI supports bidirectional energy flow and demand-response systems that balance supply and demand, reducing the need for expensive fossil fuel backups and fostering a more sustainable energy market [1]. AI approaches, combined with energy storage systems (ESSs), further amplify economic returns by injecting surplus energy during high-demand periods, mitigating the stochastic nature of RESs, and stabilizing prices [20].
Environmentally, AI implementation in the energy sector promotes sustainability by easing the penetration of RESs into SG architectures, which lowers the carbon footprint of energy production [44]. For example, AI-optimized DSBPs and pricing strategies enable efficient distribution of surplus renewable energy, reducing reliance on non-renewable sources and supporting dual energy flows that align with environmental goals [3]. However, challenges such as the energy demands of AI computations and potential vulnerabilities in IoT-integrated systems [12] must be addressed to ensure that these benefits do not inadvertently increase electronic waste or grid instability. Overall, the reviewed paradigms suggest that AI not only bolsters economic resilience through cost savings and reliability [8] but also advances environmental objectives by promoting cleaner, more balanced energy ecosystems [44], warranting further research into scalable, low-impact AI deployments.
4.3. Energy Storage Systems (ESS)
Although the Demand–Supply Balance Program (DSBP) assists the smart grid in maintaining a balanced state, this balance can be further enhanced by incorporating energy storage systems (ESSs). By utilizing ESSs, energy generated from photovoltaic (PV) systems and wind turbines during periods of high generation or favorable weather conditions can be stored in batteries. This stored energy can then be injected back into the system during peak-hour demand, thereby reducing the gap between requested demand and available renewable energy.
In smart grids, energy can be stored using multiple technologies, as illustrated in Figure 6. Among these, batteries are one of the most widely adopted methods due to their flexibility, scalability, and relatively straightforward integration. Batteries come in various chemical compositions, each with specific advantages and limitations, as also shown in Figure 6.
4.3.1. Lead–Acid Batteries
Lead–acid batteries are among the most cost-effective energy storage solutions, offering a low upfront cost and simple control mechanisms with high surge current capability. Due to these attributes, they are frequently employed in smart grid research to address energy storage challenges. Table 26 presents a comparative summary of several studies that utilized lead–acid batteries for energy storage in smart grid applications.

Table 26.
Lead–acid battery types, objectives, and strengths.
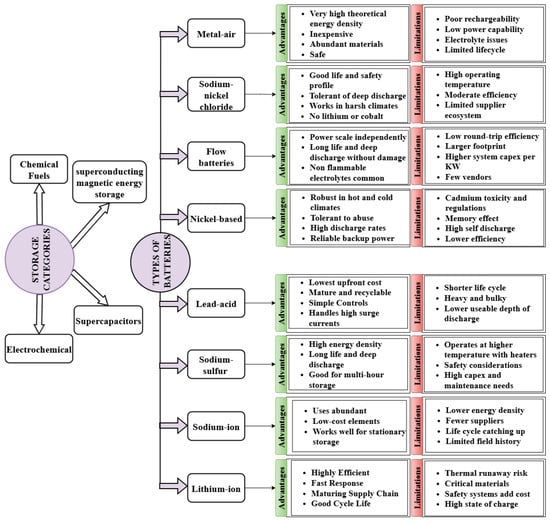
Figure 6.
Storage categories and types of batteries.
However, the main operational challenges of lead–acid batteries include their relatively short lifecycle and degraded performance under adverse weather conditions, which limits their effectiveness in long-term or harsh operating environments.
4.3.2. Nickel-Based Batteries
To address the limitations of lead–acid batteries, nickel-based batteries have been proposed for energy storage in smart grids. Compared to lead–acid batteries, nickel-based batteries offer higher tolerance to extreme weather conditions, enhanced reliability, and longer operational lifetimes, making them a more robust option for backup and renewable energy storage.
Table 27 provides a comparative overview of several studies that have implemented nickel-based batteries in smart grid applications, highlighting their performance, advantages, and deployment scenarios.

Table 27.
Nickel-based battery types, objectives, and strengths.
4.3.3. Sodium–Sulfur-Based Batteries
One of the primary drawbacks of nickel-based batteries is their high self-discharge rate, which negatively affects the overall efficiency of the storage system. To overcome this limitation, sodium–sulfur (NaS) batteries have been increasingly proposed for energy storage in smart grids. NaS batteries offer several advantages, including high energy density, long operational life, and deep discharge capabilities, making them well-suited for large-scale storage and renewable energy integration.
Table 28 summarizes several studies that have deployed sodium–sulfur batteries, highlighting their performance characteristics, deployment strategies, and operational benefits in smart grid applications.

Table 28.
Sodium–sulfur battery research, objectives, and strengths.
4.3.4. Sodium-Ion Batteries
Although sodium–sulfur batteries provide high energy density and long life, they require regular maintenance, which increases the operational costs of the energy storage system. To mitigate these costs, sodium-ion (Na-ion) batteries have been proposed as an alternative for energy storage in smart grids. Sodium-ion batteries offer reduced maintenance requirements while remaining well-suited for stationary storage applications.
Table 29 summarizes several studies that have deployed sodium-ion batteries, highlighting their advantages, deployment strategies, and performance outcomes in smart grid implementations.

Table 29.
Sodium-ion battery research, objectives, and strengths.
4.3.5. Lithium-Ion Batteries
One of the main limitations of sodium-ion batteries is their lower energy density, which restricts their full-scale deployment in smart grid energy storage applications. To address this limitation, lithium-ion (Li-ion) batteries are widely adopted due to their higher energy density, longer cycle life, and better efficiency. Many researchers have incorporated lithium-ion batteries into smart grid energy storage models to enhance performance and reliability.
Table 30 provides a comparison of several studies that implemented lithium-ion batteries, highlighting their objectives, deployment strategies, and key strengths in energy storage systems.

Table 30.
Lithium-ion battery research, objectives, and strengths.
4.4. Cost–Performance Trade-Offs Across Battery Technologies in Smart Grid Scenarios
Energy storage systems (ESSs) are integral to smart grids (SGs) for balancing demand and supply, but each battery technology presents distinct cost–performance characteristics. Lead–acid batteries are among the cheapest to deploy, offering simple control and high surge currents, which make them attractive for low-cost stationary storage. However, their shorter lifecycle and poor performance under adverse weather conditions limit their long-term cost-effectiveness [25]. Nickel-based batteries improve durability and environmental tolerance, with high cycle life (1000–1500+ cycles) and low maintenance requirements, but they suffer from higher self-discharge currents, which increase operational inefficiency [420].
Sodium–sulfur (NaS) batteries provide high energy density, long life, and deep discharge capability, offering better performance for large-scale integration. However, they require regular maintenance, which increases operational expenditure over time [427]. Sodium-ion batteries (SIBs) offer a cost-effective and sustainable alternative to lithium-ion by leveraging abundant materials. They are optimal for stationary storage models, providing moderate performance at lower cost, yet their lower energy density restricts deployment in applications requiring high power density [437].
Lithium-ion (Li-ion) batteries, conversely, deliver high energy density and scalability, making them suitable for both grid-scale and distributed applications. Nevertheless, they come with higher upfront costs and face degradation challenges over time [442]. Research on second-life Li-ion batteries has shown that reusing electric vehicle (EV) batteries for grid services can significantly reduce lifecycle costs while maintaining acceptable performance, improving both economic and environmental metrics (e.g., lowering global warming potential and cumulative energy demand compared to new battery packs) [445].
In practical SG scenarios, these cost–performance trade-offs indicate that lead–acid may be chosen for short-duration, cost-constrained backup; nickel-based and sodium–sulfur for environments demanding resilience and deep cycling; sodium-ion for cost-sensitive stationary storage with moderate performance; and lithium-ion or second-life Li-ion where high performance and integration flexibility justify higher upfront cost. Hybrid configurations combining, for instance, Li-ion and supercapacitors or lead–acid with supercapacitors, further optimize both cost and performance by distributing stress across chemistries to extend lifetime and improve round-trip efficiency [414]. A comparative analysis of cost–performance metrics of these storage systems is presented in Table 31.

Table 31.
Cost–performance trade-offs across battery technologies for smart grid (SG) applications.
4.5. Role of AI/Privacy-Preserving Techniques in ESS
Energy storage systems (ESSs), particularly their battery management systems (BMSs), introduce unique cybersecurity and privacy challenges. BMS devices control charging, discharging, and state-of-charge estimation, making them attractive targets for adversaries. False data injection into BMS signals can lead to misreporting of storage capacity, resulting in market imbalances or unsafe operating conditions.
Privacy-preserving techniques, such as differential privacy or Secure Multiparty Computation, can be applied to aggregated storage data to hide individual user behavior, while blockchain can provide tamper-proof audit trails of storage transactions. However, these mechanisms must be complemented with system-level intrusion detection and secure firmware, since privacy alone cannot prevent adversaries from disrupting storage operations.
Thus, the interaction between privacy and ESS security is twofold: cryptographic and privacy-preserving methods help protect user and market data, while robust BMS cybersecurity ensures that the underlying physical storage assets remain safe and trustworthy. A summary of privacy-preserving techniques and their interaction with ESS is presented in Table 32.

Table 32.
Privacy-preserving mechanisms for ESS/BMS interaction.
5. Case Studies
This section presents case studies based on pricing models, demand–supply management, privacy preservation, and attack identification in P2P smart grid energy trading, following recent studies [1,450,451].
5.1. Case Study: Uniform Pricing Model
Uniform pricing models bring all participants in the energy market onto a single platform, where they agree on the same price. Several factors, such as the Supply–Demand Ratio, generation costs, transmission, and grid constraints, can influence the determination of a uniform price signal. Reputation is another key factor, which can be used to determine energy prices in P2P markets. Incorporating reputation reduces bias among participants and promotes fairness in energy trading. A reputation-based pricing model has been proposed in the recent study by Amin et al. [450].
The energy trading model proposed by the authors is illustrated in Figure 7.
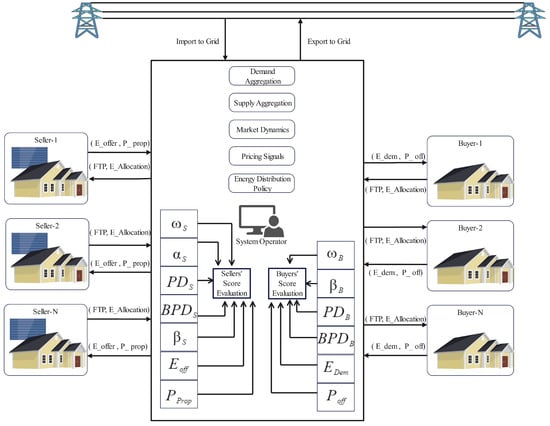
Figure 7.
Reputation-based uniform pricing model [450].
From Figure 7, it can be seen that the proposed model formulates a market where participants interact with each other to encourage energy trading under the supervision of a virtual market operator (MO), which oversees all trading activities. Sellers are weighted based on factors such as reliability , price dynamism , presence of participants , persistence factor , etc. The MO evaluates the reputation of each participant and assigns a corresponding score.
At the start of a trading session t, the MO invites participants to share their information. Sellers provide the MO with their offered price and the offered surplus energy , while buyers in the set B notify the MO of their energy demand and offered price . The MO keeps this information private and evaluates the reputation of each participant. The reputation evaluation for sellers, according to this study, can be computed using the following equations.
Similarly, buyers’ evaluation criteria are presented in equations given as
Once the scores for buyers and sellers have been evaluated, the market operator (MO) calculates the Supply–Demand Ratio (SDR) to determine the possible mode of operation. Based on the identified mode of operation, the final trading price of energy can be determined. The process is summarized as follows:
This proposed model exhibits several desirable characteristics, such as non-dictatorship, Pareto efficiency, independence of irrelevant alternatives, and collective rationality, thereby promoting fairness in the energy market while determining the uniform price of energy.
The model was evaluated using a one-year dataset consisting of varying demand and supply values. It was also compared with several state-of-the-art methods, including those proposed in [226,235,294,452]. Additionally, the proposed model considers the grid price as another baseline parameter to assess seller profitability and buyer savings. The experimental results are presented in Figure 8a,b.
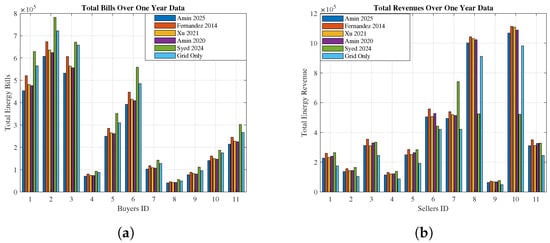
Figure 8.
Financial metrics for the reputation-based pricing model. (a) Energy bills for the reputation-based uniform pricing model over one-year dataset [450]. (b) Energy revenues for the reputation-based uniform pricing model over one-year dataset [450].
The experimental results demonstrate that the proposed reputation-based pricing model can increase the probability of sellers participating in the market by 2.1% to 20.41% compared with other state-of-the-art methods, and improve seller profitability by 22.91% compared to the grid export rate.
Similarly, buyers benefit from energy bill savings ranging from 2.81% to 44.27% compared with other state-of-the-art methods, while the savings relative to the grid import rate can reach approximately 27.78%.
5.2. Case Study: Integrated Demand–Supply Balance, Pricing, and Privacy-Preserving Model
A recent study [1] proposed an integrated model that combines demand–supply balance, pricing, and privacy-preserving techniques to ensure an effective energy trading platform in P2P energy markets. The proposed model is illustrated in Figure 9.
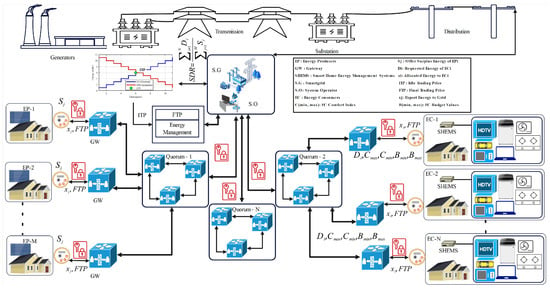
Figure 9.
Integrated demand–supply, pricing, and privacy-preserving model [1].
In this model, for each time slot t, each energy consumer (EC) i reports its energy demand , while each energy producer (EP) j reports its surplus energy . Additionally, each buyer communicates to the system operator (S.O.) their comfort indices and budgetary constraints, denoted as and , respectively.
The information shared by the participants is secured through a quorum-based architecture that integrates SHA-256 hashing, the Elliptic Curve Digital Signature Algorithm (ECDSA), and Shamir’s Secret Sharing (SSS). Each participant signs and hashes their data as follows:
After verification, the gateway encodes the data using SSS:
Each gateway receives a share:
The S.O reconstructs the secret using Lagrange interpolation:
Once the information is successfully secured, the S.O determines the market operation mode by evaluating the Supply–Demand Ratio (SDR):
If , the market operates in Sellers’ Mode, otherwise in Buyers’ Mode. At each trading time ‘t’ the ideal trading price (ITP) is determined at the equilibrium point of supply and demand, as presented in Figure 10.
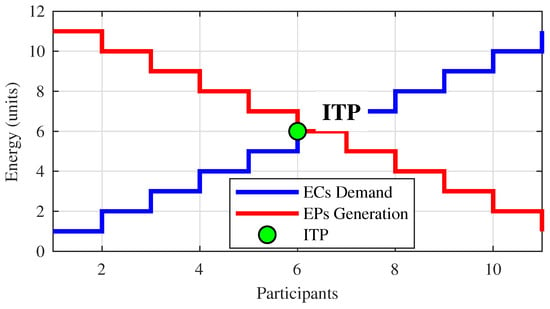
Figure 10.
Equilibrium price point determination [1].
Based on the market mode, the S.O. computes the trading price (TP). For the Sellers’ Mode, the TP is calculated as follows:
Once the price of energy has been found the next objective for the S.O is to formulate the energy allocation model as a convex optimization problem presented as follows:
For Buyers’ Mode, the objective can be expressed as follows:
The experimental results demonstrate the robustness of the proposed model against data manipulation during transmission. Any tampering results in the failure of the integrity test for affected participants, as illustrated in Figure 11.
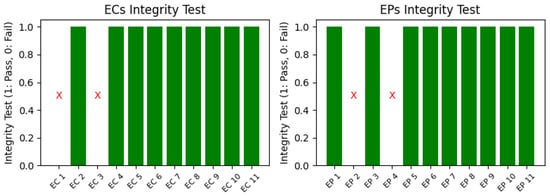
Figure 11.
Integrity test for affected participants [1]. X presents the failed participants in the integrity test.
Due to the failed integrity test, the S.O. refuses to reconstruct the information of affected participants, as shown in Figure 12.
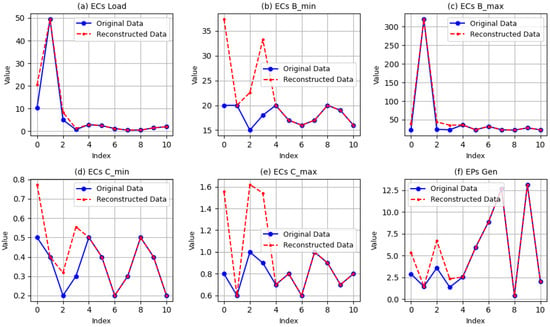
Figure 12.
Failed reconstruction of affected participants’ information by the S.O. [1].
This mechanism ensures privacy preservation in the P2P energy trading market. Furthermore, the model is computationally efficient; Figure 13 shows that it requires less execution time compared to baseline models.
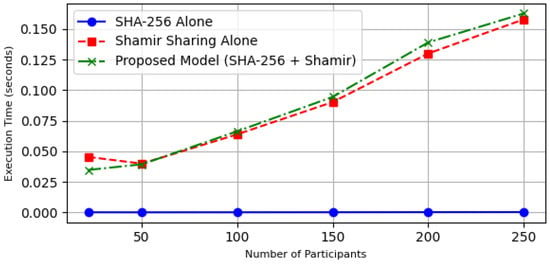
Figure 13.
Scalability analysis of the proposed model [1].
Finally, evaluation over a one-year dataset demonstrates improved grid efficiency by reducing the grid imbalance state in Buyers’ Mode, as presented in Figure 14.
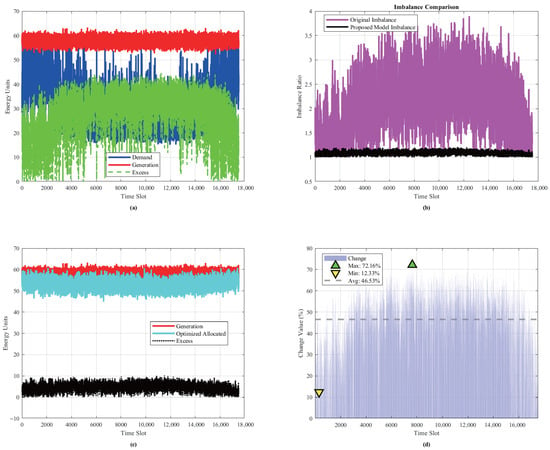
Figure 14.
Impact on grid imbalance: Buyers’ Mode over one-year dataset [1]. (a) Presents the relationship between the demand, generation and difference among them as surplus energy. (b) presents the original imbalance Vs Proposed model imbalance, (c) presents the difference in generation and optimized allocation, and (d) presents the percentage impact of grid imbalance state through the proposed model.
5.3. Cyberattack Detection in Smart Grid
This case study demonstrates the detection of cyberattacks in smart grids, specifically focusing on False Data Injection Attacks (FDIAs) that can manipulate participants’ shared information and disrupt market operations, based on the recent study [451].
With the rapid integration of renewable energy and advanced communication technologies, smart grids have become crucial for efficient power generation and distribution. However, this interconnectivity exposes grids to cyber threats such as FDIAs, which can compromise state estimation, disrupt grid operations, and potentially cause large-scale blackouts. Traditional machine learning techniques often fail to capture temporal dependencies in smart grid time-series data, reducing detection accuracy. To address this, Ref. [451] proposes a robust detection framework using a Bidirectional Long Short-Term Memory (Bi-LSTM) network integrated with an Attention Mechanism, offering high detection accuracy, computational efficiency, and interpretability.
The architecture diagram of the proposed model is shown in Figure 15.
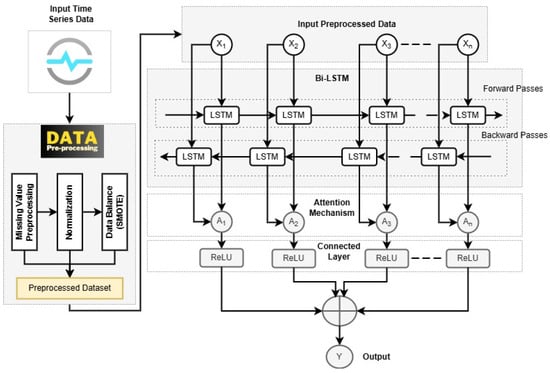
Figure 15.
Architecture of the Bi-LSTM with Attention Mechanism for FDIA detection [451].
As illustrated in Figure 15, the proposed model workflow is as follows:
- Data Acquisition: Time-series data from smart meters, including participant information such as energy demand, surplus energy, offered and proposed prices, is collected.
- Data Preprocessing: The raw input data passes through a preprocessing block to clean, normalize, and structure it for use in the Bi-LSTM model.
- Bi-LSTM Network: Captures both forward and backward temporal dependencies, enhancing recognition of subtle patterns associated with potential FDIA.
- Attention Mechanism: Dynamically assigns weights to critical time steps, focusing on significant events while filtering irrelevant information, thereby improving detection accuracy and interpretability.
This integrated Bi-LSTM and Attention framework enables the smart grid system to effectively detect FDIAs, ensuring the integrity of participant data and maintaining stable energy market operations.
The proposed model is evaluated on a real-time smart grid dataset, and the reported results are summarized in Table 33. From Table 33, it can be observed that the proposed Bi-LSTM with Attention model effectively identifies potential cyberattacks in the form of False Data Injection Attacks (FDIAs), achieving an accuracy of 92.32%, which outperforms other state-of-the-art baseline models.

Table 33.
Performance metric of the proposed model [451] in comparison with other state-of-the-art baseline models.
6. Future Research Directions
This section briefly explores potential future research directions based on the extensive literature reviewed in the preceding sections.
6.1. Privacy-Preserving Future Research Directions
The analysis of privacy-preserving techniques in smart grids reveals several limitations that highlight essential avenues for future research. For cryptographic methods such as Homomorphic Encryption (HE), the high computational overhead and latency in processing large-scale data necessitate the development of streamlined algorithms to reduce costs and enhance feasibility for real-time applications [64,65,73]. Similarly, Zero-Knowledge Proofs (ZKPs) face challenges in computational complexity and scalability, indicating the need for optimized protocols such as zk-SNARKs and zk-STARKs for efficient deployment in large-scale networks [85,86]. Secure Multiparty Computation (SMPC) also requires advancements to mitigate high communication overhead and improve scalability in decentralized systems [93,97].
In anonymization and aggregation techniques, differential privacy (DP) demands improved optimization of noise addition to balance privacy guarantees with data utility, particularly for demand-response management [100,106]. The vulnerabilities of k-Anonymity to auxiliary information attacks call for more robust models incorporating clustering and noise injection to enhance resistance [111,117]. Data aggregation models should aim to minimize generalization losses while still supporting individualized services without compromising overall grid optimization [122,123].
Blockchain-based mechanisms, including smart contracts and decentralized access control, require solutions to scalability and transaction speed limitations to accommodate increasing network traffic [130,142]. Similarly, tokenization approaches demand improved key management to prevent misuse and ensure seamless integration into energy trading systems [156,157].
Machine learning approaches, such as federated learning, must address challenges related to data heterogeneity and communication inefficiencies to achieve better model convergence for anomaly detection [160,164]. Adversarial learning, particularly using GANs, should focus on improving the quality of synthetic data and computational efficiency to develop robust privacy-preserving models [168,169].
Table 34 summarizes the key future research directions for privacy-preserving techniques in smart grids.

Table 34.
Future research directions in privacy preservation for smart grids.
Although the discussed literature presents remarkable efforts to preserve participants’ privacy and ensure grid stability, their resilience against coordinated, multi-layered state-sponsored attacks as discussed in Section 2.3 remains uncertain and highly dependent on implementation rigor and adherence to established standards.
For instance, while Homomorphic Encryption ensures data confidentiality during processing, its high computational overhead may make it susceptible to resource exhaustion attacks, a common tactic in state-sponsored DDoS campaigns, unless complemented by NIST-recommended resource management and intrusion detection systems [453]. Similarly, Zero-Knowledge Proofs, although effective for authentication without exposing data, face scalability challenges and may not withstand sustained high-volume attacks without IEC 62351-compliant key management and session integrity controls.
Blockchain-based solutions provide tamper-resistant transaction records and decentralized trust; however, their slower transaction speeds and scalability limitations (as highlighted in Table 7 and Table 13) could be exploited in prolonged attacks targeting consensus mechanisms. The International Electrotechnical Commission (IEC) [454] emphasizes the necessity of resilient consensus algorithms and real-time anomaly detection to mitigate such risks.
Although differential privacy and k-Anonymization techniques protect against data linkage attacks, they may fail under advanced adversarial inference leveraging auxiliary data, a known capability of state actors. IEC 62443-3-3 [455] recommends augmenting these techniques with continuous monitoring and adaptive noise injection to maintain utility while resisting sophisticated de-anonymization attempts.
Furthermore, the hierarchical communication architecture of smart grids (HAN/BAN, WAN) introduces multiple attack surfaces. State-sponsored actors often exploit unpatched systems, vulnerable protocols, and insider threats, as illustrated in Figure 2. NIST CSF and IEC 62351 stress the importance of defense-in-depth strategies, including (i) network segmentation and encryption across all layers, (ii) regular security audits and patch management, (iii) multi-factor authentication and strict access controls, and (iv) real-time intrusion detection and response systems.
Based on this discussion, it is recommended that future research adopt a holistic, standards-based approach integrating cryptographic methods with robust network security practices, continuous monitoring, and incident response frameworks to enhance smart grid resilience against advanced persistent threats.
6.2. Future Research Direction: Pricing Models
Future research in energy pricing mechanisms for smart grid P2P trading should focus on addressing the operational challenges and limitations observed in synchronous and asynchronous pricing models. For synchronous pricing, efforts could aim at enhancing market efficiency by mitigating manipulation in the merit order, improving congestion handling in uniform pricing, and developing more accurate grid constraint modeling for Locational Marginal Pricing (LMP) in dynamic systems with high renewable penetration. Similarly, Supply–Demand Ratio (SDR)-based pricing requires advancements to better handle fluctuating renewable energy markets through improved accuracy in supply and demand data.
Asynchronous mechanisms offer opportunities to reduce inefficiencies in pay-as-bid pricing by minimizing bid manipulation and price uncertainty, while also optimizing bilateral negotiations for greater transparency and mutual agreement on contract terms. Reserved pricing could benefit from methods to determine optimal reserve prices without hindering market clearing, and forward/futures contracts require improved models for contract pricing under market volatility.
Regarding price determination techniques, future directions include refining game-theoretic approaches to better model participant uncertainty and equilibrium calculations in large markets, as well as effectively handling non-cooperative behaviors in dynamic environments. Optimization methods should address forecasting data accuracy and computational demands for large-scale problems, particularly in systems with high renewable variability. Numerical methods can evolve to reduce computational costs in real-time simulations and improve model calibration under dynamic conditions. AI-based techniques present significant potential to overcome data quality challenges, enhance model interpretability, and reduce training time for large-scale adaptations to market dynamics.
Table 35 summarizes the future research directions for pricing models in smart grid P2P energy trading.

Table 35.
Future research directions in energy pricing.
6.3. Future Research Directions: DSBM
The Demand–Supply Balance Program (DSBP) faces several challenges, including achieving scalability, real-time adaptability, and effective integration of strategic participant interactions. Iterative models, while simple and scalable, often exhibit slow convergence and suboptimal performance in dynamic environments [20,370]. Future research should focus on accelerating convergence through advanced synchronization techniques and enhancing robustness against communication delays.
Optimization models can achieve near-optimal solutions but are computationally intensive and struggle with high-dimensional problems [21,385]. Developing hybrid algorithms that combine heuristic methods with real-time data processing could mitigate these limitations.
Game-theoretic models capture strategic interactions effectively but face challenges in ensuring unique equilibria and preserving participant privacy [22,229]. Future research should explore decentralized game-theoretic frameworks integrated with blockchain to enable secure, privacy-preserving interactions.
AI-based models offer significant potential in managing uncertainty and large datasets but require substantial training data and can face integration challenges with legacy grid infrastructure [23,408,456]. Future efforts should focus on developing lightweight AI models, leveraging transfer learning to reduce data dependency, and ensuring seamless integration with existing systems.
Table 36 summarizes the key future research directions for DSBM.

Table 36.
Future research directions for Demand–Supply Balance Program (DSBP).
6.4. Future Research Directions: ESS
Energy storage systems (ESSs) play a crucial role in balancing demand and supply in smart grids, yet each battery technology presents unique challenges. Lead–acid batteries, while low-cost, suffer from short lifecycles and limited performance under adverse conditions [25,418]. Future research should focus on enhancing lifecycle performance through advanced thermal management and hybrid configurations.
Nickel-based batteries offer durability but are constrained by high self-discharge rates [420,424]. Developing low-cost, high-efficiency electrolytes and improved cell designs could mitigate this limitation. Sodium–sulfur batteries provide high energy density but require frequent maintenance [427,428]. Research should explore low-maintenance architectures and novel electrolyte additives to improve operational stability.
Sodium-ion batteries are promising for stationary storage but exhibit lower energy density [28,437]. Future work should investigate advanced cathode materials and optimized cell designs to enhance energy density while maintaining cost-effectiveness. Lithium-ion batteries, with high energy density and scalability, face challenges related to cost and degradation [442,448]. Research should emphasize second-life applications, advanced battery management systems, and recycling strategies to extend lifespan and reduce costs.
Table 37 summarizes the key future research directions for ESSs in smart grid applications.

Table 37.
Future research directions for energy storage systems (ESSs).
7. Conclusions
The smart grid (SG) represents a transformative platform in energy management, integrating efficiency, sustainability, and reliability through two-way communication, the Internet of Things (IoT), and Advanced Metering Infrastructure (AMI). However, the extensive transfer of sensitive data exposes SGs to privacy and security risks, as evidenced by recent global incidents including data interception, energy theft, and cyberattacks such as MITM, DoS, and replay attacks. This review systematically analyzes the SG architecture and its core components substations, concentrators, aggregators, smart appliances, and renewable energy sources highlighting associated vulnerabilities and fundamental security requirements, including confidentiality, integrity, availability, secure storage, and scalability.
Effective countermeasures include cryptographic protocols (Homomorphic Encryption, Zero-Knowledge Proofs, Secure Multiparty Computation), anonymization techniques (differential privacy, k-Anonymity), and data aggregation methods. Recent studies also demonstrate that machine learning and blockchain-based solutions can complement these defenses. Further analyses of pricing models, Demand–Supply Balance Programs (DSBPs) using optimization and game-theoretic approaches, AI-driven models, and energy storage systems across various battery chemistries underscore their crucial role in maintaining grid stability amid the stochastic nature of renewable energy sources.
Finally, this review identifies persistent research gaps, such as the computational overhead of cryptographic techniques, trade-offs in the utility of anonymized data, and network scalability challenges. Addressing these issues is critical to developing resilient SGs that safeguard user privacy, mitigate cyber threats, and facilitate widespread adoption of sustainable energy technologies.
Author Contributions
I.N., N.M. and W.A. equally contributed in all sections. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author on request.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SG | Smart Grid |
| IoT | Internet of Things |
| AMI | Advanced Metering Infrastructure |
| MITM | Man-in-the-Middle |
| DoS | Denial-of-Service |
| CCs | Control Centers |
| SMs | Smart Meters |
| RESs | Renewable Energy Sources |
| DSBPs | Demand–Supply Balance Programs |
| ESSs | Energy Storage Systems |
| EVs | Electric Vehicles |
| ICT | Information and Communication Technology |
| HAN | Home Area Network |
| BAN | Building Area Network |
| WAN | Wide Area Network |
| DDoS | Distributed Denial of Service |
| HE | Homomorphic Encryption |
| ZKPs | Zero-Knowledge Proofs |
| SMPC | Secure Multiparty Computation |
| DP | Differential Privacy |
| zk-SNARKs | Zero-Knowledge Succinct Non-interactive ARguments of Knowledge |
| zk-STARKs | Zero-Knowledge Scalable Transparent ARguments of Knowledge |
References
- Amin, W.; Huang, Q.; Li, J.; Khan, A.A.; Subramaniam, U.; Selvam, S. A secure energy management model for Peer-to-Peer smart grids with user-centric constraints. Internet Things 2025, 33, 101678. [Google Scholar] [CrossRef]
- Dhaigude, R.; Chanda, R. Real-Time Data and Analytics on Building Management System to Control Energy Consumption. In Proceedings of the International Conference on Information and Communication Technology for Competitive Strategies, Jaipur, India, 15–17 December 2023; pp. 295–305. [Google Scholar]
- Dutta Pramanik, P.K.; Upadhyaya, B.K.; Kushwaha, A.; Bhowmik, D. Harnessing IoT: Transforming Smart Grid Advancements. In IoT for Smart Grid: Revolutionizing Electrical Engineering; Wiley Online Library: Hoboken, NJ, USA, 2025; pp. 127–174. [Google Scholar]
- Ahsan, F.; Dana, N.H.; Sarker, S.K.; Li, L.; Muyeen, S.M.; Ali, M.F.; Tasneem, Z.; Hasan, M.M.; Abhi, S.H.; Islam, M.R.; et al. Data-driven next-generation smart grid towards sustainable energy evolution: Techniques and technology review. Prot. Control Mod. Power Syst. 2023, 8, 43. [Google Scholar] [CrossRef]
- Althobaiti, A.; Jindal, A.; Marnerides, A.K.; Roedig, U. Energy theft in smart grids: A survey on data-driven attack strategies and detection methods. IEEE Access 2021, 9, 159291–159312. [Google Scholar] [CrossRef]
- Jain, H.; Kumar, M.; Joshi, A.M. Intelligent energy cyber physical systems (iECPS) for reliable smart grid against energy theft and false data injection. Electr. Eng. 2022, 104, 331–346. [Google Scholar] [CrossRef]
- Said, D. A survey on information communication technologies in modern demand-side management for smart grids: Challenges, solutions, and opportunities. IEEE Eng. Manag. Rev. 2022, 51, 76–107. [Google Scholar] [CrossRef]
- Amin, W.; Huang, Q.; Umer, K.; Zhang, Z.; Afzal, M.; Khan, A.A.; Ahmed, S.A. A motivational game-theoretic approach for peer-to-peer energy trading in islanded and grid-connected microgrid. Int. J. Electr. Power Energy Syst. 2020, 123, 106307. [Google Scholar] [CrossRef]
- Zhao, X.; Gao, W.; Qian, F.; Ge, J. Electricity cost comparison of dynamic pricing model based on load forecasting in home energy management system. Energy 2021, 229, 120538. [Google Scholar] [CrossRef]
- Alomari, M.A.; Al-Andoli, M.N.; Ghaleb, M.; Thabit, R.; Alkawsi, G.; Alsayaydeh, J.A.J.; Gaid, A.S.A. Security of smart grid: Cybersecurity issues, potential cyberattacks, major incidents, and future directions. Energies 2025, 18, 141. [Google Scholar] [CrossRef]
- Amanlou, S.; Hasan, M.K.; Mokhtar, U.A.; Malik, K.M.; Islam, S.; Khan, S.; Khan, M.A.; Khan, M.A. Cybersecurity challenges in smart grid systems: Current and emerging attacks, opportunities, and recommendations. IEEE Open J. Commun. Soc. 2025. [Google Scholar] [CrossRef]
- Guo, C.; Luo, F.; Cai, Z.; Dong, Z.Y. Integrated energy systems of data centers and smart grids: State-of-the-art and future opportunities. Appl. Energy 2021, 301, 117474. [Google Scholar] [CrossRef]
- Sevilla, F.R.S.; Liu, Y.; Barocio, E.; Korba, P.; Andrade, M.; Bellizio, F.; Bos, J.; Chaudhuri, B.; Chavez, H.; Cremer, J.; et al. State-of-the-art of data collection, analytics, and future needs of transmission utilities worldwide to account for the continuous growth of sensing data. Int. J. Electr. Power Energy Syst. 2022, 137, 107772. [Google Scholar] [CrossRef]
- Amuthan, N.; Sathya, M.; Rani, N.C. Empowering Consumers and Utilities for a Smarter Future: The Pivotal Role of Advanced Metering Infrastructure (AMI) in Smart Meter Technology. In Cloud Computing in Smart Energy Meter Management; Wiley Online Library: Hoboken, NJ, USA, 2025; pp. 31–65. [Google Scholar]
- Mubeen, M.; Arslan, M.; Anandhi, G. Strategies to Avoid Illegal Data Access. J. Commun. Eng. Syst. 2022, 12, 29–40. [Google Scholar]
- Shi, M.; Hoffmann, A.; Wagner, A.; Huyeng, T.; Thiele, C.-D.; Rüppel, U. Using blockchain technology to implement peer-to-peer network in construction industry. In Proceedings of the 18th International Conference on Computing in Civil and Building Engineering, Sao Paulo, Brazil, 18–20 August 2020; pp. 839–849. [Google Scholar]
- Liu, J.; Hu, H.; Yu, S.S.; Trinh, H. Electricity pricing and its role in modern smart energy system design: A review. Designs 2023, 7, 76. [Google Scholar] [CrossRef]
- Soh, C.; Markus, M.L.; Goh, K.H. Electronic marketplaces and price transparency: Strategy, information technology, and success. MIS Q. 2006, 30, 705–723. [Google Scholar] [CrossRef]
- González, F.; Arévalo, P.; Ramirez, L. Game Theory and Robust Predictive Control for Peer-to-Peer Energy Management: A Pathway to a Low-Carbon Economy. Sustainability 2025, 17, 1780. [Google Scholar] [CrossRef]
- Paul, S.; Padhy, N.P. A new iterative mixed integer linear programming based real time energy efficient management of AC–DC distribution networks. Int. J. Electr. Power Energy Syst. 2024, 157, 109793. [Google Scholar] [CrossRef]
- Zhao, Z.; Holland, N.; Nelson, J. Optimizing smart grid performance: A stochastic approach to renewable energy integration. Sustain. Cities Soc. 2024, 111, 105533. [Google Scholar] [CrossRef]
- Cheng, L.; Huang, P.; Zhang, M.; Yang, R.; Wang, Y. Optimizing electricity markets through game-theoretical methods: Strategic and policy implications for power purchasing and generation enterprises. Mathematics 2025, 13, 373. [Google Scholar] [CrossRef]
- Wang, X.; Wang, H.; Bhandari, B.; Cheng, L. AI-empowered methods for smart energy consumption: A review of load forecasting, anomaly detection and demand response. Int. J. Precis. Eng. Manuf.-Green Technol. 2024, 11, 963–993. [Google Scholar] [CrossRef]
- Antonopoulos, I.; Robu, V.; Couraud, B.; Kirli, D.; Norbu, S.; Kiprakis, A.; Flynn, D.; Elizondo-Gonzalez, S.; Wattam, S. Artificial intelligence and machine learning approaches to energy demand-side response: A systematic review. Renew. Sustain. Energy Rev. 2020, 130, 109899. [Google Scholar] [CrossRef]
- Luo, X.; Barreras, J.V.; Chambon, C.L.; Wu, B.; Batzelis, E. Hybridizing lead–acid batteries with supercapacitors: A methodology. Energies 2021, 14, 507. [Google Scholar] [CrossRef]
- Chandra Bhowmik, K.; Rahman, M.A.; Billah, M.M.; Paul, A. From lithium-ion to sodium-ion batteries for sustainable energy storage: A comprehensive review on recent research advancements and perspectives. Chem. Rec. 2024, 24, e202400176. [Google Scholar] [CrossRef]
- Miroshnyk, O.; Moroz, O.; Shchur, T.; Chepizhnyi, A.; Qawaqzeh, M.; Kocira, S. Investigation of smart grid operation modes with electrical energy storage system. Energies 2023, 16, 2638. [Google Scholar] [CrossRef]
- Dorau, F.A.; Sommer, A.; Koloch, J.; Röß-Ohlenroth, R.; Schreiber, M.; Neuner, M.; Gamra, K.A.; Lin, Y.; Schoeberl, J.; Bilfinger, P.; et al. Comprehensive analysis of commercial sodium-ion batteries: Structural and electrochemical insights. J. Electrochem. Soc. 2024, 171, 090521. [Google Scholar] [CrossRef]
- Luo, X.R.; Li, H.; Hu, Q.; Xu, H. Why individual employees commit malicious computer abuse: A routine activity theory perspective. J. Assoc. Inf. Syst. 2020, 21, 5. [Google Scholar] [CrossRef]
- Farkas, T.; Hronyecz, E. The Risks and Danger of Smart Devices Exposing Personal Information: Dark Side of Convenience. In Proceedings of the 2024 IEEE 22nd Jubilee International Symposium on Intelligent Systems and Informatics (SISY), Pula, Croatia, 19–21 September 2024; IEEE: New York, NY, USA, 2024; pp. 39–44. [Google Scholar]
- Nguyen, L.-H.; Nguyen, V.-L.; Hwang, R.-H.; Kuo, J.-J.; Chen, Y.-W.; Huang, C.-C.; Pan, P.-I. Towards secured smart grid 2.0: Exploring security threats, protection models, and challenges. IEEE Commun. Surv. Tutor. 2024, 27, 2581–2620. [Google Scholar] [CrossRef]
- Peter, J.S.P.; Babu, C.R.; Esther, B.P. Cybersecurity in ICT-Enabled Smart Metering Systems: Addressing Challenges and Implementing Solutions. In Cloud Computing in Smart Energy Meter Management; Wiley Online Library: Hoboken, NJ, USA, 2025; pp. 263–290. [Google Scholar]
- Vighneswari, B.D.; Kothai Andal, C. Smart Meter Security—Fraud Detection in Power Theft. In Cloud Computing in Smart Energy Meter Management; Wiley Online Library: Hoboken, NJ, USA, 2025; pp. 239–262. [Google Scholar]
- Abir, S.M.A.A.; Anwar, A.; Choi, J.; Kayes, A.S. Iot-enabled smart energy grid: Applications and challenges. IEEE Access 2021, 9, 50961–50981. [Google Scholar] [CrossRef]
- Senthilkumar, S.P.; Subramani, B. Internet of Things in Low-Power Wide Area Network and Short Range Network: A Review. I-Manag. J. Comput. Sci. 2023, 10, 33. [Google Scholar]
- Lounis, K.; Zulkernine, M. Attacks and defenses in short-range wireless technologies for IoT. IEEE Access 2020, 8, 88892–88932. [Google Scholar] [CrossRef]
- Suhaimy, N.; Radzi, N.A.M.; Ahmad, W.S.H.M.W.; Azmi, K.H.M.; Hannan, M.A. Current and future communication solutions for smart grids: A review. IEEE Access 2022, 10, 43639–43668. [Google Scholar] [CrossRef]
- Raza, M.H.; Rind, Y.M.; Javed, I.; Zubair, M.; Mehmood, M.Q.; Massoud, Y. Smart meters for smart energy: A review of business intelligence applications. IEEE Access 2023, 11, 120001–120022. [Google Scholar] [CrossRef]
- Rasheed, M.B.; Javaid, N.; Awais, M.; Khan, Z.A.; Qasim, U.; Alrajeh, N.; Iqbal, Z.; Javaid, Q. Real time information based energy management using customer preferences and dynamic pricing in smart homes. Energies 2016, 9, 542. [Google Scholar] [CrossRef]
- Beno, M.M.; Sivakumar, N.; Saravanan, R. Demystifying Smart Meters: Powering the Next-Generation Grid. In Cloud Computing in Smart Energy Meter Management; Wiley Online Library: Hoboken, NJ, USA, 2025; pp. 67–97. [Google Scholar]
- Noorazar, H.; Srivastava, A.; Pannala, S.; Sadanandan, S.K. Data-driven operation of the resilient electric grid: A case of COVID-19. J. Eng. 2021, 2021, 665–684. [Google Scholar] [CrossRef]
- Lang, A.; Wang, Y.; Feng, C.; Stai, E.; Hug, G. Data aggregation point placement for smart meters in the smart grid. IEEE Trans. Smart Grid 2021, 13, 541–554. [Google Scholar] [CrossRef]
- Liu, H.; Du, Z.; Xue, T.; Jiang, T. Enhancing smart building performance with waste heat recovery: Supply-side management, demand reduction, and peak shaving via advanced control systems. Energy Build. 2025, 327, 115070. [Google Scholar] [CrossRef]
- Amin, W.; Xie, S.; Vasa, L.; Mentel, U. Role of land use, green energy, and water resources for food accessibility: Evidence from emerging economies in the lens of COP 28. Land Degrad. Dev. 2024, 35, 4607–4622. [Google Scholar] [CrossRef]
- Ajayi, O.O.; Alozie, C.E.; Abieba, O.A. Enhancing cybersecurity in energy infrastructure: Strategies for safeguarding critical systems in the digital age. Trends Renew. Energy 2025, 11, 201–212. [Google Scholar] [CrossRef]
- Sivasubramanian, S.S. Detection of Man in the Middle Attack on Fog Layer Using Intrusion Detection Systems. Ph.D. Thesis, National College of Ireland, Dublin, Ireland, 2023. [Google Scholar]
- Cui, L.; Qu, Y.; Gao, L.; Xie, G.; Yu, S. Detecting false data attacks using machine learning techniques in smart grid: A survey. J. Netw. Comput. Appl. 2020, 170, 102808. [Google Scholar] [CrossRef]
- Tripathi, N.; Hubballi, N. Application layer denial-of-service attacks and defense mechanisms: A survey. ACM Comput. Surv. 2021, 54, 1–33. [Google Scholar] [CrossRef]
- Salim, M.M.; Rathore, S.; Park, J.H. Distributed denial of service attacks and its defenses in IoT: A survey. J. Supercomput. 2020, 76, 5320–5363. [Google Scholar] [CrossRef]
- Bushigampala, B.K.; Inaganti, A.C. Threat Detection in Critical Infrastructure Using AI Models. Int. J. Acta Inform. 2023, 2, 196–208. [Google Scholar]
- Lee, I. Analysis of insider threats in the healthcare industry: A text mining approach. Information 2022, 13, 404. [Google Scholar] [CrossRef]
- Medcalfe, D. Critical Infrastructure in the Face of Global Cyber Threats; Université de Sherbrooke: Sherbrooke, QC, USA, 2024. [Google Scholar]
- Lackenbauer, P.W. Situating the Yukon in Canadian Arctic Defence and Security. 2024. Available online: https://www.naadsn.ca/wp-content/uploads/2024/07/2024apr-Lackenbauer-Yukon-defence-security.pdf (accessed on 1 September 2025).
- Gomila, D.; Carreras, B.A.; Reynolds-Barredo, J.-M.; Martínez-Barbeito, M.; Colet, P.; Gomis-Bellmunt, O. Reducing Blackout Risk by Segmenting European Power Grid with HVDC Lines. J. Mod. Power Syst. Clean Energy 2025. [Google Scholar] [CrossRef]
- Konstantinoudis, G.; Riou, J. Excess mortality attributable to the 2025 Iberian Peninsula blackout. medRxiv 2025. [Google Scholar] [CrossRef]
- Iftikhar, S. Cyberterrorism as a global threat: A review on repercussions and countermeasures. PeerJ Comput. Sci. 2024, 10, e1772. [Google Scholar] [CrossRef]
- Alromih, A. Developing an Efficient and Privacy-Preserving Energy Theft Detection System for Smart Grids. Ph.D. Thesis, University of Sheffield, Sheffield, UK, 2023. [Google Scholar]
- Liu, L.; Workman, M.; Hayes, S. Net Zero and the potential of consumer data-United Kingdom energy sector case study: The need for cross-sectoral best data practice principles. Energy Policy 2022, 163, 112803. [Google Scholar] [CrossRef]
- Singh, S.K.; Kumar, S.; Garg, S.; Arora, S.; Sharma, S.K.; Arya, V.; Chui, K.T. Blockchain-Based Data Security in Smart Cities: Ensuring Data Integrity and Trustworthiness. In Digital Forensics and Cyber Crime Investigation; CRC Press: Boca Raton, FL, USA, 2025; pp. 17–41. [Google Scholar]
- Shah, M.S.M.; Leau, Y.-B.; Anbar, M.; Bin-Salem, A.A. Security and integrity attacks in named data networking: A survey. IEEE Access 2023, 11, 7984–8004. [Google Scholar] [CrossRef]
- Zografopoulos, I.; Hatziargyriou, N.D.; Konstantinou, C. Distributed energy resources cybersecurity outlook: Vulnerabilities, attacks, impacts, and mitigations. IEEE Syst. J. 2023, 17, 6695–6709. [Google Scholar] [CrossRef]
- Herath, H.M.S.S.; Herath, H.M.K.K.M.B.; Madhusanka, B.G.D.A.; Guruge, L.G.P.K. Data protection challenges in the processing of sensitive data. In Data Protection: The Wake of AI and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2024; pp. 155–179. [Google Scholar]
- Haque, A.B.; Bhushan, B.; Dhiman, G. Conceptualizing smart city applications: Requirements, architecture, security issues, and emerging trends. Expert Syst. 2022, 39, e12753. [Google Scholar] [CrossRef]
- Munjal, K.; Bhatia, R. A systematic review of homomorphic encryption and its contributions in healthcare industry. Complex Intell. Syst. 2023, 9, 3759–3786. [Google Scholar] [CrossRef] [PubMed]
- Bozduman, H.Ç.; Afacan, E. Simulation of a homomorphic encryption system. Appl. Math. Nonlinear Sci. 2020, 5, 479–484. [Google Scholar] [CrossRef]
- Xiao, Y.; Xu, J.; Lin, Z.; Xie, Y.; Liu, R.; Yan, L.; Feng, P. Privacy Protection Anomaly Detection in Smart Grids Based on Combined PHE and TFHE Homomorphic Encryption. Electronics 2025, 14, 2386. [Google Scholar] [CrossRef]
- Zhao, S. Smart Grids Data Aggregation Method on Paillier Homomorphic Encryption. Appl. Artif. Intell. 2024, 38, 2327901. [Google Scholar] [CrossRef]
- Sousa-Dias, D.; Amyot, D.; Rahimi-Kian, A.; Bashari, M.; Mylopoulos, J. Cyclic Homomorphic Encryption Aggregation (CHEA)—A Novel Approach to Data Aggregation in the Smart Grid. Energies 2024, 17, 878. [Google Scholar] [CrossRef]
- Westrich, B. Privacy-Preserving Analytics for Smart Meter (AMI) Data: A Hybrid Approach to Comply with CPUC Privacy Regulations. arXiv 2025, arXiv:2505.08237. [Google Scholar] [CrossRef]
- Parihar, V.; Malik, A.; Bhushan, B.; Bhattacharya, P.; Shankar, A. Innovative smart grid solutions for fostering data security and effective privacy preservation. In Data Analytics for Smart Grids Applications—A Key to Smart City Development; Springer: Berlin/Heidelberg, Germany, 2023; pp. 351–380. [Google Scholar]
- Syed, D.; Refaat, S.S.; Bouhali, O. Privacy preservation of data-driven models in smart grids using homomorphic encryption. Information 2020, 11, 357. [Google Scholar] [CrossRef]
- Bakar, A.A.; Yussof, S.; Ghapar, A.A.; Sameon, S.S.; Jørgensen, B.N. A review of privacy concerns in energy-efficient smart buildings: Risks, rights, and regulations. Energies 2024, 17, 977. [Google Scholar] [CrossRef]
- Mollakuqe, E.; Parduzi, A.; Rexhepi, S.; Dimitrova, V.; Jakupi, S.; Muharremi, R.; Hamiti, M.; Qarkaxhija, J. Applications of homomorphic encryption in secure computation. Open Res. Eur. 2024, 4, 158. [Google Scholar] [CrossRef]
- Singh, P.; Masud, M.; Hossain, M.S.; Kaur, A. Blockchain and homomorphic encryption-based privacy-preserving data aggregation model in smart grid. Comput. Electr. Eng. 2021, 93, 107209. [Google Scholar] [CrossRef]
- Samuel, A.J. Optimizing energy consumption through AI and cloud analytics: Addressing data privacy and security concerns. World J. Adv. Eng. Technol. Sci. 2024, 13, 789–806. [Google Scholar] [CrossRef]
- Ali, M.; Suchismita, M.; Ali, S.S.; Choi, B.J. Privacy-Preserving Machine Learning for IoT-Integrated Smart Grids: Recent Advances, Opportunities, and Challenges. Energies 2025, 18, 2515. [Google Scholar] [CrossRef]
- Cali, U.; Gourisetti, S.N.G.; Sebastian-Cardenas, D.J.; Catak, F.O.; Lee, A.; Zeger, L.M.; Ustun, T.S.; Dynge, M.F.; Rao, S.; Ramirez, J.E. Emerging technologies for privacy preservation in energy systems. In Proceedings of the European Interdisciplinary Cybersecurity Conference, Xanthi, Greece, 5–6 June 2024; pp. 163–170. [Google Scholar]
- Desai, S.; Sabar, N.; Alhadad, R.; Mahmood, A.; Chilamkurti, N. Mitigating Consumer Privacy Breach in Smart Grid Using Obfuscation-Based Generative Adversarial Network; La Trobe: Melbourne, Australia, 2022. [Google Scholar]
- Bamberger, K.A.; Canetti, R.; Goldwasser, S.; Wexler, R.; Zimmerman, E.J. Verification dilemmas in law and the promise of zero-knowledge proofs. Berkeley Tech. LJ 2022, 37, 1. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Seth, D.; Panyam, S.; Gangrade, P. Enhancing Digital Privacy: The Application of Zero-Knowledge Proofs in Authentication Systems. Int. J. Comput. Trends Technol. 2024, 72, 34–41. [Google Scholar] [CrossRef]
- Liang, W.; Liu, Y.; Yang, C.; Xie, S.; Li, K.; Susilo, W. On identity, transaction, and smart contract privacy on permissioned and permissionless blockchain: A comprehensive survey. ACM Comput. Surv. 2024, 56, 1–35. [Google Scholar] [CrossRef]
- Ballesteros-Rodríguez, A.; Sánchez-Alonso, S.; Sicilia-Urbán, M.-Á. Enhancing Privacy and Integrity in Computing Services Provisioning Using Blockchain and zk-SNARKs. IEEE Access 2024, 12, 117970–117993. [Google Scholar] [CrossRef]
- Lodder, M. Token Based Authentication and Authorization with Zero-Knowledge Proofs for Enhancing Web API Security and Privacy. 2023. Available online: https://scholar.dsu.edu/cgi/viewcontent.cgi?article=1426&context=theses (accessed on 15 August 2025).
- Giaconi, G.; Gündüz, D.; Poor, H.V. 10 smart meter data privacy. In Advanced Data Analytics for Power Systems; Cambridge University Press: Cambridge, UK, 2021; p. 230. [Google Scholar]
- El-Hajj, M.; Oude Roelink, B.; Sarmah, D. Systematic review: Comparing zk-SNARK, zk-STARK, and bulletproof protocols for privacy-preserving authentication. Secur. Priv. 2024, 7, e401. [Google Scholar]
- Manzoor, A. Performance and Security Analysis of Distributed Ledger Technologies in IoT; Oulun Yliopisto: Oulu, Finland, 2024. [Google Scholar]
- Dehalwar, V.; Kolhe, M.L.; Deoli, S.; Jhariya, M.K. Blockchain-based trust management and authentication of devices in smart grid. Clean. Eng. Technol. 2022, 8, 100481. [Google Scholar] [CrossRef]
- Koukaras, P.; Afentoulis, K.D.; Gkaidatzis, P.A.; Mystakidis, A.; Ioannidis, D.; Vagropoulos, S.I.; Tjortjis, C. Integrating blockchain in smart grids for enhanced demand response: Challenges, strategies, and future directions. Energies 2024, 17, 1007. [Google Scholar] [CrossRef]
- Rahman, H. Securing Data Privacy in Blockchain Networks. In Blockchain Technology Applications in Knowledge Management; IGI Global Scientific Publishing: Palmdale, PA, USA, 2025; pp. 367–410. [Google Scholar]
- Chen, X.; Wang, F.; Huang, Z.; Chen, Y.-C. Smart grid aggregation billing scheme based on blockchain. J. Netw. Intell. 2022, 7, 878–893. [Google Scholar]
- Kumar, R.; Khan, A.A.; Kumar, J.; Golilarz, N.A.; Zhang, S.; Ting, Y.; Zheng, C.; Wang, W. Blockchain-federated-learning and deep learning models for covid-19 detection using ct imaging. IEEE Sens. J. 2021, 21, 16301–16314. [Google Scholar] [CrossRef] [PubMed]
- Li, W. Frontiers in Blockchain for Secure Information Sharing in Next Generation Transportation Systems. Ph.D. Thesis, University of Delaware, Newark, DE, USA, 2022. [Google Scholar]
- Rahaman, M.; Arya, V.; Orozco, S.M.; Pappachan, P. Secure multi-party computation (SMPC) protocols and privacy. In Innovations in Modern Cryptography; IGI Global: Palmdale, PA, USA, 2024; pp. 190–214. [Google Scholar]
- Zhou, I.; Tofigh, F.; Piccardi, M.; Abolhasan, M.; Franklin, D.; Lipman, J. Secure multi-party computation for machine learning: A survey. IEEE Access 2024, 12, 53881–53899. [Google Scholar] [CrossRef]
- Khan, S. Secure multi-party computation for privacy preservation in big data analytics. J. Big Data Priv. Manag. 2024, 2, 168–179. [Google Scholar]
- Fowlie, M.; Wolfram, C.; Baylis, P.; Spurlock, C.A.; Todd-Blick, A.; Cappers, P. Default effects and follow-on behaviour: Evidence from an electricity pricing program. Rev. Econ. Stud. 2021, 88, 2886–2934. [Google Scholar] [CrossRef]
- Fan, C.; Chen, M.; Wang, X.; Wang, J.; Huang, B. A review on data preprocessing techniques toward efficient and reliable knowledge discovery from building operational data. Front. Energy Res. 2021, 9, 652801. [Google Scholar] [CrossRef]
- Sasikumar, K.; Nagarajan, S. Comprehensive review and analysis of cryptography techniques in cloud computing. IEEE Access 2024, 12, 52325–52351. [Google Scholar] [CrossRef]
- Bjarghov, S.; Löschenbrand, M.; Saif, A.U.I.; Pedrero, R.A.; Pfeiffer, C.; Khadem, S.K.; Rabelhofer, M.; Revheim, F.; Farahmand, H. Developments and challenges in local electricity markets: A comprehensive review. IEEE Access 2021, 9, 58910–58943. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, J. A survey on differential privacy for unstructured data content. ACM Comput. Surv. 2022, 54, 1–28. [Google Scholar] [CrossRef]
- Hu, C.; Liu, Z.; Li, R.; Hu, P.; Xiang, T.; Han, M. Smart contract assisted privacy-preserving data aggregation and management scheme for smart grid. IEEE Trans. Dependable Secur. Comput. 2023, 21, 2145–2161. [Google Scholar] [CrossRef]
- Rai, H.M.; Shukla, K.K.; Tightiz, L.; Padmanaban, S. Enhancing data security and privacy in energy applications: Integrating IoT and blockchain technologies. Heliyon 2024, 10, e38917. [Google Scholar] [CrossRef] [PubMed]
- Gai, N.; Xue, K.; Zhu, B.; Yang, J.; Liu, J.; He, D. An efficient data aggregation scheme with local differential privacy in smart grid. Digit. Commun. Netw. 2022, 8, 333–342. [Google Scholar] [CrossRef]
- Cai, Z.; Xiong, Z.; Xu, H.; Wang, P.; Li, W.; Pan, Y. Generative adversarial networks: A survey toward private and secure applications. ACM Comput. Surv. 2021, 54, 1–38. [Google Scholar] [CrossRef]
- Chen, W.-N.; Song, D.; Ozgur, A.; Kairouz, P. Privacy amplification via compression: Achieving the optimal privacy-accuracy-communication trade-off in distributed mean estimation. Adv. Neural Inf. Process. Syst. 2023, 36, 69202–69227. [Google Scholar]
- Gough, M.B.; Santos, S.F.; AlSkaif, T.; Javadi, M.S.; Castro, R.; Catalão, J.P.S. Preserving privacy of smart meter data in a smart grid environment. IEEE Trans. Ind. Inform. 2021, 18, 707–718. [Google Scholar] [CrossRef]
- Razi, Q.; Piyush, R.; Chakrabarti, A.; Singh, A.; Hassija, V.; Chalapathi, G.S.S. Enhancing Data Privacy: A Comprehensive Survey of Privacy-Enabling Technologies. IEEE Access 2025, 13, 40354–40385. [Google Scholar] [CrossRef]
- Tran, H.-Y.; Hu, J.; Pota, H.R. Smart meter data obfuscation with a hybrid privacy-preserving data publishing scheme without a trusted third party. IEEE Internet Things J. 2022, 9, 16080–16095. [Google Scholar] [CrossRef]
- Kua, J.; Hossain, M.B.; Natgunanathan, I.; Xiang, Y. Privacy preservation in smart meters: Current status, challenges and future directions. Sensors 2023, 23, 3697. [Google Scholar] [CrossRef]
- Li, M.; Zhu, L.; Zhang, Z.; Lal, C.; Conti, M.; Alazab, M. User-defined privacy-preserving traffic monitoring against n-by-1 jamming attack. IEEE/ACM Trans. Netw. 2022, 30, 2060–2073. [Google Scholar] [CrossRef]
- Etezady, N.N. A survey of privacy metrics for smart homes. Cybersecur. Pedagog. Pract. J. 2023, 2, 26–37. [Google Scholar]
- Bhattacharjee, K. Interactive Visualization Workflows for Mitigating Analytical Uncertainty. Ph.D. Thesis, New Jersey Institute of Technology, Newark, NJ, USA, 2024. [Google Scholar]
- Sakthivel, S.; Vinotha, N. An intellectual optimization of k-anonymity model for efficient privacy preservation in cloud platform. J. Intell. Fuzzy Syst. 2023, 45, 1497–1512. [Google Scholar] [CrossRef]
- Li, S.; Schneider, M.J.; Yu, Y.; Gupta, S. Reidentification risk in panel data: Protecting for k-anonymity. Inf. Syst. Res. 2023, 34, 1066–1088. [Google Scholar] [CrossRef]
- Adewole, K.S.; Torra, V. DFTMicroagg: A dual-level anonymization algorithm for smart grid data. Int. J. Inf. Secur. 2022, 21, 1299–1321. [Google Scholar] [CrossRef]
- Avraam, D.; Wilson, R.; Butters, O.; Burton, T.; Nicolaides, C.; Jones, E.; Boyd, A.; Burton, P. Privacy preserving data visualizations. EPJ Data Sci. 2021, 10, 2. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Dou, Y.; Yang, C.; Zhang, K.; Wang, J.; Yu, P.S.; He, L.; Li, B. Adversarial attack and defense on graph data: A survey. IEEE Trans. Knowl. Data Eng. 2022, 35, 7693–7711. [Google Scholar] [CrossRef]
- Arshad, R.; Asghar, M.R. Characterisation and quantification of user privacy: Key challenges, regulations, and future directions. IEEE Commun. Surv. Tut. 2024. [Google Scholar] [CrossRef]
- Ul Hassan, M. Efficient Privacy Preservation in Smart Grid. Ph.D. Thesis, Swinburne, Hawthorn, Australia, 2021. [Google Scholar]
- Kapoor, A.; Kumar, D. Federated learning for urban sensing systems: A comprehensive survey on attacks, defences, incentive mechanisms, and applications. IEEE Commun. Surv. Tut. 2024, 27, 1293–1325. [Google Scholar] [CrossRef]
- Zhan, Y.; Zhou, L.; Wang, B.; Duan, P.; Zhang, B. Efficient function queryable and privacy preserving data aggregation scheme in smart grid. IEEE Trans. Parallel Distrib. Syst. 2022, 33, 3430–3441. [Google Scholar] [CrossRef]
- Teng, F.; Chhachhi, S.; Ge, P.; Graham, J.; Gunduz, D. Balancing Privacy and Access to Smart Meter Data; Energy Futures Lab briefing paper; Imperial College: London, UK, 2022. [Google Scholar]
- Diraco, G.; Rescio, G.; Caroppo, A.; Manni, A.; Leone, A. Human action recognition in smart living services and applications: Context awareness, data availability, personalization, and privacy. Sensors 2023, 23, 6040. [Google Scholar] [CrossRef]
- Aga, D.T.; Chintanippu, R.; Mowri, R.A.; Siddula, M. Exploring secure and private data aggregation techniques for the internet of things: A comprehensive review. Discov. Internet Things 2024, 4, 28. [Google Scholar] [CrossRef]
- Xu, H.; Seng, K.P.; Ang, L.M.; Smith, J. Decentralized and distributed learning for AIoT: A comprehensive review, emerging challenges, and opportunities. IEEE Access 2024, 12, 101016–101052. [Google Scholar] [CrossRef]
- Tong, X.; Hamzei, M.; Jafari, N. Towards Secure and Efficient Data Aggregation in Blockchain-Driven IoT Environments: A Comprehensive and Systematic Study. Trans. Emerg. Telecommun. Technol. 2025, 36, e70061. [Google Scholar]
- Behrouz, P.; Khaksari, A.; Konstantinidis, O.; Pagourtzis, A.; Spyrakou, M. Privacy-preserving methods for smart meter data-a systematization of knowledge. In Proceedings of the CP904: Institute of Engineering and Technology Conference, Singapore, October 2024; pp. 64–71. Available online: https://digital-library.theiet.org/doi/10.1049/icp.2024.4638 (accessed on 1 September 2025).
- Le, M.; Huynh-The, T.; Do-Duy, T.; Vu, T.-H.; Hwang, W.-J.; Pham, Q.-V. Applications of distributed machine learning for the internet-of-things: A comprehensive survey. IEEE Commun. Surv. Tut. 2024, 27, 1053–1100. [Google Scholar] [CrossRef]
- Yan, R.; Zheng, Y.; Yu, N.; Liang, C. Multi-smart meter data encryption scheme based on distributed differential privacy. Big Data Min. Anal. 2023, 7, 131–141. [Google Scholar] [CrossRef]
- Hasan, M.K.; Alkhalifah, A.; Islam, S.; Babiker, N.B.; Habib, A.A.; Aman, A.H.M.; Hossain, M.A. Blockchain technology on smart grid, energy trading, and big data: Security issues, challenges, and recommendations. Wirel. Commun. Mob. Comput. 2022, 2022, 9065768. [Google Scholar] [CrossRef]
- Saeed, N.; Wen, F.; Afzal, M.Z. Decentralized peer-to-peer energy trading in microgrids: Leveraging blockchain technology and smart contracts. Energy Rep. 2024, 12, 1753–1764. [Google Scholar] [CrossRef]
- Nazir, I.; Mushtaq, N.; Ishfaq, H.; Amin, W.; Maaliw, R.R.; Shi, X.; Saleem, M.A. Blockchain Enabled Reserved Pricing and Privacy Preserving Model for Peer-to-Peer Energy Trading in Smart Grid. IEEE Trans. Consum. Electron. 2025, 1. [Google Scholar] [CrossRef]
- Alshahrani, H.; Islam, N.; Syed, D.; Sulaiman, A.; Al Reshan, M.S.; Rajab, K.; Shaikh, A.; Shuja-Uddin, J.; Soomro, A. Sustainability in blockchain: A systematic literature review on scalability and power consumption issues. Energies 2023, 16, 1510. [Google Scholar] [CrossRef]
- Alsheavi, A.N.; Hawbani, A.; Othman, W.; Wang, X.; Qaid, G.; Zhao, L.; Al-Dubai, A.; Zhi, L.; Ismail, A.S.; Jhaveri, R. Iot authentication protocols: Challenges, and comparative analysis. ACM Comput. Surv. 2025, 57, 1–43. [Google Scholar] [CrossRef]
- Honari, K.; Rouhani, S.; Falak, N.E.; Liu, Y.; Li, Y.; Liang, H.; Dick, S.; Miller, J. Smart contract design in distributed energy systems: A systematic review. Energies 2023, 16, 4797. [Google Scholar] [CrossRef]
- Fatima, S.; Arshad, M.J. A Comprehensive Review of Blockchain and Machine Learning Integration for Peer-to-Peer Energy Trading in Smart Grids. IEEE Access 2025, 13, 92756–92782. [Google Scholar] [CrossRef]
- Ishtaiwi, A.; Aldweesh, A.; al-Qerem, A.; Alkasassbeh, M. AI-Powered Smart Contracts for Energy Grid Optimization: A Hybrid Intelligence Approach. In Blockchain Applications for the Energy and Utilities Industry; IGI Global Scientific Publishing: Palmdale, PA, USA, 2025; pp. 235–264. [Google Scholar]
- Sigalov, K.; Ye, X.; König, M.; Hagedorn, P.; Blum, F.; Severin, B.; Hettmer, M.; Hückinghaus, P.; Wölkerling, J.; Groß, D. Automated payment and contract management in the construction industry by integrating building information modeling and blockchain-based smart contracts. Appl. Sci. 2021, 11, 7653. [Google Scholar] [CrossRef]
- Kalbantner, J. Security and Privacy Issues of Distributed, Complex P2P Smart Grid Marketplace Systems. Ph.D. Thesis, Royal Holloway University of London, London, UK, 2024. [Google Scholar]
- Zaidi, S.Y.A.; Shah, M.A.; Khattak, H.A.; Maple, C.; Rauf, H.T.; El-Sherbeeny, A.M.; El-Meligy, M.A. An attribute-based access control for IoT using blockchain and smart contracts. Sustainability 2021, 13, 10556. [Google Scholar] [CrossRef]
- AlMarshoud, M.; Sabir Kiraz, M.; Al-Bayatti, A.H. Security, privacy, and decentralized trust management in VANETs: A review of current research and future directions. ACM Comput. Surv. 2024, 56, 1–39. [Google Scholar]
- Rouhani, S.; Belchior, R.; Cruz, R.S.; Deters, R. Distributed attribute-based access control system using permissioned blockchain. World Wide Web 2021, 24, 1617–1644. [Google Scholar] [CrossRef]
- Saidi, H.; Labraoui, N.; Ari, A.A.A.; Maglaras, L.A.; Emati, J.H.M. DSMAC: Privacy-aware Decentralized Self-Management of data Access Control based on blockchain for health data. IEEE Access 2022, 10, 101011–101028. [Google Scholar] [CrossRef]
- Lankadasu, N.V.Y.; Pesarlanka, D.B.; Sharma, A.; Sharma, S. Security Aspects of Blockchain Technology. In Driving Transformative Technology Trends with Cloud Computing; IGI Global: Palmdale, PA, USA, 2024; pp. 259–277. [Google Scholar]
- Babu, S.B.; Jothi, K.R. A secure framework for privacy-preserving analytics in healthcare records using zero-knowledge proofs and blockchain in multi-tenant cloud environments. IEEE Access 2024, 13, 8439–8455. [Google Scholar] [CrossRef]
- Alladi, T.; Chamola, V.; Rodrigues, J.J.; Kozlov, S.A. Blockchain in smart grids: A review on different use cases. Sensors 2019, 19, 4862. [Google Scholar] [CrossRef]
- Uddin, S.S.; Joysoyal, R.; Sarker, S.K.; Muyeen, S.M.; Ali, M.F.; Hasan, M.M.; Abhi, S.H.; Islam, R.; Ahamed, H.; Islam, M.; et al. Next-generation blockchain enabled smart grid: Conceptual framework, key technologies and industry practices review. Energy AI 2023, 12, 100228. [Google Scholar] [CrossRef]
- Luo, H.; Yu, H.; Luo, J. PRAFT and RPBFT: A class of blockchain consensus algorithm and their applications in electric vehicles charging scenarios for V2G networks. Internet Things Cyber-Phys. Syst. 2023, 3, 61–70. [Google Scholar]
- Su, K.; Yu, Y.; Zhang, J. Blockchain-based smart grid power trading technology. J. Eng. Appl. Sci. 2024, 71, 220. [Google Scholar] [CrossRef]
- Chikezie, U.; Karacolak, T.; Do Prado, J.C. Examining the applicability of blockchain to the smart grid using proof-of-authority consensus. In Proceedings of the 2021 IEEE 9th International Conference on Smart Energy Grid Engineering (SEGE), Oshawa, ON, Canada, 11–13 August 2021; pp. 19–25. [Google Scholar]
- Khan, A.A.; Dhabi, S.; Yang, J.; Alhakami, W.; Bourouis, S.; Yee, L. B-LPoET: A middleware lightweight Proof-of-Elapsed Time (PoET) for efficient distributed transaction execution and security on Blockchain using multithreading technology. Comput. Electr. Eng. 2024, 118, 109343. [Google Scholar] [CrossRef]
- Jain, A.K.; Gupta, N.; Gupta, B.B. A survey on scalable consensus algorithms for blockchain technology. Cyber Secur. Appl. 2025, 3, 100065. [Google Scholar] [CrossRef]
- Zhang, X.; You, L.; Hu, G. An efficient and robust multidimensional data aggregation scheme for smart grid based on blockchain. IEEE Trans. Netw. Serv. Manag. 2022, 19, 3949–3959. [Google Scholar] [CrossRef]
- Akiladevi, R.; Sardha, S.; Shruthi, R. Tokenization of energy assets: A multichain blockchain approach. In Proceedings of the 5th International Conference on Mobile Computing and Sustainable Informatics (ICMCSI), Lalitpur, Nepal, 18–19 January 2024; pp. 702–709. [Google Scholar]
- Taherdoost, H. Blockchain integration and its impact on renewable energy. Computers 2024, 13, 107. [Google Scholar] [CrossRef]
- Hu, C.; Cheng, X.; Tian, Z.; Yu, J.; Lv, W. Achieving privacy preservation and billing via delayed information release. IEEE/ACM Trans. Netw. 2021, 29, 1376–1390. [Google Scholar] [CrossRef]
- Karaduman, Ö.; Gülhas, G. Blockchain-Enabled Supply Chain Management: A Review of Security, Traceability, and Data Integrity Amid the Evolving Systemic Demand. Appl. Sci. 2025, 15, 5168. [Google Scholar] [CrossRef]
- Khemaissia, R. Using Blockchain to Protect Personal Data. Ph.D. Thesis, Université Echahid Cheikh Larbi-Tebessi-Tébessa, Tébessa, Algeria, 2025. [Google Scholar]
- An, Q.; Jiang, F.; Dong, C.; Pal, S.; Li, J.; Neiat, A.G.; Yeoh, W. A blockchain-powered secure architecture for cyber marketplaces of electric vehicles. IEEE Trans. Ind. Appl. 2025, 61, 4198–4213. [Google Scholar] [CrossRef]
- Fekri, M.N.; Grolinger, K.; Mir, S. Distributed load forecasting using smart meter data: Federated learning with Recurrent Neural Networks. Int. J. Electr. Power Energy Syst. 2022, 137, 107669. [Google Scholar] [CrossRef]
- Su, Z.; Wang, Y.; Luan, T.H.; Zhang, N.; Li, F.; Chen, T.; Cao, H. Secure and efficient federated learning for smart grid with edge-cloud collaboration. IEEE Trans. Ind. Inform. 2021, 18, 1333–1344. [Google Scholar] [CrossRef]
- Alshehri, A.; Badr, M.M.; Baza, M.; Alshahrani, H. Deep anomaly detection framework utilizing federated learning for electricity theft zero-day cyberattacks. Sensors 2024, 24, 3236. [Google Scholar] [CrossRef]
- Santosh, S.H.L.; Ravi, R.M. A Enhancing Privacy in IoT Systems with Federated Learning: A Multi-Agent Solution for Smart City Networks. SGS-Eng. Sci. 2025, 1. Available online: https://spast.org/techrep/article/view/5282 (accessed on 15 August 2025).
- Qu, L.; Zhou, Y.; Liang, P.P.; Xia, Y.; Wang, F.; Adeli, E.; Fei-Fei, L.; Rubin, D. Rethinking architecture design for tackling data heterogeneity in federated learning. In Proceeding of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 10061–10071. [Google Scholar]
- Khan, A.R. Federated learning for next generation intelligent applications. Ph.D. Thesis, University of Glasgow, Glasgow, UK, 2025. [Google Scholar]
- Zhang, C.; Li, S. State-of-the-art approaches to enhancing privacy preservation of machine learning datasets: A survey. arXiv 2024, arXiv:2404.16847. [Google Scholar]
- Mohammadi, M.; Mohammadi, A. Empowering distributed solutions in renewable energy systems and grid optimization. In Distributed Machine Learning and Computing: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2024; pp. 141–155. [Google Scholar]
- Adewole, K.S.; Torra, V. Privacy Protection of Synthetic Smart Grid Data Simulated via Generative Adversarial Networks. In Proceedings of the 20th International Conference on Security and Cryptography (SECRYPT), Rome, Italy, 10–12 July 2023; pp. 279–286. [Google Scholar]
- Takiddin, A.; Ismail, M.; Serpedin, E. Robust data-driven detection of electricity theft adversarial evasion attacks in smart grids. IEEE Trans. Smart Grid 2022, 14, 663–676. [Google Scholar] [CrossRef]
- Abdi, N.; Albaseer, A.; Abdallah, M. The role of deep learning in advancing proactive cybersecurity measures for smart grid networks: A survey. IEEE Internet Things J. 2024, 11, 16398–16421. [Google Scholar] [CrossRef]
- Pelekis, S.; Koutroubas, T.; Blika, A.; Berdelis, A.; Karakolis, E.; Ntanos, C.; Spiliotis, E.; Askounis, D. Adversarial machine learning: A review of methods, tools, and critical industry sectors. Artif. Intell. Rev. 2025, 58, 226. [Google Scholar] [CrossRef]
- Ramirez, J.E.; Sebastian, C.; David, J. A Computational Review of Privacy-Preserving Mechanisms for the Smart Grid; Pacific Northwest National Laboratory (PNNL): Richland, WA, USA, 2024. Available online: https://www.pnnl.gov/main/publications/external/technical_reports/PNNL-36774.pdf (accessed on 1 September 2025).
- Zhang, J. Efficient Zero-Knowledge Proofs: Theory and Practice. Ph.D. Thesis, UC Berkeley, Berkeley, CA, USA, 2023. Available online: https://www2.eecs.berkeley.edu/Pubs/TechRpts/2025/EECS-2025-20.pdf (accessed on 1 September 2025).
- Egunjobi, O.O.; Gomes, A.; Egwim, C.N.; Morais, H. A systematic review of blockchain for energy applications. E-Prime Electr. Eng. Electron. Energy 2024, 9, 100751. [Google Scholar] [CrossRef]
- Huang, Q.; Amin, W.; Umer, K.; Gooi, H.B.; Eddy, F.Y.S.; Afzal, M.; Shahzadi, M.; Khan, A.A.; Ahmad, S.A. A review of transactive energy systems: Concept and implementation. Energy Rep. 2021, 7, 7804–7824. [Google Scholar] [CrossRef]
- Asad, M.; Shaukat, S.; Hu, D.; Wang, Z.; Javanmardi, E.; Nakazato, J.; Tsukada, M. Limitations and future aspects of communication costs in federated learning: A survey. Sensors 2023, 23, 7358. [Google Scholar] [CrossRef]
- Zhang, J.; Shi, C. Efficient Secure Data Aggregation for Real-Time Smart Grid Monitoring: A Lightweight Privacy-Preserving Approach. IEEE Trans. Comput. Soc. Syst. 2025, 12, 1563–1573. [Google Scholar] [CrossRef]
- Yang, R.; Gao, H.; Si, F.; Wang, J. Advancing User Privacy in Virtual Power Plants: A Novel Zero-Knowledge Proof-Based Distributed Attribute Encryption Approach. Electronics 2024, 13, 1283. [Google Scholar] [CrossRef]
- Hu, H.; Hsu, C.; Cui, J.; Harn, L.; Hou, Q.; Li, L. Advancing User Privacy in Virtual Power Plants: Provably secure and lightweight authentication protocol using PUF and blockchain for smart grids. J. Supercomput. 2025, 8, 949. [Google Scholar] [CrossRef]
- Soto, E.A.; Bosman, L.B.; Wollega, E.; Leon-Salas, W.D. Peer-to-peer energy trading: A review of the literature. Appl. Energy 2021, 283, 116268. [Google Scholar] [CrossRef]
- Le, H.T.; Sanseverino, E.R.; Nguyen, D.-Q.; Di Silvestre, M.L.; Favuzza, S.; Pham, M.-H. Critical assessment of feed-in tariffs and solar photovoltaic development in Vietnam. Energies 2022, 15, 556. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, J. Realizing the transactive energy future with local energy market: An overview. Curr. Sustain. Renew. Energy Rep. 2022, 9, 1–14. [Google Scholar] [CrossRef]
- Munoz, F.D.; Wogrin, S.; Oren, S.S.; Hobbs, B.F. Economic inefficiencies of cost-based electricity market designs. Energy J. 2018, 39, 51–68. [Google Scholar] [CrossRef]
- Wei, W.; Liu, F.; Mei, S. Energy pricing and dispatch for smart grid retailers under demand response and market price uncertainty. IEEE Trans. Smart Grid 2014, 6, 1364–1374. [Google Scholar] [CrossRef]
- Bouloumpasis, I.; Steen, D. Congestion management using local flexibility markets: Recent development and challenges. In Proceedings of the 2019 IEEE PES Innovative Smart Grid Technologies Europe (ISGT-Europe), Bucharest, Romania, 29 September–2 October 2019; pp. 1–5. [Google Scholar]
- Biegel, B.; Andersen, P.; Stoustrup, J.; Bendtsen, J. Congestion management in a smart grid via shadow prices. IFAC Proc. Vol. 2012, 45, 518–523. [Google Scholar] [CrossRef]
- Armstrong, M. Price discrimination. In The New Palgrave Dictionary of Economics; Macmillan: London, UK, 2008. [Google Scholar]
- Willems, B.; Yueting, Y. Bidding and Investment in Wholesale Electricity Markets: Discriminatory Versus Uniform-Price Auctions. TSE Working Paper 2023. Available online: https://www.tse-fr.eu/sites/default/files/TSE/documents/doc/wp/2023/wp_tse_1462.pdf (accessed on 15 August 2025).
- Jaskowski, P.; Biruk, S.; Czarnigowska, A. Strategy for mark-up definition in competitive tenders for construction work. In Proceedings of the IOP Conference Series Materials Science and Engineering, Bristol, UK, 19–22 August 2019; p. 112060. [Google Scholar]
- Beiranvand, N. The Role of Algorithmic Pricing in Modern Markets: Price Discrimination, Fairness, and Collusion. 2023. Available online: https://unitesi.unipv.it/bitstream/20.500.14239/27269/1/Collusion%20and%20Price%20Discrimination%20with%20Algorithmic%20Pricing%20Efficiency%20and%20Fairness%20Issue.pdf (accessed on 15 August 2025).
- Damiano, E.; Li, H. Price discrimination and efficient matching. Econ. Theory 2007, 30, 243–263. [Google Scholar] [CrossRef]
- Pollitt, M.G. Locational Marginal Prices (LMPs) for Electricity in Europe? The Untold Story. 2023. [Google Scholar]
- Li, F. Continuous locational marginal pricing (CLMP). IEEE Trans. Power Syst. 2007, 22, 1638–1646. [Google Scholar] [CrossRef]
- Tesfatsion, L. Locational marginal pricing: A fundamental reconsideration. IEEE Open Access J. Power Energy 2024, 11, 104–116. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, G.; McCalley, J.D.; Zheng, T.; Litvinov, E. Risk-based locational marginal pricing and congestion management. IEEE Trans. Power Syst. 2014, 29, 2518–2528. [Google Scholar] [CrossRef]
- Tan, Z.; Cheng, T.; Liu, Y.; Zhong, H. Extensions of the locational marginal price theory in evolving power systems: A review. IET Gener. Transm. Distrib. 2022, 16, 1277–1291. [Google Scholar] [CrossRef]
- Liyanapathirane, U.; Khorasany, M.; Razzaghi, R. Optimization of economic efficiency in distribution grids using distribution locational marginal pricing. IEEE Access 2021, 9, 60123–60135. [Google Scholar] [CrossRef]
- Chen, B. Real-Time Electricity Market Pricing Methods Incorporating Power System Frequency Dynamics. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 2025. [Google Scholar]
- Tang, W.; Shi, L.; Xu, P.; Luo, H.; Li, L. Assessing the Influencing Factors of Locational Marginal Price in Day-Ahead Hydro-Thermal Power Spot Market. IEEE Access 2025, 13, 47055–47067. [Google Scholar] [CrossRef]
- Gill, S.; MacIver, C.; Bell, K. Exploring Market Change in the GB Electricity System: The Potential Impact of Locational Marginal Pricing. 2023. Available online: https://pureportal.strath.ac.uk/en/publications/exploring-market-change-in-the-gb-electricity-system-the-potentia-2 (accessed on 15 August 2025).
- Arora, M.; Vishwanath, G.M.; Sharma, A.; Chilamkurti, N. A novel congestion based pricing model for prosumer-centric smart grid systems. Electr. Power Syst. Res. 2025, 247, 111732. [Google Scholar] [CrossRef]
- Niu, T.; Li, H.; Chen, G.; Fang, S.; Liao, R. Pricing and Distributed Scheduling Framework of Multi-Microgrid System Based on Coupled Electricity-Carbon Market. J. Mod. Power Syst. Clean Energy 2024, 13, 1026–1039. [Google Scholar] [CrossRef]
- Syed, A.A.; Qi, H.; Waqas, A.; Muhammad, A.; Fazal, H.; Muhammad Husnain, H. A fair and effective approach to managing distributed energy resources through peer-to-peer energy trading with load prioritization among smart homes. Energy Rep. 2023, 10, 4402–4419. [Google Scholar]
- Alsolami, M.; Alferidi, A.; Lami, B.; Slama, S.B. Peer-to-peer trading in smart grid with demand response and grid outage using deep reinforcement learning. Ain Shams Eng. J. 2023, 14, 102466. [Google Scholar] [CrossRef]
- Park, S.; Lee, J.; Bae, S.; Hwang, G.; Choi, J.K. Contribution-based energy-trading mechanism in microgrids for future smart grid: A game theoretic approach. IEEE Trans. Ind. Electron. 2016, 63, 4255–4265. [Google Scholar] [CrossRef]
- Amin, W.; Ahmad, F.; Umer, K.; Khawaja, A.H.; Afzal, M.; Ahmad, S.A.; Chaitusaney, S. An effective pricing mechanism for electricity trading considering customer preference and reserved price in direct P2P electricity market under uncertainty in grid supply. IEEE Access 2022, 10, 96197–96211. [Google Scholar] [CrossRef]
- Umar, A.; Kumar, D.; Ghose, T. A decentralized energy management system inculcating supply–demand ratio (SDR) and miners’ stake through blockchain smart contract for community microgrid operation. IEEE J. Emerg. Sel. Top. Ind. Electron. 2023, 5, 369–380. [Google Scholar] [CrossRef]
- Oprea, S.-V.; Bâra, A. An adaptive pricing mechanism framework for post-auction in the local electricity markets integrating a higher share of renewables. Renew. Energy 2025, 256, 124056. [Google Scholar] [CrossRef]
- Caragiannis, I.; Jiang, Z.; Skoulakis, S. Rethinking Pricing in Energy Markets: Pay-as-Bid vs Pay-as-Clear. arXiv 2025, arXiv:2507.06035. [Google Scholar]
- Akbari-Dibavar, A.; Mohammadi-Ivatloo, B.; Zare, K. Electricity market pricing: Uniform pricing vs. pay-as-bid pricing. In Electricity Markets: New Players and Pricing Uncertainties; Springer: Berlin/Heidelberg, Germany, 2020; pp. 19–35. [Google Scholar]
- Shahinzadeh, H.; Nasrabadi, M.N.; Nafisi, H.; Moazzami, M.; Jurado, F.; Abdelaziz, A.Y. Enhancing Transparency in the Peer-to-Peer Transactive Energy Market: Smart Contract Monitoring in Bilateral Negotiations with the Ethereum Platform. In Proceedings of the 9th International Conference Technology and Energy Management (ICTEM), Hoes Lane, Piscataway, NJ, USA, 14–15 February 2024; pp. 1–8. [Google Scholar]
- Cretan, A.-G. Leveraging AI to revolutionize business processes. Chall. Knowl. Soc. 2025, 504–517. [Google Scholar]
- Atanasov, A. The Economics of Water Conflict: Transaction Costs, Bargaining Failure, and Sustainable Cooperation in the Nile Dispute. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=5371192 (accessed on 15 August 2025).
- Hassan, F.; Abinader, L.G.; Kavanagh, M.M. Law and power in pandemic negotiations: Policymaking via contract in South Africa’s dealings with COVID-19 vaccine companies. Glob. Public Health 2025, 20, 2537688. [Google Scholar] [CrossRef] [PubMed]
- Talebi, E.; Mehdinejad, M.; Mohammadi-Ivatloo, B.; Abapour, M.; Tohidi, S. A robust framework for peer-to-peer energy trading with transmission costs consideration: A fuzzy possibilistic programming model. Appl. Energy 2025, 398, 126379. [Google Scholar] [CrossRef]
- van de Water, P.R.; Doumen, S.C.; Campfens, J.K.E.K.; Wieczorek, A.J.; Nguyen, P.H. An implementation pathway for price formation mechanisms in local electricity markets. Energy Rep. 2025, 13, 6384–6396. [Google Scholar] [CrossRef]
- Wang, Y.; Li, T.; Li, Y.; Shao, N.; Wang, Y. Spot market clearing model and flexibility premium assessment method considering flexible regulation of virtual power plants. IEEE Access 2024, 12, 53855–53870. [Google Scholar] [CrossRef]
- Jiang, Y.; Sioshansi, R. Optimal and incentive-compatible scheduling of flexible generation in an electricity market. Energy J. 2024, 01956574251340293. [Google Scholar] [CrossRef]
- Taslimi, M.; Khosravi, A. Flexibility and profitability in power-to-methanol plants: Integrating storage solutions and reserve market participation. Energy 2025, 327, 136438. [Google Scholar] [CrossRef]
- Xu, Y.; Bai, Y.; Zhang, Y.; Wang, P.; Wang, X.; Guo, J.; Xie, K.; Zhao, R. Analyzing the Impact of Strategic Bidding on the Reserve Capacity via a Bi-Level Model. arXiv 2025, arXiv:2506.20493. [Google Scholar] [CrossRef]
- Johnson, A.; Fraser, A.; York, D. Enabling Industrial Demand Flexibility: Aligning Industrial Consumer and Grid Benefits; White Paper; ACEEE: Washington, DC, USA, 2024. [Google Scholar]
- Cramton, P. Competitive bidding behavior in uniform-price auction markets. In Proceedings of the 37th Annual Hawaii International Conference on System Sciences Proceeding, Big Island, HI, USA, 5–8 January 2004; p. 11. [Google Scholar]
- Vlachos, A.G.; Biskas, P.N. Balancing supply and demand under mixed pricing rules in multi-area electricity markets. IEEE Trans. Power Syst. 2010, 26, 1444–1453. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Y.; Yang, T. Iterative auction for P2P renewable energy trading with dynamic energy storage management. Energies 2020, 13, 4963. [Google Scholar] [CrossRef]
- Amin, W.; Huang, Q.; Afzal, M.; Khan, A.A.; Zhang, Z.; Umer, K.; Ahmed, S.A. Consumers’ preference based optimal price determination model for P2P energy trading. Electr. Power Syst. Res. 2020, 187, 106488. [Google Scholar] [CrossRef]
- Xu, S.; Zhao, Y.; Li, Y.; Zhou, Y. An iterative uniform-price auction mechanism for peer-to-peer energy trading in a community microgrid. Appl. Energy 2021, 298, 117088. [Google Scholar] [CrossRef]
- Xu, S.-S. Pion superfluid phase transition at finite isospin chemical potential. Eur. Phys. J. A 2021, 57, 298. [Google Scholar] [CrossRef]
- Tushar, W.; Chai, B.; Yuen, C.; Huang, S.; Smith, D.B.; Poor, H.V.; Yang, Z. Energy storage sharing in smart grid: A modified auction-based approach. IEEE Trans. Smart Grid 2016, 7, 1462–1475. [Google Scholar] [CrossRef]
- Doan, H.T.; Cho, J.; Kim, D. Peer-to-peer energy trading in smart grid through blockchain: A double auction-based game theoretic approach. IEEE Access 2021, 9, 49206–49218. [Google Scholar] [CrossRef]
- Angaphiwatchawal, P.; Sompoh, C.; Chaitusaney, S. A Multi-k double auction pricing mechanism for peer-to-peer energy trading market of prosumers. In Proceedings of the 2021 18th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Chiang Mai, Thailand, 19–22 May 2021. [Google Scholar]
- Zhang, Z.; Tang, H.; Ren, J.; Huang, Q.; Lee, W.-J. Strategic prosumers-based peer-to-peer energy market design for community microgrids. IEEE Trans. Ind. Appl. 2021, 57, 2048–2057. [Google Scholar] [CrossRef]
- Salehi, Z.; Chen, Y.; Petersen, I.R.; Shi, G.; Callaway, D.S.; Ratnam, E.L. Peer-to-Peer Energy Markets with Uniform Pricing: A Dynamic Operating Envelope Approach. arXiv 2025, arXiv:2506.19328. [Google Scholar]
- Kwag, K.; Shin, H.; Oh, H.; Yun, H.; Yoon, H.; Kim, W. Quantifying the impact and policy implications of transitioning to zonal and nodal pricing in the electricity market: A South Korean case study. Appl. Sci. 2025, 15, 716. [Google Scholar] [CrossRef]
- Hu, J.; Mitchell, J.E.; Pang, J.-S.; Yu, B. On linear programs with linear complementarity constraints. J. Glob. Optim. 2012, 53, 29–51. [Google Scholar] [CrossRef]
- Fernández-Blanco, R.; Arroyo, J.M.; Alguacil, N. Consumer payment minimization under uniform pricing: A mixed-integer linear programming approach. Appl. Energy 2014, 114, 676–686. [Google Scholar] [CrossRef]
- Tierney, S.; Schatzki, T.; Mukerji, R. Uniform-Pricing versus Pay-as-bid in Wholesale Electricity Markets. Analysis Group ISO New York. 2008, 24p. Available online: https://g-city.sass.org.cn/_upload/article/files/7f/9e/6effc73d4950949afcbca0df3872/0dcf8fef-1149-428d-adb8-e0c8b0f1e18d.pdf (accessed on 15 August 2025).
- Paudel, A.; Beng, G.H. A hierarchical peer-to-peer energy trading in community microgrid distribution systems. In Proceedings of the 2018 IEEE Power Energy Soc. Gen. Meet. (PESGM), Portland, OR, USA, 5–10 August 2018; IEEE: New York, NY, USA, 2018; pp. 1–5. [Google Scholar]
- Rasheed, M.B.; Qureshi, M.A.; Javaid, N.; Alquthami, T. Dynamic pricing mechanism with the integration of renewable energy source in smart grid. IEEE Access 2020, 8, 16876–16892. [Google Scholar] [CrossRef]
- Fabra, N. Market power and price discrimination: Learning from changes in renewables regulation. EnergyEcoLab 2020. Available online: https://repository.graduateinstitute.ch/record/319894?v=pdf (accessed on 15 August 2025).
- El Gohary, F.; Nyström, S.; Reitsma, L.; Bartusch, C. Identifying challenges in engaging users to increase self-consumption of electricity in microgrids. Energies 2021, 14, 1257. [Google Scholar] [CrossRef]
- Malik, S. Peer-to-Peer Energy Trading in Microgrids: A Game-Theoretic Approach. Ph.D. Thesis, University of Galway, Galway, Ireland, 2024; pp. 1–144. [Google Scholar]
- Tushar, W.; Yuen, C.; Smith, D.B.; Poor, H.V. Price discrimination for energy trading in smart grid: A game theoretic approach. IEEE Trans. Smart Grid 2016, 8, 1790–1801. [Google Scholar] [CrossRef]
- Tushar, W.; Yuen, C.; Chai, B.; Smith, D.B.; Poor, H.V. Feasibility of using discriminate pricing schemes for energy trading in smart grid. In Proceedings of the IEEE Global Communication Conference, Austin, TX, USA, 8–12 December 2014; pp. 3138–3144. [Google Scholar]
- PVcase. Why Locational Marginal Pricing (LMP) Data Is Essential for Solar Development. 2023. Available online: https://pvcase.com/blog/why-locational-marginal-pricing-lmp-data-is-essential-for-solar-development (accessed on 31 July 2025).
- SlideServe. Locational Marginal Pricing Overview. 2023. Available online: https://www.slideserve.com/shina/locational-marginal-pricing-overview (accessed on 31 July 2025).
- Thomaßen, G.; Fuhrmanek, A. Where to build renewables in Europe? The benefits of locational auction design. Energy Econ. 2025, 147, 108579. [Google Scholar] [CrossRef]
- Hausman, E.; Fagan, R.; White, D.; Takahashi, K.; Napoleon, A.; Economics, S.E. LMP Electricity Markets: Market Operations, Market Power; Synapse Energy Economics: Cambridge, MA, USA, 2006. [Google Scholar]
- Liu, H.; Tesfatsion, L.; Chowdhury, A. Derivation of Locational Marginal Prices for Restructured Wholesale Power Markets. 2009. Available online: https://faculty.sites.iastate.edu/tesfatsi/archive/tesfatsi/DerivationLMP.HLLTAC.pdf (accessed on 15 August 2025).
- Wu, J.; Guo, X.; Zhu, Q.; Guo, J.; Han, Y.; Zhong, L.; Liu, S. Threshold effects and supply-demand ratios should be considered in the mechanisms driving ecosystem services. Ecol. Indic. 2022, 142, 109281. [Google Scholar] [CrossRef]
- Alfaverh, F.; Denai, M.; Sun, Y. A dynamic peer-to-peer electricity market model for a community microgrid with price-based demand response. IEEE Trans. Smart Grid 2023, 14, 3976–3991. [Google Scholar] [CrossRef]
- Crespo-Vazquez, J.L.; AlSkaif, T.; Gonzalez-Rueda, A.M.; Gibescu, M. A community-based energy market design using decentralized decision-making under uncertainty. IEEE Trans. Smart Grid 2020, 12, 1782–1793. [Google Scholar] [CrossRef]
- Kim, S.-J.; Giannakis, G.B. An online convex optimization approach to real-time energy pricing for demand response. IEEE Trans. Smart Grid 2016, 8, 2784–2793. [Google Scholar] [CrossRef]
- El Rahi, G.; Etesami, S.R.; Saad, W.; Mandayam, N.B.; Poor, H.V. Managing price uncertainty in prosumer-centric energy trading: A prospect-theoretic Stackelberg game approach. IEEE Trans. Smart Grid 2017, 10, 702–713. [Google Scholar] [CrossRef]
- Kim, J.-Y.; Brünner, T.; Skiera, B.; Natter, M. A comparison of different pay-per-bid auction formats. Int. J. Res. Mark. 2014, 31, 368–379. [Google Scholar] [CrossRef]
- Galgana, R.; Golrezaei, N. Learning in repeated multiunit pay-as-bid auctions. Manuf. Serv. Oper. Manag. 2025, 27, 200–229. [Google Scholar] [CrossRef]
- Carlos Carbajal, J.; Dharanan, G.V.A. GVA, Pay-as-Bid Auctions with Budget Constrained Bidders. 2025. Available online: https://www.isid.ac.in/~acegd/acegd2024/papers/GVADharanan.pdf (accessed on 15 August 2025).
- Song, Y.; Chu, Y.; Yoon, Y.; Jin, Y. Virtual Power Plant Bidding Strategies in Pay-as-Bid and Pay-as-Clear Markets: Analysis of Imbalance Penalties and Market Operations. Energies 2025, 18, 1383. [Google Scholar] [CrossRef]
- Federico, G.; Rahman, D. Bidding in an electricity pay-as-bid auction. J. Regul. Econ. 2003, 24, 175–211. [Google Scholar] [CrossRef]
- Rothkopf, M.H.; Teisberg, T.J.; Kahn, E.P. Why are Vickrey auctions rare? J. Polit. Econ. 1990, 98, 94–109. [Google Scholar] [CrossRef]
- Evans, J.R. Determining Consumer Perceptions of and Willingness to Pay for Appalachian Grass-Fed Beef: An Experimental Economics Approach; West Virginia University: Morgantown, MV, USA, 2007. [Google Scholar]
- Yassine, A.; Hossain, M.S.; Muhammad, G.; Guizani, M. Double auction mechanisms for dynamic autonomous electric vehicles energy trading. IEEE Trans. Veh. Technol. 2019, 68, 7466–7476. [Google Scholar] [CrossRef]
- Sutterer, P.; Waldherr, S.; Bichler, M. Are truthful bidders paying too much? Efficiency and revenue in display ad auctions. ACM Trans. Manag. Inf. Syst. (TMIS) 2019, 10, 1–18. [Google Scholar] [CrossRef]
- Potfer, M.; Baudry, D.; Richard, H.; Perchet, V.; Wan, C. Improved learning rates in multi-unit uniform price auctions. Adv. Neural Inf. Process. Syst. 2024, 37, 130237–130264. [Google Scholar]
- Lamp, S.; Samano, M.; Tiedemann, S. Firms’ Bidding Behavior in a New Market: Evidence from Renewable Energy Auctions. Avail. SSRN 4780866. 2024. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4780866 (accessed on 15 August 2025).
- Bertsimas, D.; Koulouras, A.G. Adaptive Pricing in Unit Commitment Under Load and Capacity Uncertainty. arXiv 2023, arXiv:2309.08162. [Google Scholar] [CrossRef]
- Just, S.; Weber, C. Pricing of reserves: Valuing system reserve capacity against spot prices in electricity markets. Energy Econ. 2008, 30, 3198–3221. [Google Scholar] [CrossRef]
- Hummon, M.; Denholm, P.; Jorgenson, J.; Palchak, D.; Kirby, B.; Ma, O. Fundamental Drivers of the Cost and Price of Operating Reserves; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2013. [Google Scholar]
- Rosen, C.; Madlener, R. An auction design for local reserve energy markets. Decis. Support Syst. 2013, 56, 168–179. [Google Scholar] [CrossRef]
- Cramton, P. How best to auction natural resources. In The Taxation of Petroleum and Minerals; Routledge: London, UK, 2010; pp. 305–332. [Google Scholar]
- Mehrtash, M.; Hobbs, B.F.; Ela, E. Reserve and energy scarcity pricing in United States power markets: A comparative review of principles and practices. Renew. Sustain. Energy Rev. 2023, 183, 113465. [Google Scholar] [CrossRef]
- Nazir, I.; Mushtaq, N.; Ziafat, B.; Fareed, M.F.; Amin, W. A Reserved Pricing Mechanism for Nano/Peco Smart Grid Peer-to-Peer Energy Trading. In Proceedings of the 3rd International Conference Emerging Trends Electrical, Control, and Telecommunication Engineering (ETECTE), Lahore, Pakistan, 26–27 November 2024; pp. 1–5. [Google Scholar]
- Deman, L.; Siddiqui, A.S.; Clastres, C.; Boucher, Q. Day-ahead and reserve prices in a renewable-based power system: Adapting electricity-market design for energy storage. Energy J. 2025, 46, 67–98. [Google Scholar] [CrossRef]
- Ribeiro, L.; Street, A.; Arroyo, J.M.; Moreno, R. A Causation-Based Framework for Pricing and Cost Allocation of Energy, Reserves, and Transmission in Modern Power Systems. arXiv 2025, arXiv:2505.24159. [Google Scholar] [CrossRef]
- Qi, N.; Pinson, P.; Almassalkhi, M.R.; Cheng, L.; Zhuang, Y. Chance-constrained generic energy storage operations under decision-dependent uncertainty. IEEE Trans. Sustain. Energy 2023, 14, 2234–2248. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, S.; Zhou, H.; Zhu, M.; Zhang, Y. A two-stage optimization strategy for VPP trading in multi-market considering setting method and marginal revenue and expenditure of standby capacity. J. Renew. Sustain. Energy 2025, 17. [Google Scholar] [CrossRef]
- Chow, Y.-F.; McAleer, M.; Sequeira, J. Pricing of forward and futures contracts. J. Econ. Surv. 2000, 14, 215–253. [Google Scholar] [CrossRef]
- Injadat, E.M.M. Futures and forwards contracts from perspective of Islamic law. J. Econ. Polit. Econ. 2014, 1, 241–252. [Google Scholar]
- Landman, D.J. Real Option Analysis of Primary Rail Contracts in Grain Shipping. Master’s Thesis, North Dakota State University, Fargo, ND, USA, 2017. [Google Scholar]
- Munné-Collado, Í.; Bullich-Massagué, E.; Aragüés-Peñalba, M.; Olivella-Rosell, P. Local and micro power markets. In Micro and Local Power Markets; Wiley: Hoboken, NJ, USA, 2019; pp. 37–96. [Google Scholar]
- Schlecht, I.; Maurer, C.; Hirth, L. Financial contracts for differences: The problems with conventional CfDs in electricity markets and how forward contracts can help solve them. Energy Policy 2024, 186, 113981. [Google Scholar] [CrossRef]
- Ordoñez, C.C.; Organero, M.M.; Ramirez-Gonzalez, G.; Corrales, J.C. Smart Contracts as a Tool to Support the Challenges of Buying and Selling Coffee Futures Contracts in Colombia. Agriculture 2024, 14, 845. [Google Scholar] [CrossRef]
- Ogundu, P.G. The Strategic Implications of Financial Derivatives in Hedging Corporate Exposure to Global Economic volatility. World J. Adv. Res. Rev. 2025, 25, 1218–1234. [Google Scholar] [CrossRef]
- Dahlberg, J.; Rehula, L. The Effect of Hedging with Derivatives on Firm Performance: Evidence from European Energy Firms During the Global Energy Crisis in 2021–2023. 2024. Available online: https://www.diva-portal.org/smash/get/diva2:1877521/FULLTEXT01.pdf (accessed on 15 August 2025).
- Mohandes, N.; Bayhan, S.; Sanfilippo, A.; Abu-Rub, H. Peer-to-peer trade and the sharing economy at distribution level: A review of the literature. IEEE Access 2023, 11, 122842–122858. [Google Scholar] [CrossRef]
- Ahmadian-Yazdi, F.; Sokhanvar, A.; Roudari, S.; Tiwari, A.K. Dynamics of the relationship between stock markets and exchange rates during quantitative easing and tightening. Financ. Innov. 2025, 11, 51. [Google Scholar] [CrossRef]
- Bensalah, N. Challenges and Opportunities in Energy Economics: Balancing Cost, Sustainability, and Innovation in the Global Energy Transition. Mod. Econ. 2024, 15, 1147–1180. [Google Scholar] [CrossRef]
- Karaki, A.; Al-Fagih, L. Evolutionary game theory as a catalyst in smart grids: From theoretical insights to practical strategies. IEEE Access 2024, 12, 186926–186940. [Google Scholar] [CrossRef]
- Wan, X.; Wen, X.; Tang, B.; Sun, Q. Trading strategy for virtual power plant clusters based on a multi-subject game model. J. Comput. Methods Sci. Eng. 2023, 23, 2261–2274. [Google Scholar] [CrossRef]
- Izanlo, A.; Sheikholeslami, A.; Gholamian, S.A.; Kazemi, M.V.; Hosseini, S.N. A combination of MILP and game theory methods for P2P energy trading by considering network constraints. Appl. Energy 2024, 374, 123916. [Google Scholar] [CrossRef]
- Wang, B.; Guo, X. Blockchain-enabled transformation: Decentralized planning and secure peer-to-peer trading in local energy networks. Sustain. Energy Grids Netw. 2024, 40, 101556. [Google Scholar] [CrossRef]
- Malik, S.; Thakur, S.; Duffy, M.; Breslin, J.G. Comparative double auction approach for peer-to-peer energy trading on multiple microgrids. Smart Grids Sustain. Energy 2023, 8, 21. [Google Scholar] [CrossRef]
- Zhang, W.; Ji, C.; Liu, Y.; Hao, Y.; Song, Y.; Cao, Y.; Qi, H. Dynamic interactions of carbon trading, green certificate trading, and electricity markets: Insights from system dynamics modeling. PLoS ONE 2024, 19, e0304478. [Google Scholar] [CrossRef]
- Abate, A.G.; Majdi, D.; Kazempour, J.; Kamgarpour, M. Learning to bid in forward electricity markets using a no-regret algorithm. Electr. Power Syst. Res. 2024, 234, 110693. [Google Scholar] [CrossRef]
- Amin, W.; Huang, Q.; Afzal, M.; Khan, A.A.; Umer, K.; Ahmed, S.A. A converging non-cooperative & cooperative game theory approach for stabilizing peer-to-peer electricity trading. Electr. Power Syst. Res. 2020, 183, 106278. [Google Scholar]
- Raja, A.A.; Grammatico, S. Online coalitional games for real-time payoff distribution with applications to energy markets. IEEE Trans. Energy Mark. Policy Regul. 2023, 1, 97–106. [Google Scholar] [CrossRef]
- Raja, A.A.; Grammatico, S. Bilateral peer-to-peer energy trading via coalitional games. IEEE Trans. Ind. Inform. 2022, 19, 6814–6824. [Google Scholar] [CrossRef]
- Mitrea, D.; Chifu, V.R.; Cioara, T.; Anghel, I.; Pop, C.B. Social Factors in P2P Energy Trading Using Hedonic Games. IEEE Access 2024, 12, 71256–71270. [Google Scholar] [CrossRef]
- Azar, A.G.; Nazaripouya, H.; Khaki, B.; Chu, C.-C.; Gadh, R.; Jacobsen, R.H. A non-cooperative framework for coordinating a neighborhood of distributed prosumers. IEEE Trans. Ind. Inform. 2018, 15, 2523–2534. [Google Scholar] [CrossRef]
- Bandeiras, F.; Gomes, Á.; Gomes, M.; Coelho, P. Application and challenges of coalitional game theory in power systems for sustainable energy trading communities. Energies 2023, 16, 8115. [Google Scholar] [CrossRef]
- Gerwin, C.; Mieth, R.; Dvorkin, Y. Compensation mechanisms for double auctions in peer-to-peer local energy markets. Curr. Sustain. Renew. Energy Rep. 2020, 7, 165–175. [Google Scholar] [CrossRef]
- Emami, I.T.; Samani, E.; Abyaneh, H.A.; Mohsenian-Rad, H.; Bakhshai, A. A conceptual analysis of equilibrium bidding strategy in a combined oligopoly and oligopsony wholesale electricity market. IEEE Trans. Power Syst. 2022, 37, 4229–4243. [Google Scholar] [CrossRef]
- Song, H.; Liu, C.-C.; Lawarrée, J. Nash equilibrium bidding strategies in a bilateral electricity market. IEEE Trans. Power Syst. 2002, 17, 73–79. [Google Scholar] [CrossRef]
- Cheng, H.; Li, Y.; Jiang, H.; Sun, W.; Wei, C.; Huang, X. A Multi-Type Distributed Renewable Energy Aggregators Collaborative Operation Model Based on Non-Cooperative Game Theory. J. Phys. Conf. Ser. 2025, 3015, 012011. [Google Scholar] [CrossRef]
- Mignoni, N. Non-Cooperative Game Theoretical Control for Green and Efficient Energy Communities; Politecnico di Bari: Bari, Italy, 2025. [Google Scholar]
- Lei, Z.; Liu, M.; Shen, Z.; Lu, J.; Lu, Z. A Nash–Stackelberg game approach to analyze strategic bidding for multiple DER aggregators in electricity markets. Sustain. Energy Grids Netw. 2023, 35, 101111. [Google Scholar] [CrossRef]
- Yu, X.; Pan, D.; Zhou, Y. A Stackelberg game-based peer-to-peer energy trading market with energy management and pricing mechanism: A case study in Guangzhou. Sol. Energy 2024, 270, 112388. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Y.; Zhang, F.; Li, Y. A Stackelberg game-based approach to load aggregator bidding strategies in electricity spot markets. J. Energy Storage 2024, 95, 112509. [Google Scholar] [CrossRef]
- Xu, N.; Hu, Y.; Zhang, J.; Hao, R. Load-Side Shared Energy Storage New Energy Consumption Strategy Based on Nash Bargaining. In Proceedings of the 7th International Conference on Renewable Energy and Power Engineering, Beijing China, 25–27 September 2024; pp. 137–142. [Google Scholar]
- Becchetti, L.; Salustri, F. Renewable energy communities and the ecological transition: A game theoretic bargaining approach. Util. Policy 2025, 96, 102006. [Google Scholar] [CrossRef]
- Tanis, Z.; Durusu, A. Cooperative behaviors and multienergy coupling through distributed energy storage in the peer-to-peer market mechanism. IEEE Access 2025, 13, 12081–12102. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, B.; Ma, J.; Jin, Q. Earning while learning: An adversarial multi-armed bandit based real-time bidding scheme in deregulated electricity market. IEEE Trans. Netw. Sci. Eng. 2022, 9, 3991–4000. [Google Scholar] [CrossRef]
- Alsalloum, H.; Merghem-Boulahia, L.; Rahim, R. A systematical analysis on the dynamic pricing strategies and optimization methods for energy trading in smart grids. Int. Trans. Electr. Energy Syst. 2020, 30, e12404. [Google Scholar] [CrossRef]
- Umer, K.; Huang, Q.; Khorasany, M.; Amin, W.; Afzal, M. A novel prosumer-centric approach for social welfare maximization considering network voltage constraints in peer-to-peer energy markets. Int. J. Electr. Power Energy Syst. 2023, 147, 108820. [Google Scholar] [CrossRef]
- Nekrasov, S.A. Reducing costs for integration of renewable energy sources: A way to making renewable energy more accessible. Therm. Eng. 2021, 68, 593–603. [Google Scholar] [CrossRef]
- Mushtaq, N.; Nazir, I.; Azad, M.; Ishfaq, H.; Fareed, M.F.; Amin, W. Optimal Selection of Trading Partner in Peer-to-Peer Energy Markets. In Proceedings of the 3rd International Conference Emerging Trends Electrical, Control, and Telecommunication Engineering (ETECTE), Lahore, Pakistan, 26–27 November 2024; pp. 1–5. [Google Scholar]
- Camelo, M.M.; de Andrade, C.F.; de Athayde Prata, B. A mixed-integer linear programming model for optimizing green hydrogen supply chain networks. Int. J. Hydrog. Energy 2025, 118, 134–145. [Google Scholar] [CrossRef]
- Yoon, S.-J.; Ryu, K.-S.; Kim, C.; Nam, Y.-H.; Kim, D.-J.; Kim, B. Optimal Bidding Scheduling of Virtual Power Plants Using a Dual-MILP (Mixed-Integer Linear Programming) Approach under a Real-Time Energy Market. Energies 2024, 17, 3773. [Google Scholar] [CrossRef]
- Jin, X.; Liu, B.; Liao, S.; Cheng, C.; Zhao, Z.; Zhang, Y. Robust optimization for the self-scheduling and bidding strategies of a hydroproducer considering the impacts of crossing forbidden zones. J. Water Resour. Plan. Manag. 2023, 149, 05022017. [Google Scholar] [CrossRef]
- Zhou, W.; Zheng, J.; Wang, H.; Yin, P.; Zhang, J.; Zhang, Y. Coordinated and optimized dispatch of smart building group-energy storage power station based on multiple games. In Proceedings of the 36th Chinese Control and Decision Conference, Xi’an, China, 25–27 May 2024; pp. 2180–2185. [Google Scholar]
- Twaisan, K.; Barışçı, N. Integrated distributed energy resources (DER) and microgrids: Modeling and optimization of DERs. Electronics 2022, 11, 2816. [Google Scholar] [CrossRef]
- Di Persio, L.; Alruqimi, M.; Garbelli, M. Stochastic Approaches to Energy Markets: From Stochastic Differential Equations to Mean Field Games and Neural Network Modeling. Energies 2024, 17, 6106. [Google Scholar] [CrossRef]
- Zheng, K.; Sun, Z.; Song, Y.; Zhang, C.; Zhang, C.; Chang, F.; Yang, D.; Fu, X. Stochastic scenario generation methods for uncertainty in wind and photovoltaic power outputs: A comprehensive review. Energies 2025, 18, 503. [Google Scholar] [CrossRef]
- Tang, J.; Qian, B.; Luo, Y.; Lin, X.; Zhou, M.; Zhang, F.; Wang, H. Evolutionary Game Theory-Based Analysis of Power Producers’ Carbon Emission Reduction Strategies and Multi-Group Bidding Dynamics in the Low-Carbon Electricity Market. Processes 2025, 13, 952. [Google Scholar] [CrossRef]
- Yu, J.; Liu, S.; Zou, Y.; Wang, G.; Hu, C. Auction Theory and Game Theory Based Pricing of Edge Computing Resources: A Survey. IEEE Internet Things J. 2025, 12, 32394–32418. [Google Scholar] [CrossRef]
- Amin, W.; Ahmad, F.; Umer, K.; Khawaja, A.H.; Afzal, M.; Ahmed, S.A.; Chaitusaney, S. P2p energy trading: An optimal solution for energy shortage in pakistan. IEEE Access 2022, 10, 89614–89633. [Google Scholar] [CrossRef]
- Zheng, Y.; Wang, Y.; Yang, Q. Bidding strategy design for electric vehicle aggregators in the day-ahead electricity market considering price volatility: A risk-averse approach. Energy 2023, 283, 129138. [Google Scholar] [CrossRef]
- Rousta, M.; Güsewell, J.; Eltrop, L. Integrated Production and Multi-Market Optimization of Biomethane in Germany: A Two-Step Linear Programming Approach. Energies 2025, 18, 2991. [Google Scholar] [CrossRef]
- Pinthanon, P.; Rianmora, S.; Chanchiewvichai, W. Decision-Making Platform for Design Optimization by Integrating Linear Programming and House of Quality. Eng. J. 2025, 29, 95–122. [Google Scholar] [CrossRef]
- Kuram, Ç.; Bilişik, Ö.N. A mixed-integer linear programming model proposal to determine material sustainability for new product development processes in production. Comput. Chem. Eng. 2025, 198, 109108. [Google Scholar] [CrossRef]
- Liaquat, S.; Hussain, T.; Kassab, F.A.; Ali, A.; Celik, B.; Fourney, R.; Hansen, T.M. An Integrated Two-Stage Hybrid P2P-DR Transactive Energy Trading Platform Using Iterative Distributed-Mixed Integer Linear Optimisation. IET Smart Grid 2025, 8, e70027. [Google Scholar] [CrossRef]
- Deng, J.; He, F.; Zeng, Q.; Yan, J.; Liu, R.; He, D.; Zhou, S. Coordinated Optimal Dispatch of Distribution Grids and P2P Energy Trading Markets. Energy Sci. Eng. 2025, 13, 2206–2219. [Google Scholar] [CrossRef]
- Yaghoubi, M. Resilient Peer-to-Peer Energy Trading: Addressing Price Uncertainty and Communication Delays in Decentralized Markets. Ph.D. Thesis, École de Technologie Supérieure, Montréal, QC, Canada, 2025. [Google Scholar]
- Akülker, H.; Alakent, B.; Aydin, E. A two-stage stochastic MINLP model to design and operate a multi-energy microgrid by addressing carbon emission regulatory policies uncertainty. arXiv 2025, arXiv:2501.18988. [Google Scholar] [CrossRef]
- Kassab, F.A. Co-Optimisation of the Sizing and Control of an Urban Microgrid. Ph.D. Thesis, Université de Technologie de Compiègne, Compiègne, France, 2024. [Google Scholar]
- Ling, J.Q.; Tan, W.-S.; Ding, Z.Y.; Wu, Y.-K. Multi-Objective Optimization of Cloud Energy Storage Placement and Sizing in Peer-to-Peer Energy Market Under Line Congestion. In Proceedings of the 2025 IEEE Industry Applications Society Annual Meeting (IAS), Taipei, Taiwan, 15–20 June 2025; IEEE: New York, NY, USA, 2025; pp. 1–8. [Google Scholar]
- dos Santos, S.A.B.; Coutinho, L.R.R.; Tofoli, F.L.; Barroso, G.C. Community energy management system for residential energy communities integrating demand response, distributed generation, and energy storage systems. J. Energy Storage 2025, 132, 117832. [Google Scholar] [CrossRef]
- Ahmadi Kamarposhti, M.; Ghandour, R.; Abdel-Aty, M.; Hafez, M.; Alfiras, M.; Alkhazaleh, S.; Colak, I.; Solyman, A. Optimizing capacitor bank placement in distribution networks using a multi-objective particle swarm optimization approach for energy efficiency and cost reduction. Sci. Rep. 2025, 15, 12332. [Google Scholar] [CrossRef]
- Vaithiyanathan, B.; Jothi, K.R.; Paramasivam, S.K. Develop a Hybrid Intelligent Fuzzy Self-Adaptive Mutated Genetic Algorithm and Deep Reinforcement Learning for Efficient Home Energy Management. Trait. Signal 2025, 42, 2. [Google Scholar] [CrossRef]
- Zubin, J.B.; Sunitha, R.; Pathirikkat, G. Integrated Bidding and Battery Scheduling in a Microgrid for Sealed-Bid Double Auction Power Trading with Peer Microgrids under Uncertainty and Its Blockchain-Based Implementation. IEEE Access 2025, 13, 117953–117970. [Google Scholar]
- Li, S.; Gu, N.; Wu, C. Electricity Tariff Insurance Design Under Real-Time Pricing. In Proceedings of the 7th Conference on Energy Internet & Energy System Integration, Hangzhou, China, 15–18 December 2023; pp. 3172–3177. [Google Scholar]
- Yang, A.; Li, A.; Li, Z.; Sun, Y.; Gao, J. Investment Analysis of Low-Carbon Yard Cranes: Integrating Monte Carlo Simulation and Jump Diffusion Processes with a Hybrid American–European Real Options Approach. Energies 2025, 18, 1928. [Google Scholar]
- Kluge, T. Pricing Derivatives in Stochastic Volatility Models Using the Finite Difference Method. Master’s Thesis, Technische Universität Chemnitz, Chemnitz, Germany, 2002. [Google Scholar]
- Baamonde-Seoane, M.A. Modelling, Mathematical Analysis and Numerical Simulation to Value Derivatives Related to Renewable Energy Certificates. 2021. Available online: https://ruc.udc.es/entities/publication/21889049-7496-4f83-8f44-3333e810ed59 (accessed on 15 August 2025).
- Voronin, S.; Partanen, J. Price forecasting in the day-ahead energy market by an iterative method with separate normal price and price spike frameworks. Energies 2013, 6, 5897–5920. [Google Scholar] [CrossRef]
- Kim, H.J.; Kim, M.K. Data-Driven Virtual Power Plant Bidding Strategy in Electricity Markets Integrating Hybrid Forecasting Model and Customized Incentive Demand Response. IEEE Internet Things J. 2025, 12, 13851–13869. [Google Scholar] [CrossRef]
- Oprea, S.-V.; Bara, A. Two-step price mechanism using Newton-Raphson method and peer-to-peer mediation for local electricity markets. Energy Strategy Rev. 2025, 59, 101701. [Google Scholar] [CrossRef]
- Shiltz, D.J.; Cvetković, M.; Annaswamy, A.M. An integrated dynamic market mechanism for real-time markets and frequency regulation. IEEE Trans. Sustain. Energy 2015, 7, 875–885. [Google Scholar] [CrossRef]
- Lu, J.; Xie, Z.; Xu, H.; Liu, J. Optimizing Joint Bidding and Incentivizing Strategy for Price-Maker Load Aggregators Based on Multi-Task Multi-Agent Deep Reinforcement Learning. IEEE Access 2024, 12, 63988–164001. [Google Scholar] [CrossRef]
- Tang, C.; Qin, Y.; Wu, F.; Tang, Z. Dynamic demand-aware power grid intelligent pricing algorithm based on deep reinforcement learning. IEEE Access 2024, 12, 75809–75817. [Google Scholar] [CrossRef]
- Basnet, M.R.; Bryan, J.A.; Dana, S.J.; Meek, A.S.; Wang, H.; Talbot, P. Stochastic optimization and uncertainty quantification of Natrium-based nuclear-renewable energy Systems for Flexible Power Applications in deregulated markets. Appl. Energy 2024, 375, 124105. [Google Scholar] [CrossRef]
- Wang, Y.; Lin, T. A novel deterministic probabilistic forecasting framework for gold price with a new pandemic index based on quantile regression deep learning and multi-objective optimization. Mathematics 2023, 12, 29. [Google Scholar] [CrossRef]
- Nizharadze, N.; Farokhi Soofi, A.; Manshadi, S. Predicting the gap in the day-ahead and real-time market prices leveraging exogenous weather data. Algorithms 2023, 16, 508. [Google Scholar] [CrossRef]
- Li, W.; Zhang, N.; Liu, Z.; Ma, S.; Ke, H.; Wang, J.; Chen, T. MLfus: A real-time forecasting architecture for low communication costs in electricity IoT based on ensemble learning. IET Commun. 2023, 17, 145–161. [Google Scholar] [CrossRef]
- Alhosani, A. Development and Application of Forecasting Machine Learning Approach for Renewable Energy-Related Products’ Prices. Ph.D. Thesis, Khalifa University of Science, Abu Dhabi, United Arab Emirates, 2023. [Google Scholar]
- Saeed, N.; Shafi, I.; Pervez, S.; Thompson, E.B.; Castilla, A.K.; Samad, M.A.; Ashraf, I. Intelligent Decision Making for Commodities Price Prediction: Opportunities, Challenges and Future Avenues. Comput. Econ. 2025, 1–59. [Google Scholar] [CrossRef]
- Liu, F.; Li, X. Integrating deep reinforcement learning with evolutionary algorithms for advanced optimization in smart city energy management. IEEE Access 2024, 12, 177103–177118. [Google Scholar] [CrossRef]
- Jeong, J.; Kim, S.W.; Kim, H. Deep reinforcement learning based real-time renewable energy bidding with battery control. IEEE Trans. Energy Mark., Policy Regul. 2023, 1, 85–96. [Google Scholar] [CrossRef]
- Yadav, D.; Mekhilef, S.; Singh, B.; Rawa, M. Deep Reinforcement Learning and Energy Price Prediction. In Artificial Intelligence-Based Smart Power Systems; Wiley Online Library: Hoboken, NJ, USA, 2023; pp. 207–231. [Google Scholar]
- Song, J.; Zheng, W.; Chen, M.; Qi, L.; Zou, Q. Analysis of collusive bidding characteristics in the power spot market based on multi-agent reinforcement learning simulation. Electr. Eng. 2025, 107, 10069–10090. [Google Scholar] [CrossRef]
- Alavi, S.A.; Mehran, K.; Vahidinasab, V.; Catalão, J.P.S. Forecast-based consensus control for DC microgrids using distributed long short-term memory deep learning models. IEEE Trans. Smart Grid 2021, 12, 3718–3730. [Google Scholar] [CrossRef]
- Aslam, S.; Ayub, N.; Farooq, U.; Alvi, M.J.; Albogamy, F.R.; Rukh, G.; Haider, S.I.; Azar, A.T.; Bukhsh, R. Towards electric price and load forecasting using cnn-based ensembler in smart grid. Sustainability 2021, 13, 12653. [Google Scholar] [CrossRef]
- Bakir, A.; Rami, A. Enhanced electricity price forecasting in smart grids using an optimized hybrid convolutional Multi-Layer Perceptron deep network with Marine Predators Algorithm for feature selection. Energy Sources Part B Econ. Plan. Policy 2025, 20, 2456058. [Google Scholar] [CrossRef]
- Guo, X.; Zhao, Q.; Zheng, D.; Ning, Y.; Gao, Y. A short-term load forecasting model of multi-scale CNN-LSTM hybrid neural network considering the real-time electricity price. Energy Rep. 2020, 6, 1046–1053. [Google Scholar] [CrossRef]
- Zhu, Z. Applications of Reinforcement Learning on Deregulated Active Distribution Networks; Hong Kong Polytechnic University: Hong Kong, China, 2023. [Google Scholar]
- Meydani, A.; Shahinzadeh, H.; Ramezani, A.; Moazzami, M.; Nafisi, H.; Askarian-Abyaneh, H. Comprehensive review of artificial intelligence applications in smart grid operations. In Proceedings of the 2024 9th International Conference on Technology Energy Management (ICTEM), 445 Hoes Lane, Piscataway, NJ, USA, 14–15 February 2024; pp. 1–13. [Google Scholar]
- Richarz, J.; Henn, S.; Osterhage, T.; Müller, D. Optimal scheduling of modernization measures for typical non-residential buildings. Energy 2022, 238, 121871. [Google Scholar] [CrossRef]
- Alghamdi, H.; Hua, L.-G.; Hafeez, G.; Murawwat, S.; Bouazzi, I.; Alghamdi, B. Optimal adaptive heuristic algorithm based energy optimization with flexible loads using demand response in smart grid. PLoS ONE 2024, 19, e0307228. [Google Scholar] [CrossRef] [PubMed]
- Gronier, T.; Fitó, J.; Franquet, E.; Gibout, S.; Ramousse, J. Iterative sizing of solar-assisted mixed district heating network and local electrical grid integrating demand-side management. Energy 2022, 238, 121517. [Google Scholar] [CrossRef]
- Li, J.; Mi, Z.; Yu, Y. Research on the classification and evaluation of large-scale user load patterns for grid supply–demand balance regulation demands. Appl. Energy 2025, 397, 126301. [Google Scholar] [CrossRef]
- Yu, S.; Fan, Y.; Shi, Z.; Zhang, J.; Zhang, T.; Zhang, J.; Liu, Z. Innovative heat management method and metaheuristic algorithm optimized power supply–demand balance for PEMFC–ASHP–CHP system. Appl. Energy 2024, 371, 123778. [Google Scholar] [CrossRef]
- Chandlekar, S.; Boroju, A.; Jain, S.; Gujar, S. A novel demand response model and method for peak reduction in smart grids–PowerTAC. arXiv 2023, arXiv:2302.12520. [Google Scholar]
- Yu, M.; Hong, S.H. Supply–demand balancing for power management in smart grid: A Stackelberg game approach. Appl. Energy 2016, 164, 702–710. [Google Scholar] [CrossRef]
- Chen, Q.; Kumar, P.; Baskonus, H.M. Modeling and analysis of demand–supply dynamics with a collectability factor using delay differential equations in economic growth via the Caputo operator. AIMS Math. 2024, 9, 7471–7491. [Google Scholar] [CrossRef]
- Toderean, L.; Cioara, T.; Anghel, I.; Sarmas, E.; Michalakopoulos, V.; Marinakis, V. Demand response optimization for smart grid integrated buildings: Review of technology enablers landscape and innovation challenges. Energy Build. 2025, 326, 115067. [Google Scholar] [CrossRef]
- Rashid, A.; Biswas, P.; Nasim, M.D.; Gupta, K.D. Power plays: Unleashing machine learning magic in smart grids. arXiv 2024, arXiv:2410.15423. [Google Scholar] [CrossRef]
- Du, Y.; Wu, J.; Li, S.; Long, C.; Onori, S. Hierarchical coordination of two-time scale microgrids with supply–demand imbalance. IEEE Trans. Smart Grid 2020, 11, 3726–3736. [Google Scholar] [CrossRef]
- Ghorbanian, M.; Dolatabadi, S.H.; Siano, P. Game theory-based energy-management method considering autonomous demand response and distributed generation interactions in smart distribution systems. IEEE Syst. J. 2020, 15, 905–914. [Google Scholar] [CrossRef]
- Naughton, J.; Wang, H.; Cantoni, M.; Mancarella, P. Co-optimizing virtual power plant services under uncertainty: A robust scheduling and receding horizon dispatch approach. IEEE Trans. Power Syst. 2021, 36, 3960–3972. [Google Scholar] [CrossRef]
- Cheng, L.; Wei, X.; Li, M.; Tan, C.; Yin, M.; Shen, T.; Zou, T. Integrating evolutionary game-theoretical methods and deep reinforcement learning for adaptive strategy optimization in user-side electricity markets: A comprehensive review. Mathematics 2024, 12, 3241. [Google Scholar] [CrossRef]
- Wen, Y.; Lu, Y.; Gou, J.; Liu, F.; Tang, Q.; Wang, R. Robust transmission expansion planning of ultrahigh-voltage AC–DC hybrid grids. IEEE Trans. Ind. Appl. 2022, 58, 3294–3302. [Google Scholar] [CrossRef]
- Lee, J.-W.; Kim, M.-K. An evolutionary game theory-based optimal scheduling strategy for multiagent distribution network operation considering voltage management. IEEE Access 2022, 10, 50227–50241. [Google Scholar] [CrossRef]
- Zhang, X.; Cai, Z.; Yang, X.; Luo, J.; Zhang, R.; Zhang, Y. Game theory-based demand-side management for efficient energy collaboration in smart networks: A neighborhood-scale optimization framework. Electr. Eng. 2024, 107, 9071–9088. [Google Scholar] [CrossRef]
- Chen, P.; Han, L.; Xin, G.; Zhang, A.; Ren, H.; Wang, F. Game theory based optimal pricing strategy for V2G participating in demand response. IEEE Trans. Ind. Appl. 2023, 59, 4673–4683. [Google Scholar] [CrossRef]
- Ding, Y.; Xie, D.; Hui, H.; Xu, Y.; Siano, P. Game-theoretic demand side management of thermostatically controlled loads for smoothing tie-line power of microgrids. IEEE Trans. Power Syst. 2021, 36, 4089–4101. [Google Scholar] [CrossRef]
- Yadav, R.K.; Bhadoria, V.S.; Hrisheekesha, P.N. Demand side management using ant colony optimization algorithm in renewable energy integrated smart grid. J. Intell. Fuzzy Syst. 2024, 46, 7627–7642. [Google Scholar] [CrossRef]
- Nanibabu, S.; Baskaran, S.; Marimuthu, P. Realisation of demand side management in smart distribution grid with commercial loads using butterfly optimization algorithm. In Proceedings of the Third International Conference on Intelligent Techniques in Control, Optimization and Signal Processing (INCOS), Tamil Nadu, India, 14–16 March 2024; pp. 1–6. [Google Scholar]
- Maity, S.; Chanda, S.; Rai, A.K.; Biswas, P.; De, A. A DE modified quantum PSO based demand response program for social welfare optimization with scalable renewable energy penetration in smart grid. SAMRIDDHI A J. Phys. Sci. Eng. Technol. 2024, 16, 9–19. [Google Scholar] [CrossRef]
- Xiong, Q.; Chen, Y.; Song, L.; Huang, Z.; Dong, C.; Zou, G.; Yu, S. Research on multi-scenario source–grid–load–storage optimization and comprehensive optimization strategies considering user satisfaction and economy. In Proceedings of the 6th International Conference on Energy, 2314 Power and Grid (ICEPG), Guangzhou, China, 27–29 September 2024; pp. 1717–1723. [Google Scholar]
- Woo, Y.-B.; Moon, I. Bilevel optimization for multi-user systems with mixed demand response programs for enhanced operational efficiency in electric power grids. Appl. Energy 2025, 399, 126507. [Google Scholar] [CrossRef]
- Xu, W.; Zhou, D.; Huang, X.; Lou, B.; Liu, D. Optimal allocation of power supply systems in industrial parks considering multi-energy complementarity and demand response. Appl. Energy 2020, 275, 115407. [Google Scholar] [CrossRef]
- Xinfa, T.; Jingjing, W.; Yonghua, W.; Youwei, W. The optimization of supply–demand balance dispatching and economic benefit improvement in a multi-energy virtual power plant within the Jiangxi power market. Energies 2024, 17, 4691. [Google Scholar] [CrossRef]
- Silva, W.N.; Henrique, L.F.; Silva, A.F.P.d.C.; Dias, B.H.; Soares, T.A. Market models and optimization techniques to support the decision-making on demand response for prosumers. Electr. Power Syst. Res. 2022, 210, 108059. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, H.; Zhang, Z.; Wang, Y. Optimization model of supply and demand matching of energy right products based on pre-listing transactions. In Proceedings of the 4th International Conference on Big Data Economy and Information Management, Tianjin, China, 27–29 October 2023; pp. 704–708. [Google Scholar]
- Stanelyte, D.; Radziukyniene, N.; Radziukynas, V. Overview of demand-response services: A review. Energies 2022, 15, 1659. [Google Scholar] [CrossRef]
- Honarmand, M.E.; Hosseinnezhad, V.; Hayes, B.; Shafie-Khah, M.; Siano, P. An overview of demand response: From its origins to the smart energy community. IEEE Access 2021, 9, 96851–96876. [Google Scholar] [CrossRef]
- Yang, P.; Jiang, H.; Liu, C.; Kang, L.; Wang, C. Coordinated optimization scheduling operation of integrated energy system considering demand response and carbon trading mechanism. Int. J. Electr. Power Energy Syst. 2023, 147, 108902. [Google Scholar] [CrossRef]
- Baldivieso Monasterios, P.R.; Verba, N.; Morris, E.A.; Morstyn, T.; Gaura, E.; McArthur, S. Incorporating forecasting and peer-to-peer negotiation frameworks into a distributed model predictive control approach for meshed electric networks. arXiv 2021, arXiv:2105.14547. [Google Scholar]
- Sampath, L.P.M.I.; Paudel, A.; Nguyen, H.D.; Foo, E.Y.S.; Gooi, H.B. Peer-to-peer energy trading enabled optimal decentralized operation of smart distribution grids. IEEE Trans. Smart Grid 2021, 13, 654–666. [Google Scholar] [CrossRef]
- Yan, M.; Shahidehpour, M.; Paaso, A.; Zhang, L.; Alabdulwahab, A.; Abusorrah, A. Distribution network-constrained optimization of peer-to-peer transactive energy trading among multi-microgrids. IEEE Trans. Smart Grid 2020, 12, 1033–1047. [Google Scholar] [CrossRef]
- Li, J.; Khodayar, M.E.; Wang, J.; Zhou, B. Data-driven distributionally robust co-optimization of P2P energy trading and network operation for interconnected microgrids. IEEE Trans. Smart Grid 2021, 12, 5172–5184. [Google Scholar] [CrossRef]
- Pop, C.; Antal, M.; Cioara, T.; Anghel, I.; Salomie, I.; Bertoncini, M. A fog computing enabled virtual power plant model for delivery of frequency restoration reserve services. Sensors 2019, 19, 4688. [Google Scholar] [CrossRef]
- Wang, W.; Chen, P.; Zeng, D.; Liu, J. Electric vehicle fleet integration in a virtual power plant with large-scale wind power. IEEE Trans. Ind. Appl. 2020, 56, 5924–5931. [Google Scholar] [CrossRef]
- Van Summeren, L.F.M.; Wieczorek, A.J.; Bombaerts, G.J.T.; Verbong, G.P.J. Community energy meets smart grids: Reviewing goals, structure, and roles in virtual power plants in Ireland, Belgium and the Netherlands. Energy Res. Soc. Sci. 2020, 63, 101415. [Google Scholar] [CrossRef]
- Phyo, P.-P.; Jeenanunta, C. Advanced ML-based ensemble and deep learning models for short-term load forecasting: Comparative analysis using feature engineering. Appl. Sci. 2022, 12, 4882. [Google Scholar] [CrossRef]
- Sivakumar, S.A. Predictive analytics for demand response management with AI. Acta Energetica 2024, 2, 12–22. [Google Scholar]
- Khan, M.A.; Saleh, A.M.; Waseem, M.; Sajjad, I.A. Artificial intelligence enabled demand response: Prospects and challenges in smart grid environment. IEEE Access 2022, 11, 1477–1505. [Google Scholar] [CrossRef]
- Aguiar-Pérez, J.M.; Pérez-Juárez, M.A. An insight of deep learning based demand forecasting in smart grids. Sensors 2023, 23, 1467. [Google Scholar] [CrossRef]
- Sangoleye, F.; Jao, J.; Faris, K.; Tsiropoulou, E.E.; Papavassiliou, S. Reinforcement learning-based demand response management in smart grid systems with prosumers. IEEE Syst. J. 2023, 17, 1797–1807. [Google Scholar] [CrossRef]
- Wen, X.; Liao, J.; Niu, Q.; Shen, N.; Bao, Y. Deep learning-driven hybrid model for short-term load forecasting and smart grid information management. Sci. Rep. 2024, 14, 13720. [Google Scholar] [CrossRef]
- El Maghraoui, A.; El Hadraoui, H.; Ledmaoui, Y.; El Bazi, N.; Guennouni, N.; Chebak, A. Revolutionizing smart grid-ready management systems: A holistic framework for optimal grid reliability. Sustain. Energy Grids Netw. 2024, 39, 101452. [Google Scholar] [CrossRef]
- Ma, R.; Yi, Z.; Xiang, Y.; Shi, D.; Xu, C.; Wu, H. A blockchain-enabled demand management and control framework driven by deep reinforcement learning. IEEE Trans. Ind. Electron. 2022, 70, 430–440. [Google Scholar] [CrossRef]
- Dascalu, A.; Cruden, A.J.; Sharkh, S.M. Experimental investigations into a hybrid energy storage system using directly connected lead-acid and Li-ion batteries. Energies 2024, 17, 4726. [Google Scholar] [CrossRef]
- Szott, M.; Wermiński, S.; Jarnut, M.; Kaniewski, J.; Benysek, G. Battery energy storage system for emergency supply and improved reliability of power networks. Energies 2021, 14, 720. [Google Scholar] [CrossRef]
- Diaz-Gonzalez, F.; Chillón-Antón, C.; Llonch-Masachs, M.; Galceran-Arellano, S.; Rull-Duran, J.; Bergas-Jane, J.; Bullich-Massagué, E. A hybrid energy storage solution based on supercapacitors and batteries for the grid integration of utility scale photovoltaic plants. J. Energy Storage 2022, 51, 104446. [Google Scholar] [CrossRef]
- Zhang, L.; Hu, X.; Wang, Z.; Ruan, J.; Ma, C.; Song, Z.; Dorrell, D.G.; Pecht, M.G. Hybrid electrochemical energy storage systems: An overview for smart grid and electrified vehicle applications. Renew. Sustain. Energy Rev. 2021, 139, 110581. [Google Scholar] [CrossRef]
- Wang, Z.; Tuo, X.; Zhou, J.; Xiao, G. Performance study of large capacity industrial lead-carbon battery for energy storage. J. Energy Storage 2022, 55, 105398. [Google Scholar] [CrossRef]
- Han, K.B.; Jung, J.; Kang, B.O. Real-time load variability control using energy storage system for demand-side management in South Korea. Energies 2021, 14, 6292. [Google Scholar] [CrossRef]
- Kebede, A.A.; Kalogiannis, T.; Van Mierlo, J.; Berecibar, M. A comprehensive review of stationary energy storage devices for large scale renewable energy sources grid integration. Renew. Sustain. Energy Rev. 2022, 159, 112213. [Google Scholar] [CrossRef]
- Theocharis, A.; Hamanee, S. Battery storage at the secondary distribution electricity grid by investigating end-users load demand measurements. Energies 2022, 15, 2743. [Google Scholar] [CrossRef]
- Barakat, S.; Emam, A.; Samy, M.M. Investigating grid-connected green power systems’ energy storage solutions in the event of frequent blackouts. Energy Rep. 2022, 8, 5177–5191. [Google Scholar] [CrossRef]
- Phogat, P.; Dey, S.; Wan, M. Powering the sustainable future: A review of emerging battery technologies and their environmental impact. RSC Sustain. 2025, 3, 3266–3306. [Google Scholar] [CrossRef]
- Zeng, Y.; Li, X.; Fu, J.; Shen, P.K.; Zhang, X. Corrigendum: High-energy-density and high-rate membraneless Ni–Fe battery enabled by a 1-butyl-3-methylimidazolium bromide-based gel electrolyte. ChemElectroChem 2023, 10, e202300354. [Google Scholar]
- Sun, H.; Wang, C.; Qi, Z.; Hu, W.; Zhang, Z. Nanostructure nickel-based selenides as cathode materials for hybrid battery–supercapacitors. Front. Chem. 2021, 8, 611032. [Google Scholar] [CrossRef]
- Salkuti, S.R. Electrochemical batteries for smart grid applications. Int. J. Electr. Comput. Eng. 2021, 11, 1849–1856. [Google Scholar]
- Li, Y.; Tan, Z.; Liu, Y.; Lei, C.; He, P.; Li, J.; He, Z.; Cheng, Y.; Wu, F.; Li, Y. Past, present and future of high-nickel materials. Nano Energy 2024, 119, 109070. [Google Scholar] [CrossRef]
- Li, F.; Wang, D.; Liu, D.; Yang, S.; Sun, K.; Liu, Z.; Yu, H.; Qin, J. A comprehensive review on energy storage system optimal planning and benefit evaluation methods in smart grids. Sustainability 2023, 15, 9584. [Google Scholar] [CrossRef]
- Huang, Z.; Song, B.; Zhang, H.; Feng, F.; Zhang, W.; Lu, K.; Chen, Q. High-capacity and stable sodium–sulfur battery enabled by confined electrocatalytic polysulfides full conversion. Adv. Funct. Mater. 2021, 31, 2100666. [Google Scholar] [CrossRef]
- Wang, L.; Wang, T.; Peng, L.; Wang, Y.; Zhang, M.; Zhou, J.; Chen, M.; Cao, J.; Fei, H.; Duan, X.; et al. The promises, challenges and pathways to room-temperature sodium–sulfur batteries. Natl. Sci. Rev. 2022, 9, nwab050. [Google Scholar]
- Wang, Y.; Zhang, Y.; Cheng, H.; Ni, Z.; Wang, Y.; Xia, G.; Li, X.; Zeng, X. Research progress toward room temperature sodium–sulfur batteries: A review. Molecules 2021, 26, 1535. [Google Scholar] [CrossRef]
- Wu, J.; Tian, Y.; Gao, Y.; Gao, Z.; Meng, Y.; Wang, Y.; Wang, X.; Zhou, D.; Kang, F.; Li, B.; et al. Rational electrolyte design toward cyclability remedy for room-temperature sodium–sulfur batteries. Angew. Chem. Int. Ed. 2022, 61, e202205416. [Google Scholar]
- Yan, Z.; Zhao, L.; Wang, Y.; Zhu, Z.; Chou, S.-L. The future for room-temperature sodium–sulfur batteries: From persisting issues to promising solutions and practical applications. Adv. Funct. Mater. 2022, 32, 2205622. [Google Scholar]
- Murugan, S.; Klostermann, S.V.; Schützendübe, P.; Richter, G.; Kästner, J.; Buchmeiser, M.R. Stable cycling of room-temperature sodium–sulfur batteries based on an in situ crosslinked gel polymer electrolyte. Adv. Funct. Mater. 2022, 32, 2201191. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, X.; Yang, Q.; Shao, Y.; Du, Y.; Qi, J.; Zhao, M.; Shang, Z.; Hao, Y.; Tang, Y.; et al. Chemical and spatial dual-confinement engineering for stable Na–S batteries with approximately 100% capacity retention. Proc. Natl. Acad. Sci. USA 2023, 120, e2314408120. [Google Scholar] [CrossRef] [PubMed]
- Basel, J.; Sapkota, N.; Parekh, M.; Rao, A.M. Electrolyte optimization for sodium–sulfur batteries. Appl. Phys. Lett. 2024, 124, 123901. [Google Scholar]
- Liu, D.; Li, Z.; Li, X.; Chen, X.; Li, Z.; Yuan, L.; Huang, Y. Stable room-temperature sodium–sulfur batteries in ether-based electrolytes enabled by the fluoroethylene carbonate additive. ACS Appl. Mater. Interfaces 2022, 14, 6658–6666. [Google Scholar] [CrossRef]
- Zhang, H.; Gao, Y.; Liu, X.; Zhou, L.; Li, J.; Xiao, Y.; Peng, J.; Wang, J.; Chou, S.-L. Long-cycle-life cathode materials for sodium-ion batteries toward large-scale energy storage systems. Adv. Energy Mater. 2023, 13, 2300149. [Google Scholar]
- Singh, A.N.; Islam, M.; Meena, A.; Faizan, M.; Han, D.; Bathula, C.; Hajibabaei, A.; Anand, R.; Nam, K.-W. Unleashing the potential of sodium-ion batteries: Current state and future directions for sustainable energy storage. Adv. Funct. Mater. 2023, 33, 2304617. [Google Scholar]
- Zhu, Q.; Wu, J.; Li, W.; Hu, X.; Tian, N.; He, L.; Li, Y. Boosting sodium-ion battery performance by anion doping in NASICON Na4MnCr(PO4)3 cathode. J. Colloid Interface Sci. 2024, 663, 191–202. [Google Scholar]
- Tyagaraj, H.B.; Marje, S.J.; Ranjith, K.S.; Hwang, S.-K.; Al Ghaferi, A.; Chodankar, N.R.; Huh, Y.S.; Han, Y.-K. Sodium-ion batteries: Charge storage mechanisms and recent advancements in diglyme-based electrolytes. J. Energy Storage 2023, 74, 109411. [Google Scholar] [CrossRef]
- Pahari, D.; Verma, P.; Puravankara, S. Are Na-ion batteries nearing the energy storage tipping point?—Current status of non-aqueous, aqueous, and solid-state Na-ion battery technologies for sustainable energy storage. J. Energy Storage 2022, 56, 105961. [Google Scholar]
- Ma, W.-L.; Zhou, Y.; Zhao, X.-W.; Cao, X.; Wu, P.; Zhu, X.-S.; Wei, S.-H.; Sun, K.; Zhou, H.; Zhou, Y.-M. Ultra-fast-charging, long-duration, and wide-temperature-range sodium storage enabled by multiwalled carbon nanotube-hybridized biphasic polyanion-type phosphate cathode materials. ACS Appl. Mater. Interfaces 2024, 16, 34819–34829. [Google Scholar]
- Parthasarathy, C.; Laaksonen, H.; Redondo-Iglesias, E.; Pelissier, S. Aging aware adaptive control of Li-ion battery energy storage system for flexibility services provision. J. Energy Storage 2023, 57, 106268. [Google Scholar]
- Rouholamini, M.; Wang, C.; Nehrir, H.; Hu, X.; Hu, Z.; Aki, H.; Zhao, B.; Miao, Z.; Strunz, K. A review of modeling, management, and applications of grid-connected Li-ion battery storage systems. IEEE Trans. Smart Grid 2022, 13, 4505–4524. [Google Scholar]
- Cheng, L.; Wan, Y.; Zhou, Y.; Gao, D.W. Operational reliability modeling and assessment of battery energy storage based on lithium-ion battery lifetime degradation. J. Mod. Power Syst. Clean Energy 2021, 10, 1738–1749. [Google Scholar] [CrossRef]
- Iqbal, H.; Sarwar, S.; Kirli, D.; Shek, J.K.H.; Kiprakis, A.E. A survey of second-life batteries based on techno-economic perspective and applications-based analysis. Carbon Neutrality 2023, 2, 8. [Google Scholar] [CrossRef]
- Kostenko, G.; Zaporozhets, A. Transition from electric vehicles to energy storage: Review on targeted lithium-ion battery diagnostics. Energies 2024, 17, 5132. [Google Scholar] [CrossRef]
- Wang, W.; Liu, S.; Ma, X.-Y.; Jiang, J.; Yang, X.-G. Advancing smart lithium-ion batteries: A review on multi-physical sensing technologies for lithium-ion batteries. Energies 2024, 17, 2273. [Google Scholar] [CrossRef]
- Nazaralizadeh, S.; Banerjee, P.; Srivastava, A.K.; Famouri, P. Battery energy storage systems: A review of energy management systems and health metrics. Energies 2024, 17, 1250. [Google Scholar] [CrossRef]
- Solyali, D.; Safaei, B.; Zargar, O.; Aytac, G. A comprehensive state-of-the-art review of electrochemical battery storage systems for power grids. Int. J. Energy Res. 2022, 46, 17786–17812. [Google Scholar] [CrossRef]
- Waqas, A.; Qi, H.; Jian, L.; Abdullah, A.K.; Umashankar, S.; Sivakumar, S.S. Reputation-based uniform pricing & energy distribution in peer-to-peer energy trading market. Ain Shams Eng. J. 2025, 16, 103715. [Google Scholar]
- Ishfaq, H.; Amin, W.; Ashfaq, S.; Mushtaq, N.; Shi, X. Attention-Enhanced Bidirectional LSTM for Accurate False Data Injection Attack Detection in Smart Grid. Trans. Emerg. Telecommun. Technol. 2025, 36, 70238. [Google Scholar] [CrossRef]
- Ahmed, S.A.; Huang, Q.; Zhang, Z.; Li, J.; Amin, W.; Afzal, M.; Hussain, J.; Hussain, F. Optimization of social welfare and mitigating privacy risks in P2P energy trading: Differential privacy for secure data reporting. Appl. Energy 2024, 356, 122403. [Google Scholar] [CrossRef]
- Force, J.T.; Benysek, G. Security and Privacy Controls for Information Systems and Organizations. National Institute of Standards and Technology. 2017. Available online: https://nvlpubs.nist.gov/nistpubs/SpecialPublications/NIST.SP.800-53r5.pdf (accessed on 1 September 2025).
- International Electrotechnical Commission (IEC). Power Systems Management and Associated Information Exchange—Data and Communications Security—Part 3: Communication Network and System Security—Profiles Including TCP/IP. International Electrotechnical Commission. 2014. Available online: https://cdn.standards.iteh.ai/samples/105100/b7a344cdd98f47e4a67e4a94e9df50b5/IEC-62351-3-2023.pdf (accessed on 1 September 2025).
- Cindrić, I.; Jurčević, M.; Hadjina, T. Mapping of Industrial IoT to IEC 62443 Standards. Sensors 2025, 25, 728. [Google Scholar] [CrossRef]
- Ishfaq, H.; Kanwal, S.; Anwar, S.; Abdussalam, M.; Amin, W. Enhancing Smart Grid Security and Efficiency: AI, Energy Routing, and T&D Innovations (A Review). Energies 2025, 18, 4747. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).