Abstract
Using the analytic method based on the Biot–Savart law for the electromagnetic field, the distribution of the magnetic field of a ribbon busbar of finite length was determined. The analytical formulas describing the magnetic field in all areas of the considered ribbon busbars were obtained. The Mathematica program was used to visualize the solutions obtained. The Mathematica programme is a good and convenient tool for analytical measurements using the integration function and conversion of the analytical solutions, for the determination of field quantities, and for the graphical visualisation of the obtained final solutions. This allowed for quick field analysis to be conducted after changes were made in the geometrical or electrical parameters of the systems under examination.
1. Introduction
In the course of teaching the electromagnetic field theory, challenges often arise that require extensive calculations, not only in numerically solving problems [1,2,3,4,5,6,7,8,9] but also in their analytical resolution—involving integration, differentiation, rearrangement, and condensation of expressions, as well as seeking special solutions for terminal values of certain parameters or terminal domains [10,11,12,13,14,15]. The swift visualization of the obtained solutions is equally important, particularly spatial visualization, which enables us to understand the geometrical changes in a given configuration, the values of electrical parameters (current, voltage, external electric and magnetic fields, frequency, etc.), and the electrical parameters of the configuration (conductivity, permittivity, and magnetic permeability, etc.) [10,12,16,17,18,19,20]. Possessing a suitable tool to accomplish these objectives is highly instructive, aiding in memorizing analysed issues and assisting students in understanding and interpreting derived formulas. This enables a deeper insight into the characteristics of the electromagnetic field [13,14].
Tools such as QuickField, Flux, Comsol, Matlab, Agros, and Ansys are specialized instruments that can be used for solving field problems [21,22,23,24,25,26,27]. However, various mathematical programs can be easily applied to solve electric field problems. MatCad and Mathematica are undoubtedly classified among these programs [28,29]. The Mathematica program offers advanced tools for data visualization and computation results, allowing for the presentation of findings in an attractive and clear manner. It is well-regarded among a wide range of users, including scientists, engineers, students, and professionals from various fields.
A precise determination of the magnetic field is necessary in the context of electromagnetic compatibility, which requires thorough determination of magnetic field intensities at industrial frequencies. Magnetic fields can be determined using analytical or analytical–numerical methods employing the vector magnetic potential [30]. From classical electrodynamics formulas, electromagnetic fields can be determined in all areas of busbar conductors, as well as the current density in phase conductors, consequently leading to the flow of phase currents. In works [31,32], authors derived formulas for the self-inductance of a finite-length rectangular busbar conductor using the method of integral equations. Similarly, in works [33,34], authors applied the method of integral equations to determine the impedance of an isolated rectangular busbar conductor at low frequencies, while also comparing the obtained results with those derived from currently used formulas available in the professional literature.
This analysis will demonstrate the process of determining the magnetic field in a busbar with a long rectangular cross-section, a busbar of finite length, and its surroundings using the Mathematica program [35]. The solution obtained will be utilized by the Mathematica program to describe the magnetic field around a ribbon busbar with finite length. The manuscript presents an extension of the author’s work [36]. All the shown formulas enable the calculation of the magnetic field at any point in systems of ribbon busbars, including three-phase systems, under both current symmetry and asymmetry. The derived formulas can be utilized in the design of rectangular busbars [32,33,34] and in superconducting applications [37,38,39]—for calculating the electromagnetic field and current densities in phase conductors—thus resulting in the distribution of phase currents [40,41,42,43,44].
2. The Magnetic Field of a Long Rectangular Busbar
Suppose we have a rectangular busbar with dimensions (Figure 1) carrying a constant or low-frequency sinusoidal current with the complex RMS value I. Therefore, at each point of the busbar, the current density is constant and equal to
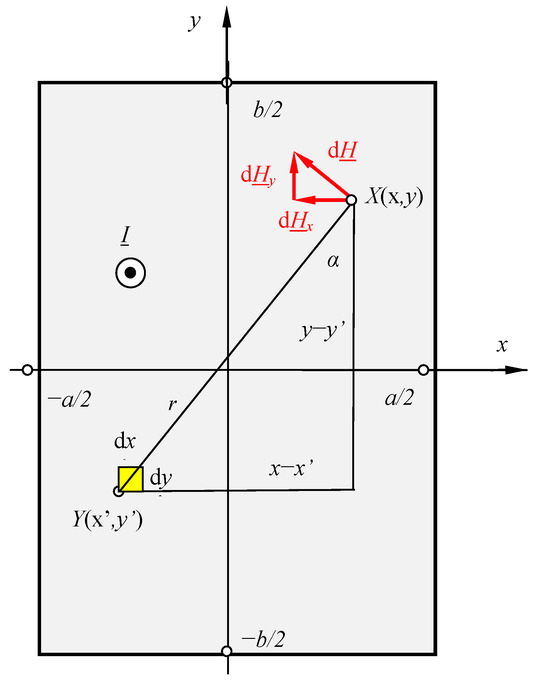
Figure 1.
Rectangular busbar carrying current I.
The magnetic field in any point , on the inside or outside of the busbar, can be calculated as a superposition of the fields generated by the current at source pointss with a distance of r from point —Figure 1. For point , we assume the elementary area as
Next, as the current density in the cross-section of the busbar is constant, the current of the busbar can be calculated as
According to the Biot–Savart law, there is an elementary magnetic field strength vector in point :
where , , and are unit vectors of the Cartesian coordinate system. is the unit vector of vector connecting point and point , while and are the components of vector . Distance can be obtained as follows:
Vector module (4):
Therefore, we can calculate the and components of the total magnetic field strength vector using the following integrals:
and
In the outer area of the busbar (i.e., for ), the observation point will never coincide with the source point , and the integrals above are proper.
In the inner area of the busbar (i.e., for ), the observation point may coincide with the source point , and the integrals above are improper but convergent. The issue of convergence for these integrals occurs in the second integration. The solution results in a component of magnetic field strength along the Ox axis
Due to the denominators of functions inverse to trigonometric functions in Formula (11), it is necessary to calculate the component on the upper and lower sides of the busbar cross-section, which results in the following:
and
Similarly, we can calculate the component of the magnetic field strength along the Oy axis to acquire the following:
In this case, it is also necessary to calculate the component on the right and left sides of the busbar cross-section, which results in
and
The formulas specified above allow us to calculate the components of the magnetic field strength in any point inside a rectangular busbar. The total magnetic field module is calculated using the following formula:
If we only use Formulas (11) and (12), it should be noted that these formulas also describe the magnetic fields of the outer area of the busbar.
The formulas derived above describe the magnetic field in a rectangular cross-section busbar and are very complex, making it difficult to predict the changes in magnetic field distribution after changing, for example, the cross-section dimension ratio of the busbar. However, any software with a graphic module (e.g., Mathematica) will offer a ready-made, excellent tool for quick visualisation of the solutions [35]. In the considered case of a busbar, the distribution of magnetic field strength module at any point on the inside or outside of the busbar is illustrated in Figure 2 [45], where the field is expressed in relative units, as the following function:
where the reference of the magnetic field is
and , as if the magnetic field at a given point was calculated for a current-carrying busbar located at the origin of the coordinate system, i.e., for a thread wire.
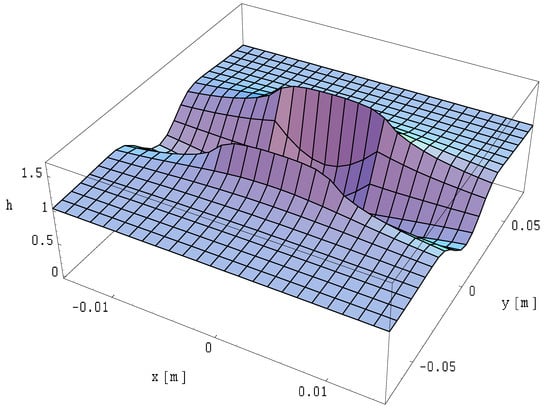
Figure 2.
Distribution of the magnetic field strength module in the inner and outer area of a rectangular cross-section busbar; .
The distribution of the module of this field on a cross-section plane of the busbar is illustrated in Figure 3.
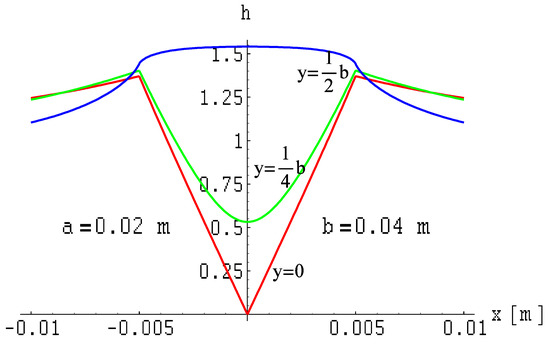
Figure 3.
Distribution of the magnetic field module on a cross-section plane of a rectangular busbar; .
From Figure 3, it follows that the magnetic field inside the busbar as well as outside the busbar significantly differs from the magnetic field calculated from the Biot–Savart law (for a thread wire). Considering the dimensions of the busbar with a uniform current density distribution, the magnetic field inside the busbar may be smaller as well as larger than the field calculated at these points from the thread wire. In the external region of the busbar, the magnetic field is greater than the field generated by the thread current, and obviously, as one moves away from the origin of the coordinate system, the field becomes that of the thread current (the relative value equals one—from a large distance, the busbar appears more and more like a thread wire).
Changing the proportions between the dimensions a and b of the busbar changes the magnetic field distribution, which is illustrated in Figure 4.
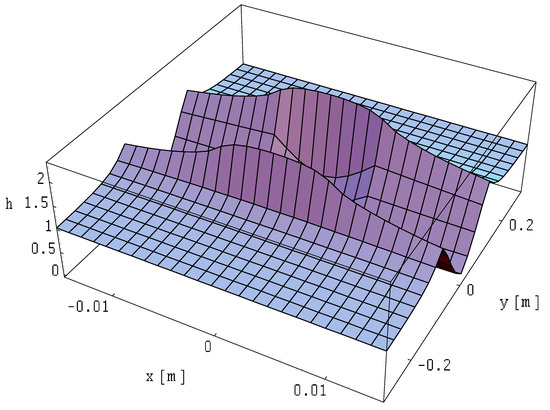
Figure 4.
Distribution of the magnetic field strength module in the inner and outer area of a rectangular cross-section busbar; .
3. The Magnetic Field of a Long Ribbon Busbar
In the case of a long ribbon busbar (i.e., a busbar with a rectangular cross-section where ), the magnetic field generated by a constant or low-frequency sinusoidal current with a complex RMS value in any point is much easier to calculate than in the case of a rectangular busbar because the calculation requires a single integration. Additionally, it is possible to limit the solution to the wire’s axis of symmetry.
However, if we already have Formulas (11) and (12), we can calculate the magnetic field components by determining the limits of these functions with the cross-section dimension of the busbar . Therefore, we have the following formulas:
and
In special cases, from the above formulas, we obtain the following:
- Field strength on the Ox axis asand
- Field strength on the Oy axis asand
The distribution of the magnetic field module around the ribbon busbar is illustrated in Figure 5. The field is expressed in relative units, with Function (14), where the reference of the magnetic field corresponds to (15).
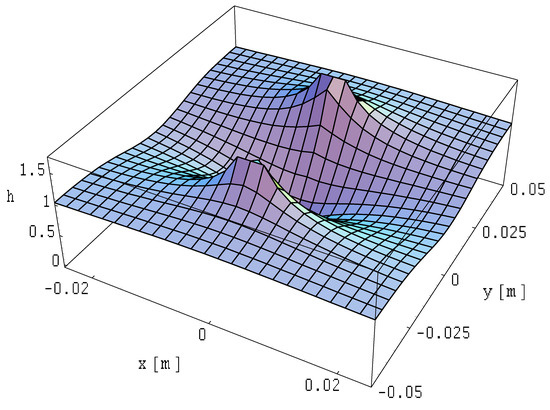
Figure 5.
Distribution of the magnetic field strength module around the ribbon busbar; .
4. The Magnetic Field of a Ribbon Busbar of Finite Length
In the case of a ribbon busbar of length l (Figure 6), if we already have formulas from the works [20,42,43,44], we can calculate the magnetic field components by determining the limits of these functions (the details are located in Appendix A) with the cross-section dimension of the busbar . Therefore, we obtain the following formulas:
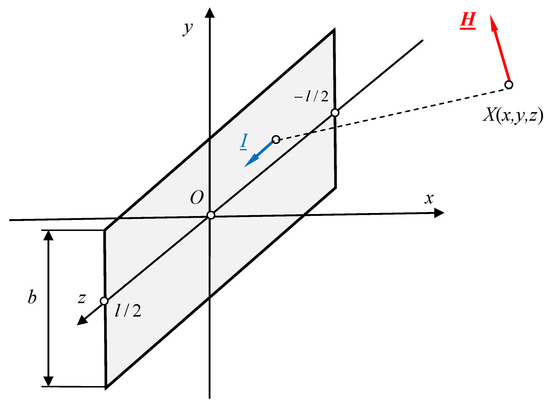
Figure 6.
Ribbon busbar of finite length.
- The magnetic field strength component along the Ox axis is
- The magnetic field strength component along the Oy axis is
In special cases where point is on the xOy plane (i.e., for ), the components can be calculated using the following formulas:
and
Moreover, on the Ox axis, these components are
and
If point is on the Oy axis, the magnetic field components are
and
The depiction of the magnetic field module distribution for a ribbon busbar of finite length on the xOy plane is presented in Figure 7. The field is represented in relative units according to Formula (14), where the magnetic field strength module is
and the reference of magnetic field is
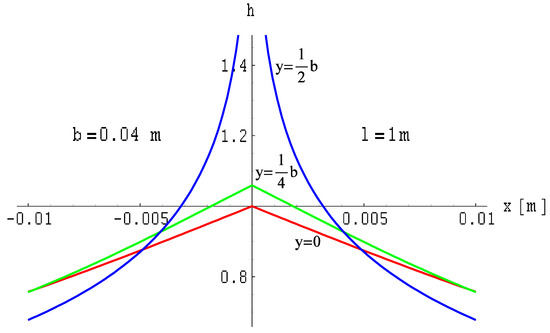
Figure 7.
Magnetic field module distribution on the xOy plane for a ribbon busbar of finite length.
The impact of the busbar length on the magnetic field distribution is depicted in Figure 8 and Figure 9.
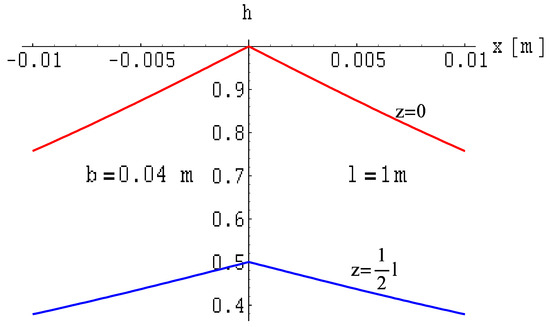
Figure 8.
Distribution of the magnetic field module on planes where z = const. of a ribbon busbar of finite length.
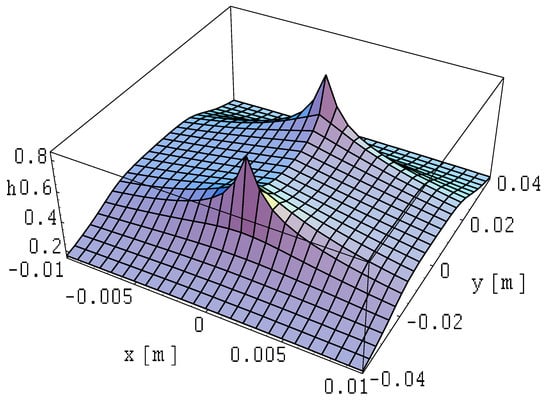
Figure 9.
Spatial distribution of the magnetic field module on the plane of a ribbon busbar of finite length; .
5. Results and Discussion
5.1. The Magnetic Field of a Line with Two Ribbon Busbars of Finite Length
Suppose we have a line made of two ribbon busbars with dimensions and distance d between the busbars (Figure 10), carrying a constant or low-frequency sinusoidal current with complex RMS values and .
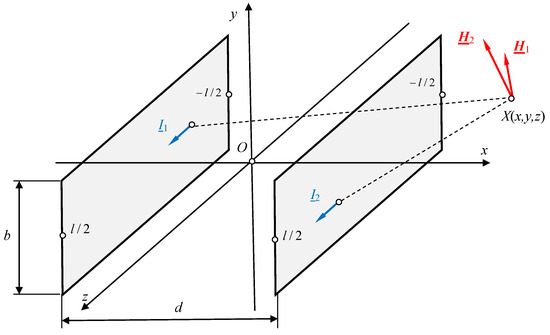
Figure 10.
A line with two ribbon busbars of finite length.
The approach for computing the magnetic field strength at any given point remains consistent, as seen in the scenario of a line featuring two rectangular busbars [30,34]. The illustration of the total magnetic field module distribution on the xOy plane for a two-busbar line, where the current direction is identical for each busbar (i.e., where ), is presented in Figure 11. The field is represented in relative units based on Formula (14) with the magnetic field reference being (31).
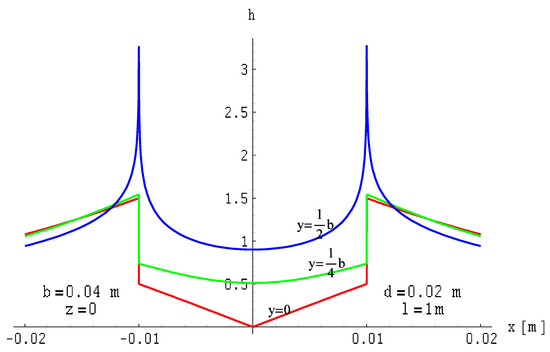
Figure 11.
Distribution of the total magnetic field module of a two-wire line with ribbon busbars of finite length on the xOy plane where the current direction is symmetrical.
The relation between the length of the busbar and total magnetic field distribution is illustrated in Figure 12 and Figure 13. If the current in the busbars flows in opposite directions (i.e., where ), the distributions of the magnetic field modules are as illustrated in Figure 14, Figure 15, and Figure 16, respectively.
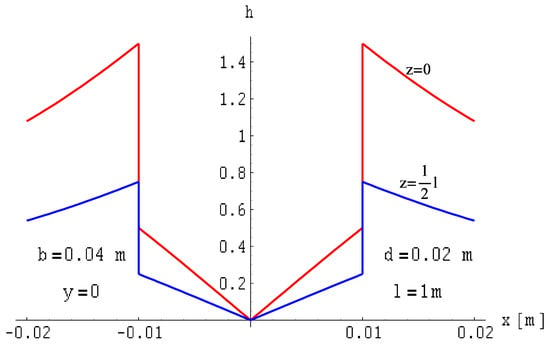
Figure 12.
Distribution of the total magnetic field module on planes where z = const. of two-wire line with ribbon busbars of finite length, where .
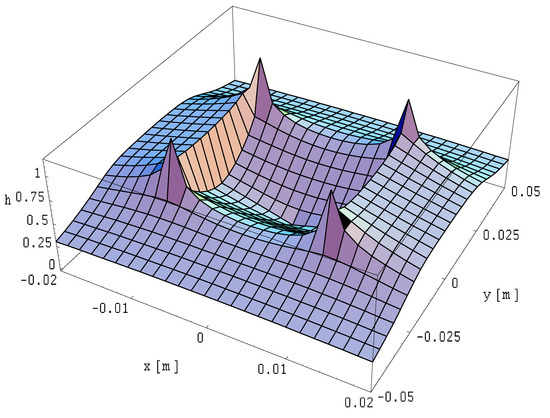
Figure 13.
Spatial distribution of the magnetic field module on plane of a two-wire line with rectangular busbars of finite length, where ; .
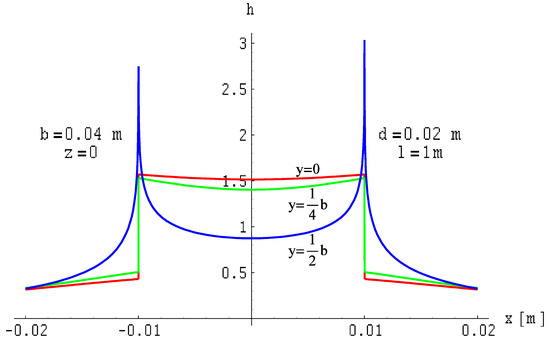
Figure 14.
Distribution of the total magnetic field module of a two-wire line with ribbon busbars of finite length on the xOy plane for opposite current.
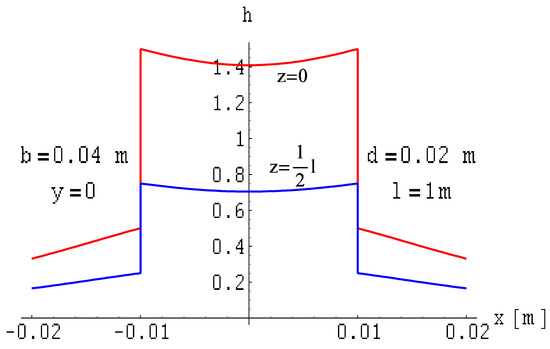
Figure 15.
Distribution of the total magnetic field module on planes where z = const. of a two-wire line with ribbon busbars of finite length, where .
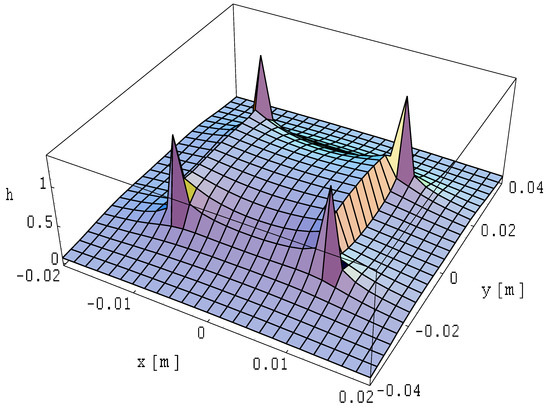
Figure 16.
Spatial distribution of the magnetic field module on a plane of a two-wire line with rectangular busbars of finite length, where ; .
5.2. The Magnetic Field Characteristics of a Three-Phase Line with Three Ribbon Busbars of Finite Length
Consider a three-phase line composed of three ribbon busbars with dimensions and a distance d between the busbars (refer to Figure 17). These busbars carry a constant or low-frequency sinusoidal current with complex RMS values , , and .
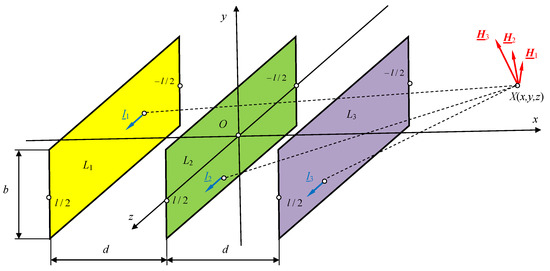
Figure 17.
Three-phase line with three ribbon busbars of finite length.
The approach for calculating the magnetic field strength at point remains consistent with the method applied in the case of a three-phase line featuring three rectangular busbars. The illustration of the total magnetic field module distribution on the xOy plane for a three-phase three-busbar line, where the current in the busbars is symmetrical (i.e., where , , and ), is presented in Figure 18. The field is quantified in relative units as a function using Formula (14), with the magnetic field reference outlined in Formula (31). The relationship between the length of the busbars and the overall magnetic field distribution in such a line is depicted in Figure 19 and Figure 20.
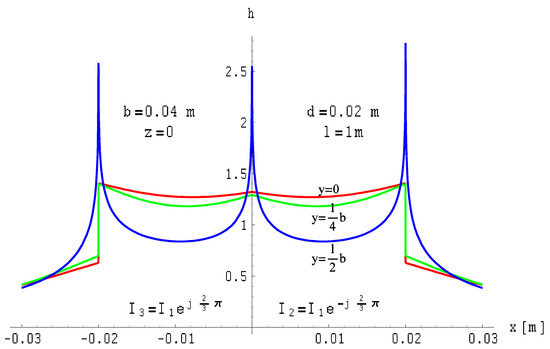
Figure 18.
Distribution of the magnetic field module of a three-wire three-phase line with ribbon busbars of finite length on the xOy plane for symmetrical currents.
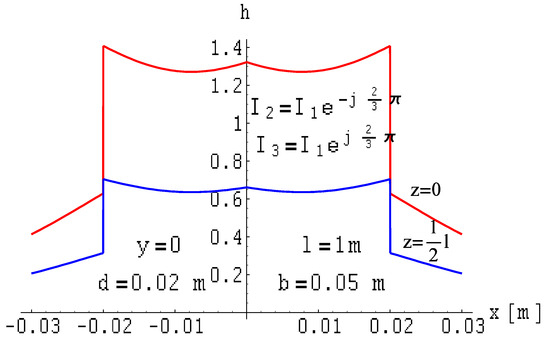
Figure 19.
Distribution of the magnetic field module of a three-wire three-phase line with ribbon busbars of finite length on planes where z = const. for symmetrical currents.
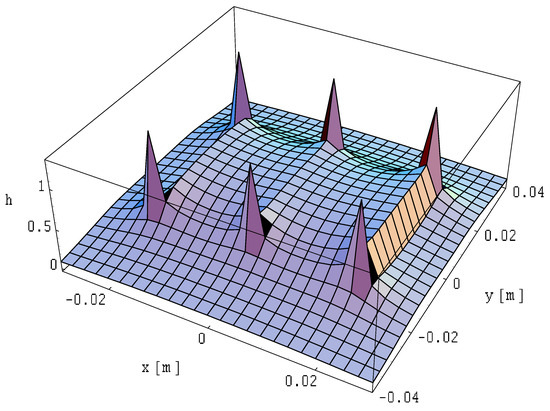
Figure 20.
Spatial distribution of the magnetic field module on the plane of a three-wire three-phase line with ribbon busbars of finite length for symmetrical currents; .
Current asymmetry changes the magnetic field distribution around the considered. As an example, the following phase currents were assumed: and . Therefore, this results in . The field distributions for this case are illustrated in Figure 21, Figure 22 and Figure 23.
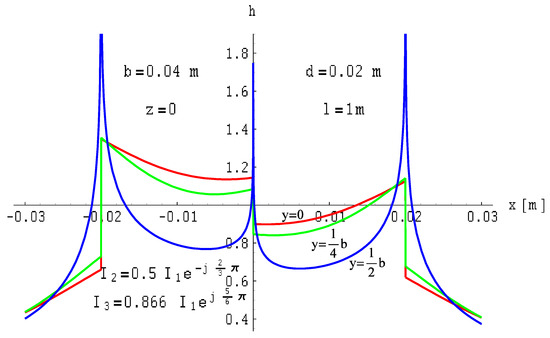
Figure 21.
Distribution of the magnetic field module of a three-wire three-phase line with ribbon busbars of finite length on the xOy plane for asymmetrical currents: , , and .
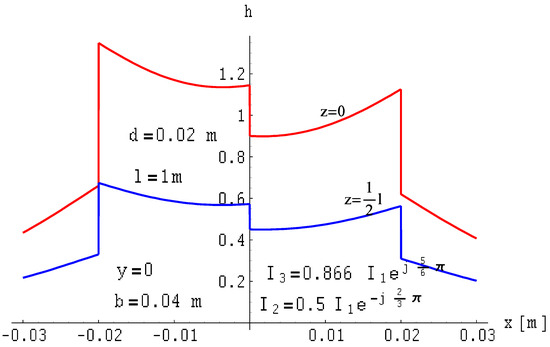
Figure 22.
Distribution of the magnetic field module of a three-wire three-phase line with ribbon busbars of finite length on planes where z = const. for asymmetrical currents: , , and .
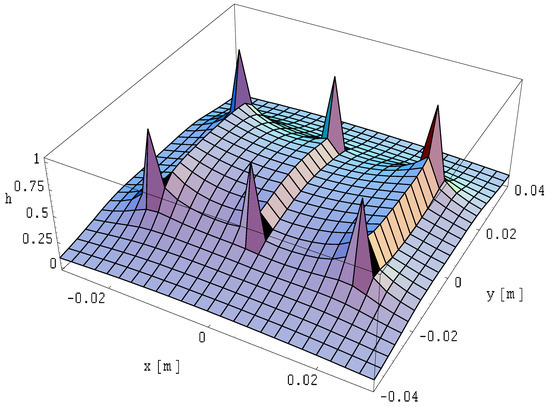
Figure 23.
Spatial distribution of the magnetic field module on a plane of a tree-wire three-phase line with ribbon busbars of finite length for asymmetrical currents: , , and ; .
5.3. The Magnetic Field of a Three-Phase Line with Four Ribbon Busbars of Finite Length
Suppose we have a four-wire hight current line with ribbon busbars of dimensions and distance d between the busbars (Figure 24), with current asymmetry , , and , with the current in the neutral rail being .
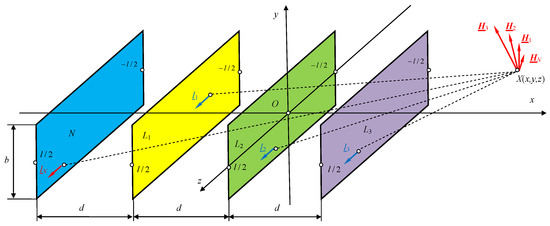
Figure 24.
Three-phase line with four ribbon busbars of finite length.
The field distributions for this case are illustrated in Figure 25, Figure 26 and Figure 27. The field is expressed in relative units as a function provided by Formula (14), where the reference of the magnetic field is expressed in Formula (31).
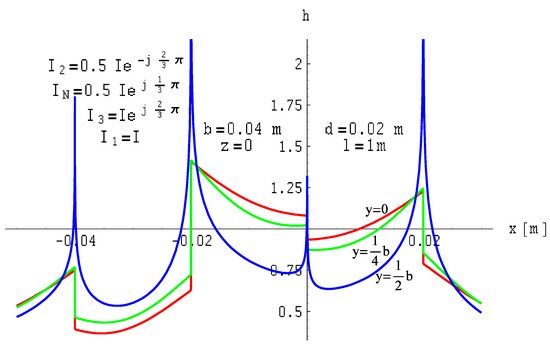
Figure 25.
Distribution of the magnetic field module of a four-wire three-phase line with ribbon busbars of finite length on the xOy plane for asymmetrical currents.
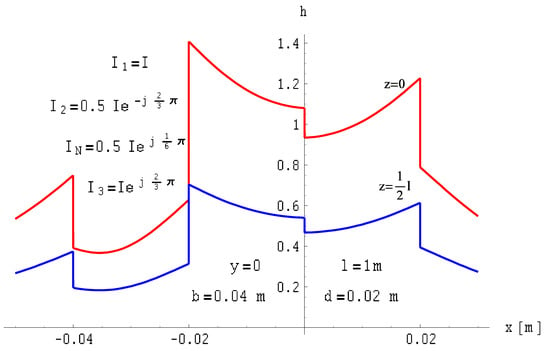
Figure 26.
Distribution of the magnetic field module of a four-wire, three-phase line with ribbon busbars of finite length on planes where z = const. for asymmetrical currents.
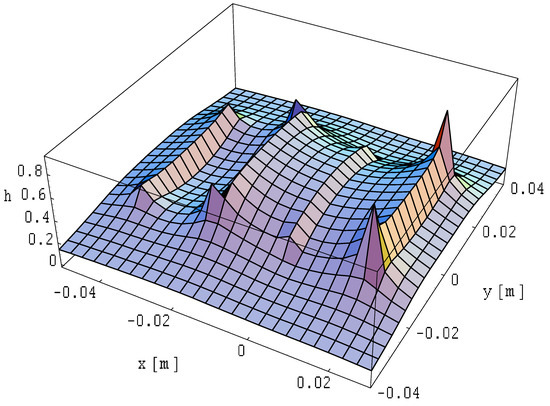
Figure 27.
Spatial distribution of the magnetic field module on plane of a four-wire three-phase line with ribbon busbars of finite length for asymmetrical currents: , , , and ; .
6. Conclusions
The formulas derived above describe the magnetic fields in ribbon busbars and are very complex, making it difficult to predict the changes in magnetic field distribution after altering, for example, the length of the busbar. However, any software with a graphic component (e.g., Mathematica), will offer a ready-made, excellent tool for a quick visualisation of solutions. Therefore, as illustrated in the figures above, it is possible to quickly analyse the magnetic field of a ribbon busbar after changes are made in the geometrical or electric parameters of the examined circuits.
This article derives analytical formulas, which is a huge advantage over numerical solutions. Analytical formulas allow us to obtain precise solutions to problems concerning the magnetic field, depending on their complexity (in this case, for various cases of strip conductors). In contrast, numerical solutions may carry some error, which can vary depending on the numerical methods used and the precision of calculations (their accuracy primarily depends, for example, on the discretization grid and associated computation time). Analytical formulas enable a deeper understanding of the nature of the problem and the mathematical relationships and theories of the electromagnetic field associated with it. They can reveal certain properties or symmetries that may be more challenging to detect with numerical solutions.
Funding
This research received no external funding. The APC was funded by the Czestochowa University of Technology.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
The author is grateful to the Dean of Faculty of Electrical Engineering, Marek Lis, for providing partial financial support to cover the APC from the statutory funds for research carried out at the Faculty of Electrical Engineering, CUT, BS/PB-3-300-3011/2024/P.
Conflicts of Interest
The author declares no conflicts of interest.
Appendix A
Equations (22) and (23) are obtained from the formulas of the magnetic field’s components for a finite-length rectangular busbar. The component of the magnetic field’s strength along the Ox axis takes the following form:
Due to the denominators of the inverses of trigonometric functions in Formula (A1), it is necessary to determine this component on the upper and lower sides of the cross-sectional area of the conductor, which results in the following:
and
The component of the magnetic field’s strength along the Oy axis takes the following form:
Due to the denominators of the inverses of trigonometric functions in Formula (A4), it is necessary to determine this component on the right and left sides of the cross-sectional area of the conductor, resulting in the following:
and
For the same reasons as above, in Formulas (A1) and (A4), it is necessary to determine these components on the xOy plane. Then, the component is as follows:
Also, on the xOy plane, it is necessary to determine the component on the upper and lower sides of the cross-sectional area of the conductor, resulting in the following:
and
The component of the magnetic field along the Oy axis on the xOy plane takes the following form:
Moreover, the above component on the right and left side of the cross-sectional area of the conductor is given by the following formulas:
and
All the above formulas determine the complex components of the magnetic field’s strength at any point inside and outside a rectangular busbar of finite length.
References
- Sarajcev, P. Numerical Analysis of the Magnetic Field of High-Current Busducts and GIL Systems. Energies 2011, 4, 2196–2211. [Google Scholar] [CrossRef]
- Kusiak, D. The magnetic field and impedances in three-phase rectangular busbars with a finite length. Energies 2019, 12, 1419. [Google Scholar] [CrossRef]
- Koch, H. Gas-Insulated Transmission Lines; John Wiley&Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Karban, P.; Pánek, D.; Orosz, T.; Petrášova, I.; Doležel, I. FEM based robust design optimization with Agros and Ārtap. Comp. Math. Appl. 2021, 81, 618–633. [Google Scholar] [CrossRef]
- Yousuf, H.; Zahid, M.A.; Khokhar, M.Q.; Park, J.; Ju, M.; Lim, D.; Kim, Y.; Cho, E.-C.; Yi, J. Cell-to-Module Simulation Analysis for Optimizing the Efficiency and Power of the Photovoltaic Module. Energies 2022, 15, 1176. [Google Scholar] [CrossRef]
- Martinez-Roman, J.; Puche-Panadero, R.; Sapena-Bano, A.; Burriel-Valencia, J. Fast Numerical Model of Power Busbar Conductors Through the FFT and the Convolution Theorem. IEEE Trans. Power Deliv. 2022, 37, 3291–3301. [Google Scholar] [CrossRef]
- Kolańska-Płuska, J.; Jabłoński, P.; Piątek, Z. Numerical Method of Computing the Impedance of a Twin High Current Busduct of Rectangular Hollow Conductors. Prog. Electromagn. Res. M 2014, 34, 9–17. [Google Scholar] [CrossRef]
- Riba, J.R. Calculation of AC to DC resistance ratio of conductive nonmagnetic straight conductors by applying FEM simulations. Eur. J. Phys. 2015, 36, 055019. [Google Scholar] [CrossRef][Green Version]
- Riba, J.R.; Capelli, F. Calculation of the inductance of conductive nonmagnetic conductors by means of finite element method simulations. Int. J. Electr. Educ. 2018, 57, 230–252. [Google Scholar] [CrossRef]
- Piątek, Z. Impedances of Tubular High Current Busducts; Series Progress in High-Voltage Technique; Polish Academy of Sciences; Committee of Electrical Engineering: Warsaw, Poland, 2008; p. 154. [Google Scholar]
- Li, B.; Shi, L.; Wen, W.; Li, B.; Gu, T. Research on the Calculation Method of Equivalent Parameters of the Core Wire for the High-Voltage GIL Metal Shell Grounded Through the Copper Bar. Front. Energy Res. 2022, 10, 813770. [Google Scholar] [CrossRef]
- Piątek, Z. Modelowanie linii, kabli i torów wielkopradowych (Modeling of Lines, Cables and High-Current Busducts); Monograph Series No. 130; Czestochowa University of Technology: Czestochowa, Poland, 2007; p. 220. (In Polish) [Google Scholar]
- Pramanik, A. Electromagnetism—Theory and Applications; PHI Learning: New Delhi, India, 2009. [Google Scholar]
- Griffiths, D.J. Introduction to Electrodynamics, 4th ed.; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Alboyacı, B.; Çınar, M.A.; Demirol, Y.B. Influence of busbar trunking system design on thermal performance operating with non-sinusoidal currents. Electr. Power Syst. Res. 2023, 214, 10881. [Google Scholar] [CrossRef]
- Wu, R.; Zou, W.; Yuan, J.; Bao, H.; Wang, S.; Liu, Y.; Yang, W. Comparison of Methods for Suppressing Circulating Current in Metal Sheath of Cables Connected in Parallel. Energies 2023, 16, 4265. [Google Scholar] [CrossRef]
- Kovalev, D.I.; Varivodov, V.N.; Golubev, D.V.; Voronkova, E.M. Calculation of Electric Fields in 6(10) kV Conductors with Solid Insulation. Power Technol. Eng. 2022, 55, 931–938. [Google Scholar] [CrossRef]
- Kotsur, M.; Yarymbash, D.; Bezverkhnia, Y.; Kotsur, I. Increasing the Accuracy of Determining the Resistance of Three-Phase Busbar’s Trolleys. In Proceedings of the 2022 IEEE 3rd KhPI Week on Advanced Technology (KhPIWeek), Kharkiv, Ukraine, 3–7 October 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Kotsur, M.; Yarymbash, D.; Bezverkhnia, Y.; Kotsur, I. Comparative analysis of a different geometric shapes of a busbar’s trolley parameters in the higher harmonic current condition. In Proceedings of the 2022 IEEE 16th International Conference on Advanced Trends in Radioelectronics, Telecommunications and Computer Engineering (TCSET), Lviv-Slavske, Ukraine, 22–26 February 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Kusiak, D.; Szczegielniak, T. Obliczenia elektromagnetyczne szynoprzewodów (Electromagnetic Calculations of Busbars); Monograph Series No. 326; Czestochowa University of Technology: Czestochowa, Poland, 2017; p. 177. (In Polish) [Google Scholar]
- QuickField. Available online: www.quickfield.com (accessed on 2 February 2024).
- COMSOL Multiphysics. Available online: www.comsol.com (accessed on 2 February 2024).
- FEMM (Finite Element Method Magnetics). Available online: www.femm.info (accessed on 2 February 2024).
- AGROS Suite. Available online: www.agros2d.org (accessed on 2 February 2024).
- MATLAB. Available online: www.mathworks.com (accessed on 2 February 2024).
- Ansys. Available online: www.ansys.com (accessed on 2 February 2024).
- Ziolkowski, M.; Gratkowski, S. Closed-Form Expressions for Local Absorbing Boundary Conditions in Electromagnetic Scattering Problems and Their Implementation into Commercial FEM Software. Energies 2024, 17, 89. [Google Scholar] [CrossRef]
- Mathcad. Available online: www.mathcad.com (accessed on 2 February 2024).
- Mathematica. Available online: www.wolfram.com/mathematica (accessed on 2 February 2024).
- Piątek, Z.; Baron, B.; Jabłoński, P.; Szczegielniak, T.; Kusiak, D.; Pasierbek, A. A numerical-analytical method for magnetic field determination in three-phase busbars of rectangular cross section. Przegląd Elektrotechniczny 2015, 91, 193–197. [Google Scholar] [CrossRef][Green Version]
- Piątek, Z.; Baron, B. Exact closed form formula for self inductance of conductor of rectangular cross section. Prog. Electromagn. Res. M 2012, 26, 225–236. [Google Scholar] [CrossRef]
- Piątek, Z.; Baron, B.; Szczegielniak, T.; Kusiak, D.; Pasierbek, A. Exact closed form formula for mutual inductance of conductors of rectangular cross section. Przegląd Elektrotechniczny 2013, 89, 61–64. [Google Scholar]
- Piątek, Z.; Baron, B.; Szczegielniak, T.; Kusiak, D.; Pasierbek, A. Inductance of a long two-rectangular busbar single-phase line. Przegląd Elektrotechniczny 2013, 89, 290–292. [Google Scholar]
- Piątek, Z.; Baron, B.; Szczegielniak, T.; Kusiak, D.; Pasierbek, A. Mutual inductance of long rectangular conductors. Przegląd Elektrotechniczny 2012, 88, 175–177. [Google Scholar]
- Gliński, H.; Grzymkowski, R.; Kapusta, A.; Słota, D. Mathematica 8; Jacek Skalmierski Publisher of the Computer Studio: Gliwice, Poland, 2012; p. 718. (In Polish) [Google Scholar]
- Kusiak, D.; Piątek, Z.; Szczegielniak, T. Magnetic Field of a Ribbon Busbar of Finite Length. In Proceedings of the Conference on Computer Applications in Electrical Engineering (ZKwE’2018), Poznań, Poland, 23–24 April 2018; ITM Web of Conferences. Volume 19, p. 0101. [Google Scholar] [CrossRef]
- Cabral, S.H.L.; Bertoli, S.L.; Medeiros, A.; Hillesheim, C.R.; De Souza, C.K.; Stefenon, S.F.; Nied, A.; Leithardt, V.R.Q.; Gonzalez, G.V. Practical Aspects of the Skin Effect in Low Frequencies in Rectangular Conductors. IEEE Access 2021, 9, 49424–49433. [Google Scholar] [CrossRef]
- Tabei, B.; Ametani, A.; Gole, A.M.; Kordi, B. Quasi-Analytical Calculation of Frequency-Dependent Resistance of Rectangular Conductors Considering the Edge Effect. Energies 2022, 15, 503. [Google Scholar] [CrossRef]
- Szczegielniak, T.; Piątek, Z.; Kusiak, D. Impedancje własne i wzajemne szynoprzewodów prostokątnych o skończonej długości (Self and mutual impedances of rectangular bus-bars of finite length). Inform. Autom. Pomiary W Gospod. I Ochr. Sr. 2014, 4, 21–24. (In Polish) [Google Scholar] [CrossRef]
- Vaskuri, A.; Curé, B.; Dudarev, A.; Mentink, M. Aluminium-Stabilized High-Temperature Superconducting Cable for Particle Detector Magnets. IEEE Trans. Appl. Supercond. 2023, 33, 4500506. [Google Scholar] [CrossRef]
- Gautam, G.; Zhang, M.; Yuan, W.; Burt, G.; Malkin, D. Fault Tolerant Superconducting Busbar With Reduced Self-Field Effect on Critical Current Design for All Electric Aircraft. IEEE Trans. Appl. Supercond. 2024, 34, 4801805. [Google Scholar] [CrossRef]
- Hou, W.; Sun, K.; Sun, S.; Li, M. Numerical Investigation of Electro-Thermal Field Distribution Law of Busbar under Different Operating Conditions. Metals 2023, 13, 1361. [Google Scholar] [CrossRef]
- Di Gerlando, A.; Negri, S.; Ricca, C. A Novel Analytical Formulation of the Magnetic Field Generated by Halbach Permanent Magnet Arrays. Magnetism 2023, 3, 280–296. [Google Scholar] [CrossRef]
- Romero-Mendez, R.; Berjano, E. Differences in the Electric Field Distribution Predicted with a Mathematical Model of Cylindrical Electrodes of Finite Length vs. Infinite Length: A Comparison Based on Analytical Solution. Mathematics 2023, 11, 4447. [Google Scholar] [CrossRef]
- Mathematica, version 7.0.1. Software Used; License Number: L4726-9731 (for Czestochowa University of Technology). Wolfram Research, Inc.: Champaign, IL, USA.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).