A Cooperative Multi-Agent Q-Learning Control Framework for Real-Time Energy Management in Energy Communities

Abstract

Residential and commercial buildings are responsible for 35% of the EU energy-related greenhouse gas (GHG) emissions. Reducing their emissions is crucial for meeting the challenging EU objective of the agenda for becoming a net-zero continent by 2050. The diffusion and integration of distributed renewable energy sources (RESs) and energy storage systems (ESSs), as well as the creation of energy communities (ECs), have proven to be crucial aspects in reducing GHG emissions. In this context, this article proposes a multi-agent AI-based control framework to solve the EC’s energy management problem in the presence of distributed RESs and ESSs as well as considering a shared ESS. The objectives of the proposed control framework are to satisfy the EC members’ load demand to maximize self-consumption and to manage ESSs charging and discharging processes, to enforce cooperative behavior among the EC members by adopting fair and personalized strategies and to maximize EC members’ profits. The proposed control procedure is based on three sequential stages, each solved by a dedicated local RL agent exploiting the Q-Learning algorithm. To reduce the computational complexity of the proposed approach, specifically defined state aggregation criteria were defined to map the RL agents’ continuous state spaces into discrete state spaces of limited dimensions. During the training phase, the EC members’ profiles and the ESSs’ and RESs’ characteristics were randomly changed to allow the RL agents to learn the correct policy to follow in any given scenario. Simulations proved the effectiveness of the proposed approach for different costumers’ load demand profiles and different EC configurations. Indeed, the trained RL agents proved to be able to satisfy the EC members’ load demands to maximize self-consumption, to correctly use the distributed and shared ESSs, to charge them according to respective personalized criteria and to sell the energy surplus, prioritizing sales to the EC. The proposed control framework also proved to be a useful tool for understanding EC performance in different configurations and, thus, for properly dimensioning the EC elements.

1. Introduction

The last decades have witnessed a constantly increasing attention toward the definition of common strategies to deal with climate change. In this respect, the Organization of United Nations (ONU) and the European Union (EU) have defined medium- and long-term strategies with challenging goals, including the reduction of 55% of net greenhouse gas (GHG) emissions by 2030 [1] and becoming a climate-neutral continent by 2050 [2], respectively. To achieve these challenging objectives, a crucial aspect is tackling residential and business buildings’ emissions. Indeed, buildings account for 35% of the EU emissions related to energy production [3]. The diffusion and integration of distributed renewable energy sources (RESs) and energy storage systems (ESSs) with the traditional electric grid and/or microgrids, peer-to-peer (P2P) energy trading, and the creation of energy communities (ECs) have been identified as crucial tools to tackle the buildings’ emissions reduction problem [4,5]. With respect to ECs, several EU directives have been published to regulate ECs’ implementation rules, principles and setup criteria and for specifying the roles of all the involved actors [6,7,8].

Energy communities are defined as citizen-driven local communities aimed at cooperating for more efficient and cleaner energy production and consumption. Beyond technical research activities on efficient materials, ECs require intensive research on the best energy management policies that allow for meeting the EU-specified criteria and maximizing customer satisfaction. These policies may include one or more of the following aspects: accurate energy production forecasts, intelligent ESS charging and discharging strategies, cooperative satisfaction of EC members’ load demands, and the smart exchange of surplus energy. In this article, the energy forecast problem will not be addressed. The proposed control framework oversees understanding, in real-time, of the best energy management strategy with respect to the EC members’ load demand satisfaction, the ESS charging problem, and the energy surplus management problem. In this respect, the next subsection will present a literature review related to these aspects. More specifically, since the most recent EU policy updates were made in 2022 and 2023, the literature review will focus on the most recent articles related to ECs in which the new directives’ principles have been considered.

1.1. Related Works

Energy communities are characterized by the presence of many members, each of whom may have a local ESS and/or RES, as well as different comfort levels. As already mentioned, beyond the load satisfaction problem, other issues shall be addressed, such as the ESS charging and discharging processes, the maximization of self-consumption, the promotion of collaborative behaviours and the management of energy surplus.

In the literature, several articles focus on the analysis of the environmental and economic benefits of real-world use cases. In [9], for example, the authors investigate the economic benefits of the joint use of multiple energy sources such as photovoltaic (PV) systems, ESSs and hydrogen sources. The article’s case study is the EC campus of the Marche Polytechnic University (UNIVPM) located in Ancona, Italy. The authors propose a mixed-integer linear programming (MILP) optimization model to reduce GHG emissions by considering energy source installation, operation and maintenance costs. In [10], the environmental and economic benefits of a renewable energy community (REC) with a shared PV system located in Rome, Italy, are discussed. In [11], the authors investigate the impact of distributed renewable energy systems in a real-world scenario located in Italy. To evaluate the benefits of distributed RESs, the authors consider not only economic aspects but also socio-economic aspects such as unemployment rates and population conformation. The particularity of this article relies on the specific application domain investigated, which is an area subject to reconstruction activities after the 2009 and 2016 earthquakes. In [12], the authors investigate the impact of climate change on PV energy production, analysing three different representative concentration pathway scenarios, starting from a pessimistic scenario to an optimistic one. The results confirmed that the average temperature increase, as a consequence of climate change, has an impact on the efficiency of RES production. Nevertheless, the article points out that the compensation due to the increase in radiation leads to a general improvement of the annual energy production of PVs, even in the pessimistic scenarios. In [13,14], the authors provide a state-of-the-art analysis on European and Italian ECs, with a focus on the city of Naples, Italy. Energy communities located in Naples have also been the focus of [15], in which several optimization methods have been adopted to foster the transition of buildings to a nearly zero-energy community by evaluating multiple possible EC features. The authors use a brute force algorithm to select the most appropriate EC features. In [16], the authors perform an analysis of a REC located in Magliano Alpi, Italy, using load shifting. The authors introduce several key performance indices (KPIs) useful for evaluating Italian EC performances. In [17], the authors analyse the performance of a REC set up in Austria, under forecasting and price uncertainties, developing a MILP-based MPC framework. In [18], the authors analyse the impact of different types of ESS management for a REC located in Florence, Italy, proposing a smart ESS management method for collective self-consumption. The results have shown better performances than the method for individual self-consumption. In [19], the authors describe a Deming Cycle-based approach for managing Italian ECs, considering both physical and virtual self-consumption to reduce GHG emissions, to prevent energy poverty and to optimize RECs’ and customers’ profits. The proposed approach has been validated in an EC located in Sicily, Italy. The results show good performance in facilitating the setup of such communities and with respect to the considered objectives. Energy poverty reduction has also been considered in [20], in which the authors present an optimization model to dimension energy source capacity and to manage shared energy under the Italian regulatory framework. The proposed model considers both physical and virtual sharing schemes in centralised and decentralised configurations, as well as the influence of different ESS configurations. The results have confirmed economic, environmental and social benefits for EC members and the EC itself. In [21], a three-stage optimization method for the management of EC shared energy under the Portuguese regulatory framework is presented. The proposed algorithm minimizes individual and collective energy costs and manages the flexible resources of EC members and the EC itself. The authors also consider grid constraints, exploiting the degrees of freedom provided by the available energy resources and, eventually, by the local energy generation and/or consumption. The proposed algorithm is based on an MILP optimization problem.

A similar solution based on a multi-stage optimal control-based approach has been presented in [22]. The authors propose a two-stage optimization algorithm to manage an EC with shiftable ESS and electric vehicles (EVs), satisfying EC members’ load demands and improving EC flexibility. The proposed model also takes into account customers’ preferences and their interaction with the community manager (who acts as a local market operator) for the energy sharing process. The presence of EVs is also considered in [23], where the authors envisage the presence of EVs, heat pumps and thermal ESSs. The objective of this approach is to minimize customers’ bill costs and EV battery degradation. The proposed solution exploits a two-stage MPC-based method that takes into account customers’ thermal preferences.

In [24], the authors propose the use of a decentralised autonomous organizational (DAO) model for the management of RECs to improve members’ participation and cooperation in sustainable projects, and to cope with scalability and flexibility issues. In [25], the integration of distributed energy resources (DERs) in microgrids is discussed. The article also explores the use of blockchain technologies to enable EC setup while preserving the microgrid’s reliability, stability and flexibility. To support investment decisions in ECs, Ref. [26] presents an optimisation model focusing on RECs for the generation of green energy and the promotion of internal energy sharing. Ref. [27] analyses the economic benefits of participating in P2P energy trading among different energy communities, developing a mathematical model with constraints as a game with multiple leaders, a distribution system operator (DSO) and a market operator. In [28], an economic analysis of ECs is proposed. The authors describe an optimization model based on self- and third-party investments while also considering different pricing schemes for determining energy costs. A smart definition of energy costs has also been addressed in [29], in which the authors propose a real-time optimization method. The proposed solution adopts a linear quasi-relaxation approach and dynamic partitioning technique. Ref. [30] performs a variance-based sensitivity analysis focusing on the influence of (i) forecasting uncertainties and (ii) resource availability and flexibility in REC management. The authors state that this sensitivity analysis can be used as a supportive decision-making tool to evaluate energy performance in uncertain environments.

An interesting solution is proposed in [31], in which the authors combine an optimal control-based approach (a MILP-based algorithm) and deep reinforcement learning (DRL) algorithm. The proposed solution is able to maximize social and economic benefits while taking into account the role of ESS in balancing REC demand. In [32], an analysis of the influence of EC customers’ preferences in a decentralised EC framework is presented. The authors focus on the assignment of collective renewable energy under different fairness policies. DRL is also adopted in [33], in which the authors focus on developing energy-aware distributed cyber-physical systems (DCPS) exploiting the cloud and edge computing paradigms. The proposed approach considers the presence of RESs and exploits DRL algorithms to forecast their energy production to optimize energy usage. In [34], the authors focus on the energy sharing problem and address it by means of a DRL algorithm. More specifically, the Deep Q-Network (DQN) algorithm is used to learn the energy consumption behaviour of a household and a centralized agent is used to compute the energy status of the EC. The individual DRL agents receive data regarding the energy status and obtain a reward which will induce a cooperative behaviour. In [35], instead, the authors focus on community energy storage systems (CESSs) allowing flexible energy sharing among EC members. Deep learning techniques are used to forecast RES energy production, whereas hybrid optimization techniques are used to cluster EC members and to provide the optimal management of RESs and the shared ESSs. In [36], the authors investigate the benefits of P2P energy trading in the presence of distributed ESSs and RESs, considering multiple application scenarios. The proposed control framework to manage the P2P energy trading is based on a multi-agent DRL algorithm trained in a decentralized environment.

Table 1. Comparison of reviewed articles.

Ref.	Problem Addressed	Methodology	F1	F2	F3	F4	F5	F6	F7	F8	F9
[9]	Optimal planning of shared energy sources applied to the campus of the Marche Polytechnic University (UNIVPM)	MILP (Calliope)	✕	✓	✕	✓	✓	✕	✕	✕	✕
[10]	PV sizing to meet customers load demand in the REC of the northwest area of the Municipality of Rome	-	✕	✓	✕	✕	✓	✕	✕	✕	✕
[15]	Multi-objective energy optimization applied to nearly zero-energy community	Brute-force search (MATLAB®)	✕	✓	✕	✓	✓	✓	✕	✕	✕
[17]	Optimal scheduling of energy sources, considering uncertainties, applied to a REC located in Austria	MILP-MPC framework	✕	✓	✕	✓	✓	✓	✓	✕	✕
[18]	Study of several battery management systems applied to a REC located in Florence	MILP-based	✕	✓	✓	✓	✓	✓	✓	✕	✕
[21]	Multi-objective optimal scheduling of EC’s energy sources to reduce individual and collective energy bill’s cost while considering economic benefits and grid constraints	MILP	✕	✓	✓	✕	✓	✓	✕	✓	✕
[22]	Optimal scheduling of EC energy sources, considering BESS and EVs as flexible units	Mathematic programming (MATLAB and GAMS solver)	✕	✓	✓	✕	✓	✓	✕	✕	✓
[31]	Optimal management of RECs, considering BESS charging and discharging processes and virtual self-consumption incentives	Hybrid DRL and MILP approach	✕	✓	✓	✕	✓	✓	✕	✕	✕
[32]	Fair scheduling of the EC’s renewable energy sources	Game theory approach based	✓	✓	✕	✕	✓	✕	✕	✓	✓
[33]	Data-driven approach to support RECs, considering load and RES forecasting	DL approaches (LSTM and BiLSTM)	✕	✓	✕	✕	✓	✕	✓	✕	✕
[34]	Maximization of the energy shared in a Zero EC using a multi-agent DRL approach	Multi-agent DQN	✓	✓	✓	✕	✓	✕	✕	✕	✕
[35]	Optimal energy management of ECs by using (i) a hybrid algorithm for PVs and a community ESS and (ii) a DRL-based method for forecasting	Clustering, and DRL-based method for forecasting	✕	✓	✕	✓	✓	✓	✓	✕	✕
[36]	Optimal P2P DRL-based framework to perform EC’s energy sharing while minimizing electricity costs and considering EV charging and discharging processes	Smart bidding and Multi-agent Fuzzy Q-Learning	✓	✓	✓	✕	✓	✓	✕	✕	✕
Present Article	Multi-objective and multi-agent EC’s energy management to minimize customers’ bill cost and Grid dependency while handling ESS charging process and surplus management	Multi-agent Q-Learning	✓	✓	✓	✓	✓	✓	✕	✓	✓

summarizes the findings of the literature review. The articles have been compared based on nine main features, as described in the following. F1 captures the nature (decentralized/distributed versus centralized) of the proposed control framework. F2 and F3 indicate whether distributed RESs and ESSs have been considered, respectively. F4 specifies whether, in the adopted EC model, a shared ESS was considered. F5 and F6 specify whether the energy surplus and ESS charging process management problems have been considered, respectively. F7 describes whether, in the proposed control framework, load demand and RESs’ energy production forecasts have been embedded. F8 captures the inclusion of fairness principles in the energy management control problem. In the context of energy communities, fairness is defined with respect to (i) decision-making processes and (ii) benefits and costs sharing [37]. The former aspect has been tackled in the literature from the design and investment point of view [38,39,40]. The latter element has been addressed by developing fair P2P energy trading strategies [41,42,43] or fair energy transactive market policies [44,45]. Table 1 describes whether at least one of these aspects has been considered. Finally, F9 specifies whether EC members’ personalized comfort levels have been considered. Based on such features, it is possible to state the following. Most of the articles based on real-world use cases focus on analysing the economic and environmental benefits of given ECs rather than on the control problems related to the EC energy management. Some articles describe the control algorithms proposed to solve the energy management problem, and they mostly involve the adoption of optimal control-based approaches (e.g., MILP and MPC). This type of solution has the advantage of providing the optimal solution at the cost of high computational costs, limiting their applicability in real-time. In this respect, AI-based solutions allow reducing the computational burden and the need to derive a precise mathematical model of the considered system. However, AI has been mostly used to forecast the energy production of RESs or to model the energy consumption of consumers/households. Furthermore, DRL algorithms are characterized by several hyperparameters whose tuning is a complex task based on trial and error. More generally, the problems addressed in the literature with respect to ECs include (i) P2P energy trading, (ii) economic and environmental analyses, (iii) management of ESSs and RESs for maximizing self-consumption, (iv) satisfaction of grid constraints and (v) dimensioning of EC elements.

The authors believe that there is a lack of an integrated scalable approach jointly tackling the EC members’ load demand, the optimization of the members’ RES energy production and ESS usage, the consideration of shared ESSs and the energy trading with the EC and the grid, and the consideration of personalized criteria based on EC members’ preferences. Motivated by these considerations, the proposed control framework adopts a hierarchical multi-agent reinforcement learning (RL) approach. To each EC member, there is associated a RL agent in charge of learning the best energy management strategy with respect to all the above-mentioned problems.

1.2. Article’s Contributions

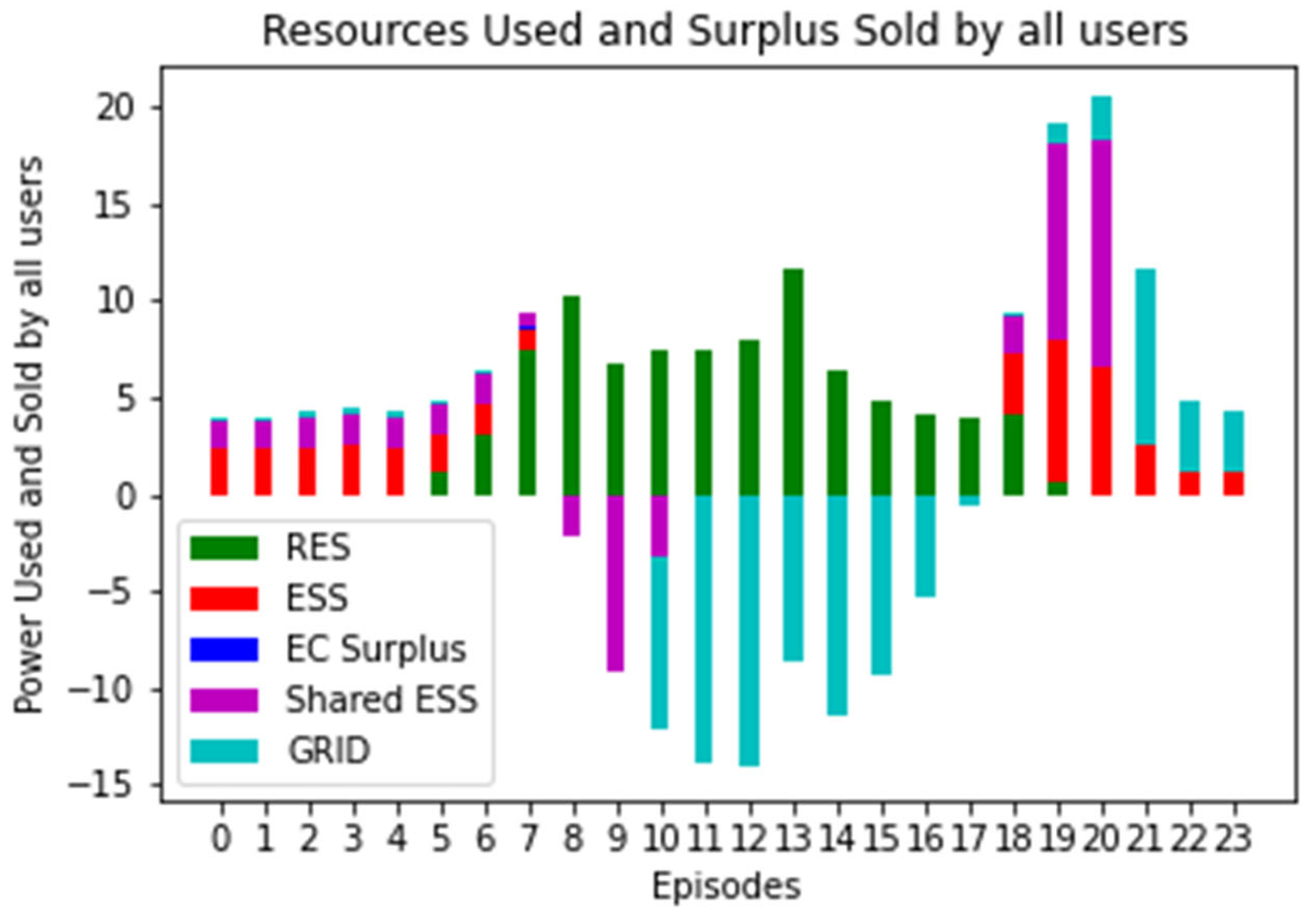
The major contribution of this paper is the development of a cooperative multi-agent AI-based control framework able to learn the optimal energy management strategy in a given EC. The proposed solution can be used to solve the EC energy management problem as well as to understand EC performances in different configurations and thus to dimension the EC elements (e.g., ESSs, RESs, community members, member profiles, etc.). The EC energy management problem consists of understanding the best way to exploit the available energy sources. The load demand of a given EC member can be satisfied through (i) the energy produced by the RES, (ii) the energy stored in the ESS, (iii) the energy stored in the shared ESS, (iv) the EC’s energy surplus and (v) the electric grid. Furthermore, it is necessary to understand the best control strategy to charge the shared ESS and to manage the EC’s energy surplus. With the proposed solution, each building in the EC can be equipped with local energy management software, exploiting the trained artificial RL agents in charge of deciding the energy exchanges between the building and (i) the distributed RES and ESS, (ii) the EC and (iii) the electric grid.

To the best of the authors’ knowledge, a multi-agent AI-based control framework for simultaneously tackling the load demand satisfaction problem, the individual and shared ESS and RES management and the management of the EC energy surplus has not been proposed yet in the literature. From a technical perspective, the proposed multi-agent solution is based on the well-known Q-Learning algorithm.

Furthermore, under specific conditions, the Q-Learning algorithm guarantees that the learned policy is the optimal one. This property is not guaranteed by Deep Reinforcement Learning algorithms. However, the convergence property comes at the cost of low scalability. To address this aspect, the considered control problems were decoupled into three sequential stages. In addition, an ad hoc state aggregation procedure was developed to map the RL agents’ continuous state spaces into discrete state spaces of limited dimensions, further reducing the algorithms’ computational complexity. Finally, the proposed solution captures the most recent EU directive principles with respect to EC structures, member cooperation and energy management that is privacy-preserving and fair.

1.3. Article’s Structure

The remainder of this article is organized as follows: Section 2 describes the considered energy community model. Section 3 describes the proposed control framework. Section 4 presents the simulations performed to validate the proposed approach and a discussion of the achieved results. Finally, Section 5 draws the conclusions of the performed work and outlines future developments.

2. Problem Description

EU directives specify several criteria that shall be followed when creating an energy community (EC). An important aspect that shall be considered is the cooperation between the community members. In this respect, transparent and fair decision-making processes shall be enforced. Indeed, it has been proven that, beyond environmental and economic aspects, the elements increasing costumers’ willingness to become community members are the provision of privacy-preserving, flexible and fair services [19,20]. Flexibility can be enforced by considering personalized energy management policies. As an example, members’ needs and comfort levels shall be considered by the adopted energy management policy to charge and discharge their energy storage systems (ESSs). Beyond these aspects, efficient energy management policies shall maximize the community independence from the electric grid and optimize other performance criteria such as the maximization of the energy consumption from the available renewable energy sources (RESs), the minimization of greenhouse gas (GHG) emissions, the optimization of the energy profile fed to the grid and, of course, to satisfy the members’ load demand. As detailed in Section 3 and Section 4, the proposed control framework will consider all these elements.

Figure 1 depicts the scenario considered. The EC’s members can be divided into residential and/or business consumers and prosumers, both having a crucial role. Prosumers provide the community with RESs generating clean energy and ESSs which can be exploited by the EC members. On the other hand, consumers allow the consumption of the locally generated energy, avoiding waste and stabilizing the community’s energy profile. Each EC member is also connected to the main electric grid. The prosumers’ ESS can provide energy to the EC members. The presence of a shared ESS is also considered, which can be charged by the available RESs and/or by the electric grid, if deemed convenient.

From an energy management point of view, each customer is characterized by their own load demand $P_i^L$, the RES generation profile $P_i^{RES}$, and the ESS capacity and characteristics. Load demand and RES production profiles are typically defined as one-day curves, discrete in time but continuous in amplitude. For ESSs, they are characterized in terms of their (i) minimum $C_i^{MIN}$ and maximum $C_i^{MAX}$ capacities, (ii) charge $P_i^{IN}$ and discharge $P_i^{OUT}$ power rates, and (iii) battery efficiency ${\mu }_i$. Batteries are typically modelled as “black box” components capable of providing and/or storing energy [46,47]. Let $\mathsf{\Delta }T$ be the sampling time, then the dynamics of the ESSs charging and discharging processes can be described by

$$C_i\left[k+1\right]=C\left[k\right]+{\mu }_i{P}_i^{IN}\mathsf{\Delta }T-{\displaystyle \frac{P_i^{OUT}\mathsf{\Delta }T}{{\mu }_i}}, \forall i$$

(1)

and it must satisfy the following constraint:

$$C_i^{MIN}\le C_i\left[k\right]\le C_i^{MAX}, \forall i$$

(2)

With respect to Equation (1), it can be observed that the first term on the equation’s right-hand characterizes the charge level of the $i$-th ESS in the previous time instant, whereas the second and third terms capture the impact of the charging and discharging processes, respectively. Equations (1) and (2) can also be used to characterize the shared ESS. In traditional electric grids, energy purchase and sale costs are determined by day-ahead policies. When considering ECs, these costs also consider internal and external incentives. The former is defined within the EC, while the latter is defined by the energy services management company.

3. Problem Formalization and Control Framework

3.1. Generalities on Markov Decision Processes and Q-Learning

The mathematical framework provided by Markov decision processes (MDPs) is particularly useful to define reinforcement learning algorithms [48]. Indeed, MDPs are used to model decision-making problems in which an agent (i.e., the decision maker) interacts with a given environment by performing an action. More specifically, at the generic time instant $k$, the agent observes the environment and measures its state $s_k$. Based on this observation, the agent performs an action $a_k$, inducing a state transition in the environment. After that, the environment transitions to the new state $s_{k+1}$, and the agent receives a reward $r_{k+1}$ capturing the effectiveness of the action performed. The final goal of an MDP consists of finding the optimal policy ${\pi }^{\ast }\left(s\right)$ mapping states and actions. In other words, the policy specifies which action shall be taken when the environment’s state is $s$. Figure 2 depicts the above-described interaction between the agent and the environment in a deterministic environment. MDPs can thus be defined by the tuples $〈\begin{array}{cccc}S& A& P_a& R\end{array}〉$, where $S$ and $A$ are the state and action spaces, respectively, and $P_a$ is the state transition distribution probability defined as

$$P_a\left(s,s’\right)=\mathrm{Pr}\left(\begin{array}{ccc}{s}_{k+1}=\mathrm{s}\mathrm{’}& |& s_k=s,a_k=a\end{array}\right)$$

(3)

and $R$ is the reward function.

Reinforcement learning (RL) is one of the three machine learning paradigms together with supervised and unsupervised learning. RL algorithms consist of training an artificial agent, which, by interacting with a given environment and following a given policy, learns how to behave. The objective of an RL agent is to maximize the total expected reward

$$E\left[\sum _{k=0}^{\infty }{\gamma }^k{r}_{k+1}\left(s_k,s_{k+1}\right)\right]$$

(4)

where $\gamma \in \left[0;1\right]$ is referred to as the discount factor allowing the weighting of the importance given to future rewards. The function(s) optimizing the expected reward is referred to as the optimal policy ${\pi }^{\ast }$. For estimating the expected reward, RL algorithms rely on two functions referred to as the state-value function $V^{\pi }\left(s\right)$ and the action-state value function $Q^{\pi }\left(s,a\right)$, also known as the Q-Function. The state-value function provides a measure of how good it is to be in a given state. In particular, it provides a measure of the expected reward that can be obtained when being in a given state $s$ and when adopting policy $\pi$. In formal terms it is defined as follows:

$$V^{\pi }\left(s\right)=E^{\pi }\left[\begin{array}{ccc}{\displaystyle \sum _{k=0}^{\infty }}{\gamma }^k{r}_{k+1}& |& s_0=s\end{array}\right]$$

(5)

The Q-Function, instead, provides a measure of how good it is to perform a given action when being in a given state and following policy $\pi$. In formal terms, it is defined as follows:

$$Q^{\pi }\left(s,a\right)=E^{\pi }\left[\begin{array}{ccc}{\displaystyle \sum _{k=0}^{\infty }}{\gamma }^k{r}_{k+1}& |& s_0=s, a_0=a\end{array}\right]$$

(6)

It is clear that, if an optimal Q-Function can be learned, the agent is able to understand the optimal action to be taken when the environment is in any possible state.

A well-known RL algorithm is the Q-Learning algorithm, allowing the agent to learn the optimal Q-Function. Indeed, if at each interaction between the agent and the environment the value of the Q-Function of a given state-action pair is properly updated, it has been proven that the Q-Function will approach the optimal one. More specifically, at the generic time instant $k$, the agent receives a measure of the environment state $s_k$ and, based on a given policy $\pi$, selects an action $a_k$. The environment transitions in a new state $s_{k+1}$ and the agent receives a reward $r_{k+1}$. At this point, the Q-learning algorithm requires that the Q-Function of the state-action pair $〈s_k,a_k〉$ is updated as follows:

$$Q^{\pi }\left(s_k,a_k\right)=Q^{\pi }\left(s_k,a_k\right)+{\alpha }_k\left(s_k,a_k\right)\left[r_{k+1}+\gamma \underset{a_{k+1}}{\max }{Q}^{\pi }(s_{k+1},a_{k+1})-Q^{\pi }\left(s_k,a_k\right)\right]$$

(7)

where ${\alpha }_k\left(·\right)\in \left(0;1\right]$ is the learning rate weighting the impact of future interactions. Let $n^i\left(s,a\right)$ be the number of times in which action $a$ was selected when the environment is in state $s$. Provided that (i) the rewards $r_k$ are bounded, (ii) the learning rate ${\alpha }_k\in \left(0;1\right]$ and (iii) that

$$\begin{array}{cccc}{\displaystyle \sum _{i=1}^{\infty }}{\alpha }_{n^i\left(s,a\right)}=\infty & ,& {\displaystyle \sum _{i=1}^{\infty }}{\left[{\alpha }_{n^i\left(s,a\right)}\right]}^2<\infty & \forall s,a\end{array}$$

(8)

then, it has been proven [49] that

$$\underset{n\to \infty }{\lim }{Q}_n^{\pi }\left(s,a\right)=Q^{{\pi }^{\ast }}\left(s,a\right), \forall s,a$$

(9)

In other words, if each state-action pair is visited infinitely times and the corresponding value of the Q-Function is updated following Equation (7), the agent will learn the optimal Q-Function $Q^{{\pi }^{\ast }}(s,a)$. The condition of visiting infinitely times each state-action pair can be satisfied stochastically by using an $ϵ$-greedy policy defined as follows:

$$a_k=\left\{\begin{array}{cc}\underset{a}{\max }Q\left(s_k,a\right)& \mathrm{with} \mathrm{probability} 1-ϵ\\ \mathrm{random} \mathrm{action}& \mathrm{with} \mathrm{probability} ϵ\end{array}\right.$$

(10)

The $ϵ$-greedy policy allows balancing of the exploration phase (in which random actions are selected) and the exploitation phase (in which the gained experience is used to perform the best action). One of the challenges of the Q-Learning algorithm, and in general of machine learning, is the possibility of being stuck in a local optimum. To avoid this, several solutions can be adopted. In [50], the authors propose to de-randomize the $ϵ$-greedy policy by incrementing the values of the Q-Table, mapping state and actions, with respect to the actions not taken. Alternative approaches consist in smoothing the greedy action by considering the first $n$ best actions to randomly choose from or choosing the less visited state-action pair. In the present article, the local optimum avoidance problem was addressed by means of two modeling choices. First, as detailed in Section 3.2.1, state aggregation criteria were defined to map the continuous states spaces into discrete ones of limited dimensions. This latter aspect allows identifying, for each state, the best possible action. Second, the reward function was shaped to encourage the selection of the best action.

3.2. Distributed Cooperative Multi-Objective RL Control Framework

As mentioned in Section 2, the approach proposed in this article has the ambition of addressing the many criteria that EU policies specified for energy communities. These criteria include cooperation among the EC members, maximization of self-consumption, fairness and personalization of the energy management policies. From a technical perspective, the energy management policies shall address the satisfaction of the EC members’ load demand, the management of the energy produced by the available RESs, the ESSs’ charging and discharging strategies and the management of the surplus energy. Dealing with all these aspects requires the definition of many control variables and complex control frameworks. To reduce the computational complexity of the proposed solution, a distributed multi-agent control framework was developed. The energy management problem of each EC member is tackled by a dedicated RL agent. Furthermore, due to the multiple control objectives, a multi-stage control procedure was defined. This procedure hierarchically addresses the load demand satisfaction, the ESSs’ charging and the management of the energy surplus problems, respectively. This multi-stage procedure renders the proposed control framework modular, meaning that it can be applied to deal with one or more of the energy management problems considered and scalable with respect to the number of EC members.

As depicted in Figure 3, the internal architecture of each RL agent envisages the presence of three sub-agents. The load demand RL agent is in charge of understanding the best strategy to satisfy the $i$-th EC members’ load demand, considering the energy produced by the EC’s RESs, the EC’s ESSs and, if necessary, the electric grid. The objective of this first stage of the control procedure is to minimize the energy bill while maximizing self-consumption. The second stage of the proposed control procedure, tackled by the ESS RL agent, consists of learning the best strategy to charge the EC’s ESSs. This was done after the load demand satisfaction problem was addressed. In other words, the load demand agent provides the ESS agent with the updated state variables. Finally, the surplus RL agent is in charge of learning how to manage the possible surplus energy. In the considered EC scenario (described in Section 2), this implies considering the individual ESS, the shared ESS and also the electric grid.

Cooperation among EC members is enforced by the sharing of the surplus energy that each member renders available to the EC. Furthermore, the presence of the shared ESS increases the availability of a shared energy source. This ESS can be charged by each EC member (when selling the surplus energy to the EC) and used when the RES and ESS are not able to satisfy the load demand of a given EC member. This cooperative behavior is privacy-preserving, meaning that each EC member does not have the information regarding the energy production and consumption profiles of the other members. Indeed, each EC member (and the associated distributed controller) receives the data relative to the cumulative energy surplus of the EC.

The proposed distributed RL control framework relies on the well-known Q-Learning algorithm, briefly described in Section 3.1. Q-Learning is based on a table, referred to as the Q-Table, matching states and actions. More specifically, the values of the Q-Table (which will be learned by the RL agent after the training phase) capture the goodness of taking a given action when the environment is in a given state. The energy management problem is characterized by a continuous state space. To reduce the computational complexity of the algorithm and to adopt the Q-Learning algorithm, aggregation criteria were defined with the purpose of mapping the continuous state space into a discrete and limited one.

As mentioned in Section 3.1, RL algorithms can be defined by exploiting the MDPs’ mathematical framework. This requires defining the state and action spaces, the state transition probability distribution and the reward function. With respect to the state transition probability distribution, a deterministic scenario will be considered, and thus its definition will not be addressed. All the other elements will be detailed in the next sub-sections. The variables used to model the considered control problem and to define the proposed control framework are reported in

Table 2. Nomenclature.

Variable	Description	Algorithm Stage
$k$	Discrete time instant	1–3
$i$	$\mathrm{Index} \mathrm{for} \mathrm{characterizing} \mathrm{the} i$-th community member	1–3
$j$	$\mathrm{Index} \mathrm{for} \mathrm{characterizing} \mathrm{the} j$-th artificial agent	1–3
$\mathsf{\Delta }T$	Sampling time	1–3
$C_i^{MIN}$	$i$-th ESS minimum capacity	1–3
$C_i^{MAX}$	$i$-th ESS maximum capacity	1–3
${\mu }_i$	$\mathrm{Efficiency} \mathrm{of} \mathrm{the} i$-th ESS	1–2
$C_{HUB}^{MIN}$	Shared ESS minimum capacity	1–3
$C_{HUB}^{MAX}$	Shared ESS maximum capacity	1–3
${\mu }^{HUB}$	Efficiency of the shared ESS	1–3
$P_i^L\left[k\right]$	$\mathrm{Load} \mathrm{demand} \mathrm{at} \mathrm{time} k$$\mathrm{of} \mathrm{the} i$-th community member	1
$P_i^{RES}\left[k\right]$	$\mathrm{Available} \mathrm{RES} \mathrm{power} \mathrm{of} \mathrm{the}$  $i\text{-}\mathrm{th} \mathrm{community} \mathrm{member} \mathrm{at} \mathrm{time} k$	1–3
$C_i^{ESS}\left[k\right]$	$\mathrm{Charge} \mathrm{level} \mathrm{of} \mathrm{the}$  $i\text{-}\mathrm{th} \mathrm{ESS} \mathrm{at} \mathrm{time} k$	1–2
$P_i^{IN}\left[k\right]$	$\mathrm{Available} \mathrm{charging} \mathrm{power} \mathrm{of} \mathrm{the}$  $i\text{-}\mathrm{th} \mathrm{ESS} \mathrm{at} \mathrm{time} k$	2
$P_i^{OUT}\left[k\right]$	$\mathrm{Available} \mathrm{discharging} \mathrm{power} \mathrm{of} \mathrm{the}$  $i\text{-}\mathrm{th} \mathrm{ESS} \mathrm{at} \mathrm{time} k$	1
$P_i^S\left[k\right]$	$\mathrm{EC} \mathrm{energy} \mathrm{surplus} \mathrm{available} \mathrm{for} \mathrm{the}$  $i\text{-}\mathrm{th} \mathrm{EC} \mathrm{member} \mathrm{at} \mathrm{time} k$	1–2
$P_{OUT}^{HUB}\left[k\right]$	$\mathrm{Shared} \mathrm{ESS}’\mathrm{s} \mathrm{output} \mathrm{power} \mathrm{available} \mathrm{at} \mathrm{time} k$	1–2
$P_{IN}^{HUB}\left[k\right]$	$\mathrm{Shared} \mathrm{ESS}’\mathrm{s} \mathrm{input} \mathrm{power} \mathrm{available} \mathrm{at} \mathrm{time} k$	3
$C_{GRID}^{BUY}\left[k\right]$	$\mathrm{Unit} \cos \mathrm{t} \mathrm{of} \mathrm{purchasing} \mathrm{energy} \mathrm{from} \mathrm{the} \mathrm{grid} \mathrm{at} \mathrm{time} k$	1–2
$C_{EC}^{BUY}\left[k\right]$	$\mathrm{Unit} \cos \mathrm{t} \mathrm{of} \mathrm{purchasing} \mathrm{energy} \mathrm{from} \mathrm{the} \mathrm{EC} \mathrm{at} \mathrm{time} k$	1–2
$C_{GRID}^{SELL}\left[k\right]$	$\mathrm{Unit} \cos \mathrm{t} \mathrm{of} \mathrm{selling} \mathrm{energy} \mathrm{to} \mathrm{the} \mathrm{grid} \mathrm{at} \mathrm{time} k$	3
$C_{EC}^{SELL}\left[k\right]$	$\mathrm{Unit} \cos \mathrm{t} \mathrm{of} \mathrm{selling} \mathrm{energy} \mathrm{to} \mathrm{the} \mathrm{EC} \mathrm{at} \mathrm{time} k$	3
$C_i^{CH}\left[k\right]$	$\mathrm{Cumulative}$  $i\text{-}\mathrm{th} \mathrm{ESS} \mathrm{charging} \cos \mathrm{t} \mathrm{at} \mathrm{time} k$	2
$C_i^{Tr}$	$\mathrm{Maximum} \mathrm{daily} \cos \mathrm{t} \mathrm{the} i$-th EC member is willing to spend to charge its ESS	2
$S_{i,j}$	$\mathrm{State} \mathrm{space} \mathrm{of} \mathrm{the}$ $i\text{-}\mathrm{th} \mathrm{EC} \mathrm{member} \mathrm{for} \mathrm{the} j$-th artificial agent	1–3
$A_{i,j}$	$\mathrm{Action} \mathrm{space} \mathrm{of} \mathrm{the}$ $i\text{-}\mathrm{th} \mathrm{EC} \mathrm{member} \mathrm{for} \mathrm{the} j$-th artificial agent	1–3
$R_{i,j}\left(·\right)$	$\mathrm{Reward} \mathrm{function} \mathrm{of} \mathrm{the}$ $i\text{-}\mathrm{th} \mathrm{EC} \mathrm{member} \mathrm{for} \mathrm{the} j$-th artificial agent	1–3

. The table also specifies in which stage of the control algorithm such variables are used.

3.2.1. Q-Learning-Based Cooperative Multi-Agents

The proposed hierarchical multi-agent control framework is based on three stages. The control problems associated with each stage are solved by a specific RL agent. That is, for each RL agent, it is necessary to define the tuples $〈\begin{array}{ccc}{S}_{i,j}& A_{i,j}& R_{i,j}\end{array}〉$ (as already specified, state transitions are assumed to be deterministic and thus the state transition distribution probability function will not be addressed).

With respect to the agents’ state spaces, it is necessary to define state vectors capturing the goals of each algorithm’s stage. The first stage is in charge of satisfying the EC members’ load demand. Hence, at each discrete time instant $k$, the $i$-th RL load demand agent state shall capture the EC members’ load demand profile $P_i^L\left[k\right]$, the power generated by their available RESs $P_i^{RES}\left[k\right]$, the level of charge and the available power output of their ESSs, $C_i^{ESS}\left[k\right]$ and $P_i^{OUT}\left[k\right]$, respectively, the available surplus energy in the EC and the available power output of the shared ESS, $P_i^S\left[k\right]$ and $P_{OUT}^{HUB}\left[k\right]$, respectively, and the unit cost of energy purchased from the grid and from the EC, $C_{GRID}^{BUY}\left[k\right]$ and $C_{EC}^{BUY}\left[k\right]$, respectively. The generic state $s_{i,1}\in S_{i,1}$ of the first RL agent will thus be a vector in the following form:

$$s_{i,1}\left[k\right]=〈\begin{array}{cccccccc}{P}_i^L\left[k\right]& P_i^{RES}\left[k\right]& C_i^{ESS}\left[k\right]& P_i^{OUT}\left[k\right]& P_i^S\left[k\right]& P_{OUT}^{HUB}\left[k\right]& C_{GRID}^{BUY}\left[k\right]& C_{EC}^{BUY}\left[k\right]\end{array}〉$$

(11)

The second algorithm’s stage focuses on learning the best strategy to charge the available ESS and is tackled by the RL ESS agent. Relevant variables that shall be captured by the state vector are those allowing for charging the ESSs and those related to the ESS charging dynamics, namely the energy produced by the RES $P_i^{RES}\left[k\right]$, the EC’s surplus energy $P_i^S\left[k\right]$, the input ESS charging power $P_i^{IN}\left[k\right]$, the output power of the shared ESS $P_{OUT}^{HUB}\left[k\right]$, the cumulative cost already spent to charge the $i$-th ESS $C_i^{CH}\left[k\right]$, and the unit costs of purchasing energy from the grid and from the EC, $C_{GRID}^{BUY}\left[k\right]$ and $C_{EC}^{BUY}\left[k\right]$, respectively. The generic state $s_{i,2}\in S_{i,2}$ of the second RL agent will thus be a vector in the following form:

$$s_{i,2}\left[k\right]=〈\begin{array}{ccccccc}{P}_i^{RES}\left[k\right]& P_i^S\left[k\right]& P_i^{IN}\left[k\right]& P_{OUT}^{HUB}\left[k\right]& C_i^{CH}\left[k\right]& C_{GRID}^{BUY}\left[k\right]& C_{EC}^{BUY}\left[k\right]\end{array}〉$$

(12)

Finally, the third algorithm’s stage is in charge of managing the surplus energy. The underlying control problem of this stage requires learning the best actions allowing for charging the shared ESS and/or selling the surplus energy to the grid or the EC. Hence, the state shall capture the energy produced by the RES $P_i^{RES}\left[k\right]$, the input power of the shared ESS $P_{IN}^{HUB}\left[k\right]$, and the unit selling costs to the grid and to the EC, $C_{GRID}^{SELL}\left[k\right]$ and $C_{EC}^{SELL}\left[k\right]$, respectively. The generic state $s_{i,3}\in S_{i,3}$ of the third RL agent will thus be a vector in the following form:

$$s_{i,3}\left[k\right]=〈\begin{array}{cccc}{P}_i^{RES}\left[k\right]& P_{IN}^{HUB}\left[k\right]& C_{GRID}^{SELL}\left[k\right]& C_{EC}^{SELL}\left[k\right]\end{array}〉$$

(13)

The three RL agents are in charge of learning the best energy management strategy with respect to different control problems (i.e., load satisfaction, ESS charging and energy surplus management). Hence, it is possible to define three distinct finite action spaces as follows:

$$\begin{array}{ccc}{a}_{i,1}\left[k\right]=\left\{\begin{array}{c}\mathrm{do} \mathrm{nothing}\\ \mathrm{use} \mathrm{the} \mathrm{RES}\\ \mathrm{use} \mathrm{the} \mathrm{ESS}\\ \mathrm{use} \mathrm{EC} \mathrm{surplus}\\ \mathrm{use} \mathrm{shared} \mathrm{ESS}\\ \mathrm{use} \mathrm{energy} \mathrm{grid}\end{array}\right.& a_{i,2}\left[k\right]=\left\{\begin{array}{c}\mathrm{do} \mathrm{nothing}\\ \mathrm{use} \mathrm{the} \mathrm{RES}\\ \mathrm{use} \mathrm{EC} \mathrm{surplus}\\ \mathrm{use} \mathrm{shared} \mathrm{ESS}\\ \mathrm{use} \mathrm{energy} \mathrm{grid}\end{array}\right.& a_{i,3}\left[k\right]=\left\{\begin{array}{c}\mathrm{do} \mathrm{nothing}\\ \mathrm{sell} \mathrm{to} \mathrm{the} \mathrm{EC}\\ \mathrm{sell} \mathrm{to} \mathrm{the} \mathrm{grid}\end{array}\right.\end{array}$$

(14)

It should be noted that the three state spaces $S_{i,1}, S_{i,2},$ and $S_{i,3}$—see Equations (12)–(14)—are discrete in time but continuous in the values that the entries can assume (e.g., the charge level of a given ESS). To reduce the computational complexity of the proposed control framework, a set of aggregation criteria was defined to map such continuous states into discrete state spaces with limited possible values that can be assumed. Aggregation techniques have been widely adopted in the literature to reduce the complexity of the problems to be solved. In [51], the author describes several different feature-based approaches to aggregate states in finite-state MDPs. The state aggregation procedure can be based on specifically designed aggregation functions, can be inferred by means of neural networks or can be based on static rules. The approach adopted in this article, and summarized in

Table 3. Aggregation criteria for first stage.

Aggregation Criteria	Description	Best Action
$\mathbf{if} P_i^L=0$ $\mathbf{then} s_{i,1}=s_1$	$s_1$ captures the scenario in which the load demand of the EC member is zero or it has been already satisfied. This state is a terminal state for the first algorithm’s stage.	do nothing
$\mathbf{if} \left\{\begin{array}{c}{P}_i^L>0\\ P_i^{RES}>0\end{array}\right.$ $\mathbf{then} s_{i,1}=s_2$	$s_2$ describes a scenario in which the EC member load demand is not zero and the RES is producing energy to satisfy such demand.	use the RES
$\mathbf{if} \left\{\begin{array}{c} P_i^L>0\\ P_i^{RES}=0\\ P_i^{OUT}>0\end{array}\right.$ $\mathbf{then} s_{i,1}=s_3$	$s_3$ captures a scenario in which the load demand of the EC member is not zero, the RES is not producing energy while the ESS is (at least partially) charged.	use the ESS
$\mathbf{if} \left\{\begin{array}{c}{P}_i^L>0\\ P_i^{RES}=0\\ P_i^{OUT}=0\\ P_i^S>0\end{array}\right.$ $\mathbf{then} s_{i,1}=s_4$	$s_4$ describes a scenario in which only the EC surplus energy can be used to satisfy the EC member’s load demand.	use the EC surplus
$\mathbf{if} \left\{\begin{array}{c} P_i^L>0\\ P_i^{RES}=0\\ P_i^{OUT}=0\\ P_i^S=0\\ P_{OUT}^{HUB}>0\end{array}\right.$ $\mathbf{then} s_{i,1}=s_5$	$s_5$ captures the scenario in which the RES and the ESS cannot be used to satisfy the EC member’s load demand, and the EC does not have an energy surplus to be used.	use the shared ESS
$\mathbf{if} \left\{\begin{array}{c} P_L>0\\ P_i^{RES}=0\\ P_i^{OUT}=0\\ P_i^S=0\\ P_{OUT}^{HUB}=0\end{array}\right.$ $\mathbf{then} s_{i,1}=s_6$	$s_6$ describes the scenario in which the only energy source to satisfy the EC member’s load demand is the electric grid.	use energy grid

,

Table 4. Aggregation criteria for second stage.

Aggregation Criteria	Description	Best Action
$\mathbf{if} (P_i^{IN}=0 \mathrm{A}\mathrm{N}\mathrm{D} C_i^{CH}<C_i^{Tr})$ $\mathrm{OR} (C_i^{CH}\ge C_i^{Tr})$ $\mathbf{then} s_{i,2}=s_7$	$s_7$$\mathrm{captures} \mathrm{the} \mathrm{scenario} \mathrm{in} \mathrm{which} \mathrm{either} \mathrm{the} \mathrm{ESS} \mathrm{is} \mathrm{fully} \mathrm{charged}, \mathrm{or} \mathrm{the} \cos \mathrm{t} \mathrm{already} \mathrm{spent} \mathrm{to} \mathrm{charge} \mathrm{the} i$-th ESS is equal or greater than the personalized threshold that each EC member specified.	do nothing
$\mathbf{if} \left\{\begin{array}{c}{P}_i^{IN}>0\\ P_i^{RES}>0\end{array}\right.$ $\mathbf{then} s_{i,2}=s_8$	$s_8$ describes the scenario in which the ESS can be charged, and the RES is producing energy.	use the RES
$\mathbf{if} \left\{\begin{array}{c}{P}_i^{IN}>0\\ P_i^{RES}=0\\ P_{SurpluEC}>0\\ C_i^{CH}<C_i^{Tr}\end{array}\right.$ $\mathbf{then} s_{i,2}=s_9$	$s_9$ describes the scenario in which the ESS shall be charged but the RES cannot be used.	use the EC surplus
$\mathbf{if} \left\{\begin{array}{c}{P}_i^{IN}>0\\ P_i^{RES}=0\\ P_i^S=0\\ P_{OUT}^{HUB}>0\\ C_i^{CH}<C_i^{Tr}\end{array}\right.$ $\mathbf{then} s_{i,2}=s_{10}$	$s_{10}$ describes the scenario in which the ESS shall be charged, but RES is not producing energy, and there is no EC energy surplus.	use the shared ESS
$\mathbf{if} \left\{\begin{array}{c}{P}_i^{IN}>0\\ P_i^{RES}=0\\ P_i^S=0\\ P_{OUT}^{HUB}=0\\ C_i^{CH}<C_i^{Tr}\end{array}\right.$ $\mathbf{then} s_{i,2}=s_{11}$	$s_{11}$ describes the scenario in which the only available energy source for charging the ESS is the electric grid.	use energy grid

and

Table 5. Aggregation criteria for third stage.

Aggregation Criteria	Description	Best Action
$\mathbf{if} (P_i^{RES}=0)$ $\mathbf{then} s_{i,3}=s_{12}$	$s_{12}$ describes the scenario in which the EC member has no energy surplus.	do nothing
$\mathbf{if} \left\{\begin{array}{c}{P}_i^{RES}>0\\ P_{IN}^{HUB}>0\end{array}\right.$ $\mathbf{then} s_{i,3}=s_{13}$	$s_{13}$ describes the scenario in which the EC member has an energy surplus, and the EC shared ESS is not fully charged.	sell to EC
$\mathbf{if} \left\{\begin{array}{c}{P}_i^{RES}>0\\ P_{IN}^{HUB}=0\end{array}\right.$ $\mathbf{then} s_{i,3}=s_{14}$	$s_{14}$ describes the scenario in which the EC member has an energy surplus, and the EC shared ESS is fully charged.	sell to grid

, exploits the latter strategy. The aggregation criteria (or features) reported in the first columns are used to define representative states that deterministically capture a given operation point. The reduced and discretized state spaces also allow for easy identification of the best possible action when the environment is in each discrete state. The aggregation criteria, the definition of each discrete state and the associated best possible action are reported in Table 3, Table 4 and Table 5 below, one for each algorithm’s stages.

The last element that must be defined to properly instantiate an RL control framework is the reward function. For fostering artificial agents to select the best action, a positive reward is assigned when the best action is selected, whereas a negative reward is assigned otherwise. Hence, the rewards that the agents can receive are the following:

$$r_{a_{i,j}\left[k\right]}\left(s_{i,j}\left[k\right],s_{i,j}\left[k+1\right]\right)=\left\{\begin{array}{ccc}+2& \mathbf{if}& a_{i,j} \mathrm{is} \mathrm{the} \mathrm{best} \mathrm{action} \mathrm{for} \mathrm{state} s_{i,j}\\ -1& \mathbf{if}& \mathrm{otherwise}\end{array}\right., \forall i,j$$

(15)

The structure of the reward function plays a crucial role in the RL agents’ learning process since it is the mathematical object based on which the agents understand how to behave. The solution proposed in Equation (15), together with the criteria summarized in Table 2, Table 3 and Table 4, is aimed at maximizing the EC’s grid independence and self-consumption. Additional criteria to be optimized can be considered by modifying the reward function.

4. Simulations and Results

Simulations were implemented in Python, version Python 3.8.10 (tags/v3.8.10:3d8993a, 3 May 2021, 11:48:03), on a HP Pavilion Laptop 15-EH1xxx equipped with an AMD Ryzen 7 5700U processor, 16 GB and Windows version 11 Home.

4.1. Training Set-Up

The EC model considered during the training phase consists of six members, classified into three different clusters, i.e., associated with different energy load demand profiles. Figure 4 depicts the baseline RESs’ energy production in three different scenarios and the load demand profiles for three considered EC member profiles. In each training episode, the number of EC members belonging to these profiles is randomly selected. As can be seen, the load demand and RES energy production profiles capture both energy-intensive buildings (e.g., an industrial building belonging to the EC) and residential buildings. This lets the RL agents visit all the possible state-action pairs and thus learn policies that can be adopted in many possible scenarios. These load demand and energy production profiles are used as a baseline: at each training episode, random variations of 20% are considered. In other words, the load demand of the $i$-th EC member used during the $e$-th training episode is

$$P_i^L\left[k\right]=P_t^L\left[k\right]+{\rho }_i\left[k\right], \forall i,k$$

(16)

where $P_t^L\left[k\right]$ is the instantaneous value of the load demand profile depicted in Figure 4 and ${\rho }_i\left[k\right]$ is a random number in the range $\left[-0.2\ast P_t^L\left[k\right];0.2\ast P_t^L\left[k\right]\right]$. The same applies to the RES energy production profiles. Such variations are in line with the findings of several reports [52,53]. Furthermore, the consideration of different EC members’ load demand profiles allows the RL agents to be trained in a significant variety of application scenarios.

The battery type of each EC member was randomly chosen from the ESS types whose datasheets are reported in

Table 6. ESSs’ characteristics used for the training phase.

ESS Type	${\mathit{C}}_{\mathit{i}}^{\mathit{M}\mathit{I}\mathit{N}}\left(\mathbf{k}\mathbf{w}\mathbf{h}\right)$	${\mathit{C}}_{\mathit{i}}^{\mathit{M}\mathit{A}\mathit{X}}$(kwh)	${\mathit{P}}_{\mathit{i}}^{\mathit{I}\mathit{N}}$(kw)	${\mathit{P}}_{\mathit{i}}^{\mathit{O}\mathit{U}\mathit{T}}$$\left(\mathbf{k}\mathbf{w}\right)$	${\mathit{\mu }}_{\mathit{i}}$
Lead-acid	2.295	7.65	2	2	0.89
Lead-acid	2.295	7.65	0.2	2	0.89
Li-ion	0,5	3	0.3	0.3	0.95

, without considering the load demand profile of that member. For the shared ESS, the datasheet of the considered battery is reported in

Table 7. Shared ESSs’ characteristics used for the training phase.

ESS Type	${\mathit{C}}_{\mathit{i}}^{\mathit{M}\mathit{I}\mathit{N}}\left(\mathbf{k}\mathbf{w}\mathbf{h}\right)$	${\mathit{C}}_{\mathit{i}}^{\mathit{M}\mathit{A}\mathit{X}}$(kwh)	${\mathit{P}}_{\mathit{i}}^{\mathit{I}\mathit{N}}$(kw)	${\mathit{P}}_{\mathit{i}}^{\mathit{O}\mathit{U}\mathit{T}}$$\left(\mathbf{k}\mathbf{w}\right)$	${\mathit{\mu }}_{\mathit{i}}$
Lead-acid	11.475	38.25	10	10	0.89

. The considered datasheets were selected from different manufacturers, including Pylontech US2000, Pylontech 81/36, Polytech PowerCube H2, the FerroAmp PSM series and the CSBatteries SM12 Series. ESSs with different characteristics were voluntarily selected to evaluate their impact on the performance of the proposed control framework.

Finally, in relation to the unit costs of selling and purchasing energy from/to the grid and the EC, the average values applied in Italy by some grid operators were considered. These costs are reported in Figure 5.

4.2. Training Phase

The number of training episodes $E$ was set to $E=9840$, corresponding to 410 days. The discount factor $\gamma$ and the learning rate of the Q-Learning update rule reported in Equation (7) are $\gamma =0.85$ and $\alpha =0.05$. Finally, in the adopted $ϵ$-greedy policy, the $ϵ$ parameter decays according to the following law:

$${ϵ}_e=\left\{\begin{array}{cc}1+{\displaystyle \frac{\log \left(0.01\right)}{E}}& e=1\\ {ϵ}_{e-1}\ast \left(1+{\displaystyle \frac{\log \left(0.01\right)}{E}}\right)& \begin{array}{ccc}e>1& \bigwedge & {ϵ}_{e-1}\ge 0.01\end{array}\\ 0.01& \begin{array}{ccc}e>1& \bigwedge & {ϵ}_{e-1}<0.01\end{array}\end{array}\right.$$

(17)

Due to Equation (17), at the beginning of the training phase, the artificial agents are most likely to explore new state-action pairs. When the number of training episodes increases instead, the agents are encouraged to exploit the gained experience. For a design choice, a lower threshold of 0.01 was defined for the $ϵ$ parameter. The pseudocode of the training phase is reported in

Table 8. Pseudo code of the training phase.

Step	Action	Description
1.	$\mathbf{for} e=1,\dots ,E$	for each training episode
3.	for $k=1,\dots ,24$	for each discrete time slot
4.	$\hspace{1em} {ϵ}_e\leftarrow {ϵ}_e\ast \delta ϵ$	$\mathrm{update} ϵ$-greedy parameter
5.	for $i=1,\dots ,N$	for each EC member
6.	$\hspace{1em}\hspace{1em}\overline{i}\leftarrow$ random index from the set	select a random EC member
7.	$\hspace{1em}\hspace{1em}\mathrm{while} P_i^L>0$	until the first stage is completed, i.e., until load demand is satisfied
8.	$\hspace{1em}\hspace{1em} s_{\overline{i},1}\leftarrow$ get observation from the environment	observe the environment
9.	$\hspace{1em}\hspace{1em} 〈\begin{array}{cc}{a}_{\overline{i},1}& s_{{\overline{i}}^{’},1}\end{array}〉\leftarrow {\pi }_{\overline{i},1}\left(s_{\overline{i},1}\right)$	$\mathrm{follow} \mathrm{policy} {\pi }_{\overline{i},1}\left(·\right)$$, \mathrm{get} \mathrm{action} a_{\overline{i},1}$$\mathrm{and} \mathrm{observe} \mathrm{new} \mathrm{state} s_{{\overline{i}}^{’},1}$
10.	$\hspace{1em}\hspace{1em} r_{\overline{i},1}\leftarrow R_{a_{\overline{i},1}}\left(s_{\overline{i},1},s_{{\overline{i}}^{’},1}\right)$	get reward
11.	$\hspace{1em}\hspace{1em} Q_{\overline{i},1}^{OLD}\left(s_{\overline{i},1},a_{\overline{i},1}\right)\leftarrow Q_{\overline{i},1}^{NEW}\left(s_{\overline{i},1},a_{\overline{i},1}\right)$	update Q-Function using Equation (7)
12.	for $i=1,\dots ,N$	for each EC member
13	$\hspace{1em} \overline{i}\leftarrow$ random index from the set	select a random EC member
14.	$\hspace{1em} \mathrm{while} (P_i^{IN}=0\mathrm{O}\mathrm{R}{C}_i^{CH}\ge C_i^{Tr}$)	$\mathrm{until} \mathrm{the} \sec \mathrm{ond} \mathrm{stage} \mathrm{is} \mathrm{completed}, \mathrm{i}.\mathrm{e}., \mathrm{until} \mathrm{the} \mathrm{ESS} \mathrm{is} \mathrm{charged} \mathrm{or} \mathrm{the} \mathrm{personalized} \mathrm{threshold} C_i^{Tr}$ is already reached
15.	$\hspace{1em}\hspace{1em} s_{\overline{i},2}\leftarrow$ get observation from the environment	observe the environment
16.	$\hspace{1em}\hspace{1em} 〈\begin{array}{cc}{a}_{\overline{i},2}& s_{{\overline{i}}^{’},2}\end{array}〉\leftarrow {\pi }_{\overline{i},2}\left(s_{\overline{i},2}\right)$	$\mathrm{follow} \mathrm{policy} {\pi }_{\overline{i},2}\left(·\right)$$, \mathrm{get} \mathrm{action} a_{\overline{i},2}$$\mathrm{and} \mathrm{observe} \mathrm{new} \mathrm{state} s_{{\overline{i}}^{’},2}$
17.	$\hspace{1em}\hspace{1em} r_{\overline{i},2}\leftarrow R_{a_{\overline{i},2}}\left(s_{\overline{i},2},s_{{\overline{i}}^{’},2}\right)$	get reward
18.	$\hspace{1em}\hspace{1em} Q_{\overline{i},2}^{OLD}\left(s_{\overline{i},2},a_{\overline{i},2}\right)\leftarrow Q_{\overline{i},1}^{NEW}\left(s_{\overline{i},2},a_{\overline{i},2}\right)$	update Q-Function using Equation (7)
19.	for $i=1,\dots ,N$	for each EC member
20.	$\hspace{1em} \overline{i}\leftarrow$ random index from the set	select a random EC member
21.	$\hspace{1em} \mathrm{while} P_i^{RES}>0$	until the third stage is completed, i.e., until there is no energy surplus
22.	$\hspace{1em}\hspace{1em} s_{\overline{i},2}\leftarrow$ get observation from the environment	observe the environment
23.	$\hspace{1em}\hspace{1em} 〈\begin{array}{cc}{a}_{\overline{i},3}& s_{{\overline{i}}^{’},3}\end{array}〉\leftarrow {\pi }_{\overline{i},3}\left(s_{\overline{i},3}\right)$	$\mathrm{follow} \mathrm{policy} {\pi }_{\overline{i},3}\left(·\right)$$, \mathrm{get} \mathrm{action} a_{\overline{i},3}$$\mathrm{and} \mathrm{observe} \mathrm{new} \mathrm{state} s_{{\overline{i}}^{’},3}$
24.	$\hspace{1em}\hspace{1em} r_{\overline{i},3}\leftarrow R_{a_{\overline{i},3}}\left(s_{\overline{i},3},s_{{\overline{i}}^{’},3}\right)$	get reward
25.	$\hspace{1em}\hspace{1em} Q_{\overline{i},3}^{OLD}\left(s_{\overline{i},3},a_{\overline{i},3}\right)\leftarrow Q_{\overline{i},3}^{NEW}\left(s_{\overline{i},3},a_{\overline{i},3}\right)$	update Q-Function using Equation (7)

. The defined training procedure enforces fairness in the proposed energy management strategy through a random selection of an EC member’s energy management problem. More specifically, at each stage of the algorithm, the EC members’ requests are addressed in a sequential manner based on a random order (steps 6, 13 and 20). Solving the problem in a sequential manner allows for avoiding conflicts between the control actions selected by each RL agent. An alternative solution to deal with this aspect would be to limit the number of shared resources that each agent is able to control. In other words, let $N$ be the number of EC members, $C^{HUB}\left[k\right]$ be the shared ESS charge level at time $k$ and $P^{SURPLUS}\left[k\right]$ be the EC energy surplus available at time $k$. If each RL agent is able to decide only about a fraction of $1/N$ of $C^{HUB}\left[k\right]$ and $P^{SURPLUS}\left[k\right]$, there would not be conflicts. The same applies to the shared ESS charging process. With this solution, a complete distributed control framework could be implemented. However, the implemented control actions would not be optimal since, in a given discrete time instant, an EC member may not need to use the shared resources.

The training phase lasted 234 s, i.e., less than 4 min. It should be noted that the training could be arrested by defining specific stop conditions. As an example is the case when the updates of the visited Q-Function values are below a given threshold or when each state-action pair has been visited enough times. Of course, the Q-Learning convergence criteria shall always be considered. Figure 6 depicts the number of iterations required by the control algorithm and the $ϵ$ evolution during the training phase. As can be seen from the left figure, the artificial agents are able to learn the optimal policy, and indeed, the required algorithms’ iterations converge.

4.3. Simulations

To validate the effectiveness of the learned energy management policies, the trained agents were deployed in an EC with a configuration similar to the one described in Section 4.1. The baseline EC members’ load demand and RESs’ energy production profiles were selected, as depicted in Figure 7, for capturing a residential EC scenario. Data used for simulations were generated starting from the baseline profiles reported in Figure 7, capturing realistic residential EC quantities. More specifically, Figure 7 reports RESs’ energy production (on the left) and EC members’ load demand (on the right) profiles. Each EC member is associated with a specific load demand profile. The actual load demand profile considered during the simulations was generated starting from the baseline profile reported in Figure 7, plus random noise to capture different users’ behaviours. The same applies to the RESs’ energy production profiles. The considered baseline profiles were selected based on realistic scenarios.

The following subsections will present and discuss three sets of simulations. The first sets, reported in Section 4.3.1, are aimed at proving that, after the training phase, the agents are able to properly solve the EC energy management problem. The second sets, reported in Section 4.3.2, will focus on analyzing the impact of a different dimensioning of the shared ESS. Similarly, the third set of simulations, reported in Section 4.3.3, will investigate the impact of different EC members’ ESS configurations.

4.3.1. Validation

In this first set of simulations, the members’ and the shared ESS characteristics are the same as those mentioned in Section 4.1. It was assumed that the EC members’ load demand profiles are equally distributed among the three load demand profiles depicted in Figure 7. The simulation and resolution of the EC energy management problem for a day required 436 milliseconds, meaning that, for each discrete time instant, around 18 milliseconds were required to apply the learned control policy. This computational complexity renders the proposed algorithm suitable for real-time energy management policies. Figure 8 depicts the resources used to solve the considered energy management problem. More specifically, the green and red bars capture the usage of the distributed RESs and ESSs to satisfy the EC members’ load demand, respectively; the dark blue bars describe the amount of EC energy surplus consumed by the EC members; the violet bars describe the EC’s shared ESS charging process, where positive values mean that the shared ESS is used by the EC members, whereas negative values mean that the shared ESS is charged through the EC’s energy surplus; the light blue bars describe the energy exchange between the EC and the electric grid, where positive values express the power absorbed from the grid to satisfy EC members’ load demand, whereas negative values mean that the EC’s energy surplus is sold to the grid. As can be seen in Figure 8, during the hours in which the RESs produce little or no energy (i.e., in the time intervals 01:00–08:00 and 18:00–24:00), the artificial agents correctly absorb energy from the distributed and shared ESSs (the red and dark blue bars in the figure, respectively). Conversely, when the RESs produce energy, the EC members’ load demand is mostly satisfied by their RESs (green bars). During daylight hours, when a consumer is not able to satisfy their load demand through their RES, the EC surplus energy (in dark blue) can be used. Furthermore, during daylight hours, the EC members sell the energy surplus to the EC (to charge the shared ESS, in violet) and to the grid (to maximize their profit, in light blue).

4.3.2. Impact of Shared ESS Size

In this set of simulations, the impact of different shared ESS types was analysed for two different scenarios. The shared ESS characteristics are reported in

Table 9. Shared ESS datasheets.

Scenario	ESS Type	${\mathit{C}}_{\mathit{i}}^{\mathit{M}\mathit{I}\mathit{N}}\left(\mathbf{k}\mathbf{w}\mathbf{h}\right)$	${\mathit{C}}_{\mathit{i}}^{\mathit{M}\mathit{A}\mathit{X}}$(kwh)	${\mathit{P}}_{\mathit{i}}^{\mathit{I}\mathit{N}}$(kw)	${\mathit{P}}_{\mathit{i}}^{\mathit{O}\mathit{U}\mathit{T}}$$\left(\mathbf{k}\mathbf{w}\right)$	${\mathit{\mu }}_{\mathit{i}}$
1	Lead-acid	11.475	38.25	10	10	0.89
2	Lead-acid	27	90	36	36	0.93

. The remaining EC model elements were not changed. Figure 9 depicts the outcomes of the simulations in the two different scenarios. The top graphs show the energy sources from which energy is absorbed and to which energy is given. The bottom figures, instead, focus on the energy purchased and sold from and to the grid. As expected, when the shared ESS has lower energy storage capacity (first scenario, figures on the left), the EC community is not able to achieve grid independence. On the contrary, with proper dimensioning of the shared ESS, grid independence can be achieved. The proposed control framework can thus be used to evaluate the economic benefits of different EC configurations, both in the design phase and to improve the performance of already-implemented ECs.

4.3.3. Impact of Individual ESSs’ Charging Rates and Capacities

Similarly to what was done in the previous subsection, the objective of this third set of simulations is to assess the impact of the EC members’ ESSs on EC performance.

Table 10. EC members’ ESSs’ datasheets.

Scenario	ESS Type	${\mathit{C}}_{\mathit{i}}^{\mathit{M}\mathit{I}\mathit{N}}\left(\mathbf{k}\mathbf{w}\mathbf{h}\right)$	${\mathit{C}}_{\mathit{i}}^{\mathit{M}\mathit{A}\mathit{X}}$(kwh)	${\mathit{P}}_{\mathit{i}}^{\mathit{I}\mathit{N}}$(kw)	${\mathit{P}}_{\mathit{i}}^{\mathit{O}\mathit{U}\mathit{T}}$$\left(\mathbf{k}\mathbf{w}\right)$	${\mathit{\mu }}_{\mathit{i}}$
1	Lead-acid	2.295	7.65	0.2	2	0.89
2	Lead-acid	2.295	7.65	2	2	0.89
3	Li-ion	0.5	3	0.3	0.3	0.95

reports the datasheets of the EC members’ ESSs. Three different scenarios were envisioned. In the first two scenarios, the ESSs belong to the same class of batteries. What changes is the input power $P_i^{IN}$, capturing the charging rate of the ESS. Lower values correspond to slower charging processes. Furthermore, in these first two scenarios, it is assumed that the EC members did not specify a personalized threshold $C_i^{TR}$ bounding the daily cost they are willing to pay to charge their ESS. In the third scenario, an ESS with greater storage capacity and a limited charging rate was considered. It was also assumed that, in this scenario, the EC members had specified a personalized threshold $C_i^{TR}$.

Figure 10 depicts the energy absorbed and provided to the grid in the three considered scenarios. As expected, the ESS charging rates heavily impact EC independence from the grid. This is particularly evident during night hours. The first figure from the left (related to the first scenario) shows that energy is sold to the grid when RESs are producing and bought when there is no production. This is because the slow charging rate does not allow for charging the members’ ESS, and so, the surplus energy is sold to the grid. Since, in this scenario, no thresholds on ESS charging costs were specified, energy was purchased from the grid to charge them. The center figure (related to the second scenario with identical ESSs but a faster charging rate) shows that grid independence during nighttime is significantly higher. Indeed, the slower ESS charging rate limited the amount of energy purchased from the grid to charge their ESSs. Finally, the figure on the right is associated with ESSs that have higher capacities but slow charging rates. In this grid, independence during nighttime is similar to the second scenario. Indeed, ESSs’ charging rates and capacities are both directly related to the capabilities of the EC in making the most of the RESs energy production and, in turn, to the control framework’s degrees of freedom. Furthermore, the presence of the personalized thresholds $C_i^{TR}$ limits the amount of energy that can be bought from the grid.

5. Discussion

The proposed control framework focused on (i) satisfying each customer’s load demand, guaranteeing customers’ privacy and a flexible fairness principle among EC customers; (ii) optimizing the EC’s energy source usage to maximize self-consumption, with the goal of achieving grid independence; and (iii) promoting cooperation between EC members, ensuring transparent decisional processes and procedural fairness at the EC level. Indeed, many works highlight the impact of flexible, fair and personalized energy management strategies on customers’ willingness to actively participate in eco-sustainable initiatives and projects, such as being part of an energy community [54,55,56,57]. Given this context, a complex EC model, including distributed RESs and ESSs as well as a shared ESS, was considered. Such models give rise to a significant number of control variables, rendering optimal control-based approaches unsuitable for real-time applications. AI-based methodologies, on the other hand, are particularly useful for handling large-scale systems from a scalability point of view [58]. In contrast to [9,15,17,18,21,22], the proposed approach adopts an AI-based control algorithm: the Q-Learning algorithm. Moreover, the proposed control framework exploits (i) a distributed multi-agent problem formulation and (ii) state aggregation criteria to reduce the computational complexity of the control algorithm. These elements allow for achieving computational times suitable for real-time applications: For each discrete time instant and for each EC member, around 18 milliseconds are required to apply the learned control policy.

The proposed user-centric control framework is aimed at aiding ECs in satisfying EC members’ load demands while managing their ESS charging processes and handling their energy surplus with an intelligent usage and scheduling of personal and community energy sources. Distributed ESSs play a crucial role in augmenting the flexibility, availability, reliability and stability of energy generation and distribution networks. Differently from [10,15,17,18,35], the proposed control framework deals with the EC members’ ESSs in a distributed control environment. Moreover, the proposed approach is able to handle the distributed ESSs charging processes, in contrast to [33,34]. Finally, with respect to [31,33,34,36], the proposed approach implements fairness principles among the EC members and considers a shared ESS. This latter element allows the EC members to use the EC energy surplus generated by other EC members, as well as an additional energy source represented by the shared ESS, which can be charged by the EC members as well as by the grid. Simulations proved that the proposed control framework is able to successfully solve the energy management problem in this setting. The multi-stage control procedure is able to satisfy the EC members’ load demands, prioritizing the usage of the distributed RESs. In addition, the RESs are also used to charge the distributed ESSs as well as, when an energy surplus is available, the shared ESS. The adopted EC model allows the EC members to use the energy surplus generated by other users as well as the energy stored in the shared ESS. This latter element increases the EC’s flexibility and grid independence. As shown in Figure 8, during night hours, the EC members benefit from the shared ESS, and the need to resort to using the grid is minimized. The EC’s performance is directly linked to the technical characteristics of the distributed and shared ESSs. Figure 9 and Figure 10 show the impact of different ESS capacities and charging rates on EC performance. The proposed control framework can indeed also be used as a tool to understand the proper dimensioning of the EC elements when designing and creating an EC. In addition, Figure 10 shows the impact of EC members’ personalized criteria with respect to the ESS recharge costs. High ESS recharge cost thresholds may not translate to higher degrees of EC grid independence. Indeed, it is necessary to balance individual and EC objectives without penalizing the customers’ comfort.

More sophisticated energy management policies can be developed by including, in the control framework, real-time dynamic energy costs, eventually also based on the available energy surplus. Furthermore, by embedding grid constraints in the control problem, it is possible to define more realistic energy management strategies with respect to the energy surplus management problem. Both grid-connected and off-grid communities must deal with this aspect [59,60]. The necessity of advanced energy surplus management strategies is due to stability and reliability issues caused by energy excess [61]. In this respect, the presence of distributed ESSs plays a crucial role. Alternative approaches include power-to-gas systems for absorbing the excess energy [62,63].

6. Conclusions and Future Works

To achieve the challenging objectives set out in the 2030 and 2050 EU agendas on climate change, it is crucial to develop strategies to reduce buildings’ GHG emissions. The EU identified energy communities as important instruments for addressing this issue. This article investigates the problem of energy management in ECs.

The developed EC model considers the presence of both consumers and prosumers. The latter class of EC members is equipped with local RESs and ESSs. In the developed model, the EC members can benefit from the EC’s RES energy surplus as well as from a shared ESS. The proposed control framework is aimed at (i) satisfying the EC members’ load demand while maximizing self-consumption, (ii) optimizing the ESSs’ charging and discharging processes and (iii) managing the EC energy surplus, in a fair and cooperative way. This is achieved through the definition of a scalable multi-agent reinforcement learning-based control framework that exploits the Q-Learning algorithm. The scalability of the proposed control framework was achieved through the definition of (i) a multi-agent control framework, (ii) state aggregation criteria and (iii) a multi-stage control procedure. The multi-agent problem formulation allows for considering local control problems, one for each EC member. With a centralised approach, the number of control variables to be considered would significantly increase the required training times as well as the algorithm’s complexity. Furthermore, the trained RL agents can be immediately deployed in new buildings entering the EC later without the need to re-train them. The state aggregation criteria allow for mapping the RL agents’ continuous state spaces (arising from the continuous nature of energy-related quantities) into discrete state spaces of limited dimensions. This, together with the previous aspect, translates to fewer state-action pairs. The multi-stage control procedure allows for decomposing the considered energy management problem into three smaller sub-problems with fewer control variables, further reducing the algorithm’s complexity.

The energy management problem is solved by a multi-stage cooperative procedure in which the RL agent assigned to a given EC member is able to learn the optimal energy policy while also considering personalized optimization criteria. The RL agents exploit (i) locally available data regarding the ESS charge level, the current load demand and the local production of green energy and (ii) global variables, such as the EC energy surplus, the shared ESS charge level and the energy purchasing and selling unit costs. Simulations demonstrated the possibility of adopting the proposed approach in real time. During the training phase, several variables were randomly changed, allowing the RL agents to learn the optimal policy for any possible state-action pairs. Hence, the trained agents can also be successfully deployed in different EC configurations. Indeed, the abstraction level provided by the mentioned state aggregation criteria translated to a technology independent solution.

Future work may focus on the integration of real-time dynamic pricing strategies, the integration of P2P energy trading strategies and the inclusion of grid constraints. The authors are currently investigating alternative approaches based on deep reinforcement learning algorithms. With respect to the EC members’ energy surplus management, in the proposed approach, the primary objective is to maximize EC independence from the grid. Due to this, energy surplus trading was controlled through static hierarchical rules. When an EC member has an energy surplus, the proposed control algorithm first tries to sell it to EC members. Secondly, it tries to use this surplus to charge the shared ESS. As a last resort, it considers selling the surplus to the grid. By integrating real-time dynamic pricing and P2P energy trading strategies, it is possible to give more relevance to the EC members’ economic benefits. As an example, by considering a centralized EC controller defining the energy costs for internal energy exchanges and by defining P2P energy trading strategies (replacing the static rules defined for managing the energy surplus), it is possible to modify the EC members’ cooperativeness level. This could be useful for increasing the willingness of users to enter a given EC, since more relevance can be given to economic aspects.