Impacts of Renewable Sources of Energy on Bid Modeling Strategy in an Emerging Electricity Market Using Oppositional Gravitational Search Algorithm

Abstract

Power suppliers in a dynamic power market can achieve full benefit by introducing a bidding strategy mechanism. In the power sector, renewable resources have significant gradual usage and their effect on the production of detailed bidding approaches is becoming further complicated in the industry. Due to the irregular nature of these renewable resources and because they are subject to several fluctuations, there is an inherent issue with generating electricity. Taking these considerations into account, attempts have been made to create a model of bidding strategy to optimize the benefit of the electricity producers using the oppositional gravitational search algorithm. The Weibull and Beta distribution functions are utilized to describe the stochastic characteristics of the wind-speed profile and solar-irradiation, respectively. For the IEEE-30 and IEEE-57 frameworks, the suggested method is being checked and explained. In comparison to other optimization approaches, the results of this approach were taken into account, and it was discovered that it outperformed other techniques in addressing bid difficulties. In addition, it is worth noting that the impact of renewable energy on the bidding strategy lowered market clearing and thermal power generating costs, and encouraged renewable influenced producers to put forward the excess electricity into the real-time market.

1. Introduction

For economic growth and welfare of developing countries, one of the most critical infrastructure essentials is electricity. Over the last few years, the electric industry has seen drastic shifts all over the world. This shift occurs as a result of open bidding, bilateral power sharing, and the implementation of a power exchange [1]. The modernization of the electrical power industry eliminates the monopoly existence of generation, allowing consumers to choose between different providers and bringing competition to multiple stages. This type of electricity market allows generation companies (GENCOs) to establish optimum competitive bidding strategies in order to optimize benefit [2]. In a perfect competitive world, the marginal production rate and the bid rates of generating firms (GENCOs) are quite comparable. This theory, however, is entirely false, because in practice, the competitive system is an oligopoly, with premiums greater than the marginal output expense [3]. This is attributed to a variety of characteristics of the electricity sector, including the effects of various generation restrictions and the small number of suppliers [4]. In this setting, all GENCOs depend on optimal bidding strategy (BS) to maximize profits. The benefit of a power producer is primarily determined by the market clearing price (MCP). The MCP is calculated by independent system operators (ISO), which is the intersection point among the power supply and demand. MCP uses the market clearing process to determine the price of the next unit of energy generated, resulting in a viable solution to the issue of strategic bidding. When the electricity market is not fully competitive, oligopolistic market structures are used. As a result, in the oligopolistic pool model, power producers increase their benefit by conducting strategic bidding.

In the past few decades, numerous strategies for optimizing bidding issues have been developed and found to be effective in removing the traditional monopoly in the electric industry. In [5], the authors published a short review of the literature summary regarding competing bidding techniques within the energy sector. Since, instead of being deterministic, the strategic bidding dilemma is stochastic, a variety of studies using stochastic optimization methods have been reported in recent years. Complexity of the electricity market is modeled by the allocation of competing bids in these optimization methods, and the problem is solved for power suppliers benefit maximization. In [6], a stochastic optimization technique was suggested that used the Monte Carlo (MC) approach to forecast opponent actions and the bidding issue was solved by utilizing the golden section search method. MC simulation was used in this approach to repeatedly compute the best one player’s bid strategy when competing against unsystematic opponents. An optimum bidding strategy was determined by the average bidding constraint importance. Following that, a number of research papers using stochastic optimization methods such as genetic algorithm (GA) [7], particle swarm optimization (PSO) [8], fuzzy adaptive particle swarm optimization (FAPSO) [9], gravitational search algorithm (GSA) [10], fuzzy adaptive gravitational search algorithm (FAGSA) [11], krill herd algorithm (KHA) [12], bat inspired algorithm (BIA) [13], and many more to study strategic bidding mechanisms for finding optimal solution in day-ahead energy markets were published. In terms of profit, this produces a suboptimal result. Still, there is an opportunity to increase the solution’s quality in order to maximize profits.

Electricity generation is transitioning from fossil fuel conventional power plants to greener facilities throughout the world, but there has not been a total change yet [14]. It may take a few more years to achieve carbon-free electricity generation on a long-term basis. In order to sell their power, fossil fuel producers compete with renewable in energy markets [15]. Renewable energy facilities have minimal operating expenses, allowing them to offer their energy at a low cost [16]. Due to this reason, fossil fuel producers may not be able to sell their energy at high rates on a continuous basis. Therefore, researchers have been interested in the bidding strategies of renewable power producers with amalgamation of the fossil fuel power producers in recent years [17]. However, owing to weather dependence, many green energy sources, such as solar PV or wind, are uncertain, posing problems such as suggesting bidding quantity will differ from the quantity produced, which are leading to financial penalties [18]. As a result, these renewable energy providers should be supplied with a well-thought-out strategy in a deregulated electricity market. Moreover, to decrease the uncertainty and maximize profit, precise renewable energy sources modeling is required.

There are a variety of optimization techniques that may be used to address the issue of bidding strategy and maximize supplier advantage. A functional heuristic optimization strategy must necessarily meet three criteria, according to literature. To begin, regardless of the original system’s parameter settings, the technique should discover the global solution. Second, rapid convergence is needed. Third, the method can include a small set of control parameters to make it easier to use. The GA [7], PSO [8], GSA [10], KHA [12], and BIA [13] are examples of heuristic optimization approaches that are sensitive to parameter selection such as selections of crossover and mutation in GA, learning factors and inertia weight selection in PSO, initialization of population in GSA, poor exploitation capability in KHA, and control and tuning of parameters in BIT. The no-free-lunch (NFL) algorithm [19] reasonably demonstrates that a single method cannot be credited with dealing with a variety of optimization problems. As a result, this algorithm enables researchers to suggest novel approaches or alter existing strategies for tackling complicated problems in the literature. The strategic bidding challenge is one of these difficult issues. Therefore, the idea of oppositional based learning (OBL) has been used in a number of studies. OBL has also been shown to improve the performance of algorithms. Tizoosh [20] proposed an OBL concept. When dealing with the curse of dimensionality, OBL is a very useful paradigm. Because of the large exploration space and the random temperament of variables, the curse of dimensionality is unavoidable in the strategic bidding formulation issue. As a result, in dynamic replication, establishing a global best might be difficult. OBL provides a one-of-a-kind solution to this problem and may provide a way out of the local minima trap. By producing opposing points in search space, OBL improve the exploration ability of any algorithm.

Therefore, in this paper, the authors suggested and considered the following:

• A new variation of the GSA algorithm to tackle the strategic bidding issue with renewable sources in an emerging electricity market. In OGSA, the opposing number concept is incorporated with the GSA for population initialization and new population generation to improve the exploration ability of the algorithm;
• The proposed version is assessed first on standard IEEE 30-bus and 57-bus arrangements and then standard arrangements with the renewable sources;
• The Weibull and Beta probability distribution functions have been used to build an authentic uncertainty modeling of wind and solar respectively in order to decrease projected error while maintaining the profit. Furthermore, the probabilities for wind and solar have been adjusted to reflect physical circumstances;
• The Kantorovich distance (KD) technique to decrease the scenarios for wind and solar;
• Cost formulas for underestimation and overestimation to compute the renewable power anomalies.

2. Wind Power Modeling

Long-term meteorological data are required to make a wind prospective and attributes must be accurately assessed. Wind speed is a random variable, and functions of probability density (pdf) are employing to describe changes in wind speed over time. Detailed understanding of the dispersion and properties of the wind are essential elements to pick best a wind force translation arrangement to maximize force efficiency and reduction of the price of power production. The Lognormal, Gamma, Rayleigh, Weibull, and three-parameter Beta distributions have all been used to depict the wind speed frequency distribution. In literature, the Weibull pdf has become one among the most popular, recognized, and optional distributions for estimating wind force potential. However, it is worth noting that the Weibull distribution is not appropriate for representing wind dispersion in every geographical area on the planet. Therefore, it is possible to infer that the method’s appropriateness varies depending on sample data size, distribution, layout, and tests for the quality of fit. The data fit test was used to assess the appropriateness of suggested techniques for the distribution of wind speeds in a given area. Hourly mean wind statistics at 39 m above ground level for Barnstable city, MA, USA areas were collected from the University of Massachusetts Amherst [21], Wind Energy Center during the period of 1300–1400 h from 1 August to 31 August 2005, in order to compare the distributions. Fit tests for considered historical wind speed for different distributions are shown in Figure 1 and different parameters values for considered distributions are given in Table 1.

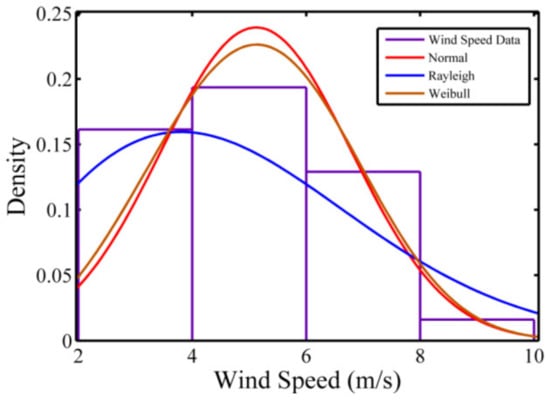
Figure 1. Past wind speed data fittings.

Table 1. Past wind data fitting results for different pdfs.

	Normal	Rayleigh	Weibull
Log Likelihood Value	−59.3305	−64.7905	−59.2297
Mean	5.12151	4.76584	5.12102
Variance	2.77917	6.20614	2.8617

It can be noted that from Table 1 the speed data of past wind was better fixed in the Weibull pdf found on the maximum value of likelihood as compared to other considered distributions. Therefore, Weibull distribution function is utilized for wind speed scenario generations.

2.1. Weibull Parameters Estimation

The Weibull probability distribution [22] is considered as:

$$W_{pdf}=\frac{k}{c}{\left(\frac{v}{c}\right)}^{\left(k-1\right)}\left(exp{\left(-\frac{v}{c}\right)}^k\right)$$

(1)

W_pdf is the likelihood of sensing speed of wind v, dimensionless form of shape parameters are k, while c is a scaling constraint in wind speed divisions. Estimating Weibull parameters may be done in a number of ways. In this study, one of them is represented as:

$$k={\left(\frac{{\sigma }_{std}}{{\mu }_{hws}}\right)}^{\left(-1.086\right)}$$

(2)

$$c=\left(\frac{{\mu }_{hws}}{\Gamma \left(1+\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$k$}\right.\right)\right)}\right)$$

(3)

where standard deviation and mean are ${\sigma }_{std}$ and ${\mu }_{hws}$ respectively.

Among the key characteristics of the Weibull distribution that makes it more suitable for wind turbines is that once these settings have been set at particular altitude, they may be adjusted to various heights. At various heights, the wind speed is approximated as follows:

$$v\left(h_{est}\right)=v\left(h_{rkh}\right){\left(\frac{h_g}{h_{kah}}\right)}^{\left(\gamma \right)}$$

(4)

here $\gamma$ is the shear coefficient parameter that controls the surface’s irregularity and environment; $v\left(h_{est}\right)$ denotes the anticipated speed of wind at the hub height of a turbine; $h_{kah}$ is the height of anemometer; $h_g$ is the height of the generating wind turbine base (m); and Wind speed at known hub heights is represented by $v\left(h_{rkh}\right)$.

2.2. Wind Power Calculation

Wind power may be represented as follows using the Weibull distribution.

$$W_a\left(v\right)=\left\{\begin{array}{ll}0& v\le v_{in}\\ \frac{1}{2}{\eta }_p\left(v\right)\rho A_s{v}^3& v_{in}\le v\le v_r\\ W_r& v_r\le v\le v_o\\ 0& v\ge v_o\end{array}\right.$$

(5)

where $W_a\left(v\right)$ is the deliberated accessible power of wind at considered wind speed site; $W_r$ is the rated output of the wind energy production; ${\eta }_p\left(v\right)$ is the effectiveness of considered wind turbine; $A_s$ is the wind turbines rotor swept area; $\rho$ is the considered site air density (kg/m³).

Furthermore, a random variable transformation is performed to convert it into a power variable. Due to the fact that the wind power function is represented in discrete form (5). As a result, wind power pdf has discontinuous probability. Wind power has a 0% chance of succeeding, i.e.: $f_w=f_w\left[(v\le v_{in})\mathrm{and}(v\ge v_o)\right]=0$

$$f_w\left[(v\le v_{in})\mathrm{and}(v\ge v_o)\right]=1-\exp \left[-{\left(\frac{v_{in}}{c}\right)}^k\right]+\exp \left[-{\left(\frac{v_o}{c}\right)}^k\right]$$

(6)

Wind power has linear output chance of succeeding as:

$$f_w\left(v_{in}\le v\le v_r\right)=\left(\frac{kz{v}_{in}}{c{W}_r}\right)\left[\frac{(1+z{W}_a/W_r)v_{in}}{c}\right]\times \left\{-{\left[\frac{(1+z{W}_a/W_r)v_{in}}{c}\right]}^k\right\}$$

(7)

here $z=\frac{\left(v_r-v_{in}\right)}{v_{in}}$.

Wind power has the rated output chance of succeeding as:

$$f_w{(v}_r\le v\le v_o)=\exp \left[-{\left(\frac{v_r}{c}\right)}^k\right]+\exp \left[-{\left(\frac{v_o}{c}\right)}^k\right]$$

(8)

3. Solar Power Modeling

Solar radiation data show how much of the sun’s energy reaches a surface at a certain point on the planet over a given time period. This information is required for effective solar-energy research. Due to established sun direction and limited hour availability, solar irradiation has some predictability. To establish an accurate assessment of solar energy potential and characteristics, long-term meteorological data are necessary. Hourly solar statistics for Barnstable city, MA, USA [23] areas were collected from the solar anywhere, during the period of 1300–1400 h from 1 January 2013 to 31 December 2013, in order to compare the distributions. Fit tests for considered historical solar irradiance for different distributions are shown in Figure 2 and different parameters values for considered distributions are given in Table 2.

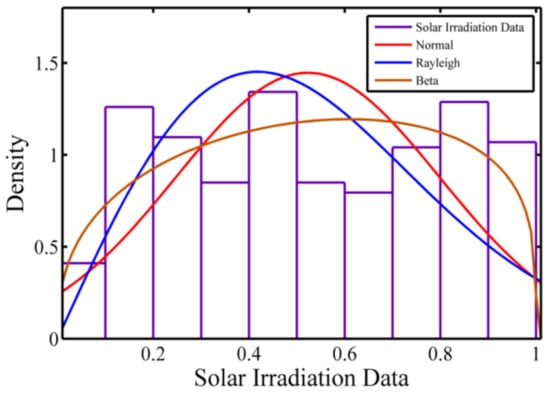
Figure 2. Past solar irradiance data fitting.

Table 2. Past solar data fitting results for different pdfs.

	Normal	Rayleigh	Beta
Log Likelihood Value	−47.2392	−34.9839	10.1446
Mean	0.52266	0.523565	0.526305
Variance	0.0760555	0.0749005	0.06844

It can be noted that from Table 2, the data of historical solar irradiance is better fitted in the Beta distribution based on the maximum value of likelihood as compared to other considered distributions. Therefore, Beta distribution function is utilized for solar irradiance scenario generations.

3.1. Beta Distribution Parameters Estimation Method

A Beta pdf [22] is used to explain the random phenomena of the irradiance data, as seen below:

$$B_{pdf}\left(S_{i,t}\right)=\left\{\frac{\Gamma \left(A_t+B_t\right)}{\Gamma \left(A_t\right)\Gamma \left(B_t\right)}{\left(\frac{S_{i,t}}{S_{i\max ,t}}\right)}^{\left(A_t-1\right)}{\left(1-\frac{S_{i,t}}{S_{i\max ,t}}\right)}^{\left(B_t-1\right)}\right\},0\le \left(\frac{S_{i,t}}{S_{i\max ,t}}\right)\le 1,A_t>0,B_t>0$$

(9)

where $A_t,B_t$ are the Beta pdf parameters; S_i,t is the irradiance of solar in kW/m²; S_imax,t is the maximum solar irradiance.

The standard deviation and mean of the random variable are used to determine the parameters of the Beta distribution function as follows:

$$A_t={\mu }_{si}^2\left(\frac{1-{\mu }_{si}}{{\sigma }_{si}}-\frac{1}{{\mu }_{si}}\right)$$

(10)

$$B_t=A_t\left(\frac{1}{{\mu }_{si}}-1\right)$$

(11)

while the Beta pdf variable falls inside a range between 0 to 1. As a result, a notional value of solar irradiance $\left(\frac{S_{i,t}}{S_{i\max ,t}}\right)$ is taken into account. In addition, the solar power is organized according to the Beta pdf as calculated by the model.

$$B_{pdf}\left(S_{PV,t}\right)=\left\{\begin{array}{l}\frac{1}{S_{PV}^{\max }}\times \frac{\Gamma \left(A_t+B_t\right)}{\Gamma \left(A_t\right)\Gamma \left(B_t\right)}{\left(\frac{S_{PV,t}}{S_{PV,t}^{\max }}\right)}^{\left(A_t-1\right)}\\ {\left(1-\frac{S_{PV,t}}{S_{PV,t}^{\max }}\right)}^{\left(B_t-1\right)}\end{array}\right\},0\le \left(\frac{S_{PV,t}}{S_{PV,t}^{\max }}\right)\le 1,A_t>0,B_t>0$$

(12)

3.2. PV Module Output Calculation

The PV module’s output power is determined by the site’s solar irradiation and ambient temperature, as well as the module’s specifications. As a result, after the Beta pdf for a given time segment is created, the output power for that segment is computed using the following formula:

$$T_{cell,t}=T_a+S_{i,t}\left(\frac{T_{NO}-20}{0.8}\right)$$

(13)

$$I_t=S_{i,t}\left[I_{sc}+I_{TK}\left(T_{cell,t}-25\right)\right]$$

(14)

$$V_t=V_{oc}-V_{TK}\times T_{cell,t}$$

(15)

$$S_{PO,t}\left(S_{i,t}\right)=n\times I_t\times V_t\times FF$$

(16)

$$\mathrm{here},FF=\frac{I_{mpp}\times V_{mpp}}{I_{sc}\times V_{oc}}$$

(17)

The specifications of the considered PV module in this study are given in Table 3.

Table 3. Data on considered PV modules.

Features of the Module	Unit
Peak output (PVmax)	340 W
VTK	0.335 mV/°C
ITK	0.047 mA/°C
Fill factor (FF)	0.755
Current at maximum power (Impp)	8.99 Amp.
Ambient temperature and nominal cell operating temperature (Ta and TNO)	25 °C and 46 °C
Vmpp (voltage at maximum power)	37.8 V
Short circuit current (Isc)	9.78 A
Open circuit voltage (Voc)	46 V

4. Handling of the Uncertainty Related to Renewable Energy Sources

A vast number of possibilities is required for every stochastic process for proper modeling. The amount of computing power required to solve scenario-based optimization representation is relative to the number of possible situations. As a result, the original scenario set must be decreased so that the reduced set contains a lesser number of possibilities, but the stochastic characteristics remain same. The quantity of reduced scenarios depends according to the problem’s form and character to be improved and it has to be less than one-fourth of all scenarios created [24].

The scenario reduction’s primary premise is to eliminate possibilities with extremely low probability and group those that are extremely similar. As a result, scenario-reduction algorithms choose a subset of situations and compute probabilities for new scenarios in such a way that in terms of a given probability distance, the reduced probability measure approaches the original probability measure.

Using the Kantorovich distance (KD) matrix [25], the scenario-reduction method reduces and bundles the scenarios. The probability distance between two separate scenario sets representing the same stochastic process is known as KD. It is most commonly used to compare the similarity of several situations’ positions. KD ensures that the highest number of potential situations is minimized while adhering to a set of tolerance requirements. All removed possibilities are considered to have a probability of zero. The fresh prospect of conserved possibilities is the sum of their previous probabilities and the likelihood of deleting instances that are the most similar to it. Steps for the Kantorovich distance (KD) matrix are as follows:

Step 1: Compute the Euclidian detachment involving each case and all other potential circumstances. The distance linking any two distinct possibilities ${\upsilon }^i$ and ${\upsilon }^j$ is computed as:

$$KD\left({\upsilon }^i,{\upsilon }^j\right)={\left({\displaystyle \sum _{l=0}^{{\eta }_l}{\left(v_l^i-v_l^j\right)}^2}\right)}^{\frac{1}{2}}$$

(18)

Step 2: Find the least separation $\min \left\{KD\left({\upsilon }^i,{\upsilon }^j\right)\right\}$ between every opportunity ${\upsilon }^i$ and the opportunity ${\upsilon }^j,j\ne i$.

Step 3: Replicate or develop with the same likelihood calculated in Step 2.

$$\min \left\{KD\left({\upsilon }^i,{\upsilon }^j\right)\right\}\times P\left[{\upsilon }^i\right]$$

(19)

Step 4: Diminish the smallest feasible gap and situation. Then, for the next closest possibility, apply the likelihood of the removed circumstances.

Step 5: Repeat Steps 2–4 until the stoppage condition is met.

5. Calculation of Bidding Amount for Renewable Energy Sources

The predicted solar and wind energy is calculated with KDM, and the proper probability are planned as follows [18]:

$$S_g={\displaystyle \sum _{i=1}^{{\upsilon }_i}{S}_{ai}\times {\mathrm{prob}}_i}$$

(20)

$$W_g={\displaystyle \sum _{i=1}^{{\upsilon }_i}{W}_{ai}\times {\mathrm{prob}}_i}$$

(21)

where the probability of a predicted ith scenario is represented by ${\mathrm{prob}}_i$.

6. Formulation of Strategic Bidding with Renewable Sources

The revenue and production costs of thermal generators, as well as the revenues and imbalance costs of wind and solar facilities are represented as the objective function of stochastic strategic bidding.

Maximize:

$$F({\pi }_m,{\varphi }_m)=R\times P{g}_m-P{C}_m(P{g}_m)+R\times W{g}_n-IMC(W{g}_n)+R\times S{g}_n-IMC(S{g}_n)$$

(22)

The revenue of the thermal generator is defined by the first term of the objective function. Every power suppler submits their bid as a linear supply function (non-decreasing) as given in Equation (23) to the impendent system operator in the single sided pool-based electricity market.

$$C{P}_m(P{g}_m)={\pi }_m+{\varphi }_{m}P{g}_m,m=1,2,\dots \dots ,\mathrm{TPS}$$

(23)

where $P{g}_m$ is the bidding amount in MW; and ${\pi }_m$ and ${\varphi }_m$ are non-negative bidding parameters.

The ISO matches total bidding amount with total forecasted demand of the system after receiving bid data from power utilities. After that, it reduces the cost of procuring while increasing profit. Furthermore, it takes use of the provider for power dispatch while taking into account other market limitations such as inequality and equality constraints. Following are the equality constraints of the power market:

$${\pi }_m+{\varphi }_{m}P{g}_m=R$$

(24)

where R is the market clearing price.

$${\displaystyle \sum _{m=1}^{cps}P{g}_m+{\displaystyle \sum _{n=1}^{sg}s{g}_n}+{\displaystyle \sum _{n=1}^{wg}W{g}_n}=Q(R)}$$

(25)

Following are the inequality constraints of the power market:

$$P{g}_{\min ,m}\le P{g}_m\le P{g}_{\max ,m}$$

(26)

The generating limits of thermal generators are shown in Equation (26).

$Q(R)$ reflects the load predicted by pool, as follows:

$$Q(R)=L_c-k\ast R$$

(27)

where L_c is the regular load and k is the load flexibility factor.

Without taking inequality restrictions into account, the solutions to Equations (24) and (25) become:

$$R=\frac{L_c-{\displaystyle \sum _{n=1}^{sg}S{g}_n}-{\displaystyle \sum _{n=1}^{wg}W{g}_n}+{\displaystyle \sum _{m=1}^{cps}\frac{{\pi }_m}{{\varphi }_m}}}{k+{\displaystyle \sum _{m=1}^{cps}\frac{1}{{\varphi }_m}}}$$

(28)

$$P{g}_m=\frac{R-{\pi }_m}{{\varphi }_m}$$

(29)

If the solution breaches its limit for Equation (29) after getting the value of MCP, it must be brought to the appropriate limit as indicated by Equation (26).

The production cost of a thermal generator is expressed in the second objective function term. It is considered as:

$$P{C}_m(P{g}_m)=a_{m}P{g}_m+b_{m}P{g}_m^2$$

(30)

where a_m and b_m are the production cost parameters.

The revenues of the considered renewable power sources are defined by the third (for wind source) and fifth (for solar source) terms of the objective function.

Imbalance costs of the considered renewable power sources are defined by the fourth (for wind source) and sixth (for solar source) terms of objective function. The imbalance costs of the wind and solar power sources are calculated as follows [18]:

$$IMC(W{g}_n)=O_c(w_g)+U_c(w_g)$$

(31)

$$IMC(S{g}_n)=O_c(S_g)+U_c(S_g)$$

(32)

where $O_c(w_g)$ and $O_c(S_g)$ are the cost for overestimation of the renewable power output (wind and solar), respectively. $U_c(w_g)$ and $U_c(S_g)$ are the cost for underestimation of the wind and solar power output respectively. The costs for overestimation and underestimation of the renewable (wind and solar) power output are calculated as follows:

$$O_c(w_g)=K_o\ast {\displaystyle \underset{0}{\overset{W_g}{\int }}(W_g-W_a)\ast f_{W_a}}(W_a)\ast d{W}_a$$

(33)

$$O_c(S_g)=K_o\ast {\displaystyle \underset{0}{\overset{S_g}{\int }}(S_g-S_a)\ast f_{S_a}}(S_a)\ast d{S}_a$$

(34)

$$U_c(w_g)=K_u\ast {\displaystyle \underset{W_g}{\overset{W_{\max }}{\int }}(W_a-W_g)\ast f_{W_a}}(W_a)\ast d{W}_a$$

(35)

$$U_c(S_g)=K_u\ast {\displaystyle \underset{S_g}{\overset{S_{\max }}{\int }}(S_a-S_g)\ast f_{S_a}}(S_a)\ast d{S}_a$$

(36)

here $K_o$ and $K_u$ are the penalty coefficients for overestimation and underestimation of the wind and solar power output, respectively.

Probabilistic Modeling of Bid Parameters

Because the power market model is based on secret bids, the data necessary for following bidding periods are unknown, making the optimization problem difficult to solve. Using the probability density function and bidding data from previous bids, the estimation of rival bidding coefficients may be derived [6]. From the ith utility standpoint, bidding coefficients ${\pi }_m$ and ${\varphi }_m$ are follow the probability density function (PDF) of a joint normal distribution obeyed by jth rivals is as follows:

$$\mathrm{pdf}({\pi }_m,{\varphi }_m)=\frac{1}{{2\pi \sigma }_m{}^{\left(\pi \right)}{\sigma }_m{}^{\left(\varphi \right)}\sqrt{1-{\rho }_m^2}}\times \exp \left\{-\frac{1}{2\left(1-{\rho }_m^2\right)}\right.\left.\left.\left[{\left(\frac{{\pi }_m-{\mu }_m^{\left(\pi \right)}}{{\sigma }_m^{\left(\pi \right)}}\right)}^2+\left(\frac{{\varphi }_m-{\mu }_m^{\left(\varphi \right)}}{{\sigma }_m^{\left(\varphi \right)}}\right)\right.-\frac{{2\rho }_m\left({\pi }_m-{\mu }_m{}^{\left(\pi \right)}\right)\left({\varphi }_m-{\mu }_m{}^{\left(\varphi \right)}\right)}{{\sigma }_m^{\left(\pi \right)}{\sigma }_m^{\left(\varphi \right)}}\right]\right\}$$

(37)

This pdf can be viewed in a compressed format. −×)

$$({\pi }_m,{\varphi }_m)\sim N\left\{\left[\begin{array}{c}{\mu }_m^{(\pi )}\\ {\mu }_m^{(\varphi )}\end{array}\right]\right.,\left.\left[\begin{array}{cc}{({\sigma }_m^{(\pi )})}^2& {\rho }_m{\sigma }_m^{(\pi )}{\sigma }_m^{(\varphi )}\\ {\rho }_m{\sigma }_m^{(\pi )}{\sigma }_m^{(\varphi )}& {({\sigma }_m^{(\varphi )})}^2\end{array}\right]\right\}$$

(38)

where ${\rho }_n$ is the parameter of correlation; ${\mu }_m^{(\pi )}$ and ${\mu }_m^{(\varphi )}$ are the mean values; ${\sigma }_m^{(\pi )}$ and ${\sigma }_m^{(\varphi )}$ are the standard deviations values.

The problem described in Equation (22) is optimized using the OGSA method in subsequent sections, taking into account all of the restrictions listed above, to discover the best solution for the strategic bidding issue that maximizes generator profit during an one hour trading period.

7. An Overview of Gravitational Search Algorithm

Agents are treated such as objects in GSA [26], and their presentation is assessed by their masses. The gravitational strength attracts all of these things, causing a universal progress of all substance towards the ones through heavier weights. The masses collaborate through gravitational force, which is the shortest form of contact. The heavier weights (which are appropriate for high-quality solutions) travel at a slower rate than the lighter masses. This ensures the algorithm’s exploitation stage.

Inertial mass, position, passive, and active gravitational mass are the four parameters for each mass (agent) in GSA. A fitness function is used to determine the gravitational and inertial masses, which correlates to the problem’s solution. To put it another way, each mass is a solution. By appropriately changing the inertial and gravitational masses, the algorithm may be navigated. It is predicted that the heaviest mass would attract masses over time. In the exploration space, this mass will provide an optimal clarification.

Let us take a look at a structure with n representatives (masses). The kth agent’s location is determined by:

$${\lambda }_k=({\lambda }_k^1,\dots \dots ,{\lambda }_k^D,\dots \dots ,{\lambda }_k^M)\mathrm{For}k=1,2,\dots \dots ,N$$

(39)

where ${\lambda }_k^D$ represents the kth agent’s location in the Dth dimension. The force exerted on the kth mass from the jth mass is described as in the following equation at a given time t.

$$F_{kj}^D(t)=G(t)\frac{M_{passive,k}\left(t\right)\times M_{active,j}(t)}{R_{kj}(t)+\epsilon }({\lambda }_j^D(t)-{\lambda }_k^D(t))$$

(40)

where $\epsilon$ is the small constant; G(t) represents the gravitational constant at time t; $M_{passive,k}\left(t\right)$ is the kth agent’s passive gravitational mass linked at time t; $M_{active,j}\left(t\right)$ is the active gravitational mass associated with the jth agent at time t; R_kj(t) is the Euclidian distance between the two agents k and j is given by the equation:

$$R_{kj}\left(t\right)=\parallel {\lambda }_k\left(t\right)-{\lambda }_j\left(t\right){\parallel }_2$$

(41)

To give the method a stochastic quality, the total force acting on the kth agent in the Dth dimension is anticipated to be a randomly weighted sum of the Dth components of the forces exerted by other agents, as indicated by the equation:

$$F_k^d={\displaystyle \sum _{j=1,j\ne k}^{N}ran{d}_j\times F_{kj}^D(t)}$$

(42)

where rand_j is a random number between 0 and 1. As a result of Newton’s law of motion, the acceleration of the kth agent in the Dth dimension at time t is given by the equation:

$$a_k^D(t)=\frac{F_k^D(t)}{M_{initial}(t)}$$

(43)

where $M_{initial}(t)$ is the kth agent’s inertial mass. Equations (44) and (45) can be used to compute an agent’s position and velocity, respectively.

$$v_k^D(t+1)=ran{d}_k\times v_k^D(t+1)+a_k^D(t)$$

(44)

$${\lambda }_k^D(t+1)={\lambda }_k^D\left(t\right)+v_k^D(t+1)$$

(45)

In Equation (44) rand_k is a random number between 0 and 1. This random integer is used to give the search a randomized characteristic. To regulate the search accuracy, the gravitational constant (G) is established at the start and lowered over time. In other terms, G is represented as the following Equation as a function of the starting value (G₀) and time (t):

$$G(t)=G(G_0,t)=G(t_0)\times {\left(\frac{t_0}{t}\right)}^{X}X\text{<}1$$

(46)

G(t) is the gravitational constant value at time t in Equation (46). The gravitational constant G(t₀) is the value at the first cosmic quantum period of time, t₀. G(t) is calculated in GSA using the following equation:

$$G(t)=G_0\times e^{-\tau \left(\frac{iteration}{iteratio{n}_{\max }}\right)}$$

(47)

where $\tau$ is set to 20, G₀ is set to 100, iteration is the current number of iterations, and iteration_max is the total number of iterations. The fitness evaluation can easily compute inertial and gravitational masses. A more efficient agent has a higher mass. Better agents are more attractive and move more slowly as a result of this. Assuming that the gravitational mass and the mass of inertia are identical, the map of fitness is used to determine the mass values. The following equations are used to calculate gravitational and inertial masses:

$$M_{active}=M_{passive}=M_{Initial}\mathrm{for}k=1,2,\dots n$$

(48)

$$m_k(t)=\frac{fi{t}_k(t)-worst(t)}{best(t)-worst(t)}$$

(49)

$$M_k(t)=\frac{m_k(t)}{{\displaystyle \sum _1^N{m}_k(t)}}$$

(50)

where for a maximization issue, fit_k(t) is the fitness value of the kth agent at time t, and worst(t) and best(t) are defined in Equations (51) and (52), respectively.

$$best(t)=\underset{j\in \{1,..,n\}}{\max }fi{t}_j(t)$$

(51)

$$worst(t)=\underset{j\in \{1,..,n\}}{\min }fi{t}_j(t)$$

(52)

The progressive reduction of the number of agents is one way to establish a good balance between exploration and exploitation. As a result, a collection of agents with bigger masses is supposed to exert their forces on one and all. However, this strategy must be implemented with caution because it has the potential to diminish exploration power while increasing exploitation capabilities. To prevent becoming trapped in a neighboring best, the algorithm be required to employ exploration at the start. Investigation must fade away and exploitation must emerge after a number of cycles. Only the Kbest agents will entice the others to increase GSA’s performance by regulating exploration and exploitation. Kbest is a time-dependent function that starts at K0 and lowers with time. As a result, all agents apply the pressures at the start, and Kbest decreases linearly with time. In the end, just one agent will be using force against the others. As a result, Equation (42) may be changed as follows:

$$F_k^D(t)={\displaystyle \sum _{\begin{array}{cc}j\in kbest& j\ne k\end{array}}ran{d}_j\times F_{kj}^D(t)}$$

(53)

In Equation (53), Kbest refers to the first 2% K agents having the highest fitness values and the largest populations.

7.1. An Overview of Oppositional Gravitational Search Algorithm

Starting with certain starting solutions (initial population), evolutionary optimization methods aim to enhance them until they reach a most favorable result (s). When certain preset criteria are met, the search procedure comes to an end. We generally start with random guesses when we do not have any a priori information about the answer. The gap between these initial estimations and the best answer, among other things, affects computing time. By testing the opposing solution at the same time, we can increase our chances of starting with a closer (better) solution. As a result, the best match (guess or opposite guess) can be selected as the first answer. In reality, based on theory of probability, a guess is 50% more likely to be inaccurate than the opposing guess. As a result, starting with the closer of the two predictions (as determined by fitness) has the potential to speed up convergence. Not only can the same method be used to find initial solutions, but it can also be used to find each solution in the present population. The components of the opposing point $O{\lambda }_k=[O{\lambda }_k^1,\dots \dots ,O{\lambda }_k^D,\dots \dots ,O{\lambda }_k^M]$ entirely characterize as:

$$O{\lambda }_k^D=L_k^D+U_k^D-{\lambda }_k^D$$

(54)

$O{\lambda }_k^D\in [L_k^D,U_k^D]$ is the agent’s (kth) opposing placement in the oppositional community’s Dth aspect; $L_k^D,$ and $U_k^D$ are the lower bound and upper bound values.

7.2. Opposition Based Fitness Evaluation

At the same time, the algorithm assesses the strength of an agent and its adversary. Further computations are performed using the agent with the better fitness score, while the additional agent is rendered worthless.

$${\lambda }_k(i)=\left\{\begin{array}{lll}O{\lambda }_k(i)& if& fit(O{\lambda }_k(i)>fit({\lambda }_k(i))\\ {\lambda }_k(i)& otherwise\end{array}\right.$$

(55)

8. Results

The proposed algorithm has been tested on IEEE 30 bus and IEEE 57 bus systems. For the IEEE 30-bus [18] and 57-bus [18] networks, the load demands are as 500 and 1500 MW, respectively. Firstly, the standard evaluation bus systems are used to develop the bidding approach initially. Secondly, one solar photovoltaic generator and one wind power generator, each with a capacity of 200 megawatts, have been considered to be installed at any two different buses. The proposed procedure was investigated in a MATLAB R-2014a setting with 4 GB of RAM and an i5 Core Processor. The OGSA is put to the test using a search agent that prefers 1000 iterations. The maximum number of distinct runs is set at 100.

To prove the superiority of the suggested version, the proposed technique was first tested on standard IEEE 30-bus and 57-bus arrangements. Bidding criteria are exercised to build bidding approach in a dynamic power market. As a consequence, it is calculated using a combined pdf (Equation (13)) and optimized using the OGSA approach. The bidding criteria cannot be preferred independently in order to get the desired results (optimize revenues while generating utilities). One coefficient ${\pi }_m$ of bidding is fixed for each utility, while another coefficient ${\varphi }_m$ is calculated with OGSA in the selected criteria [b_m, 10b_m] [6]. MCP is then computed using the optimal bid constraints. The computed MCP is used to evaluate the overall profit of generating energy and total energy production dispatch in this scenario. Table 4 and Table 5 describe the results of different optimization approaches such as OGSA, GSA [26], PSO [27], and GA [28] for the standard IEEE 30-bus and 57-bus arrangements, correspondingly. Table 4 and Table 5 shows that the utilization of OGSA, the overall advantages of power supplies with IEEE 30-bus and 57-bus systems have increased to $5317.72 and $14,077.77, respectively. In addition, the values of MCPs for IEEE 30-bus and 57-bus systems have increased to 14.15 $/MW and 12.97 $/MW, respectively. In contrast to GSA [26], PSO [27], and GA [28], for both cases for IEEE 30-bus and 57-bus systems, the total profit of power supplies and values of MCPs are the largest. The superiority of the OGSA method is demonstrated by judging against simulation results of GSA, PSO, and GA.

Table 4. Findings for the IEEE standard 30-bus exclusive of renewable influence.

TPSs	${\mathit{\pi }}_{\mathit{m}}$	OGSA			GSA [26]			PSO [27]			GA [28]
		${\mathit{\varphi }}_{\mathit{m}}$	PG	Profit	${\mathit{\varphi }}_{\mathit{m}}$	PG	Profit	${\mathit{\varphi }}_{\mathit{m}}$	PG	Profit	${\mathit{\varphi }}_{\mathit{m}}$	PG	Profit
1	2.0	0.049984	160	1848.47	0.049231	160	1815.32	0.042666	160	1645.73	0.044090	160	1592.4
2	1.75	0.223528	78.68	867.49	0.224134	77.45	839.65	0.211031	74.81	735.14	0.19429	75.05	712.19
3	1.0	0.680919	42.5	446.15	0.722945	40.95	425.33	0.436374	49.28	433.95	0.300167	57.94	459.54
4	3.25	0.099466	100	1006.9	0.097653	100	986.18	0.103585	100	880.18	0.094465	100	846.85
5	3.0	0.307913	59.41	574.36	0.289934	60.80	573.06	0.275273	57.95	488.96	0.280553	53.50	439.52
6	3.0	0.307913	59.41	574.36	0.289934	60.80	573.06	0.275273	57.95	488.96	0.280553	53.50	439.52
MCP		14.15			13.9458			12.89			12.55
Profit		5317.72			5212.6			4672.93			4490.02
Total PG		500			500			500			500

Table 5. Findings for the IEEE standard 57-bus exclusive of renewable influence.

TPSs	${\mathit{\pi }}_{\mathit{m}}$	OGSA			GSA [26]			PSO [27]			GA [28]
		${\mathit{\varphi }}_{\mathit{m}}$	PG	Profit	${\mathit{\varphi }}_{\mathit{m}}$	PG	Profit	${\mathit{\varphi }}_{\mathit{m}}$	PG	Profit	${\mathit{\varphi }}_{\mathit{m}}$	PG	Profit
1	1.7365	0.022239	505.16	5241.2	0.021819	510.26	5238.34	0.020393	520.21	5058.66	0.019718	530.23	5065.65
2	10	0.076760	38.7	99.99	0.092598	30.99	79.34	0.098836	23.73	50.02	0.095015	23.07	45.23
3	7.1429	0.088860	65.58	351.7	0.081198	70.53	368.62	0.082602	62.98	299.48	0.078495	64.32	295.35
4	10	0.076760	38.7	99.99	0.092598	30.99	79.34	0.098836	23.73	50.02	0.095015	23.07	45.23
5	1.81	0.023240	480.23	4944.7	0.02278	485.52	4945.47	0.021487	490.3	4732.82	0.020843	498.08	4724.32
6	10	0..076760	38.7	99.99	0.092598	30.99	79.34	0.098836	23.73	50.02	0.095015	23.07	45.23
7	2.4390	0.031635	332.92	3240.2	0.030615	340.71	3275.32	0.02788	355.3	3216.81	0.028839	338.18	3023.63
MCP		12.97			12.87			12.35			12.19
Total profit		14,077.77			14,065.79			13,457.81			13,244.65
Total PG		1500			1500			1500			1500

Due to inherent unpredictability, the success of evolutionary algorithms cannot be measured by the results of a sole run. Several pursuits among varied initializations should be conducted to make a clear finish regarding the effectiveness of the techniques. It is important to remember that an algorithm is only regarded stable if it provides acceptable results in a variety of scenarios. Because the OGSA, GA, GSA, and PSO algorithms are indiscriminate, as a result, the bidding data were run 20 times for each technique. Table 6 shows a comparison of the outcomes of several approaches for the OGSA method’s robustness and validation. When compared to other approaches, it can be deduced that the OGSA methodology has the lowest standard deviation for the IEEE 30-bus and IEEE 57 bus arrangements, correspondingly. Furthermore, in terms of best, worst, and mean, OGSA delivers better results. The suggested approach accuracy is higher, allowing producers to gain a bigger profit by using OGSA. For both the standard bus arrangements, the OGSA approach is more successful, perfect, and the modeling of the strategic bidding practice is achievable, according to the outcome’s investigation.

Table 6. Relative analysis of a variety of methods for checking the strength of OGSA.

Takings	IEEE 57-bus				IEEE 30-bus
	GA [28]	PSO [27]	GSA [26]	OGSA	GA [28]	PSO [27]	GSA [26]	OGSA
Best	13,244.65	13,457.81	14,065.79	14,077.77	4490.02	4672.93	5212.59	5317.719
Worst	11,448.63	12,009	12,982.51	13,212.03	3941.41	4253.56	4798.86	4944.638
Mean	11,927.7	12,509.51	13,446.45	13,590.17	4187.19	4395.08	4944.70	5046.50
SD	415.5907	386.71	350.59	262.77	155.87	124.91	109.75	94.66

After demonstrating the superiority of the suggested version, OGSA was used to evaluate the proposed optimum bidding methods with three cases, i.e., with wind, with solar, and with both wind and solar. The values of 7.93 and 3.34 m/s for scale and shape parameters, respectively, were derived from Equations (2) and (3). Then, utilizing the wind speed power connection, a thousand speeds for wind possibilities were created and transformed into power situations at 100 m hub height for considered turbine [29]. To make their total equal to unity, each produced scenario was given a probability of normalization calculated using the Weibull distribution. For produced power situations, we used the density of the Weibull pdf as shown in Figure 3.

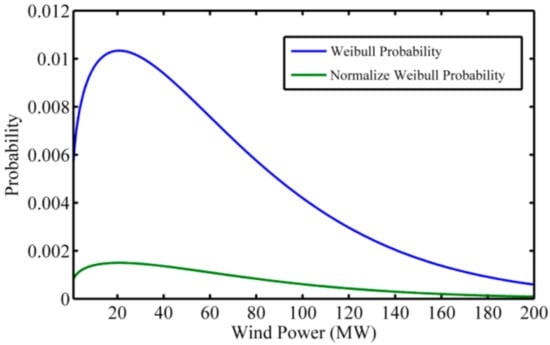
Figure 3. Density of Weibull pdf.

For the past date of solar irradiation, the values of Beta pdf parameters A and B were 1.3909 and 1.2518, respectively, as determined by Equations (10) and (11). Following that, a thousand sun irradiation scenarios were generated and translated into power scenarios using PV module specs. To make their total equal to unity, each created scenario was given a possibilities’ normalization calculated with the Beta pdf. For generated power situations, we took the Beta and normalized the probability density curve as shown in Figure 4.

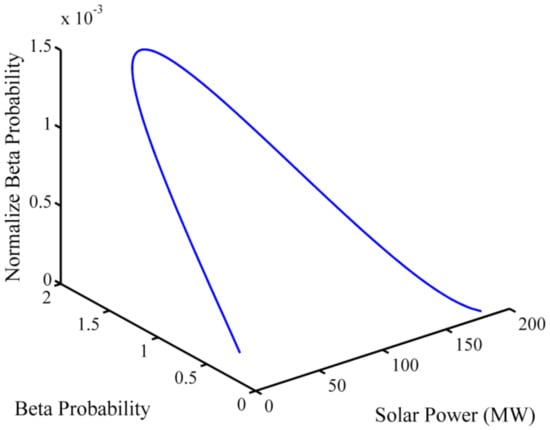
Figure 4. Density of Beta pdf.

The unpredictability of renewable power (wind and solar) was predicted by the vast variety of possibilities. However, only a few cases showed the same conclusion. The KDM approach was used to remove such scenarios in order to improve renewable power modeling. Table 7 shows 10 concentrated situations created from 1000 possibilities for considered renewable sources, respectively. The predicted values of solar and wind powers are 73.29 and 49.54 MW, respectively, depending on the ultimate values of renewable (wind and solar) power outputs, as well as the likelihood associated with them.

Table 7. Ten reduced renewable power scenarios.

Scenarios	For Wind		For Solar
	Wind Power (MW)	Probability	Solar Power (MW)	Probability
1	14.39	0.234229	16	0.022218
2	42.24	0.443626	27.42	0.075345
3	66.09	0.17126	50.23	0.268311
4	90.74	0.080668	62.35	0.163971
5	106.5	0.025689	78.47	0.277874
6	123.3	0.025047	96.74	0.09117
7	141.5	0.011009	114.7	0.046975
8	155.6	0.005085	130.8	0.042748
9	179.2	0.002536	147.1	0.00999
10	193.9	0.000852	166.2	0.001399

After calculating the wind and solar power outputs, suggested optimum bidding methods were then examined on both the arrangements using OGSA with solar, wind, and both the solar and wind together. Table 8 and Table 9 show the optimal values for factors of bidding for TPS with solar only, wind only, and combined wind-solar electricity using OGSA for both systems, respectively. The impacts of renewable energy sources were studied in order on both systems. For the bidding approach considering renewable influence, the ISO was permitted to alter the current requirement, which was a real requirement apart from renewable influence contribution, and the bidding factors were then updated to reflect the changing demand.

Table 8. Results for standard IEEE 30-bus system with renewable.

Power Suppliers	πm	With Wind			With Solar			With Both Wind and Solar
		ϕm	Pg (MW)	Profit ($)	ϕm	Pg (MW)	Profit ($)	ϕm	Pg (MW)	Profit ($)
1	2.0	0.049984	160	1661.96	0.049886	160	1570.03	0.050156	160	1432.87
2	1.75	0.223528	64.70	653.79	0.208066	60.99	585.25	0.229582	48.81	436.93
3	1.0	0.680919	32.03	319.85	0.747376	25.02	246.39	0.66874	21.89	201.09
4	3.25	0099466	100	890.32	0.108838	93.93	787.09	0.109776	81.76	623.31
5	3.0	0.307913	46.86	413.13	0.279827	43.38	361.31	0.325901	32.35	250.64
6	3.0	0.307913	46.86	413.13	0.279827	43.38	361.31	0.325901	32.35	250.64
MCP		12.99			12.41			11.56
Total TPS profit		4352.19			3911.38			3195.48
Total TPS production		450.46			426.71			377.17
$Wg$		49.5406			00			49.5406
$O_c(w_g)$		46.7718			00			41.6230
$U_c(w_g)$		368.7903			00			328.1921
$IMC(W{g}_n)$		415.5621			00			369.8151
Wind profit		227.9703			00			202.8742
$Sg$		00			73.2897			73.2897
$O_c(S_g)$		00			119.1724			111.0099
$U_c(S_g)$		00			257.9840			240.3139
$IMC(S{g}_n)$		00			377.1564			351.3238
Solar profit		00			532.3688			495.9051

Table 9. Results for standard IEEE 57-bus system with renewable.

Power Suppliers	πm	With Wind			With Solar			With Both Wind and Solar
		ϕm	Pg (MW)	Profit ($)	ϕm	Pg (MW)	Profit ($)	ϕm	Pg (MW)	Profit ($)
1	1.7365	0.021880	501.65	5078.29	0.022239	485.76	4846.56	0.022531	466.59	4535.04
2	10	0.123756	21.92	54.65	0.076760	33.08	73.07	0.094126	23.9	48.04
3	7.1429	0.071514	77.88	390.7	0.088860	60.73	301.56	0.076142	67.06	310.52
4	10	0.123756	21.92	54.65	0.076760	33.08	73.07	0.094126	23.9	48.04
5	1.81	0.023322	467.47	4703.2	0.023240	461.68	4569.9	0.024014	434.71	4197.96
6	10	0.123756	21.92	54.65	0.076760	33.08	73.07	0.094126	23.9	48.04
7	2.4390	0.030421	337.71	3195.7	0.031635	319.29	2980.3	0.029101	337.11	3034.43
MCP		12.71			12.54			12.25
Total TPSs profit		13,531.86			12,917.50			12,222.07
Total TPSs production		1450.46			1426.7103			1377.1697
$Wg$		49.5406			00			49.5406
$O_c(w_g)$		45.7637			00			44.1074
$U_c(w_g)$		360.8410			00			347.7815
$IMC(W{g}_n)$		406.6047			00			391.8888
WPS profit		223.0564			00			214.9835
$Sg$ (MW)		00			73.2897			73.2897
$O_c(S_g)$		00			120.4208			117.6360
$U_c(S_g)$		00			260.6865			254.6578
$IMC(S{g}_n)$		00			381.1073			372.2938
Solar profit		00			537.9455			525.5050

The new MCP was determined using this technique, which considered wind and solar electricity amount. First, the wind supplier was taken into account, and a new MCP value was considered by revising the bidding coefficients at the modified demand. In the same way, MCP considered the collective benefits of wind and solar suppliers, as well as the incorporation of solar supplier. The operational costs of these renewable energy sources were not taken into description of this work. However, because of the intermittent nature of renewable energy sources, it is necessary to assess the cost of their imbalance. This cost was calculated based on overestimation and underestimating of solar and wind power, and the impact of this cost was measured in terms of total income minus the imbalance cost for renewable energy providers. Furthermore, the coefficients for penalty and reserve associated with underestimation and overestimation, respectively, were treated as 50% of MCP and identical to MCP [18]. Table 8 and Table 9 show the outcomes of the suggested bidding method on examined systems with only wind, solely solar, and combined solar and wind, respectively, using OGSA.

Table 4 shows that the market was secured at an MCP of 14.15 $/MW, total production for TPS was 500 MW, and total profit TPSs was $5317.72 with an IEEE 30 bus system that excludes solar and wind electricity. However, if just wind power was included, MCP dropped to $12.99 per MW, and TPSs total production fell to 450.46 MW. TPSs net profit was also down $4352.19, owing to the decreased value of MCP and traditional system production. The expenses of wind power overestimation and underestimation were $227.9703 and $46.7718, respectively, with a net profit $368.7903 for the wind supplier. The total earnings, overestimation, and underestimating costs in the next situation only solar with TPSs were $532.3688, $119.1724, and $257.9840, respectively. The MCP value in this scenario was $12.41 per MW, with a total production of TPSs 426.71 MW, which was less than traditional with wind because of the large amount of solar energy produced. Finally, MCP was 11.56 $/MW when both solar and wind were included with TPSs, which was the lowest of all the previously studied situations.

Table 5 shows that the market was cleared at 12.97 $/MW, total TPSs production was 1500 MW, and total profit for TPSs was $14,077.77 for IEEE 57 bus system without renewable suppliers. However, if just wind influence was incorporated with TPSs, MCP fell to $12.71 per MW, and net TPSs production fell to 1450.46 MW. Furthermore, the total profit for TPSs was lowered by $1426.7103, owing to the lower value of MCP and conventional production. The wind power total profit, overestimation, and underestimating, respectively, were $223.0564, $45.7637, and $360.8410. The total profit, overestimation, and underestimating costs in the second scenario, i.e., solely solar power with TPSs, respectively, were $537.9455, $120.4208, and $260.6865. The MCP in this scenario was $12.54/MW, with total TPSs output of 1426.7103 MW, which was lesser than traditional and wind because of the large amount of solar energy produced. Finally, MCP was $12.25/MW when both wind and solar were included with TPSs, which was the lowest of all the previously studied scenarios of IEEE 57-bus system.

9. Discussion

From the aforementioned examples, it can be shown that the inferior MCP price would meet all of the purchase offers. There would be less TPSs needed in power system operating owing to the involvement of solar and wind energy providers in the process of power dispatch. Furthermore, when compared to the underestimating of solar and wind power uncertainty, the overestimation estimate is extremely less. As a result, using KDM to reduce possibilities is superior for modeling uncertainty. If the underestimate is optimistic, this will encourage renewable influenced producers to put forward the excess electricity into the real-time market.

10. Conclusions

Due to the combination of unpredictable competing bid parameters and uncertain renewable power providers, the problem of strategic bidding is regarded as a challenging stochastic optimization issue. The theory and method presented in this work illustrated how a power supplier might determine the charges at which a particular capacity of energy may be provided to the grid structure while accounting for opponent prediction performance, renewable power uncertainty, and anticipated structure requirements. Grants for varying fluctuation in these variables were effectively integrated in the model, which is an important element of the model. The KDM method is well suited to dealing with solar and wind uncertainty. To tackle the strategic bidding, an opposition-based GSA was developed. The suggested version was evaluated over standard two benchmark functions, i.e., IEEE 30-bus system and IEEE 57-bus arrangements. The suggested OGSA has been found to perform well to obtained high profitable bids compared to that of several current algorithms. It was discovered that the proposed technique generates extra profit and might be a useful implement for a power generation business that participates in market activities. The impact of renewable energy on bidding strategy decreases market clearing price, conventional generation costs, and encourages renewable suppliers to sell excess electricity in real time. The future scope of this study will include bi-level bidding model using the suggested approach to create an adaptive framework.