Application of Norm Optimal Iterative Learning Control to Quadrotor Unmanned Aerial Vehicle for Monitoring Overhead Power System

Abstract

Wind disturbances and noise severely affect Unmanned Aerial Vehicles (UAV) when monitoring and finding faults in overhead power lines. Accordingly, we propose repetitive learning as a new solution for the problem. In particular, the performance of Iterative Learning Control (ILC) that are based on optimal approaches are examined, namely (i) Gradient-based ILC and (ii) Norm Optimal ILC. When considering the repetitive nature of fault-finding tasks for electrical overhead power lines, this study develops, implements and evaluates optimal ILC algorithms for a UAV model. Moreover, we suggest attempting a learning gain variation on the standard optimal algorithms instead of heuristically selecting from the previous range. The results of both simulations and experiments of gradient-based norm optimal control reveal that the proposed ILC algorithm has not only contributed to good trajectory tracking, but also good convergence speed and the ability to cope with exogenous disturbances such as wind gusts.

1. Introduction

Overhead electrical power lines are a vital component of the power supply infrastructure. It is essential to carry out preventive monitoring of high voltage transmission lines more safely and efficiently in order to meet consumer demand [1,2,3]. UAVs have the potential to perform these monitoring tasks, due to their inherent advantages of cost, manoeuvrability, speed, and easy set-up [4,5]. They can attain the required heights and positions that are needed for performing major inspection tasks and do not require contact. However, UAVs are susceptible to aerodynamic disturbances [6,7]. Because of this, the autonomous identification of faults in terms of performance and accuracy for overhead power lines remains a difficult problem. To ensure the quality of the tasks in fault-finding operations for overhead power lines, precise and accurate trajectory tracking is important [8,9].

The UAV performance relies both on the chosen control strategy and on the underlying vehicle dynamics. Quadrotors are under-actuated and open-loop unstable with significant non-linearity and strong dynamic coupling. Furthermore, exogenous disturbances can easily compromise quadrotor stability [10]. These make the control problem non-trivial. To design and test the control system, models of the dynamics are required. However, the system is subject to modelling, plant and disturbance uncertainties that should be accounted for.

Researchers have developed an ongoing design capability to overcome limitations using various control methods. Some depend on classical control (e.g., PID controller), which is simple and capable of providing acceptable performance [11]. Nevertheless, this method needs an accurate mathematical model, as do Linear Quadratic Regulator (LQR) [12] approaches. Others are based on non-linear control such as sliding-mode [13] or back-stepping [14]. These works make use of conventional feedback and feedforward and to improve the control performance by augmenting the previous controllers (i.e., PID controller). Consequently, the feedback controllers react on the basis of the observation of information using reference signal and disturbance that results in a delayed tracking response [15]. In these regimes, it can be observed that feedback is unable to react in time.

To achieve high performance, extending classical control methods with learning schemes is another approach. Iterative Learning Control (ILC) algorithms provide some advantages over conventional feedback controllers in that they develop an element of intelligence by memorizing from previous practice [16]. ILC has been applied to quadrotors using various approaches. These include derivative-type ILC [17], Proportional-Interactive-Derivative (PID-type) ILC [18], and basic optimal ILC approaches [19] that assume the reference (r) is specified over the entire finite time horizon, $\left[0,T\right]$, and they also do not require a model. On the other hand, ILC has been applied to some complicated systems, such as precise speed-tracking control of a robotic fish [20], for multi-agent systems in [21], and recently in [22] for the distributed ILC of multiple flexible manipulators in the presence of uncertain disturbances and actuator dead zones.

We propose using two ILC methods that are based on optimal approaches. These are the Gradient-based ILC and the Norm Optimal ILC. They are chosen because of their prevalence, their use of the same underlying cost function, and because they have similar implementations [23]. This paper seeks to determine whether the proposed optimal algorithms can be applied to quadrotors for tracking performance. Furthermore, it proceeds to motivate, develop, and evaluate the flight controller required to address and if it can address this deficiency of these previous methods.

Existing ILC approaches to UAV control are reviewed in the next section. The ILC design, application, and optimal algorithm designs are described in Section 3. A suitable experimental system is selected in order to provide a test platform and results for the proposed algorithm G-ILC and NO-ILC presented in Section 5 and Section 4, respectively. Section 6 provides some concluding remarks.

2. ILC Controllers

2.1. Basic ILC

ILC relies on performing similar missions multiple times, so that the control can be modified to improve performance over previous operations (i.e., trials, iterations, and passes) through learning. However non-learning systems do not improve their performance due to the same tracking error on each iteration in which despite large model uncertainty and repeating disturbances [23]. Learning-type control strategies can accordingly be classified into ILC, Repetitive Control (RC), neural networks, and adaptive control. Whilst ILC strategies modify the input signal (i.e., the control input), adaptive and neural network learning control methods modify the system (i.e., the controller), and controller parameters, respectively [24]. Additionally, ILC usually guarantees fast convergence within just a few iterations, but the alternative strategies may not [25].

ILC has been applied to quadrotors in a few cases. ILC can be used for systems for which a finite-duration task is repeated. Every iteration should have the same initial conditions and, as the number of trials increase, ILC updates the input signal to ensure that the system output converges to a reference signal. ILC has been applied to many fields, including robotics [26].

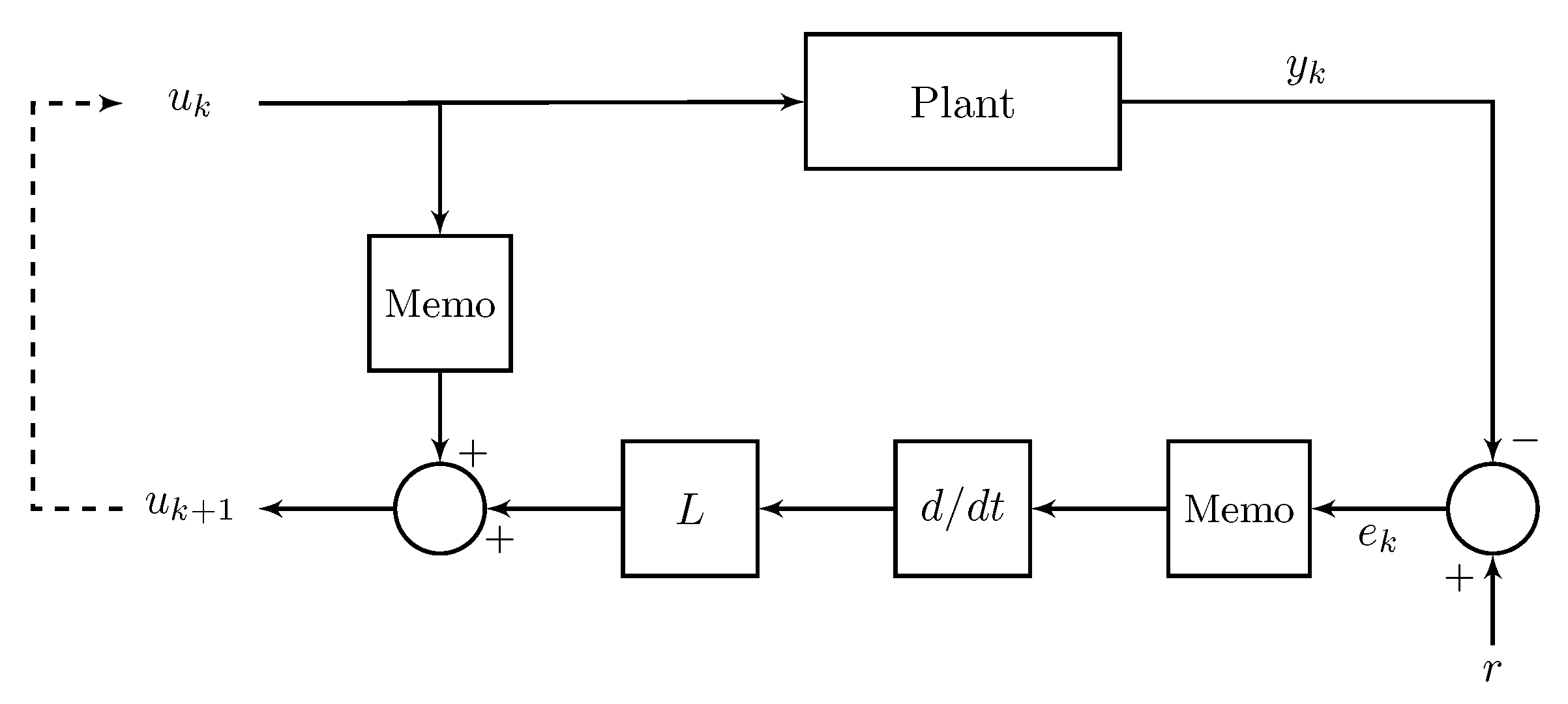
The simple D-type ILC form used in [27] for UAV trajectory tracking was based on the Additive State Decomposition (ASD) method. The block diagram shown in Figure 1 demonstrates the D-type algorithm, which employs the change of error rate to modify the input for the next iteration in lieu of the error itself. It is evident that the derivative part in the ILC algorithm amplifies small noise signals which may destabilize the system. Ref. [28] has developed another special case of D-type in UAV applications in order to obtain a better tracking performance and lower errors than the typical D-type update rule in [27]. However, although both [27] and [28] use the D-type ILC, they still do not guarantee the rate of convergence in the presence of disturbances.

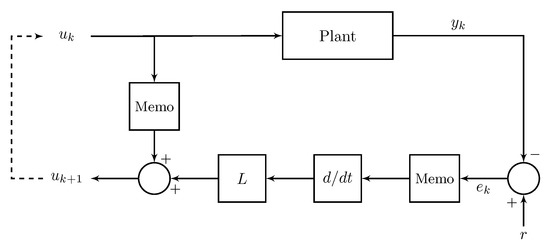
Figure 1. Block diagram for D-type ILC:- here the ${\displaystyle u_k\left(n\right)}$ it is the input signal was used on kth iterations, ${\displaystyle L_{opt}}$ is the D-type gain, ${\displaystyle e_k\left(n\right)}$ the derivative of error, and ${\displaystyle r\left(n\right)}$ and ${\displaystyle y_k\left(n\right)}$ are the reference and the plant output, respectively.

In [29,30], the P and D-term ILCs are combined as a PD-type ILC to increase the convergence rate. In [29], three different methods are additionally applied: offline ILC, online ILC, and a combination of both ILCs. These have the respective forms for P-type ILC

$$u_{k+1}\left(n\right)=\underset{\mathrm{offline}\mathrm{P}\text{-}\mathrm{type}}{\underbrace{u_k\left(n\right)+K_P{e}_k\left(n\right)}},$$

(1)

$$u_{k+1}\left(n\right)=\underset{\mathrm{online}\mathrm{P}\text{-}\mathrm{type}}{\underbrace{u_k\left(n\right)+K_P{e}_{k+1}\left(n\right)}},$$

(2)

where subscript k denotes the iteration number and subscript n the the sample number.

An inner online PD type ILC update was designed by [29] for quadrotor trajectory tracking control to stabilise the UAV system without taking disturbances into account. The algorithm is

$$u_{k+1}\left(n\right)=u_k\left(n\right)+K_P{e}_k(n+1)+K_D\left[e_k(n+1)-e_k\left(n\right)\right]$$

(3)

The results show a high tracking error. However, the ILC was able to reduce it over subsequent iterations but with low convergence. In [30], ILC was implemented by an adaptive term for enhancing the performance and robustness. This controller term was implemented on a quadrotor platform, where the test results showed improvement in tracking performance, despite the presence of disturbances.

In [31], another ILC form is proposed that includes a combination of the previous two simple structures to include an integral term and is termed PID-type ILC. A controllable flight was optimized using the PID-type ILC after a chnge in mass of the quadrotor. The method is based only on manual auto-tuning for parameters. In summary, all the previous structures (D-type, PD type, PID-type ILC) are susceptible to process disturbance and measurement error, while rarely being utilized in practical applications.

ILC was applied to achieve quadrotor trajectory tracking while balancing an inverted pendulum [32]. The learning algorithm used was of the form

$$\left\{\begin{array}{c}\underset{u_{k+1}}{\min }\parallel S(F{u}_{k+1}+\widehat{d_k})\parallel +\alpha \parallel D{u}_{k+1}\parallel \hfill \\ \mathrm{subject}\mathrm{to}{L}_{opt}{u}_{k+1}\le q_{max},\hfill \end{array}\right.$$

(4)

where F is the lifted system matrix, $\alpha$ weights the additional penalty term, and $\widehat{d_k}$ is an updated estimate of disturbance. Via the matrix D, the input derivatives can be penalized. The matrix S allows for the error signal to be scaled or filtered.

The aforementioned approaches are very limited in accuracy. Apart from initial identification procedures and tuning, it is also noted that these approaches demand a large level of computation and do not require an explicit model. Although usability is an advantage of this simplicity, it necessarily degrades performance. There is a great opportunity to assess a wide variety of ILC approaches on UAVs. There is no single algorithm that delivers all of the required features for high performance control while facing uncertain dynamics and environmental factors. Overall, ILC approaches demonstrated the best tracking performance only with medium complexity. Relatively few ILC schemes have been applied to quadrotors, and their evaluation is quite limited.

2.2. Optimal Approach ILCs

The properties of linear optimal algorithms have been studied extensively [33,34,35,36,37]. Leading ILC examples are now introduced with their own specific features.

2.2.1. Gradient-Based Iterative Learning Control

Due to their attractive theoretical properties, Gradient-based (G-ILC) algorithms have received considerable attention in the literature. When compared to generic ILC approaches, the optimal gradient ILC achieves faster error convergence by relying on the system model and utilizing the characteristics of gradient-descent in order to structure the ILC control action update. In [38,39,40], Gradient ILC has been used for SISO systems and was derived for MIMO systems.

The common form of standard ILC employed by the input update law is specified as [23]

$$\begin{array}{c}\hfill u_{k+1}\left(n\right)=u_k\left(n\right)+L_{opt}{e}_k\left(n\right)\end{array}$$

(5)

where $L_{opt}$ is a learning operator, $y_d$ is the desired reference signal, and $e_k=y_d-y_k$ is the error. By taking the transpose, $G^T$, an alternative method of guaranteeing Equation (5) can be obtained. The lifted form of the more general adjoint operator $G^{*}$ leads to

$$L_{opt}=\beta G^{*}$$

(6)

which yields the update law

$$u_{k+1}=u_k+\beta G^T{e}_k$$

(7)

where the scalar $\beta$ is the learning gain. Equation (7) is interpreted to be the gradient descent solution to the minimisation problem $\underset{u}{\min }J\left(u_k\right)={\parallel y_d-G{u}_k\parallel }^2$. The spectral radius condition is a necessary and sufficient condition for convergence

$$\rho (I-G{L}_{opt})<1.$$

(8)

Substituting $L_{opt}=\beta G^T$ into the general convergence conditions Equation (8) yields

$$\rho \left(I-\beta G{G}^T\right)=\parallel I-\beta G{G}^T\parallel <1$$

(9)

Here, the $G{G}^T$ is positive definite, so the convergence condition becomes

$$0<\beta <\frac{2}{\parallel G{G}^T\parallel }=\frac{2}{{\parallel G\parallel }^2}.$$

(10)

Therefore, it should be noted, when the number of trials, k, approaches infinity, Equation (10) ensures the error converges monotonically to zero.

2.2.2. Norm Optimal ILC

The model-based Norm Optimal ILC (NO-ILC) algorithm was introduced in [41]. The ILC input to the following trial is acquired through optimising a specific performance index that allows a balance between the error convergence and input energy. NO-ILC has been used for many applications and extended, for instance a predictive approach based on norm-optimal ILC [42]. NO-ILC uses the quadratic cost function:

$$J\left(u_{k+1}\right)={\displaystyle \frac{1}{2}}\{{[u_{k+1}-u_k]}^{T}R[u_{k+1}-u_k]+{[y_d-y_{k+1}]}^{T}Q[y_d-y_{k+1}]\}$$

(11)

where the weighting matrices $R\left(t\right)$ and $Q\left(t\right)$ are positive semi-definite and symmetric.

The requirement is to minimize the tracking error by modifying the input control from one trial pass to the next. This can be done by generating the control action $u_{k+1}$ for the next trial. The problem at each iteration is thus

$$minJ\left(u_{k+1}\right)$$

(12)

which can be solved by applying a partial differentiation to $J_{k+1}$ with respect to u, and determining the stationary point, $\partial J_{k+1}/\partial u=0$. This leads to the update law

$$u_{k+1}=u_k+G^{\mathsf{T}}{e}_{k+1}$$

(13)

where $G^{\mathsf{T}}$ is the adjoint operator of the system G, where $G^{\mathsf{T}}=R^{-1}{G}^{T}Q$. It can be demonstrated that the convergence condition in Equation (8) is always satisfied and, moreover,

$$\parallel {\mathbf{e}}_{k+1}\parallel \le \frac{1}{1+{\sigma }^2\left(G{G}^{\mathsf{T}}\right)}\parallel {\mathbf{e}}_k\parallel \le \parallel {\mathbf{e}}_k\parallel$$

(14)

where ${\sigma }^2\left(G{G}^{\mathsf{T}}\right)$ is the smallest spectral radius value of the symmetric, positive definite operator $G{G}^{\mathsf{T}}$. Equation (14), being non-causal, can be manipulated to either generate a causal feed-forward form or feedback and feed-forward form by [43], where

$$L_{opt}=G^{\mathsf{T}}{(I-G{G}^{\mathsf{T}})}^{-1}.$$

(15)

Therefore, the updated law is

$$u_{k+1}=u_k+G^{\mathsf{T}}{(I-G{G}^{\mathsf{T}})}^{-1}{e}_k.$$

(16)

Note that the implementation of optimal algorithms in such cases needs to be investigated. This is more crucial in the application of UAVs for the monitoring overhead power system, especially since the quadrotor UAV has more than one degree of freedom. Moreover, the electric power system inspection task is inherently repetitive while detecting errors that require using optimal algorithms to critically compare performance and inform design.

3. ILC Design and Application to Quadrotor

This section purports to put forward the optimal algorithms (G-ILC, NO-ILC) for the UAV quadrotor. The design of the optimal algorithm is based on the following assumptions and steps:

I.

The system is presumed to operate in a repetitive manner (iteratively) for both optimal algorithms, G-ILC and NO-ILC.

II.

At the end of every iteration, the state is reset operation toward a particular repetition that have independent initial condition to the next operation.

III.

A new control signal might be utilized during this time. A reference signal, $r\left(t\right)$, is presumed to be known and the ultimate control objective is to determine an input function $u^{*}\left(t\right)$ such the output function $y\left(t\right)=r\left(t\right)$ on $[1;N]$.

IV.

For G-ILC, the value of the learning gain ${\beta }_{old}\left(k\right)$ is heuristically selected for the first step, and then calculated automatically using the the gain ${\beta }_{new}\left(k\right)$ by establishing the varying gain equations. The established variable will be repeated again for NO-ILC, but with a different learning gain $Q_k$.

V.

To guarantee error convergence, the necessary conditions are $J\left({\beta }_{new}\left(k\right)\right)={\parallel {\mathrm{e}}_{k+1}\parallel }^2+\zeta {\beta }_{new}{\left(k\right)}^2$.

Now, the SISO model is a non-linear, discrete, state space system:

$$\begin{array}{cc}\hfill x_k(n+1)& =f(x_k\left(n\right),u_k\left(n\right))\hfill \\ \hfill y_k\left(n\right)& =h\left(x_k\left(n\right)\right)\hfill \end{array}$$

(17)

where $x_k\left(t\right)\in {\mathbb{R}}^n,u_k\left(t\right)\in {\mathbb{R}}^m,y_k\left(t\right)\in {\mathbb{R}}^p$ and $A\in {\mathbb{R}}^{n\times n},B\in {\mathbb{R}}^{n\times m},C\in {\mathbb{R}}^{p\times n}$ are the system matrices. Moreover, $x_k$, $u_k$, and $y_k$ are the state vector, input and output respectively, for trial k.

3.1. Gradient-Based ILC (G-ILC)

When compared to generic ILC approaches, the optimal gradient ILC depends on the system model to obtain faster error convergence. It constructs the ILC control action update while using the properties of gradient descent. This happens through minimising the cost function

$$\underset{}{\min }J\left(u_k\right)={\displaystyle \frac{1}{2}}\parallel e_k{\parallel }^2={\displaystyle \frac{1}{2}}{\parallel y_d-G{u}_k\parallel }^2$$

(18)

where

$$\begin{array}{cc}\hfill G& =\left[\begin{array}{cccc}{g}_0& 0& \cdots & 0\\ g_1& g_0& \cdots & ⋮\\ ⋮& ⋮& \ddots & 0\\ g_{h-1}& g_{h-2}& \cdots & g_0\end{array}\right]\hfill \end{array}$$

(19)

$$g_N=C{A}^{N+r-1}BN=0,1,2....,h-1$$

and the tracking error ${\mathbf{e}}_k$ from the $N^{th}$ trial. This is the error between the actual outputs ${\mathbf{y}}_k$ of the system and their desired reference signal ${\mathbf{y}}_d$ is then

$$\begin{array}{c}\hfill e_k=y_d-y_k.\end{array}$$

(20)

Using gradient descent to solve the optimisation problem given by Equation (18) gives

$$\begin{array}{cc}\hfill u_{k+1}& =u_k-\beta ▽J\left(u_k\right)\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill & =u_k-\beta ▽{\displaystyle \frac{1}{2}}{\parallel y_d-G{u}_k\parallel }^2\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill & =G{u}_k\beta +u_k-y_d{G}^T\beta \hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill & =u_k+\beta G^T{e}_k\hfill \end{array}$$

(24)

where $\beta$ represents the learning gain.

From Equation (24), the error evolution of the G-ILC can be derived as

$$\begin{array}{cc}\hfill e_{k+1}& =y_d-G{u}_{k+1}\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill & =G^{T}G{e}_k\beta +y_d-u_{k}G\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill & =(I-\beta G{G}^T)e_k.\hfill \end{array}$$

(27)

By choosing the learning gain $\beta$ from the range $0<\beta <2/\overline{\sigma }\left(G\right)$, where $\overline{\sigma }\left(G\right)$ is the largest singular of the matrix G, it can be easily shown that $\parallel I-\beta G{G}^T\parallel <1$. Therefore, the error converges monotonically to zero, as the trials k goes to infinity.

Instead of arbitrarily selecting a value of ${\beta }_{old}\left(k\right)$ from the range, the error convergence rate can be optimized. Repeating Equations (23) and (27)

$$\begin{array}{cc}\hfill u_{k+1}& =u_k+{\beta }_{old}\left(k\right)G^T{e}_k\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill e_{k+1}& =(I-{\beta }_{old}\left(k\right)G{G}^T)e_k\hfill \end{array}$$

(29)

the optimal iteration-varying ${\beta }_{new}\left(k\right)$ can be obtained by minimising:

$$\begin{array}{c}\hfill J\left({\beta }_{new}\left(k\right)\right)={\parallel {\mathrm{e}}_{k+1}\parallel }^2+\zeta {\beta }_k^2.\end{array}$$

(30)

where $\zeta$ is a small positive weighting constant. Substituting Equation (29) into Equation (30) we get

$$\begin{array}{cc}\hfill J\left({\beta }_{new}\left(k\right)\right)& ={\left((I-{\beta }_{k}G{G}^T)e_k\right)}^T\left((I-{\beta }_{k}G{G}^T)e_k\right)+\zeta {\beta }_k^2\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill & =e_k^T{e}_k-2{\beta }_k{e}_k^{T}G{G}^T{e}_k+{\beta }_k^2{e}_k^{T}G{G}^{T}G{G}^T{e}_k+\zeta {\beta }_k^2.\hfill \end{array}$$

(32)

Differentiating Equation (32) with respect to ${\beta }_{new}\left(k\right)$ and equating to zero gives the optimal learning gain:

$$\begin{array}{cc}\hfill {\beta }_{new}\left(k\right)& ={\displaystyle \frac{e_k^{T}G{G}^T{e}_k}{e_k^{T}G{G}^{T}G{G}^T{e}_k+\zeta }}\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill & ={\displaystyle \frac{{\left(G^T{e}_k\right)}^T{G}^T{e}_k}{{\left(G{G}^T{e}_k\right)}^{T}G{G}^T{e}_k+\zeta }}\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill & ={\displaystyle \frac{\parallel G^T{e}_k{\parallel }^2}{\parallel G{G}^T{e}_k{\parallel }^2+\zeta }}.\hfill \end{array}$$

(35)

Thus the necessary and sufficient conditions for guaranteeing a convergence of error are

$$\begin{array}{c}\hfill \parallel {\mathrm{e}}_{k+1}\parallel <\parallel e_k\parallel \mathrm{for}\mathrm{all}k\ge 0\mathrm{and}\underset{k\to \infty }{lim}{e}_k=0.\end{array}$$

(36)

From Equation (29) we get

$$\begin{array}{cc}\hfill \parallel {\mathrm{e}}_{k+1}{\parallel }^2-{\parallel e_k\parallel }^2& =e_k^T{e}_k(I-{\beta }_{k}G{G}^T){(I-{\beta }_{k}G{G}^T)}^T-e_k^T{e}_k\hfill \end{array}$$

(37)

$$\begin{array}{c}\hfill =e_k^T({(I-{\beta }_{k}G{G}^T)}^2-I)e_k\end{array}$$

(38)

$$\begin{array}{c}\hfill =e_k^T(-2{\beta }_{k}G{G}^T+{\beta }_k^{2}G{G}^{T}G{G}^T)e_k\end{array}$$

(39)

$$\begin{array}{c}\hfill ={\beta }_k^2(-2{\displaystyle \frac{e_k^{T}G{G}^T{e}_k}{{\beta }_k}}+e_k^{T}G{G}^{T}G{G}^T{e}_k)\end{array}$$

(40)

$$\begin{array}{c}\hfill ={\beta }_k^2(-2{\displaystyle \frac{\parallel G^T{e}_k{\parallel }^2}{{\beta }_k}}+\parallel G{G}^T{e}_k{\parallel }^2).\end{array}$$

(41)

Furthermore from Equation (34), we get

$$\begin{array}{cc}\hfill {\displaystyle \frac{\parallel G^T{e}_k{\parallel }^2}{{\beta }_{new}\left(k\right)}}& =\parallel G{G}^T{e}_k{\parallel }^2+\zeta .\hfill \end{array}$$

(42)

Substituting Equation (41) into Equation (42) gives

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \parallel {\mathrm{e}}_{k+1}{\parallel }^2-{\parallel e_k\parallel }^2& ={\beta }_{new}{\left(k\right)}^2(-2(\parallel G{G}^T{e}_k{\parallel }^2+\zeta )+\parallel G{G}^T{e}_k{\parallel }^2\hfill \\ \hfill & =-{\beta }_{new}{\left(k\right)}^2(2\zeta +\parallel G{G}^T{e}_k{\parallel }^2)\le 0.\hfill \end{array}\end{array}$$

(43)

From Equation (43) it can be deduced that $\parallel {\mathrm{e}}_{k+1}\parallel =\parallel e_k\parallel$ if and only if ${\beta }_k=0$. Because $G{G}^T$ is a positive definite matrix, from Equation () we have that ${\beta }_{new}\left(k\right)=0$ if and only if $e_k=0$, Thus the conditions of Equation (36) are satisfied and the and the system has monotonic convergence.

3.2. Norm Optimal ILC (NO-ILC)

To produce the optimal action ILC ${\mathbf{u}}_{k+1}$, we recall the Equation (11). Setting the gradient to zero gives

$$\begin{array}{c}\hfill ▽J\left({\mathbf{u}}_{k+1}\right)=-G^{T}Q{\mathbf{e}}_{k+1}+R({\mathbf{u}}_{k+1}-{\mathbf{u}}_k)=0.\end{array}$$

(44)

Since matrix R is a positive definite so is non-singular, rearranging gives

$$\begin{array}{cc}\hfill {\mathbf{u}}_{k+1}& ={\mathbf{u}}_k+R^{-1}{G}^{T}Q{\mathbf{e}}_{k+1}.\hfill \end{array}$$

(45)

From Equation (45), the error evolves as

$$\begin{array}{cc}\hfill {\mathbf{e}}_{k+1}& ={\mathbf{y}}_d-G{\mathbf{u}}_{k+1}\hfill \end{array}$$

(46)

$$\begin{array}{cc}\hfill & ={\mathbf{y}}_d-R^{-1}G{G}^{T}Q-\mathbf{u}{G}_k{\mathbf{e}}_{k+1}\hfill \end{array}$$

(47)

$$\begin{array}{cc}\hfill & ={(I-G{R}^{-1}{G}^{T}Q)}^{-1}{\mathbf{e}}_k\hfill \end{array}$$

(48)

However Equation (11) is implicit. However, it can be solved by supposing that $G^{*}=R^{-1}{G}^{T}Q$ and substituting the Equation () into Equation (11) gives

$$\begin{array}{cc}\hfill {\mathbf{u}}_{k+1}& ={\mathbf{u}}_k+G^{*}{e}_k{(I-G{G}^{*})}^{-1}.\hfill \end{array}$$

(49)

Monotonic convergence can be shown as follows

$$\begin{array}{c}\hfill \underset{k\to \infty }{\lim }\parallel {\mathbf{e}}_k{\parallel }^2=\underset{k\to \infty }{\lim }{\parallel {\mathbf{J}}_k\parallel }^2:J_{\infty }⩾0,\end{array}$$

(50)

implying

$$\begin{array}{c}\hfill \underset{k\to \infty }{\lim }{\parallel u_{k+1}-u_k\parallel }^2=0.\end{array}$$

(51)

Thus

$$\begin{array}{c}\hfill \underset{k\to \infty }{\lim }(u_{k+1}-u_k)=\underset{k\to \infty }{\lim }{R}^{-1}{G}^{T}Q{\mathbf{e}}_{k+1}=0.\end{array}$$

(52)

We get error convergence if either there exist no e such that $G^{T}e=0$ so $\underset{k\to \infty }{\lim }{e}_{k+1}=0$, or if ${\mathbf{y}}_d\in \mathrm{range}\left(G\right)$.

3.3. Application to Quadrotors

The dynamics of standard quadrotors are well established, the main equations are given here. Details of the dynamics model can be found in [34], for example.

The control inputs are related to each rotor speed ${\mathsf{\Omega }}_i$ by:

$$\mathbf{u}=\left[\begin{array}{c}{u}_1\\ u_2\\ u_3\\ u_4\end{array}\right]=\left[\begin{array}{cccc}b& b& b& b\\ 0& lb& 0& -lb\\ lb& 0& -lb& 0\\ d& d& d& d\end{array}\right]\left[\begin{array}{c}{\mathsf{\Omega }}_1^2\\ {\mathsf{\Omega }}_2^2\\ {\mathsf{\Omega }}_3^2\\ {\mathsf{\Omega }}_4^2\end{array}\right]$$

(53)

where and l is the arm length and b and d are rotor thrust and drag coefficients respectively.

The dynamic model for the quadrotor attitude is given by

$$\begin{array}{cc}\hfill \dot{p}& =\frac{1}{I_{xx}}\left[u_2+qr(I_{yy}-I_{zz})+q{J}_p{\mathsf{\Omega }}_r\right]\hfill \end{array}$$

(54)

$$\begin{array}{cc}\hfill \dot{q}& =\frac{1}{I_{yy}}\left[u_3+pr(I_{zz}-I_{xx})+p{J}_p{\mathsf{\Omega }}_r\right]\hfill \end{array}$$

(55)

$$\begin{array}{cc}\hfill \dot{r}& =\frac{1}{I_{zz}}\left[u_4+qp(I_{xx}-I_{yy})\right]\hfill \end{array}$$

(56)

where the triplet $(p,q,r)$ are the rotation rates about the body axes, $I_{xx}$, $I_{yy}$, $I_{zz}$ are the moments of inertia about the body axes, and $J_p$ is the rotor moment of inertia about the rotor rotation axis.

We define a state variable vector as

$$\mathbf{x}={\left[\begin{array}{cccccccccccc}\varphi & \theta & \psi & x& y& z& \dot{\varphi }& \dot{\theta }& \dot{\psi }& \dot{x}& \dot{y}& \dot{z}\end{array}\right]}^T$$

(57)

where the triplet $(x,y,z)$ is the position of the vehicle in the earth axes, and $(\varphi ,\theta ,\psi )$ are the standard aerospace Euler angles. By approximating the rotation rate triplet $(p,q,r)$ by the Euler angle derivative $(\dot{\varphi },\dot{\theta },\dot{\psi })$ and from the standard aeronautics navigation equations we get the dynamic model in the form $\dot{\mathbf{x}}=f(\mathbf{x},u)$ where

$$f(\mathbf{x},\mathbf{u})=\left[\begin{array}{c}\dot{\varphi }\\ \dot{\theta }\dot{\psi }{a}_1+\dot{\theta }{a}_2\overline{\mathsf{\Omega }}+b_1{u}_2\\ \dot{\theta }\\ \dot{\varphi }\dot{\psi }{a}_3-\dot{\varphi }{a}_4\overline{\mathsf{\Omega }}+b_2{u}_3\\ \dot{\psi }\\ \dot{\theta }\dot{\varphi }{a}_5+b_3{u}_4\\ \dot{x}\\ \frac{1}{m}(cos\varphi sin\theta cos\psi +sin\varphi sin\psi )u_1\\ \dot{y}\\ \frac{1}{m}(cos\varphi sin\theta sin\psi -sin\varphi cos\psi )u_1\\ \dot{z}\\ g-\frac{1}{m}(cos\varphi cos\theta )u_1\end{array}\right],$$

and where m is the mass, g is the gravitational constant, $\overline{\mathsf{\Omega }}$ is the rotor rotation rate sum, $a_1=(I_{yy}-I_{zz})/I_{xx}$, $a_2=J_p/I_{xx}$, $a_3=(I_{zz}-I_{xx})/I_{yy}$, $a_4=J_p/I_{yy}$, $a_5=(I_{xx}-I_{yy})/I_{zz}$, $b_1=l/I_{xx}$, $b_2=l/I_{yy}$, and $b_3=l/I_{zz}$.

The SISO structure of Equation (17) is extended to a MIMO dynamics to give

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill x_k(n+1)& =f(x_k\left(n\right),u_k\left(n\right)),\hfill \\ \hfill y_k\left(n\right)& =h(x_k\left(n\right),u_k\left(n\right)),x\left(0\right)=x_0.\hfill \end{array}\end{array}$$

(58)

The model $\dot{\mathbf{x}}=f(\mathbf{x},\mathbf{u})$ can be discretized by an Euler approximation. Full state feedback is assumed, that is $y_k=x_k$.

4. Experimental Platform Selection

4.1. Physical Parameters

The AscTec Hummingbird is chose as the experimental test platform. This quadrotor is popular, has good performance and is light-weight maneuverable. It has a payload of 200 g and a flight endurance of nearly 20 min.The aircraft component frame is made out of balsa wood and carbon fiber. The vehicle is powered by four brushless DC motors running off an 11.1V Lithium Polymer (LiPo) battery pack. It is equipped with an accelerometer, pressure sensor, magnetic sensor, gyros, and GPS module. These can provide the vehicle state. Some of the technical details are listed in Table 1 [44]. The model parameters are given in Table 2.

Table 1. Technical Details of the Quadrotor.

Type of Platform	AscTec HB. UAV
The Producer	AscTec GmbH + Intel
Take-off Weight	480 g
Battery	2100 mAh LiPo
Distance between motors	34 cm
Propeller	Standard propellers (8${}^{\prime \prime }$), flexible (PP) plastics
Motors	HACKER Motors Germany (X-BL 52 s)
Motor Controllers	X-BLDC controllers
Transmitter	Futaba 2.4 GHz
Wireless Link	Xbee 2.4 GHz

Table 2. Quadrotor model parameters.

Parameters	Description	Value	Unit
${\displaystyle I_{xx}}$	x axis-Moment Inertia	$10.7$ × ${10}^{-3}$	kg·m${}^2$
$I_{yy}$	y axis-Moment of Inertia	$10.7$ × ${10}^{-3}$	kg·m${}^2$
$I_{zz}$	z axis-Moment of Inertia	$18.4$ × ${10}^{-3}$	kg·m${}^2$
$J_p$	Rotor Inertia	47 × ${10}^{-6}$	kg·m${}^2$
m	Mass	0.547	kg
l	Arm Length	0.168	m
g	Gravitational constant	9.81	ms${}^2$
${\mathsf{\Omega }}_{max}$	Maximum rotor speed	200	rad/s

4.2. Test Bed

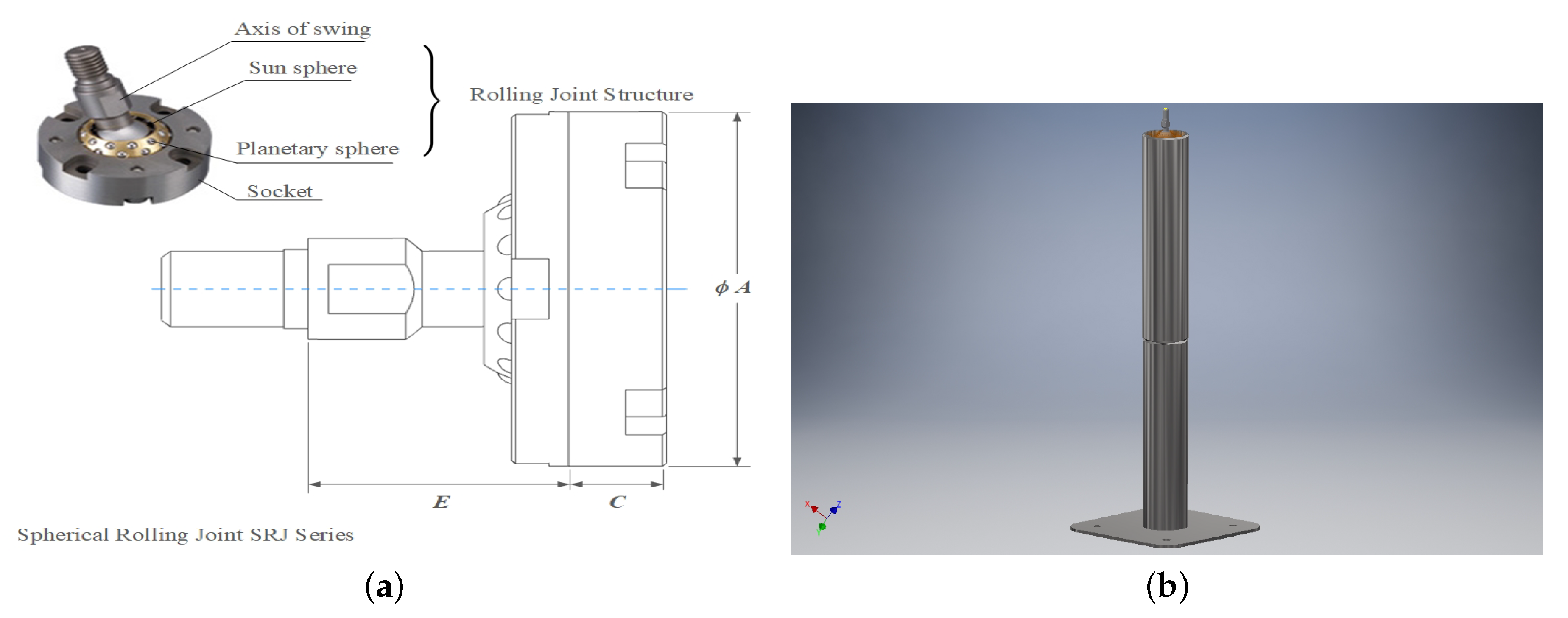
A test bed, designed for analysing the motor’s performance and enabling controller tuning, is constructed from steel and finished in black paint and bearings, so that it allows three DOF of rotation. Steel tube was selected because of its easy availability and high density gives the rig stability and rigidity. The UAV is secured in place with a spherical rolling joint. The assembled mechanical design is shown in Figure 2 and Figure 3, The UAV installed on the top. A Raspberry Pi 3 is used for the control.

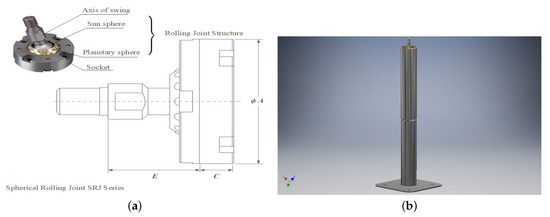
Figure 2. The complete assembly of proposed mechanical test-bed for quadrotor: (a) High precision spherical rolling joints with its features. (b) Mechanical-bed reconfiguration with precision rolling joints.

Figure 3. Quadrotor system with complete hardware test frame design for Iterative Learning Control (ILC) controllers.

5. Results and Discussion

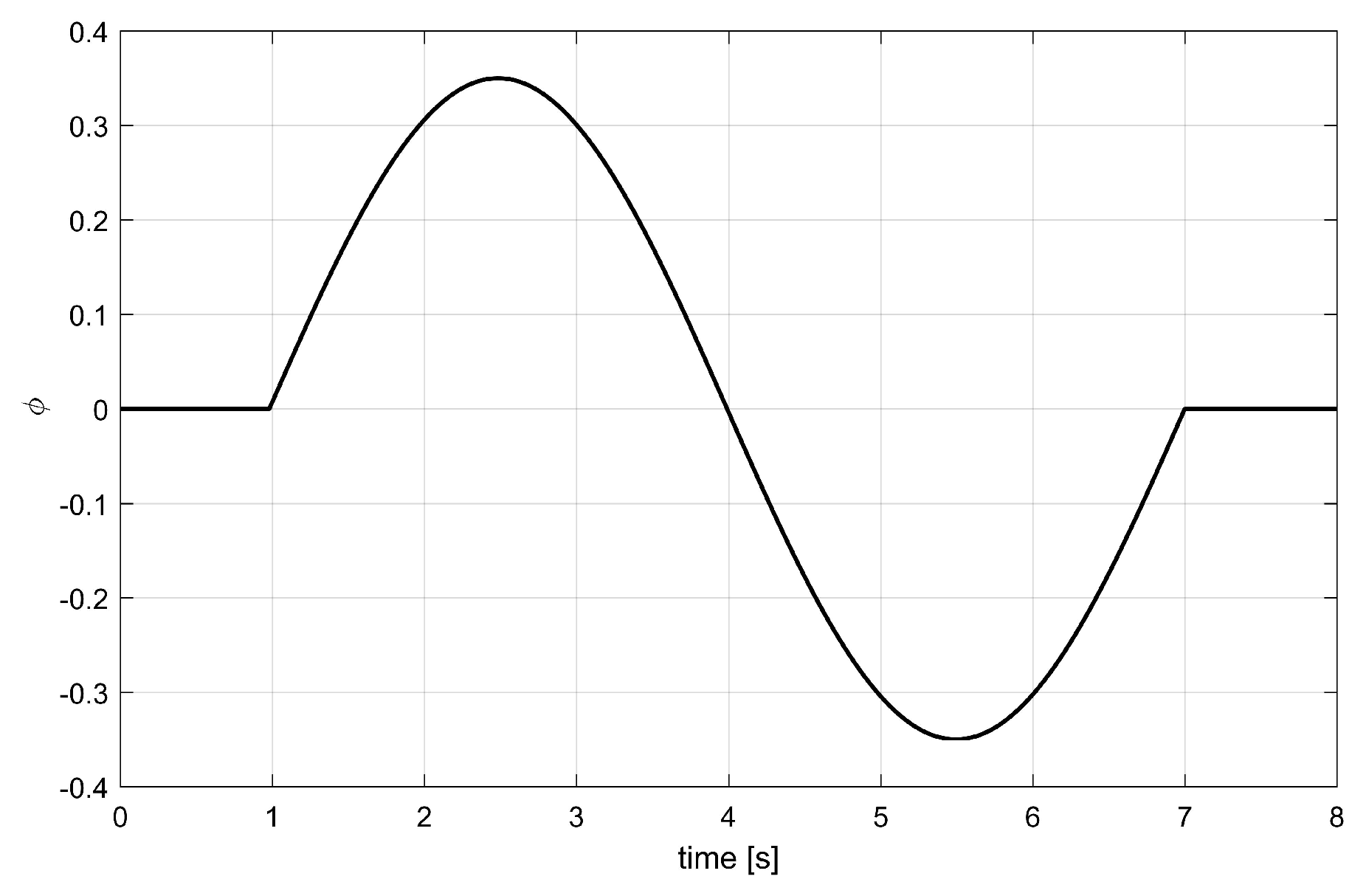
The G-ILC and NO-ILC algorithms are applied to the test system. Simulations are also performed. The simulations and experiments were conducted on a Laptop (i7) ThinkPad P1 Mobile WorkStation with 16 GB RAM/2.20 GHz via MATLAB R2018b. The reference trajectory is shown in Figure 4. The trajectory consists of a single period sin wave and is non-smooth; hence is a challenging task for the ILC algorithm. Sixteen iteration trials were performed for each algorithm. The input update for the G-ILC and NO-ILC algorithms was acquired by Equations (28) and (35), respectively, with the help of the linearized quadrotor dynamics from Equation (49).

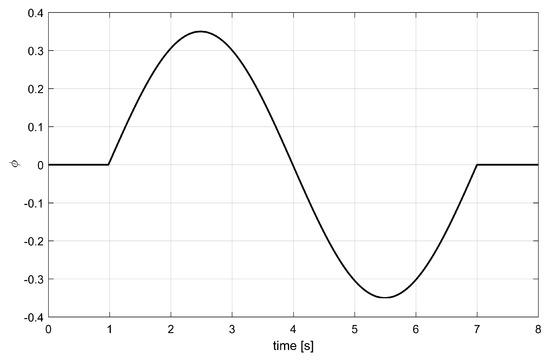
Figure 4. References for ILC controllers.

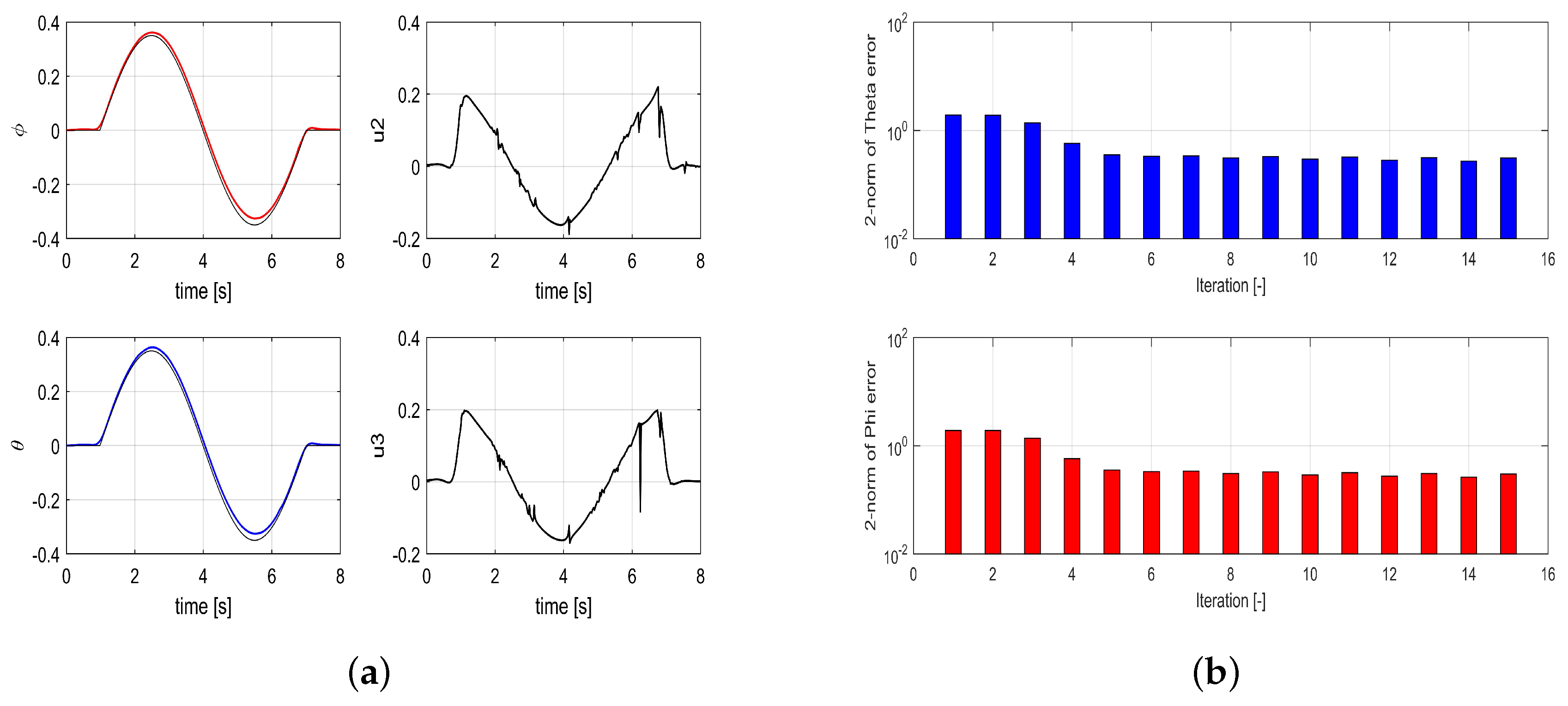
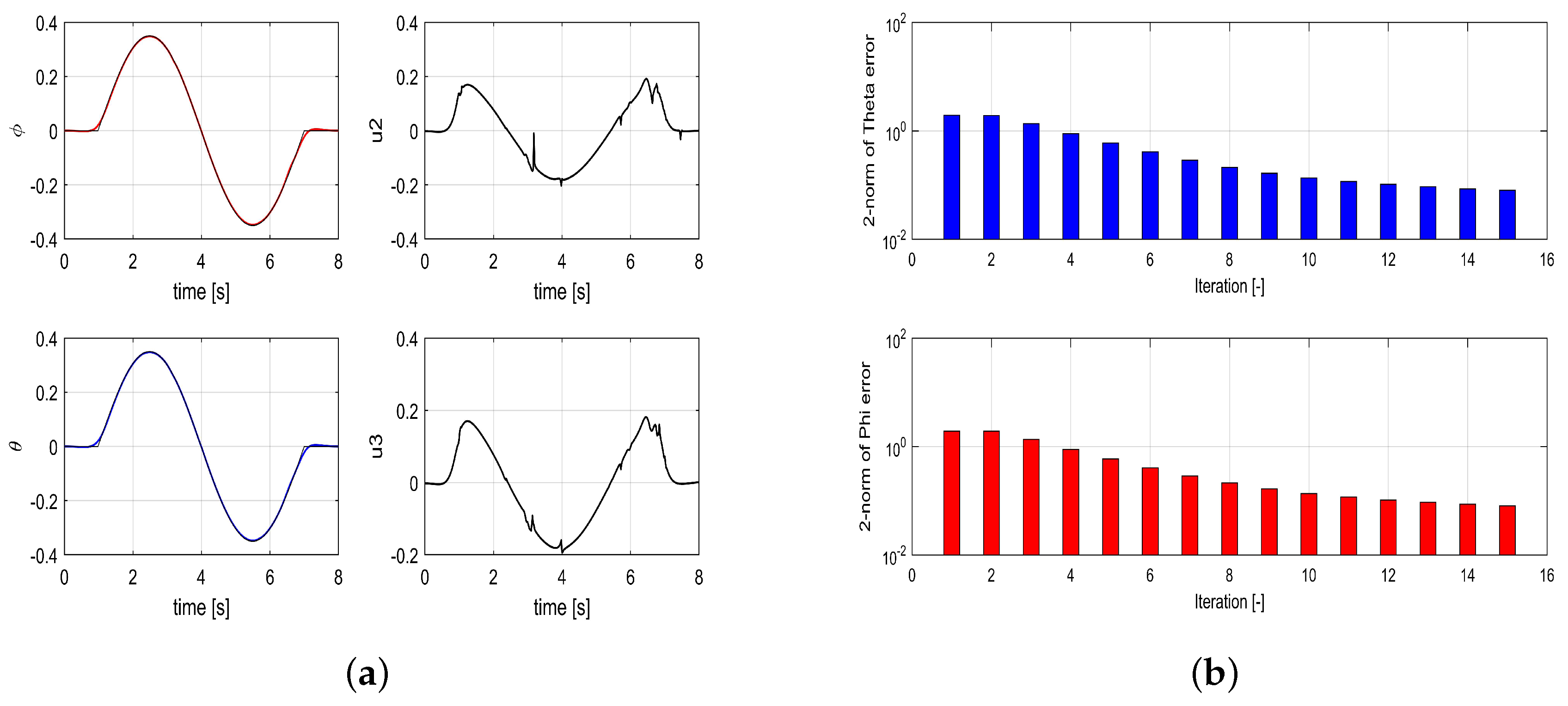
Demonstrating the monotonic convergence of the G-ILC algorithm is also important. The simulation results show a notable decrease in the error over different trial iterations. Figure 5 shows the decrease of the 2-norm of the error, with a value of 0.3092 at the 16th iteration. The variation in $\varphi$ and $\theta$ over time for different iterations are also shown in Figure 5.

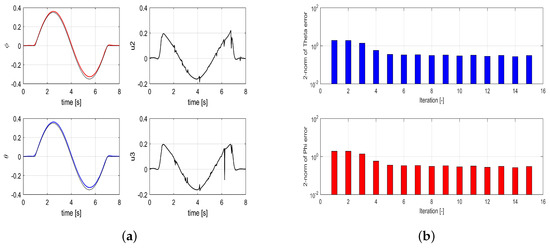
Figure 5. G-ILC for different iterations without disturbance: (a) the variation in theta over time for different iterations. (b) two norm for roll and pitch over time for different iterations.

Figure 6 similarly shows the results for the NO-ILC algorithms, The improvement over the G-ILC is noticeable. Again the convergence is shown by the decrease of the error 2-norm. The error 2-norm is 0.1215 at 16th iteration, a considerable improvement over the G-ILC approach .

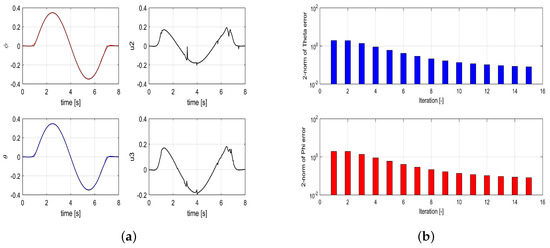
Figure 6. Norm Optimal ILC (NO-ILC) for different iterations without disturbance: (a) the variation in theta over time for different iterations. (b) two norm for roll and pitch over time for different iterations.

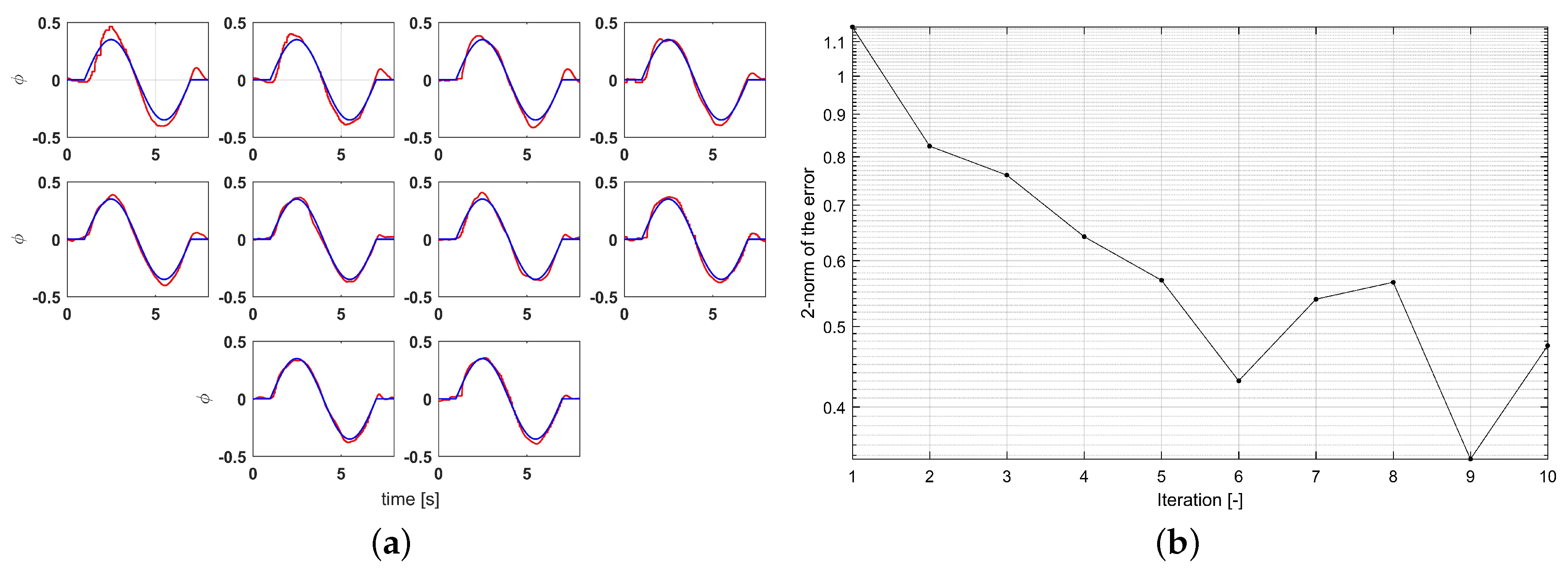
The G-ILC with updating Equations (28) and (29) was implemented to track the reference signal. An optimal value of gain, $\beta$, is chosen between 0.01 and 1.0. After testing a wide range of values of $\beta$, the best performance was found with $\beta =0.1$. The experimental results show a significant decline in the error over the first five trial iterations as shown in Figure 7a. A slight increase occurred at the 7th and 10th trials but the trend was from 1.277 at first trial to the value of 0.574 at the 6th trial.

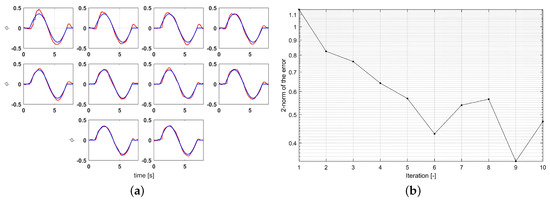
Figure 7. Experimental results of G-ILC for different iterations with disturbance. (a) Experimental tracking with different iteration. (b) Monotonic convergence result.

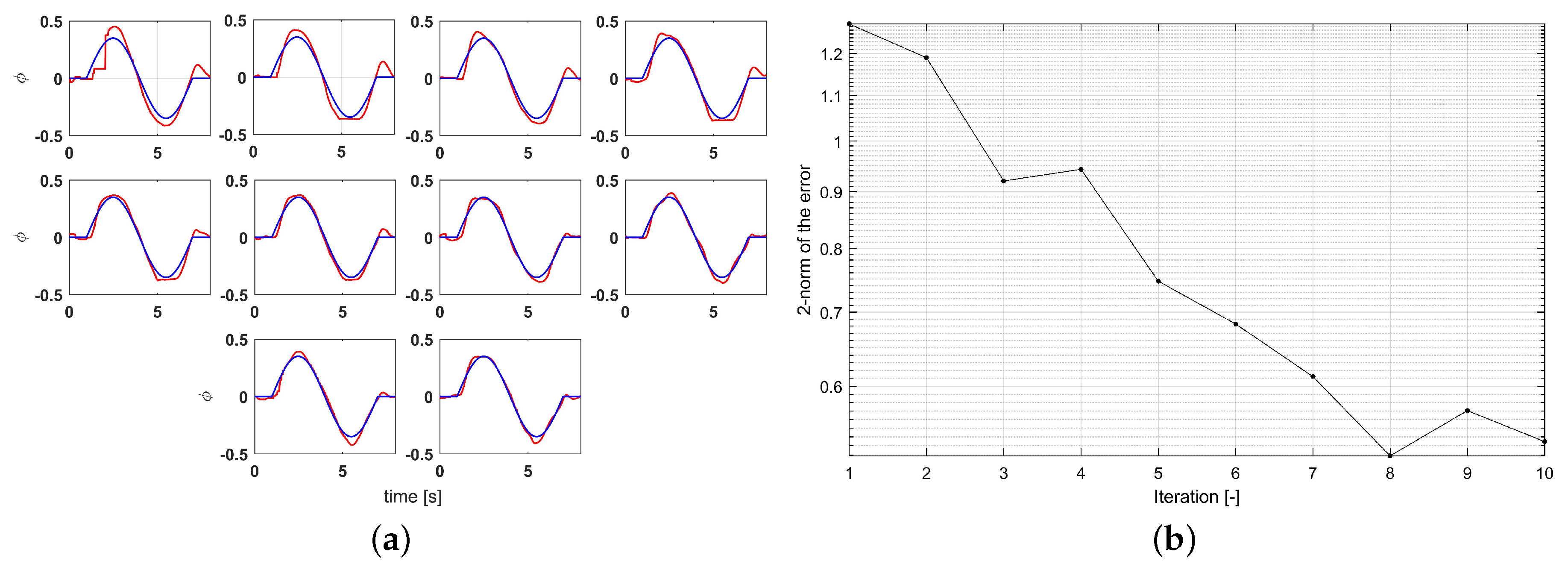
The performance of the NO-ILC algorithm is also investigated with the reference signal shown in Figure 4. The results are shown in Figure 8a. The weighting parameter is set to $Q=0.1$. The value of Q can be increased to improve convergence, but Figure 8b shows the convergence is similar to that of the G-ILC experiment, with the latter slightly better. Convergence was achieved after 8 iterations.

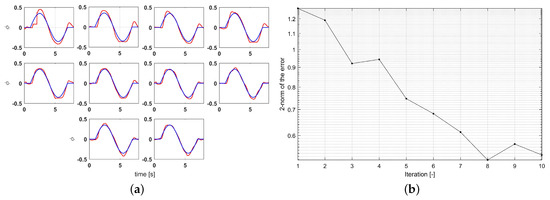
Figure 8. Experimental results of NO-ILC for different iterations with disturbance. (a) Experimental tracking with different iteration. (b) Monotonic convergence result.

Note that although convergence is established theoretically, in practice the system is subject to disturbances and uncertainty. The effect of disturbances is evaluated in simulation and by experiment for the two approaches. First the performances of the two methods in sumulation without disturbance are quantified and compared. The results are shown in Table 3. The NO-ILC method had significantly better performance and convergence properties in simulation.

Table 3. Simulation norm error results for attitude angles without disturbance.

ILC Approaches	Passes No.	$\parallel \widehat{\mathit{\theta }}-\mathit{\theta }\parallel$	$\parallel \widehat{\mathit{\varphi }}-\mathit{\varphi }\parallel$
G-ILC (without disturbance)	1	1.92	1.92
	3	1.38	1.38
	6	0.532	0.532
	16	0.309	0.303
NO-ILC (without disturbance)	1	1.92	1.92
	3	1.24	1.24
	6	0.476	0.476
	16	0.121	0.119

The disturbances took the form of torques that were injected in the $\varphi$ and $\theta$ channels. The disturbances defined as exponentially decaying sinusoidal functions $\delta \tau =e^{-0.1t}(sint),cost,0)$ for $t\in (2,6)$ s. The results for experiment are shown in Table 4. These show the better performance of the NO-ILC but the difference is less marked.

Table 4. Experimental norm error results for ILC algorithms with Disturbance Injection.

ILC Approaches	Trial (1)		Trial (3)		Trial (7)		Trial (10)
	$\parallel {\mathit{e}}_{\theta }\parallel$	$\parallel {\mathit{e}}_{\psi }\parallel$	$\parallel {\mathit{e}}_{\theta }\parallel$	$\parallel {\mathit{e}}_{\psi }\parallel$	$\parallel {\mathit{e}}_{\theta }\parallel$	$\parallel {\mathit{e}}_{\psi }\parallel$	$\parallel {\mathit{e}}_{\theta }\parallel$	$\parallel {\mathit{e}}_{\psi }\parallel$
G-ILC + Disturbance Injection	1.277	2.834	0.920	1.281	0.612	0.705	0.574	0.534
NO-ILC + Disturbance Injection	1.283	3.214	0.926	1.212	0.562	0.633	0.434	0.446

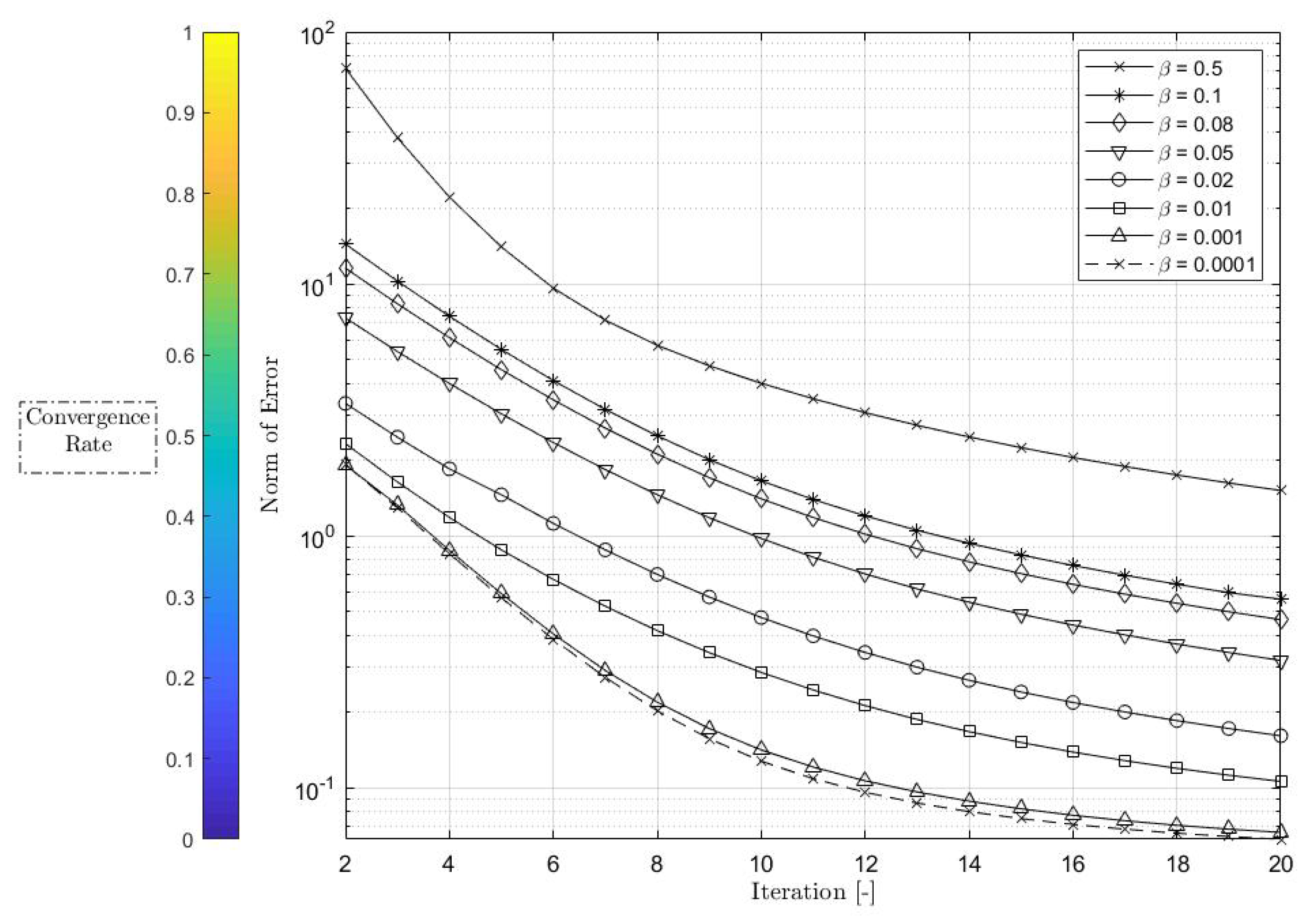
To improve the performance of the G-ILC algorithm, the value of the learning gain $\beta$ can be changed. Figure 9 shows the effect of $\beta$ on the convergence rate.

Figure 9. Optimized error convergence rate with a variation on the learning gain $\beta$ values, as proposed in Equations (35) and (42).

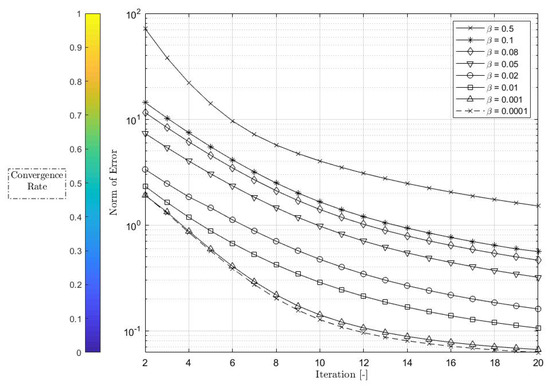
For a large class of practical systems, such as UAV reference tracking (as required for power line surveillance and monitoring) it is required that the output achieves perfect tracking at more than one defined time and enables the system error to converge to zero norm as rapidly as possible. Consequently, it includes future work on an alternative controller (i.e., ILC with hybrid controller) as an extension to enhance the tracking performance at subset (instantaneous in time) for many critical positions.

6. Conclusions

The suggested G-ILC and NO-ILC have been formulated and applied to the problem of reference tracking for UAV. When comparing the findings, the NO-ILC has shown superior tracking performance. Furthermore, the suggested NO-ILC has shown substantially improvement over the G-ILC in terms of error decrease and monotonic convergence. The results of the simulations and experiments both with and without an external disturbance show the proposed ILC performance for the two methods. The results the potential potential to achieve good trajectory tracking.

The NO-ILC method could form the basis for a power line inspection system. The repetitive nature of the power line geometries lends itself to this approach. However there are many control challenges to be faced, such as disturbances in the form of steady wind and unsteady wind gusts, and decision-making in the face of uncertainty. This points to the urgent need for additional future work for expanding ILC (i.e., point-to-point with hybrid controller) for tracking identification, for instance, through a straight conductor for a electrical overhead conductors monitoring-task.