Improvement in Voltage Conversion Ratio of Ultrahigh Step-Down Converter

Abstract

A modified step-down converter is presented herein, which is mainly based on one coupled inductor and several energy-transferring capacitors to improve the voltage conversion ratio as well as to reduce the switch voltage stress. In addition, the portion of the leakage inductance energy can be recycled to the input via the active clamp circuit during the turn-off period and the switches have zero-voltage switching (ZVS) during the turn-on transient. In this paper, the basic operating principles of the proposed converter are firstly described and analyzed, and its effectiveness is finally demonstrated by experiment based on a prototype with input voltage of 60 V, output voltage of 3.3 V and rated output power of 33 W.

1. Introduction

Recently, with the fast development of the servo power and the cloud, the converter with a high step-down voltage conversion ratio is indispensable. However, regarding the traditional buck converter, if a high step-down voltage conversion ratio is required, the corresponding duty cycle is extremely low, thereby causing the control to be difficult, the power loss on the switch to be increased, and the accompanying efficiency to be decreased. Consequently, there are many researches presented to overcome these problems. The literatures [1,2] apply transformers to half-bridge buck converters so as to improve the step-down voltage conversion ratio. The literatures [3,4,5] present switched-capacitor converters, whose step-down voltage conversion ratios are enhanced via capacitor voltage dividers. The literatures [6,7] adopt input voltage dividers along with two transformers to improve step-down voltage conversion ratios as well as to cause voltage stresses on switches to be three-level. The circuits shown in [8,9] are improvements of the circuits shown in [7,10]. The literatures [11,12,13,14,15,16] apply central-tapped coupling inductors to synchronously rectified (SR) buck converters so as to obtain relatively high step-down voltage conversion ratios. In the literatures [17,18,19], via changing the turns ratios of coupling inductors, not only the voltage stresses on switches can be reduced but also relatively high step-down voltage conversion ratios can be achieved. The literature [20] applies a coupling inductor to an SR buck converter so as to improve the step-down voltage conversion ratio. The literatures [21,22,23,24] apply coupling inductors and energy-transferring capacitors to SR buck converters to improve the step-down voltage conversion ratio, and besides, the last employs an active clamp circuit to reduce the switch voltage stress. The circuit shown in [25], with an active clamp circuit included, adopts two forward converters connected in parallel to reduce the voltage conversion ratio. The literature [26] utilizes multiple voltage-bucking modules and energy-transferring capacitors to improve the step-down voltage conversion ratio as well as to reduce the voltage stresses on switches. However, a large number of modules causes the circuit to be complex and the corresponding size to be relatively huge. The literature [27] employs one buck-boost connected in series with two half-bridge DC transformers and three energy-transferring capacitors so as to improve the step-down voltage conversion ratio. As compared with the literature [21], literature [28] utilizes one additional capacitor and one additional inductor so as to obtain more advantages, such as improvement of core size utilization, reduction of output current ripple, etc. In addition, both have the same voltage conversion ratio.

In this paper, a modified step-down converter is presented. As compared with the work [24], the proposed circuit, based on only one additional capacitor inserted and some circuit connections changed, has a relatively wide voltage conversion ratio as well as relatively small voltage stresses on switches. By the way, both have inherent some merits, such as the voltage clamp during the turn-off period, and the zero-voltage switching (ZVS) for switches during the turn-on transient.

2. Circuit Configuration and Its Operating Behavior

Figure 1 shows the proposed converter, which is built up by four switches Q₁, Q₂, Q₃ and Q₄, three energy-transferring capacitors C₁, C₂ and C₃, and one coupling inductor with one primary winding N₁, one secondary winding N₂ and one magnetic inductor L_m. As for the load, it is constructed by one output resistor R_o. Figure 2 displays an equivalent circuit model of the proposed converter.

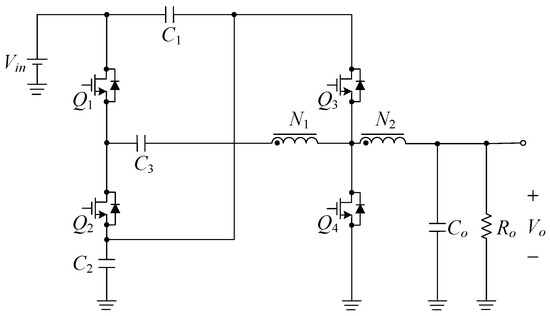
Figure 1. Proposed improved ultrahigh step-down converter.

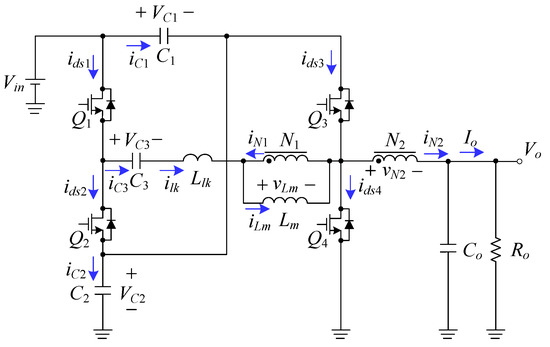
Figure 2. Equivalent circuit model of the proposed converter.

Prior to tackling this section, there are some associated symbols and assumptions in Figure 2, to be described as follows: (i) the input voltage is V_i; (ii) the output voltage is V_o; (iii) the primary-side and second-side turns are N₁ and N₂, respectively; (iv) the currents i_ds1, i_ds2, i_ds3, i_ds4, i_c1, i_c2, i_c3, i_lk, i_Lm, i_N1, i_N2 and i_o are the currents in Q₁, Q₂, Q₃, Q₄, C₁, C₂, C₃, L_lk, L_m, N₁, N₂ and R_o, respectively; (v) the voltages across L_m, N₂, C₁, C₂, C₃ and C_o are v_Lm, v_N2, V_C1, V_C2, V_C3 and V_o; (vi) the switching period is signified by T_s; (vii) the turn-on times for Q₁ and Q₃ are DT_s, whereas the turn-on times for Q₂ and Q₄ are (1 - D)T_s, where D is a duty cycle; (viii) all the switches are ideal, and all the capacitors are ideal without their equivalent series resistances (ESRs) included, that is, the capacitance for each capacitor is assumed to be large enough to keep the voltage on it constant at some value; (ix) the gate driving signals v_gs1 and v_gs3, for Q₁ and Q₃ respectively, are identical, whereas the gate driving signals v_gs2 and v_gs4, for Q₂ and Q₄ respectively, are identical; and (x) the circuit operates with no negative current. There are six states over one switching period, to be shown in Figure 3.

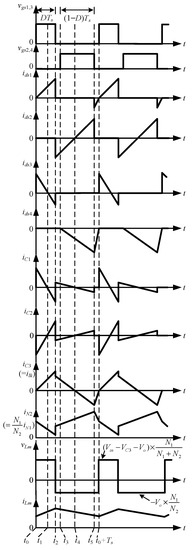
Figure 3. Key waveforms relevant to the proposed converter operating.

2.1. Operating Principles

2.1.1. State 1: [t₀ ≤ t ≤ t₁]

As shown in Figure 4, the switches Q₁ and Q₃ are in the on-state but the switches Q₂ and Q₄ are in the off-state. The switch Q₁ is turned on with zero-voltage switching (ZVS) because the body diode of Q₁ is switched on before turn-on of Q₁. During this state, the voltages across the magnetizing inductance L_m and leakage inductance L_lk are positive voltages, thereby causing L_m and L_lk to be magnetized. At the same time, the voltage V_in charges the capacitors C₁ and C₃, and, together with the capacitor C₂, supplies energy to the load. To speak lucidly, at t = t₀, the current in C₁ has some positive value and then linearly decreases due to the leakage reflected from the primary-side leakage; at t = t₀, the current in C₂ has some negative value and then linearly decreases due to the leakage reflected from the primary-side leakage; At t = t₀, the current in C₃ is zero and then linearly increases due to the primary-side leakage. As soon as i_C1 and i_C2 reach zero, this mode ends at t = t₁.

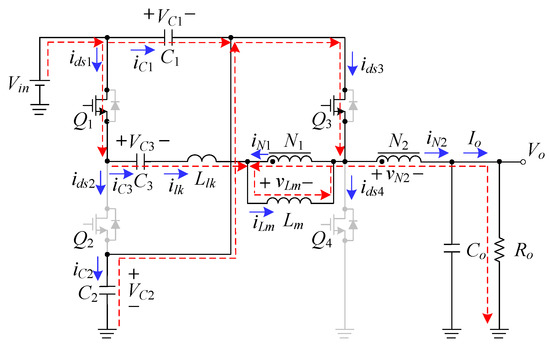
Figure 4. Current flow during state 1.

2.1.2. State 2: [t₁ ≤ t ≤ t₂]

As shown in Figure 5, the switches Q₁ and Q₃ are still in the on-state, but the switches Q₂ and Q₄ are still in the off-state. During this state, the magnetizing inductance L_m and leakage inductance L_lk are still magnetized. At the same time, the input voltage V_in charges the capacitor C₂ and, together with the capacitor C₁, charges the capacitor C₃ as well as supplies energy to the load. Once Q₁ is turned off, this mode ends at t = t₂.

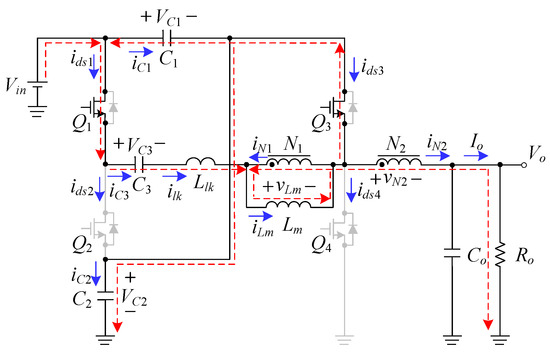
Figure 5. Current flow during state 2.

2.1.3. State 3: [t₂ ≤ t ≤ t₃]

As shown in Figure 6, all the switches are turned off with the body diode of Q₂ turned on, and this state is called one blanking time over one switching period. During such a state, the voltages across the magnetizing inductance L_m and leakage inductance L_lk are negative voltages, thereby causing L_m and L_lk to be demagnetized as well as to transfer their energy to the load. At the same time, the capacitor C₁ is charged by the input voltage V_in, and the capacitor C₂ discharges and, together with V_in, charges the capacitor C₃ as well as supplies energy to the load. The moment Q₂ and Q₄ is turned on, this mode ends at t = t₃.

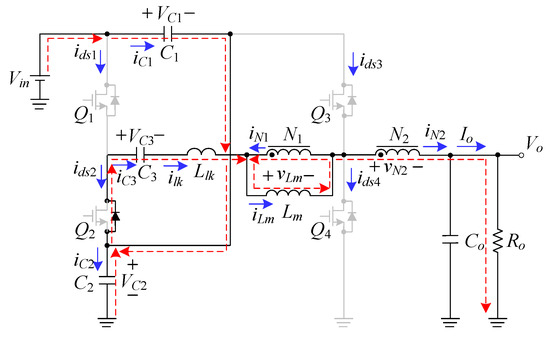
Figure 6. Current flow during state 3.

2.1.4. State 4: [t₃ ≤ t ≤ t₄]

As shown in Figure 7, the switches Q₂ and Q₄ are turned on but the switches Q₁ and Q₃ are still in the off-state. The switch Q₂ is turned on with ZVS because the body diode of Q₂ is switched on before turn-on of Q₂. During this state, the magnetizing inductance L_m and leakage inductance L_lk are still demagnetized, transferring their energy to the load. At the same time, the capacitor C₁ is charged by the input voltage V_in, and the capacitor C₂ still discharges and, together with the input voltage V_in, still charges the capacitor C₃ as well as still supplies energy to the load. As soon as i_ds2 reaches zero, this mode ends at t = t₄.

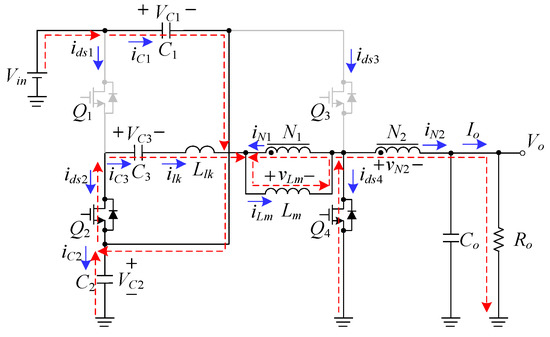
Figure 7. Current flow during state 4.

2.1.5. State 5: [t₄ ≤ t ≤ t₅]

As shown in Figure 8, the switches Q₂ and Q₄ are still in the on-state but the switches Q₁ and Q₃ are still in the off-state. During this state, the magnetizing inductance L_m and leakage inductance L_lk are still demagnetized, transferring their energy to the load. At the same time, the capacitor C₃ charges the capacitor C₂ and, together with the capacitor C₁, releases energy to the input voltage V_in. Once Q₂ and Q₄ are turned off, this mode ends at t = t₅.

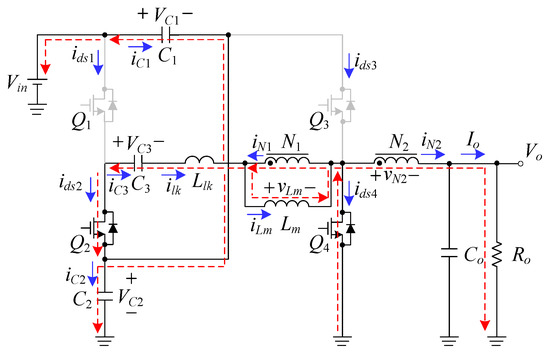
Figure 8. Current flow during state 5.

2.1.6. State 6: [t₅ ≤ t ≤ t₀ + T_s]

As shown in Figure 9, all the switches are turned off with the body diodes of Q₁ and Q₄ turned on and this state is called the other blanking time over one switching period. During such a state, the capacitor C₃ still discharges. At the same time, the magnetizing inductance L_m and leakage inductance L_lk are still demagnetized, transferring their energy to the load. The moment Q₁ and Q₃ are turned on, this mode ends and the next cycle is repeated.

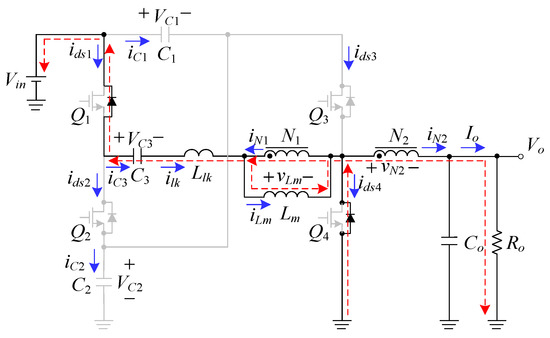
Figure 9. Current flow during state 6.

2.2. Voltage Conversion Ratio

In order to obtain the voltage conversion ratio, the voltages across the magnetizing inductance L_m, the secondary winding N₂, and the energy-transferring capacitors C₁, C₂ and C₃, that is, v_Lm, v_N2, V_C1, V_C2 and V_C3, are first obtained. In the following analysis, the blocking times and the leakage inductance are negligible, and hence only states 1 and 4 are considered. From state 1, the voltages v_Lm and v_N2 can be expressed as

$$v_{Lm}=(V_{in}-V_{C3}-V_o)\times \frac{N_1}{N_1+N_2}$$

(1)

$$v_{N2}=V_{C2}-V_o$$

(2)

From state 4, the voltages v_Lm and v_N2 can be represented by

$$v_{Lm}=-V_o\times \frac{N_1}{N_2}=V_{C2}-V_{C3}$$

(3)

$$v_{N2}=-V_o$$

(4)

Since the magnetizing inductance L_m on the primary side can be reflected to the secondary side, the voltage-second balance should be obeyed over one switching period. Therefore, the following equation can be obtained to be

$$(V_{C2}-V_o)\times D=V_o\times (1-D)$$

(5)

From (5), we can obtain

$$V_{C2}=\frac{V_o}{D}$$

(6)

Substituting (6) into (3) yields

$$V_{C3}=V_o\times (\frac{1}{D}+\frac{N_1}{N_2})$$

(7)

In addition, since the magnetizing inductance L_m on the primary side also needs to obey the voltage-second balance, the following equation can be obtained to be

$$(V_{in}-V_{C3}-V_o)\times \frac{N_1}{N_1+N_2}\times D=\frac{V_o\times N_1}{N_2}\times (1-D)$$

(8)

By substituting (7) into (8), the voltage conversion ratio can be obtained to be

$$\frac{V_o}{V_{in}}=D\times (\frac{n}{1+2n})$$

(9)

where n is the turns ratio equal to N₂/N₁.

2.3. Boundary Condition Analysis

The boundary condition for L_m is described as follows.

$$\{\begin{array}{l}2I_{Lm}\ge \Delta i_{Lm}\Rightarrow L_m\mathrm{operated}\mathrm{without}\mathrm{negative}\mathrm{current}\\ 2I_{Lm}\le \Delta i_{Lm}\Rightarrow L_m\mathrm{operated}\mathrm{with}\mathrm{negative}\mathrm{current}\end{array}$$

(10)

where I_Lm and $\Delta i_{Lm}$ are the DC and AC values of i_Lm, respectively, and the latter is also called the magnetizing current ripple.

For analysis convenience, it is assumed that there is no power consumption in the converter. According to the voltage-second balance of the inductor and the current second balance of the capacitor, the DC voltage across the coupling inductor and the DC current in the energy-transferring capacitor are zero. Therefore, as shown in Figure 10, the secondary DC current I_N2 is equal to the output current I_o, namely,

$$I_{N1}=\frac{N_2}{N_1}\times I_{N2}=\frac{N_2}{N_1}\times I_o$$

(11)

$$I_{Lm}=I_{N1}=\frac{N_2}{N_1}\times I_o$$

(12)

$$I_o=\frac{V_o}{R_o}$$

(13)

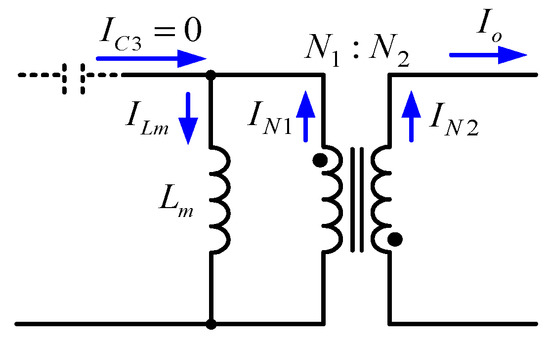
Figure 10. Equivalent model for the coupling inductor under DC analysis.

From (12) and (13), it can be obtained

$$I_{Lm}=I_{N1}=\frac{N_2}{N_1}\times \frac{V_o}{R_o}$$

(14)

Since the current ripple $\Delta i_{Lm}$ can be expressed as

$$\Delta i_{Lm}=\frac{v_{Lm}\Delta t}{L_m}=\frac{\frac{N_1}{N_2}{V}_o(1-D)T_s}{L_m}$$

(15)

Hence, as $2I_{Lm}\ge \Delta i_{Lm}$, the magnetizing inductance L_m will be operated without negative current, that is,

$$\begin{array}{l}2I_{Lm}\ge \Delta i_{Lm}\\ \Rightarrow 2\times \frac{N_2}{N_1}\times \frac{V_o}{R_o}\ge \frac{\frac{N_1}{N_2}{V}_o(1-D)T_s}{L_m}\\ \Rightarrow \frac{2L_m}{R_o{T}_s}\ge {\left(\frac{N_1}{N_2}\right)}^2\times (1-D)\\ \Rightarrow K\ge K_{crit}(D)\end{array}$$

(16)

where $K=\frac{2L_m}{R_o{T}_s}$ and $K_{crit}(D)={\left(\frac{N_1}{N_2}\right)}^2\times (1-D)$.

From (16), it can be seen that as K ≥ K_crit(D), the magnetizing inductance L_m will be operated without negative current; otherwise, L_m will be operated with negative current. Hence, by assuming that N₁/N₂ = 3, the boundary curve for L_m operating mode can be drawn as shown in Figure 11.

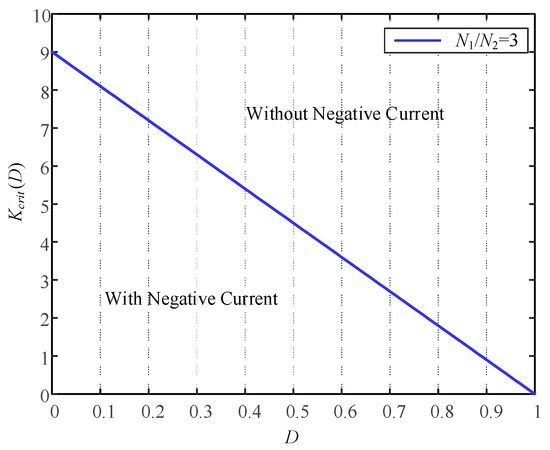
Figure 11. Boundary curve for L_m operating mode.

2.4. Comparison of Proposed Circuit with Existing Circuits

Table 1 shows the comparison of the proposed circuit with the existing circuits, in terms of voltage conversion ratio, component number, switch voltage stress, and output inductor. From Table 1, the proposed circuit has a more component number than the circuits shown in [24,28] have. As shown in Figure 12, the proposed circuit has a lower voltage conversion ratio than the circuits shown in [24,28] have. In practice, the lower the turns ratio n (= N₂/N₁) is, the larger the leakage inductance. Consequently, the value of n, set at 1/3 for the comparison in step-down voltage conversion ratio, is reasonable. The proposed circuit has lower voltage stresses on Q₁ and Q₂ than the circuits shown in [24,28] have. In addition, the proposed circuit has lower voltage stresses on Q₃ and Q₄ than the circuits shown in [24,28] have. In addition, only the circuit shown in [28] has an output inductor.

Table 1. Comparison of the proposed circuit with the existing circuits.

Converter	Voltage Conversion Ratio	Component Number	Switch Voltage Stress	Output Inductor
Proposed	$D\cdot (\frac{n}{1+2n})$	9	$V_{ds1}=V_{ds2}=\frac{1+n}{1+2n}{V}_{in}$ $V_{ds3}=V_{ds4}=\frac{n}{1+2n}{V}_{in}$	No
[24]	$D\cdot (\frac{n}{1+n})$	8	$V_{ds1}=V_{ds2}=V_{in}$ $V_{ds3}=V_{ds4}=\frac{n}{1+n}{V}_{in}$	No
[28]	$D\cdot (\frac{n}{1+n})$	8	$V_{ds1}=V_{ds2}=V_{in}$ $V_{ds3}=V_{ds4}=\frac{n}{1+n}{V}_{in}$	Yes

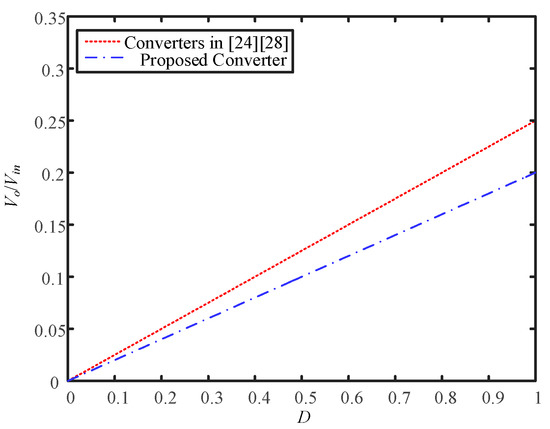
Figure 12. Voltage conversion curves of the circuit shown in Table 1 with n = 1/3.

3. Control Strategy

Figure 13 shows the system block diagram for the proposed high step-down converter, including main power stage and feedback control circuit. As for the feedback control circuit, it is constructed by one voltage divider used to obtain the analogue signal of the output voltage, one analogue-to-digital converter (ADC) used to transfer this analogue signal to the digital signal, and one field-programmable gate array (FPGA) chip used to generate four digital pulse-width modulation (DPWM) signals, which are sent to four switches after four gate drivers so as to stabilize the output voltage at the desired value. Speaking lucidly, the digital signal obtained from the ADC is sent to the proportional-integral (PI) controller embedded in the FPGA to create DPWM signals, v_gs1, v_gs2, v_gs3 and v_gs4, where v_gs1 equal to v_gs2 is complimentary to v_gs2 equal to v_gs4.

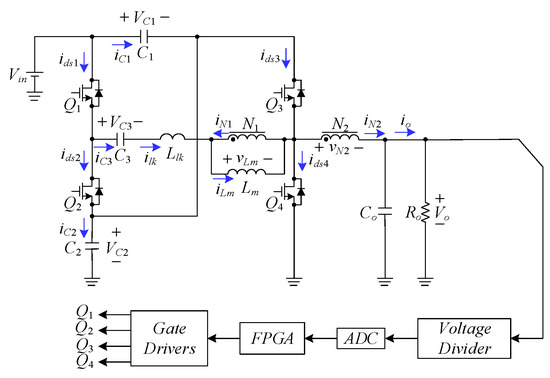
Figure 13. System configuration block diagram.

How to Set Switching Frequency from FPGA and How to Get DPWM Signal

The FPGA needs an external oscillator of 20 MHz, and this frequency will be increased to 100 MHz, which will be used as a system clock as well as a subsystem clock of the DPWM generator. As soon as the system get started, the counting value of one counter will be increased from zero to 999, and then be initialized such that the next cycle is to be repeated. That is to say, the switching frequency is 100 MHz divided by 1000, equal to 100 kHz. As the counting value of the counter is smaller than the control force created from the PI controller embedded in the FPGA, the DPWM signal will be “high”; otherwise, the DPWM signal will be “low”.

4. Design Considerations

Prior to this section, system specifications should be given as shown in Table 2. The two blanking times between Q₁ (or Q₃) and Q₂ (or Q₄) are set at 100 ns and 150 ns, respectively. It is noted that in order to verify that the voltage conversion ratio of the proposed circuit is wider than that of the circuit shown in [24], the former has an input voltage of 60 V and an output voltage of 3.3 V, whereas the latter has an input voltage of 48 V and an output voltage of 3.3 V.

Table 2. System specifications.

Parameters	Specifications
Converter Operating Mode	CCM
Input Voltage (Vin)	60 V
Rated Output Voltage (Vo,rated)	3.3 V
Rated Output Current (Io,rated)/Power (Po,rated)	10 A/33 W
Minimum Output Current (Io,min)/Power (Po,min)	2 A/6.6 W
Switching Frequency (fs)/Period (Ts)	100 kHz/10 μs

4.1. Design of Coupling Inductor

4.1.1. Design of Turns Ratio

From (9), the following equation can be obtained to be

$$D=\frac{V_o}{V_{in}}\times \left(\frac{1+2n}{n}\right)$$

(17)

Since the converter mainly transfers energy to the load during the turn-off period of Q₁, the duty cycle is set between 0.2 and 0.3. According to Table 2, together with this desired duty cycle range, the turns ratio inequality can be obtained to be

$$\begin{array}{l}0.2\le \frac{V_o}{V_{in}}\times \left(\frac{1+2n}{n}\right)\le 0.3\\ \Rightarrow 0.2\le \frac{3.3}{60}\times \left(\frac{1+2n}{n}\right)\le 0.3\Rightarrow 0.289\le n\le 0.61\end{array}$$

(18)

Based on (18), the value of n is chosen to be

$$n=\frac{1}{3}$$

(19)

Substituting (19) and some system specifications shown in Table 2 into (19) yields

$$D=\frac{V_o}{V_{in}}\times \left(\frac{1+2n}{n}\right)=\frac{3.3}{60}\times \left(\frac{1+2\times \frac{1}{3}}{\frac{1}{3}}\right)=0.275$$

(20)

4.1.2. Design of Magnetizing Inductance

From (16), it can be seen that if the magnetizing inductance L_m operates without negative current, the value of L_m should obey the following inequality:

$$\begin{array}{l}{L}_m\ge {\left(\frac{N_1}{N_2}\right)}^2\times (1-D)\times \frac{R_{o,max}\times T_s}{2}\\ \Rightarrow L_m\ge {\left(\frac{N_1}{N_2}\right)}^2\times (1-D)\times \frac{V_o\times T_s}{2\times I_{o,min}}\end{array}$$

(21)

where R_o,max indicates the maximum output resistance.

Substituting the results shown in (19) and (20), and some specifications shown in Table 2 into (21) yields

$$L_m\ge \frac{9\times (1-0.275)\times 3.3\times 10\mu }{2\times 2}\Rightarrow L_m=53.8\mu H$$

(22)

Before calculating the primary and secondary turns of the coupled inductor, N₁ and N₂, the peak current of the magnetizing inductance, I_Lm,peak, should be first obtained, namely,

$$I_{Lm,peak}=I_{Lm}+\frac{\Delta i_{Lm}}{2}$$

(23)

By substituting (14) and (15) into (23), the following equation can be obtained to be

$$\begin{array}{ll}{I}_{Lm,peak}& =I_{Lm}+\frac{\Delta i_{Lm}}{2}\\ & =\frac{N_2}{N_1}\times I_o+\frac{\frac{N_1}{N_2}\times V_o\times (1-D)}{2\times L_m\times f_s}\end{array}$$

(24)

By substituting the results shown in (19) and (20), and some specifications shown in Table 2 into (30), the value of I_Lm,pesak can be obtained to be

$$I_{Lm,peak}=\frac{1}{3}\times 10+\frac{3\times 3.3\times (1-0.275)}{2\times 53.8\mu \times 100k}=4\mathrm{A}$$

(25)

After this, via the Faraday law, the value of N₁ can be represented by

$$N_1=\frac{L_m\times I_{Lm,peak}}{A_e\times B_{max}}\times {10}^8$$

(26)

where A_e is the effective area of the core size and B_max is the maximum flux density.

Since the saturation flux density B_s will be reduced due to the temperature rising, the value of B_max is designed to be 80% of B_s. By the way, the high-μ core is used herein, whose product name is PQ20/16-3C90, made by FERROXCUBE Co. Table 3 shows the specifications of this core.

Table 3. Core specifications.

Parameters	Specifications
Product name	PQ20/16-3C90
Inductor constant (AL)	3250 nH/N2 ± 25%
Saturation flux density (Bs)	380 mT
Residual flux density (Br)	60 mT
Effective area (Ae)	0.619 cm2
Effective volume (Ve)	2.33 cm3
Effective magnetic length (le)	3.76 cm

By substituting the results shown in (22) and (25), and some specifications shown in Table 3 into (26), the value of N₁ can be obtained to be

$$N_1=\frac{53.8\mu \times 4}{0.619\times 0.8\times 3800}\times {10}^8\approx 12\mathrm{Turns}$$

(27)

Since the value of n is 1/3, the value of N₂ is set at four turns. However, by substituting the result of (27) and the value of A_e shown in Table 3 into the following equation, the corresponding value of L_m, much larger than the value of L_min shown in (22), can be obtained to be

$$L_m=N_1{}^2\times A_L={12}^2\times 3250\times {10}^{-9}=468\mu \mathrm{H}$$

(28)

Consequently, the air gap needs to be adjusted in order to obtain the desired value of L_m. Without considering the fringing effect, the desired value of the airgap l_g can be obtained according to the following two equations:

$$L_m=\frac{4\pi A_e{N}_{{}_1}^2{\mu }_e}{l_e}\times {10}^{-8}$$

(29)

$${\mu }_e\cong \frac{l_e}{l_a}$$

(30)

where μ_e is the equivalent magnetic permeability.

Combining (29) and (30) yields

$$l_a=\frac{4\pi A_e{N}_{{}_1}^2}{L_m}\times {10}^{-8}$$

(31)

By substituting the result shown in (22) and some specifications shown in Table 3 into (31), the required value of l_a can be obtained to be

$$l_a=\frac{4\pi \times 0.619\times 144}{53.8\mu }\times {10}^{-8}\approx 0.21\mathrm{mm}$$

(32)

Finally, the actual value of L_m is designed and measured to be 81.6 μH.

4.2. Component Specifications

In the following, the specifications of the used components are listed in Table 4.

Table 4. Specifications of the components used in the proposed converter.

Components		Specifications
MOSFET	Q1, Q2	STP120NF10
	Q3, Q4	IRF3205Z
Energy-TransferringCapacitor	C1	220 μF/100 V Rubycon Electrolytic Capacitor
	C2, C3	680 μF/35 V Rubycon Electrolytic Capacitor
Capacitor	Co	1000 μF/16 V Rubycon Electrolytic Capacitor
Coupled Inductor		Core: PQ20/16-3C90 N = 1/3, Lm = 81.6 μH, Llk = 0.82 μH

5. Experimental Results

5.1. Test Bench for Measuring Efficiency and Waveforms

In the following, how to measure the efficiency will be described. First, as shown in Figure 14, the input current is obtained by measuring the voltage across one current sensing resistor based on one digital meter. After this, the input voltage is obtained also by another digital meter. Hence, the input power can be attained. Regarding the output power, the output current is read from one electronic load and the output voltage is obtained also by the other digital meter. Therefore, the output power can be attained. Finally, the corresponding efficiency can be obtained. As for measured waveforms, they are obtained by the instruments shown in Figure 14, along with two additional current amplifiers, two additional current probes and one additional isolated oscilloscope.

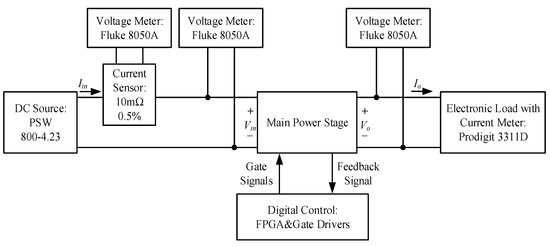
Figure 14. Test bench for measuring efficiency.

5.2. Measured Waveforms and Efficiency

The waveforms shown in Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21 are measured at rated load. Figure 15 shows the gate driving signal for Q₁, v_gs1, the voltage across Q₁, v_ds1, the gate driving signal for Q₃, v_gs3, and the voltage across Q₃, v_ds3. Figure 16 shows the gate driving signal for Q₂, v_gs2, the voltage across Q₂, v_ds2, the gate driving signal for Q₄, v_gs4, and the voltage across Q₄, v_ds4. Figure 17 shows the voltages on C₁, V_C1, the voltage on C₂, V_C2, and the voltage on C₃, V_C3. Figure 18 shows the gate driving signal for Q₁, v_gs1, the gate driving signal for Q₂, v_gs2, the current flowing through L_lk, i_lk, and the current in N₂, i_N2. Figure 19 shows the input voltage V_in and the output voltage V_o. Figure 20 and Figure 21 show the turn-on ZVS of Q₁ and Q₂, respectively. Figure 22 shows load transient responses and Figure 23 displays a curve of efficiency versus load current percentage.

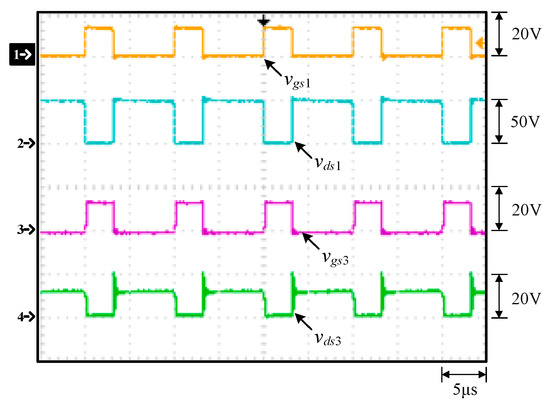
Figure 15. Measured waveforms at rated load: (1) v_gs1; (2) v_ds1; (3) v_gs3; (4) v_ds3.

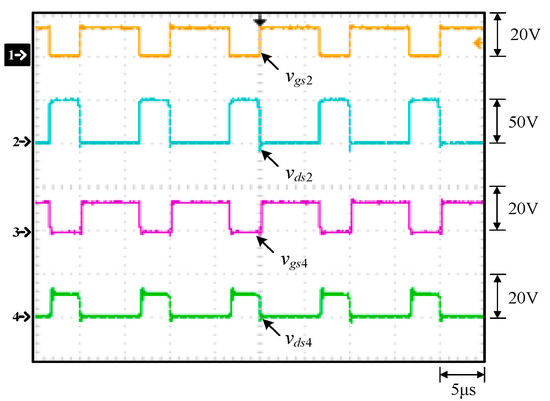
Figure 16. Measured waveforms at rated load: (1) v_gs2; (2) v_ds2; (3) v_gs4; (4) v_ds4.

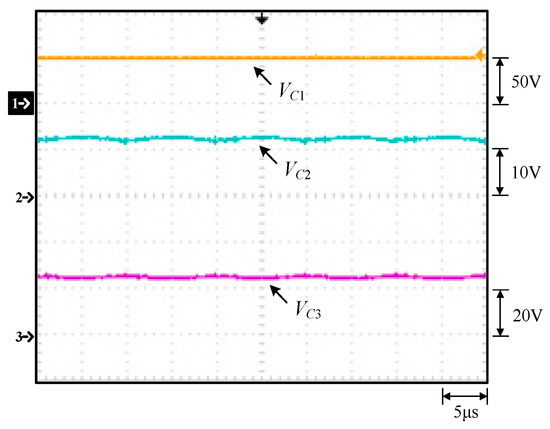
Figure 17. Measured waveforms at rated load: (1) V_C1; (2) V_C2; (3) V_C3.

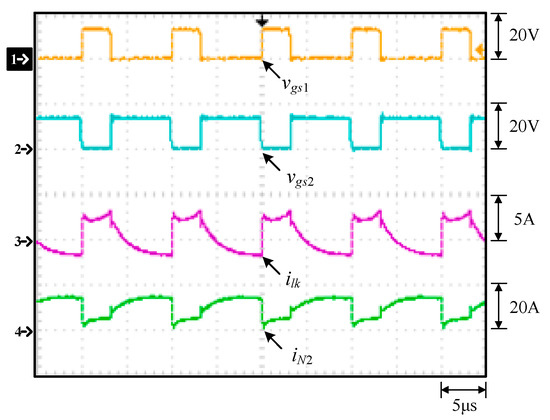
Figure 18. Measured waveforms at rated load: (1) v_gs1; (2) v_gs2; (3) i_lk; (4) i_N2.

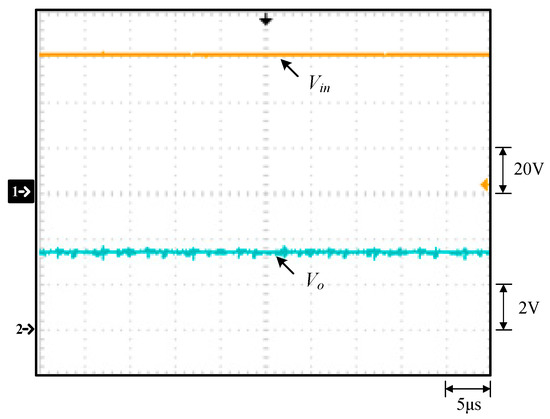
Figure 19. Measured waveforms at rated load: (1) V_in; (2) V_o.

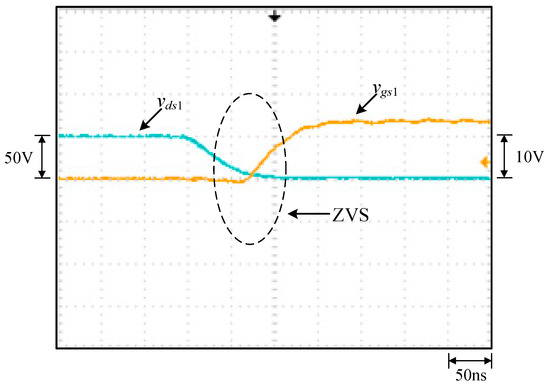
Figure 20. Zoom-in of the turn-on transient of Q₁.

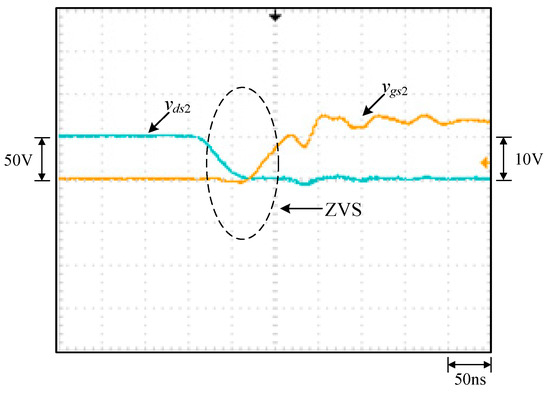
Figure 21. Zoom-in of the turn-on transient of Q₂.

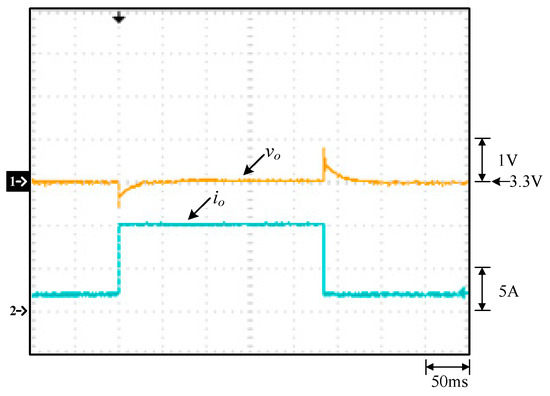
Figure 22. Output voltage responses due to load transients from light/rated load to rated/light load.

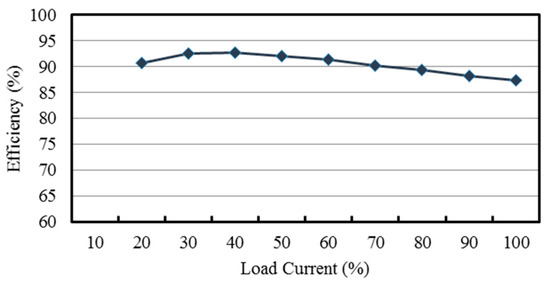
Figure 23. Curve of efficiency versus load current percentage.

From Figure 15, it can be seen that the voltage stress across Q₁ is 48 V, equal to V_in minus V_C2 (= 60 V − 12 V), whereas it can be seen that the voltage stress across Q₃ is 12 V, equal to V_in minus V_C1 (= 60 V − 48 V) with the voltage spike on Q₃ due to the parasitic capacitance of the switch resonating with the line parasitic inductance and the leakage inductance of the coupling inductor. From Figure 16, it can be seen that the voltage stress across Q₂ is 48 V, equal to V_in minus V_C2 (= 60 V − 12 V), whereas it can be seen that the voltage stress across Q₄ is 12 V, equal to V_in minus V_C1 (= 60 V − 48 V). From Figure 17, the voltages on C₁, C₂ and C₃, namely, V_C1, V_C2 and V_C3, are almost kept constant at some values. From Figure 18, it can be seen that there are some differences in i_lk and i_N2 between the waveforms shown in Figure 4 and these measured waveforms. This is because the leakage inductance of the coupled inductor will resonate with the energy-transferring capacitors. From Figure 19, it can be seen that the output voltage can be stably kept at 3.3 V under the input voltage of 60 V. From Figure 20 and Figure 21, it can be seen that the switches Q₁ and Q₂ have ZVS turn-on since these two switches are switched on after individual body diodes are turned on, corresponding to states 1 and 4 in Section 2. Figure 22 shows the load transient response from light load to rated load with a undershoot of 600 mV and a recovery time of 30 ms, and the load transient response from rated to light load with an overshoot of 800 mV and a recovery time of 55ms. Figure 23 shows that the overall efficiency is above 87.4% and can be up to 92.7%.

6. Conclusions

The proposed step-down converter comes from the converter [28]. Although the former, with one additional capacitor, has larger number of components than the latter has, the former has a higher voltage conversion ratio and lower voltage stresses on the switches than the latter has if the value of turns ratio is chosen reasonably. In addition, the portion of the leakage inductance energy in the former can be recycled to the input via the active clamp circuit during the turn-off period.