Electromagnetic Vibration Simulation of a 250-MW Large Hydropower Generator with Rotor Eccentricity and Rotor Deformation
Abstract
1. Introduction
2. Transient 2D Modelling
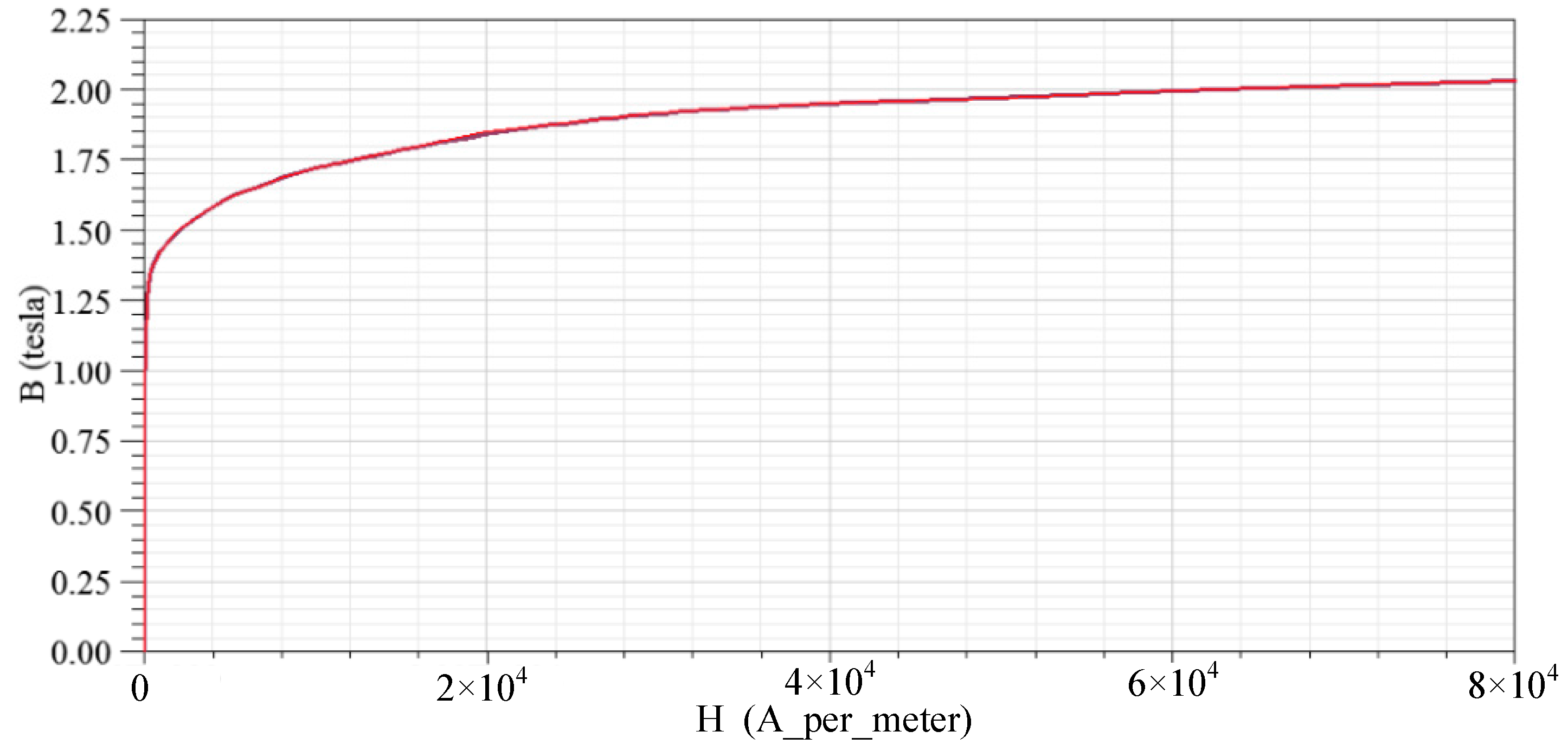
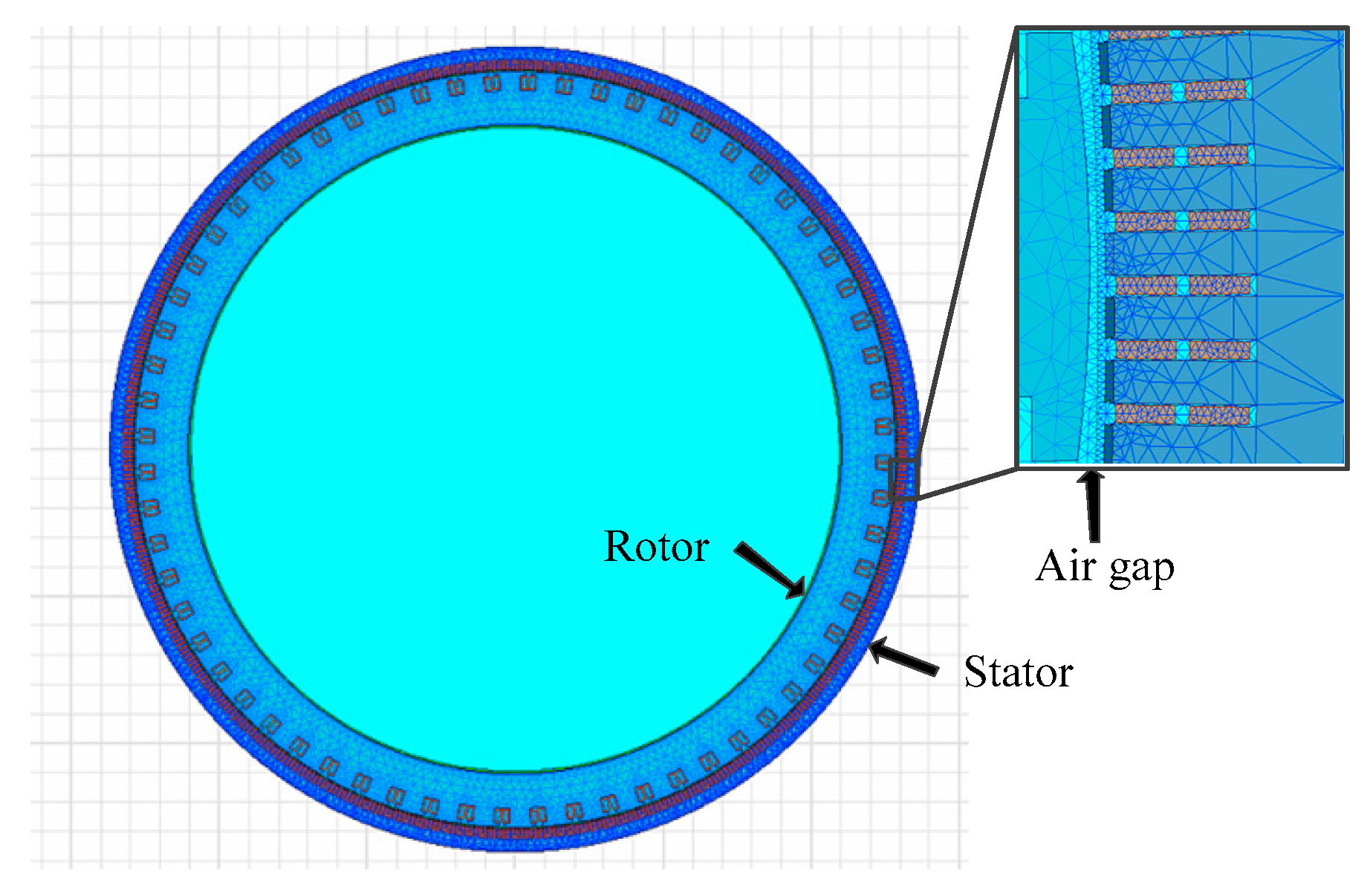
2.1. The Basic Model of the Hydropower Generator
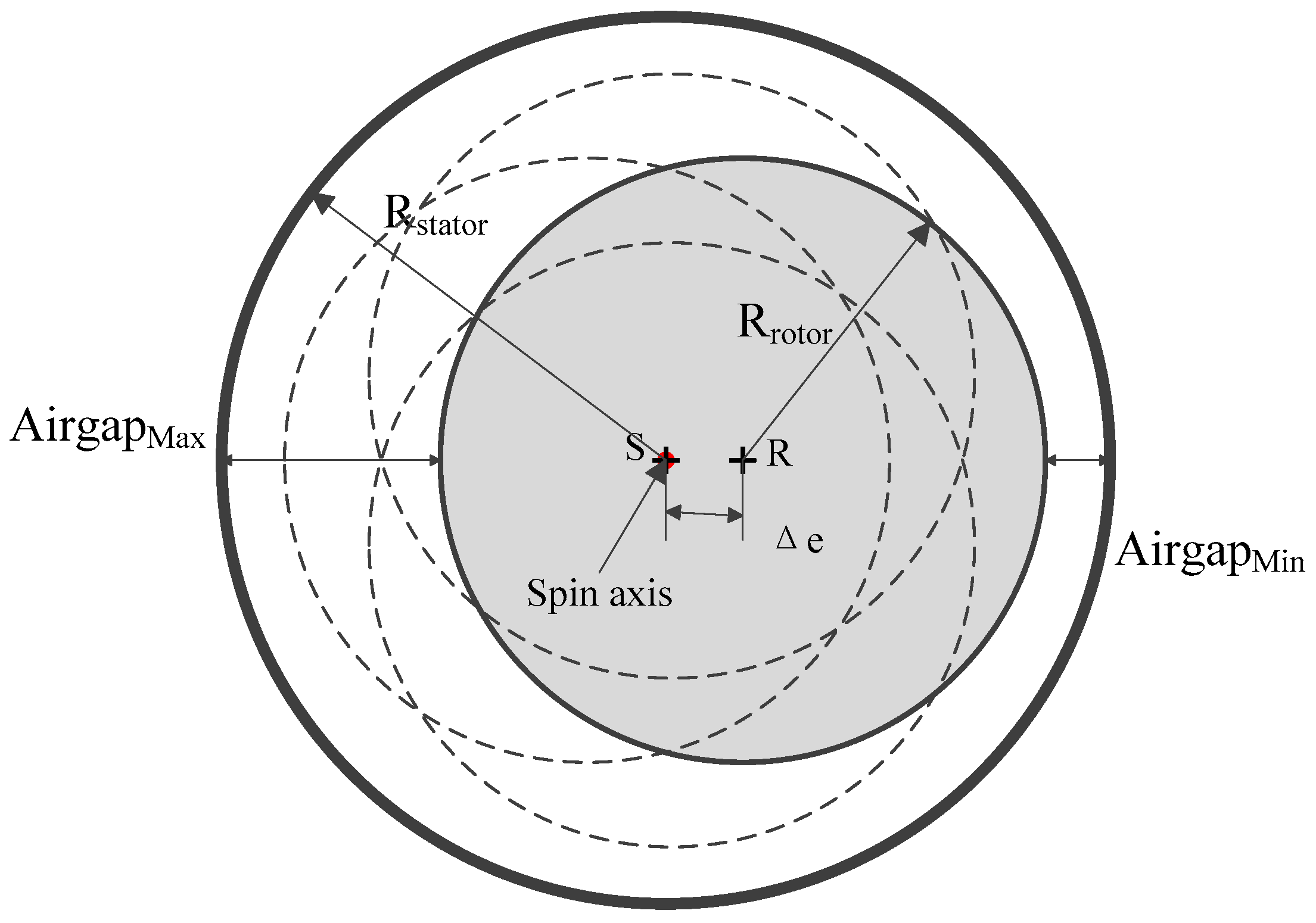
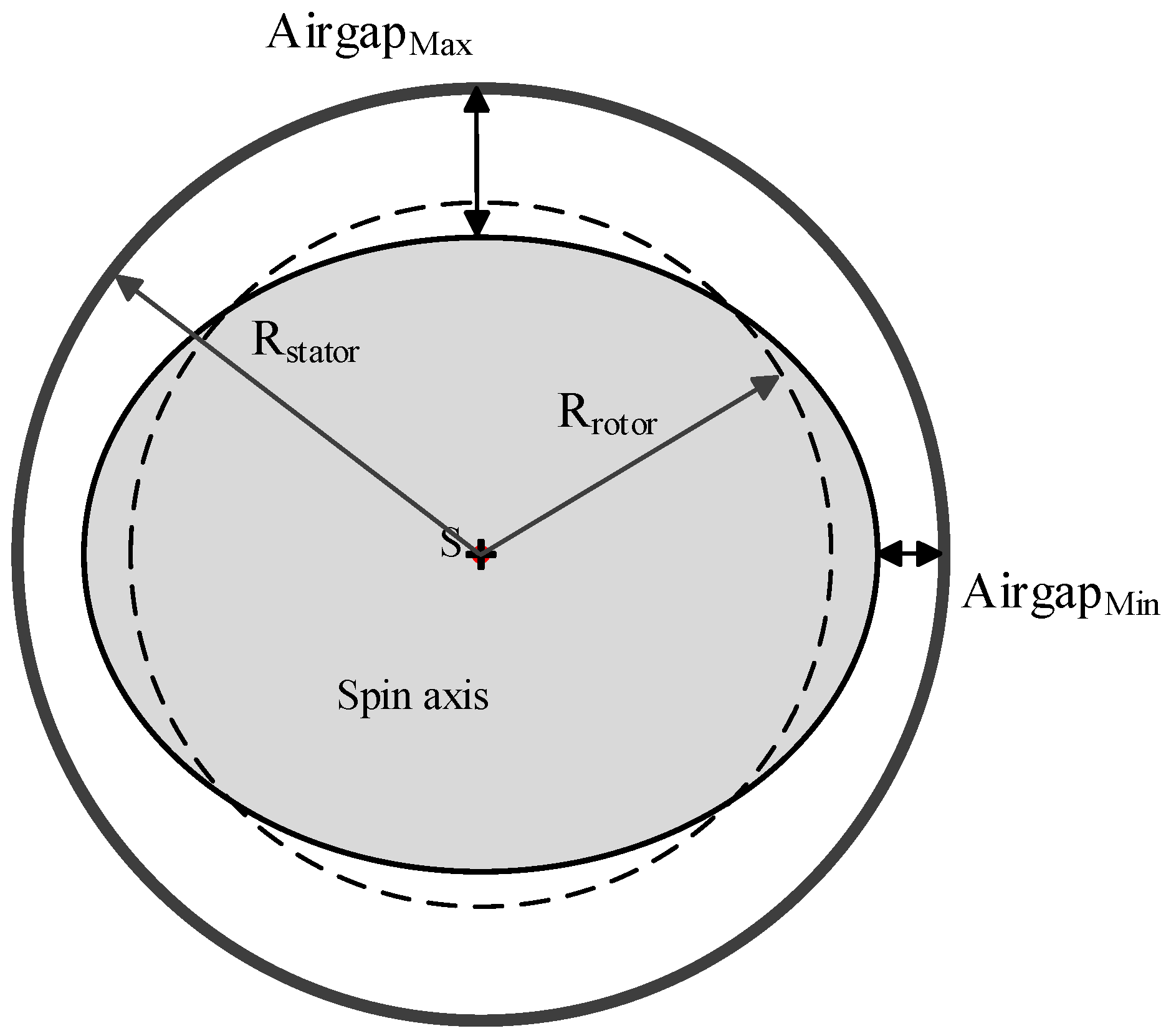
2.2. Rotor Eccentricity and Rotor Ellipse Deformation Models of the Hydropower Generator
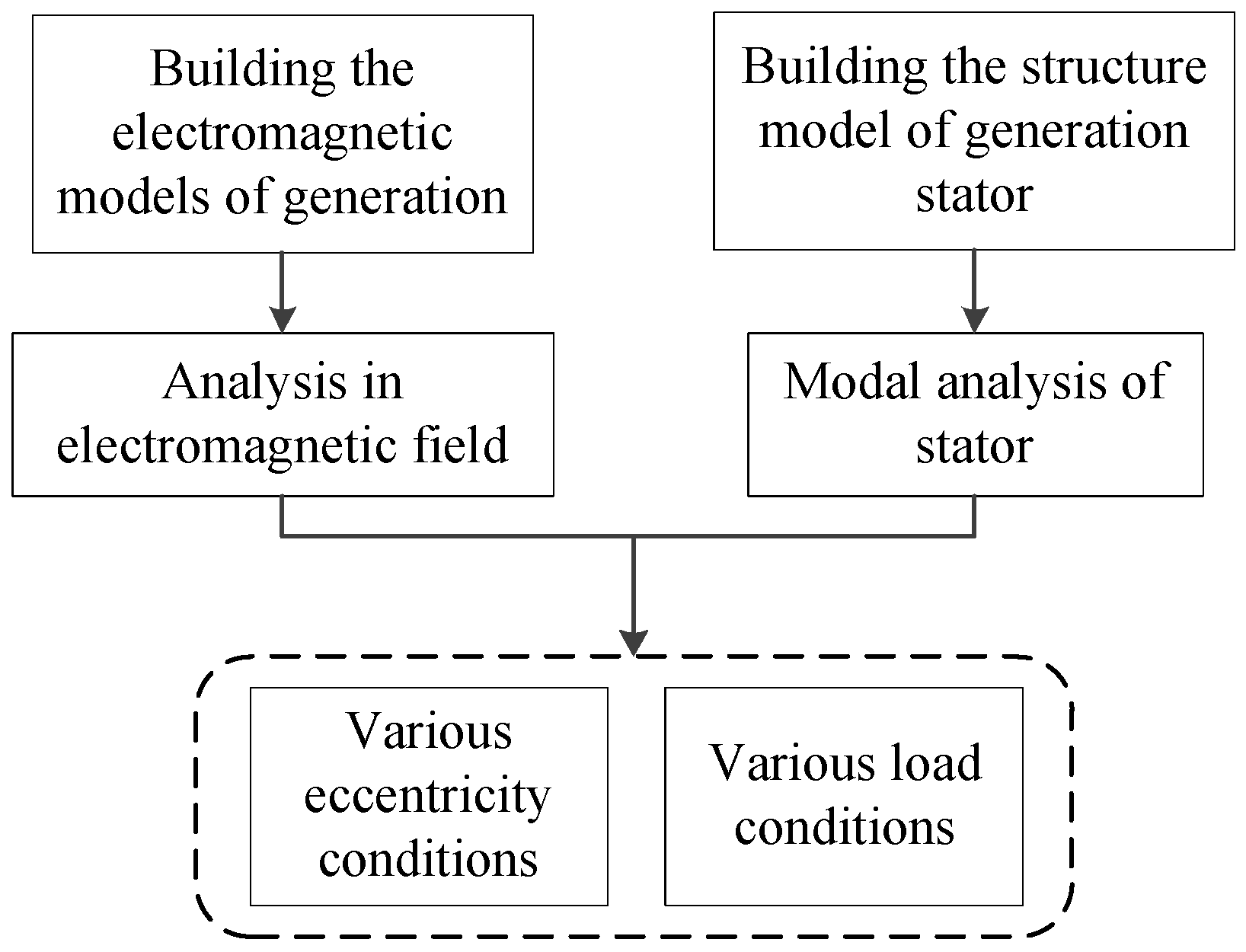
3. Simulation Principle of Electromagnetic Field
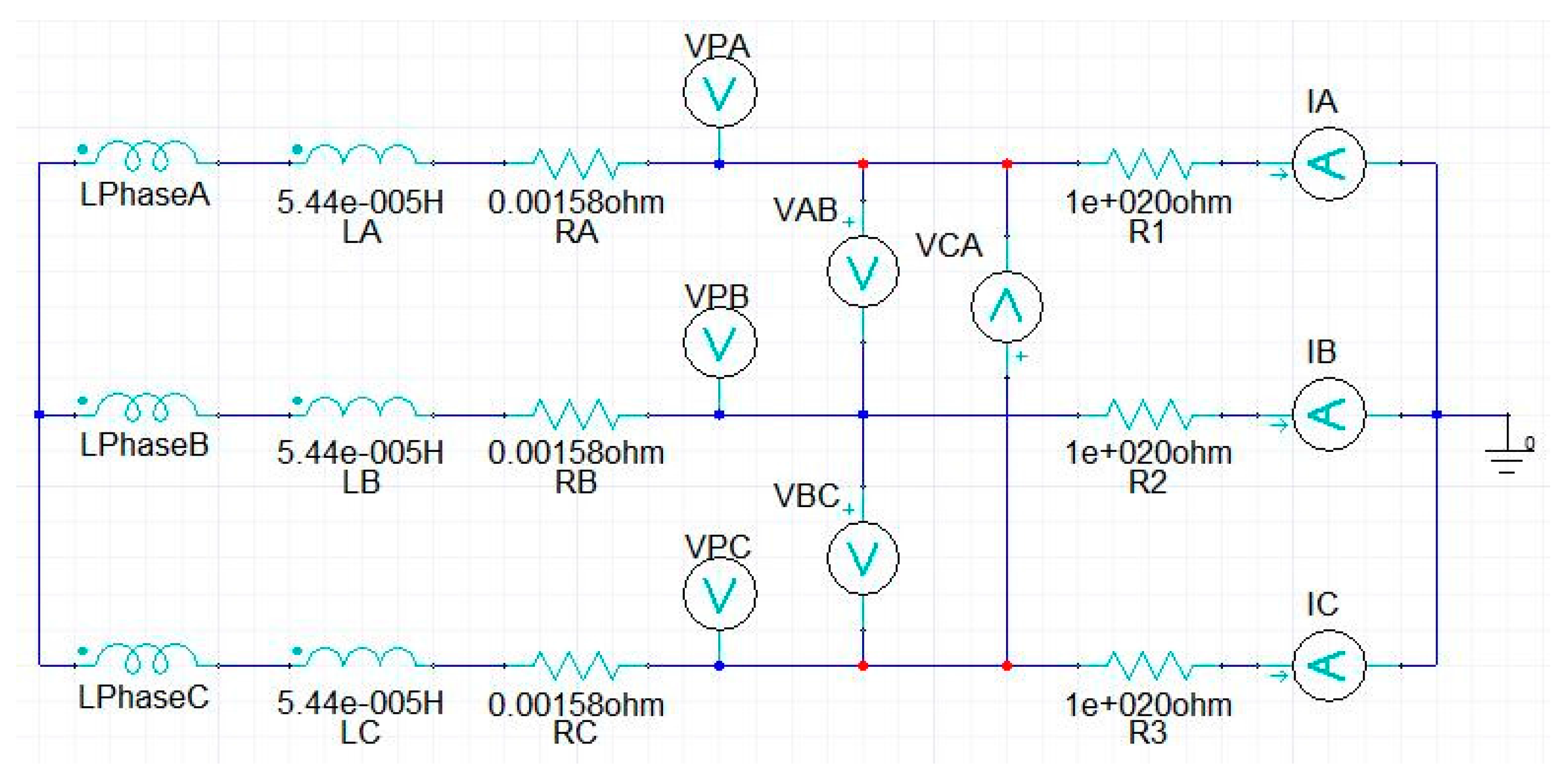
3.1. Transient Electromagnetic Analysis
3.2. Electromagnetic Force Analysis
4. The Results of Electromagnetic Simulations
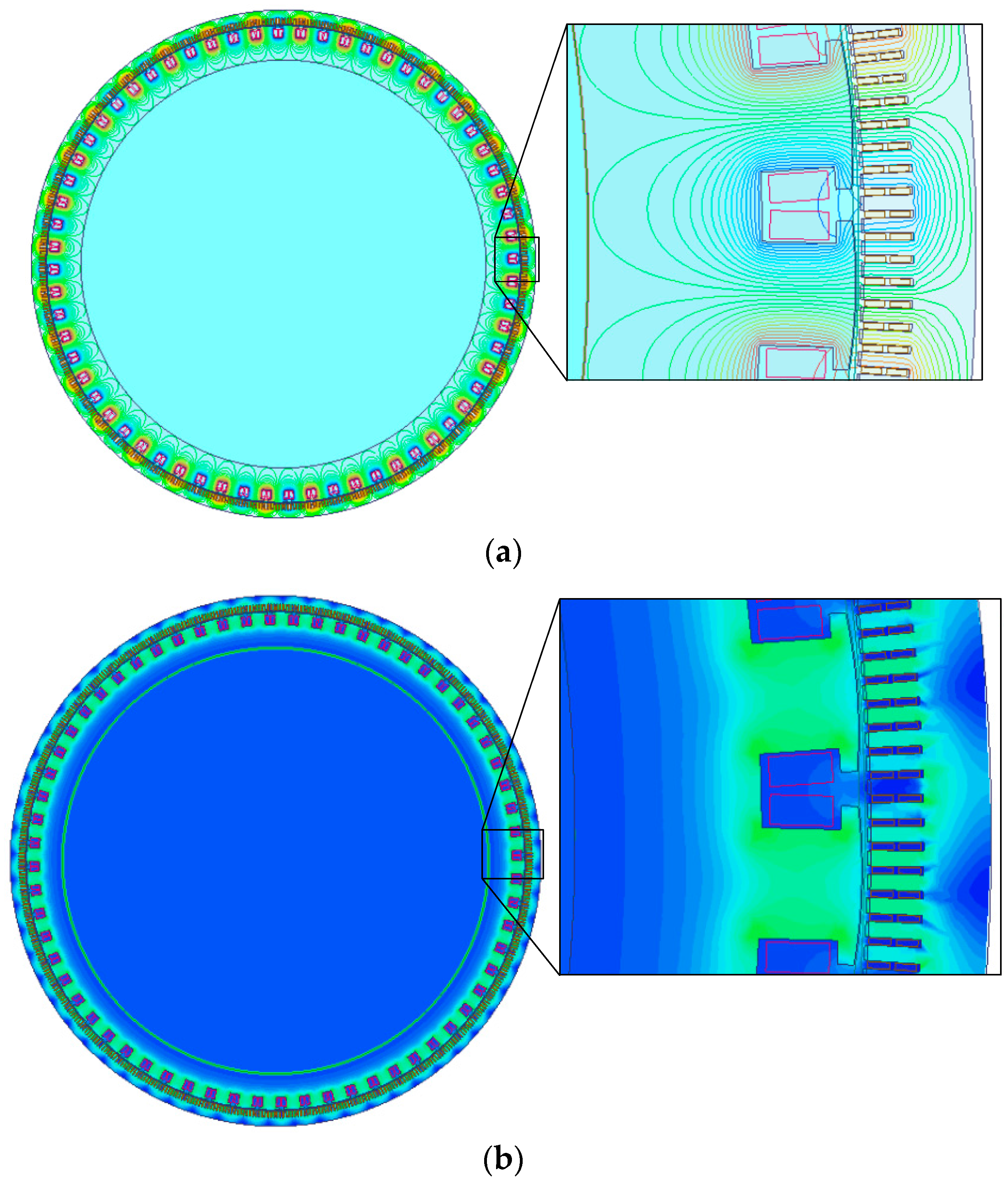
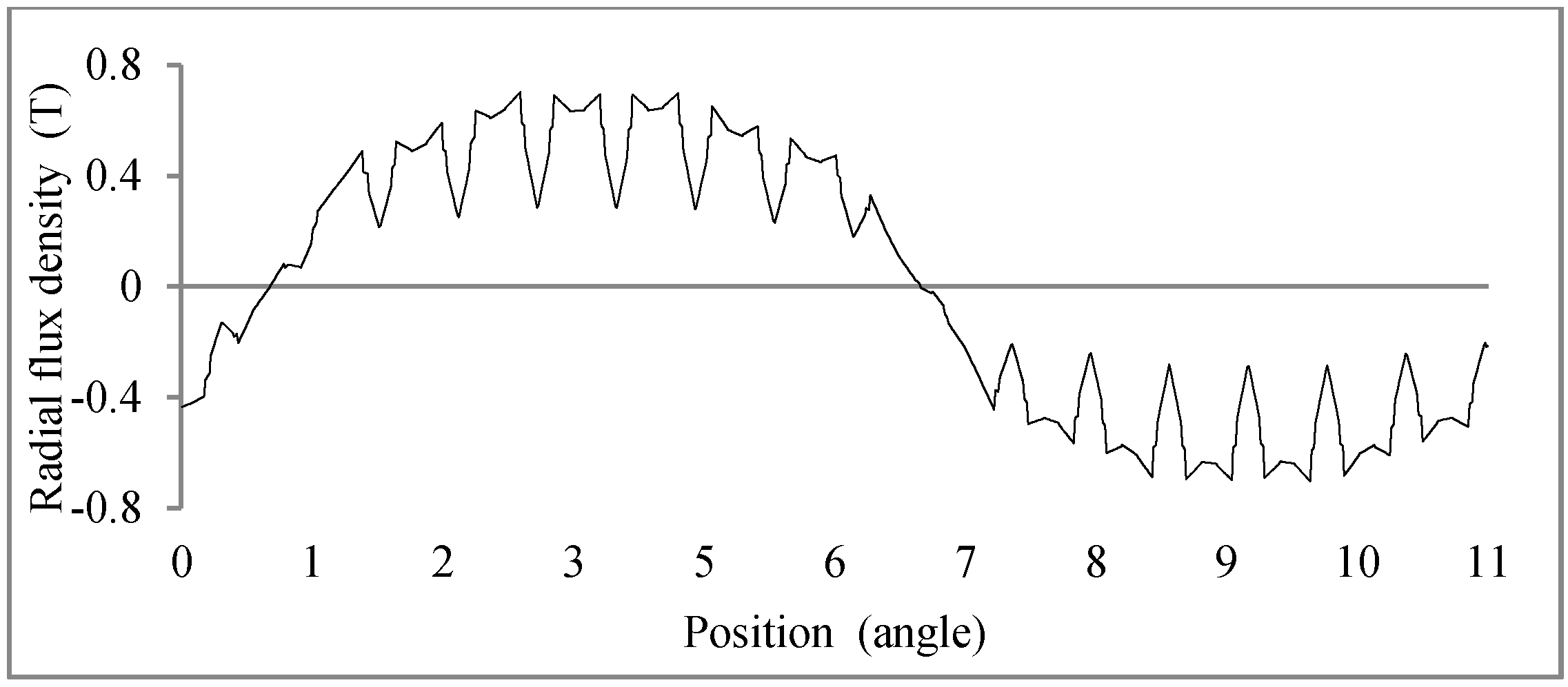
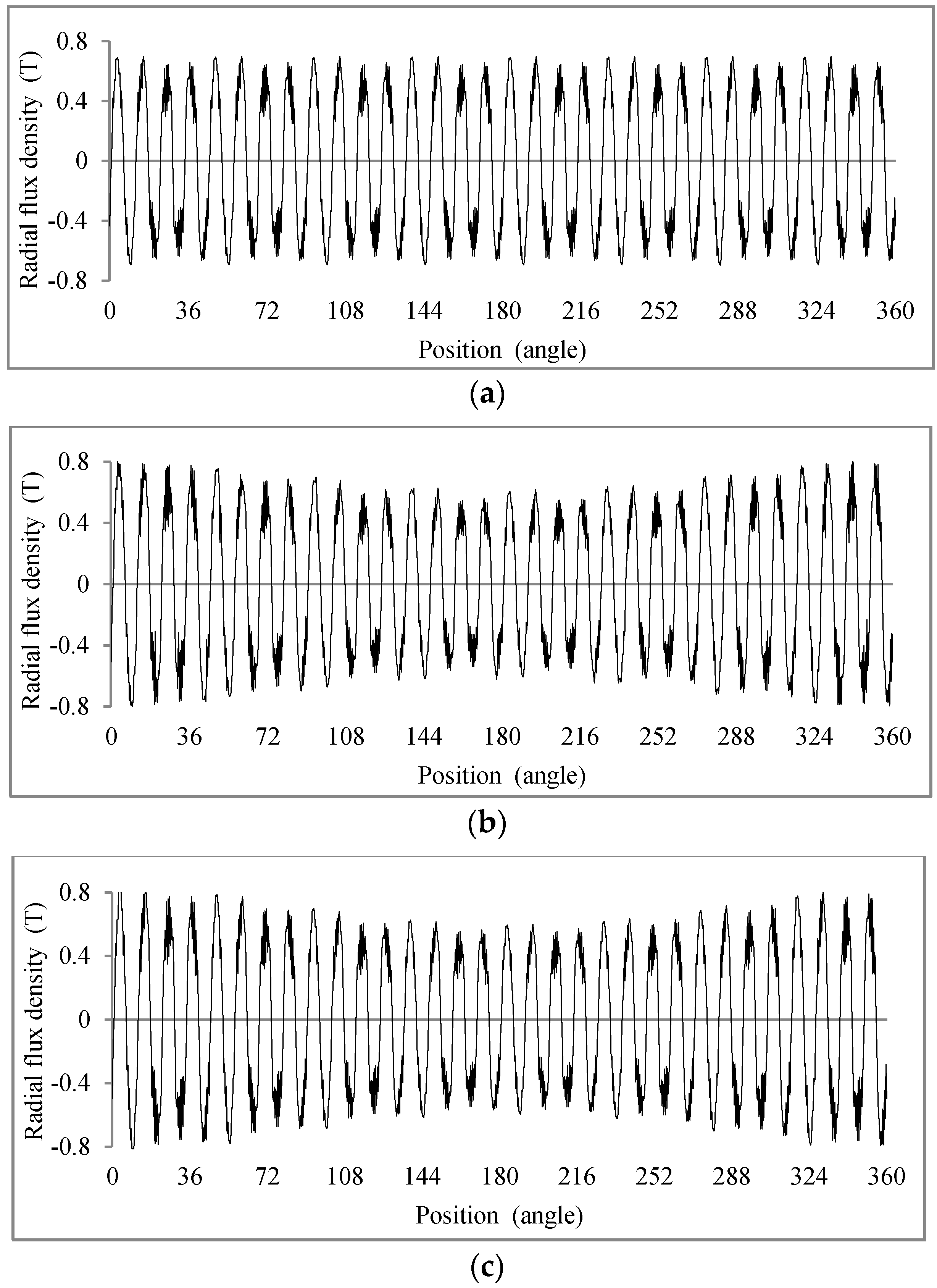
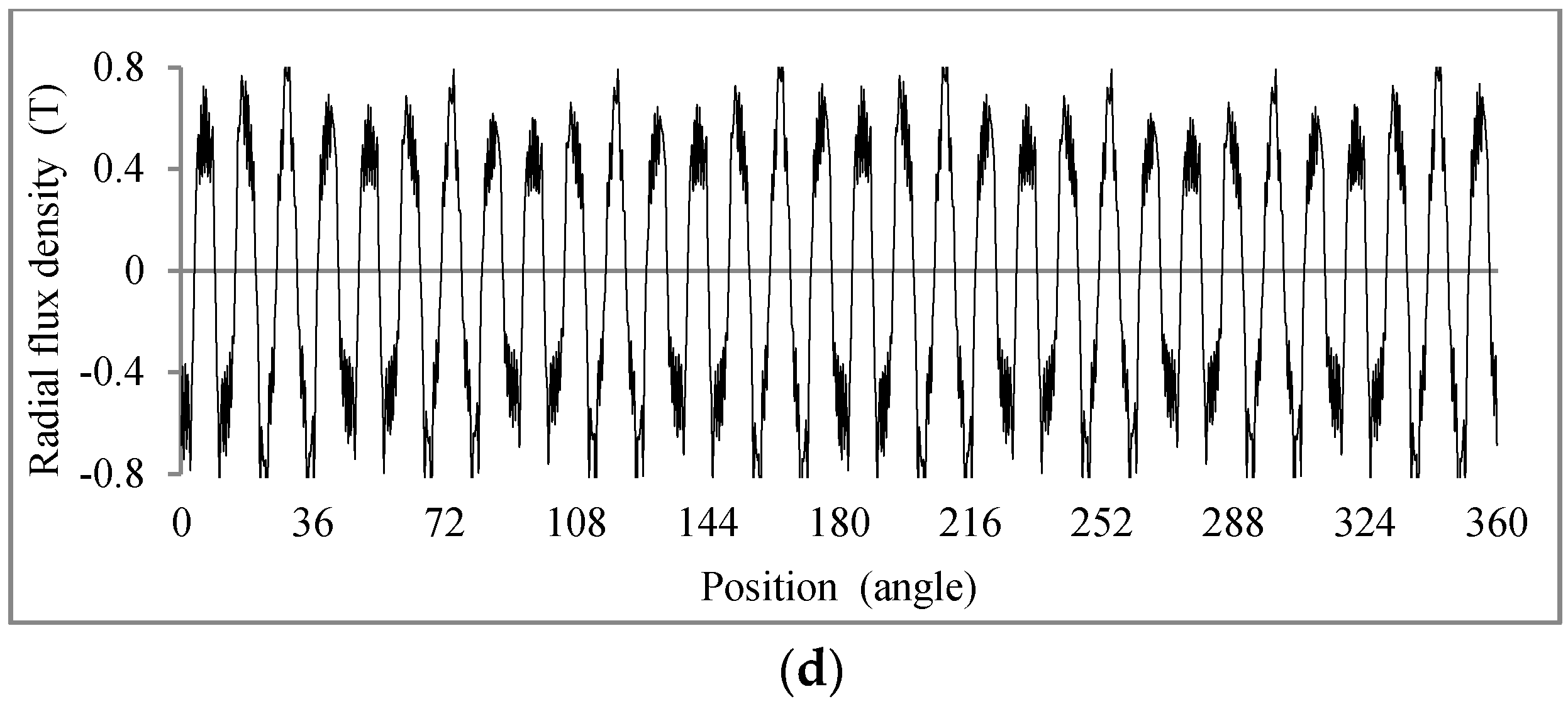
4.1. Flux Density on the Stator Teeth End
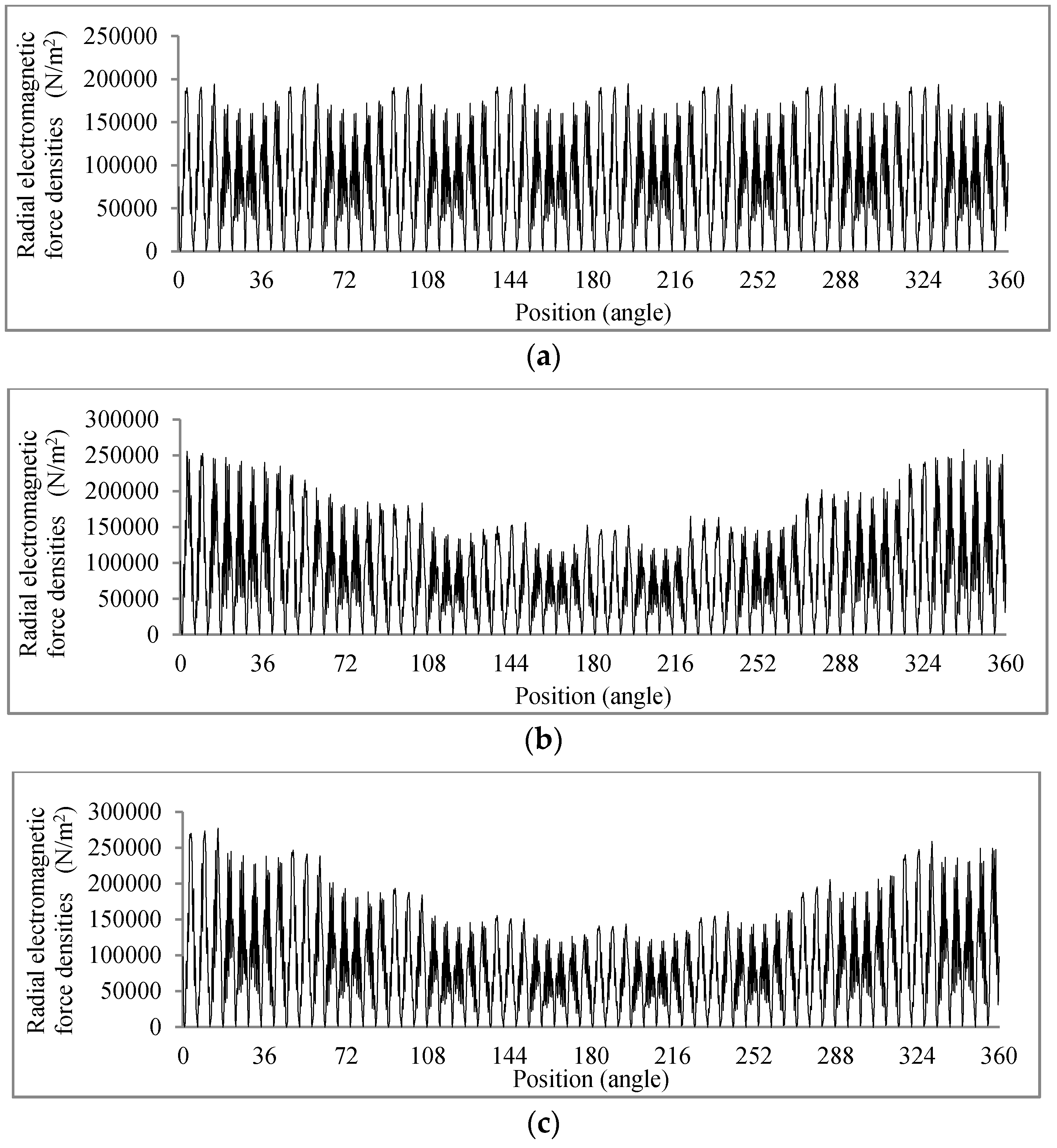
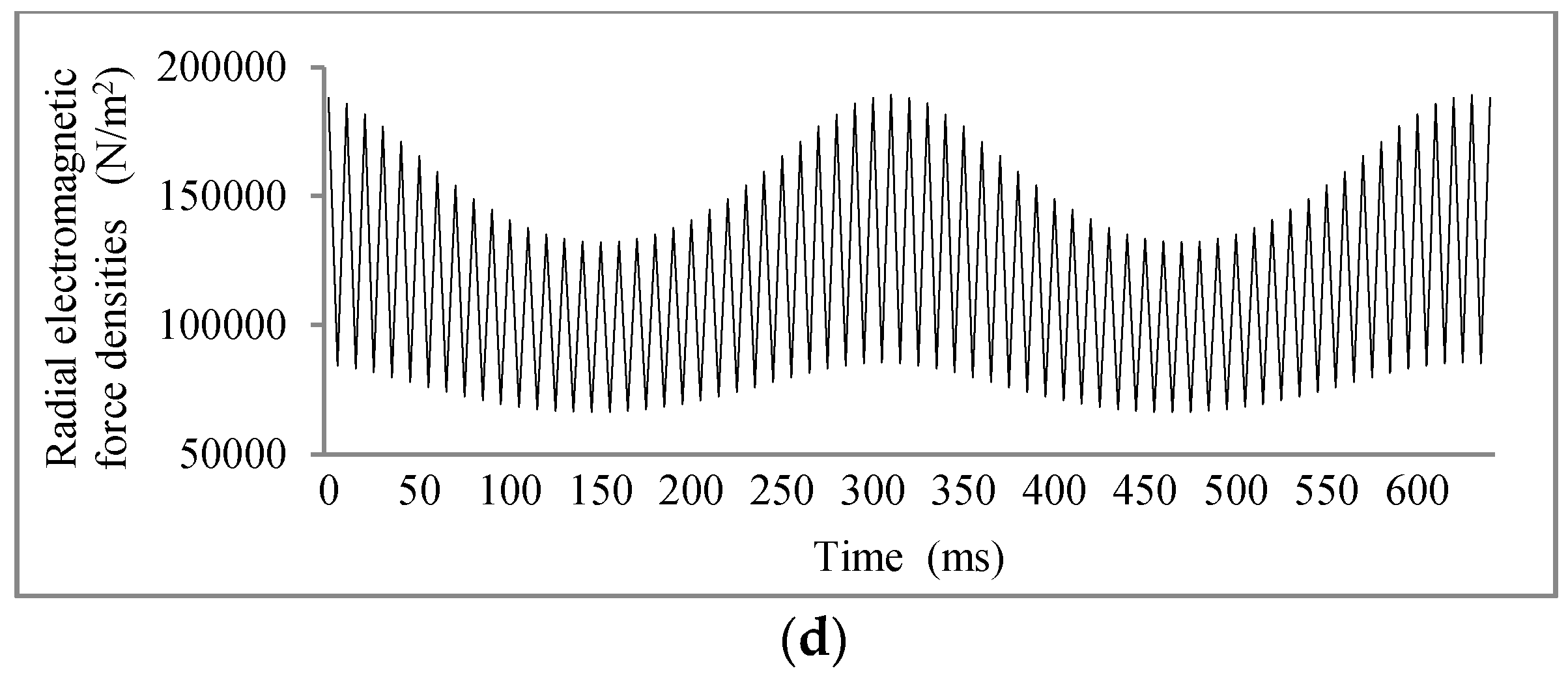
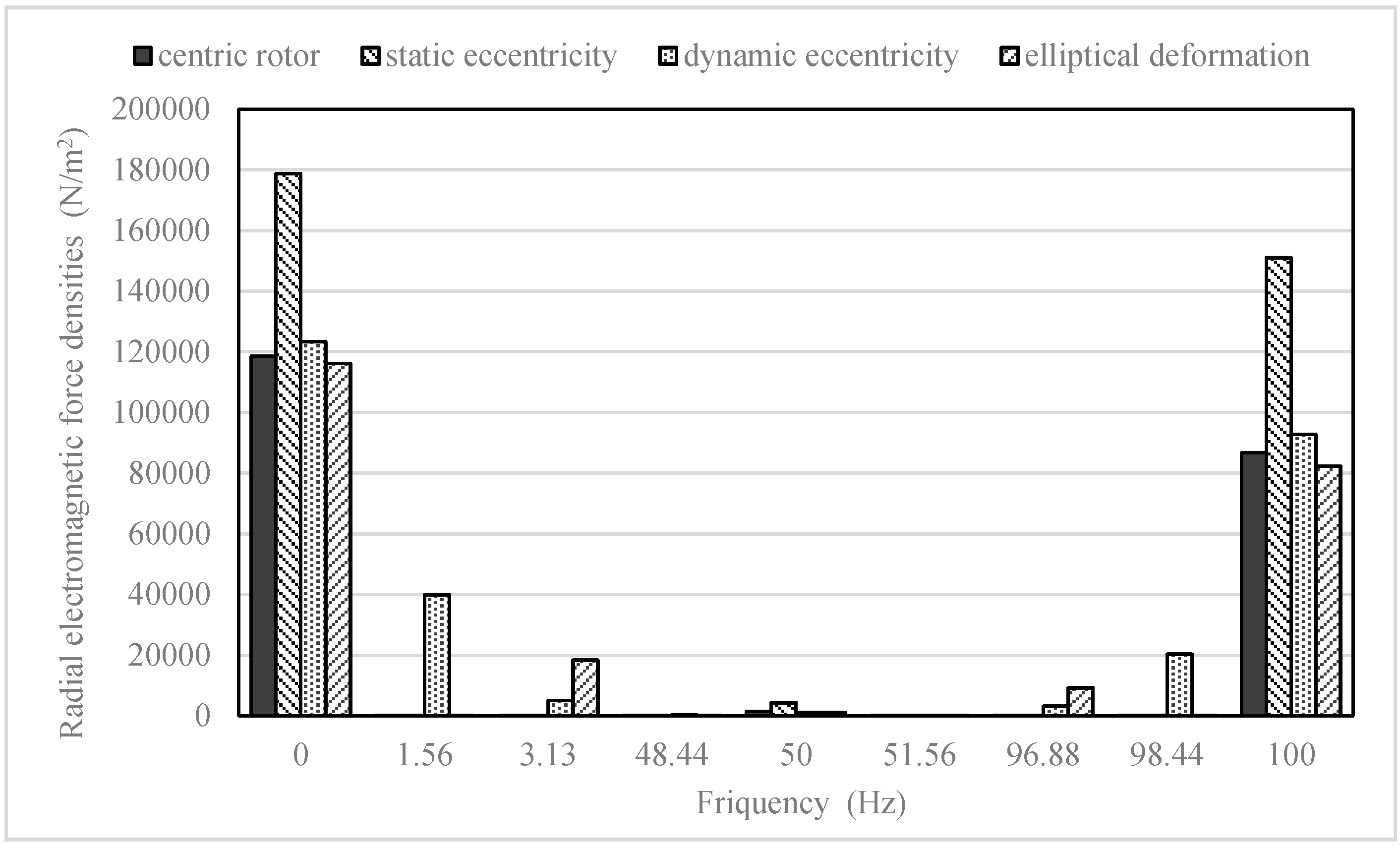
4.2. Electromagnetic Force Density Simulation
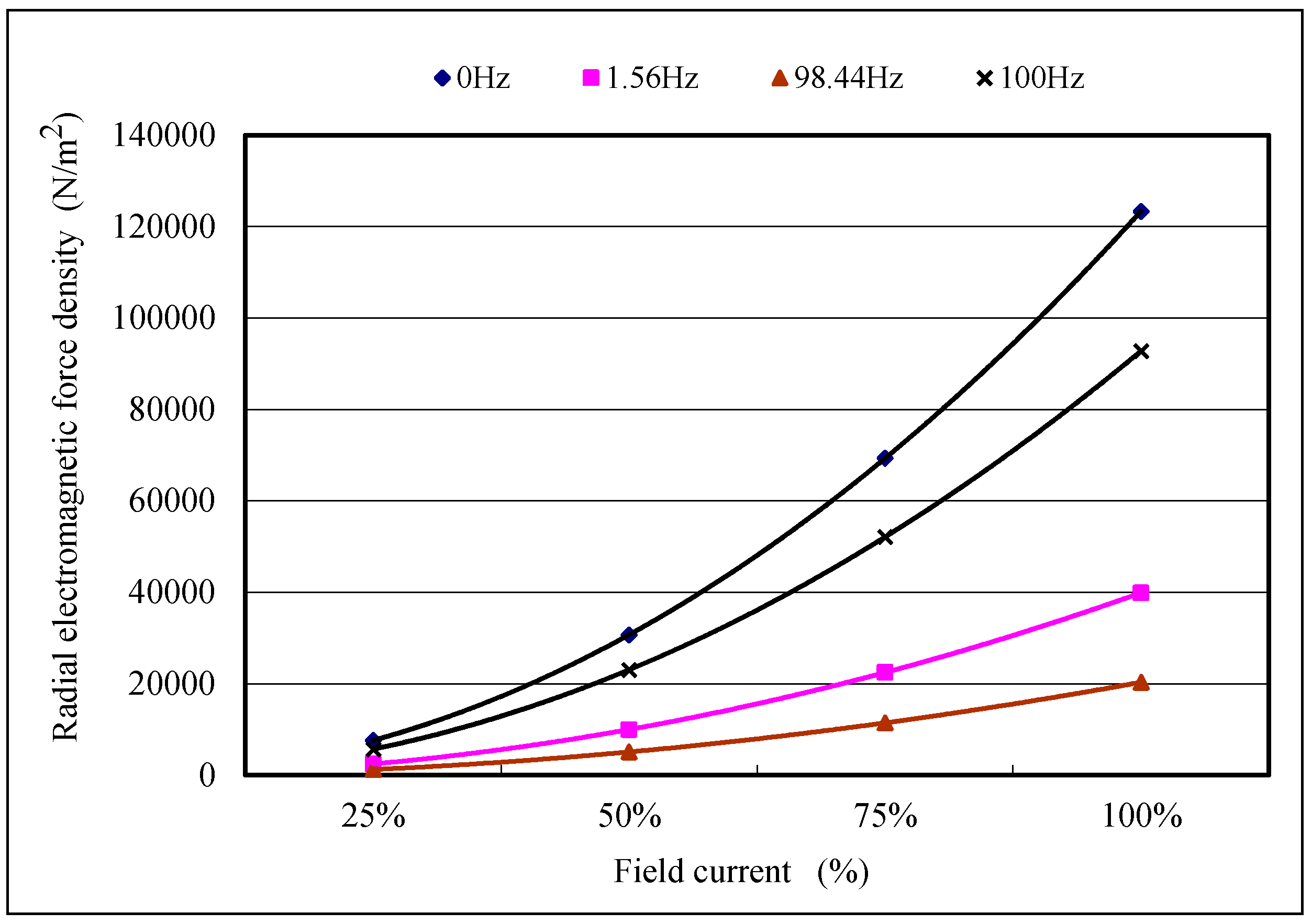
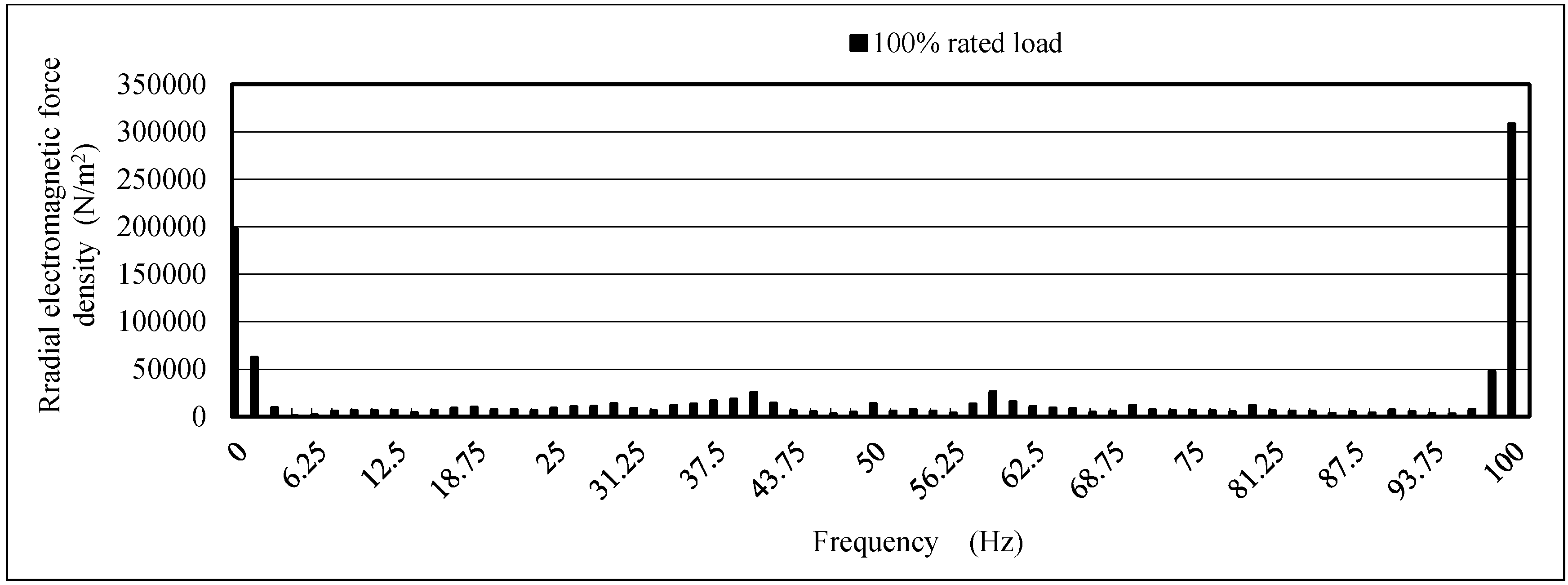
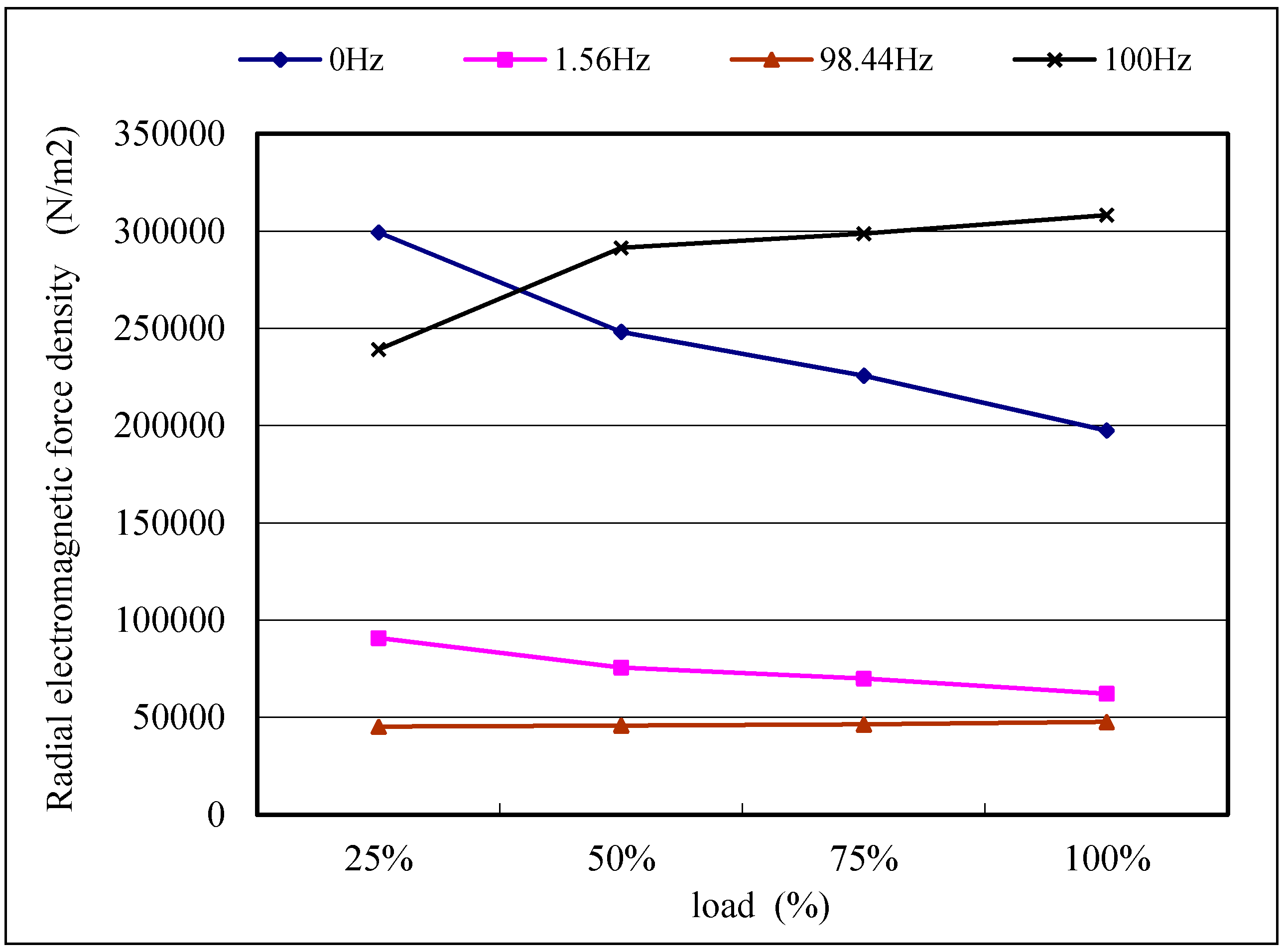
4.3. The Influence of Variable Field Currents and Loads
5. Electromagnetic Vibration Analysis
5.1. Principle of Harmonic Response Analysis
5.2. Geometry Modelling
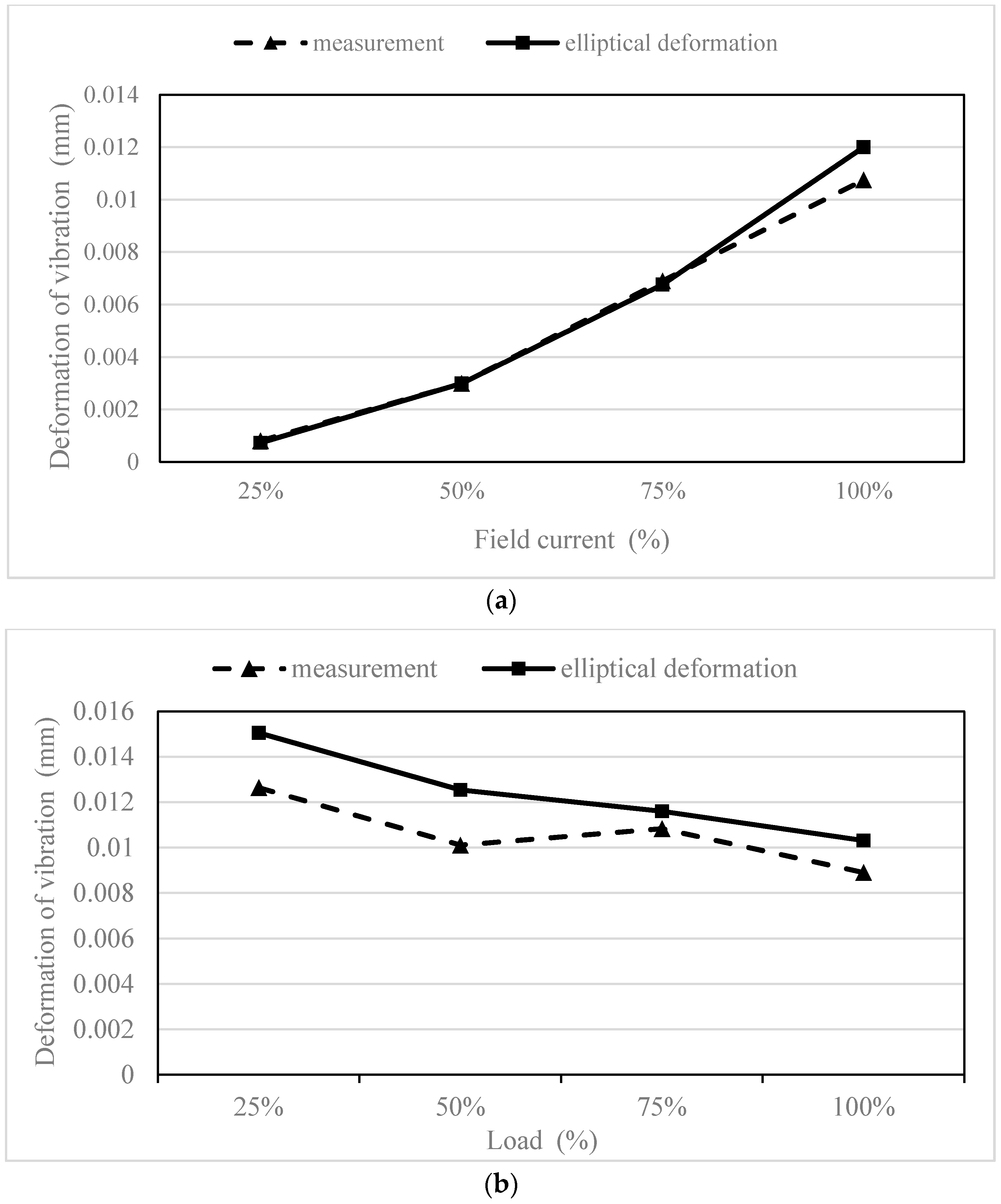
5.3. Electromagnetic Harmonic Response Vibration Coupled Analysis
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Pluk, K.J.W.; Jansen, J.W.; Lomonova, E.A. Three-Dimensional Modeling of Shielding of Magnetic Stray Fields based on Superposition of 2-D Models. IEEE Trans. Ind. Appl. 2015, 51, 3656–3665. [Google Scholar] [CrossRef]
- Sun, T.; Kim, J.M.; Lee, G.H. Effect of Pole and Slot Combination on Noise and Vibration in Permanent Magnet Synchronous Motor. IEEE Trans. Magn. 2011, 47, 1038–1041. [Google Scholar] [CrossRef]
- Koo, M.M.; Choi, J.Y.; Jeong, J.H. Characteristic Analysis of Permanent-Magnet Synchronous Generator with Slotless Stator Structure Considering Magnetic/Mechanical Air Gap Using Semi-3-D Analytical Method. IEEE Trans. Magn. 2015, 51. [Google Scholar] [CrossRef]
- Jia, H.; Wang, J.; Cheng, M. Mathematical Model of Radial Suspending Force for a New Stator-Permanent Magnet Bearingless Machine. IEEE Trans. Magn. 2015, 51. [Google Scholar] [CrossRef]
- Pennacchi, P.; Frosini, L. Dynamical behaviour of a three-phase generator due to unbalanced magnetic pull. IEE Proc. Electr. Power Appl. 2005, 152, 1389–1400. [Google Scholar] [CrossRef]
- Lundstrom, N.L.P.; Aidanpaa, J.O. Dynamic consequences of electromagnetic pull due to deviations in generator shape. J. Sound Vib. 2007, 301, 207–225. [Google Scholar] [CrossRef]
- Di, C.; Bao, X.; Wang, H. Modeling and Analysis of Unbalanced Magnetic Pull in Cage Induction Motors with Curved Dynamic Eccentricity. IEEE Trans. Magn. 2015, 51. [Google Scholar] [CrossRef]
- Naderi, P. Eccentricity Fault Diagnosis and Torque Ripple Analysis of a Four-pole Synchronous Reluctance Machine in Healthy and Faulty Conditions. Electr. Power Compon. Syst. 2015, 43, 1236–1245. [Google Scholar] [CrossRef]
- Dorrell, D.G. Calculation of unbalanced magnetic pull in small cage induction motors with skewed rotors and dynamic rotor eccentricity. IEEE Trans. Energy Convers. 1996, 11, 483–488. [Google Scholar] [CrossRef]
- Stoll, R.L. Simple computational model for calculating the unbalanced magnetic pull on a two-pole turbogenerator rotor due to eccentricity. IEE Proc. Electr. Power Appl. 1997, 144, 263–270. [Google Scholar] [CrossRef]
- Abdi, S.; Abdi, E.; McMahon, R. Optimization of Magnetic Circuit for Brushless Doubly Fed Machines. IEEE Trans. Energy Convers. 2015, 30, 1611–1619. [Google Scholar] [CrossRef]
- Wang, L.; Cheung, R.W.; Ma, Z. Finite-Element Analysis of Unbalanced Magnetic Pull in a Large Hydro-Generator under Practical Operations. IEEE Trans. Magn. 2008, 44, 1558–1561. [Google Scholar] [CrossRef]
- Abdi, S.; Abdi, E.; McMahon, R. A Study of Unbalanced Magnetic Pull in Brushless Doubly Fed Machines. IEEE Trans. Energy Convers. 2015, 30, 1218–1227. [Google Scholar] [CrossRef]
- Khalf, M.A.; Wamkeue, R.; Aguglia, D. Finite Element Approach for Performances Prediction of a Small. In Proceedings of the 2012 25th IEEE Canadian Conference on Electrical & Computer Engineering (CCECE), Montreal, QC, Canada, 29 April–2 May 2012; Volume 25. [Google Scholar]
- Edrington, C.S.; Kaluvagunta, D.C.; Joddar, J.; Fashimi, B. Investigation of electromagnetic force components in SRM under single and multiphase excitation. IEEE Trans. Ind. Appl. 2005, 41, 978–988. [Google Scholar] [CrossRef]
- Afsari, S.A.; Heydari, H.; Dianati, B. Cogging Torque Mitigation in Axial Flux Magnetic Gear System based on Skew Effects Using an Improved Quasi 3-D Analytical Method. IEEE Trans. Magn. 2015, 51. [Google Scholar] [CrossRef]
- Ishibashi, F.; Noda, S.; Mochizuki, M. Numerical simulation of electromagnetic vibration of small induction motors. IEE Proc. Electr. Power Appl. 1998, 145, 528–534. [Google Scholar] [CrossRef]
- Jung, A.W.; Kim, D.J.; Hong, J.P. Experimental Verification and Effects of Step Skewed Rotor Type IPMSM on Vibration and Noise. IEEE Trans. Magn. 2011, 47, 3661–3664. [Google Scholar] [CrossRef]





| Parameters (Units) | Values |
|---|---|
| Number of poles | 64 |
| Number of slots | 528 |
| Rated Speed (rpm) | 93.75 |
| Number of phases | 3 |
| Rated frequency (Hz) | 50 |
| Air gap thickness (mm) | 19 |
| Rated Power (MW) | 250 |
| Rated Line Voltage (kV) | 15.75 |
| Rated line current (A) | 10,182.6 |
| Rated Power Factor | 0.9 |
| Winding Connection | Wye |
| Coil Pitch | 7 |
| Parameters (Units) | Values | |
|---|---|---|
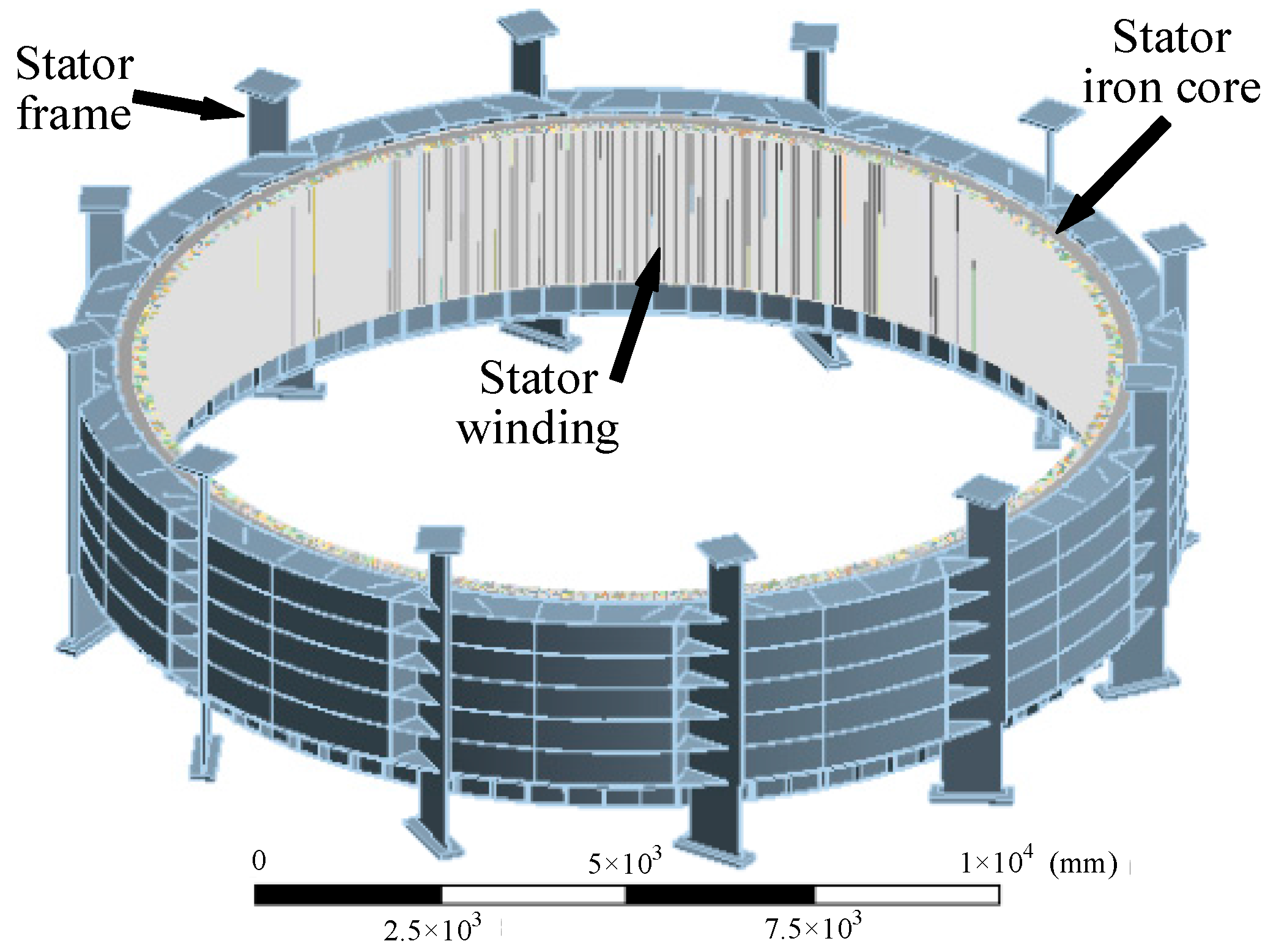
| Stator iron core | Internal diameter (mm) | 12,900 |
| Outside diameter (mm) | 13,700 | |
| Material | coiled silicon steel sheet | |
| Density (Kg/m3) | 7650 | |
| Young’s Modulus (Pa) | 2.05 × 1011 | |
| Poisson’s Ratio | 0.25 | |
| Stator frame | Internal diameter (mm) | 13,700 |
| Outside diameter (mm) | 14,900 | |
| Material | structural steel | |
| Density (Kg/m3) | 7850 | |
| Young’s Modulus (Pa) | 2.0 × 1011 | |
| Poisson’s Ratio | 0.30 | |
| Winding | Material | Copper Alloy |
| Density (Kg/m3) | 8300 | |
| Young’s Modulus (Pa) | 1.1 × 1011 | |
| Poisson’s Ratio | 0.34 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, R.; Li, C.; Peng, X.; Wei, W. Electromagnetic Vibration Simulation of a 250-MW Large Hydropower Generator with Rotor Eccentricity and Rotor Deformation. Energies 2017, 10, 2155. https://doi.org/10.3390/en10122155
Li R, Li C, Peng X, Wei W. Electromagnetic Vibration Simulation of a 250-MW Large Hydropower Generator with Rotor Eccentricity and Rotor Deformation. Energies. 2017; 10(12):2155. https://doi.org/10.3390/en10122155
Chicago/Turabian StyleLi, Ruhai, Chaoshun Li, Xuanlin Peng, and Wei Wei. 2017. "Electromagnetic Vibration Simulation of a 250-MW Large Hydropower Generator with Rotor Eccentricity and Rotor Deformation" Energies 10, no. 12: 2155. https://doi.org/10.3390/en10122155
APA StyleLi, R., Li, C., Peng, X., & Wei, W. (2017). Electromagnetic Vibration Simulation of a 250-MW Large Hydropower Generator with Rotor Eccentricity and Rotor Deformation. Energies, 10(12), 2155. https://doi.org/10.3390/en10122155




