Abstract
Forming solid solutions is one of the most effective strategies to suppress the thermal conductivity of thermoelectric materials. However, the accompanying increase in impurity ion scattering usually results in an undesirable loss in hall mobility, negatively impacting the electrical transport properties. In this work, a tellurium–selenium (Te-Se) solid solution with trace antimony (Sb) doping was synthesized via the high pressure and high temperature method. It was found that slight Se doping into the Te sites not only had no impact on the hall mobility and carrier concentration, but also enhanced the density-of-state effective mass of Sb0.003Te0.997, leading to an enhanced power factor near room temperature. Additionally, the presence of Se doping caused a significant reduction in the phonon thermal conductivity of Te due to fluctuations in the mass and strain field. The lowest phonon thermal conductivity was as low as ~0.42 Wm−1K−1 at 600 K for Sb0.003Se0.025Te0.972, which approached the theoretical minimum value of Te (~0.28 Wm−1K−1). The effects of Se doping suppressed thermal conductivity, while Sb doping enhanced the power factor, resulting in a larger ZT of ~0.94 at 600 K. Moreover, these findings demonstrate that Sb and Se doping can effectively modulate the electrical and thermal transport properties of Te in a synergistic manner, leading to a significant increase in the average ZT across a wide temperature range.
1. Introduction
The use of thermoelectric (TE) materials has been recognized as a viable and environmentally friendly solution to address the global energy crisis [1,2,3,4,5]. The efficacy of TE devices in converting heat into electricity is primarily influenced by the dimensionless figure of merit, denoted as ZT = S2T/ρκ, where S, ρ, and T represent the Seebeck coefficient, electrical resistivity, and absolute temperature, respectively. Additionally, κ is the total thermal conductivity, comprising both electronic (κe) and phonon (κph) thermal conductivities [6,7,8,9]. The optimization of ZT is constrained by the significant trade-off correlation observed between S, ρ, and κ as predicted by the Boltzmann transport theories and the Wiedemann–Franz relationship [10]. Consequently, achieving performance optimization becomes challenging due to the interdependence of these parameters [11,12,13]. In addition to possessing high ZT values, TE materials should also exhibit environmentally friendly characteristics and consist of non-toxic elements [14,15,16,17,18,19,20].
For an extended period, advanced TE materials have primarily consisted of compounds such as Bi2Te3 [21,22], PbTe [23], Mg2Si [24,25], half-Heuslers [26,27], and oxides [28]. Nevertheless, a significant drawback of these materials is their susceptibility to precipitation, segregation, and volatilization during the application process, making it challenging to achieve uniformity in the preparation process. Consequently, there is a pressing need to identify TE materials with simpler compositions. In 2014, elemental tellurium (Te) was found to exhibit promising characteristics as a promising TE material due to its relatively high band degeneracy (Nv = 4) near the valence band maximum (VBM), resulting in a large density-of-state (DOS) effective mass m*DOS and reaching a peak Seebeck coefficient (S) value of 450 μVK−1 at a hole concentration around 1017 cm−3, with an average value ranging from 200 to 250 μVK−1 at room temperature [29]. Recent studies have shown that the thermoelectric performance of the p-type Te-based system can be improved through the introduction of dopants such as arsenic (As) [30,31], antimony (Sb) [32], and bismuth (Bi) [33], which serve to modulate the carrier concentration in the Te substrate. The highest ZT value up to 1.0 at 650 K was successfully achieved in As-doped Te with a carrier density of 2.65 × 1019 cm−3 [30]. Previous studies have indicated that doping with non-equivalent elements is a fundamental and direct approach to enhance the thermoelectric performance of Te. However, the improvement in the electrical transport properties inevitably leads to a negative impact on the thermal performance. If the thermal conductivity can be mitigated while maintaining excellent electrical performance, the thermoelectric efficiency of Te can be significantly enhanced. According to our previous work, an extremal low thermal conductivity can be obtained in a Te-Se solid solution [34]. However, a large amount of Se alloying induces pronounced carrier scattering, thereby diminishing the hall mobility and adversely affecting the power factor. According to prior research, the application of high pressure has been found to induce abundant defects in the crystal structure, thereby facilitating the reduction in κph. Furthermore, the utilization of high-pressure technology has the potential to significantly decrease the preparation time from several days to a mere 30 min [35].
In this work, we investigated the effect of Sb doping and slight Se alloying on the thermoelectric properties of Te (Sb0.003SexTe0.997−x, x = 0–0.05). Due to the strong phonon scattering from the mass and strain fluctuations, a remarkably low phonon thermal conductivity of ~0.42 Wm−1K−1 was achieved at 600 K, which was in close proximity to the theoretical minimum. Furthermore, we found that the formation of Te-Se solid solutions did not significantly affect the electrical properties of Sb0.003Te0.997 when the Se doping content was below 3.75 at.%. The low thermal conductivity and optimized power factor led to a high ZT of ~0.94 at 600 K for Sb0.003Se0.025Te0.972. This work provides significant insights into the optimization of thermoelectric properties through strategic doping and alloying. The findings suggest that the careful modulation of the material composition can lead to a balance between the thermal and electrical properties, ultimately enhancing the thermoelectric performance. The results establish a promising foundation for the development of highly efficient thermoelectric materials.
2. Results
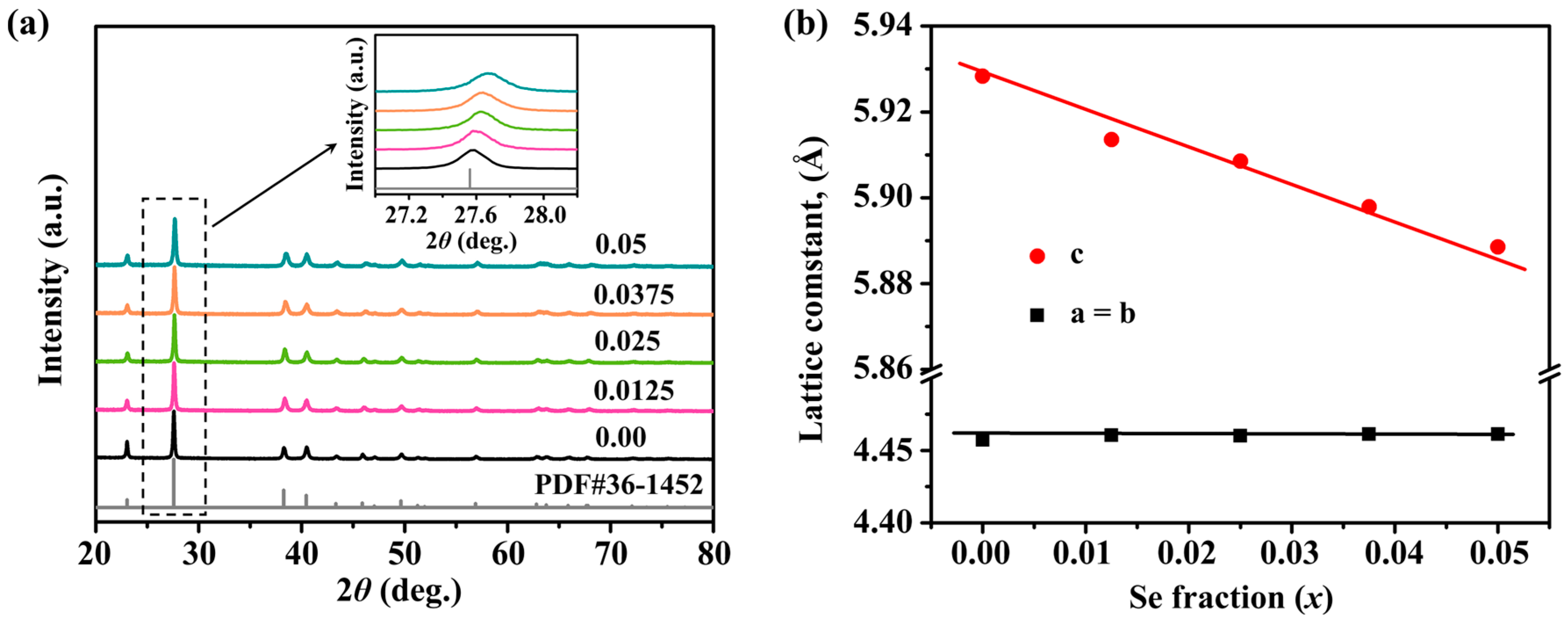
Figure 1a provides the X-ray Diffraction (XRD) patterns of the Sb0.003SexTe0.997−x (x = 0–0.05) samples. In these patterns, all peaks align perfectly with the trigonal structure of Te, conforming to the P3121 space group. Importantly, no discernible impurity phase is detected within the sensitivity limits of the measurements for all of the samples under consideration. This observation attests to the purity of the synthesized compounds, indicating that the synthesis process is well controlled and free of extraneous elements. The inset in Figure 1a illustrates a magnified view of the main peaks. Here, a gradual shift towards higher angles is seen with the increasing Se concentrations. This trend signifies the successful integration of Se into the Te matrix. It also points towards a contraction of the lattice, a consequence of the smaller atomic radius of Se (1.16 Å) compared to that of Te (1.36 Å). Figure 1b presents the lattice parameter (a) of the Sb0.003SexTe0.997−x samples, as determined via the Rietveld refinement method using the General Structure Analysis System (GSAS) program. As the Se content increases, a corresponding decrease in the lattice parameters is observed. This change is aligned with the shift of the peaks towards higher angles that were previously noted in the XRD patterns, and it is consistent with Vegard’s law, which states that the lattice parameter of an alloy will linearly change with the concentration in a solid solution. These results strongly suggest that Te is being substituted by Se, leading to the formation of a solid solution. This conclusion corroborates the existing literature [36] and underscores the potential of Se alloying for tailoring Te’s structural properties. The findings provide critical insights into the crystallographic changes induced by Se alloying and its role in tuning the material’s thermoelectric performance.
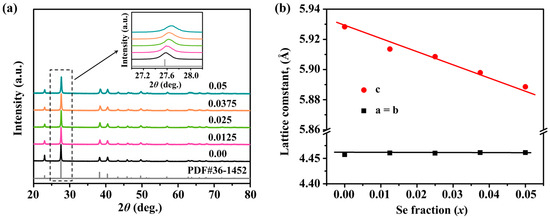
Figure 1.
(a) Powder XRD patterns (inset is a close-up of the main peaks); (b) lattice parameters of Sb0.003SexTe0.997−x (x = 0–0.05) samples.
Figure 2 presents a comprehensive visual depiction of the sectional morphology of the Sb0.003SexTe0.997−x compounds, where x varies as 0, 0.0125, 0.025, and 0.05. These compounds are synthesized by employing the high pressure and high temperature (HPHT) methodology, a technique renowned for its capability to generate materials with unique properties. In the figure, we can observe a clear pattern in the grain size of the synthesized samples. The Se-free sample, that is, when x = 0, exhibits a sizable grain structure with a measurement exceeding 20 µm, as shown in Figure 2a. This large grain size is indicative of the material’s characteristics in the absence of the Se alloy. Contrastingly, as we introduce the Se into the SbTe compound (increasing x value), a discernible shift in the grain structure is noted. The average grain size begins to decrease progressively, as visualized in Figure 2b–d. This trend is particularly interesting as it suggests a correlation between the Se concentration and the morphological characteristics of the synthesized compound. In a striking comparison, the Se-alloyed samples (where x > 0) present significantly smaller grain sizes, often less than 5 µm. This is a stark contrast to the Se-free samples and introduces a denser configuration of grains, leading to a considerable increase in the number of grain boundaries. This morphological modification, ushered by the introduction of the Se alloy, is expected to offer consequential impacts on the thermal properties of the resultant compound. The abundance of grain boundaries is theorized to lower the thermal conductivity (κ). This is because the increased grain boundaries serve as scattering centers for heat-carrying phonons, resulting in a reduction in the thermal conductivity. Hence, this research provides valuable insights into the structural and thermal properties of Sb0.003SexTe0.997−x compounds, highlighting the important role of the Se alloy in controlling these properties.

Figure 2.
SEM images of the fresh fracture surface of Sb0.003SexTe0.997−x with (a) x = 0, (b) x = 0.0125, (c) x = 0.025, and (d) x = 0.05. Inset in (a–d): grain size distribution corresponding to (a–d).
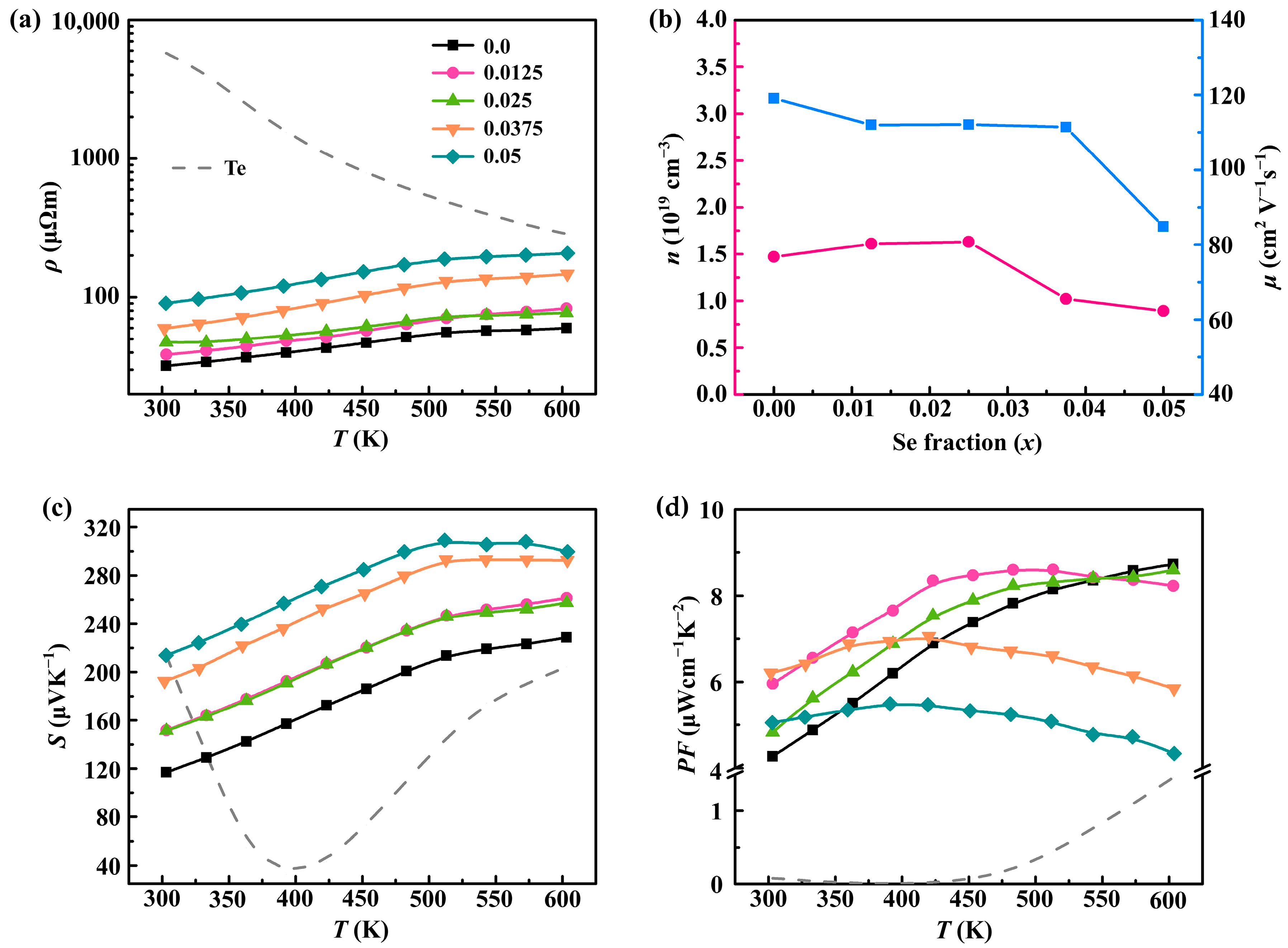
Figure 3 plots the electrical transport properties of pristine Te and Sb0.003SexTe0.997−x (x = 0–0.05) samples. As depicted in Figure 3a, the ρ of all samples increases with the increasing temperature (except for pristine Te), indicating degenerate semiconducting behavior. Furthermore, the ρ of Sb0.003SexTe0.997−x remains relatively constant for x ≤ 0.025, but experiences a sharp increase with the increasing Se content. Specifically, the ρ rises from ∼32 μΩm for Sb0.003Te0.997 to ∼89 μΩm for Sb0.003Se0.05Te0.947 at 300 K. Based on the Hall measurement results (Figure 3b), the observed increase in ρ at x > 0.025 can be primarily attributed to the decreased carrier concentration (nH) and mobility (μH). This decrease is caused by the introduction of Se alloying, which induces variations in the band structure and the carrier scattering [37]. Notably, the returned ρ of the Se-alloyed sample remains significantly lower than that of the pristine Te, as Sb is utilized to adjust the nH. Figure 3c displays the temperature dependence of the Seebeck coefficient (S) for the Sb0.003SexTe0.997−x samples. The results indicate that all samples synthesized by HTHP exhibit a positive Seebeck coefficient (S), suggesting a predominance of hole (p-type) conduction. Moreover, the addition of Se to the matrix significantly enhances the Seebeck coefficient (S) value, with the sample alloyed with 5 at.% Se displaying a Seebeck coefficient (S) value of 213.8 μVK−1 at 300 K compared to 116.9 μVK−1 for the Sb0.003Te0.997 sample. However, for samples with x > 0.025, the Seebeck coefficient (S) value decreases with the increasing temperature beyond 500 K, indicating the occurrence of bipolar diffusion. The temperature dependence of the power factor (PF) is depicted in Figure 3d. It can be observed that the PF does not experience significant deterioration when the Se content remains below 2.5 at.%. Although the PF of samples with x > 0.025 deteriorate compared to the pristine Te0.997Sb0.003, it is still noticeably higher than that of pristine Te.
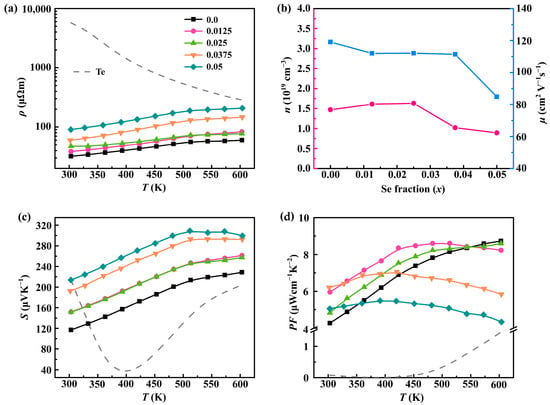
Figure 3.
Temperature dependence of electrical transport properties: (a) electrical resistivity; (b) carrier concentration (pink line) and mobility (blue line); (c) Seebeck coefficient (S); and (d) power factor of both pristine Te and Sb0.003SexTe0.997−x (x = 0–0.05) samples.
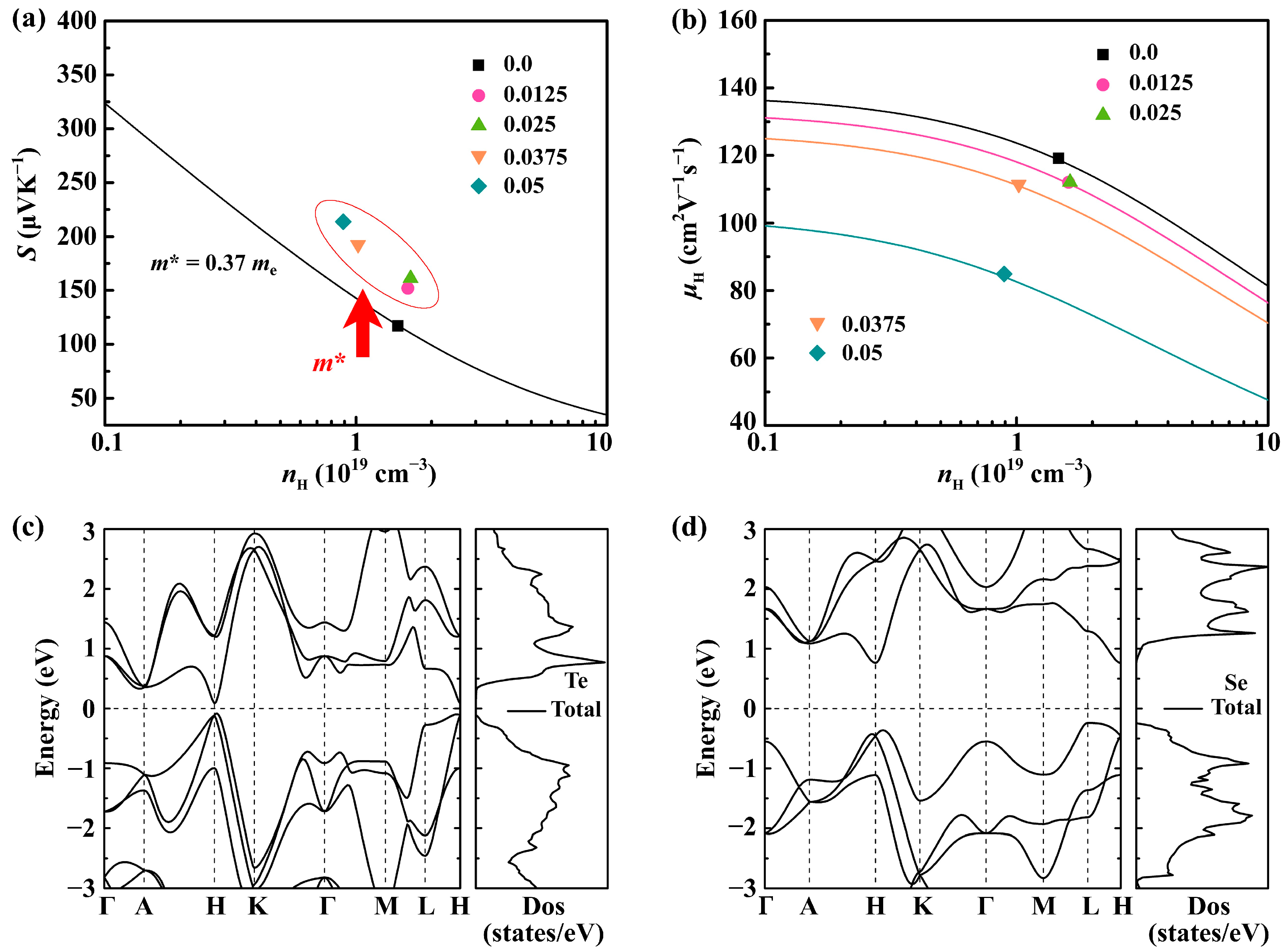
To further shed light on the electrical transport mechanism in the Sb0.003SexTe0.997−x (x = 0–0.05) samples, we employed the single parabolic band (SPB) model [38] to estimate the m*DOS, as depicted in Figure 4a. The m*DOS of the Se-doped samples exhibits a slight increase, leading to an effective enhancement in the Seebeck coefficient. This also means that the band structure was altered after Se doping. However, it is worth noting that the substantially increased m*DOS in the highly doped sample (x~0.05) also hinders the carrier transport, as shown in Figure 4b. To elucidate the underlying mechanisms, we performed comprehensive electronic band structure calculations for pure Te and Se, as depicted in Figure 4c,d. While both materials exhibit generally similar band structures due to their comparable valence electron configurations, notable distinctions arise in the vicinity of the Valence Band Maximum (VBM), which plays a crucial role in determining the thermoelectric performance. Specifically, the VBM of Te is located near the H point and is characterized by a smaller effective mass. Conversely, the VBM of Se is situated at the L point and exhibits a larger effective mass. This higher effective mass contributes to a steeper density of states, thereby positively impacting the Seebeck coefficient. These computational results indicate that Se doping is advantageous for enhancing the effective mass, aligning well with our initial experimental observations.
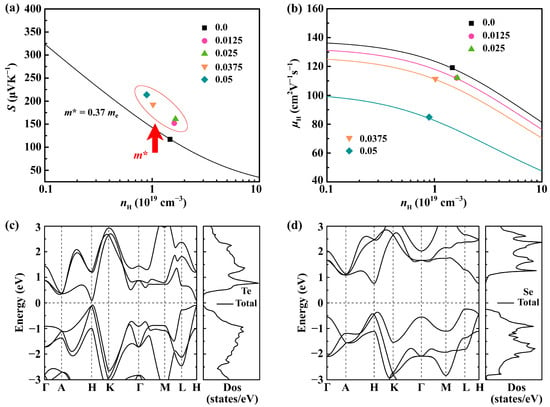
Figure 4.
The relationship of (a) Seebeck coefficient (S); (b) Hall carrier mobility with carrier concentration of Sb0.003SexTe0.997−x (x = 0–0.05) samples; and the calculation results of electronic band structure for (c) Te and (d) Se, respectively.
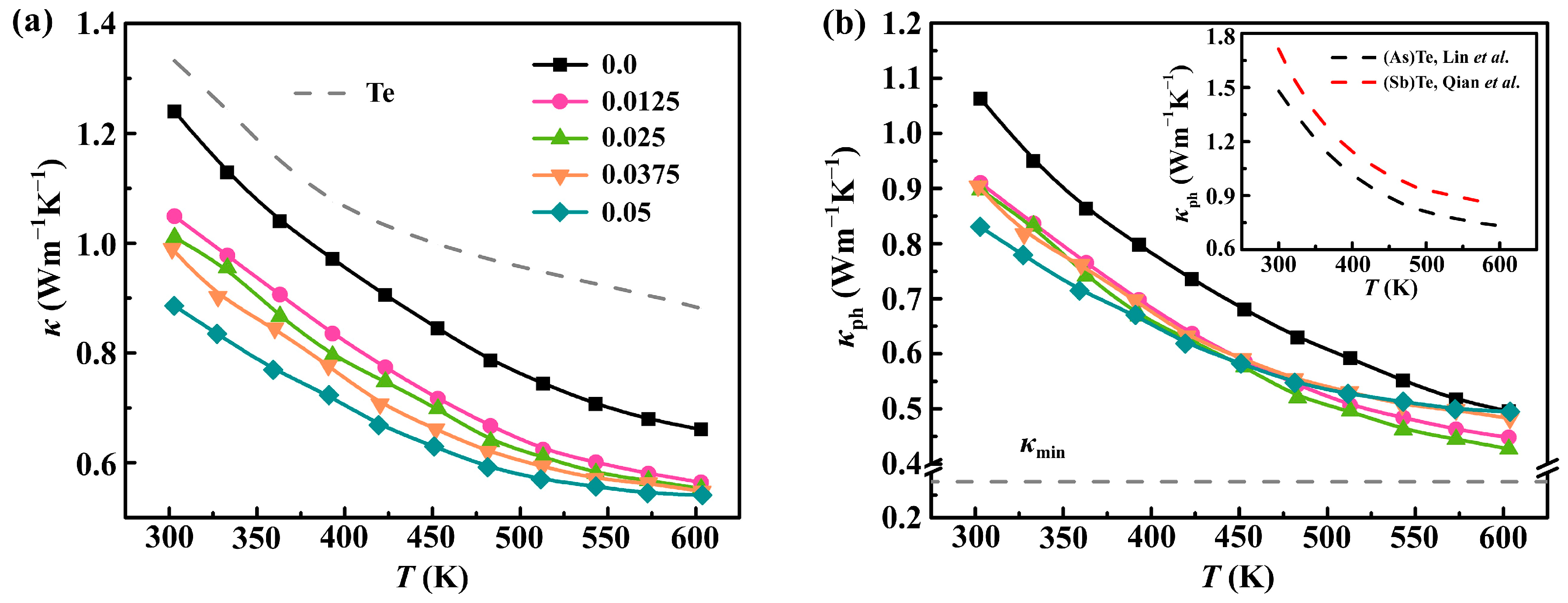
As we know, achieving an extremely lower κ value and understanding the underlying phonon transport mechanism are extremely significant to the improvement of ZT for thermoelectric materials. Figure 5a plots the composition-dependent κ as a function of the temperature (T), revealing a nearly identical temperature dependence. The κ values exhibit a pronounced decrease with the increasing temperature, following the T−1 trend, suggesting the prevalence of phonon scattering through the Umklapp process. The κ decreases from 1.33 Wm−1K−1 for the pristine Te to 0.83 Wm−1K−1 for the sample alloyed with 5 at.% Se and doped with 0.3 at.% Sb. This represents reductions of approximately 22% and 38% compared to the Se-free sample (Sb0.003Te0.997) and pristine Te at 300 K, respectively. It is well known that κ is composed of two components, κe and κph. The value of κe can be determined using the Wiedemann–Franz law, κe = LT/ρ, where the Lorenz number (L) is estimated using the equation, L = 1.5 + exp[−|S|/116], in this study [39]. The κph is obtained by subtracting the electronic component from κ as shown in Figure 5b. Obviously, the κ and κph show a similar trend with Se doping and the increasing temperature. A significantly suppressed κph, reaching ~0.42 Wm−1K−1 at 600 K, is observed in the Sb0.003Se0.025Te0.9753 sample, approaching the amorphous limit of ~0.28 Wm−1K−1 calculated via Cahill’s model [40]. This reduction in κph is nearly 50% lower than that of pristine Te at 600 K. Therefore, the decrease in κ is strongly correlated with the decrease in κph for Sb0.003SexTe0.997−x. Importantly, the κph value of this work is considerably lower compared to that of Te(As) [30] and Te(Sb) [41] prepared using the conventional melt quench technique. It is worth noting that all the TE properties were assessed at an ambient pressure, indicating that the characteristics of the samples under a high pressure can be retained at an ambient pressure. This demonstrates that the HTHP-prepared samples possess residual stress, which aids in capturing the character, including the low conductance activation energy of the TE materials. The effect of a high pressure on the TE performance in this work was proven.
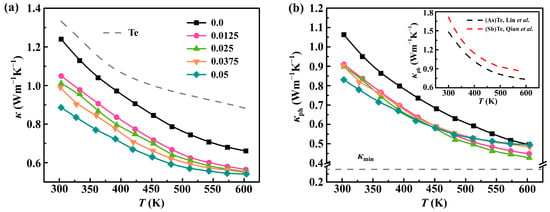
Figure 5.
Temperature dependence of thermal transport properties: (a) total thermal conductivity; (b) phonon thermal conductivity for both pristine Te and Sb0.003SexTe0.997−x (x = 0–0.05) samples, inset in (b) reference data of Te-As [30] and Te-Sb [41] for comparison.
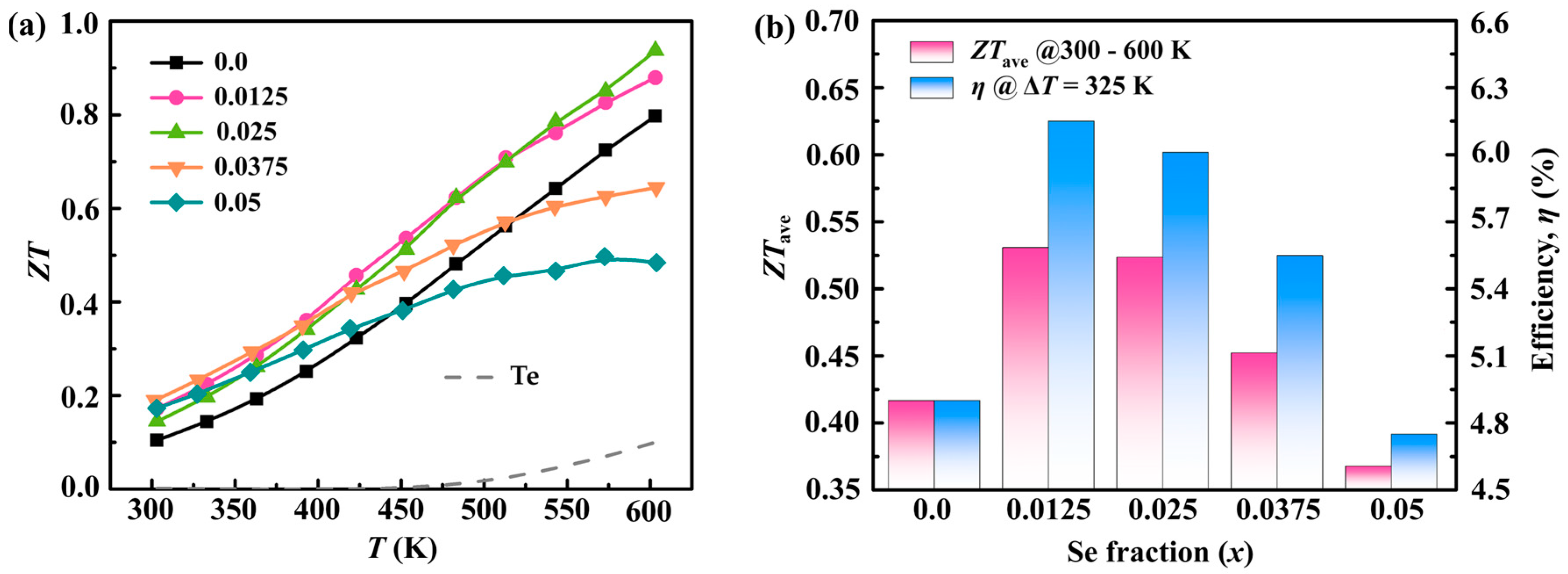
Figure 6 delves into the thermoelectric performance of pristine Te and the Sb0.003SexTe0.997−x (x = 0–0.05) samples, providing a detailed analysis of the key metrics related to thermoelectric efficiency. Figure 6a specifically exhibits the temperature dependence of the dimensionless thermoelectric figure of merit (ZT) for the aforementioned samples. In the field of thermoelectrics, ZT is a crucial metric that combines both the electrical and thermal properties of a material. It is noteworthy that the peak ZT value achieved is approximately 0.94 at a temperature of 600 K, as shown by the Sb0.003Se0.025Te0.9753 sample. This impressive performance can be attributed to the significant reduction in the thermal conductivity (κ), coupled with a relatively stationary power factor (PF), which suggests a commendable balance between electrical and thermal properties. Moving on to Figure 6b, the average ZT values (ZTave) of the Sb0.003SexTe0.997−x (x = 0–0.05) samples, in the temperature range of 300 to 600 K, are summarized. The optimization of the density of states effective mass (m*DOS) and a decrease in the phonon thermal conductivity (κph) contribute to the peak average ZT (ZTave) of approximately 0.53 for Sb0.003Se0.0125Te0.9845. It is paramount to achieve a high ZTave across an extensive temperature range to enhance thermoelectric conversion efficiency, a crucial factor in thermoelectric applications. In pursuit of this goal, calculations were carried out to ascertain the thermoelectric power generation efficiency of p-type legs composed of Sb0.003SexTe0.997−x (x = 0–0.05) samples [42]. As per the conditions set for these calculations, the temperatures of the hot and cold sides of the legs were maintained at a steady 273/600 K, and neither thermal nor electrical losses were factored in. The outcomes of these calculations indicated a significant enhancement in efficiency, with an approximate 26% increase for the x = 0.0125 sample in comparison to the Se-free sample. These findings underscore the potential of defect engineering in achieving an optimal thermoelectric performance. The results highlight the delicate balance between carrier transport and phonon scattering, emphasizing the importance of the careful modulation of material defects to optimize these interactions and enhance the overall thermoelectric performance.
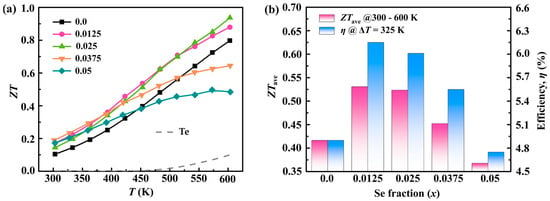
Figure 6.
(a) Temperature-dependent ZT values; (b) ZTave values within the temperature range of 300–600 K and power generation efficiency for the pristine Te and Sb0.003SexTe0.997−x (x = 0–0.05) samples.
3. Experimental Procedure
3.1. Sample Preparation
The preparation of the samples involved a precise and controlled process to ensure the synthesis of the target compounds, namely pristine Te and Sb0.003SexTe0.997−x, where x = 0, 0.0125, 0.025, 0.0375, and 0.05. High-purity materials were used as the starting ingredients: Te (99.99%), Sb (99.999%), and Se (99.95%). The proportions of these elements were carefully measured to align with the stoichiometric requirements of the targeted compounds. The first step in the preparation process was to thoroughly mix these elemental powders. This task was accomplished using a planetary ball mill, a device renowned for its ability to achieve highly homogeneous mixtures. To protect the materials from unwanted reactions with atmospheric gases, the milling process was conducted under an inert Ar gas atmosphere. Absolute alcohol was also employed to facilitate the milling process. Following the milling, the resultant mixture of Te, Sb, and Se elements was dried and then transformed into a cylindrical shape, preparing it for the subsequent high-pressure synthesis process. This shaping process helps to achieve uniform pressure and temperature conditions during the synthesis. The cylindrical samples were then subjected to a high-pressure synthesis process using a cubic anvil high-pressure apparatus (ZN-460, China). This process involved conditions of 4 GPa of pressure and a temperature of 1000 K, maintained for a duration of 30 min. After synthesis, the samples were rapidly quenched to room temperature within a span of 2 min to ensure a sharp transition and to preserve the high-temperature phase. The obtained ingots were then slowly heated to a temperature of 600 K over a span of 5 h, and then held at this temperature for an additional hour. This slow heating and soaking process helps to relieve any internal stresses in the material and to homogenize the sample. The ingots were then cut and polished, preparing them for subsequent structural and property characterizations. This meticulous preparation process ensures the synthesis of highly pure and structurally consistent samples, thereby providing a reliable basis for the subsequent analysis and evaluation of their thermoelectric properties.
3.2. Physical Measurements
To understand the characteristics of the synthesized materials, a series of comprehensive physical measurements were conducted. The phase structure of all samples was discerned through X-ray diffraction (XRD) analysis, employing Cu-Kα radiation (λ = 1.5406 Å) on a Rigaku SmartLabSE system, a high-performance XRD platform. This technique allows for the determination of crystallographic structures and the identification of any impurity phases. Microstructure morphology, providing insights into the grain size and distribution, was investigated using Scanning Electron Microscopy (SEM) on a Carl Zeiss Sigma 500 VP. SEM provides high-resolution images that reveal the surface features and structural details of the samples. The Hall effect, which provides valuable information on the type and concentration of charge carriers, was measured using the van der Pauw method facilitated by a Lake Shore 8400 Hall setup. The Seebeck coefficient (S), a measure of the thermoelectric power, and electrical resistivity(ρ), an indicator of charge transport efficiency, were simultaneously measured in the temperature range of 300 to 600 K. The measurements were carried out using the CTA-3S apparatus (Cryoall, China) with a temperature increment of 30 K and a heating rate of 5 K min−1. The thermal conductivity (κ), a critical parameter dictating the heat transport property of a material, was computed using the equation κ = DCPρ. In this equation, D refers to the thermal diffusivity coefficient obtained through the laser flash method on a Netzsch LFA457 instrument. The parameter ρ denotes the pellet density measured via the Archimedes method. CP signifies the specific heat capacity, which was estimated based on the Dulong–Petit law, under the assumption that it is not significantly influenced by temperature. The uncertainties associated with these measurements were within acceptable limits: ±5–7% for κ and ρ, and ±5% for S. These measurements provide a holistic understanding of the synthesized materials’ physical properties, contributing to our understanding of their thermoelectric performances.
3.3. Computational Method
The computational investigations into the properties of Te and Se were carried out using the projector-augmented wave (PAW) method, a highly revered technique for efficient and accurate quantum mechanical calculations. This method was implemented via the Vienna Ab initio Simulation Package (VASP), a widely recognized computational toolset for atomic-scale materials modeling [43]. In our computations, the exchange-correlation potential was treated using the Perdew–Burke–Ernzerhof (PBE) functional [44]. This functional, which is based on the generalized gradient approximation (GGA), is popular for its reliability and performance in predicting the properties of a wide array of materials. Further, we established an energy cutoff for the plane-wave basis set at 350 eV. This relatively high cutoff energy ensures the precision of the simulations by incorporating a sufficient number of plane waves in the calculations. To secure the convergence of our simulations, we required the total energy differences between consecutive steps to be less than 1 × 10−6 eV. This strict criterion ensures a high level of accuracy in the computation of the electronic structure. For the geometry optimizations, we employed a Monkhorst–Pack uniform k-point spacing of 0.15 Å−1. This parameter is crucial to adequately sample the Brillouin zone, and hence, to accurately determine the electronic properties of the material. Furthermore, the relaxation of the atomic positions was carried out until the Hellmann–Feynman force on each atom was less than 0.01 eV Å−1. This stringent force criterion ensures that the final atomic positions are at or very near their minimum-energy configurations. In conclusion, the computational methodology adopted in this study is designed to achieve a fine balance between the computational efficiency and the precise calculation of material properties. The results derived from these calculations provide valuable insights into the behaviors of Te and Se at the atomic level, helping to better understand the observed experimental results.
4. Conclusions
In this study, we successfully synthesized a series of samples comprising pristine Te and Sb0.003SexTe0.997−x (x = 0–0.05) using HPHT technology. Our aim was to enhance the TE properties of elemental Te through strategic Sb doping and Se alloying, and the results demonstrate the success of these techniques. The Sb doping proved instrumental in providing Te with superior electrical transport performance. The advantageous impact of Sb doping on the electrical properties lays the foundation for the high thermoelectric performance of these compounds. Meanwhile, the introduction of a modest amount of Se into the Te sites had a marked effect in suppressing the thermal conductivity of Sb0.003Te0.997. Given the disparities in mass and atomic radius between Se and Te, an extremely low phonon thermal conductivity of approximately 0.42 Wm−1K−1 was achieved at 600 K for the Sb0.003Se0.025Te0.972 composition. Interestingly, this significant reduction in thermal conductivity did not cause a detrimental effect on the carrier concentration and Hall mobility. This finding suggests that the slight Se alloying does not impinge on the power factor of the pristine Sb0.003Te0.997, preserving its exceptional electrical performance despite the addition of Se. Given the combination of reduced phonon thermal conductivity and a consistent power factor, the thermoelectric figure of merit (ZT) reaches a maximum value of approximately 0.94 at 600 K in the case of Sb0.003Se0.025Te0.972. This represents an appreciable increment of about 19% over the ZT value for Sb0.003Te0.997, highlighting the advantage of Se alloying in enhancing thermoelectric performance. In brief, our work demonstrates the viability of Sb doping and Se alloying as effective strategies for optimizing the thermoelectric properties of Te. The findings of this study pave the way for further investigations into the fine-tuning of material properties through doping and alloying, with potential implications for the design of high-performance thermoelectric materials.
Author Contributions
Conceptualization, T.S. and J.J.; investigation, M.Y. (Manman Yang) resources, T.S. and J.J.; methodology, M.Y. (Manman Yang) and M.Y. (Mengxiang Yang); data curation, T.S. and J.J.; software, Y.C. and Y.S.; writing—original draft, Y.L. and M.Y. (Manman Yang); writing—review and editing, T.S. and J.J.; funding acquisition, T.S. and J.J. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Natural Science Foundation of China (12364006), the Guangxi Natural Science Foundation (AD20297014), the Anhui Province Higher Education Innovation Team: Key Technologies and Equipment Innovation Team for Clean Energy (2023AH010055), and the Doctor Research Startup Foundation of Suzhou University (2022 B-SK005).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
Sample Availability
Not applicable.
References
- He, R.; Zhu, H.; Sun, J.; Mao, J.; Reith, H.; Chen, S.; Schierning, G.; Nielsch, K.; Ren, Z. Improved thermoelectric performance of n-type half-heusler MCo1−xNixSb (M = Hf, Zr). Mater. Today Phys. 2017, 1, 24–30. [Google Scholar] [CrossRef]
- Sun, J.; Shuai, J.; Ren, Z.; Singh, D. Computational modelling of the thermoelectric properties of p-type zintl compound CaMg2Bi2. Mater. Today Phys. 2017, 2, 40–45. [Google Scholar] [CrossRef]
- He, J.; Terry, M.T. Advances in thermoelectric materials research: Looking back and moving forward. Science 2017, 357, eaak9997. [Google Scholar] [CrossRef]
- Olabi, A.G.; Elsaid, K.; Sayed, E.T.; Mahmoud, M.S.; Wilberforce, T.; Hassiba, R.J.; Abdelkareem, M.A. Application of nanofluids for enhanced waste heat recovery: A review. Nano Energy 2021, 84, 105871. [Google Scholar] [CrossRef]
- Luo, D.; Sun, Z.; Wang, R. Performance investigation of a thermoelectric generator system applied in automobile exhaust waste heat recovery. Energy 2022, 238, 121816. [Google Scholar] [CrossRef]
- Sootsman, J.R.; Chung, D.Y.; Kanatzidis, M.G. New and old concepts in thermoelectric materials. Angew. Chem. Int. Ed. 2009, 48, 8616–8639. [Google Scholar] [CrossRef]
- Kanatzidis, M.G. Nanostructured thermoelectrics: The new paradigm?†. Chem. Mater. 2010, 22, 648–659. [Google Scholar] [CrossRef]
- Yang, M.; Li, X.; Duan, S.; Zhang, X.; Sun, H.; Chen, X.; Su, T.; Gu, L.; Liu, X. Superior Thermoelectric performance of black phosphorus in elemental tellurium. Adv. Energy Mater. 2022, 12, 2203014. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Yang, T.; Ma, Z.; Zhang, H.; Li, H.; Xia, A. Alloying engineering for thermoelectric performance enhancement in p-type skutterudites with synergistic carrier concentration optimization and thermal conductivity reduction. J. Adv. Ceram. 2023, 12, 539–552. [Google Scholar] [CrossRef]
- Fan, J.; Schnelle, W.; Antonyshyn, I.; Veremchuk, I.; Carrillo-Cabrera, W.; Shi, X.; Grin, Y.; Chen, L.-D. Structural evolvement and thermoelectric properties of Cu3−xSnxSe3 compounds with diamond-like crystal structure. Dalton Trans. 2014, 43, 16788–16794. [Google Scholar] [CrossRef]
- Liu, Z.; Gao, W.; Guo, F.; Cai, W.; Zhang, Q.; Sui, J. Challenges for thermoelectric power generation: From a material perspective. Mater. Lab. 2022, 1, 220003. [Google Scholar] [CrossRef]
- Pei, Y.; Zheng, L.; Li, W.; Lin, S.; Chen, Z.; Wang, Y.; Xu, X.; Yu, H.; Chen, Y.; Ge, B. Interstitial point defect scattering contributing to high thermoelectric performance in SnTe. Adv. Electron.Mater. 2016, 2, 1600019. [Google Scholar] [CrossRef]
- Qin, B.; Wang, D.; Zhao, L.-D. Slowing down the heat in thermoelectrics. InfoMat 2021, 3, 755–789. [Google Scholar] [CrossRef]
- Zhang, Q.; Liao, B.; Lan, Y.; Lukas, K.; Liu, W.; Esfarjani, K.; Opeil, C.; Broido, D.; Chen, G.; Ren, Z. High thermoelectric performance by resonant dopant indium in nanostructured SnTe. Proc. Natl. Acad. Sci. USA 2013, 110, 13261–13266. [Google Scholar] [CrossRef]
- Tan, G.; Zhao, L.; Shi, F.; Doak, J.W.; Lo, S.-H.; Sun, H.; Wolverton, C.; Dravid, V.P.; Uher, C.; Kanatzidis, M.G. High thermoelectric performance of p-type SnTe via a synergistic band engineering and nanostructuring approach. J. Am. Chem. Soc. 2014, 13, 7006–7017. [Google Scholar] [CrossRef] [PubMed]
- Nolas, G.S.; Cohn, J.L.; Slack, G.A.; Schujman, S.B. Semiconducting Ge clathrates: Promising candidates for thermoelectric applications. Appl. Phys. Lett. 1998, 73, 178–180. [Google Scholar] [CrossRef]
- Liu, W.; Yin, K.; Su, X.; Li, H.; Yan, Y.; Tang, X.; Uher, C. Enhanced hole concentration through Ga doping and excess of Mg and thermoelectric properties of p-type Mg2(1+z)(Si0.3Sn0.7)1−yGay. Intermetallics 2013, 32, 352–361. [Google Scholar] [CrossRef]
- Fulkerson, W.; Moore, J.P.; Williams, R.K.; Graves, R.S.; McElroy, D.L. Thermal conductivity, electrical resistivity, and Seebeck coefficient of silicon from 100 to 1300 K. Phys. Rev. 1968, 167, 765–782. [Google Scholar] [CrossRef]
- Dismukes, J.P.; Ekstrom, L.; Steigmeier, E.F.; Kudman, I.; Beers, D.S. Thermal and electrical properties of heavily doped Ge-Si alloys up to 1300 K. J. Appl. Phys. 1964, 35, 2899–2907. [Google Scholar] [CrossRef]
- Yim, W.M.; Amith, A. Bi-Sb alloys for magneto-thermoelectric and thermomagnetic cooling. Solid State Electron. 1972, 15, 1141–1165. [Google Scholar] [CrossRef]
- Zhu, B.; Liu, X.; Wang, Q.; Qiu, Y.; Shu, Z.; Guo, Z.; Tong, Y.; Cui, J.; Gu, M.; He, J. Realizing record high performance in n-type Bi2Te3-based thermoelectric materials. Energy Environ. Sci. 2020, 13, 2106–2114. [Google Scholar] [CrossRef]
- Meroz, O.; Ben-Ayoun, D.; Beeri, O.; Gelbstein, Y. Development of Bi2Te2.4Se0.6 alloy for thermoelectric power generation applications. J. Alloys Compd. 2016, 679, 196–201. [Google Scholar] [CrossRef]
- Ananya, B.; Shenoy, U.S.; Anand, S.; Waghmare, U.V.; Kanishka, B. Mg alloying in SnTe facilitates valence band convergence and optimizes thermoelectric properties. Chem. Mater. 2015, 27, 581–587. [Google Scholar]
- Kim, C.E.; Soon, A.; Stampfl, C. Unraveling the origins of conduction band valley degeneracies in Mg2Si1−xSnx thermoelectrics. Phys. Chem. Chem. Phys. 2016, 18, 939–946. [Google Scholar] [CrossRef] [PubMed]
- Lai, H.; Peng, Y.; Wang, M.; Shi, R.; Chen, J.; Liu, C.; Wang, Y.; Miao, L.; Wei, H. Thermoelectric enhancement of p-type Si80Ge20 alloy via co-compositing of dual oxides: Respective regulation for power factor and thermal conductivity by β-Ga2O3 and SiO2 aerogel powders. J. Adv. Ceram. 2023, 012, 228–241. [Google Scholar] [CrossRef]
- Fu, C.; Zhu, T.; Pei, Y.; Xie, H.; Wang, H.; Snyder, G.J.; Liu, Y.; Liu, Y.; Zhao, X. High band degeneracy contributes to high thermoelectric performance in p-type half-heusler compounds. Adv. Energy Mater. 2014, 4, 1400600. [Google Scholar] [CrossRef]
- Rani, B.; Wani, A.F.; Sharopov, U.B.; Patra, L.; Singh, J.; Ali, A.M.; Abd El-Rehim, A.F.; Khandy, S.A.; Dhiman, S.; Kaur, K. Effective mass-related thermoelectric properties of PdXSn (X = Zr, Hf) half heuslers. Molecules 2022, 27, 6567. [Google Scholar] [CrossRef]
- Liu, Y.; Zhi, J.; Li, W.; Yang, Q.; Zhang, L. Oxide materials for thermoelectric conversion. Molecules 2023, 28, 5894. [Google Scholar] [CrossRef]
- Peng, H.; Kioussis, N.; Snyder, G.J. Elemental tellurium as a chiral p-type thermoelectric material. Phys. Rev. B 2014, 89, 195206. [Google Scholar] [CrossRef]
- Lin, S.; Li, W.; Chen, Z.; Shen, J.; Ge, B.; Pei, Y. Tellurium as a high-performance elemental thermoelectric. Nat. Commun. 2016, 7, 10287. [Google Scholar] [CrossRef]
- Yang, M.; Su, T.; Zhu, H.; Li, S.; Hu, M.; Hu, Q.; Ma, H.; Jia, X. Thermoelectric performance of Te doped with As and alloyed with Se. J. Mater. Sci. 2018, 53, 11524–11533. [Google Scholar] [CrossRef]
- Lin, S.; Li, W.; Zhang, X.; Li, J.; Chen, Z.; Pei, Y. Sb induces both doping and precipitation for improving the thermoelectric performance of elemental Te. Inorg. Chem. Front. 2017, 4, 1066–1072. [Google Scholar] [CrossRef]
- Yang, M.; Su, T.; Zhou, D.; Zhu, H.; Li, S.; Hu, M.; Hu, Q.; Ma, H.; Jia, X. High-pressure synthesis and thermoelectric performance of tellurium doped with bismuth. J. Mater. Sci. 2017, 52, 10526–10532. [Google Scholar] [CrossRef]
- Yang, M.; Zhu, H.; Yi, W.; Li, S.; Hu, M.; Hu, Q.; Du, B.; Liu, X.; Su, T. Electrical transport and thermoelectric properties of Te-Se solid solutions. Phys. Lett. A 2019, 383, 2615–2620. [Google Scholar] [CrossRef]
- Yang, M.; Su, T.; Li, S.; Li, S.; Hu, M.; Liu, X. Facile synthesis and high thermoelectric performance of tellurium with antimony doping. J. Alloys Compd. 2021, 887, 161342. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, Q.; Liu, F.; Fang, T.; Zhu, T.; Zhao, X. Scattering mechanisms and compositional optimization of high performance elemental Te as a thermoelectric material. Adv. Electron Mater. 2020, 6, 202000038. [Google Scholar] [CrossRef]
- Saparamadu, U.; Li, C.; He, R.; Zhu, H.; Ren, Z.; Mao, J.; Song, S.; Sun, J.; Chen, S.; Zhang, Q.; et al. Improved thermoelectric performance of Tellurium by alloying with a small concentration of selenium to decrease lattice thermal conductivity. ACS Appl. Mater. Interfaces 2019, 11, 511–516. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, X.; Guo, M.; Li, J.; Hu, J.; Cai, S.; Cai, W.; Zhang, Y.; Sui, J. Restructured single parabolic band model for quick analysis in thermoelectricity. npj Comput. Mater. 2021, 7, 116. [Google Scholar] [CrossRef]
- Kim, H.S.; Gibbs, Z.M.; Tang, Y.; Wang, H.; Snyder, G.J. Characterization of lorenz number with Seebeck coefficient measurement. APL Mater. 2015, 3, 041506. [Google Scholar] [CrossRef]
- Cahill, D.G.; Pohl, R.O. Heat flow and lattice vibrations in glasses. Solid State Commun. 1989, 70, 927–930. [Google Scholar] [CrossRef]
- Qian, X.; Xiao, Y.; Zheng, L.; Qin, B.; Zhou, Y.; Pei, Y.; Yuan, B.; Gong, S.; Zhao, L.-D. Effective dopants in p-type elementary Te thermoelectrics. RSC Adv. 2017, 7, 17682–17688. [Google Scholar] [CrossRef]
- Nandihalli, N.; Wijethunge, D.; Kim, K.; Kim, J.; Gayner, C. High efficient nanostructured PbSe0.5Te0.5 exhibiting broad figure-of-merit plateau. J. Alloys Compd. 2019, 785, 862–870. [Google Scholar] [CrossRef]
- Kresse, G.G.; Furthmüller, J.J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1997, 78, 3865. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).