Abstract
An approach for the cryptographic security enhancement of encryption is proposed and analyzed. The enhancement is based on the employment of a coding scheme and degradation of the ciphertext. From the perspective of the legitimate parties that share a secret key, the degradation appears as a transmission of the ciphertext through a binary erasure channel. On the other hand, from the perspective of an attacker the degradation appears as a transmission of the ciphertext over a binary deletion channel. Cryptographic security enhancement is analyzed based on the capacity of the related binary deletion channel. An illustrative implemementation framework is pointed out.
1. Introduction
Enhancing the security of certain cryptographic primitives by employing randomness has been employed in a number of reported designs (see, e.g., [1,2]), as well as in the context of wire-tap coding. Following these approaches, two main directions have appeared. One approach is based on the employment of a cryptograhic key control of error correction encoding and decoding, given, for example, in [3,4,5,6,7]. The other approach is the employment of error-correction coding and noisy channels for cryptographic security enhancement of a given encryption scheme: This approach has been reported, for example, in [8,9,10,11,12,13,14,15].
Motivation. The employment of coding and noisy channel based techniques for the security enhancement of given encryption appears as an important topic. In particular, this approach could significantly increase the cryptographic security margin of a lightweight encryption scheme. On the other hand, this approach also implies additional complexity overhead. Accordingly, it appears as an interesting issue to design security enhancement with a number of parameters that provide control over desired security enhancement and required implementation and execution overheads of the encryption. The main motivation for this paper was addressing the security enhancement of a given encryption that provides the opportunity for trade-off between the security margin increasing and the required overhead.
Summary of the Results. This paper proposes a novel approach for the security enhancement of an encryption scheme. The proposed encryption is analyzed employing certain results of information theory. The enhancement is based on the employment of an error-correction coding scheme and degradation of the ciphertext. From the perspective of the legitimate parties that share a secret key, the degradation appears as a transmission of the ciphertext through a binary erasure channel. On the other hand, from the perspective of an attacker, the degradation appears as a transmission of the ciphertext over a binary deletion channel. The degradation is performed by employing a simulated noisy channel that consists of two sub-channels so that an additional flexibility is provided for the selection of the parameters to achieve the desired security and the enhancement overhead. Cryptographic security enhancement is analyzed based on the capacity of the related binary deletion channel. It is shown that the enhancement is a function of the following parameters: probabilities of deletion in the sub-channels, capacity of the sub-channels, and the probability of the sub-channel selection for a transmission. An illustrative implementation framework is pointed out which employs a stream cipher.
Organization of the Paper. A novel scheme for cryptographic security enhancement of an encryption employing error-correction coding and a simulated channel that on an attacker’s side appears as a channel with synchronization errors is proposed in Section 2. Preliminaries and background for the security evaluation are given in Section 3. Section 4 provides a cryptographic security evaluation of the proposed enhanced encryption. An illustrative approach for the implementation is discussed in Section 5. Concluding notes are given in Section 6.
2. Proposal for a Security Enhanced Encryption
This section proposes the cryptographic security enhancement of an encryption scheme employing error-correction coding and a simulator of a channel with synchronization errors displayed in Figure 1.
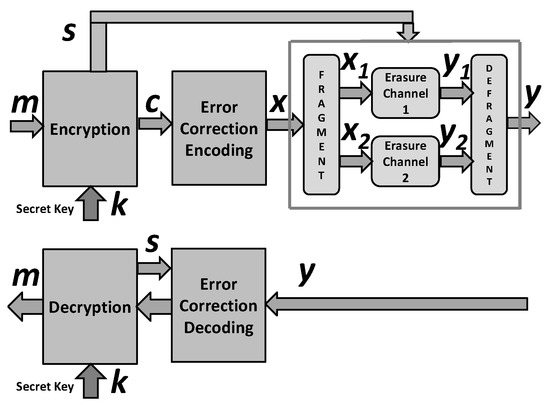
Figure 1.
Security enhanced encryption scheme.
We use the following notation. The message, a data vector subject to encryption is denoted by and we assume that it is a realization of the binary vector variable M. Encrypted form of m is denoted by and we assume that it is a realization of the binary vector variable :
where denotes the encryption mapping controlled by the secret key . The vector denotes the encoded version of employing an error-correction encoding , that performs mapping , :
and is a realization of a random binary variable .
We consider a channel in which the input sequence is divided into subsequences and these subsequences are transmitted through independent i.i.d. binary deletion channels and the arrived bits after the deletion channels are combined preserving their order in the original input sequence. Consequently, the resulting channel is an i.i.d. binary deletion channel with parameters which depend on the parameters of the considered subchannels.
A simulator of the considered channel is controlled by a vector generated by the encryption algorithm which is considered as a realization of a binary random vector .
An attacker on the encryption scheme at Figure 1 faces the problem of cryptanalysis in a known plaintext attack displayed in Figure 2.
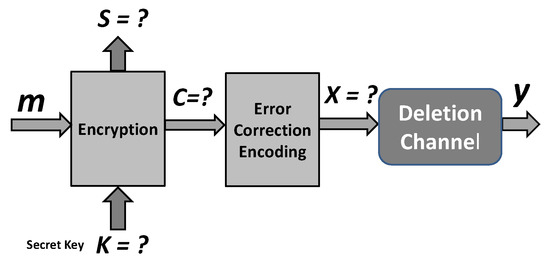
Figure 2.
Model of encryption for cryptanalysis at the attacker’s side under known plaintext attack.
Note that the legitimate parties face the problem of decoding after a binary erasure channel, but the attacker faces a much harder problem of dealing with the decoding after a deletion channel. The knowledge of attackers is limited to the following. Each channel input bit is transmitted through Channel 1 with probability , and through Channel 2 with probability , independently of each other. If transmitted through Channel 1 a bit is deleted with the probability , and if transmitted through Channel 2 a bit is deleted with the probability d2. The attacker does not know the specific realization of the “individual channel selection events”, i.e., they do not know which specific sub-channel bit is transmitted through, and which specific sub-channel each output symbol is received from.
An illustrative instantiate of the proposed framework is given in Section 5.
3. Preliminaries and Background
3.1. Entropy, Mutual Information, and Shannon Capacity
This section provides a summary explanation on the entropy, mutual information and Shannon capacity. A random variable is denoted by an upper-case letter (e.g., A) and its realization is denoted by a lower-case letter (e.g., a). The entropy of a random object A is denoted by , and the mutual information between two random objects A and B is denoted by . The binary entropy function is denoted by .
The entropy of a random variable A is defined as:
The mutual information between jointly distributed random variables A and B is defined as follows:
where conditional entropy is defined as:
and:
Consequently, the conditional mutual information when the third variable Z is given as:
The Shannon capacity of a channel is denoted by C and is defined as:
where A corresponds the channel input, B corresponds to the channel output, and the supremum is over the choice of the distribution of A.
3.2. Mutual Information and Capacity of the Deletion Channel with Fragmentation
The considered communication channel is displayed in Figure 3 and it consists of two sub-channels: and .
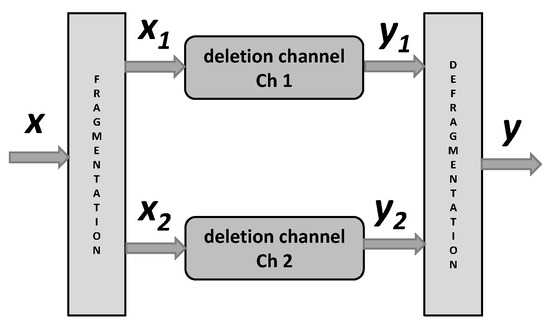
Figure 3.
Model of the deletion channel with frangmentation.
An i.i.d. binary input deletion channel is considered in which every transmitted bit is either randomly deleted with probability d or received correctly with probability while there is no information about the values or the positions of the lost symbols at the transmitter or at the receiver. In the transmission of n symbols through the channel, the input sequence is denoted by in which , and . The output binary sequence is denoted by in which m is a realization of a binomial random variable with parameters n and d (due to the characteristics of the i.i.d. deletion channel).
Let and denotes input and output codewords of the considered channel, respectively.
Further on, let denotes part of the codeword transmiied through , , and let denotes numbers of the codeword bits transmitted through , . Finally, let denotes the vector received trough when the channel input is , . We assume that the vectors , , , and , are realizations of the random variables , , , and , respectively, .
In continuation, we consider , , following [16]:
where in deriving the first inequality we have used the fact that:
and in deriving the second equality the fact that:
where denotes the probability of deletions through the transmission of bits over the i-th channel and , is realization of the corresponding random variable , .
Accordingly:
and
where denotes the expected value of the variable and the last inequality results since , . Finally:
It is shown in [16] that:
where , , . , .
3.3. The Probability of Error and the Equivocation after a Noisy Channel
Suppose the random variables A and B represent input and output messages (out of m possible messages), and the given conditional entropy represents the average amount of information lost on A when B is given. According to [17,18], for example, we have the following general upper bound on the equivocation:
where is the binary entropy function and , and following [15], when A is such that it has the maximum possible entropy , we have:
4. Security Evaluation of the Enhanced Encryption
4.1. Security Notation
We employ a traditional approach for analyzing cryptographic security (see [19], for example) based on the following two issues: (i) a description of what a “break” of the scheme means, and (ii) a specification of the assumed power of the adversary. A cryptographic scheme is considered as a secure one in a computational sense, if for every probabilistic polynomial-time adversary performing an attack of some specified type, and for every polynomial , there exists an integer N such that the probability that succeeds (where success of the attack is also well-defined) is less than for every . Accordingly, the following two definitions specify a security evaluation scenario and a security statement.
Definition 1
([19]). The Adversarial Indistinguishability Experiment consists of the following steps:
- 1.
- The adversary chooses a pair of messages of the same length n, and passes them on to the encryption system for encrypting.
- 2.
- A bit is chosen uniformly at random, and only one of the two messages , precisely , is encrypted into ciphertext and returned to ;
- 3.
- Upon observing , and without knowledge of b, the adversary outputs a bit ;
- 4.
- The experiment output is defined to be 1 if , and 0 otherwise; if the experiment output is 1, denoted shortly as the event , we say that has succeeded.
Definition 2
([19]). An encryption scheme provides indistinguishable encryption in the presence of an eavesdropper, if for all probabilistic polynomial-time adversaries :
where is a negligibly small function.
Definitions 1 and 2 are more precisely discussed in [19].
4.2. Evaluation of the Security Gain
We consider the encryption/decryption scheme proposed in Section 2 which is a security enhanced scheme of a certain basic one. Our goal is to estimate the advantage of in the indistinguishability game specified by Definition 1 when where is a particular realization of , assuming that the advantage of is known when and are two chosen realizations of and the corresponding realization of is given, i.e., the advantage of is known for the basic (security non-enhanced) scheme.
We assume that in the corresponding statistical model, the considered encryption scheme is such that:
i.e., the knowledge of and does not leak (provide) any information on .
Lemma 1.
We consider the advantage of the adversary (specified by Definition 2) to win the indistinguishability game (specified by Definition 1), assuming that the mapping of into is such that equals the advantage of the adversary to win the game. Under these assumptions:
Proof.
For simplicity, it is assumed that equals the advantage of the adversary (specified by Definition 2) to win the indistinguishability game. Consequently, let b which denotes the index of the selected message by realization of the random variable B.
The probability that wins the game is determined by the following:
The lemma assumption implies:
where corresponds to the selected , and:
Note that the encoding mapping is a deterministic one-to-one mapping and consequently has no impact on the advantage of adversary , i.e., we have:
Consequently:
Finally, we obtain:
QED. □
Definition 1 implies that the security of an encryption scheme increases as the difference on the adversary advantage from decreases: The factor shows the reduction rate of the advantage, and so we call it the advantage reduction factor.
Theorem 1.
We consider the adversary (specified by Definition 2) to win the indistinguishability game (specified by Definition 1). Let the basic encryption mapping of into , be such that equals the advantage of the adversary. Consequently, the advantage of the adversary , in the security enhanced scheme specified in Section 2 is:
where:
and , , . , .
Proof.
Finally, taking into account (12) we have:
Substitution of (29) into the statement of Lemma 1 yields the proof. QED. □
Lemma 1 shows that the encryption mapping enhances the security because the probability that wins the game becomes closer to , which corresponds to random guessing, by the factor , and Theorem 1 shows that the upper bound on is .
5. Notes on Implementation Issues
As an illustration, this section proposes an instantiate of the generic framework given in Section 2. This section yields particular designs for the following three main parts of the generic framework: (i) encryption scheme; (ii) coding scheme; (iii) simulated noisy channel.
Encryption. The following Figure 4 displays a model of the encryption box based on a stream cipher: The inputs are the session secret key and the plaintext message , and the outputs are the ciphertext and the control of simulated noisy channel.
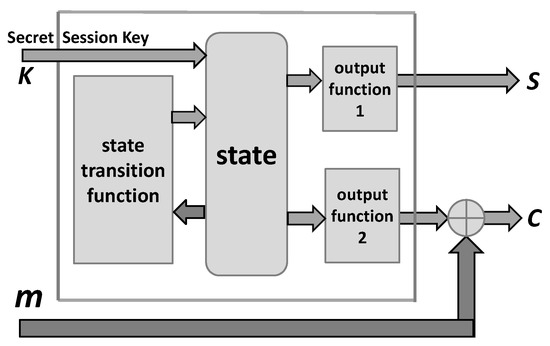
Figure 4.
Model of encryption based on a stream cipher.
Note that the above scheme provides all vectors (sequences) required by encryption box in Figure 1, and in particular the vector required for the simulation of a noisy channel.
Coding. As an option for suitable error correction coding we point to the LDPC codes reported in [20,21]. The time and space complexity of these codes is and , respectively. In order to keep decoding complexity as claimed, the number of errors introduced by the simulated noisy channel should be below the error capability of the employed code, [22]. Otherwise if we are at the error-correcting capability limit we face an increase of the decoding complexity. We assume that up to errors can be corrected with the claimed complexity. In a particular case as reported in [21] (Algorithm C), the time complexity will be , where is a parameter, providing at the same decoding error-rate.
As an alternative option for suitable error correction coding we also point to the polar codes proposed in [23] and considered in [6,7,24], for example.
Simulated Noisy Channel. The simulated noisy channel box takes the sequence as the input and performs its mapping block-by-block in order to obtain three sequences required for the simulated noisy channel composed of two binary erasure channels. Let denotes an n-bit segment of , and let the functions , , perform mapping generating the following three binary n-dimensional vectors:
We assume that the functions are such that the following is valid, where and are the vector weight and the expected value of the weight: (i) ; (ii) ; (iii) .
Let be the codeword after the encoding box, and denotes the degraded codeword after the simulated noisy channel according to the following algorithm. Please note that in order to keep the number of the erased bits within the error correction capability of the employed code, the parameter is used: When the number of already erased bits is greater than , the probability of erasures should be reduced, and accordingly, there are two different rules regarding appearance of the output bit as “?”. Consequently, we consider the following simulator of the noisy channel.
Simulated Noisy Channel
- Input: , the parameter
- set w = 1.
- do i = 1, n
- -
- if= ? and if orotherwise
- -
- if= ? ifotherwise
- Output:
Note that for the legitimate receiver, appears as the codeword after the binary erasures channels. On the other hand, because the attacker does not know the sequence , appears as the codeword after the binary deletion channels displayed in Figure 3.
6. Conclusions
This paper proposes a generic design for a measurable cryptographic security enhancement of certain secret key encryption schemes. This security enhancement is based on the following (see Figure 1): (i) employment of an error correction coding, (ii) splitting the codeword into two parts in the secret key dependent manner; and (iii) degradation each of the codeword parts by simulated binary erasure channels where the erasures are secret key dependent.
Note that for an attacker that does not know the secret key, the resulting channel appears as a simulated deletion channel. The security enhancement is quantified employing reported results on the capacity of the related two parallel binary deletion channels. The reported upper bound on the resulting channel capacity is established employing the upper bound on the mutual information between the inputs and outputs of the component deletion channels. The final lower bound on the achieved security gain is derived by employing relations between the probability of correct decoding and the mutual information between input and output of the resulting channel.
It is shown that the enhancement is a function of the following parameters: probabilities of deletion in the sub-channels, capacity of the sub-channels and the probability of the sub-channel selection for the transmission. Consequently, a desirable security enhancement, as well as, the implementation complexity could be achieved based on a suitable selection of the parameters related to the the employed channels and the coding scheme.
Accordingly, the main contributions of this paper are: (i) novel design of an encryption scheme which employs dedicated coding and simulated noisy channels that, from an attacker perspective, appear as binary deletion channels; and (ii) its cryptographic security evaluation, based on mutual information between input and output of certain channel with bits deletion, employing the adversarial indistinguishably experiment. It is out of the scope of this paper to discuss in detail particular implementations of the proposed framework, and so just illustrative notes are given regarding a possible implementation approach.
Author Contributions
Conceptualization, M.J.M.; methodology, M.J.M.; validation, M.J.M., L.W. and S.X.; formal analysis, M.J.M.; writing–original draft preparation, M.J.M.; writing–review and editing, M.J.M., L.W. and S.X.; supervision, L.W. and S.X.; project administration, L.W. and S.X.; funding acquisition, L.W. and S.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Shandong Provincial Key Research and Development Program (2020CXGC010107, 2019JZZY020129), the Science, Education and Industry Integration Innovation Program of Qilu University of Technology (Shandong Academy of Science) (2020KJC-GH11).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rivest, R.; Sherman, T. Randomized Encryption Techniques. In Advances in Cryptology: Proceedings of CRYPTO ’82; Plemum: New York, NY, USA, 1983; pp. 145–163. [Google Scholar]
- Willett, M. Deliberate noise in a modern cryptographic system. IEEE Trans. Inf. Theory 1980, 26, 102–104. [Google Scholar] [CrossRef]
- Esmaeili, M.; Dakhilalian, M.; Gulliver, T.A. New secure channel coding scheme based on randomly punctured quasi-cyclic-low density parity check codes. IET Commun. 2014, 8, 2556–2562. [Google Scholar] [CrossRef]
- Esmaeili, M.; Gulliver, T.A. Joint channel coding-cryptography based on random insertions and deletions in quasi-cyclic-low-density parity check codes. IET Commun. 2015, 9, 1555–1560. [Google Scholar] [CrossRef]
- Esmaeili, M.; Gulliver, T.A. A Secure Code Based Cryptosystem via Random Insertions, Deletions, and Errors. IEEE Commun. Lett. 2016, 20, 870–873. [Google Scholar] [CrossRef]
- Hooshmand, R.; Aref, M.R.; Eghlidos, T. Physical layer encryption scheme using finite-length polar codes. IET Commun. 2015, 9, 1857–1866. [Google Scholar] [CrossRef]
- Hooshmand, R.; Aref, M.R. Efficient Polar Code-Based Physical Layer Encryption Scheme. IEEE Wirel. Commun. Lett. 2017, 6, 710–713. [Google Scholar] [CrossRef]
- Mihaljević, M.J.; Imai, H. An approach for stream ciphers design based on joint computing over random and secret data. Computing 2009, 85, 153–168. [Google Scholar] [CrossRef]
- Khiabani, Y.S.; Wei, S.; Yuan, J.; Wang, J. Enhancement of Secrecy of Block Ciphered Systems by Deliberate Noise. IEEE Trans. Inf. Forensics Secur. 2012, 7, 1604–1613. [Google Scholar] [CrossRef] [Green Version]
- Mihaljević, M.J. An Approach for Light-Weight Encryption Employing Dedicated Coding. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Anaheim, CA, USA, 3–7 December 2012; pp. 892–898, ISBN 978-1-4673-0919-6. [Google Scholar]
- Wei, S.; Wang, J.; Yin, R.; Yuan, J. Trade-Off Between Security and Performance in Block Ciphered Systems with Erroneous Ciphertexts. IEEE Trans. Inf. Forensics Secur. 2013, 8, 636–645. [Google Scholar]
- Oggier, F.; Mihaljević, M.J. An Information-Theoretic Security Evaluation of a Class of Randomized Encryption Schemes. IEEE Trans. Inf. Forensics Secur. 2014, 9, 158–168. [Google Scholar] [CrossRef]
- Mihaljević, M.J.; Kavčić, A.; Matsuura, K. An Encryption Technique for Provably Secure Transmission from a High Performance Computing Entity to a Tiny One. Math. Probl. Eng. 2016, 2016, 7920495. [Google Scholar] [CrossRef] [Green Version]
- Mihaljevic, M.J.; Oggier, F. Security Evaluation and Design Elements for a Class of Randomized Encryptions. IET Inf. Secur. 2019, 13, 36–47. [Google Scholar] [CrossRef]
- Mihaljevic, M.J. A Security Enhanced Encryption Scheme and Evaluation of Its Cryptographic Security. Entropy 2019, 21, 701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rahmati, M.; Duman, T.M. Upper Bounds on the Capacity of Deletion Channels Using Channel Fragmentation. IEEE Trans. Inf. Theory 2015, 61, 146–156. [Google Scholar] [CrossRef]
- Tebbe, D.L.; Dwyer, S.J., III. Uncertainty and the Probability of Error. IEEE Trans. Inf. Theory 1968, IT-24, 516–518. [Google Scholar] [CrossRef]
- Feder, M.; Merhav, N. Relations between entropy and error probability. IEEE Trans. Inf. Theory 1994, 40, 259–266. [Google Scholar] [CrossRef] [Green Version]
- Katz, J.; Lindell, Y. Introduction to Modern Cryptography; CRC Press: Boca Ratton, FL, USA, 2007. [Google Scholar]
- Luby, M.G.; Mitzenmacher, M.; Shokrollahi, M.A.; Spielman, D.A. Efficient Erasure Correcting Codes. IEEE Trans. Inf. Theory 2001, 47, 569–584. [Google Scholar] [CrossRef] [Green Version]
- Pishro-Nik, H.; Fekri, F. On Decoding of Low-Density Parity-Check Codes Over the Binary Erasure Channel. IEEE Trans. Inf. Theory 2004, 50, 439–454. [Google Scholar] [CrossRef] [Green Version]
- Rybin, P.; Andreev, K.; Zyablov, V. Error Exponents of LDPC Codes under Low-Complexity Decoding. Entropy 2021, 23, 253. [Google Scholar] [CrossRef]
- Arıkan, E. Channel polarization: A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels. IEEE Trans. Inf. Theory 2009, 55, 3051–3073. [Google Scholar] [CrossRef]
- Thomas, E.K.; Tan, V.Y.F.; Vardy, A.; Motani, M. Polar coding for the binary erasure channel with deletions. IEEE Commun. Lett. 2017, 21, 710–713. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).