Abstract
The article aimed to analytically investigate the thermophysical behaviors of a ferrofluid in a vertical rectangle with the variation of intensity of the magnetic field, viscosity of the ferrofluid and boundary conditions. The governing equations of the ferrofluid include the continuity, momentum and energy equations for describing the thermal-fluidic behaviors of the ferrofluid and the Maxwell equation and magnetization equation are also added to consider rotating effect of the nano-sized particles. The flow behavior and heat transfer characteristics of the ferrofluid with the intensity of the magnetic field, viscosities of the ferrofluid and boundary conditions were analyzed through isotherms, velocity profiles and both mean and local Nusselt numbers. As a result, the isotherms of the ferrofluid in the vertical rectangle increased with the increase of the magnetic volume fractions and magnetic field intensities. In addition, the mean Nusselt numbers increased with the increase of magnetite volume fractions at all magnetic field intensities because of the combined effects of both heat conduction by magnetite and the magnetic volume force.
1. Introduction
With increasing international concerns about saving energy and environmental regulations, new functional fluids have been widely considered and developed in various industries. Recently, many studies on the enhancement of cooling performance for electronics with high heat flux are conducted by many researchers due to the high integration and compactification of electronics.
Ferrofluids are very promising working fluids for high efficiency thermal systems. Numerous scientific articles on the thermo-physical characteristics of the ferrofluids in the cavities as basic and fundamental research topics have been published in the open literature for a long time. A ferrofluid is a kind of nanofluid and it has been researched as a novel cooling material to facilitate better heat transfer for better energy savings and longer lifetime of electronics with high heat fluxes [1–7]. The basic and applicable characteristics of ferrofluids as working fluids have also been studied and discussed in the open literature for a long time. Sheikholeslami et al. [8] studied the effects of natural convection heat transfer in a cold outer circular enclosure containing a hot inner elliptic circular cylinder. They used a Cu-water nanofluid as the working fluid in the enclosure. They reported that Nusselt number increases with an increase of nanoparticle volume fraction, Rayleigh numbers and inclination angle. The heat transfer enhancement of the nanofluid also decreased with an increase of Rayleigh number. Akbar et al. investigated the interaction of copper nanoparticles with the base fluid water in an asymmetric channel under an induced magnetic field. They showed the mutual relations between various parameters using graphs [9]. Ellahi investigated the magneto-hydrodynamic flow of a non-Newtonian nanofluid in a pipe. The author discussed the effects of various physical parameters on velocity, temperature and nano concentration through a graphical approach [10]. Kim et al. studied the local and mean Nusselt numbers of a magnetic fluid (MF) in thin channels with variations of the inclination angles and aspect ratio. They reported the mean Nusselt numbers of the magnetic fluid in the thin channel was increased with the increase of the inclination angles and also increased with the increased of the aspect ratio [11]. Lee and Seo reported numerical results of some natural convection characteristics such as flow velocity and an isotherm of the temperature-sensitive ferrofluid in a square cavity with variations of the Rayleigh number. As a result, they reported that the heat and flow characteristics of the ferrofluids within the tested cavity were found to depend on both magnetic intensity and magnetic volume fractions of magnetite [12]. Wang et al. considered the natural convection characteristics in a porous medium enclosure under a magnetic field. They explained the heat and flow characteristics in a porous enclosure due to the effects of the inclination angle, Darcy number, and magnetic force parameter [13]. Extensive studies have been conducted on the thermo-physical characteristics of ferrofluids in the various channels and cavities. However, concise and precise studies in the open literature on ferrofluids as working fluids in a vertical rectangular channel for heat exchangers of thermal systems are very few. Therefore, this study analyzed the flow behaviors and heat transfer characteristics of a ferrofluid as a working fluid in a vertical rectangle for the purpose of application in heat exchangers for thermal systems by varying the viscosity of the ferrofluid, the magnetic field intensity and boundary conditions at all walls. In addition, the mean and local Nusselt numbers were calculated with these boundary conditions and the magnetic field intensities.
2. Numerical Method
In order to analyze the flow behaviors and heat transfer characteristics of the ferrofluid, the physical model and numerical analysis condition are derived. Figure 1 shows the physical model of the vertical rectangle filled with the nano-sized ferrofluid. The temperature of the bottom (T1) wall was basically maintained at 340 K and the temperatures of the left (T2), right (T4) and top (T3) walls were maintained at 300 K. The temperatures of the right (T4) and left (T2) walls were varied to 290 K, 300 K and 310 K. Magnetic field intensities ranged from 0 to 3000 A/m with an interval of 1000 A/m and were applied uniformly along the y-direction at the bottom wall. Velocities at the initial conditions were assumed to be 0 in both the x- and y-directions, and all walls were under no-slip boundary conditions. Table 1 shows the numerical conditions.
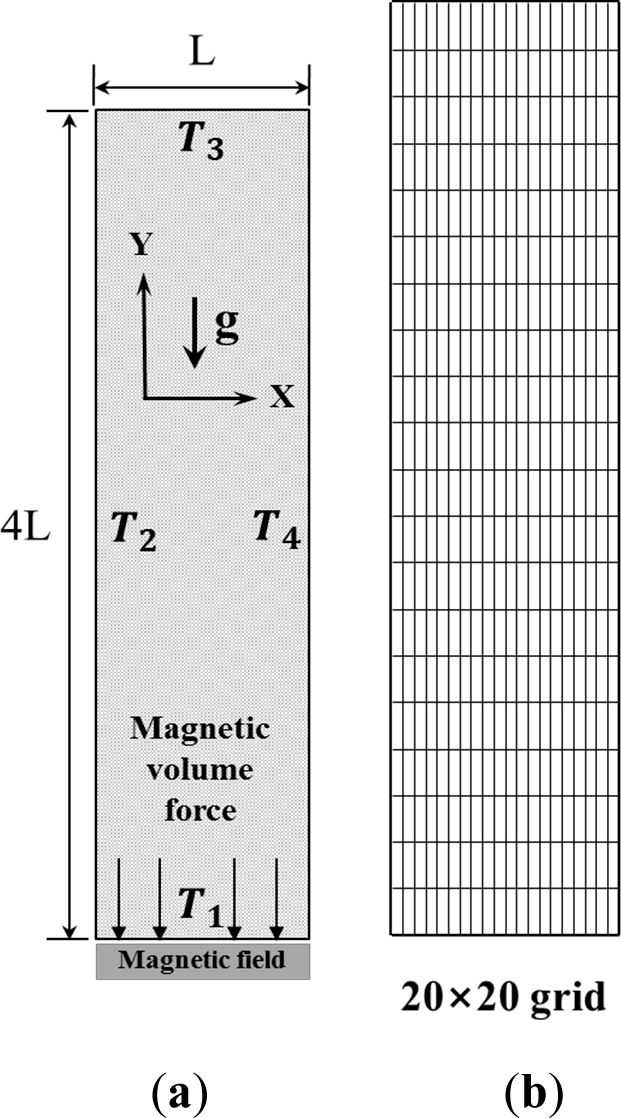
Figure 1.
The physical model for ferrofluid in the vertical rectangle: (a) Rectangle; (b) Mesh.

Table 1.
Numerical conditions.
The viscosities at 300 K of the ferrofluids used in the physical model were 0 (water) 0.854, 1.9, 2.95 and 4.0 mPa·s. The volume fractions of magnetite were 0 (water), 1.5, 3.0 and 4.5%. The Rayleigh number was fixed at 105 as suggested by Hollands et al. [14]. The thermodynamic properties of the ferrofluids used in this study were based on the data supplied by the manufacturing company [15]. Table 2 lists the thermodynamic properties of the ferrofluids used in this study.

Table 2.
Thermo-dynamic properties of the used ferrofluids.
Mesh size of the vertical rectangle used 20 × 20 grids and numerical analysis was performed until the temperature difference between the initial state and final state was 10−5 K during 0.5 s. The elapsed time was t = 20,000 s. The conservation equations for mass, momentum and energy were used to analyze the heat and flow characteristics of the ferrofluid in the vertical rectangle. In addition, the magnetization and Maxwell equations are used to predict the ferrofluid behaviors with consideration of the rotating effect of the nano-sized magnetic particles [16]. In addition, the governing equations were solved with several physical assumptions as well as the well-known Boussinesq approximation [17]. The local Nusselt number on the near heated wall (T1) was defined as an Equation (7) and the mean Nusselt number was calculated as an Equation (8), based on the research results of Seo and Lee [18]:
3. Results and Discussion
The numerical model for investigation on the thermophysical characteristics of the ferrofluid in a vertical rectangle in this study was developed based on the existing model suggested by Lee and Seo et al. and the developed model was sufficiently validated with their data and other numerical models explained in their articles [11,12]. Also, all data predicted by the present model showed good agreement within 5% of the existing models and thus we confirmed that the present model is valid.
3.1. Thermal-Flow Characteristics
Generally, the flow characteristics of the working fluid in the closed system are discussed with isotherms and velocity profiles. Figure 2 shows the isotherms of the ferrofluid with various magnetite volume fractions in the vertical rectangle. In order to compare the flow characteristics between the water and the ferrofluid in the vertical rectangle, isotherms were considered with the variation of the volume fractions from 1.5% to 4.5% under H = 0 A/m, T1 = 340 K and T3 = 300 K.
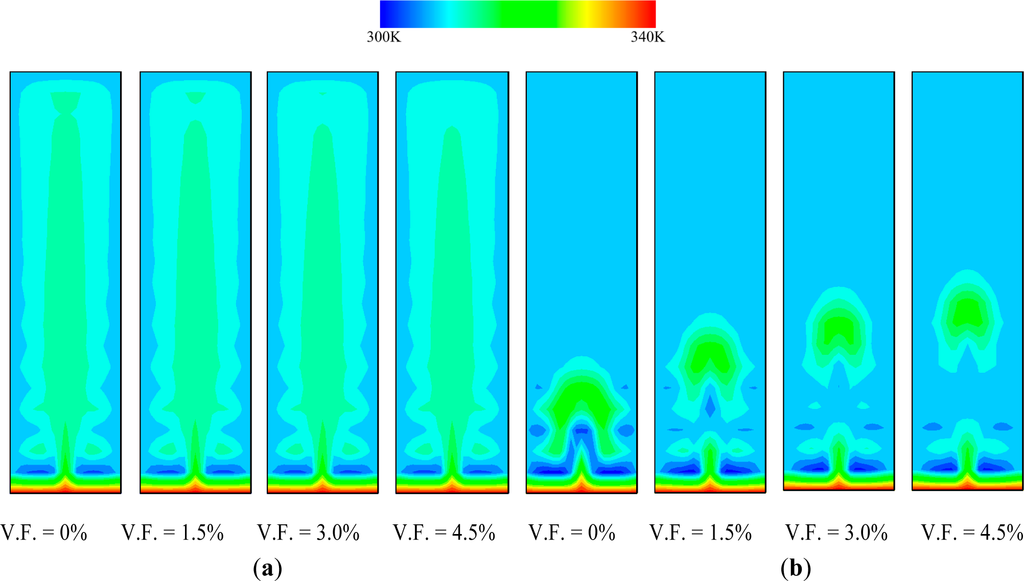
Figure 2.
Comparisons of the isotherms with various magnetite volume fractions of ferrofluids at H = 0 A/m. (a) 20,000 s; (b) 4000 s.
Figure 3 shows the isotherms of the ferrofluid in the vertical rectangle with various intensities of the magnetic field at the magnetite volume fraction of 1.5%, T1 = 340 K and T3 = 300 K. The thermal diffusion of the ferrofluid in the vertical rectangle was enhanced with the rise of the magnetic field intensities. This is because the magnetic volume force for the y-direction increased with the rise of the magnetic field intensities at the bottom wall of the rectangle [19].
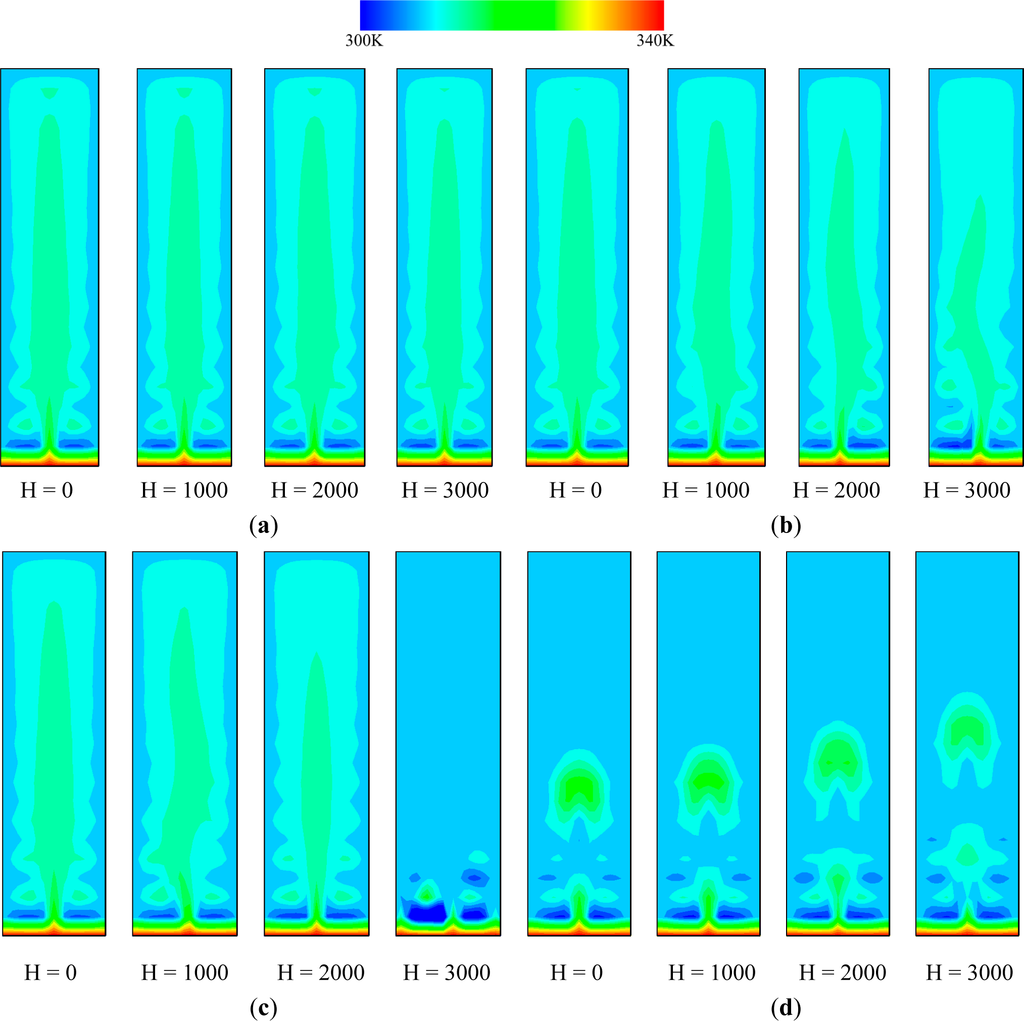
Figure 3.
Isotherms of ferrofluid with various intensities of magnetic field at the magnetite volume fractions of 1.5%, 3.0% and 4.5%. (a) Volume fraction (1.5%) at 20,000 s; (b) Volume fraction (3.0%) at 20,000 s; (c) Volume fraction (4.5%) at 20,000 s; (d) Volume fraction (3.0%) at 4000 s.
In addition, the isotherms of the ferrofluids in the vertical rectangle were enhanced with the increase of the viscosities of the ferrofluids under given magnetic fields. The height of the core column in the isotherm for ferrofluid with the volume fraction of 4.0% at H = 2000 A/m is less than that with the volume fraction of 1.5% due to the faster cooling with the cold walls by increasing the heat transfer velocity to opposite direction of the bottom wall. The reason is that the effect of magnetic field intensity on the ferrofluid was increased with the rise of the volume fraction of the ferrofluids.
As shown in Figure 3d at the same elapsed time of 4000 s, the magnetic volume force was increased with the intensities of the magnetic field [20]. From the results of Figures 2 and 3, the isotherms of the ferrofluid in the vertical rectangle increased with the increase of the magnetic volume fractions and magnetic field intensities. In addition, the natural convection heat transfer of the ferrofluid in the vertical rectangle was increased.
3.2. Nusselt Numbers and Heat Transfer Characteristics
The local and mean Nusselt numbers of the ferrofluid in the vertical rectangle were considered with variations of the magnetic volume fractions and magnetic field intensities. Figure 4 shows the variation of mean Nusselt numbers of the ferrofluid in the vertical rectangle with the magnetite volume fractions. The mean Nusselt number of the ferrofluid with the volume fraction of 4.5% at H = 0 A/m is 0.08% larger than that with the volume fraction of 1.5%. Also the mean Nusselt number of the ferrofluid with the volume fraction of 4.5% at H = 3000 A/m is 15.84% larger than that with the volume fraction of 1.5% because the magnetic volume force of the ferrofluid increased with the increase of the ferrofluid volume fractions [21]. The cooling area at the isotherms of the ferrofluid in the vertical rectangle increased with the increase of the magnetic volume fractions and magnetic field intensities due to increasing of the cooling speed with increased magnetic volume force [22]. Namely, the ferrofluid with more magnetite content yields a higher heat transfer. However, when the ferrofluid used as the working fluid in the thermal devices such as a micro-heat exchanger, a channel and an enclosed cavity, the manufacturing costs of the ferrofluid get more expensive with increasing amount of magnetite. Therefore, in order to practically use the ferrofluid in thermal devices with a lower manufacturing cost, a larger magnetic field intensity at lower magnetic volume fraction of the ferrrofluid is necessary to have the same heat transfer performance with the higher magnetic volume fractions. In addition, these results could contribute as a basic research result applicable to heat exchangers like solar thermal collectors in real industries.
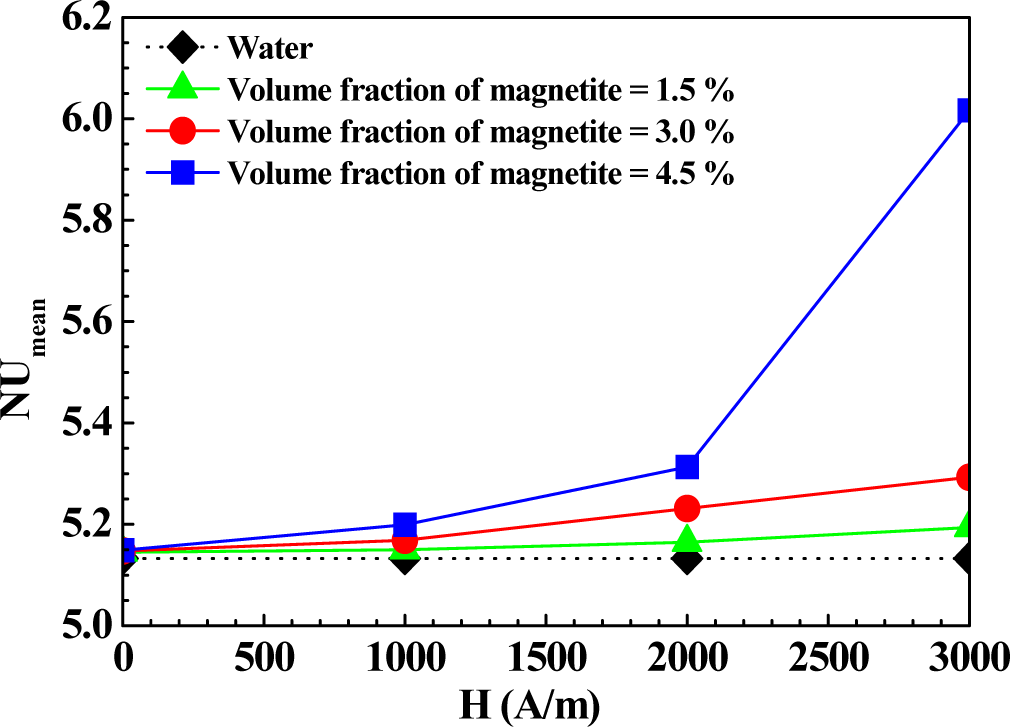
Figure 4.
Mean Nusselt numbers of the ferrofluid in the vertical rectangle with the magnetite volume fractions.
As a result, the mean Nusselt numbers increased with the increase of magnetite volume fractions at all magnetic field intensities because of the combined effects of both heat conduction by magnetite and the magnetic volume force [23]. In addition, at H = 1000, 2000 and 3000 A/m, the mean Nusselt numbers at the magnetite volume fraction of 4.5% increased by 0.98%, 3.19% and 16.85%, respectively, compared with the water reduced convective heat transfer rate. Also, the mean Nusselt numbers at the bottom wall show higher values than those at the top wall because of the larger temperature difference with the faster velocity profiles and isotherms as shown in Figure 5d where the isotherms of the ferrofluid in the vertical rectangle with various temperatures of the left wall at H = 0 A/m and magnetite volume fraction of 3.0% are seen.
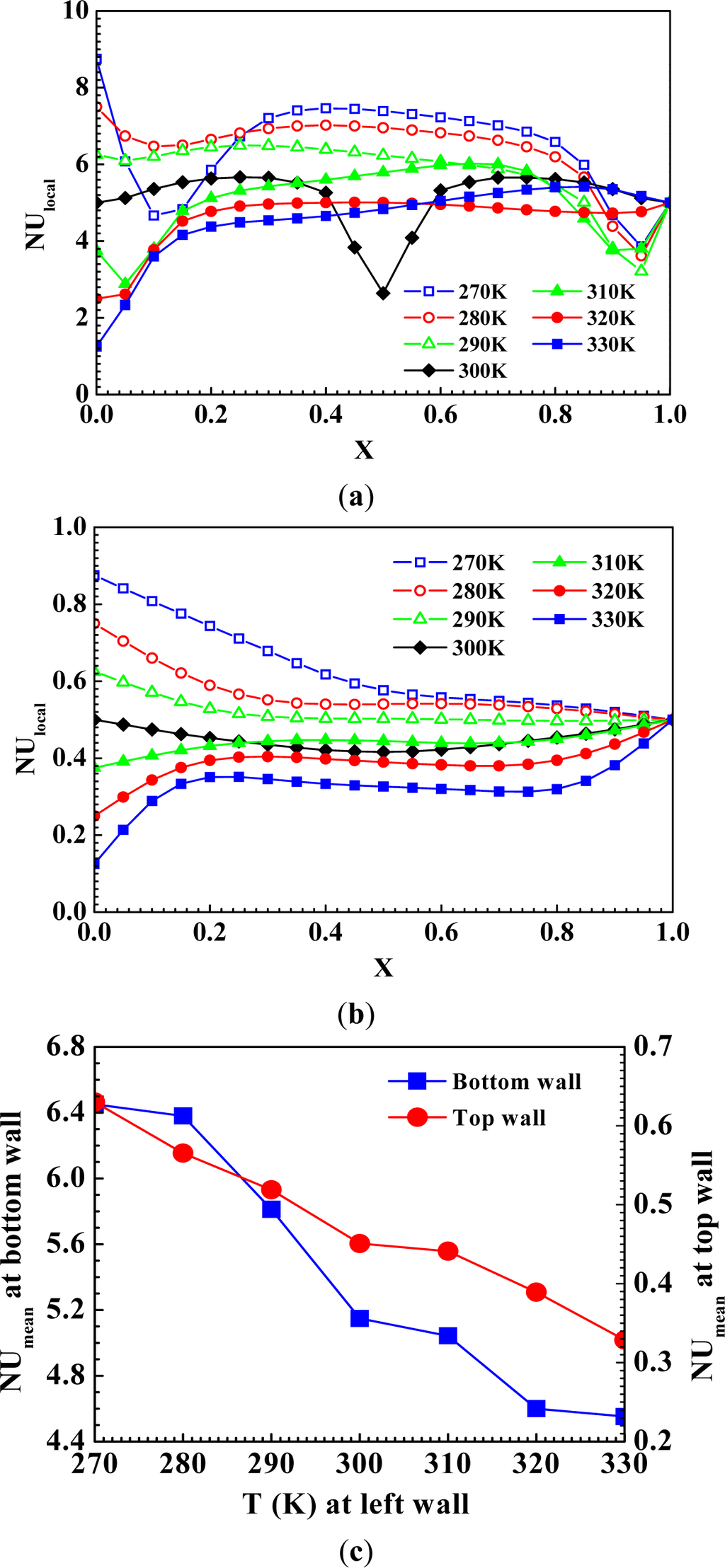
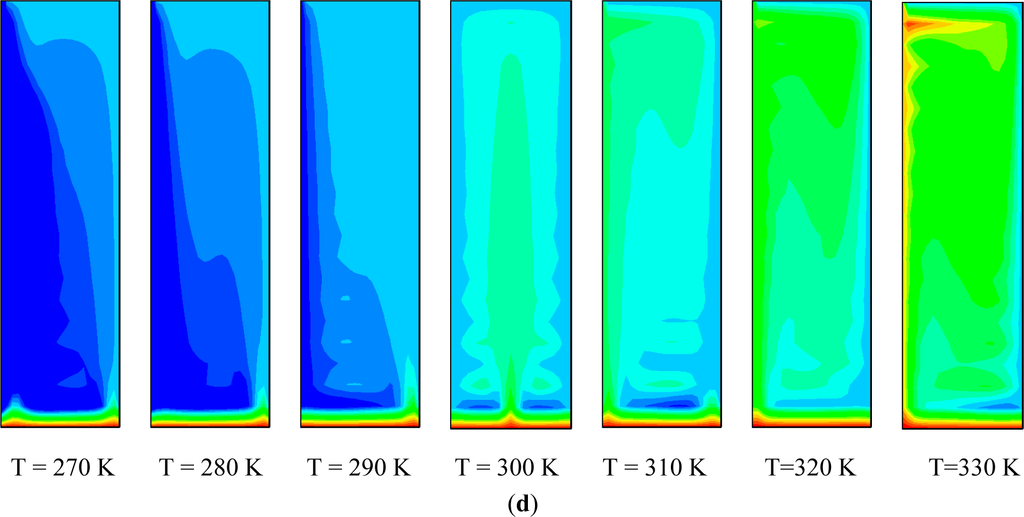
Figure 5.
Both local and mean Nusselt numbers and isotherms of ferrofluid in the vertical rectangle with various temperatures of the left wall at H = 0 A/m and magnetite volume fraction of 3.0%. (a) Local Nu at bottom wall; (b) Local Nu at top wall; (c) Mean Nu at top and bottom walls; (d) Isotherms.
4. Conclusions
This study investigated numerically the thermophysical behaviors of a nanosized ferrofluid in a vertical rectangle with the variation of intensity of the magnetic field, viscosity of the ferrofluid and boundary conditions. The variation of the flow behavior and heat transfer characteristics of the ferrofluid were analyzed through isotherms, velocity profiles and both mean and local Nusselt numbers with the intensity of the magnetic field, viscosities of the ferrofluid and boundary conditions. As results, the flow and heat transfer characteristics of the ferrofluid in the vertical rectangle were affected by the intensities of the magnetic field and the boundary conditions at all walls. The cooling area in the isotherms of the ferrofluid in the vertical rectangle increased with the increase of the magnetic volume fractions and magnetic field intensities due to the increased cooling speed with increased magnetic volume force. The mean Nusselt numbers were increased with the rise of the magnetic field intensities and the rise of viscosities of the ferrofluids due to the increased magnetic volume force of the ferrofluids. The mean Nusselt numbers also increased with the increase of magnetite volume fractions at all magnetic field intensities because of the combined effects of both heat conduction by magnetite and the magnetic volume force. In addition, the mean Nusselt numbers of the ferrofluid in the vertical rectangle at both the top and bottom walls decreased with the left wall being heated from 270 K to 330 K because the local Nusselt numbers at top and bottom walls decreased with left wall heating due to the reduced temperature between the left wall and bottom wall with the reduced convective heat transfer rate.
Acknowledgments
This research was supported in part by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT and Future Planning (2013R1A1A1062152). This work (Grants No. C0200054) was supported by Business for Cooperative R&D between Industry, Academy, and Research Institute funded Korea Small and Medium Business Administration in 2014. Some contents of this article were already presented at the 7th Asia-Pacific Conference on Transducers and Micro/Nano Technologies in 2014.
Author Contributions
Both Moo-Yeon Lee and Dong-Yeon Lee are corresponding authors and they designed and wrote the paper. Jae-Hyeong Seo is the first author and analyzed the data obtained by numerical analysis. He also wrote part of the results and discussions in the paper. Both Byoung-Hee You and Sang-Seuk Kwen are co-authors and helped prepare the review and summary of the published articles in the introduction part in the paper. They assisted with the corrections for the English expressions and typos of the article during the revision process. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Horng, H.E.; Hong, C.Y.; Yang, S.Y.; Yang, H.C. Novel properties and applications in magnetic fluids. J. Phys. Chem. Solids 2001, 62, 1749–1764. [Google Scholar]
- Jin, L.; Zhang, X.; Niu, X. Lattice Boltzmann simulation for temperature-sensitive magnetic fluids in a porous square cavity. J. Magn. Magn. Mater 2012, 324, 44–51. [Google Scholar]
- Zhao, Y.; Zhang, Y.; Lv, R.; Wang, Q. Novel optical devices based on the tunable refractive index of magnetic fluid and their characteristics. J. Magn. Magn. Mater 2011, 323, 2987–2996. [Google Scholar]
- Torii, S. Experimental study on thermal transport phenomenon of nanofluids as working fluid in heat exchanger. Int. J. Air Cond. Refrig 2014, 22, 1450005. [Google Scholar]
- Yun, R.; Hwang, Y. Inflow condensation heat transfer characteristics of CO2 in microchannel. Int. J. Air Cond. Refrig 2014, 22, 1450011. [Google Scholar]
- Jang, D.S.; Lee, E.J.; Lee, S.H.; Kim, Y.C. Thermal Performance of Flat Plate Pulsating Heat Pipes with Mini- and Micro-Channels. Int. J. Air Cond. Refrig 2014, 22, 1450025. [Google Scholar]
- Cho, H.G.; Kim, T.H.; Kim, J.H.; Lee, C.S.; Choi, J.H. Simulation Results for the Effect of Fin Geometry on the Performance of a Concentric Heat Exchanger. Int. J. Air Cond. Refrig 2014, 22, 1450026. [Google Scholar]
- Sheikholeslami, M.; Ellahi, R.; Hassan, M.; Soleimani, S. A study of natural convection heat transfer in a nanofluid filled enclosure with elliptic inner cylinder. Int. J. Numer. Methods Heat Fluid Flow 2014, 24, 1906–1927. [Google Scholar]
- Akbar, N.S.; Raza, M.; Ellahi, R. Interaction of nano particles for the peristaltic flow in an asymmetric channel with the induced magnetic field. Eur. Phys. J. Plus 2014, 129, 1–12. [Google Scholar]
- Ellahi, R. The effects of MHD and temperature dependent viscosity on the flow of non-Newtonian nanofluid in a pipe: Analytical solutions. Appl. Math. Model 2013, 37, 1451–1467. [Google Scholar]
- Kim, S.C.; Seo, J.H.; Lee, D.Y.; Hong, D.P.; Kang, S.J.; Lee, M.Y. Thermodynamic behaviors of magnetic-fluid in a thin channel with magnetic field and aspect ratio. Int. J. Precis. Eng. Manuf 2014, 15, 1377–1382. [Google Scholar]
- Lee, M.Y.; Seo, J.H. Numerical investigation on heat and flow characteristics of temperature-sensitive ferrofluid in a square cavity. Adv. Mech. Eng 2013, 2013, 240438. [Google Scholar]
- Wang, Q.W.; Zeng, M.; Huang, Z.P.; Wang, G.; Ozoe, H. Numerical investigation of natural convection in an inclined enclosure filled with porous medium under magnetic field. Int. J. Heat Mass Transfer 2007, 50, 3684–3689. [Google Scholar]
- Hollands, K.G.T.; Unny, T.E.; Raithby, G.D.; Konicek, L. Free convective heat transfer across inclined air layers. J. Heat Transfer 1976, 98, 189–193. [Google Scholar]
- Ferrotec Corporation. Available online: http://www.ferrotec.com/ accessed on 5 January 2014.
- Sawada, T.; Kikura, H.; Tanahashi, T. Visualization of wall temperature distribution caused by natural convection of magnetic fluids in a cubic enclosure. Int. J. Appl. Electromagn. Mater 1994, 4, 329–335. [Google Scholar]
- Park, J.W. A Study on the Heat Transfer Characteristics and Fluid Flow of Magnetic Fluids in Concentric Double Pipe Annuli. Ph.D. Thesis, Dong-A University, Busan, Korea, 2002. [Google Scholar]
- Seo, J.H.; Lee, M.Y. Numerical analysis on thermal-fluidic characteristics of the magnetic fluid in a cavity using GSMAC. J. Korea Acad. Ind. Coop. Soc 2013, 14, 997–1002. [Google Scholar]
- Seo, J.H.; Lee, M.Y.; Seo, L.S. Study of natural convection of magnetic fluid in cubic cavity. Trans. Korean Soc. Mech. Eng. B 2013, 37, 637–646. [Google Scholar]
- Odenbach, S.; Liu, M. Invalidation of the Kelvin force in ferrofluids. Phys. Rev. Lett 2001, 86, 328–331. [Google Scholar]
- Seo, J.H.; Kim, D.W.; Lee, M.Y. Heat transfer characteristics of the magnetic fluid in the inclined rectangular cavity using finite element method, Proceedings of the International Conference of Saving Energy in Refrigeration and Air-Conditioning, Yeosu, Korea, 23–25 October 2013; pp. 77–80.
- Grosan, T.; Revnic, C.; Pop, I.; Ingham, D.B. Magnetic field and internal heat generation effects on the free convection in a rectangular cavity filled with a porous medium. Int. J. Heat Mass Transfer 2009, 52, 1525–1533. [Google Scholar]
- Lajvardi, M.; Moghimi-Rad, J.; Hadi, I.; Gavili, A.; Isfahani, T.D.; Zabihi, F.; Sabbaghzadeh, J. Experimental investigation for enhanced ferrofluid heat transfer under magnetic field effect. J. Magn. Magn. Mater 2010, 322, 3508–3513. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).