A Review of Methods for Improving Microwave Heating Uniformity

Abstract

Microwave heating technology has gained extensive application in various fields, including food processing and drying, material synthesis, and waste treatment, due to its advantages of high efficiency, selectivity, and rapid response. However, the inherent non-uniform electromagnetic field distribution within metallic microwave cavities leads to uneven heating. This issue severely constrains the large-scale industrial application of microwave heating, particularly its extension into high-precision, high-value-added industrial sectors like 3D printing, curing, and microwave plasma micro/nano-fabrication. To address this challenge, extensive research efforts have been undertaken in both academia and industry, focusing on improving microwave heating uniformity, resulting in the proposal of various methods. This review summarizes these methods for enhancing microwave heating uniformity and specifically outlines recent research progress on novel techniques based on artificial electromagnetic surfaces. It aims to offer valuable references and guidance for the broader application of microwave heating technology.

1. Introduction

Microwave heating, which utilizes electromagnetic (EM) waves—typically in the industrial, scientific, and medical (ISM) frequency bands—to heat materials, has evolved significantly since its inception in the mid-20th century. The underlying mechanism relies on the interaction between EM waves and the dielectric properties of the materials, where dipolar polarization and polar molecules exposed to alternating electric fields result in volumetric and efficient heating. Compared to conventional heating techniques based on thermal conduction or radiation, microwave heating offers unique advantages, including accelerated heating rates, improved energy efficiency, and the ability to selectively target specific materials or regions. Owing to these benefits, microwave heating has been widely adopted in recent two decades (Figure 1) across the diverse application domains, such as chemical production [1,2,3,4,5], materials processing or synthesis [6,7], food processing [8,9,10,11,12,13,14], medical therapy [15,16], agriculture [17], etc., as summarized in Figure 2.

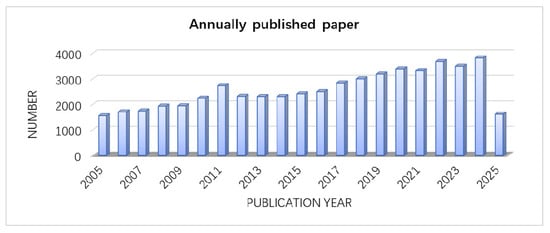
Figure 1. Number of annually published papers on microwave heating based on the Science Citation Index (SCI) library.

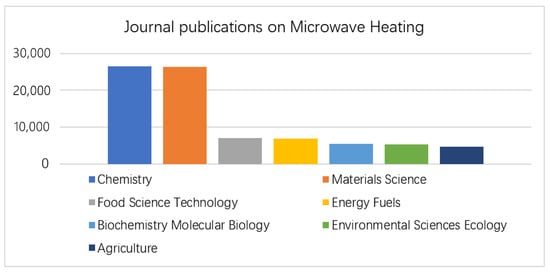
Figure 2. Journal publication summary on Microwave heating based on the SCI library.

In food processing, microwave heating significantly reduces processing times for cooking, thawing, baking, and sterilization, while helping to preserve nutritional value, flavor, and texture [18,19]. In chemical engineering, microwave-assisted process enhances intermolecular energy transfer, thereby accelerating reaction kinetics and improving yields in both fine chemical synthesis and large-scale industrial applications [4,5]. Similarly, in medical applications, microwave heating is extensively employed for tumor ablation, where precise spatial control enables localized thermal treatment with minimal damage to surrounding healthy tissue [20,21,22]. In materials science, microwave-assisted synthesis and sintering techniques have demonstrated not only improved production efficiency but also enhancements in microstructures and material properties, particularly for nanomaterials [7], polymers [23], and ceramics [6].

Despite these advantages, achieving uniform heating remains a critical challenge in the practical implementation of microwave technologies [24,25,26,27,28,29,30]. Non-uniform heating, often manifesting as localized “hot spots” and “cold spots”, can degrade process quality, causing problems such as scorching or insufficient cooking in food processing, process instability in chemical reactions, and inconsistent material properties during synthesis. In demanding applications such as premium food manufacturing, complex chemical syntheses, precision medical therapy, and advanced materials fabrication, heating uniformity is directly linked to product quality, safety, and reliability. Therefore, improving uniformity and controllability of microwave heating remains a central research objective.

Although numerous review papers have examined the microwave heating fundamentals [6] and its diverse applications [31,32,33,34,35,36,37,38,39,40,41], a comprehensive survey dedicated to strategies for improving heating uniformity from the perspective of microwave engineering is notably absent in the literature. To address this gap, this paper presents a focused review of recent technological advances aimed at alleviating non-uniformity in microwave heating systems.

Research indicates that the inherent non-uniform distribution of the EM field within microwave cavities [33,42,43,44,45,46,47,48,49,50,51,52,53,54,55] is a primary cause of uneven heating. The absorbed power density P within a dielectric material can be expressed as

$$P={\displaystyle \frac{1}{2}}\omega {\epsilon }^{″}{\left|\mathit{E}\right|}^2$$

(1)

where ω is the angular frequency, ε″ is the imaginary part of the complex permittivity, and |E| is the local electric field amplitude. Any spatial non-uniformity in |E| translates into uneven power absorption and heating.

The electric field in (1) can be determined by solving Maxwell’s wave equation

$$\nabla \times {\mu }_r^{-1}(\nabla \times \mathit{E})-k_0^2\left({\epsilon }_r-{\displaystyle \frac{j\sigma }{\omega {\epsilon }_0}}\right)\mathit{E}=0$$

(2)

where ε_r, μ_r, and σ are relative permittivity, permeability and conductivity, respectively. Notably, the specific boundary conditions of metallic cavities result in a set of resonant eigenmodes. The total electromagnetic field is a linear superposition of these modes. However, the amplitude of each mode (which is zero if the mode is unexcited) is determined exclusively by the feed. Consequently, the EM field distribution is significantly dependent on the cavity geometry, boundary conditions, excitation source (frequency, phase, position, number, etc.), sample (geometry, placement, constitutive properties), and other factors.

The temperature-dependent properties of materials also directly affect heating uniformity. For many materials, constitutive parameters are functions of temperature. As a result, the entire heating process is nonlinear, with either positive or negative feedback. For example, the permittivity of water is higher than that of ice, causing thawed regions of food to heat up rapidly. In contrast, the frozen regions absorb less energy, thereby exacerbating the non-uniformity of heating. In addition, the thermal conductivity of materials affects temperature uniformity, too. The heat conduction equation can describe the internal temperature distribution as

$$\rho C_p{\displaystyle \frac{\partial T}{\partial t}}=\nabla \cdot \left(k\nabla T\right)+P$$

(3)

where ρ is the density, C_p is the specific heat capacity, k is the thermal conductivity. The term P denotes the heat source, which corresponds to the microwave energy dissipated within the material and is calculated using Equation (1). A higher thermal conductivity is more favorable for achieving uniform heating.

In the field of microwave heating, the coefficient of variation (COV) of temperature is commonly used as a key quantitative indicator for evaluating heating uniformity. It is calculated as

$$COV={\displaystyle \frac{\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n{\left(T_i-\overline{T}\right)}^2}}}{\overline{T}-T_0}}$$

(4)

where $\overline{T}$ is the average temperature, and n is the number of sampling points within a cavity. A lower COV value directly corresponds to a more uniform distribution of electromagnetic energy and a more consistent temperature rise in the material. It is therefore widely used to evaluate the effectiveness of various uniformity improvement strategies. Additionally, the maximum temperature difference and the standard deviation of temperature can also be used to evaluate heating uniformity.

Since the non-uniformity of microwave heating originates from the standing wave distribution of the electric field, some studies have evaluated heating uniformity based on the uniformity of the electric field. The uniformity of the electric field can be assessed using the normalized standard deviation

$$s_{norm}={\displaystyle \frac{1}{\overline{\left|\mathit{E}\right|}}}\sqrt{{\displaystyle \frac{1}{n}}{{\displaystyle \sum _{i=1}^n\left(\left|{\mathit{E}}_i\right|-\overline{\left|\mathit{E}\right|}\right)}}^2}$$

(5)

where $\overline{\left|\mathit{E}\right|}$ is the average temperature, and n is the number of sampling points.

To date, numerous studies have been conducted on improving microwave heating uniformity, proposing a variety of strategies. These strategies are mainly classified into three categories: dynamic field distribution, movement of objects being heated, and the metasurface-based method. This review will provide a detailed examination of these investigations.

2. Strategies for Dynamic Field Modulation to Enhance Heating Uniformity

The uneven EM field distribution within a metallic cavity primarily stems from the inherent standing wave characteristics of the cavity. Consequently, a variety of EM field modulation-based heating improvement methods have been developed, aiming to mitigate the formation of stationary hot spots and cold spots. Based on their underlying principles, strategies for modulating the cavity field can be broadly classified into two categories: those that modify the boundary conditions and those that optimize the feed.

For methods based on boundary conditions, the boundaries directly determine the spatial structure and resonant frequencies of the electromagnetic modes within the cavity, thereby influencing the overall field. This influence arises through two mechanisms. First, as the fundamental components constituting the total field, changes in the modal structures directly alter the overall field distribution. Second, whether a mode can be excited depends not only on the feed but also on the mode’s own spatial structure and resonant frequency. Therefore, by controlling the boundary conditions, the excitation of different modes can be indirectly influenced, ultimately shaping the total electromagnetic field.

Excitation control primarily shapes the electromagnetic field inside the cavity by governing the excitation strength of specific modes. This can be achieved through several means. The feed configuration—including the number, position, and geometry of the feed elements—can be optimized. Alternatively, since resonant modes occur at distinct frequencies, tuning the excitation frequency offers direct control over mode selection. In multi-feed systems, the output power and phase of each feed can be independently adjusted to synthesize a superimposed field with improved uniformity.

Building upon these two approaches, the electric field can be uniformly distributed over the heated sample, thereby improving heating uniformity. This represents a static control strategy. Alternatively, a dynamic control strategy can be implemented by introducing moving parts, which enables the time-averaged electric field within the cavity to achieve uniform distribution across the sample.

As mentioned, the cavity geometry, boundary condition, excitation style, and sample’s characteristics are the main factors that impact the EM distribution within the microwave heating cavity. Since the sample is generally an inflexible constraint to microwave heating, the practical ways to modulate the EM field distribution includes: introduction of mode stirrers [45,46,47,48,49], modification of cavity geometry [50,51], and optimization of the excitation which involves power sources [52,53,54,55,56,57,58,59,60], frequency [61,62,63,64,65,66,67,68,69,70,71], and phase [72,73,74]. These approaches mitigate stationary EM field patterns, creating dynamic field distributions to enhance heating uniformity.

2.1. Mode Stirring-Based Techniques

The most prevalent method for heating uniformity improvement employs mode stirrers to dynamically reconfigure EM field distributions within cavities. The mode stirrers, which are widely implemented in microwave ovens, can continuously redistribute EM fields during heating by altering standing wave patterns. Early in 2005, Plaza-González et al. comparatively analyzed stirrer configurations for low-, medium-, and high-loss dielectric materials, proposing optimized designs for field uniformity [45]. The results indicate that, when heating samples with a low dielectric constant, the mode stirrer can significantly improve heating uniformity. However, for media with a high dielectric constant, the effect of the mode stirrer is relatively limited. This is because the electric field within the cavity tends to concentrate in materials with a high dielectric constant, making it difficult for the stirrer to alter the field distribution.

Later, Cuccurullo et al. demonstrated the significant improvement of the final product quality and drying time by using a mode stirrer and air renewal in microwave drying of sliced zucchini [46]. Compared with the conventional method, the drying time was reduced by approximately 48%. Huang’s group proposed a simulation model to analyze the function of the turntable and the mode stirrer in microwave heating. Results demonstrate that the mode stirrer contributes to maintaining a relatively high heating efficiency and improving heating uniformity [47].

In 2021, Wang et al. developed a dual-pendulum mode stirrer [48] with more complex chaotic trajectories than the conventional single-pendulum design, significantly improving heating uniformity (COV: 0.35 vs. 0.18) without compromising efficiency. This design demonstrates superior field perturbation and reduced temperature differentials under specific initial conditions.

In 2023, Wang et al. developed a controllable time-varying EM boundary microwave reaction cavity by using 20 circularly arranged controllable eccentric rotary copper columns [49]. Results demonstrate that the optimized rotation angles of the copper columns can effectively improve heating uniformity while maintaining high efficiency. When the columns are fixed at 0°, 45°, 90°, and 180°, the COV is 0.6317, 0.7543, 0.4133, and 0.6188, respectively, whereas the dynamic rotational heating process achieves a much lower COV of 0.2338. This rotation at different angles constitutes another type of mode stirring.

Research indicates that mode stirrers can significantly improve microwave heating uniformity and are relatively insensitive to the size, shape, or position of the sample, demonstrating broad applicability. Consequently, they are widely used in commercial and industrial applications such as food processing. However, the incorporation of stirrers also introduces several drawbacks: (1) moving parts reduce system reliability and increase maintenance requirements; (2) additional drive motors are needed, further raising costs; and (3) Corona discharge at metallic edges under high-power conditions can affect the system’s power capacity.

2.2. Cavity Geometry Modification-Based Techniques

Cavity geometry modification offers another EM field adjustment approach. Recent work has proposed an accordion-like deformable cavity [50], where compression/expansion during operation dynamically shifts modes, enabling the co-optimization of uniformity and efficiency. Its experimental validation was conducted based on a cavity with a tunable short-circuit plunger. When the plunger was fixed, the COV was 0.51 with an average temperature rise of 5.88 °C; when the plunger was varied, the COV improved to 0.36, with an increased average temperature rise of 9.68 °C. This method improves both heating uniformity and efficiency. However, the plunger suffers from significant wear during prolonged operation, resulting in low reliability. Furthermore, inherent gaps in its structure pose a risk of electrical breakdown, resulting in poor overall safety performance.

Zhou et al. proposed an Arbitrary Lagrangian-Eulerian (ALE)-based shape optimization algorithm [51], enhancing uniformity through boundary shape optimization while maintaining the cavity topology. After optimization, the COV improved from 0.544 to 0.279, with a slight increase in the average temperature. This method does not require the addition of moving parts. However, the optimized cavity typically has an irregular structure, making it difficult to manufacture, and it is only applicable to a single type of sample, limiting its general applicability.

2.3. Optimal Feeding-Based Methods

Optimizing microwave power feeding offers alternatives for improving heating uniformity. Those methods involve multi-source configurations, feed position optimization, frequency control (selective or sweeping), phase tuning, and other techniques. All of them try to establish an improved uniform EM field distribution.

2.3.1. Multiple Sources and Rotary Feeding Ports

Utilizing multiple power sources in a microwave heating system is an effective method for enhancing heating uniformity, particularly in large-scale industrial applications. In 2007, Tortajada et al. proposed a method to enhance EM field uniformity by optimizing the configuration of a multi-feed system in a multimode cavity using genetic algorithms [52]. Compared to the single-feed system, the normalized standard deviation of the electric field decreased from 0.3648 to 0.1445, improving uniformity. However, the average electric field intensity dropped from 671.25 V/m to 575 V/m. In 2020, Ahn et al. developed a 1.5-kW microwave applicator that employs three slotted waveguides with longitudinal or transverse slots to improve heating uniformity. With the aid of power control, a uniformity improvement of approximately 67% was achieved [53]. The uniformity enhancement in the microwave applicator with one waveguide consisting of orthogonal slots is also experimentally demonstrated in [54].

These studies enhance electric field uniformity by optimizing the multi-feed configuration (e.g., position, power, polarization, etc.), without introducing moving parts, and demonstrate strong adaptability to different samples, making them suitable for a wide range of applications. However, the increased number of feeds raises the cost, limiting their use to high-end products.

Subsequently, Yang’s group introduced a layered control framework for temperature uniformity in the microwave heating of heterogeneous materials. The proposed approach was experimentally validated by heating alumina ceramic in a ducted microwave reactor with six microwave sources [55], achieving a COV of 0.015. They further simulated a multi-source microwave heating system integrated with a power-frequency control strategy and demonstrated the improved temperature uniformity [56]. Compared to the case with a fixed frequency, heating uniformity was improved by 44.4–76.6%. More recently, the same group presented a gradient descent-based coordinated control strategy for multi-source microwave heating, aiming to simultaneously enhance the heating efficiency and temperature uniformity by coordinating the power fed by each microwave source [57]. Compared with constant power heating, heating efficiency increased by 10.7%, while temperature uniformity improved by 41.5–73.8%. Seo et al. also proposed a multi-source cooperative phase-shifting technique to rotate the electric field, achieving a more uniform temperature distribution (COV = 0.05) [58].

These studies collectively indicate that, in multi-source microwave heating systems, adaptively manipulating the power, frequency, and phase of each source is the key to improving both heating efficiency and temperature uniformity. However, this approach significantly increases the complexity and cost of the system, making it suitable only for scenarios that require extremely uniform temperature and precise control.

Rotating microwave feeding ports change the polarization of incident EM waves and thus result in different modes within the heating cavity, which inspire new uniformity improvement approaches. For example, Zhu et al. developed a rotary radiation structure [59] which dynamically alters the polarization of the incidence wave, effectively disrupting stationary hot/cold spots. Compared to the stationary case, the COV decreased from 0.6332 to 0.3122, while the average temperature after heating increased from 24.63 °C to 41.2 °C. Follow-up research optimized the positioning and rotation angles of dual sources, showing superior field uniformity and reduced local overheating compared to static heating or turntable systems, achieving a COV of 0.2637 [60]. However, it should be noted that, compared to turntables and mode stirrers, a rotating feed requires a more complex mechanical structure and exhibits lower operational stability, posing notable challenges for practical implementation.

2.3.2. Frequency-Tuning Strategies

Microwave heating efficiency exhibits high sensitivity to operational frequency. This dependence arises from two factors: (i) distinct field distributions within the same cavity at different frequencies, and (ii) frequency-dependent complex permittivity of heated materials, which leads to differential microwave power absorption. Advances in solid-state microwave systems now enable flexible frequency manipulation, facilitating the exploration of frequency-tuning-based methods that improve heating uniformity.

In early 1996, Fathi et al. reviewed the application of variable frequency microwave energy in polymerization, composite processing, bonding, and plasma [61]. Then, Antonio et al. numerically and experimentally compared different frequency sweep rate regimes (linear or non-linear) and demonstrated that a much greater heating uniformity was achieved using the variable frequency method than conventional fixed-frequency methods in terms of materials processing [62]. Compared to the traditional method, which dried less than 25% of the area, the two frequency sweep strategies dried over 80% and 90% of the area, respectively. The same improvement was also observed in food samples by Taghian et al. [63]. Tang et al. numerically and experimentally compared the impact of frequency variation strategies (fixed, continuously variable, and selected) on heating uniformity, with the results showing COV values of 0.78, 0.68, and 0.57, respectively, and corresponding average temperature rises of 9.8 °C, 8.6 °C, and 10.9 °C [64]. These results demonstrate that the selected frequency strategy can significantly enhance both heating uniformity and efficiency. Wu et al. reported a four-port heating method with sweep frequency output from the magnetrons, indicating that both high heating efficiency and uniformity can be achieved when the ports are fed in sweep frequency microwaves with inconsistent polarization [65].

Yang and Chen et al. proposed a complementary-frequency heating strategy that can selectively use specific frequencies (identified based on temperature profile) in the microwave heating process. Consequently, this method can trade off power absorption efficiency and heating uniformity to deliver a higher heating rate than the sweeping-frequency strategy does [66]. They also developed three online frequency-shifting strategies: ordered, predetermined complementary, and dynamic complementary, that simultaneously collected heating performances and provided closed-loop feedback through customized algorithms to control the frequency shifting during the heating processes. Experimental results demonstrated that the dynamic complementary frequency shifting yielded significantly better heating uniformity than the other two shifting strategies [67]. Later, they investigated a dual-source microwave heating system with four frequency shifting strategies, i.e., non-shifting, synchronized-shifting, inverse-shifting, and distinct-shifting, for both stationary and rotatory conditions. Similarly, frequency shifting was again demonstrated to significantly improve heating uniformity compared to the fixed-frequency heating [68]. Other frequency-tuning-based heating uniformity strategies can be found in [69,70,71].

A well-designed frequency sweeping strategy can significantly enhance microwave heating uniformity without altering the cavity structure, thereby ensuring high stability and adaptability. However, reliance on high-power solid-state sources increases system costs and limits the maximum power.

2.3.3. Phase-Controlled Method

Around 1999, Bows et al. pioneered phase-controlled microwave heating using a waveguide system. They demonstrated that varying the relative phases of two coherent microwave signals can effectively improve heating uniformity [72]. In their approach, the relative phase difference was obtained by using transmission lines of different lengths. Later, Wang et al. developed a dual-feed phase-shifting heating technique based on a resonant cavity system [73]. This technique dynamically adjusts the phase difference (either fixed or varying) between two feeding ports via phase shifters during heating, thereby modifying the EM field patterns to enhance uniformity. As a result, the COV values decreased from 0.64 to 0.4. Both studies rely on dual-port feeding and tuning of the relative phase difference between these two input signals.

Liao et al. also introduced a phase-shifting approach to improve heating uniformity in a single-mode rectangular cavity [74]. However, in this case, the phase adjustment is realized by moving a sliding short, which essentially changes the cavity geometry. Consequently, this technique is more accurately classified as a cavity geometry modification method, rather than a genuine phase-shifting strategy.

Across these studies, a unifying theme emerges: despite differences in implementation, each phase modulation technique exploits the interference of two coherent waves to generate a standing wave. By precisely tuning the phase difference, the resulting pattern of antinodes and nodes can be spatially reconfigured, enhancing energy distribution uniformity during heating and allowing control over the extent of the heated area. It should be noted, however, that phase-controlled strategies generally require phase shifters and multiple feeding ports, which are implemented using either multiple power sources or power dividers. These additional components increase system complexity and cost, posing challenges for practical applications.

2.3.4. Methods Based on Injection-Locked Magnetron

Owing to the low cost of high-power sources based on injection-locked magnetrons [75,76,77,78,79], methods for achieving uniform microwave heating using these sources have recently gained attention. Zhu et al. proposed a phase-frequency simultaneous modulation technique based on injection pulling to improve microwave heating uniformity [80]. Experimental results confirmed that this approach enhances uniformity while offering improved controllability in magnetron-based heating systems. Similarly, Zhao et al. developed a quasi-dual-frequency microwave generator that produces nearly identical amplitudes by injecting signals at specific powers and frequencies outside the Adler locking band [81]. This technique shows great potential for improving microwave heating uniformity in large-scale industrial applications.

Injection-locked magnetrons eliminate the dependence on high-power solid-state sources in frequency-tuning strategies, alleviating the challenges they face in practical applications.

3. Enhancing Uniformity via Material Movement

Beyond improving the uniformity of electromagnetic field distribution within cavities, researchers have pursued enhanced uniformity of EM energy absorption by moving materials throughout both high- and low-intensity E-field regions [82,83,84,85,86,87,88,89,90,91,92,93]. The predominant methods employ turntables or conveyor belts. As the material traverses different field regions, statistically uniform energy absorption is achieved, thereby mitigating localized overheating or underheating.

3.1. Rotating Turntable

Owing to its advantages in structural simplicity and low cost, the rotating turntable has been widely implemented in commercial and domestic microwave ovens. Geedipalli et al. found that rotating the sample during a 35 s microwave heating process improved the uniformity by about 40%, with the COV decreasing from 0.871 to 0.497 [82]. Pedreño-Molina et al. numerically investigated the way samples move in the EM field using different optimization methods and found that optimized movement control (i.e., controlling the sample dwell time in the different field regions) could improve the temperature distribution uniformity, compared to constantly moving in the EM field [83].

Ye et al. studied the turntable composed of the combination of two different materials (polyethylene (PE) and alumina, PE and aluminum, and alumina and aluminum). Results show that a multi-material turntable can achieve a 26–47% increase in temperature uniformity compared to a single-material turntable [84].

Meng et al. have numerically and experimentally demonstrated that a metal patch placed on a turntable is an efficient method for improving heating uniformity. Furthermore, the rotating speed has little influence once the heating time exceeds a single rotation period [85].

Yang and Chen utilized modeling tools to comprehensively investigate the turntable function in microwave ovens, indicating that the turntable’s high/vertical position is more critical to power efficiency and heating uniformity. At the same time, rotation primarily works to decrease the temperature difference between hot and cold spots [86]. The results showed that the temperature difference between hot and cold spots decreased by 45%, and the heating uniformity index (HUI) decreased by 51%.

These increasingly detailed studies deepen the understanding of the turntable’s role in enhancing microwave heating uniformity, thereby facilitating the design of the high-performance systems.

3.2. Conveyor Belts and Other Moving Elements

The conveyor belt is typically used in large-scale industrial applications involving microwave heating or drying processes [87]. In these systems, samples placed on the conveyor belt are constantly moved through the microwave system, which is fed by multiple power sources.

For example, the good drying quality of bamboo and impressive time reduction from days to hours using a conveyor belt microwave dryer have been reported [88]. Bae et al. developed a continuous power-controlled method, which achieves a heating uniformity improvement of approximately 34% compared to a simultaneous multiple input method [89].

Additionally, Chao et al. proposed a rotary microwave applicator to rapidly dry high-moisture biofuel materials [90]. This cylindrical applicator features dual movement, combining drum rotation and material stirring, which not only promotes heating uniformity but also mitigates the formation of hot and cold spots.

3.3. Cooperation of Mode Stirrer and Material Movement

Research indicates that both field stirring and material motion enhance heating uniformity [91]. Consequently, several studies integrate these strategies for synergistic improvement.

Cuccurullo et al. implemented an infrared thermography-based online temperature-controlled microwave system for zucchini drying. They experimentally evaluated individual and combined effects of turntable rotation, mode stirring, and airflow control on drying kinetics and product quality [46]. Yi et al. analyzed heating effects under varying component positions/velocities and compared the impact of stirrer material properties and sample geometry on uniformity. Results demonstrate that cavity designs combining dual stirrers with conveyor motion effectively enhance both heating uniformity and energy utilization [92].

To heat the fluid, Zhu et al. integrated a screw propeller into a continuous-flow microwave reactor. Results demonstrate effective enhancement of heating uniformity through dynamic fluid mixing and field redistribution, offering a robust strategy for industrial microwave processing applications [93].

3.4. Numerical Modeling for Heating Systems with Moving Components

Multiphysical simulation is an effective method for elucidating microwave heating dynamics and provides quantitative theoretical guidance for optimizing system designs [94]. However, the simulation becomes significantly challenging when moving components (stirrers, turntables, conveyors) are involved, due to their varied geometries, motion patterns, and velocities.

In the early stage, an iterative method is proposed to address the continuous rotation of the turntable [95,96]. The sliding interface between the rotating and stationary parts is specially assigned and treated, and the temperatures are estimated by coupling electromagnetic and heat transfer analysis. During simulation, the heat generation is updated at time steps according to the sample’s position and renewed spatial temperature-dependent dielectric properties, as shown in Figure 3. However, the method’s reliance on per-time-step remeshing generates considerable computational overhead and cumulative inaccuracies from inter-step mesh misalignment.

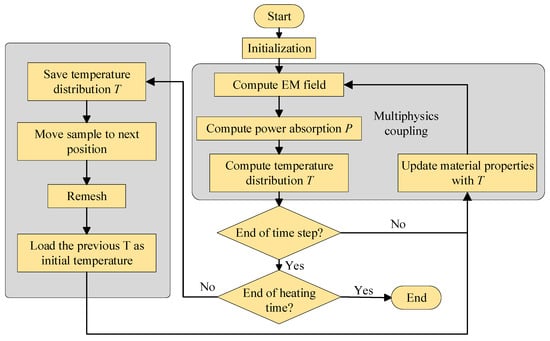
Figure 3. Basic flowchart of the iterative method.

Zhu et al. presented a transformation optics-based novel simulation method for the microwave applicator with moving elements [97]. This approach exploits transformation optics, surrounding the object with a time-varying anisotropic layer. The layer’s material properties are mathematically derived to “twist” EM waves, mimicking the motion of an object while the mesh remains static. They began by defining a coordinate transformation

$$r^{\prime }=F(r)$$

(6)

where $r=(x,y,z)$ denotes the original position, and $r^{\prime }=(x^{\prime },y^{\prime },z^{\prime })$ represents the transformed position. Based on this transformation, the permittivity and permeability of the surrounding material are defined as

$$\overline{\overline{\epsilon }}=\epsilon \overline{\overline{\gamma }}\hspace{1em}\hspace{1em}\overline{\overline{\mu }}=\mu \overline{\overline{\gamma }}$$

(7)

$$\overline{\overline{\gamma }}={\displaystyle \frac{{\overline{\overline{J}}}^T\cdot \overline{\overline{J}}}{\det \overline{\overline{J}}}}$$

(8)

where $\overline{\overline{J}}$ is the Jacobian tensor:

$$\overline{\overline{J}}=\left[\begin{array}{ccc}\partial x^{\prime }/\partial x& \partial x^{\prime }/\partial y& \partial x^{\prime }/\partial z\\ \partial y^{\prime }/\partial x& \partial y^{\prime }/\partial y& \partial y^{\prime }/\partial z\\ \partial z^{\prime }/\partial x& \partial z^{\prime }/\partial y& \partial z^{\prime }/\partial z\end{array}\right]$$

(9)

This model allows for direct field coupling within the transformed space, simplifying the simulation. Despite a significant reduction in remeshing steps, the method cannot eliminate remeshing altogether, which leads to persistent error accumulation. Furthermore, it is less general, as deriving the material parameters is complex and typically restricted to simple, predefined motions, such as rotation.

Ye et al. developed a novel continuous algorithm to simulate the heating process with moving elements [98]. This method utilizes an implicit function φ to define the boundaries of moving objects on a fixed grid. The level set equation updates φ to model motion, entirely avoiding remeshing. The level set equation is

$${\displaystyle \frac{d\phi }{dt}}+\mathit{V}\cdot \nabla \phi =0$$

(10)

where V is the velocity of the element. As a result, the moving region’s properties are set as a function of space coordinate and time. However, it requires an additional coordinate transformation to couple the electromagnetic and thermal fields due to the moving reference frame. Moreover, the requirement for an analytical description of the sample boundary poses a significant challenge for modeling objects with complex geometries.

Zhou et al. proposed a continuous algorithm based on the Arbitrary Lagrangian-Eulerian (ALE) method [99]. This approach maintains a fixed mesh in the moving region while introducing the ALE formulation, which allows the surrounding domain’s mesh to deform freely under the influence of the moving boundary. This ensures computational accuracy and continuity, enabling precise simulations of complex models. Nonetheless, the method still requires remeshing and is therefore often referred to as the ALE-remeshing method. In 2021, Ye et al. proposed a hybrid ALE/implicit function method. This approach utilizes the Arbitrary Lagrangian-Eulerian (ALE) method to track object motion, while representing the object’s position through a time-varying implicit function [100]. By integrating the advantages of both the Implicit Function and Level Set Method (IFLSM) and the ALE-remeshing technique, this method can effectively handle complex geometries without requiring remeshing.

Li et al. introduced a Ray Casting Method for microwave heating simulation of moving, complex-shaped samples. It determines a point’s location (inside/outside a sample) by counting ray-triangle intersections from its mesh file, enabling implicit boundary definition. This overcomes a key limitation of Level Set methods, which required mathematical formulas for boundaries and struggled with arbitrary shapes [101].

These studies collectively advance microwave heating uniformity through innovative computational and physical strategies. Each method has distinct strengths and limitations, as detailed in Table 1, highlighting the need for context-specific solutions in microwave heating applications.

Table 1. Comparison of different numerical modeling methods.

Method	Sample Shape	Motion	Remesh Required	Accuracy	Complexity
Iterative method [95,96]	Arbitrary	Complex	Yes	Low	Low
Transformation Optics-based [97]	Arbitrary	Simple	Yes (low freq)	Medium	High
IFLSM [98]	Regular	Complex	No	High	Medium
ALE-remeshing [99]	Arbitrary	Complex	Yes	Medium	Medium
Hybrid ALE/Implicit Function [100]	Arbitrary	Complex	No	High	Medium
Ray Casting [101]	Arbitrary	Complex	No	High	Medium

4. Innovative Approaches Based on Metamaterials/Metasurfaces

While the strategies above significantly improve microwave heating uniformity, methods involving field modulation or material motion typically require additional mechanical components, multiple microwave sources, phase shifters, or high-performance solid-state power sources. These elements increase manufacturing and operational costs, and introduce potential mechanical wear, thereby compromising system reliability. Recent advances in artificial EM structures offer innovative pathways for further uniformity enhancement.

Metamaterials are artificially engineered structures that exhibit electromagnetic properties not readily found in natural materials, typically achieved by arranging subwavelength-scale inclusions to tailor effective permittivity and permeability [102]. Metasurfaces are their two-dimensional counterparts, consisting of subwavelength or quasi-subwavelength elements arranged on a surface to manipulate EM waves in terms of amplitude, phase, polarization, or wavefront [103]. Due to their extraordinary wave-manipulation capability, these structures have garnered considerable attention for enhancing the uniformity of microwave heating. The introduction of metamaterials or metasurfaces into the cavity enables modification of the effective boundary conditions, thereby facilitating precise control over the electromagnetic field distribution. Based on this principle, well-designed structures can be employed to improve heating uniformity significantly.

4.1. Metamaterial-Based Method

In 2022, a method employing photonic crystal structures to enhance both heating efficiency and uniformity was presented [104,105]. These structures, consisting of copper pillars or Al₂O₃ ceramic rods, are placed inside heating cavities to redistribute the EM field. Though simulations demonstrated the improvement of heating efficiency and uniformity, with increases of approximately 35% and 40%, respectively, the installation of 132 copper pillars [104] or 72 Al₂O₃ ceramic rods [105] in the cavity severely restricts available space for samples, greatly limiting practical applicability.

A gradient-index metamaterial-based EM black hole has also been proposed for microwave heating in a cylindrical multimode cavity [106], which experimentally increased energy efficiency by 35%. However, this method primarily increases heating efficiency by reducing reflections rather than enhancing uniformity.

It is important to note that metamaterials used in these studies are inherently 3D structures and occupy considerable space, which significantly hinders their practical application. In contrast, frequency-selective surfaces (FSSs) and metasurfaces are 2D structures that can be integrated onto the walls of microwave heating chambers, offering more compact and practical solutions.

4.2. Frequency Selective Surface-Based Method

Frequency selective surfaces (FSSs), often referred to as spatial filters [107,108,109], can be regarded as a specific class of metasurfaces characterized by uniform unit cells patterns.

In 2021, Kim et al. proposed a microwave heating applicator comprising FSS absorptive walls and a Fresnel zone plate (FZP)-based beamforming antenna for microwave heating uniformity enhancement [110]. In this applicator, FSS absorptive walls suppress the diffuse reflections, approximating a free-space radiation environment. The FZP-based antenna, composed of a dual-polarized waveguide antenna and a reconfigurable FSS loaded with varactors, enables beam steering by electrically controlling the transparency of EM waves through bias on the varactors. Consequently, microwave power can be delivered to the desired location. While this approach demonstrates temperature control, heating uniformity was not experimentally validated. Furthermore, the use of absorptive FSS walls significantly reduces heating efficiency and increases manufacturing cost, both of which hinder practical deployment.

Wang et al. proposed a dynamic electromagnetic boundary control technique employing a switchable FSS, as shown in Figure 4a [111]. By biasing PIN diodes embedded within the FSS unit cells, the structure toggles between reflective and transmissive states, allowing for dynamic EM boundary reconfiguration without the need for mechanical actuators. The application of an FSS improves both heating uniformity and efficiency, as indicated by a decrease in COV from 0.48 to 0.35 and a rise in the average temperature from 31.4 °C to 41.8 °C. More recently, Xiao et al. also introduced an active FSS approach, where the states of PIN diodes are selectively controlled across unit cells to redistribute the EM field, thereby enhancing heating uniformity [112].

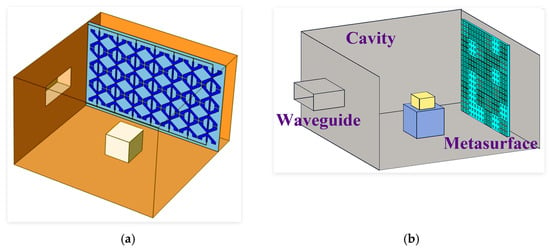
Figure 4. Heating uniformity improvement methods based on (a) switchable FSS and (b) metasurface.

It should be noted that the incorporation of diodes in both designs introduces several issues: First, transistors have an on-state resistance that increases energy loss and may cause overheating or even combustion under high-power, long-duration operation. Second, transistors are typically placed between two metal patches where the electric field is highly concentrated. Considering the breakdown voltage of the diodes, the overall system exhibits a reduced power handling capacity. Additionally, the introduction of a DC feed network increases system complexity, reduces stability, and raises costs. Consequently, their practical applicability is severely limited.

4.3. Metasurface-Based Method

To mitigate these problems, scattering metasurfaces have been recently integrated into microwave heating cavities by Peng et al. [113,114] to enhance heating uniformity. The idea is to design a beam-splitting metasurface and mount it on the wall of the heating cavity (Figure 4b) to scatter incident waves into multiple directions, rather than a single dominant path, thereby improving the uniformity of the EM field distribution [114]. Based on this idea, a 2-bit digitally coded metasurface combining cross-shaped and L-branch elements was designed, and the array arrangement is optimized using a genetic algorithm (GA) [113]. When integrated into the cavity, the metasurface facilitates a uniform electromagnetic field distribution without requiring mechanical or active electronic regulation. Both simulations and experiments validated the proposed idea. Compared to the empty cavity, the introduction of the metasurface reduced the COV from 0.694 to 0.425 and significantly increased the sample temperature. In this study, the scattering effect of the metasurface facilitates the excitation of cavity modes. Since the standing wave structures of different modes vary, the superposition of multiple modes results in a more uniform total field distribution compared to that of a single mode, thereby improving heating uniformity. It should be noted, however, that the impact of the metasurface on the intrinsic structure of the electromagnetic modes themselves was not discussed. Furthermore, while the study aimed to achieve broader scattering coverage to enhance performance, a more refined design approach—such as controlling the scattering intensity in different directions to precisely adjust the excitation strength of specific modes—could lead to further improvements in field uniformity.

Compared with active FSS-based method, this passive design, which relies on mature PCB fabrication and a low-profile structure, offers a cost-effective and practical solution with higher power tolerance. However, the current fabrication cost of a metasurface with sufficiently large aperture remains higher than that of conventional approaches, such as incorporating mode stirrers or turntables. Moreover, the circuit layout on the metasurface inherently induces localized electric field concentrations, which imposes constraints on power handling capacity, thus, such metasurface structures are suitable primarily for relatively low power applications.

In summary, metasurfaces offer a promising alternative for improving microwave heating uniformity and provide distinct advantages. Nevertheless, several technical challenges remain to be addressed before their widespread deployment in industrial applications. Microwave technologies have long been central to scientific and engineering advancement [115]. Beyond microwave heating, wireless power transmission has also become a significant research direction [116,117,118], where metasurface or cavity-based structures are frequently introduced to achieve more uniform electromagnetic field distribution [119,120].

5. Conclusions

This review has provided a comprehensive overview of strategies for improving microwave heating uniformity, focusing on dynamic electromagnetic field control, sample movement and rotation, and the utilization of advanced structures such as metasurfaces for field shaping, as illustrated in Figure 5. These approaches have demonstrated significant potential in enhancing electromagnetic field distribution/heating uniformity.

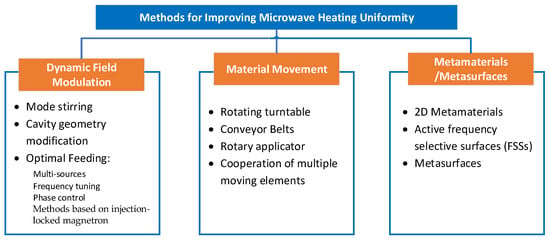
Figure 5. Summary of strategies for improving microwave heating uniformity.

Despite these advancements, several critical challenges remain. First, the inherent complexity of multimode cavity fields under varying load conditions complicates precise prediction and control. Second, most reported techniques have been validated only under laboratory conditions, and their scalability to large-scale continuous processes requires further investigation. Table 2 provides a qualitative assessment of the heating uniformity and efficiency of various methods, along with a summary of their practical constraints. Based on the respective advantages and limitations of these methods, Figure 6 identifies the most suitable approach for different application fields by analyzing their alignment with fundamental domain requirements.

Table 2. Performance and practical constraints of different methods.

Method	Uniformity Improvement	Efficiency Improvement	Practical Constraints
Mode Stirring [49]	44% to 69%	up to 31%	—
Deformable Cavity [50]	11% to 29%	28% to 73%	Risk of EM Leakage
Cavity Optimization [51]	45%	29%	Sample-Specific
Multi-Feed [52]	60%	−14%	—
Multi-Feed Control Strategy [56,57]	42% to 94% (vs. Multi-Feed)	11% (vs. Multi-Feed)	Complex & High-Cost
Feed Rotation [59,60]	25% to 26%	−19% to 332%	Complex & Unstable
Frequency-Tuning [64,68]	22% to 27%	11%	—
Phase-Controlled [73,74]	25% to 57%	Marginal	—
Material Movement [82]	37% to 43%	6%	—
Metamaterial-based [105]	12% to 34%	15% to 34%	Low Space Efficiency
FSS-Based [111]	27%	33%	Low Power Capacity (<220 W)
Metasurface-Based [113]	39%	29%	—

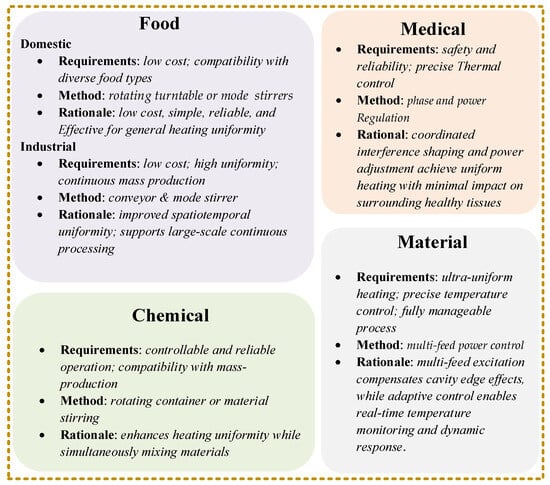
Figure 6. Overview of optimal heating uniformity methods for various application fields.

Future research may focus on the following directions: (1) developing neural network (NN)-assisted intelligent design of microwave heating applicators that integrate with multiple strategies; (2) designing reconfigurable components to achieve on-demand field shaping; (3) conducting theoretical analysis of microwave cavities loaded with metasurfaces; and (4) establishing highly efficient and accurate multiphysical simulation methods. Advances in these areas are expected to significantly improve heating uniformity, energy efficiency, and industrial applicability.

Overall, this review aims to serve as a reference for researchers and engineers seeking to optimize microwave heating systems and to inspire future innovations toward more uniform, efficient, and adaptive heating solutions.