Mergers and Tidal Breakups of Binary Systems of Primordial DM Planets with Baryon Admixture and Emission of Gravitational Waves ^†

Abstract

Here, we discuss the possibility of the admixture of baryons to the DM primordial planets, with the DM particles varying in mass from 20 GeV to 100 GeV. We have considered different fractions of admixture particles to form the planet. The mass of the primordial planet made completely of DM ranges from asteroid mass to Neptune mass. However, the mass of primordial planets (admixed with DM and baryonic matter) is found to increase with the fraction of baryonic matter in the planets, and the mass of these objects can go well beyond the mass of Jupiter (around 40 times Jupiter’s mass) and can also approach sub-stellar mass (brown dwarf mass). So far, thousands of exoplanets have been discovered by the Kepler mission and more will be found by NASA’s Transiting Exoplanet Survey Satellite (TESS) mission, which is observing the entire sky to locate planets orbiting the nearest and brightest stars. Many exoplanets, such as exo-Jupiter, discovered so far fall in this mass range, and unsure whether these exoplanets are entirely made of baryons. Some of the exoplanets with a mass several times Jupiter’s mass could be possible signatures of the presence of primordial planets with an admixture of baryonic and DM particles. It is also found that some of these planets could reach even sub-stellar mass (10³² g), such as that of a brown dwarf. Additionally, even if a small fraction of DM particles is trapped in these objects, the flux of ambient DM particles would be reduced significantly. This could be one of the many reasons for not detecting the DM particles in various experiments, such as XENON1T, etc., as suggested earlier. If two such primordial planets (in a binary system) merge, they will release a lot of energy. The energy released in gravitational waves, as well as the time scale of the merger of these objects, is found to increase with the mass of primordial objects. The frequency of gravitational waves emitted in these systems is matching within the range of LIGO. The objects near the galactic center could consist of such primordial objects, planets, comets, etc. We also discuss the possibility of the tidal break up of these primordial objects in the presence of a BH. The mass of BH required for tidal break up is calculated, and it is found that the mass of BH required for tidal break up increases with the DM particle mass and also with the increase in the fraction of baryons in these objects. The energy released during tidal breakup will be emitted as gravitational waves. The energy released, as well as the frequency of waves, is tabulated, and the frequency is in the sensitivity range of LIGO.

1. Introduction

Dark matter (DM) is theorized as one of the basic constituents of the Universe. DM is five times as abundant as ordinary matter in the Universe [1,2]. Many experiments with very sensitive detectors in different parts of the world have been operating for many years trying to catch traces of these DM particles (Xenon 1T, Cd-Te experiment, the Iodine or Argon detectors, the LUX or DAMA experiments, etc.); however, the results so far have been negative. In recent works, we had discussed the possibility of primordial planets composed entirely of dark matter (DM) [3] and considered this to be a possible reason for not detecting DM particles. The evolution of such planets as the Universe expands is discussed in detail in [4]. The formation of such objects and their presence in large numbers in our galaxy could significantly reduce the number of free DM particles moving around in the Universe.

In cosmology, the missing baryon problem remains an unidentified mystery at low redshifts. White and Rees [5] explained this missing baryon problem with the existence of primordial free-floating planets. Many such planets have been discovered so far. Most of these primordial planetary-mass objects are not bound to any host star.

Here, we discuss the possibility of baryons becoming mixed with DM particles in the formation of these primordial objects. During the phase of formation of these primordial objects, as the primeval ambient cloud collapses, we consider the presence of baryonic matter in addition to the DM particles.

2. Mass and Radius of DM Planet Admixed with Baryonic Matter

For forming the planet admixed with DM and baryonic particles, the gravitational binding energy density of the planet must be in balance with the radiation pressure, thermal pressure, and degeneracy pressure of baryonic and DM particles. Thus,

$$\frac{G{M}_T^2}{R^4}=\frac{{\hslash }^2{M}_D^{\raisebox{1ex}{$5$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}{R^5{m}_d^{\raisebox{1ex}{$8$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}+\frac{{\hslash }^2{M}_B^{\raisebox{1ex}{$5$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}{R^5{m}_p^{\raisebox{1ex}{$8$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}+\frac{G{M}_T{M}_B}{R^4}+a{\left(\frac{G{M}_T{m}_p}{k_{B}R}\right)}^4$$

(1)

where $M_T$ is the total mass of the planet, $M_B$ is the total mass of baryonic particles, $M_D$ is the total mass of DM particles, R is the radius of the planet, $m_d$ is the mass of DM particle, $m_p$ is mass of proton, $a$ is Stefan’s constant, and $k_B$ is the Boltzmann constant.

If we assume the $f$ fraction of baryonic particles becomes mixed with the $\left(1-f\right)$ fraction of DM particles, then $M_B$ and $M_D$ in Equation (1) can be replaced by $f{M}_T$ and $\left(1-f\right)M_T$, respectively. Thus, Equation (1) becomes

$$\frac{G{M}_T^2}{R^4}=\frac{{\hslash }^2{\left(1-f\right)}^{\raisebox{1ex}{$5$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}{M}_T^{\raisebox{1ex}{$5$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}{R^5{m}_d^{\raisebox{1ex}{$8$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}+\frac{{\hslash }^2{f}^{\raisebox{1ex}{$5$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}{M}_T^{\raisebox{1ex}{$5$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}{R^5{m}_p^{\raisebox{1ex}{$8$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}+\frac{Gf{M}_T^2}{R^4}+a{\left(\frac{G{M}_T{m}_p}{k_{B}R}\right)}^4$$

(2)

The mass of the planet formed with these particles [6] is given by

$$\mathrm{M}=\frac{M_{Pl}^3}{m_{eff}^2}$$

(3)

where $m_{eff}$ is the effective mass of the constituent particles forming the planet, which is given by

$$m_{eff}=\left(1-f\right)m_d+f{m}_B$$

(4)

Consider such a planet with 50% DM, assuming an $m_d$ of 60 GeV [7] and 50% of baryonic matter, the mass of the planet is $~2M_J$, where $M_J$ is the mass of Jupiter. For a planet of this mass, the baryonic radiation pressure will be very small compared with the degeneracy and thermal pressures. Thus, the radius of the object from Equation (2) becomes

$$R=\frac{{\hslash }^2{M}_T^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}{G}\left(\frac{{\left(1-f\right)}^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}{m_d^{\raisebox{1ex}{$8$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}+\frac{f^{\raisebox{1ex}{$5$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}{\left(1-f\right)m_p^{\raisebox{1ex}{$8$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}\right)$$

(5)

For the planet with a mass $~2M_J$, as discussed in the above case, the radius is worked out to be $9.8\times {10}^5$ cm.

3. Binary Systems of DM Objects Admixed with Baryonic Matter

These primordial planetary objects can form binary systems. Considering a binary system, each with a mass of $2M_J$ and size of $9.8\times {10}^5$ cm, as well as a separation of about 10 times their size, the orbital period P is given by

$$G{M}_T{P}^2=4{\pi }^2{R}^3$$

(6)

where $R$ is the orbital radius and $M_T$ is the total mass of the system. The orbital period is worked out to be P = 0.27 s, and the corresponding frequency is ω = 23 Hz. The binary system will be emitting energy as it revolves, and the energy emitted per unit time is given by

$$\dot{E}=\frac{32}{5}\frac{G}{c^5}{\mu }^2{R}^4{\omega }^6{ϵ}^2$$

(7)

where ϵ is the eccentricity of orbit and μ is the reduced mass of the system, which is given by

$$\mu =\frac{M_1{M}_2}{M_1+M_2}$$

(8)

$M_1$ and $M_2$ are the masses of individual objects in the binary system.

4. Mergers of Binary System

During the orbit of planets around one another, they lose energy, and the orbital radius keeps decreasing until it becomes $2R_{obj}.$ The final merger period and merger frequency of the binary system will be $P=0.0243\mathrm{s}$ and $\omega =260 \mathrm{Hz}$. This frequency is also within the existing range of LIGO [8]. The binding energy of the binary system will be emitted as gravitational waves, and is given by

$$E=\frac{G{M}_T^2}{R}$$

(9)

Table 1 shows the gravitational wave energy emitted by the binary system for different fractions of baryons admixed with DM particles of masses ranging from 20 to 100 GeV when forming the planet. It is found that for greater-mass DM particles, the energy emitted as gravitational waves decreases. As the fraction of baryons increases, the energy emitted by the binary system will increase. If we consider these binary systems to be situated at distance r from the Earth, then the strain h on Earth, due to the gravitational radiation emissions from them, is given by

$$h=\frac{2GE}{r{c}^4}$$

(10)

Table 1. Total energy emitted as gravitational waves by the binary system for different mass of DM particles and with different fractions of baryons for forming the planet.

f(%)	E (ergs) for mD = 20 GeV	E (ergs) for mD = 40 GeV	E (ergs) for mD = 80 GeV	E (ergs) for mD = 100 GeV
10	1.16 × 1050	4.68 × 1048	1.86 × 1047	6.57 × 1046
20	5.51 × 1049	2.24 × 1048	8.94 × 1046	3.17 × 1046
30	4.40 × 1049	1.82 × 1048	7.35 × 1046	2.61 × 1046
40	4.54 × 1049	1.93 × 1048	7.90 × 1046	2.81 × 1046
50	5.67 × 1049	2.50 × 1048	1.04 × 1047	3.72 × 1046
60	8.50 × 1049	3.95 × 1048	1.69 × 1047	6.08 × 1046
70	1.58 × 1050	8.00 × 1048	3.59 × 1047	1.30 × 1047
80	4.00 × 1050	2.36 × 1049	1.16 × 1048	4.27 × 1047
90	1.73 × 1051	1.49 × 1050	9.21 × 1048	3.58 × 1048

If this binary system is assumed to be at distances $1\mathrm{kpc}$ and $10\mathrm{kpc}$ from Earth, then the strains due to the gravitational wave are $2\times {10}^{-23}$ and $2\times {10}^{-24}, \mathrm{respectively}$. The corresponding flux on Earth at these distances will be $8\times {10}^{-9} \mathrm{ergs}/{\mathrm{m}}^2\mathrm{s}$ and $8\times {10}^{-11} \mathrm{ergs}/{\mathrm{m}}^2\mathrm{s}$, respectively.

5. Tidal Breakup of Objects

When a primordial degenerate object approaches a BH, the object can break if the tidal force is greater than the self-gravitational force of the object, i.e.,

$$\frac{4G{M}_{BH}{M}_{T}R}{d^3}\ge \frac{G{M}_T^2}{R^2}$$

(11)

where $M_T$ is the total mass of the object, $M_{BH}$ is the mass of BH required for the tidal breakup of the object, R is the radius of the object, and $d$ is the separation between the BH and the primordial object.

Considering the distance between the BH and object to be around 10 times the Schwarzchild radius ($d\approx 10(\frac{2G{M}_{BH}}{c^2})$), the minimum mass of BH required for the tidal break up of the object is given by

$$M_{BH}=\frac{c^3{R}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{45G^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{M}_T^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}$$

(12)

Figure 1 shows the mass of BH required for the tidal break up of the primordial planet when it comes near the BH. The mass of the BH required for tidal break up increases with an increase in the mass of DM particles, as well as with the fraction of baryons in the primordial planet. As these objects orbit the BH, they lose energy according to Equation (7). Table 2 shows the gravitational wave energy emitted per second by the DM object consisting of different-mass DM particles with different fractions of baryons when forming the primordial object. It is found that energy decreases with an increase in the mass of DM particles. When they lose energy, the orbital radius keeps decreasing until the radius becomes equal to the Schwarzschild radius ($R_{sch}$). At the Schwarzschild radius, the frequency is given by [9]

$$\omega =\sqrt{\frac{G{M}_T}{R^3}}$$

(13)

where $M_T$ is the total mass of the system and the orbital radius $R=R_{sch}$. The orbital binding energy will be emitted as the gravitational wave at this frequency. The time of the merger of the primordial object with the BH is given by [10]

$$t=\frac{5c^5{r}_i^4}{256M^2\mu G^3}$$

(14)

where c is speed of light, r_i is the initial orbital radius, M is the total mass of system involving BH and the object, μ is the reduced mass of system, and G is gravitational constant. Figure 2 shows the relation between the merger time and fraction of baryons in forming the primordial planet. It is found that the merger time increases with the increase in DM particle mass. Additionally, the merger time increases with the fraction of baryons, reaching a maximum for planets made of 60% baryonic matter.

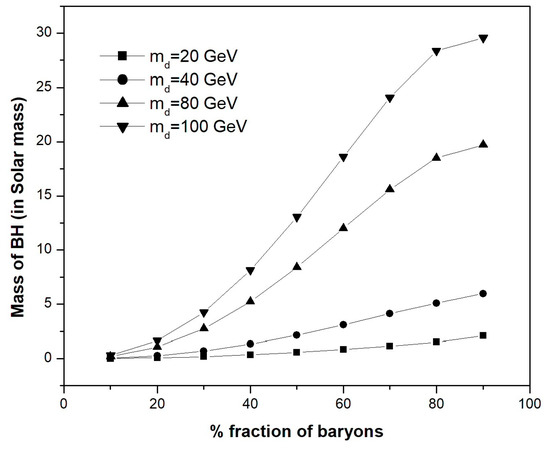
Figure 1. Mass of BH for tidal break up versus fraction of baryonic particles admixed to form the primordial planet for different-mass DM particles ranging from 20 GeV to 100 GeV.

Table 2. Gravitational radiation energy emitted per second by the DM planet admixed with baryons for different-mass DM particles.

f(%)	E (ergs) for mD = 20 GeV	E (ergs) for mD = 40 GeV	E (ergs) for mD = 60 GeV	E (ergs) for mD = 80 GeV	E (ergs) for mD = 100 GeV
10	9.39 × 1051	2.79 × 1049	1.08 × 1048	1.08 × 1047	1.82 × 1046
20	3.97 × 1050	1.51 × 1048	5.95 × 1046	6 × 1045	1.01 × 1045
30	9.13 × 1049	3.72 × 1047	1.49 × 1046	1.51 × 1045	2.56 × 1044
40	4.21 × 1049	1.82 × 1047	7.41 × 1045	7.58 × 1044	1.29 × 1044
50	3.01 × 1049	1.39 × 1047	5.79 × 1045	5.98 × 1044	1.02 × 1044
60	3.06 × 1049	1.55 × 1047	6.65 × 1045	6.99 × 1044	1.21 × 1044
70	4.43 × 1049	2.58 × 1047	1.16 × 1046	1.26 × 1045	2.2 × 1044
80	9.85 × 1049	7.38 × 1047	3.67 × 1046	4.17 × 1045	7.55 × 1044
90	4.03 × 1050	5.59 × 1048	3.58 × 1047	4.66 × 1046	9.21 × 1045

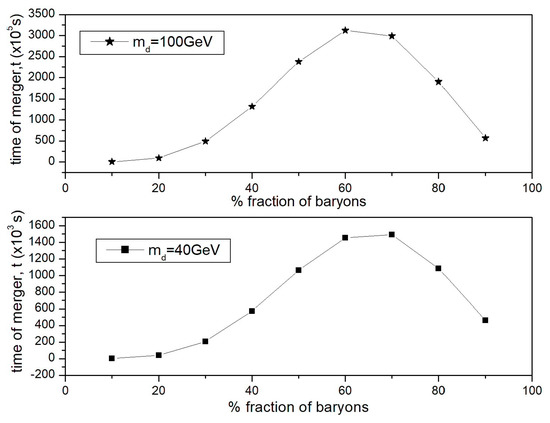
Figure 2. Merger time versus fractions of baryons in forming the primordial planet for DM particles of masses of 40 GeV and 100 GeV.

6. Conclusions

Here, we discussed the possibility of the admixture of baryons to DM primordial planets, with the DM particles varying in mass from 20 GeV to 100 GeV. We have considered different fractions of admixture to form the planet. The mass of primordial planets (admixed with DM and baryonic matter) is found to increase with the fraction of baryonic matter in the planets, and the mass of these objects can go well beyond the mass of Jupiter (around 40 times Jupiter’s mass), approaching sub-stellar mass (brown dwarf mass). The Kepler mission so far has found thousands of exoplanets, and more will be found by the Transiting Exoplanet Survey Satellite (TESS) mission. Many exoplanets (exo-Jupiters) discovered so far fall into this mass range, and we are unsure whether these exoplanets are entirely made of baryons. Some of the exoplanets with a mass several times Jupiter’s mass could be possible signatures of the presence of primordial planets with an admixture of baryonic and DM particles. Even if a small fraction of DM particles is trapped in these objects, the flux of ambient DM particles would be reduced significantly. This could be one of the many reasons for not detecting the DM particles in various experiments, such as XENON1T, etc., as suggested earlier. If two such primordial planets merge, they will release a lot of energy. The energy released and the time scale of the merger of these objects is found to increase with the mass of primordial objects. The frequency of the merger is matched with the frequency of LIGO. Here, we also discussed the possibility of the tidal break up of these primordial objects in the presence of BH. The mass of BH required for tidal break up is calculated, and it is found that the mass of BH required for tidal break up increases with DM particle mass and also with the increase in the fraction of baryons in these objects. DM, since decoupled from radiation during tidal breakup, will emit energy as gravitational waves.