Game of Life-like Opinion Dynamics: Generalizing the Underpopulation Rule

Abstract

Graph dynamics for a node-labeled graph is a set of updating rules describing how the labels of each node in the graph change in time as a function of the global set of labels. The underpopulation rule is graph dynamics derived by simplifying the set of rules constituting the Game of Life. It is known that the number of label configurations met by a graph during the dynamic process defined by such rule is bounded by a polynomial in the size of the graph if the graph is undirected. As a consequence, predicting the labels evolution is an easy problem (i.e., a problem in P) in such a case. In this paper, the generalization of the underpopulation rule to signed and directed graphs is studied. It is here proved that the number of label configurations met by a graph during the dynamic process defined by any so generalized underpopulation rule is still bounded by a polynomial in the size of the graph if the graph is undirected and structurally balanced, while it is not bounded by any polynomial in the size of the graph if the graph is directed although unsigned unless P = PSpace.

1. Introduction

Social networks, traffic networks (ant colonies and distributed message passing algorithms included), biological cell systems and cellular automata are all examples of sets of relations between pairs of “individuals” in which the “state” of an individual is somehow influenced by the set of its relations and evolves over time. As a couple of examples, an individual may join some event occurring in a pub if the amount of people joining the same event is reasonably large (so as to ensure opportunities to his/her social life) but not too large (so avoiding staying in an overcrowded pub), or an individual moves to a novel (expensive and complex) operating system only if a reasonable amount of her/his colleagues has already moved to it (in order, for instance, to ease the cooperation). In this paper, the second scenario is considered, in which a critical amount of an individual acquaintances getting some state is needed for that individual to obtain the same state.

Networks are naturally modeled as graphs, with nodes corresponding to individuals and edges/arcs to the symmetric/asymmetric relations between pairs of individuals. In fact, while many relations behave symmetrically (as friendship in some kinds of social networks), many real-world complex networks are directed (as people following famous stars but not followed by them, or the biological signal flow in biological networks; see, for instance, the discussion in [1]). In social network analysis, signed graphs, in which a labeling of the edges/arcs with values in $\{-1,+1\}$ is given, are used for distinguishing between relations ruled by friendship/trusting and relations ruled by antagonism/distrusting (see [2] and references quoted therein). Individuals’ state evolution in a network is then studied in terms of graph dynamics.

Following the definition in [3], an opinion dynamics is a state update rule in which the state of a node at step t only depends on its state at time $t-1$ and on the value of a function of the states of its neighbors at step $t-1$; the update rule is the same for every graph and for every node, and it does not change over time.

Many opinion dynamics stochastic models have been considered for unsigned graphs, such as the French–DeGroot model [4,5] and its extensions, the majority rule model [6], and the social impact model [7]; see also [3,8] for a survey. Some of these models have been adapted to the case of signed graphs [9,10,11,12].

Goles and Olivos [13] proposed single-threshold deterministic opinion dynamics for weighted graphs in which every node at each step is either in state 0 or in state 1, and at the next step, it obtains state 1 if and only if the sum of the products between the current state of each of its k neighbors with the weight of the edge connecting the neighbor to the individual is at least $\theta \left(k\right)$ for a given function $\theta$ defined on the node set. In [14], a couple of deterministic opinion dynamics models, the overpopulation and theunderpopulation rules, that still work with binary node states are defined for unsigned graphs as a simplification of the Game-of-Life rules [15]; according to the underpopulation rule, nodes’ opinion changes are controlled by two constant values, $c^{+}$ and $c^{-}$. A node gets a positive opinion if either its opinion is already positive and at least $c^{+}$ neighbors have a positive opinion, or its opinion is negative and at least $c^{-}$ neighbors have a positive opinion. The local threshold-based rules defined in [16] generalize the underpopulation rule both in that they are designed for arc-signed directed graphs and in that the nodes’ opinion changes are now controlled by two functions of the node degree, ${\theta }^{+}$ and ${\theta }^{-}$, instead of by two constant values.

• Related literature. The study of various aspects of graph dynamics has received very wide attention in the literature, and a detailed discussion of papers and results about this topic is out of the scope of this paper. Broadly speaking, two scenarios may be identified in this setting.

In the first scenario, each node is in one of two states (with possible generalizations), say “old state” and “new state”, and once a node moves from an old state to a new state, it will remain in the new state forever. Within this scenario, two problems have been largely studied, in several variations and with respect to several dynamics: the influence maximization and the target set selection problems. In the influence maximization problem, the goal is detecting a small set of nodes to put in the new state in order to make a maximum size subset of nodes move to the new state [17,18,19]. Somehow symmetrically, in the target set selection problem, the goal is detecting a minimum size set of nodes to put in the new state in order to make all the other nodes in the graph move to the new state. Initially, the setting of only positive influences (that is, the underlying graph is unsigned) was considered in which whenever an individual knows that a neighbor has obtained the new state, such an individual will gain some evidence that getting the new state is a good idea. In other words, any individual always increases its support in favor of the new state whenever one of its neighbors obtains it. Among the many models introduced in this setting, the voter model [20], the linear threshold model [21], and the independent cascade model [22,23] have had a large impact in the study of diffusion processes over networks.

In several network settings, also negative link effects are to be considered. In [24,25,26,27], it is assumed that individuals may develop a positive or negative opinion about getting the new state and, in the latter case, they may negatively influence their neighbors. In [28,29,30], it is taken into account the possibility that some relations between individuals are ruled by, for instance, antagonism and distrusting while being assumed that node opinions about getting the new state are always positive: here, receiving positive feedback from an untrusted/antagonist neighbor results in increasing the support for not obtaining the new state. For instance, in [30], the target set selection is studied in the model in which a node obtains the new state at step t if and only if for the first step, one of its neighbors obtains the new state $t-1$, and all its node neighbors that obtain the new state at step $t-1$ are joined to the node by a positive link. In [31,32], the two approaches (positive/negative opinions and positive/negative relationships) are jointly considered.

In the second scenario, each node is in one of two states (with possible generalizations), say “$-1$” and “1”, and it can move from one state to the other an unlimited number of times. As noticed in several papers on the topic, being allowed to change from one state to the other well fits to describe people changing opinions (see [8,33] among the others), so that the graph dynamics in this scenario are often referred to as opinion dynamics.

Within this scenario, problems that have been considered concern the study of the reachability of a consensus configuration in which all nodes have the same opinion, starting from a given opinion configuration [33,34,35,36] or in a random graph [37]; the reachability of an equilibrium configuration in a random graph in which no node changes its opinion any longer [38]; if an opinion obtained by a minority of nodes may become the opinion of the majority of nodes [39]; and if a Nash equilibrium in a game theoretic setting can be reached [40]. In [41], the case of multiple (not binary) alternatives is considered with respect to the influence maximization. A review of topics in consensus and coordination of multi-agent systems, also considering signed networks, is provided in [42].

The reachability problems studied in the cited papers mainly contain some degree of randomness, either in the graph [37,38] or in the opinion dynamics (the models in [33,34,35,36] assume that not all nodes that could change their opinion actually do it). Furthermore, [33,34,35,36] (somehow) search for an initial opinion configuration from which a consensus configuration is reachable. In [16,43], the setting is different in two aspects. First, no randomness is considered: in particular, the opinion dynamics forces all nodes in the condition of changing their opinion to simultaneously doing it. Then, a graph is given in a given initial opinion configuration, and the question is something like whether a (given) target configuration is reachable from the initial one or not. It is worthwhile to be observed that the answer to such a question can be derived by simply letting the dynamics work (one opinion configuration after the other) till the target configuration is eventually met. This procedure is in fact effective in the first scenario (when nodes never go back to the old state) since, in this case, the number of configurations that a graph can meet during its evolution is bounded by the number n of its nodes. Conversely, as to the second scenario, since each node has the possibility of changing its opinion more and more times, the procedure could require a sequence of $2^n$ steps, so putting its complexity outside the tractability threshold.

In [43], it is proved a tight bound $\Theta \left(n^2\right)$ on the number of configurations met by an unsigned undirected graph evolving according to a deterministic majority dynamics (in which a node changes its opinion if and only if the majority of its neighbors has the other opinion) starting from any initial configuration. In [14], a polynomial bound in the graph size on the number of configurations met by an unsigned undirected graph evolving according to an underpopulation rule and starting at any initial opinion configuration is provided. In [16], a similar polynomial bound is first proved for unsigned undirected graphs evolving according to any local threshold-based dynamics; then, the bound is proved when the graph is signed and undirected, and it evolves according to an extension of the deterministic majority dynamics to signed graphs. All this makes the reachability problems tractable when considered with respect to a local threshold-based dynamics and the graph is undirected and unsigned, or when considered with respect to the deterministic majority dynamics and the (signed or unsigned) graph is undirected. In [16], it is also proved that the reachability problems are PSPACE-complete when the graph is directed, although unsigned, and evolves with respect to the deterministic majority dynamics.

• Paper contribution. This paper is devoted to the study of the generalization of the underpopulation rule to signed and directed graphs. Both the underpopulation rule and the deterministic major dynamics are special occurrences of local threshold-based dynamics: indeed, as it will become clear in the next section, the underpopulation rule occurs by choosing ${\theta }^{+}=c^{+}$ and ${\theta }^{-}=c^{-}$, that is, as two constant functions, while the deterministic majority dynamics occurs by choosing ${\theta }^{+}\left(k\right)=\lceil \frac{k}{2}\rceil$ and ${\theta }^{-}\left(k\right)=\lfloor \frac{k}{2}\rfloor +1$. Hence, on the majority dynamics side, the amount of a node’s neighbors in a given opinion needed to make that node change or keep its current opinion linearly increases with the node degree, while such an amount is independent of the node degree in the underpopulation rule.

Of course, each of the two dynamics well fits in different contexts. The spread of technologies, such as cellular phones platforms, is suitable to be described by majority dynamics in that the adoption of a new technology also depends on the incentives people have to communicate with friends who have already adopted it. On the other hand, an individual may decide to assume a new drug after observing the good effects of the drug on a large enough amount of its acquaintances—independent of the percentage of its acquaintances that have tested the drug.

From a theoretical point of view, it is interesting to study if the just outlined dichotomy between “constant size requirements” and “linear increase in the node degree requirements” entails meaningful differences in the size of the set of opinion configurations a graph enters in while evolving according to the two dynamics. The main result of this paper is proving that, in fact, in many cases, the sizes of such sets in the two opinion dynamics are strictly related. Specifically, we have the following:

• Like in the majority dynamics case, unless P = PSpace, the total number of opinion configurations an unsigned directed graph enters while evolving according to an underpopulation rule is not polynomially bounded in the size of the graph, and this is true even when the maximum indegree of the graph is 6 and $c^{+}=3$ and $c^{-}=4$.
• The total number of opinion configurations a structurally balanced undirected graph enters while evolving according to an underpopulation rule is polynomially bounded in the size of the graph.

As for the former point, actually, it is here proved that it is PSpace-complete to decide if a given node will ever obtain one of the two opinions when a directed unsigned graph in a given initial opinion configuration evolves according to undepopulation dynamics. The PSpace-completeness is proved by the a technique similar to that in Cook’s theorem, namely, it will be shown that the computation of any deterministic Turing machine T on any input x can be simulated by the underpopulation evolution of a related graph $G\left(T\right)$, starting from an opinion configuration $\omega \left(x\right)$ and that $G\left(T\right)$ and $\omega \left(x\right)$ can be computed in polynomial time in the sizes of T and x.

As for the latter point, we recall that a signed undirected graph is structurally balanced [44] if the set of its nodes can be partitioned into two subsets X and Y such that all edges joining a node in X to a node in Y are negative, and all the other edges are positive. The proof of the latter point occurs in two steps, both by the simulation technique.

The first step has somehow independent interest. Specifically, it is here shown how to simulate the opinion evolution of a structurally balanced graph according to symmetric dynamics by the opinion evolution of a related unsigned undirected graph according to related symmetric dynamics, where symmetric dynamics is a local threshold-based dynamics such that ${\theta }^{+}\left(k\right)+{\theta }^{-}\left(k\right)=k$ for all $k\in \mathbb{N}$. Such a simulation and the result in [16] on the number of configurations met by an unsigned undirected graph evolving according to any local threshold based dynamics jointly prove that a polynomial bound exists on the total number of configurations met by a structurally balanced graph evolving according to a symmetric dynamics. The simulation technique also deserves to be mentioned in that it requires the definition of edge-labels dynamics and of the support graph of a graph in some opinion configuration; after that, it is shown that the opinion evolution of the original graphs may be, somehow concisely, described by the edge-labels evolution of its support graph.

The second step shows how to simulate the opinion evolution of a signed graph according to any underpopulation dynamics by the opinion evolution of a related signed graph according to related symmetric dynamics and that if the first graph is structurally balanced, then the second graph is structurally balanced as well.

It is worth noticing that the structural balance property of a graph was already considered in several papers [9,10,11,44], proving to be useful to the convergence of the dynamics to specific opinion distributions.

The above outlined achievements are formally stated in the next section, together with some of their consequences.

2. Results

Before formally stating the results obtained in this paper, some formal definitions are required. Table 1 lists some of the notations introduced in this paper.

Table 1. List of symbols.

Notation	Meaning
$\lambda$	arc/edge sign function
$\omega$ (and sometimes $\pi$)	opinion configuration
$\mathbf{d}$	generic opinion dynamics
for $t>0$, ${\mathbf{d}}^t$	the application of dynamics $\mathbf{d}$ for t times
	(${\mathbf{d}}^t(G,\omega )$ is the opinion configuration met by G after
	t steps of its $\mathbf{d}$-evolution starting at $\omega$)
${\mathbf{d}}_{({\theta }^{+},{\theta }^{-})}$	local threshold-based opinion dynamics ruled by
	${\theta }^{+}:\mathbb{N}\to \mathbb{N}$ and ${\theta }^{-}:\mathbb{N}\to \mathbb{N}$
${\mathbf{d}}_{\theta }$	symmetric dynamics ruled by $\theta :\mathbb{N}\to \mathbb{N}$
	(${\mathbf{d}}_{\theta }={\mathbf{d}}_{({\theta }^{+},{\theta }^{-})}$ with ${\theta }^{+}\left(k\right)=\theta \left(k\right)$ and ${\theta }^{-}\left(k\right)=k-\theta \left(k\right)$)
${\mathbf{d}}_{(c^{+},c^{-})}$	underpopulation opinion dynamics ruled by $c^{+},c^{-}\in \mathbb{N}$
	(${\mathbf{d}}_{(c^{+},c^{-})}={\mathbf{d}}_{({\theta }^{+},{\theta }^{-})}$ with ${\theta }^{+}\left(k\right)=c^{+}$ and ${\theta }^{-}\left(k\right)=c^{-})$)
${\mathcal{E}}_{\mathbf{d}}(G,\omega )$	sequence of distinct opinion configurations met by graph G
	while evolving according to dynamics $\mathbf{d}$
	(it becomes ${\mathcal{E}}_{{\mathbf{d}}_{({\theta }^{+},{\theta }^{-})}}(G,\omega )$, ${\mathcal{E}}_{{\mathbf{d}}_{\left(\theta \right)}}(G,\omega )$, ${\mathcal{E}}_{{\mathbf{d}}_{\left(c^{+}{c}^{-}\right)}}(G,\omega )$
	in the specific dynamics)
u-RT	the problem of deciding if ${\omega }^{\prime }\in {\mathcal{E}}_{{\mathbf{d}}_{(c^{+},c^{-})}s}(G,\omega )$ exists
	such that ${\omega }^{\prime }\left(u\right)=1$ for all $u\in U$, given: dynamics ${\mathbf{d}}_{(c^{+},c^{-})}$,
	graph G, opinion configuration $\omega$, subset of nodes U.

A directed signed graph $G=(V,A,\lambda )$ is a directed graph together with an arc-labeling function $\lambda :A\to \{-1,1\}$. An undirected signed graph $G=(V,E,\lambda )$ is similarly defined, with $\lambda$ being an edge labeling function, that is, $\lambda :E\to \{-1,1\}$. Within this paper, for any node v of a directed (undirected) signed graph G, $N\left(u\right)$ denotes the set of in-neighbors (respectively, neighbors) of u and ${\delta }_u=\left|N\left(u\right)\right|$. Finally, $\Delta =max\{{\delta }_u:u\in V\}$.

An opinion configuration of a signed graph G is a node-labeling function $\omega :V\to \{-1,1\}$, stating whether a given node is in favor of or against a specific topic. Nodes influence each other so that their opinions change over time: in particular, positive in-neighbors of a node u positively influence u, that is, their influence works in favor of u obtaining their same opinion, while negative in-neighbors of u negatively influence u, that is, their influence works in favor of u obtaining their opposite opinion. In this respect, for any in-neighbor v of any node u, we say that v pushes u to 1 at $\omega$ if $\omega \left(v\right)=1$ and $\lambda (v,u)=1$ or $\omega \left(v\right)=-1$ and $\lambda (v,u)=-1$, and that v pushes u to $-1$ at $\omega$ if $\omega \left(v\right)=-1$ and $\lambda (v,u)=1$ or $\omega \left(v\right)=1$ and $\lambda (v,u)=-1$. Finally, $P^{+}\left(u\right)$ and $P^{-}\left(u\right)$ shall denote the number of in-neighbors of u pushing u, respectively, to 1 and to $-1$ at $\omega$.

An opinion dynamics is functional $\mathbf{d}$ which specifies, for a given signed graph G and an opinion configuration $\omega$ of G, the next opinion configuration $\mathbf{d}(G,\omega )$ of G. In the remainder of this paper, for any $u\in V$, $\mathbf{d}(G,\omega )\left(u\right)$ is the opinion of node u obtained after the influence of its neighbors according to $\mathbf{d}$, that is, the opinion of u after one step of the opinion evolution process of G starting at $\omega$; similarly, for any $t>0$, $\mathbf{d}{(G,\omega )}^t\left(u\right)$ is the opinion of u after t steps of the opinion evolution process of G starting at $\omega$ and occurring according to $\mathbf{d}$.

The opinion configuration evolution of a signed graph G in a configuration $\omega$ with respect to opinion dynamics $\mathbf{d}$ (or, in short, the $\mathbf{d}$-evolution of G) is the sequence ${\mathcal{E}}_{\mathbf{d}}(G,\omega )=⟨{\omega }_1=\omega ,{\omega }_2,\dots ,{\omega }_T⟩$ of distinct opinion configurations such that $T\le 2^{\left|V\right|}$ (the number of configurations of V) and the following:

• For $t=2,\dots ,T$, ${\omega }_t=\mathbf{d}(G,{\omega }_{t-1})$;
• There exists $h\le T$ such that ${\omega }_h=\mathbf{d}(G,{\omega }_T)$.

With a slight abuse of notation, the sequence ${\mathcal{E}}_{\mathbf{d}}(G,\omega )$ shall be dealt with as a set as well.

A local threshold-based dynamics is a dynamics ${\mathbf{d}}_{({\theta }^{+},{\theta }^{-})}$ ruled by a pair of threshold functions ${\theta }^{+}:\mathbb{N}\to \mathbf{N}$ and ${\theta }^{-}:\mathbb{N}\to \mathbf{N}$ as described in the following: for any node u and for any opinion configuration $\omega$, ${\mathbf{d}}_{({\theta }^{+},{\theta }^{-})}(G,\omega )={\omega }^{\prime }$ is defined as

$${\omega }^{\prime }\left(u\right)=\left\{\begin{array}{cc}1\hfill & \mathrm{if} \omega \left(u\right)=1 \mathrm{and} P^{+}\left(u\right)\ge {\theta }^{+}\left({\delta }_u\right)\hfill \\ & \mathrm{or} \omega \left(u\right)=-1 \mathrm{and} P^{+}\left(u\right)\ge {\theta }^{-}\left({\delta }_u\right),\hfill \\ -1\hfill & \mathrm{if} \omega \left(u\right)=1 \mathrm{and} P^{+}\left(u\right)<{\theta }^{+}\left({\delta }_u\right)\hfill \\ & \mathrm{or} \omega \left(u\right)=-1 \mathrm{and} P^{+}\left(u\right)<{\theta }^{-}\left({\delta }_u\right),\hfill \end{array}\right.$$

or, equivalently, as

$${\omega }^{\prime }\left(v\right)=\left\{\begin{array}{cc}\omega \left(v\right)\hfill & \mathrm{if} \omega \left(v\right)=1 \mathrm{and} P^{+}\left(v\right)\ge {\theta }^{+}\left({\delta }_v\right)\mathrm{or}\hfill \\ \hfill & \omega \left(v\right)=-1 \mathrm{and} P^{-}\left(v\right)\ge {\delta }_v-{\theta }^{-}\left({\delta }_v\right),\hfill \\ -\omega \left(v\right)\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(1)

A local threshold-based dynamics is symmetric if ${\theta }^{+}\left(k\right)+{\theta }^{-}\left(k\right)=k$ for any $k\in \mathbb{N}$. Notice that symmetric dynamics is actually ruled by a single threshold function, in that ${\theta }^{-}\left(k\right)=k-{\theta }^{+}\left(k\right)$; hence, in the remaining of this paper, the notation ${\mathbf{d}}_{\theta }$ will denote a symmetric dynamics and will stand for ${\mathbf{d}}_{({\theta }^{+},{\theta }^{-})}$ with ${\theta }^{+}\left(k\right)=\theta$ and ${\theta }^{-}\left(k\right)=k-\theta \left(k\right)$.

The underpopulation opinion dynamics considered in [14] is a noticeable example of a (family of) local threshold-based opinion dynamics, which corresponds to having, for any $u\in V$, ${\theta }^{+}\left(u\right)=c^{+}$ and ${\theta }^{-}\left(u\right)=c^{-}$ for some pair of constants $c^{+},c^{-}\in \mathbf{N}$. The underpopulation dynamics ruled by the constants $c^{+}$ and $c^{-}$ will be denoted as ${\mathbf{d}}_{(c^{+},c^{-})}$.

In what follows, theorems and corollaries constituting this paper contribution, which will be mainly proved in the next section, are stated.

Theorem 1. 

For any structurally balanced signed graph $G=(V,E,\lambda )$ of maximum degree Δ, for any opinion configuration ω of G and for any symmetric local threshold-based opinion dynamics ${\mathbf{d}}_{\theta }$,

$$\left|{\mathcal{E}}_{{\mathbf{d}}_{\theta }}(G,\omega )\right|\le 4\left|E\right|+2\left|V\right|+4\Delta (\Delta +1)\left|V\right|+2.$$

Theorem 2. 

For any structurally balanced signed graph $G=(V,E,\lambda )$, for any opinion configuration ω of G and for any underpopulation opinion dynamics ${\mathbf{d}}_{(c^{+},c^{-})}$, it holds that $\left|{\mathcal{E}}_{{\mathbf{d}}_{(c^{+},c^{-})}}(G,\omega )\right|\in O\left(\right|E|+\left|V\right|{\Delta }^4)$. More precisely,

$$\left|{\mathcal{E}}_{{\mathbf{d}}_{(c^{+},c^{-})}}(G,\omega )\right|<4\left|E\right|+2\left|V\right|+{2\left|V\right|(2\Delta +3)(2\Delta +4)}^3+2.$$

Within the framework defined in this paper, the underpopulation-ReachTarget problem (in short, u-RT) asks for deciding, given underpopulation opinion dynamics ${\mathbf{d}}_{(c^{+},c^{-})}$, a signed oriented graph G, a target set of nodes U and an opinion configuration $\omega$ of G, if a configuration ${\omega }^{\prime }\in {\mathcal{E}}_{{\mathbf{d}}_{(c^{+},c^{-})}s}(G,\omega )$ exists such that ${\omega }^{\prime }\left(u\right)=1$ for all $u\in U$.

Theorem 3. 

The problem u-RT is PSpace-complete, even when restricted to the dynamics ${\mathbf{d}}_{(3,4)}$, to unsigned (directed) graphs with maximum indegree 6 and to size 1 target sets.

The following corollary is a remarkable consequence of Theorem 3.

Corollary 1. 

If $\mathrm{P}\ne \mathrm{P}\mathrm{S}\mathrm{p}\mathrm{a}\mathrm{c}\mathrm{e}$, then there does not exist any polynomial $\mathcal{P}$ such that, for every directed graph $G=(V,A)$ and for every opinion configuration $\omega :V\to \{-1,1\}$ of G, $|{\mathcal{E}}_{{\mathbf{d}}_{(3,4)}}(G,\omega )|\le \mathcal{P}(\left|G\right|)$.

Needless to say, the PSpace-completeness proved in Theorem 3 allows to state in a more general form the above corollary, as described in what follows.

Let $h,k\in \mathbb{N}$ and let $f:\mathbb{N}\times \mathbb{N}\to \mathbb{N}$; ${\mathcal{P}}^{f(h,k)}$ shall denote the class of polynomials whose degree is $f(h,k)$.

Corollary 2. 

If $\mathrm{P}\ne \mathrm{P}\mathrm{S}\mathrm{p}\mathrm{a}\mathrm{c}\mathrm{e}$ then, for any $f:\mathbb{N}\times \mathbb{N}\to \mathbb{N}$, there does not exist $p\in {\mathcal{P}}^{f(c^{+},c^{-})}$ such that, for every underpopulation opinion dynamics ${\mathbf{d}}_{(c^{+},c^{-})}$, for every unsigned directed graph $G=(V,A)$ and for every opinion configuration $\omega :V\to \{-1,1\}$ of G, $|{\mathcal{E}}_{{\mathbf{d}}_{(c^{+},c^{-})}}(G,\omega )|\le p(\left|G\right|)$.

3. Proofs

3.1. Proof of Theorem 1: Polynomial Bound to $\left|{\mathcal{E}}_{{\mathbf{d}}_{\theta }}(G,\omega )\right|$ in Structurally Balanced Graphs

It is well-known that a signed graph $G=(V,E,\lambda )$ is structurally balanced if and only if no cycle in G contains an odd number of edges labeled $-1$.

The aim of this section is showing that, for any structurally balanced signed graph $G=(V,E,\lambda )$, for any opinion configuration $\omega$ of G and for any symmetric local threshold-based opinion dynamics ${\mathbf{d}}_{\theta }$, the size of ${\mathcal{E}}_{{\mathbf{d}}_{\theta }}(G,\omega )$ is polynomially bounded in the size of G. This goal is met by reducing the ${\mathbf{d}}_{\theta }$-opinion evolution of a structurally balanced signed graph $G=(V,E,\lambda )$ starting at some opinion configuration $\omega$ to the ${\mathbf{d}}_{\theta }$-opinion evolution of the undirected unsigned graph $\overline{G}=(V,E)$ corresponding to G and starting at a properly defined opinion configuration $\overline{\omega }$.

The reduction occurs in two steps. First, in Section 3.1.1, the edge-sign dynamics and the support graph associated with a signed graph in some initial opinion configuration are defined, and it is shown that the opinion evolution of the original signed graph with respect to a symmetric local threshold-based dynamics can be simulated by the edge-signs evolution of its support graph. Then, in Section 3.1.2, we show that the support graph of a structurally balanced signed graph $G=(V,E,\lambda )$ in any opinion configuration $\omega$ is the support graph of the undirected unsigned graph $\overline{G}=(V,E)$ in some opinion configuration $\overline{\omega }$. All this will lead to the following lemma, formally proved in Section 3.1.3.

Lemma 1. 

For any structurally balanced signed graph $G=(V,E,\lambda )$, for any opinion configuration ω of G and for any symmetric local threshold-based opinion dynamics ${\mathbf{d}}_{\theta }$, there exists an opinion configuration $\overline{\omega }$ of the undirected unsigned graph $\overline{G}=(V,E)$ such that

$$|{\mathcal{E}}_{{\mathbf{d}}_{\theta }}(G,\omega )|=|{\mathcal{E}}_{{\mathbf{d}}_{\theta }}(\overline{G},\overline{\omega })|.$$

In [16], the following theorem was proved.

Theorem 4. 

For any local threshold-based opinion dynamics ${\mathbf{d}}_{({\theta }^{+},{\theta }^{-})}$, for any undirected unsigned graph $G=(V,E)$ of maximum degree Δ and for any opinion configuration ω of G, $\left|{\mathcal{E}}_{({\mathbf{d}}_{{\theta }^{+},{\theta }^{-})}}(G,\omega )\right|\le 4\left|E\right|+2\left|V\right|+4\Delta (\Delta +1)\left|V\right|+2$.

From Lemma 1 and Theorem 4, the bound on the number of configurations met by a structurally balanced graph during its evolution according to a symmetric dynamics stated by Theorem 1 finally follows.

3.1.1. First Step: Symmetric Dynamics and Support Graphs

Given a signed graph $G=(V,E,\lambda )$ and an opinion configuration $\omega$ of G, we say that edge $(u,v)\in E$ $\omega$-supports $\omega \left(v\right)$ if $\lambda (u,v)\omega \left(u\right)=\omega \left(v\right)$ (and, hence, $\lambda (u,v)\omega \left(v\right)=\omega \left(u\right)$ so that $(u,v)$ $\omega$-supports $\omega \left(u\right)$ as well).

Let $G=(V,E,\lambda )$ be a signed graph and let $\omega$ be an opinion configuration of G. The support graph associated with G and $\omega$ is the edge-signed graph ${\mathcal{S}}_{G,\omega }=(V,E,\sigma )$ such that $\sigma :E\to \{-1,1\}$ is defined as follows: for every $(u,v)\in E$

$$\sigma (u,v)=\left\{\begin{array}{cc}1\hfill & \mathrm{if} (u,v) \omega \text{-}\mathrm{supports} \omega \left(v\right),\mathrm{that} \mathrm{is},\lambda (u,v)\omega \left(u\right)=\omega \left(v\right),\hfill \\ -1\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

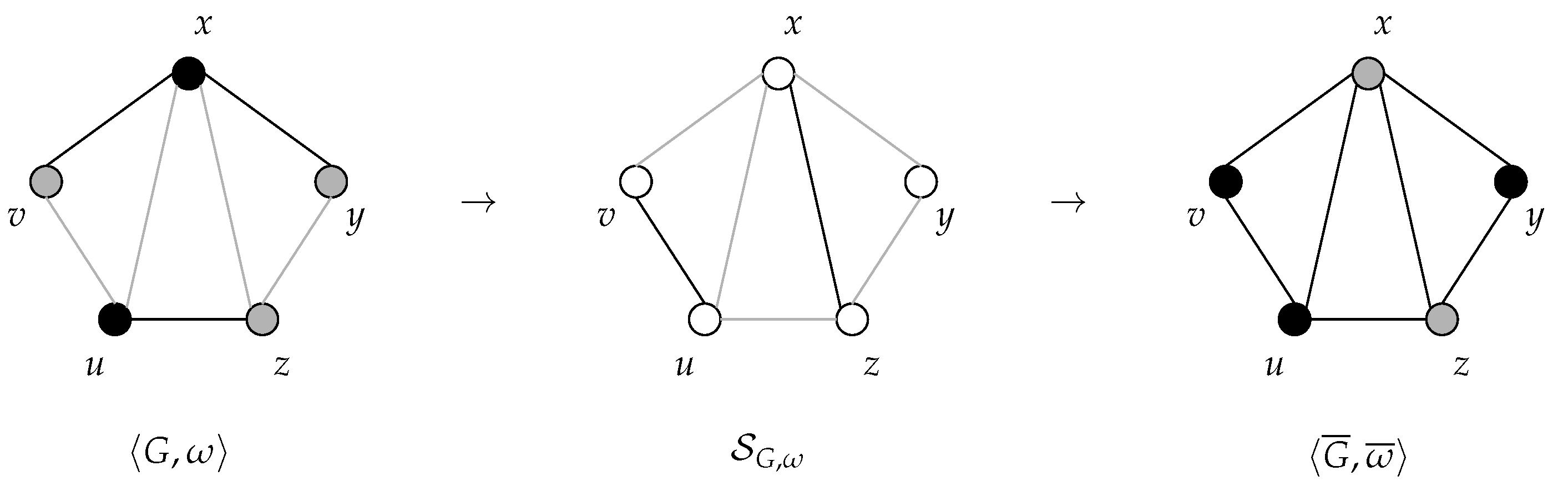
In Figure 1, an example of the support graph of a signed graph in a given opinion configuration is shown.

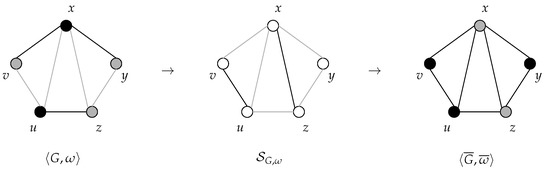
Figure 1. An example of the construction of the structurally balanced support graph ${\mathcal{S}}_{G,\omega }$ of a structurally balanced graph $G=(V,E,\lambda )$ in an opinion configuration $\omega$ and, then, of the construction of an opinion configuration $\overline{\omega }$ of the unsigned graph $\overline{G}=(V,E)$ such that ${\mathcal{S}}_{G,\omega }={\mathcal{S}}_{\overline{G},\overline{\omega }}$. Negative edges as well as negative node labels are grey, and positive ones are black.

Let ${\mathbf{d}}_{\theta }$ be a symmetric local threshold-based opinion dynamics. The following edge dynamics ${\mathbf{a}}_{\theta }$ is defined for ${\mathcal{S}}_{G,\omega }$: by denoting as ${\sigma }^{\prime }={\mathbf{a}}_{\theta }\left({\mathcal{S}}_{G,\omega }\right)$, for any $(u,v)\in E$ it is

$${\sigma }^{\prime }(u,v)=\left\{\begin{array}{cc}\sigma (u,v)\hfill & \mathrm{if} p_{\sigma }\left(u\right)\ge \theta \left(u\right)\wedge p_{\sigma }\left(v\right)\ge \theta \left(v\right)\hfill \\ & \mathrm{or} p_{\sigma }\left(u\right)<\theta \left(u\right)\wedge p_{\sigma }\left(v\right)<\theta \left(v\right),\hfill \\ -\sigma (u,v)\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

where, for $u\in V$, $p_{\sigma }\left(u\right)=\left|\{(u,v)\in E:\sigma (u,v)=1\}\right|$.

The next lemma proves that the ${\mathbf{d}}_{\theta }$-evolution of a signed graph G in an opinion configuration $\omega$ reflects in the ${\mathbf{a}}_{\theta }$-edge-evolution of ${\mathcal{S}}_{G,\omega }$.

Lemma 2. 

For any signed graph $G=(V,E,\lambda )$ and for any opinion configuration ω of G, it holds that ${\mathcal{S}}_{G,{\mathbf{d}}_{\theta }(G,\omega )}=(V,E,{\mathbf{a}}_{\theta }\left({\mathcal{S}}_{G,\omega }\right))$.

Proof. 

We set ${\omega }^{\prime }={\mathbf{d}}_{\theta }(G,\omega )$ and as ${\sigma }^{\prime }={\mathbf{a}}_{\theta }\left({\mathcal{S}}_{G,\omega }\right)$.

For every $u\in V$, by the definition of $\sigma$ and of ${\mathbf{d}}_{\theta }$, the following holds:

• if $\omega \left(u\right)=1$ then $p_{\sigma }\left(u\right)=P^{+}\left(u\right)$ and, hence, ${\omega }^{\prime }\left(u\right)=1$ if and only if $p_{\sigma }\left(u\right)=P^{+}\left(u\right)\ge \theta \left(u\right)$,
• if $\omega \left(u\right)=-1$ then $p_{\sigma }\left(u\right)=P^{-}\left(u\right)$ and, hence, ${\omega }^{\prime }\left(u\right)=-1$ if and only if $p_{\sigma }\left(u\right)=P^{-}\left(u\right)\ge \theta \left(u\right)$.

This proves that, for every $u\in V$, ${\omega }^{\prime }\left(u\right)=\omega \left(u\right)$ if and only if $p_{\sigma }\left(u\right)\ge \theta \left(u\right)$.

Let $(u,v)\in E$. If $\sigma (u,v)=1$, that is, $\lambda (u,v)\omega \left(u\right)=\omega \left(v\right)$, the following holds:

• If ${\omega }^{\prime }\left(u\right)=\omega \left(u\right)$ and ${\omega }^{\prime }\left(v\right)=\omega \left(v\right)$ then

  $$\lambda (u,v){\omega }^{\prime }\left(u\right)=\lambda (u,v)\omega \left(u\right)=\omega \left(v\right)={\omega }^{\prime }\left(v\right),$$

  so that $(u,v)$${\omega }^{\prime }$-supports ${\omega }^{\prime }\left(v\right)$. On the other hand, if ${\omega }^{\prime }\left(u\right)=\omega \left(u\right)$ and ${\omega }^{\prime }\left(v\right)=\omega \left(v\right)$ then $p_{\sigma }\left(u\right)\ge \theta \left(u\right)$ and $p_{\sigma }\left(v\right)\ge \theta \left(v\right)$, so that ${\sigma }^{\prime }(u,v)=\sigma (u,v)=1$.
  Similarly, if ${\omega }^{\prime }\left(u\right)\ne \omega \left(u\right)$ and ${\omega }^{\prime }\left(v\right)\ne \omega \left(v\right)$, then $\lambda (u,v){\omega }^{\prime }\left(u\right)\ne \lambda (u,v)\omega \left(u\right)=\omega \left(v\right)$ so that $\lambda (u,v){\omega }^{\prime }\left(u\right)={\omega }^{\prime }\left(v\right)$, that is, $(u,v)$ ${\omega }^{\prime }$-supports ${\omega }^{\prime }\left(v\right)$. On the other hand, if ${\omega }^{\prime }\left(u\right)\ne \omega \left(u\right)$ and ${\omega }^{\prime }\left(v\right)\ne \omega \left(v\right)$ then $p_{\sigma }\left(u\right)<\theta \left(u\right)$ and $p_{\sigma }\left(v\right)<\theta \left(v\right)$, so that ${\sigma }^{\prime }(u,v)=\sigma (u,v)=1$.
• If ${\omega }^{\prime }\left(u\right)=\omega \left(u\right)$ and ${\omega }^{\prime }\left(v\right)\ne \omega \left(v\right)$ then $\lambda (u,v){\omega }^{\prime }\left(u\right)\ne {\omega }^{\prime }\left(v\right)$, so that $(u,v)$ does not ${\omega }^{\prime }$-support ${\omega }^{\prime }\left(v\right)$. On the other hand, if ${\omega }^{\prime }\left(u\right)=\omega \left(u\right)$ and ${\omega }^{\prime }\left(v\right)\ne \omega \left(v\right)$ then $p_{\sigma }\left(u\right)\ge t\left(u\right)$ and $p_{\sigma }\left(v\right)<t\left(v\right)$, so that ${\sigma }^{\prime }(u,v)\ne \sigma (u,v)$, that is, ${\sigma }^{\prime }(u,v)=-1$.

This proves that, for any $(u,v)\in A$, if $\sigma (u,v)=1$ then ${\sigma }^{\prime }(u,v)=1$ if and only if $(u,v)$${\omega }^{\prime }$-supports ${\omega }^{\prime }\left(v\right)$. Similarly, it can be proved that, for any $(u,v)\in A$, if $\sigma (u,v)=-1$ then ${\sigma }^{\prime }(u,v)=1$ if and only if $(u,v)$${\omega }^{\prime }$-supports ${\omega }^{\prime }\left(v\right)$ in ${\omega }^{\prime }$ as well.

This completes the proof of the lemma. □

3.1.2. Second Step: Structurally Balanced Graphs

In this subsection, we exploit the results in Section 3.1.1 to show how to simulate the ${\mathbf{d}}_{\theta }$-opinion evolution of a structurally balanced signed graph $G=(V,E,\lambda )$ starting at some opinion configuration $\omega$ by the ${\mathbf{d}}_{\theta }$-opinion evolution of the related undirected unsigned graph $\overline{G}=(V,E)$ starting at some opinion configuration $\overline{\omega }$.

The first achievement of this subsection is that the structural balance property of a graph, at any opinion configuration, also holds for its support graph, as stated in the next lemma.

Lemma 3. 

If $G=(V,E,\lambda )$ is a structurally balanced graph, then for any opinion configuration $\omega :V\to \{-1,+1\}$ of G, ${\mathcal{S}}_{G,\omega }=(V,E,\sigma )$ is structurally balanced.

Proof. 

Suppose, by contradiction, that ${\mathcal{S}}_{G,\omega }$ is not structurally balanced, that is, there exists a cycle C in ${\mathcal{S}}_{G,\omega }$ containing an odd number of edges $(u,v)$ such that $\sigma (u,v)=-1$. This means that there exists $h\in \mathbb{N}$ such that

$$C^{-}=\{(u,v)\in C:\sigma (u,v)=-1\}=\{(u_0,v_0),(u_1,v_1),\dots ,(u_{2h},v_{2h})\},$$

(possibly $u_i=v_{i\oplus 1}$ (within this proof, ⊕ will denote the sum modulo $2h$.) for some $i\in \{0,\dots ,2h\}$). For any $i=0,\dots ,2h$, denote as $C_i$ the set of edges in C between $v_i$ and $u_{i\oplus 1}$.

Without loss of generality, assume that $\omega \left(u_0\right)=1$; hence, since $\sigma (u_0,v_0)=-1$, it is $\lambda (u_0,v_0)\omega \left(u_0\right)\ne \omega \left(v_0\right)$, that is, $\omega \left(v_0\right)=-\lambda (u_0,v_0)\omega \left(u_0\right)$. Similarly, since $\sigma \left(e\right)=1$ for all edges $e\in C$ between $v_0$ and $u_1$, then

$$\omega \left(u_1\right)=-\lambda (u_0,v_0)\omega \left(u_0\right)\prod _{(u,v)\in C_0}\lambda (u,v)$$

and, since $\sigma (u_1,v_1)=-1$, $\omega \left(v_1\right)=\lambda (u_0,v_0)\lambda (u_1,v_1)\omega \left(u_0\right){\prod }_{(u,v)\in C_0}\lambda (u,v).$

Again, since $\sigma \left(e\right)=1$ for all edges $e\in C$ between $v_1$ and $u_2$, then

$$\omega \left(u_2\right)=\lambda (u_0,v_0)\lambda (u_1,v_1)\omega \left(u_0\right)\prod _{(u,v)\in C_0\cup C_1}\lambda (u,v)$$

and, since $\sigma (u_2,v_2)=-1$,

$$\omega \left(v_2\right)=-\lambda (u_0,v_0)\lambda (u_1,v_1)\lambda (u_2,v_2)\omega \left(u_0\right)\prod _{(u,v)\in C_0\cup C_1}\lambda (u,v).$$

By iterating, we obtain that

$$\omega \left(v_{2h}\right)=-\omega \left(u_0\right)\prod _{0\le i\le 2h}\lambda (u_i,v_i)\prod _{(u,v)\in {\cup }_{1\le i\le 2h-1}{C}_i}\lambda (u,v)$$

and, finally,

$$\omega \left(u_0\right)=-\omega \left(u_0\right)\prod _{0\le i\le 2h}\lambda (u_i,v_i)\prod _{(u,v)\in {\cup }_{1\le i\le 2h}{C}_i}\lambda (u,v)=-\omega \left(u_0\right)\prod _{(u,v)\in C}\lambda (u,v).$$

Notice now that, since G is structurally balanced, then ${\prod }_{(u,v)\in C}\lambda (u,v)>0$. Hence, the last equality obtains the contradiction $\omega \left(u_0\right)=-\omega \left(u_0\right)$. □

Given a signed graph $G=(V,E,\lambda )$ and an opinion configuration $\omega$ of G, it may well happen that ${\mathcal{S}}_{G,\omega }={\mathcal{S}}_{G^{\prime },{\omega }^{\prime }}$, with $G^{\prime }=(V,E,{\lambda }^{\prime })$, for some arc-labeling function ${\lambda }^{\prime }$ and some opinion configuration ${\omega }^{\prime }$ of $G^{\prime }$.

In particular, thanks to Lemma 3, this has a noticeable consequence when G is structurally balanced, as stated in the next lemma.

Lemma 4. 

For any structurally balanced signed graph $G=(V,E,\lambda )$ and for any opinion configuration ω of G there exists an opinion configuration $\overline{\omega }$ of the unsigned graph $\overline{G}=(V,E)$ such that ${\mathcal{S}}_{G,\omega }={\mathcal{S}}_{\overline{G},\overline{\omega }}$.

Proof. 

Let $G=(V,E,\lambda )$ be a structurally balanced graph, let $\omega$ be an opinion configuration of G and let ${\mathcal{S}}_{G,\omega }=(V,E,\sigma )$ be the support graph associated with G and $\omega$: hence, by Lemma 3, ${\mathcal{S}}_{G,\omega }$ is structurally balanced as well. We choose any $x\in V$, and compute the following opinion configuration $\overline{\omega }$ of $\overline{G}=(V,E)$:

• set $\overline{\omega }\left(x\right)=+1$ and $V^{\prime }=\left\{x\right\}$;
• set $i=0$ and $V_0=\left\{x\right\}$;
• while $V^{\prime }\ne V$, repeat the following steps

  –

  set $i=i+1$ and $V_i=\varnothing$;

  –

  for each $u\in V_{i-1}$ and for each $v\in N\left(u\right)$, set $\overline{\omega }\left(v\right)=\sigma (u,v)\overline{\omega }\left(u\right)$, $V_i=V_i\cup \left\{v\right\}$ and $V^{\prime }=V^{\prime }\cup \left\{v\right\}$.

We claim that ${\mathcal{S}}_{G,\omega }={\mathcal{S}}_{\overline{G},\overline{\omega }}$. In fact, denote as $\overline{\sigma }$ the edge-sign function in ${\mathcal{S}}_{\overline{G},\overline{\omega }}$, and suppose the claim does not hold, that is, there exists $(u,v)\in E$ such that $\overline{\sigma }(u,v)\ne \sigma (u,v)$: since $\overline{G}$ is unsigned and, hence, by definition of support graph, $\overline{\omega }\left(v\right)=\overline{\sigma }(u,v)\overline{\omega }\left(u\right)$, this means that $\overline{\omega }\left(v\right)\ne \sigma (u,v)\overline{\omega }\left(u\right)$ (and $\overline{\omega }\left(u\right)\ne \sigma (u,v)\overline{\omega }\left(v\right)$).

Without loss of generality, assume that $u\in V_i$ and $v\in V_j$ with $i\le j$, and let $⟨x=u_0,u_1,\dots ,u_i=u⟩$ and $⟨x=v_0,v_1,\dots v_j=v⟩$ be the two sequences of nodes leading to the assignments $\overline{\omega }\left(u\right)$ and $\overline{\omega }\left(v\right)$: that is, according to the just outlined algorithm, for $h>0$, $u_h,v_h\in V_h$ and $\overline{\omega }\left(u_h\right)=\sigma (u_{h-1},u_h)\overline{\omega }\left(u_{h-1}\right)$ and $\overline{\omega }\left(v_h\right)=\sigma (v_{h-1},v_h)\overline{\omega }\left(v_{h-1}\right)$. Notice that, since $\overline{\omega }\left(v\right)\ne \sigma (u,v)\overline{\omega }\left(u\right)$, it is $u\ne v_{j-1}$.

Let $\ell \le i$ be such that $u_{\ell }=v_{\ell }$ and, for every $\ell +1\le h\le i-1$, $u_h\ne v_h$ (eventually, $\ell =0$), and denote as y the node $u_{\ell }=v_{\ell }$. Since $u\ne v_{j-1}$ and $(u,v)\in E$, the sequence of nodes

$$C=⟨u=u_i,u_{i-1},\dots ,u_{\ell }=y=v_{\ell },v_{\ell +1},\dots ,v_j=v⟩$$

is actually a cycle.

Suppose first $\sigma (u,v)=1$ so that $\overline{\omega }\left(v\right)\ne \overline{\omega }\left(u\right)$. The following holds:

-

If $\overline{\omega }\left(u\right)\ne \overline{\omega }\left(y\right)$ then the path $⟨u=u_i,u_{i-1},\dots ,u_{\ell }=y⟩$ contains an odd number of edges e such that $\sigma \left(e\right)=-1$. Furthermore, since $\overline{\omega }\left(u\right)\ne \overline{\omega }\left(v\right)$, then $\overline{\omega }\left(v\right)=\overline{\omega }\left(y\right)$ and, hence, the number of edges e in the path $⟨y=v_{\ell },v_{\ell +1},\dots ,v_j=v⟩$ such that $\sigma \left(e\right)=-1$ is even. This would imply that the number of edges e in C such that $\sigma \left(e\right)=-1$ is odd, so contradicting that ${\mathcal{S}}_{G,\omega }$ is structurally balanced.

-

If $\overline{\omega }\left(u\right)=\overline{\omega }\left(y\right)$, then the path $⟨u=u_i,u_{i-1},\dots ,u_{\ell }=y⟩$ contains an even number of edges e such that $\sigma \left(e\right)=-1$. Furthermore, since $\overline{\omega }\left(u\right)\ne \overline{\omega }\left(v\right)$, then $\overline{\omega }\left(v\right)\ne \overline{\omega }\left(y\right)$ and, hence, the number of edges e in the path $⟨y=v_{\ell },v_{\ell +1},\dots ,v_j=v⟩$ such that $\sigma \left(e\right)=-1$ is odd. Again, this would imply that the number of edges e in C is such that $\sigma \left(e\right)=-1$ is odd.

The same reasoning can be applied if we suppose that $\sigma (u,v)=-1$, and this completes the proof that ${\mathcal{S}}_{G,\omega }={\mathcal{S}}_{\overline{G},\overline{\omega }}$. □

In Figure 1, an example of the construction of $\overline{\omega }$ from a structurally balanced graph G in an opinion configuration $\omega$ according to Lemma 4 is shown.

3.1.3. Summarizing

Let ${\mathbf{d}}_{\theta }$ be a symmetric local threshold-based dynamics, let $G=(V,E,\lambda )$ be a structurally balanced graph and let $\omega$ be an opinion configuration of G. By Lemma 3, the support graph ${\mathcal{S}}_{G,\omega }$ associated with G and $\omega$ is structurally balanced so that, by Lemma 4, there exists an opinion configuration $\overline{\omega }$ of the unsigned graph $\overline{G}=(V,E)$ such that ${\mathcal{S}}_{G,\omega }={\mathcal{S}}_{\overline{G},\overline{\omega }}$.

By Lemma 2, there is a one-to-one correspondence between the opinion configurations met by G while evolving according to ${\mathbf{d}}_{\theta }$ starting at $\omega$ and the configurations met by ${\mathcal{S}}_{G,\omega }$ while evolving according to the edge dynamics ${\mathbf{a}}_{\theta }$ described in Section 3.1.1. Similarly, there is a one-to-one correspondence between the opinion configurations met by $\overline{G}$ while evolving according to ${\mathbf{d}}_{\theta }$ starting at $\overline{\omega }$ and the configurations met by ${\mathcal{S}}_{\overline{G},\overline{\omega }}$ while evolving according to ${\mathbf{a}}_{\theta }$. Hence, there is a one-to-one correspondence between the opinion configurations met by G while evolving according to ${\mathbf{d}}_{\theta }$ starting at $\omega$, and the configurations met by $\overline{G}$ while evolving according to ${\mathbf{d}}_{\theta }$ starting at $\overline{\omega }$. This proves Lemma 1.

3.2. Proof of Theorem 2: Polynomial Bound to $\left|{\mathcal{E}}_{{\mathbf{d}}_{(c^{+},c^{-})}}(G,\omega )\right|$ in Structurally Balanced Graphs

The aim of this section is to show that, for any structurally balanced signed graph $G=(V,E,\lambda )$, for any opinion configuration $\omega$ of G and for any underpopulation opinion dynamics ${\mathbf{d}}_{(c^{+},c^{-})}$, the size of ${\mathcal{E}}_{{\mathbf{d}}_{(c^{+},c^{-})}}(G,\omega )$ is polynomially bounded in the size of G.

The first step to this goal is reducing the ${\mathbf{d}}_{(c^{+},c^{-})}$-opinion evolution of a signed graph $G=(V,E,\lambda )$ starting at some opinion configuration $\omega$ to the ${\mathbf{d}}_{\widehat{\theta }}$-opinion evolution of a related signed graph $\widehat{G}=(\widehat{V},\widehat{E},\widehat{\lambda })$ starting at a properly defined opinion configuration $\widehat{\omega }$, where $\widehat{\theta }$ is a properly defined threshold function.

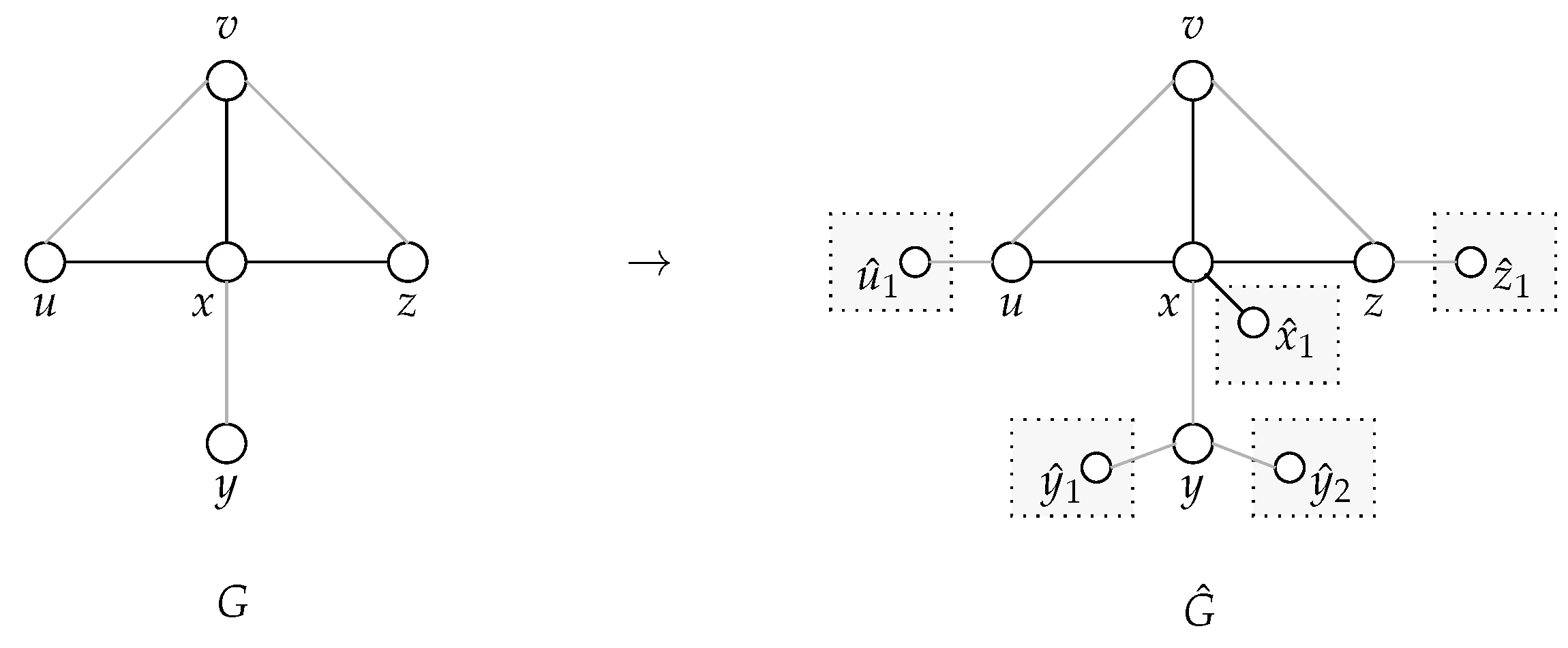
Let $G=(V,E,\lambda )$ be a signed graph, let $\omega$ be an opinion configuration of G and let $c^{+},c^{-}\in \mathbb{N}$ be a pair of constant values. The $(c^{+},c^{-})$-degree controller graph $\widehat{G}=(\widehat{V},\widehat{E},\widehat{\lambda })$ associated to $⟨G,c^{+},c^{-}⟩$ is obtained by adding to G a set of nodes suitably connected to the nodes in V, as described in what follows, and by setting $\widehat{\lambda }(u,v)=\lambda (u,v)$ for all $(u,v)\in E$. In order to avoid confusion, for any $v\in V$, ${\delta }_v$ and ${\widehat{\delta }}_v$ shall denote, respectively, the degree of v in G and in $\widehat{G}$; similarly, $P^{+}\left(v\right)$ and ${\widehat{P}}^{+}\left(v\right)$ shall denote the number of neighbors of v pushing v to 1, respectively, in G and in $\widehat{G}$, and $P^{-}\left(v\right)$ and ${\widehat{P}}^{-}\left(v\right)$ shall denote the number of neighbors of v pushing v to $-1$, respectively, in G and in $\widehat{G}$. Finally, $\Delta$ and $\widehat{\Delta }$ are, respectively, the maximum node degree in G and in $\widehat{G}$.

For every node v in G, a set of ${\mu }_v=|{\delta }_v-c^{-}-c^{+}|$ dummy cliques $K_1^v,\dots ,K_{{\mu }_v}^v$ of $2\Delta +3$ nodes each is added to G with exactly one node in each clique adjacent to v in $\widehat{G}$: more specifically, for $i=1,\dots ,{\mu }_v$, there exists exactly one degree-controller node ${\widehat{v}}_i$ in $K_i^v$ such that $({\widehat{v}}_i,v)\in \widehat{E}$. All edges in all dummy cliques are positive and, for $i=1,\dots ,{\mu }_v$, $\widehat{\lambda }({\widehat{v}}_i,v)=-1$ if $c^{+}>{\delta }_v-c^{-}$ and $\widehat{\lambda }({\widehat{v}}_i,v)=1$ otherwise (see Figure 2). Hence, for any node $v\in \widehat{V}$, the degree of v in $\widehat{G}$ is

$${\widehat{\delta }}_v=\left\{\begin{array}{cc}{\delta }_v+{\mu }_v\hfill & \mathrm{if} v\in V,\hfill \\ 2\Delta +3\hfill & \mathrm{if} v\in \widehat{V}-V\mathrm{and} v \mathrm{is} \mathrm{a} \mathrm{degree}\text{-}\mathrm{controller} \mathrm{node},\hfill \\ 2\Delta +2\hfill & \mathrm{if} v\in \widehat{V}-V \mathrm{and} v \mathrm{is} \mathrm{not} \mathrm{a} \mathrm{non}\text{-}\mathrm{degree}\text{-}\mathrm{controller} \mathrm{node}.\hfill \end{array}\right.$$

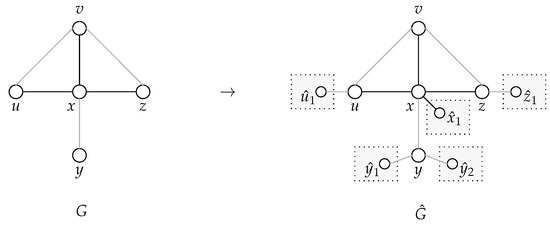
Figure 2. An example of the construction of the $(c^{+},c^{-})$-degree controller graph $\widehat{G}$ associated to the signed graph G when $c^{+}=1$ and $c^{-}=2$: in this case, ${\mu }_u={\mu }_x={\mu }_z=1$, ${\mu }_v=0$ and ${\mu }_y=2$. The dummy cliques (of 11 nodes each) are depicted as dotted light grey rectangles and only the degree-controller nodes in them are explicitly drawn. Negative edges are grey, and positive edges are black.

Notice that, since ${\mu }_v\le \Delta +1$, it holds that ${\widehat{\delta }}_v\le 2\Delta +1$ for every $v\in V$.

Then, for every $v\in V$, we set $\widehat{\omega }\left(v\right)=\omega \left(v\right)$ and, for every node x in every dummy clique, we set $\widehat{\omega }\left(x\right)=1$.

Finally, $\widehat{\theta }$ has to be defined. To this aim, a function $\phi :\widehat{V}\to \mathbb{N}$ is first introduced as follows: for any $v\in \widehat{V}$,

$$\phi \left(v\right)=\left\{\begin{array}{cc}\max \{c^{+},{\delta }_v-c^{-}\}\hfill & \mathrm{if} v\in V,\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

We now show that, for every pair of nodes $u\in \widehat{V}$ and $v\in \widehat{V}$, it holds that ${\widehat{\delta }}_u={\widehat{\delta }}_v$ if and only if $\phi \left(u\right)=\phi \left(v\right)$. If $u\in \widehat{V}-V$ then ${\widehat{\delta }}_u>2\Delta +1\ge max\{{\widehat{\delta }}_x:x\in V\}$ and hence ${\widehat{\delta }}_u={\widehat{\delta }}_v$ only if $v\in \widehat{V}-V$ so that $\phi \left(u\right)=\phi \left(v\right)=0$. If $u\in V$ and $v\in V$, then the following cases are possible:

• If ${\delta }_u-c^{-}>c^{+}$ and ${\delta }_v-c^{-}>c^{+}$ then: $\phi \left(u\right)={\delta }_u-c^{-}$ and $\phi \left(v\right)={\delta }_v-c^{-}$, and ${\widehat{\delta }}_u=2{\delta }_u-c^{-}-c^{+}$ and ${\widehat{\delta }}_v=2{\delta }_v-c^{-}-c^{+}$; hence, $\phi \left(u\right)=\phi \left(v\right)$ if and only if ${\widehat{\delta }}_u={\widehat{\delta }}_v$.
• If ${\delta }_u-c^{-}\le c^{+}$ and ${\delta }_v-c^{-}\le c^{+}$ then $\phi \left(u\right)=c^{+}=\phi \left(v\right)$, and ${\widehat{\delta }}_u=c^{+}+c^{-}={\widehat{\delta }}_v$.
• If ${\delta }_u-c^{-}\le c^{+}$ and ${\delta }_v-c^{-}>c^{+}$ then: $\phi \left(u\right)=c^{+}$ and $\phi \left(v\right)={\delta }_v-c^{-}$ so that $\phi \left(u\right)\ne \phi \left(v\right)$, and ${\widehat{\delta }}_v=2{\delta }_v-c^{-}-c^{+}>2(c^{+}+c^{-})-c^{-}-c^{+}=c^{+}+c^{-}\ge {\widehat{\delta }}_u$.

As a consequence, the following function $\widehat{\theta }:\mathbb{N}\to \mathbb{N}$ can be defined: for any $k\in \mathbb{N}$,

$$\widehat{\theta }\left(k\right)=\left\{\begin{array}{cc}\phi \left(u\right)\hfill & \mathrm{if}\exists u\in \widehat{V}:{\widehat{\delta }}_u=k,\hfill \\ \widehat{\Delta }+2\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

The next lemma proves that the ${\mathbf{d}}_{(c^{+},c^{-})}$-evolution of G starting at $\omega$ can be simulated by the ${\mathbf{d}}_{\widehat{\theta }}$-evolution of $\widehat{G}$ starting at $\widehat{\omega }$.

Lemma 5. 

For any underpopulation dynamics ${\mathbf{d}}_{(c^{+},c^{-})}$ and for any signed graph $G=(V,E,\lambda )$ in any opinion configuration ω, it holds that, for every $v\in V$ and for every $t>0$,

$${\mathbf{d}}_{(c^{+},c^{-})}{(G,\omega )}^t\left(v\right)={\mathbf{d}}_{\widehat{\theta }}{(\widehat{G},\widehat{\omega })}^t\left(v\right).$$

Proof. 

Firstly, we show that, for every $v\in V$, v does not change its opinion in one step of the ${\mathbf{d}}_{(c^{+},c^{-})}$-evolution of G starting at $\omega$ if and only if v does not change its opinion in one step of the ${\mathbf{d}}_{\widehat{\theta }}$-evolution of $\widehat{G}$ starting at $\widehat{\omega }$, that is, $\omega \left(v\right)={\mathbf{d}}_{(c^{+},c^{-})}(G,\omega )\left(v\right)$ if and only if $\widehat{\omega }\left(v\right)={\mathbf{d}}_{\widehat{\theta }}(\widehat{G},\widehat{\omega })\left(v\right)$.

Let $v\in V$ be such that $c^{+}>{\delta }_v-c^{-}$ so that $\widehat{\theta }\left({\widehat{\delta }}_v\right)=c^{+}$ and v has $c^{+}+c^{-}-{\delta }_v$ in-neighbors in $\widehat{V}-V$ supporting $-1$. Hence, ${\widehat{P}}^{+}\left(v\right)=P^{+}\left(v\right)$ and ${\widehat{P}}^{-}\left(v\right)=P^{-}\left(v\right)+[c^{+}+c^{-}-{\delta }_v]$ and the following holds:

• If $\omega \left(v\right)=1$ then

  –

  if ${\mathbf{d}}_{(c^{+},c^{-})}(G,\omega )\left(v\right)=1$ then $P^{+}\left(v\right)\ge c^{+}$ and, hence, ${\widehat{P}}^{+}\left(v\right)\ge \widehat{\theta }\left({\delta }_v\right)$;

  –

  if ${\mathbf{d}}_{(c^{+},c^{-})}(G,\omega )\left(v\right)=-1$ then $P^{+}\left(v\right)<c^{+}$ and, hence, ${\widehat{P}}^{+}\left(v\right)<\widehat{\theta }\left({\delta }_v\right)$.

• If $\omega \left(v\right)=-1$ then

  –

  if ${\mathbf{d}}_{(c^{+},c^{-})}(G,\omega )\left(v\right)=1$ then $P^{-}\left(v\right)<{\delta }_v-c^{-}$ and, hence,

  $${\widehat{P}}^{-}\left(v\right)<{\delta }_v-c^{-}+[c^{+}+c^{-}-{\delta }_v]=c^{+}=\widehat{\theta }\left({\delta }_v\right);$$

  –

  if ${\mathbf{d}}_{(c^{+},c^{-})}(G,\omega )\left(v\right)=-1$ then $P^{-}\left(v\right)\ge {\delta }_v-c^{-}$ and, hence,

  $${\widehat{P}}^{-}\left(v\right)\ge {\delta }_v-c^{-}+[c^{+}+c^{-}-{\delta }_v]=c^{+}=\widehat{\theta }\left({\delta }_v\right).$$

This proves that if $c^{+}>{\delta }_v-c^{-}$ then $\omega \left(v\right)={\mathbf{d}}_{({\theta }^{+},{\theta }^{-})}(G,\omega )\left(v\right)$ if and only if $\widehat{\omega }\left(v\right)={\mathbf{d}}_{\widehat{\theta }}(\widehat{G},\widehat{\omega })\left(v\right)$.

Symmetrically, if $c^{+}\le {\delta }_v-c^{-}$ then $\widehat{\theta }\left({\delta }_v\right)={\delta }_v-c^{-}$ and v has ${\delta }_v-c^{-}-c^{+}$ neighbors in $\widehat{V}-V$ supporting 1. Hence, ${\widehat{P}}^{+}\left(v\right)=P^{+}\left(v\right)+{\delta }_v-c^{-}-c^{+}$ and ${\widehat{P}}^{-}\left(v\right)=P^{-}\left(v\right)$. Similar to before, this allows to prove that $\omega \left(v\right)={\mathbf{d}}_{({\theta }^{+},{\theta }^{-})}(G,\omega )\left(v\right)$ if and only if $\widehat{\omega }\left(v\right)={\mathbf{d}}_{\widehat{\theta }}(\widehat{G},\widehat{\omega })\left(v\right)$ in this case too.

Secondly, it is immediate to verify that, for every $t\ge 0$ and for every $u\in \widehat{V}-V$, ${\mathbf{d}}_{\widehat{\theta }}{(\widehat{G},\widehat{\omega })}^t\left(u\right)=1$.

Hence, the first step can be iterated and the assertion follows. □

Lemma 5 proves that there is a one-to-one correspondence between the opinion configurations met by G during its ${\mathbf{d}}_{(c^{+},c^{-})}$-evolution staring at $\omega$ and the opinion configurations met by $\widehat{G}$ during its ${\mathbf{d}}_{\widehat{\theta }}$-evolution staring at $\widehat{\omega }$. As a consequence, it holds that $|{\mathcal{E}}_{{\mathbf{d}}_{(c^{+},c^{-})}}(G,\omega )|=|{\mathcal{E}}_{{\mathbf{d}}_{\widehat{\theta }}}(\widehat{G},\widehat{\omega })|$.

Notice now that since adding the dummy cliques to G does not create any cycle involving negative edges, if G is structurally balanced, then $\widehat{G}$ is structurally balanced as well. Hence, since $|\widehat{V}|\le |V|+|V|(\Delta +1)(2\Delta +3)$, $|\widehat{E}|\le |E|+|V|(\Delta +1)\frac{(2\Delta +2)(2\Delta +3)}{2}$ and $\widehat{\Delta }=2\Delta +3$, by Theorem 1, the bound on the number of configurations met by a structurally balanced graph during its evolution according to any underpopulation dynamics stated by Theorem 2 follows.

3.3. Proofs of Theorem 3: u-RT Is PSpace-Complete in Directed Graphs

It will now be proved that u-RT is a complete problem for PSpace even when $c^{+}=3$ and $c^{-}=4$. The instance graph is unsigned, and its maximum indegree is 6, and when the target set U contains a single node.

Given a graph G, a subset U of nodes in G, and an initial opinion configuration $\omega$, a simple procedure can be exploited to decide if a configuration $\pi \in {\mathcal{E}}_{{\mathbf{d}}_{(3,4)}}(G,\omega )$ exists such that $\pi \left(u\right)=1$. Indeed, as already observed in the Introduction, such a procedure simply lets the ${\mathbf{d}}_{(3,4)}$-evolution of G starting at $\omega$ occur, checking each time the graph enters a new configuration, which is the opinion of each node in U in the new configuration. Trivially, running the procedure requires a space proportional to the size of G. This proves that u-RT belongs to PSpace.

The completeness for PSpace of u-RT will be shown by providing a polynomial-time transformation of any computation C of a deterministic recognizer Turing machine working in polynomial space into the following:

• An oriented unsigned graph $G=(V,A)$;
• An opinion configurations ${\omega }_0:V\to \{-1,+1\}$ for G;
• A subset U of V.

This is such that C is an accepting computation if and only if there exists an opinion configuration ${\omega }^{\prime }\in {\mathcal{E}}_{{\mathbf{d}}_{(3,4)}}(G,{\omega }_0)$ such that ${\omega }^{\prime }\left(u\right)=1$ for all $u\in U$.

Let $\mathit{TM}=⟨\{0,1\},Q,P,\{q_0,q_A,q_R\}⟩$ be a deterministic semi-infinite single tape recognizer Turing machine working on alphabet $\{0,1\}$ with set of states Q and set of quintuples P, which uses at most $N=f\left(\right|x\left|\right)$ tape cells with input x, for some polynomial f. Without loss of generality, it will be assumed that P is total (that is, for every $q\in Q-\{q_A,q_R\}$ and for every $s\in \{0,1,\bcancel{b}\}$ (where $\bcancel{b}$ is the empty cell symbol) P contains a quintuple $⟨q,s,s^{\prime },q^{\prime },mov⟩$) and that every quintuple in P, but the ones entering a final state, moves right or left the tape head. Additionally, it will be assumed that, for every $u\in \{0,1,\bcancel{b}\}$, P contains both a quintuple that reads u and does not write u and a quintuple that does not read u and writes u: if P does not satisfy such a constraint, it is sufficient to add some dummy quintuples to P. Finally, it is assumed that, after having decided to accept its input, $\mathit{TM}$ still performs a sequence of tape-cleaning operations before entering the accepting state $q_A$, so that every accepting computation of $\mathit{TM}$ ends, executing a quintuple that writes $\bcancel{b}$ in the leftmost cell and enters $q_A$, and leaves $\mathit{TM}$ in the global state (a global state of $\mathit{TM}$ is the description of the content of its tape, its internal state and the cell that its head is positioned on at a given step of a computation) in which the tape is empty and the head is positioned on the leftmost cell.

In what follows, a numbering of the $p=\left|P\right|$ quintuples in P will be assumed with $⟨q_b^i,s_r^i,s_w^i,q_e^i,m^i⟩$ denoting the ith quintuple in P, where $q_b^i,q_e^i\in Q$, $s_r^i,s_w^i\in \{0,1,\bcancel{b}\}$ and $m^i\in \{\mathtt{left},\mathtt{right}\}$. Finally, the ith quintuple will be said to begin at state $q_b^i$, to read symbol $s_r^i$, to end at state $q_e^i$ and to write symbol $s_w^i$; correspondingly, $q_b^i$ and $q_e^i$ are, respectively, the beginning and ending state, and $s_r^i$ and $s_w^i$ are, respectively, the read and written symbol of the ith quintuple.

3.3.1. Connecting Components of G

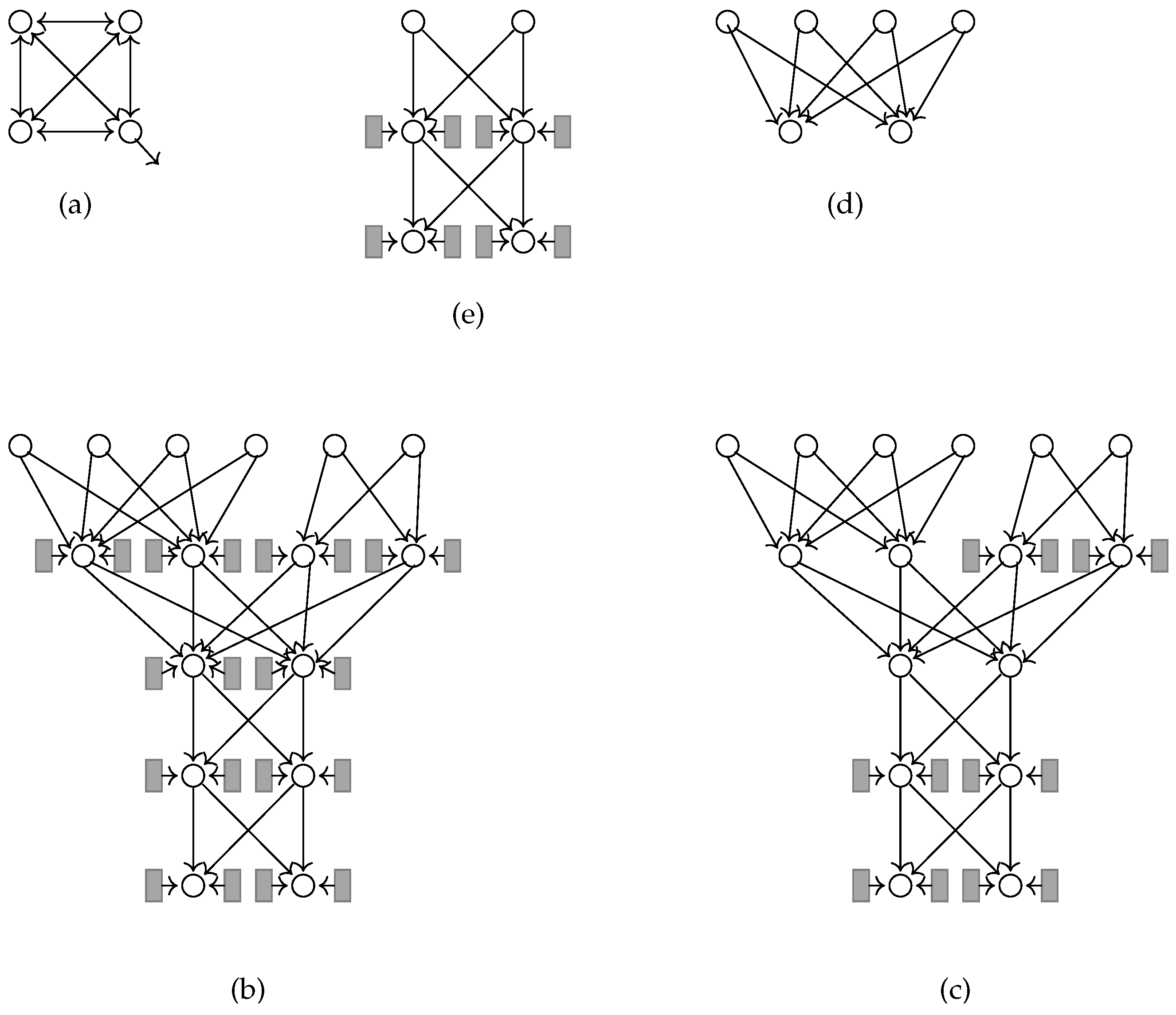
Graph G is built over the three structural components we are going to describe; an example of these components is shown in Figure 3.

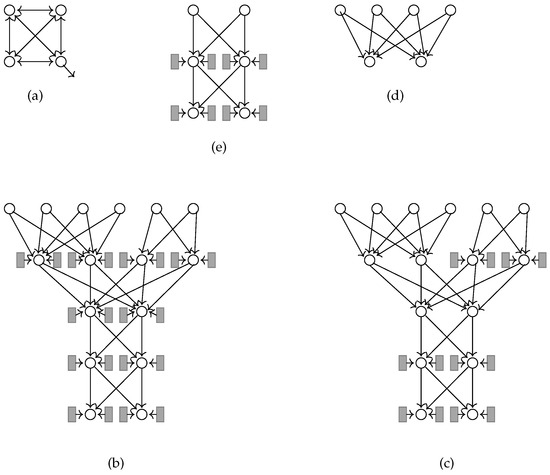
Figure 3. (a) A stable clique. (b) A $(3,2)$-selector. (c) A $(3,1)$-reverse selector. (d) A $(2,0)$-reverse selector. (e) A $(1,2)$-selector (or, equivalently, a $(1,2)$-reverse selector).

A stable clique is made of four nodes connected to each other; it has no input node and one output node (see Figure 3a). The following property trivially holds.

Property 1. 

If all nodes in a stable clique are initialized to 1, then the opinion of any node does not change all the ${\mathbf{d}}_{(3,4)}$-evolution process long.

A stable clique will be said to be positive under an opinion configuration if the opinion of all its nodes is 1 in such a configuration.

For $k\ge 1$ and $h\ge 0$, a $(k,h)$-selector (Figure 3b,e) is the connection of a double sink tree with $2k$ leaves and two roots with a pair of directed chains of $h+1$ nodes each. In fact, a $(k,h)$-selector is a layered graph with $k+h$ layers, layer 0 containing k pairs of nodes $({\alpha }_{0,1}^1,{\alpha }_{0,1}^2),\dots ({\alpha }_{0,k}^1,{\alpha }_{0,k}^2)$. The remaining layers are then recursively defined:

• if $k>1$, for $1\le i\le k-1$, layer i contains the $k-i$ pairs of nodes $({\alpha }_{i,1}^1,{\alpha }_{i,1}^2),\dots ({\alpha }_{i,k-i}^1,{\alpha }_{i,k-i}^2)$; each node in the first pair has an incoming arc from each node in the first 2 pairs of nodes of layer $i-1$ and, for $2\le j\le k-i$, each node in the jth pair of nodes has an incoming arc from each node of the $(j+1)$th pair of layer $i-1$
• if $h>0$, for $k\le i\le k+h-1$, layer i contains the pair of nodes $({\alpha }_{i,1}^1,{\alpha }_{i,1}^2)$ with each such node having an incoming arc from each node in layer $i-1$.

Finally, for $1\le i\le k+h-1$, two stable cliques are linked to any node of any layer $i>0$ of the $(k,h)$-selector. The $2k$ nodes in layer 0 are the inputs and the pair of nodes in layer $k+h-1$ are the outputs of the $(k,h)$-selector. Notice that the indegree of any non-input node is at most 6, and that the distance between any input and any output of a $(k,h)$-selector is $k+h-1$.

A $(k,h)$-reverse selector (Figure 3c–e) is defined similarly to a $(k,h)$-selector, with the only difference that no stable clique is linked to the first pair of nodes $({\alpha }_{i,1}^1,{\alpha }_{i,1}^2)$ in layers $1\le i\le k-1$. Hence, the indegree of any non-input node is 4.

Whenever the number of levels is not relevant, we shall generally speak about selectors and reverse selectors. Let u and v be any pair of nodes in a (reverse) selector H: v is a descendant of u if there is a path in H from u to v. The following properties directly follow from the definition of the ${\mathbf{d}}_{(3,4)}$ dynamics and from Property 1.

Property 2. 

Let H be a $(k,h)$-selector and let ω be an opinion configuration of H such that all its stable cliques are positive under it, then the following holds:

• If there exists a level i of H such that both nodes of a pair in level i of H have a positive opinion at ω, then for every $1\le t\le k+h-1-i$, all descendants of such nodes in level $t+i$ obtain a positive opinion at step t of the dynamic process.
  Formally, if there exist $0\le i\le k+h-1$ and $1\le j\le max\{k-i,1\}$ such that $\omega \left({\alpha }_{i,j}^1\right)=\omega \left({\alpha }_{i,j}^2\right)=1$ then, for any $t=1,\dots ,k+h-1-i$, ${\mathbf{d}}_{(3,4)}{(H,\omega )}^t\left({\alpha }_{t+i,\ell }^1\right)={\mathbf{d}}_{(3,4)}{(H,\omega )}^t\left({\alpha }_{t+i,\ell }^2\right)=1$ where $\ell =max\{j-t,1\}$.
• If there exists a level i of H such that all nodes in level i of H have a negative opinion at ω then, for every $1\le t\le k+h-1-i$, all nodes in level $t+i$ obtain a negative opinion at step t of the dynamic process.
  Formally, if there exists $0\le i\le k+h-1$ such that, for every $1\le j\le max\{k-i,1\}$, $\omega \left({\alpha }_{i,j}^1\right)=\omega \left({\alpha }_{i,j}^2\right)=-1$ then, for any $t=1,\dots ,k+h-1-i$ and for any $1\le \ell \le max\{k-t,1\}$, ${\mathbf{d}}_{(3,4)}{(H,\omega )}^t\left({\alpha }_{t+i,\ell }^1\right)={\mathbf{d}}_{(3,4)}{(H,\omega )}^t\left({\alpha }_{t+i,\ell }^2\right)=-1$.

Property 3. 

Let H be a $(k,h)$-reverse selector and let ω be an opinion configuration of H such that all its stable cliques are positive under it, then the following holds:

• If there exists a level i of H such that both nodes of a pair in level i of H have a negative opinion at ω then, for every $1\le t\le k+h-1-i$, all descendants of such nodes in level $t+i$ obtain a negative opinion at step t of the dynamic process.
  Formally, if there exist $0\le i\le k+h-1$ and $1\le j\le max\{k-i,1\}$ such that $\omega \left({\alpha }_{i,j}^1\right)=\omega \left({\alpha }_{i,j}^2\right)=-1$ then, for any $t=1,\dots ,k+h-1-i$, ${\mathbf{d}}_{(3,4)}{(H,\omega )}^t\left({\alpha }_{t+i,\ell }^1\right)={\mathbf{d}}_{(3,4)}{(H,\omega )}^t\left({\alpha }_{t+i,\ell }^2\right)=-1$ where $\ell =max\{j-t,1\}$;
• If there exists a level i of H such that all nodes in level i of H have a positive opinion at ω then, for every $1\le t\le k+h-1-i$, all nodes in level $t+i$ obtain a positive opinion at step t of the dynamic process.
  Formally, if there exists $0\le i\le k+h-1$ such that, for every $1\le j\le max\{k-i,1\}$, $\omega \left({\alpha }_{i,j}^1\right)=\omega \left({\alpha }_{i,j}^2\right)=1$ then, for any $t=1,\dots ,k+h-1-i$ and for any $1\le \ell \le max\{k-t,1\}$, ${\mathbf{d}}_{(3,4)}{(H,\omega )}^t\left({\alpha }_{t+i,\ell }^1\right)={\mathbf{d}}_{(3,4)}{(H,\omega )}^t\left({\alpha }_{t+i,\ell }^2\right)=1$.

Let H be a $(k,h)$-selector or a $(k,h)$-reverse selector; the internal nodes of H are all nodes in the set $\{{\alpha }_{i,j}^1,{\alpha }_{i,j}^2:1\le i\le k+h-1\wedge 1\le j\le k-min\{i,k-1\}\}$ (that is, a node in H is internal if it is not an input node of H and it does not belong to any stable clique in H).

A $(k,h)$-selector H is positive under an opinion configuration $\omega$ if there exists $1\le j\le k-1$ such that $\omega \left({\alpha }_{1,j}^1\right)=\omega \left({\alpha }_{1,j}^2\right)=1$ and $\omega \left(u\right)=1$ for all internal nodes u in H such that there is a path in H from ${\alpha }_{0,j}^1$ (and, hence, from ${\alpha }_{0,j}^2$) to u. A $(k,h)$-selector H is negative under an opinion configuration $\omega$ if $\omega \left(u\right)=-1$ for all internal nodes u in H.

Symmetrically, a $(k,h)$-reverse selector H is positive under an opinion configuration $\omega$ if $\omega \left(u\right)=1$ for all internal nodes u in H. A $(k,h)$-reverse selector H is negative under an opinion configuration $\omega$ if there exists $1\le j\le k-1$ such that $\omega \left({\alpha }_{1,j}^1\right)=\omega \left({\alpha }_{1,j}^2\right)=-1$ and $\omega \left(u\right)=-1$ for all internal nodes u in H such that there is a path in H from ${\alpha }_{0,j}^1$ (and, hence, from ${\alpha }_{0,j}^2$) to u.

Again, the following property directly follows from the definition of the ${\mathbf{d}}_{(3,4)}$ dynamics and from Property 1, where ${\mathbf{d}}_{(3,4)}{(H,\omega )}^0=\omega$.

Property 4. 

Let H be a $(k,h)$-selector or a $(k,h)$-reverse selector and let ω be an opinion configuration of H such that all its stable cliques are positive under ω.

If H is positive under ω, then both its outputs have a positive opinion at all steps $t=0,\dots ,k+h-1$ of the dynamic process. Formally,

$$\forall 0\le t\le k+h-1[{\mathbf{d}}_{(3,4)}{(H,\omega )}^t\left({\alpha }_{k+h-1,1}^1\right)={\mathbf{d}}_{(3,4)}{(H,\omega )}^t\left({\alpha }_{k+h-1,1}^2\right)=1].$$

If H is negative under ω, then both its outputs have negative opinion at all steps $t=0,\dots ,$$k+h-1$ of the dynamic process; formally,

$$\forall 0\le t\le k+h-1[{\mathbf{d}}_{(3,4)}{(H,\omega )}^t\left({\alpha }_{k+h-1,1}^1\right)={\mathbf{d}}_{(3,4)}{(H,\omega )}^t\left({\alpha }_{k+h-1,1}^2\right)=-1].$$

3.3.2. Graph G

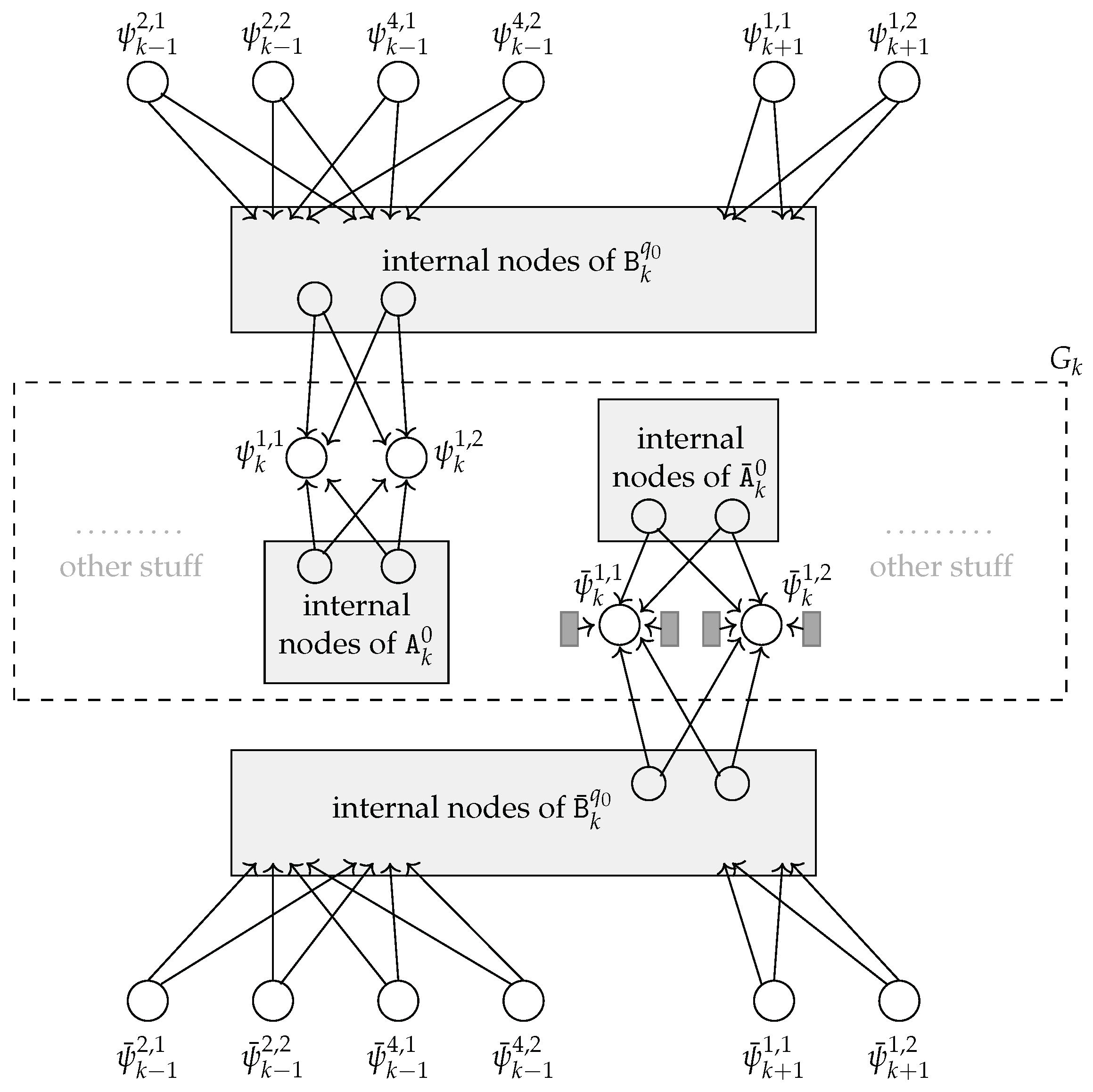
Graph G consists of the $N+1$ subgraphs $G_0,G_1,\dots ,G_N$, where $G_0$ is the initialization/ termination subgraph and, for each $k\in \{1,\dots ,N\}$, the subgraph $G_k$ is associated with tape cell k of $\mathit{TM}$ (recall that the computation $\mathit{TM}\left(x\right)$ uses N tape cells). The main nodes in each subgraph are called acting, and connections between subgraphs occur by them; the remaining nodes belong to (reverse) selectors and they are just functional to the graph evolution properties.

The description of G rests on an integer parameter $\gamma$ whose value will be fixed later on.

• Subgraph $G_k$, with $1\le k\le N$.
  $G_k$ consists of the following set of acting nodes: the cell nodes $0_k^1$, $0_k^2$, $1_k^1$, $1_k^2$, ${\bcancel{b}}_k^1$ and ${\bcancel{b}}_k^2$ and ${\overline{0}}_k^1$, ${\overline{0}}_k^2$, ${\overline{1}}_k^1$, ${\overline{1}}_k^2$, ${\overline{\bcancel{b}}}_k^1$ and ${\overline{\bcancel{b}}}_k^2$, designed to describe the content of tape cell k of $TM$, and, for $1\le i\le p$, the quintuple nodes${\psi }_k^{i,1}$, ${\psi }_k^{i,2}$, ${\overline{\psi }}_k^{i,1}$ and ${\overline{\psi }}_k^{i,2}$, designed to point out which quintuple of $TM$ is to be executed at any step of the computation $TM\left(x\right)$ when the head tape of $TM$ reads cell k.

For $u\in \{0,1,\bcancel{b}\}$, $u_k^1$ and $u_k^2$ are the inputs of the $(1,\gamma -1)$-selector ${\mathtt{A}}_k^u$ and ${\overline{u}}_k^1$ and ${\overline{u}}_k^2$ are the inputs of the $(1,\gamma -1)$-reverse selector ${\overline{\mathtt{A}}}_k^u$: for any i such that $⟨q_b^i,u,s_w^i,q_e^i,m^i⟩$, the outputs of ${\mathtt{A}}_k^u$ are in-neighbors of nodes ${\psi }_k^{i,1}$ and ${\psi }_k^{i,2}$ and the outputs of ${\overline{\mathtt{A}}}_k^u$ are in-neighbors of nodes ${\overline{\psi }}_k^{i,1}$ and ${\overline{\psi }}_k^{i,2}$ (recall that in our assumptions about P, u is read by at least one quintuple).

For $u\in \{0,1,\bcancel{b}\}$, let $P_{u,w}$ be the set of indexes of the quintuples in P writing but not reading u, that is, $P_{u,w}=\{i:1\le i\le p\wedge ⟨q_b^i,s_r^i,u,q_e^i,m^i⟩\in P\wedge s_r^i\ne u\}$: notice that by the assumptions on P, it holds that $P_{u,w}\ne \varnothing$. Then, $\{{\psi }_k^{i,1},{\psi }_k^{i,2}:i\in P_{u,w}\}$ is the input set of the $\left(\right|P_{u,w}|,\gamma -|P_{u,w}\left|\right)$-selector ${\mathtt{W}}_k^u$ each output of which is an in-neighbor of both $u_k^1$ and $u_k^2$. Symmetrically, $\{{\overline{\psi }}_k^{i,1},{\overline{\psi }}_k^{i,2}:i\in P_{u,w}\}$ is the input set of the $\left(\right|P_{u,w}|,\gamma -|P_{u,w}\left|\right)$-reverse selector ${\overline{\mathtt{W}}}_k^u$, each output of which is an in-neighbor of both ${\overline{u}}_k^1$ and ${\overline{u}}_k^2$.

Finally, for $u\in \{0,1,\bcancel{b}\}$, let $P_{u,r}$ be the set of indexes of the quintuples in P reading but not writing u, that is, $P_{u,r}=\{i:1\le i\le p\wedge ⟨q_b^i,u,s_w^i,q_e^i,m^i⟩\in P\wedge s_w^i\ne u\}$: notice that by the assumptions on P, it holds that $P_{u,r}\ne \varnothing$. Then, $\{{\overline{\psi }}_k^{i,1},{\overline{\psi }}_k^{i,2}:i\in P_{u,r}\}$ is the input set of the $\left(\right|P_{u,r}|,\gamma -|P_{u,r}\left|\right)$-reverse selector ${\mathtt{D}}_k^u$ each output of which is an in-neighbor of both $u_k^1$ and $u_k^2$. Symmetrically, $\{{\psi }_k^{i,1},{\psi }_k^{i,2}:i\in P_{u,r}\}$ is the input set of the $\left(\right|P_{u,r}|,\gamma -|P_{u,r}\left|\right)$-selector ${\overline{\mathtt{D}}}_k^u$ each output of which is an in-neighbor of both ${\overline{u}}_k^1$ and ${\overline{u}}_k^2$.

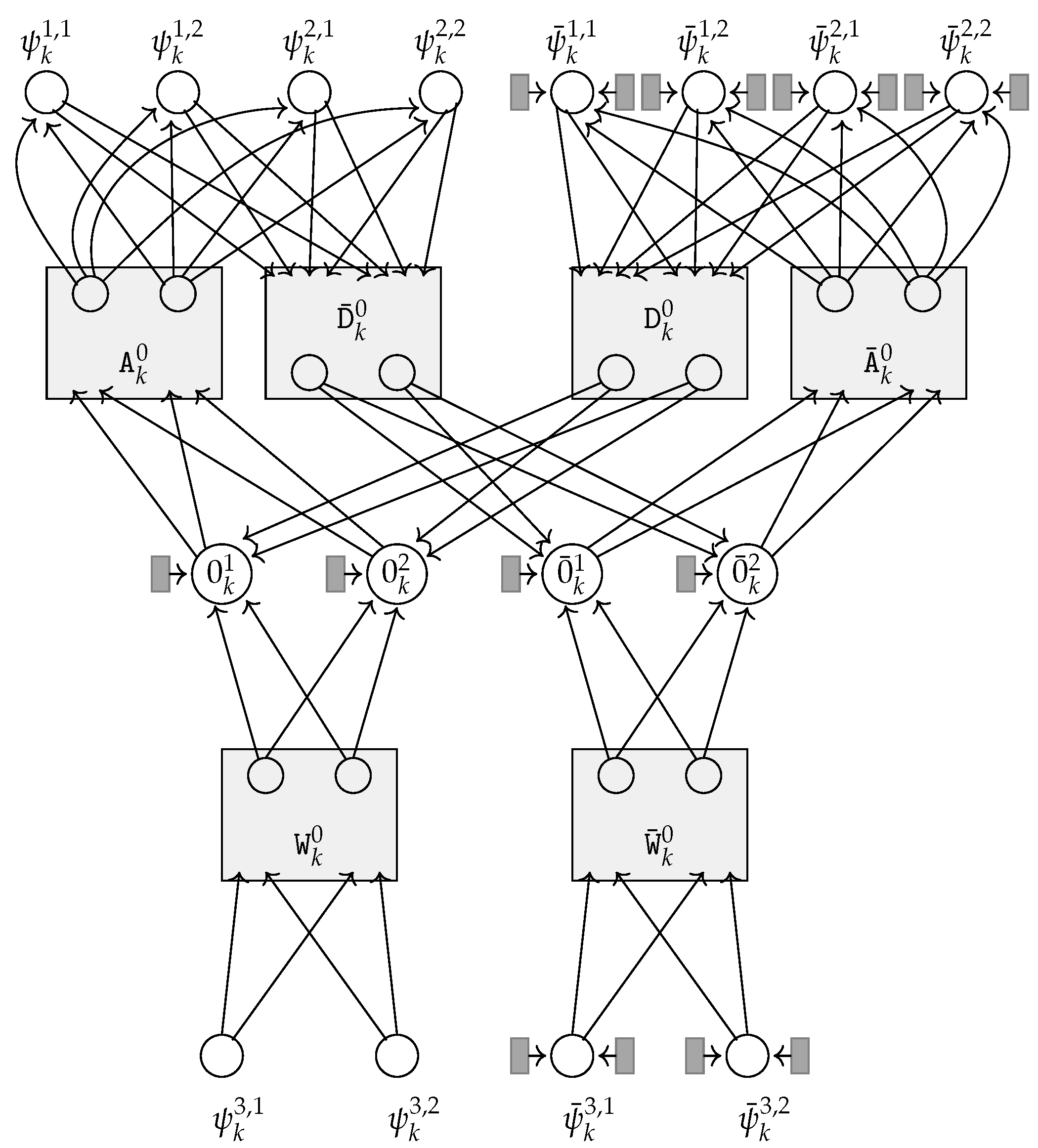
Graph $G_k$ is completed by adding a set of stable cliques: a stable clique is added for every cell node and, for every $1\le i\le p$, a pair of stable cliques is added for ${\overline{\psi }}_k^{i,1}$ and a pair of stable cliques is added for ${\overline{\psi }}_k^{i,2}$, with the output node of each stable clique being in-neighbor of the corresponding cell or quintuple node. Figure 4 depicts the portion related to cell nodes $0_k^1$ and $0_k^2$ of an example of a subgraph $G_k$: in the case in the example $P_{0,w}=\left\{3\right\}$ and $P_{0,r}=\{1,2\}$.

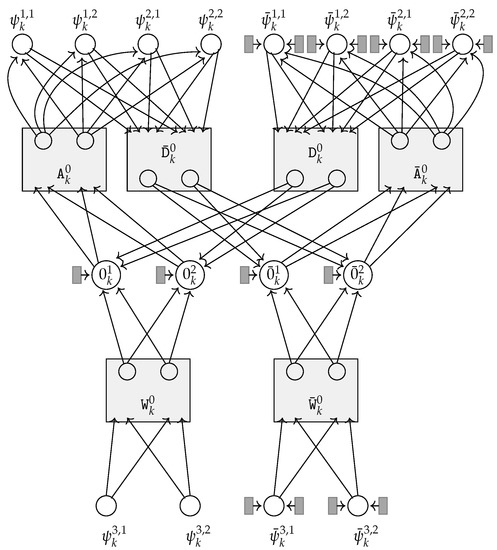
Figure 4. Example of the part of subgraph $G_k$, for some $1\le k\le N$, related to cell nodes $0_k^1,0_k^2$ and ${\overline{0}}_k^1,{\overline{0}}_k^2$ when the quintuples in P (listed with their order number) are: (1): $⟨q_0,0,1,q_0,\mathtt{left}⟩$, (2): $⟨q_1,0,1,q_0,\mathtt{right}⟩$, (3): $⟨q_0,1,0,q_1,\mathtt{left}⟩$, (4): $⟨q_1,1,\bcancel{b},q_0,\mathtt{right}⟩$, (5): $⟨q_0,\bcancel{b},1,q_1,\mathtt{right}⟩$, (6): $⟨q_1,\bcancel{b},\bcancel{b},q_A,\mathtt{right}⟩$. For the sake of readability, a machine $\mathit{TM}$ was considered, defined with a very small and meaningless set of quintuples that does not even satisfy all the constraints described at the beginning of this section (rejecting quintuples are missing, and the accepting conditions are not fulfilled). As in Figure 3, stable cliques are depicted as dark grey rectangles. The inner nodes in selectors and reverse selectors are depicted as light grey rectangles containing their names: the input nodes of the structures are explicitly depicted and named (since they are acting nodes) and the output nodes are shown within the rectangles.

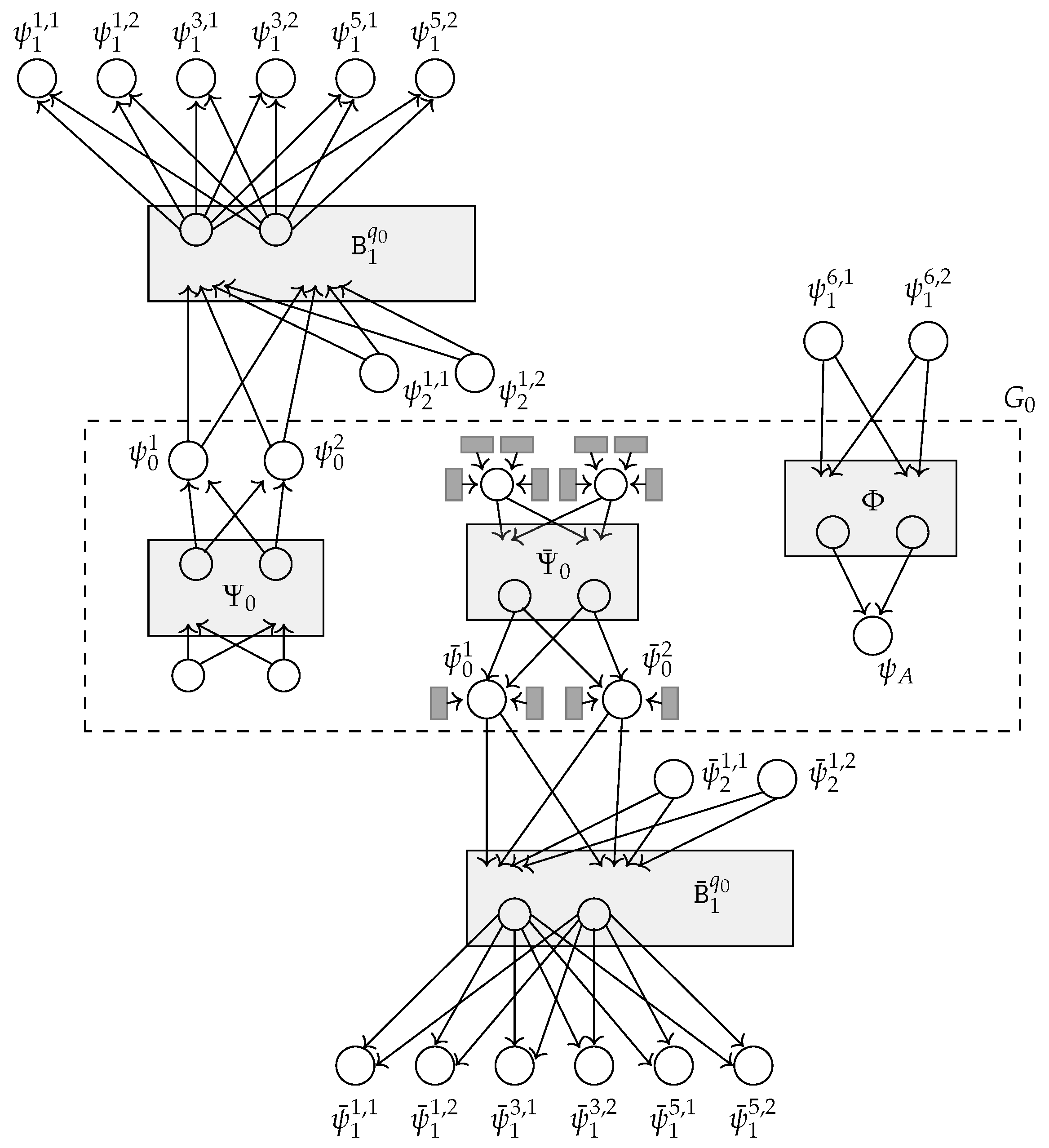
• Subgraph $G_0$.
  $G_0$ consists of the $(1,\gamma -1)$-selector ${\mathsf{\Psi }}_0$, having as outputs, the acting starting nodes ${\psi }_0^1$, ${\psi }_0^2$, of the the $(1,\gamma -1)$-selector ${\overline{\mathsf{\Psi }}}_0$ having as outputs the acting starting nodes ${\overline{\psi }}_0^1$ and ${\overline{\psi }}_0^2$, and of the acting accepting node ${\psi }_A$. The input nodes of ${\mathsf{\Psi }}_0$ have indegree 0 in G, the in-neighbors of each input node of ${\overline{\mathsf{\Psi }}}_0$ are the output nodes of 4 stable cliques, and the output nodes of 2 stable cliques are in-neighbors of ${\psi }_A$. In Figure 5, an example of the subgraph $G_0$ is shown (together with its connections to $G_1$ that will be described in a few lines).

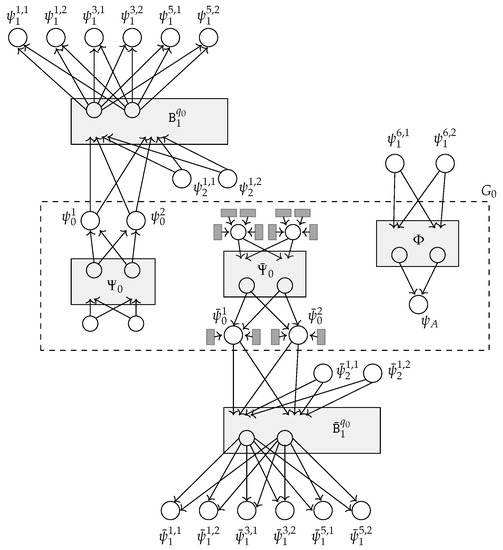
Figure 5. Subgraph $G_0$ and its connections with $G_1$, for the same $TM$ in Figure 4: the quintuples in P are (1): $⟨q_0,0,1,q_0,\mathtt{left}⟩$, (2): $⟨q_1,0,1,q_0,\mathtt{right}⟩$, (3): $⟨q_0,1,0,q_1,\mathtt{left}⟩$, (4): $⟨q_1,1,\bcancel{b},q_0,\mathtt{right}⟩$, (5): $⟨q_0,\bcancel{b},1,q_1,\mathtt{right}⟩$, (6): $⟨q_1,\bcancel{b},\bcancel{b},q_A,\mathtt{right}⟩$. Again, stable cliques are depicted as dark grey rectangles, and the inner nodes in selectors and reverse selectors are depicted as light grey rectangles containing their names with only their input and output nodes explicitly depicted (the input nodes shown outside the rectangles).

• Connections among subgraphs. They connect quintuple-nodes in $G_k$ (or ${\psi }_0^1$, ${\psi }_0^2$, ${\overline{\psi }}_0^1$ and ${\overline{\psi }}_0^2$ if $k=0$) to quintuple-nodes in $G_{k-1}$ or $G_{k+1}$. For every $q\in Q-\{q_A,q_R\}$, we have the following:
  • $R^q$ denotes the set of indexes of the quintuples in P ending at q and moving right, that is,

    $$R^q=\{i:1\le i\le p\wedge ⟨q_b^i,s_r^i,s_w^i,q,\mathtt{right}⟩\in P\};$$
  • Similarly, $L^q$ denotes the set of indexes of the quintuples in P ending at q and moving left, that is, $L^q=\{i:1\le i\le p\wedge ⟨q_b^i,s_r^i,s_w^i,q,\mathtt{left}⟩\in P\}$;
  • $F^q$ denotes the set of indexes of the quintuples in P starting at q, that is, $F^q=\{i:1\le i\le p\wedge ⟨q,s_r^i,s_w^i,q_e^i,\mathtt{left}⟩\in P\}$.

• For every $1<k<N$: for every $q\in Q$, G contains a $\left(\right|L^q|+|R^q|,\gamma -|L^q|-|R^q\left|\right)$-selector ${\mathtt{B}}_k^q$ and a $\left(\right|L^q|+|R^q|,\gamma -|L^q|-|R^q\left|\right)$-reverse selector ${\overline{\mathtt{B}}}_k^q$ such that

  -

  $\{{\psi }_{k+1}^{i,1},{\psi }_{k+1}^{i,2}:i\in L^q\}\cup \{{\psi }_{k-1}^{i,1},{\psi }_{k-1}^{i,2}:i\in R^q\}$ is the input set of ${\mathtt{B}}_k^q$ and each output of its is an in-neighbor of both ${\psi }_k^{j,1}$ and ${\psi }_k^{j,2}$ for every $j\in F^q$,

  -

  $\{{\overline{\psi }}_{k+1}^{i,1},{\overline{\psi }}_{k+1}^{i,2}:i\in L^q\}\cup \{{\overline{\psi }}_{k-1}^{i,1},{\overline{\psi }}_{k-1}^{i,2}:i\in R^q\}$ is the input set of ${\overline{\mathtt{B}}}_k^q$ and each output of its is and in-neighbor of both ${\overline{\psi }}_k^{j,1}$ and ${\overline{\psi }}_k^{j,2}$ for every $j\in F^q$.

Figure 6 shows an example of part of the connections of $G_k$ with $g_{k-1}$ and $G_{k+1}$.

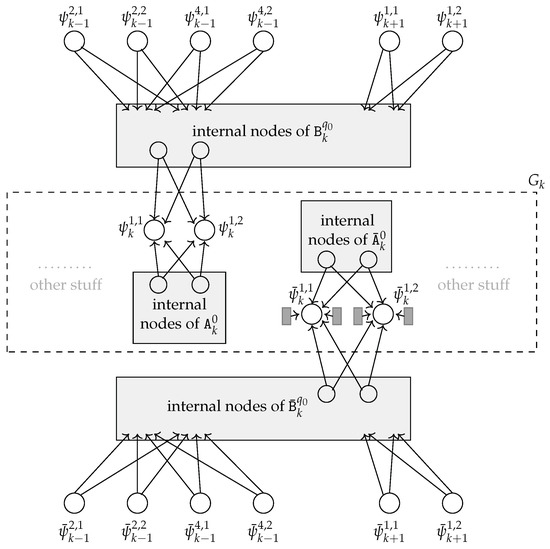
Figure 6. For $k>1$, the in-neighborhood of nodes ${\psi }_k^{1,1},{\psi }_k^{1,2},{\overline{\psi }}_k^{1,1},{\overline{\psi }}_k^{1,2}$, related to quintuple $⟨q_0,0,1,q_0,\mathtt{left}⟩$, for the same $TM$ in Figure 4: the quintuples in P are (1): $⟨q_0,0,1,q_0,\mathtt{left}⟩$, (2): $⟨q_1,0,1,q_0,\mathtt{right}⟩$, (3): $⟨q_0,1,0,q_1,\mathtt{left}⟩$, (4): $⟨q_1,1,\bcancel{b},q_0,\mathtt{right}⟩$, (5): $⟨q_0,\bcancel{b},1,q_1,\mathtt{right}⟩$, (6): $⟨q_1,\bcancel{b},\bcancel{b},q_A,\mathtt{right}⟩$. As in Figure 3, stable cliques are depicted as dark grey rectangles. The inner nodes in selectors and reverse selectors are depicted as light grey rectangles containing their names. The input nodes of ${\mathtt{B}}_k^{q_0}$ and ${\overline{\mathtt{B}}}_k^{q_0}$ are explicitly depicted and named, and the output nodes of all (reverse) selectors are shown within the rectangles.

• For $k=1$: G contains the $\left(\right|L^{q_0}|+1,\gamma -|L^{q_0}|-1)$-selector ${\mathtt{B}}_1^{q_0}$, the $\left(\right|L^{q_0}|+1,\gamma -|L^{q_0}|-1)$-reverse selector ${\overline{\mathtt{B}}}_1^{q_0}$, and, for every $q\in Q-\{q_0,q_A,q_R\}$, the $\left(\right|L^q|,\gamma -|L^q\left|\right)$-selector ${\mathtt{B}}_1^q$ and the $\left(\right|L^q|,\gamma -|L^q\left|\right)$-reverse selector ${\overline{\mathtt{B}}}_1^q$ such that

  -

  if $q\ne q_0$ then the input and the output sets of ${\mathtt{B}}_1^q$ and of ${\overline{\mathtt{B}}}_1^q$ are identically defined as for $1<k<N$,

  -

  if $q=q_0$ then $\{{\psi }_2^{i,1},{\psi }_2^{i,2}:i\in L^{q_0}\}\cup \{{\psi }_0^1,{\psi }_0^2\}$ is the input set of ${\mathtt{B}}_1^{q_0}$ and each output of its is an in-neighbor of both ${\psi }_1^{j,1}$ and ${\psi }_1^{j,2}$ for every $j\in F^{q_0}$; similarly, $\{{\overline{\psi }}_2^{i,1},{\overline{\psi }}_2^{i,2}:i\in L^{q_0}\}\cup \{{\overline{\psi }}_0^1,{\overline{\psi }}_0^2\}$ is the input set of ${\overline{\mathtt{B}}}_1^{q_0}$ and each output of its is and in-neighbor of both ${\overline{\psi }}_1^{j,1}$ and ${\overline{\psi }}_1^{j,2}$ for every $j\in F^{q_0}$.

  Denote as $I_A$ the set of indexes of the quintuples in P ending at $q_A$ (namely, $j\in I_A$ if and only if $q_e^j=q_A$). G finally contains the $\left(\right|I_A|,\gamma -|I_A\left|\right)$-selector $\mathsf{\Phi }$ having $\{{\psi }_1^{i,1},{\psi }_1^{i,2}:i\in I_A\}$ as its input set and each output of which has an outgoing arc to ${\psi }_A$.

• For $k=N$: for every $q\in Q-\{q_A,q_R\}$, G contains the $\left(\right|R^q|,\gamma -|R^q\left|\right)$-selector ${\mathtt{B}}_N^q$ and the $\left(\right|R^q|,\gamma -|R^q\left|\right)$-reverse selector ${\overline{\mathtt{B}}}_N^q$ such that

  -

  $\{{\psi }_{N-1}^{i,1},{\psi }_{N-1}^{i,2}:i\in R^q\}$ is the input set of ${\mathtt{B}}_N^q$ and each output of its is an in-neighbor of both ${\psi }_N^{j,1}$ and ${\psi }_N^{j,2}$ for every $j\in F^q$,

  -

  $\{{\overline{\psi }}_{N-1}^{i,1},{\overline{\psi }}_{N-1}^{i,2}:i\in R^q\}$ is the input set of ${\overline{\mathtt{B}}}_N^q$ and each output of its is and in-neighbor of both ${\overline{\psi }}_N^{j,1}$ and ${\overline{\psi }}_N^{j,2}$ for every $j\in F^q$.

Refer to Figure 5 and Figure 6 for an example of the construction yielding G.

We explicitly remark that the distance between an input and an output of every selector and of every reverse selector in G but ${\mathsf{\Psi }}_0$ and ${\overline{\mathsf{\Psi }}}_0$ is $\gamma -1$: this implies that the distance between any pair of acting nodes connected by a (reverse) selector is $\gamma$.

We are now ready to fix the value of $\gamma$: in order to have $\gamma -y\ge 0$, for $y\in \left\{\right|I_A\left|\right\}\cup \left\{\right\{|P_{u,w}|,|P_{u,r}|:u\in \{0,1,\bcancel{b}\}\}\cup \left\{\right|R^q|+|L^q|:q\in Q-\{q_0,q_A,q_R\}\}\cup \{|L^{q_0}|+1\}\}$, and $\gamma >1$ we set

$$\begin{array}{c}\hfill \gamma =1+max\left\{\right|I_A|,|P_{u,w}|,|P_{u,r}|,|R^q|+|L^q|,|L^{q_0}|+1:\\ \hfill u\in \{0,1,\bcancel{b}\},q\in Q-\{q_0,q_A,q_R\}\}.\end{array}$$

3.3.3. Global States and Mirroring Configurations

Recall that a global state of a (one tape) Turing machine is the description of its internal state, of the position of the tape head, and of the content of the non-blank portion of its tape. Any non-final global state of $\mathit{TM}$ occurring during the computation $\mathit{TM}\left(x\right)$ may well be described by an opinion configuration $\omega$ for G. Let S be a non-final global state met by $\mathit{TM}$ during the computation $\mathit{TM}\left(x\right)$: an opinion configuration $\omega$ for G mirrors S (or, equivalently, $\omega$ is the mirror configuration of S) if the following hold:

• For every $1\le k\le N$ and for every $u\in \{0,1,\bcancel{b}\}$, if cell k contains u in S then $\omega \left(u_k^1\right)=\omega \left(u_k^2\right)=1$ and ${\mathtt{W}}_k^u$ is positive or ${\mathtt{D}}_u^k$ is positive, and, symmetrically, $\omega \left({\overline{u}}_k^1\right)=\omega \left({\overline{u}}_k^2\right)=-1$ and ${\overline{\mathtt{W}}}_k^u$ is negative or ${\overline{\mathtt{D}}}_k^u$ is negative;
• For every $1\le k\le N$ and for every $u\in \{0,1,\bcancel{b}\}$, if cell k does not contain u in S then $\omega \left(u_k^1\right)=\omega \left(u_k^2\right)=-1$ and ${\mathtt{W}}_k^u$ is negative or ${\mathtt{D}}_u^k$ is negative, and, symmetrically, $\omega \left({\overline{u}}_k^1\right)=\omega \left({\overline{u}}_k^2\right)=1$ and ${\overline{\mathtt{W}}}_k^u$ is positive or ${\overline{\mathtt{D}}}_k^u$ is positive;
• For every $1\le k\le N$ and for every $1\le i\le p$, if in S the head of $\mathit{TM}$ is positioned on cell k, the internal state of $\mathit{TM}$ is $q_b^i$, and cell k contains $s_r^i$ then $\omega \left({\psi }_k^{i,1}\right)=\omega \left({\psi }_k^{i,2}\right)=1$ and ${\mathtt{B}}_k^{q_b^i}$ is positive and ${\mathtt{A}}_k^{s_r^i}$ is positive, and, symmetrically, $\omega \left({\overline{\psi }}_k^{i,1}\right)=\omega \left({\overline{\psi }}_k^{i,2}\right)=-1$ and ${\overline{\mathtt{B}}}_k^{q_b^i}$ is negative and ${\overline{\mathtt{A}}}_k^{s_r^i}$ is negative;
• For every $1\le k\le N$ and for every $1\le i\le p$, if in S the head of $\mathit{TM}$ is not positioned on cell k or the internal state of $\mathit{TM}$ is not $q_b^i$ or cell k does not contain $s_r^i$ then $\omega \left({\psi }_k^{i,1}\right)=\omega \left({\psi }_k^{i,2}\right)=-1$ and ${\mathtt{B}}_k^{q_b^i}$ is negative (if $\mathit{TM}$ is not in state $q_b^i$) or ${\mathtt{A}}_k^{s_r^i}$ is negative (if the head of $\mathit{TM}$ is not positioned on cell k), and, symmetrically, $\omega \left({\overline{\psi }}_k^{i,1}\right)=\omega \left({\overline{\psi }}_k^{i,2}\right)=1$ and ${\overline{\mathtt{B}}}_k^{q_b^i}$ is positive or ${\overline{\mathtt{A}}}_k^{s_r^i}$ is positive;
• $\omega \left({\psi }_0^1\right)=\omega \left({\psi }_0^2\right)=\omega \left({\psi }_A^1\right)=\omega \left({\psi }_A^2\right)=-1$, $\omega \left({\overline{\psi }}_0^1\right)=\omega \left({\overline{\psi }}_0^2\right)=1$ and every stable clique is positive under $\omega$.

We now show that, if an opinion configuration $\omega$ of G mirrors a non-final global state S, then the opinion evolution of G starting at $\omega$ somehow describes the computation of $TM$ starting at S. Before proceeding, we establish a property of mirroring opinion configurations that is functional to our goal and that claims that acting nodes have somehow stable opinions in a configuration mirroring a global state of $TM$.

Property 5. 

If an opinion configuration ω mirrors a global state S of $TM$ then, for any acting node v and for any $1\le \ell \le \gamma -1$, it holds that

$${\mathbf{d}}_{(3,4)}{(G,\omega )}^{\ell }\left(v\right)=\omega \left(v\right).$$

Proof. 

Since $\omega$ mirrors S, then by the positiveness/negativeness of the selectors and of the reverse selectors under $\omega$ and by Property 4, for any node v in G, we have the following:

• If $v=u_k^1$ or $v=u_k^2$ then v has 5 in-neighbors (the pair of outputs of ${\mathtt{W}}_k^u$, the pair of outputs of ${\mathtt{D}}_k^u$ and the output of a stable clique). As a consequence, we have the following:

  –

  If $\omega \left(v\right)=1$ then ${\mathtt{W}}_k^u$ is positive or ${\mathtt{D}}_k^u$ is positive so that, by Property 4, at least 3 in-neighbors of v push it to 1 at ${\mathbf{d}}_{(3,4)}{(G,\omega )}^{\ell }$ for any $0\le \ell \le \gamma -2$ and, hence, ${\mathbf{d}}_{(3,4)}{(G,\omega )}^{\ell +1}\left(v\right)=1$ for any $0\le \ell \le \gamma -2$;

  –

  If $\omega \left(v\right)=-1$ then ${\mathtt{W}}_k^u$ is negative or ${\mathtt{D}}_k^u$ is negative so that, by Property 4, at most 3 in-neighbors of v push it to 1 at ${\mathbf{d}}_{(3,4)}{(G,\omega )}^{\ell }$ for any $0\le \ell \le \gamma -2$ and, hence, ${\mathbf{d}}_{(3,4)}{(G,\omega )}^{\ell +1}\left(v\right)=-1$ for any $0\le \ell \le \gamma -2$;

• If $v={\overline{u}}_k^1$ or $v={\overline{u}}_k^2$ then, again, v has 5 in-neighbors (the pair of outputs of ${\overline{\mathtt{W}}}_k^u$, the pair of outputs of ${\overline{\mathtt{D}}}_k^u$ and the output of a stable clique). As a consequence, we have the following:

  –

  If $\omega \left(v\right)=1$ then ${\overline{\mathtt{W}}}_k^u$ is positive or ${\overline{\mathtt{D}}}_k^u$ is positive so that, by Property 4, at least 3 in-neighbors of v push it to 1 at ${\mathbf{d}}_{(3,4)}{(G,\omega )}^{\ell }$ for any $0\le \ell \le \gamma -2$ and, hence, ${\mathbf{d}}_{(3,4)}{(G,\omega )}^{\ell +1}\left(v\right)=1$ for any $0\le \ell \le \gamma -2$;

  –

  If $\omega \left(v\right)=-1$ then ${\overline{\mathtt{W}}}_k^u$ is negative or ${\overline{\mathtt{D}}}_k^u$ is negative so that, by Property 4, at most 3 in-neighbors of v push it to 1 at ${\mathbf{d}}_{(3,4)}{(G,\omega )}^{\ell }$ for any $0\le \ell \le \gamma -2$ and, hence, ${\mathbf{d}}_{(3,4)}{(G,\omega )}^{\ell +1}\left(v\right)=-1$ for any $0\le \ell \le \gamma -2$;

• If $v={\psi }_k^{i,1}$ or $v={\psi }_k^{i,2}$ then v has 4 in-neighbors (the pair of outputs of ${\mathtt{A}}_k^{s_r^i}$ and the pair of outputs of ${\mathtt{B}}_k^{q_b^i}$). As a consequence, we have the following:

  –

  If $\omega \left(v\right)=1$ then ${\mathtt{A}}_k^{s_r^i}$ is positive and ${\mathtt{B}}_k^{q_b^i}$ is positive so that, by Property 4, all the 4 in-neighbors of v push it to 1 at ${\mathbf{d}}_{(3,4)}{(G,\omega )}^{\ell }$ for any $0\le \ell \le \gamma -2$ and, hence, ${\mathbf{d}}_{(3,4)}{(G,\omega )}^{\ell +1}\left(v\right)=1$ for any $0\le \ell \le \gamma -2$;

  –

  If $\omega \left(v\right)=-1$ then ${\mathtt{A}}_k^{s_r^i}$ is negative or ${\mathtt{B}}_k^{q_b^i}$ is negative so that, by Property 4, at most 2 of the 4 in-neighbors of v push it to 1 at ${\mathbf{d}}_{(3,4)}{(G,\omega )}^{\ell }$ for any $0\le \ell \le \gamma -2$ and, hence, ${\mathbf{d}}_{(3,4)}{(G,\omega )}^{\ell +1}\left(v\right)=-1$ for any $0\le \ell \le \gamma -2$;

• If $v={\overline{\psi }}_k^{i,1}$ or $v={\overline{\psi }}_k^{i,2}$ then v has 6 in-neighbors (the pair of outputs of ${\overline{\mathtt{A}}}_k^{s_r^i}$, the pair of outputs of ${\overline{\mathtt{B}}}_k^{q_b^i}$ and the output nodes of 2 stable cliques). As a consequence, we have the following:

  –

  If $\omega \left(v\right)=1$ then ${\overline{\mathtt{A}}}_k^{s_r^i}$ is positive or ${\overline{\mathtt{B}}}_k^{q_b^i}$ is positive so that, by Property 4, at least 4 in-neighbors of v push it to 1 at ${\mathbf{d}}_{(3,4)}{(G,\omega )}^{\ell }$ for any $0\le \ell \le \gamma -2$ and, hence, ${\mathbf{d}}_{(3,4)}{(G,\omega )}^{\ell +1}\left(v\right)=1$ for any $0\le \ell \le \gamma -2$;

  –

  If $\omega \left(v\right)=-1$ then ${\overline{\mathtt{A}}}_k^{s_r^i}$ is negative and ${\overline{\mathtt{B}}}_k^{q_b^i}$ is negative so that, by Property 4, at most 2 of the 6 in-neighbors of v push it to 1 at ${\mathbf{d}}_{(3,4)}{(G,\omega )}^{\ell }$ for any $0\le \ell \le \gamma -2$ and, hence, ${\mathbf{d}}_{(3,4)}{(G,\omega )}^{\ell +1}\left(v\right)=-1$ for any $0\le \ell \le \gamma -2$.

□

Recall that the computation $\mathit{TM}\left(x\right)$ occurs in $N=f\left(\right|x\left|\right)$ cells so that it always halts; hence, $\mathit{TM}\left(x\right)$ is described by a sequence $⟨S_0,S_1,\dots ,S_{\tau }⟩$ of global states such that $S_0$ is the initial global state (in which the tape contains x, the head is positioned on cell 1, and the internal state is $q_0$), $S_{\tau }$ is a final state (no quintuple can be executed from it), and, for any $0\le t\le \tau -1$, $S_{t+1}$ is derived from $S_t$ by executing a quintuple in P. The main lemma of this subsection can now be proved.

Lemma 6. 

For any $1\le t\le \tau -2$, if an opinion configuration ω mirrors $S_t$ then ${\omega }^{\prime }={\mathbf{d}}_{(3,4)}{(G,\omega )}^{\gamma }$ mirrors $S_{t+1}$.

Proof. 

Let us denote ${\omega }_{\gamma -1}={\mathbf{d}}_{(3,4)}{(G,\omega )}^{\gamma -1}$ and ${\omega }_{\gamma }={\mathbf{d}}_{(3,4)}{(G,\omega )}^{\gamma }$.

Let $q\in Q$, $k\in \{1,\dots ,N\}$ and $u\in \{0,1,\bcancel{b}\}$ be, respectively, the state, the cell read by the head tape, and the content of cell k described by $S_t$. Since $S_t$ is not a final global state, there exists $1\le i\le p$ such that $⟨q,u,v,q_e^i,m_i⟩$ is the ith quintuple in P, and since $TM$ is deterministic the ith quintuple in P is the only one beginning at state q and reading u. Hence, since $\omega$ mirrors $S_t$, $\omega \left({\psi }_k^{i,1}\right)=\omega \left({\psi }_k^{i,2}\right)=1$ and $\omega \left({\overline{\psi }}_k^{i,1}\right)=\omega \left({\overline{\psi }}_k^{i,2}\right)=-1$, and $\omega \left({\psi }_h^{\ell ,1}\right)=\omega \left({\psi }_h^{\ell ,2}\right)=-1$ and $\omega \left({\overline{\psi }}_k^{\ell ,1}\right)=\omega \left({\overline{\psi }}_k^{\ell ,2}\right)=1$ whenever $h\ne k$ or $\ell \ne i$. Without loss of generality (the other cases being similar), let us assume $k<N$ and $m^i=\mathtt{right}$, and $u\ne v$ (so that $i\in P_{u,r}$, $i\notin P_{u,w}$, $i\notin P_{v,r}$, $i\in P_{v,w}$).

Recall that, for any $z\in \{0,1,\bcancel{b}\}$ and for any $h\in \{1,\dots ,N\}$, nodes $z_h^1$ and $z_h^2$ have 5 in-neighbors each: the outputs of the selector ${\mathtt{W}}_h^z$, the outputs of the reverse selector ${\mathtt{D}}_h^z$, and the output of a stable clique. Hence, since the stable clique is positive by hypothesis and since the distance between an input and an output of any (reverse) selector in G is $\gamma -1$, then, by Properties 1, 2 and 3, the following holds:

• If $h=k$ and $z=u$ ($=s_r^i$), since $i\in P_{u,r}$ and $i\notin P_{u,w}$ then ${\overline{\psi }}_k^{i,1}$ and ${\overline{\psi }}_k^{i,2}$ are in the input set of ${\mathtt{D}}_k^u$ and ${\psi }_k^{i,1}$ and ${\psi }_k^{i,2}$ are not in the input set of ${\mathtt{W}}_k^u$ and, hence, the opinion of both the outputs of ${\mathtt{D}}_k^u$ and the outputs of ${\mathtt{W}}_k^u$ at ${\omega }_{\gamma -1}$ is $-1$ so that ${\omega }_{\gamma }\left(u_k^1\right)={\omega }_{\gamma }\left(u_k^2\right)=-1$;
• If $h=k$ and $z\notin \{u,v\}$ or if $h\ne k$, then ${\psi }_k^{i,1}$ and ${\psi }_k^{i,2}$ are not in the input set of the selector ${\mathtt{W}}_h^z$ and ${\overline{\psi }}_k^{i,1}$ and ${\overline{\psi }}_k^{i,2}$ are not in the input set of the reverse selector ${\mathtt{D}}_h^z$ and, hence, the opinion of the outputs of ${\mathtt{W}}_h^z$ is $-1$ and the opinion of the outputs of ${\mathtt{D}}_h^z$ is 1 at ${\omega }_{\gamma -1}$; hence, since exactly 3 in-neighbors push $z_h^1$ and $u_h^2$ to 1 at ${\omega }_{\gamma -1}$, this implies that ${\omega }_{\gamma }\left(z_h^1\right)={\omega }_{\gamma }\left(z_h^2\right)={\omega }_{\gamma -1}\left(z_h^1\right)={\omega }_{\gamma -1}\left(z_h^2\right)$ and, by Property 5, ${\omega }_{\gamma }\left(z_h^1\right)={\omega }_{\gamma }\left(z_h^2\right)=\omega \left(z_h^1\right)=\omega \left(z_h^2\right)$.

Symmetrically, for any $u\in \{0,1,\bcancel{b}\}$ and for any $h\in \{1,\dots ,N\}$, nodes ${\overline{u}}_h^1$ and ${\overline{u}}_h^2$ have 5 in-neighbors each: the outputs of the selector ${\overline{\mathtt{W}}}_h^u$ with input set $\{{\overline{\psi }}_h^{\ell ,1},{\overline{\psi }}_h^{\ell ,2}:\ell \in P_{u,w}\}$, the outputs of the reverse-selector $\overline{\mathtt{D}}$ with input set $\{{\psi }_h^{\ell ,1},{\psi }_h^{\ell ,2}:\ell \in P_{u,r}\}$, and the output of a stable clique. Hence, by the same reasoning applied above, the following can be proved:

• If $h=k$ and $z=u$ ($=s_r^i$) then ${\omega }_{\gamma }\left({\overline{u}}_k^1\right)={\omega }_{\gamma }\left({\overline{u}}_k^2\right)=1$;
• If $h=k$ and $z=v$ ($=s_w^i$) then ${\omega }_{\gamma }\left({\overline{v}}_k^1\right)={\omega }_{\gamma }\left({\overline{v}}_k^2\right)=-1$;
• If $h=k$ and $z\notin \{u,v\}$ or if $h\ne k$ then ${\omega }_{\gamma }\left({\overline{z}}_h^1\right)={\omega }_{\gamma }\left({\overline{z}}_h^2\right)=\omega \left({\overline{z}}_h^1\right)=\omega \left({\overline{z}}_h^2\right)$.

Since the content of only cell k is different in $S_t$ and in $S_{t+1}$, this proves that ${\omega }_{\gamma }$ actually mirrors the tape content in $S_{t+1}$, that is, for every $u\in \{0,1,\bcancel{b}\}$ and for every $1\le h\le N$, if cell h of $TM$ contains u in $S_{t+1}$ then ${\omega }_{\gamma }\left(u_h^1\right)={\omega }_{\gamma }\left(u_h^2\right)=1$ and ${\omega }_{\gamma }\left({\overline{u}}_h^1\right)={\omega }_{\gamma }\left({\overline{u}}_h^2\right)=-1$, otherwise ${\omega }_{\gamma }\left(u_h^1\right)={\omega }_{\gamma }\left(u_h^2\right)=-1$ and ${\omega }_{\gamma }\left({\overline{u}}_h^1\right)={\omega }_{\gamma }\left({\overline{u}}_h^2\right)=1$.

Since $S_{t+1}$ is not a final configuration, then there exists one (and only one) quintuple to be executed in $S_{t+1}$ and such a quintuple begins at state $q_e^i$; let the jth quintuple $⟨q_b^j=q_e^i,s_r^j=a,s_w^j,q_e^j,m^j⟩$ be the quintuple to be executed in $S_{t+1}$, with $a\in \{0,1,\bcancel{b}\}$.

Nodes ${\psi }_{k+1}^{j,1}$ and ${\psi }_{k+1}^{j,2}$ have 4 in-neighbors each: the outputs of the selector ${\mathtt{B}}_{k+1}^{q_b^j}$ and the outputs of the selector ${\mathtt{A}}_{k+1}^a$. Since $q_b^j=q_e^i$ then ${\psi }_k^{i,1}$ and ${\psi }_k^{i,2}$ are a pair of inputs of ${\mathtt{B}}_{k+1}^{q_b^j}$ and since $\omega \left({\psi }_k^{i,1}\right)=\omega \left({\psi }_k^{i,2}\right)=1$ then, by Property 2, the outputs of ${\mathtt{B}}_{k+1}^{q_b^j}$ have positive opinions at ${\omega }_{\gamma -1}$. Furthermore, since cell $k+1$ contains a in $S_{t+1}$, since the content of cell $k+1$ does not change when $TM$ moves from $S_t$ to $S_{t+1}$, and since $\omega$ mirrors $S_t$ then $\omega \left(a_{k+1}^1\right)=\omega \left(a_{k+1}^2\right)=1$; hence, still by Property 2, the outputs of ${\mathtt{A}}_{k+1}^a$ have positive opinions at ${\omega }_{\gamma -1}$. As a consequence, all four in-neighbors of ${\psi }_{k+1}^{j,1}$ and ${\psi }_{k+1}^{j,2}$ push them to 1 at ${\omega }_{\gamma -1}$ so that ${\omega }_{\gamma }\left({\psi }_{k+1}^{j,1}\right)={\omega }_{\gamma }\left({\psi }_{k+1}^{j,2}\right)=1$.

On the other hand, nodes ${\overline{\psi }}_{k+1}^{j,1}$ and ${\overline{\psi }}_{k+1}^{j,2}$ have 6 in-neighbors each: the outputs of the reverse selector ${\overline{\mathtt{B}}}_{k+1}^{q_b^j}$, the outputs of the reverse selector ${\overline{\mathtt{A}}}_{k+1}^a$ and the outputs of two stable cliques. Since ${\overline{\psi }}_k^{i,1}$ and ${\overline{\psi }}_k^{i,2}$ are a pair of inputs of ${\overline{\mathtt{B}}}_{k+1}^{q_b^j}$ and since $\omega \left({\overline{\psi }}_k^{i,1}\right)=\omega \left({\overline{\psi }}_k^{i,2}\right)=-1$ then, by Property 3, the outputs of ${\overline{\mathtt{B}}}_{k+1}^{q_b^j}$ have negative opinions at ${\omega }_{\gamma -1}$. Furthermore, similar to before, it can be shown that $\omega \left({\overline{a}}_{k+1}^1\right)=\omega \left({\overline{a}}_{k+1}^2\right)=-1$: since ${\overline{a}}_{k+1}^1$ and ${\overline{a}}_{k+1}^2$ are the two inputs of ${\overline{\mathtt{A}}}_{k+1}^a$ then, by Properties 3, both outputs of ${\overline{\mathtt{A}}}_{k+1}^a$ have negative opinions at ${\omega }_{\gamma -1}$. As a consequence, ${\overline{\psi }}_{k+1}^{j,1}$ and ${\overline{\psi }}_{k+1}^{j,2}$ are pushed to 1 at ${\omega }_{\gamma -1}$ by the outputs of two stable cliques only so that ${\omega }_{\gamma }\left({\overline{\psi }}_{k+1}^{j,1}\right)={\omega }_{\gamma }\left({\overline{\psi }}_{k+1}^{j,2}\right)=-1$.

By recalling that $TM$ is deterministic, a similar reasoning allows to prove that, for any $\ell \ne j$ or $h\ne k+1$, at most 2 in-neighbors of ${\psi }_h^{\ell ,1}$ and ${\psi }_h^{\ell ,2}$ push them to 1 at ${\omega }_{\gamma -1}$ so that ${\omega }_{\gamma }\left({\psi }_h^{\ell ,1}\right)={\omega }_{\gamma }\left({\psi }_h^{\ell ,2}\right)=-1$, and at least 4 in-neighbors of ${\overline{\psi }}_h^{\ell ,1}$ and ${\overline{\psi }}_h^{\ell ,2}$ push them to 1 at ${\omega }_{\gamma -1}$ so that ${\omega }_{\gamma }\left({\overline{\psi }}_h^{\ell ,1}\right)={\omega }_{\gamma }\left({\overline{\psi }}_h^{\ell ,2}\right)=1$.

It remains to show the positiveness/negativeness of selectors and reverse selectors under ${\omega }_{\gamma }$. We observe that, by Properties 5, 2 and 3, it follows that any selector in G is positive under ${\omega }_{\gamma }$ if and only if at least one pair of its inputs has opinion 1 at $\omega$ and any reverse selector in G is positive under ${\omega }_{\gamma }$ if and only if all its inputs have opinion 1 at $\omega$.

We just proved that ${\omega }_{\gamma }\left({\psi }_{k+1}^{j,1}\right)={\omega }_{\gamma }\left({\psi }_{k+1}^{j,2}\right)=1$: since $\omega \left({\psi }_k^{i,1}\right)=\omega \left({\psi }_k^{i,2}\right)=1$ and $\omega \left(a_{k+1}^1\right)=\omega \left(a_{k+1}^2\right)=1$ with $a=s_r^j$, by the above observation, it follows that both ${\mathtt{B}}_{k+1}^{q_b^j}$ and ${\mathtt{A}}_{k+1}^a$ are positive under ${\omega }_{\gamma }$. Symmetrically, ${\omega }_{\gamma }\left({\overline{\psi }}_{k+1}^{j,1}\right)={\omega }_{\gamma }\left({\overline{\psi }}_{k+1}^{j,2}\right)=-1$ and, since $\omega \left({\overline{\psi }}_k^{i,1}\right)=\omega \left({\overline{\psi }}_k^{i,2}\right)=-1$ and $\omega \left({\overline{a}}_{k+1}^1\right)=\omega \left({\overline{a}}_{k+1}^2\right)=-1$, ${\overline{\mathtt{B}}}_{k+1}^{q_b^j}$ and ${\overline{\mathtt{A}}}_{k+1}^a$ are negative under ${\omega }_{\gamma }$.

Recall that $⟨q,u,v,q_e^i,m_i⟩$ is the ith quintuple in P, and the ith quintuple is the one being to be executed at $S_t$ (with $u\ne v$). Let $1\le h\le N$ and $1\le \ell \le p$ be such that $h\ne k+1$ or $\ell \ne j$: similar to before, it can be proved that ${\mathtt{B}}_h^{q_b^{\ell }}$ is negative, or ${\mathtt{A}}_h^{s_r^{\ell }}$ is negative at ${\omega }_{\gamma }$ and, symmetrically, ${\overline{\mathtt{B}}}_h^{q_b^{\ell }}$ is positive or ${\overline{\mathtt{A}}}_h^{s_r^{\ell }}$ is positive at ${\omega }_{\gamma }$.

Let $z\in \{0,1,\bcancel{b}\}$ and $1\le h\le N$:

• if $h=k$ and $z=v$ then, on one side, it is ${\omega }_{\gamma }\left(z_h^1\right)={\omega }_{\gamma }\left(z_h^2\right)=1$ and, on the other side, the pair of inputs ${\psi }_h^{i,1}$ and ${\psi }_h^{i,2}$ of ${\mathtt{W}}_h^z$ have opinion 1 at $\omega$ so that ${\mathtt{W}}_h^z$ is positive under ${\omega }_{\gamma }$; symmetrically, ${\omega }_{\gamma }\left({\overline{z}}_h^1\right)={\omega }_{\gamma }\left({\overline{z}}_h^2\right)=1$ and a pair of inputs of ${\overline{\mathtt{W}}}_h^z$ have opinion $-1$ at $\omega$ so that ${\overline{\mathtt{W}}}_h^z$ is negative under ${\omega }_{\gamma }$;
• Similar to before, it can be proved that if $h=k$ and $z=u$ then ${\mathtt{D}}_h^z$ is negative and ${\overline{\mathtt{D}}}_h^z$ is positive under ${\omega }_{\gamma }$, and that if $h\ne k$ or $z\notin \{u,v\}$, then ${\mathtt{W}}_h^z$ is negative, ${\mathtt{D}}_h^z$ is positive, ${\overline{\mathtt{W}}}_h^z$ is positive and ${\overline{\mathtt{D}}}_h^z$ is negative under ${\omega }_{\gamma }$.

Since $\omega$ mirrors $S_t$ and by Property 1, it holds that all stable cliques are positive under ${\omega }_{\gamma }$, ${\omega }_{\gamma }\left({\psi }_0^1\right)={\omega }_{\gamma }\left({\psi }_0^2\right)=-1$, ${\omega }_{\gamma }\left({\overline{\psi }}_0^1\right)={\omega }_{\gamma }\left({\overline{\psi }}_0^2\right)=1$, and, since $q_e^i\ne q_A$, ${\omega }_{\gamma }\left({\psi }_A^1\right)={\omega }_{\gamma }\left({\psi }_A^2\right)=-1$.

Finally, since $S_{t+1}$ is not an accepting global state, then all inputs of the $\left(\right|I_A|,\gamma -|I_A\left|\right)$-selector whose outputs are in-neighbors of ${\psi }_A^1$ and ${\psi }_A^2$ have negative opinion al $\omega$: hence, ${\omega }_{\gamma }\left({\psi }_A^1\right)={\omega }_{\gamma }\left({\psi }_A^2\right)=-1$. □

As to the evolution of an opinion configuration $\omega$ mirroring $S_{\tau -1}$, the next lemma holds.

Lemma 7. 

If the opinion configuration ω mirrors $S_{\tau -1}$ then ${\omega }_{\gamma }={\mathbf{d}}_{(3,4)}{(G,\omega )}^{\gamma }$ is such that ${\omega }_{\gamma }\left({\psi }_A\right)=1$ if and only if $S_{\tau }$ is the accepting global state.

Proof. 

Since $S_{\tau -1}$ is not a final global state, there exists $1\le i\le p$ such that the ith quintuple in P, namely $⟨q_b^i,s_r^i,s_w^i,q_e^i,m^i⟩$, has to be executed in $S_{\tau -1}$. Let k be the tape cell being read by $TM$ in $S_{\tau -1}$.

Since $\omega$ mirrors $S_{\tau -1}$ then $\omega \left({\psi }_k^{i,1}\right)=\omega \left({\psi }_k^{i,2}\right)=1$ and $\omega \left({\psi }_h^{j,1}\right)=\omega \left({\psi }_h^{j,2}\right)=-1$ for every pair $(h,j)$ such that $h\ne k$ or $j\ne i$.

Node ${\psi }_A$ has 4 in-neighbors: the outputs of two stable cliques and the outputs of $\mathsf{\Phi }$. Since $\omega$ mirrors $S_{\tau -1}$, then $\omega \left({\psi }_A\right)=-1$ and, as a consequence of Property 2, ${\omega }_{\gamma }\left({\psi }_A\right)=1$ if and only if at least one input of the selector $\mathsf{\Phi }$ has opinion 1 at $\omega$.

Thus, ${\omega }_{\gamma }\left({\psi }_A\right)=1$ if and only if $k=1$ and $q_e^i=q_A$. □

3.3.4. Finishing the Reduction

We now define the initial opinion configuration ${\omega }_0$.

For every $1\le k\le N$, for every $u\in \{0,1,\bcancel{b}\}$ and for every $q\in Q$, we do the following:

• We set ${\omega }_0\left(v\right)=1$ for all nodes v in ${\mathtt{D}}_k^u$, in ${\overline{\mathtt{W}}}_k^u$ and ${\overline{\mathtt{B}}}_k^q$;
• We set ${\omega }_0\left(v\right)=-1$ for all nodes v in ${\overline{\mathtt{D}}}_k^u$, in ${\mathtt{W}}_k^u$ and ${\mathtt{B}}_k^q$.

Notice that, the above setting implies that, for every $1\le k\le N$ and for every $1\le j\le p$, ${\omega }_0\left({\psi }_k^{j,1}\right)={\omega }_0\left({\psi }_k^{j,2}\right)=-1$ and ${\omega }_0\left({\overline{\psi }}_k^{j,1}\right)={\omega }_0\left({\overline{\psi }}_k^{j,2}\right)=1$.

Let $x=x_1{x}_2\dots x_n$ be the input string; for $k=1,\dots ,N$ and $u\in \{0,1,\bcancel{b}\}$:

• If $1\le k\le n$ and $u=x_k$ or if $n+1\le k\le N$ and $u=\bcancel{b}$ then we set ${\omega }_0\left(v\right)=1$ for all nodes v in ${\mathtt{A}}_k^u$ and we set ${\omega }_0\left(v\right)=-1$ for all nodes v in ${\overline{\mathtt{A}}}_k^u$;
• If $1\le k\le n$ and $u\ne x_k$ or if $n+1\le k\le N$ and $u\ne \bcancel{b}$ then we set ${\omega }_0\left(v\right)=-1$ for all nodes v in ${\mathtt{A}}_k^u$ and we set ${\omega }_0\left(v\right)=1$ for all nodes v in ${\overline{\mathtt{A}}}_k^u$.

Notice that, by the assumptions about $TM$ described at the beginning of this section, the above setting implies that, for every $1\le k\le N$ and for every $u\in \{0,1,\bcancel{b}\}$, if cell k contains u in the initial global state $S_0$ of $TM\left(x\right)$ then ${\omega }_0\left(u_k^1\right)={\omega }_0\left(u_k^2\right)=1$ and ${\omega }_0\left({\overline{u}}_k^1\right)={\omega }_0({\overline{u}}_k^2)=-1$, otherwise ${\omega }_0\left(u_k^1\right)={\omega }_0\left(u_k^2\right)=-1$ and ${\omega }_0\left({\overline{u}}_k^1\right)={\omega }_0{\left(\overline{u}\right)}_k^2=1$.

Finally, we set ${\omega }_0\left({\psi }_A^1\right)={\omega }_0\left({\psi }_A^2\right)=-1$, for every node v in ${\mathsf{\Psi }}_0$ we set ${\omega }_0\left(v\right)=1$, and for every node v in ${\overline{\mathsf{\Psi }}}_0$ we set ${\omega }_0\left(v\right)=-1$.

Notice that, since ${\omega }_0\left({\psi }_k^{i,1}\right)={\omega }_0\left({\psi }_k^{i,2}\right)=-1$ for every $1\le k\le N$ and $1\le i\le p$, ${\omega }_0$ does not mirror any global state of $\mathit{TM}$. However, it evolves in an opinion configuration mirroring the initial global state $S_0$ of $\mathit{TM}\left(x\right)$. This is shown in the next lemma.

Lemma 8. 

The opinion configuration ${\mathbf{d}}_{(3,4)}{(G,{\omega }_0)}^{\gamma }$ mirrors $S_0$.

Proof. 

As in the proof of Lemma 6, we denote as ${\omega }_{\gamma -1}={\mathbf{d}}_{(3,4)}{(G,\omega )}^{\gamma -1}$ and as ${\omega }_{\gamma }={\mathbf{d}}_{(3,4)}{(G,\omega )}^{\gamma }$.

Since ${\omega }_0\left({\psi }_k^{i,1}\right)={\omega }_0\left({\psi }_k^{i,2}\right)=-1$ and ${\omega }_0\left({\overline{\psi }}_k^{i,1}\right)={\omega }_0\left({\overline{\psi }}_k^{i,2}\right)=1$ for every $1\le k\le N$ and $1\le i\le p$, by similar arguments to those in the proof of Lemma 6, the following hold:

• ${\omega }_{\gamma }\left(u_k^1\right)={\omega }_{\gamma }\left(u_k^2\right)={\omega }_0\left(u_k^1\right)={\omega }_0\left(u_k^2\right)$ and ${\omega }_{\gamma }\left({\overline{u}}_k^1\right)={\omega }_{\gamma }\left({\overline{u}}_k^2\right)={\omega }_0\left({\overline{u}}_k^1\right)={\omega }_0\left({\overline{u}}_k^2\right)$ for every $1\le k\le N$ and $u\in \{0,1,\bcancel{b}\}$;
• ${\mathtt{D}}_k^u$ is positive and ${\mathtt{W}}_k^u$ is negative at ${\omega }_{\gamma }$, and ${\overline{\mathtt{D}}}_k^u$ is negative and ${\overline{\mathtt{W}}}_k^u$ is negative at ${\omega }_{\gamma }$, for every $1\le k\le N$ and $u\in \{0,1,\bcancel{b}\}$;
• ${\omega }_{\gamma }\left({\psi }_k^{i,1}\right)={\omega }_{\gamma }\left({\psi }_k^{i,1}\right)={\omega }_0\left({\psi }_k^{i,1}\right)={\omega }_0\left({\psi }_k^{i,2}\right)=-1$ and ${\omega }_{\gamma }\left({\overline{\psi }}_k^{i,1}\right)={\omega }_{\gamma }\left({\overline{\psi }}_k^{i,1}\right)={\omega }_0\left({\overline{\psi }}_k^{i,1}\right)={\omega }_0\left({\overline{\psi }}_k^{i,2}\right)=1$ for every pair $(k,i)$ such that $1\le k\le N$ and $1\le i\le p$ and $q_b^i\ne q_0$ or $s_r^i\ne x_1$;
• ${\mathtt{B}}_k^q$ is negative and ${\overline{\mathtt{B}}}_k^q$ is positive for every pair $(k,q)$ such that $1\le k\le N$ and $q\ne q_0$.

Let the jth quintuple $⟨q_b^j,s_r^j,s_w^j,m_j⟩$ be the one to be executed by $TM$ in $S_0$: hence, $q_b^j=q_0$ and $s_r^j=x_1$. As a consequence, since ${\omega }_0\left({\psi }_0^1\right)={\omega }_0\left({\psi }_0^2\right)=1$, since the outputs of ${\mathtt{B}}_1^{q_0}$ are in-neighbors of ${\psi }_1^{j,1}$ and ${\psi }_1^{j,2}$ and since the inputs of ${\mathtt{A}}_1^{s_r^j}$ have opinion 1 at ${\omega }_0$ then, by Property 2, nodes ${\psi }_1^{j,1}$ and ${\psi }_1^{j,2}$ are pushed to 1 by all their 4 in-neighbors. Symmetrically, since ${\omega }_0\left({\overline{\psi }}_0^1\right)={\omega }_0\left({\overline{\psi }}_0^2\right)=-1$, since the outputs of ${\overline{\mathtt{B}}}_1^{q_0}$ are in-neighbors of ${\overline{\psi }}_1^{j,1}$ and ${\overline{\psi }}_1^{j,2}$ and and since the inputs of ${\overline{\mathtt{A}}}_1^{s_r^j}$ have opinion $-1$ at ${\omega }_0$ then, by Property 3, nodes ${\overline{\psi }}_1^{j,1}$ and ${\overline{\psi }}_1^{j,2}$ are pushed to $-1$ by 4 in-neighbors out of 6 at ${\omega }_{\gamma -1}$. All this implies that ${\omega }_{\gamma }\left({\psi }_1^{j,1}\right)={\omega }_{\gamma }\left({\psi }_1^{j,2}\right)=1$ and ${\omega }_{\gamma }\left({\overline{\psi }}_1^{j,1}\right)={\omega }_{\gamma }\left({\overline{\psi }}_1^{j,2}\right)=-1$.

Since the input nodes of ${\mathsf{\Psi }}_0$ have positive opinion at ${\omega }_0$ and the input nodes of ${\overline{\mathsf{\Psi }}}_0$ have negative opinion at ${\omega }_0$, then, by Properties 2 and 3, ${\mathbf{d}}_{(3,4)}{(G,{\omega }_0)}^{\ell }\left({\psi }_0^1\right)={\mathbf{d}}_{(3,4)}{(G,{\omega }_0)}^{\ell }\left({\psi }_0^2\right)=1$ and ${\mathbf{d}}_{(3,4)}{(G,{\omega }_0)}^{\ell }\left({\overline{\psi }}_0^1\right)={\mathbf{d}}_{(3,4)}{(G,{\omega }_0)}^{\ell }\left({\overline{\psi }}_0^2\right)=-1$ for all $\ell =1,\dots ,\gamma -1$. Correspondingly, by Properties 5, 2 and 3, it follows that ${\mathtt{B}}_1^j$ is positive and ${\overline{\mathtt{B}}}_1^j$ is negative under ${\omega }_{\gamma }$.

Furthermore, again similar to the proof of Lemma 6, it can be proved that for $u\in \{0,1,\bcancel{b}\}$ and $k=1,\dots ,N$, ${\mathtt{A}}_k^u$ is positive at ${\omega }_{\gamma }$ if and only if ${\omega }_{\gamma }\left(u_k^1\right)={\omega }_{\gamma }\left(u_k^2\right)=1$; correspondingly, ${\overline{\mathtt{A}}}_k^u$ is negative at ${\omega }_{\gamma }$ if and only if ${\omega }_{\gamma }\left({\overline{u}}_k^1\right)={\omega }_{\gamma }\left({\overline{u}}_k^2\right)=-1$: hence, ${\mathtt{A}}_1^{s_r^j}$ is positive and ${\overline{\mathtt{A}}}_1^{s_r^j}$ is negative at ${\omega }_{\gamma }$.

Since the input nodes $i^1$ and $i^2$ of ${\mathsf{\Psi }}_0$ have indegree 0 in G then ${\mathbf{d}}_{(3,4)}{(G,{\omega }_0)}^t\left(i^1\right)={\mathbf{d}}_{(3,4)}{(G,{\omega }_0)}^t\left(i^2\right)=-1$ for every $t>0$: hence, by Property 2, ${\mathsf{\Psi }}_0$ is negative at ${\omega }_{\gamma }$. Symmetrically, since the output nodes of 4 stable cliques are in-neighbors of the input nodes ${\overline{i}}^1$ and ${\overline{i}}^2$ of ${\overline{\mathsf{\Psi }}}_0$ then ${\mathbf{d}}_{(3,4)}{(G,{\omega }_0)}^t\left({\overline{i}}^1\right)={\mathbf{d}}_{(3,4)}{(G,{\omega }_0)}^t\left({\overline{i}}^2\right)=1$ for every $t>0$: hence, by Property 3, ${\overline{\mathsf{\Psi }}}_0$ is negative at ${\omega }_{\gamma }$.

Finally, similar to the proof of Lemma 6, it can be shown that all stable cliques are positive at ${\omega }_{\gamma }$ and that ${\omega }_{\gamma }\left({\psi }_A^1\right)={\omega }_{\gamma }\left({\psi }_A^2\right)=-1$. □

From Lemmas 8, 6 and 7, it directly follows that ${\psi }_A$ gets a positive opinion starting from the configuration ${\omega }_0$ if and only if $\mathit{TM}\left(x\right)$ is an accepting computation. Since G, ${\omega }_0$ and $V_A$ are computable in polynomial time in $\left|x\right|$, by defining the target set as $U=\left\{{\psi }_A\right\}$, this completes the proof of Theorem 3.

3.4. Proof of Corollary 1: Unlikeliness of a Polynomial Bound to $|{\mathcal{E}}_{{\mathbf{d}}_{(3,4)}}(G,\omega )|$ in Directed Graphs

Let us denote as ${\mathbf{d}}_{(c^{+},c^{-})}$-ReachTarget the restriction of u-RT in which only the ${\mathbf{d}}_{(c^{+},c^{-})}$ opinion dynamics is considered, and let $⟨G=(V,E,\lambda ),\omega ,U⟩$ be an instance of ${\mathbf{d}}_{(c^{+},c^{-})}$-ReachTarget (that is, $⟨{\mathbf{d}}_{(3,4)},G=(V,E,\lambda ),\omega ,U⟩$ is an instance of u-RT).

Recall that, for any opinion dynamics $\mathbf{d}$, deciding if ${\omega }^{\prime }\in {\mathcal{E}}_{\mathbf{d}}(G,\omega )$ exists such that ${\omega }^{\prime }\left(u\right)=1$ for every $u\in U$ may occur by just computing, one after the other, all the opinion configurations in ${\mathcal{E}}_{\mathbf{d}}(G,\omega )$ and testing if any of them makes positive the opinions of all nodes in U. Then, ${\mathbf{d}}_{(c^{+},c^{-})}$-ReachTarget should belong to P if ${\mathcal{E}}_{{\mathbf{d}}_{(c^{+},c^{-})}}$ has polynomial size $\left|G\right|$.

4. Discussion

Theoretical issues are considered in this paper. The main achievements of the paper are the proof that, like in the case of undirected unsigned graphs, a polynomial bound in the graph size on the number of opinion configurations met during the underpopulation opinions evolution process exists for (undirected) structurally balanced graphs, and the proof that such a polynomial bound is unlikely to exist for directed (although unsigned) graphs. The former results extend the set of instances for which deciding if the reachability of some opinion configurations from one other is a problem in P.

As mentioned in the introduction, two features were introduced for proving the existence of the polynomial bound, namely, the support graph of a graph in some opinion configuration, and a procedure allowing the simulation of the opinion evolution of a signed graph according to underpopulation dynamics by the opinion evolution of a related signed graph according to related symmetric dynamics. Since the support graph evolves according to its edge labels only (instead of according to a combination of edge and node labels), it allows to concisely describe the opinion configurations and, hence, the evolution of a signed graph. This argument suggests that it might prove to be a useful tool for new achievements on this topic. Additionally, the possibility of generalizing the procedure yielding Lemma 5 in order to obtain simulations between other pairs of local threshold-based dynamics seems worthwhile to be investigated.

At first glance, the underpopulation rule looks like a minor change to the set of rules governing the Game of Life. In this respect, it has to be remarked that the Game of Life is a Turing-complete system (that is, it can simulate the behavior of any Turing-based computation models) also when played on an (infinite) undirected grid. On the other hand, the underpopulation rule is a much weaker model when considered in undirected unsigned graphs or even (as proved in this paper) on structurally balanced graphs: this is the downside of having the reachability problems in P in such cases.