Effects of the Queue Discipline on System Performance
Abstract
:1. Introduction
2. Influence of Service Disciplines
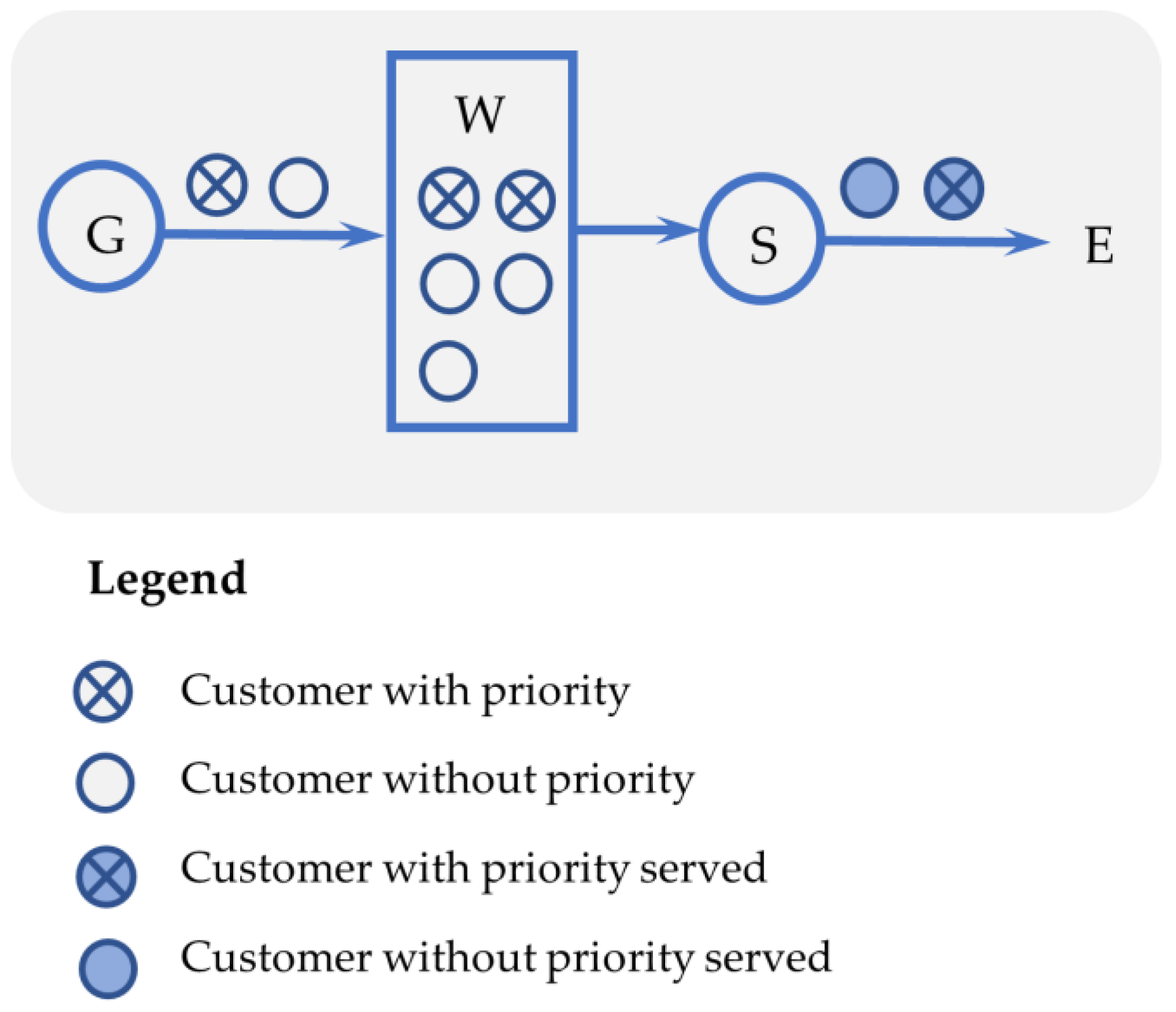
2.1. Formulation of the Problem
- Time in the queue, .
- Time in the system (between the arrival time and departure time).
- Without interruptions: the priorities of customers in the queue are examined; the FIFO discipline is applied to customers in the highest priority class.
- With interruptions: the arrival of a customer with priority causes the service interruption of a non-priority (or lower priority) customer, which returns to the queue. If several levels of priorities are applied, the customer in service must have the highest priority.
2.2. Priority Service with Same Service Rates
2.2.1. Single Server, Service without Interruptions
- —arrival rate of customers in class k, for k ∈ {1, 2}.
- —service rate of customers in class k.
- —utilisation for customers in class k (ratio between arrival rate and service rate).
- —system utilisation.
2.2.2. Single Sever, Service with Interruptions and Additional Idle Time
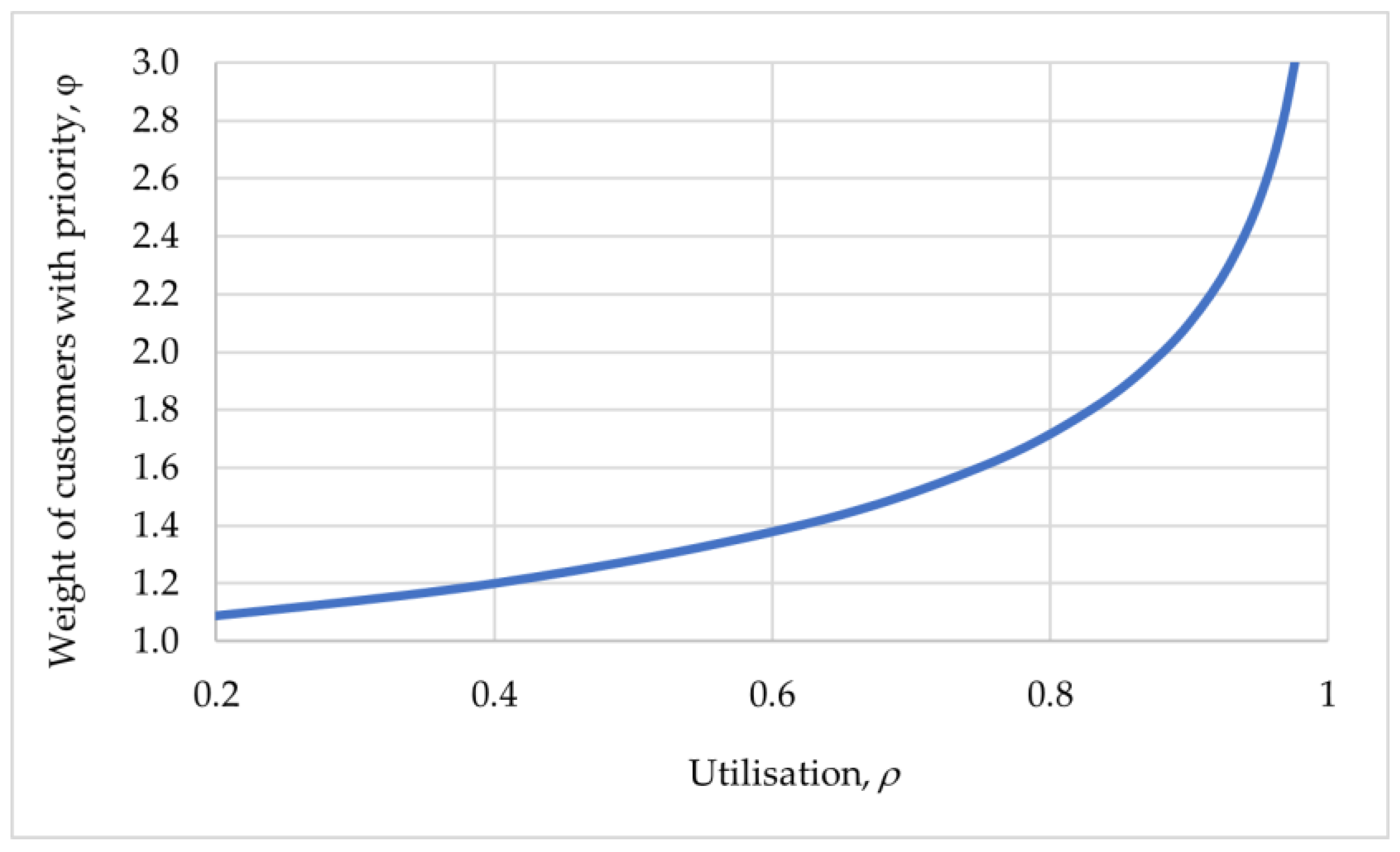
2.3. Priority Service with Different Service Rates
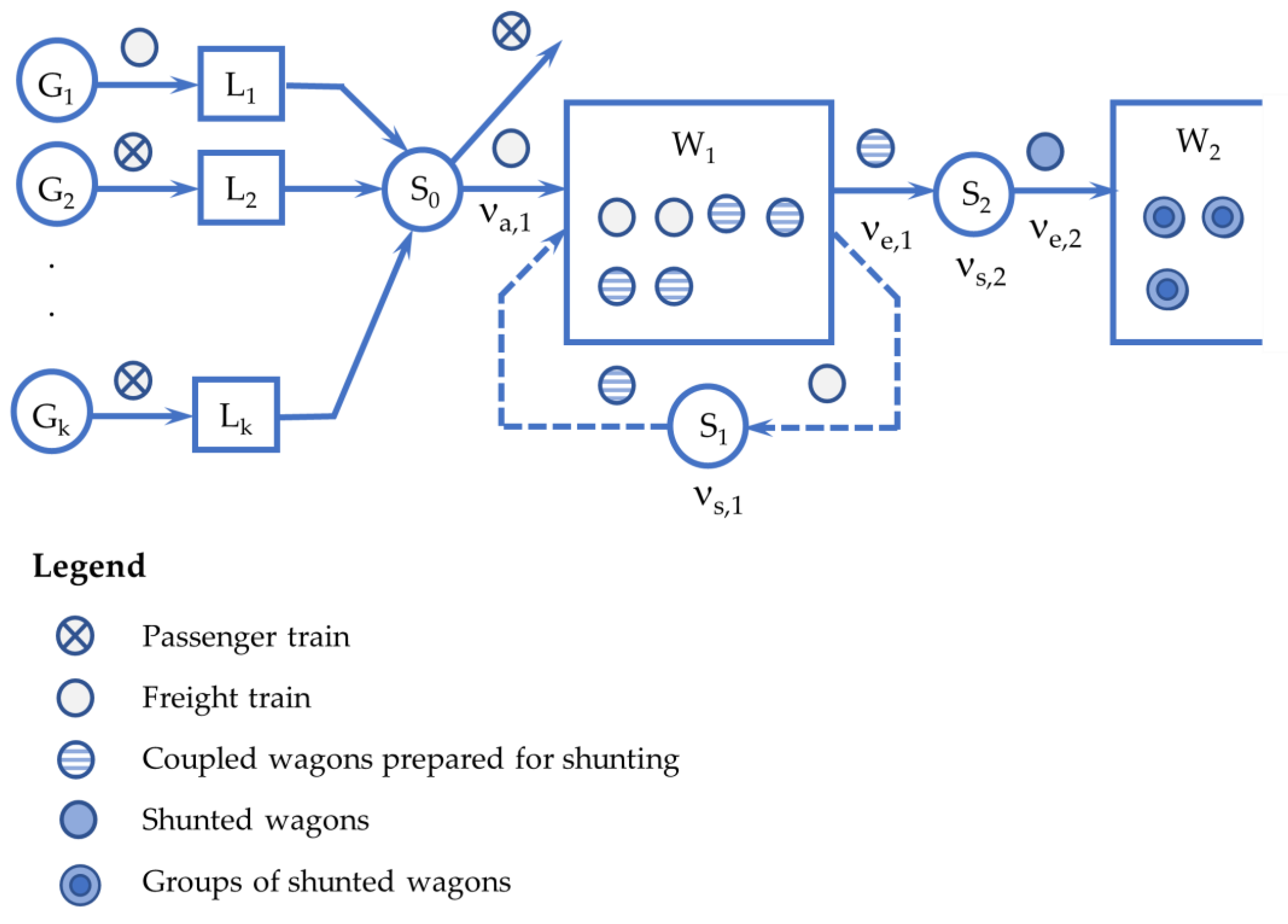
3. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Raicu, S. Transport Systems; AGIR Press: Bucharest, Romania, 2007; pp. 323–385. (In Romanian) [Google Scholar]
- Raicu, R.; Raicu, S. Complex Aspects of Transport Quality. In Urban Transport XI. WIT Transactions on the Built Environment; WIT Press: Southampton, UK, 2005; Volume 77, pp. 281–290. [Google Scholar] [CrossRef]
- Newell, G.F. Airport capacity and delays. Transp. Sci. 1979, 13, 201–241. [Google Scholar] [CrossRef]
- Jacyna, M.; Żak, J.; Gołębiowski, P. The Use of the Queueing Theory for the Analysis of Transport Processes. Log. Transp. 2019, 41, 101–111. [Google Scholar] [CrossRef]
- Raicu, S.; Popa, M. Some Difficult Problems in Using the Models of Queuing Theory for the Real Systems Study. In Proceedings of the 9th Symposium on Modelling, Simulation and Identification Systems, “Dunarea de Jos” University, Galati, Romania, 24–25 October 1996; pp. 247–251. [Google Scholar]
- Hall, R.W. Transportation Queueing. In Handbook of Transportation Science. International Series in Operations Research & Management Science; Hall, R.W., Ed.; Springer: Boston, MA, USA, 1999; Volume 23, pp. 109–150. [Google Scholar]
- Cox, D.R.; Smith, W. Queues, 1st ed.; Chapman & Hall: London, UK, 1991. [Google Scholar]
- Lee, A.M. Applied Queueing Theory; Studies in Management; Palgrave: London, UK, 1966. [Google Scholar]
- Ackoff, R.L.; Sasieni, M.W. Fundamentals Of Operations Research; John Wiley and Sons Inc.: New York, NY, USA, 1968. [Google Scholar]
- Hall, R.W. Queueing Methods for Services and Manufacturing; Prentice Hall: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]
- Varghese, V.N.; Verghese, V.; Chandran, A. Application of Queuing Theory in Transportation. Intern. J. Eng. Res. Techn. 2021, 9, 55–58. [Google Scholar]
- Itoh, E.; Mitici, M. Queue-Based Modelling of the Aircraft Arrival Process at a Single Airport. Aerospace 2019, 6, 103. [Google Scholar] [CrossRef] [Green Version]
- Higasa, K.; Itoh, E. Controlling Aircraft Inter-Arrival Time to Reduce Arrival Traffic Delay via a Queue-Based Integer Programming Approach. Aerospace 2022, 9, 663. [Google Scholar] [CrossRef]
- Itoh, E.; Mitici, M. Analyzing tactical control strategies for aircraft arrivals at an airport using a queuing model. J. Air Transp. Manag. 2020, 89, 101938. [Google Scholar] [CrossRef]
- Dorda, M.; Teichmann, D. Modelling of Freight Trains Classification Using Queueing System Subject to Breakdowns. Math. Prob. Eng. 2013, 2013, 307652. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, Y.; Li, L.; Delahaye, D. A Queuing Network Model of a Multi-Airport System Based on Point-Wise Stationary Approximation. Aerospace 2022, 9, 390. [Google Scholar] [CrossRef]
- Bychkov, I.; Kazakov, A.; Lempert, A.; Zharkov, M. Modeling of Railway Stations Based on Queuing Networks. Appl. Sci. 2021, 11, 2425. [Google Scholar] [CrossRef]
- Huisman, T.; Boucherie, R.J.; van Dijk, N.M. A solvable queueing network model for railway networks and its validation and applications for the Netherlands. Eur. J. Oper. Res. 2002, 142, 30–51. [Google Scholar] [CrossRef]
- Arseni, O.; Racioppi, F. (Coord.). Making THE (Transport, Health and Environment) Link. Transport, Health and Environment Pan-European Programme and the Sustainable Development Goals. World Health Organization Regional Office for Europe, 2018. Available online: https://thepep.unece.org/sites/default/files/2018-09/online%20version.pdf (accessed on 7 December 2022).
- Lee, H.W.; Lee, S.S.; Chae, K.C.; Nadarajan, R. On a batch service queue with single vacation. Appl. Math. Modell. 1992, 16, 36–42. [Google Scholar] [CrossRef]
- Staniuk, W.; Staniuk, M.; Chamier-Gliszczynski, N.; Jacyna, M.; Kłodawski, M. Decision-Making under the Risk, Uncertainty and COVID-19 Pandemic Conditions Applying the PL9A Method of Logistics Planning—Case Study. Energies 2022, 15, 639. [Google Scholar] [CrossRef]
- Barrena, E.; Canca, D.; Coelho, L.C.; Laporte, G. Single-line rail rapid transit timetabling under dynamic passenger demand. Transp. Res. Part B Method. 2014, 70, 134–150. [Google Scholar] [CrossRef]
- Alotaibi, F.M.; Ullah, I.; Ahmad, S. Modelling and Performance Evaluation of Multi-Class Queuing System with QoS and Priority Constraints. Electronics 2021, 10, 500. [Google Scholar] [CrossRef]
- Klimenok, V.; Dudin, A.; Dudina, O.; Kochetkova, I. Queuing System with Two Types of Customers and Dynamic Change of a Priority. Mathematics 2020, 8, 824. [Google Scholar] [CrossRef]
- Lee, S.; Dudin, S.; Dudina, O.; Kim, C.; Klimenok, V. A Priority Queue with Many Customer Types, Correlated Arrivals and Changing Priorities. Mathematics 2020, 8, 1292. [Google Scholar] [CrossRef]
- Dudin, A.; Dudina, O.; Dudin, S.; Samouylov, K. Analysis of Single-Server Multi-Class Queue with Unreliable Service, Batch Correlated Arrivals, Customers Impatience, and Dynamical Change of Priorities. Mathematics 2021, 9, 1257. [Google Scholar] [CrossRef]
- Afroun, F.; Aïssani, D.; Hamadouche, D.; Boualem, M. Q-matrix method for the analysis and performance evaluation of unreliable M/M/1/N queueing model. Math. Meth. Appl Sci. 2018, 41, 9152–9163. [Google Scholar] [CrossRef]
- Jain, M.; Dhibar, S.; Sanga, S.S. Markovian working vacation queue with imperfect service, balking and retrial. J. Amb. Intell. Hum. Comput. 2022, 13, 1907–1923. [Google Scholar] [CrossRef]
- Powell, W.B. Analysis of vehicle holding and cancellation strategies in bulk arrival, bulk service queues. Transp. Sci. 1985, 19, 352–377. [Google Scholar] [CrossRef]
- Cox, D.R.; Titterington, D.M. Complex Stochastic Systems; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raicu, S.; Costescu, D.; Popa, M. Effects of the Queue Discipline on System Performance. AppliedMath 2023, 3, 37-48. https://doi.org/10.3390/appliedmath3010003
Raicu S, Costescu D, Popa M. Effects of the Queue Discipline on System Performance. AppliedMath. 2023; 3(1):37-48. https://doi.org/10.3390/appliedmath3010003
Chicago/Turabian StyleRaicu, Serban, Dorinela Costescu, and Mihaela Popa. 2023. "Effects of the Queue Discipline on System Performance" AppliedMath 3, no. 1: 37-48. https://doi.org/10.3390/appliedmath3010003
APA StyleRaicu, S., Costescu, D., & Popa, M. (2023). Effects of the Queue Discipline on System Performance. AppliedMath, 3(1), 37-48. https://doi.org/10.3390/appliedmath3010003







