Abstract
Total ankle arthroplasty (TAA) is a motion-preserving treatment for end-stage ankle arthritis. An effective tool for analyzing these implants’ mechanical performance and longevity in silico is finite element analysis (FEA). An FEA in ABAQUS was used to statically analyze the mechanical behavior of the ultra-high-molecular-weight polyethylene (UHMWPE) bearing component at varying dorsiflexion/plantarflexion ankle angles and axial loading conditions during the stance phase of the gait cycle for a single cycle. The von Mises stress and contact pressure were examined on the articulating surface of the bearing component in two newly installed fixed-bearing TAA implants (Wright Medical INBONE II and Exactech Vantage). Six different FEA models of variable ankle compressive load levels and ankle angle positions, for the varying subphases of the stance phase of the gait cycle, were created. The components in these models were constrained to be conducive to the bone–implant interface, where implant loosening occurs. Our results showed that the von Mises stress and contact pressure distributions increased as the compressive load increased. The highest stress was noted at dorsiflexion angles > 15°, in areas where the UHMWPE liner was thinnest, at the edges of the talar and UHMWPE components, and during the terminal stance phase of the gait cycle. This static structural analysis highlighted these failure regions are susceptible to yielding and wear and indicated stress magnitudes that are in agreement (within 25%) with those in previous static structural TAA FEAs. The mechanical wear of the UHMWPE bearing component in TAA can lead to aseptic loosening and peri-implant cyst formation over time, requiring surgical revision. This study provides ankle replacement manufacturers and orthopedic surgeons with a better understanding of the stress response and contact pressure sustained by TAA implants, which is critical to optimizing implant longevity and improving patient care.
1. Introduction
The ankle, or the tibiotalar joint, is a hinged synovial articulation between the distal tibia, talus, and fibula bones. The distal fibula’s lateral malleolus forms the joint’s outer border, while the medial malleolus of the distal tibia forms the inner border of the joint. The distal tibia, or the tibial plafond, forms the superior border, and the talar dome trochlear surface forms the inferior border. All joint surfaces are lined by articular cartilage, a viscoelastic connective tissue that facilitates load transmission [1,2]. The bony articulations are further stabilized by strong collateral ligaments medially and laterally. A schematic of an ankle joint is shown in Figure 1.
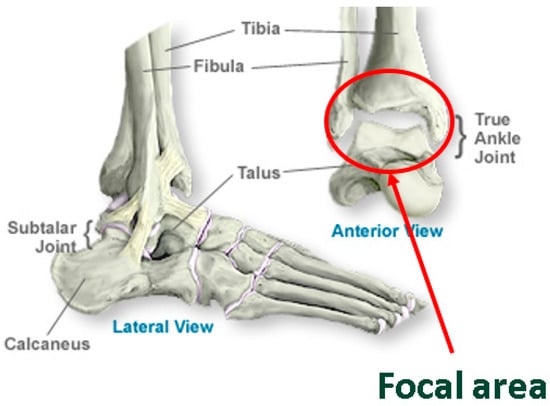
Figure 1.
Schematic of the ankle joint [2].
The ankle joint has six degrees of freedom. The greatest motion occurs in the sagittal plane, providing dorsiflexion and plantarflexion. Dorsiflexion refers to the motion when the foot moves upwards towards the tibia, whereas plantarflexion refers to the foot moving downwards towards the ground. Normal, non-arthritic ankles have a total range of motion (ROM) of approximately 50–75° in the sagittal plane, 10–20° on average for dorsiflexion and 40–55° for plantarflexion [3,4,5]. Ankle planes of motion are shown in Figure 2.
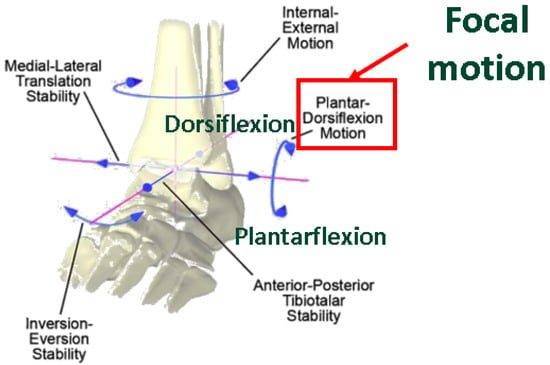
Figure 2.
Ankle planes of motion, with emphasis on dorsiflexion/plantarflexion [6]. Licensed permission for use granted by Elsevier.
Gait refers to the pattern of walking. One gait cycle is the time between the heel strikes of a limb. The stance phase of the gait cycle, which makes up 60% of the gait cycle, is when the foot is in contact with the ground. This phase is of primary significance when analyzing stress on the ankle joint. The swing phase is the period of time when the foot is not in direct contact with the ground and comprises the remainder of the gait cycle.
The stance phase is subdivided into the initial contact and loading response, mid-stance, terminal stance, and pre-swing stages, as shown in Figure 3.
Data from Martinelli [7] of normal ankle dorsiflexion and plantarflexion angles are plotted in Figure 4. During the first 10% of the gait cycle, the initial contact and loading response, the heel contacts the ground, the foot everts, and the ankle dorsiflexors eccentrically contract. During the subsequent mid-stance stage, 10–30% of the stance phase, the tibia externally rotates, and the plantarflexors eccentrically contract. At the terminal stance and pre-swing stages, 30–60% of the stance phase, the plantarflexors concentrically contract, and the foot internally rotates [8].
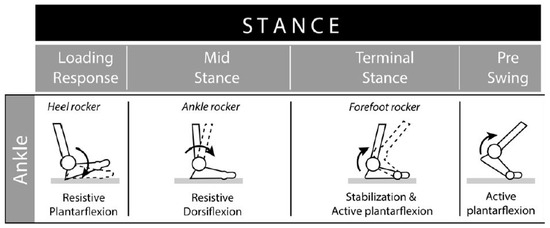
Figure 3.
Subphases of the stance phase of the gait cycle [8]. Used with permission from BioMed Central under Creative Commons Attribution 4.0.
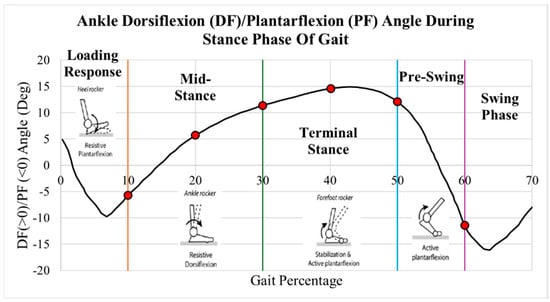
Figure 4.
Dorsiflexion/plantarflexion gait data of a healthy ankle during stance phrase of gait cycle. Figure created by author using healthy ankle data of Martinelli’s [7] study. Permission granted through BMC Musculoskeletal Disorders with Creative Commons Attribution 4.0.
Ankle joint osteoarthritis is a debilitating degenerative disorder resulting in the loss of articular cartilage, causing pain and a loss of motion [9]. Surgical treatment to address end-stage ankle arthritis includes ankle fusion (arthrodesis) or total ankle arthroplasty (TAA) [10]. Ankle fusion involves joining the tibia and talus bones with plates and screws in order for them to consolidate and combine into one bony unit. This eliminates any remaining motion within the ankle joint but also eliminates the pain associated with the ankle arthritis. A total ankle arthroplasty involves removing a portion of the degenerated bone and cartilage from the ankle joint and placing an artificial implant. This addresses the pain from the ankle arthritis while preserving ankle motion.
Ankle arthroplasty (TAA) offers several advantages over ankle arthrodesis. These include preserving the ankle’s range of motion, promoting more natural walking mechanics, and reducing stress on adjacent joints [7]. The surgical technique involves resectioning of the degraded tibial plafond and talar dome articular and subchondral bone surfaces and replacing them with the corresponding TAA components. Figure 5 shows a labeled diagram of a TAA implant.
TAA results in significant improvement in patient-reported outcome measures, including decreased pain and improved mobility, physical and mental function, and quality of life [11,12,13].
The tibial and talar components typically have porous coated pegs and stems that are inserted into native bone for primary fixation and bony ingrowth. Bone cement can be used to augment the fixation if needed [14,15]. These components are typically made of cobalt chromium molybdenum (CoCrMo), a high-stiffness and high-strength material.
The bicondylar bearing component comprises ultra-high-molecular-weight polyethylene (UHMWPE). This material has a low wear rate, is chemically inert, and has high levels of biocompatibility, crystallinity, ductility, and toughness. Typically, it is cross-linked and injected with Vitamin E as an antioxidant to eliminate free radicals, decrease the wear rate, and promote longevity [16,17].

Figure 5.
Labeled diagram of Vantage TAA implant [15].
The primary failure modes of TAA are polyethylene wear and aseptic loosening [18]. Figure 6 shows the location of these failure modes. Aseptic loosening is a non-infectious failure of prosthetic component fixation, leading to unstable and unintended motions of the component [19].

Figure 6.
Labeled locations of failure modes on TAA implant [15].
Polyethylene wear occurs from abnormal stress concentration, leading to particulate formation which can function as debris within the joint. This leads to the activation of specialized cells called macrophages, which lead to bone destruction, or osteolysis, around the implant components [6,20]. Further micromotion at the bone and implant interface leads to gross loosening, which eventually leads to painful implant subsidence [21]. The von Mises stress is an equivalent stress that is important in determining whether a material yields under maximum loading.
The long-term TAA implant survivorship rate is greater than 90% at 10 years [20]. However, the longer-term results of fourth-generation implants at 15–20 years are still limited [22], highlighting the need for the in silico testing of these TAA implants.
An effective method to test TAA implants in silico is finite element analysis (FEA). An FEA is useful for the static structural analysis of the stress response on the bearing component while loaded during the stance phase of the gait cycle. It is also beneficial to analyze the longevity of the bearing to indicate long-term results. Several researchers have performed FEAs in this regard within the past ten years. Yu [23] created a model of the INBONE II within a patient’s foot based on CT scans. They performed a sensitivity analysis with different material combinations for the bearing component and metallic components to determine the static von Mises stress response on the implant. Zhang [24] analyzed the stresses on the bearing component of the INBONE II, as well as the tibial and talar bone micromotion of the implant. Saad [25] performed a cyclic analysis on the BOX fixed-bearing implant. He computed the wear rate on the bearing while loaded and utilized an algorithm to adjust the bearing geometry based on the volumetric wear. He used the contact pressure due to the bearing and talar component to compute this wear over millions of gait cycles.
The primary aim of this study was to investigate the mechanical behavior of two commonly used TAA fixed-bearing implants, the Wright Medical INBONE II and the Exactech Vantage, under axial loading and varying ankle positions during the stance phase of the gait cycle. A static structural analysis was performed to highlight the implant areas most susceptible to failure based on the identified points of maximum loading. The von Mises stress response and contact pressure distribution on the bearing component were further sub-characterized during all four components of the stance phase.
To the authors’ knowledge, this is the first FEA study on the Vantage publicly available in the literature. Figure 7 shows these two fixed-bearing implants. Figure 8 shows the long-term benefits of FEAs of TAA implants, ultimately improving patient care.

Figure 7.
Focal implants of this study. (a) Wright Medical INBONE II [26], (b) Exactech Vantage [15].
Figure 8.
Long-term benefits of FEA structural analyses of TAA implants.
2. Methods
The implant geometry was created in SolidWorks 2023, and the FEA was performed using ABAQUS 6.25. The FEA model process involved creating the geometry, establishing the material model, specifying the solver increment, constraining the component interactions, applying the load and boundary conditions, and meshing. For a more detailed description of these processes, refer to the Methods chapter in the Master’s thesis written by Jain [27].
2.1. Implant Geometry Development
The precise geometry of the implants could not be obtained due to the proprietary nature of their designs. Wright Medical and Exactech provided limited dimensions of the implant components in their surgical technique guides, including each component’s length, width, and height. Therefore, we used a reverse-engineering process to model the implants. We chose a size 2 implant based on a prior study by Yu [23] in their FEA study of the INBONE II. This is the smallest size available and is suitable for a conservative estimate of implant stresses, as the highest stresses are expected from the smallest size. The coronal and sagittal views of the INBONE II tibial component with the corresponding implant dimensions per size are shown in Figure 9a. We assumed that the proportions of the component elements were true to the real implant. Screen clips were taken from these images and optimized using Microsoft Paint. Then, these views were saved as DXFs to import into SolidWorks (Figure 9b). This process maintains the feature-to-feature relationships as the assumed proportions remain consistent. The features were exported to create the completed part in Figure 9c.
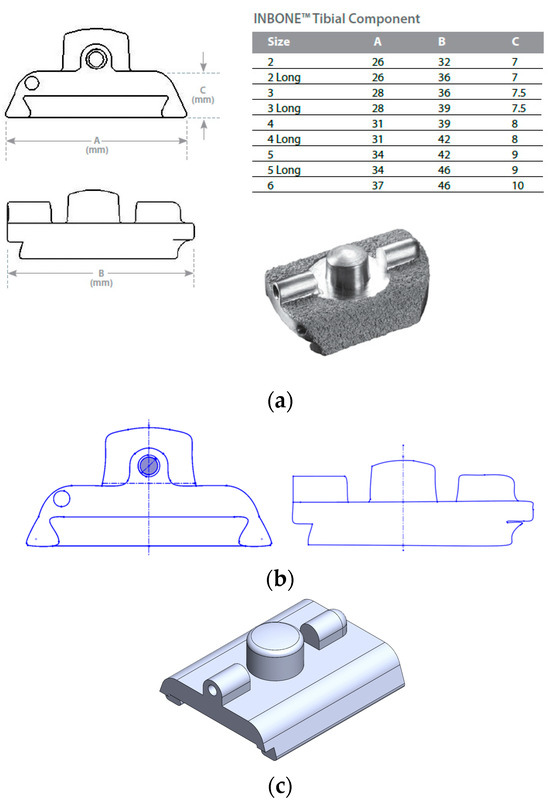
Figure 9.
Geometry modeling process for implant components. (a) Limited dimensions provided by implant manufacturer, (b) DXF of the component as a sketch, (c) Sketch with adjustments and extruded CAD components.
The manufacturer did not disclose the exact dimensions of the INBONE II bearing, only the thickness of the bearing for the Vantage. Therefore, we used data from Zhang [28] to help design the CAD model of the INBONE II bearing. We created models with similar tibial and talar surfaces for both implants. The components, including the bearing and condylar radii, are labeled for the INBONE II (Figure 10) and the Vantage (Figure 11). Arrows indicate the relevant radii on these figures.
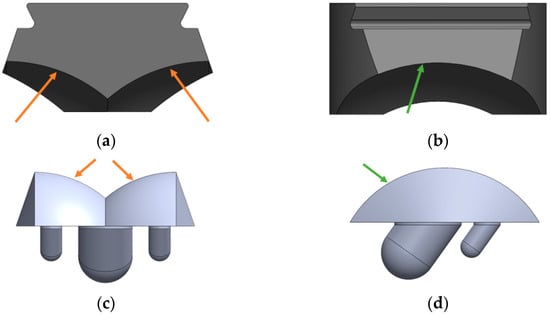
Figure 10.
Critical radii for congruency of INBONE II articulating surfaces. (a) Bearing condylar radii, (b) Bearing medial radius, (c) Talar component condylar radii, (d) Talar component medial radius.
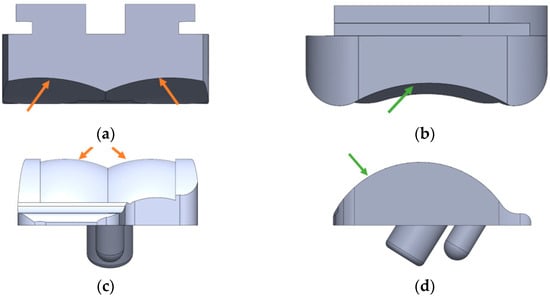
Figure 11.
Important radii for congruency of Vantage articulating surfaces. (a) Bearing condylar radii, (b) Bearing medial radius, (c) Talar component condylar radii, (d) Talar component medial radius.
The final modeled CAD assemblies of each implant with each labeled component are shown in Figure 12.
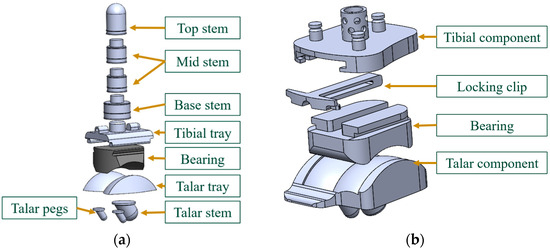
Figure 12.
Labeled assembly for both implants in study. (a) INBONE II, (b) Vantage.
2.2. ABAQUS Material Properties
The bearing component is made of UHMWPE, and the tibial and talar components are made of CoCrMo (Figure 13). The settings for the elastic behavior of these materials are shown in Table 1. Since the Young’s modulus of CoCrMo is significantly higher than that of UHMWPE, the Young’s modulus was set from the real value of 210 × 103 MPa to 210 × 106 MPa, and the Poisson’s ratio was kept the same. This condition is called “Pseudo-Rigid”, and it has a very high Young’s modulus to replicate the effect of a rigid body having an infinite stiffness. This significantly decreased run-time and yielded the same results as assigning them as “Deformable” within ABAQUS. It also permitted boundary conditions and loading to be placed on any portions of the metallic components, which would be limited with “Rigid” behavior in ABAQUS since all nodes of a rigid body move with the same motion. For our study, the stresses and strains were not of concern on the metallic components. The bearing was modeled as “elastic-plastic,” which was assumed in other FEA studies [7,24]. This indicates that the elastic behavior is assumed to have a single Young’s modulus and Poisson’s ratio.
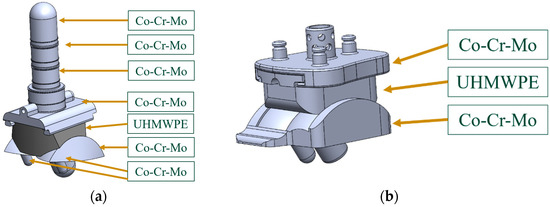
Figure 13.
Material assignments for both the (a) INBONE II and (b) Vantage.

Table 1.
Elastic behavior for materials settings on implants in ABAQUS.
In addition to the elastic behavior, plastic behavior was modeled for the UHMWPE to represent the material’s response after yielding. This behavior was extracted from a true stress–strain curve. This curve (Figure 14) was created with data for UHMWPE with a grade of virgin GUR 1020 provided by Miller [29]. This specific true stress and true strain data for this grade of UHMWPE have been used consistently in other FEA studies by Martinelli, Zhang, and Yu [7,23,24]. The yield strength for this grade of UHMWPE is 10.86 MPa, the lowest value reported in the literature among grades of this polyethylene [30]. A conservative estimate of von Mises stress on the bearing is obtained, predicting yielding earlier than expected. The manufacturers did not provide specifics on the grade of UHMWPE. It is also important to note that the Poisson’s ratio of UHMWPE is 0.46, which is close to the incompressible value of 0.5 observed on rubbers. This indicates that minimal volume changes are expected as the material expands laterally and contracts longitudinally under compression.
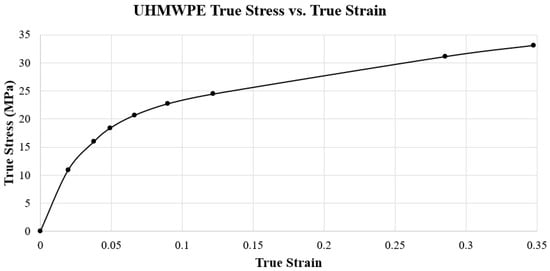
Figure 14.
UHMWPE GUR 1020 true stress vs. true strain curve.
2.3. ABAQUS Step/Interactions
The analysis step in ABAQUS was set at a fixed increment for both implants (INBONE II: 0.05, Vantage: 0.01). Using this small step increment ensured proper convergence as the ABAQUS equation solver computed the stiffness matrix to calculate stress and strain outputs.
The interactions between components consisted of ties and contacts. Ties were utilized for components that have no relative motion between them, making the two components one piece. For the INBONE II, the tibial tray was tied to the stem subassembly and the bearing. The talar tray was tied to the pegs and stem. For the Vantage, the tibial tray was tied to the bearing and the locking clip, and the locking clip was tied to the bearing. A visualization of the tibial tray-to-bearing tie interaction is shown in Figure 15. Contact interactions are appropriate for surfaces with sliding relative motion between them and where the pressure between them is relevant. These surfaces were the articulating surfaces of the implant, which were the top bicondylar surface of the talar tray and the bottom bicondylar surface of the bearing. These surfaces and the corresponding settings for this contact interaction were inputted into ABAQUS, as shown in Table 2. They were determined as the best fit for this analysis based on an FEA study of an indenter–block contact interaction performed by the authors [27]. The normal behavior was assumed to be “hard” to indicate that the contact pressure would be computed as the surfaces are in contact. The tangential behavior was assumed to be based on a Coulomb friction model. The friction coefficient of μ = −0.04 has been used vastly within TAA FEA studies with CoCrMo and UHMWPE [7,24]. It has been benchmarked as the appropriate coefficient in an experimental analysis of friction on joint replacement implants performed by Godest [31]. The surface-to-surface behavior is most relevant for curved surfaces, and finite sliding is utilized in regions that expect significant frictional behavior.

Figure 15.
Visualization of tie constraint between tibial tray and bearing for Vantage.

Table 2.
Summary of Vantage contact settings.
2.4. Implant Loading
Gait and loading data were extracted from the literature. This study aimed to evaluate the maximum stress on the implants during the stance phase and the behavior during each of the four subphases of the stance phase of the gait cycle. Dorsiflexion/plantarflexion data were collected by Zhang [24,32] on a post-operative INBONE II TAA patient while walking on force plates in a gait lab. These data are plotted with images of the ankle position during the four subphases of gait in Figure 16a. In particular, points of interest are indicated in red for 10%, 20%, 30%, 40%, 49%, and 60%. These characterize the entire spectrum of the stance phase of the gait cycle. With the angle for each of these points of interest, six separate CAD models were developed within SolidWorks to rotate the implant. When the ankle is flexed, the tibial component and bearing flex to the corresponding angle while the talar component is stationary. These rotated models are shown next to their corresponding gait percentages on the INBONE II dorsiflexion/plantarflexion angle plot in Figure 16b.
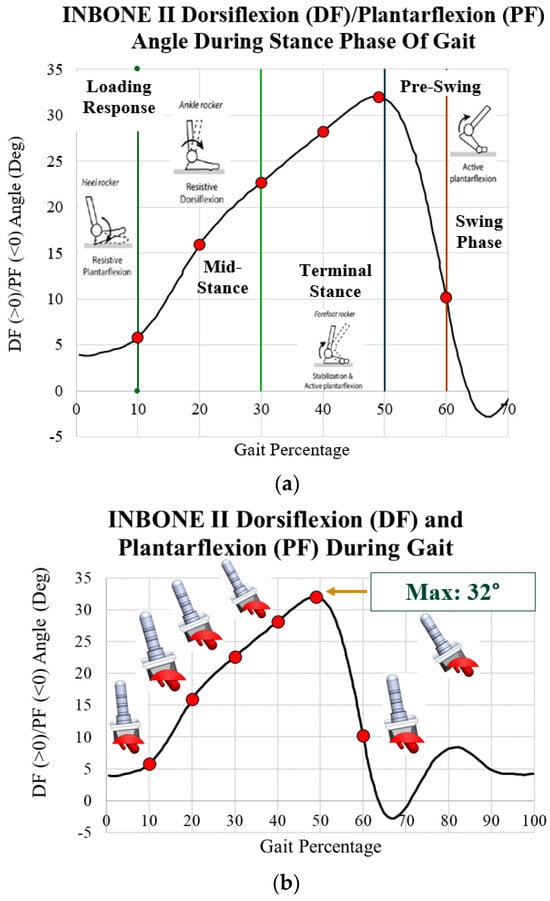
Figure 16.
Dorsiflexion/plantarflexion curve of INBONE II patient [24] with (a) subphases of stance indicated; (b) rotated CAD implant models. Maximum DF angle of 32° at 49% gait.
The load used for the INBONE II was the total ankle joint contact force. This contact force was assumed to be purely axial as a compressive load on the tibial component. Axial loading is 10x greater than shear loading on the ankle during the gait cycle and thus was the only force considered [33]. The axial compressive load on the INBONE II during the gait cycle is shown in Figure 17. The same gait percentage points of interest are emphasized in red. These load data and the flexion data were based on a 50-year-old male patient weighing 75.3 kg with a height of 172 cm, corresponding to a BMI of 25.5 [34]. The maximum load was 4787 N, which, if normalized to the patient’s body weight of 75 kg (736 N), corresponds to a load of 6.5x his body weight (BW). This also corresponds to the point of maximum dorsiflexion on the implant.
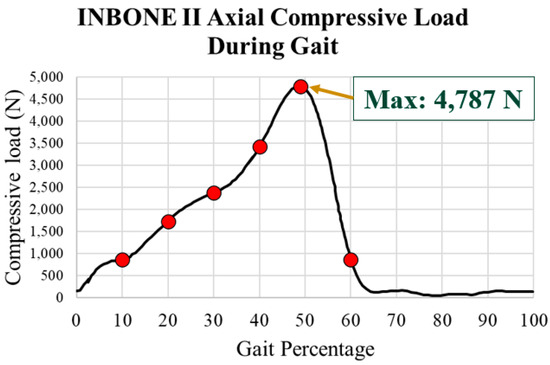
Figure 17.
Axial compressive load on INBONE II patient during gait cycle [24]. Maximum load of 4787 N at 49% gait.
The axial compressive load aligned with the axis of the tibial stem (Figure 18a). The load was applied uniformly across the surfaces of the stem and top of the tibial tray because these are the areas where the implant contacts the bone (Figure 18b). The uniformly distributed load was calculated based on the axial compressive load divided by the summation of areas of the loading surfaces. A local coordinate axis was attached to the front of the tibial component (Figure 18b) to ensure that the loading and boundary conditions were applied relative to the rotated coordinate system.
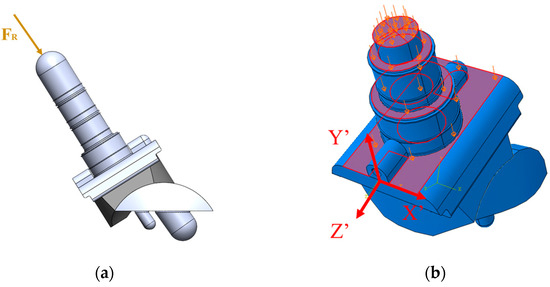
Figure 18.
Loading distribution on INBONE II tibial component with the (a) resultant force and (b) distributed load on stem and tray surfaces.
The process for determining the loading of the Vantage was similar. Gait and load data were taken based on a healthy ankle from Bell’s [35] experiment on ankle joint prostheses wear, which was used in Martinelli’s [7] study on the Zimmer fixed-bearing implant. Exactech did not provide load data [33]; however, they did reveal the dorsiflexion range is 15 degrees and the plantarflexion range is 15 degrees, which are nearly identical to the data used by Martinelli. These data are plotted in Figure 19a, with the subphases of gait and points of interest indicated on the plot. These points of interest were at gait percentages of 10%, 20%, 30%, 40%, 50%, and 60%. Images of the six rotated Vantage CAD models are shown next to their corresponding gait percentages on the dorsiflexion/plantarflexion plot in Figure 19b.
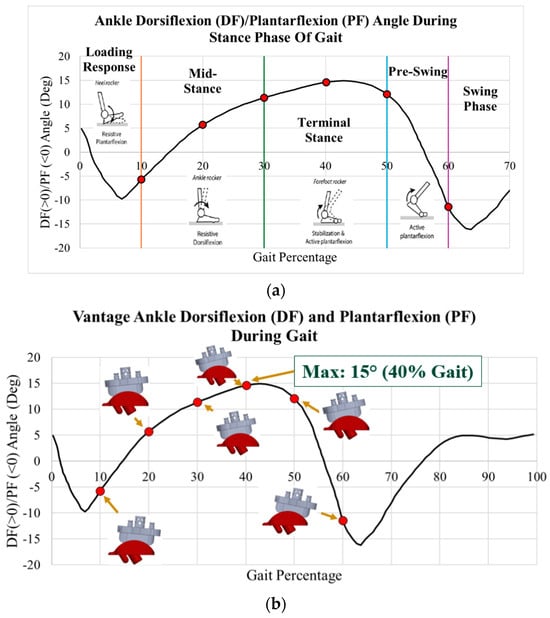
Figure 19.
Dorsiflexion/plantarflexion curve of healthy patient used for Vantage [35]. (a) Subphases of stance; (b) rotated CAD models indicated on plot.
The axial load data were also taken from Bell’s [35] study. This is plotted in Figure 20 with a maximum load of 3158 N at 40% gait.
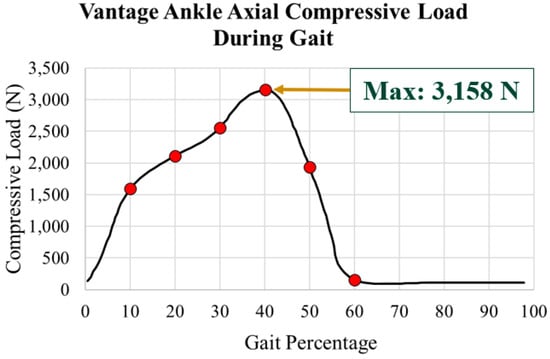
Figure 20.
Axial compressive load on ankle during gait cycle used for Vantage [35]. Maximum load of 3158 N (40% gait).
The resultant axial load was applied along the axis of the central peg of the tibial tray (Figure 21a). The loading among the pegs was computed using a statically indeterminate approach. The internal loads within the pegs were calculated based on the resultant axial load and compatibility relations. The forces in each peg were calculated using a MATLAB script and a system of three linear equations for all gait percentages of interest. The corresponding load per peg was uniformly distributed on the top of the pegs’ surfaces as shown in Figure 21b. A local coordinate system was attached to the side of the tibial component.
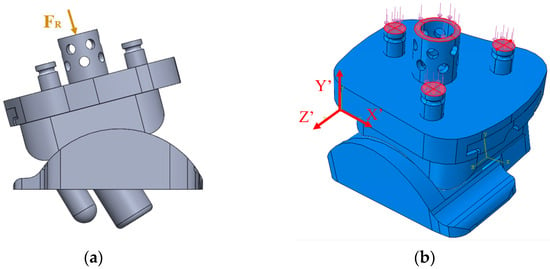
Figure 21.
Loading on Vantage pegs with (a) resultant force and (b) distributed peg loading.
2.5. ABAQUS Boundary Conditions
Boundary conditions were considered based on two primary conditions. The implant was constrained based on how the implant interfaces with the bone. It was assumed that there was no loosening of the implant from the bone. Rigid body modes were eliminated when these constraints were placed. For both implants, the bottom of the talar component was constrained with rollers to restrict vertical translations. Pins were generally placed on the center of the pegs to constrain lateral translations. For the INBONE II, the top of the mid stem and the bottom of the pegs on the talar component were pin-constrained. For the Vantage, the top of the small tibial pegs, the edges of the large tibial peg, and the bottom of the talar pegs were pin-constrained. Boundary conditions placed on the tibial pegs were defined relative to the local coordinate system since the tibial component rotated based on the ankle angle for the corresponding gait percentage. By pin-constraining the implant, rigid body modes were eliminated. The element type used in meshing is a linear tetrahedral element with 3 translational degrees of freedom per node. However, translational and rotational rigid body modes were constrained by constraining the translational degrees of freedom. All boundary conditions, including roller and pin constraints, are shown for the INBONE II (Figure 22) and Vantage (Figure 23). The orange arrows indicate the pins and rollers with constraints in their respective directions based on the global or local coordinate axes. Local coordinate axes are indicated by the X’ or Z’ directions.
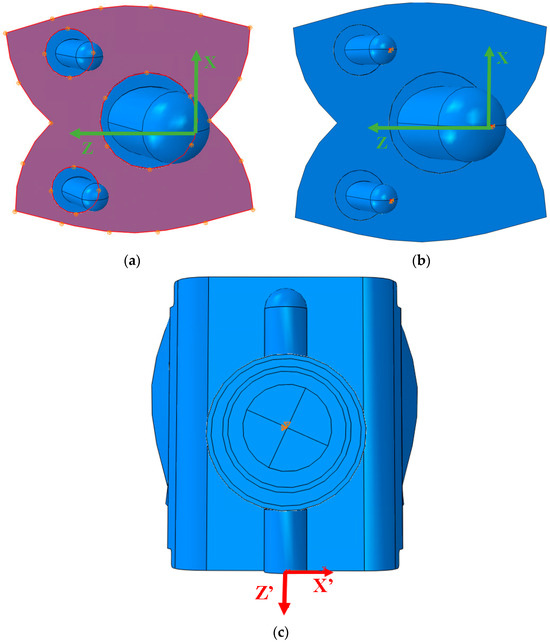
Figure 22.
INBONE II boundary conditions with (a) roller constraint on talar face, (b) pin constraint on talar pegs, and (c) pin constraint on mid stem center.
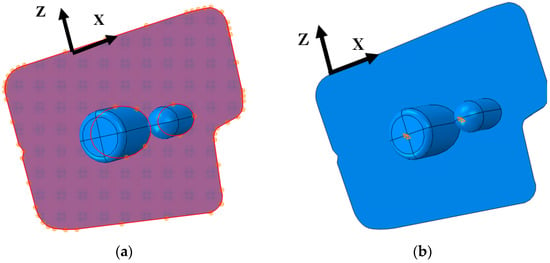
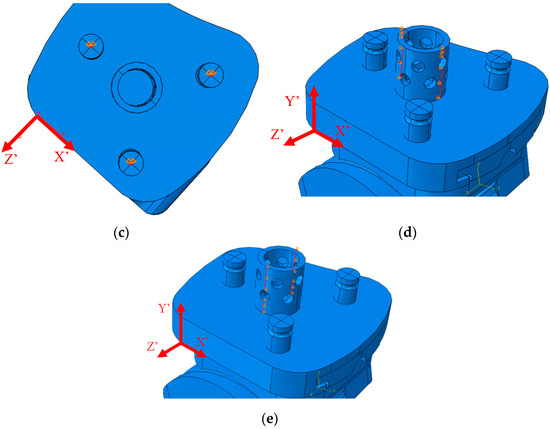
Figure 23.
Vantage boundary conditions with (a) roller constraint on talar face, (b) pin constraint on talar pegs, (c) pin constraint on tibial pegs, (d) pin constraint on tibial pegs’ edges normalized to X’ axis, and (e) pin constraint on tibial pegs’ edges normalized to Z’ axis.
2.6. ABAQUS Meshing
The element type used for meshing was C3D4, a 4-noded linear tetrahedron element. ABAQUS free meshing was utilized to mesh these elements. These have been used consistently across TAA studies [22,36]. They are appropriate for regions of fine meshes and are computationally efficient. In particular, the surfaces in contact were meshed finely with local seeding for accurate results. A mesh sensitivity test was performed on the middle of the articulating surface of the bearing, as shown in the top row of Figure 24. The von Mises stress and contact pressure were evaluated in this region for seed sizes of 5, 3, 1, 0.75, 0.65, and 0.50 mm. Convergence for mesh seed size was determined by comparing the results from one seed size to the lowest seed size (0.50 mm). If the results for von Mises were within 1% and the results for contact pressure were within 5%, the mesh was determined to have converged. For the INBONE II, this was reached at a seed size of 0.75 mm (48,102 DOF), and for the Vantage, this was reached at 0.65 mm (33,294 DOF). A side-by-side summary of the mesh convergence study for both implants is shown in Figure 24.
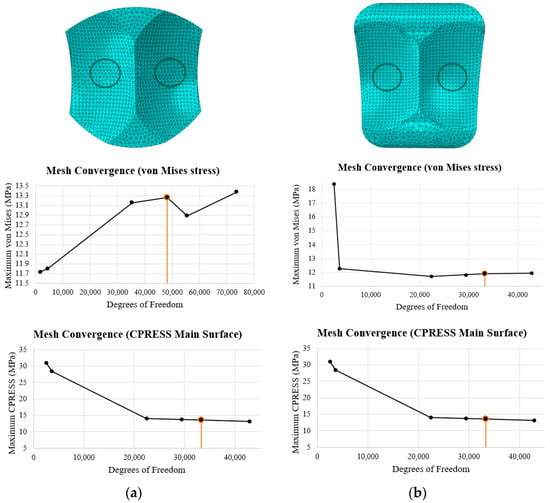
Figure 24.
Summary of mesh convergence for bearing surface of both implants. (a) INBONE II converged at 0.75 mm with 48,102 DOF; and (b) Vantage converged at 0.65 mm with 33,294 DOF.
3. Results
The results were collected for the von Mises stress and contact pressure on the articulating surface of the bearing to investigate the mechanical performance of the implant’s weakest component during the stance phase of the gait cycle.
3.1. Von Mises Stress
The von Mises stress is a metric for determining the equivalent stress for ductile materials. Comparing the equivalent stress to the yield strength, it is a failure criterion. The safety factor quantifies how close the material is to yielding. It was important to investigate the maximum von Mises stress on the implants to find how close the UHMWPE was to yielding under the load applied.
The maximum von Mises stresses for both implants occurred in the regions where the bearing was thinnest: the middle of each condyle on the articulating surface. The stress distributions were uniform across both condyles (Figure 25). Both implants were plastically deformed and yielded since their maximums were above the yield strength for the material (10.86 MPa). As mentioned earlier, this yield strength is the most conservative estimate since it is the lowest value reported in the literature [30].
Figure 25.
Von Mises stress distributions at maximum loading for both implants.
The stress results for all six gait configurations for the INBONE II are shown in Table 3 and Figure 26. The compressive load increased with gait percentages from 10 to 50%, and the von Mises stress increased correspondingly. The maximum stress occurred at the 49% gait during the terminal stance phase of the gait cycle. During the pre-swing stage, the load and corresponding stress decreased significantly. Uniformity was maintained on both condyles of the bearing with maximum values on the middle of the bearing surface. The maximum values of each configuration are indicated. The safety factor is less than one for the 40% gait and 49% gait due to the low yield strength used for UHMWPE (10.86 MPa). Design modifications to improve this are suggested in Section 4.4: Future Recommendations.

Table 3.
INBONE II von Mises stress gait configuration results.
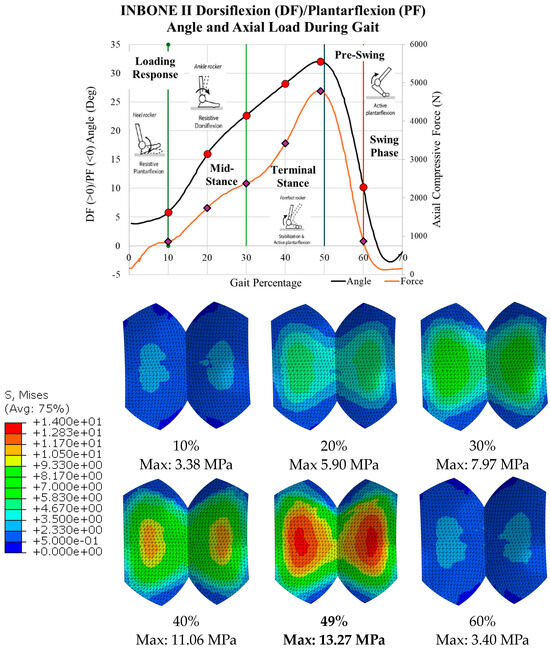
Figure 26.
INBONE II von Mises stress for all configurations with maximum values.
The stress distributions for all six gait configurations for the Vantage are shown in Table 4 and Figure 27. The compressive load increased with gait percentages from 10 to 40%, and the von Mises stress increased correspondingly. The maximum stress occurred at the 40% gait during the terminal stance phase of the gait cycle. Around 50%, however, the load and corresponding stress decreased significantly. Again, uniformity was seen on both condyles of the bearing with maximum values in the expected areas. The maximum values of each configuration are indicated.

Table 4.
Vantage von Mises stress gait configuration results.
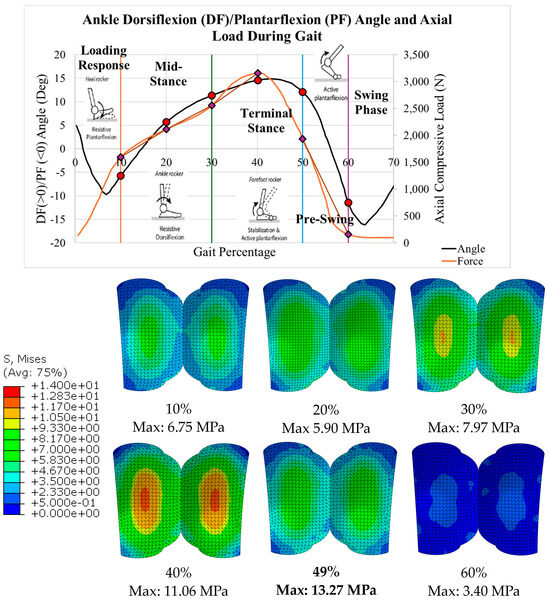
Figure 27.
Vantage von Mises stress for all configurations with maximum values.
3.2. Contact Pressure
Contact pressure is defined as the normal contact force on each element divided by the contact area between two bodies. In our study, it was calculated to determine the amount of pressure applied between the stiffer CoCrMo talar component on the softer UHMWPE bearing and the friction between the two surfaces. This was utilized to evaluate the bearing wear rate. The maximum contact pressure for both implants is shown in Figure 28. The central area of the bearing exhibited high congruence and conformity with the talar component and experienced the highest von Mises stress and highest uniform contact pressure.
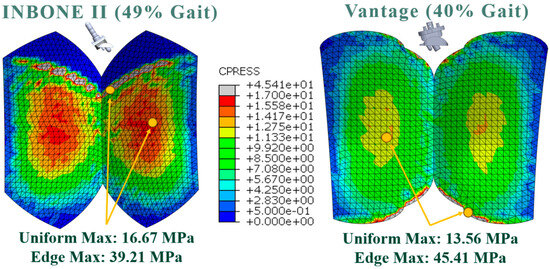
Figure 28.
Contact pressure distribution for both implants at maximum loading.
Our modeling also identified edge loading at specific angles. At a dorsiflexion angle of 32, the INBONE II bearing component was noted to sit slightly anterior to the talar component. This led to the talar component anterior edge, which was in contact with the bearing to sustain contact pressures over twice as high as the uniform maximum contact pressure.
Similarly, the Vantage implant exhibited edge loading on the posteroinferior aspect of the bearing surface. Additionally, the posterior tibial peg sustained a distributed load twice as large as the anterior pegs (73 MPa vs. 48 MPa), leading to high normal contact forces and contact pressures on the edge of the bearing surface in these areas. This edge maximum was over three times larger than the uniform maximum.
The contact pressure results for all six gait configurations for the INBONE II are shown in Table 5 and Figure 29. As the uniformly distributed pressure load increased, the contact pressure increased. Values on the edge of the bearing were only recorded when the edge of the talar component caused high magnitudes of contact pressure, as shown for the gait percentages of 40% and 50%.

Table 5.
INBONE II contact pressure gait configuration results.
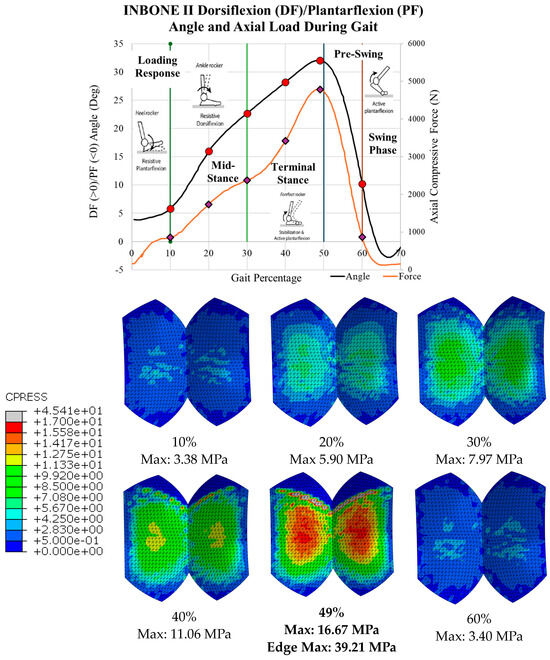
Figure 29.
INBONE II contact pressure distributions for all configurations with maximum values.
The contact pressure results for all six gait configurations for the Vantage are shown in Table 6 and Figure 30. Like the INBONE II, the contact pressure increased as the compressive load and dorsiflexion angle increased. The edge effect was visible throughout the entire gait cycle since the posterior peg loading was higher than the anterior peg loading.

Table 6.
Vantage contact pressure gait configuration results.
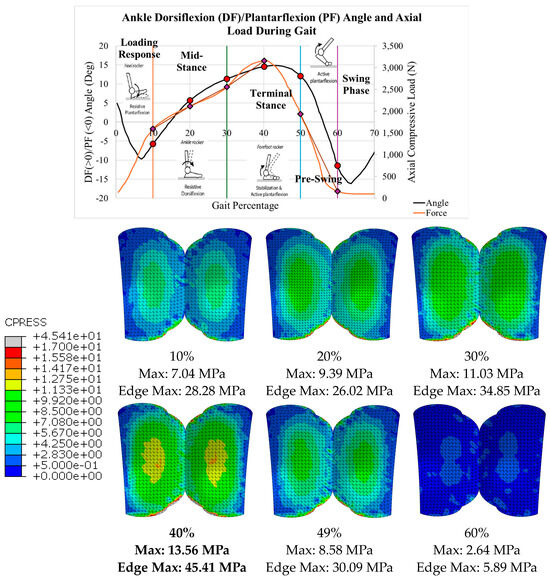
Figure 30.
Vantage contact pressure distributions for all configurations with maximum values.
4. Discussion
4.1. Indications of Results
The goal of this study was to perform a static structural analysis to investigate the mechanical behavior of the UHMWPE bearing for a single gait cycle across different subphases of the stance phase of the gait cycle. These regions of highest von Mises stress are most susceptible to yielding, and the regions with the highest contact pressure are most vulnerable to wear.
In both implants, the highest von Mises stress was observed on the condyles in the central region of the bearing. These regions corresponded to the areas where the bearing was the thinnest. It is biomechanically and clinically important to recognize that the stress is magnified in these regions.
In the Vantage, the load is transmitted through the pegs, through the thin region of the tibial tray, and onto the superior surface of the bearing (Figure 31a). In the frontal cross-sectional cut (normalized to the X’ axis) at the midplane of the bearing, the smallest thickness of the bearing is indicated by t, and it lies along the condylar radius of the bearing. Stress concentrations at the sharp corners of the bearing were identified and circled in red, where the stress propagates as it reaches the condylar radii. In the region shown in green, the highest stresses are seen by the bearing (10–15 MPa). A medial view of the bearing with a cross-sectional cut (normal to the Z’-axis) at the region of the smallest thickness is shown in Figure 31b. This thickness, t, is smallest at the middle of the medial radius. The same principle occurs for the lateral radius since the stress is symmetric on both condyles of the bearing. The corresponding highest stress regions on the bearing are circled in yellow in a view with multiple cross-sectional cuts in Figure 31c.
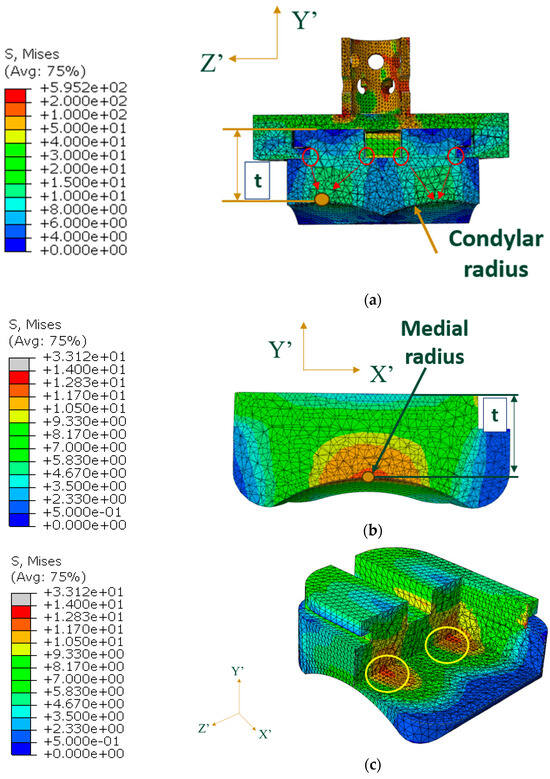
Figure 31.
Stress flow through Vantage bearing on (a) condylar radii, (b) medial radius, and (c) corresponding highest regions of stress.
High magnitudes of contact normal forces exist in regions where the bearing is small. These regions have uniform maximum contact pressure distributions, making them the most vulnerable to linear wear and pitting.
Similarly, the regions where the edge effect was identified on the bearing surface are most susceptible to accelerated wear. For the INBONE II, the edge effect starts on the anterior aspect of the bearing at around 30% of the stance phase or at 22.7° DF. At this point, the model shows that the bearing is rotated slightly off the edge of the talar component, causing this stress concentration. It is important to note that the average maximum clinical dorsiflexion values are no more than 20°. A clinical trial by Mulcahy [37] reported the average dorsiflexion of patients after receiving an INBONE II to be 14.3°. Therefore, the anterior edge loading, regarding the tibial side, noted at greater dorsiflexion angles, is unlikely to be experienced in vitro. Understanding this edge effect from a biomedical standpoint is essential, but there is no direct clinical relevance to anterior edge loading.
For the Vantage, the greatest loading magnitude occurs on the tibial peg that is located posteriorly. Thus, higher stresses occur on the posterior edge of the bearing than on the uniform surface where the bearing is thinnest.
These results can aid in implant design to determine if modifications could be made to the UHMWPE liner, where it is the thinnest and experiencing the highest stress. Clinicians need information on the loading magnitude for different implant systems. For the Vantage, higher stress occurs on the posterior edge of the bearing, which can influence the surgeon’s ultimate implant placement. Additionally, this information can help surgeons counsel patients on extreme range of motions of the ankle with dorsiflexion angles >15 degrees, leading to more potential wear of the liner over time.
It should be noted that the presence of areas of a high localized stress concentration is of clinical concern, as this may lead to implant loosening and peri-implant lucency in these regions after the implant is repetitively loaded with use. This would lead to a decreased range of motion, pain, implant wear, and possible eventual implant subsidence, requiring revision surgery. From a surgical technique standpoint, it may be worth considering augmenting the implants in regions where we observed the highest stress, such as with cement or bone graft augmentation in this area. Alternatively, this information suggests that the implant thickness should be increased in this area to combat localized stress, prevent complications, and optimize implant longevity and patient outcomes. Moreover, this information can influence the surgeon’s ultimate implant placement. For example, with the identified area of posterior edge loading with the Vantage implant, more anterior placement may be beneficial to mitigate this area of stress concentration.
4.2. Unloading and Reloading
This study only loaded the implants once, and since yielding occurred, it is important to investigate the effect of unloading and re-loading the materials. The maximum plastic strain occurred on the bearing surface and at the maximum von Mises stress region. When unloaded (Figure 32a), the material would incur a permanent plastic deformation and lead to elastic recovery strain. As the material is re-loaded (Figure 32b), it would load at the permanent set until it reaches the true strain corresponding to the elastic recovery strain, raising the yield strength. The new yield strength would correspond to the true strain corresponding to the maximum plastic strain at the maximum von Mises stress location (Figure 32c). This repeats with each gait cycle in a strain-hardening process.
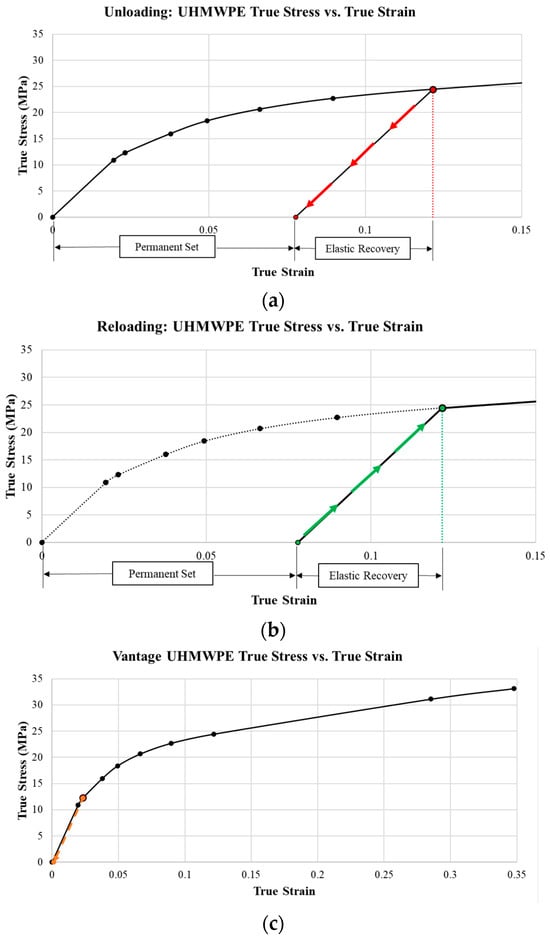
Figure 32.
Effect of (a) unloading (exaggerated for clarity) and (b) re-loading (exaggerated for clarity) on UHMWPE on (c) the yield strength.
4.3. Comparison to Other Studies
It was not possible to directly compare our study to other studies due to the limitations of this study. Other studies included different components within their models, including bone or soft tissue. However, a general agreement was seen between other studies and the present work.
The INBONE II model was compared to Yu’s [23] study on the INBONE II. Despite incorporating the entire foot with the implant in their model, the von Mises stress on the INBONE II was noted to be 15 MPa, a difference of only 12% from the results of this study. Similarly, a slight uniformity across the condyles of the stress on the bearing was noted, which is consistent with this work.
Zhang [24] performed a comparative FEA study in ABAQUS of three different TAA implants, including the Wright INBONE II. He post-processed gait data from TAA patients with these implants using multibody dynamics modeling (MSK-MBD) software [33]. A comparison of our contact pressure results found the edge effect of the contact pressure to be consistent with that of Zhang’s work with a magnitude of 41 MPa, which is only a 5% difference. There was a strong uniformity across both condyles in their model. However, the maximum value in the uniform region was higher by 24% (21 MPa).
Our analysis of the Vantage is unique in that no existing FEA studies exist for this implant within the literature. To the authors’ knowledge, this is the first study with open access to the community. With this limitation, a comparison was made against other implants similar in geometry. The results of the von Mises stress were compared to Martinelli’s [7] work on the Zimmer fixed-bearing implant, from which the gait and load data for the Vantage were taken. The stress observed by Martinelli was 17% higher (14 MPa); however, uniformity was observed on both condyles of the bearing. A similar implant to the Vantage, with multiple pegs on the tibial component, was custom designed by Elliot [38], and the difference in stress magnitude was a mere 4%. For contact pressure, uniformity was seen on both condyles of the bearing in Martinelli’s work. The edge effect was observed in Rodrigues’ [36] work on the Agility implant and was 14% higher in magnitude (45 MPa). Despite the limitations and simplicity of this study, there is still a reasonable agreement within 25% between the present work and most of the aforementioned studies.
4.4. Future Recommendations
Future improvements on this work should implement several facets so that the FEA model is more reflective of the interaction of in vitro implants with the surrounding anatomy.
Biological factors such as bone remodeling, tissue response, and changes in patient anatomy over time could significantly impact the mechanical performance and longevity of TAA implants. Although these factors were not documented in the studies we reviewed, it would be important to include them in future work.
It would be beneficial to investigate additional fixed-bearing implant systems to provide a more comprehensive understanding of TAA implants. While our current results can be extrapolated to other fixed-bearing total ankle systems, it is important to note that there are nuanced differences among implants.
It was difficult to model the geometry of the implants precisely due to the lack of manufacturer-provided specifications. One alternative method of obtaining these dimensions would be to measure implant sizes from CT scans of patients and input this geometry into ABAQUS. Adjacent patient bony geometry could also be obtained from this imaging, as Zhang et al. did for the INBONE II [24].
For the INBONE II, examining the effect of longer and shorter stems within the model would be clinically relevant. With longer stem lengths, buckling becomes a concern, and consequently, the implant loosens from the bone. For both implants, it would be most relevant to test all sizes of the implant that the manufacturer specifies to accurately capture the effect of the implant across the full spectrum of patients.
Different grades of UHMWPE vary in yield strength and Young’s modulus values [26]. The precise grade of UHMWPE should be obtained from the manufacturers to ensure the accuracy of results and yield predictions. In this study, UHMWPE GUR 1020 was utilized for the most conservative estimate of yield strength (10.86 MPa). Consequently, Table 3 and Table 4 indicate that the safety factor was below one at certain gait configurations. To improve this, a variety of grades of UHMWPE with higher yield strengths should be tested within the model.
C3D4 linear tetrahedron elements are generally too stiff for three-dimensional structural analysis. A linear approximation cannot be applied to curved surfaces unless many individual elements are used to approximate the displacement, as used in this study. This analysis could be improved by using C3D10M elements, i.e., modified quadratic tetrahedron elements. Quadratic elements have a quadratic shape function approximation for displacements between two nodes. This yields a better precision for elements that are on curved surfaces. Remeshing would need to be considered within the components that do not have a contact interaction in order to run this simulation within the 250,000 node limit of the ABAQUS teaching license provided by the university.
The tibial and talar bones adjacent to the implants are cancellous, trabecular bone. A better assumption than attaching the talar component to this bone with rollers would be to use nonlinear one-dimensional springs.
The analysis only considered axial compression. However, during the gait cycle, loading is not truly uniform. Shear and lateral loading cause combined loading across the implant. Although axial loading is ten times greater than shear loading, it is still important to consider these shear and lateral loads to determine if they contribute to aseptic loosening.
Since plantarflexion/dorsiflexion are the primary motions of the ankle, our analysis focused solely on these for simplicity. However, to fully capture the complete range of motion of the ankle, it is necessary to also incorporate other biomechanical motions, such as inversion/eversion, internal/external rotation, and anterior/posterior translation.
The goal of this study was to analyze the mechanical behavior of newly installed implants during a single gait cycle. However, this static analysis does not account for potential effects over millions of gait cycles. There are limited clinical data on long-term, 15–20-year implant longevity. The FEA model can only reflect real patient scenarios if dynamic loading and wear on the UHMWPE bearing are considered. This could be predicted by performing a wear analysis using Hertzian contact mechanics on the bearing to calculate the amount of linear wear over millions of cycles. This can be performed by evaluating the linear wear based on the contact pressure and adjusting the bearing geometry after each cycle before re-running the simulation. Paris’ equation could also be used to understand the fracture mechanics better and predict the likelihood of the subsurface bearing cracking over time. To be most effective, these models can be implemented within an FEA model in conjunction with supercomputing to obtain results efficiently. The long-term data on the survivorship of modern TAR implants are limited due to the multiple generations of implants developed over the past few decades. Additionally, TAR has a significantly higher revision rate than other joint arthroplasties, such as total knee and total hip arthroplasties. Five-year TAR revision rates have been reported as high as 6.8%, compared to 2.3% for total hip replacement and 2.7% for total knee replacement [39,40], with complication rates up to 52% [41]. Ten-year TAR revision rates are reported up to 22% [42]. A retrospective cohort with 3.5-year follow-up showed that tibial failure leading to revision TAR occurred relatively early, on average 1.3 years post-operatively. In contrast, talar component failure necessitating revision TAR occurred on average 2.3 years post-operatively [43].
Aseptic loosening in total ankle replacement (TAR) requiring revision is a complex surgical issue. The appearance of radiolucent lines around the implant, known as peri-implant lucency, is a common complication of all joint replacements. Medium-term follow-up studies of TAR have revealed that up to 50% of cases experience periprosthetic lucency. This lucency can later result in implant subsidence and instability, causing erosion of the remaining tibia and talus around the TAR implant [44]. Surgical options for revision may involve another TAR, a conversion to ankle fusion, tibiotalocalcaneal fusion, or below-knee amputation, depending on the extent of bone loss and the available remaining bone stock. A recent systematic review found that 26.9% of patients who underwent revision to another TAR required additional surgeries, with an overall 14.4% failure rate for these revisions. Conversion to ankle fusion was associated with a 13% failure rate [45].
Furthermore, the number of yearly TARs performed increases, leading to more potential future revisions due to implant failure. It is crucial to gain a better understanding of the ideal implant geometry and placement to extend the implant lifespan and reduce the need for future revisions caused by aseptic component loosening due to an uneven stress distribution.
Historically, total ankle arthroplasty has been revised to address talar component loosening and subsidence. Future research could involve using finite element modeling to determine if there are stress concentration areas in the talar component, similar to what was done for the tibial component in this study.
5. Conclusions
In this study, the results for the von Mises stress and contact pressure indicated a great amount of uniformity on both condyles of the bearing articulating surface. Although this model was limited in the number of components utilized, our results demonstrated a close agreement with the previous literature.
With uniformly distributed loading, the highest magnitudes occurred in the thinnest areas of the bearing. Unsurprisingly, a higher compressive load led to higher stresses experienced by the implant. Increased ankle dorsiflexion angles were also correlated to higher loads and stress experienced at the bearing surface. Clinically, this raises a question of how increased body weight affects these patterns and whether there is a threshold BMI above which there should be a concern for unacceptably accelerated bearing wear.
The axial compressive load, transferred through the distal tibia, acted axially on the tibial component and acted normally on the pegs or surfaces. In the maximum load cases for the von Mises stress, the safety factor was calculated to be below one compared to the yield strength of 10.86 MPa. This indicates that the material plastically deformed under these conditions, and the yield strength was raised to the true stress corresponding to the true strain from the plastic deformation. The contact area between the bearing and talar components demonstrated close congruency in the uniform regions.
In certain configurations, the contact pressure revealed concentrated areas of increased magnitude consistent with edge loading. This raises clinical concern for focal areas of increased wear and possible subsurface bearing cracking.
Our work contributes to the body of data available on TAA biomechanics and implant wear patterns, laying the foundation for future research to understand implant longevity better and improve patient outcomes.
Author Contributions
Conceptualization, T.S.J., N.N., A.A. and J.J.R.; methodology, T.S.J., J.J.R. and S.H.; software, T.S.J., J.J.R. and S.H.; validation, T.S.J., J.J.R. and S.H.; formal analysis, T.S.J., J.J.R. and S.H.; investigation, T.S.J., M.N. and J.J.R.; resources, M.N. and N.N.; data curation, T.S.J., M.N. and J.J.R.; writing—original draft preparation, T.S.J.; writing—review and editing, T.S.J., M.N., N.N., A.A. and J.J.R.; visualization, T.S.J. and J.J.R.; supervision, M.N., J.J.R. and N.N.; project administration, M.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The Master’s thesis by Timothy Jain that this work is based on is provided below. This provides a thorough review of how the analyses were performed in this work. https://digitalcommons.calpoly.edu/theses/2766/.
Acknowledgments
We would like to express our special thanks to the following colleagues for their contributions which made this research possible. Mason Kaseeska from Cal Poly IT department for his assistance working the remote desktop for ABAQUS. Erik Hallgrimson, a current Cal Poly ME undergraduate student, for helping with the design of the components of the Vantage model. Nicolo Martinelli (Orthopedic Surgeon at Instituto Ortopedico Galeazzi, Milan, Italy) for granting us permission to use the gait and load data from his study for the Exactech Vantage. Yanwei Zhang (Xi’an Jiaotong University, X’ian, China) for providing gait and load data and a reference model of the bearing for the Wright Medical INBONE II. Stephen Klisch (Cal Poly, San Luis Obispo, CA, USA) for providing biomechanics and continuum mechanics advice for the appropriate model setup.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ankle Joint. Cleveland Clinic. 2023. Available online: https://my.clevelandclinic.org/health/body/24909-ankle-joint (accessed on 28 July 2023).
- Anatomy of the Ankle. Southern California Orthopedic Institute. 2023. Available online: https://www.scoi.com/specialties/ankle-doctor/anatomy-ankle (accessed on 28 July 2023).
- Brockett, C.L.; Chapman, G.J. Biomechanics of the ankle. Orthop. Trauma 2016, 30, 232–238. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Grimston, S.K.; Nigg, B.M.; Hanley, D.A.; Engsberg, J.R. Differences in ankle joint complex range of motion as a function of age. Foot Ankle 1993, 14, 215–222. [Google Scholar] [CrossRef] [PubMed]
- Stauffer, R.N.; Chao, E.Y.; Brewster, R.C. Force and motion analysis of the normal, diseased, and prosthetic ankle joint. Clin Orthop. Relat. Res. 1977, 127, 189–196. [Google Scholar] [CrossRef] [PubMed]
- Pappas, M.J.; Buechel, F.F. Failure Modes of Current Total Ankle Replacement Systems. Clin. Podiatr. Med. Surg. 2013, 30, 123–143. [Google Scholar] [CrossRef] [PubMed]
- Martinelli, N.; Baretta, S.; Pagano, J.; Bianchi, A.; Villa, T.; Casaroli, G.; Galbusera, F. Contact stresses, pressure and area in a fixed-bearing total ankle replacement: A finite element analysis. BMC Musculoskelet. Disord. 2017, 18, 493. [Google Scholar] [CrossRef] [PubMed]
- Gil-Castillo, J.; Alnajjar, F.; Koutsou, A.; Torricelli, D.; Moreno, J.C. Advances in neuroprosthetic management of foot drop: A review. J. NeuroEng. Rehabil. 2020, 17, 46. [Google Scholar] [CrossRef]
- Arthritis of the Foot and Ankle. American Academy of Orthopedic Surgeons. 2023. Available online: https://orthoinfo.aaos.org/en/diseases--conditions/arthritis-of-the-foot-and-ankle/ (accessed on 30 July 2023).
- Coester, L.M.; Saltzman, C.L.; Leupold, J.; Pontarelli, W. Long-term results following ankle arthrodesis for post-traumatic arthritis. J. Bone Jt. Surg. Am. 2001, 83, 219–228. [Google Scholar] [CrossRef] [PubMed]
- Kofoed, H.; Stürup, J. Comparison of ankle arthroplasty and arthrodesis. A prospective series with long-term follow-up. Foot 1994, 4, 6–9. Available online: https://api.semanticscholar.org/CorpusID:71193582 (accessed on 30 July 2023). [CrossRef]
- Glazebrook, M.; Burgesson, B.N.; Younger, A.S.; Daniels, T.R. Clinical outcome results of total ankle replacement and ankle arthrodesis: A pilot randomised controlled trial. Foot Ankle Surg. 2021, 27, 326–331. [Google Scholar] [CrossRef]
- Dekker, T.J.; Hamid, K.S.; Federer, A.E.; Steele, J.R.; Easley, M.E.; Nunley, J.A.; Adams, S.B., Jr. The Value of Motion: Patient-Reported Outcome Measures Are Correlated with Range of Motion in Total Ankle Replacement. Foot Ankle Spec. 2018, 11, 451–456. [Google Scholar] [CrossRef] [PubMed]
- DeOrio, J.K.; Nunley, J.A.; Easley, M.E.; Valderrabano, V. Vantage Total Ankle Replacement, Published in Primary and Revision Total Ankle Replacement, pp 151–163. 2021. Available online: https://link.springer.com/chapter/10.1007/978-3-030-69269-8_13 (accessed on 30 July 2023).
- A New Perspective in Total Ankle: Vantage Total Ankle. Exactech Extremities. Available online: https://it.exac.com/wp-content/uploads/sites/33/2022/04/721-00-11-Rev-B_Vantage_Ankle-Product_Sheet_OUS.pdf (accessed on 30 July 2023).
- Baena, J.C.; Wu, J.; Peng, Z. Wear performance of UHMWPE and reinforced UHMWPE composites in arthroplasty applications: A review. Lubricants 2015, 3, 413–436. [Google Scholar] [CrossRef]
- Patil, N.A.; Njuguna, J.; Kandasubramanian, B. UHMWPE for biomedical applications: Performance and functionalization. Eur. Polym. J. 2020, 125, 109529. [Google Scholar] [CrossRef]
- Hauer, G.; Hofer, R.; Kessler, M.; Lewis, J.; Leitner, L.; Radl, R.; Leithner, A.; Sadoghi, P. Revision Rates After Total Ankle Replacement: A Comparison of Clinical Studies and Arthroplasty Registers. Foot Ankle Int. 2022, 43, 176–185. [Google Scholar] [CrossRef] [PubMed]
- Anil, U.; Singh, V.; Schwarzkopf, R. Diagnosis and Detection of Subtle Aseptic Loosening in Total Hip Arthroplasty. J. Arthroplast. 2022, 37, 1494–1500. [Google Scholar] [CrossRef] [PubMed]
- Noori, N.B.; Ouyang, J.Y.; Noori, M.; Altabey, W.A. A Review Study on Total Ankle Replacement. Appl. Sci. 2023, 13, 535. [Google Scholar] [CrossRef]
- Jones, M.D.; Buckle, C.L. How does aseptic loosening occur and how can we prevent it? Orthop. Trauma 2020, 34, 146–152. [Google Scholar] [CrossRef]
- Frequently Asked Questions about Total Ankle Replacement. Washington University Orthopedics. Available online: https://www.ortho.wustl.edu/content/Education/2915/Patient-Education/Educational-Materials/Total-Ankle-Replacements-FAQs.aspx#:~:text=While%20results%20at%205%20and,years%20after%20the%20original%20surgery (accessed on 13 March 2024).
- Yu, J.; Zhao, D.; Chen, W.-M.; Chu, P.; Wang, S.; Zhang, C.; Huang, J.; Wang, X.; Ma, X. Finite element stress analysis of the bearing component and bone resected surfaces for total ankle replacement with different implant material combinations. BMC Musculoskelet. Disord. 2022, 23, 70. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Chen, Z.; Zhao, H.; Zhao, D.; Zhang, X.; Ma, X.; Jin, Z. Comparison of joint load, motions and contact stress and bone-implant interface micromotion of three implant designs for total ankle arthroplasty. Comput. Methods Programs Biomed. 2022, 223, 106976. [Google Scholar] [CrossRef]
- Saad, A.P.B.M.; Syahrom, A.; Harun, M.N.; Kadir, M.R.A. Wear of Total Ankle Replacement (TAR). In Wear Prediction on Total Ankle Replacement; SpringerBriefs in Applied Sciences and Technology; Springer: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- INBONE Total Ankle System. Wright Medical Total Ankle Institute. 2023. Available online: http://www.totalankleinstitute.com/inbone-products/inbone-ankle/ (accessed on 22 August 2023).
- Timothy, S. Jain, Finite Element Analysis of The Bearing Component of Total Ankle Replacement Implants during the Stance Phase of Gait, California Polytechnic State University, San Luis Obispo, CA, USA. Available online: https://digitalcommons.calpoly.edu/theses/2766/ (accessed on 10 March 2024).
- Zhang, Y.; Chen, Z.; Zhao, D.; Yu, J.; Ma, X.; Jin, Z. Articular geometry can affect joint kinematics, contact mechanics, and implant-bone micromotion in total ankle arthroplasty. J. Orthop. Res. 2023, 41, 407–417. [Google Scholar] [CrossRef]
- Miller, M.C.; Smolinski, P.; Conti, S.; Galik, K. Stresses in polyethylene liners in a semiconstrained ankle prosthesis. J. Biomech. Eng. 2004, 126, 636–640. [Google Scholar] [CrossRef]
- Malito, L.G.; Arevalo, S.; Kozak, A.; Spiegelberg, S.; Bellare, A.; Pruitt, L. Material properties of ultra-high molecular weight polyethylene: Comparison of tension, compression, nanomechanics and microstructure across clinical formulations. J. Mech. Behav. Biomed. Mater. 2018, 83, 9–19. [Google Scholar] [CrossRef] [PubMed]
- Godest, A.C.; Beaugonin, M.; Haug, E.; Taylor, M.; Gregson, P.J. Simulation of a knee joint replacement during a gait cycle using explicit finite element analysis. J. Biomech. 2002, 35, 267–275. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Chen, Z.; Zhao, H.; Liang, X.; Sun, C.; Jin, Z. Musculoskeletal modeling of total ankle arthroplasty using force-dependent kinematics for predicting in vivo joint mechanics. Proc. Inst. Mech. Eng. H 2020, 234, 210–222. [Google Scholar] [CrossRef] [PubMed]
- Nunley, J.M.M.; Valderrabano, V.M.P.; DeOrio, J.M.; Easley, M.M. Vantage Ankle Design Rationale. Exactech Extremities. Available online: https://www.exac.com/wp-content/uploads/2019/04/721-00-40_Vantage_Ankle_Design_Rationale_Web_6835600.pdf (accessed on 30 July 2023).
- National Heart, Lung, and Blood Institute. Calculate Your Body Mass Index. National Institute of Health. 2024. Available online: https://www.nhlbi.nih.gov/health/educational/lose_wt/BMI/bmi-m.htm (accessed on 10 March 2024).
- Bell, C.J.; Fisher, J. Simulation of polyethylene wear in ankle joint prostheses. J. Biomed. Mater. Res. B Appl. Biomater. 2007, 81, 162–167. [Google Scholar] [CrossRef]
- Rodrigues, D.S.S. Biomechanics of the Total Ankle Arthroplasty: Stress Analysis and Bone Remodeling. 2013. Available online: https://api.semanticscholar.org/CorpusID:53547308 (accessed on 12 February 2024).
- Mulcahy, H.; Chew, F.S. Current Concepts in Total Ankle Replacement for Radiologists: Features and Imaging Assessment. Am. J. Roentgenol. 2015, 205, 1038–1047. [Google Scholar] [CrossRef]
- Elliot, B.J.; Gundapaneni, D.; Goswami, T. Finite element analysis of stress and wear characterization in total ankle replacements. J. Mech. Behav. Biomed. Mater. 2014, 34, 134–145. [Google Scholar] [CrossRef]
- National Joint Registry Steering Committee. 16th Annual Report 2019: National Joint Registry for England, Wales, Northern Ireland and the Isle of Man; 20th National Joint Registry Annual Report. 2019. Available online: https://reports.njrcentre.org.uk/Portals/0/PDFdownloads/NJR%2016th%20Annual%20Report%202019.pdf (accessed on 5 February 2024).
- Shaffrey, I.; O’Malley, E.; Henry, J.K.; Rajan, L.; Deland, J.T.; O’Malley, M.; Ellis, S.J.; Demetracopoulos, C.A. Midterm Clinical Outcomes, Radiographic Outcomes, and Survivorship of the Infinity Total Ankle Arthroplasty. Foot Ankle Int. 2023, 44, 1247–1255. [Google Scholar] [CrossRef] [PubMed]
- Vale, C.; Almeida, J.F.; Pereira, B.; Andrade, R.; Espregueira-Mendes, J.; Gomes, T.M.; Oliva, X.M. Complications after total ankle arthroplasty- A systematic review. Foot Ankle Surg. 2023, 29, 32–38. [Google Scholar] [CrossRef] [PubMed]
- van der Plaat, L.W.; Hoornenborg, D.; Sierevelt, I.N.; van Dijk, C.N.; Haverkamp, D. Ten-year revision rates of contemporary total ankle arthroplasties equal 22%. A meta-analysis. Foot Ankle Surg. 2022, 28, 543–549, Erratum in Foot Ankle Surg. 2023, 29, 177. https://doi.org/10.1016/j.fas.2022.10.005. [Google Scholar] [CrossRef] [PubMed]
- Henry, J.; Teehan, E.; Ellis, S.J.; Deland, J.; Demetracopoulos, C. Lessons from Revision Total Ankle Replacement: Tibias Fail Early, and Taluses Fail Late (And Fail Again). Foot Ankle Orthop. 2024, 9, 10711007241255112. [Google Scholar] [CrossRef]
- Millstein, I.D.; Koneru, M.; Dibato, J.E.; Gentile, P.; Mahjoub, A.; Freeland, E. Comparing Rates of Radiographic Baseplate Loosening Between Cement and Cementless INFINITY Total Ankle Prostheses. Foot Ankle Spec. 2024, Epub ahead of print. 19386400241247456. [Google Scholar] [CrossRef] [PubMed]
- Jennison, T.; Spolton-Dean, C.; Rottenburg, H.; Ukoumunne, O.; Sharpe, I.; Goldberg, A. The outcomes of revision surgery for a failed ankle arthroplasty: A systematic review and meta-analysis. Bone Jt. Open 2022, 3, 596–606. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).