Diffusion-Based Image Synthesis or Traditional Augmentation for Enriching Musculoskeletal Ultrasound Datasets

Abstract

Background: Machine learning models can provide quick and reliable assessments in place of medical practitioners. With over 50 million adults in the United States suffering from osteoarthritis, there is a need for models capable of interpreting musculoskeletal ultrasound images. However, machine learning requires lots of data, which poses significant challenges in medical imaging. Therefore, we explore two strategies for enriching a musculoskeletal ultrasound dataset independent of these limitations: traditional augmentation and diffusion-based image synthesis. Methods: First, we generate augmented and synthetic images to enrich our dataset. Then, we compare the images qualitatively and quantitatively, and evaluate their effectiveness in training a deep learning model for detecting thickened synovium and knee joint recess distension. Results: Our results suggest that synthetic images exhibit some anatomical fidelity, diversity, and help a model learn representations consistent with human opinion. In contrast, augmented images may impede model generalizability. Finally, a model trained on synthetically enriched data outperforms models trained on un-enriched and augmented datasets. Conclusions: We demonstrate that diffusion-based image synthesis is preferable to traditional augmentation. Our study underscores the importance of leveraging dataset enrichment strategies to address data scarcity in medical imaging and paves the way for the development of more advanced diagnostic tools.

1. Introduction

Musculoskeletal ultrasound (MSK-US) is a type of medical imaging used to non-invasively assess the health of bones, muscles, tendons, and ligaments. MSK-US is preferable over alternatives such as magnetic resonance imaging given its lower-cost, bedside point of care, and safety [1]. One prevalent application of MSK-US is the assessment of knee osteoarthritis (OA), a common degenerative joint disease affecting over 25% of adults in the United States [2]. Effusion and thickened synovium have been identified as key indicators of OA, contributors to the disease’s development, and potential targets for its treatment. Effusion refers to the increase of fluid within the joint space. This may cause the joint recess to distend and inflammation (thickening) of the synovial membrane lining the joint space. The latter is known as synovitis, and may lead to further buildup of synovial fluid in the joint space, worsening the effusion [3]. Joint recess distension and thickened synovium may occur together or separately. 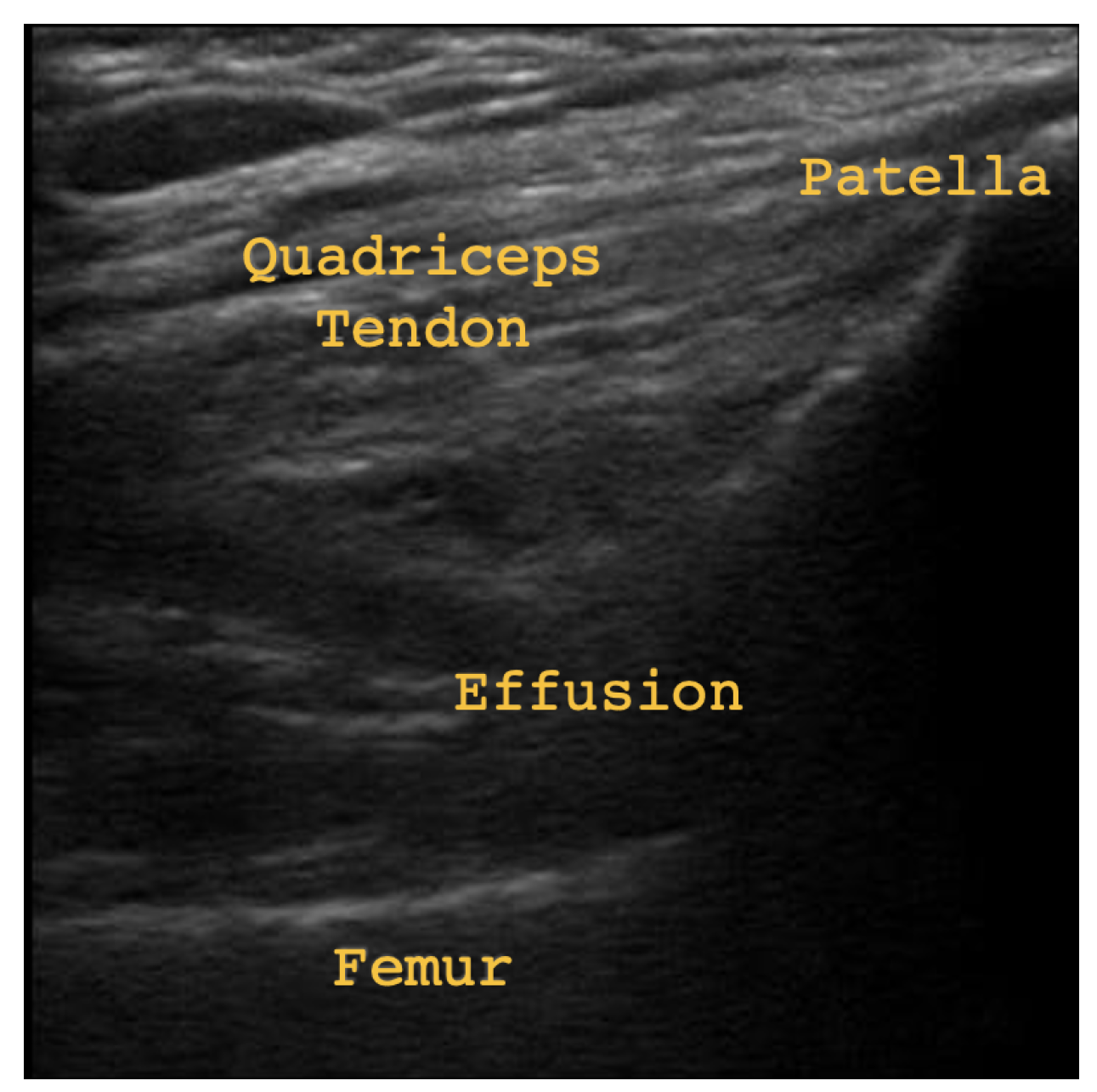In Figure 1 some subtle effusion may be discerned by darker patches (echo-free space) in the region labeled Effusion, indicating joint recess distension. In Figure 2, thickened synovium and significantly more effusion may be discerned by the clear presence of echo-free space in the area labeled Effusion/Thickened Synovium. The presence of echo-free space is an indicator of fluid, since the waves emitted by the ultrasound probe are absorbed instead of reflected [3]. Therefore, Figure 2 provides evidence of both joint recess distension and thickened synovium.

Assessing thickened synovium in the presence of joint recess distension is very difficult [4]. Hence, a new procedure to help clinicians more confidently assess joint recess distension and thickened synovium would help over 50 million patients suffering from OA within only the United States. This work develops such a procedure, incorporating recent advancements in machine learning (ML).

ML has become integral to the development of new diagnostic procedures in medical imaging [5]. These models help to increase the accessibility of medicine, aid in the interpretation of clinical data, and expedite the rate at which diagnostic results are returned to patients. In the domain of medical imaging, convolutional neural networks (CNNs) have demonstrated success in the segmentation and classification of tumors, lesions, cancers, COVID-19, and many other medical conditions [6]. These networks consist of a series of locally-connected layers (called convolutional layers), and fully-connected layers. Each convolutional layer applies a linear filter across the previous layer’s output, or across the input in the case of the first layer. These filters are learned during training, and can be thought of as feature detectors, where each filter tries to extract some defining characteristic of the image (edges, shapes, boundaries). Layers are connected by non-linear activation functions, increasing the complexity of the representations learnable by the network. Once the input moves through every convolutional layer, its final representation is passed to a sequence of fully-connected layers to obtain the output [6]. The type of output depends on the task. In the diagnosis of cancer, for example, it is usually the probability that a given patient has cancer based on the input image.

CNNs are an example of supervised learning, whereby they are trained on input and output pairs. The performance and reliability of these models is highly dependent on the quality and quantity of their training data. Yet, large datasets are not feasibly obtained in medical imaging due to the ethical regulations protecting patient data, the rarity of certain medical conditions, and the costs of data labeling and healthcare [5]. Therefore, numerous methods have been proposed to enrich datasets without requiring new patient data or annotations for that data. This paper will compare two such methods, using a MSK-US dataset to train a CNN for the diagnosis of thickened synovium and joint recess distension. The methodology and findings we present are relevant for other neural network architectures, such as vision transformers, and is not restricted to CNNs. We have decided to focus on neural networks and other supervised approaches over semi-supervised and unsupervised learning, which require less or no labeled data, due to their demonstrated success and fast growing prevalence in medical imaging, as well as other fields.

The first method is augmentation and involves enriching the model’s training set with transformations of existing images. Typically, these transformations include rotation, vertical and horizontal flipping, brightness and hue adjustment, and other similar geometric, intensity, and color transformations [7]. With augmentation, the model learns potentially natural variations in the data to improve the robustness of its decision making.

Although augmentation is widely used, augmented images may be too similar to existing images, and not offer the model any additional information about the conditional distribution of outputs given inputs [5]. Furthermore, augmented images may not be reflective of the inputs received by the model for inference. For example, in medical imaging, augmentation can suppress important biological markers in the training images, reducing the model’s reliability on un-augmented inputs from real patients. Hence, to do better than traditional augmentation, several generative ML models have been developed to synthesize new images as opposed to modifying existing ones. Ideally, synthetic images should contain the defining attributes of real images, while offering sufficient diversity to provide the model with new information about the distribution it must learn.

Generative ML models are characterized by their ability to sample from the unknown data generating distribution of the observed data. In some cases, it is possible to learn the parameters of this unknown distribution directly using maximum likelihood or maximum a posteriori estimation, and then a sampling procedure can be defined over the distribution. In the case of images, however, these distributions may be impossible to sample from directly by being extremely high dimensional. Alternatively, energy-based models learn the parameters of an un-normalized density function to avoid having to compute the normalizing constant (usually an intractable and high dimensional integral) [8]. Finally, variational inference estimates the data generating distribution using a simpler distribution (such as a Gaussian), at the cost of any mathematical guarantees on the goodness of the approximation. These challenges with probabilistic models arising from the curse of dimensionality, have encouraged the development of numerous deep learning (DL) methods for generating synthetic images [9]. One example is the generative adversarial network (GAN).

A GAN is a DL model capable of synthesizing high-quality images. It consists of a generator whose goal is to produce images that will fool the discriminator, a neural network trained to classify images as real or fake [5]. Once the generator’s synthetic images are consistently classified as real by the discriminator, they can be used to enrich a dataset. In [10], a GAN was used to generate MSK-US images of the gastrocnemius medialis muscle. They showed that synthetic images were similar in pixel intensity distribution to real images, and contained the desired muscle architecture. However, as pointed out by [11], they did not train a DL model on the synthetic images to determine how these images might affect the performance of such a model in a real-world diagnostic task.

In [11], they used a de-noising diffusion probabilistic model (DDPM) to generate MSK-US images opposed to a GAN. The advantage of DDPMs over GANs is their ability to generate equally high quality samples with greater diversity, ease of training, and avoidance of mode collapse, where the generator repeatedly produces the same set of images that have been found to fool the discriminator [12]. DDPMs are trained via a forward process, where the model learns to predict the random Gaussian noise added to an image. New samples are then synthesized via a reverse process, beginning with an image of pure Gaussian noise, and incrementally de-noising it over a sequence of time steps until a noise-free image is obtained [9]. In [11], they synthesized images of muscle texture for the tibialis anterior, rectus femoris, gastrocnemius, and biceps brachii and brachialis anterior muscles using a DDPM trained on 1223 MSK-US images. Their synthetic images were found to be similar in pixel intensity distribution to the real images and depicted desired muscle textures. Finally, they trained a DL segmentation model on a mixture of real and synthetic images, resulting in a Dice coefficient and IoU 0.01 greater than the same model trained only on real images, indicating that the synthetic images marginally improved the model’s performance.

This work extends [11], and goes beyond generating muscle texture by applying a DDPM to the significantly more difficult task of generating MSK-US images of synovial thickening and joint recess distension in the knee joint space. Moreover, it directly compares two methods to enrich a MSK-US dataset. First, we augment a subset of existing images using geometric and intensity transformations. Second, we train two DDPMs to generate brand-new synthetic images. The similarity between real, synthetic, and augmented images is assessed qualitatively and quantitatively. Then, the usefulness of the images is evaluated in a challenging clinical task, where we train a CNN using the enriched datasets to diagnose thickened synovium and compare its decision-making against human opinion.

To our knowledge, we are the first to compare augmentation and diffusion-based image synthesis for enriching medical imaging datasets. Our purpose is to determine the most appropriate methodology for enriching medical imaging datasets to train DL models in challenging clinical tasks. We therefore set the following objectives:

• Train two DDPMs to generate MSK-US images of synovial thickening and joint recess distension.
• Compare the performance of a DL model at diagnosing synovial thickening when trained on datasets of real images, augmented images, and synthetic images.
• Offer conclusions regarding the usefulness of augmentation and diffusion-based image synthesis to train DL models within the context of medical imaging.

The contributions of this work are:

• Provide evidence of the utility of dataset enrichment methods for deep learning in an important and challenging medical imaging problem.
• Directly evaluate diffusion-based dataset enrichment against augmentation-based dataset enrichment in the context of medical imaging.
• Facilitate the interpretability of deep learning models in medical imaging by comparing the decision-making heuristics of trained models against human opinion.

2. Materials and Methods

2.1. Data

The complete MSK-US dataset contained 9987 images of joint recess distension without thickened synovium (negatives), and 1799 images of joint recess distension with thickened synovium (positives). The 9987 negatives belonged to 3800 patients, of whom 180 were children or adolescents, accounting for 310 images. The 1799 positives belonged to 713 patients, of whom 166 were children or adolescents, accounting for 455 images. All images were filtered for the suprapatellar longitudinal view of the knee using a neural network. Of the negatives, 9311 depicted the suprapatellar longitudinal view, while 1651 of the positives depicted the desired view. The suprapatellar longitudinal view is the most appropriate for the diagnosis of recess distension and thickened synovium. Landmarks visible in this view include the patella, quadriceps tendon, and femur. Additionally, the view depicts areas of possible effusion and thickened synovium. See annotations in Figure 1 and Figure 2 for an example. The filtered images were then cropped to remove any annotations in the margins, and their pixel values were normalized to the range $[-1,1]$. See

Table 1. MSK-US dataset summary. Classes: negative for thickened synovium with knee joint recess distension, positive for thickened synvoium with knee joint recess distension.

Class	Adult	Pediatric	Total	Suprapatellar Longitudinal
Negative	9677	310	9987	9311
Positive	1344	455	1799	1651

for a summary.

2.2. MSK-US Image Synthesis with DDPM

2.2.1. Background

As described in the Introduction, DDPMs synthesize a new image $x_0$ by beginning with an image of pure Gaussian noise $x_T$ and de-noising it over a fixed sequence of time steps T. The number of time steps is a hyperparameter. This de-noising process is called the reverse process. More specifically, diffusion models are latent variable models, where the joint distribution of $x_{0:T}$ is defined as a first-order Markov chain [13].

$$\begin{array}{c}\hfill p\left(x_{0:T}\right)=p\left(x_T\right)\prod _{t=0}^{T-1}p\left(x_t\right|x_{t+1})\end{array}$$

(1)

This chain, p in Figure 3, is called the reverse process with initial state $x_T\sim \mathcal{N}(0,I)$. Note that each $x_t,\forall t\in \{0,\cdots ,T\}$ has the same dimension as the final state (the synthesized image) $x_0$. Transitions in this chain of the form $x_{t+1}\to x_t$ are determined by a conditional Gaussian distribution [13].

$$\begin{array}{c}\hfill p\left(x_t\right|x_{t+1})=\mathcal{N}(x_t;\mu (x_{t+1},t+1),\Sigma (x_{t+1},t+1))\end{array}$$

(2)

The parameters of these transitions (conditional Gaussians) are learned during the forward process. The approximation of the posterior distribution, q in Figure 3, is called the forward process and is another first-order Markov chain with initial state $x_0$. Transitions in this chain of the form $x_t\to x_{t+1}$ are also determined by a conditional Gaussian distribution [13].

$$\begin{array}{c}\hfill q\left(x_{t+1}\right|x_t)=\mathcal{N}(x_{t+1};\sqrt{1-{\beta }_{t+1}}{x}_t,{\beta }_{t+1}I)\end{array}$$

(3)

However, unlike the reverse process, these transitions have no learnable parameters. Each transition can be intuitively interpreted as the addition of Gaussian noise to the previous state $x_t$, where the distribution of the noisy output $x_{t+1}$ is parameterized by a variance schedule ${\left\{{\beta }_t\right\}}_{t=1}^T$ depending on the current time step [13]. The variance schedule is fixed as a hyperparameter in [13], where it is defined as a linearly increasing sequence from 0.0001 to 0.02. However, as shown by [14], a linear schedule introduces noise too quickly and thereby reduces the model’s ability to learn from later time steps. To solve this problem, the authors define a cosine schedule where each ${\beta }_t$ is non-linearly determined by a cosine function of the current time step t. This schedule succeeds in introducing noise more gradually to facilitate learning [14].

$$\begin{array}{c}\hfill {\beta }_t=min(1-{\displaystyle \frac{{\overline{\alpha }}_t}{{\overline{\alpha }}_{t-1}}},0.999),{\overline{\alpha }}_t={\displaystyle \frac{f\left(t\right)}{f\left(0\right)}},f\left(t\right)=cos{\left({\displaystyle \frac{t/T+s}{1+s}}\ast {\displaystyle \frac{\pi }{2}}\right)}^2\end{array}$$

(4)

In [13], they implement the entire model using a U-Net architecture, since the input and output dimensions are equal, and train it by minimizing a loss function defined as the $L_1$-norm of the difference between the actual and predicted noise in an image $x_t$ at time step t.

2.2.2. Training

Two separate DDPMs were used. The first DDPM was trained to generate negative samples and the second DDPM was fine-tuned to generate positive samples. The first DDPM was trained on the set of 9311 negatives as depicted in Figure 4, where each image had been filtered for the suprapatellar longitudinal view, cropped, and normalized. Each image was resized to $256\times 256$ when passed to the model, with a probability of 0.5 for being horizontally flipped. Random horizontal flips during training were found to improve sample quality in [13]. The model implemented a variant of the U-Net architecture, including residual connections across convolutional layers, time and position embedding, and a cosine variance schedule with 1000 time steps. The cosine schedule was found to be more effective at introducing noise during the forward process compared to a linear schedule in [14]. The number of chosen time steps matched that originally used in [13]. The loss function was given by the $L_1$-norm between the model’s predicted noise and the actual random noise in an image. The resolution of $256\times 256$ was chosen after observing that $128\times 128$ images lacked sufficient detail for diagnosing thickened synovium. Further increasing the resolution to $512\times 512$ would have necessitated excessive compute and training time as found by [11].

The first DDPM was trained using Adam over 90 epochs with a learning rate of 0.00001, and batch size of 32, then for another 35 epochs with a reduced learning rate of 0.000001. The choice of Adam is consistent with both [13,14]. In [13], they found that a smaller learning rate of the order ${10}^{-5}$ worked better for images with resolution $256\times 256$. The second DDPM was created by fine-tuning the first DDPM using an additional set of 1651 positives as depicted in Figure 4, where each image had been filtered for the suprapatellar longitudinal view, cropped, and normalized. Each image was resized to $256\times 256$ when passed to the model, with a probability of 0.5 for being horizontally flipped. The second diffusion model was fine-tuned using Adam over 95 epochs with a learning rate of 0.00001, and batch size of 32. Both DDPMs were trained on NVIDIA V100-SMX2-32GB GPUs.

2.2.3. Sampling

Both diffusion models were sampled over 1000 time steps to synthesize 320,256 × 256 RGB images. Each sampled image was converted to gray scale, its contrast was doubled, and its brightness reduced by 30%. In addition, bilateral filtering was applied to smooth the unwanted noise created by contrast enhancement. These operations were chosen for the synthetic images to appear perceptually more similar to real images (see Section 3 and Section 4).

2.3. Augmentation and Detecting Synovial Thickening with CNN

2.3.1. Experimentation

A CNN was used to diagnose synovial thickening with joint recess distension, and its accuracy was compared across five experiments. Each experiment was conducted with 5-fold cross validation. The same dataset used to train the DDPMs, consisting of 9311 negatives and 1651 positives, was randomly sub-sampled to obtain 3200 images, 1600 images per class. These were then split into 5 folds with 100 additional images set aside to be used as a balanced testing set (50 images per class). If multiple images belonged to the same patient, each was contained in the same fold, or in the test set. This dataset was then used as the un-enriched training set. All images were filtered for the suprapatellar longitudinal view, cropped, and their pixel values normalized. Each image was resized to $380\times 380$ when passed to the model, including the $256\times 256$ synthetic images. A higher resolution was chosen for the CNNs because it was found to improve their performance, however, increasing the resolution of the DDPM would have been too computationally expensive as described above. The model was trained on four of the five folds in every iteration, where the fifth fold was used as a validation set. Each experiment consisted of five iterations, meaning each fold was used as a validation set exactly once. Finally, the model was evaluated on the test set using its best set of weights. A description of each experiment is provided below and graphically summarized in Figure 5.

• Trained on un-enriched MSK-US dataset of 3200 images, 1600 per class.
• Trained on dataset enriched 20% with augmentation (320 augmented images per class).
• Trained on dataset enriched with augmentation at runtime (number of augmented images is probabilistic).
• Trained on dataset enriched 20% with diffusion-based image synthesis (320 synthetic images per class).
• Trained on dataset enriched with 20% diffusion-based image synthesis and augmentation at runtime.

Augmentations included horizontal and vertical flips, rotation, as well as contrast, sharpness, and brightness enhancement. All augmentations at runtime were performed with probability 0.5. The set of augmentations was chosen to not overly distort the training images, so that the model learns on mostly realistic input and output pairs. We chose to include experiments where augmentation was applied at runtime since this is the standard approach used by most researchers when writing ML code. However, probabilistic augmentation at runtime makes it impossible to determine the final number of augmented images in the training set, whereby we chose to compare synthetic and augmented images using a fixed 20% enrichment. Our choice of 20% was influenced by the amount of time and compute required to sample from a DDPM.

2.3.2. Training

The model implemented the EfficientNet-B4 architecture, pre-trained on ImageNet1K. In each experiment, the model was fine-tuned on the corresponding dataset. Transfer learning with this architecture on image classification tasks was shown to be effective in [15]. The model was trained with Adam for a minimum of 25 epochs and a maximum of 50 epochs, early stopping with a patience of 5 epochs, learning rate of 0.001, batch size of 64, and gradient accumulation across 2 batches. The loss function was given by the binary cross entropy loss. The model was trained in parallel on a NVIDIA V100-SMX2-32GB GPU.

3. Results

3.1. Image Similarity

3.1.1. Qualitative Comparison

In Figure 6 and Figure 7, a visual comparison reveals that synthetic images are noticeably brighter than real and augmented images. This phenomenon was also observed in [11]. Additionally, real and augmented images exhibit more contrast, even after the brightness and contrast levels of synthetic images were adjusted. Anatomically, there are inconsistencies in the synthetic images, for example in the bottom row of Figure 1 within the red circled region, where the quadriceps tendon is abruptly cut off. Note, however, that the generation of anatomically correct synthetic images was not a primary objective of our work. Lastly, the geometric transformations applied to augmented images including horizontal and vertical flips, as well as rotation by up to $\pm {10}^{\circ }$, makes them difficult to interpret, given the absence or repositioning of biological landmarks pertaining to the suprapatellar longitudinal view. The yellow annotations in Figure 6 and Figure 7 illustrate how flips and rotations affect the landmarks.

3.1.2. Pixel Intensity Histograms

Pixel intensity histograms for 100 real, synthetic, and augmented images are depicted in Figure 8. The mean and standard deviation of pixel intensity was computed for each set of images. In support of our qualitative observation that synthetic images appear brighter than real images, the mean of the distribution over synthetic pixel intensity is much greater than the means of the distributions over real and augmented pixel intensities. Moreover, the standard deviation is lower for synthetic images, given their lower levels of contrast compared to real and augmented images, which is again consistent with our qualitative observation. Finally, upon visual inspection, the distributions over pixel intensity for real and augmented images are near identical. This is attributable to the fact that many augmentations were geometric not intensity transformations.

3.1.3. Quantitative Metrics

Three metrics were computed to quantitatively measure the similarity between real, synthetic, and augmented images. Peak signal-to-noise ratio (PSNR) is inversely proportional to the mean squared error (MSE) of pixel values between two images, whereby higher PSNR indicates lower MSE, and so greater similarity [16]. The expression for PSNR is given below for images f and g, each of size $M\times N$ [16].

$$\begin{array}{c}\hfill PSNR(f,g)=10{log}_{10}{\displaystyle \frac{{255}^2}{MSE(f,g)}},MSE(f,g)={\displaystyle \frac{1}{MN}}\sum _{i=0}^{M-1}\sum _{j=0}^{N-1}{(f_{ij}-g_{ij})}^2\end{array}$$

(5)

Given that PSNR depends entirely on pixel values, however, means that it is not correlated with human perceived similarity. In contrast, the structural similarity index measure (SSIM) was found to be aligned with human perceived similarity, where values close to 1 imply greater similarity [16]. Its expression is given below for images f and g, where ${\mu }_f$ denotes mean of f, ${\sigma }_f^2$ denotes variance of f, and ${\sigma }_{fg}$ denotes covariance across $f,g$ [16].

$$\begin{array}{c}\hfill SSIM(f,g)=l(f,g)c(f,g)s(f,g)\end{array}$$

(6)

$$\begin{array}{cc}\hfill l(f,g)={\displaystyle \frac{2{\mu }_f{\mu }_g+C_1}{{\mu }_f^2+{\mu }_g^2+C_1}},c(f,g)& ={\displaystyle \frac{2{\sigma }_f{\sigma }_g+C_2}{{\sigma }_f^2+{\sigma }_g^2+C_2}},s(f,g)={\displaystyle \frac{{\sigma }_{fg}}{{\sigma }_f{\sigma }_g+C_3}}\hfill \end{array}$$

(7)

Finally, learned perceptual image patch similarity (LPIPS) was found to be the most representative metric of human perceived similarity. It is computed by extracting the activations for each layer l across L layers of AlexNet for both images, denoted ${\widehat{y}}_f^l,{\widehat{y}}_g^l$, then scaling the difference of these activations element-wise by a learned vector w, taking the $L_2$-norm, and summing across feature maps and layers. The expression for LPIPS is given below for images f and g, where $H^l,W^l$ denote the dimensions of the feature map for layer l [17].

$$\begin{array}{c}\hfill LPIPS(f,g)=\sum _l{\displaystyle \frac{1}{H_l{W}_l}}\sum _{i,j}\left|\right|w_l\odot ({\widehat{y}}_{f,ij}^l-{\widehat{y}}_{g,ij}^l){\left|\right|}_2^2\end{array}$$

(8)

LPIPS values close to 0 suggest greater similarity [17].

Table 2. Quantitative metrics PSNR, SSIM, LPIPS to compare similarity between real, augmented, and synthetic images in both classes. Classes: negative for thickened synovium with knee joint recess distension, positive for thickened synovium with knee joint recess distension.

Class	Comparison	PSNR	SSIM	LPIPS
Negatives	Real and augmented	12.65	0.1218	0.6301
Positives		12.52	0.1216	0.6149
Negatives	Real and synthetic	6.478	0.1063	0.7475
Positives		6.581	0.1091	0.7340
Negatives	Synthetic and augmented	6.563	0.1011	0.7531
Positives		6.801	0.1064	0.7372

records the mean PSNR, SSIM, and LPIPS, computed using 320 images for each dataset pair.

3.2. Experiments

The results of the experiments outlined in Section 2.3.1 are given in

Table 3. CNN 5-fold cross validation results for Ex. 1–5. All accuracies are balanced. Accuracy measures ability to determine if image is positive for thickened synovium with knee joint recess distension given images positive and negative for thickened synovium with knee joint recess distension.

Training Set	Validation Set Mean	Validation Set Standard Deviation	Test Set	Test Set Sensitivity	Test Set Specificity
Un-enriched	0.6858	0.0094	0.7100	0.8200	0.6000
Augmented 20%	0.6734	0.0127	0.6900	0.8800	0.5000
Augmented Runtime	0.6712	0.0108	0.7200	0.8600	0.5800
Synthetic 20%	0.6906	0.0168	0.7300	0.8600	0.6000
Synthetic and Augmented Runtime	0.6690	0.0176	0.7100	0.8800	0.5400

. Importantly, the classifier trained on an enriched dataset of synthetic images (Ex. 4) outperforms the rest with respect to every metric but sensitivity. A decision threshold of 0.5 was used for computing sensitivity and specificity.

3.3. Heat Maps

Heat maps were generated with gradient-weighted class activation mapping (Grad-CAM) to verify if the CNN identified points of interest consistent with human opinion, and whether these points were the same across real and synthetic images. The heat maps were created using back-propagated gradients in the last convolutional layer [18]. The weights of the network corresponded to those trained in Ex. 4, given that they performed the best across experiments. The top rows of Figure 9 and Figure 10 illustrate output on real images, while the bottom rows contain output on synthetic images. On each instance the model confidently made the right decision, where confidence is quantified by the probability that the given input image contains thickened synovium. Therefore, small probabilities in Figure 9 suggest high confidence in the absence of thickened synovium, while large probabilities in Figure 10 suggest high confidence in the presence of thickened synovium.

4. Discussion

Our work compares two methods to enrich a MSK-US dataset for thickened synovium and joint recess distension. First, we augment a subset of existing images using geometric and intensity transformations. Second, we train two DDPMs to generate brand-new synthetic images. The similarity between real, synthetic, and augmented images is assessed qualitatively and quantitatively. Then, the usefulness of the images is evaluated in a challenging clinical task, where we train a CNN using the enriched datasets to diagnose thickened synovium and compare its decision-making against human opinion.

Given the synthetic and augmented images, a qualitative analysis suggested that the synthetic images appear noticeably brighter than real and augmented images. This observation was reflected in the mean of the pixel intensity histogram for synthetic images being significantly greater than the means of the histograms for real and augmented images. Furthermore, synthetic images exhibited less contrast, which was again reflected in the standard deviation of the histogram for synthetic images being smaller than the standard deviations of the histograms for real and augmented images. These observations are consistent with [11], where they also found the synthetic MSK-US images from a DDPM to be brighter than their real counterparts to some extent. In [19], they found that generating extremely bright or extremely dark images is a general problem with diffusion models stemming from the fact that variance schedules do not produce pure noise by the last time step T.

The near perfect correspondence between pixel intensity histograms for real and augmented images is due to many augmentations being geometric transformations. Unlike intensity or color transformations, geometric transformations do not affect the pixel intensity histogram of an image. Importantly, however, geometric transformations may reposition or conceal biological landmarks, meaning the augmented image becomes difficult to interpret and inconsistent with real images. This is particularly a concern for the CNN, which may then be encouraged to learn incorrect representations when trained on augmented images. In contrast, synthetic images portray more consistent anatomical structures than augmented images and contain resemblances to the three landmarks of the suprapatellar longitudinal view: The patella, femur, and quadriceps tendon. We emphasize, however, that the generation of anatomically accurate synthetic images was not a primary objective of our work and acknowledge that the synthetic images contain anatomical inaccuracies.

Next, similarity between images was assessed quantitatively using the PSNR, SSIM, and LPIPS metrics. Across all metrics, the similarity between augmented and real images was higher than between synthetic and real images. This was expected given that augmented images do not contain any new content. Of the three metrics, PSNR suggested that augmented images were approximately twice as similar to real images as synthetic images were to real images. This is because PSNR heavily penalized the brightness and contrast discrepancies across real and synthetic images. Even so, according to SSIM, augmented images were more similar by only 0.014 on average to real images than synthetic images were to real images. Likewise, according to LPIPS, augmented images were more similar by only 0.1183 on average to real images than synthetic images were to real images. Given that SSIM and LPIPS are most representative of human perceived similarity, these values should be attributed more importance than PSNR. It is worth noting, however, that MSK-US images consist mostly of black and gray pixels, and SSIM has been shown to severely underestimate similarity when comparing dark images [20]. Furthermore, our PSNR, SSIM, and LPIPS all suggest significantly less similarity between real and synthetic images than in [11]. We attribute this to the fact that suprapatellar longitudinal view is visually much more complex than their images of muscle textures. This complexity arises from the structures within the images, but also the greater variability across the images. Hence, the diffusion model is prone to performing worse than in [11]. Nevertheless, applying diffusion models to a more challenging learning problem, even for humans, was one of the original motivators of our work. A final point is that a higher dissimilarity between real and synthetic images is not necessarily a limitation of synthetic images but may suggest that they are more diverse than augmented images. Capturing greater diversity was an original motivator for choosing DDPMs, since it provides the CNN with more information about the conditional distribution over labels given inputs.

The most important contribution of our work is the training of a CNN to perform the challenging clinical task of detecting synovial thickening in the presence of joint recess distension, with reasonable accuracy and precision. Five variants of this CNN were trained across our five experiments. In each experiment, the network was trained on a dataset of un-enriched or enriched images, using five-fold cross validation. This allowed us to directly compare its performance when trained on augmented and synthetic images. The results revealed that the CNN trained on an enriched dataset of synthetic images demonstrated maximal performance in all but one metric, across validation sets and test set. Moreover, the small value of the standard deviation for validation accuracy suggests that the model was consistent and reliable throughout the entire training set. This is a necessary condition for the model to be deployable in a clinical setting. Another desirable property demonstrated by our model trained with 20% synthetic images was its preference for sensitivity, which is vital in the medical imaging domain to ensure patients in need do not go undetected. In summary, our experimental results coincide with [11], where their DL model trained on a mixture of synthetic and real images outperformed the base model (trained only on real images). As in [11], the improvement offered by the synthetically enriched dataset is small (1%), however, the difficulty of detecting synovial thickening underscores the practical relevance of our results.

The fact that the synthetically enriched dataset yielded a better model than any augmented dataset can be attributed to the qualitative and quantitative comparisons made between synthetic and augmented images. To reiterate, synthetic images depict anatomical structures and landmarks with greater consistency than augmented images, exposing the model to more images representative of those it will receive from real patients. Therefore, the anatomical inaccuracies in synthetic images do not necessarily detract from their value in training a DL model, which was one of the primary objectives of our work. Moreover, synthetic images are more diverse, providing the model with more information about the conditional distribution of outputs given inputs. All of this is to say that synthetic images help the CNN achieve greater generalizability.

In our experiments, unlike the synthetic model which outperformed the base model across both validation and test sets, the augmented models performed unpredictably. To be exact, the model trained with 20% augmentation performed worse than the base model across both validation and test sets. Yet, it performed better on average across the validation sets than the model trained on images augmented at runtime, which in turn performed better than the base model over the test set. This unreliable performance makes augmentation an undesirable choice in high-risk clinical applications where lives are at stake. In our opinion, these observations are a result of the visual inconsistencies and distortions introduced by augmentation. The lack of realism in some of the augmented images may lead the model to learn incorrect representations, and thereby explain why the base model might outperform one trained with augmentation. In Ex. 5, the model was trained with both synthetic images and augmentation at runtime, and its performance decreased across validation and test sets compared to the models in Ex. 3 and Ex. 4. Augmentation at runtime likely decreased performance in these cases by devaluing both the real and synthetic images, as well as increasing the standard deviation of the model’s accuracy, whereby the model was unable to benefit from the synthetic images and experienced greater variability in its performance. In summary, through these observations we show that augmentation may degrade model performance in certain medical imaging tasks.

To rigorously understand and validate our CNN’s performance, heat maps were used to verify if points of interest identified by the model aligned with human opinion, and if these points were the same across real and synthetic images. The heat maps illustrated that the CNN attributed importance to relevant regions, near areas of noticeable effusion. Moreover, the regions identified in synthetic images matched those identified in real images for similar views. These observations suggest that the CNN’s decision-making is aligned with human opinion, and that the synthetic images maintain enough biological and visual fidelity for thickened synovium and joint recess distension to be identified consistently.

In summary, the reasons above indicate that diffusion-based image synthesis is preferable over traditional augmentation to enrich medical imaging datasets of DL models. Our results also substantiate the findings of [11]. We proposed a successful methodology to enrich a MSK-US dataset for training a CNN in a diagnostic task, and demonstrated that traditional augmentation may actually degrade model performance at such a task. However, our study has limitations. Using augmentation at runtime, dictated by probabilities, means that it is impossible to verify the number of augmented images present in the training set. Although, this is the standard approach. Moreover, future work would incorporate attention block fine-tuning opposed to traditional fine-tuning to potentially reduce over-fitting [21]. Furthermore, experimentation involving de-noising diffusion implicit models (DDIMs) would help compare the sampling quality between DDIMs and DDPMs, to determine the extent of the trade off between sample quality and improved sampling speed in the context of medical imaging [22]. Our choice of 20% synthetic enrichment was influenced by the computational cost and time required to sample a DDPM. This slow iterative sampling process is a limitation of DDPMs addressed by DDIMs.

5. Conclusions

We compared traditional augmentation techniques and diffusion-based image synthesis for enriching a MSK-US dataset for thickened synovium and joint recess distension. Our results indicate that diffusion-based image synthesis is a viable alternative to traditional augmentation for enriching the training set of DL models in medical imaging. Concretely, synthetic images seemed to maintain greater anatomical consistency, diversity, and appeared more representative of the images received from real patients. Furthermore, synthetic images improved the performance of a DL model in a diagnostic task corroborating the findings of [11], and seemed to encourage the model to learn representations consistent with human opinion.

With synthetic dataset enrichment, we overcome persistent problems in medical imaging related to ethical regulations over the distribution of data, cost of data labeling, cost of accessing healthcare, and the rarity of medical conditions. Thereby, we pave the way for the development of more reliable diagnostic tools in medical imaging. These diagnostic tools, such as our CNN, provide medical practitioners with a second set of eyes, and a second opinion during potentially life-altering decisions. These models work for free, 24 h a day, 7 days a week, and immediately return results to patients. Therefore, they evolve the provision of healthcare today.