Abstract
A comprehensive investigation of the chemical bonding, electronic structure, and spectroscopic properties of the lanarkite-type Pb2SO5 (PSO) structure was conducted, for the first time, using density functional theory simulations. Thus, different functionals, PBE, PBE0, PBESOL, PBESOL0, BLYP, WC1LYP, and B3LYP, were used, and their results were compared to predict their fundamental properties accurately. All DFT calculations were performed using a triple-zeta valence plus polarization basis set. Among all the DFT functionals, PBE0 showed the best agreement with the experimental and theoretical data available in the literature. Our results also reveal that the [PbO5] clusters were formed with five Pb–O bond lengths, with values of 2.29, 2.35, 2.57, 2.60, and 2.79 Å. Meanwhile, the [SO4] clusters exhibited uniform S–O bond lengths of 1.54 Å. Also, a complete topological analysis based on Bader’s Quantum Theory of Atoms in Molecules (QTAIM) was applied to identify atom–atom interactions in the covalent and non-covalent interactions of the PSO structure. Additionally, PSO has an indirect band gap energy of 4.83 eV and an effective mass ratio (/) of about 0.192 (PBE0) which may, in principle, indicate a low degree of recombination of electron–hole pairs in the lanarkite structure. This study represents the first comprehensive DFT investigation of Pb2SO5 reported in the literature, providing fundamental insights into its electronic and structural properties.
1. Introduction
In materials science, the quest for novel advanced materials, including nanostructures, with highly tailored properties and unique functionality has always been closely related to technological advancement. From this perspective, the discovery, design, and optimization of such materials can currently be achieved using various synthetic methods, significantly influencing their properties [1,2,3,4,5]. Notably, these advanced materials have historically been designed and manufactured empirically, primarily through extensive trial and error using a combinatorial synthesis strategy [6,7,8,9,10]. It is widely recognized that the traditional approach is not only time-consuming and costly but also involves a vast number of potential combinations, adding to its complexity. In recent decades, the approach to designing and discovering advanced materials has undergone a profound transformation, driven by the integration of theoretical and experimental strategies. This combined methodology has facilitated a deeper understanding of the intricate relationships between structure, composition, and properties in these novel materials [3,9,11,12,13,14,15,16].
Therefore, new emerging technologies currently focus on the design process of new materials based on classes little explored in the literature [17,18,19,20]. In this direction, more recently, researchers have found that the combination of the lanarkite-type PSO structure with copper phosphide (Cu3P) leads to the formation of Pb10−xCux(PO4)6O which can be in a room-temperature superconducting state [21,22]. Such results generated great debates, and new studies are, in turn, already calling this discovery into question [23,24,25,26,27]. Thus, from this perspective, PSO is now in the spotlight of the attention of the scientific community.
As is commonly recognized, the PSO structure under certain synthesis conditions crystallizes in the monoclinic phase belonging to the C2/m space group (no 12) [28,29]. This mineral was first discovered in Lanarkshire, Scotland, and was named after its location [30,31]. Notably, the initial structural description of these ceramic materials was provided by Schrauf in 1877. Despite being relatively scarce in the literature, experimental and theoretical studies involving PSO-based material applications hold significant potential. These structures can exhibit a range of attractive physical and chemical properties that need to be correctly understood and exploited for successful commercialization in the future. Therefore, a comprehensive understanding of their electronic structure, spectroscopic properties, and chemical bonding is crucial for the development of new technologies based on PSO.
In this paper, for the first time, a comprehensive perspective is provided on the chemical bonding, electronic structure, and Raman spectroscopy properties of the lanarkite-type PSO structure from a computational perspective, through density functional theory (DFT), and the influence of seven different functionals on structural and electronic properties is investigated to unravel which one best describes PSO’s properties. In this case, the proposed computational strategy is of great interest in order to obtain a more accurate description of electronic parameters, which govern much of PSO’s technological applications.
2. Computational Method and Model System
All the periodic DFT calculations were performed using seven density functionals, PBE [32], PBE0 [33], PBESOL [34], PBESOL0, BLYP [35,36], WC1LYP [37], and B3LYP [35,36,38], for comparison as implemented in CRYSTAL17 [39] software. This methodology for evaluating the most suitable functional was successfully applied in our previous studies [40,41], consistently demonstrating its reliability in ensuring the accuracy and robustness of the results. The Pb, S, and O atomic centres were described by a triple-zeta valence plus polarization (TZVP) [42]. It is important to note that the Pb basis set employs a scalar relativistic effective core potential (ECP), which has been extensively benchmarked for accuracy and reliability [42,43]. The minimum energy structure was confirmed by diagonalizing the Hessian matrix with respect to the lattice parameters and internal coordinates, followed by the confirmation of the absence of imaginary frequencies. Structural convergence was checked on gradient components and nuclear displacements, with tolerances on their root mean square set to 0.0001 and 0.0004 a.u., respectively.
The precision of the infinite Coulomb and HF exchange series is controlled by five parameters αi, with i = 1–5, such that two-electron contributions are neglected when the overlap between atomic functions is lower than . In our simulation, the five αi parameters were set to 8, 8, 8, 8, and 18, and the shrinking factor for the Pack–Monkhorst and Gilat nets was set to 9. The band structure and density of states (DOS) were analyzed using the Properties17 routine implemented in the CRYSTAL code, with the same k-point sampling employed for the diagonalization of the Fock matrix in the optimization process, for the DOS, and the high-symmetry points in the Brillouin zone, with a grid of 100 points along the path, for the band structure. The vibrational frequencies were determined at the Γ point using the numerical second derivatives of the total energies, which were estimated using the coupled perturbed Hartree–Fock/Kohn–Sham algorithm [44,45,46]. Raman intensities were determined analytically by computing the derivatives of polarizability with respect to atomic displacements, in accordance with Placzek’s approximation.
The chemical bonds and electron density distribution properties were investigated by applying the Quantum Theory of Atoms in Molecules and Crystal (QTAIMAC) [47], as implemented in CRYSTAL17 with the Topond program [48]. In this case, the critical points of the bonds, referred to as bond critical points (BCPs), were evaluated here by analyzing the electron density, ρ(r). Notably, this analysis of BCPs involves evaluating various quantities to define the bond character, including electron density, Laplacian (∇2ρ(r)), the ratio of potential energy density to kinetic energy density (V(r)/G(r)), and the total electronic energy density (H = V(r) + G(r)) which defines the bond degree H/ρ(r). In turn, these values can indicate the nature of the bond, whether it be covalent, ionic, or transient.
Additionally, the shape of the bond was described using the ellipticity parameter (ε), which indicates the degree and direction of polarization of the density. From this perspective, a value of ε close to zero suggests a localized density characteristic of an ionic or covalent bond in a polar molecule. Conversely, ε ≈ 1 indicates an elliptical bond shape with more scattered density between the two attractors.
Also, it is important to highlight that we do not include the Spin–Orbit Coupling (SOC) effects in our calculations, since we are interested in properties other than superconductivity. Furthermore, there is no implementation of SOC in CRYSTAL23 since it is not yet in its complete form, as not all basis sets are available to consider such an effect. Although SOC significantly impacts the electronic structure of heavy elements like Pb, its omission may alter absolute band gap values but does not affect the overall qualitative trends observed.
3. Results and Discussion
3.1. Structural Properties
Figure 1a shows a representation of the PSO unit cell, with experimental lattice parameters of a = 13.746 ; b = 5.696 ; and c = 7.066 and angles α = γ = 90° and β = 115.79° [49]. The lanarkite PSO structure has monoclinic symmetry (belonging to the C2/m space group) and is composed of a combination of altered penta-coordinated lead [PbO5] and tetra-coordinated sulphur [SO4] clusters. Figure 1b,c show the results of our investigation of the influence of the density functional on the lattice parameters. The dashed lines indicate the experimental values for the respective parameters.
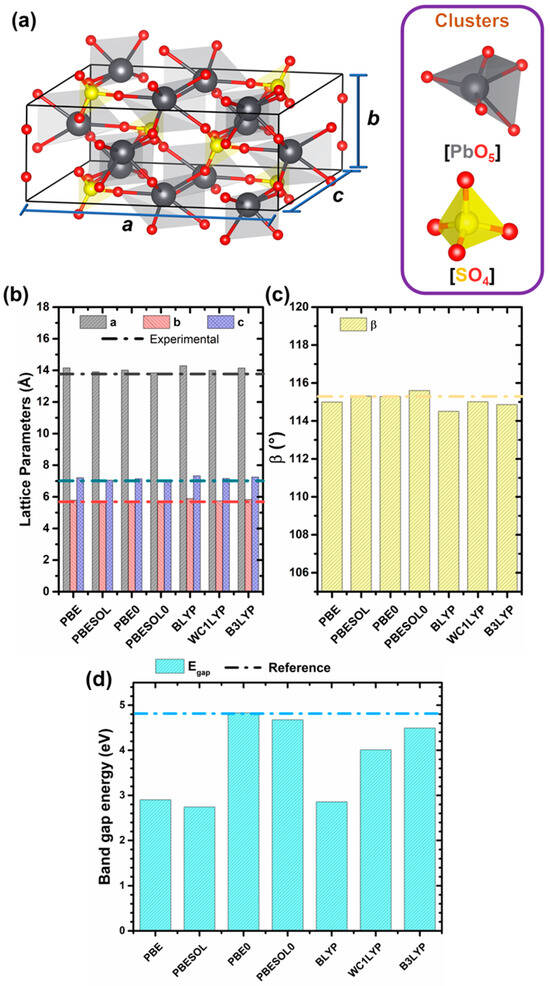
Figure 1.
(a) Bulk structure unit cell and its constituting clusters, (b) lattice parameters, (c) β (angle between a and c), and (d) band gap energy variations in function of density functional. Dashed dotted line represents reference values for each parameter [49].
As shown in Figure 1b,c, all density functionals used in this study can accurately describe the PSO lattice (see Table S1 for further details), with small variations observed between the theoretical and experimental values. For instance, the sum of the deviations found for all these lattice parameters (in percentage) was 0.71% for WC1LYP, 0.67% for PBE0, 0.21% for PBESOL, and 0.16% for PBESOL0. However, it is well known that in the development of new semiconductor materials, the band gap is the most fundamental property [3]. So, among all the density functionals tested in this study, PBE0 presented a band gap value closest to what is expected for the structure, as can be seen in Figure 1d. Therefore, all subsequent analyses of this system were performed using the PBE0 functional. It is important to note that exploring the influence of various density functionals is crucial to accurately describing the electronic structure and properties of complex materials. Standard GGA functionals, such as PBE, often underestimate band gaps due to their lack of exact exchange, leading to discrepancies in electronic property predictions. PBE0, a hybrid functional incorporating a fraction of Hartree–Fock exchange, provides a significant improvement by correcting for delocalization errors, yielding more reliable band gap estimations. Its balance between accuracy and computational cost makes it particularly suitable for materials where electronic structure plays a key role in functionality. Additionally, the use of an all-electron basis set ensures higher precision in resolving both core and valence interactions, further refining the computed electronic properties. The selection of PBE0 in this study represents an optimal trade-off, offering enhanced predictive capability while maintaining feasibility for larger systems.
In terms of PBE0, the calculated lattice parameters of our structure are a = 14.02 Å (−1.97%); b = 5.73 Å (−0.67%); and c = 7.14 Å (−1.08%), with an angle β of 115.3° (0.43%), all of which are in good agreement with most of the experimental studies [28,49]. In this lanarkite structure, the [PbO5] clusters are formed with five Pb–O bond lengths, with values of approximately 2.29, 2.35, 2.57, 2.60, and 2.79 Å, while the [SO4] clusters have the same S–O bond lengths of 1.54 Å. The bond lengths estimated in this study agree with the experimental data reported for PSO (lanarkite-type) [30], highlighting the high computational accuracy used. Therefore, we believe that these distortions in the [PbO5] clusters are the origin of their physical properties.
This study also evaluated the spectroscopic properties of the optimized structure calculated at the PBE0 level through Raman spectroscopy and XRD, as they provide chemical and structural fingerprints for the monoclinic PSO structure. Figure 2a,b show the XRD patterns and the simulated Raman spectra of the PSO structure. Furthermore, the results are similar to those obtained experimentally and are more pronounced at lower angles [50]. Moreover, PSO has 24 active Raman modes, of which only 6 are the most relevant and intense, as shown in Figure 2b. These intense modes are located at 142.95 cm−1 (Ag, high lead rocking and small sulphur wagging), 344.85 cm−1 (Bg, lead rocking and sulphur scissoring), 357.11 cm−1 (Ag, lead and sulphur symmetrical stretching), 844.55 cm−1 (Ag, sulphur symmetrical stretching), 957.91 cm−1 (Bg, sulphur asymmetrical stretching), and 974.43 cm−1 (Ag, sulphur asymmetrical stretching and wagging). A video animation of the vibrational Raman-active mode movements is provided in the Supplementary Material.
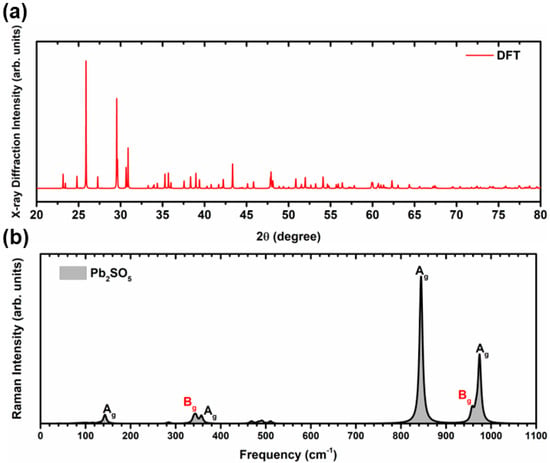
Figure 2.
The theoretical (a) X-ray diffraction curves and (b) vibrational Raman spectra of the PSO structure. The XRD pattern of the optimized structure was determined through the RIETAN-RF methodology [51] implemented in VESTA software [52].
The observed lower-frequency vibrational modes can be attributed to a combination of the vibrations of the [PbO5] and [SO4] clusters, with a dominant vibration from [PbO5], whereas at higher frequencies, we observed that [SO4] is the only cluster that vibrates.
3.2. Bond Analysis
Table 1 shows the topological parameters for four different bond critical points (BCPs) found in the [PbO5] cluster and two in the [SO4] cluster, obtained from the QTAIM analysis performed using the PBE0 functional.

Table 1.
Topological properties of PSO measured at BCPs: bond distance (Å), electron density (ρ(r)), Laplacian of electron density (∇2ρ(r)), |V|/G ratio, bond degree (H/ρ(r)), ellipticity (ε), and bond type. Labels “cov”, “T”, and “ionic” denote covalent, transitory, and ionic bond (interactions) types, respectively.
The [PbO5] cluster BCPs are arranged in a crescent order of bond length, which shows that the smaller bond distances have a greater concentration of electron density at the BCP and exhibit a transitory incipient covalent bond character owing to the negative covalent degree. The |V|/G ratio and ellipticity values serve as quantitative indicators of bond nature, distinguishing covalent, ionic, and transient interactions within Pb2SO5, where values for |V|/G < 1, 1 < |V|/G < 2, and |V|/G > 2 indicate a closed shell, transitory region, and shared shell, respectively. As the bond distance increases, the ratio |V|/G approaches unity, and the incipient covalent starts to change to a more directional form. Consequently, a transitory ionic behaviour is induced, which is, of course, confirmed by the small concentration of electron density at this point, and the bond degree (H/ρ(r)) is close to 0. At greater bond distances, the bonding changes to completely ionic, where the electron density is almost completely at the atoms and not at the BCP; however, the ellipticity suggests a small covalent behaviour (no such spherical shape of the bond). For [SO4], the bonds have a high concentration of charge density, a high |V|/G ratio, and a negative bond degree, indicating an incipient covalent bond with a spherical bond shape. To generate a three-dimensional visualization of the QTAIMAC descriptors, TopIso3D Viewer was used in this study [53]. The results of this can be seen in the HTML file in the Supplementary Material.
Additionally, Mulliken analysis showed that in the [PbO5] cluster, the Pb–O bonds had an overlap population of 64, 40, and 34 m|e|, whereas in the [SO4] clusters, the S–O bonds had a bond overlap of about 528 m|e|. This result suggests that the sharing of electrons is greater in the [SO4] cluster than in [PbO5], as expected.
3.3. Electronic Properties
Figure 3a displays the band structure and DOS of the monoclinic PSO structure obtained through the high-symmetry path (Γ—C|C2—Y2—Γ—M2—D|D2—A—Γ|L2—Γ—V2) along the Brillouin zone. As is well known, the band gap is indeed a crucial property in the design and engineering of new semiconductor materials [1,2,3,4]. For the PSO (lanarkite-type) system, this information is only available on the Materials Project website. Based on these theoretical results found on the Materials Project website, PSO has an indirect band gap of approximately 3.13 eV [15]. However, we know that the accuracy of this parameter is very sensitive to the density functional and the basis set used [54,55,56]. Figure 1d compares the estimated band gap values for the PSO structure from the seven density functionals used in this study. A higher band gap value obtained with a specific density functional indicates that it provides a better description of the electronic structure and properties of the material. This parameter is therefore best described by PBE0 followed by the PBESOL0 and B3LYP functionals. To this end, it is important to understand that theoretical predictions are crucial for Pb2SO5 due to the lack of experimental band gap data. The Materials Project reports a 3.13 eV band gap using GGA-PBE, which is known to underestimate electronic gaps due to delocalization errors. In contrast, our PBE0 calculation yields 4.83 eV, offering improved accuracy through exact exchange contributions. This value aligns well with trends in similar lead-based oxysulphides, reinforcing its reliability. While GW or HSE06 could provide further refinements, PBE0 offers a practical balance between precision and computational efficiency, making it a robust choice for describing the electronic structure of Pb2SO5.
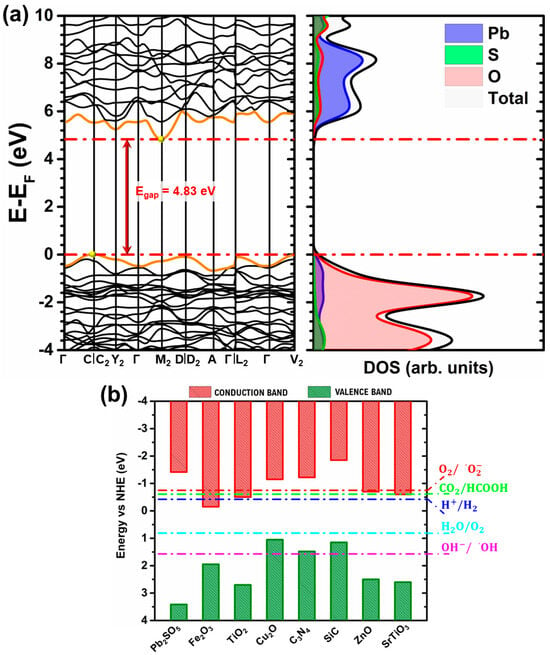
Figure 3.
(a) Band structure of PSO in high-symmetry path in Brillouin zone and its density of states (DOS) and (b) band edge positions for PSO (our work) and for other materials [57,58].
The analysis of PBE0 calculations shows that the band are well defined, and it has an indirect band gap energy of 4.83 eV, where the valence band (VB) maximum is located at the C point, while the conduction band (CB) minimum is at M2 (Figure 3a). The projected DOS (Figure 3a) shows that the O states have a major influence on the band gap in relation to the 2px, 2py, and 2pz orbitals and a minor influence on the Pb 6s, 6py, and 6pz states in the VB, with no presence of S states around the band gap. In the CB, one major influence is from the Pb 6px, 2py, and 2pz orbitals and a minor influence is from the O 2pz, S 2s, and 2px orbitals. Interestingly, S atoms have a greater influence at lower and higher energy values, far from the forbidden zone. For clarity, Figure S1 (see Supplementary Material) shows the DOS as a function of the elemental orbital.
The band edge positions (Figure 3b) were also elaborated to analyze the potential uses of PSO, along with other materials [57,58], in the photocatalytic water separation process using solar energy to produce oxygen (O2) and hydrogen (H2) and to photodegrade pollutants via reduced oxygen species (ROS). For a semiconductor photocatalyst to work well, it needs to have the right energy levels of its CB and VB so that they can match the energy needed to split water into hydrogen and oxygen. This property can be evaluated through the redox potentials and , which was highlighted to evaluate the possibility of ROS generation. As can be seen in Figure 3b, PSO, which is a p-type semiconductor, has a good band edge positioning for the reduction processes of CO2, , and , as well as the oxidation process of and , as indicated by the dashed dotted lines.
To better understand the mobility of electrons in the bands, the effective masses of electrons () and holes () were determined, and they are inversely proportional to the second derivative of the band energy with respect to the k-point, which implies that the greater the effective mass, the more difficult it is to drive electrons through the bands [59,60]. Hence, the effective mass tensor definition is given by the following:
where En(k) is the n-th band energy, and kμ and kν are the k-points in the Brillouin zone in the μ and ν directions, respectively [59,60]. This indicates that the hole effective mass is greater than the electron effective mass because the lowest-energy CB has a parabolic shape, as indicated by the yellow point in Figure 3a. For the effective mass analysis, a symmetrical path in the Brillouin zone of Γ-C-Γ (VB) and Γ-M2-Γ (CB) was used. PBE0 calculations showed that PSO has an effective mass of electrons (/) and holes (/ and mass ratios (/) of about 5.408, 1.041, and 0.192. As the / ratio is small, we have a lower recombination ratio of electron–hole pairs, which can, in principle, be interesting for p-type conductivity [61]. In photocatalysis, this enhances the availability of reactive species for surface reactions, boosting efficiency. In solar cells, a low mh/me ratio improves carrier transport, enabling higher charge extraction and better power conversion. In sensor applications, it increases sensitivity and accelerates response time.
3.4. Mechanical Properties and Dynamical Stability
The elastic properties of the PSO system were also calculated. As PSO belongs to the C2/m monoclinic symmetry space group, thirteen independent elastic constants were obtained by applying small displacements to the equilibrium structure, as implemented in CRYSTAL17 software. So, the calculated elastic constants are summarized in Table 2.

Table 2.
Elastic constants of monoclinic (C2/m) Pb2SO5 structure, in GPa.
To verify mechanical stability, it is important to verify whether the Born–Huang criteria for stability are satisfied. Hence, for a monoclinic structure, the Born stability criteria are given by the following eight equations [62]:
Our results indicate that the PSO elastic constants fully satisfy the Born stability criteria, confirming its mechanical stability, where the calculated values of each equation were ~, , , , , , and , from Equations (2) to (8). Beyond these, we also calculated phonon dispersion to confirm dynamical stability. To this end, the tight-binding density functional theory (DFTB) was employed, using DFTB+ software [63], along with the extended tight-binding method (xTB/GFN1) [64,65] combined with the Phonopy package [66,67]. This approach was the right choice due to the size of the supercell (3 × 3 × 3), which implies a supercell with 432 atoms, and it was used in our previous works successfully [68,69]. Moreover, the loss of symmetry in the displacement phonon supercell imposed feasibility restrictions and significantly increased computational costs, making this approach the most practical option. Our calculations show the absence of imaginary frequencies, as can be seen in the phonon band structure (Figure 4), also confirming that our structures are not metastable.
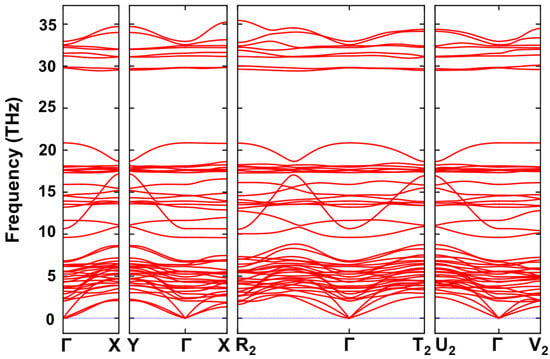
Figure 4.
Phonon band structure of PSO in high-symmetry path in Brillouin zone.
4. Conclusions
In summary, we provided very rich computational information to better understand the physical and chemical properties of the monoclinic PSO structure. For bulk calculations, different DFT functionals (e.g., PBE, PBE0, PBESOL, PBESOL0, BLYP, WC1LYP, and B3LYP) were applied to accurately predict their structural, electronic, and spectroscopic properties. All the density functionals employed in this study were proven to be suitable for accurately reproducing the experimental lattice parameters of PSO. Notably, PBE0 exhibited the closest agreement with the experimental band gap values. Our DFT calculations show that PSO is a p-type semiconductor with an indirect band gap of about 4.83 eV and an effective mass ratio (/) of about 0.192 (using PBE0 calculations). These theoretical findings open new opportunities in research with lanarkite-type materials and hence are of great importance for describing their exotic functional properties, allowing for an in-depth understanding of the nature of their chemical bonds as well. As the first in-depth investigation using DFT, this study establishes a fundamental benchmark, paving the way for future explorations and advanced computational assessments in this field.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/physchem5020022/s1, Figure S1: Partial Density of States of lanarkite PSO; Table S1: Influence of the functional in the lattice parameters (a, b and c in Å; and β in degrees) and band gap energy (Egap, in eV). The Δ indicates the percentual difference from the experimental to the calculated data; Video S1: Lanarkite PSO vibrational modes.
Author Contributions
Conceptualization, J.R.S. and F.A.L.P.; Methodology, G.S.L.F., J.R.S. and F.A.L.P.; Software, M.M.F. and J.R.S.; Validation, M.M.F., C.A.P., J.R.S. and F.A.L.P.; Formal analysis, G.S.L.F., M.M.F., J.R.S. and F.A.L.P.; Investigation, G.S.L.F., C.R.R.A., C.A.P., J.R.S. and F.A.L.P.; Resources, J.R.S.; Data curation, G.S.L.F., C.R.R.A., C.A.P. and F.A.L.P.; Writing—original draft, G.S.L.F., M.M.F., C.R.R.A., C.A.P., J.R.S. and F.A.L.P.; Writing—review & editing, G.S.L.F., M.M.F., J.R.S. and F.A.L.P.; Visualization, C.R.R.A. and C.A.P.; Supervision, J.R.S. and F.A.L.P.; Project administration, J.R.S. and F.A.L.P.; Funding acquisition, J.R.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Council for Scientific and Technological Development—CNPq (grant numbers 150187/2023-8, 482473/2010-0, 446126/2014-4, 308548/2014-0, 307236/2018-8, and 302887/2022-9), Fundação de Amparo à Pesquisa do Estado do Rio Grande do Sul—FAPERGS (grant number 23/2551-0000153-5), and Fundação de Amparo à Pesquisa do Estado de São Paulo—FAPESP (grant numbers 2022/03959-6 and 2013/07296-2).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
G. S. L. Fabris is grateful for the postdoc scholarship financed by CNPq—and FAPERGS. C. A. Paskocimas acknowledges CNPq for financial support. J. R. Sambrano thanks FAPESP for financial support. F. A. La Porta acknowledges financial support from Fundação Araucária. The computational facilities were supported by resources supplied by the Molecular Simulations Laboratory (São Paulo State University, Bauru, Brazil).
Conflicts of Interest
The authors declare no conflict of interest.
References
- La Porta, F.A.; Taft, C.A. Functional Properties of Advanced Engineering Materials and Biomolecules; Springer International Publishing: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- La Porta, F.A.; Taft, C.A. Emerging Research in Science and Engineering Based on Advanced Experimental and Computational Strategies; Springer International Publishing: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Longo, E.; La Porta, F.A. Recent Advances in Complex Functional Materials; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- de Jesus, J.P.A.; Santos, A.C.L.; Pinto, F.M.; Taft, C.A.; La Porta, F.A. Review: Theoretical and experimental investigation of the intrinsic properties of Zn2GeO4 nanocrystals. J. Mater. Sci. 2021, 56, 4552–4568. [Google Scholar] [CrossRef]
- de Conti, M.C.M.D.; Dey, S.; Pottker, W.E.; La Porta, F.A. An overview into advantages and applications of conventional and unconventional hydro(solvo)thermal approaches for novel advanced materials design. Mater. Today Sustain. 2023, 23, 100458. [Google Scholar] [CrossRef]
- de Pablo, J.J.; Jackson, N.E.; Webb, M.A.; Chen, L.Q.; Moore, J.E.; Morgan, D.; Jacobs, R.; Pollock, T.; Schlom, D.G.; Toberer, E.S.; et al. New frontiers for the materials genome initiative. npj Comput. Mater. 2019, 5, 41. [Google Scholar] [CrossRef]
- Zhou, T.; Song, Z.; Sundmacher, K. Big Data Creates New Opportunities for Materials Research: A Review on Methods and Applications of Machine Learning for Materials Design. Engineering 2019, 5, 1017–1026. [Google Scholar] [CrossRef]
- Nosengo, N. Can artificial intelligence create the next wonder material? Nature 2016, 533, 22–25. [Google Scholar] [CrossRef]
- Alberi, K.; Nardelli, M.B.; Zakutayev, A.; Mitas, L.; Curtarolo, S.; Jain, A.; Fornari, M.; Marzari, N.; Takeuchi, I.; Green, M.L.; et al. The 2019 materials by design roadmap. J. Phys. D Appl. Phys. 2019, 52, 013001. [Google Scholar] [CrossRef]
- Choudhary, K.; DeCost, B.; Chen, C.; Jain, A.; Tavazza, F.; Cohn, R.; Park, C.W.; Choudhary, A.; Agrawal, A.; Billinge, S.J.; et al. Recent advances and applications of deep learning methods in materials science. npj Comput. Mater. 2022, 8, 59. [Google Scholar] [CrossRef]
- Resasco, J.; Abild-Pedersen, F.; Hahn, C.; Bao, Z.; Koper, M.T.; Jaramillo, T.F. Enhancing the connection between computation and experiments in electrocatalysis. Nat. Catal. 2022, 5, 374–381. [Google Scholar] [CrossRef]
- Seh, Z.W.; Kibsgaard, J.; Dickens, C.F.; Chorkendorff, I.B.; Nørskov, J.K.; Jaramillo, T.F. Combining theory and experiment in electrocatalysis: Insights into materials design. Science 2017, 355, eaad4998. [Google Scholar] [CrossRef]
- Chen, X.; Hou, T.; Persson, K.A.; Zhang, Q. Combining theory and experiment in lithium–sulfur batteries: Current progress and future perspectives. Mater. Today 2019, 22, 142–158. [Google Scholar] [CrossRef]
- Yang, R.X.; McCandler, C.A.; Andriuc, O.; Siron, M.; Woods-Robinson, R.; Horton, M.K.; Persson, K.A. Big Data in a Nano World: A Review on Computational, Data-Driven Design of Nanomaterials Structures, Properties, and Synthesis. ACS Nano 2022, 16, 19873–19891. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.; Ong, S.P.; Hautier, G.; Chen, W.; Richards, W.D.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G.; et al. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 011002. [Google Scholar] [CrossRef]
- Jain, A.; Hautier, G.; Moore, C.J.; Ong, S.P.; Fischer, C.C.; Mueller, T.; Persson, K.A.; Ceder, G. A high-throughput infrastructure for density functional theory calculations. Comput. Mater. Sci. 2011, 50, 2295–2310. [Google Scholar] [CrossRef]
- Walsh, A.; Zunger, A. Instilling defect tolerance in new compounds. Nat. Mater. 2017, 16, 964–967. [Google Scholar] [CrossRef]
- Laranjeira, J.A.S.; Martins, N.F.; Azevedo, S.A.; Fabris, G.S.L.; Sambrano, J.R. Novel octa-graphene-like structures based on GaP and GaAs. J. Mol. Model. 2023, 29, 202. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, V.Y.; Amorin, L.H.; Fabris, G.S.; Dey, S.; Sambrano, J.R.; Cohen, H.; Oron, D.; La Porta, F.A. Enhanced Photocatalytic and Photoluminescence Properties Resulting from Type-I Band Alignment in the Zn2GeO4/g-C3N4 Nanocomposites. Catalysts 2022, 12, 692. [Google Scholar] [CrossRef]
- Zhu, H.; Hautier, G.; Aydemir, U.; Gibbs, Z.M.; Li, G.; Bajaj, S.; Pöhls, J.H.; Broberg, D.; Chen, W.; Jain, A.; et al. Computational and experimental investigation of TmAgTe 2 and XYZ 2 compounds, a new group of thermoelectric materials identified by first-principles high-throughput screening. J. Mater. Chem. C 2015, 3, 10554–10565. [Google Scholar] [CrossRef]
- Lee, S.; Kim, J.; Im, S.; An, S.; Kwon, Y.W.; Auh, K.H. Consideration for the development of room-temperature ambient-pressure superconductor (LK-99). J. Korean Cryst. Growth Cryst. Technol. 2023, 33, 61–70. [Google Scholar]
- Lee, S.; Kim, J.; Kim, H.T.; Im, S.; An, S.; Auh, K.H. Superconductor Pb10−xCux(PO4)6O showing levitation at room temperature and atmospheric pressure and mechanism. arXiv 2023, arXiv:2307.12037. [Google Scholar]
- Griffin, S.M. Origin of correlated isolated flat bands in copper-substituted lead phosphate apatite. arXiv 2023, arXiv:2307.16892. [Google Scholar]
- Kumar, K.; Karn, N.K.; Kumar, Y.; Awana, V.P.S. Absence of superconductivity in LK-99 at ambient conditions. ACS Omega 2023, 8, 41737–41743. [Google Scholar] [CrossRef] [PubMed]
- Kumar, K.; Karn, N.K.; Awana, V.P.S. Synthesis of possible room temperature superconductor LK-99: Pb9Cu(PO4)6O. Supercond. Sci. Technol. 2023, 36, 10LT02. [Google Scholar] [CrossRef]
- Liu, L.; Meng, Z.; Wang, X.; Chen, H.; Duan, Z.; Zhou, X.; Yan, H.; Qin, P.; Liu, Z. Semiconducting Transport in Pb10−XCux(PO4)6O Sintered from Pb2SO5 and Cu3P. Adv. Funct. Mater. 2023, 33, 2308938. [Google Scholar] [CrossRef]
- Lai, J.; Li, J.; Liu, P.; Sun, Y.; Chen, X.-Q. First-principles study on the electronic structure of Pb10−xCux(PO4)6O (x = 0, 1). J. Mater. Sci. Technol. 2024, 171, 66–70. [Google Scholar] [CrossRef]
- Richmond, W.E.; Wolfe, C.W. Crystallography of lanarkite. Am. Mineral. J. Earth Planet. Mater. 1938, 23, 799–804. [Google Scholar]
- Mentzen, B.F.; Latrach, A. Crystal data for dilead(II) pentaoxosulfate(VI), Pb2SO5. J. Appl. Crystallogr. 1983, 16, 430. [Google Scholar] [CrossRef]
- Mentzen, B.F.; Latrach, A.; Bouix, J.; Hewat, A.W. The crystal structures of PbO.PbXO4 (X = S, Cr, Mo) at 5K by neutron powder profile refinement. Mater. Res. Bull. 1984, 19, 549–554. [Google Scholar] [CrossRef]
- Abdul-Samad, F.A.; Thomas, J.H.; Williams, P.A.; Symes, R.F. Chemistry of formation of lanarkite, Pb2OSO4. Mineral Mag. 1982, 46, 499–501. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Demichelis, R.; Civalleri, B.; Ferrabone, M.; Dovesi, R. On the performance of eleven DFT functionals in the description of the vibrational properties of aluminosilicates. Int. J. Quantum Chem. 2010, 110, 406–415. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Dovesi, R.; Erba, A.; Orlando, R.; Zicovich-Wilson, C.M.; Civalleri, B.; Maschio, L.; Rérat, M.; Casassa, S.; Baima, J.; Salustro, S.; et al. Quantum-mechanical condensed matter simulations with CRYSTAL. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018, 8, e1360. [Google Scholar] [CrossRef]
- Gomes, E.O.; Fabris, G.S.; Ferrer, M.M.; Motta, F.V.; Bomio, M.R.; Andres, J.; Longo, E.; Sambrano, J.R. Computational procedure to an accurate DFT simulation to solid state systems. Comput. Mater. Sci. 2019, 170, 109176. [Google Scholar] [CrossRef]
- Fabris, G.S.L.; Marana, N.L.; Longo, E.; Sambrano, J.R. Theoretical study of porous surfaces derived from graphene and boron nitride. J. Solid State Chem. 2018, 258, 247–255. [Google Scholar] [CrossRef]
- Vilela Oliveira, D.; Laun, J.; Peintinger, M.F.; Bredow, T. BSSE-correction scheme for consistent gaussian basis sets of double- and triple-zeta valence with polarization quality for solid-state calculations. J. Comput. Chem. 2019, 40, 2364–2376. [Google Scholar] [CrossRef]
- Lima, E.F.; Bredow, T. Extended benchmark set for lattice parameters of inorganic solids. J. Comput. Chem. 2024, 45, 2702–2709. [Google Scholar] [CrossRef]
- Ferrero, M.; Rérat, M.; Kirtman, B.; Dovesi, R. Calculation of first and second static hyperpolarizabilities of one- to three-dimensional periodic compounds. Implementation in the CRYSTAL code. J. Chem. Phys. 2008, 129, 244110. [Google Scholar] [CrossRef] [PubMed]
- Ferrero, M.; Rérat, M.; Orlando, R.; Dovesi, R. The calculation of static polarizabilities of 1-3D periodic compounds. the implementation in the crystal code. J. Comput. Chem. 2008, 29, 1450–1459. [Google Scholar] [CrossRef] [PubMed]
- Ferrero, M.; Rérat, M.; Orlando, R.; Dovesi, R. Coupled perturbed Hartree-Fock for periodic systems: The role of symmetry and related computational aspects. J. Chem. Phys. 2008, 128, 014110. [Google Scholar] [CrossRef]
- Casassa, S.; Erba, A.; Baima, J.; Orlando, R. Electron density analysis of large (molecular and periodic) systems: A parallel implementation. J. Comput. Chem. 2015, 36, 1940–1946. [Google Scholar] [CrossRef]
- Gatti, C.; Casassa, S. TOPOND User’s Manual; CNR-CSRSRC: Milano, Italy, 2013. [Google Scholar]
- Binnie, W.P. The crystal structure of lanarkite, PbO.PbSO4. Acta Crystallogr. 1951, 4, 471–472. [Google Scholar] [CrossRef]
- Singh, H.; Gautam, A.; Singh, M.; Saha, P.; Kumar, P.; Das, P.; Lamba, M.; Yadav, K.; Mishra, P.K.; Patnaik, S.; et al. On the experimental evidence for possible superconductivity in LK99. arXiv 2023, arXiv:2308.06589. [Google Scholar]
- Izumi, F.; Momma, K. Three-Dimensional Visualization in Powder Diffraction. Solid State Phenom. 2007, 130, 15–20. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA: A three-dimensional visualization system for electronic and structural analysis. J. Appl. Crystallogr. 2008, 41, 653–658. [Google Scholar] [CrossRef]
- Silva, J.F.; Fabris, G.S.L.; Sambrano, J.R.; Albuquerque, A.R.; Maia, A.S. TopIso3D Viewer: Enhancing Topological Analysis through 3D Isosurfaces. J. Chem. Inf. Model. 2023, 63, 1999–2013. [Google Scholar] [CrossRef]
- Xiao, H.; Tahir-Kheli, J.; Goddard, W.A. Accurate Band Gaps for Semiconductors from Density Functional Theory. J. Phys. Chem. Lett. 2011, 2, 212–217. [Google Scholar] [CrossRef]
- Arı, H.; Büyükmumcu, Z. Comparison of DFT functionals for prediction of band gap of conjugated polymers and effect of HF exchange term percentage and basis set on the performance. Comput. Mater. Sci. 2017, 138, 70–76. [Google Scholar] [CrossRef]
- Ody, K.S.; Jesus, J.P.D.; Cava, C.E.; Albuquerque, A.R.; Maia, A.S.; Sambrano, J.R.; Porta, F.A.L. Avaliação da Estrutura Eletrônica da Fase Monoclinica do Óxido de Nióbio Com Base No Uso de Diferentes Funcionais de Densidade. Química Nova 2021, 44, 1124–1131. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, X.; Xu, Z.; Loo, J.S.C. Hybrid catalysts for photoelectrochemical reduction of carbon dioxide: A prospective review on semiconductor/metal complex co-catalyst systems. J. Mater. Chem. A 2014, 2, 15228. [Google Scholar] [CrossRef]
- Underwood, T.M.; Robinson, R.S. Adducing Knowledge Capabilities of Instrumental Techniques Through the Exploration of Heterostructures’ Modification Methods. ChemPhysChem 2022, 23, e202200241. [Google Scholar] [CrossRef]
- Sze, S.M.; Ng, K.K. Physics of Semiconductor Devices; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar] [CrossRef]
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics; Cengage Learning: Boston, MA, USA, 1976. [Google Scholar]
- Yim, K.; Youn, Y.; Lee, M.; Yoo, D.; Lee, J.; Cho, S.H.; Han, S. Computational discovery of p-type transparent oxide semiconductors using hydrogen descriptor. NPJ Comput. Mater. 2018, 4, 17. [Google Scholar] [CrossRef]
- Wu, Z.J.; Zhao, E.J.; Xiang, H.P.; Hao, X.F.; Liu, X.J.; Meng, J. Crystal structures and elastic properties of superhard IrN2 and IrN3 from first principles. Phys. Rev. B 2007, 76, 054115. [Google Scholar] [CrossRef]
- Hourahine, B.; Aradi, B.; Blum, V.; Bonafe, F.; Buccheri, A.; Camacho, C.; Cevallos, C.; Deshaye, M.Y.; Dumitrică, T.; Dominguez, A.; et al. DFTB+, a software package for efficient approximate density functional theory based atomistic simulations. J. Chem. Phys. 2020, 152, 124101. [Google Scholar] [CrossRef]
- Grimme, S.; Bannwarth, C.; Shushkov, P. A Robust and Accurate Tight-Binding Quantum Chemical Method for Structures, Vibrational Frequencies, and Noncovalent Interactions of Large Molecular Systems Parametrized for All spd-Block Elements (Z = 1–86). J. Chem. Theory Comput. 2017, 13, 1989–2009. [Google Scholar] [CrossRef]
- Bannwarth, C.; Caldeweyher, E.; Ehlert, S.; Hansen, A.; Pracht, P.; Seibert, J.; Spicher, S.; Grimme, S. Extended tight-binding quantum chemistry methods. WIREs Comput. Mol. Sci. 2021, 11, e1493. [Google Scholar] [CrossRef]
- Togo, A. First-principles Phonon Calculations with Phonopy and Phono3py. J. Phys. Soc. Jpn. 2023, 92, 012001. [Google Scholar] [CrossRef]
- Togo, A.; Chaput, L.; Tadano, T.; Tanaka, I. Implementation strategies in phonopy and phono3py. J. Phys. Condens. Matter 2023, 35, 353001. [Google Scholar] [CrossRef] [PubMed]
- Martins, N.F.; Laranjeira, J.A.; de Azevedo, S.A.; Fabris, G.S.L.; Sambrano, J.R. Tuning the electronic properties of the SiC graphenylene by transition metal (Fe, Mn and Co) doping. Phys. B Condens. Matter 2024, 691, 416369. [Google Scholar] [CrossRef]
- Martins, N.F.; Laranjeira, J.A.S.; Azevedo, S.A.; Fabris, G.S.L.; Sambrano, J.R. Structural, electronic and mechanical properties of a novel graphenylene-like structure based on GeC. J. Phys. Chem. Solids 2023, 181, 111518. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).