Urban Hybrid Electric Vehicle with Kinetic Energy Storage System and Friction Transmission ^†

Abstract

The subject of this study is the dynamic analysis of the energy flow in the transient mode of the movement of the vehicle with a kinetic accumulator, implemented with a purely mechanical transmission. The elements of which include—a flywheel, planetary gears with two degrees of freedom, some ordinary gears, a friction mechanism with a variable transmission ratio (CVT), and a certain number of brake clutches, etc. A control algorithm is proposed; the differential equations of motion are derived and solved. The effectiveness and applicability of such a purely mechanical transmission for accumulating and realizing energy during braking and accelerating of the electro-mobile are proven, in which it is possible to extend the range by up to 12–14%.

1. Introduction

In the 1950s, Oerlicon (Switzerland) produced an experimental trolleybus with a propulsion system containing a kinetic energy storage system–flywheel. It was a reversible electric machine and a motor/generator was built into its core. The flywheel was monolithic, with mass of 3 × 10³ [kg], a diameter of about 1.5 [m], and a maximum permissible rotation speed of 300 [s⁻¹] [1]. This trolleybus, later called the Gyrobus, could in a charged state travel a distance of about 2 [km] until the next charging with energy.

In essence, from that moment on a very active scientific research activity began all over the world in the field of kinetic technologies in various areas of the industry.

Prof. D. W. Rabenhorst from John Hopkins University—USA, can be noted as one of the pioneers in this direction [1].

At beginning of the century, stationary kinetic storage systems with a maximum power in the range of 10 to 500 [kw] were put in regular production and offered on the market [2]:

• As a variety of substations along the largest railway high-lines in the USA and EU, with a power of up to 500 [kw] [3];
• As Uninterruptible Power Systems (UPSs) [4];
• As lifting facilities (hydraulic elevators, container handling equipment at large ports) [5];
• Stationary storage devices with general purpose [6];
• As well as in transport equipment with the ability to recover energy during vehicle braking and other scenarios.

Kinetic energy systems are used in wind farms and recently they have replaced high-power, pumped-energy accumulating plants in the USA and China [7,8]. It is quite possible that these technologies will find their place in military affairs and in space under the natural conditions of vacuum and weightlessness.

A kinetic storage system is added in the propulsion systems of Formula One cars [9,10,11] to the main source of energy in an internal combustion engine (ICE),—a super flywheel and a continuous variable transmission (CVT). When cornering on a track, when the speed is sharply reduced the braking energy is stored in the super flywheel, which is subsequently released when the car accelerates.

There are studies in the scientific literature on similar propulsive systems consisting of a main and additional source of energy [12], with the ability to recuperate energy during braking of the vehicle [13], and with a different topological structure [14]—parallel, in series, and some combinations.

A computer simulation in [15] proves that an electric vehicle with a kinetic storage system has about 11–14% increased mileage on one charge of its electric battery, with the research demonstrating it for five of the most common transport cycles in a large city.

The purpose of this study is to analyze the proposed structural scheme for driving a hybrid urban electric vehicle, characterized by:

• A minimum number of energy transformations from one type to another;
• The electric battery not participating in the energy recovery processes during vehicle stops.

The analysis of energy flows to and from the kinetic energy recovery system is oriented towards two of the standardized and widely used transport cycles—FTP-72 and NEUDC.

The use of energy realized during frequently repeated transient modes (start and stops) has practical meaning only at speeds greater than 3 [m/s] and mainly under big city traffic conditions.

There have been developments in hybrid electric vehicles with kinetic energy recovery systems (KERSs), in which the energy from the battery is inverted from DC to AC, enters a reversible motor/generator, and then the mechanical energy enters the driving wheels of the electric vehicle. The path of the energy flow from and to the KERS is similar [16,17,18,19].

In hydrostatic transmissions [20] the number of energy transformations is also very high, centering on the recovery of energy when stopping the vehicle.

2. Theoretical Considerations

2.1. Nomenclature

The following Table 1 introduces the nomenclature of the denotations of the parameters of the vehicle analyzed in this article.

Table 1. Nomenclature of used variables.

Variable	Dim.	Description
m	[kg]	mass of the electro-mobile
g	[m/s2]	earth acceleration
f	[m]	rolling friction coefficient
h	[kg/m3]	drag coefficient
S	[m2]	cross-sectional area
rw	[m]	wheel’s radius
V	[m/s]	car’s velocity
T	[s]	motor’s time constant
Θ	[-]	speed limiter
δ	[-]	inertial coefficient
ωm, ωv, ωf	[1/s]	angular velocities of the motor, wheel, and flywheel
K	[Nms]	coefficient of motor’s static characteristic
iD, ig1, ig2, iV	[-]	transmission ratio of differential D
g1, g2 and iV	[-]	transmission ratio of variator
M, Mc	[Nm]	moment of motor and resistance
Jm, Jf	[kgm2]	mass moment of inertia-motor and flywheel
η, ηV, ηf, ηg	[-]	efficiency coefficients for variator, flywheel, and gears

2.2. Numerical Data Used in the Simulations

m = 1200 [kg]; rw = 0.35 [m]; k = 6 [Nms]; ω₀ = 600 [1/s]; ω_N = 513 [1/s]; i₁ = 5 [-]; i₂ = 2.5 [-]; i_D = 1/−1 [-]; Jf = 3 [kgm²]; ηg = 0.8 [-]; η_V = 0.75 [-]; ηf = 0.7 [-]; δ = 1.06 [-]; h = 0.935 [kg³]; f = 0.013 [m]; T = 0.3 [s]; and numeric arrays of NEUDC and WLTC-3 cycles.

2.3. Structural and Block Diagrams

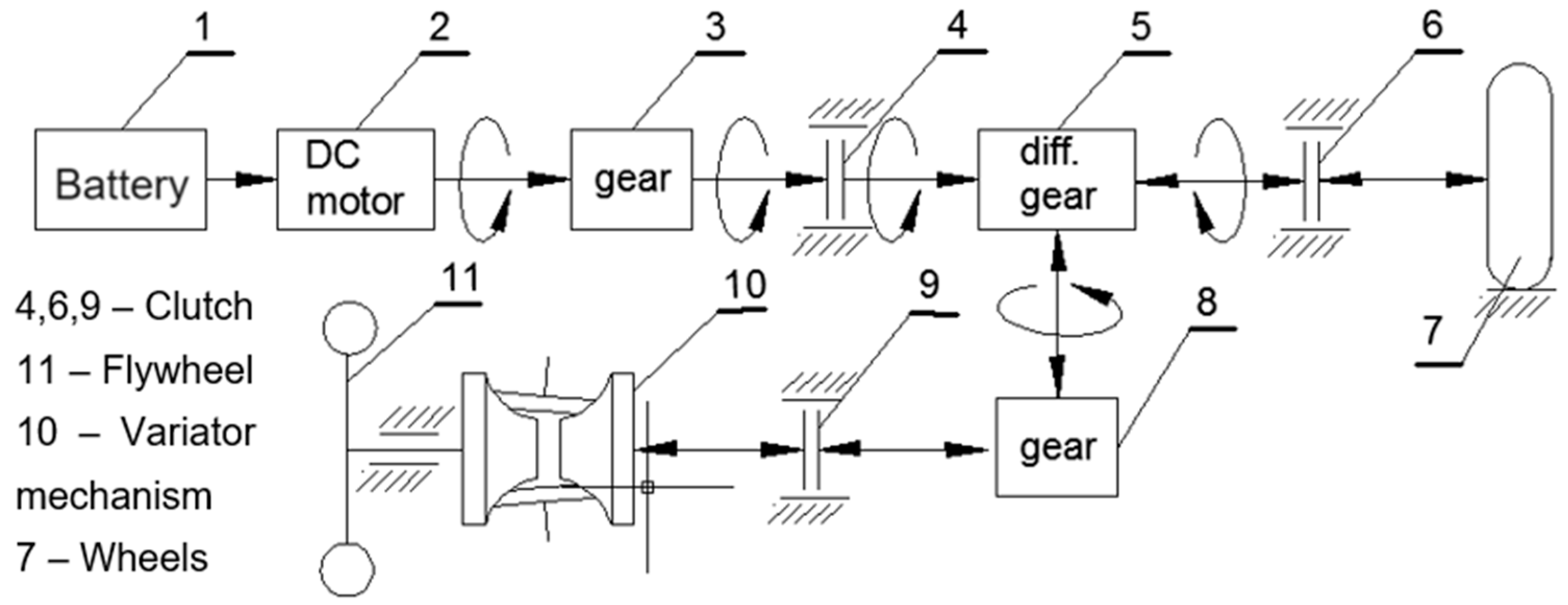
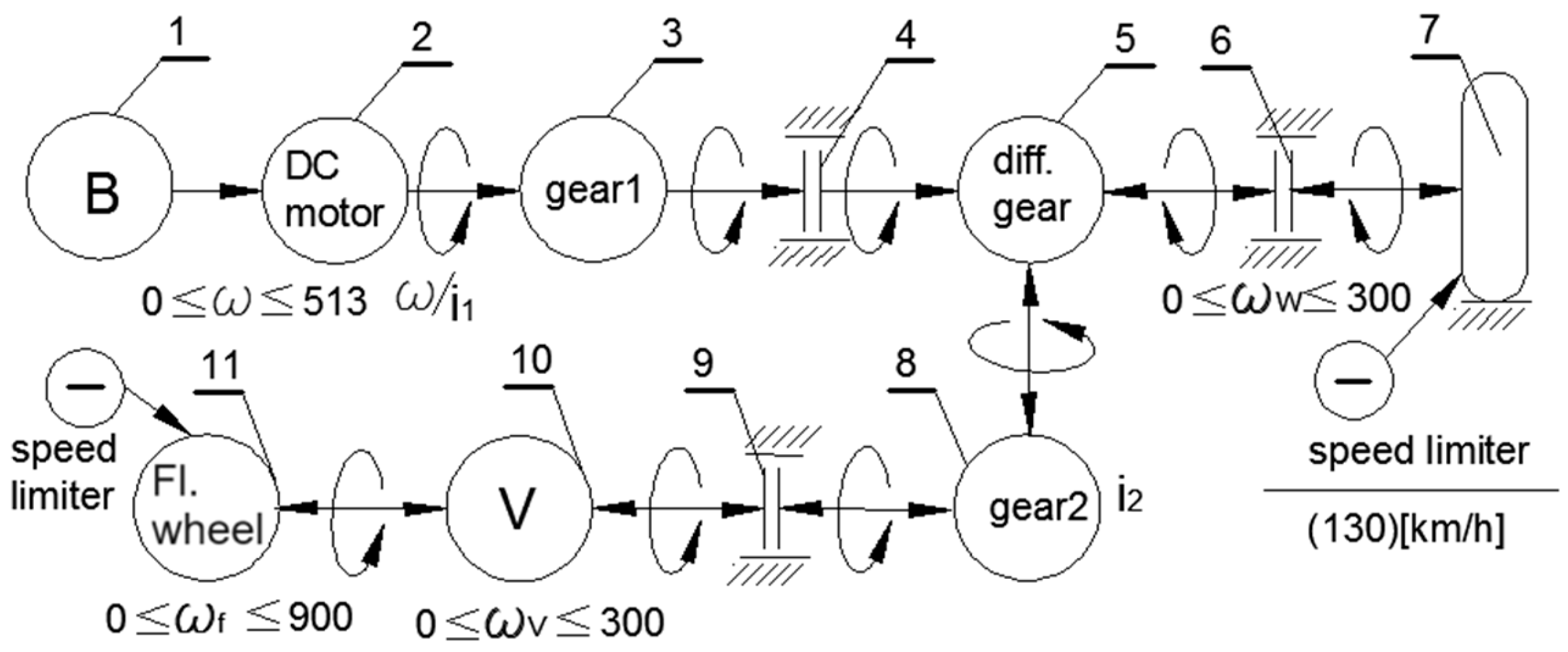
Figure 1 shows the structural diagram of the considered hybrid city electric vehicle with a kinetic energy storage system (KERS). The block diagram for controlling the different modes of motion of the transport vehicle in the conditions of a big city is presented in Figure 2.

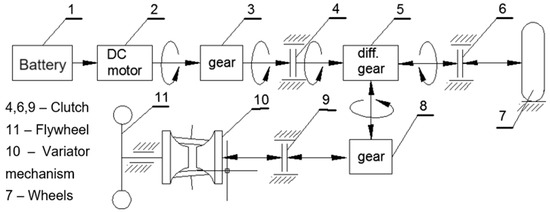
Figure 1. Structural diagram.

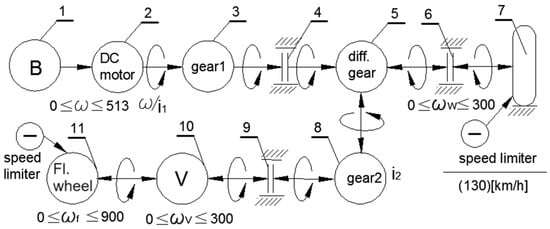
Figure 2. Block diagram.

3. Control Algorithms and Solutions

3.1. Initial Charging of KERS with Energy

The direction of the energy flow in accordance with Figure 2 is from the electric motor to the flywheel in the sequence 1-2-3-4-5-8-9-10-11, with clutches 4 and 9 and brake 6 engaged.

To the axis of the engine, the equation of motion has the following form:

$$\{J_m+J_f({\displaystyle \frac{{\omega }_f}{{\omega }_m}}{)}^2\}{\displaystyle \frac{d{\omega }_m}{dt}}=M_m-M_c , \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}{ M}_m=k({\omega }_0-{\omega }_m)$$

(1)

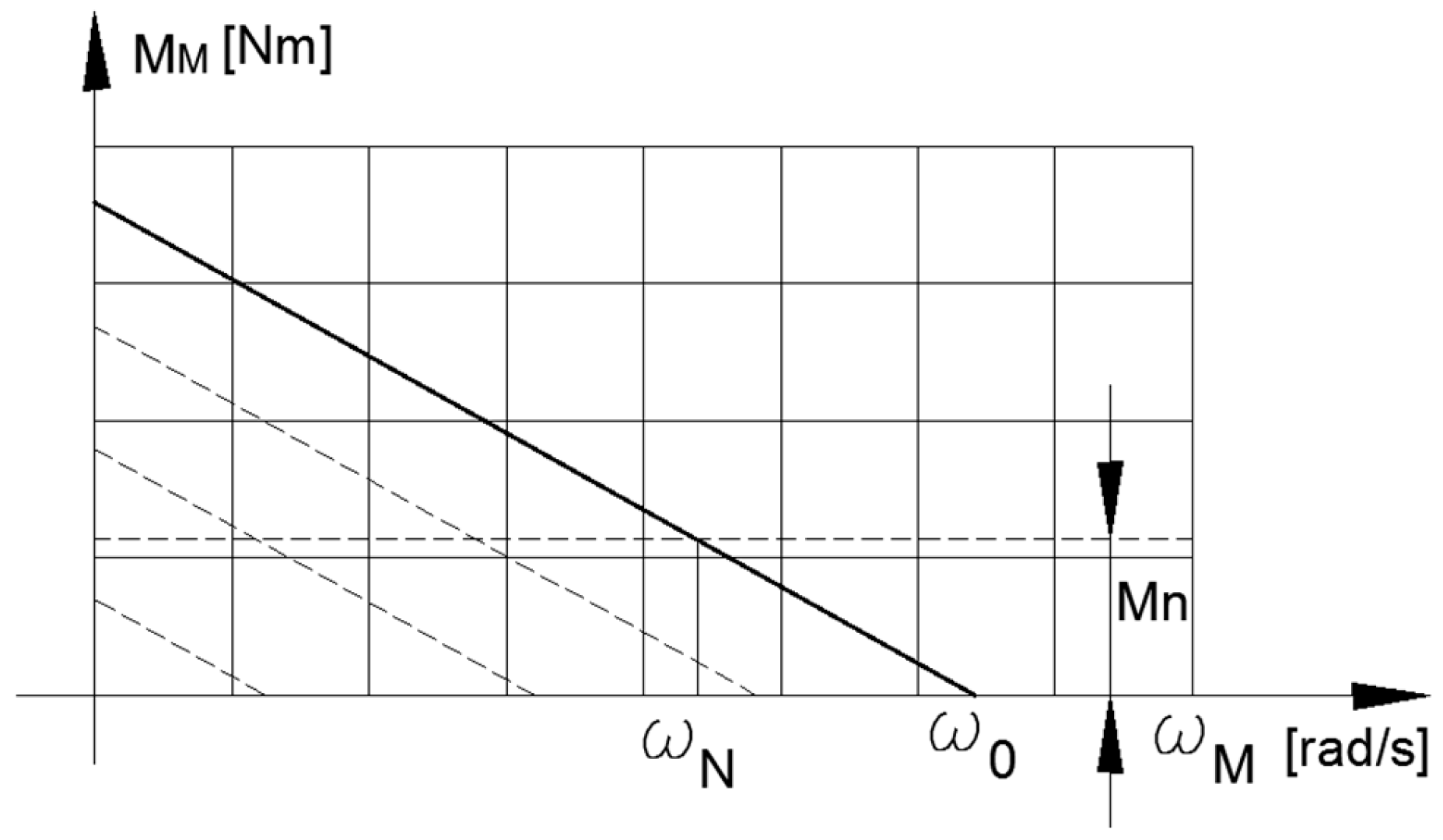
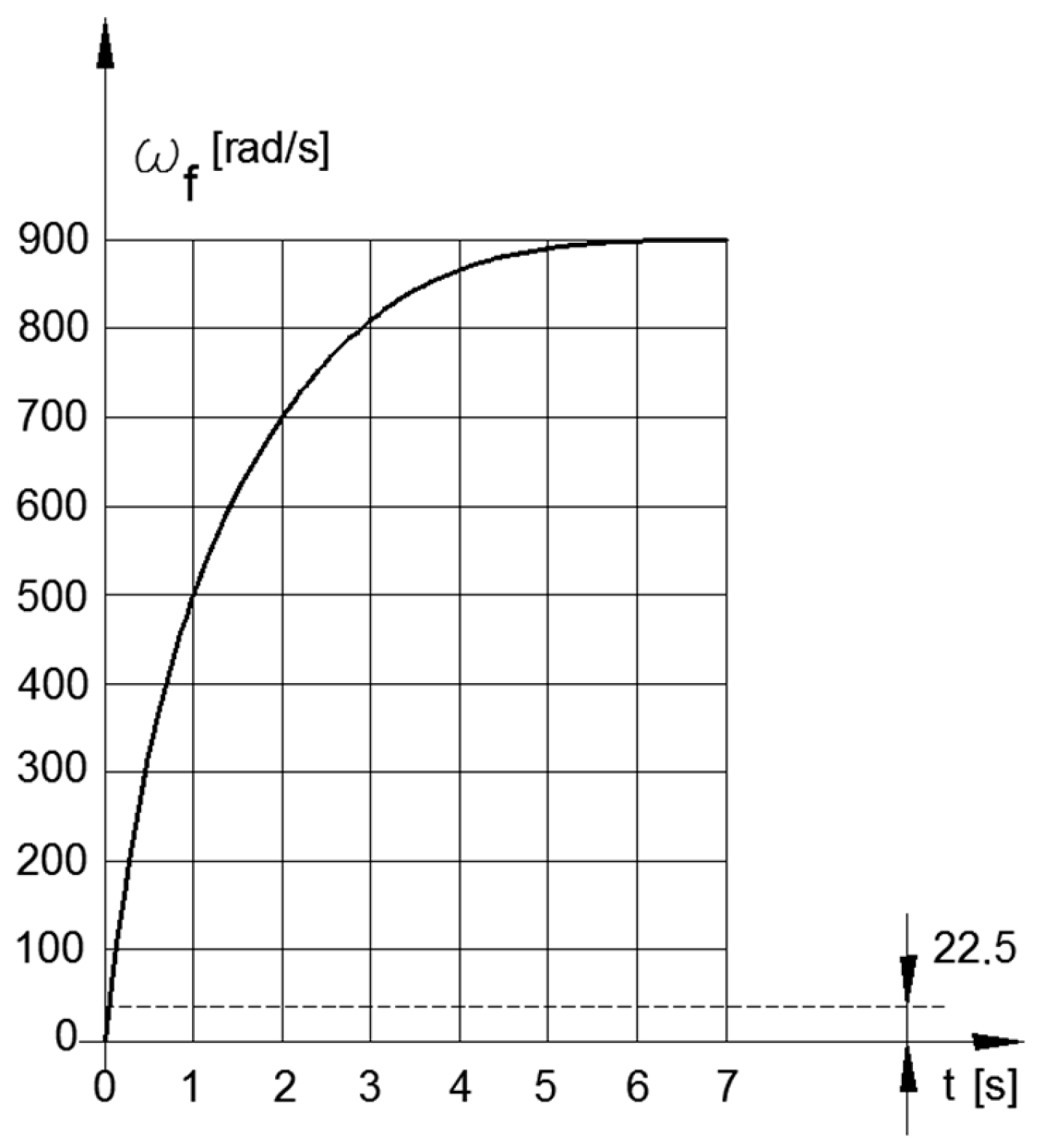
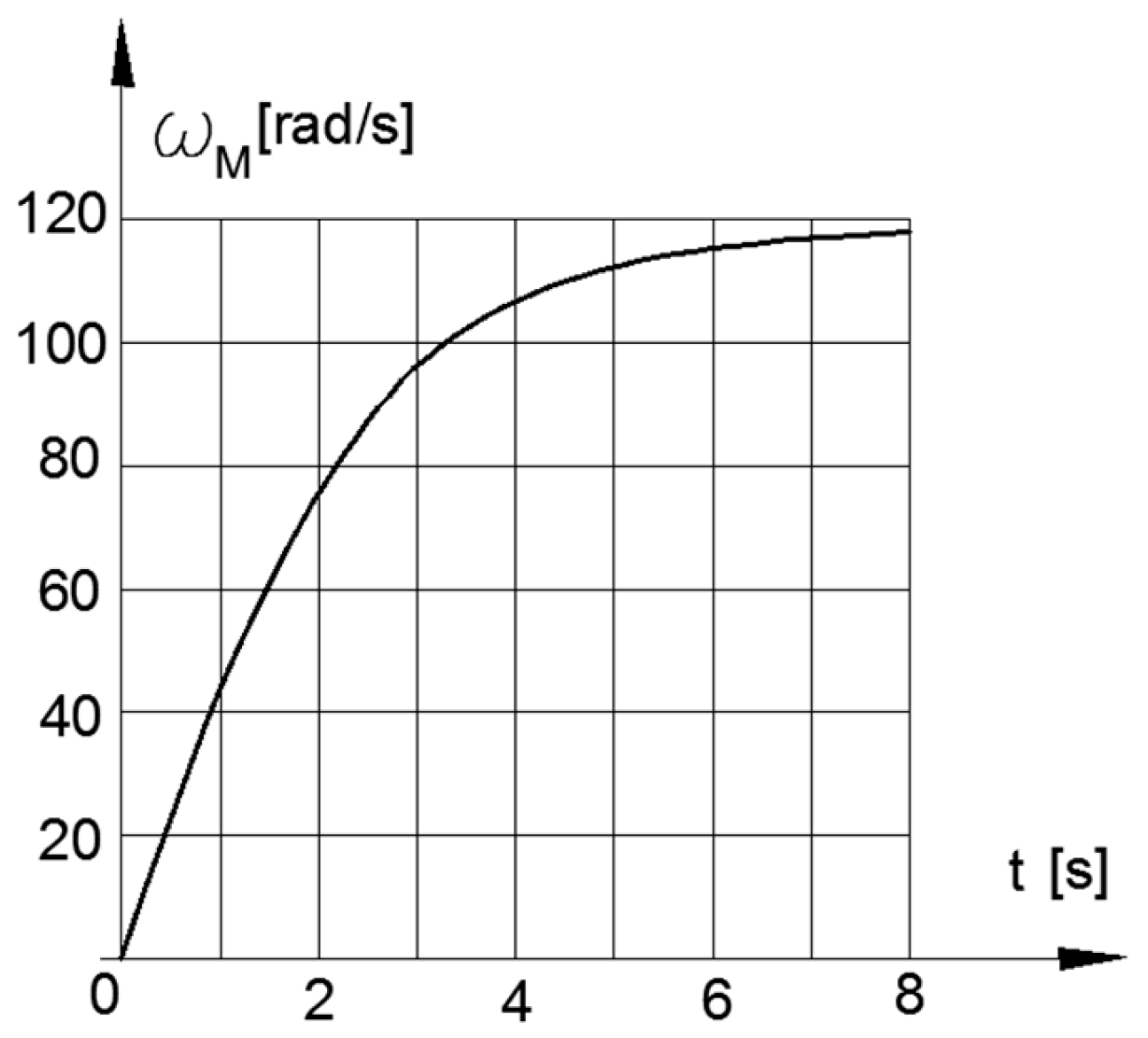
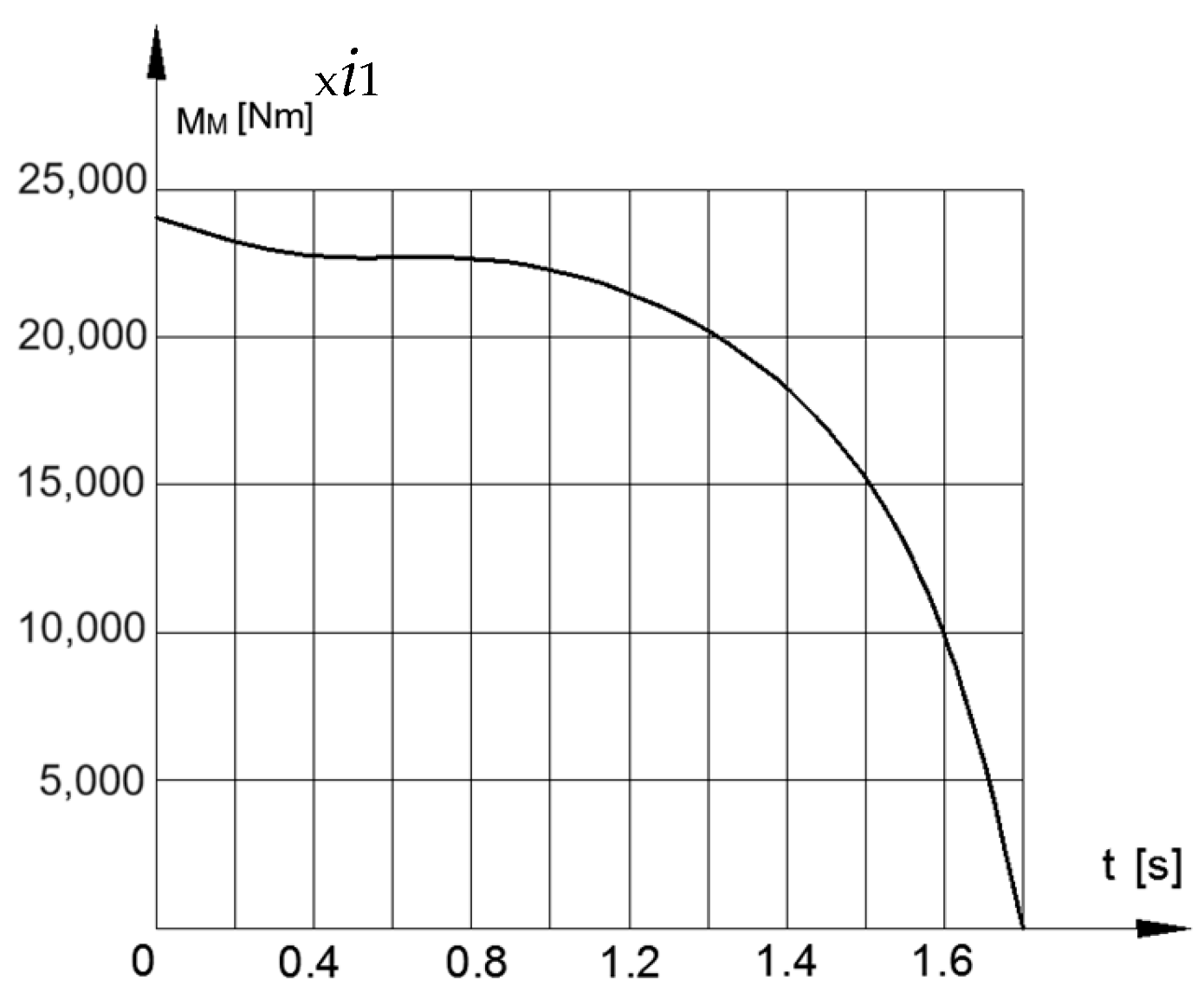
Figure 3 and Figure 4 present the graphs of the static characteristic of the engine and the angular velocity of the flywheel as a function of time.

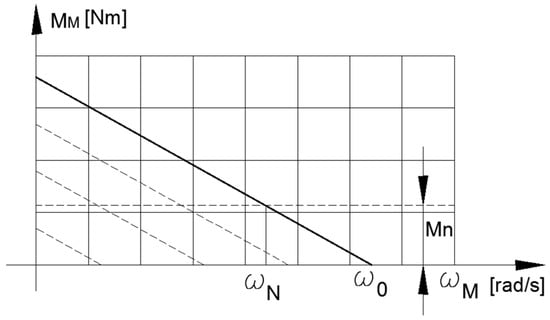
Figure 3. Motor’s static characteristic.

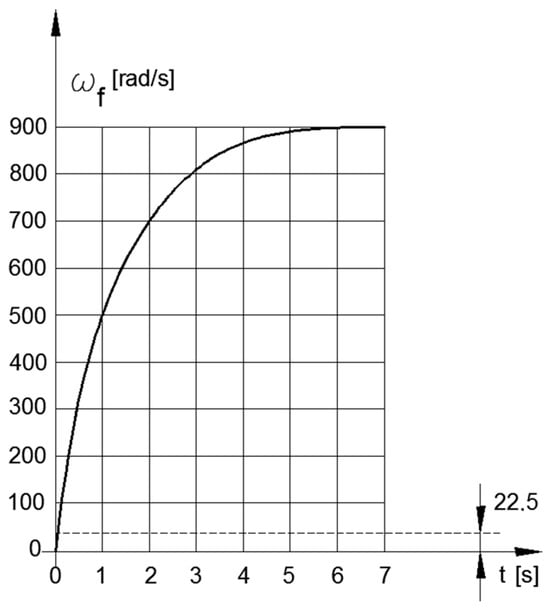
Figure 4. Flywheel’s angular velocity.

3.2. Motion of the Vehicle by Electric Motor

The flow of the energy direction is in the sequence 1-2-3-4-5-6-7 (Figure 2), with couplings 4 and 6 switched on and coupling 10 switched off. The differential equation of motion for the driving wheels takes the following form:

$$(J_m+{\displaystyle \frac{m\delta {r_w}^2}{i_1}}){\displaystyle \frac{d{\omega }_m}{dt}}=M -{ M}_{c_1}-M_{c_2}T{\displaystyle \frac{dM}{dt}}+M=k({\omega }_0-{\mathsf{\omega }}_m),$$

(2)

where M_c1 = m g f/i₁; M_c2 = h S r_w³ ω_m ²/i₁²; and V = r_w ω_m/i₁.

Figure 5 and Figure 6 show the changes in the angular velocity of the motor’s rotor, and the dynamic characteristic of the engine as a function of time.

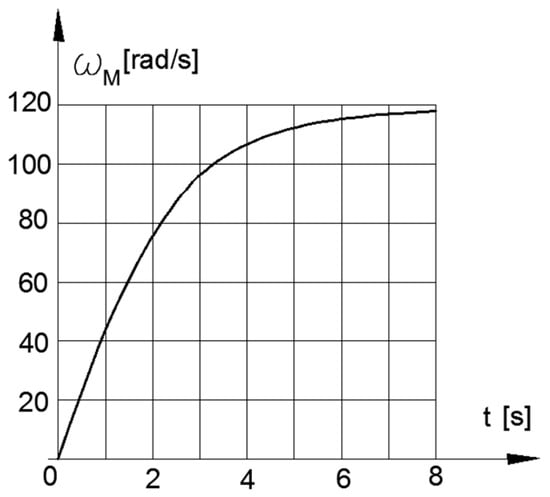
Figure 5. Velocities ω_m.

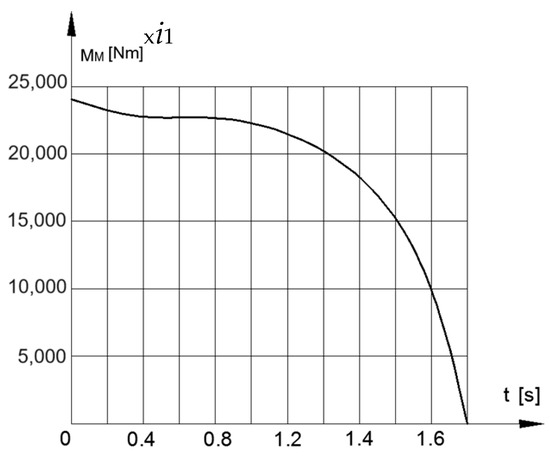
Figure 6. Engine’s dynamic moment.

3.3. Stopping Process

For charging with energy from the kinetic recovery system, the direction of energy flow is in the sequence 7-6-5-8-9-10-11 (Figure 2), with brake 4 and clutches 6 and 9 engaged.

The differential equation of motion of the electric vehicle, brought to the axis of drive wheels 7 (Figure 2), is derived using the Lagrange equation of the second kind [21]. The kinetic energy of the vehicle has the following form:

$$E={\displaystyle \frac{1}{2}}(m\delta {r_w}^2+J_f{i^2}_{\sum }){{\omega }_w}^2,$$

(3)

where $i_{å }= {\mathrm{i}}_{2.}.{\mathrm{i}}_{\mathrm{D} .}.{\mathrm{i}}_V = \mathrm{f}(\mathsf{\phi },{\mathsf{\omega }}_w);{\displaystyle \frac{\mathrm{d}{\mathrm{i}}_{å}}{\mathrm{d}{\mathsf{\omega }}_w}} = -{\mathrm{i}}_2.{\mathrm{i}}_D.{\displaystyle \frac{i_V}{{\omega }_w}}.$.

The generalized force in the right-hand side has three components: moments, reduced by losses in the flywheel and in the variator (CVT), and the road resistances. This can be depicted as follows:

$$Q =-m.g.f + J_{f.}{.}^{.}\omega {\ast }_{f.}r{.}_w.n,$$

(4)

where $\mathrm{n} = ( {\mathrm{i}}_{å}.{\mathsf{\eta }}_f.{\mathsf{\eta }}_V.{\mathsf{\eta }}_g+{\mathrm{i}}_{\mathrm{V}.}{\eta }_V.{\mathsf{\eta }}_g)$.

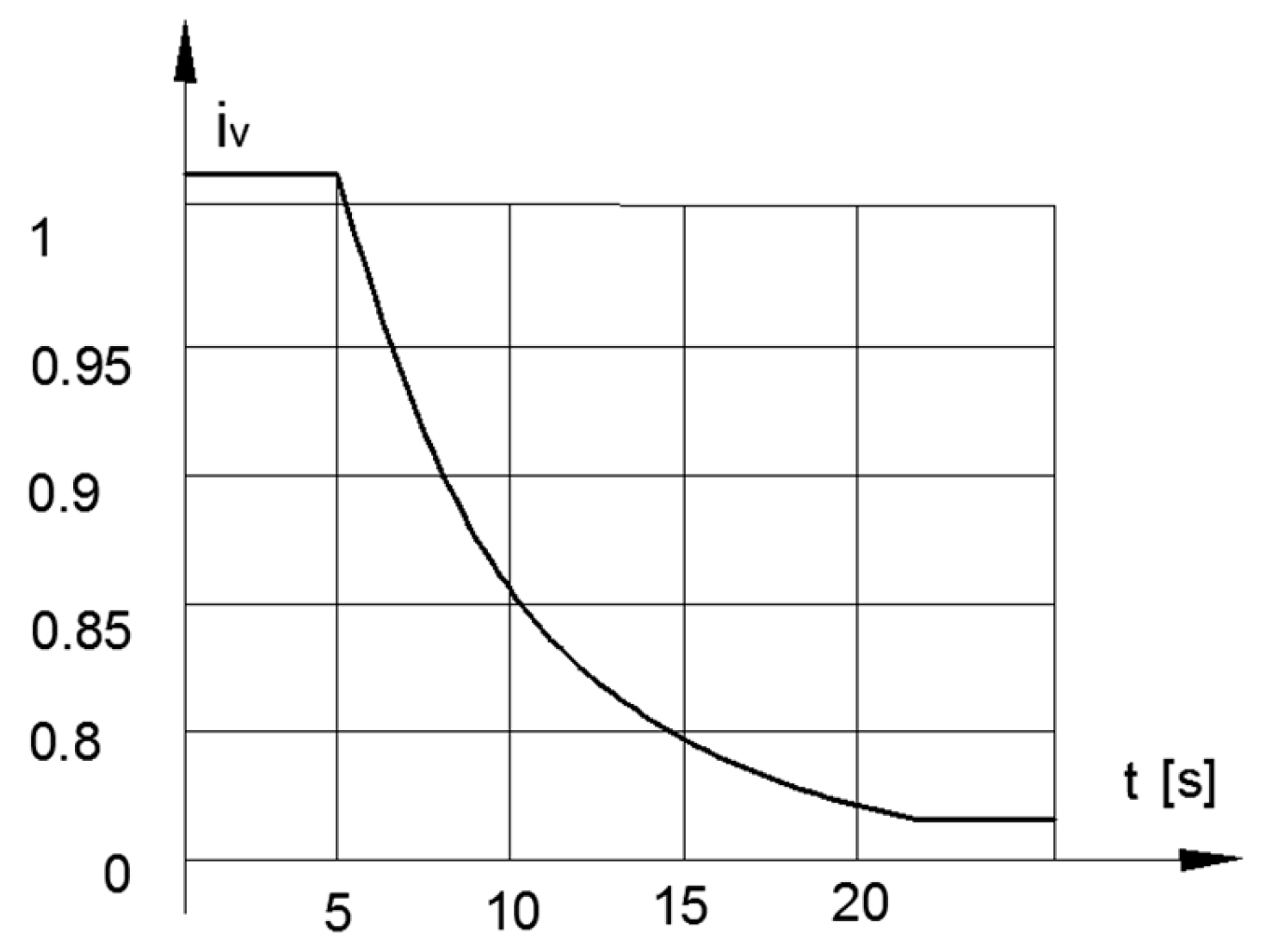
After finding the derivatives of energy (3) with respect to phi φ, omega ωw, and time t, the differential equation of the transmission ratio iV of the variator (CVT) acquires the following form:

$$i_V{\displaystyle \frac{d{i}_V}{dt}}+{\displaystyle \frac{1}{3}}{\displaystyle \frac{{\dot{\omega }}_W}{{\omega }_W}}{i_V}^2=Q^{*},$$

(5)

where ${\mathrm{Q}}^{*}={\displaystyle \frac{\mathrm{Q}}{3{.(\mathrm{J}}_{\mathrm{f}}{.\mathsf{\omega }}_{\mathrm{w}}.{{\mathrm{i}}^2}_{\mathrm{D}}.{{\mathrm{i}}^2}_2)}}$.

If the following assumptions are made

$$F_1(t)={\displaystyle \frac{2}{3}}.{\displaystyle \frac{{\dot{\omega }}_w}{{\omega }_w}};F_2(t)=2,Q^{*},$$

(6)

then differential Equation (5) is reduced to a linear equation with variable coefficients relative to the square of the transmission function of the variator (CVT) of the type

$$\dot{Y}(t)+F_1(t).Y(t)=F_2(t),$$

(7)

whose solution has the form

$$Y(t)={e^{-{\int }_0^t{F}_1}}^{(t)dt}{F}_2(t).e^{{\int }_0^t{F}_1(t)dt},$$

(8)

at t = 0; ω_w = 103 [1/s] and ω*= 0 [1/s²].

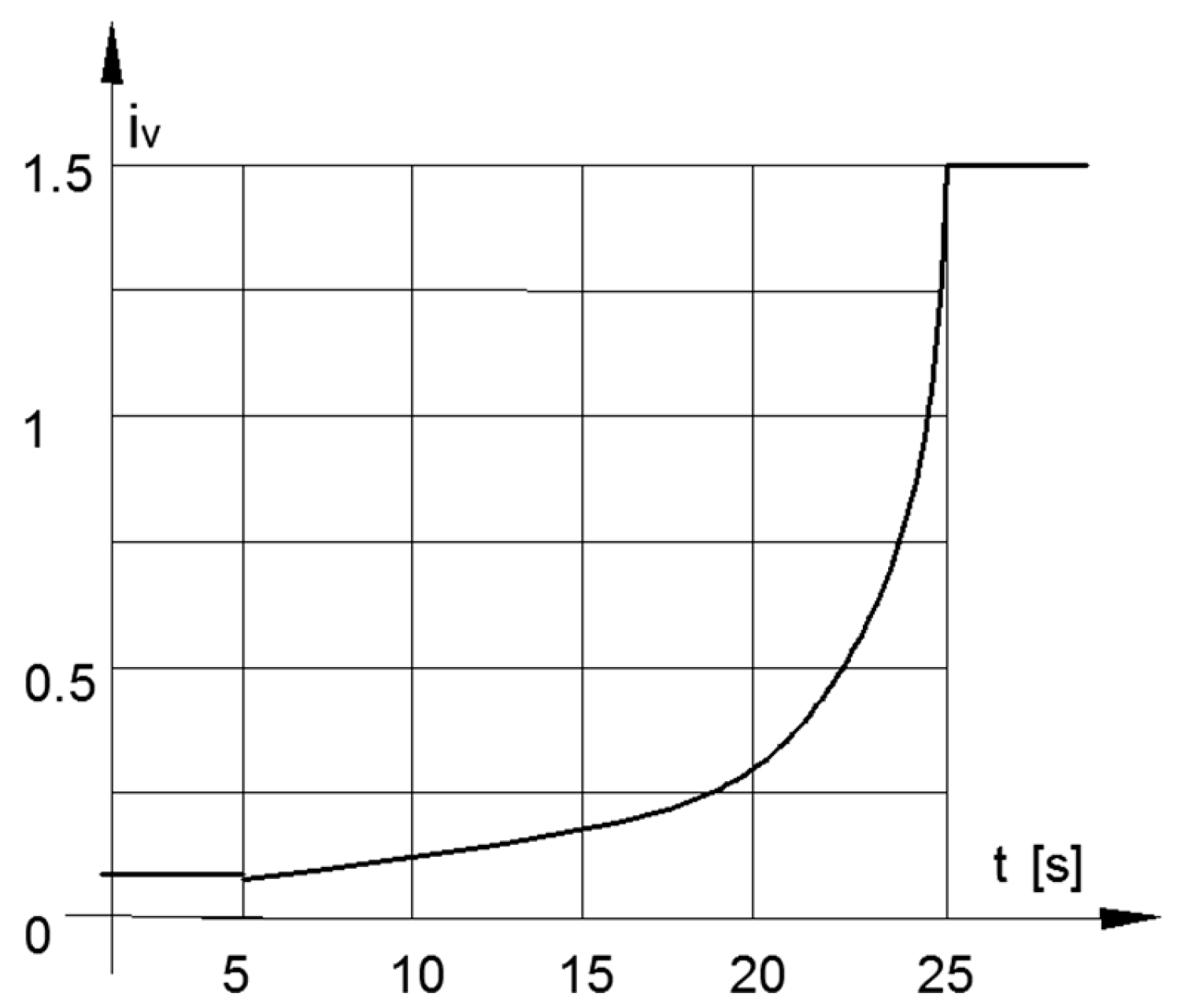
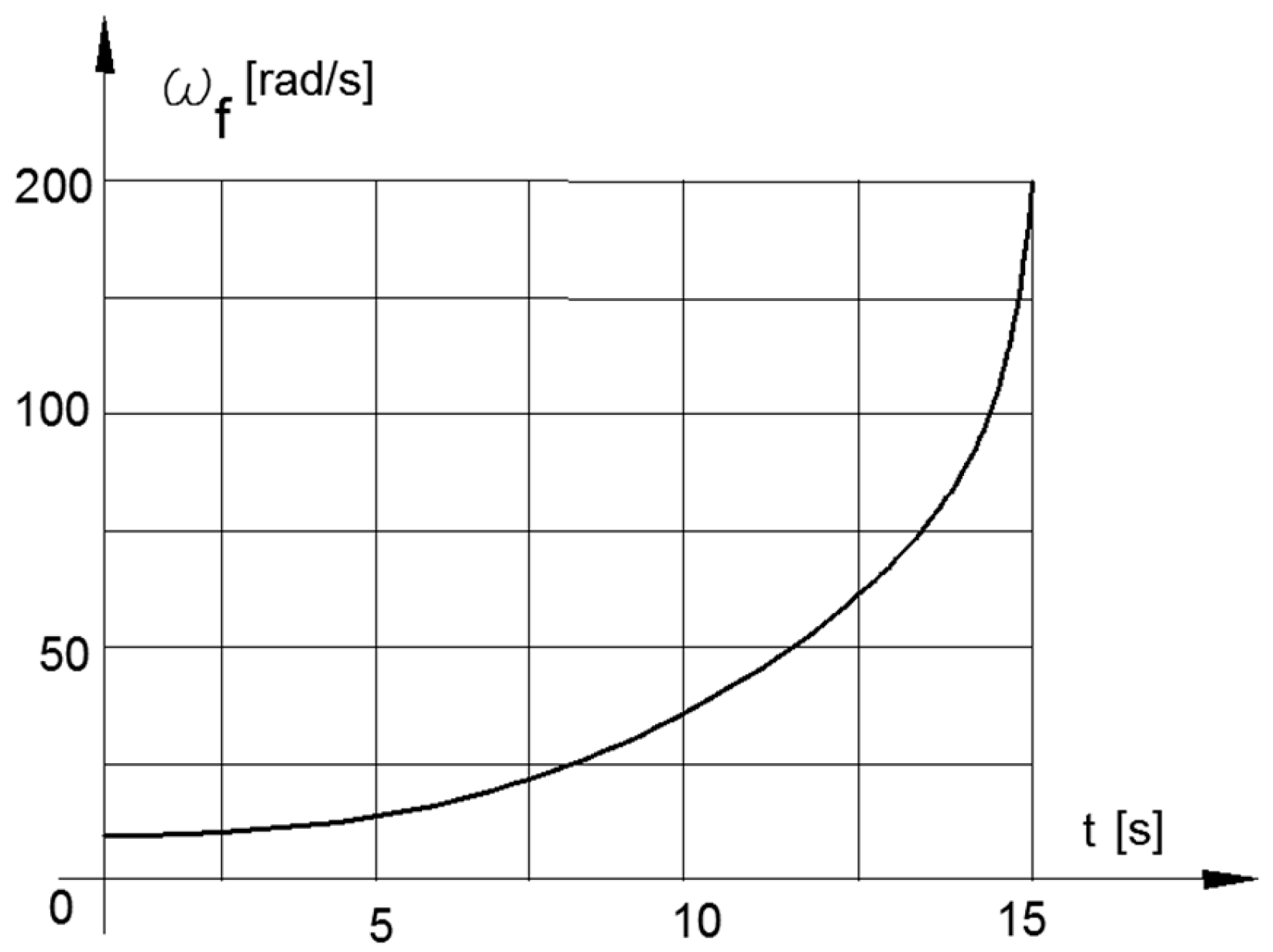
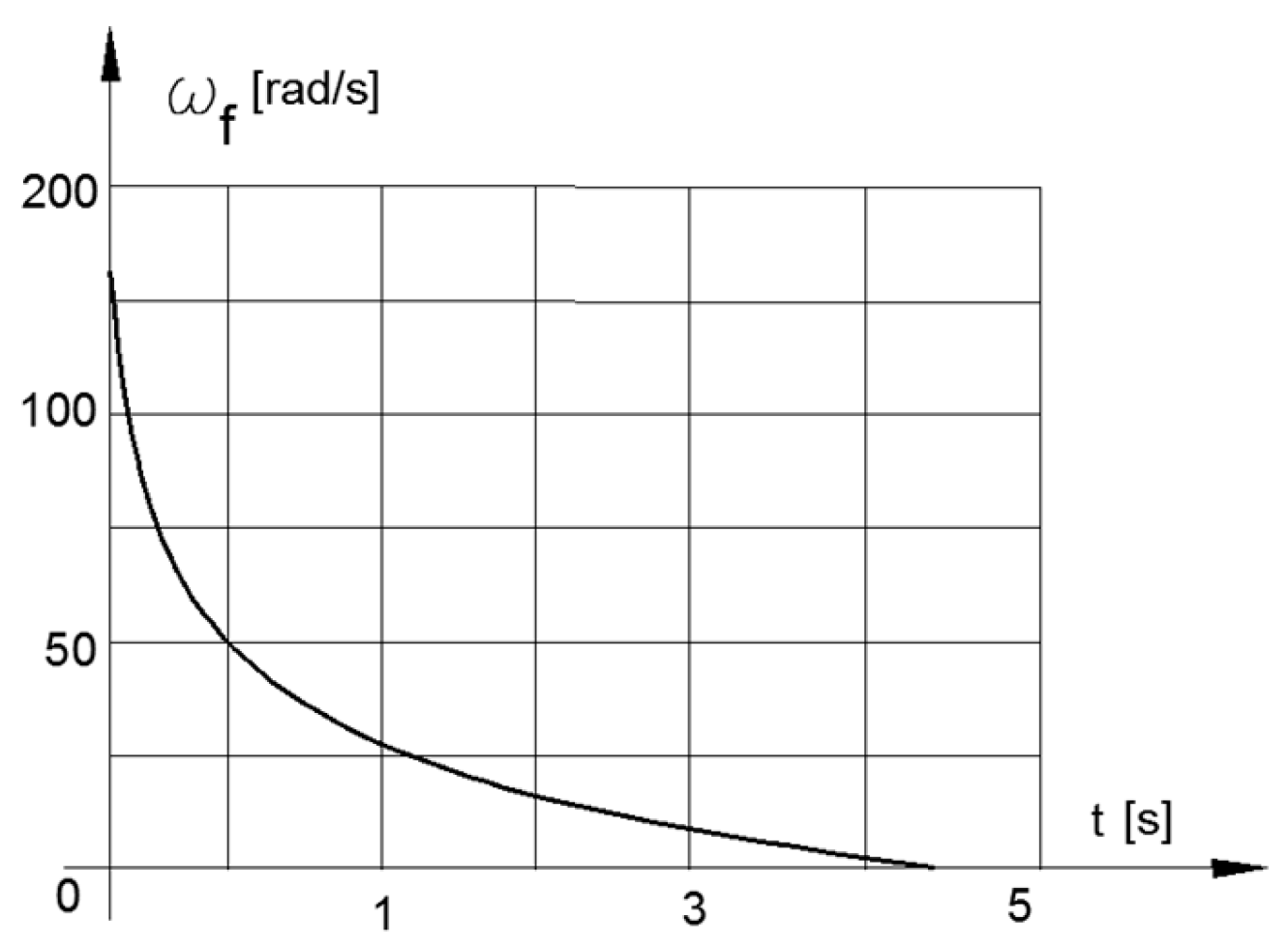
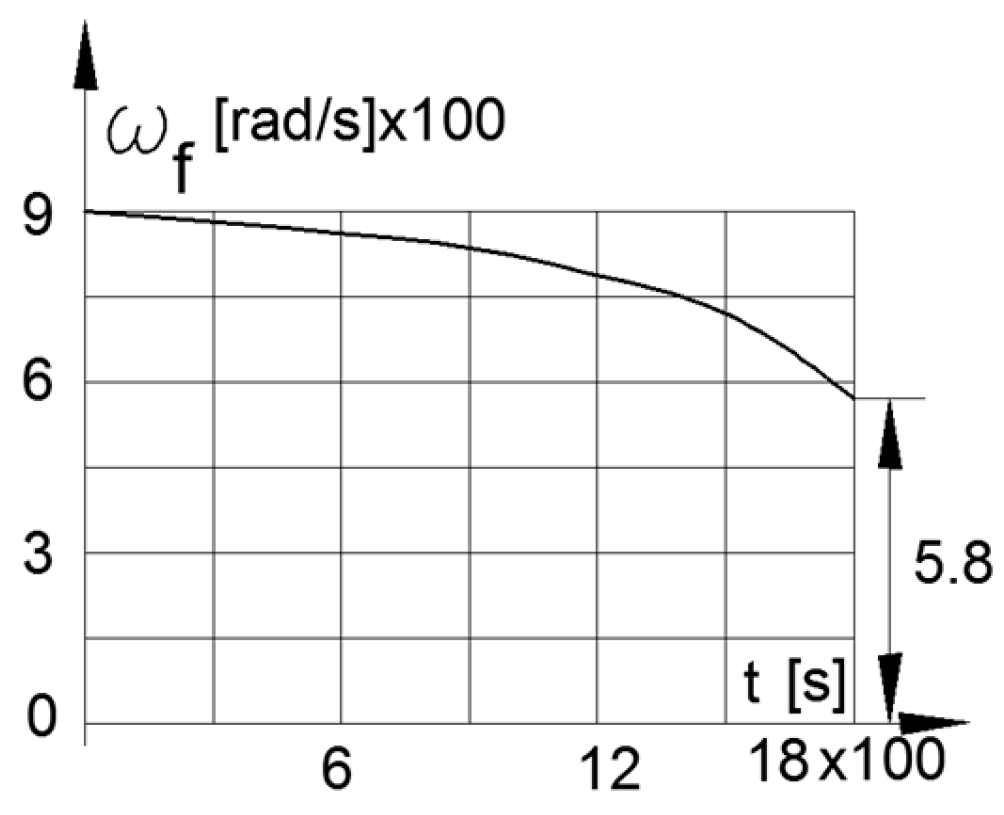
By test function ω_w= 103–0.25. t² (103 ≥ ω_w ≥ 3), the solutions of Equation (8) are presented in Figure 7 for i_V(t) and in Figure 8 for ω_f(t) as functions of time.

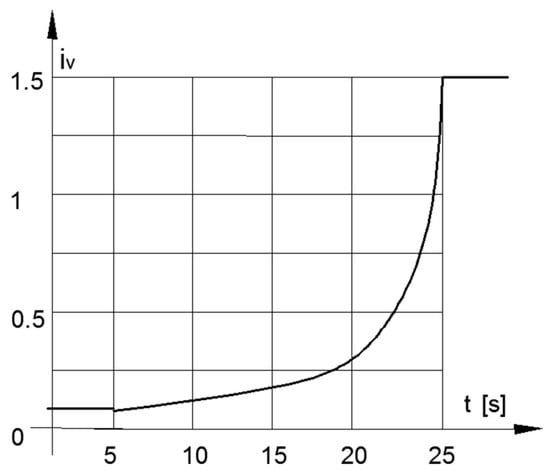
Figure 7. Transmission ratio of CVT in stopping mode.

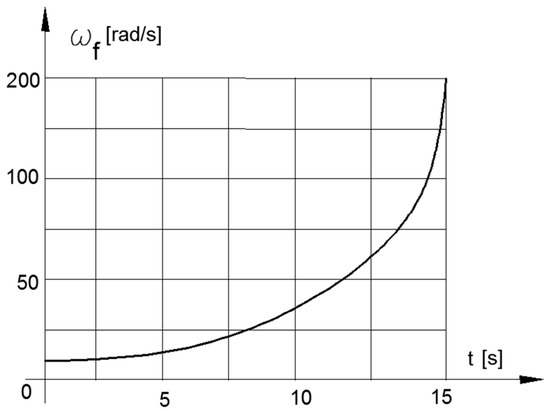
Figure 8. Angular velocity of the flywheel in stopping mode.

3.4. Accelerating the Vehicle from (KERS) Kinetic Storage System

The direction of the energy flow in accordance with Figure 2 is in the sequence 11-10-9-8-5-6 and 7, with clutches 6 and 9 and brake 4 engaged.

The differential equation describing the behavior of the variator (CVT) as a function of time is the same (6), but under a different initial condition where t = 0; ω_w = 3 [1/s]; and ω_w^∗ = 0.175 [1/s²]. The high friction coefficient of 0.7 in the variator mechanism is provided by the applied nanostructure multilayer (AlTiN) ml.

The test function constitutes a positive gradient (${\mathsf{\omega }}_{\mathrm{w}}= 3+ 0{.25 \mathrm{t}}^{2 }$) and changes in (4), where the coefficients of efficiencies have degrees in the power of −1 or (η_i⁻¹).

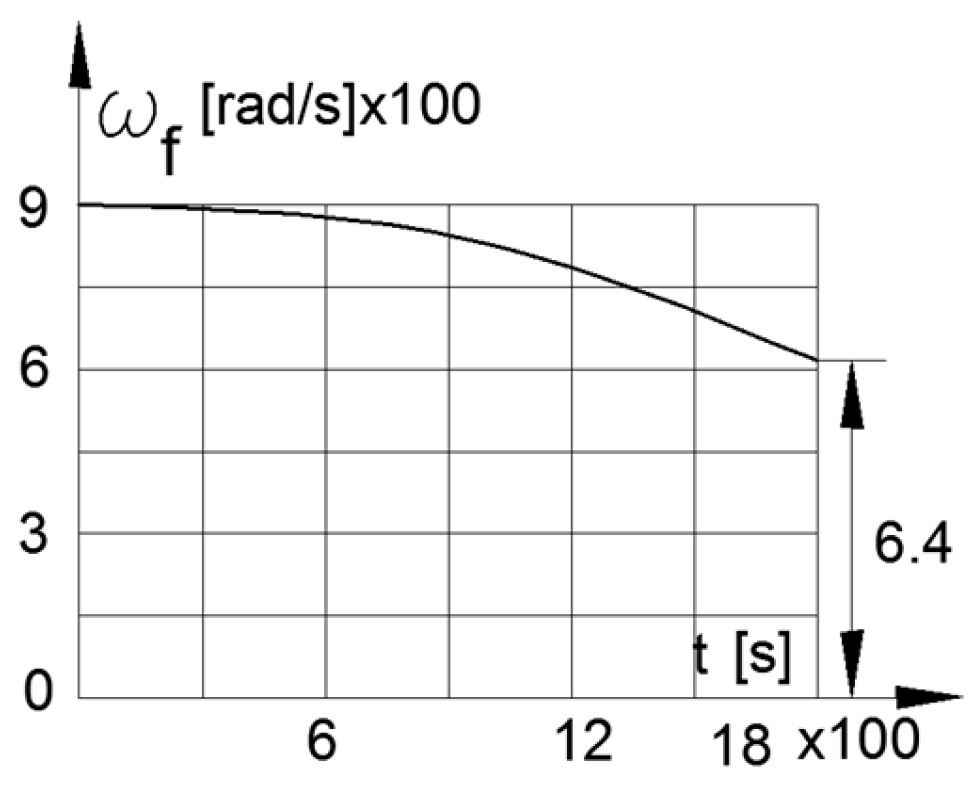
The solutions of Equation (8) for this case are presented in Figure 9 for i_V(t) and for angular velocity of the flywheel ω_f(t), and in Figure 10 for ω_f(t) as functions of time.

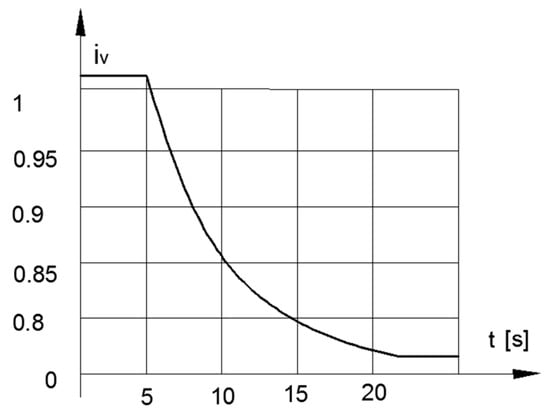
Figure 9. Transmission ratio of the CVT in acceleration mode.

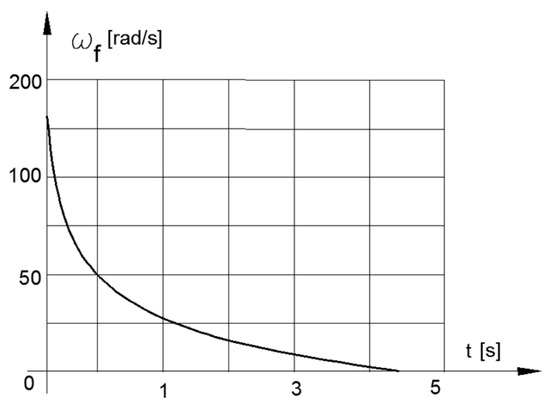
Figure 10. Angular velocity of the Flywheel in acceleration mode.

3.5. Accelerating the Vehicle (Split)

The following is for driving the electric vehicle simultaneously from the motor and the flywheel. The directions of the energy flows are in the following sequence, simultaneously—1-2-3-4-5, 11-10-9-8-5-6-7—with clutches 4, 6, and 9 engaged.

The kinetic energy of the electro-mechanical system of the electric vehicle in split drive with respect to the drive wheels is represented by

$$\mathrm{E}={\displaystyle \frac{1}{2}}(J_0+{\mathrm{J}}_1.{{\mathrm{i}}^2}_V).{{\mathsf{\omega }}^2}_w,$$

(9)

where ${\mathrm{J}}_0{=\mathrm{J}}_{\mathrm{m}},{{\mathrm{i}}_1}^2+\mathrm{m}.\mathsf{\delta }.{{\mathrm{r}}_{\mathrm{w}}}^2{;\mathrm{J}}_1{=\mathrm{J}}_{\mathrm{f}}.{{\mathrm{i}}_2}^2.{{\mathrm{i}}_{\mathrm{D}}}^2{;\mathrm{i}}_{å}{=\mathrm{i}}_2{.\mathrm{i}}_{\mathrm{D}}{.\mathrm{i}}_{\mathrm{V}}={\displaystyle \frac{{\omega }_{\mathrm{f}}}{{\omega }_{\mathrm{w}}}}{=\mathrm{f}(\mathsf{\phi },\omega }_{\mathrm{W}})$.

The reduced moment of the active forces has the form

$$M_r=M-m.g.f \pm { J}_f.n.{\dot{\omega }}_w.i_V-h.S.{{\omega }^2}_w.r^3;n={ i}_2.i_D.{{{\eta }_V}^{\pm }}^1.{{{\eta }_g}^{\pm }}^1({{\eta }_f}^{\pm 1}+1).$$

(10)

where M is the dynamic characteristic (moment) of the engine and n is a number depending on the gear ratios i₁, i2, and i_D, with efficiencies of the degree of +1 or −1 depending on the direction of the energy flow.

The dynamic characteristic of the DC electric motor is represented with one time constant T, which is represented by the following first-order differential equation:

$$T.{\dot{F}}_r +{ F}_r ={{ i}_1}^2.k.(42-V),$$

(11)

which is analogical of the second equation of (2), where F_r is equal to ${\mathrm{M}}_r.{\mathrm{r}}_{\mathrm{w} }$ and ${\omega }_0.{\mathrm{r}}_w= 42 \left[\mathrm{m}/\mathrm{s}\right],$ and reduced external force is $F_r= {\mathrm{M}}_r.{\mathrm{r}}_{\mathrm{w} }$.

After successively calculating the derivatives of the kinetic energy (9) with respect to position, velocity, and time and substituting in the Lagrange equation and known transformations, we arrive at the following systems of differential Equations (11) and (12):

$$i_V.{\displaystyle \frac{\mathrm{d}{\mathrm{i}}_V}{\mathrm{dt}}}+{\displaystyle \frac{1}{3}}.{\displaystyle \frac{\dot{V}}{V}}.{{\mathrm{i}}_V}^{2}m{\displaystyle \frac{J_f}{3{\mathrm{J}}_1}}.{\displaystyle \frac{\dot{V}}{V}}.\mathrm{n}.{\mathrm{i}}_V = \mathsf{\Phi }(t),$$

(12)

where

$$\Phi (t)={\displaystyle \frac{1}{3.J_1.V}}.(m.g.f.r_w+h.S.V^2-F_r)$$

(13)

The differential equation above in relation to the transmission ratio of the variator (CVT) has variable coefficients and does not have an analytical solution. It has a physical meaning with known V and V^⃰ values

From the analysis of the numerical values in front of the derivatives in the system of Equations (12) and (13), it can be easily established that this system belongs to the so-called “stiff” from mathematical equations point of view. The difference in the orders of this value reaches three. For this reason, the numerical solutions were obtained using special methods [22,23].

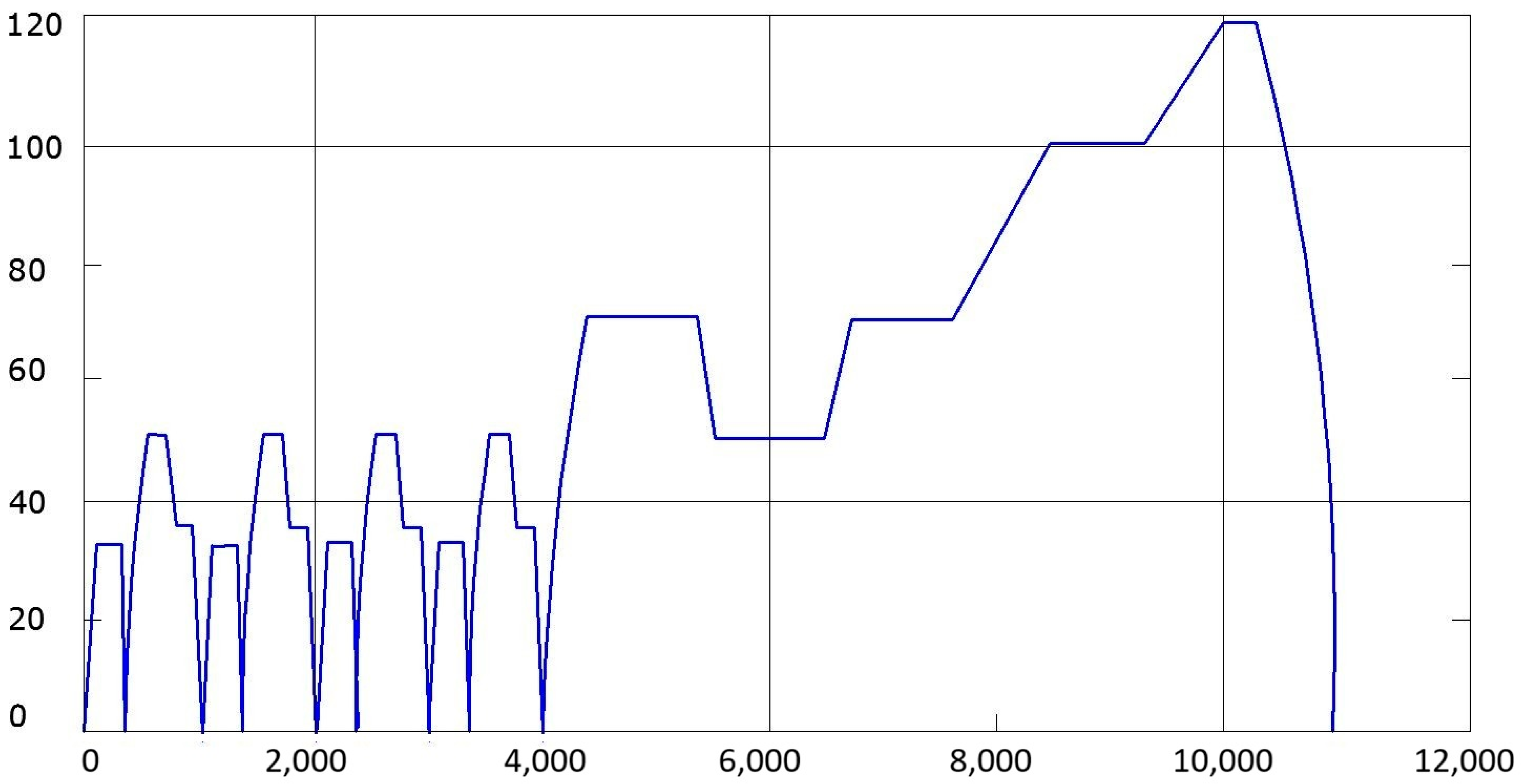
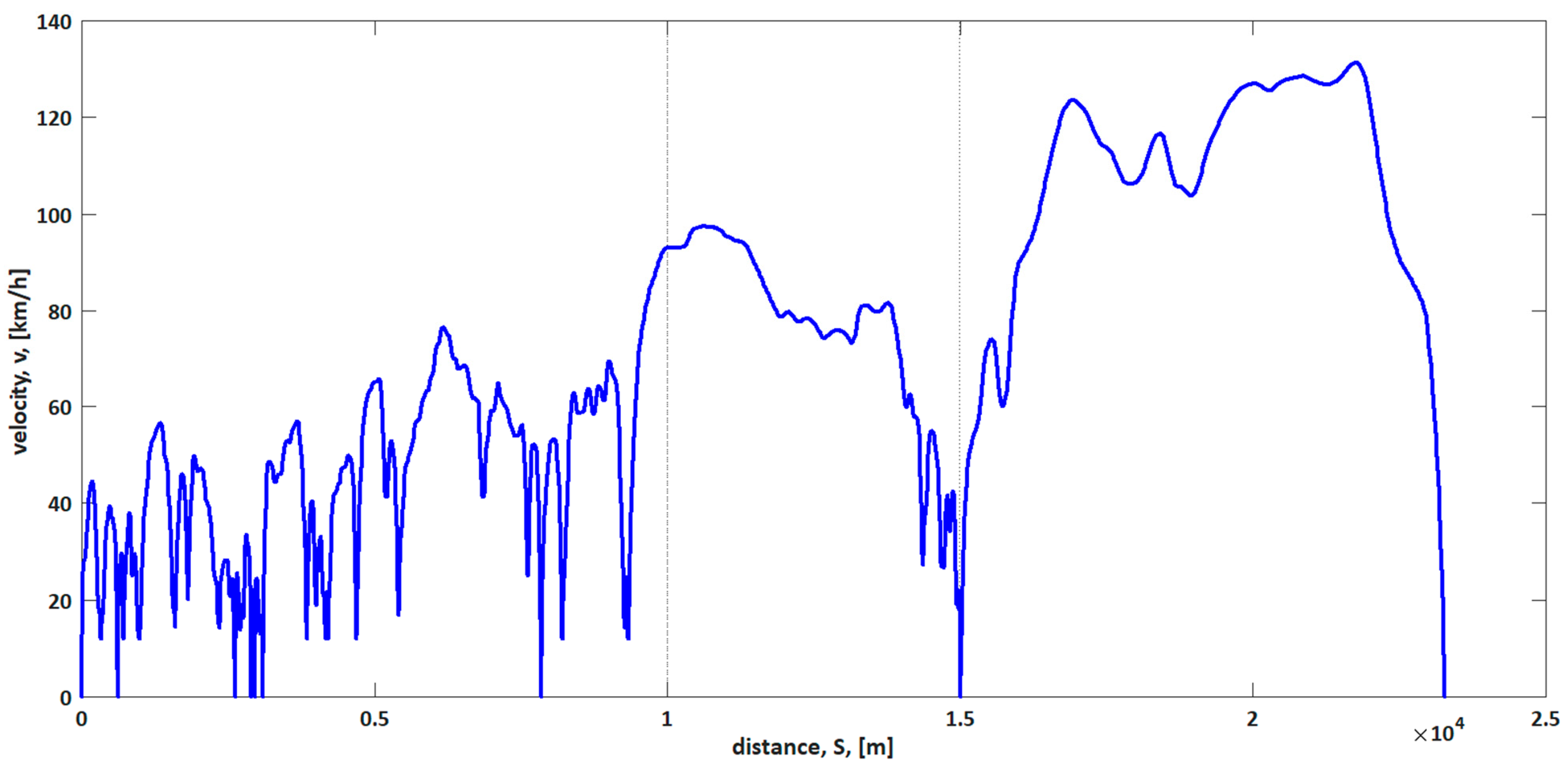
The computer simulations were performed on a digital array of the standardized transport cycles NEUDC and WLTC-3 (Figure 11 and Figure 12).

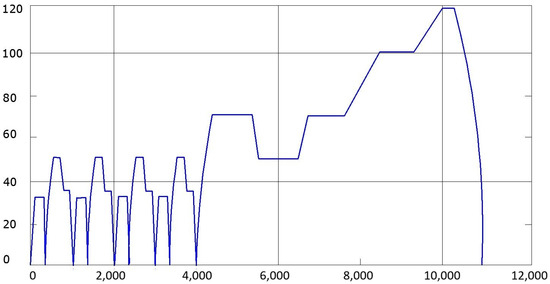
Figure 11. NEUDC cycle.

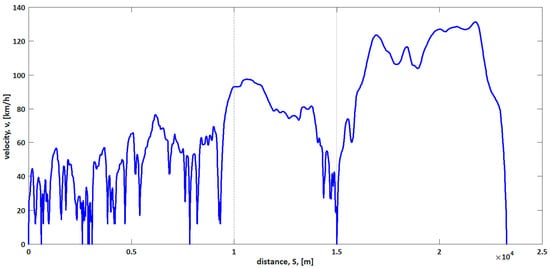
Figure 12. WLTC 3 cycle.

The results of the numerical solutions of the system differential Equations (11) and (12) for the angular velocities of the flywheel within the durations of the aforementioned transport cycles are presented in Figure 13 and Figure 14.

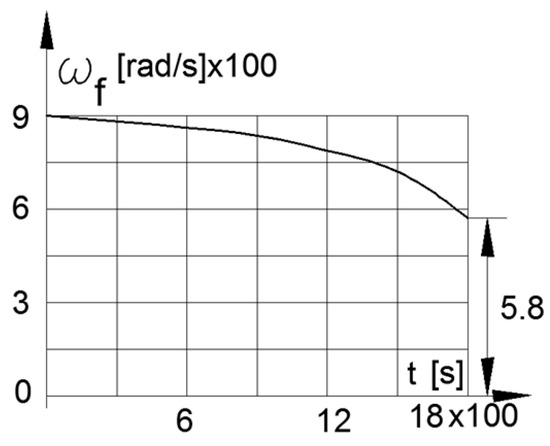
Figure 13. ω_f by NEUDEC cycle.

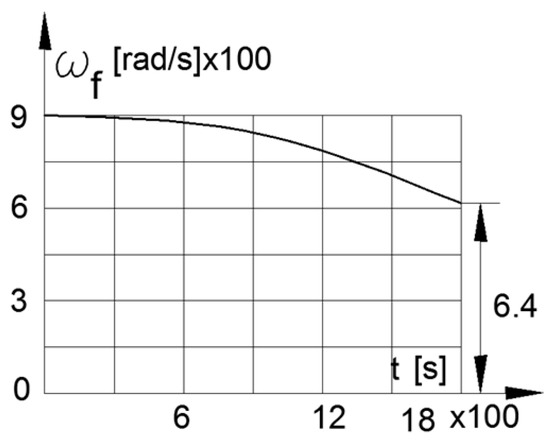
Figure 14. ω_f by WLTC 3 cycle.

4. Conclusions

An innovative structure and algorithm [24] for controlling a hybrid urban electric vehicle with a kinetic energy storage system are proposed, satisfying the set goals:

• Elimination of shock loads on the electric battery during the stopping of the vehicle;
• A single transformation from electrical to mechanical energy;
• The possibility of increasing the mileage/range of the electric vehicle with a single charge of the electric battery is preserved.

The efficiency, reliability, and security of the proposed algorithm for controlling the energy flows between the electric motor and the kinetic energy storage system are proven.

5. Patents

A corresponding utility model has been developed with the name “System for hybrid electric vehicle propulsion with kinetic energy accumulator” and respective number BG/U/2025/6462 [24].