Enhancing Classification Performance on Imbalanced Data by Combining Autoencoder Generative Adversarial Networks with Synthetic Minority Over-Sampling Technique-Particle Swarm Optimization ^†

Abstract

Class imbalance is a common issue in machine learning, often causing bias in learning models toward the majority class and leading to poor predictive performance for the minority class data. To address the class imbalance problem, this paper presents the autoencoder-based generative adversarial network-synthetic minority over-sampling technique-particle swarm optimization (AEGAN-SMOTE-PSO) model. We compared the AEGAN-SMOTE-PSO model with three other state-of-the-art oversampling techniques. Those experimental results demonstrate that the AEGAN-SMOTE-PSO model effectively improves the classification performance of two support vector machine prediction models on two imbalanced medical cases. Compared to the other three oversampling methods, the AEGAN-SMOTE-PSO model effectively provides satisfactory predictive performance in terms of recall, precision, and F1-score.

1. Introduction

Machine learning and deep learning have been widely applied in medicine. They have shown great effectiveness in disease classification and medical diagnosis, aiding doctors in making correct clinical decisions [1]. However, class imbalance is frequently encountered in actual medical data. In breast cancer datasets, for example, benign tumor samples often outnumber malignant ones [2]. The class imbalance may cause the classification model to tend to predict the majority class during training [3], due to insufficient representations of the minority class. If the learning model cannot accurately identify malignant tumor samples, it may lead to delayed treatment, thereby reducing therapeutic drug efficacy.

Currently, various data-driven solutions have been proposed to address the class imbalance problem. Those solutions include under-sampling, over-sampling, and hybrid-sampling. In terms of under-sampling, it can effectively improve classifiers’ classification accuracy by randomly removing samples from the original dataset. On the downside, it may lead to the loss of key information in the majority class samples, which would affect the model’s ability to distinguish the majority class [4]. Among over-sampling methods, the synthetic minority over-sampling technique (SMOTE) is one of the most representative techniques. It increases the number of minority class examples by generating synthetic samples, thereby balancing class distribution. Additionally, compared with other oversampling techniques, SMOTE is less prone to overfitting [5]. It synthesizes new samples by performing linear interpolation on minority class samples [6]. However, when the minority class is sparsely distributed, SMOTE might produce unrepresentative examples (i.e., noise), which may negatively affect the performance of traditional learning models [7]. On the other hand, classical generative adversarial networks (GANs) are often used to learn the data distribution of the minority class to produce new samples resembling the original minority class data [8]. However, GAN has the mode collapse problem during training, which generates high-quality but low-variant synthetic samples, which may be invalid for improving the performance of predictive models.

As a result, we developed a novel hybrid oversampling model, termed AEGAN-SMOTE-PSO, which integrates an autoencoder GAN (AEGAN) model and SMOTE with a particle swarm optimization (PSO) algorithm. The developed generative model contains an autoencoder deep learning network, which enables the generative model to extract deep-detailed features to generate high-quality samples. Different from traditional GAN, AEGAN effectively alleviates the mode collapse problem during training [9,10]. Additionally, it can generate more diverse samples via a combination of SMOTE and GAN [11]. Using PSO, potential noise and low-quality samples can be filtered out [12]. Moreover, the classification performance of the predictive model for minority class data can be further enhanced [13].

To evaluate the effectiveness of the AEGAN-SMOTE-PSO model, we compared it with three oversampling methods: SMOTE, SMOTE-PSO, and AEGAN (without SMOTE-PSO). The three evaluation metrics included recall, precision, and F1-score to measure the classification results of these algorithms. Two breast cancer datasets—downloaded from the UCI repository [14], the breast cancer Wisconsin original, and the breast cancer Wisconsin diagnostic datasets—were used in the experiment. Two SVM classifiers with two kernel functions: polynomial (poly) and radial basis function (rbf) were deployed to verify efficacy in using these oversampling methods. Experimental results demonstrated that the AEGAN-SMOTE-PSO model outperforms the other oversampling methods across the three metrics for two SVM prediction models.

2. Related Works

2.1. GAN

In the GAN architecture, a random latent variable $z\sim p_z\left(z\right)$ is fed into the generator $G$ to produce synthetic samples $G\left(z\right)$. The discriminator $D$ is used to determine whether an input sample $X$ comes from the real data distribution $p_{data}\left(x\right)$. The training of GAN is carried out through a minimax adversarial learning process. The objective function is expressed as Equation (1).

$$mi{n}_{G}ma{x}_{D}V\left(D, G\right)=E_{x\sim p_{data}\left(x\right)}\left[logD\left(x\right)\right]+E_{z\sim p_z\left(z\right)}\left[log\left(1-D\left(G\left(z\right)\right)\right)\right].$$

(1)

The training objective of the generator is to produce artificial samples that can fool the discriminator. Its loss function is expressed as Equation (2).

$$mi{n}_G=E_{z\sim p_z\left(z\right)}\left[log\left(1-D\left(G\left(z\right)\right)\right)\right],$$

(2)

where D(.) represents the probability that the input sample is from the real data. By minimizing this function, the generator aims to increase the probability that the artificial samples are judged as real samples. Conversely, the training objective of the discriminator is to correctly classify the input samples as real or artificial samples. Its loss function is expressed as Equation (3).

$$ma{x}_D=E_{x\sim p_{data}\left(x\right)}\left[log D\left(x\right)\right]+E_{z\sim p_z\left(z\right)}\left[log\left(1-D\left(G\left(z\right)\right)\right)\right].$$

(3)

2.2. PSO

To select the most representative synthetic samples, we adopted a PSO algorithm. PSO elucidates the optimal artificial samples via simulating the movement behavior of particles in the feature space. The velocity and position of each particle are updated based on its personal best solution and the global best solution. The formulas for updating velocity and position are expressed as Equations (4) and (5).

$${v_i}^{\left(t+1\right)}=w\cdot {v_i}^{\left(t\right)}+c_1\cdot r_1\cdot \left(p_{best,i}-{x_i}^{\left(t\right)}\right)+c_2\cdot r_2\cdot \left(g_{best}-{x_i}^{\left(t\right)}\right),$$

(4)

$${x_i}^{(t+1)}={x_i}^{\left(t\right)}+{v_i}^{(t+1)},$$

(5)

where ${x_i}^{\left(t\right)}$ and ${v_i}^{\left(t\right)}$ represent the current position and velocity of the $i$-th particle at iteration $t$, respectively. $p_{best,i}$ is the personal best position, and $g_{best}$ is the global best position. The parameters $w$, $c_1$, and $c_2$ denote the inertia weight and acceleration coefficients, while $r_1$ and $r_2$ are random variables uniformly distributed in the range [0, 1].

3. Method

3.1. Procedure

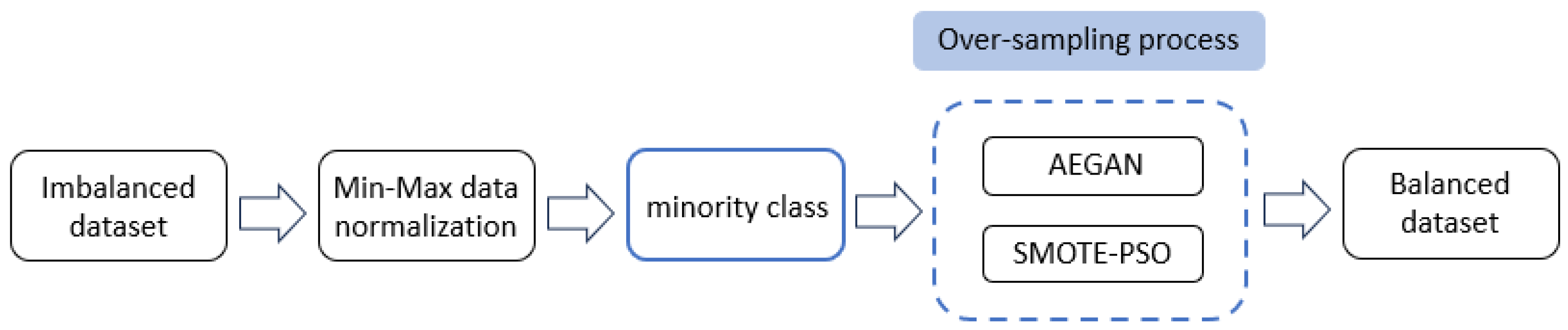
The AEGAN-SMOTE-PSO method was applied to generate samples for the various examples of the minority class. After using AEGAN for generating new minority class samples, SMOTE was used to generate synthetic minority class examples, and PSO was applied to select the best synthetic samples among them. Figure 1 displays the implementation procedure of the proposed AEGAN-SMOTE-PSO method.

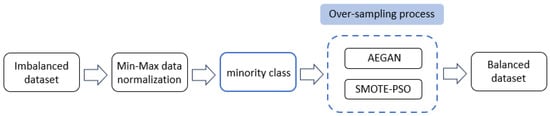
Figure 1. Implementation of the AEGAN-SMOTE-PSO model.

Before performing AEGAN-SMOTE-PSO, we applied min-max normalization to scale the original imbalanced dataset into the domain [0, 1]. The mathematical formula for the normalization is defined as Equation (6).

$$X_{normalized}={\displaystyle \frac{X-X_{min}}{X_{max}-X_{min}}}$$

(6)

where $X$ represents the original feature value, while $X_{min }$ and $X_{max}$ denote the minimum and maximum values of features in datasets, respectively.

3.2. Autoencoder GAN

The generator is composed of an autoencoder neural network, where the number of neurons in the hidden layers is set to 64, 32, and 64. Both the hidden and output layers employ the sigmoid activation function to ensure the features of the generated sample $\widehat{X}$ are constrained within the range [0, 1]. The sigmoid function is defined as Equation (7).

$$\sigma \left(x\right)={\displaystyle \frac{1}{1+e^{-x}}}$$

(7)

During the training process, the discriminator architecture consists of a single hidden layer with 64 neurons. In this study, the discriminator is trained with a batch size of 1. The AEGAN is trained for 50 iterations, with each iteration updating all weights of AEGAN using $z\sim N\left(0,1\right)$ noises in a 64-dimensional space. The weights of the generator and discriminator are optimized using the Adam optimizer. In the proposed method, the number of generated samples is set to half the difference between the number of majority class samples and the minority class sample size. The mathematical formulation is expressed as Equation (8).

$$N_{AEGAN}=\left[{\displaystyle \frac{N_{maj}-N_{min}}{2}}\right]$$

(8)

where $N_{AEGAN}$ denotes the number of generated samples with AEGAN, and $N_{maj}$($N_{min}$) represents the number of samples in the majority (minority) classes, respectively. In the feature space, SMOTE is used to identify the nearest neighbors for each minority class sample and generates new synthetic samples through linear interpolation. The parameters of SMOTE are set to k_nei = 1 and n_nei = 1, meaning that each minority class sample is interpolated with only one nearest neighbor. The interpolation formula is defined as Equation (9):

$$X_{new}=X_i+\lambda \cdot \left(X_{zi}-X_i\right)$$

(9)

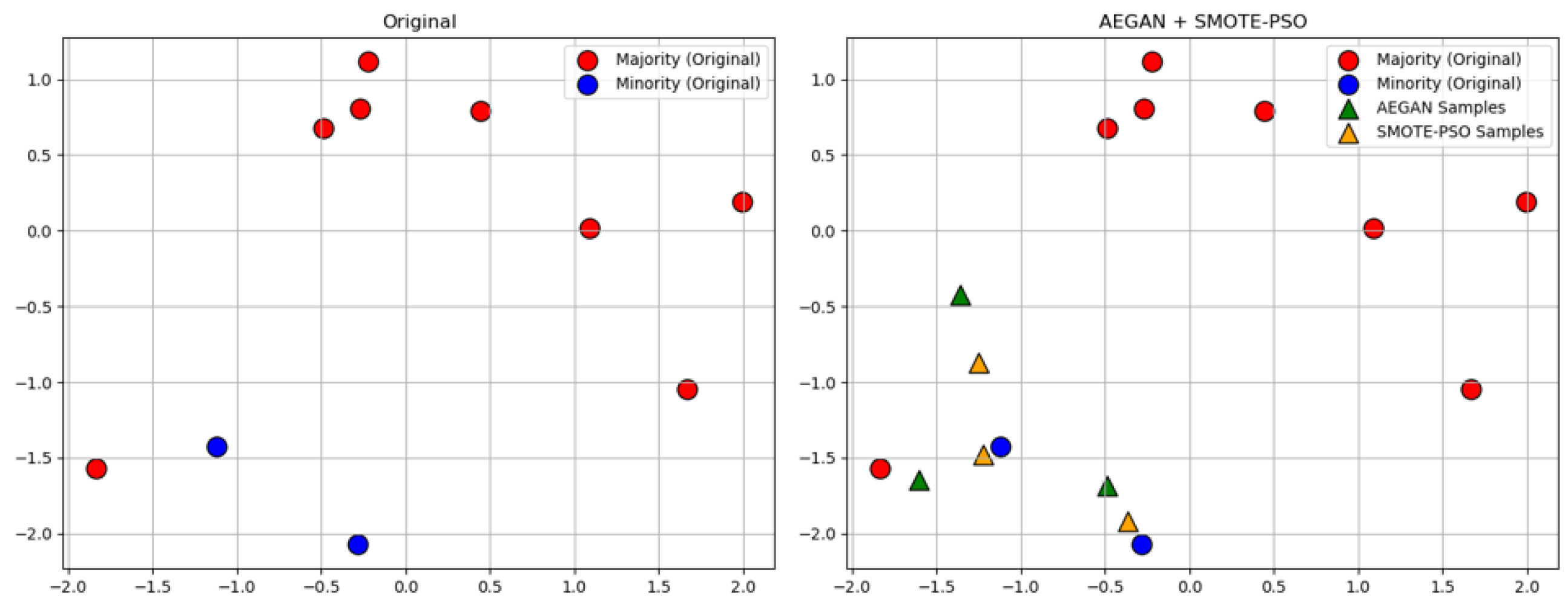
where $X_i$ represents ith original minority class sample, while $X_{zi}$ is a neighboring sample selected from its nearest neighbors. The parameter $\lambda$ is a real number randomly chosen from the interval [0, 1]. For example, half of the synthetic minority class samples are generated by AEGAN and the other half by SMOTE-PSO, as shown in Figure 2.

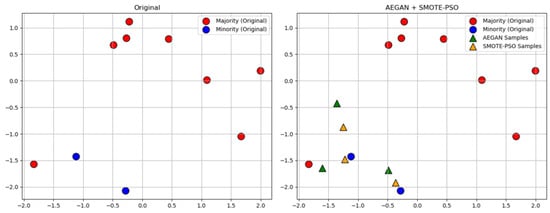
Figure 2. Generate synthetic samples using AEGAN-SMOTE-PSO.

4. Results

After completing the balance of the imbalanced data using AEGAN-SMOTE-PSO, based on this balanced training dataset, we built two SVM classification models with two kernel functions: polynomial (SVM_poly) and radial basis function (SVM_rbf).

4.1. Case Description

We utilized two breast cancer datasets: the Wisconsin original and the Wisconsin diagnostic data. The Wisconsin original data and Wisconsin diagnostic data contain 699 and 569 samples with 9 and 30 features, respectively. To ensure the stability and reliability of the predictive results, the experimental process was repeated 30 times.

4.2. Experiment

For SVM with polynomial and radial basis function kernels, the cost parameter was set at 1 and the polynomial degree 3. Additionally, the gamma parameter was set to “scale.”, calculated by the following Equation (10).

$$Gamma={\displaystyle \frac{1}{n_{\mathit{features}}\times Var\left(X\right)}}$$

(10)

where $n_{features}$ is the number of features and Var(X) is the variance of X. In our experiments, we set the imbalance ratio to 9, meaning that the number of samples in the majority class was nine times that of the minority class. This is used to evaluate the effectiveness of our method under imbalanced conditions. After balancing the imbalanced data, we built the SVM model based on the balanced training dataset. In this study, we evaluate the performance of the model with a confusion matrix, as shown in Table 1. The four valuation indicators can be used to assess the classification performance of imbalanced data.

Table 1. Confusion matrix.

	Actual Positive	Actual Negative
Predicted positive	True positive (TP)	False positive (FP)
Predicted negative	False negative (FN)	True negative (TN)

In this study, we evaluated prediction accuracy using recall, precision, and F1-score indicators, as expressed in Equations (11)–(13).

$$Recall={\displaystyle \frac{TP}{TP+FP}}$$

(11)

$$Precision={\displaystyle \frac{TP}{TP+FN}}$$

(12)

$$F1-Score=2\times {\displaystyle \frac{Precision\times Recall}{Precision+Recall}}$$

(13)

where recall measures the proportion of actual positive instances that are correctly identified by the classification model, precision indicates the proportion of predicted positive instances that are truly positive, and F1-score is a harmonic mean of recall and precision.

4.3. Experimental Results

4.3.1. Wisconsin Original Data

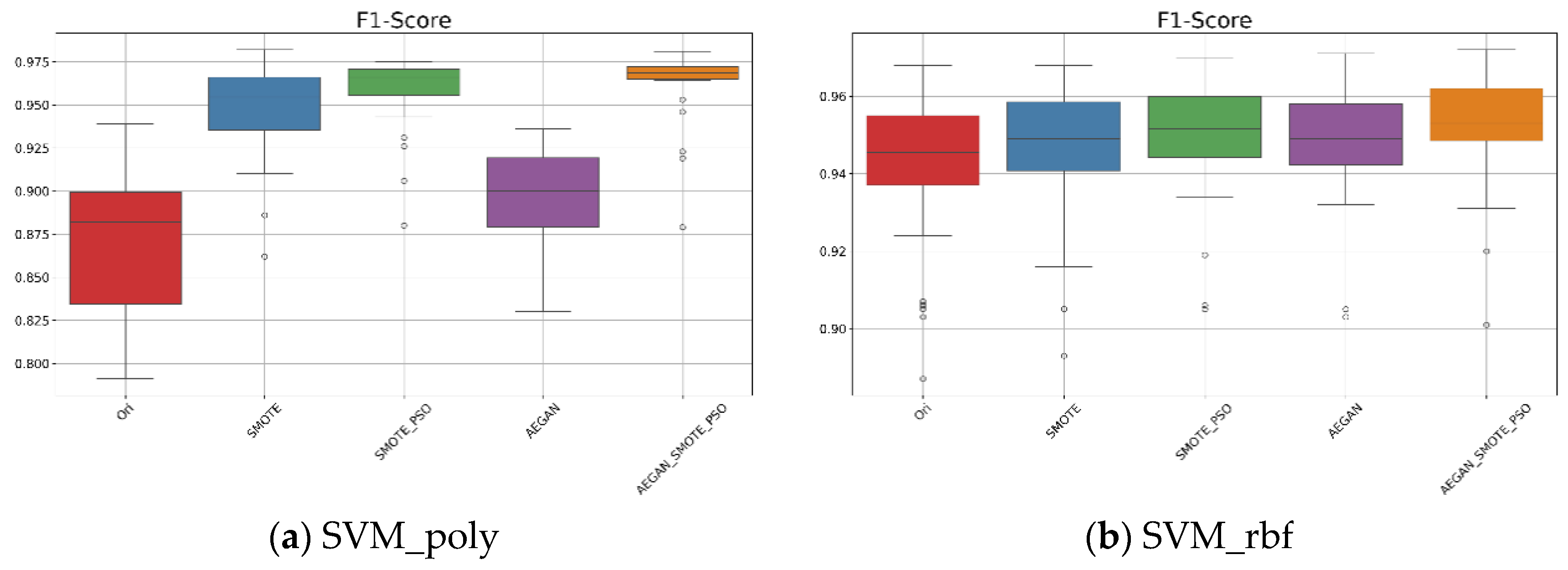
According to Table 2, when the kernel is set to polynomial, the AEGAN-SMOTE-PSO model showed an average F1-score of 0.962 with a standard deviation of 0.021 for the SVM_poly model. From Figure 3, these experimental results demonstrate that the proposed AEGAN-SMOTE-PSO method (orange box plot) outperforms Ori for using original dataset (red box plot), SMOTE (blue box plot), SMOTE-PSO (green box plot), and AEGAN (purple box plot). Additionally, as illustrated in Figure 3a, for the SVM_poly model, the F1-score results of the AEGAN-SMOTE-PSO model are more concentrated with a narrower interquartile range. This further highlights the AEGAN-SMOTE-PSO model’s robustness and its ability to enhance classification performance. When the kernel function is switched to RBF, AEGAN-SMOTE-PSO still yields the best results. As shown in Figure 3b and Table 2, the average F1-score was 0.952, slightly higher than that of SMOTE-PSO, which was 0.949.

Table 2. Average and standard deviation of the two SVM models using the techniques on the Wisconsin original data.

Classifier	SVM_poly
Performance	Metric	Ori	SMOTE	SMOTE-PSO	AEGAN	AEGAN-SMOTE-PSO
Average	Recall	0.837	0.941	0.959	0.870	0.963
	Precision	0.908	0.953	0.957	0.924	0.962
	F1-score	0.871	0.947	0.958	0.896	0.962
Standard deviation	Recall	0.052	0.039	0.028	0.042	0.028
	Precision	0.023	0.017	0.017	0.018	0.015
	F1-score	0.039	0.028	0.022	0.031	0.021
Classifier	SVM_rbf
Performance	Metric	Ori	SMOTE	SMOTE-PSO	AEGAN	AEGAN-SMOTE-PSO
Average	Recall	0.933	0.940	0.943	0.941	0.947
	Precision	0.948	0.953	0.955	0.954	0.956
	F1-score	0.941	0.946	0.949	0.948	0.952
Standard deviation	Recall	0.028	0.025	0.023	0.020	0.020
	Precision	0.013	0.011	0.010	0.011	0.010
	F1-score	0.021	0.018	0.017	0.015	0.015

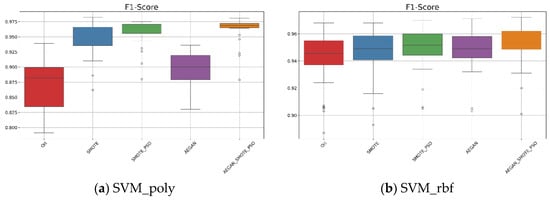
Figure 3. Boxplots for the SVM results on the Wisconsin original data.

4.3.2. Wisconsin Diagnostic Data

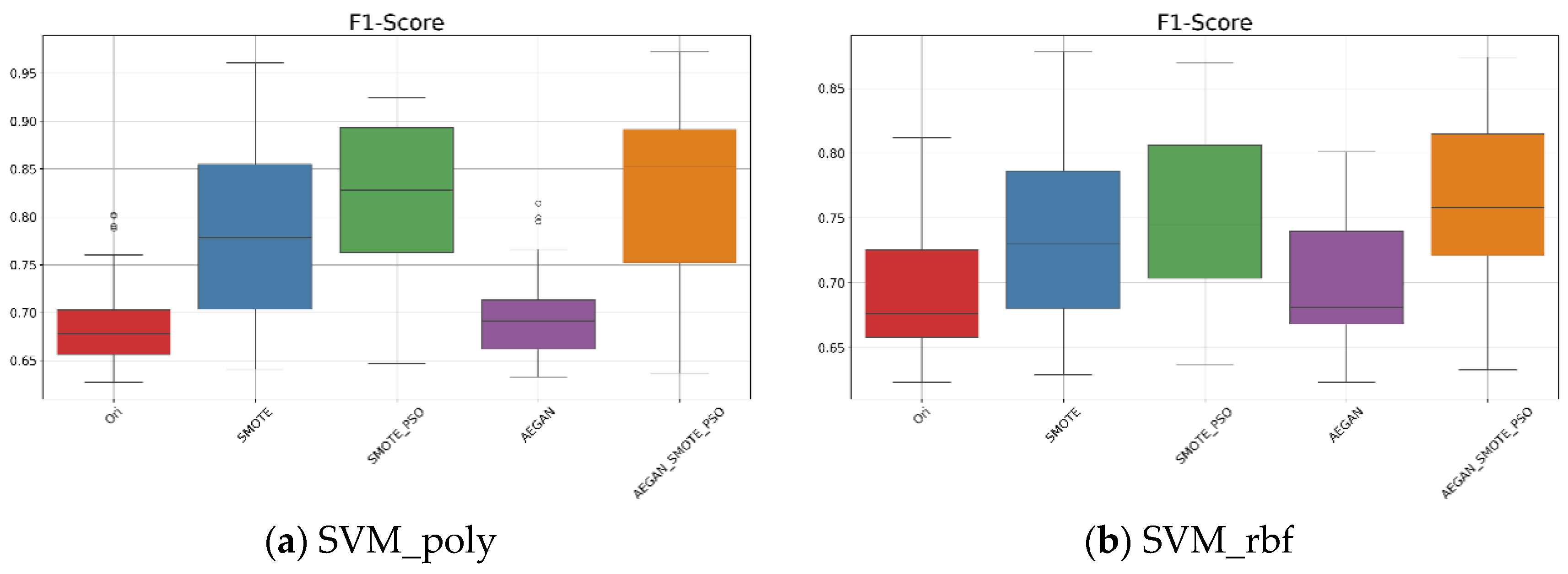
In Table 3 and Figure 4a, based on the original dataset, when the kernel function is set to polynomial, it can be seen that the average F1-score was 0.691. After applying the AEGAN-SMOTE-PSO model, the F1-score was increased to 0.823. The model effectively generated representative synthetic samples. The standard deviation of the F1-score was 0.094, indicating that the classification results using the AEGAN-SMOTE-PSO model are relatively stable. When the kernel function is changed to RBF, as illustrated in Figure 4b, the AEGAN-SMOTE-PSO model demonstrates the best predictive performance among all compared methods, where its average F1-score reached 0.762.

Table 3. Average and standard deviation of the two SVM models using the techniques on the Wisconsin diagnostic data.

Classifier	SVM_poly
Performance	Metric	Ori	SMOTE	SMOTE-PSO	AEGAN	AEGAN-SMOTE-PSO
Average	Recall	0.602	0.728	0.773	0.609	0.778
	Precision	0.813	0.859	0.874	0.815	0.879
	F1-score	0.691	0.785	0.818	0.697	0.823
Standard deviation	Recall	0.066	0.119	0.116	0.062	0.125
	Precision	0.021	0.046	0.044	0.020	0.049
	F1-score	0.050	0.089	0.086	0.047	0.094
Classifier	SVM_rbf
Performance	Metric	Ori	SMOTE	SMOTE-PSO	AEGAN	AEGAN-SMOTE-PSO
Average	Recall	0.605	0.660	0.680	0.616	0.696
	Precision	0.814	0.833	0.839	0.817	0.845
	F1-score	0.693	0.735	0.750	0.701	0.762
Standard deviation	Recall	0.065	0.089	0.082	0.065	0.082
	Precision	0.021	0.031	0.029	0.020	0.029
	F1-score	0.050	0.067	0.062	0.049	0.062

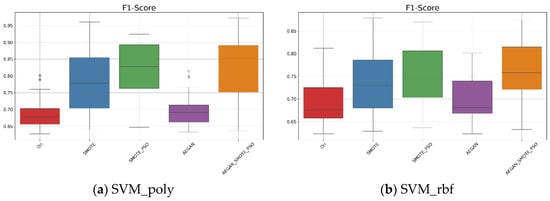
Figure 4. Boxplots for the SVM results on the Wisconsin diagnostic data.

5. Conclusions

In medicine, class imbalance may lead to incorrect disease classification and misdiagnosis. To tackle the class imbalance problem, we developed the AEGAN-SMOTE-PSO model. By combining AEGAN with SMOTE-PSO, the diversity of the minority class examples is enhanced to effectively boost predictive performance for imbalanced data. A comparative analysis was performed using three oversampling methods—SMOTE, SMOTE-PSO, and AEGAN—alongside the original data. The experimental results indicate that under an imbalance ratio of nine, the developed AEGAN-SMOTE-PSO model consistently outperforms the other four methods for two SVM models across three evaluation indicators. This demonstrates its superior classification performance and effectiveness in addressing class imbalance. In the future, the developed model needs to be extended to other imbalanced medical datasets.