FGM Sandwich Curved Beam Under Thermomechanical Loads for Hydrogen Mechanical Applications ^†

Abstract

In this study, a curved sandwich beam with Functionally Graded Materials (FGM) face sheets and a homogeneous core under thermomechanical loads is investigated. The problem is studied numerically by the finite element method (FEM). Plane, eight nodes isoparametric elements are used, where the gradient of the material properties is incorporated into the formulation of the element. The effect of the thickness and volume fraction index (VFI) of the FGM face sheets on the stress and the temperature fields are studied. The results are valuable in the design of hydrogen mechanical applications, since the FGM sandwich curved beam could be a part of hydrogen storage tanks.

1. Introduction

Liquid hydrogen (LH₂) offers high specific energy and zero-emission potential for aviation, but its storage at extremely low temperatures (−253 °C) introduces severe thermomechanical challenges. Thermal gradients, heat ingress, and repeated thermal cycling could induce significant thermal stresses in LH₂ storage tank structures, affecting material performance and structural integrity. As the aviation sector moves toward decarbonization goals (e.g., the European Green Deal), research increasingly focuses on the coupled thermal and mechanical behavior of LH₂ storage tanks, with emphasis on insulation efficiency, stress mitigation, and material durability under extreme thermal loads [1].

A way to handle the aforementioned issues appearing on storage tanks is to structure them with Functionally Graded Materials (FGM). The proposed use of FGMs was made in Japan (1984) as a preparation of thermal barrier materials [2]. Initially, FGMs were used in aerospace but there are applications in other fields, like industrial materials, optoelectronics, biomaterials, energy materials, Nuclear Energy, Electronics, Cutting Tools, and Automotive [3,4]. The use of FGMs has the following advantages [5,6]: (a) smoothing of the thermal stress distribution, (b) mitigated or eliminated interfacial cracking or debonding caused by stress concentration due to abrupt change in material properties between distinct materials, (c) minimization or elimination of stress concentrations and singularities at the free edges, and (d) increase in the bond strength of two materials and improved fracture toughness.

The materials commonly used in applications are as follows [7]: FGM Alloys: Aluminum, Copper, and Titanium and, as reinforcements, Aluminum oxide, Silicon carbide, Silicon nitride, Silicon dioxide, Titanium nitride, Titanium dioxide, and Aluminum nitride.

In this study, a curved sandwich beam which may be used as a storage tank component, with FGM face sheets and a homogeneous core under thermomechanical loads, is investigated. In particular, we study two cases of core material, the Silicon carbide (SiC) and Titanium carbide (TiC), and in both cases, Aluminum alloy is the metal material. The finite element method (FEM) is used to deal with the problem. Plane isoparametric eight-node elements are used, where the gradient of the material properties is incorporated in the formulation of the element. In our investigation, the Gauss quadrature method is applied, and the material properties are sampled at the Gauss points. The effect of the thickness and volume fraction index (VFI) of the FGM face sheets on the stress and the temperature fields are studied.

2. Thermoelasticity Governing Equations

The equations of motion and energy equation are given below [8,9,10]:

$${\mathsf{\sigma }}_{ij,j}=0,q_{i,i}=0$$

(1)

where ${\mathsf{\sigma }}_{ij}$ is the stress tensor and the $q$ is the heat flux. The kinematic equations are [9,11,12]

$${\mathsf{\epsilon }}_{ij}={\displaystyle \frac{1}{2}}\left(u_{i,j}+u_{j,i}\right)={\mathsf{\epsilon }}_{ij}^{el}+{\mathsf{\epsilon }}_{ij}^{th}\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mathsf{\epsilon }}_{ij}^{th}=\alpha {\delta }_{ij}\mathsf{\theta },$$

(2)

where $a$ is the coefficient of thermal expansion, ${\mathsf{\epsilon }}_{ij}$ total strain, ${\delta }_{ij}$ the Kronecker’s delta and $\mathsf{\theta }$ is the temperature difference, and $u_i$ is the displacement. Furthermore, the constitutive equations are given by [8,9,10,13]

$${\mathsf{\sigma }}_{ij}=C_{ijkl}{\mathsf{\epsilon }}_{kl}-{\beta }_{ij}\mathsf{\theta },\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{q}_i=-k_{ij}\mathsf{\theta }{,}_j$$

(3)

where $C_{ijkl}$ is the fourth order tensor of elastic moduli, ${\beta }_{ij}$ is the thermoelasticity tensor, and $k_{ij}$ is the thermal conductivity tensor. The equations of thermoelasticity for nonhomogeneous graded materials are [11]

$${\left(\mu \left(x,y\right)\left(u_{i,j}+u_{j,i}\right)\right)}_{,j}+{\left(\lambda \left(x,y\right)u_{k,k}\right)}_{,i}-{\left(\beta \left(x,y\right)\mathsf{\theta }\right)}_{,i}=0,{\left(k\left(x,y\right){\mathsf{\theta }}_{,i}\right)}_{,i}=0$$

(4)

3. Numerical Implementation

3.1. FEM

In FEM, for a plane element with n nodes, the $\left(u, v\right)$ and the $\mathsf{\theta }$ fields are approximated by the shape functions $N_i$ [8,9,14] and take the following form:

$$u\left(x,y\right)={\displaystyle \sum _{i=1}^n{u}_i^{\left(e\right)}{N}_i\left(x,y\right),}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}v\left(x,y\right)={\displaystyle \sum _{i=1}^n{v}_i^{\left(e\right)}{N}_i\left(x,y\right),}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathsf{\theta }\left(x,y\right)={\displaystyle \sum _{i=1}^n{\mathsf{\theta }}_i^{\left(e\right)}{N}_i^{\mathsf{\theta }}\left(x,y\right)}$$

(5)

Applying the Galerkin method [8,9,10] for Equation (4), it is obtained:

$$\begin{array}{l}{\displaystyle {\int }_{V^{\left(e\right)}}\mu N_{m,j}{N}_{l,j}dV{u}_{mi}^{(e)}}+{\displaystyle {\int }_{V^{\left(e\right)}}\mu N_{m,j}{N}_{l,j}dV{u}_{mj}^{(e)}}+{\displaystyle {\int }_{V^{\left(e\right)}}\lambda N_{m,j}{N}_{l,j}dV{u}_{mj}^{(e)}}\\ -{\displaystyle {\int }_{V^{\left(e\right)}}\beta N_{l,j}{N}_m^{\mathsf{\theta }}dV{\mathsf{\theta }}_m^{(e)}}={\displaystyle {\int }_{A^{\left(e\right)}}{t}_i^{(n)}{N}_{l}dA}\end{array}$$

(6)

Similarly, the energy equation becomes

$${\displaystyle {\int }_{V^{\left(e\right)}}k{N}_{m,i}^{\mathsf{\theta }}{N}_{l,i}^{\mathsf{\theta }}dV{\mathsf{\theta }}_m^{(e)}}={\displaystyle {\int }_{A^{\left(e\right)}}{q}_i{n}_i{N}_l^{\mathsf{\theta }}dA}$$

(7)

3.2. Graded FEM

In the GFEM, the material properties are sampled at the Gauss points, which is referred to as Direct Gaussian integration formulation (DGIF) [15].

The displacements for the isoparametric elements are given by [15,16,17]:

$$u={\displaystyle \sum _{i=1}^n{N}_i(\mathsf{\xi },\mathsf{\eta })u_i^e}$$

(8)

For the case of the functionally graded materials, the matrices are [11]

$$\begin{array}{l}{K}_{MM}^{(e)}={\displaystyle {\int }_{V^{(e)}}{\left[B\right]}^T\left[D\left(x\right)\right]\left[B\right]dV,}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{K}_{M\mathsf{\theta }}^{(e)}={\displaystyle {\int }_{V^{(e)}}{\left[B\right]}^T\left[\beta \left(x\right)\right]\left[N^{\mathsf{\theta }}\right]dV},\\ K_{\mathsf{\theta }\mathsf{\theta }}^{(e)}={\displaystyle {\int }_{V^{(e)}}{\left[B^{\mathsf{\theta }}\right]}^T\left[\kappa \left(x\right)\right]\left[B^{\mathsf{\theta }}\right]dV}\end{array}$$

(9)

Flux at a boundary due to convection is given by Newton’s law of cooling [18,19]:

$$q_B=h\left(T_s-T_{\infty }\right)$$

(10)

where $q_B$ is the heat flux on the boundary [19]. Temperature in the fluid varies from $T_{\infty }$ to the surface temperature $T_s$ through the thickness of a boundary layer adjacent to the solid [18]. The convection matrix and convection vector for $\mathsf{\eta }=1$ are given by [18,19]

$$K_h^{(e)}={\displaystyle {\int }_{-1}^1{\left[N^{\mathsf{\theta }}\right]}^{T}h\left[N^{\mathsf{\theta }}\right]t{J}_{s}d\mathsf{\xi }}\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{r}_h^{(e)}={\displaystyle {\int }_{-1}^1{\left[N^{\mathsf{\theta }}\right]}^{T}h{T}_{\infty }t{J}_{s}d\mathsf{\xi }},$$

(11)

where $J_s=\sqrt{\left({\left({\displaystyle \frac{dx}{d\mathsf{\xi }}}\right)}^2+{\left({\displaystyle \frac{dy}{d\mathsf{\xi }}}\right)}^2\right)}$

The local material properties of the element are obtained by substituting the Cartesian coordinates $\left(x, y\right)$ in terms $\left(\mathsf{\xi },\mathsf{\eta }\right)$ [20]:

$$P_e\left(\mathsf{\xi },\mathsf{\eta }\right)=P\left({\displaystyle \sum _{k=1}^n{x}_k{N}_k(\mathsf{\xi },\mathsf{\eta }),{\displaystyle \sum _{k=1}^n{y}_k{N}_k(\mathsf{\xi },\mathsf{\eta })}}\right)$$

(12)

Finally, the general matrix has the following form:

$$\left[\begin{array}{cc}{K}_{MM}^{(e)}& -K_{M\mathsf{\theta }}^{(e)}\\ 0& K_{T\mathsf{\theta }}^{(e)}\end{array}\right]\left\{\begin{array}{c}{u}^{(e)}\\ {\mathsf{\theta }}^{(e)}\end{array}\right\}=\left\{\begin{array}{c}{F}_M^{(e)}\\ F_{\mathsf{\theta }}^{(e)}\end{array}\right\}$$

(13)

where $K_{T\mathsf{\theta }}^{(e)}=K_{\mathsf{\theta }\mathsf{\theta }}^{(e)}+K_h^{(e)}$.

4. The Curved Beam Application

From the problem presented in Figure 1 [21], the boundary conditions (BCs) are fixed support at both beam ends, a temperature $T_1$ at the lower outer surface, and a pressure $p$ and the convection BC $\left(h_s,T_{\infty }\right)$ at the upper–outer surface. The radius differences $h_1:=\left|R_2-R_1\right|=\left|R_4-R_3\right|$ define the FGM sheets’ thickeness. Moreover, the parameteres are reference temperature $T_0=0 °\mathrm{C}$, convection coefficient $h_s=2.183\hspace{0.17em}{ \mathrm{W}/\mathrm{m}}^2·\mathrm{K}$, pressure $p=170 \mathrm{kPa}$, height $h=1 \mathrm{m}$, free flow temperature $T_{\infty }=-25 °\mathrm{C}$, boundary temperature $T_1=25 °\mathrm{C}$, and radius $R_3-R_2=\left\{0.6,0.33\right\} \mathrm{m},R_1=199.5 \mathrm{m},R_4=200.5 \mathrm{m}$.

The variation of material properties for the ceramic core configuration is given by [21,22]

$$P\left(r\right)=P_m+\left(P_c-P_m\right)V_c$$

(14)

where $P$ is the material property, $P_c$ is the ceramic material property, $P_m$ is the metal material property, $V_c$ is the volume fraction of the ceramic phase, and $p_1$ is the volume fraction index (VFI) [21,22]. In particular, we have

$${\mathrm{V}}_c^{\left(1\right)}={\left({\displaystyle \frac{r-R_1}{R_2-R_1}}\right)}^{p_1},\hspace{0.17em}\hspace{0.17em}r\in \left[R_1,R_2\right]\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mathrm{V}}_c^{\left(2\right)}=1,\hspace{0.17em}\hspace{0.17em}r\in \left[R_2,R_3\right]\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em},\hspace{0.17em}{\mathrm{V}}_c^{\left(3\right)}={\left({\displaystyle \frac{r-R_4}{R_3-R_4}}\right)}^{p_1},\hspace{0.17em}\hspace{0.17em}r\in \left[R_3,R_4\right]$$

(15)

We study two cases of core material, SiC and TiC, with Aluminum as the metal material (

Table 1. Material properties [23,24,25].

	TiC	SiC	Aluminum 6061-T651
Young’s modulus (GPa)	410–510	410	68.9
Poisson’s ratio	0.191	0.14	0.33
Thermal conductivity (W/m∙°K)	21	120	167
Thermal expansion (×10−6/°C)	7.6	4.0	23.6

).The solution of the problems conducted with plane isoparametric quadratic eight-node elements, where the gradient of the material properties is incorporated into the formulation of the element. For the integration, the Gauss quadrature method is used and the material properties are sampled at the Gauss points. The number of elements is 1800 in each layer (FGM sheets and core) and, in total, 5400 (Figure 2).

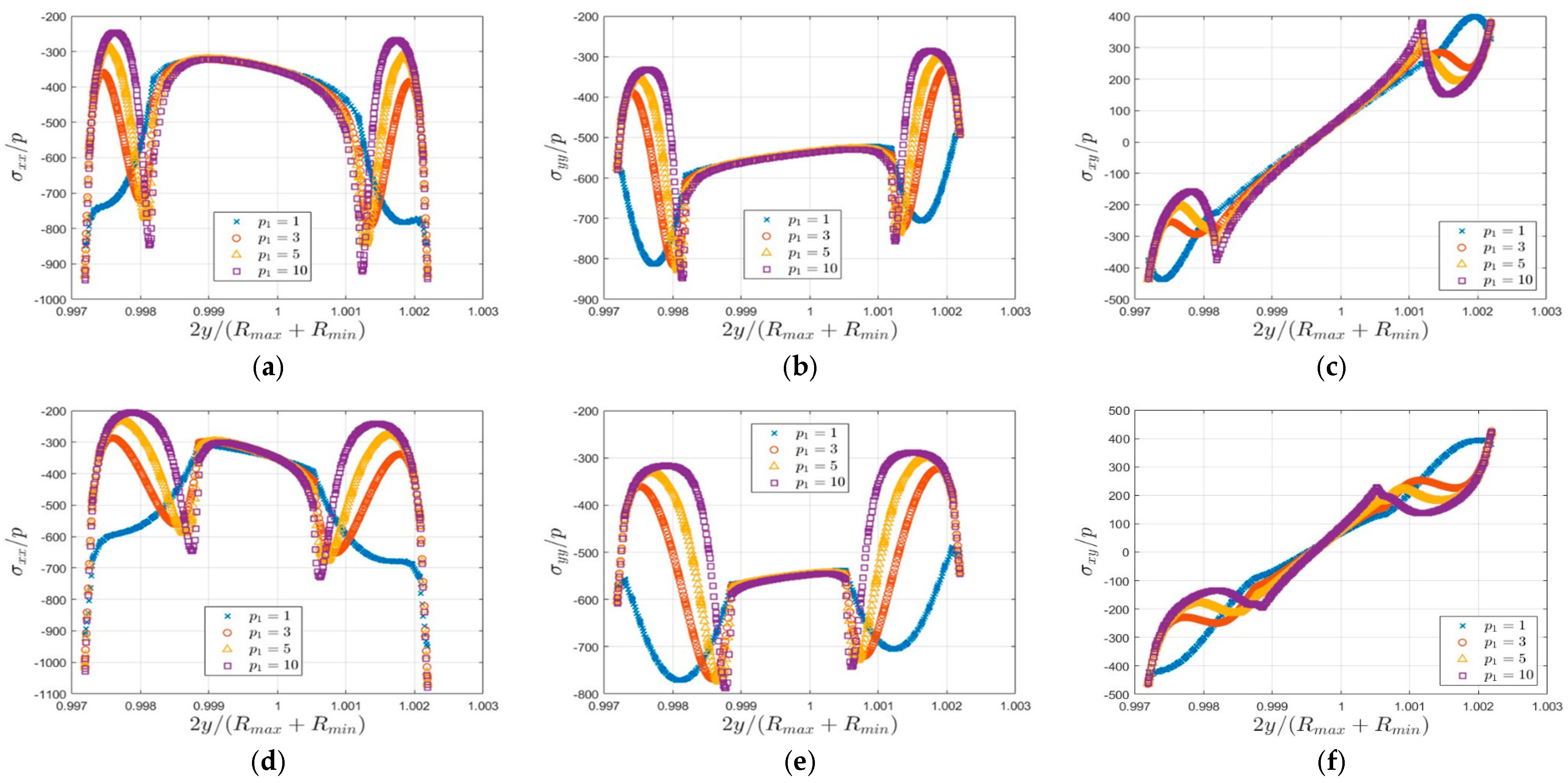
5. Results and Discussion

In this section, the stress distributions ${\mathsf{\sigma }}_{xx}$, ${\mathsf{\sigma }}_{yy}$, ${\mathsf{\sigma }}_{xy}$ and the temperature through the height of the beam section are presented for the left fixed end. Figure 2 and Figure 3 referred to the SiC core and Figure 4 and Figure 5 to TiC.

Figure 3. SiC’s stress distributions (i) ${\displaystyle \frac{h_1}{h}}=0.2$, (a–c) and (ii) ${\displaystyle \frac{h_1}{h}}=0.33$, (d–f).

Figure 3. SiC’s stress distributions (i) ${\displaystyle \frac{h_1}{h}}=0.2$, (a–c) and (ii) ${\displaystyle \frac{h_1}{h}}=0.33$, (d–f).

Figure 4. SiC’s temperature distributions (a) ${\displaystyle \frac{h_1}{h}}=0.2$, (b) ${\displaystyle \frac{h_1}{h}}=0.33$ and (c) a comparison for the two different FGM sheets’ thickness in the case of $p_1$ = 1.

Figure 4. SiC’s temperature distributions (a) ${\displaystyle \frac{h_1}{h}}=0.2$, (b) ${\displaystyle \frac{h_1}{h}}=0.33$ and (c) a comparison for the two different FGM sheets’ thickness in the case of $p_1$ = 1.

Figure 5. TiC’s stress distributions (i) ${\displaystyle \frac{h_1}{h}}=0.2$, (a–c) and (ii) ${\displaystyle \frac{h_1}{h}}=0.33$, (d–f).

Figure 5. TiC’s stress distributions (i) ${\displaystyle \frac{h_1}{h}}=0.2$, (a–c) and (ii) ${\displaystyle \frac{h_1}{h}}=0.33$, (d–f).

The temperature $T$ is quite similar both for SiC and TiC materials for the different values of VFIs (Figure 4 and Figure 6). For the case of the TiC with $p_1=1$ and ${\displaystyle \frac{h_1}{h}}=0.33$, there is a distinguished difference in the upper face sheet (Figure 6b,c).

Figure 6. TiC’s temperature distributions (a) ${\displaystyle \frac{h_1}{h}}=0.2$, (b) ${\displaystyle \frac{h_1}{h}}=0.33$ and (c) a comparison for the two different FGM sheets’ thickness in the case of $p_1$ = 1.

Figure 6. TiC’s temperature distributions (a) ${\displaystyle \frac{h_1}{h}}=0.2$, (b) ${\displaystyle \frac{h_1}{h}}=0.33$ and (c) a comparison for the two different FGM sheets’ thickness in the case of $p_1$ = 1.

In the cases of the SiC and TiC, the stress distributions ${\mathsf{\sigma }}_{xx}$, ${\mathsf{\sigma }}_{yy}$, ${\mathsf{\sigma }}_{xy}$ are almost identical for all values of $p_1$ along the core (Figure 3 and Figure 5). For the cases of $p_1=3,5,10$ the stress distributions at the face sheets are quite similar. However, a significant difference between the stresses distributions of $p_1=1$ and the stresses distributions of $p_1=3,5,10$ is appeared (Figure 3 and Figure 5).

In addition, for both materials (SiC and TiC) and for the different values of $p_1$, the stresses ${\mathsf{\sigma }}_{xx}$ have the maximum values at the outer surfaces of the beam. The stresses ${\mathsf{\sigma }}_{yy}$ have the maximum values at the interfaces between the face sheets and the core of the beam. There is an exception regarding the TiC material, in the case of $p_1$ where the maximum value of ${\mathsf{\sigma }}_{yy}$ is located on the inner part of the face sheets.Finally, the stresses ${\mathsf{\sigma }}_{xy}$ have the maximum values at the outer surfaces of the beam (Figure 3 and Figure 5).

The FGM face sheets’ thickness affectsneither the maximum (or the minimum) of the stress distributions nor the quality form of them (Figure 3 and Figure 5), except for the case of ${\mathsf{\sigma }}_{xy}$ distributions of SiC (Figure 3c,f).

6. Conclusions and Perspectives

In the present study, an aircraft/aerospace LH₂ storage component is investigated for its structural response under thermomechanical loadings. The component is simulated as a curved sandwich beam comprising FGM face sheets and a homogeneous core. The numerical study is performed by the FEM, utilizing eight-node, plane, isoparametric elements. The computational analysis is based on the incorporation of the spatial variation of material properties directly into the element formulation, thereby enabling an accurate representation of the gradient effects within the FGM layers. The influence of both the thickness and the VFI of the FGM face sheets on the resulting stress and temperature fields is examined. As in our best knowledge, this is the first time that the aforementioned problem has been attempted to be handled.

The numerical results indicate that, for all configurations considered, the maximum stress values occur at the outer FGM surfaces or at the interface between the core and the face sheets of the curved beam for both SiC and TiC materials, regardless of the face-sheet thickness. Furthermore, the stress distributions corresponding to $p_1=1$ exhibit smoother gradients compared with those of $p_1=3,5,10$. The temperature field is found to be nearly linear across the FGM thickness for SiC, whereas for TiC it exhibits a linear variation with a different slope across the distinct material regions.

The scope of our study highlights the necessity for a detailed and rigorous design methodology in the development of LH₂ storage components to mitigate the risk of fracture and failure under severe thermomechanical BCs.

The present results provide preliminary valuable insights toward the identification and optimization of suitable advanced materials for reliable LH₂ containment in engineering applications.