Abstract
Fiber-Metal Laminates (FMLs) are hybrid composite structures of alternating metal layers and fiber-reinforced preimpregnated (prepreg) layers. The purpose of this article is to study numerically the elastic buckling behavior of simply supported FML plates compressed by two equal and opposite forces. More specifically, the main objective of the present study is the calculation of buckling coefficients of thin GLARE plates and the construction of diagrams of these coefficients as a function of their aspect ratio. It is found that the diagrams of the buckling coefficient versus the aspect ratio of aluminum and GLARE plates present a very similar trend.
1. Introduction
Laminated composites have been studied and used extensively as main materials for many modern applications in automotive and aerospace engineering, such as hydrogen storage [1]. However, considering that further research is required to improve the potential of laminated materials and extend their applications, future research should focus on advanced materials by developing multifunctional materials and hybrid composites such as Fiber-Metal Laminates (FMLs).
FMLs are hybrid composite and laminated structures consisting of alternating metal layers and fiber-reinforced preimpregnated (prepreg) layers. FMLs have exceptional mechanical properties, and they are mainly applied in the aerospace and automotive industries [2]. Due to the epoxy-based polymer matrix of the composite layers and the low-density aluminum sheets, FMLs are a weight-saving structural material in comparison to classical metal alloys. It is noted that aluminum alloys are used in the majority of the industrial FMLs. Furthermore, taking into account that weight saving is of critical importance in aerospace and automotive engineering, most FML structures are thin-walled. Consequently, the buckling behavior of FMLs is very important for mechanical engineers.
The purpose of this article is to study the elastic buckling behavior of simply supported GLARE (GLAss REinforced) plates compressed by two equal and opposite forces. GLARE is the most successful FML up to now, with respect to the variety and extent of its applications. More specifically, the main objective of the present study is the calculation of buckling coefficients of thin GLARE plates and the construction of diagrams of these coefficients as a function of their aspect ratio.
The scientific research concerning the buckling of isotropic and composite materials is intensive. Teter and Kolakowski [3] studied the phenomenon of multimodal buckling of wide stiffened plates made of Functionally Graded Materials subject to uniform compression in the elastic range. York and Williams [4] presented a theory and buckling results for skewed plate assemblies that are infinitely wide. Their results illustrated the beneficial effect of shear loading on the load-carrying capacity of stiffened panels under certain conditions. Prasad and Sahu [5] investigated the numerical and experimental investigation of the buckling behavior of glass fiber metal laminated plates. More specifically, they examined the effects of various parameters such as aspect ratio, side-to-thickness ratio, ply orientation and boundary conditions on buckling loads of the considered materials. In the study of Jasion and Magnucki [6], the strength and elastic buckling of a sandwich cylindrical pressure vessel with an individual functionally graded core was investigated numerically through the finite element method. These materials may be used in various applications related to the automotive industry, such as hydrogen tanks. Kim et al. [7] proposed a simplified and useful design formula for the elastic buckling and the ultimate strength of a plate under longitudinal compression.
The main objective of the present study is the calculation of buckling coefficients of thin wide GLARE plates subjected to transverse compression and the construction of pertinent diagrams of these coefficients as a function of their aspect ratio. The axial compression is applied through two equal and opposite forces at the large edges of the plates (loading vertical to the length direction of the plates). According to the authors’ knowledge, the buckling of thin and wide FML plates subjected to transverse compression has not been published so far. In the previous authors’ work [8], the examined plates were subjected to longitudinal loading along the small edges of the plate (loading parallel to the length direction of the plates).
2. Problem Delineation
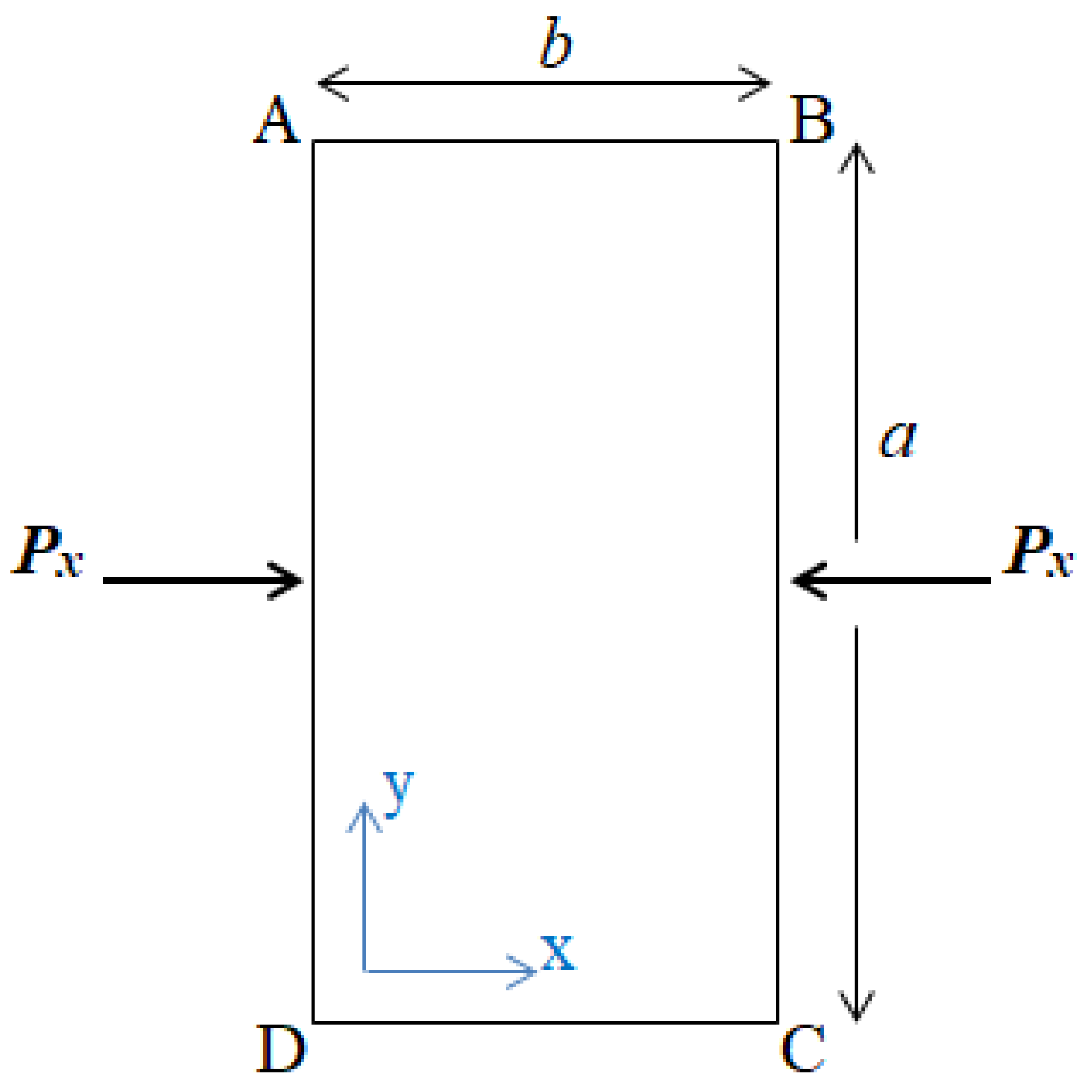
A thin simply supported rectangular GLARE plate is considered with length a, width b and thickness t. The plate consists of aluminum and unidirectional (UD) glass–epoxy layers. The static loading of the plate is applied through two equal and opposite forces, Px, along the vertical (long) edges (AD and BC), as it is illustrated in Figure 1. Taking into account the simply supported boundary conditions of the plate and the applied loading, the plate will buckle for a critical value of this loading Pcr, which corresponds to the critical buckling load of the plate. It is noted that the elastic buckling of the plate is examined.
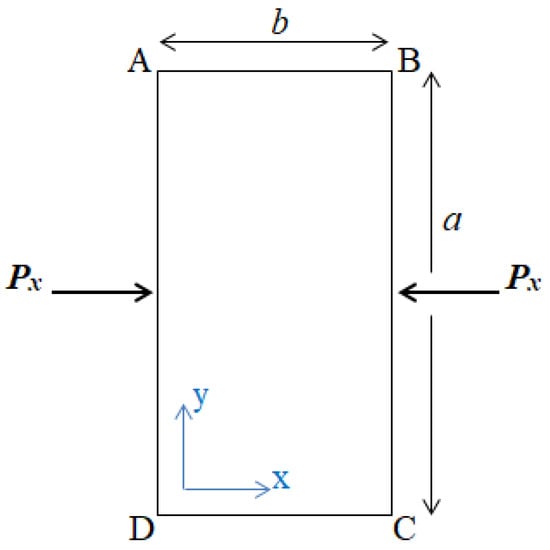
Figure 1.
Top view of a rectangular plate along with the compressive loading.
3. Numerical Modeling
The critical buckling load of the examined thin rectangular plates is calculated through a finite element modeling procedure using the finite element software ANSYS 15.0 [9]. SHELL 181 elements are used for the modeling of the considered thin plates. These elements are suitable for analyzing thin to moderately thick layered structures, and they have four nodes with six degrees of freedom per node (three translational and three rotational).
The metal layers of the considered materials are composed of 2024-T3 aluminum alloy, and they are modeled as isotropic linear elastic material, whereas the composite (UD glass–epoxy) layers are modeled as orthotropic linear elastic material. The compressive loading is applied at the points located at the middle of the long edges of the plate (Figure 1). The compressive force Px is equal to unity.
The critical buckling load and the corresponding mode shape of the examined plates are predicted using the eigenvalue buckling analysis of ANSYS 15.0 software. The convergence of the finite element results is always checked through a comparison between a fine and a very fine meshed model. It is noted that the convergence check is carried out for the buckling load and for the mode shape as well. The stress levels of the plies of the examined plates are checked in all models, in order to ensure that the aluminum and composite layers remain in the elastic range.
The buckling coefficient k corresponding to the critical buckling load of the isotropic aluminum plates is calculated as follows [10]:
where D is the bending stiffness of the aluminum plate.
The buckling coefficient k of the specially orthotropic GLARE plates is calculated [11]:
where Dii are the bending stiffnesses of the GLARE plate.
The width b of all plates is constant and equals 0.2 m, while the length a varies, in order to obtain the curves of the buckling coefficient and the buckling load as a function of the aspect ratio. The aspect ratio a/b is between the range 1 to 5. The total thickness of all considered plates is also constant (1.875 mm). Apart from the 2024-T3 aluminum plate, the presented numerical modeling procedure is also applied to four different GLARE grades, which are described below:
GLARE 2A-3/2-0.458, [Alum/0°/0°/Alum/0°/0°/Alum]
GLARE 2B-3/2-0.458, [Alum/90°/90°/Alum/90°/90°/Alum]
GLARE 3/2-0.292 (0°), [Alum/0°/0°/0°/0°/Alum/0°/0°/0°/0°/Alum]
GLARE 3/2-0.292 (90°), [Alum/90°/90°/90°/90°/Alum/90°/90°/90°/90°/Alum]
The 0° fiber orientation angle is parallel to the x-axis (Figure 1). According to the nomenclature of the aforementioned GLARE grades, the thickness of each aluminum layer is indicated by the last number in mm (e.g., 0.458 mm), whereas the thickness of each composite layer is always 0.125 mm. The mechanical properties of the considered materials are described in the following Table 1 and Table 2 [12].

Table 1.
Mechanical properties of 2024-T3 aluminum (Data from [12]).

Table 2.
Mechanical properties of S2 glass–epoxy composite layers (Data from [12]).
4. Validation of Numerical Procedure
It is necessary to apply suitable boundary conditions in the buckling problem, considering that the critical buckling load is sensitive with respect to different boundary conditions. The validation of the numerical procedure along with the suitability of the simply supported boundary conditions is carried out through comparison of the numerical with corresponding analytical results [13] concerning isotropic plates.
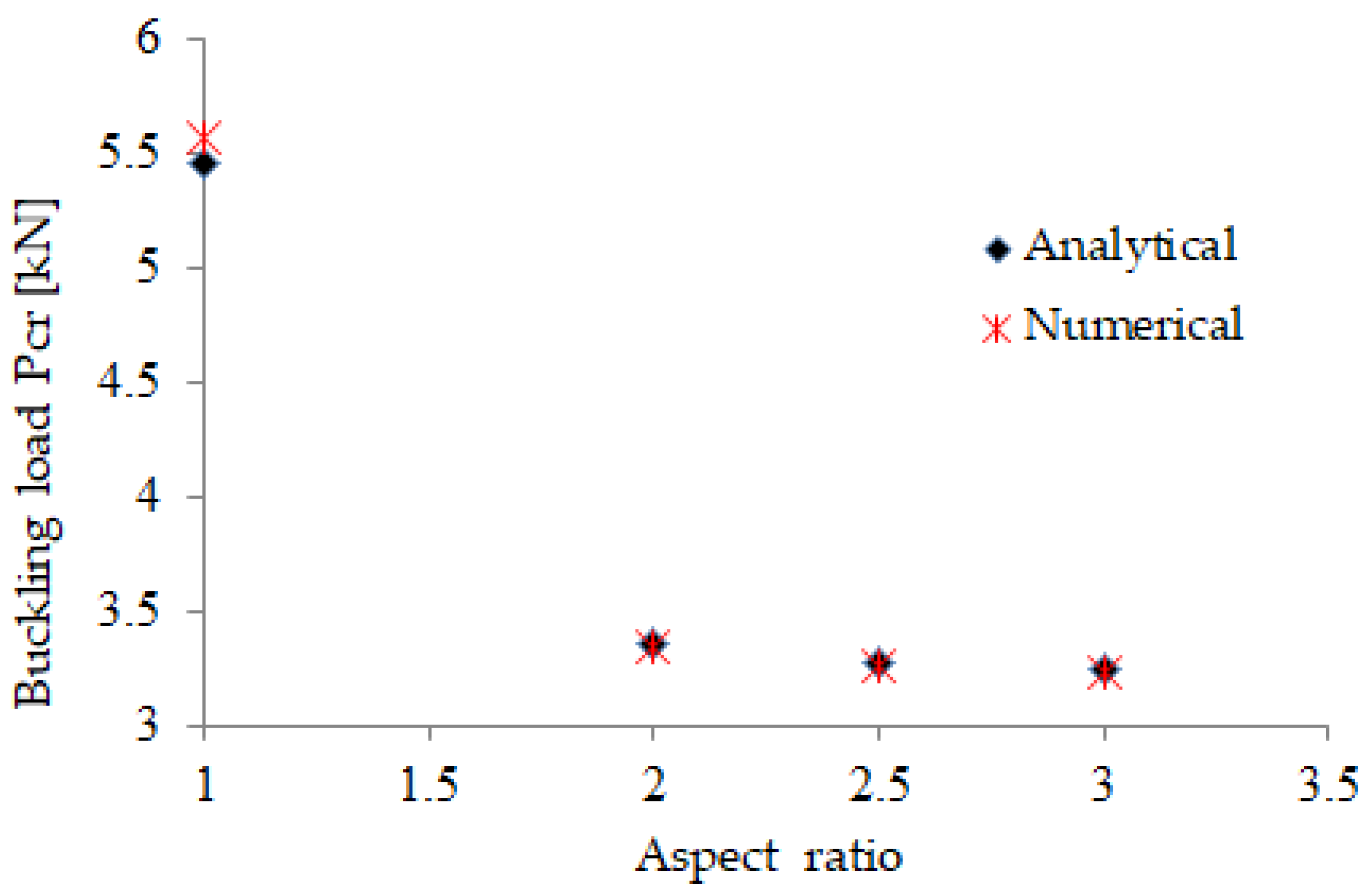
An excellent agreement has been found between the analytical results [13] and the finite element results, indicating that the implemented numerical procedure has been validated. More specifically, the absolute value of the divergence between the analytical and numerical results for the isotropic aluminum plates is lower than 2%, as it is graphically depicted in Figure 2. Taking into account the fact that the implemented numerical procedure and the boundary conditions are applied unchanged on the GLARE laminates, we consider that this procedure is valid for the examined GLARE FMLs as well. It is noted that the same consideration has been used in reference [8], where the numerical procedure for GLARE plates subjected to longitudinal compression had been successfully validated through comparison of the FEM results with analytical calculations.
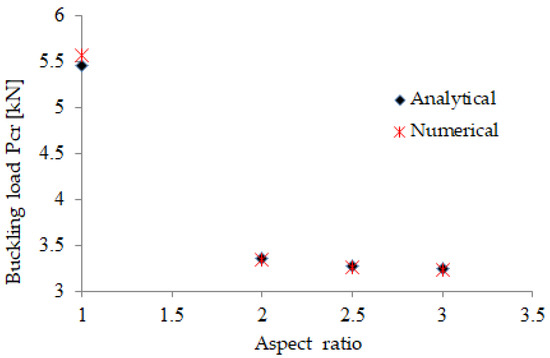
Figure 2.
Numerical [9] versus analytical [13] critical buckling load of simply supported aluminum plates.
5. Results and Discussion
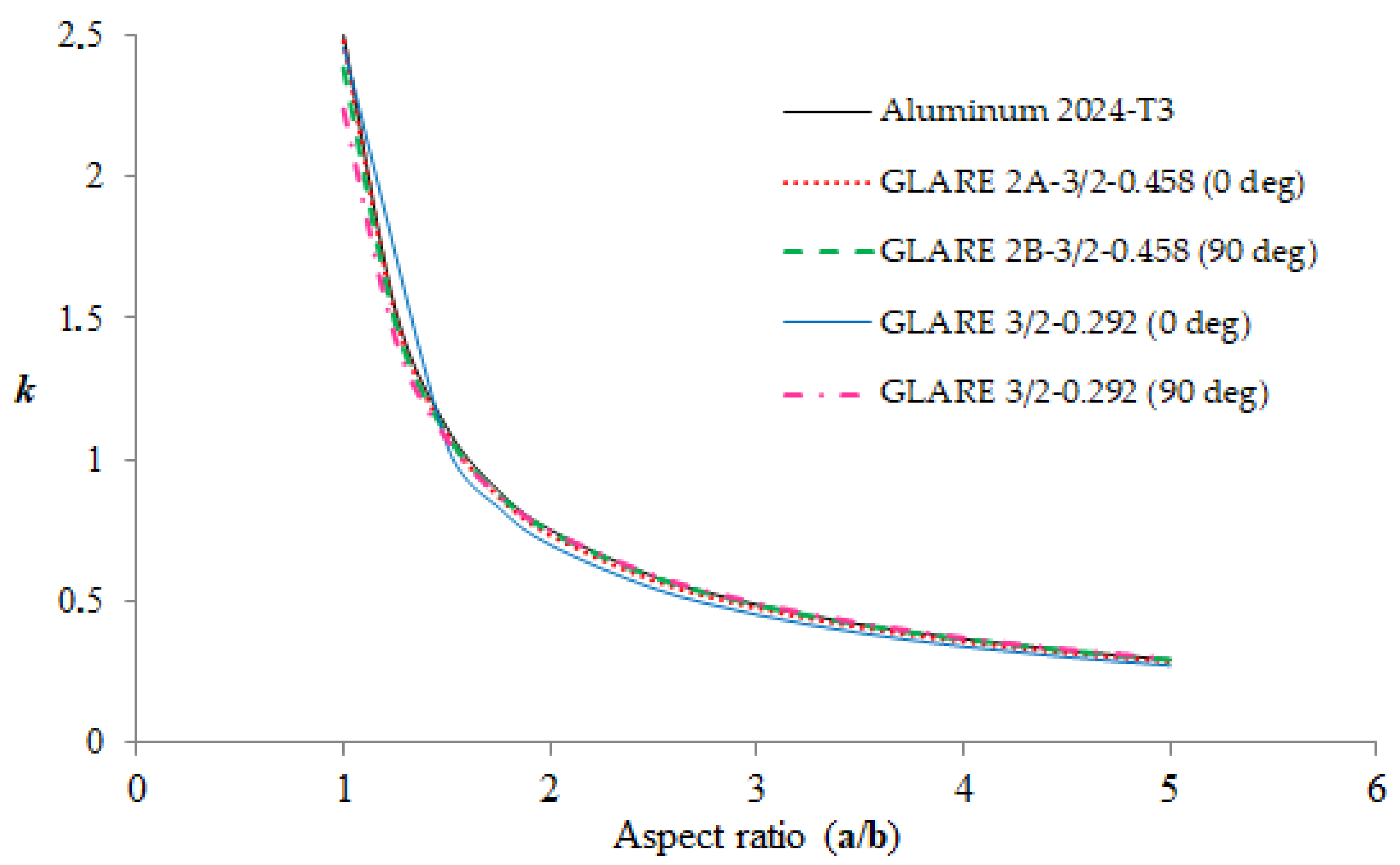
In Figure 3, the diagrams of buckling coefficients corresponding to the examined wide plates subjected to axial loading are illustrated. It is noted that the usefulness of these diagrams has to do with the fact that the buckling strength of the plates can be easily obtained, utilizing Equations (1) and (2).
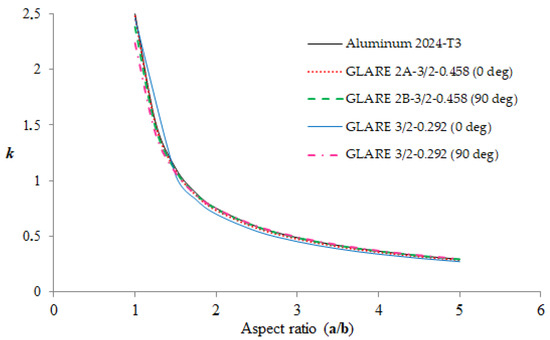
Figure 3.
Buckling coefficients of simply supported aluminum and GLARE plates subjected to uniaxial compression.
It is shown from Figure 3 that the (k, a/b) curves of the examined materials present a very similar trend (practically coincide), since it is difficult to even distinguish the curve of each material. This is an interesting finding, taking into account the fact that the different materials have different buckling strengths due to their different structural properties, as it is shown in Figure 4.
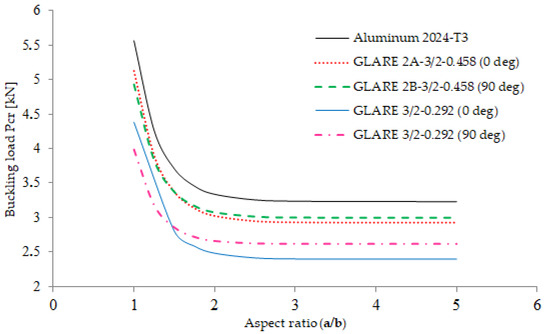
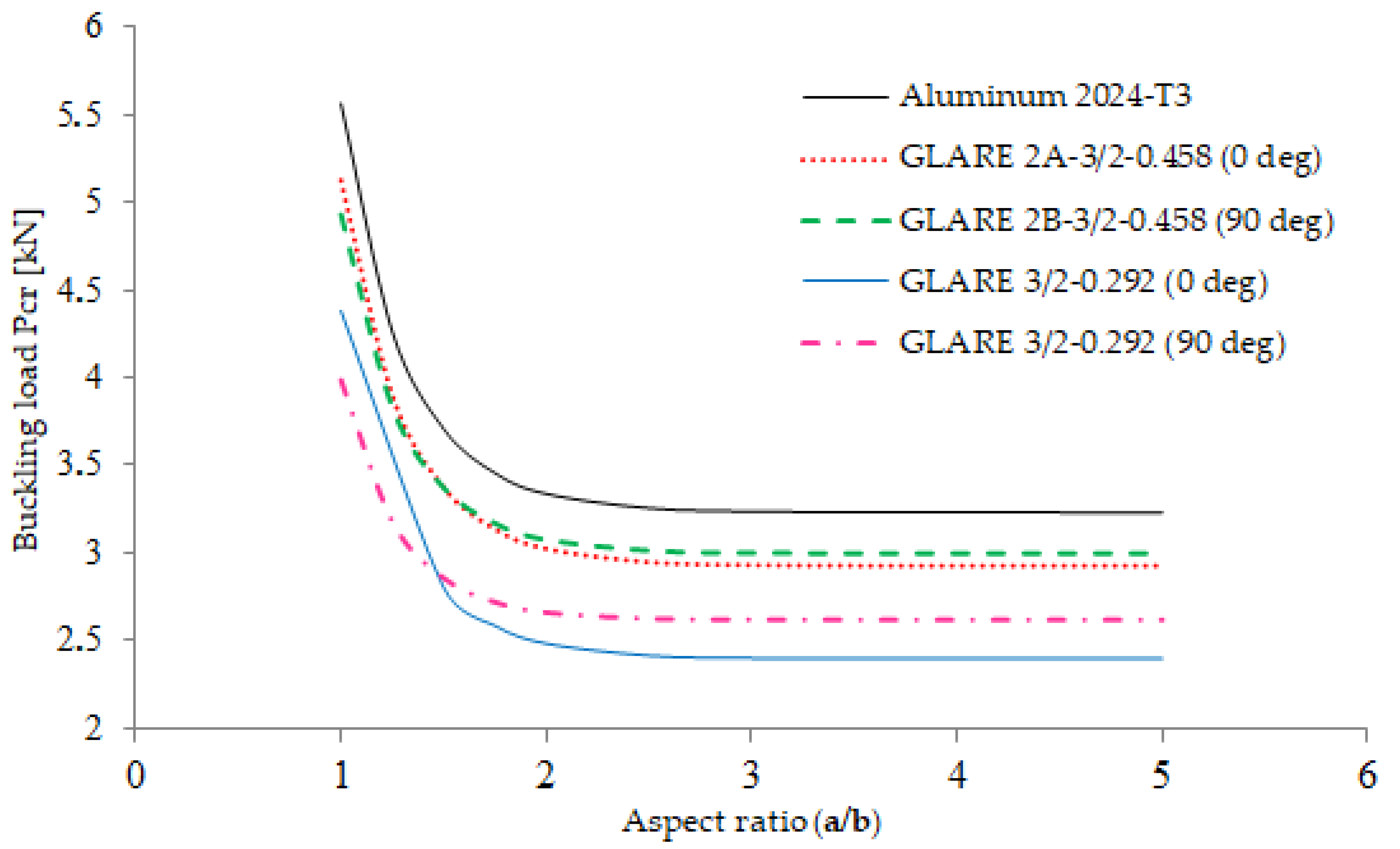
Figure 4.
Comparison of critical buckling load of simply supported aluminum and GLARE plates.
Although the buckling coefficient is a reliable indicator of the buckling strength of a plate, it is not convenient to directly compare the buckling strength of different materials using their buckling coefficients. This is attributed to the fact that k depends on the bending stiffness of each material, as it is indicated in Equations (1) and (2). Consequently, the direct comparison of the buckling strength of the considered materials is carried out using the values of their critical buckling loads. In Figure 4, the critical buckling loads are given as a function of their aspect ratio values.
It is observed from Figure 4 that aluminum plates have the highest buckling strength among the considered materials, and the two GLARE 3/2 laminates (with 0° and 90°) have the lowest buckling strength. Aluminum has a metal volume fraction (MVF) = 1, GLARE 2A and 2B have a MVF = 0.73 and GLARE 3/2 grades have a MVF = 0.47. As a result, it is observed from Figure 4 that the MVF is the most decisive parameter with respect to the critical buckling load of the considered materials.
An interesting observation concerning the fiber orientation angle is also observed from Figure 4. More specifically, it is observed that when comparing GLARE 2A and GLARE 2B, which have identical structural properties except for the fiber orientation of their composite layers, GLARE 2A (0°) is more buckling resistant than GLARE 2B (90°) when the aspect ratio is approximately lower than 1.5. On the other hand, when the aspect ratio is approximately higher than 1.5, GLARE 2B (90°) has a higher critical buckling load.
The same observation regarding the fiber orientation angle is also valid and more obvious between GLARE 3/2-0.292 (0°) and GLARE 3/2-0292 (90°), where the 90° fiber orientation angle yields clearly higher critical buckling load in comparison with the 0° fiber orientation angle when the aspect ratio is higher than 1.5.
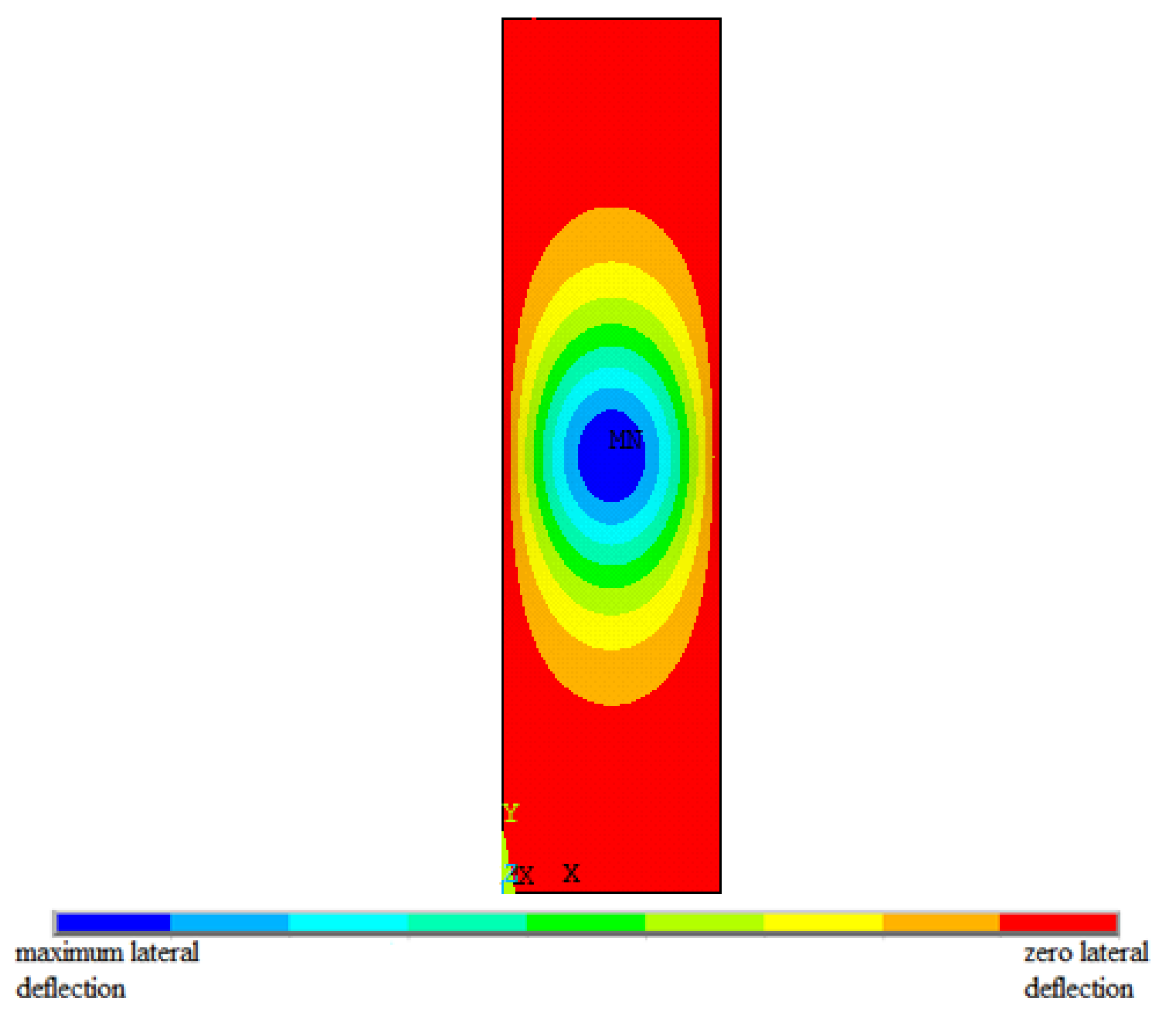
The critical mode shapes of the examined laminates have been calculated and studied in order to locate the areas on the plate surface where the higher stresses are developed. These are the areas that should be strengthened in order for the critical buckling load to be increased. Figure 5 illustrates the representative mode shape corresponding to the critical buckling load of a GLARE plate with aspect ratio a/b = 4. It is shown that one symmetrical half-wave is formed, and the maximum lateral deflection is located at the center of the plate. This finding is valid for all examined plates.
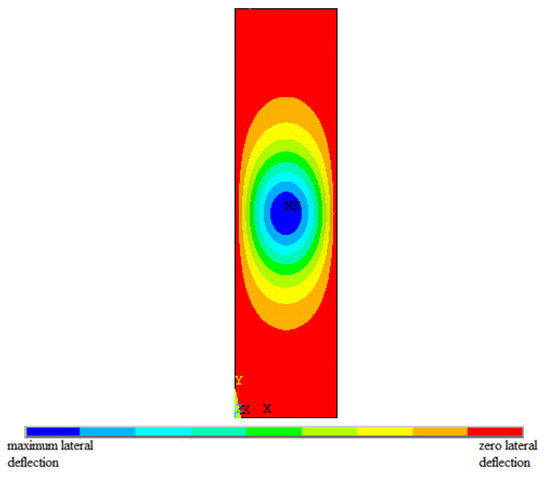
Figure 5.
FEM contour of the lateral deflection of the critical buckling mode shape of a simply supported FML plate (a/b = 4 (GLARE 3/2-0.292, 90°)) subjected to uniaxial compression.
6. Conclusions
This article investigates the elastic buckling of wide, simply supported GLARE laminates subjected to transverse compression. The two equal and opposite forces are applied at the middle of the long sides of the plate (vertically to the length direction). The classical eigenvalue buckling analysis is employed using ANSYS 15.0 FEM software in order to calculate the critical buckling load. It is found that the metal volume fraction is the most crucial factor determining the buckling strength of the considered materials. Another interesting finding is that the curves of the buckling coefficients as a function of the aspect ratio values practically coincide for all examined materials, although they have different structural properties. This study provides useful results and will help engineers and researchers to understand the elastic buckling behavior of wide rectangular GLARE plates when they are subjected to uniaxial compression. Additionally, considering that FMLs are advanced materials with exceptional properties, further research is required in order to extend their applications in other fields, such as hydrogen storage for the automotive or aerospace industry, which is a promising solution to the energy crisis.
Author Contributions
Conceptualization, G.S.E.B.; methodology, C.D.K.; software, C.D.K.; validation, G.S.E.B.; formal analysis, E.E.T.; investigation, G.S.E.B. and C.D.K.; writing—original draft preparation, C.D.K.; writing—review and editing, E.E.T.; visualization, G.S.E.B.; supervision, E.E.T.; project administration, E.E.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Feki, I.; Shirinbayan, M.; Nouira, S.; Bi, R.T.; Maeso, J.B.; Thomas, C.; Fitoussi, J. Composites in high pressure hydrogen storage: A review of multiscale characterization and mechanical behavior. Compos. Part C Open Access 2025, 16, 100555. [Google Scholar] [CrossRef]
- Sinmazçelik, T.; Avcu, E.; Bora, M.O.; Çoban, O. A review: Fibre metal laminates, background, bonding types and applied test methods. Mater. Des. 2011, 32, 3671–3685. [Google Scholar] [CrossRef]
- Teter, A.; Kolakowski, Z. Interactive buckling of wide plates made of Functionally Graded Materials with rectangular stiffeners. Thin-Walled Struct. 2022, 171, 108750. [Google Scholar] [CrossRef]
- York, C.B.; Williams, F.W. Theory and buckling results for infinitely wide, stiffened skew plate assemblies. Comp. Struct. 1994, 28, 189–200. [Google Scholar] [CrossRef]
- Prasad, E.V.; Sahu, S.K. Buckling of fiber-metal laminated plates—Numerical and experimental studies. Aircr. Eng. Aerosp. Tecnol. Int. J. 2020, 92, 472–481. [Google Scholar] [CrossRef]
- Jasion, P.; Magnucki, K. Strength and elastic buckling of a sandwich cylindrical pressure vessel with an individual functionally graded core. Int. J. Press. Vessels Pip. 2024, 210, 105238. [Google Scholar] [CrossRef]
- Kim, D.K.; Yang, H.Y.; Li, S.; Kim, S. An updated design formula for predicting the compressive strength of plate: Elastic buckling and ultimate compressive strength. J. Mar. Sci. Eng. 2025, 13, 113. [Google Scholar] [CrossRef]
- Bikakis, G.S.E.; Kalfountzos, C.D.; Theotokoglou, E.E. Elastic buckling of rectangular fiber-metal laminated plates under uniaxial compression. J. Thermoplast. Compos. Mater. 2019, 33, 1629–1651. [Google Scholar] [CrossRef]
- ANSYS. Structural Analysis Guide; ANSYS Inc.: Canonsburg, PA, USA, 2014. [Google Scholar]
- Hughes, O.F.; Paik, J.K. Ship Structural Analysis and Design; SNAME: Jersey City, NJ, USA, 2010. [Google Scholar]
- Gay, D.; Hoa, S.V.; Tsai, S.W. Composite Materials Design and Applications; CRC Press LLC: Mississauga, ON, Canada, 2003; Appendix 2. [Google Scholar]
- Yaghoubi, A.S.; Liaw, B. Influences of thickness and stacking sequence on ballistic impact behaviors of GLARE 5 FML plates: Part II—Numerical studies. J. Compos. Mater. 2014, 48, 2363–2374. [Google Scholar] [CrossRef]
- Leggett, D.M.A. The effect of two isolated forces on the elastic stability of a flat rectangular plate. Math. Proc. Cambridge Philos. Soc. 1937, 33, 325–339. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).