Event-Triggered Control Protocols for Achieving Bipartite Consensus in Switched Multi-Agent Systems

Abstract

This paper investigates the bipartite consensus problem for multi-agent systems subject to both switching dynamics and external disturbances within an event-triggered control (ETC) framework. The investigation commences with an analysis of time-invariant systems to establish bipartite consensus, and subsequently expands the framework to accommodate the complexities of switched systems. In time-invariant systems, agents update their states only when the event-triggering threshold is exceeded; the convergence of this mechanism can be rigorously established via an error dynamics mode. For switched systems, the system state is also updated solely when the event-triggering condition is met. Once all subsystems are stabilized, we design an appropriate mean sojourn time to mitigate state jumps caused by switching, thus ensuring bipartite consensus. Finally, four case studies based on numerical simulations to verify the theoretical results.

1. Introduction

In multiagent systems, a common value for the state variables across all agents is achieved through control protocols and coordination mechanisms, an outcome known as consensus. Classical consensus theory demonstrates that interactions based on nearest-neighbor rules enable agents to asymptotically align their motion directions [1]. Systematic investigations have addressed consensus problems under directed network topologies (both fixed and switching), while also revealing the influence of communication delays on consensus in fixed undirected networks [2]. In multi-vehicle system coordination, distributed protocols are designed for agents governed by first-order and second-order dynamics, under the necessary condition that the communication graph admits a directed spanning tree [3]. Further studies established convergence criteria for second-order algorithms in fixed and switching-directed topologies [4]. For higher-order agent dynamics, linear coordination protocols have been formulated, with convergence criteria—both necessary and sufficient—rigorously derived for consensus in networks of order greater than two [5]. Refined criteria for linear systems have provided crucial theoretical support for stability analysis and controller design [6]. In nonlinear systems, researchers have explored leader-follower frameworks with heterogeneous agents, addressing complexities arising from asymmetric interactions [7]. Additionally, consensus theories under input saturation constraints have been developed to address practical implementation challenges with bounded control inputs [8].

Traditional multi-agent systems typically assume cooperative interactions through non-negative communication networks. However, practical scenarios often involve both cooperative and competitive relationships. This challenge has been addressed through bipartite consensus frameworks that extend conventional non-negative topologies to signed networks [9]. A distributed control protocol partitions agents into two distinct groups, achieving intra-group state consensus while inter-group states converge to opposite values under structurally balanced signed networks. Recent research has significantly advanced this field. Systematic analyses have been conducted for bipartite consensus in homogeneous and heterogeneous networks [10]. Later studies generalized these results to broader classes of linear agent networks operating over signed digraphs [11,12]. Input saturation constraints in bipartite consensus for linear systems have also been addressed [13]. Further developments in bipartite consensus research are documented [14,15,16].

Depending on application requirements, multi-agent systems have branched into various specialized control paradigms. For example, prescribed-time control employs time-varying gains that increase when the tracking error is large to achieve desired performance within a user-specified finite time. However, the resulting sharp increase in control effort may lead to actuator saturation and excessive energy consumption [17]. In scenarios involving unknown or uncertain dynamics, multi-agent reinforcement learning (MARL) has recently emerged as a prominent approach due to its strong adaptability. Nevertheless, MARL-based methods typically lack rigorous stability guarantees and often rely on powerful computational platforms for extensive offline training [18].

Practical constraints from limited energy and bandwidth necessitate resource-efficient communication strategies in multi-agent systems. The two primary approaches are time-triggered control (actions executed at fixed sampling intervals) and event-triggered control (ETC) (communication activated only upon predefined state/output-related events). In ETC frameworks, control updates occur solely upon detecting significant changes in system states or outputs, offering enhanced resource efficiency [19,20]. This efficiency has driven extensive research interest in ETC methodologies. Early contributions include the development of error function-based event-triggering mechanisms, where communication is activated upon threshold violations [21]. The integration of ETC into multi-agent systems was first explored in [22], with subsequent extensions to consensus problems across diverse dynamics: single-integrator systems [23,24], second-order systems [25,26], and linear multi-agent systems [27,28]. Recent advancements have adapted ETC principles to bipartite consensus scenarios. For first-order systems, event-triggered bipartite consensus protocols have been systematically analyzed [29]. Operating under both undirected and directed graph topologies, dynamic event-triggered (DET) mechanisms further generalize these results, addressing distributed bipartite consensus for multi-agent systems [30]. Compared to static event-triggering laws, DET strategies significantly extend inter-event intervals, improving resource utilization efficiency [31,32].

However, the existing literature primarily focuses on time-invariant systems. To address this gap, research on switched systems has gradually emerged, with relevant surveys provided in [33,34,35]. Notably, prior works on event-triggered control (ETC) for multi-agent systems have mainly considered switching communication topologies [36,37,38,39]. In contrast, this paper investigates ETC for achieving bipartite consensus in switched multi-agent systems where the switching arises from changes in the agents’ intrinsic dynamics. Research of this form remains relatively scarce.

This paper makes the following key contributions:

• Research on multi-agent consensus under dynamically varying system dynamics remains relatively scarce; this paper provides incremental contributions to this direction.
• By integrating switched systems and disturbed systems within the event-triggered control (ETC) framework, the proposed approach better reflects real-world application scenarios, thereby enhancing the generality and practical relevance of the theoretical results.
• This work extends the study of multi-agent systems to the domain of bipartite consensus. Specifically, by introducing a transformation matrix, the bipartite consensus problem is reformulated as a standard consensus problem.

The subsequent sections of this paper are arranged as follows: Section 2 introduces the theory of signed graphs and related lemmas; Section 3, Section 4, Section 5 and Section 6 address ETC bipartite consensus for linear and nonlinear MASs, under time-invariant and switched systems; In Section 7, we present our simulation studies and results; A summary of the entire paper is presented in the final section.

Notations: Given a symmetric matrix $M\in {\mathbb{R}}^{n\times n}$, denote its eigenvalues by ${\lambda }_i$ ($i=1,\dots ,n$). These eigenvalues satisfy ${\lambda }_{min}={\lambda }_1\le {\lambda }_2\le \dots \le {\lambda }_n={\lambda }_{max}$. For a positive definite (respectively, negative definite) matrix N, we write $N>0$.

The notation $I_N$ denotes the $N\times N$ identity matrix, and I for an identity matrix of any appropriate size. Furthermore, the notation $D=diag\{d_1,d_2,\dots ,d_n\}$ defines a diagonal matrix with diagonal the elements $d_1,d_2,\dots ,d_n$. ⊗ signifies the Kronecker product. The function of the sign function $sgn\left(\alpha \right)$ satisfies:

$$sgn\left(\alpha \right)=\left\{\begin{array}{cc}1,& \alpha >0\\ 0,& \alpha =0\\ -1,& \alpha <0\end{array}\right.$$

2. Materials and Methods

A weighted signed graph is modeled by a triple $\mathcal{G}=(V,E,A)$. Here, $V=\left\{v_1,\dots ,v_n\right\}$ is the vertex set of cardinality n, E is the set of edges where $\epsilon \subseteq \left\{\left(v_j,v_i\right)\mid v_j,v_i\in V\right\}$, with the weighted adjacency matrix $A=\left[a_{ij}\right]\in {\mathbb{R}}^{n\times n}$ associated to the graph. Let $a_{ii}=0$ indicate that the node has no self-loop, and $a_{ij}\ne 0$ indicates $\epsilon \subseteq E$, otherwise $a_{ij}=0$. Additionally, cooperation between agents i and j is indicated by $a_{ij}>0$, while $a_{ij}<0$ signifies that these two agents are competitive. Evidently, the matrix A is not necessarily a non-negative matrix, except in cases where the multi-agent system involves only cooperative interactions. For a node i, its neighborhood is denoted by $N_i=v_j\mid (v_j,v_i)\in E$ and its in-degree is expressed as $d_i={\sum }_{j=1}^n\left|a_{ij}\right|$.

Let $D=diag\left\{d_1,d_2,\dots ,d_n\right\}$ represent the degree matrix of the weighted signed graph, with the Laplacian matrix $L=\left[l_{ij}\right]$ of $\mathcal{G}$ defined as $L=D-A$, where:

$$l_{ij}=\left\{\begin{array}{cc}{\sum }_{j=1}^n\left|a_{ij}\right|,\hfill & i=j\hfill \\ -a_{ij},\hfill & i\ne j\hfill \end{array}\right.$$

We define matrix $H=diag\{h_1,h_2,\dots ,h_n\}$ to represent the interaction topology between the leader and followers, where $h_i$ denotes the leader-follower coupling weight.

Definition 1 (Structure Balance).

A signed graph $\mathcal{G}$ is considered structurally balanced if and only if all its vertices can be partitioned into two disjoint subsets $V_1$ and $V_2$ (where $V_1\cap V_2=⌀$), satisfying the following specific conditions:

1. 

For every positive edge weight $a_{ij}>0$, the corresponding vertices $v_i$ and $v_j$ are grouped within the common subset (i.e., both in $v_1$ or both in $V_2$).

2. 

For every negative edge weight $a_{ij}<0$, the corresponding nodes $v_i$ and $v_j$ belong to different subsets (i.e., one in $v_1$, the other in $V_2$).

Lemma 1.

To convert the signed Laplacian L of a structurally balanced graph $\mathcal{G}$ into a standard non-negative Laplacian, a gauge transformation $T=diag\{t_1,t_2,\dots ,t_N\}$ ($t_i=\pm 1$) is applied, producing $L_T=TLT$. This transformation ensures all edge weights in the underlying network are positive ([9]).

Remark 1.

By applying the transformation matrix $T=diag\{t_1,t_2,\dots ,t_N\}$ where $T_i=\pm 1$, we can convert the signed graph into an unsigned graph. This conversion transforms the bipartite consensus challenge into a conventional consensus problem. Furthermore, the matrix $\overline{L}$, defined as $\overline{L}=T(L+H)T$, can be shown to be positive definite.

2.1. Problem Statements

Consider an MAS with n linear follower agents subject to disturbances, whose dynamics can be given by the following equations:

$${\dot{x}}_i\left(t\right)=A_{\sigma }{x}_i\left(t\right)+B_{\sigma }{u}_i\left(t\right)+C_i\left(t\right),i=1,\dots ,N$$

(1)

where $x_i\left(t\right)\in {\mathbb{R}}^n$ represents the state of agent i, and $u_i\left(t\right)\in {\mathbb{R}}^m$ is referred to as the control input or control protocol of agent i. The matrices $A_{\sigma }\in {\mathbb{R}}^{n\times n}$ and $B_{\sigma }\in {\mathbb{R}}^{n\times m}$, governed by the switching signal $\sigma$, are piecewise constant. They are fixed during the sojourn time of each subsystem and change values only at the switching instants. $C_i\left(t\right)$ is an external disturbance. The leader’s dynamics are given by:

$${\dot{x}}_0\left(t\right)=A_{\sigma }{x}_0\left(t\right)$$

(2)

where $x_0\left(t\right)\in {\mathbb{R}}^n$ represents the state of the leader. As an independent entity, the leader is autonomous. Hence, its dynamics remain unaffected by the follower agents.

Consider a multi-agent system comprising nonlinear followers that are subject to disturbances. The dynamical model for each agent is given by:

$${\dot{x}}_i\left(t\right)=f_{\sigma }\left(x_i\left(t\right)\right)+u_i\left(t\right)+C_i^{\prime }\left(t\right),i=1,2,\dots ,N$$

(3)

where $f_{\sigma }\left(x_i\left(t\right)\right)\in {\mathbb{R}}^n$ denotes the dynamics of agent i, governed by the switching signal $\sigma$, and $u_i\left(t\right)\in {\mathbb{R}}^n$ represents the control input of this agent. The leader’s dynamics are given by:

$${\dot{x}}_0\left(t\right)=f_{\sigma }\left(x_0\left(t\right)\right)$$

(4)

Assumption 1.

The pair $(A_{\sigma },B_{\sigma })$ possesses the ANCBC property—it is stabilizable with all eigenvalues of $A_{\sigma }$ in the closed left-half plane. This guarantees the existence of a positive definite matrix $P_{\sigma }$ fulfilling the following linear matrix inequality:

$$P_{\sigma }{A}_{\sigma }+A_{\sigma }^{\mathsf{T}}{P}_{\sigma }-2\xi P_{\sigma }{B}_{\sigma }{B}_{\sigma }^{\mathsf{T}}{P}_{\sigma }+\xi I_n<0,$$

(5)

where $\xi >0$ is the smallest eigenvalue of the matrix $\overline{L}$ and the matrix $P_{\sigma }$ can be obtained by solving the LMI (using standard convex optimization tools such as YALMIP in MATLAB R2023a).

Note: In the case of a time-invariant system, the switching signal $\sigma$ is either absent or remains constant, implying that the matrices A, B, and P are constant.

Assumption 2.

The $C_i\left(t\right)={[C_1^T,\dots ,C_N^T]}^T$ is bounded above, and its norm satisfies $\left|\right|C_i\left(t\right)\left|\right|<c$, where c is a positive constant.

Assumption 3.

The ${C^{\prime }}_i\left(t\right)={[{C^{\prime }}_1^T,\dots ,{C^{\prime }}_N^T]}^T$ is bounded above, and its norm satisfies $\left|\right|{C^{\prime }}_i\left(t\right)\left|\right|<c$, where $c^{\prime }$ is a positive constant.

2.2. Controller Design

This section develops a distributed event-triggered control scheme to attain bipartite consensus for leader-follower MASs.

To ensure bipartite consensus, the following distributed control input is introduced:

$$\begin{array}{cc}\hfill u_i\left(t\right)=-K& \{{\displaystyle \sum _{j=1}^n}\left|a_{ij}\left(t\right)\right|\left[x_i\left(t\right)-sgn\left(a_{ij}\left(t\right)\right)x_j\left(t\right)\right]\hfill \\ \hfill & +|h_i\left(t\right)|\left[x_i\left(t\right)-t_i{x}_0\left(t\right)\right]\}\hfill \end{array}$$

(6)

To reduce system communication overhead, we develop a event-triggered communication strategy, where each agent transmits its actual states to neighbors at event-triggered time instants, while during non-triggering intervals, it does not communicate and instead utilizes approximated values of both its own states and neighbors’ states. Let $\hat{x}$ denote the approximated value, which satisfies the following condition:

$$\left\{\begin{array}{c}{\hat{x}}_i\left(t\right)=x_j\left(t_k^i\right)t\in [t_k^i,t_{k+1}^i)\hfill \\ t_{k+1}^i=inf(t>t_k^i+t_{min}\left|\right|Q\ge 0)\hfill \end{array}\right.$$

(7)

where $t=t_k^i$ denotes the event-triggering instant of the k-th event for agent i, with i being the agent index; Q refers to the triggering function and $t_{min}$ denotes the minimum communication time interval.

Remark 2.

In (7), agents receive neighbors’ states only during event triggering. Notably, the leader’s estimated initial state equals its true initial value, i.e., ${\hat{x}}_0\left(0\right)=x_0$.

When introducing the event-triggered mechanism, for $t\in [t_k^i,t_{k+1}^i)$, the control protocol satisfies:

$$\begin{array}{cc}\hfill u_i\left(t\right)=-K& \{{\displaystyle \sum _{j=1}^n}\left|a_{ij}\left(t\right)\right|\left[{\hat{x}}_i\left(t\right)-sgn\left(a_{ij}\right){\hat{x}}_j\left(t\right)\right]\hfill \\ \hfill & +h_i\left(t\right)\left[{\hat{x}}_i\left(t\right)-t_i{\hat{x}}_0\left(t\right)\right]\}\hfill \end{array}$$

(8)

The error between the approximated state and the actual state of the agent is given by $e_i={\hat{x}}_i-x_i$. Meanwhile, the tracking error between the agent and the leader during leader-following tasks is defined as $x_e=x_i-t_i{x}_0$.

Define the matrices $X_e$ and E as

$$X_e=\left[\begin{array}{c}[x_1-t_1{x}_0]\\ [x_2-t_2{x}_0]\\ ⋮\\ [x_n-t_i{x}_0]\end{array}\right],E=\left[\begin{array}{c}[{\hat{x}}_1-x_1]\\ [{\hat{x}}_2-x_2]\\ ⋮\\ [{\hat{x}}_n-x_n]\end{array}\right].$$

We incorporate the variables into the protocol(8), so it follows that:

$$\begin{array}{cc}\hfill & u_i\left(t\right)=-K\times \{{\displaystyle \sum _{j=1}^n}\left|a_{ij}\left(t\right)\right|\left[x_i\left(t\right)+e_i\left(t\right)-sgn\left(a_{ij}\left(t\right)\right)\left(x_j\left(t\right)+e_j\left(t\right)\right)\right]\hfill \\ \hfill & +h_i\left(t\right)\left[x_i\left(t\right)+e_i\left(t\right)-t_i\left(x_0\left(t\right)+e_0\left(t\right)\right)\right]\}\hfill \end{array}$$

(9)

Definition 2.

MASs reach bipartite tracking consensus once the following requirements are met:

$$\underset{t\to \infty }{lim}\left|x_i\left(t\right)-t_i{x}_0\left(t\right)\right|=0,i=1,2,\dots ,N$$

(10)

3. Linear Time-Invariant System

Here, we investigate the problem of bipartite consensus under an event-triggered mechanism for a linear time-invariant system.

To achieve bipartite consensus in a leader-based multi-agent system, we employ the controller defined in Equation (8). To demonstrate the effectiveness of this control protocol, we introduce two distinct sets of error variables—formulated in Equation (9)—and substitute them into the system dynamics (1). This transformation recasts the consensus problem as a stability analysis of the resulting error system, which is described as follows:

$$\dot{X_e}=A{X}_e-L_H\otimes BKE-L_H\otimes BK{X}_e+C$$

(11)

where $L_H=L+H$.

Define ${\overline{x}}_{ei}\left(t\right)=t_i{x}_{ei}\left(t\right)$ and ${\overline{e}}_i\left(t\right)=t_i{e}_i\left(t\right)$, ${\overline{X}}_e=(T\otimes I_n)X_e$, $\overline{E}=(T\otimes I_n)E\left(t\right)$, we can obtain:

$$\dot{\overline{X_e}}=A{\overline{X}}_e-\overline{L}\otimes BK\overline{E}-\overline{L}\otimes BK{\overline{X}}_e+\overline{C}$$

(12)

Remark 3.

By employing a transformation matrix, we reformulate the bipartite consensus problem as a conventional consensus problem, followed by stability analysis. A similar procedure is applied in all subsequent sections.

Assumption 4.

In the signed graph $\overline{\mathcal{G}}$ (which includes one leader and N follower), structural balance and connectivity are maintained.

Theorem 1.

Suppose the MASs described by (1) satisfy Assumptions 1, 2, and 4. Then, under the event-triggered controller given by (8) with the feedback gain matrix chosen as $K=B^{\mathsf{T}}P$, the consensus in the multi-agent system is achieved. The triggering function Q is designed as follows:

$$Q={∥\overline{E}∥}^2-{\displaystyle \frac{a_1(\xi -a_1{\beta }_1-a_2{\beta }_2)}{{\beta }_1}}\parallel {\overline{X}}_e{\parallel }^2+{\displaystyle \frac{a_1{\beta }_2}{a_2{\beta }_1}}{\parallel \overline{C}\parallel }^2$$

(13)

where $0<a_1,0<a_2,\xi ={\lambda }_{min}\left(\overline{L}\right)$, ${\beta }_1={\lambda }_{max}(\overline{L}\otimes PB{B}^{T}P)$, ${\beta }_2={\lambda }_{max}\left(P\right)$ and $a_1{\beta }_1+a_2{\beta }_2-\xi <0$.

Proof. 

We define a Lyapunov function for the error dynamics:

$$V_1\left(t\right)={\overline{X}}_e^T(I_n\otimes P){\overline{X}}_e$$

(14)

then we obtain

$$\begin{array}{cc}\hfill {\dot{V}}_1\left(t\right)& ={\dot{\overline{X}}}_e^T(I_n\otimes P){\overline{X}}_e+{\overline{X}}_e^T(I_n\otimes P){\dot{\overline{X}}}_e\hfill \\ \hfill & ={\overline{X}}_e^T\left(I_n\otimes A^T-{\overline{L}}^T\otimes PB{B}^T\right)(I_n\otimes P){\overline{X}}_e+{\overline{X}}_e^T(I_n\otimes P)\left(I_n\otimes A-\overline{L}\otimes B{B}^{T}P\right){\overline{X}}_e\hfill \\ \hfill & +{\overline{E}}^T(-\overline{L}\otimes B{B}^{T}P)(I_n\otimes P){\overline{X}}_e+{\overline{X}}_e^T(I_n\otimes P)(-\overline{L}\otimes B{B}^{T}P)\overline{E}\hfill \\ \hfill & ={\overline{X}}_e^T\left[I_n\otimes (A^{T}P+P^{T}A)-2\overline{L}\otimes PB{B}^{T}P\right]{\overline{X}}_e-2{\overline{E}}^T(\overline{L}\otimes PB{B}^{T}P){\overline{X}}_e+2{\overline{C}}^T(I_n\otimes P){\overline{X}}_e\hfill \\ \hfill & \le {\overline{X}}_e^T\left[(A^{T}P+P^{T}A)-2\xi PB{B}^{T}P\right]{\overline{X}}_e+2{\beta }_1\parallel \overline{E}\parallel \parallel {\overline{X}}_e\parallel +2{\beta }_2\parallel \overline{C}\parallel \parallel {\overline{X}}_e\parallel \hfill \\ \hfill & =-\xi \parallel {\overline{X}}_e{\parallel }^2+2{\beta }_1\parallel \overline{E}\parallel \parallel {\overline{X}}_e\parallel +2{\beta }_2\parallel \overline{C}\parallel \parallel {\overline{X}}_e\parallel \hfill \end{array}$$

(15)

where $\xi ={\lambda }_{min}\left(\overline{L}\right)$, ${\beta }_1={\lambda }_{max}(\overline{L}\otimes PB{B}^{T}P)$ and ${\beta }_2={\lambda }_{max}\left(P\right)$.

We apply the Young’s inequality: $m^{\top }n\le {\displaystyle \frac{1}{2a}}{\parallel m\parallel }^2+{\displaystyle \frac{a}{2}}{\parallel n\parallel }^2$, $a>0$, if the following inequality is satisfied:

$$\left\{\begin{array}{c}{a}_1{\beta }_1+a_2{\beta }_2-\xi <0\hfill \\ {∥\overline{E}∥}^2<{\displaystyle \frac{a_1(\xi -a_1{\beta }_1-a_2{\beta }_2)}{{\beta }_1}}\parallel {\overline{X}}_e{\parallel }^2-{\displaystyle \frac{a_1{\beta }_2}{a_2{\beta }_1}}{\parallel \overline{C}\parallel }^2\hfill \end{array}\right.$$

(16)

then we have

$$\begin{array}{cc}\hfill {\dot{V}}_1\left(t\right)& =-\xi \parallel {\overline{X}}_e{\parallel }^2+2{\beta }_1\parallel \overline{E}\parallel \parallel {\overline{X}}_e\parallel +2{\beta }_2\parallel \overline{C}\parallel \parallel {\overline{X}}_e\parallel \hfill \\ \hfill & \le -\xi \parallel {\overline{X}}_e{\parallel }^2+2{\beta }_1\left({\displaystyle \frac{1}{2a_1}}\parallel \overline{E}{\parallel }^2+{\displaystyle \frac{a_1}{2}}{\parallel {\overline{X}}_e\parallel }^2\right)+2{\beta }_2\left({\displaystyle \frac{1}{2a_2}}\parallel \overline{C}{\parallel }^2+{\displaystyle \frac{a_2}{2}}{\parallel {\overline{X}}_e\parallel }^2\right)\hfill \\ \hfill & =\left(a_1{\beta }_1+a_2{\beta }_2-\xi \right)\parallel {\overline{X}}_e{\parallel }^2+{\displaystyle \frac{{\beta }_1}{a_1}}\parallel \overline{E}{\parallel }^2+{\displaystyle \frac{{\beta }_2}{a_2}}{\parallel \overline{C}\parallel }^2\hfill \\ \hfill & <0,\hfill \end{array}$$

(17)

Therefore, the transformed error system can achieve consensus, that is, the original system can achieve bipartite consensus. □

Remark 4.

When the function $Q=0$, it is at the event-triggered moment $t_{k+1}^i$. At this time, the network will communicate and update the state, then the state measurement error will be reset to 0. As time increases, the error will accumulate until the next trigger moment when it is reset again, repeating this process. Moreover, to prevent Zeno behavior, this paper set a minimum inter-event time $t_{min}$ (with $t_{min}>0$) is enforced for each agent.

4. Linear Switched System

Here, we address the issue of bipartite consensus under an event-triggered mechanism with switching system.

In a linear switched system, for arbitrary time instances ${\tau }_b>{\tau }_a\ge 0$, define $M_{\sigma }({\tau }_a,{\tau }_b)$ as the total count of discontinuities in the switching signal $\sigma \left(t\right)$ within the time interval $({\tau }_a,{\tau }_b)$. Suppose there are constants $\tau >0$ and $M_0\ge 0$ for which the following inequality holds:

$$M_{\sigma }({\tau }_a,{\tau }_b)\le M_0+{\displaystyle \frac{{\tau }_b-{\tau }_a}{\tau }}$$

then $\tau$ is called the mean sojourn time of switching signal $\sigma \left(t\right)$, and $M_0$ is called the jitter bound.

Remark 5.

The switching signal $\sigma \left(t\right)$(denoted by σ) maps $\sigma \left(t\right):[0,\infty )\to \mathcal{P}$, where $\mathcal{P}=\{1,2,\dots ,N\}$ represents the set of all subsystems. This signal governs the system’s switching behavior over time, with each subsystem $\sigma \in \mathcal{P}$ corresponding to a graph ${\overline{\mathcal{G}}}_{\sigma \left(t\right)}$. A jitter bound $M_0=0$ indicates that no switching occurs on any time interval shorter than τ. When $M_0=1$, this implies that at most one switching event can take place over any time interval of length less than τ. In this case, the mean sojourn time switching is equivalent to standard sojourn time switching.

When the system switches, the system dynamics are represented by the following equations:

$${\dot{x}}_i\left(t\right)=A_{\sigma }{x}_i\left(t\right)+B_{\sigma }{u}_i\left(t\right)+C_i\left(t\right),i=1,\dots ,N$$

(18)

and the control input is given by

$$\begin{array}{cc}\hfill u_i\left(t\right)=-K_{\sigma }& \{{\displaystyle \sum _{j=1}^n}\left|a_{ij}\left(t\right)\right|\left[{\hat{x}}_i\left(t\right)-sgn\left(a_{ij}\left(t\right)\right){\hat{x}}_j\left(t\right)\right]\hfill \\ \hfill & +h_i\left(t\right)\left[{\hat{x}}_i\left(t\right)-t_i\left(t\right){\hat{x}}_0\left(t\right)\right]\}\hfill \end{array}$$

(19)

then, the dynamics of the error system can be expressed as:

$$\begin{array}{cc}\hfill {\dot{\overline{X}}}_e=& A_{\sigma }\otimes I_N{\overline{X}}_e-{\overline{L}}_{\sigma }\otimes B_{\sigma }{K}_{\sigma }\overline{E}\hfill \\ \hfill & -{\overline{L}}_{\sigma }\otimes B_{\sigma }{K}_{\sigma }{\overline{X}}_e+\overline{C}\hfill \end{array}$$

(20)

Assumption 5.

For each subsystem $\sigma \in \mathcal{P}$, the graph ${\overline{\mathcal{G}}}_{\sigma }$ is connected and satisfies structural balance.

Assumption 6.

If there exist a positive number $\eta >0$ and $\mu >1$, positive definite matrices $P_{\sigma }>0$ for all $\sigma \in \mathcal{P}$, such that $\forall a,b\in \mathcal{P},a\ne$ b, $P_a\le \mu P_b$ hold, and the mean sojourn time τ satisfies

$$\tau >{\tau }^{*}={\displaystyle \frac{ln\mu }{\eta }}$$

Remark 6.

When switching occurs in the system, energy transitions arise between the pre-switching and post-switching states. From an energetic perspective, the parameter μ represents the multiplicative factor of energy growth. Across multiple switching transitions, the energy growth factor admits a finite upper bound. Specifically, after independently solving for each subsystem’s Lyapunov matrix $P_{\sigma }$, the discrepancy between any two matrices $P_a$ and $P_b$ can be quantified by the maximum eigenvalue of their product $P_a{P}_b^{-1}$. The parameter μ is then defined as:

$$\mu =\underset{a,b\in \mathcal{P}}{max}\left\{{\lambda }_{max}\left(P_a{P}_b^{-1}\right)\right\}$$

Theorem 2.

Suppose the MASs described by (18) satisfies Assumptions 1, 2, 5, and 6. Then, under the event-triggered controller given by (19) with the feedback gain matrix chosen as $K_{\sigma }=B_{\sigma }^{\mathsf{T}}{P}_{\sigma }$, the consensus in the MASs is achieved. The triggering function Q is designed as follows:

$$Q=\parallel \overline{E}{\parallel }^2-{\displaystyle \frac{a_1({\xi }_2-a_1{\beta }_1-a_2{\beta }_2)}{{\beta }_1}}\parallel {\overline{X}}_e{\parallel }^2+{\displaystyle \frac{a_1{\beta }_2}{a_2{\beta }_1}}{\parallel \overline{C}\parallel }^2$$

(21)

where $0<a_1,0<a_2$, ${\beta }_1={\lambda }_{max}({\overline{L}}_{\sigma }\otimes P_{\sigma }{B}_{\sigma }{B}_{\sigma }^T{P}_{\sigma })$ and ${\beta }_2={\lambda }_{max}\left(P_{\sigma }\right)$, $0<\xi ={\xi }_1+{\xi }_2={\lambda }_{min}\left(P_{\sigma }\right)$, $a_1{\beta }_1+a_2\beta -{\xi }_2<0$.

Proof. 

First, we establish the stability of each subsystem within the switched system. For every subsystem $\sigma \in \mathcal{P}$, we define the error Lyapunov function:

$$V_{\sigma }\left(t\right)={\overline{X}}_e^T(I_n\otimes P_{\sigma }){\overline{X}}_e,$$

(22)

where $P_{\sigma }=P_{\sigma }^T>0$. For notational convenience, we drop the subscript $\sigma$ and denote $P_{\sigma }$, $A_{\sigma }$, $B_{\sigma }$, and $\overline{L}$ simply as P, A, B, and $\overline{L}$, respectively. Then, the time derivative of $V_{\sigma }\left(t\right)$ along the error dynamics satisfies

$$\begin{array}{cc}\hfill {\dot{V}}_{\sigma }\left(t\right)& ={\dot{\overline{X}}}_e^T(I_n\otimes P){\overline{X}}_e+{\overline{X}}_e^T(I_n\otimes P){\dot{\overline{X}}}_e\hfill \\ \hfill & ={\overline{X}}_e^T\left(I_n\otimes A^T-{\overline{L}}^T\otimes PB{B}^T\right)(I_n\otimes P){\overline{X}}_{e}d+{\overline{X}}_e^T(I_n\otimes P)\left(I_n\otimes A-\overline{L}\otimes B{B}^{T}P\right){\overline{X}}_e\hfill \\ \hfill & +{\overline{E}}^T(-\overline{L}\otimes B{B}^{T}P)(I_n\otimes P){\overline{X}}_e+{\overline{X}}_e^T(I_n\otimes P)(-\overline{L}\otimes B{B}^{T}P)\overline{E}\hfill \\ \hfill & ={\overline{X}}_e^T\left[I_n\otimes (A^{T}P+PA)-2\overline{L}\otimes PB{B}^{T}P\right]{\overline{X}}_e-2{\overline{E}}^T(\overline{L}\otimes PB{B}^{T}P){\overline{X}}_e+2{\overline{C}}^T(I_n\otimes P){\overline{X}}_e\hfill \\ \hfill & \le {\overline{X}}_e^T\left[(A^{T}P+PA)-2\xi PB{B}^{T}P\right]{\overline{X}}_e+2{\beta }_1\parallel \overline{E}\parallel \parallel {\overline{X}}_e\parallel +2{\beta }_2\parallel \overline{C}\parallel \parallel {\overline{X}}_e\parallel \hfill \\ \hfill & =-\xi \parallel {\overline{X}}_e{\parallel }^2+2{\beta }_1\parallel \overline{E}\parallel \parallel {\overline{X}}_e\parallel +2{\beta }_2\parallel \overline{C}\parallel \parallel {\overline{X}}_e\parallel ,\hfill \end{array}$$

(23)

where $\xi ={\lambda }_{min}\left(\overline{L}\right)$, ${\beta }_1={\lambda }_{max}(\overline{L}\otimes PB{B}^{T}P)$, and ${\beta }_2={\lambda }_{max}\left(P\right)$. We apply the Young’s inequality: $m^{\top }n\le {\displaystyle \frac{1}{2a}}{\parallel m\parallel }^2+{\displaystyle \frac{a}{2}}{\parallel n\parallel }^2$, $a>0$. One can observe if ${\xi }_1>0,{\xi }_2>0$, ${\xi }_1+{\xi }_2=\xi$, and the following inequality is satisfied:

$$\left\{\begin{array}{c}{a}_1{\beta }_1+a_2{\beta }_2-{\xi }_2<0\hfill \\ {∥\overline{E}∥}^2<{\displaystyle \frac{a_1({\xi }_2-a_1{\beta }_1-a_2{\beta }_2)}{{\beta }_1}}\parallel {\overline{X}}_e{\parallel }^2-{\displaystyle \frac{a_1{\beta }_2}{a_2{\beta }_1}}{\parallel \overline{C}\parallel }^2\hfill \end{array}\right.$$

(24)

then we have

$$\begin{array}{cc}\hfill {\dot{V}}_{\sigma }\left(t\right)& =-\xi \parallel {\overline{X}}_e{\parallel }^2+2{\beta }_1\parallel \overline{E}\parallel \parallel {\overline{X}}_e\parallel +2{\beta }_2\parallel \overline{C}\parallel \parallel {\overline{X}}_e\parallel \hfill \\ \hfill & \le -\xi \parallel {\overline{X}}_e{\parallel }^2+2{\beta }_1\left({\displaystyle \frac{1}{2a_1}}\parallel \overline{E}{\parallel }^2+{\displaystyle \frac{a_1}{2}}{\parallel {\overline{X}}_e\parallel }^2\right)+2{\beta }_2\left({\displaystyle \frac{1}{2a_2}}\parallel \overline{C}{\parallel }^2+{\displaystyle \frac{a_2}{2}}{\parallel {\overline{X}}_e\parallel }^2\right)\hfill \\ \hfill & =(a_1{\beta }_1+a_2{\beta }_2-{\xi }_1-{\xi }_2)\parallel {\overline{X}}_e{\parallel }^2+{\displaystyle \frac{{\beta }_1}{a_1}}\parallel \overline{E}{\parallel }^2+{\displaystyle \frac{{\beta }_2}{a_2}}{\parallel \overline{C}\parallel }^2\hfill \\ \hfill & \le -{\xi }_1{\parallel {\overline{X}}_e\parallel }^2\hfill \end{array}$$

(25)

Since $V_{\sigma }\left(t\right)$ is positive definite, we obtain

$${ϵ}_1\parallel {\overline{x}}_e{\left(t\right)\parallel }^2\le V_{\sigma }\left(t\right)\le {ϵ}_2{\parallel {\overline{x}}_e\left(t\right)\parallel }^2$$

(26)

where ${ϵ}_1={min}_{\sigma \in \mathcal{P}}\left\{{\lambda }_{min}\left(P_{\sigma }\right)\right\}>0$ and ${ϵ}_2={max}_{\sigma \in \mathcal{P}}\left\{{\lambda }_{max}\left(P_{\sigma }\right)\right\}>0$ are constants.

According to inequality (25) and (26) we have

$${\dot{V}}_{\sigma }\left(t\right)<-{\displaystyle \frac{{\xi }_1}{{ϵ}_2}}{V}_{\sigma }\left(t\right)=-\eta V_{\sigma }\left(t\right)$$

(27)

this implies that $V_{\sigma }\left(t\right)$, $\sigma \in \mathcal{P}$, decreases exponentially along the trajectories of each subsystem.

Without loss of generality, consider an arbitrary time interval $[t_0,t]$, and assume the number of switchings in this interval is $M_{\sigma }(t_0,t)=k$, with switching times $t_1,t_2,\dots ,t_k$.

Then, based on the comparison lemma and inequality (27), we obtain

$$\left\{\begin{array}{c}{V}_{\sigma \left(t_k\right)}\left(t\right)<e^{-\eta (t-t_k)}{V}_{\sigma \left(t_k\right)}\left(t_k\right)\hfill \\ V_{\sigma \left(t_{j-1}\right)}\left(t\right)<e^{-\eta (t_j-t_{j-1})}{V}_{\sigma \left(t_{j-1}\right)}\left(t_{j-1}\right)\hfill \end{array}\right.$$

(28)

In other words, when no switching occurs, the Lyapunov function is always exponentially decreasing. On the other hand, at switching instants, we allow the Lyapunov function to increase, but this increase is bounded. Specifically, according to $P_a\le \mu P_b$ for all $a,b\in \mathcal{P}$, we have

$$\begin{array}{cc}\hfill & V_{\sigma \left(t_j\right)}\left(t_j\right)\le \mu V_{\sigma \left(t_j^{-}\right)}\left(t_j\right)\iff \hfill \\ \hfill & x{\left(t_j\right)}^T(I_n\otimes P_a)x\left(t_j\right)\le \mu x{\left(t_j\right)}^T(I_n\otimes P_b)x\left(t_j\right)\hfill \end{array}$$

(29)

By combining inequalities (28), with the jitter bound $M_0=0$ and $\tau >{\tau }^{*}={\displaystyle \frac{ln\mu }{\eta }}$ we derive:

$$\begin{array}{cc}\hfill V_{\sigma \left(t\right)}\left(t\right)& <e^{-\eta (t-t_k)}{V}_{\sigma \left(t_k\right)}\left(t_k\right)\hfill \\ \hfill & \le \mu e^{-\eta (t-t_k)}{V}_{\sigma \left(t_k^{-}\right)}\left(t_k\right)\hfill \\ \hfill & <\mu e^{-\eta (t-t_k)}{e}^{-\eta (t_k-t_{k-1})}{V}_{\sigma \left(t_{k-1}\right)}\left(t_{k-1}\right)\hfill \\ \hfill & <{\mu }^{N_{\sigma }(t_0,t)}{e}^{-\eta (t-t_k)}\dots e^{-\eta (t_1-t_0)}{V}_{\sigma \left(t_0\right)}\left(t_0\right)\hfill \\ \hfill & \le {\mu }^{{\displaystyle \frac{t-t_0}{\tau }}}{e}^{-\eta (t-t_0)}{V}_{\sigma \left(t_0\right)}\left(t_0\right)\hfill \\ \hfill & =e^{-2\gamma (t-t_0)}{V}_{\sigma \left(t_0\right)}\left(t_0\right)\hfill \end{array}$$

(30)

where $\gamma ={\displaystyle \frac{1}{2}}\left(\eta -{\displaystyle \frac{ln\mu }{\tau }}\right)$ is the exponential decay rate. This demonstrates that the Lyapunov function of the system is exponentially decreasing. Furthermore, the condition $\tau >{\tau }^{*}$ ensures $\gamma >0$. This guarantees the exponential decay rate is positive, thereby establishing global exponential stability. Therefore, leader-follower consensus is guaranteed. It can therefore be concluded that bipartite consensus is reachable. □

5. Nonlinear Time-Invariant System

This section addresses a nonlinear multi-agent system whose dynamics are given by the following equation:

$${\dot{x}}_i\left(t\right)=f\left(x_i\left(t\right)\right)+u_i\left(t\right)+C_i^{\prime },i=1,2,\dots ,N$$

(31)

We derive the dynamics of the error system as follows:

$$\begin{array}{cc}\hfill {\dot{x}}_{ei}=& f\left(x_i\left(t\right)\right)-f\left(x_0\left(t\right)\right)\hfill \\ \hfill & -k{\displaystyle \sum _{j=1}^n}\left|a_{ij}\left(t\right)\right|\left[{\overline{x}}_i\left(t\right)-sgn\left(a_{ij}\right){\overline{x}}_j\left(t\right)\right]\hfill \\ \hfill & -k|h_i\left(t\right)|\left[{\overline{x}}_i\left(t\right)-t_i{\overline{x}}_0\left(t\right)\right]\}+{C^{\prime }}_i\hfill \end{array}$$

(32)

The compact form of the error system dynamics can be formulated as:

$${\dot{\overline{X}}}_e=F_e-\Gamma \otimes \overline{L}\overline{E}-\Gamma \otimes \overline{L}{\overline{X}}_e+{\overline{C}}^{\prime }$$

(33)

where $F_e=\left[\begin{array}{c}f\left(x_1\left(t\right)\right)-f\left(x_0\left(t\right)\right)\\ f\left(x_2\left(t\right)\right)-f\left(x_0\left(t\right)\right)\\ ⋮\\ f\left(x_i\left(t\right)\right)-f\left(x_0\left(t\right)\right)\end{array}\right]$, and $\Gamma =diag\{k_1,k_2,\dots ,k_n\}$ (where $k_i>0$ for all $i=1,2,\dots ,n$ is a positive definite matrix.

Assumption 7.

The function f is nonlinear and bounded, and satisfies the following Lipschitz condition:

$$\parallel f\left(x\right)-f\left(y\right)\parallel \le \rho \parallel x-y\parallel ,\forall x,y\in R^n$$

(34)

where ρ is the positive constant.

Theorem 3.

Consider the MASs described by (31) under Assumptions 1, 3, and 7. Using the event-triggered controller (8) with gain parameter k, consensus of the multi-agent system can be achieved. The corresponding triggering function is designed as follows:

$$Q=\parallel \overline{E}{\parallel }^2-{\displaystyle \frac{{\beta }_3-{\beta }_5(2\rho +1)}{{\beta }_4}}{\parallel {\overline{X}}_e\parallel }^2+{\displaystyle \frac{{\beta }_5{\parallel {\overline{C}}^{\prime }\parallel }^2}{{\beta }_4}}$$

(35)

where ${\beta }_3={\lambda }_{min}({\Gamma }^2\otimes \overline{L}),$${\beta }_4={\lambda }_{max}({\Gamma }^2\otimes \overline{L})$, ${\beta }_5={\lambda }_{max}(\Gamma \otimes I_n)$ and ${\beta }_5(2\rho +1)-{\beta }_3<0$.

Proof. 

Define the error Lyapunov function candidate as:

$$V_2={\overline{X}}_e^T(\Gamma \otimes I_n){\overline{X}}_e$$

(36)

To analyze its time evolution, we compute the derivative along system trajectories:

$$\begin{array}{cc}\hfill {\dot{V}}_2\left(t\right)& =2{\overline{X}}_e^T{\dot{\overline{X}}}_e\hfill \\ \hfill & =2{\overline{X}}_e^T(\Gamma \otimes I_n)(F_e-\Gamma \otimes \overline{L}\overline{E}-\Gamma \otimes \overline{L}{\overline{X}}_e+\overline{C})\hfill \\ \hfill & \le 2\rho {\overline{X}}_e^T(\Gamma \otimes I_n){\overline{X}}_e-2{\overline{X}}_e^T({\Gamma }^2\otimes \overline{L})\overline{E}-2{\overline{X}}_e^T({\Gamma }^2\otimes \overline{L}){\overline{X}}_e\hfill \\ \hfill & +2{\overline{X}}_e^T(\Gamma \otimes I_n){\overline{C}}^T\hfill \end{array}$$

(37)

To bound the cross terms, we apply the Young’s inequality:

$$m^{\top }n\le {\displaystyle \frac{1}{2}}{\parallel m\parallel }^2+{\displaystyle \frac{1}{2}}{\parallel n\parallel }^2$$

(38)

where $a>0$ which yields:

$$\begin{array}{cc}\hfill & -2{\overline{X}}_e^T({\Gamma }^2\otimes \overline{L})\overline{E}+2{\overline{X}}_e^T(\Gamma \otimes I_n){\overline{C}}^T\hfill \\ \hfill & \le {\overline{X}}_e^T({\Gamma }^2\otimes \overline{L}){\overline{X}}_e+{\overline{E}}^T({\Gamma }^2\otimes \overline{L})\overline{E}+{\overline{X}}_e^T(\Gamma \otimes I_n){\overline{X}}_e+{\overline{C}}^{\prime }(\Gamma \otimes I_n){\overline{C}}^{\prime T}\hfill \end{array}$$

(39)

Substituting this bound into (37), we obtain if the following inequality holds:

$$\left\{\begin{array}{c}{\beta }_5(2\rho +1)-{\beta }_3<0\hfill \\ \parallel \overline{E}{\parallel }^2<{\displaystyle \frac{{\beta }_3-{\beta }_5(2\rho +1)}{{\beta }_4}}{\parallel {\overline{X}}_e\parallel }^2-{\displaystyle \frac{{\beta }_5{\parallel {\overline{C}}^{\prime }\parallel }^2}{{\beta }_4}}\hfill \end{array}\right.$$

(40)

Then we obtain:

$$\begin{array}{cc}\hfill {\dot{V}}_2\left(t\right)& \le 2\rho {\overline{X}}_e^T(\Gamma \otimes I_n){\overline{X}}_e-{\overline{X}}_e^T({\Gamma }^2\otimes \overline{L}){\overline{X}}_e+{\overline{E}}^T({\Gamma }^2\otimes \overline{L})\overline{E}+{\overline{X}}_e^T(\Gamma \otimes I_n){\overline{X}}_e+\overline{C}\overline{(}\Gamma \otimes I_n)C^T\hfill \\ \hfill & \le \{{\beta }_5(2\rho +1)-{\beta }_3\}\parallel {\overline{X}}_e{\parallel }^2+{\beta }_4\parallel \overline{E}{\parallel }^2+{\beta }_5{\parallel {\overline{C}}^{\prime }\parallel }^2\hfill \\ \hfill & <0\hfill \end{array}$$

(41)

Thus, the nonlinear MAS with disturbances can achieve bipartite consensus. □

6. Nonlinear Switched System

This section examines consensus in nonlinear and switched MASs using event-triggered mechanisms.

Analogous to the case of linear switching system, we assume that the subsystem $\sigma \in \mathcal{P}$ satisfying Assumption 1, 5. The dynamics of the nonlinear multi-agent system are governed by the following equation:

$${\dot{x}}_i\left(t\right)=f_{\sigma }\left(x_i\left(t\right)\right)+u_i\left(t\right)+C_i^{\prime },i=1,2,\dots ,N$$

(42)

When the system switches, the control input is defined as

$$\begin{array}{cc}\hfill u_i\left(t\right)=-K_{\sigma }& \{{\displaystyle \sum _{j=1}^n}\left|a_{ij}\left(t\right)\right|\left[{\overline{x}}_i\left(t\right)-sgn\left(a_{ij}\left(t\right)\right){\overline{x}}_j\left(t\right)\right]\hfill \\ \hfill & +|h_i\left(t\right)|\left[{\overline{x}}_i\left(t\right)-t_i{\overline{x}}_0\left(t\right)\right]\}\hfill \end{array}$$

(43)

Assumption 8.

Given $\eta >0$ and $\mu >1$, if there exist a family of continuously differentiable functions $V_i:{\mathbb{R}}^n\to \mathbb{R}$, a switching signal $\sigma \left(t\right):[0,+\infty )\to \mathcal{P}=\{1,2,\dots ,m\}$, and two $r_{\infty }$ functions $r_1$ and $r_2$ such that satisfies

$$\left\{\begin{array}{c}{r}_1(\parallel x\left(t\right)\parallel )\le V_{\sigma }\left(x\left(t\right)\right)\le r_2(\parallel x\left(t\right)\parallel )\forall x,\forall \sigma \in \mathcal{P}\hfill \\ {\displaystyle \frac{\partial V_{\sigma }}{\partial x}}{f}_{\sigma }\left(x\right)\le -\eta V_{\sigma }\left(x\right)\forall x,\forall \sigma \in \mathcal{P}\hfill \\ V_a\left(x\left(t_j\right)\right)\le \mu V_b\left(x\left(t_j\right)\right)(\sigma \left(t_j\right)=a,\sigma \left(t_j^{-}\right)=b\in \mathcal{P},a\ne b)\hfill \end{array}\right.$$

(44)

and the mean sojourn time τ satisfies the following inequality:

$$\tau >{\tau }^{*}={\displaystyle \frac{ln\mu }{\eta }}$$

Theorem 4.

Under Assumptions 1,3, 5, 7, and 8, we establish that the multi-agent system (42) under controller (43) achieves bipartite consensus using the event-triggered function Q.

$$\begin{array}{c}\hfill Q=\parallel \overline{E}{\parallel }^2-{\displaystyle \frac{{\beta }_3^{\prime }-{\beta }_5(2\rho +1)}{{\beta }_4}}{\parallel {\overline{X}}_e\parallel }^2+{\displaystyle \frac{{\beta }_5{\parallel {\overline{C}}^{\prime }\parallel }^2}{{\beta }_4}}\end{array}$$

(45)

where ${\beta }_3={\lambda }_{min}({\Gamma }_{\sigma }^2\otimes \overline{L}),\eta >0,{\beta }_4>0,{\beta }_3^{\prime }=\eta +{\beta }_3^{\prime }$, ${\beta }_4={\lambda }_{max}({\Gamma }_{\sigma }^2\otimes \overline{L})$ and ${\beta }_5(2\rho +1)-{\beta }_3^{\prime }<0$.

Proof. 

The proof is conducted in two steps. First, we establish the stability of each subsystem. Under Assumption 8, the stability of each individual subsystem is guaranteed; the detailed proof follows a similar approach to that used for nonlinear time-invariant systems. Second, we assume that the energy jumps at switching instants are bounded above (${\Gamma }_a\le \mu {\Gamma }_b$). The overall switched system remains stable under the average dwell time condition. Since the stability argument adopted in these proofs closely resembles the method used for linear switched systems in Equation (30), the proofs are omitted here for brevity. □

7. Simulation Results

We consider an MAS comprising one leader and five followers, as illustrated in Figure 1. In this structure, the leader (agent 0) and agents 1 and 5 belong to one category, while agents 2, 3, and 4 are grouped into another category with opposite values.

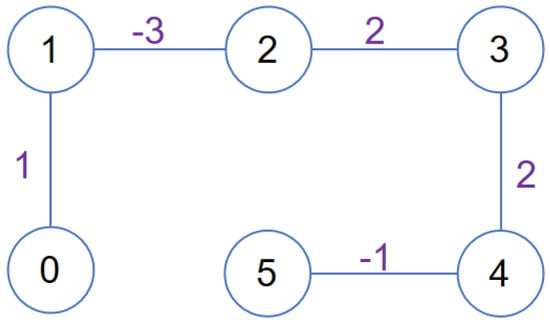
Figure 1. Topology of Muti-Agent Systems.

The matrices L and H are set as follows:

$$L=\left(\begin{array}{ccccc}3& 3& 0& 0& 0\\ 3& 5& -2& 0& 0\\ 0& -2& 4& -2& 0\\ 0& 0& -2& 3& 1\\ 0& 0& 0& 1& 1\end{array}\right),H=\left(\begin{array}{ccccc}1& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right).$$

7.1. Linear Time-Invariant Systems

The parameter is designed as

$$A=\left(\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ -1& -2& -3\end{array}\right),B=\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right).$$

It is evident that Assumption 1 is satisfied. One can see that eigenvalues of $\overline{L}=SLS+H$ are 8.2613, 5.3120, 2.3812, 0.9207, 0.1247. Combining the min eigenvalue $\xi =0.1247$, we can compute that

$$\begin{array}{cc}\hfill X& =\left(\begin{array}{ccc}0.6097& 0.5508& 0.1295\\ 0.5508& 1.1850& 0.3280\\ 0.1295& 0.3280& 0.1519\end{array}\right)\hfill \\ \hfill K& =\left(\begin{array}{ccc}0.1295& 0.3280& 0.1519\end{array}\right)\hfill \end{array}$$

Considering disturbances with c less than 0.05, and the initial states of the agents are configured as follows:

$$\begin{array}{cccc}\hfill {\zeta }_0& ={[20,25,15]}^{\top },\hfill & \hfill {\zeta }_1& ={[50,30,10]}^{\top },\hfill \\ \hfill {\zeta }_2& ={[-60,70,-5]}^{\top },\hfill & \hfill {\zeta }_3& ={[70,-40,15]}^{\top },\hfill \\ \hfill {\zeta }_4& ={[80,10,-10]}^{\top },\hfill & \hfill {\zeta }_5& ={[40,-40,20]}^{\top }.\hfill \end{array}$$

(46)

where ${\zeta }_i={[x_i,y_i,z_i]}^{\top }$ denotes the 3D state vector of agent i.

By computing ${\beta }_1={\lambda }_{max}\left(L\otimes \left(K^{\top }K\right)\right)=1.2178,{\beta }_2={\lambda }_{max}\left(P\right)=1.6022,$ and to satisfy the stability condition $a_1{\beta }_1+a_2{\beta }_2-\xi <0$, we select $a_1=a_2=0.04$.

As shown in Figure 2, the state trajectories of all agents are depicted in subfigures (a), (b), and (c), while the event-triggering instants are illustrated in subfigure (d). It can be observed that all agents eventually achieve bipartite consensus.

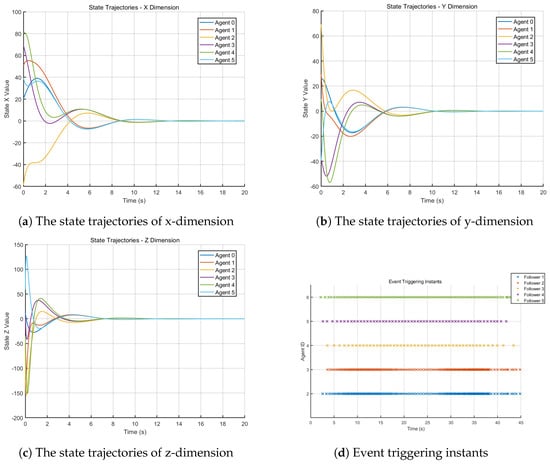
Figure 2. Multi-Agent Systems In A Linear Time-Invariant System.

7.2. Linear Switched Systems

In the switching system, the parameters are configured as follows:

$$A_1=\left(\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ -1& -2& -3\end{array}\right),B_1=\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right).$$

$$A_2=\left(\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ -2& -3& -4\end{array}\right),B_2=\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right).$$

It can be clearly observed that these parameters also satisfy Assumption 1. Through computation, we determine that

$$\begin{array}{cc}\hfill P_1& =\left(\begin{array}{ccc}0.6097& 0.5508& 0.1295\\ 0.5508& 1.1850& 0.3280\\ 0.1295& 0.3280& 0.1519\end{array}\right),P_2=\left(\begin{array}{ccc}0.5732& 0.4264& 0.0664\\ 0.4264& 0.9134& 0.1838\\ 0.0664& 0.1838& 0.0790\end{array}\right)\hfill \\ \hfill K_1& =\left(\begin{array}{ccc}0.0664& 0.1838& 0.0790\end{array}\right),K_2=\left(\begin{array}{ccc}0.0311& 0.0869& 0.0373\end{array}\right)\hfill \end{array}$$

The initial states of the leader and the other five agents are defined as follows:

$$\begin{array}{cccc}\hfill {\zeta }_0& ={[5,10,15]}^{\top },\hfill & \hfill {\zeta }_1& ={[40,30,40]}^{\top },\hfill \\ \hfill {\zeta }_2& ={[-20,5,5]}^{\top },\hfill & \hfill {\zeta }_3& ={[20,30,30]}^{\top },\hfill \\ \hfill {\zeta }_4& ={[20,30,30]}^{\top },\hfill & \hfill {\zeta }_5& ={[-35,-5,-10]}^{\top }.\hfill \end{array}$$

Through calculation, ${\beta }_1={\lambda }_{max}({\overline{L}}_{\sigma }\otimes k^T{k}_{\sigma })=1.2178$, ${\beta }_2={\lambda }_{max}\left(P_{\sigma }\right)=1.6022$, $\mu =1.9$, $\eta =0.16$ by setting $a_1=a_2=0.04$, we obtain $\tau =4.01$ s. With the switching signal and its corresponding state trajectories shown in Figure 3, the system switches between Subsystem 1 and Subsystem 2 under a mean sojourn time.

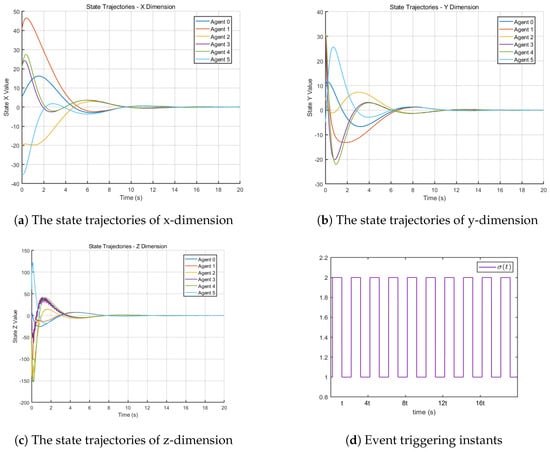
Figure 3. Multi-Agent Systems in linear switched Systems.

7.3. Nonlinear Time-Invariant Systems

The nonlinear terms are given by $f\left(x\left(t\right)\right)=-x+tanh\left(x\right)$, with $\rho =3$. The following initial states are used for the agents:

$$\begin{array}{cccc}\hfill {\zeta }_0& ={[1.0,0.5]}^{\top },\hfill & \hfill {\zeta }_1& ={[4.0,3.0]}^{\top },\hfill \\ \hfill {\zeta }_2& ={[-2.0,5.0]}^{\top },\hfill & \hfill {\zeta }_3& ={[2.0,3.0]}^{\top },\hfill \\ \hfill {\zeta }_4& ={[2.0,1.0]}^{\top },\hfill & \hfill {\zeta }_5& ={[-3.5,-5.0]}^{\top }.\hfill \end{array}$$

(47)

The event-driven parameters for the agents are chosen as: $k\ge 25$. Throughout the simulations, we have ${\beta }_3=k_{min}{\lambda }_{min}=3.11$, which satisfies the stability condition ${\beta }_3>2\rho +1$. Using protocol (Equation (9)), Figure 4 presents the state trajectories of all agents, along with their corresponding event-triggering instants, demonstrating that bipartite consensus is achieved.

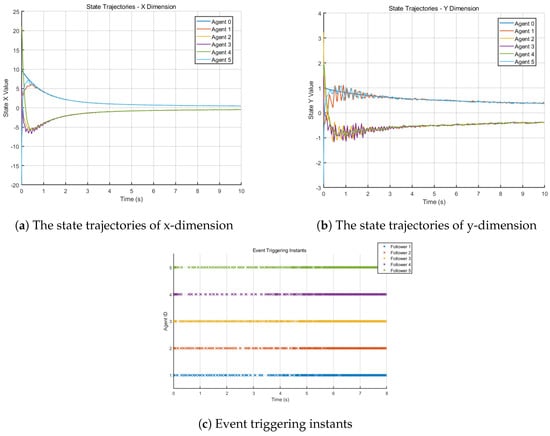
Figure 4. Multi-Agent Systems in Noninear Time-Invariant System System.

7.4. Nonlinear Switched Systems

The nonlinear terms of the agents are described by $f_1\left(x\left(t\right)\right)=-x+tanh\left(x\right)$, $f_2\left(x\left(t\right)\right)=-x+sin\left(x\right)$.

The following initial states are used for the agents:

$$\begin{array}{cccc}\hfill {\zeta }_0& ={[10,10]}^{\top },\hfill & \hfill {\zeta }_1& ={[30,50]}^{\top },\hfill \\ \hfill {\zeta }_2& ={[-20,50]}^{\top },\hfill & \hfill {\zeta }_3& ={[20,30]}^{\top },\hfill \\ \hfill {\zeta }_4& ={[20,30]}^{\top },\hfill & \hfill {\zeta }_5& ={[-35,50]}^{\top }.\hfill \end{array}$$

(48)

For $f_1\left(x\right)$, the system has a Lipschitz constant $\rho =1$ and $f_2\left(x\right)$ has a Lipschitz constant $\rho =2$. We choose the control gain $k\ge 50$. Throughout the simulations, we have $\mu =2$, $\eta =1.235,{\beta }_3=k_{min}{\lambda }_{min}=6.235$, which satisfies the stability condition ${\beta }_3>2\rho +1$. Then we obtain ${\tau }_a=0.56s$. Under the settings of mean sojourn time and event-triggered mechanism, the system achieves bipartite consensus illustrated in Figure 5.

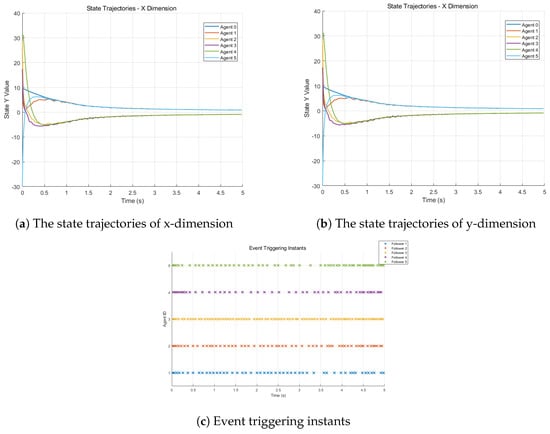
Figure 5. Multi-Agent Systems in Noninear Switched Systems.

8. Conclusions

This paper studies event-triggered bipartite consensus for MASs with linear/nonlinear dynamics for both time-invariant and switched systems. In time-invariant systems, we analyze consensus using an error transformation model and Lyapunov theory. For switched systems, we first establish the stability of each subsystem, then address the switching-induced jumps by designing an appropriate mean sojourn time, thereby achieving asymptotic consensus. Simulations confirm the validity and efficacy of the introduced method. How to integrate the existing model with reinforcement learning and how to investigate bipartite consensus under unbalanced network structures will be the focus of our future research.