Survey on Graph-Based Reinforcement Learning for Networked Coordination and Control

Abstract

A networked system consists of a collection of interconnected autonomous agents that communicate and interact through a shared communication infrastructure. These agents collaborate to pursue common objectives or exhibit coordinated behaviors that would be difficult or impossible for a single agent to achieve alone. With widespread applications in domains such as robotics, smart grids, and communication networks, the coordination and control of networked systems have become a vital research focus—driven by the complexity of distributed interactions and decision-making processes. Graph-based reinforcement learning (GRL) has emerged as a powerful paradigm that combines reinforcement learning with graph signal processing and graph neural networks (GNNs) to develop policies that are relationally aware, scalable, and adaptable to diverse network topologies. This survey aims to advance research in this evolving area by providing a comprehensive overview of GRL in the context of networked coordination and control. It covers the fundamental principles of reinforcement learning and graph neural networks, examines state-of-the-art GRL models and algorithms, reviews training methodologies, discusses key challenges, and highlights real-world applications. By synthesizing theoretical foundations, empirical insights, and open research questions, this survey serves as a cohesive and structured resource for the study and advancement of GRL-enabled networked systems.

1. Introduction

The rapid emergence of large-scale, networked systems, such as multi-robot teams, autonomous vehicle fleets, wireless sensor networks, and smart grids, has brought renewed attention to the challenges of coordination and control in complex, distributed environments [1,2,3]. These systems consist of multiple autonomous agents that interact with one another over structured topologies, exchanging information and making decisions to achieve global objectives. The inherent graph-structured nature of these systems, characterized by dynamic inter-agent relationships, spatial constraints, and localized communication, presents unique opportunities and challenges for learning-based control [4].

Reinforcement learning (RL) has gained popularity as a powerful framework for sequential decision making under uncertainty [5]. It enables agents to learn optimal control policies through trial-and-error interactions with their environment. However, conventional RL methods typically assume flat or unstructured observation spaces, making them ill-suited for multi-agent systems with relational dependencies. In contrast, graph neural networks (GNNs) offer a principled way to model such relational structures by leveraging the underlying graph topology to encode spatial or communication dependencies among agents [6,7].

The integration of GNNs with MARL has emerged as an effective approach for scalable and generalizable coordination in networked systems. GNN-enhanced MARL methods enable agents to learn policies that are permutation-invariant, localized, and transferable across varying graph topologies and scales. By embedding the message-passing principles of GNNs into policy learning, these approaches can exploit both structural and dynamic regularities to enhance learning outcomes and coordination effectiveness.

This survey provides a comprehensive overview of recent advances in GNN-MARL for networked coordination and control. We examine how GNNs enhance fundamental RL elements, including state representation, action selection, and reward design; analyze the architectural principles underlying message-passing and agent coordination mechanisms; and evaluate different training frameworks from centralized approaches to distributed coordination strategies. We discuss representative applications spanning autonomous systems, traffic networks, wireless communications, smart energy systems, and supply chain management, and identify open research challenges, including computational complexity, convergence properties, and cross-domain generalization. By synthesizing theoretical foundations, architectural innovations, and practical insights, this survey aims to provide a structured guide for researchers and practitioners seeking to leverage graph-enhanced learning approaches for coordination and control in complex networked environments.

The remainder of this survey is organized as follows. Section 2 provides background on RL and GNNs. Section 3, the core technical contribution, examines how GNNs enhance MARL systems through several aspects: fundamental RL elements (state representation, action selection, reward design), multi-agent communication and coordination mechanisms, training methods, and performance evaluation criteria. Section 4 presents real-world applications in robotics, transportation, wireless networks, and manufacturing. Section 5 identifies research challenges and future directions on scalability, communication efficiency, and theoretical foundations. Finally, Section 6 concludes the survey. Throughout, we emphasize both theoretical advances and empirical validations to provide a comprehensive resource for researchers and practitioners.

2. Related Work

In recent years, the integration of graph neural networks (GNNs) with reinforcement learning (RL), especially multi-agent reinforcement learning (MARL), has emerged as a rapidly growing research area. Along with this development, several surveys have been published to provide overviews of the field. These works are valuable for positioning current progress, yet they differ in scope, focus, and level of detail. In this section, we briefly review representative surveys and outline how our work builds upon and complements them.

The survey Challenges and Opportunities in Deep Reinforcement Learning with Graph Neural Networks: A Comprehensive Review of Algorithms and Applications [8] provides a broad overview of how GNNs can be combined with deep RL. It systematically discusses algorithmic advances and a wide range of applications, but its emphasis is largely on single-agent RL. As a result, MARL-specific challenges such as inter-agent communication, coordination, and credit assignment are not addressed in depth.

Another early effort, Graph Neural Networks and Reinforcement Learning: A Survey [9], offers wide coverage, from theoretical foundations to practical algorithms. While the work carefully categorizes existing approaches, MARL is not treated as a central analytical focus. Moreover, the survey does not provide a systematic discussion of learning and training frameworks, which are critical for scaling GNN-enhanced MARL to practical systems.

Closer to our topic, Graph Neural Network Meets Multi-Agent Reinforcement Learning: Fundamentals, Applications, and Future Directions [10] specifically addresses the intersection of GNNs and MARL. It clearly presents the fundamentals of GNNs in MARL and organizes existing applications around functional roles such as communication and representation learning. However, given its time of publication, it does not capture several recent algorithmic directions such as symmetry-aware architectures (e.g., PEnGUiN), hypergraph-based coordination (e.g., HYGMA), or advanced decomposition methods (e.g., QMIX-GNN, ExpoComm). Furthermore, its perspective is primarily function-oriented, whereas our work takes a more fundamental view by aligning GNN methods with the core components of RL.

Compared with these surveys, our contribution is threefold. First, we adopt an inside-out organization that begins with the essential building blocks of RL—state, action, and reward—and we systematically analyze how GNNs enhance each component. Second, we highlight MARL-specific mechanisms by dedicating separate sections to message passing and multi-agent coordination, showing how GNNs reshape interaction and cooperation. Finally, we provide a structured overview of learning and training frameworks, including centralized training, decentralized execution, and heterogeneous-agent settings, which are essential for bridging theoretical advances with real-world deployment. Therefore, our survey not only complements prior reviews but also provides methodological guidance for future research in GNN-enhanced MARL.

3. Background: Concepts and Principles

In this section, fundamental concepts and principles of RL and GNNs are presented, serving as a basis for detailed discussion on GRL in later sections.

3.1. Reinforcement Learning

This subsection is focused on fundamental RL algorithms, starting with single-agent RL, followed by multi-agent RL.

3.1.1. Single-Agent Reinforcement Learning (RL)

Single-agent reinforcement learning (RL) [11] is a computational framework for learning goal-oriented behavior through trial-and-error. The core of RL lies in the continuous interaction loop between an agent and its environment, as depicted in Figure 1 and formalized as a Markov decision process (MDP). This interaction unfolds sequentially over discrete timesteps. At each timestep t, the process begins with the agent observing the environment’s current state, $S_t$, which provides a complete description of the situation. Based on this state, the agent consults its policy, $\pi \left(a\right|s)$, to select an action, $A_t$. This action is then executed, causing the environment to change. In the subsequent timestep, $t+1$, the environment responds with two crucial pieces of information: a new state, $S_{t+1}$, and a scalar reward, $R_{t+1}$. The reward signal provides evaluative feedback, indicating how beneficial the action $A_t$ was in state $S_t$. The agent’s objective is to learn a policy that refines its decision making over time by leveraging this reward feedback to maximize the expected cumulative discounted reward, known as the return: $G_t={\sum }_{k=0}^{\infty },{\gamma }^k{R}_{t+k+1}$ where the discount factor $\gamma \in [0,1)$ determines the present value of future rewards.

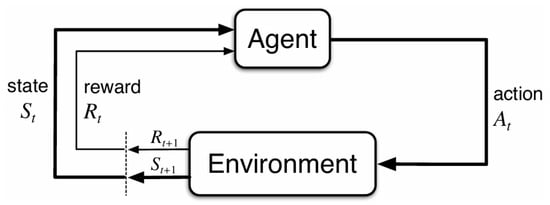
Figure 1. The agent–environment interaction in a Markov decision process [11].

Typical single-agent RL algorithms and their advantages and disadvantages are briefly explained below.

Q-learning [12] is a model-free, off-policy algorithm that learns an action-value function $Q(s,a)$ through temporal difference updates:

$$Q(s,a)\leftarrow Q(s,a)+\alpha [r+\gamma \underset{a^{\prime }}{max}Q(s^{\prime },a^{\prime })-Q(s,a)].$$

(1)

The algorithm directly learns optimal action-values regardless of the followed policy, effectively handling discrete action spaces. However, its tabular nature becomes impractical for large state spaces, motivating the development of function approximation methods.

Policy gradient methods [13] directly optimize parameterized policies $\pi \left(a\right|s;\theta )$ by ascending the gradient of the expected return as

$${\nabla }_{\theta }J\left(\theta \right)=E[{\nabla }_{\theta }log\pi \left(a\right|s;\theta )G_t].$$

(2)

The REINFORCE algorithm [13] implements this using Monte Carlo estimates. While these methods naturally support continuous action spaces and stochastic policies, they suffer from high variance in gradient estimates, motivating the development of variance reduction techniques such as baselines or advantage functions.

Actor–critic methods [14,15] combine value-based and policy-based approaches to reduce variance. The actor learns the policy $\pi \left(a\right|s;\theta )$, while the critic learns the value function $V(s;\omega )$, with updates using the advantage $A(s,a)=Q(s,a)-V\left(s\right)$. This advantage function serves as a lower-variance replacement for the full return $G_t$ used in the vanilla policy gradient update, Equation (2), leading to more stable learning. This hybrid architecture provides more stable learning than pure policy gradient methods while maintaining their flexibility.

Advantage actor–critic (A2C) is a synchronous variant derived from A3C [16], using the advantage function to compute policy gradients as

$${\nabla }_{\theta }J\left(\theta \right)\approx \mathbb{E}[{\nabla }_{\theta }log\pi \left(a\right|s;\theta )·A(s,a)]$$

(3)

where $A(s,a)$ is typically estimated using temporal-difference returns.

Asynchronous advantage actor–critic (A3C) [16] introduced asynchronous parallel training to actor–critic methods, significantly improving their scalability and stability. Multiple workers independently interact with separate environment instances, computing policy updates using n-step advantage estimates:

$$A(s_t,a_t)=\sum _{i=0}^{k-1}{\gamma }^i{r}_{t+i}+{\gamma }^{k}V(s_{t+k};{\theta }_v)-V(s_t;{\theta }_v).$$

(4)

These workers asynchronously update shared global parameters, eliminating the need for experience replay. The diversity of parallel trajectories improves exploration and leads to more stable and efficient learning.

Deep Q-network (DQN) [17] extends Q-learning to high-dimensional state spaces by approximating the action-value function with deep neural networks. Two key innovations help stabilize training: experience replay mitigates temporal correlations by sampling transitions from a replay buffer; target networks, updated periodically, provide more stable learning targets. The loss function

$$L\left(\theta \right)=\mathbb{E}[{(r+\gamma \underset{a^{\prime }}{max}Q(s^{\prime },a^{\prime };{\theta }_{\mathrm{target}})-Q(s,a;\theta ))}^2]$$

(5)

allows learning directly from raw pixel inputs and enables DQN to reach human-level performance on Atari games.

Double deep Q-network (DDQN) [18] addresses DQN’s overestimation bias by decoupling action selection and evaluation:

$$\mathrm{Target}=r+\gamma Q(s^{\prime },arg\underset{a^{\prime }}{max}Q(s^{\prime },a^{\prime };\theta );{\theta }_{\mathrm{target}}).$$

(6)

Unlike the standard DQN target in Equation (5), which uses the target network for both selecting the best next action and evaluating its value, the DDQN target in Equation (6) uses the online network ($\theta$) to select the action and the target network (${\theta }_{\mathrm{target}}$) to evaluate it. The current network selects actions while the target network evaluates them, significantly reducing overestimation and improving learning stability across various domains.

Deep deterministic policy gradient (DDPG) [19,20] extends actor–critic methods to continuous control using deterministic policies $\mu (s;{\theta }_{\mu })$. The algorithm employs experience replay, separate target networks with soft updates (${\theta }^{\prime }\leftarrow \tau \theta +(1-\tau ){\theta }^{\prime }$), and exploration noise (typically the Ornstein–Uhlenbeck process). The critic updates minimize the loss function,

$$L=E\left[{(r+\gamma Q(s^{\prime },\mu (s^{\prime };{\theta }_{\mu }^{\prime });{\theta }_Q^{\prime })-Q(s,a;{\theta }_Q))}^2\right],$$

(7)

while the actor maximizes expected Q-values.

Twin delayed deep deterministic policy gradient (TD3) [21] improves DDPG through three modifications: twin Q-functions with minimum target values to reduce overestimation

$$y=r+\gamma \underset{i=1,2}{min}{Q}_i(s^{\prime },{\mu }_{{\theta }^{\prime }}\left(s^{\prime }\right)+ϵ),$$

(8)

delayed policy updates relative to value updates, and target policy smoothing with clipped noise. These changes significantly enhance stability and performance in continuous control tasks.

Soft actor–critic (SAC) [22] incorporates maximum entropy reinforcement learning to balance exploration and exploitation:

$$J\left(\pi \right)=E[\sum _t(r_t+\alpha H\left(\pi (·|s_t)\right))].$$

(9)

This objective modifies the standard expected return by adding a weighted entropy term, encouraging the policy to be as random as possible while still maximizing rewards. The algorithm uses stochastic policies, twin soft Q-functions, and automatic temperature tuning for the entropy coefficient $\alpha$. SAC’s robustness to hyperparameters and sample efficiency make it highly effective for continuous control.

Proximal policy optimization (PPO) [23] simplifies trust region methods using a clipped surrogate objective

$$L^{CLIP}\left(\theta \right)=E[min(r_t\left(\theta \right)A_t,\mathrm{clip}(r_t\left(\theta \right),1-ϵ,1+ϵ)A_t)]$$

(10)

where $r_t\left(\theta \right)={\displaystyle \frac{{\pi }_{\theta }\left(a_t\right|s_t)}{{\pi }_{{\theta }_{old}}\left(a_t\right|s_t)}}$. This prevents destructively large policy updates while maintaining simplicity. PPO typically includes generalized advantage estimation (GAE) and has become the standard choice for policy optimization due to its stability and performance.

3.1.2. Multi-Agent Reinforcement Learning (MARL)

MARL [24,25] extends the reinforcement learning framework to environments with multiple simultaneously learning agents. Figure 2 illustrates this setting: each agent (e.g., Agent1, Agent2, Agent3) interacts with its local observation and reward from the environment, while their actions are combined into a joint action that drives the next state transition. This joint dependence highlights that each agent’s learning process is coupled with others, unlike the single-agent case. Additionally, agents often need to collaborate to achieve a common goal, as indicated by dashed lines in the figure representing their interactions. These relationships could be used to construct a graph neural network (GNN), enabling the development of GNN-MARL models that effectively capture inter-agent dependencies.

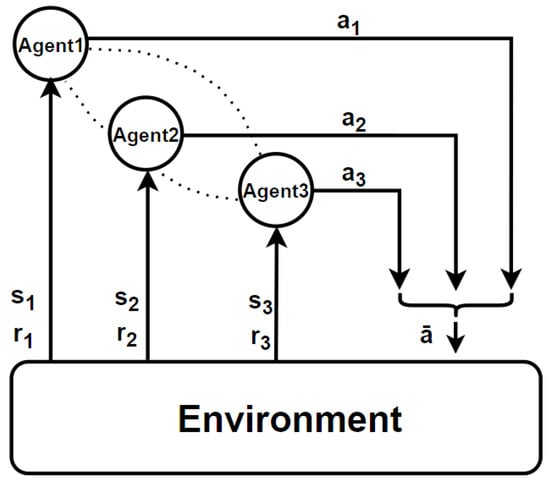
Figure 2. The diagram of multi-agent reinforcement.

By contrast, Figure 1 shows the classical single-agent RL setup, where the agent interacts with the environment in isolation, receiving a state $S_t$ and reward $R_t$ and producing an action $A_t$ that solely determines the next state. MARL generalizes this to Markov games (also known as stochastic games), formalized as $⟨N,S,A_i{i=1}^N,T,R_i{i=1}^N,\gamma ⟩$. Here, N agents share a global state space S, each with its own action space $A_i$ and reward function $R_i:S\times A_1\times \cdots \times A_N\to \mathbb{R}$. The transition function T depends on the joint action of all agents, distinguishing it from the single-agent setting where transitions depend only on one agent’s action. Similarly, each agent’s reward $R_i$ is a function of the global state and the joint action, a significant departure from the single-agent reward $R_{t+1}$, which results from an individual agent’s action $A_t$. This coupling is the primary source of non-stationarity in MARL. When $N=1$, the Markov game reduces to the standard MDP.

This multi-agent extension introduces new challenges [24], such as non-stationarity, partial observability, and coordination complexity. Consequently, specialized MARL algorithms are required to address cooperation, competition, or mixed interactions among agents.

Multi-agent policy optimization. Policy-based optimization is widely used in multi-agent reinforcement learning (MARL) due to several key advantages: handling high-dimensional and continuous action spaces, decentralized execution with centralized training, stable convergence in cooperative and mixed environments, support for stochastic policies for exploration and robustness, flexibility with shared or individual policies, and compatibility with actor–critic methods. Some typical policy-based MARL methods are:

• Multi-agent deep deterministic policy gradient (MADDPG) [26] addresses non-stationarity through centralized training with decentralized execution (CTDE). Each agent i maintains a decentralized actor ${\mu }_i\left(o_i\right)$ using only local observations, while training employs centralized critics $Q_i(x,a_1,...,a_N)$ accessing all agents’ information. This design stabilizes learning while maintaining practical deployability.
• Multi-agent proximal policy optimization (MAPPO) [27] demonstrates that properly configured PPO achieves strong multi-agent performance. Key modifications include centralized value functions conditioned on global state, PopArt value normalization, and careful hyperparameter tuning. This adapts the single-agent PPO framework, whose objective is shown in Equation (10), to the multi-agent domain by ensuring the advantage estimates used for the clipped objective are derived from a centralized critic aware of all agents’ states. MAPPO’s simplicity and effectiveness have established it as a standard baseline for cooperative multi-agent tasks.
• Counterfactual multi-agent policy gradients (COMA) [28] addresses the credit assignment problem in cooperative multi-agent settings by using counterfactual baselines. Each agent’s advantage function compares the joint action value with a counterfactual baseline computed by marginalizing over that agent’s actions while keeping other agents’ actions fixed, providing a more sophisticated way to calculate the advantage term $A_t$ seen in single-agent actor-critic updates like Equation (3) for the multi-agent case, enabling more accurate individual contribution assessment.
• Mean field actor–critic (MFAC) [29] tackles large-scale multi-agent systems by approximating the complex many-agent interactions through mean field theory. Instead of modeling all pairwise interactions, each agent considers the mean effect of neighboring agents, significantly reducing computational complexity while maintaining effective coordination in dense multi-agent environments.

3.2. Graph Neural Networks

Graph neural networks (GNNs) [30] generalize neural network models to graph-structured data, capturing complex relational patterns. A graph is defined as $G=(V,E)$, where V is a set of nodes and E are edges. The original GNN model uses an information diffusion mechanism in which nodes iteratively update their states until a stable equilibrium is reached. For a node v, the state update is

$$x_v=f_w(l_v,l_{co\left[v\right]},x_{ne\left[v\right]},l_{ne\left[v\right]})$$

(11)

where $x_v$ is the state of node v, $l_v$ is its label, $l_{co\left[v\right]}$ are the labels of edges connected to v, $x_{ne\left[v\right]}$ are the states of neighboring nodes, and $l_{ne\left[v\right]}$ are their labels. The output is computed as $o_v=g_w(x_v,l_v)$. The model ensures convergence by requiring the transition function $f_w$ to be a contraction mapping, with states being iteratively updated until a fixed point is reached.

The foundational GNN framework has inspired numerous variants that simplify the computational requirements while maintaining the core message-passing paradigm. These modern approaches have led to the widespread adoption of graph neural networks across diverse domains:

Graph convolutional networks (GCN) [31] extends convolution to graphs by efficiently aggregating neighbor features through spectral graph theory. The model is motivated by a first-order approximation of spectral graph convolutions, leading to the layer-wise propagation rule:

$$H^{(l+1)}=\sigma \left({\tilde{D}}^{-{\displaystyle \frac{1}{2}}}\tilde{A}{\tilde{D}}^{-{\displaystyle \frac{1}{2}}}{H}^{\left(l\right)}{W}^{\left(l\right)}\right)$$

(12)

where $H^{\left(l\right)}$ contains node features at layer l, $\tilde{A}=A+I_N$ adds self-loops to prevent vanishing gradients, ${\tilde{D}}_{ii}={\sum }_j{\tilde{A}}_{ij}$ is the degree matrix, $W^{\left(l\right)}$ is a trainable weight matrix, and $\sigma$ is an activation function. The symmetric normalization ${\tilde{D}}^{-{\displaystyle \frac{1}{2}}}\tilde{A}{\tilde{D}}^{-{\displaystyle \frac{1}{2}}}$ ensures stable training by controlling the eigenvalue range. This propagation rule scales linearly with the number of edges $O\left(\right|E\left|\right)$ and enables semi-supervised node classification by conditioning on both node features and graph structure. GCNs have proven effective for citation networks, knowledge graphs, and social network analysis.

Graph sample and aggregate (GraphSAGE) [32] addresses the limitation of transductive GCNs by enabling inductive learning on unseen nodes. Instead of training individual embeddings for each node, GraphSAGE learns aggregator functions that generate embeddings by sampling and aggregating features from a node’s local neighborhood:

$$h_v^{(l+1)}=\sigma \left(W^{\left(l\right)}·\mathrm{CONCAT}\left(h_v^{\left(l\right)},{\mathrm{AGGREGATE}}^{\left(l\right)}\left(\{h_u^{\left(l\right)}:u\in \mathcal{N}\left(v\right)\}\right)\right)\right)$$

(13)

where $\mathcal{N}\left(v\right)$ represents a fixed-size uniform sample of node v’s neighbors to maintain constant computational complexity. The concatenation operation acts as a skip connection, preserving the node’s representation while incorporating neighborhood information. GraphSAGE explores multiple aggregator architectures: the mean aggregator (similar to GCN’s spectral convolution), LSTM aggregators for higher expressive capacity, and pooling aggregators that apply element-wise max-pooling after transforming each neighbor through a neural network. The framework uses an unsupervised loss function based on random walks to encourage nearby nodes to have similar representations. This inductive capability enables GraphSAGE to generalize to entirely unseen graphs and dynamically handle evolving networks, making it particularly valuable for production systems processing streaming graph data.

Graph attention networks (GAT) [33] introduce learnable attention mechanisms to selectively weight neighbor contributions, addressing GraphSAGE’s uniform treatment of neighbors. GAT computes attention coefficients through a shared neural network that evaluates pairwise node interactions:

$$e_{ij}=\mathrm{LeakyReLU}\left({\mathbf{a}}^T\left[W{\mathbf{h}}_i\parallel W{\mathbf{h}}_j\right]\right)$$

(14)

where W transforms node features, $\mathbf{a}$ is a learnable attention vector, and ∥ denotes concatenation. These raw attention scores are normalized via softmax to obtain attention weights:

$${\alpha }_{ij}={\displaystyle \frac{exp\left(e_{ij}\right)}{{\sum }_{k\in \mathcal{N}\left(i\right)}exp\left(e_{ik}\right)}}.$$

(15)

The final node representation aggregates neighbor features weighted by attention:

$${\mathbf{h}}_i^{\prime }=\sigma \left(\sum _{j\in \mathcal{N}\left(i\right)}{\alpha }_{ij}W{\mathbf{h}}_j\right).$$

(16)

This attention-based aggregation, defined in Equation (16), allows the model to learn the importance of different neighbors dynamically. This contrasts sharply with the graph convolutional network’s propagation rule, Equation (12), where neighbor contributions are weighted by a fixed, pre-computed normalization constant derived from the graph structure itself. GAT employs multi-head attention for stability, computing K independent attention mechanisms and concatenating (or averaging) their outputs. This design enables the model to focus on different aspects of neighborhood relationships simultaneously. Unlike spectral methods, GAT operates locally without requiring global graph structure knowledge, making it naturally applicable to both transductive and inductive settings. The attention mechanism provides interpretability by revealing which neighbors contribute most to each node’s representation, though careful regularization is needed to prevent attention collapse on small neighborhoods.

Relational graph convolutional networks (R-GCN) [34] extends standard GCNs to handle multi-relational graphs where edges have different semantic meanings. R-GCNs modify the aggregation mechanism to use relation-specific transformations:

$$h_i^{(l+1)}=\sigma \left(\sum _{r\in \mathcal{R}}\sum _{j\in {\mathcal{N}}_i^r}{\displaystyle \frac{1}{c_{i,r}}}{W}_r^{\left(l\right)}{h}_j^{\left(l\right)}+W_0^{\left(l\right)}{h}_i^{\left(l\right)}\right)$$

(17)

where $\mathcal{R}$ denotes the set of relation types, ${\mathcal{N}}_i^r$ represents neighbors of node i under relation r, $W_r^{\left(l\right)}$ is a relation-specific weight matrix, and $c_{i,r}$ is a normalization constant (typically $|{\mathcal{N}}_i^r|$). The self-loop term $W_0^{\left(l\right)}{h}_i^{\left(l\right)}$ preserves the node’s own information across layers.

To address the parameter explosion problem when dealing with many relation types, R-GCNs employ two regularization techniques: basis decomposition, where $W_r^{\left(l\right)}={\sum }_{b=1}^B{a}_{rb}^{\left(l\right)}{V}_b^{\left(l\right)}$ shares basis matrices $V_b^{\left(l\right)}$ across relations with learned coefficients $a_{rb}^{\left(l\right)}$; and block-diagonal decomposition, which constrains weight matrices to block-diagonal structure. These techniques enable R-GCNs to scale to knowledge graphs with hundreds of relation types while maintaining expressive power. R-GCNs have proven particularly effective for knowledge base completion tasks, where understanding the semantic differences between relations is crucial for accurate link prediction and entity classification.

Graph isomorphism networks (GIN). Many GNNs struggle to distinguish certain graph structures. Graph isomorphism networks [35] address this by matching the Weisfeiler–Lehman (WL) test’s power. GIN uses:

$$h_v^{\left(k\right)}={\mathrm{MLP}}^{\left(k\right)}\left(\left(1+{ϵ}^{\left(k\right)}\right)·h_v^{(k-1)}+\sum _{u\in \mathcal{N}\left(v\right)}{h}_u^{(k-1)}\right)$$

(18)

where MLP is a learnable multi-layer perceptron and ${ϵ}^{\left(k\right)}$ is a learned (or fixed) scalar parameter. The use of a multi-layer perceptron (MLP) within the update rule, Equation (18), is a key distinction from models like GCN and GAT, which typically use a single linear transformation (e.g., $W^{\left(l\right)}$ in Equation (12)). This allows GIN to learn more complex, non-linear aggregation functions, granting it greater expressive power. By combining a tunable self-loop weight $(1+ϵ)$ with sum aggregation of neighbors, GIN can produce distinct embeddings for different multiset neighborhoods.

The key theoretical insight is that GIN satisfies the conditions for maximal representational power: it uses injective aggregation functions that can distinguish any two different multisets of node features. Specifically, GIN’s aggregation scheme can represent any injective multiset function through the universal approximation properties of MLPs combined with sum pooling.

For graph-level tasks, GIN employs a concatenated readout across all layers:

$$h_G=\mathrm{CONCAT}\left(\mathrm{READOUT}\left(\left\{h_v^{\left(k\right)}\mid v\in G\right\}\right)\mid k=0,1,\dots ,K\right).$$

(19)

This design makes GIN provably as powerful as the one-dimensional Weisfeiler–Lehman test in distinguishing graph structures. The enhanced expressiveness benefits applications like molecular property prediction, where distinguishing subtle structural differences is crucial for accurate predictions.

Graph Transformers. Graph Transformers [36] generalize the Transformer architecture to handle graph-structured data by adapting self-attention mechanisms to respect graph topology. Unlike traditional GNNs that aggregate information only from local neighbors, graph Transformers can model long-range dependencies by allowing attention across the entire graph or within a defined neighborhood. To preserve structural information, they incorporate positional encodings derived from Laplacian eigenvectors, which generalize the sinusoidal encodings used in NLP Transformers. These encodings help the model distinguish node positions and capture distance-aware patterns in the graph.

To improve training efficiency and stability, graph Transformers replace LayerNorm with BatchNorm, which leads to better generalization and faster convergence in graph tasks. Additionally, for graphs with edge attributes—such as molecules or knowledge graphs—the model integrates edge features directly into the attention mechanism. By modifying attention scores based on edge embeddings, the model enhances its ability to leverage pairwise relationships. Though computationally demanding, graph Transformers perform particularly well in scenarios where graph sparsity and long-range semantic interactions are important, such as in document graphs or molecular property prediction.

4. GNN-RL Methods and Algorithms

Building on the introduction of GNNs and RL, this section focuses on a review of the state-of-the-art GNN-RL methods and algorithms. First, we explore how GNNs enhance key elements of RL such as state representation, action selection, and reward design. Then, we examine their role in enabling inter-agent communication and coordination, followed by system-level training and evaluation strategies.

4.1. MARL Elements Enhanced by GNNs

This section examines how GNNs transform the core elements of MARL: state representation, action selection, and reward design. Each demonstrates how GNN integration addresses fundamental multi-agent coordination challenges while maintaining computational tractability. Table 1 presents a summary of the methods for the enhanced MARL elements by GNNs.

Table 1. Summary of the methods for the enhanced MARL elements by GNNs.

Component	Method
State Representation	Graph convolutional networks (GCN) [31]
	Multi-agent graph embedding communication (MAGEC) [37]
	Graph attention networks (GAT) [33]
	Hierarchical graph attention networks (HGAT) [38]
	Partially equivariant graph unified networks (PEnGUiN) [39]
	Graph-assisted predictive state representation (GAPSR) [40]
	Hypergraph-based multi-agent coordination (HYGMA) [41]
	Graph-based multi-agent actor–critic network (G2ANet) [42]
	Relational state abstraction [43]
	Multimodal graph fusion [44]
	Generalized graph drawing [45]
Action Selection	Graph-based multi-agent actor–critic network (G2ANet) [42]
	Multi-actor-attention-critic (MAAC) [46]
	Exponential communication (ExpoComm) [47]
	QMIX with graph neural networks (QMIX-GNN) [48]
	Role-based multi-agent deep reinforcement learning (RODE) [49]
	Hypergraph-based multi-agent coordination (HYGMA) [41]
	Heterogeneous multi-agent graph Q-network (HMAGQ-Net) [50]
Reward Design	Reward propagation GCN [51]
	CoHet [52]
	Graph conv. value decomposition [53]
	QMIX [48]
	VDN [54]

4.1.1. State Representation in GNN-Enhanced MARL

State representation in MARL faces the challenge of capturing both individual agent states and complex interactions within dynamic environments [26]. GNN integration introduces novel approaches leveraging inherent graph structures in multi-agent systems, moving beyond traditional vector representations to enable richer coordination modeling [39,55].

The state representation methods can be systematically classified across multiple dimensions based on their underlying network architectures, learning paradigms, and coordination mechanisms. These approaches span from fundamental graph convolutional networks (GCNs) [31] to advanced architectures including hierarchical attention networks [38], partially equivariant systems [39], and hypergraph neural networks [41]. The classification reveals three primary architectural categories: spectral-based methods that provide Laplacian-based neighbor aggregation [31], attention-based approaches that enable selective information processing through learnable attention mechanisms [33,38,42], and advanced specialized architectures including inductive learning methods [37], symmetry-aware networks [39], and hypergraph-based systems [41]. Table 2 provides a comprehensive comparison of these methods across network architectures, learning paradigms, coordination mechanisms, theoretical foundations, and scalability characteristics.

Table 2. State representation methods in GNN-enhanced MARL.

Algorithm	Net Arch.	Learning	Coordination Mechanism	Theoretical Foundation	Scale
GCN [31]	GCN	CTDE	Laplacian-based message passing	Spectral graph theory	Medium
MAGEC [37]	GraphSAGE	CTDE	Spatial graph encoding with inductive learning	Inductive representation learning	Medium
GAT [33]	GAT	CTDE	Learnable attention coefficients for neighbor prioritization	Attention mechanism	Medium
HGAT [38]	Hierarchical GAT	CTDE	Two-level attention (node + hyper-node)	Hierarchical attention mechanism	Large
PEnGUiN [39]	Partially equivariant GNN	CTDE	Learnable symmetry score blending	Partial equivariance theory	Medium
GAPSR [40]	Graph-assisted PSR	CTDE	Primitive predictive states aggregation	Predictive state theory	Medium
HYGMA [41]	Hypergraph neural network	CTDE	Spectral clustering + hypergraph convolution	Hypergraph theory	Large
G2ANet [42]	Two-stage GAT	CTDE	Hard attention (BiLSTM) + soft attention	Gumbel-Softmax + attention	Medium
Relational State Abstraction [43]	R-GCN	CTDE	Spatial relation encoding	Relational learning theory	Medium
Multimodal Graph Fusion [44]	Multiplexed GNN	CTDE	Modality-specific autoencoders + graph layers	Multimodal fusion theory	Medium-large
Generalized Graph Drawing [45]	Laplacian eigenvectors	Individual	Spectral state embedding with unique minimizer	Spectral graph optimization	Medium-large

The evolution from traditional vector representations to graph-based encoding represents a paradigm shift in MARL. Early approaches struggled with exponential state space growth, while modern GNN-based methods naturally model spatial-temporal relationships through dynamic graph structures, enabling efficient neighbor aggregation without full enumeration of the global state space.

Graph-based encoding transforms environments into structured representations where agents are represented as nodes and their interactions as edges. The environment can be modeled as a graph $\mathcal{G}=(\mathcal{V},\mathcal{E})$, where $\mathcal{V}$ denotes the set of nodes (agents) and $\mathcal{E}$ the set of edges (interactions), enabling localized and topology-aware feature learning.

Graph convolutional network (GCN). A standard graph convolutional network (GCN) [31] performs layer-wise propagation using a message aggregation scheme based on the graph Laplacian. Specifically, the node representations are updated according to:

$$H^{(l+1)}=\sigma \left({\tilde{D}}^{-1/2}\tilde{A}{\tilde{D}}^{-1/2}{H}^{\left(l\right)}{W}^{\left(l\right)}\right)$$

(20)

where $\tilde{A}=A+I$ is the adjacency matrix with added self-connections, $\tilde{D}$ is the degree matrix of $\tilde{A}$, $H^{\left(l\right)}$ is the node feature matrix at layer l, $W^{\left(l\right)}$ is the trainable weight matrix, and $\sigma (·)$ is an activation function such as ReLU. This update rule is identical to the foundational GCN propagation mechanism previously introduced in Equation (12), which forms the basis for many advanced graph-based MARL models. A well-documented issue with GCNs is the tendency towards over-smoothing, where repeated neighborhood averaging can make node representations overly similar after several layers. For state representation, this may cause distinct agent states to become indistinguishable, potentially hindering fine-grained policy learning.

Multi-agent graph embedding-based coordination (MAGEC). Multi-agent graph embedding methods enhance continuous-space representation by constructing spatial graphs that encode agent–obstacle–target relations [37]. In such spatial graphs, nodes represent agents and relevant environmental entities. To learn coordination policies over this representation, GNNs such as GraphSAGE [32] are applied:

$$h_i^{\left(k\right)}=\sigma \left(W^{\left(k\right)}·{\mathrm{AGGREGATE}}^{\left(k\right)}\left(\left\{h_i^{(k-1)}\right\}\cup \{h_j^{(k-1)}:j\in \mathcal{N}\left(i\right)\}\right)\right).$$

(21)

Here, ${\mathrm{AGGREGATE}}^{\left(k\right)}$ denotes a neighborhood aggregation function. This formulation directly applies the inductive GraphSAGE framework from Equation (13), where the aggregator function learns to generate embeddings from sampled local neighborhoods. This spatial-graph plus GraphSAGE pipeline improves coordination robustness by leveraging spatial locality and inductive generalization.

Multi-agent state aggregation enhancement. Traditional state aggregation in multi-agent systems suffers from the curse of dimensionality. GNN-based models address this by enabling structured and localized message passing. In particular, GCNs enhance state aggregation by embedding agent states within relational graphs, allowing each agent to integrate neighborhood information without full enumeration of the global state space. To extract compact global features, a permutation-invariant pooling function is applied over the final node embeddings:

$$h_{\mathrm{global}}=\mathrm{POOL}\left(\{h_i^{\left(L\right)}:i\in V\}\right),$$

yielding a fixed-size global state descriptor. To further improve adaptivity, graph attention networks (GAT) employ learnable attention coefficients to prioritize important neighbors [33]:

$${\alpha }_{ij}={\displaystyle \frac{exp\left(\mathrm{LeakyReLU}\left({\mathbf{a}}^{\top }[\mathbf{W}{h}_i\parallel \mathbf{W}{h}_j]\right)\right)}{{\sum }_{k\in {\mathcal{N}}_i}exp\left(\mathrm{LeakyReLU}\left({\mathbf{a}}^{\top }[\mathbf{W}{h}_i\parallel \mathbf{W}{h}_k]\right)\right)}},$$

(22)

which allows agents to adaptively focus on the most relevant peers under dynamic conditions. The calculation of these attention weights is the core mechanism of GATs, as detailed earlier in Equations (14) and (15). While GAT’s attention offers expressive weighting, its performance can be sensitive to the graph topology. In sparse neighborhoods, attention weights may become concentrated or noisy, leading to state representations that are unstable or disproportionately influenced by a small subset of neighbors.

Hierarchical graph attention network (HGAT). To address scalability and relational complexity, Ryu et al. [38] propose a Hierarchical Graph Attention Network (HGAT) with a two-level attention architecture. At the lower level, node-level attention models fine-grained interactions. At the higher level, hyper-node attention aggregates representations of predefined agent groups. The local embedding of an agent i is computed using attention-weighted message passing:

$$h_i^{\prime }=\sigma \left(\sum _{j\in \mathcal{N}\left(i\right)}{\alpha }_{ij}W{h}_j\right)$$

(23)

where ${\alpha }_{ij}$ is the attention coefficient. This local update rule directly mirrors the GAT aggregation mechanism previously shown in Equation (16). The effectiveness of HGAT’s hierarchical representation, however, is heavily dependent on the predefined agent grouping strategy. An improperly designed hierarchy can create information bottlenecks or misrepresent the true coordination structure, potentially leading to suboptimal state abstractions. This structure enables HGAT to generate context-aware agent embeddings that are invariant to the number of agents.

Equivariant and symmetry-aware state representations (PEnGUiN). Recent advances leverage structural symmetries to enhance sample efficiency. McClellan et al. [39] introduce partially equivariant graph neural networks (PEnGUiN), which selectively enforces equivariance to agent permutations. Each agent’s representation is decomposed into equivariant and invariant components: $h_i=\left[h_i^{\mathrm{equiv}},h_i^{\mathrm{inv}}\right]$. The framework introduces a learnable symmetry score $\alpha \in [0,1]$ to blend fully equivariant and non-equivariant updates:

$$h_i^{(l+1)}=\alpha f_{\mathrm{equiv}}^{\left(l\right)}\left(h^{\left(l\right)}\right)+(1-\alpha )f_{\mathrm{inv}}^{\left(l\right)}\left(h^{\left(l\right)}\right).$$

(24)

While partial equivariance enhances sample efficiency in symmetric tasks, it remains a strong inductive bias. In environments with subtle but critical asymmetries, the equivariant component of the representation might overly constrain the policy space, making it difficult for agents to learn specialized, non-symmetric behaviors. This architecture generalizes both equivariant GNNs and standard GNNs, adapting dynamically to varying degrees of environmental symmetry.

Predictive and hypergraph state representations. Graph-assisted predictive state representations (GAPSR) extend single-agent PSR to multi-agent partially observable systems by leveraging agent connectivity graphs [40]. The framework constructs primitive predictive states $q_{t,i,j}$ between agent pairs: $q_{t,i,j}{\psi }_{t,j}^a=\mathbb{E}\left[{\psi }_{t,i}^o\right|{\psi }_{t,j}^a;{\psi }_{t,i,j}^h]$. The final predictive representation is obtained through graph-based aggregation: $q_{t,i}={\sum }_j{I}_{i,j}{q}_{t,i,j}$. This approach enables decentralized agents to capture interactions while avoiding the complexity of joint state estimation.

Hypergraph coordination networks (HYGMA). HYGMA addresses multi-agent coordination through dynamic spectral clustering and hypergraph neural networks to capture higher-order agent relationships [41]. The framework constructs hypergraphs by solving a normalized cut minimization problem:

$$\underset{A\in {\mathbb{R}}^{n\times k}}{min}\mathrm{Tr}\left(A^{T}LA\right)\mathrm{s}.\mathrm{t}.A^{T}A=I$$

(25)

where $L=D-W$ is the graph Laplacian. The resulting hypergraph enables attention-enhanced information processing through hypergraph convolution:

$$h_i^{(l+1)}=\sigma \left(\sum _{e\in E_i}{\alpha }_{ie}·D^{-{\displaystyle \frac{1}{2}}}HW{B}^{-1}{H}^T{D}^{-{\displaystyle \frac{1}{2}}}{h}_i^{\left(l\right)}{P}^{\left(l\right)}\right)$$

(26)

where ${\alpha }_{ie}$ represents learned attention coefficients. Representing states with hypergraphs allows for capturing higher-order relationships, but this comes at the cost of increased computational complexity. The performance is critically dependent on the hyperedge construction step (e.g., spectral clustering), which is often a non-trivial and computationally intensive preprocessing task.

Relationship modeling enhancement via graph edges. Liu et al. [42] propose a two-stage graph attention network (G2ANet) for automatic game abstraction. G2ANet constructs an agent-coordination graph where agents are initially fully connected, then uses hard attention to identify and remove unrelated edges, followed by soft attention to learn importance weights. Hard attention employs Bi-LSTM, and its weight is computed as $W_{i,j}^h=\mathrm{gumbel}\left(f\left(\mathrm{BiLSTM}(h_i,h_j)\right)\right)$. Soft attention then uses query-key mechanisms: $W_{i,j}^s\propto exp\left(e_j^T{W}_k^T{W}_q{e}_i{W}_{i,j}^h\right)$. The resulting sub-graph for each agent is processed by GNNs to obtain joint encodings $x_i={\sum }_{j\ne i}{W}_{i,j}^h{W}_{i,j}^s{h}_j$.

Relational state abstraction [43] transforms observations into spatial graphs where entities are connected through directional spatial relations. The method employs R-GCNs to aggregate information, $z_v^{\prime }=\sigma ({\sum }_{r\in R}{\sum }_{u\in N_r\left(v\right)}{\displaystyle \frac{1}{|N_r\left(v\right)|}}{W}_r{z}_u+W_0{z}_v)$, achieving translation invariance. This update rule is a direct application of the R-GCN framework described in Equation (17), using relation-specific weight matrices $W_r$ to process different spatial relationships. A max-pooling operation generates fixed-size representations $e\left(o_i\right)=\max -\mathrm{pool}\left(Z^{\prime }\right)$ for the critic network, demonstrating significant sample efficiency improvements.

Multimodal graph fusion. Graph-based multimodal fusion demonstrates superior integration capabilities by explicitly modeling structural relationships between modalities [44]. D’Souza et al. propose a multiplexed GNN approach that creates targeted encodings for each modality through autoencoders, with multiplexed graph layers representing different relationships. This framework processes different data types and addresses challenges where not all modalities are present for all samples.

Generalized graph drawing for Laplacian state representations. Wang et al. [45] develop an improved Laplacian state representation learning method by modeling states and transitions as graph structures. The approach views the MDP as a graph $G=(S,E)$. The graph Laplacian is defined as $L=D-A$. Notably, this is the unnormalized graph Laplacian, whereas the propagation in GCNs, as seen in Equation (12), typically utilizes a symmetrically normalized version for stable feature propagation. The d-dimensional Laplacian representation of a state is constructed from the smallest eigenvectors of L. To address the non-uniqueness of the standard spectral graph drawing objective

$$\underset{u_1,\dots ,u_d}{min}\sum _{i=1}^d{u}_i^{T}L{u}_i\mathrm{s}.\mathrm{t}.u_i^T{u}_j={\delta }_{ij},\forall i,j=1,\dots ,d,$$

(27)

the authors propose a generalized objective with decreasing coefficients:

$$\underset{u_1,\dots ,u_d}{min}\sum _{i=1}^d{c}_i{u}_i^{T}L{u}_i\mathrm{s}.\mathrm{t}.u_i^T{u}_j={\delta }_{ij},\forall i,j=1,\dots ,d$$

(28)

where $c_1>c_2>\cdots >c_d>0$. This generalized objective has the smallest eigenvectors as its unique global minimizer, ensuring a faithful approximation to the ground truth Laplacian representation.

Summary

The evolution of state representation architectures reflects a consistent shift toward capturing richer structural information in multi-agent environments. While GCN-based models rely on spectral aggregation across local neighborhoods, recent approaches such as GAT and hypergraph neural networks have advanced toward modeling high-order relations and multi-scale dependencies. In particular, GraphSAGE introduces behavior-driven aggregation schemes that emphasize stable abstraction over selective attention. Alongside architectural advancements, the theoretical foundations behind these methods, ranging from spectral graph theory to equivariant representation learning, remain heterogeneous and often incomplete. This inconsistency highlights the need for more unified and interpretable frameworks to support generalization across diverse multi-agent structures. Table 3 provides a summary of the advantages and limitations of different categories of state representation methods.

Table 3. Advantages and limitations of key state representation methods.

Category	Strengths	Limitations	Best Use Cases
GCN-based (Spectral)	Simple, efficient; captures local neighborhood structure; well-grounded in spectral theory	Limited expressivity; assumes uniform neighbor importance; scalability issues for dense graphs	Medium-scale systems with stable topologies and moderate agent counts
Attention-based (GAT, G2ANet)	Learns importance weights; adaptive to dynamic interactions; robust to heterogeneous agents	Higher computational cost; soft attention may dilute key neighbors (unless combined with hard attention)	Dynamic or heterogeneous environments where selective coordination is critical
Hypergraph-based (HYGMA)	Models higher-order/group interactions; scales better for clustered agents; strong theoretical grounding in hypergraph spectral theory	Graph construction overhead; hyperedge design is task-dependent	Large-scale multi-agent systems with group-level or higher-order relations
Symmetry-aware (PEnGUiN)	Exploits symmetry for efficiency; blends equivariant and invariant features; strong generalization	Less effective in highly asymmetric environments; requires identifying symmetry structures	Tasks with interchangeable agents or partial environmental symmetry
Hierarchical (HGAT)	Captures both local and global group interactions; scales to large populations	Requires meaningful group partitioning; design complexity grows with system heterogeneity	Large-scale systems with natural group hierarchies (e.g., swarm robotics, clustered agents)

In practice, the selection of state representation methods is highly task-dependent. GCN-based methods are appealing in medium-scale systems with relatively stable interaction topologies, but their uniform aggregation limits performance when neighbor importance is uneven. Attention-based approaches (e.g., GAT, G2ANet) provide stronger adaptability to dynamic or heterogeneous environments by selectively weighting neighbors, though at the cost of increased computation. Hypergraph-based models (e.g., HYGMA) naturally capture higher-order or group-level interactions, making them suitable for large-scale systems, yet they require careful hyperedge construction. Symmetry-aware networks (e.g., PEnGUiN) are particularly effective when environments exhibit agent interchangeability or partial symmetry, improving sample efficiency and generalization but offering less benefit in asymmetric domains. Hierarchical models (e.g., HGAT) strike a balance between scalability and structure by integrating both local and group-level interactions, though they depend on meaningful group partitioning for effectiveness.

4.1.2. Action Selection in GNN-Enhanced MARL

GNN-enhanced MARL frameworks fundamentally transform action selection by leveraging graph structures to process agent interactions and environmental information. Based on the core mechanisms that differentiate action generation approaches, we identify three primary categories of GNN-enhanced action selection strategies:

• Information-Aggregation-Based Action Selection: Methods that focus on how agents collect and process neighborhood information during action generation, including attention-based critic mechanisms [46], graph-based attention networks [42], and scalable exponential topology communication [47].
• Decomposition-Based Action Selection: Approaches that address exponential joint action spaces by factorizing complex multi-agent decisions, including heterogeneous value decomposition with graph neural networks [48] and effect-based role decomposition [49].
• Hierarchical and Heterogeneous Decision Making: Systems that structure action selection across multiple organizational levels and adapt to different agent capabilities, including hypergraph-based group coordination [41] and class-specific relational learning for heterogeneous agents [50].

Table 4 categorizes representative methods according to these action selection paradigms, highlighting their core innovations and scalability characteristics.

Table 4. Representative GNN-enhanced action selection methods.

Algorithm	Network Architecture	Paradigm	Action Selection Category	Key Innovation	Scalability
G2ANet [42]	Two-stage attention (hard + soft) + GNN	Centralized	Agent-coordination graph	Dynamic interaction learning with game abstraction	Medium (5–20)
MAAC [46]	Multi-head attention (query-key-value)	CTDE	Critic enhancement	Attention-based critic for value estimation	Small (8)
ExpoComm [47]	Exponential graph + memory-based message processing	CTDE	Rule-based communication topology	Small diameter + linear scaling	Large (100+)
QMIX-GNN [48]	GAT + projection + tower	CTDE	Heterogeneous value decomposition	k-NN graph construction with multi-head attention fusion	Medium
RODE [49]	Effect-based action encoder + role selector	CTDE	Effect-based decomposition	Action clustering by effects	Large
HYGMA [41]	Hypergraph GNN	Hierarchical (group-agent)	Dynamic group coordination	Attention-based information aggregation	Large
HMAGQ-Net [50]	RGCN + class-specific encoders + multi-Q networks	CTDE	Heterogeneous agent classes	Relational convolution for inter-class communication with specialized policies	Medium

Information-Aggregation-Based Action Selection

Information-aggregation-based methods focus on how agents collect and process information from their neighborhood to generate actions. The core innovation lies in developing sophisticated mechanisms for weighting and combining neighbor information.

Multi-agent actor–attention-critic (MAAC). MAAC [46] enhances action selection through an attention-based critic design. The critic for each agent learns by selectively attending to information from other agents. For agent i, the Q-value function is computed as:

$$Q_i^{\psi }(o,a)=f_i(g_i(o_i,a_i),x_i)$$

(29)

where $x_i$ represents the contribution from other agents through the attention mechanism:

$$x_i=\sum _{j\ne i}{\alpha }_j{v}_j=\sum _{j\ne i}{\alpha }_{j}h\left(V{g}_j(o_j,a_j)\right)$$

(30)

The attention weight ${\alpha }_j$ is calculated using a query-key system:

$${\alpha }_j\propto exp\left(e_j^T{W}_k^T{W}_q{e}_i\right)$$

(31)

where $e_i=g_i(o_i,a_i)$ is agent i’s embedding. This query-key mechanism shares the same principle as the attention score calculation in GAT, shown in Equation (14), by learning pairwise importance scores. This graph-inspired information aggregation provides more accurate value estimates. While the attention-based critic is expressive, its requirement to process information from all other agents can present a scalability challenge, as the critic’s input and the attention computation grow with the number of agents. This leads to improved action selection compared to methods that simply concatenate all agents’ information.

Graph-based multi-agent actor–critic network (G2ANet). G2ANet [42] addresses the scalability challenge through a two-stage attention mechanism. It utilizes hard attention to identify which agents need to interact and soft attention to learn the importance weights of these interactions. This graph-based game abstraction achieves significantly higher success rates than baselines in complex coordination tasks.

Exponential communication (ExpoComm). Exponential topology methods [47] enable scalable communication through rule-based graph structures. In the static exponential graph, agents communicate according to

$$E_{ij}^{t\left(\mathrm{stat}\right)}=\left\{\begin{array}{cc}1\hfill & \mathrm{if}{log}_2((j-i)modN)\mathrm{is}\mathrm{an}\mathrm{integer}\mathrm{or}i=j\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(32)

This rule-based approach for defining a static communication topology contrasts with the data-driven, dynamic weighting found in attention-based models like GAT (Equation (16)), offering a trade-off between communication efficiency and adaptive interaction modeling. The primary trade-off for its high scalability is a lack of adaptivity; the static topology does not adjust to the dynamic state of the environment, which may be suboptimal in tasks where coordination needs are highly context-dependent. This topology ensures agents can exchange messages within $\lceil {log}_2(N-1)\rceil$ timesteps with communication overhead scaling efficiently, enabling coordination in systems with 100+ agents.

Decomposition-Based Action Selection

Decomposition-based methods address the exponential growth of joint action spaces by breaking down complex multi-agent decisions into manageable components.

QMIX with graph neural networks (QMIX-GNN). QMIX-GNN [48] is a GNN-based heterogeneous MARL algorithm built on the QMIX framework. It inherits monotonic value factorization to enable decentralized execution while learning a centralized value function. To enable information sharing, the method introduces a GAT that aggregates observations from each agent’s k-nearest neighbors. This aggregation employs the same principles of learnable, input-dependent weights as described in the foundational GAT model (Equation (16)). This produces a fused team-level representation $o_{\mathrm{all}}$. Each agent then computes its individual Q-value by combining its projected local observation with the global team context:

$$Q_i={\mathrm{tow}}_{{\varphi }_i}\left(\mathrm{bott}\left(\mathrm{concat}[M_{{\varphi }_i}·o_i,o_{all}]\right)\right)$$

(33)

where projection matrices $M_{{\varphi }_i}$ handle heterogeneous feature spaces. During decentralized execution, agents select actions via $a_i^t=arg{max}_{a_j}{Q}_i\left(a_j\right)$. While inheriting the benefits of QMIX, this approach is also subject to its primary structural limitation: the monotonicity constraint. This assumption limits the class of joint action-value functions that can be represented, which may be insufficient for tasks with complex, non-monotonic agent rewards.

Role-based multi-agent deep reinforcement learning (RODE). RODE [49] decomposes the action selection problem by first learning effect-based action representations, then clustering actions into role-specific action spaces. The performance of this framework is critically dependent on the quality of the learned action-effect representations and the resulting role clustering. In environments with highly stochastic action effects, the learned roles may not be distinct or meaningful. The framework employs a bi-level hierarchical structure where a role selector assigns roles and role policies operate within restricted action spaces, reducing policy search complexity.

Hierarchical and Heterogeneous Decision Making

Hierarchical and heterogeneous methods structure action selection across multiple organizational levels, adapting to different agent capabilities and enabling decisions that consider both multi-scale coordination and agent diversity.

Hypergraph-based multi-agent coordination (HYGMA). HYGMA [41] enhances action selection through hypergraph-based group-aware representations. The method integrates hypergraph convolution features into both value-based and policy-based frameworks: $Q_i({\tau }_i,a_i,h_i)=f_Q\left(\right[{\tau }_i|a_i|h_i\left]\right)$ and ${\pi }_i\left(a_i\right|{\tau }_i,h_i)=f_{\pi }\left(\left[{\tau }_i\right|h_i]\right)$, where $h_i$ is the group-aware representation generated by the hypergraph network. Although hypergraphs capture higher-order team structures, the dynamic construction of hyperedges via spectral clustering is a computationally expensive step that must be performed regularly, which can pose a challenge for real-time applications. This approach achieves faster convergence and high win rates in challenging MARL benchmarks.

Heterogeneous multi-agent graph Q-network (HMAGQ-Net). HMAGQ-Net [50] addresses action selection when agents have different capabilities. It employs relational graph convolutional networks (RGCN) to establish class-specific communication channels between different agent types. Through hierarchical feature aggregation across K-layer graph convolutions, agents aggregate neighbor information:

$${\mathbf{v}}_i^{(l+1)}=\sigma \left(\sum _{r\in R}\sum _{j\in N_i^r}{\displaystyle \frac{1}{c_{i,r}}}{\mathbf{W}}_r^{\left(l\right)}{\mathbf{v}}_j^{\left(l\right)}+{\mathbf{W}}_0^{\left(l\right)}{\mathbf{v}}_i^{\left(l\right)}\right)$$

(34)

where r represents inter-class relations. This update mechanism is identical to the one introduced for relational graph convolutional networks in Equation (17), demonstrating its effectiveness in handling heterogeneous relationships. A key requirement of this approach is the pre-specification of agent classes. In scenarios where agent roles are fluid or not easily categorized, this fixed class-based structure may be too rigid and limit the model’s adaptive capacity. For class-specific policy learning, each agent class c learns specialized Q-functions $Q_c$, enabling personalized policies.

Summary

In GNN-enhanced MARL, action selection has gradually developed along four main directions: information aggregation, decomposition, hierarchical reasoning, and heterogeneity-aware strategies. Information aggregation methods work well when agent interactions are sparse or change over time, since attention can highlight the most relevant neighbors. Decomposition methods are designed for very large action spaces, breaking them into smaller factors or roles to make decision making more manageable. Hierarchical or hypergraph-based approaches are suited for tasks with clear group structures or multiple scales, where agents need to balance local and global objectives. Heterogeneity-aware approaches are essential in realistic settings where agents differ in sensing, actuation, or goals, helping to keep coordination effective despite these differences. In practice, combining these ideas—such as using decomposition together with attention or hierarchy—has shown strong potential in applications like autonomous driving fleets, distributed energy systems, and mixed-agent robotics.

4.1.3. GNN-Enhanced Reward Design in MARL

Graph neural networks (GNNs) have been increasingly adopted for reward modeling in reinforcement learning due to their ability to capture structural dependencies among agents, states, and actions. Existing methods span a variety of strategies, including potential-based reward shaping [51,56,57], representation-based shaping using Laplacian embeddings [45], value function decomposition via graph-based architectures [53], and decentralized intrinsic reward modeling based on local message passing [52,58]. Some works also explore relational reward sharing grounded in graph-structured inter-agent preferences [59]. These approaches collectively demonstrate how GNNs enable more structured and adaptive reward signals, particularly in sparse or multi-agent environments.

We summarize representative methods and their characteristics in Table 5.

Table 5. Representative GNN-enhanced reward modeling methods.

Method	GNN Architecture	Reward Type	Design Focus	Coordination Awareness	Application Domain
Reward Propagation [51]	GCN and graph Laplacian for the transition matrix	Potential-based reward shaping	Automatic learning of potential functions	No	Gridworld, Atari
Hierarchical Graph Topology [56]	Hierarchical GCN with subgraph decomposition	Potential-based reward shaping	Hierarchical decomposition of probability graphs for long-range dependencies	No	Atari, MuJoCo continuous control
Laplacian Representation [45]	Graph Laplacian with weighted eigenvectors	Distance-based reward shaping	Laplacian representation geometry for goal-directed tasks	No	Gridworld, Continuous Navigation
GCRN [57]	GCN + Bi-GRU with Krylov basis approximation	Potential-based reward shaping	Spatio-temporal dependencies with look-ahead advice mechanism	No	Atari, MuJoCo continuous control
GraphMIX [53]	GIN/GCN with Attention	Global team reward	Value decomposition & Credit assignment	Attention-based dynamic	Real-time strategy games
DGRM [58]	Graph-based neighborhood aggregation	Reward machine encoded	Computational efficiency	$\kappa$-hop local coordination	Multi-UAV & Pandemic control
CoHet [52]	Message-passing GNN	Intrinsic reward	Heterogeneous cooperation	Neighborhood-based	Multi-agent navigation/transport
RSRN-MARL [59]	Relational graph (GNN-adaptable)	Shared relational reward	Social interaction modeling	Network structure-based	Multi-agent navigation

Reward shaping methods. Reward shaping methods tackle the challenge of sparse reward environments by intelligently designing auxiliary reward signals. Reward propagation [51] employs graph convolutional networks (GCNs) to propagate reward information from rewarding states through message-passing mechanisms, learning potential functions for potential-based reward shaping that preserve the optimal policy. This propagation is a direct application of the GCN update rule shown in Equation (12), where reward signals are treated as node features that are diffused across the state graph. By approximating the underlying state transition graph through sampled trajectories and using the graph Laplacian as a surrogate for the true transition matrix, this method draws connections to the proto-value functions framework. Extensive validation across tabular domains (FourRooms), vision-based navigation tasks (MiniWorld), Atari 2600 games, and continuous control problems (MuJoCo) reveals significant performance improvements over actor–critic baselines while maintaining computational efficiency.

Hierarchical graph topology (HGT). Building upon potential-based reward shaping principles, hierarchical graph topology (HGT) [56] constructs an underlying graph where states serve as nodes and edges represent transition probabilities within the Markov decision process (MDP). Rather than operating on flat graph structures, HGT decomposes complex probability graphs into interpretable subgraphs and aggregates messages from these components for enhanced reward shaping effectiveness. The hierarchical architecture proves especially valuable in environments with sparse and delayed rewards by enabling agents to capture long-range dependencies and structured transition patterns.

Reward shaping with Laplacian representations. Wang et al. [45] explore a geometric approach to reward design by leveraging learned Laplacian representations for pseudo-reward signal generation in goal-achieving tasks. Their strategy centers on Euclidean distance computation within the representation space, where the pseudo-reward corresponds to the negative L2 distance between the current and goal states in the Laplacian representation space:

$$r_t=-{\parallel \varphi \left(s_{t+1}\right)-\varphi \left(s_{\mathrm{goal}}\right)\parallel }_2$$

(35)

Given that Laplacian representations can effectively capture the geometric properties of environment dynamics, this representation-space distance metric provides meaningful guidance signals for agent learning. Further analysis reveals that different dimensions of the Laplacian representation contribute varying degrees of effectiveness to reward shaping, with lower dimensions (corresponding to smaller eigenvalues) demonstrating superior learning acceleration. This observation establishes both theoretical foundations and practical guidelines for dimension-selective reward shaping, where pseudo-rewards can be computed using individual dimensions as

$$r_t=-{(f_i\left(s_{t+1}\right)-f_i\left(s_{\mathrm{goal}}\right))}^2$$

(36)

for the i-th dimension $f_i\left(s\right)$ of the learned representation.

Graph convolutional recurrent networks for reward shaping. Addressing fundamental limitations in existing potential-based reward shaping methods, the graph convolutional recurrent network (GCRN) algorithm [57] introduces three complementary innovations for enhanced reward shaping optimization.

Spatio-Temporal Dependency Modeling: By integrating graph convolutional networks (GCN) with bi-directional gated recurrent units (Bi-GRUs), GCRN simultaneously captures both spatial and temporal dependencies within the state transition graph. The forward computation proceeds as:

$$\begin{array}{c}\mathrm{GCN}\left(X\right)=\sigma (K·\mathrm{ReLU}\left(KX{W}_1\right)W_0)\end{array}$$

(37)

$$\begin{array}{c}{\tilde{h}}_t={\mathrm{GRU}}_{\mathrm{fwd}}(\mathrm{GC}{\left(X\right)}_t,{\tilde{h}}_{t-1})\end{array}$$

(38)

$$\begin{array}{c}{h}_t^{\leftarrow }={\mathrm{GRU}}_{\mathrm{bwd}}(\mathrm{GC}{\left(X\right)}_t,h_{t+1}^{\leftarrow })\end{array}$$

(39)

$$\begin{array}{c}{\varphi }_{\mathrm{GCRN}}\left(X\right)=\mathrm{LogSoftmax}({\tilde{h}}_t\oplus h_t^{\leftarrow })\end{array}$$

(40)

where K represents the Krylov basis, X combines state and action information, and ⊕ denotes concatenation.

Augmented Krylov Basis for Transition Matrix Approximation: While traditional approaches rely on the graph Laplacian $L_c=I-D^{-1/2}A{D}^{-1/2}$ as the GCN filter under value function smoothness assumptions, GCRN develops an augmented Krylov algorithm for more precise transition matrix P approximation. This reliance on the Laplacian $L_c$ connects to the core mechanism of standard GCNs, as its structure is fundamentally related to the symmetrically normalized adjacency matrix used in Equation (12). The resulting Krylov basis K combines top eigenvectors from the sampled transition matrix $P_0$ with Neumann series vectors, yielding superior short-term and long-term behavior modeling compared to standard graph Laplacian approaches.

Look-Ahead Advice Mechanism: Departing from conventional state-only potential functions, GCRN incorporates a look-ahead advice mechanism that exploits both state and action information. The enhanced shaping function becomes:

$$F(S_t,A_t,S_{t+1},A_{t+1})=\gamma \varphi (S_{t+1},A_{t+1})-\varphi (S_t,A_t)$$

(41)

where $\varphi$ now operates on state–action pairs S and A, facilitating more precise action-level guidance.

Training combines base and recursive loss components derived from hidden Markov model message-passing techniques:

$$\begin{array}{c}L=L_0(S,A)+\lambda L_{\mathrm{rec}}(S,A)\end{array}$$

(42)

$$\begin{array}{c}{L}_0=\sum _{s,a\in S,A}p\left(O\right|s,a)log{\varphi }_{\mathrm{GCRN}}(s,a)\end{array}$$

(43)

$$\begin{array}{c}{L}_{\mathrm{rec}}=\sum _{i=1}^{\left|d\right|}\sum _{j=1}^{\left|e\right|}{A}_{i,j}{\parallel {\varphi }_{\mathrm{GCRN}}(S_i,A_i)-{\varphi }_{\mathrm{GCRN}}(S_j,A_j)\parallel }_2\end{array}$$

(44)

where $p\left(O\right|s,a)$ represents the optimality probability calculated through forward and backward message passing.

By maintaining the policy invariance guarantee of potential-based reward shaping, GCRN achieves substantial improvements in both convergence speed and final performance, as validated through comprehensive experiments on Atari 2600 and MuJoCo environments.

Graph convolutional value decomposition. GraphMIX [53] proposes a GNN-based framework for value function factorization in MARL, enabling fine-grained credit assignment through graph attention mechanisms. It models agents as nodes in a fully connected directed graph, where edge weights, computed via attention, capture dynamic inter-agent influence. This approach leverages the expressive power of architectures like GCN (Equation (12)) or the more powerful GIN (Equation (18)) to process the graph structure and inform the value decomposition. The initial assumption of a fully connected graph, however, introduces a significant scalability bottleneck, as its computational complexity grows quadratically ($O\left(N^2\right)$) with the number of agents, making it less suitable for systems with very large agent populations.

To optimize reward allocation, GraphMIX introduces a dual-objective loss structure. A global loss encourages accurate estimation of team-level returns by evaluating joint actions over the full state, while a local loss guides individual agents based on their assigned share of the global reward, computed from learned node-level embeddings. This design ensures that agents not only cooperate effectively but also learn to attribute outcomes to their actions.

The overall training objective combines both components:

$$L=L_{\mathrm{global}}+{\lambda }_{\mathrm{local}}\sum _{v\in V}{L}_{v,\mathrm{local}}$$

(45)

This integrated loss promotes coordinated learning by balancing team performance with personalized reward feedback, thereby improving both training stability and credit assignment precision.

Decentralized graph-based multi-agent reinforcement learning using reward machines (DRGM). DGRM [58] integrates GNNs with formal reward machine representations to support decentralized reward optimization in multi-agent settings. The method encodes complex, non-Markovian reward structures using reward machines, while leveraging truncated Q-functions that rely only on information from each agent’s local $\kappa$-hop neighborhood.

By exploiting the structure of agent interaction graphs, DGRM significantly reduces computational overhead—limiting the scope of each agent’s decision making to a small, relevant subgraph. This reliance on local $\kappa$-hop neighborhoods is a principle central to inductive GNNs like GraphSAGE (Equation (13)), enabling scalability by restricting message passing to immediate neighbors. The authors theoretically show that the influence of distant agents on local policy gradients diminishes exponentially with distance, ensuring that this approximation remains accurate. While this design promotes scalability, the truncation to a local neighborhood represents a fundamental trade-off; the model may fail to learn globally optimal strategies in tasks where critical long-range dependencies exist beyond the $\kappa$-hop communication radius. This decentralized design allows agents to coordinate effectively without requiring full access to global information, achieving scalable learning in large systems.

Reward-sharing relational networks. While Haeri et al. [59] do not directly implement graph neural network architectures, their reward-sharing relational networks (RSRN) framework establishes crucial theoretical foundations and design insights for GNN applications in multi-agent reward optimization. RSRN conceptualizes multi-agent systems as directed graphs $G=(V_G,E_G,W_G)$, where $V_G$ denotes the agent set, $E_G$ represents inter-agent relational edges, and weight matrix elements $w_{i,j}$ in $W_G$ quantify how much agent i “cares about” agent j’s success. Relational rewards emerge through scalarization functions ${\overline{r}}_i=f(r_k,w_i)$, with the weighted product model specified as ${\overline{r}}_i=f_p(r,w_i)={\prod }_{j=1}^N{r}_j^{w_{i,j}}$.

Policy learning occurs through long-term shared return maximization:

$${\overline{R}}_i=\mathbb{E}\left[\sum _{k=0}^T{\gamma }^k{\overline{r}}_{i,k}\right]=\mathbb{E}\left[\sum _{k=0}^T{\gamma }^{k}f(r_k,w_i)\right]$$

(46)

The relational graph structure naturally accommodates GNN processing, enabling graph convolutional operations to learn and optimize agent reward propagation patterns. Specifically, architectures like R-GCNs (Equation (17)) are well suited to process such explicitly relational graphs, where each edge type (or weight) can be modeled with a distinct transformation. A primary challenge for this framework is its dependence on a pre-defined relational graph. The design of an effective weight matrix $W_G$ requires significant, often unavailable, domain knowledge about agent social dynamics, and a misspecified structure can lead to unintended behaviors. Different network topologies (survivalist, communitarian, authoritarian, tribal) generate distinct emergent behaviors, suggesting that GNN-based approaches could exploit similar relational inductive biases to enhance multi-agent coordination and reward optimization.

GNN-driven intrinsic rewards for heterogeneous MARL. The CoHet algorithm [52] develops a graph-neural-network-based intrinsic reward mechanism for cooperative challenges in decentralized heterogeneous multi-agent reinforcement learning. CoHet optimizes reward design through GNN message-passing mechanisms, specifically employing local neighborhood observation predictions for intrinsic reward calculation. Coordinated behavior emerges by minimizing deviations between agents’ actual observations and their neighbors’ predictions. The central reward is calculated as

$$r_{in{t}_i}^t(o_i^t,a_i^t)=-\sum _{j\in {\mathcal{N}}_i^t\cap {\mathcal{N}}_i^{t+1}}{w}_j\times \parallel o_i^{t+1}-{\widehat{o}}_{j,i}^t\parallel$$

(47)

where $w_j={\displaystyle \frac{d(i,j)}{{\sum }_{k\in {\mathcal{N}}_i^t\cap {\mathcal{N}}_i^{t+1}}d(i,k)}}$ represents the Euclidean-distance-based weight, and ${\widehat{o}}_{j,i}^t=f_{{\theta }_j}(o_i^t,a_i^t)$ corresponds to neighbor j’s prediction of agent i’s next observation. Local information processing occurs through the GNN architecture $h_i={\psi }_{{\theta }_i}\left(z_i\right)+{\sum }_{j\in {\mathcal{N}}_i}{\varphi }_{{\theta }_i}(z_j\parallel e_{ij})$. This update function embodies the general message passing paradigm central to GNNs, where a node’s representation is updated by aggregating features from its neighbors.

By enabling decentralized training based exclusively on local neighborhood information, this design promotes effective coordination among heterogeneous agents through intrinsic reward signals.

Summary

GNN-enhanced reward design methods in MARL can be broadly grouped into several categories, each addressing different challenges. Potential-based reward shaping methods (e.g., reward propagation, HGT, GCRN) are effective in sparse-reward settings, as they propagate or decompose reward signals to provide denser guidance, though they may introduce training overhead or require accurate graph approximations. Representation-based shaping with Laplacian embeddings offers geometric insights into environment dynamics and goal distances, making it useful for navigation and goal-reaching tasks, but performance depends heavily on representation quality. Value decomposition methods such as GraphMIX leverage graph attention to balance global team rewards and individual credit assignment, excelling in cooperative domains but requiring careful loss balancing. Decentralized or relational reward designs (e.g., DGRM, RSRN) scale well to large multi-agent systems by exploiting local neighborhoods or inter-agent preference structures, though they may lose global optimality. Finally, intrinsic reward modeling (e.g., CoHet) is particularly suited for heterogeneous teams, as it encourages coordination from local prediction errors, but the design of intrinsic signals can be task-dependent. In practice, potential-based and representation-based shaping are preferable in structured single-task domains, while decentralized and intrinsic reward strategies are more practical in large-scale or heterogeneous environments. Hybrid designs that combine decomposition with relational or intrinsic signals are promising directions for real-world systems such as UAV coordination, mixed-robot teams, and resource allocation networks. Table 6 provides a summary of the applicable scenarios and limitations of different categories of GNN-enhanced reward design methods in MARL.

Table 6. Reward design paradigms and their applicability.

Category	Best Suited For	Limitations
Potential-based Shaping	Sparse or delayed rewards; structured environments	High training cost; requires accurate graphs
Representation-based Shaping	Navigation, goal-reaching, geometric tasks	Strongly depends on representation quality
Value Decomposition	Cooperative domains with shared rewards	Balancing global vs. local objectives is difficult
Decentralized/Relational	Large-scale multi-agent coordination	Risk of losing global optimality
Intrinsic Rewards	Heterogeneous teams with diverse roles	Task-dependent signal design

4.2. GNN-Based Multi-Agent Communication and Coordination

Communication and coordination among agents are central to networked system control. For GNN-MARL approaches, communication and coordination mainly involve three aspects: graph construction that encodes multi-agent environments, distributed information processing for coordination signal flow, and integrated decision-making frameworks that translate graph representations into collective actions.

4.2.1. Graph Construction Strategies

The effectiveness of GNN-based MARL critically depends on how the interaction graph is constructed, as this determines the structure of information flow among agents and with the environment. In practice, the choice of construction strategy should be guided by the characteristics of the target domain. Agent-centric graphs are suitable when modeling direct agent-to-agent interactions is essential, such as in swarm coordination or cooperative control. Environment-centric graphs are preferable when the spatial or topological structure of the environment dominates, e.g., navigation, patrolling, or coverage. Dynamic graph strategies are necessary in scenarios where communication patterns or environment states evolve, enabling agents to adapt to real-time changes. Finally, heterogeneous graph constructions are indispensable when multiple types of agents or entities interact through diverse relations, as in mixed-agent systems or hierarchical control. As summarized in Table 7, each strategy offers distinct advantages for different multi-agent scenarios.

Agent-Centric Graph Construction

Agent-centric graph construction is a fundamental approach in GNN-MARL, where each agent is modeled as a node, and edges represent interactions like proximity or communication. This design captures local dependencies and is widely used due to its simplicity and effectiveness. A representative example is the graph convolutional reinforcement learning presented by Jiang et al. (2018) [55], which models agents’ local interactions via graph convolutions. The information flow in such models typically follows the neighborhood aggregation principle defined in the GCN propagation rule (Equation (12)), where each agent updates its state based on its immediate neighbors. Later works, such as Huang et al. (2021) [60] and Zhao et al. (2024) [61], follow similar agent-centric constructions in process control and UAV swarm coordination.

Environment-Centric Graph Construction

In graph-neural-network-based multi-agent reinforcement learning (GNN-MARL), the environment-centric modeling approach represents key environmental locations or waypoints as graph nodes, with edges denoting feasible connections or relationships between them. Robots (agents) are typically modeled as dynamic nodes, integrated into the graph based on their positions, while edge attributes (e.g., distances or weights) capture interaction or path costs. GNNs leverage message passing to aggregate node and edge features, generating environment-aware embeddings for distributed decision making. For example, waypoints are modeled as grid points for path planning in [62], as patrol nodes for optimizing patrolling tasks in [37], and as spatial nodes for coverage and exploration in [63]. This strategy, however, often abstracts away direct agent-to-agent interactions in favor of agent–environment relationships, making it less suitable for tasks where complex, dynamic inter-agent negotiation is the core challenge. This approach effectively captures environmental topology, enhancing coordination and generalization in multi-agent systems.

Dynamic Graph Construction

Dynamic graph construction aims to reflect the evolving communication topology and environment state in multi-robot systems. Both Li et al. [62] and Tolstaya et al. [63] emphasize that dynamically updating the graph structure allows agents to make decentralized decisions based on real-time information.

In Li et al. [62], each agent is modeled as a graph node, with edges defined by proximity under a communication radius $r_{\mathrm{COMM}}$. The graph ${\mathcal{G}}_t=(\mathcal{V},{\mathcal{E}}_t,{\mathcal{W}}_t)$ is updated at every timestep t, where edges are formed if agents are within range. This time-varying graph captures changes in local connectivity due to agent movement, ensuring decentralized processing through the dynamic adjacency matrix ${\mathbf{S}}_t$.

In contrast, Tolstaya et al. [63] introduces a spatial graph structure where both agents and waypoints (environmental interest points) form the graph’s nodes. Edges represent reachable paths or spatial proximity. As robots explore and discover new regions, nodes and edges dynamically expand, forming a growing graph that captures both inter-agent connectivity and environment-aware exploration capabilities.

While highly adaptive, dynamic graphs introduce significant computational overhead, as the graph structure may need to be reconstructed or updated at each timestep. This can become a performance bottleneck in scenarios with many agents or high-frequency state changes. These dynamic constructions enable the GNN to operate efficiently in partially observable and communication-limited scenarios.

Heterogeneous Graph Structure

In many MARL scenarios, agents and environments exhibit heterogeneity—different types of entities with distinct characteristics interact through various relations. Heterogeneous graph neural networks have emerged to model such diverse multi-agent systems.

The heterogeneous graph attention network (HAN) employs a hierarchical attention mechanism with two levels: node-level attention that learns the importance between a node and its meta-path-based neighbors, and semantic-level attention that automatically selects important meta-paths for specific tasks [64]. This enables HAN to capture different semantic information in heterogeneous graphs through meta-path-based neighbor aggregation.

To handle larger-scale heterogeneous graphs, the heterogeneous graph Transformer (HGT) introduces meta-relation-based attention, decomposing transformations based on node-type and edge-type triplets $⟨\tau \left(s\right),\varphi \left(e\right),\tau \left(t\right)⟩$ [65]. This concept of handling diverse, explicit relations is an advanced evolution of the principles seen in R-GCNs (Equation (17)), which also use relation-specific transformations. This design achieves better parameter efficiency while maintaining dedicated representations for different entity types. HGT also incorporates relative temporal encoding (RTE) to handle dynamic heterogeneous graphs, enabling the model to capture temporal dependencies with arbitrary durations.

The power of heterogeneous GNNs comes at the cost of increased design complexity. Defining a meaningful graph schema, including node types and meta-paths or meta-relations, requires substantial domain knowledge and can be a critical point of failure if specified incorrectly. In GNN-MARL applications, these heterogeneous graph methods effectively handle complex interactions between different types of agents (such as UAVs, ground robots, sensor nodes), capturing diverse semantic relationships through meta-path and meta-relation mechanisms, thereby enhancing coordination capabilities and decision quality in multi-agent systems.

Table 7 summarizes various graph construction strategies in GNN-MARL, categorized into static, dynamic, and heterogeneous approaches. Each strategy is evaluated based on its primary focus, scalability, adaptability, and typical application domains.

Table 7. Comparison of graph construction strategies in GNN-MARL.

Strategy	Primary Focus	Scalability	Application Domain
Agent-centric [55,60,61]	Local interaction modeling via agent nodes	Moderate ($O\left(n^2\right)$ with sparse edges)	UAV swarm, process control
Environment-centric [37,62,63]	Modeling environment topology via waypoint or spatial nodes	High (fixed graph size, independent of agent count)	Multi-robot path planning, patrolling, coverage
Dynamic Graph [62,63]	Time-varying topology reflecting agent movement and environment discovery	High (localized updates)	Coverage, path planning in unknown or dynamic environments
Heterogeneous Graph [64,65]	Multi-type entities with semantic relations	High with parameter sharing	Mixed autonomous systems, hierarchical control

Table 7. Comparison of graph construction strategies in GNN-MARL.

Strategy	Primary Focus	Scalability	Application Domain
Agent-centric [55,60,61]	Local interaction modeling via agent nodes	Moderate ($O\left(n^2\right)$ with sparse edges)	UAV swarm, process control
Environment-centric [37,62,63]	Modeling environment topology via waypoint or spatial nodes	High (fixed graph size, independent of agent count)	Multi-robot path planning, patrolling, coverage
Dynamic Graph [62,63]	Time-varying topology reflecting agent movement and environment discovery	High (localized updates)	Coverage, path planning in unknown or dynamic environments
Heterogeneous Graph [64,65]	Multi-type entities with semantic relations	High with parameter sharing	Mixed autonomous systems, hierarchical control

4.2.2. Message Passing and Information Sharing

Message-passing mechanisms in GNN-based multi-agent reinforcement learning have evolved through distinct phases of development, each addressing specific challenges in multi-agent coordination. We categorize these approaches into five main categories based on their core design principles and evolutionary progression: (1) fundamental message passing frameworks establish the basic principles of learnable communication and graph-based information aggregation; (2) attention-based message passing introduces selective communication through attention mechanisms that enable agents to focus on relevant neighbors; (3) adaptive communication architecture advances beyond fixed topologies by learning optimal communication structures dynamically; (4) heterogeneous and hierarchical communication addresses complex systems with diverse agent types and multi-level coordination; and (5) robust and efficient communication ensures reliable performance under adversarial conditions while maintaining computational efficiency. This categorization reflects the field’s progression from simple broadcast mechanisms to sophisticated, context-aware communication protocols that adapt to varying environmental demands.

Fundamental Message Passing Frameworks

The development of effective message-passing mechanisms in GNN-based multi-agent reinforcement learning builds upon fundamental approaches that establish core principles for learnable communication and graph-based information aggregation. These seminal works provide the theoretical and architectural foundations that enable agents to exchange information effectively in distributed environments.

Communication neural network (CommNet). CommNet [66] introduces a foundational approach to learnable communication in multi-agent reinforcement learning through continuous message-passing mechanisms. The architecture enables agents to communicate through a broadcast channel where each agent receives the averaged transmissions from all other agents. The message-passing mechanism is formalized through two key equations:

$$\begin{array}{c}{h}_j^{i+1}=f^i(h_j^i,c_j^i)\end{array}$$

(48)

$$\begin{array}{c}{c}_j^{i+1}={\displaystyle \frac{1}{J-1}}\sum _{j^{\prime }\ne j}{h}_{j^{\prime }}^{i+1}\end{array}$$

(49)

where $h_j^i$ represents the hidden state of agent j at communication step i, and $c_j^i$ denotes the communication vector. The averaging operation in Equation (49) is an early instance of a permutation-invariant mean aggregator, a concept later generalized in frameworks like GraphSAGE. This framework enables agents to exchange information iteratively across K communication steps before taking actions. While effective for broadcasting, the uniform averaging of all messages can become an information bottleneck, as it prevents agents from engaging in specialized or targeted communication with specific peers. The model’s strength lies in its ability to handle dynamic agent compositions while maintaining permutation invariance, making it particularly suitable for scenarios where the number of agents may vary. The continuous nature of communication enables end-to-end learning through standard backpropagation.

GraphSAGE (graph sample and aggregate). GraphSAGE [32] introduces an inductive framework for generating node embeddings in large graphs, enabling generalization to unseen nodes at test time. Rather than learning a unique embedding for each node, GraphSAGE learns a set of aggregation functions that combine feature information from a node’s local neighborhood. This approach operationalizes the general aggregation scheme shown in formulas like Equation (13), providing concrete aggregator designs (mean, LSTM, pooling).

The method employs a hierarchical message-passing process, where node representations are updated layer by layer by aggregating and transforming features from neighboring nodes. The performance of this framework is highly dependent on the availability of rich initial node features, as the aggregation process primarily refines and propagates existing information rather than creating it anew. To scale to large graphs, GraphSAGE uses fixed-size neighborhood sampling, which controls memory usage and computational cost by limiting the number of neighbors sampled per layer. This makes the method highly efficient and well suited for inductive learning on dynamic or partially observed graphs.

The fundamental message passing frameworks are summarized in Table 8.

Table 8. Fundamental message passing frameworks.

Framework	Communication Mechanism	Advantages	Limitations	Best Applications
CommNet [66]	Broadcast + mean pooling	Simple architecture, end-to-end trainable, permutation invariant	Limited expressiveness, all agents treated equally	Cooperative tasks with dynamic team sizes
GraphSAGE [32]	Sample + aggregate from local neighborhood	Inductive learning, fixed computational cost, multiple aggregators	Requires sufficient node features	Large-scale evolving graphs

Attention-Based Message Passing

Building upon foundational approaches like CommNet and GraphSAGE, attention-driven methods [42,55,67] introduce sophisticated mechanisms that enable agents to selectively focus on relevant neighbors and adaptively weight communication importance, moving beyond uniform information aggregation towards more targeted coordination strategies.

Graph convolutional reinforcement learning framework. The graph convolutional reinforcement learning approach [55] constructs the multi-agent environment as a dynamic graph where agents are represented as nodes and neighboring relationships define edges that change over time as agents move. The message-passing mechanism employs multi-head attention as relation kernels to compute interactions between agents. For each agent i with neighbors $B_i$, let $B_i^{+}$ denote the set including both $B_i$ and agent i itself. The relation between agent i and agent $j\in B_i^{+}$ is computed using attention weights

$${\alpha }_{ij}^m={\displaystyle \frac{exp(\tau ·W_Q^m{h}_i·{\left(W_K^m{h}_j\right)}^T)}{{\sum }_{k\in B_i^{+}}exp(\tau ·W_Q^m{h}_i·{\left(W_K^m{h}_k\right)}^T)}}$$

(50)

where $\tau$ is a scaling factor, and $W_Q^m$, $W_K^m$ are learned query and key transformation matrices for attention head m. The output of each convolutional layer integrates information from neighboring agents through weighted aggregation

$$h_i^{\prime }=\sigma \left(\mathrm{concatenate}\left[\sum _{j\in B_i^{+}}{\alpha }_{ij}^m{W}_V^m{h}_j,\forall m\in M\right]\right)$$

(51)

where $W_V^m$ represents the value transformation matrix, and $\sigma$ is a non-linear activation function. This aggregation in Equation (51) is a direct implementation of the graph attention network update rule previously detailed in Equation (16). This mechanism adapts to the dynamic nature of multi-agent environments while enabling agents to extract latent features from gradually increased receptive fields.

Targeted multi-agent communication (TarMAC). TarMAC [67] develops a targeted communication architecture for multi-agent reinforcement learning that enables agents to learn both what messages to send and whom to address them to. The signature-based soft attention mechanism allows each message $m_i^t$ to consist of a signature $k_i^t\in {\mathbb{R}}^{d_k}$ to encode properties of intended recipients and a value $v_i^t\in {\mathbb{R}}^{d_v}$: $m_i^t=[k_i^t,v_i^t]$. At the receiving end, each agent predicts a query vector $q_j^{t+1}\in {\mathbb{R}}^{d_k}$, which computes attention weights through ${\alpha }_j=\mathrm{softmax}\left({\displaystyle \frac{q_j^{t+1T_{k_i^t}}}{\sqrt{d_k}}}\right)$, which results in the aggregated message $c_j^{t+1}={\sum }_{i=1}^N{\alpha }_{ji}{v}_i^t$. This targeting mechanism allows agents to implicitly encode recipient properties without explicit addressing, enabling adaptive communication strategies that scale to variable team sizes. The architecture further supports multi-round communication where agents engage in multiple rounds of collaborative reasoning before taking actions, significantly improving coordination in complex cooperative tasks.

Selective message passing in G2ANet. G2ANet [42] constructs a customized, dynamic communication subgraph for each agent, departing from traditional message passing frameworks where agents exchange information with fixed or fully connected neighbors. This subgraph is determined by a two-stage attention mechanism: hard attention filters out irrelevant agents, and soft attention scores the importance of the remaining ones. Based on this filtered and weighted subgraph, message passing is conducted via a weighted aggregation $x_i={\sum }_{j\ne i}{w}_j{h}_j,\mathrm{with}{w}_j=W_{i,j}^h{W}_{i,j}^s$. This selective message-passing allows each agent to focus only on contextually important peers, reducing unnecessary communication. The two-stage process, while effective, introduces notable complexity. Specifically, the hard attention step requires making discrete edge selection decisions differentiable, often through techniques like the Gumbel-Softmax trick. This approximation can introduce significant variance into the training gradients and requires careful hyperparameter tuning, potentially complicating convergence compared to simpler single-stage attention mechanisms. This results in more scalable and interpretable coordination, especially in large-scale or dynamically structured environments.

The attention-based message passing frameworks are summarized in Table 9.

Table 9. Attention-based message passing.

Framework	Communication Mechanism	Advantages	Limitations	Best Applications
Graph Convolutional RL [55]	Multi-head attention on dynamic graphs	Order-independent relations, temporal consistency	Fixed neighbor size in implementation	Tactical coordination, dynamic environments
TarMAC [67]	Signature-based soft attention with multi-round communication	Targeted messaging, multi-round reasoning, interpretable attention	Requires continuous vectors, attention overhead	Variable team sizes, complex coordination
G2ANet [42]	Two-stage attention (hard + soft attention)	Learns sparse, weighted communication adaptively	Requires extra computation from two-stage model	Large-scale systems with dynamic interaction patterns

Adaptive Communication Architecture

While attention-based methods improve selective communication, adaptive architecture approaches [10,68,69] further advance the field by learning optimal communication topologies and protocols dynamically, enabling more efficient and flexible coordination strategies.

CommFormer: learning multi-agent communication from graph modeling perspective. CommFormer [68] addresses the fundamental challenge of communication architecture design in GNN-based MARL by treating the communication structure as a learnable graph. CommFormer formulates the problem as a bi-level optimization task that simultaneously learns the optimal communication graph and updates architectural parameters. The method employs continuous relaxation of graph representation using the Gumbel-Max trick to enable gradient-based optimization of the discrete adjacency matrix $\alpha \in {\mathbb{R}}^{N\times N}$. The relation-enhanced attention mechanism augments implicit attention scores with explicit edge information: $s_{ij}=(o^i+r_{i\to j})W_q^T{W}_k(o^j+r_{j\to i})$, where $r_{*\to *}$ represents edge embeddings. During message passing, agents can only access information from connected neighbors through masked attention.

$$s_{ij}=\left\{\begin{array}{cc}{s}_{ij},\hfill & e_{j\to i}=1\hfill \\ -\infty ,\hfill & e_{j\to i}=0\hfill \end{array}\right.$$

(52)

The formulation as a bi-level optimization problem, while powerful, presents a challenging non-convex landscape that can be sensitive to hyperparameters and difficult to stabilize during training. This approach enables CommFormer to achieve comparable performance to fully connected methods while using significantly fewer communication edges.

GNNComm-MARL (graph-neural-network-aided communication MARL). This framework [10] tackles the fundamental challenges of conventional MARL systems by introducing graph-neural-network-aided communication protocols to enhance message passing between agents. GNNComm-MARL utilizes graph attention networks (GAT) to intelligently sample neighborhoods and selectively aggregate messages from neighboring agents. The adaptive communication protocol consists of GNN-aided schedulers and integrators, where schedulers determine when and with whom agents communicate, while integrators use weighted attention mechanisms to combine received messages. This approach effectively addresses partial observability and non-stationarity by enabling agents to focus on their most relevant neighbors.

Adaptively controlled two-hop communication (AC2C). AC2C [69] develops a dynamic two-hop communication protocol for agents with limited-range communication. AC2C explicitly enables long-range message exchange via two-hop relaying and selectively activates it based on a learned controller. In the first round, each agent aggregates messages from its one-hop neighbors:

$${\mathbf{c}}_i^{\left(1\right)}=f^{\left(1\right)}\left({\mathbf{c}}_i^{\left(0\right)},{\left\{{\mathbf{c}}_j^{\left(0\right)}\right\}}_{j\in {\mathcal{N}}_i^{\left(1\right)}}\right)$$

(53)

where ${\mathbf{c}}_i^{\left(0\right)}$ is the initial embedding. A controller then determines the necessity of a second round:

$$z_i=\mathbf{1}\left[h\left({\mathbf{c}}_i^{\left(0\right)},{\mathbf{c}}_i^{\left(1\right)};{\theta }_c\right)>T\right]$$

(54)

If triggered ($z_i=1$), agent i initiates a second communication round by broadcasting a request through its one-hop neighbors, who act as relays to forward embeddings from two-hop neighbors. Agent i then aggregates the received two-hop messages as

$${\mathbf{c}}_i^{\left(2\right)}=f^{\left(2\right)}\left({\mathbf{c}}_i^{\left(1\right)},{\left\{{\mathbf{c}}_j^{\left(1\right)}\right\}}_{j\in {\mathcal{N}}_i^{\left(2\right)}}\right)$$

(55)

Through this selectively triggered message passing, AC2C achieves broader information coverage with minimal communication cost, offering an advantage over conventional GNN-based communication in bandwidth-constrained MARL environments.

The adaptive communication architecture frameworks are summarized in Table 10.

Table 10. Adaptive communication architecture.

Framework	Communication Mechanism	Advantages	Limitations	Best Applications
CommFormer [68]	Learnable graph + masked attention	Automated architecture search, 40% bandwidth reduction	Requires bi-level optimization	Bandwidth-constrained environments
GNNComm-MARL [10]	GAT-based selective aggregation + adaptive scheduling	Intelligent neighbor sampling, reduced overhead	Increased computational complexity for attention mechanisms	Communication networks, mobility management
AC2C [69]	Attention-based + two-hop relay with adaptive control	Long-range info access with selective activation	Requires relay agents, threshold tuning	Sparse topologies with limited communication range

Heterogeneous and Hierarchical Communication

Complex multi-agent systems often require handling diverse agent types and multi-level coordination structures. Advanced frameworks [56,65,70,71,72] address these challenges through specialized mechanisms for heterogeneous graph processing and hierarchical message propagation.

Heterogeneous graph transformer (HGT). The heterogeneous graph transformer (HGT) [65] introduces an approach to optimize message passing in heterogeneous graphs by leveraging meta relation-aware transformations. HGT addresses this limitation through a message passing mechanism that respects the heterogeneous nature of the graph. The message passing process in HGT computes multi-head messages as:

$${\mathrm{Message}}_{\mathrm{HGT}}{(s,e,t)=\parallel }_{i\in [1,h]}{\mathrm{MSG}-\mathrm{head}}^i(s,e,t)$$

(56)

where each message head is calculated as:

$${\mathrm{MSG}-\mathrm{head}}^i(s,e,t)={\mathrm{M}-\mathrm{Linear}}_{\tau \left(s\right)}^i\left(H^{(l-1)}\left[s\right]\right)W_{\varphi \left(e\right)}^{\mathrm{MSG}}$$

(57)

HGT parameterizes these transformations based on the meta relation triplet $⟨\tau \left(s\right),\varphi \left(e\right),\tau \left(t\right)⟩$. This design is a sophisticated extension of the core idea in R-GCNs (Equation (17)), which also use relation-specific matrices but without HGT’s type-based decomposition and attention. A practical challenge for HGT is its reliance on a well-defined heterogeneous schema; its effectiveness depends on the prior specification of meaningful node and edge types, which requires significant domain expertise. This design enables HGT to preserve heterogeneous graph properties while achieving effective parameter sharing.

Adversarial communication in heterogeneous GNN-MARL. Blumenkamp and Prorok [72] tackle heterogeneity by introducing adversarial communication patterns in systems with conflicting objectives. The approach extends aggregation graph neural networks (AGNNs) to support heterogeneous policies through agent-specific filter taps:

$$X^{\prime }=g_{\eta }(X;S)=\sum _{k=0}^K\left[\begin{array}{c}{\left[S^k\right]}_1^{T}X{H}_1^k\\ ⋮\\ {\left[S^k\right]}_N^{T}X{H}_N^k\end{array}\right]$$

(58)

where $\eta ={\left\{{\eta }^i\right\}}_{i\in V}$ and ${\eta }^i={\left\{H_i^k\right\}}_{k=1}^K$ represent individual communication policies. The framework demonstrates that self-interested agents can learn manipulative communication strategies without explicit adversarial training. This emergence of deceptive communication provides insights for developing robust multi-agent systems capable of handling non-cooperative participants.

Hierarchical message propagation mechanisms. Hierarchical graph structures enable efficient message passing in multi-agent systems through multi-level information propagation. Sang et al. [56] propose a hierarchical graph topology approach that decomposes probabilistic graphs into multiple subgraphs. Zhong et al. [70] introduce a hierarchical message-passing GNN employing a three-layer propagation system: bottom-up aggregation, intra-layer propagation, and top-down propagation. Vonessen et al. [71] constructs hierarchical support graphs through recursive coarsening algorithms, utilizing METIS partitioning to create supernodes representing node clusters. This achieves multi-level information flow through horizontal and vertical edges, providing logarithmic communication paths for distant nodes and significantly enhancing the capability to capture long-range dependencies.

The heterogeneous and hierarchical communication frameworks are summarized in Table 11.

Table 11. Heterogeneous and hierarchical communication.

Framework	Communication Mechanism	Advantages	Limitations	Best Applications
HGT [65]	Type-specific transformations with meta relations	Handles multiple node/edge types, parameter sharing	Type complexity, requires heterogeneous graph structure	Multi-type agent systems
Adversarial AGNN [72]	Heterogeneous filter taps with adversarial learning	Handles mixed objectives, emergent deception strategies	Requires resource contention, complex training	Mixed cooperative-competitive environments
Hierarchical Message Passing [56,70,71]	Multi-level propagation with recursive coarsening	Logarithmic communication paths, efficient global-local flow	Computational overhead for graph construction	Large-scale hierarchical coordination

Robust and Efficient Communication

As multi-agent systems are deployed in complex environments, ensuring robust and efficient communication becomes critical. Recent advances [73,74] focus on developing resilient message-passing mechanisms.

MAGI: robust communication via graph information bottleneck. The MAGI framework proposes a robust communication mechanism for GNN-based MARL by leveraging the information bottleneck (IB) principle. The objective is to learn minimal and sufficient message representations that are robust to adversarial attacks and noise. MAGI formulates communication learning as the following optimization problem:

$$\underset{\mathrm{MAGI}}{min}\beta (D,Y;M)=\left[-I(Y;M)+\beta I(D;M)\right]$$

(59)

where $D=(A,H)$ represents the graph and features, M is the message, and $I(·;·)$ denotes mutual information. To approximate this objective, variational bounds are introduced:

$$\begin{array}{cc}\hfill I(Y;M_H^L)& \ge \mathbb{E}\left[log{\displaystyle \frac{{\prod }_{i\in V}{V}_1(Y_i\mid M_{H,i}^L)}{V_2\left(Y\right)}}\right]\hfill \end{array}$$

(60)

$$\begin{array}{cc}\hfill I(D;M_H^L)& \le \sum _{l\in {\mathcal{S}}_A}{\mathrm{AIB}}_l+\sum _{l\in {\mathcal{S}}_H}{\mathrm{HIB}}_l\hfill \end{array}$$

(61)

where AIB_l and HIB_l are regularizers. The use of the information bottleneck principle introduces a complex objective that relies on variational approximations, which can present optimization challenges and require careful tuning to stabilize training. MAGI integrates this mechanism into multi-round message passing via GAT layers, enabling robust communication under perturbed environments.

Diversifying message aggregation. Zhai et al. [73] addresses the homogeneity problem in GAT-based message aggregation, where agents often over-attend to a few ’core’ agents. To tackle this, they propose measuring message aggregation diversity through the normalized tensor rank of the communication graph’s adjacency tensor. Since rank optimization is NP-hard, they introduce the Normalized Tensor Nuclear Norm (NTNN) as a convex surrogate ${\parallel A\parallel }_{*}={\displaystyle \frac{1}{K}}{\parallel \widehat{A}\parallel }_{*}$. Building on this, they develop the normalized tensor nuclear norm regularization (NTNNR) framework. The overall optimization objective becomes

$$L\left(\theta \right)=L_{RL}\left(\theta \right)+\sum _l{\lambda }_l{L}_{NTNNR}\left({\theta }_l\right)$$

(62)

where $L_{NTNNR}\left({\theta }_l\right)=-{\parallel A\parallel }_{*}$ for the l-th GAT layer. Their evaluation demonstrates that NTNNR-enhanced GAT significantly improves performance compared to existing methods.

Recurrent message passing (RMP). Weil et al. [74] propose a recurrent message-passing approach for generalizability across different graph environments. The method decouples graph representation learning from agent control. The recurrent message-passing mechanism is defined as

$$\begin{array}{cc}\hfill h_v^0& =\mathrm{encode}(h_v,m_v)\hfill \\ \hfill M_v^k& ={\mathrm{aggregate}}^k\left({\left\{h_w^k\right\}}_{w\in N\left(v\right)}\right)\hfill \\ \hfill h_v^{k+1}& ={\mathrm{update}}^k(h_v^k,M_v^k)\hfill \end{array}$$

(63)

where $h_v$ is the state of node v. Agents receive location-dependent graph observations through a differentiable readout function ${\psi }^i=\Psi \left(H_{v_i}\right)$. The approach enables decentralized execution at runtime. Evaluation across diverse graphs in communication network routing demonstrates that the method enables agents to generalize and adapt to graph changes.

The robust and efficient communication frameworks are summarized in Table 12.

Table 12. Robust and efficient communication.

Framework	Communication Mechanism	Advantages	Limitations	Best Applications
MAGI [73]	Information bottleneck + GAT layers	Robust to noise and adversarial attacks	Requires variational inference optimization	Noisy/dynamic multi-agent environments
NTNNR-GAT [73]	Multi-head attention with tensor nuclear norm regularization	Diverse message aggregation, prevents homogeneity	Requires hyperparameter tuning for regularization	Complex coordination requiring message diversity
Recurrent Message Passing [74]	LSTM + iterative aggregation with graph generalization	Generalizes across different graph topologies	Message overhead, requires graph structure knowledge	Multi-graph routing and network management

Summary

The evolution of message passing in GNN-based MARL demonstrates a clear trajectory from basic broadcast mechanisms to sophisticated, adaptive, and resilient communication protocols. Fundamental frameworks such as CommNet and GraphSAGE laid the groundwork by introducing learnable communication and inductive aggregation, enabling scalability to dynamic and unseen agents. These early methods are particularly suitable in relatively simple or homogeneous settings where uniform aggregation suffices. Building on this foundation, attention-based methods like TarMAC and G2ANet enhanced coordination efficiency by enabling selective, targeted, and interpretable message exchange, making them well suited for environments where agent interactions are dense but not all equally relevant. Moving further, adaptive communication architectures such as CommFormer and AC2C elevated scalability and efficiency by learning task-specific communication topologies and selectively expanding information horizons; such designs shine in large-scale systems where communication needs vary dynamically across tasks. In parallel, heterogeneous and hierarchical communication frameworks like HGT and hierarchical propagation networks extended message passing to systems with diverse agent types and multi-level structures, offering clear advantages in mixed-agent teams or organizationally structured domains. Finally, robust and efficient communication approaches such as MAGI and RMP emphasized resilience against redundancy, adversarial conditions, and distribution shifts, ensuring reliable deployment in dynamic and uncertain real-world environments where failures or perturbations are inevitable.

Overall, these developments illustrate a progression from uniform and static aggregation → selective and context-aware messaging → adaptive topology learning → heterogeneous and multi-level propagation → robust and efficient communication. Each stage addresses limitations of its predecessors while pushing toward more scalable, interpretable, and reliable coordination. This progression highlights the central role of message passing as both the theoretical foundation and practical bottleneck of GNN-based MARL, suggesting that future advances will likely integrate robustness, adaptability, and hierarchy into unified frameworks that balance efficiency with expressiveness.

4.2.3. Multi-Agent Coordination

Multi-agent coordination represents one of the most challenging aspects of multi-agent reinforcement learning, where agents must learn to work together effectively while maintaining individual decision-making capabilities. In GNN-enhanced MARL systems, coordination mechanisms leverage graph neural networks to model complex inter-agent relationships and facilitate information exchange. We categorize existing GNN-MARL coordination approaches into four main classes based on their underlying coordination mechanisms, as summarized in Table 13.

Table 13. Taxonomy of GNN-MARL coordination mechanisms.

Category	Key Strengths	Primary Limitations	Best Suited For
Attention-based	Dynamic partner selection; no predefined structures; multi-round reasoning support	Quadratic complexity with agent count; high computational overhead in large systems	Navigation, traffic control, targeted communication scenarios
Graph Structure Learning	Discovers optimal topology automatically; solves relative overgeneralization; adapts to state-dependent needs	High sample complexity; training instability; slow initial convergence	StarCraft micromanagement, predator-prey, dynamic coordination patterns
Heterogeneous Graph	Handles diverse entity types naturally; rich semantic modeling; effective under partial observability	Complex graph construction; requires entity type specification; over-engineering for simple scenarios	Pursuit-evasion, multi-robot tasks with heterogeneous entities
Communication-based	Optimized for bandwidth constraints; robust to agent failures; lightweight and scalable	Protocol design dependency; performance is bounded by communication limits	Multi-robot patrolling, UAV swarms, unreliable communication environments

These four categories represent fundamentally different approaches to solving the coordination problem. Attention-based methods use learnable attention weights to dynamically select relevant coordination partners without requiring predefined graph structures, offering maximum flexibility but suffering from quadratic computational complexity as agent numbers scale. Graph structure learning methods automatically discover optimal coordination topologies through end-to-end differentiable mechanisms, effectively addressing the relative overgeneralization problem but requiring substantial training data and potentially experiencing unstable learning dynamics. Heterogeneous graph methods explicitly model different entity types and relationship semantics, providing natural expressiveness for complex multi-entity environments but introducing additional complexity in graph construction and requiring domain knowledge for entity type specification. Communication-based methods integrate explicit message-passing protocols with GNNs to achieve efficient coordination under bandwidth constraints and agent failures, excelling in resource-constrained real-world deployments but depending on carefully designed communication protocols.

The key distinction lies in their fundamental trade-offs: attention-based methods prioritize coordination flexibility over computational efficiency; graph structure learning methods achieve coordination optimality at the cost of sample efficiency; heterogeneous graph methods trade modeling complexity for semantic expressiveness; and communication-based methods balance coordination capability with practical deployment constraints. Understanding these trade-offs is essential for selecting the appropriate mechanism based on application requirements.

Attention-Based Coordination

Attention-based coordination methods leverage learnable attention mechanisms to enable agents to selectively focus on relevant teammates and information during decision making. TarMAC [67] introduces targeted communication through signature-based soft attention. MAGIC [75] extends this by simultaneously solving when, with whom, and how to communicate. QMIX-GNN [48] integrates graph attention networks into the CTDE framework. The attention-augmented inverse reinforcement learning framework [76] employs a dual-attention architecture to learn coordination from demonstrations.

TarMAC: targeted multi-agent communication. TarMAC introduces a novel architecture for multi-agent coordination that enables agents to learn both what messages to send and whom to address them to [67]. Its signature-based soft attention mechanism facilitates targeted communication. Each agent’s message $m_i^t$ consists of a signature $k_i^t$ and a value $v_i^t$. At the receiving end, agents compute attention weights through:

$${\alpha }_j=\mathrm{softmax}\left({\displaystyle \frac{q_j^{t+1T}{k}_i^t}{\sqrt{d_k}}}\right)$$

(64)

where $q_j^{t+1}$ is the query vector. The aggregated message is $c_j^{t+1}={\sum }_{i=1}^N{\alpha }_{ji}{v}_i^t$. This query-key mechanism is a specialized application of the attention principles seen in GAT (e.g., Equation (14)), adapted here for targeted messaging rather than structural feature aggregation. While highly flexible, the need to compute pairwise scores between agents results in a computational complexity that scales quadratically with the number of agents, which can be prohibitive in large-scale systems. Furthermore, TarMAC supports multi-round communication where agents engage in collaborative reasoning before acting, with the internal state updated as $h_j^{{\prime }^t}=tanh\left(W_{h\to h^{\prime }}[c_j^{t+1}\parallel h_j^t]\right)$.

MAGIC (multi-agent graph-attention communication). MAGIC [75] addresses three critical communication problems: when to communicate, whom to communicate with, and how to process messages. It introduces a graph-attention protocol with a scheduler and a message processor. The scheduler uses a differentiable hard attention mechanism to generate directed communication graphs $G_t^{\left(l\right)}$. The message processor employs GATs on these dynamic graphs. A crucial advancement involves enabling GATs to work with differentiable graphs through modified attention coefficients:

$${\alpha }_{ij}^P={\displaystyle \frac{g_{ij}^{\left(l\right)}exp\left(LeReLU\right({\left(a_P^{\left(l\right)}\right)}^T[W_P^{\left(l\right)}{m}_i^{(l-1)}\left|\right|W_P^{\left(l\right)}{m}_j^{(l-1)}\left]\right))}{{\sum }_{k=1}^N{g}_{ik}^{\left(l\right)}exp\left(LeReLU\right({\left(a_P^{\left(l\right)}\right)}^T[W_P^{\left(l\right)}{m}_i^{(l-1)}\left|\right|W_P^{\left(l\right)}{m}_k^{(l-1)}\left]\right))}}$$

(65)

where $g_{ij}^{\left(l\right)}\in \{0,1\}$ represents the binary communication decisions from the scheduler. Equation (65) directly extends the standard GAT attention (Equation (15)) by incorporating a learnable binary gate $g_{ij}$ to explicitly control the communication topology. This enables end-to-end training while maintaining gradient flow. However, the introduction of a learnable scheduler adds another layer of complexity to the optimization problem, as the model must learn the communication protocol concurrently with the task policy, which can sometimes lead to training instability.

Coordination mechanism in QMIX-GNN. QMIX-GNN [48] extends the standard CTDE paradigm by embedding a GNN-based information sharing mechanism. To address the limitation of local observations, QMIX-GNN constructs a graph over agents and uses graph attention networks (GATs) to model and weigh the influence of neighboring agents. The resulting team-level representation aggregates information from each agent’s local neighborhood, dynamically weighted by attention scores. This global context is shared across all agents to enrich their local decision making. Each agent combines this shared representation with its own observation, using a type-specific encoder. Finally, the agents’ Q-values are combined using a monotonic mixing network, ensuring overall team value remains sensitive to individual contributions.

Attention-augmented inverse reinforcement learning for multi-agent coordination. The framework proposed by [76] addresses coordination challenges by using a dual-attention architecture to learn from expert demonstrations. The primary advancement lies in the hierarchical integration of multi-head self-attention (MHSA) for trajectory encoding and graph attention networks (GAT) for global coordination modeling. The framework processes agent trajectory information through MHSA to capture temporal dependencies:

$${\mathrm{head}}_n=\mathrm{softmax}\left({\displaystyle \frac{Q_n{K}_n^T}{\sqrt{d_{\mathrm{head}}}}}\right)V_n$$

(66)

Simultaneously, the global coordination module models agent–task relationships through graph attention:

$${\alpha }_{ik}={\displaystyle \frac{exp\left(\sigma \left(a^T[W{q}_i\parallel W{q}_k]\right)\right)}{{\sum }_{u\in N_e\left(i\right)}exp\left(\sigma \left(a^T[W{q}_i\parallel W{q}_u]\right)\right)}}$$

(67)

This dual-attention approach enables the system to optimize individual behaviors and global coordination patterns. The framework’s strength is its ability to infer coordination strategies from demonstrations without manual reward engineering.

The attention-based coordination methods are summarized in Table 14.

Table 14. Attention-based coordination.

Method	Embedding Mechanism	Coordination Type	Key Advantages	Best Applications
TarMAC [67]	Signature-based soft attention with multi-round communication	Targeted collaborative	Learns both message content and addressing; multi-round reasoning before actions	Navigation, traffic control, 3D environments
MAGIC [75]	GAT with dynamic directed graphs and differentiable hard attention	Targeted multi-round	Simultaneous “when/whom/how” communication decisions with 27.4% efficiency improvement	Complex coordination with sparse rewards
QMIX-GNN [48]	GAT-based neighbor fusion with projection matrix	Centralized training with decentralized execution	Heterogeneous information fusion and team-aware Q-learning	SMAC mixed-type combat scenarios
IRL-MHSA-GAT [76]	MHSA for trajectories + GAT for global states	Hierarchical coordination through reward inference	Eliminates manual reward design while capturing temporal and spatial dependencies	Multi-agent task allocation with dynamic environments

Graph Structure Learning Coordination

This category focuses on methods that learn dynamic coordination structures through differentiable graph construction. DMCG [77] proposes meta coordination graphs. DICG [78] introduces fully differentiable coordination graphs. GraphMIX [53] models agents as nodes in a complete directed graph where edge weights are determined by attention.

Deep meta coordination graph (DMCG) [77]. DMCG proposes a framework for learning cooperative policies by capturing complex coordination patterns beyond pairwise interactions. At its foundation lies the meta coordination graph (MCG), a dynamic graph structure that models higher-order relationships. The algorithm constructs a set of interaction-specific adjacency matrices ${\left\{A_k\right\}}_{k=1}^K$, which are dynamically combined through soft attention. These graphs are then fed into a graph convolutional module to extract agent embeddings:

$$Z=\underset{i=1}{\overset{o}{\parallel }}\sigma \left({\tilde{D}}_i^{-1}{\tilde{A}}_M^{\left(i\right)}XW\right),$$

(68)

where ∥ is the concatenation operator, o denotes the number of channels, and X is the agent feature matrix. This update rule is a variant of GCN propagation (Equation (12)), modified to operate over multiple learned interaction channels. By integrating multi-hop reasoning and edge-type heterogeneity, DMCG enhances coordination quality.

Deep implicit coordination graphs (DICG). DICG [78] addresses the trade-off between centralized control and decentralized execution through learnable dynamic coordination structures. It introduces a differentiable architecture that infers coordination relationships using self-attention. The primary advancement lies in replacing binary coordination edges with soft attention weights, computed as

$${\mu }_{ij}={\displaystyle \frac{exp\left(\mathrm{Attention}(e_i,e_j,W_a)\right)}{{\sum }_{k=1}^{n}exp\left(\mathrm{Attention}(e_i,e_k,W_a)\right)}}$$

(69)

where $\mathrm{Attention}(e_i,e_j,W_a)=e_j^T{W}_a{e}_i$. A key challenge for methods like DICG that learn the graph structure from scratch is their high sample complexity; the agent policies and the coordination graph must be learned concurrently, often requiring extensive environmental interaction to converge to a stable and effective topology. The architecture then applies graph convolution operations to integrate information across the learned structure: $H^{(l+1)}=\sigma \left(M{H}^{\left(l\right)}{W}_c^{\left(l\right)}\right)$. This approach solves the relative overgeneralization pathology that plagues decentralized methods.

GraphMIX: graph convolutional value decomposition. GraphMIX [53] addresses coordination through GNN-based value function factorization. The method models agents as nodes in a complete directed graph, where edge weights are dynamically determined by an attention mechanism. The central contribution is a mixing GNN module that factorizes the global state-action value function into individual value functions while maintaining monotonicity constraints. While allowing for maximum flexibility, GraphMIX’s approach of starting with a complete graph inherently faces a scalability challenge due to its quadratic complexity with respect to the number of agents. The framework demonstrates superior coordination by capturing complex agent-to-agent relationships dynamically.

The graph structure learning coordination methods are summarized in Table 15.

Table 15. Graph structure learning coordination.

Method	Embedding Mechanism	Coordination Type	Key Advantages	Best Applications
DMCG [77]	GCN over multi-type dynamic graphs	Higher-order and indirect	Captures multi-hop dependencies and dynamic edge types	Hallway, Gather, Pursuit (MACO)
DICG [78]	Self-attention + GCN over soft coordination graphs	Dynamic implicit	Learns state-dependent coordination structure, solves relative overgeneralization	Predator-prey, SMAC, traffic junction
GraphMIX [53]	GNN with attention-based edge weights	Dynamic graph-based	Attention-driven coordination and size-invariant value decomposition	StarCraft II multi-agent scenarios

Heterogeneous Graph Coordination

Methods in this category explicitly model different entity types and relationship semantics. EMAC [79] addresses scalability through a heterogeneous graph network that models different entity types. HRG-SAC [80] introduces hierarchical relation graphs that capture local spatial relationships.

EMAC (efficient multi-agent cooperation). EMAC [79] addresses scalability and efficiency challenges through a heterogeneous graph network (HGN) architecture. EMAC employs a heterogeneous graph that explicitly models different entity types (pursuers, evaders, obstacles). The primary contribution lies in its hierarchical aggregation mechanism:

$$\begin{array}{c}{\overline{e}}_v^r=\mathrm{AGG}(\sigma ,{\mathbf{W}}_{\mathrm{VAGG}}^r,\{e_n^r,\forall n\in {\mathcal{N}}_r\left(v\right)\})\end{array}$$

(70)

$$\begin{array}{c}{h}_v^1=\mathrm{AGG}(\sigma ,{\mathbf{W}}_{\mathrm{SAGG}},\{{\overline{e}}_v^r,\forall r\in \mathcal{R}\})\end{array}$$

(71)

Most importantly, EMAC introduces the frame-wise communication reduction algorithm (FCRA), which approximates multi-hop communication using only one-hop exchanges. The effectiveness of this approach is contingent upon a well-designed heterogeneous graph schema, which requires prior domain knowledge to correctly identify and categorize the different entity and relation types in the environment. EMAC’s ability to handle partial observability and heterogeneous entity types makes it suited for complex real-world multi-agent scenarios.

Hierarchical relation graph soft actor–critic (HRG-SAC). HRG-SAC [80] addresses the challenge of capturing local spatial relationships under partial observability. It introduces a hierarchical graph generation mechanism that maintains stable graph dimensions. The primary contribution is its two-layer hierarchical relationship graph construction. For each agent, the algorithm identifies the closest agent for the first layer and the nearest entities for the second. The coordination mechanism operates through GCNs that extract latent spatial features: $F^{l+1}=\sigma (D_g^{\left(i\right)-{\displaystyle \frac{1}{2}}}{A}_g^{\left(i\right)}{D}_g^{\left(i\right)-{\displaystyle \frac{1}{2}}}{F}^l{W}^l)$. This update is a direct application of the standard GCN propagation rule (Equation (12)) on the locally constructed hierarchical graph. What distinguishes HRG-SAC is its ability to handle multiple entity types while maintaining efficiency through fixed graph dimensions.

The heterogeneous graph coordination methods are summarized in Table 16.

Table 16. Heterogeneous graph coordination.

Method	Embedding Mechanism	Coordination Type	Key Advantages	Best Applications
EMAC [79]	Heterogeneous graph network with hierarchical vertex-level and semantic-level aggregation	Communication-efficient multi-hop approximation	30% efficiency improvement, scalable to arbitrary agent numbers, handles partial observability	Multi-agent pursuit-evasion, dynamic unstructured environments
HRG-SAC [80]	Hierarchical GCN with two-layer spatial graphs	Local spatial coordination	Stable graph dimensions in dynamic environments, captures agent-entity relationships	Multi-agent food collection, cooperative tasks with entities

Communication-Based Coordination

This category combines GNNs with explicit communication protocols. MAGEC [37] employs modified GraphSAGE for resilient coordination. The framework by [81] integrates GNNs with Transformers for lightweight information exchange.

Multi-agent graph embedding-based coordination. MAGEC is a GNN-enhanced MARL method designed for resilient distributed coordination [37]. Built upon MAPPO within the CTDE paradigm, MAGEC employs a modified GraphSAGE backbone. This backbone relies on the inductive neighborhood aggregation principle of GraphSAGE, as detailed in Equation (13), to generate embeddings. The policy is trained using a reward function designed to minimize average idleness $\overline{\zeta }$:

$$r_{\mathrm{local},i}\left(t\right)={\displaystyle \frac{\zeta \left(v_i\right)}{\overline{\zeta }+ϵ}},r_{\mathrm{terminal},i}\left(t\right)={\displaystyle \frac{t}{\overline{\zeta }}},r_i\left(t\right)=\left\{\begin{array}{cc}\alpha r_{\mathrm{local},i}+\beta r_{\mathrm{terminal},i},\hfill & \mathrm{if}t=T-1\hfill \\ \alpha r_{\mathrm{local},i},\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(72)

Experiments in multi-robot patrolling scenarios demonstrate that MAGEC outperforms baselines under communication disturbance and agent failures.

Graph-based DRL with Transformer-enhanced coordination. Elrod et al. [81] introduce a framework integrating GNNs, Transformers, and DDQNs for coordination under constrained communication. The approach operates on a dynamically constructed graph, where agents and goals are represented as nodes. The primary contribution lies in the adaptive graph construction mechanism that uses distance-based thresholding:

$$e_{ij}=\left\{\begin{array}{cc}{d}_{ij}\hfill & \mathrm{if}(i,j)\in E_{\mathrm{valid}}\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(73)

where $E_{\mathrm{valid}}$ constrains connections to the k-nearest neighbors within communication range $r_v$. The transformer-based message-passing mechanism with edge-feature-enhanced attention captures complex interaction patterns through:

$${\alpha }_{ij}^h={\mathrm{softmax}}_j\left({\displaystyle \frac{\left(W_Q^h{z}_i^l\right){\left(W_K^h{z}_j^l\right)}^T}{\sqrt{d_k}}}+b_{ij}\right)$$

(74)

where $b_{ij}=W_e{e}_{ij}$ incorporates edge features. The reliance on a k-nearest neighbors heuristic for graph construction, while essential for efficiency, may inadvertently prune strategically important long-range connections that fall outside the immediate neighborhood. This architecture addresses scenarios where traditional centralized approaches fail due to scalability constraints.

The communication-based coordination methods are summarized in Table 17.

Table 17. Communication-based coordination.

Method	Embedding Mechanism	Coordination Type	Key Advantages	Best Applications
MAGEC [37]	GraphSAGE with edge features	Resilient distributed	Robust to attrition and communication loss	Multi-robot patrolling
GNN-Transformer DRL [81]	Entity embedding + transformer message-passing with edge-enhanced attention	Adaptive distributed with k-nearest neighbor constraints	Dynamic graph construction, lightweight communication, attention-based prioritization	Multi-drone navigation, disaster response, environmental monitoring

Summary

The evolution of GNN-based coordination mechanisms reveals a clear progression from rigid, predefined structures toward adaptive, learnable coordination patterns. Early approaches relied on static graph topologies, while recent methods like DMCG and DICG demonstrate the power of fully differentiable coordination discovery. The emergence of heterogeneous graph modeling in EMAC and HRG-SAC addresses the reality that multi-agent systems involve diverse entity types with distinct roles, moving beyond the uniform treatment of all agents.

Most importantly, the integration of attention mechanisms across all coordination categories highlights a fundamental insight: effective coordination requires selective information processing rather than exhaustive communication. Whether through TarMAC’s targeted messaging, MAGIC’s selective communication scheduling, or DICG’s attention-based graph construction, successful coordination emerges from agents’ ability to identify and focus on relevant relationships. This suggests that future coordination efficiency should be measured not just by task performance, but by the quality and selectivity of inter-agent information exchange.

4.3. Learning and Training Frameworks

GNN-enhanced MARL has witnessed remarkable advances in training methodologies that address heterogeneous agent coordination, scalability challenges, and deployment constraints. While traditional MARL approaches rely on homogeneous assumptions, real-world systems demand frameworks that preserve agent diversity while enabling effective coordination learning. The integration of graph neural networks introduces additional complexity, requiring specialized training approaches that can simultaneously learn individual policies and graph-based interaction patterns.

Recent developments from 2023–2025 demonstrate significant breakthroughs beyond traditional centralized training paradigms, introducing novel approaches for permutation-invariant coordination, latent graph learning, and population-based training methodologies. Table 18 provides a comprehensive overview of the major learning and training frameworks in GNN-enhanced MARL.

Table 18. Overview of GNN-enhanced MARL learning and training methods.

Method	Key Contribution	Training Paradigm	Heterogeneous Focus	Ref.
HGAP	Permutation-invariant graph attention coordination	Enhanced CTDE	Entity ordering robustness	[82]
QMIX-GNN	Heterogeneous information fusion	Enhanced CTDE	Spatial proximity modeling	[48]
BenchMARL	Standardized benchmarking infrastructure	Evaluation framework	Multi-algorithm comparison	[83]
LTS-CG	Latent temporal coordination graphs	Adaptive graph learning	Multi-scale coordination	[84]
InforMARL	Intelligent local information aggregation	Decentralized learning	Scalable coordination	[85]
Graph Conv. RL	Foundational graph convolution integration	Decentralized learning	Relation-based learning	[55]
ACORM	Attention-guided contrastive role learning	Advanced methodologies	Emergent role discovery	[86]
MAGEC	Resilient coordination under disruption	Advanced methodologies	Failure-aware training	[37]

This subsection examines three primary categories of GNN-enhanced training frameworks, analyzing their technical contributions and coordination mechanisms with particular emphasis on heterogeneous agent coordination challenges.

4.3.1. Enhanced Centralized Training with Graph-Based Coordination

Traditional centralized training with decentralized execution (CTDE) [55] frameworks have evolved significantly through graph neural network integration, addressing fundamental limitations in heterogeneous multi-agent coordination. The challenge of coordinating agents with different observation spaces, action dimensions, and capabilities requires specialized training architectures that handle diversity while maintaining coordination effectiveness.

Foundational graph convolutional training. Graph convolutional reinforcement learning [55] established foundational principles for integrating graph convolution with heterogeneous coordination learning, though it represents more of a model design contribution that significantly influenced subsequent training methodologies. The framework introduces relation kernels capturing agent interactions through relation representations, enabling agents to learn coordination policies using local graph structures while preserving agent heterogeneity through type-specific relation processing. While primarily a modeling approach, its training innovations in relation-based learning have become fundamental building blocks for many subsequent GNN-enhanced training frameworks.

Permutation-invariant graph attention training. The HGAP framework [82] addresses permutation sensitivity issues in multi-agent training where heterogeneous agents observe entities in different orders, leading to inconsistent training signals. HGAP introduces a hyper graphical attention policy network that maintains permutation invariance through graph attention mechanisms, ensuring consistent policy learning regardless of observation ordering. During training, HGAP’s graph-based entity relation embedding module constructs correlation matrices between entities and transforms them into attention weight matrices using hypernetworks, enabling agents to rapidly learn inter-entity relationships through graph attention. The framework incorporates GRUs for temporal learning and trains both ego and engagement actions using TD-error optimization, allowing integration with various MARL paradigms, including QMIX, MADDPG, and MAPPO.

Heterogeneous value decomposition with graph networks. The QMIX-GNN framework [48] extends the centralized training and decentralized execution (CTDE) paradigm to heterogeneous multi-agent systems through a novel training architecture integrating graph neural networks with monotonic value decomposition. The training process employs three interconnected components: an information infusion network utilizing graph attention networks (GAT) with six attention heads to aggregate k-nearest neighbor information (k = 5), agent networks with projection matrices $M_{{\varphi }_i}$ and shared-bottom tower structures for heterogeneous feature alignment, and a mixing network preserving monotonic decomposition constraints. During training, the GAT-based infusion mechanism computes team-level representations $o_{all}$ through multi-head attention over agent graphs, enabling each agent’s Q-value computation to incorporate both local observations and aggregated team information via RNN processing. This architecture demonstrates substantial performance gains in complex coordination tasks, achieving a 92.8% win rate in the MMM scenario (5.1% improvement) and 65.5% in MMM2 (11.3% improvement), with convergence accelerated from 800k to 640k episodes compared to baseline QMIX.

Evaluation infrastructure and standardization. The BenchMARL framework [83] establishes a comprehensive benchmarking infrastructure for multi-agent reinforcement learning, leveraging TorchRL as its backend to provide high-performance implementations and standardized training protocols. While the framework itself supports various MARL algorithms, including QMIX, MADDPG, and MAPPO, its modular design enables the integration of graph neural network models alongside traditional architectures like MLPs and CNNs. The framework’s experiment-agnostic architecture allows for systematic configuration and reporting across different algorithms, models, and environments, addressing the reproducibility crisis in MARL research. BenchMARL supports both on-policy and off-policy training strategies, with options for parameter sharing among agent groups for policies and critics. The framework’s support for vectorized environments enables efficient parallel training, particularly important for scaling GNN-based approaches that may have higher computational requirements. Through its integration with standardized reporting tools and comprehensive hyperparameter management via Hydra, BenchMARL provides the infrastructure necessary for fair comparison of GNN-enhanced coordination methods against traditional approaches, though the framework itself is methodology-agnostic rather than specifically optimizing for graph-based coordination.

Scalable MARL through intelligent information aggregation. The InforMARL framework [85] addresses the challenge of learning effective multi-agent policies with limited local information through a graph-based training architecture. The framework utilizes a centralized-training-decentralized-execution (CTDE) paradigm where graph neural networks process local agent–entity relationships during both actor and critic learning phases. The training process employs a UniMP-based message-passing mechanism with multi-head attention, allowing agents to learn which neighboring entities are most relevant for decision making without requiring global state access. A key innovation is the graph information aggregation module for the centralized critic, which maintains a fixed-dimensional representation through mean pooling regardless of agent count, enabling curriculum learning and transfer to larger agent populations. The architecture learns to construct dynamic sensing graphs based on proximity, with bidirectional edges for agent–agent communication and unidirectional edges for agent-obstacle sensing. This approach achieves superior sample efficiency compared to baselines, reaching convergence with similar training steps as methods using full global information while operating solely on local observations.

Temporal coordination graph inference. The LTS-CG framework [84] proposes a learning architecture that unifies graph inference and policy optimization through end-to-end training. By leveraging agents’ historical observation trajectories, it infers a latent temporal sparse coordination graph that dynamically evolves over time. This structure captures both long-term behavioral dependencies and current relational uncertainty, which are critical for coordinating agents under partial observability and dynamic interaction patterns.

To facilitate this, LTS-CG introduces two inductive biases: Predict-Future, which uses a diffusion convolutional GRU to model temporal dependencies and forecast future observations; and Infer-Present, which integrates attention-based GNNs to help agents reconstruct the global context from partial local observations. The graph itself is constructed via Gumbel-sampled adjacency matrices, allowing differentiable, stochastic graph learning without full connectivity assumptions. This architecture departs from static graph baselines by allowing trajectory-conditioned, stochastic communication topologies during training and execution.

4.3.2. Adaptive Coordination Graph Learning and Decentralized Training

Adaptive graph learning represents a fundamental advancement in handling dynamic coordination requirements and heterogeneous agent capabilities. Unlike static approaches, adaptive frameworks modify the coordination structure based on task requirements, agent availability, and environmental conditions, enabling more flexible training paradigms.

DGRM: k-hop neighborhood decentralization. DGRM (decentralized graph-based reinforcement learning using reward machines) [58] achieves decentralized training through a k-hop neighborhood approach where each agent only accesses information from agents within k graph hops rather than global state information. The key innovation is the truncated Q-function that approximates the full Q-function using only local information while maintaining theoretical guarantees on approximation error.

Each agent employs a localized policy depending solely on its own MDP state and reward machine state, enabling independent execution after training. The reward machines encode complex temporally extended tasks and expose reward function structure, helping agents understand high-level objectives with limited local information. The authors prove that Q-function dependency on distant agents decreases exponentially with graph distance, and demonstrate that one-hop neighborhood information often suffices for complex coordination tasks like UAV delivery and pandemic mitigation.

Decentralized graph-based MARL (DGMARL) with digital twin. DGMARL with a digital twin [87] employs a fully decentralized training paradigm where each intersection operates as an independent agent with its own multi-agent advantage actor–critic (MA2C) networks. Rather than relying on centralized control, agents learn optimal signal timing policies through local observations and neighbor communication via message passing in a graph structure. The key decentralization features include autonomous local decision making at each intersection, distributed experience replay buffers, and dynamic phase selection based on real-time traffic demand. Agents exchange state information and policies with spatially adjacent intersections through a communication graph $G(V,E)$, where intersections serve as vertices and road links as edges. This enables coordinated optimization while maintaining scalable, independent operation across large traffic networks without centralized coordination overhead.

4.3.3. Advanced Training Methodologies for Complex Systems

Modern training strategies for heterogeneous multi-agent systems focus on enhancing role specialization, robustness, and rapid scalability.

Attention-guided role embedding and robust coordination. The ACORM framework [86] delivers latent role discovery by integrating attention mechanisms with contrastive learning, maximizing mutual information between role representations and agent behaviors. This design helps agents learn specialized coordination in dynamic team settings. Furthermore, techniques such as actor–attention-critic (ATOC) [46] and ROMA [88] also leverage attention or emergent role structures to decompose policies and foster coordination in heterogeneous environments.

For robust system behavior, methods such as MA2CL [89] employ masked attentive contrastive representation learning as auxiliary tasks, improving resilience under partial observability and communication noise.

Population curriculum and meta-adaptation. The evolutionary population curriculum (EPC) [90] gradually increases the size and diversity of the agent population, combining evolutionary hyperparameter tuning to generalize across unseen team configurations.

Model-agnostic meta-learning (MAML) [91] enables rapid adaptation to new tasks with just a few gradient steps. When combined with GNN-based policy representations in multi-agent settings, this approach is ideal for deployment scenarios requiring quick adjustment to heterogeneous teams.

Together, these methodologies—attention-guided role learning, curriculum-based population scaling, and meta-learning adaptation—form a versatile toolkit for building scalable, resilient, and adaptable coordination in complex heterogeneous multi-agent systems.

4.4. Performance Evaluation and Validation

GNN-MARL methods based on performance criteria. To systematically assess the advancements in graph-neural-network-based multi-agent reinforcement learning (GNN-MARL), we classify the enabling methodologies according to the key performance criteria they target. This structured categorization highlights how various approaches address critical challenges in MARL systems, providing insights into their strengths and potential trade-offs.

The main performance criteria/metrics in GNN-MARL research encompass six fundamental dimensions:

• Scalability: Maintain performance as agent populations grow from tens to thousands through hierarchical architectures, intelligent sampling, and parameter sharing to achieve sub-quadratic scaling in computation and communication.
• Fidelity: Ensure distributed representations accurately capture global states despite partial observability through permutation equivariance, adaptive readout functions, and multi-fidelity approaches.
• Coordination Accuracy: Measure collective goal achievement via attention-based communication, consensus mechanisms, and dynamic graph learning for optimal coordination discovery.
• Convergence: Guarantee stable learning in non-stationary environments using value decomposition with monotonicity constraints, multi-timescale updates, and variance-reducing attention mechanisms.
• Complexity Management: Optimize computational efficiency through selective communication, graph sampling approximations, and hierarchical information processing.
• Robustness: Ensure reliability under failures and adversarial conditions through resilient embeddings, adversarial training, and redundant communication pathways.

Each methodology in Table 19 addresses these criteria with different trade-offs: scalability-focused methods may sacrifice coordination accuracy, while robust approaches often increase computational overhead. The selection of methods depends on the specific requirements of the application and the deployment constraints.

Table 19. Main performance criteria and their enabling methodologies.

Criteria	Enabling Methodology	References
Scalability	Intelligent information aggregation and local observability	GCN [31], GAPSR [40], GraphSAGE [32], MAGI [92], MARC [43], InforMARL [85]
	Hierarchical multi-agent RL	HGAT [38], HGT [56], RODE [49], HRG-SAC [80], HMAGQ-Net [50]
	GNN-aided communication	GNNComm-MARL [10], TarMAC [67], MAGIC [75], AC2C [69], ATOC [46]
	Parameter sharing and distributed learning	QMIX-GNN [48], GraphMIX [53], RSRN [59], CoHet [52]
	Graph sampling and decomposition	G2ANet [42], Heterogeneous Graph Transformer [65], DGRM [58], GNN-Transformer DRL [81], LTS-CG [84]
Fidelity	Partially equivariant GNNs	PEnGUiN [39]
	Multi-fidelity graph neural networks	Towards Better Laplacian Representation [45], QMIX-GNN [48]
	Adaptive readout functions	MARC [43], Relational State Abstraction [43], DMCG [77]
	Graph attention-based protocols	GAT [33], MAGEC [37], HYGMA [41], G2ANet [42], AC2C [69], HGAP [82], InforMARL [85], DGMARL [87]
Coordination Accuracy	GAT-aided communication	GNNComm-MARL [10], MAGIC [75], TarMAC [67], EMAC [79]
	Multi-agent graph embedding	MAGEC [37], DMCG [77], IRL-MHSA-GAT [76], HGAP [82], InforMARL [85], LTS-CG [84], DGMARL [87]
	Connectivity-driven communication	HRG-SAC [80], Adversarial Communication Framework [72], NTNNR [73]
	Learnable communication graph	CommFormer [68], GNN-Transformer DRL [81], DICG
	Consensus-based coordination	CoHet [52], GraphMIX [53], HYGMA [41]
Convergence	GNN-enhanced value decomposition	QMIX-GNN [48], GraphMIX [53], DICG
	GAT for stabilization	GNNComm-MARL [10], MAGIC [75]
	Partially equivariant GNNs	PEnGUiN [39]
	Multi-timescale learning	ExpoComm [47], CommFormer [68], MAGEC [37]
Complexity	GAT-based selective communication	GNNComm-MARL [10], AC2C [69], EMAC [79], G2ANet [42], ATOC [46]
	Partial equivariance mechanisms	PEnGUiN [39], MARC [43]
	Hierarchical graph networks	HGAT [38], HYGMA [41], HMAGQ-Net [50], RODE [49]
	Graph sampling and approximation	G2ANet [42], DGRM [58], ExpoComm [47]
Robustness	Resilient graph embedding	MAGEC [37], GraphSAGE [32], CoHet [52], Recurrent Message Passing [74]
	Adversarial training	Adversarial Communication Framework [72], MAGI [92]
	Communication robustness	CommFormer [68], AC2C [69], ExpoComm [47]
	GAT-based adaptive communication	GCN [31], Relational State Abstraction [43], GNNComm-MARL [10]

To facilitate research and development in GNN-MARL, we provide a curated list of essential open-source libraries in Table 20. These libraries can be categorized into five main groups: (1) graph neural network libraries that provide implementations of various GNN architectures and efficient graph operations; (2) multi-agent RL frameworks that offer standardized interfaces and algorithm implementations for MARL research; (3) environment suites that supply diverse testbeds for evaluating multi-agent systems; (4) graph manipulation and analysis tools for constructing and analyzing graph structures; and (5) auxiliary tools for experiment tracking, visualization, and hyperparameter optimization. Together, these libraries form a comprehensive toolkit that enables researchers to efficiently implement, train, and evaluate GNN-MARL algorithms.

Table 20. Key open-source libraries for GNN-MARL development.

Category	Library	Description
Graph Neural Network Libraries	PyTorch Geometric	Comprehensive GNN library with 100+ architectures, efficient sparse operations, and heterogeneous graph support
	DGL	Framework-agnostic GNN library with message passing primitives, multi-GPU acceleration, and distributed training
	Spektral	GNN library based on Keras/TensorFlow 2 for quick prototyping with various layer implementations
Multi-Agent RL Frameworks	RLlib	Scalable MARL framework built on Ray with distributed training support and integration with major environments
	MARLlib	Unified MARL library supporting cooperative, competitive, and mixed tasks with 18 pre-built algorithms
	PettingZoo	Standard API for multi-agent environments with diverse built-in scenarios and parallel execution support
	EPyMARL	Extended PyMARL with flexible algorithm configurations and support for various cooperative MARL algorithms
Environment Suites	Gymnasium	Standard single-agent RL environment API, maintained fork of OpenAI Gym with 60+ environments
	SMAC	StarCraft II multi-agent challenge for decentralized micromanagement scenarios with multiple difficulty levels
	MPE	Multi-agent particle environments for communication-oriented tasks with continuous/discrete action spaces
	Google Research Football	Multi-agent football simulation with physics-based 3D environment for team coordination research
Graph Manipulation and Analysis	NetworkX	Pure Python library for graph creation and analysis with extensive algorithms and visualization tools
	igraph	High-performance C/C++ library with Python bindings, efficient for large-scale network analysis
	NetworKit	Parallel toolkit for analyzing large networks (thousands to billions of edges) with OpenMP support
Auxiliary Tools	Stable Baselines3	High-quality RL algorithm implementations with a clean, tested codebase for benchmarking
	Weights & Biases	Experiment tracking and hyperparameter optimization platform for ML workflows
	TensorBoard	Visualization toolkit for monitoring and analyzing ML training experiments

5. Real-World Applications of GNN-MARL

The integration of graph neural networks (GNNs) with multi-agent reinforcement learning (MARL) has shown concrete progress in addressing coordination problems in real-world multi-agent systems. Rather than relying on generic architectures, recent studies emphasize domain-specific designs that capture unique environmental structures and agent interaction patterns. Given the rapid development of GNN-MARL research, this survey focuses primarily on more recent publications and emerging applications that reflect the state of the art. Applications now span from distributed robot navigation and real-time traffic signal control to wireless resource allocation and industrial scheduling, where GNNs help encode structured spatial or relational information, and MARL enables agents to learn decentralized policies under dynamic and partially observable conditions. This section surveys representative systems that demonstrate how GNN-MARL frameworks are being adapted to practical multi-agent challenges across key infrastructure and automation domains.

5.1. Automation and Robotic Systems

In the context of large-scale target-tracking missions, Zhou et al. address the challenge of decentralized submodular action selection, where coordinating up to 100 robots to maximize collective information gain is computationally prohibitive for centralized expert algorithms. Their approach trains a GNN policy by imitating a centralized greedy planner, so that each robot (node) learns to select actions consistent with greedy marginal gains using only local observations and neighbor messages. In effect, the GNN provides a surrogate for the expert’s marginal-utility evaluations, but without explicit centralized computation. This enables the distributed policy to achieve about 89% of the expert’s coverage while running several orders of magnitude faster, making real-time operation and scalability to large teams feasible.

For multi-robot navigation in environments with unpredictable pathways, Yu et al. introduce MARVEL, a model that formulates the problem as a partially observable Markov decision process (POMDP). The challenge is that the traversability of edges in the topological map is only revealed upon arrival, requiring robots to adapt their plans dynamically. MARVEL employs dynamic adaptive graph embeddings combined with a graph attention network (GAT) to allow each agent to weigh the importance of information from different neighboring nodes and teammates. This attention mechanism lets a robot prioritize reliable paths or more informative neighbors when planned routes are obstructed. Trained with online expert guidance and policy gradient optimization, MARVEL learns a robust policy that adapts to evolving topology. Its effectiveness is validated both in simulation and in a physical maze experiment with Pioneer 3-DX robots, where it achieves significantly higher on-time arrival probabilities than baseline methods.

To achieve decentralized formation control, Jiang et al. developed an end-to-end GNN-based policy trained from LiDAR-based expert demonstrations. Raw LiDAR occupancy maps are first encoded by a CNN, then passed through a GNN that aggregates neighbor information defined by the formation graph, and finally mapped by a feedforward network to differential-drive motor commands. This decentralized architecture enables each robot to adjust its velocity and angular velocity based only on local sensing and limited communication. The learned policy is permutation invariant and demonstrates scalable triangular-formation behavior across different team sizes in simulation, despite being trained with a fixed nominal team size. These results confirm that GNNs can effectively learn coordinated decentralized control directly from sensory data.

In the domain of unmanned aerial vehicle (UAV) swarm control, Zhao et al. [61] propose a position-based graph attention network (PGAT) combined with multi-agent reinforcement learning to address large-scale UAV coordination challenges. Their framework encodes UAV positions, obstacles, and reference points as nodes in a dynamic spatial graph, enabling each UAV to generate collision-free actions based solely on local information. Simulation results with swarms of up to 225 UAVs demonstrate that the PGAT-MAPFL algorithm achieves faster convergence, lower collision rates, and superior formation recovery compared to traditional potential field methods and baseline MARL approaches. This work illustrates how graph-based representations can scale to hundreds of agents while maintaining computational efficiency and real-time performance.

Beyond aerial systems, graph-based MARL has also been applied to military training simulations. Liu et al. [93] develop a graph attention network to predict synthetic character behaviors in multi-agent combat scenarios, where non-player characters (NPCs) must cooperate with simulated human teammates. By training the GAT on trajectories generated from an initial RL phase, the model learns to predict teammate actions with 89.3% accuracy. When these predictions are integrated as additional observations in a subsequent RL training phase, new agents learn effective cooperation strategies significantly faster—reaching performance thresholds up to 74,000 episodes earlier than baselines without behavior prediction. This demonstrates how graph learning can facilitate coordination in partially observable, stochastic environments where agents must reason about teammates’ intentions.

5.2. Intelligent Transportation Systems

Graph-neural-network-based multi-agent reinforcement learning (GNN-MARL) has become a powerful paradigm for creating intelligent, coordinated traffic signal control systems. By modeling road networks as graphs, these methods enable signal controllers (agents) to learn from both local conditions and the states of neighboring intersections, leading to more efficient and adaptive traffic management. A primary challenge is transferability: a policy trained under a particular demand scenario or topology often fails on different, unseen traffic conditions. Yoon et al. address this by proposing a graph-centric state representation in which each intersection’s state is formed as a local subgraph (node features such as queue lengths/vehicle counts and neighbor connectivity). A GNN encodes this graph-structured state into a permutation-invariant embedding that captures relational dynamics across neighbors; that embedding is used by an RL agent (and evaluated against a conventional vector-valued DQN baseline). In experiments across multiple unseen demand scenarios, the GNN-based representation produces a more transferable policy that adapts better to previously unexperienced traffic states than the vector-DQN baseline.

To improve coordination and reduce congestion across a multi-intersection area, Jia et al. combine a GNN-based feature extractor with a soft actor–critic (SAC)-style controller augmented by a dynamic entropy constraint (their G-DESAC). The GNN aggregates spatial features from each intersection and its neighbors (e.g., vehicle counts/positions, local flow statistics) into compact, permutation-invariant embeddings that carry contextual spatial information. These embeddings are supplied to the DESAC actor–critic pipeline; the dynamic entropy constraint adaptively regulates policy randomness to balance exploration and exploitation and to stabilize learning in complex, high-dimensional traffic states. Evaluated in the CityFlow simulation (single- and multi-intersection scenarios), the G-DESAC framework demonstrates improved training stability and reduced average wait times and queues compared to baseline controllers.

Standard graph models capture pairwise (first-order) relations between intersections but may miss higher-order corridor- or group-level interactions. To address this, Wang et al. introduce a spatio-temporal hypergraph representation for traffic networks and integrate hypergraph learning into the critic of a multi-agent SAC (MA-SAC) framework. Hyperedges connect multiple intersections that jointly form meaningful corridors or routes, allowing the hypergraph neural module to encode group-level spatial dependencies (and their temporal evolution). By placing this hypergraph module inside the critic, the value-estimation step can account for the broader, multi-intersection consequences of local actions, improving credit assignment for coordinated behaviors (e.g., creating and sustaining green waves). Empirical results show that the spatio-temporal hypergraph MA-SAC reduces average travel time and queue lengths and outperforms standard GNN-based critics in the authors’ testbeds.

Beyond signal control, GNN-MARL is being applied to the fundamental problem of network-level traffic engineering (TE). Bernárdez et al. [94] introduced MAGNNETO, a distributed framework that utilizes GNNs and MARL to optimize routing protocols like OSPF. In their system, agents are deployed on network routers and communicate with neighbors to learn a cooperative policy for setting link weights to minimize overall network congestion. A key innovation of MAGNNETO is its fully decentralized architecture, which distributes and parallelizes the optimization process across the network. This allows it to achieve performance comparable to state-of-the-art centralized optimizers but with execution times that are orders of magnitude faster, often completing in sub-second timescales on large networks. Furthermore, MAGNNETO has demonstrated strong generalization capabilities, successfully operating on dozens of real-world network topologies unseen during its training phase.

In the domain of autonomous driving, GNN-MARL frameworks are critical for enabling cooperative decision making in complex, interactive scenarios. Liu et al. [95] developed an open-source framework to model vehicle interactions on a highway with multiple ramps using graph representations. In their model, each vehicle is a node in the graph, and a graph convolutional network (GCN) is used to extract features that capture the mutual effects between them. This graph-based representation is then fed into a DRL module to generate cooperative lane-changing behaviors for autonomous vehicles (AVs). The study conducted a detailed comparative analysis of several DRL algorithms, including DQN, double DQN, dueling DQN, and D3QN, demonstrating that the GNN-based approach significantly outperforms traditional rule-based methods in achieving safer and more efficient traffic flow. Their results confirmed that combining GNN for interaction modeling with advanced DRL techniques like D3QN yields the highest rewards and the most stable performance.

5.3. Wireless Communication Networks

Graph neural networks (GNNs) have recently been integrated with multi-agent reinforcement learning (MARL) to address large-scale wireless resource management problems, where dynamic topologies, interference coupling, and heterogeneous user distributions make flat feature representations inadequate. By exploiting the relational structure among users, base stations, or links, GNNs enable agents to generalize across varying network sizes and capture spatial dependencies that traditional RL models often overlook. For example, Alablani [96] frames the user–base-station association problem as a graph where users and base stations are nodes and candidate links are edges, then uses a LocalGNN to encode each node’s K-hop neighborhood into a compact, topology-aware representation that is robust to changing user and BS counts. Those node embeddings feed into a DQN (the policy network) so that Q-value estimation leverages spatial load distribution and interference structure instead of raw flat features; the reward is defined to encourage throughput fairness (log-sum throughput). This GNN→DQN pipeline allows the agent to reason about both local channel/state and neighbor load, improving adaptability to dynamic arrivals and noisy CSI; in simulation, the approach converges quickly and outperforms heuristic and RL baselines.

Building on this idea of embedding topology into learning, Ji et al. [97] investigate decentralized spectrum and power allocation for V2X communications, where vehicles must simultaneously maintain reliable V2V links while avoiding interference with V2I transmissions. They represent interference among vehicles as a dynamic graph and adopt GraphSAGE to encode local structures, enabling each vehicle agent to learn representations that capture neighborhood interference patterns. These embeddings feed into a MARL framework where agents apply DRL-based policies for distributed resource control. Compared with non-graph counterparts, the proposed scheme achieves higher reliability of V2V links and reduces V2I interference, demonstrating how GNN-encoded relational awareness enhances policy coordination in highly dynamic vehicular networks. The contribution here lies in making MARL scalable and decentralized by ensuring that each agent learns from graph-structured local observations rather than relying on global state information.

At a larger scale, Liu et al. [98] consider mobile cell-free massive MIMO, where dense deployments of distributed antennas must serve moving users under stringent coordination constraints. A key challenge is that the number of antennas and users is large and constantly changing, making centralized optimization intractable. The authors design a scalable MARL framework where GNNs encode the interaction graph between antennas and users, capturing spatial locality and mobility effects. These GNN-based embeddings allow agents to cooperate in distributed beamforming and user association without exchanging full state information. By combining GNNs with MARL under a CTDE (centralized training, decentralized execution) paradigm, the framework achieves near-optimal throughput and fairness while keeping the decision making scalable to very large networks. This work highlights how GNN-MARL can fundamentally enable cell-free massive MIMO systems by compressing high-dimensional topology into structured representations that agents can act upon efficiently.

5.4. Manufacturing and Scheduling Systems

Manufacturing and scheduling problems are particularly well suited to graph-based modeling, since jobs, machines, processes, and even supply-chain entities are inherently relational. GNN-enhanced multi-agent reinforcement learning (MARL) has therefore been increasingly applied to optimize decision making across multiple layers of industrial systems, from shop-floor task allocation to supply-chain inventory management.

At the shop-floor level, Pu et al. [99] model flexible job-shop scheduling as a bipartite graph between jobs (or operations) and machines, and build a distributed multi-agent scheduling architecture (DMASA). They employ a heterogeneous graph neural network (HetGNN) to encode both job and machine nodes—capturing compatibility, workload, and precedence constraints—into embeddings. These embeddings feed into a multi-agent proximal policy optimization (PPO) scheme, allowing agents to jointly decide task assignments and sequencing. Their experiments in dynamic environments show that the GNN-MARL method reduces makespan and improves throughput compared to classical heuristics and flat RL baselines.

On a similar trajectory, Tang et al. [100] propose a heterogeneous graph neural network with relation encoding (HGNNR) integrated with PPO (HGNNR-PPO) to directly learn scheduling policies end-to-end. They construct a heterogeneous graph whose nodes are operations and machines, while edges encode diverse relations such as precedence, shared machines, and routing constraints. This relational encoding provides rich context that the PPO agent exploits to optimize sequencing and assignment. Across public flexible job shop benchmarks, HGNNR-PPO achieves superior performance and generalization to unseen shop configurations compared to state-of-the-art heuristics and pure RL methods.

Beyond scheduling, GNN-MARL has also been extended to integrated machine– process–system control. Wang et al. [101] formulate production systems as graphs where nodes represent machines, processes, and their interdependencies. By coupling GNN-based feature extraction with multi-agent RL, their framework enables coordinated decision making that balances local machine control with global process objectives. The policy learns to dynamically allocate resources and adapt to disturbances, leading to improvements in overall production yield. This demonstrates that GNN-MARL can capture cross-level dependencies not only between jobs and machines, but also between different layers of a production system.

At an even higher abstraction level, Kotecha and del Rio Chanona [102] apply GNN-MARL to supply-chain inventory control. In their setting, the supply network is represented as a graph of facilities and transportation links. A GNN encoder aggregates local and neighboring inventory states, while MARL agents learn ordering and distribution policies that account for both local demand and upstream-downstream dependencies. The graph structure ensures scalability to large supply chains, while the MARL framework enables decentralized yet coordinated inventory decisions. Experiments show that this approach outperforms rule-based policies in minimizing stockouts and reducing holding costs, highlighting the versatility of GNN-MARL in industrial decision making.

5.5. Resource Allocation

Resource allocation problems in wireless, edge, and IoT systems often involve nontrivial topologies shaped by interference, connectivity, and task dependencies. Instead of flat RL, GNN-MARL frameworks leverage graph encoders to capture these relations, allowing agents to make more coordinated and adaptive allocation decisions. Recent studies show that such designs can improve spectral efficiency, load balancing, and energy–latency trade-offs compared to conventional decentralized RL or heuristic policies.

Agila et al. [103] tackle spectrum sharing in 6G heterogeneous networks (HetNets). They model base stations and users as nodes in a graph and edges reflecting potential interference or connectivity. Their approach integrates MARL with GNN encoders: each node uses the GNN to aggregate interference, load, and neighbor state features, producing embeddings that feed into decentralized agents that choose spectrum and power allocation actions. The GNN module helps each agent reason not only on its own channel/load state but also the interference coupling with neighbors, thereby improving global spectral efficiency and fairness over heuristic baselines.

Bo et al. (2025) address green edge-cloud computation offloading, using a graph-based MARL design (though full architectural details are in the paper). The system constructs a graph over devices, edge servers, and cloud nodes to encode offloading relationships and connectivity. Through a GNN representation layer, task/energy/latency relationships are embedded, which agents use to make offloading and resource allocation decisions. This graph encoding helps handle topology changes and interactions between neighboring nodes, resulting in improved energy efficiency and lower latency compared to non-graph RL baselines.

5.6. Summary and Future Outlook

The integration of graph neural networks with multi-agent reinforcement learning has demonstrated promising results across diverse domains, including robotics, traffic management, wireless networks, and industrial scheduling. These studies highlight how GNNs enable agents to exploit structured relational information in complex environments, while MARL provides a framework for decentralized and scalable decision making.

Although the reported improvements are encouraging, most evaluations are still simulation-based, and the robustness of GNN-MARL in large-scale real-world deployments remains an open question. Future work may focus on testing these methods in practical infrastructure settings such as energy systems, water distribution, and warehouse automation, as well as in edge computing scenarios like autonomous driving and IoT. Another direction is to integrate richer input modalities—such as vision, text, or temporal sequences—into graph structures, which may enhance adaptability in dynamic and partially observable environments.

6. Research Challenges and Future Directions

Despite promising advances, GNN-enhanced MARL systems face core unresolved research challenges. We identify six directions where fundamental investigation into scalability, efficiency, communication, and model understanding remains crucial.

6.1. Scalability to Ultra-Large Agent Networks

While GNN-MARL methods have shown promising results in coordinating dozens of agents in simulation environments, many real-world applications—such as multi-robot coordination, industrial resource allocation, and traffic management—involve scenarios where the number of agents can reach thousands or more. This raises significant challenges for scalability and generalization beyond the fixed-size or small-scale benchmarks commonly seen in the literature. Most existing architectures assume a fixed-size network or fully connected graph, which does not naturally generalize to variable or very large populations. For example, recent work on scalable MARL observes that dense GNNs and self-attention mechanisms incur prohibitive computational costs as the number of agents grows [104]. Open questions include how to design hierarchical or modular graph representations (e.g., clustering agents into communities) and permutation-invariant architectures that allow arbitrary agent counts without retraining. One promising direction is to learn sparse communication graphs on the fly, using techniques like graph sampling or attention to restrict message passing only to relevant neighbors [37,42,67]. Another is the notion of a “foundation” GNN-MARL model: pre-training a large, general-purpose graph-based policy on diverse multi-agent tasks and then fine-tuning it for specific scenarios [105]. Such an approach could amortize training costs across tasks and improve generalizability. In summary, enabling truly large-scale GNN-MARL will likely require new architectures (e.g., multi-scale or recursive GNNs), dynamic graph refinement, and mechanisms for asymptotically bounded complexity as agents proliferate.

6.2. Communication Overhead and Topological Design

A core appeal of GNN-MARL is efficient agent communication via learned graph structures, but communication overhead remains a concern. While GNN-based protocols can reduce unnecessary messaging (e.g., by attention-based neighbor selection), even sparse graphs can become costly in dense agent networks. Recent work (e.g., MAGIC) demonstrates learning when and with whom to communicate, achieving about a 27% reduction in transmitted messages [67]. This highlights that adaptive communication scheduling (learning when to send messages) and targeting (learning whom to address) can significantly cut overhead. However, many questions are open: how to co-design message encoding with policy learning so that critical information is conveyed in minimal bits; how to incorporate constraints like limited bandwidth or latency; and how to structure hierarchical communication (e.g., intermediate aggregator agents or multi-hop topologies). Robustness to unreliable communication links (e.g., lossy or delayed transmission) is also critical, motivating research into resilient and event-triggered protocols.

6.3. Computational Efficiency and Resource Constraints

The combined cost of GNN encoding and MARL optimization can be prohibitive, especially for real-time or edge deployment. Most GNN-MARL models consist of deep GNNs coupled with parameter-heavy policies, leading to high memory and energy usage. Training requirements are growing super-linearly in many RL domains, and the addition of graph structure only increases this [8]. Future directions include graph sparsification, quantized GNNs, and lightweight policy distillation. Distributed or asynchronous training schemes could reduce memory bottlenecks. The idea of a large, pretrained GNN-MARL backbone that can be fine-tuned per task (analogous to foundation models) also shows promise [105]. Another avenue is adaptive computation—pruning redundant high-order neighbors during inference via local contribution scores (LCS), which enables sparse message passing focused only on the most informative neighbors [106]. Although many methods have been proposed to address scalability or computational efficiency, most remain at an experimental stage. In real-world applications, specialized assumptions may not align with practical demands, and resource constraints can further exacerbate these mismatches. A key challenge lies in how to integrate and coordinate these approaches such that they work together effectively under realistic conditions.

6.4. Interpretability and Explainability of GNN-MARL Models

The decision processes of GNN-MARL agents remain largely opaque. Their actions are conditioned on deep message-passing layers across potentially non-local neighborhoods, making post-hoc attribution difficult. While explainable RL has progressed in single-agent contexts, little has been done to explain multi-agent policies under graph-based coordination. Future work should investigate graph-level attribution (e.g., identifying critical neighbors or subgraphs), attention- or gradient-based explanations [107], or symbolic abstractions (e.g., latent roles, rule distillation). Models with structured intermediate representations—such as modular or role-based GNNs—may offer improved transparency.

6.5. Learning in Dynamic and Heterogeneous Environments

Many real-world MAS environments are dynamic: agents can join or leave, graph topologies shift, and heterogeneous agents may carry different modalities. Current GNN-MARL approaches often assume static, homogeneous graphs. Future work should extend to spatial-temporal graph RL models [63], where the graph structure evolves and the model adapts accordingly. Heterogeneous GNNs that treat different agents or interaction types distinctly [64] could allow richer reasoning. Coupling these with meta-learning or continual learning frameworks can enable rapid adaptation to novel team compositions or task variants.

6.6. Theoretical Foundations and Convergence Guarantees

Despite practical success, the theoretical understanding of GNN-MARL remains limited. It is still unclear how GNN representations affect convergence rates, sample complexity, or equilibrium stability in non-stationary games. While permutation-equivariant architectures offer symmetry advantages [108], their effect on generalization or exploration efficiency is under-analyzed. Meanwhile, as real-world systems increasingly involve thousands of interacting agents, convergence becomes not only a computational challenge but also an uncertain issue in mathematics. Balancing such large-scale interactions in training raises open questions about stability, scalability, and expressivity of the underlying GNN architectures. Future research should aim to formalize GNN-induced policy spaces by drawing on mathematical frameworks such as topological invariants, manifold embeddings, and dynamical systems theory, with the goal of analyzing stability, convergence trajectories, and the expressive geometry of multi-agent interactions at scale.

7. Conclusions

This survey has systematically examined graph-based multi-agent reinforcement learning (MARL) for networked coordination and control, demonstrating how graph neural network (GNN)-enhanced MARL effectively addresses challenges in distributed decision making through structured representations, selective communication, and scalable architectures. The integration of GNNs and MARL enables agents to capture relational dependencies, reduce communication overhead via attention mechanisms, and generalize across varying network topologies—capabilities validated through successful deployments in robotics, traffic control, wireless networks, and industrial automation. Despite these advances, critical challenges remain: scaling to a very large scale of systems with thousands of agents, ensuring computational efficiency for edge deployment, providing theoretical convergence guarantees, and improving model interpretability. Future research should focus on developing foundation GNN-MARL models that can be fine-tuned across domains, designing hierarchical architectures for ultra-large networks, and establishing rigorous theoretical frameworks for stability analysis. As autonomous systems and networked infrastructure become ubiquitous, the demand for robust multi-agent coordination will intensify. Graph-based reinforcement learning provides a principled approach that bridges local agent autonomy with global coordination objectives, positioning it as a key enabler for next-generation distributed intelligent systems.