Abstract
DFT calculations at the B3LYP/aug-cc-pVDZ level of theory on some aromatic substrates showed that in the HOMO (Highest Occupied Molecular Orbital) of nitrobenzene, the atomic coefficients are not in agreement with the meta-directing behavior of this compound. The atomic coefficients are the same in the ortho and in the meta positions. The HOMO (or NHOMO (Next Occupied Molecular Orbital) in the case of benzaldehyde) is not in agreement with the experimental results when deactivating, meta-orienting compounds are considered. Mulliken charges sometimes are not able to explain the observed reactivity. Hirshfeld charges allow us to predict the orientation of the attack of an electrophile on the aromatic ring, with the exception of nitrobenzene. Both HOMO atomic coefficients and charges are in agreement with the experimental results when deactivating, ortho-para orienting, and activating compounds are tested.
1. Introduction
Electrophilic aromatic substitution has been the object of extensive work in the history of organic chemistry [1]. Koerner, a student of Cannizzaro in Palermo, studied in detail the electrophilic aromatic substitution reaction. Already in a first article published in 1869 [2], Koerner identified the equivalence of the carbon atoms present in the benzene ring. This work will find its maximum expression a few years later in a monumental article published by Koerner in the Gazzetta Chimica Italiana [3]. In this article Koerner prepares hundreds of aromatic compounds derived from benzene at different degrees of substitution. Beyond the preparative aspect, in itself relevant, Koerner at the end of the article tries to draw some conclusions. Let us retrace them using his words: «1. If chlorine, bromine, iodine, or nitric acid acts on chloro-, bromo-, or iodobenzene, on aniline, phenol, or toluene, in such a way as to replace a single hydrogen atom in the aforementioned bodies, thus generating a bisubstituted derivative, a derivative belonging to the 1,4 series is always formed as the main derivative, and at the same time a derivative of the 1,2 series originates as a secondary product. 2. Where the group already existing in the petrol is of an acid nature, being constituted by the residues COOH, NO2, and SO3H, the action of the same agents […] results in the main derivative being a body belonging to the 1,3 series […].» [3]. Koerner therefore identified the correct orienting effect of the substituents.
Around the 1920s, Lapworth and Robinson formulated the first theory used to justify the progress of chemical reactions: the theory of alternating polarity [4,5,6]. This theory marks the birth of studies on reaction mechanisms. What are the bases of this theory? The most electronegative atom induced a polarization of the bond that propagated to adjacent atoms. This type of approach has also been used in the case of electrophilic aromatic substitution reactions, as described in a book of organic chemistry written by Paul Karrer in 1942, which also had a certain success in the following years [7].
In accordance with this theory, the carbon atoms of the benzene ring were positively and negatively charged in alternation as a function of the electronegativity of the atoms bonded to it. If the benzene ring contained ortho-para orienting substituents, the carbon atoms in ortho and para were negatively charged: this will cause the electrophile to attack mainly in those positions. If the ring contained meta-directing substituents, the negative charge will be found essentially on the carbon atoms in meta. In this case, therefore, the electrophile will attack mainly in the meta position. Furthermore, this theory is not able to explain the activating or deactivating nature of the substituents. On the other hand, at that time the kinetic studies of the reactions had not yet been performed.
In 1942 Wheland proposed, on the basis of quantum mechanical calculations, the formation of an arenium ion as an intermediate in electrophilic aromatic substitution reactions (Figure 1) [8]. On the basis of the different stability of this intermediate, preceded or not by the formation of π complexes and/or by single-electron transfers, in relation to the substitution model present in the molecule, it was possible to interpret the reactivity of various aromatic compounds. The formation of the arenium ion has been demonstrated in some cases both via NMR [9,10,11] and by trapping reactions [12,13].
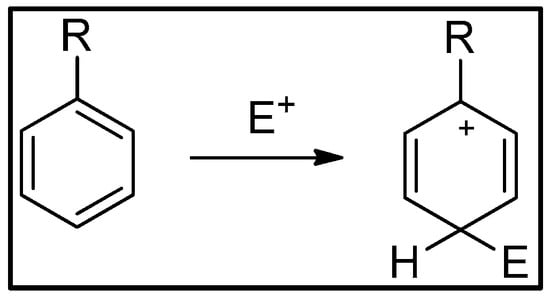
Figure 1.
Formation of the arenium ion.
This theory changed the approach from a “static” to a “dynamic” theory. The formation of the arenium ion (or σ complex) is generally the slow stage of the reaction. This species had a high energy compared to the reagents since it was not aromatic. It can be thought, on the basis of Hammond’s postulate, that the factors that stabilized the σ complex also stabilized the transition state of the slow stage of the reaction. Therefore, all the isomers could be formed, and the respective reactions were in competition with each other: the factors that preferentially stabilized a transition state made this reaction faster than the others. The groups -OH, -OR, -NR2 are all activating groups. The atom bonded to the ring is more electronegative than carbon: this makes these substituents electron-withdrawing ones, and therefore deactivating substituents, by inductive effect. They also have an electron-donating conjugative effect and, therefore, an activating effect. All these substituents, in fact, have a lone pair that they can share with the ring. The two effects are in contrast with each other; however, the conjugative effect is much more important than the inductive effect; overall, therefore, these substituents are electron donors and activators of electrophilic aromatic substitution. The attack in the ortho and para positions leads to intermediates that can be stabilized by resonance through the formation of an additional resonance structure. These substituents are, therefore, all activating and ortho-para orienting ones.
A still different case occurs when the substituent is a halogen. The halogen is clearly more electronegative than carbon: by the inductive effect, the halogen is an electron-withdrawing substituent. However, since all halogens have lone pairs, they are electron donors by the conjugative effect. Also, in this case we have two contrasting effects: unlike the -OH group, however, in halogens the inductive effect prevails. Overall, halogens are electron-withdrawing substituents and, therefore, deactivate electrophilic aromatic substitution. Since the conjugative effect can stabilize the σ complex intermediates deriving from ortho-para attack more than that deriving from meta attack, these substituents are ortho-para orienting ones.
Other substituents such as -CONR2, -CO2R, -SO3H, and -NO2 have the characteristic that the atom directly bonded to the ring has at least a partial positive charge. This charge makes these substituents inductively electron-withdrawing ones; an electron-withdrawing conjugative effect is present, since these substituents, being deficient in electrons on the atom bonded to the ring, will tend to attract them from the ring and are able, given their structure, to host the excess of electrons. The two effects are consistent, and both define these substituents as electron withdrawers and deactivators of electrophilic aromatic substitution.
This description of the reactivity of aromatic compounds is not free from limitations. It does not allow to distinguish the reactivity of benzofuran and indole. If the resonance structures of the respective σ complexes are written, no substantial difference between the two compounds is observed, and both should orient the electrophilic substitution in the α position, while indole essentially gives the β substitution product. Furthermore, the approach followed to describe the electrophilic aromatic substitution does not assign any role to the electrophile: often in the graphics it is not specified at all which electrophile is being used, and, in any case, no role of the entering group in the stabilization of the σ complex is assumed. This assumption is different from reality, where significant variations can also be observed depending on the type of reaction to which the substrate is subjected. The role of the electrophile has been explained, more recently, by admitting that, with reactive electrophiles, the transition state is reached in an initial state (early). In this way the transition state will not present a real positive charge on the ring and therefore will not be affected by the presence of substituents: the result will be a poor selectivity in the reaction. On the contrary, when the electrophile is not very reactive, the transition state will be reached when the bond of the electrophile on the aromatic ring is almost formed, the positive charge on the ring will be clear, and the reaction will be greatly affected by the presence of substituents, with a consequent increase in selectivity [14].
During 1952 Fukui proposed frontier orbital control in the aromatic substitution reactions [15,16,17]. A few decades ago, a theoretical hypothesis was formulated that allows us to describe the energy variation in a reaction along the reaction coordinate. The equation that describes energy variation is called the Klopman-Salem equation [18,19,20]. In 2016, Domingo proposed the Molecular Electron Density Theory, where the changes in the electron density are responsible for the reactivity of organic molecules [21]. The mechanism of aromatic substitution has been discussed by using DFT calculation [22,23]. In 2014, charges were considered as the determining factor in ortho/para and meta directing effects in aromatic substitutions [24].
In this article, we want to discuss the role of frontier orbitals and charges in some monosubstituted aromatic compounds, with particular attention to compounds showing deactivating properties.
2. Materials and Methods
Gaussian09 has been used for discussions about computed geometries [25]. All the computations were based on the density functional theory (DFT) by using the B3LYP hybrid xc functional [26,27]. Geometry optimizations from the Gaussian09 program have been obtained at the B3LYP/aug-cc-pVDZ level of approximation. In the case of nitrobenzene, HSEH1PBE [28], PBEPBE [29], and TPSSTPSS [30] functionals have been used. Geometry optimizations were performed with default settings on geometry convergence (gradients and displacements), integration grid, and electronic density (SCF) convergence. Redundant coordinates were used for geometry optimization as produced by the Gaussian09 program. Analytical evaluation of the energy second derivative matrix with respect to. Cartesian coordinates (Hessian matrix) at the B3LYP/aug-cc-pVDZ level of approximation confirmed the nature of minima on the energy surface points associated with the optimized structures. Z-matrix of optimized structures are collected in the Supporting Information.
3. Results
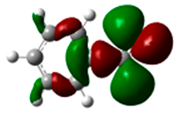
Nitrobenzene is a compound deactivated towards electrophilic aromatic substitution and a meta-orienting compound. Nitration of nitrobenzene at 35 °C gave the following results: ortho-dinitrobenzene 0.81%, meta-dinitrobenzene 90.1%, and para-dinitrobenzene 1.7% [31]. Chlorination of nitrobenzene in acetic acid at room temperature gave ortho-chloronitrobenzene (24.1%), meta-choronitrobenzene (68.7%), para-chloronitrobenzene (7.1%)ss [32]. We performed DFT calculations at the B3LYP/aug-cc-pVDZ level of theory on Gaussian09, and the HOMO was found at −7.90 eV (Figure 2). The basis set has been selected considering that, in a previous article in this field [24], the aug-cc-pVDZ basis set has been used and that that work concluded for a charge control in electrophilic substitution. The atomic coefficients are not in agreement with the meta-directing behavior of this compound. The atomic coefficients are the same in the ortho and in the meta positions.
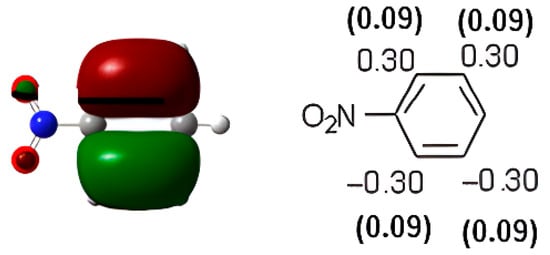
Figure 2.
HOMO of nitrobenzene. In parentheses is the electronic density (|ci|2|).
The analysis of Mulliken charges gave the distribution of charges represented in Figure 3. All the atoms have a positive charge, and this result is not in agreement with the possibility of having an electrophilic substitution reaction.
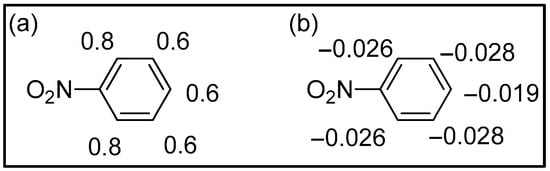
Figure 3.
Mulliken (a) and Hirshfeld (b) charges on nitrobenzene.
However, the smallest charges on the ring are those in the meta position, in agreement with the experimental results. It is noteworthy that also the para position on the ring has the same positive charge as the carbon atoms in the meta position. This result is not in agreement with the experimental results. However, recently Mulliken charges have not been considered appropriate in discussing properties [33]. On the contrary, Hirshfeld charges describe well the reactivities of aromatic compounds [34]. If we consider Hirshfeld charges, all the carbon atoms have negative charges; the highest charges are in the meta position, in agreement with the experimental results. However, the difference between the charges in the ortho and in the meta positions is very small.
Therefore, on the basis of these data, the observed reactivity of nitrobenzene when it is subjected to a nitration reaction can be explained by considering a charge effect. Nevertheless, the increase in percent yields in the ortho-substituted product observed when a chlorination reaction was performed could be explained by assuming a role for the HOMO in the reaction, considering that the atomic coefficient in the ortho and meta positions are the same. However, the observed increase in the yields for the para-substituted product (o-chloronitrobenzene) in comparison with those observed for the formation of o-dinitrobenzene cannot be explained considering the absence of the atomic coefficient in the para position in the HOMO of nitrobenzene.
To confirm this result, we also performed DFT calculations using different functionals (Table 1). The B3LYP functional was able to give the best description of the reactivity of nitrobenzene as charge-directed reactivity.

Table 1.
Atomic coefficients and electronic densities on HOMO and NHOMO, Mulliken charges, and Hirshfeld charges for nitrobenzene.
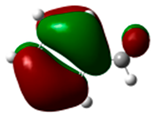
Benzonitrile showed the same behavior as nitrobenzene. Nitration of nitrobenzene gave 16% o-nitrobenzonitrile, 80% m-nitrobenzonitrile, and 4% p-nitrobenzonitrile [35,36]. On the other hand, chlorination of benzonitrile gave 34% o-chlorobenzonitrile, 55% m-chlorobenzonitrile, and 11% p-chlorobenzonitrile [36]. The HOMO of benzonitrile has been observed at −7.59 eV (Figure 4). These data are not in agreement with the experimental results. In fact, the HOMO favored the ortho-para substitution. The highest atomic coefficients and the highest electronic density are in the para position.
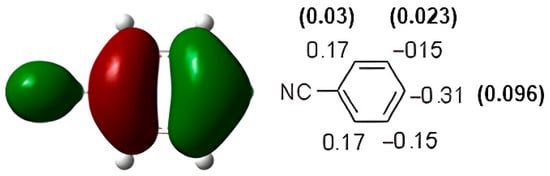
Figure 4.
HOMO of benzonitrile. In parentheses is the electronic density (|ci|2|).
The distribution of the Mulliken charges confirms this behavior (Figure 5a). All the carbon atoms show positive charges, and the smallest charges are in the ortho-para position. In conclusion, neither frontier orbital control nor charge control of the reaction can explain the observed behavior.
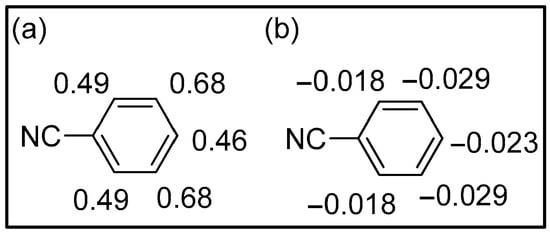
Figure 5.
Mulliken (a) and Hirshfeld (b) charges in benzonitrile.
On the contrary, Hirshfeld charges are in agreement with the experimental results (Figure 5b). All the carbon atoms have negative charges, and the highest charges are in the meta position.
The increase in ortho- and para-substituted derivatives when chlorination was performed could be due to the contribution of the HOMO in determining the substitution sites in the reaction.
Some other deactivating meta-directing compounds have been examined. Nitration of benzaldehyde at a temperature lower than 15 °C gave m-nitrobenzaldehyde in 80% yields [37]. Nitration of benzoic acid gave 22% o-nitrobenzoic acid, 76% m-nitrobenzoic acid, and 2% p-nitrobenzoic acid [38]. Nitration of methylbenzoate at 0 °C gave methyl m-nitrobenzoate in 81% yields [39]. Chlorination of benzoic acid in HCl at reflux gave 50% m-chlorobenzoic acid [40], while bromination of methyl benzoate at 60 °C afforded methyl m-bromobenzoate in 85% yields [41].
The results of calculations are reported in Table 2. The HOMO of the benzaldehyde is an n orbital, and, then, it is not involved in the aromatic substitution. The next HOMO (NHOMO = Next Highest Occupied Molecular Orbital) is a p orbital. However, the atomic coefficients and electronic densities in ortho and para are the same. These data are not in agreement with the experimental results, where the main reaction occurs in the meta position. Mulliken charges do not allow for a better criterion able to explain the chemical behavior of this compound. All the carbon atoms show positive charges, and the smallest charges are in the ortho and para positions. Only Hirshfeld charges gave results that could justify the observed behavior. In fact, all the carbon atoms show negative charges, and the highest charges are in the meta position.

Table 2.
Atomic coefficients and electronic densities on HOMO and NHOMO, Mulliken charges, and Hirshfeld charges for benzaldehyde, benzoic acid, and methyl benzoate.
The HOMO of benzoic acid showed that both the highest atomic coefficients and electronic densities are in the ortho and meta positions. Clearly, the HOMO does not allow us to justify the meta-directing property of this compound. Considering Mulliken charges, all the carbon atoms show positive charges, and the smallest charges are in the ortho and para positions. Also, Mulliken charges cannot be used to justify the orientation of benzoic acid substitution. On the contrary, Hirshfeld charges allow us to justify the observed results. In fact, all the carbon atoms show negative charges, and the highest ones are in the meta position, in agreement with the experimental results.
Methyl benzoate gave a HOMO where the highest atomic coefficients and electronic densities are in the ortho and meta positions, showing potential chemical behavior not in agreement with the experimental results. On the contrary, both Mulliken and Hirshfeld charges are in agreement with the observed behavior. In fact, considering Mulliken charges, all the carbon atoms show positive charges, and the smallest one is in the meta position. Furthermore, considering Hirshfeld charges, all the carbon atoms in the aromatic ring show negative charges, and the highest ones are in the meta position.
Bromobenzene is a deactivating compound towards electrophilic substitution. However, it is an ortho-para orienting compound. Thus, nitration gave 37% o-nitrobromobenzene, 1% meta-nitrobromobenzene, and 62% p-nitrobromobenzene. Chlorination gave 39% o-chlorobromobenzene and 61% p-chlorobromobenzene [36].
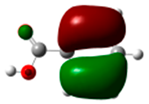
The HOMO of bromobenzene (−6.90 eV) is represented in Figure 6. Both the atomic coefficients and electronic densities are in agreement with the formation of the ortho-para bisubstituted compounds. In fact, the highest atomic coefficients are in the ortho and para positions.
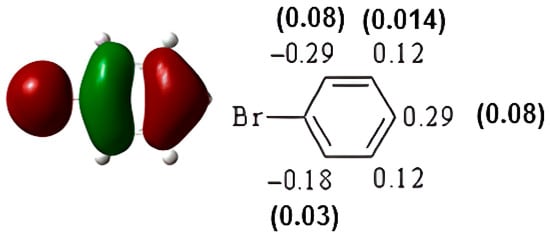
Figure 6.
HOMO of bromobenzene. In parentheses is the electronic density (|ci|2|).
Mulliken and Hirshfeld charges in this case are in agreement with the observed behavior (Figure 7). Considering Mulliken charges, all the carbon atoms show positive charges, and the smallest ones are in ortho and para positions, while, considering Hirshfeld charges, all the carbon atoms show negative charges, and the highest ones are in the same positions.
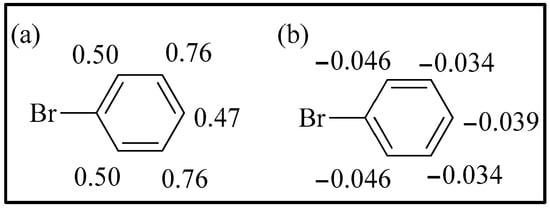
Figure 7.
(a) Mulliken charges on bromobenzene; (b) Hirshfeld charges on bromobenzene.
This section may be divided by subheadings. It should provide a concise and precise description of the experimental results and their interpretation, as well as the experimental conclusions that can be drawn.
Finally, we tested our approach on the basis of DFT calculations on an activating ortho-para orienting compound, anisole. Nitration of anisole gave 44% o-nitroanisole and 56% p-nitroanisole. Chlorination gave 21% o-chloroanisole and 79% p-chloroanisole [37].
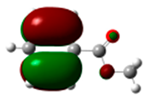
The HOMO of anisole was found at −6.92 eV (Figure 8). The highest atomic coefficients and electronic densities are in the ortho-para position, in agreement with the experimental results. Mulliken charges are not in agreement with experimental behavior (Figure 9). Considering Mulliken charges, all the carbon atoms show positive charges, and the smallest is in para. Considering Hirshfeld charges, all the carbon atoms in the aromatic ring show a negative charge, and the highest ones are in the ortho-para position. Furthermore, the increase in para isomer when chlorination had been performed clearly indicates a significant role of the HOMO in this reaction. In fact, the Hirshfeld charges are the same in ortho and para, while the atomic coefficient in the para position is very different from that in ortho.
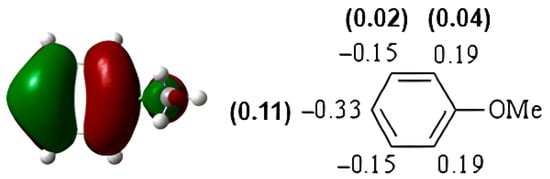
Figure 8.
HOMO of anisole. In parentheses is the electronic density (|ci|2|).
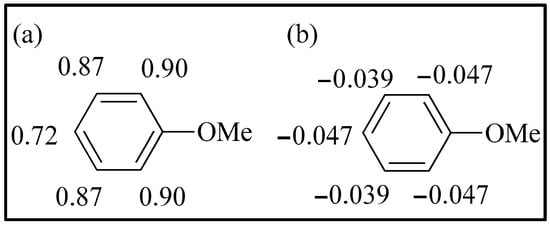
Figure 9.
(a) Mulliken charge on anisole; (b) Hirshfeld charges on anisole.
4. Conclusions
In conclusion, our analysis of the electrophilic aromatic substitution showed that, when activating or deactivating ortho-para directing substrates are considered, the description of the reaction using Hirshfeld charges when a hard electrophile (nitronium ion) is used is able to reproduce the experimental results. When a softer electrophile is used (chlorine), a role of the HOMO has to be considered. On the contrary, in the presence of deactivating, meta-directing substrates are considered, and both frontier orbital and charge approaches fail, sometimes for one factor, sometimes for another.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/org6030034/s1: Z matrix of optimized structures.
Author Contributions
Conceptualization, M.D.; data curation, L.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All the data are available in the Supporting Materials section.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Crampton, M.R. Organic Reaction Mechanisms; Knipe, A.C., Moloney, M.G., Eds.; Wiley: New York, NY, USA, 2020; pp. 213–295. [Google Scholar]
- Koerner, W. Fatti per servire alla determinazione del luogo chimico nelle sostanze aromatiche. G. Sci. Nat. Ed. Econ. 1869, 5, 212–256. [Google Scholar]
- Koerner, W. Studi sull’isomeria delle così dette sostanze aromatiche a sei atomi di carbonio. Gaz. Chim. Ital. 1874, 4, 305–446. [Google Scholar]
- Kermack, W.O.; Robinson, R. An explanation of the property of induced polarity of atoms and an interpretation of the theory of partial valencies on an electronic basis. J. Chem. Soc. Trans. 1922, 121, 427–440. [Google Scholar] [CrossRef]
- Lapworth, A. A theoretical derivation of the principle of induces alternate polarities. J. Chem. Soc. Trans. 1922, 121, 416–427. [Google Scholar] [CrossRef][Green Version]
- Saltzman, M. Arthur Lapworth. J. Chem. Educ. 1972, 49, 750–752. [Google Scholar] [CrossRef]
- Karrer, P. Trattato di Chimica Organica; Sansoni: Firenze, Italy, 1965. [Google Scholar]
- Wheland, G.W. A quantum mechanical investigation of the orientation of substitution in aromatic molecules. J. Am. Chem. Soc. 1942, 64, 900–908. [Google Scholar] [CrossRef]
- Olah, G.A. Stable carbonium ions. IX. Methylbenzenonium hexafluoroantimonates. J. Am. Chem. Soc. 1965, 87, 1103–1108. [Google Scholar] [CrossRef]
- Olah, G.A.; Kiovsky, T.E. Stable carbonium ions. LI. Fluorobenzenonium ions. J. Am. Chem. Soc. 1967, 89, 5692–5694. [Google Scholar] [CrossRef]
- Olah, G.A.; Schlosberg, R.H.; Richard, D.; Porter, R.D.; Mo, Y.K.; Kelly, D.P.; Mateescu, G.D. Stable carbocations. CXXIV. Benzenium ion and monoalkylbenzenium ions. J. Am. Chem. Soc. 1972, 94, 2034–2043. [Google Scholar] [CrossRef]
- Corey, E.J.; Barcza, S.; Klotmann, G. Directed conversion of the phenoxy grouping into a variety of cyclic polyfunctional systems. J. Am. Chem. Soc. 1969, 91, 4782–4786. [Google Scholar] [CrossRef]
- Hahn, R.C.; Strack, D.L. Ipso nitration. II. Novel products and true positional selectivities in nitration of p-cymene. J. Am. Chem. Soc. 1974, 96, 4335–4337. [Google Scholar] [CrossRef]
- Carey, F.A.; Sundberg, R.J. Advanced Organic Chemistry; Part A: Structure and Mechanisms; Springer: New York, HY, USA, 2008. [Google Scholar]
- Fukui, K.; Yonezawa, T.; Shingu, H. A molecular orbital theory of reactivity of aromatic hydrocarbons. J. Chem. Phys. 1952, 20, 722–725. [Google Scholar] [CrossRef]
- Seeman, J.I. Kenichi Fukui, Frontier Molecular Orbital Theory, and the Woodward-Hoffmann Rules. Part II. A Sleeping Beauty in Chemistry. Chem. Rec. 2022, 22, e202100300. [Google Scholar]
- Elliott, R.J.; Sackwild, V.; Richards, W.G. Quantitative frontier orbital theory: Part I. Electrophilic aromatic substitution. J. Mol. Struct. 1982, 86, 301–314. [Google Scholar]
- Klopman, G. Chemical reactivity and the concept of charge- and frontier-controlled reactions. J. Am. Chem. Soc. 1968, 90, 223–234. [Google Scholar] [CrossRef]
- Salem, L. Intermolecular orbital theory of the interaction between conjugated systems. I. General theory. J. Am. Chem. Soc. 1968, 90, 543–552. [Google Scholar] [CrossRef]
- Salem, L. Intermolecular orbital theory of the interaction between conjugated systems. II. Thermal and photochemical cycloaddition. J. Am. Chem. Soc. 1968, 90, 553–566. [Google Scholar] [CrossRef]
- Domingo, L.R. Molecular Electron Density Theory: A Modern View of Reactivity in Organic Chemistry. Molecules 2016, 21, 1319. [Google Scholar] [CrossRef]
- Stuyver, T.; Danovich, D.; De Proft, F.; Shaik, S. Electrophilic aromatic substitution reactions: Mechanistic landascape, electrostatic and electric-field control of reaction rates, and mechanistic crossovers. J. Am. Chem. Soc. 2019, 141, 9719–9730. [Google Scholar] [CrossRef]
- Galabov, B.; Nalbantova, D.; Schleyer, P.v.R.; Schaefer, H.F., III. Electrophilic aromatic substitution: New insighta into an old class of reactions. Acc. Chem. Res. 2016, 49, 1191–1199. [Google Scholar] [CrossRef]
- Liu, S. Where does the electron go? The nature of ortho/para and meta group directing in electrophilic aromatic substitution. J. Chem. Phys. 2014, 141, 194109. [Google Scholar] [CrossRef] [PubMed]
- Gaussian 09. 2009. Available online: https://barrett-group.mcgill.ca/tutorials/Gaussian%20tutorial.pdf (accessed on 28 July 2025).
- Parr, R.G.; Yang, W. Density Functional Theory of Atoms and Molecules; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar]
- Krukau, A.V.; Vydrov, O.A.; Izmaylov, A.F.; Scuseria, G.E. Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 2006, 125, 224106. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Tao, J.M.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the density functional ladder: Nonempirical meta-generalized gradient approximation designed for molecules and solids. Phys. Rev. Lett. 2003, 91, 146401. [Google Scholar] [CrossRef]
- Pounder, F.E. The Nitration of Nitrobenzene. Ph.D. Thesis, Durham University, Durham, UK, 1935. [Google Scholar]
- Baciocchi, E.; Cacace, F.; Ciranni, G.; Illuminati, G. Isomeric distributions and relative reactivities in the uncatalyzed chlorination of benzonitrile, nitrobenzene, and benzotrifluoride. The directive effects of electron-withdrawing substituents as a function of reagent and solvent. J. Am. Chem. Soc. 1972, 94, 7030–7034. [Google Scholar] [CrossRef]
- Heidar-Zadeh, F.; Ayers, P.W.; Verstraelen, T.; Vinogradov, I.; Vöhringer-Martinez, E.; Bultinck, P. Information-theoretic approaches to atoms-in.molecules: Hirshfeld family of partitioning schemes. J. Phys. Chem. A 2018, 122, 4219–4245. [Google Scholar] [CrossRef] [PubMed]
- Liu, S. Quantifying reactivity of electrophilic aromatic substitution reactions with Hirshfeld charge. J. Phys. Chem. A 2015, 119, 3107–3111. [Google Scholar] [CrossRef]
- Johnstone, J.F.; Ridd, J.H.; Sandall, J.P.B. The borderline between the classical and the electron transfer process in nitration by the nitronium ion. Chem. Commun. 1989, 244–246. [Google Scholar] [CrossRef]
- Brown, J.J.; Cockroft, S.L. Aromatic reactivity revealed: Beyond resonance theory and frontier orbitals. Chem. Sci. 2013, 4, 1772–1780. [Google Scholar] [CrossRef]
- Davey, W.; Gwilt, J.R. The preparation of mononitrobenzaldehdes. J. Chem. Soc. 1950, 204–208. [Google Scholar] [CrossRef]
- Stock, L.M. Aromatic Substitution Reactions; Prentice-Hall: Englewood Cliffs, NJ, USA, 1968; p. 63. [Google Scholar]
- Kamm, O.; Segur, J.B. Methyl m-nitrobenzoate. Org. Synth. 1923, 3, 71–72. [Google Scholar] [CrossRef]
- Yee, H.Y.; Boyle, A.J. The chlorination of benzoic acid in aqueous system by use of oxidizing acids. J. Chem. Soc. 1955, 4139–4140. [Google Scholar] [CrossRef]
- Pearson, D.E.; Stamper, W.E.; Suthers, B.R. The swamping catalyst effect. V. The halogenation of aromatic acid derivatives. J. Org. Chem. 1963, 28, 3147–3149. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).