Model-Free Identification of Heat Exchanger Dynamics Using Convolutional Neural Networks

Abstract

Heat exchangers are widely used process equipment in industrial sectors, making the study of their temperature dynamics particularly appealing due to the nonlinearities involved. Model-free approaches enable the use of input and output data to generate specific and accurate estimations for each proposed system. In this work, a model-free identification strategy is proposed using a convolutional neural network to estimate the system’s behavior. Notably, the model does not rely on direct temperature measurements; instead, temperature is inferred from other system signals such as reference, flow, and control inputs. This data-driven approach offers greater specificity and adaptability, often outperforming manufacturer-provided coefficients whose performance may vary from design expectations. The results yielded an $R^2$ index of 0.9951 under nominal conditions and 0.9936 when the system was subjected to disturbances.

1. Introduction

In primary and transformation industries such as oil, gas, mining, power generation, and pharmaceuticals, among others, there are various subprocesses where heat transfer equipment is used to provide and remove heat from process streams. These devices are known as heat exchangers, with the shell and tube type being one of the most commonly used in process plants [1]. Their importance lies in the fact that heat exchangers are crucial for the transformation of raw materials through responsible and efficient energy use, as well as offering advantages in resource utilization and economic costs. However, thermal and mechanical design is often complex, despite the apparent simplicity of their physical structure. The actual operation of these devices often deviates from their design due to both internal and external uncertainty and variability [2]. Some key factors contributing to this deviation include the following: variations in flow rate and temperature of the streams, changes in stream composition, imprecise correlations for heat transfer, and pressure drop, among others. As a result of these deviations, the variability associated with the input variables and uncertainty in the internal parameters arises, causing the performance of the equipment to fluctuate, which can even become a risk factor for the process plant [3,4]. From the perspective of Automatic Control, this represents a significant challenge due to the large number of external and internal factors involved in capturing the dynamics of these systems. Although it is possible to mathematically model these devices to obtain a theoretical expression of their behavior, the literature clearly indicates that there are notable discrepancies between theoretical predictions and practical performance. Therefore, to contribute to the improvement of equipment performance from the field of Automatic Control, the following proposal can be considered: Parametric identification is ruled out because of the high number of parameters involved in a heat exchanger, the strong nonlinearity reported in the existing literature, and the presence of unmodeled dynamics. Instead, a recursive non-parametric identification approach appears to be more suitable for this type of system. Since it does not rely on a predefined mathematical structure that forces the system to resemble something known, it allows for greater flexibility and adaptability, which is a key advantage of this kind of methodology.

For Control Theory to have a significant impact on industrial production systems, it is important that some research efforts focus on the pursuit of knowledge in real-world problems. From this perspective, understanding the dynamics of a system becomes essential, since the main factor of interest concerning system modeling is its practical use and utility for the personnel in charge. Some advantages of this include the ability to perform plant testing during the design stage, the possibility of using the model for operator training, and the opportunity to experiment via simulation with hardware improvements or control system enhancements before final approval. The use of knowledge to construct a mathematical model requires making assumptions based on principles of physics and chemistry. From the implications derived from such studies, it is possible to obtain a set of ordinary or partial differential equations. This leads to the development of a theoretical mathematical model with a defined structure and parameters, which in most cases is difficult to solve. However, there are ways to avoid the complications of a theoretical model, and one of them is through experimental analysis using identification methods, which result in a mathematical model derived from the measurement of the input and output of the system [5]. It is important to emphasize that although theoretical mathematical models are elegant, they involve significant effort and often face practical challenges in industrial applications, such as: they tend to be complex even for simple systems and can be time-consuming to develop; theoretical coefficients are not exact, as system parameters tend to change over time due to usage; there are unmodeled dynamics that are omitted, making the mathematical model incomplete, among other issues. According to [6], Figure 1 shows a way to classify systems.

Figure 1. Classification of mathematical model types according to their method of derivation [6].

White box models allow for both the mathematical structure and parameters of the system to be known. Grey-box models have a known mathematical structure but unknown parameters. Meanwhile, black box models lack both a defined mathematical structure and known parameters. At first glance, white box models may seem preferable, as their mathematical formulation has a physical meaning and can be interpreted. However, in an industrial environment, this is often impractical because of the large number of coupled systems required to produce a product. Grey-box models offer more flexibility, since parameter identification can be performed by measuring the input and output of the system [7]. Nevertheless, this approach only works effectively when the assumed mathematical structure adequately reflects the production system. Otherwise, it forces the system to behave like something it is not, leading to discrepancies between the real-world behavior and the approximated model. Black box models and non-parametric identification, on the other hand, do not rely on predefined structures or parameters [8]. Although the resulting model lacks physical interpretation, it can provide a closer approximation to reality, as it is tailored specifically to each system based on its input–output behavior. It is important to note that these classifications are not absolute rules. There are cases where exact models and parameters can be determined, such as in industrial robotics. What truly matters is that individuals learn to identify the type of system they are dealing with and determine the most appropriate modeling approach to address the problem effectively.

Several efforts aimed at uncovering the dynamic behavior of heat exchanger systems are outlined in the following. In [9], a non-parametric modeling approach is presented for a heat exchanger, intended for testing a fuzzy logic-based control strategy. Meanwhile, ref. [10] describes a model-based, step-by-step methodology to predict dynamic pressure profiles during tube rupture events in liquid–liquid, vapor–liquid, and flashing liquid–liquid systems. In [11], system identification is performed using experimental data, followed by the proposal of a cascade-type control strategy in simulation. Furthermore, ref. [12] presents a system identification approach based on input–output measurements for a linear system. Similarly, ref. [13] employs nonlinear modeling techniques, including Nonlinear ARX, Box–Jenkins, and Output-Error models, derived from collected data. In [14], a parametric system identification procedure is developed to obtain a single-input single-output, linear time-invariant, time-delay model of a liquid–liquid heat exchanger system. These examples reflect the broad interest across disciplines in the challenge of accurately capturing the dynamic behavior of heat exchangers.

The use of different types of neural network algorithms has gained significant relevance in recent years due to advances in information processing [15]. Among the most commonly used algorithms is the multilayer neural network (MLP). In biodiesel production, in [16] a MLP is proposed to predict the biodiesel fuel ratio, engine load, air consumption, and fuel flow rate data, comparing it with other neural models such as the adaptive neuro-fuzzy interference system (ANFIS) and the radial basis function network (RBFN). In terms of heat exchangers, machine learning models have come to improve some activities related to them, such as in [17] where four machine learning models were used as a prediction method of the fouling factor to schedule cleaning cycles. Also in [18], an LSTM model was implemented to monitor the fouling layer in the heat exchanger plate. In the case of compact heat exchangers designs, an SVM and MLP were used in [19] to estimate some parameters of these designs such as outlet temperatures, heat transfer rate, etc. In [20], a similar estimation of the heat transfer rate was estimated by means of an MLP for helically coiled tube heat exchangers. Some other examples can be found in [21].

CNN is also a very common neural model algorithm, used in many areas, such as estimation of variables in industrial processes, as mentioned in [22], or in image classification for the detection of faulty parts in manufacturing processes as presented in [23]. This neural models, like many others, can be classified as a black box model that only depends on input and output data from the system; no more knowledge from the system is required. One of the main applications of CNN is still in image classification for various purposes, such as for the detection of anomalies in the manufacturing of cable adhesive as presented in [24]. One more application of CNNs is to use them in time series prediction by proposing a new architecture as in [25], where a CNN combined with an auto-encoder generates better performance using MSE over state-of-the-art methods for one-step prediction using data sets for this matter. Also, in [26], the use of CNN in the prediction of oil spill areas in submarine pipelines is considered, where different neural network models are compared using performance metrics to perform an adequate analysis of the results, along with various training techniques for the models used. In dynamic system identification CNN has some recent applications, such as the one presented in [27] where a CNN model and an LSTM are compared using three different examples. And in [28] a convolutional recurrent network is used to model nonlinear dynamics in a heat exchanger.

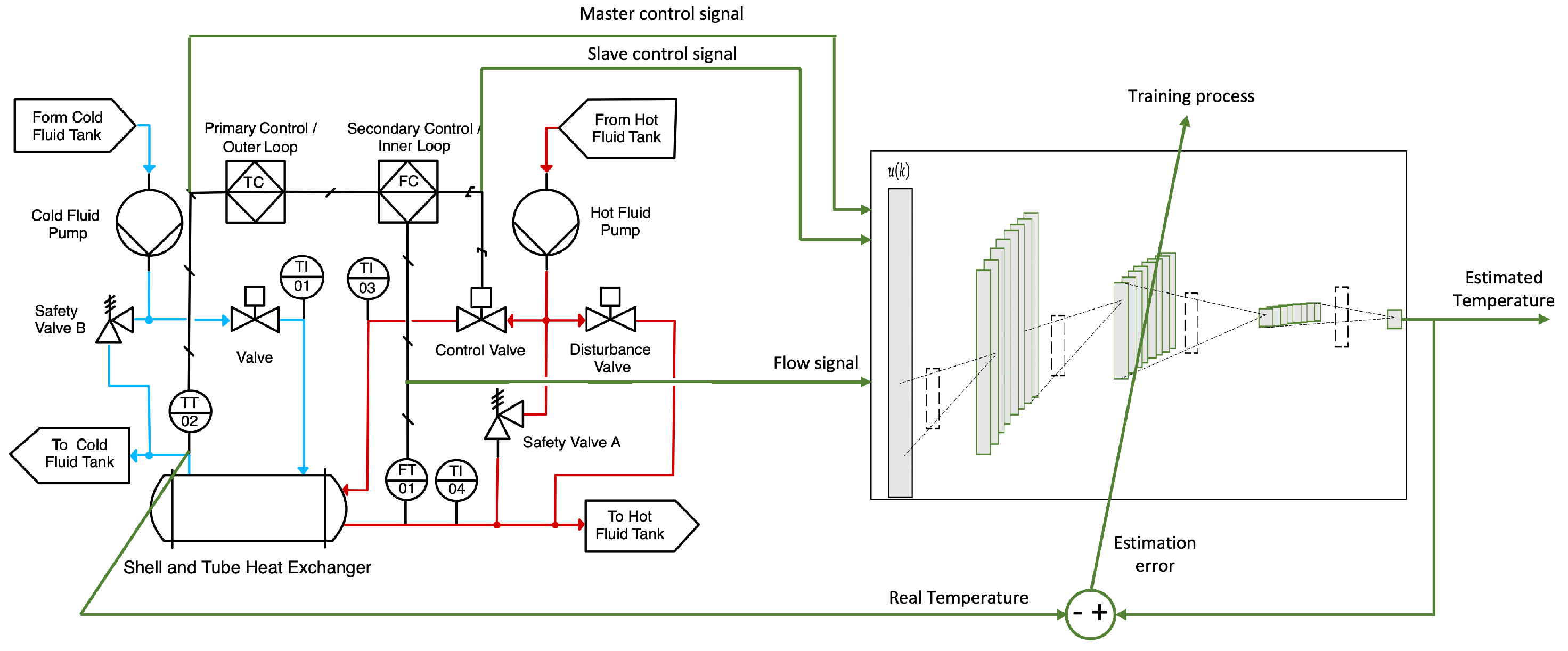
The main contribution of this work is the proposal of an estimation method for the temperature in a heat exchanger, using a convolutional neural network with a new architecture that only uses convolutional layers without the need of a fully connected layer; this is applied in the control of the temperature of the exchanger as an estimator of the variable temperature used in the closed loop of the system, also involving information of the flow variable. This methodology is used in two cases of study in which there are no output disturbances and in which there are output disturbances. In both cases, the CNN estimate is very accurate regarding the system dynamics of the heating section; this is verified using performance indexes for this matter. Moreover, a comparison with a MLP is shown, where both models estimate the temperature but using noisy data, which is a very common issue in industrial environments.

2. Materials and Methods

2.1. Case of Study

According to the experimental system [11], Figure 2 shows a control system based on the cascade control strategy, where the main function is to maintain the temperature in the shell and tube heat exchanger. To achieve this, the system is composed of two pumps responsible for recirculating a hot fluid and a cold fluid, respectively. Safety valves are included in case of overpressure in the pipeline. In addition, primary measuring instruments are installed, including temperature indicators, a temperature transmitter with an analog voltage signal, and a flow transmitter that also has an analog voltage signal. The system includes a control valve and a disturbance valve located at the pump discharge in the hot fluid pipeline. The cold fluid pipeline only includes a valve for system alignment.

Figure 2. Heat exchanger taken as a case study [11].

The operation of the system focuses on a cascade-type control system, where two nested control loops are present. The outer control loop is known as the primary or leader control loop, and the inner control loop is known as the secondary or follower control loop. In this control strategy, it is necessary for the controlled variable (leader loop) to have slower dynamics compared to the manipulated variable (follower loop). For the case study considered in this work, this condition is met by having temperature as the controlled variable and flow as the manipulated variable. The control philosophy is based on the idea that once a Set-Point achievable by the system is selected and compared with the temperature acquired directly by the temperature transmitter installed in the shell and tube heat exchanger, the error signal of the leader control loop is obtained. This signal is then used by the primary controller, which in most cases according to the literature and successful cases reported in the industry, is a PID/PI controller. This signal functions as a Set-Point for the follower control loop, where it is compared with the signal acquired by the flow transmitter installed in the shell and tube heat exchanger. The error signal produced is used by a PI/P controller, and this control signal is sent to the final control element, which in this case is the control valve in the hot fluid pipeline. By reducing or increasing the flow of the hot fluid, it is possible to control the temperature of the fluid in a shell and tube heat exchanger. Figure 3 illustrates the control philosophy described.

Figure 3. Cascade control scheme for a heat exchanger.

2.2. Convolutional Neural Network

A convolutional neural network architecture was developed to act as an estimation method. Consider a system where the temperature signal is the output of it, which can be estimated by the following CNN:

$$\widehat{T}\left(k\right)=\mathrm{CNN}\left(u\left(k\right)\right),$$

(1)

where $u\left(k\right)$ is the vector constructed from the signals from the leader controller, follower controller, reference, and flow signal; each of these variables are used in the same instant that the output signal would be estimated, and the previous one up to their own regression order, each with a specific one. These values are determined by trial and error.

The proposed CNN architecture consists of 4 convolutional layers, one after the other. Each convolutional layer consists of the convolutional operator between the filters in this layer, $F_{\ell }\in {\Re }^4$, and the input of the layer, $y_{\ell -1}$; considering a padding $P=0$ and a stride $S=3$ with this configuration, the output of this each layer is reduced. Mathematically, this operation is defined by the following:

$$x_{\ell }=\mathrm{conv}\left(y_{\ell -1},F_{\ell },P,S\right),$$

(2)

where $x_{\ell }$ is an auxiliary vector. The size of the output is calculated by $\left(S_I-S_F+2P\right)/\left(S+1\right)$, with $S_I$ being the input size and $S_F$ the filters size. After the convolution operator, an activation function is applied to the vector $x_{\ell }$; in this case the ReLU operation has been used, described by (3):

$$y_{\ell }=\mathrm{ReLU}\left(x_{\ell }\right).$$

(3)

The CNN is designed to generate a single value output, so four convolutional layers are used in the architecture considering that eight filters in each layer are used for this matter, and in the output layer, $\ell =4$, there is only one filter that uses as input the output of the previous layer, generating one single output signal, corresponding to the estimation of temperature of the system. This is shown in Figure 4, where each filter in all previous layers only considers one filter from the previous layers, generating in this architecture 8 different ways of acquiring features of the system. The hyper-parameters, number of layers, and filters per layer were chosen to ensure that the output size is 1, given that we estimate a single data point per iteration of the algorithm. By selecting this number of filters for each layer, in addition to the activation function, we can generate a size reduction sufficient for our objective. They were also selected in this way because several tests were performed to ensure that the CNN obtained adequate estimation results. This was achieved using an input with a significant amount of system data. To consider more features of the system, the initial value of the convolutional filters are set randomly which has been proven to have similar results than using a methodology especifically for the initialization of hyper-parameters.

Figure 4. Proposed architecture for CNN.

As mentioned previously, the CNN input considers 4 signals with their respective previous values, all of them adding up to 192 input data. This vector is defined as follows:

$$\begin{array}{cc}u\left(k\right) = [\hfill & u_F\left(k\right)\cdots u_F\left(k-r_F\right)u_{Ref}\left(k\right)\cdots u_{Ref}\left(k-r_{Ref}\right)\hfill \\ \hfill & u_{PIDm}\left(k\right)\cdots u_{PIDm}\left(k-r_{PIDm}\right)u_{PIDs}\left(k\right)\cdots u_{PIDs}\left(k-r_{PIDs}\right)]\hfill \end{array}$$

(4)

where $u_F,r_F,u_{Ref},r_{Ref},u_{PIDm},r_{PIDm},u_{PIDs},r_{PIDs}$ are the signal values and the regression order of the flow, the reference, PID leader, and the PID follower signal, respectively.

One of the main contributions of this paper is that no fully connected layer is used as the output layer; instead, only convolutional layers are used. This is successfully performed by considering the correct amount of hyper-parameters of the CNN such as the number of filters, their size, the padding, and stride and size of the input vector. One more advantage is the inner noise reduction that CNN can do with the processed data. The training process is performed using the backpropagation algorithm; using offline data, this process is described in the next section. The estimation process is defined in Figure 5. Data from the real process are acquired and used as input to the CNN, generating the estimated temperature to be compared with the one obtained from the temperature sensor for the training process.

Figure 5. Estimation process of temperature variable.

2.3. CNN Training

The training consists of updating the values of the filters in the CNN; this is achieved using the backpropagation algorithm (BP), which minimizes a cost function:

$$J={\displaystyle \frac{1}{2}}{e}^2,$$

(5)

where e is defined as the estimation error between the real temperature measure of the system and the CNN output, $e=\widehat{T}-T$. The estimation error has to be propagated using the gradient calculated to each filter in the CNN; then, the update of the numerical values is determined by the delta rule:

$$F_{\ell }\left(k+1\right)=F_{\ell }\left(k\right)-\eta {\displaystyle \frac{\partial J}{\partial F_{\ell }}}$$

(6)

where $\eta$ is the learning rate for the training, which is a numerical value between 0 and 1, defined by the user.

The gradient for the convolutional filters is the following:

$${\displaystyle \frac{\partial J}{\partial F_{\ell }}}=\mathrm{conv}\left(y_{\ell -1},\mathrm{rot}\left({\chi }_{\ell },90\right),P,S\right)$$

(7)

where the function $\mathrm{rot}\left(·,90\right)$ is equivalent to a 90° rotation of the first parameter of the function and ${\chi }_{\ell }$ is the gradient up to the filters in that layer, which is calculated as follows:

$${\chi }_{\ell }={\displaystyle \frac{\partial J}{\partial x_{\ell }}}={\displaystyle \frac{\partial J}{\partial y_{\ell }}}\max \left(y_{\ell }\right)$$

(8)

with the $\max \left(·\right)$ function defined as the opposite of the ReLU operation, this operation passes the gradient in the specific position where the maximum value was obtained by the ReLU operation in the feedforward process, and passes zero values in the rest of the position otherwise. Finally, the propagated error through a convolutional layer can be computed as follows:

$${\displaystyle \frac{\partial J}{\partial y_{\ell -1}}}=\mathrm{conv}\left({\chi }_{\ell },\mathrm{rot}\left(F_{\ell },90\right),P,S\right)$$

(9)

Equations previously described in this section are used in each iteration of the training in order to obtain the best possible values for the convolutional filters; after this training is completed, the testing stage consists of verifying how well the estimation can be achieved with the trained CNN using similar data for this matter.

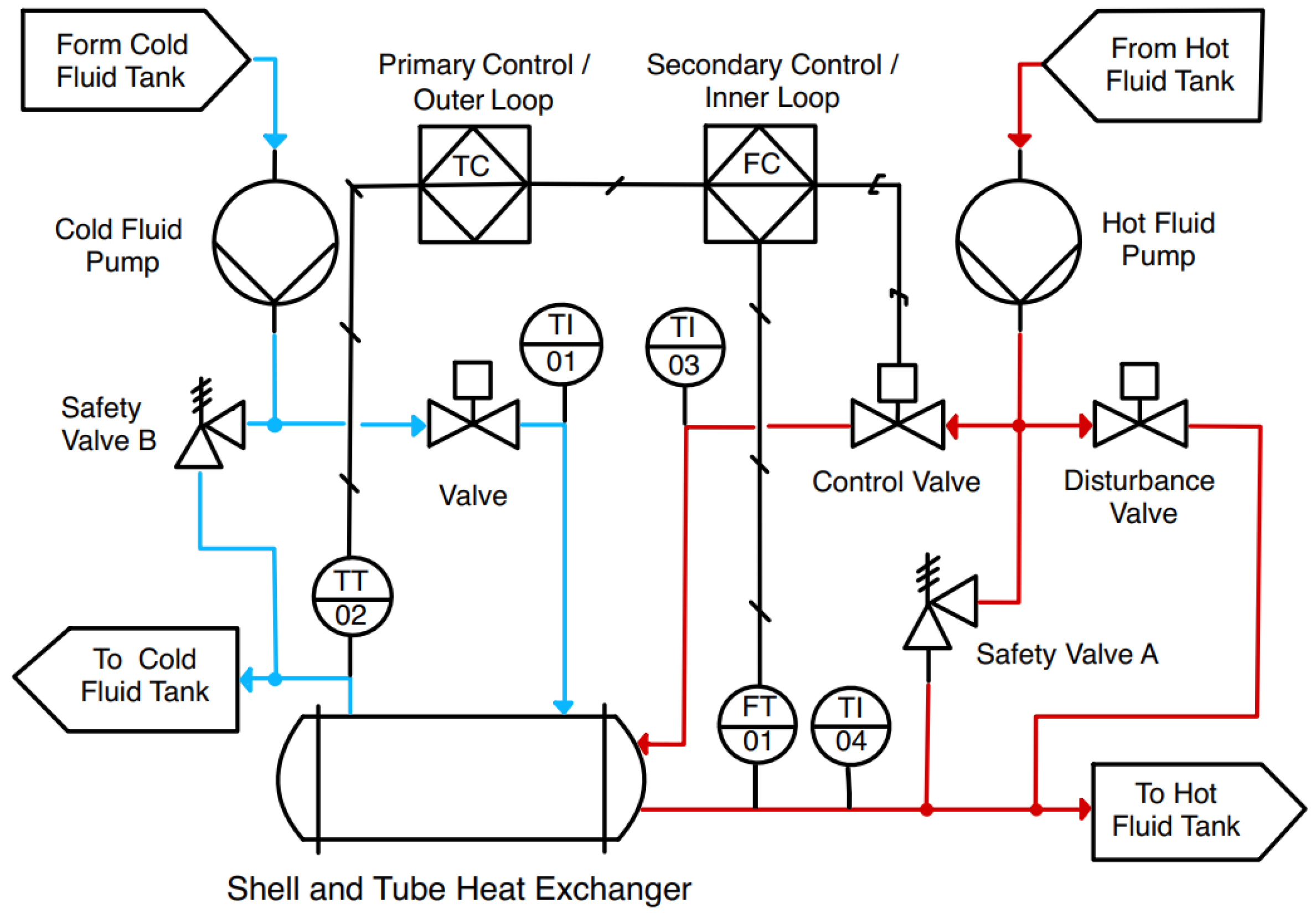
3. Experiments and Results

The experiments were performed in a M3 processor laptop with 16 GB of RAM using the MATLAB 2024b version. As described in Algorithm 1, first the hyper-parameters of the CNN must be defined, then it receives data from the system, such as control signals, references, and flow values, then the CNN computes the estimated temperature to calculate the estimation error for this iteration, and these steps are repeated until the total training data are used. In the training stage, 10,000 data points were used for this matter, which is a very similar signal to the one used for the testing stage, considering five training epochs. No extra processing such as scaling or normalization was required on the data to be used as input to the CNN.

Algorithm 1 Temperature estimation in heat exchanger.

Propose CNN hyper-parameters, $u_F,u_{Ref},u_{PIDm},u_{PIDs},P,S,F_{\ell }$. while $i\le N$ do                                        ▹N -> total of data        Use leader and follower control signal, reference and flow values into $u\left(k\right)$.        Generate $\widehat{T}$ using CNN.        Compute estimation error $e=\widehat{T}-T$.        Update hyper-parameters $F_{\ell }$ using gradient descendant method. end while Realize a testing stage to verify the training process. Compare performance indexes such as MSE and $R^2$. if $MSE\ge Mm$ then                        ▹Mm -> minimum value for acceptance estimation      Repeat previous steps varying CNN hyper-parameters. end if

For the simulation, the input values are as follows: $u_F=5$, $u_{Ref}=1$, $u_{PIDm}=180$, and $u_{PIDs}=6$. The number of filters in convolutional layers is defined as 8, and the size of filters is set at 4. The learning rate is set to 0.7 and five training epochs are needed for this. All these numerical values were obtained by trial and error after performing several simulations with different combinations of input numbers. It was observed that the leader PID signal was the most important for making the estimation; therefore, this signal has the highest number of inputs in the CNN. The first estimation was performed using the ideal system with no disturbances; the simulation results are shown in Figure 6, where the mainly high estimation error is presented when there is a drastic change in the reference.

Figure 6. System identification with no disturbances.

It is important to note that the proposed reference signal is time-varying, as many processes involve thermal treatments of materials and substances to obtain a final product. Such is the case in biodiesel production, where it is necessary to raise the temperature at different operating points. The heat exchanger is responsible for supplying the hot fluid to the reactor through a coil or jacketed system that enables its heating.

Similar simulations were carried out but this time the system output presents disturbance at four different moments and with different amplitudes, one occurring at 2000 s of 4 °C, one more at 5000 s of 7 °C, at 6500 s of 12 °C, and one last one at 9000 s of 3 °C. Estimation results are presented in Figure 7. As in the previous case, the estimation error obtained a high value when the reference changed drastically, but in other moments the CNN behaves the same as the real system.

Figure 7. System identification with output disturbances.

Disturbances in industrial production systems are inevitable, as processes generally do not form part of a fully coupled system. Instead, they interact with an environment where various conditions arise, often driven by external excitation sources, such as the nonlinear behavior of the surrounding medium. It is important to highlight that the identifier proposed in this work, based on the model presented in (4), is capable of delivering accurate estimations of the temperature variable of the heat exchanger, even in the presence of disturbances.

To evaluate the performance of the estimation method, five metrics were used for this matter, Mean Absolute error (MAE), Mean Square Error (MSE), Root Mean Square Error (RMSE), $R^2$, and Root Mean Square Logarithm Error (RMSLE), which are defined by the following equations from (10) to (14).

$$\mathrm{MAE}={\displaystyle \frac{1}{n}}\sum _{i=1}^n\left|T_i-{\widehat{T}}_i\right|$$

(10)

$$\mathrm{MSE}={\displaystyle \frac{1}{n}}\sum _{i=1}^n{\left(T_i-{\widehat{T}}_i\right)}^2$$

(11)

$$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{n}}\sum _{i=1}^n{\left(T_i-{\widehat{T}}_i\right)}^2}$$

(12)

$$R^2=1-{\displaystyle \frac{{\sum }_{i=1}^n{\left(T_i-{\widehat{T}}_i\right)}^2}{{\sum }_{i=1}^n{\left(T_i-\overline{T}\right)}^2}}$$

(13)

where $\overline{T}={\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{T}_i$ is the mean of the real temperature values from the system.

$$\mathrm{RMSLE}=\sqrt{{\displaystyle \frac{1}{n}}\sum _{i=1}^n{\left(log(1+{\widehat{T}}_i)-log(1+T_i)\right)}^2}$$

(14)

From these metrics, Figure 8 shows the behavior of the system comparing the pairs of data, estimation with the real value; for perfect fitting, each pair should be above the identity line. As is shown, at the beginning several points are outliers, this is due to the initialization of the CNN inputs, which requires around 200 data to be completed; this is only if considering there are no data to work with. After this point, there are around 10 points out of the 20% error lines in this estimation, which represents 0.1% of data used.

Figure 8. Comparison between temperature system and CNN with no disturbances.

For the simulation with disturbances, Figure 9 shows the behavior of the data. Similarly to the previous case, at the beginning of the estimation, outlier data are generated due to the CNN input; later, few data, of less than 10 points, are out of the 20% range of estimation error, occurring when the reference changes.

Figure 9. Comparison between temperature system and CNN with output disturbances.

The comparison of all metrics employee in this work for both cases is shown in Table 1.

Table 1. Performance indexes.

	MAE (°C)	MSE (°C2)	RMSE (°C)	${\mathit{R}}^2$	RMSLE
No disturbance	0.0121	0.0068	0.0825	0.9951	0.0754
Disturbance	0.0253	0.0088	0.0938	0.9936	0.0762

3.1. Noisy Data

One of the main challenges in applying control or system identification algorithms in industrial environment is dealing with noisy signals: sensor failures, connection cable failures, external agents, etc. To overcome this problem, it is important to perform adequate signal processing to ensure a better performance of the controller or the system in general. One advantage of CNN over some other estimation algorithms is that it can internally reduce signal noise. In this regard, a comparison was made between the proposed CNN and a multilayer perceptron, using the aforementioned metrics to assess the efficiency of the proposed algorithm. A two-layer MLP is designed, with 100 neurons in the hidden layer and the same amount of input data. This approach is implemented because a significant amount of system information is also required for system estimation. It is trained using the backpropagation algorithm, using a learning rate of 0.5. Five training epochs are used, each with 10,000 training data points, which are different for the testing stage. Random numbers representing temperature variations within a range of $\pm 2 °\mathrm{C}$ are used to generate noise in the simulation; this is performed for both training and testing purposes.

Table 2 shown the comparison between these two algorithms using the proposed metrics, where the numerical values are better for CNN in each of the metrics.

Table 2. Noisy data comparison.

	MAE (°C)	MSE (°C2)	RMSE (°C)	${\mathit{R}}^2$	RMSLE
CNN	0.0159	0.0069	0.0829	0.9951	0.0750
MLP	0.0695	0.0130	0.1141	0.9907	0.0931

In Figure 10, an MLP and CNN comparison is shown. The MLP signal could not reduce the noise in the output; it has more noise in the output than the real system, while CNN reduces almost all the noise in the output, proving the efficiency of the proposed algorithm.

Figure 10. Comparison between MLP and CNN with noisy data.

3.2. Discussion

As presented in Table 1, the methodology proposed in this paper obtained very similar results in each metric. Considering $R^2$, the values obtained in both cases are very close to 1, which is what is sought when applying this metric. Considering metrics such as MSE or RMSE, both penalize large estimation errors generated through the simulation, seeking results close to zero, as in this case. The RMSLE metric is used to eliminate the effect of outliers that arises at the beginning of the estimation, for which results close to zero are also sought. Although it is possible to observe a noticeable deviation in the temperature estimation when a reference change occurs, even if only for a short period, this may be attributed to issues related to the hyper-parameters of the CNN. In general, learning-based approaches often face challenges in hyper-parameter selection. It would be valuable in future work to incorporate a heuristic-based search algorithm to mitigate these effects, especially considering that transients can significantly impact controllers when dealing with faster system variables.

The nonlinear behavior reported and observed in heat exchangers poses a challenge not only for design but also for the estimation of their dynamics and subsequent closed-loop control. The results obtained in this work will enable future studies to explore certain types of model-free controllers, which tend to be more flexible than model-based approaches. Noisy data can be reduced using a CNN in real-world environments, such as industrial. The comparison with an MLP shows that CNN can drastically reduce the output noise in the data without the need of an extra data processing.

4. Conclusions

This work addresses the non-parametric identification of the temperature variable in a heat exchanger using a convolutional neural network, which relies on reference, flow, and control signals as input data. This aspect is particularly important to highlight, as the model does not rely on direct temperature measurements. Instead, temperature is estimated from other available system signals, reinforcing the value of data driven approaches that infer key variables from indirect observations. The result is a black box model intended for use as a model-free approach. Among the advantages of this methodology are its flexibility and adaptability, which are particularly valuable in real-world applications. The results yielded an $R^2$ index of 0.9951 under nominal conditions and 0.9936 when the system was subjected to disturbances. One limitation of our proposal is that it cannot be generalized for all systems, since it requires some knowledge of the system to consider a proper input to the model. Also, the amount of input data for this system was somewhat high given that almost 200 iterations are required for CNN to adequately identify the system. Finally, the hyper-parameter selection remains a challenge for this type of algorithm, as the accuracy of the identification largely depends on choosing appropriate values and there is no previous defined methodology to select them. Nevertheless, this approach enables the development of more specific models by extracting information directly from the live process, which is often preferable to relying on manufacturer-provided coefficients especially considering that their stated performance may differ from actual behavior due to design variations. The study of complex and large-scale systems in the industrial sector can lead to more efficient resource utilization, with not only economic benefits but also positive environmental impacts due to improved process efficiency.