A Hybrid Estimation Model for Graphite Nodularity of Ductile Cast Iron Based on Multi-Source Feature Extraction
Abstract
1. Introduction
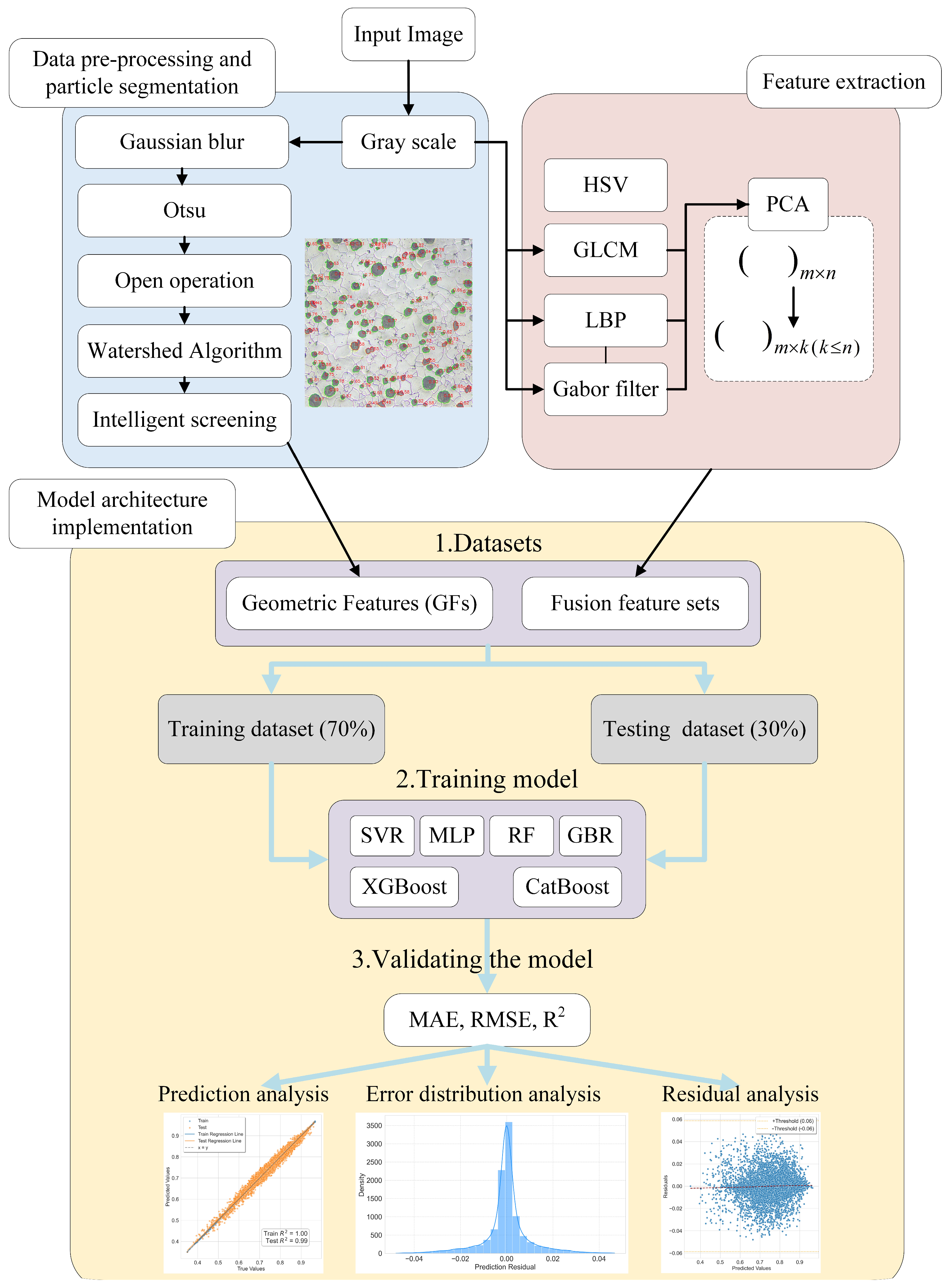
2. Materials and Methods
2.1. Image Pre-Processing
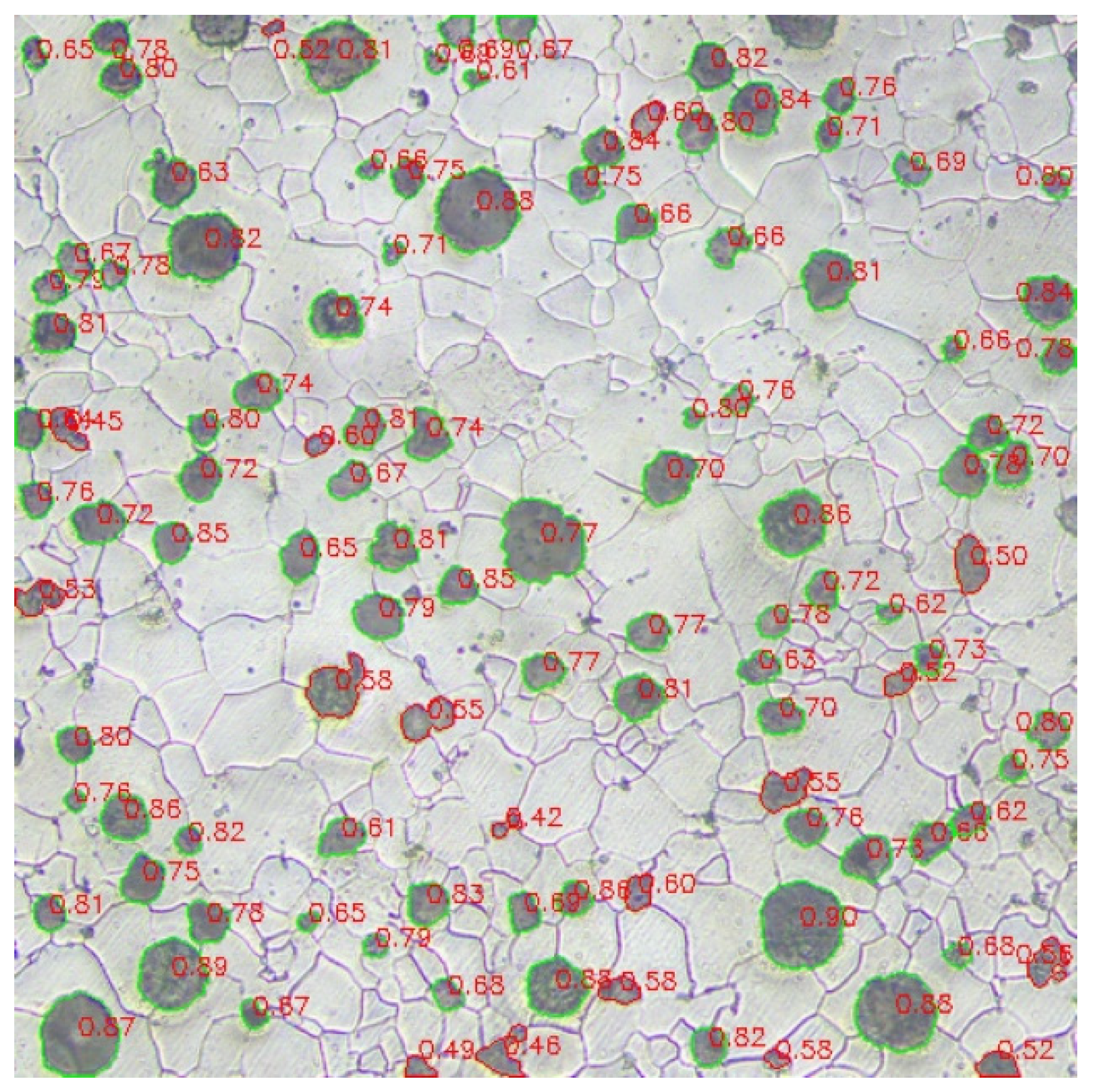
2.2. Graphite Particle Extraction
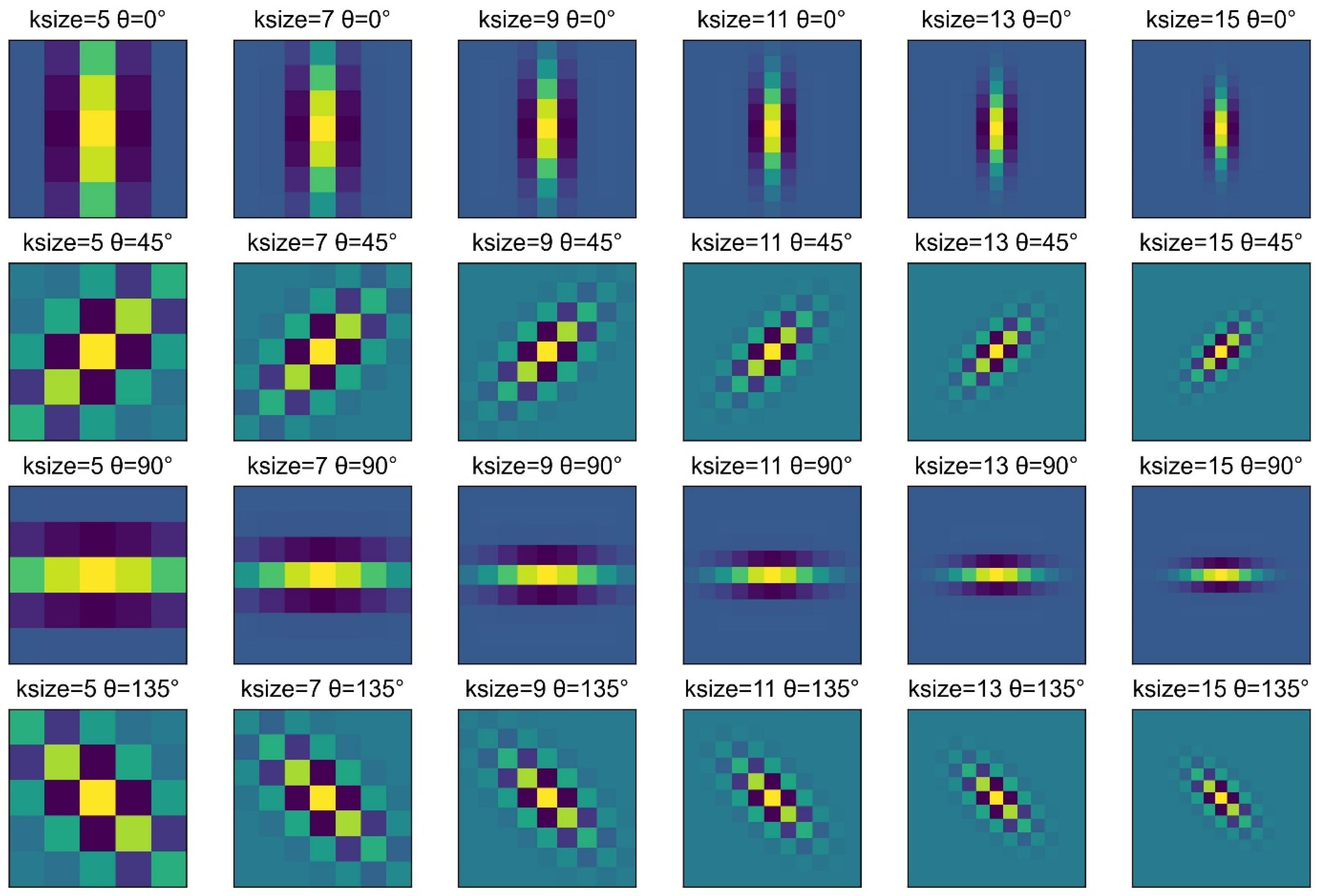
2.3. Multi-Feature Extraction Methods
2.4. CatBoost Model
3. Results
3.1. Particles Division Results
3.2. PCA Results
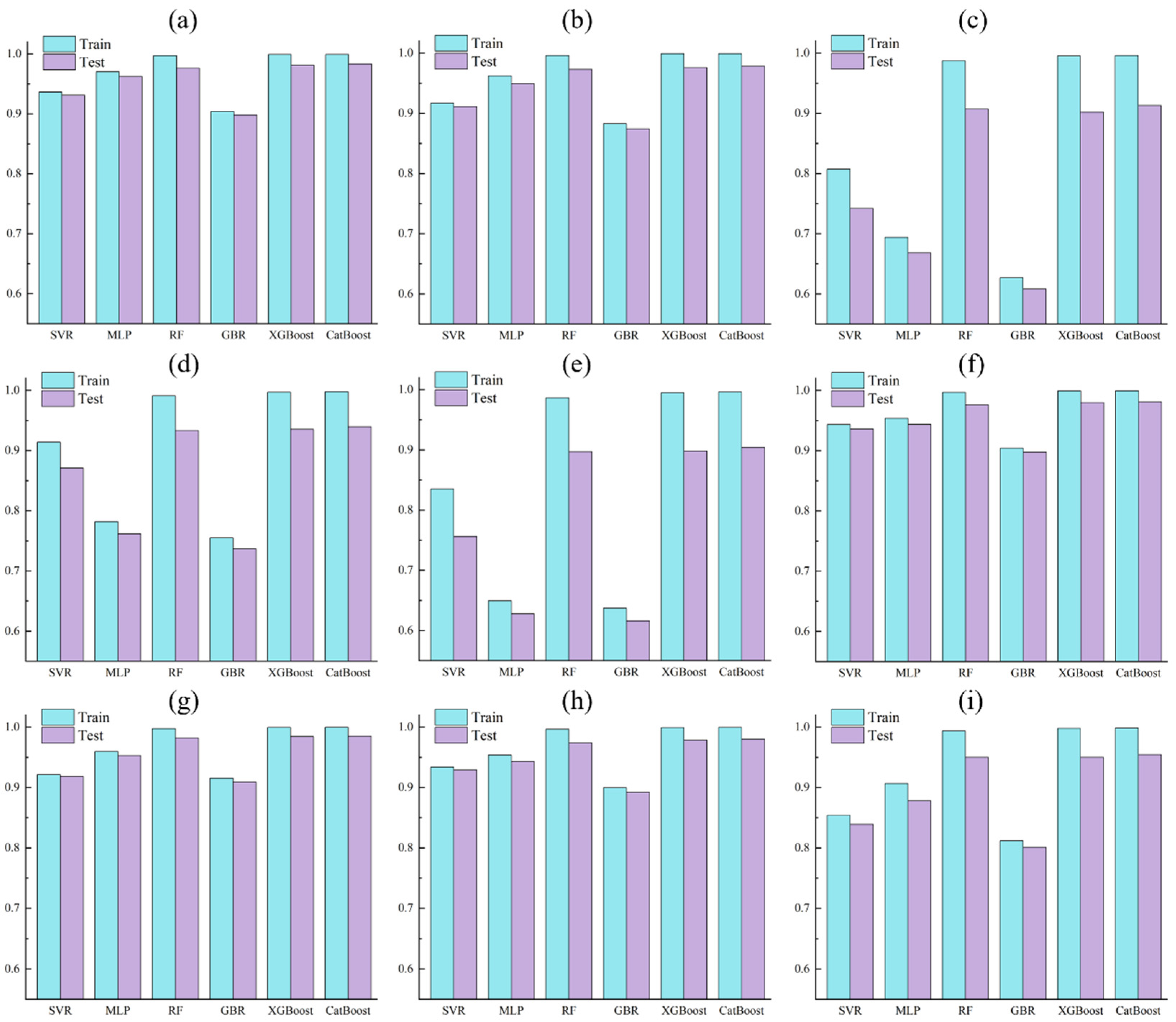
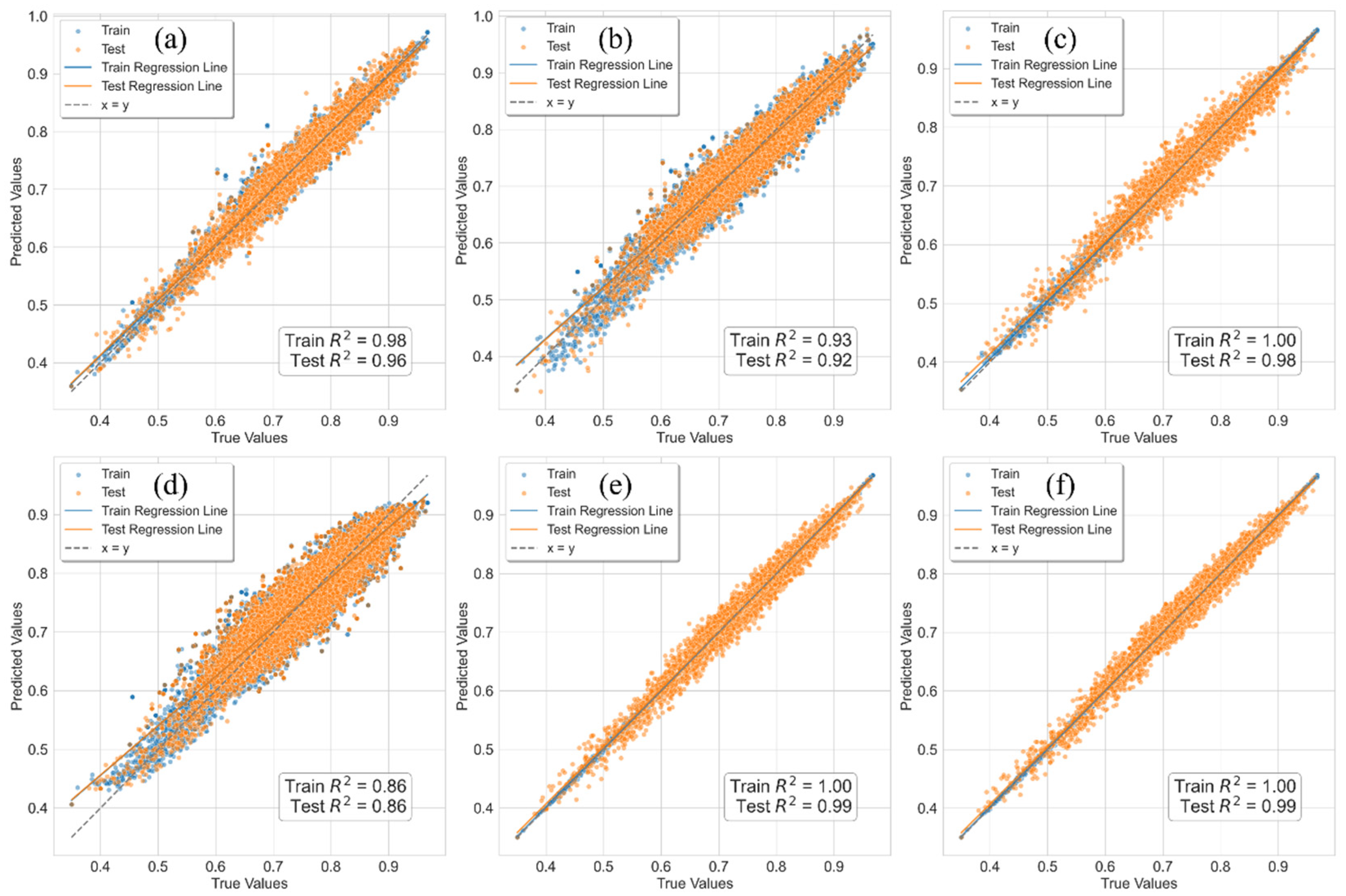
3.3. Comparative Analysis of GFs Estimation Results
3.4. Comparative Analysis of GFs Model Estimation Results
4. Conclusions
- (1)
- The improved watershed segmentation method effectively addresses the over-segmentation issues of traditional algorithms when dealing with complex graphite morphologies. Combined with GFs extracted by the intelligent screening algorithm, it can accurately characterize the geometric parameters of graphite particles.
- (2)
- The multimodal feature fusion strategy significantly enhances feature representation capability; however, the CatBoost model trained solely on the fused features exhibits overfitting when estimating geometric features, resulting in considerable errors between the training and test sets.
- (3)
- By reintegrating the GFs back into the fused feature set, the model achieves a feature self-enhancement mechanism: the geometric features serve as prior knowledge to guide the model’s focus on intrinsic morphological patterns, completely eliminating CatBoost’s overfitting problem and significantly improving both estimation accuracy (R2 ≈ 0.98) and robustness.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, J.H.; Yan, J.S.; Zhao, X.B.; Fu, B.G.; Xue, H.T.; Zhang, G.X.; Yang, P.H. Precipitation and evolution of nodular graphite during solidification process of ductile iron. China Foundry 2020, 17, 260–271. [Google Scholar] [CrossRef]
- Hsu, C.H.; Lin, K.T. A study on microstructure and toughness of copper alloyed and austempered ductile irons. Mater. Sci. Eng. A 2011, 528, 5706–5712. [Google Scholar] [CrossRef]
- Ricotta, M. Simple expressions to estimate the Manson–Coffin curves of ductile cast irons. Int. J. Fatigue 2015, 78, 38–45. [Google Scholar] [CrossRef]
- Wróbel, T.; Studnicki, A.; Stawarz, M.; Baron, C.; Jezierski, J.; Bartocha, D.; Dojka, R.; Opiela, J.; Lisiecki, A. Improving the Abrasion Resistance of Nodular Cast Iron Castings by Remelting Their Surfaces by Laser Beam. Materials 2024, 17, 2095. [Google Scholar] [CrossRef] [PubMed]
- Katuku, K. Regime features of austempered ductile iron cutting. J. Manuf. Process. 2022, 83, 374–386. [Google Scholar] [CrossRef]
- EN ISO 945-1; Microstructure of Cast Irons—Part 1: Graphite Classification by Visual Analysis. ISO: Geneva, Switzerland, 2017.
- ASTM A247–16a; Standard Test Method for Evaluating the Microstructure of Graphite in Iron Castings. ASTM International: West Conshohocken, PA, USA, 2016. Available online: www.astm.org (accessed on 1 April 2016).
- SAC/TC 54; Metallographic Examination of Ductile Iron: GB/T 9441-2021. Standards Press of China: Beijing, China, 2021.
- Anca, D.-E.; Stan, I.; Riposan, I.; Stan, S. Graphite Compactness Degree and Nodularity of High-Si Ductile Iron Produced via Permanent Mold versus Sand Mold Casting. Materials 2022, 15, 2712. [Google Scholar] [CrossRef]
- Germain, L.; Sertucha, J.; Hazotte, A.; Lacaze, J. Classification of graphite particles in metallographic images of cast irons–Quantitative image analysis versus deep learning. Mater. Charact. 2024, 217, 114333. [Google Scholar] [CrossRef]
- Song, L.; Zhang, H.; Zhang, J.; Guo, H. Prediction of heavy-section ductile iron fracture toughness based on machine learning. Sci. Rep. 2024, 14, 4681. [Google Scholar] [CrossRef]
- Pedro, D.; Dommarco, R. Rolling contact fatigue resistance of Carbidic Austempered Ductile Iron (CADI). Wear 2019, 418–419, 94–101. [Google Scholar] [CrossRef]
- Zhang, H.; Sun, S.; Liu, C.; Zhu, Y.; Liu, Q.; Wang, Y.; Wang, J.; Wang, M. Effect of Annealing Process on Properties of Ferritic Ductile Iron for Subway. Sci. Adv. Mater. 2018, 10, 1658–1663. [Google Scholar] [CrossRef]
- Wu, W.-H.; Lee, J.-C.; Wang, Y.-M. A Study of Defect Detection Techniques for Metallographic Images. Sensors 2020, 20, 5593. [Google Scholar] [CrossRef]
- Friess, J.; Sonntag, U.; Steller, I.; Bührig-Polaczek, A. From Individual Graphite Assignment to an Improved Digital Image Analysis of Ductile Iron. Int. J. Met. 2020, 14, 1090–1104. [Google Scholar] [CrossRef]
- Tchórz, A.; Korona, K.; Krzak, I.; Bitka, A.; Książek, M.; Jaśkowiec, K.; Małysza, M.; Głowacki, M.; Wilk-Kołodziejczyk, D. Development of a CT Image Analysis Model for Cast Iron Products Based on Artificial Intelligence Methods. Materials 2022, 15, 8254. [Google Scholar] [CrossRef] [PubMed]
- Mucllari, E.; Cao, Y.; Ye, Q.; Zhang, Y. Modeling imaged welding process dynamic behaviors using Generative Adversarial Network (GAN) for a new foundation to monitor weld penetration using deep learning. J. Manuf. Process. 2024, 124, 187–195. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, Y.; Pan, L. A feature-based physics-constrained active dictionary learning scheme for image-based additive manufacturing process monitoring. J. Manuf. Process. 2023, 103, 261–273. [Google Scholar] [CrossRef]
- Rossi, A.; Moretti, M.; Senin, N. Layer inspection via digital imaging and machine learning for in-process monitoring of fused filament fabrication. J. Manuf. Process. 2021, 70, 438–451. [Google Scholar] [CrossRef]
- Jiang, R.; Xiao, R.; Chen, S. Prediction of penetration based on infrared thermal and visual images during pulsed GTAW process. J. Manuf. Process. 2021, 69, 261–272. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, L.; Liu, Y.; Wang, R.; Li, D. Laser spheroidization combined with coaxial powder feeding: A novel strategy for preparing spherical powders for additive manufacturing. J. Manuf. Process. 2025, 137, 82–99. [Google Scholar] [CrossRef]
- Ruelas-Santoyo, E.A.; Ríos-Lira, A.J.; Pantoja-Pacheco, Y.V.; Jiménez-García, J.A.; Hernández-González, S.; Cruz-Domínguez, O. Recognition of Intergranular Corrosion in AISI 304 Stainless Steel by Integrating a Multilayer Perceptron Artificial Neural Network and Metallographic Image Processing. Appl. Sci. 2024, 14, 5077. [Google Scholar] [CrossRef]
- Naik, D.L.; Kiran, R. Identification and characterization of fracture in metals using machine learning based texture recognition algorithms. Eng. Fract. Mech. 2019, 219, 106618. [Google Scholar] [CrossRef]
- Jing, X.-Y.; Chang, H.; Li, S.; Yao, Y.-F.; Liu, Q.; Bian, L.-S.; Man, J.-Y.; Wang, C. Face recognition based on a Gabor-2DFisherface approach with selecting 2D Gabor principal components and discriminant vectors. In Proceedings of the 2009 Third International Conference on Genetic and Evolutionary Computing, Guilin, China, 14–17 October 2009; IEEE: New York, NY, USA, 2009; pp. 565–568. [Google Scholar] [CrossRef]
- Azimi, S.M.; Britz, D.; Engstler, M.; Fritz, M.; Mücklich, F. Advanced Steel Microstructural Classification by Deep Learning Methods. Sci. Rep. 2018, 8, 2128. [Google Scholar] [CrossRef]
- Velichko, A. Quantitative 3D Characterization of Graphite Morphologies in Cast Iron Using FIB Microstructure Tomography. Doctoral Thesis, Saarland University, Saarbrücken, Germany, 2008. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Durmaz, A.R.; Müller, M.; Lei, B.; Thomas, A.; Britz, D.; Holm, E.A.; Eberl, C.; Mücklich, F.; Gumbsch, P. A deep learning approach for complex microstructure inference. Nat. Commun. 2021, 12, 6272. [Google Scholar] [CrossRef] [PubMed]
- Thomas, A.; Durmaz, A.R.; Alam, M.; Gumbsch, P.; Sack, H.; Eberl, C. Author Correction: Materials fatigue prediction using graph neural networks on microstructure representations. Sci. Rep. 2023, 13, 13598. [Google Scholar] [CrossRef] [PubMed]
- Johannes, R.; Johannes, T.; Sebastian, M. Deep learning based initial crack size measurements utilizing macroscale fracture surface segmentation. Eng. Fract. Mech. 2023, 293, 109686. [Google Scholar] [CrossRef]
- Wilk-Kołodziejczyk, D.; Nowotny, A.; Krzak, I.; Tchórz, A.; Jaśkowiec, K.; Małysza, M.; Bitka, A.; Głowacki, M.; Książek, M.; Marcjan, Ł. Development of a model for detection and analysis of inclusions in tomographic images of iron castings using decision trees. Sci. Rep. 2025, 15, 1880. [Google Scholar] [CrossRef]
- Schmies, L.; Botsch, B.; Le, Q.-H.; Yarysh, A.; Sonntag, U.; Hemmleb, M.; Bettge, D. Classification of fracture characteristics and fracture mechanisms using deep learning and topography data. Pract. Metallogr. 2023, 60, 76–92. [Google Scholar] [CrossRef]
- Schmies, L.; Hemmleb, M.; Bettge, D. Relevant input data for crack feature segmentation with deep learning on SEM imagery and topography data. Eng. Fail. Anal. 2024, 156, 107814. [Google Scholar] [CrossRef]
- Bárcena, M.; Iglesias, L.L.; Ferreño, D.; Carrascal, I. Classification of Cast Iron Alloys through Convolutional Neural Networks Applied on Optical Microscopy Images. Steel Res. Int. 2024, 95, 2400120. [Google Scholar] [CrossRef]
- Zheng, X.; Zhang, X.; Chen, T.; Watanabe, I. Deep learning in mechanical metamaterials: From prediction and generation to inverse design. Adv. Mater. 2023, 35, 2302530. [Google Scholar] [CrossRef]
- Choudhary, K.; DeCost, B.; Chen, C.; Jain, A.; Tavazza, F.; Cohn, R.; Park, C.W.; Choudhary, A.; Agrawal, A.; Billinge, S.J.L.; et al. Recent advances and applications of deep learning methods in materials science. Npj Comput. Mater. 2022, 8, 59. [Google Scholar] [CrossRef]
- Ying, X. An Overview of Overfitting and its Solutions. J. Phys. Conf. Ser. 2019, 1168, 022022. [Google Scholar] [CrossRef]
- Kanopoulos, N.; Vasanthavada, N.; Baker, R.L. Design of an image edge detection filter using the Sobel operator. IEEE J. Solid-State Circuits 1988, 23, 358–367. [Google Scholar] [CrossRef]
- Hancock, J.T.; Khoshgoftaar, T.M. CatBoost for big data: An interdisciplinary review. J. Big Data 2020, 7, 94. [Google Scholar] [CrossRef]
- Prasshanth, C.V.; Sugumaran, V. Tire wear monitoring using feature fusion and CatBoost classifier. Artif. Intell. Rev. 2024, 57, 337. [Google Scholar] [CrossRef]


| Features Name | Description | Physical Meaning |
|---|---|---|
| total_particles | Total number of valid graphite particles detected in the image | Reflects the overall particle count available for statistical analysis |
| qualified_particles | Total number of graphite particles classified as spheroidal (roundness > 0.6) | Indicates the number of particles contributing positively to graphite nodularity |
| Graphite_nodularity | Ratio of qualified particles to total particles | Quantitative index of graphite nodularity degree and microstructural quality |
| avg_roundness | Mean roundness of all particles | Reflects the average shape tendency of particles relative to a perfect circle |
| avg_ratio | Mean short-to-long axis ratio of fitted ellipses | Describes the average elongation of particles; values closer to 1 indicate better roundness |
| avg_feret | Mean Feret diameter, defined as the distance between two parallel tangents on opposite sides of a particle | Provides an orientation-independent measure of particle size |
| angaria | Mean projected area of all particles | Represents the average size of graphite particles |
| avg_perimeter | Mean perimeter length of all particles | Indicates boundary complexity; larger values may correspond to irregular shapes |
| avg_distance | Mean nearest centroid distance between particles | Reflects spatial distribution and dispersion of particles in the microstructure |
| SVR | MLP | RF | GBR | XGBoost | CatBoost | ||
|---|---|---|---|---|---|---|---|
| total_particles | MAE: | 5.1930 | 3.8797 | 2.0946 | 6.3771 | 1.9682 | 1.8469 |
| RMSE: | 6.7529 | 4.9847 | 3.9970 | 8.2041 | 3.5164 | 3.3572 | |
| R2: | 0.9308 | 0.9623 | 0.9758 | 0.8979 | 0.9812 | 0.9829 | |
| qualified _particles | MAE: | 5.3382 | 4.0057 | 2.0623 | 6.3698 | 2.0717 | 1.9598 |
| RMSE: | 6.9026 | 5.1884 | 3.8095 | 8.1798 | 3.5760 | 3.4389 | |
| R2: | 0.9105 | 0.9494 | 0.9727 | 0.8743 | 0.9760 | 0.9778 | |
| graphite_nodularity | MAE: | 0.0328 | 0.0396 | 0.0153 | 0.0434 | 0.0158 | 0.0147 |
| RMSE: | 0.0445 | 0.0505 | 0.0268 | 0.0548 | 0.0274 | 0.0258 | |
| R2: | 0.7415 | 0.6680 | 0.9067 | 0.6078 | 0.9024 | 0.9131 | |
| avg_roundness | MAE: | 0.0096 | 0.0130 | 0.0048 | 0.0136 | 0.0049 | 0.0046 |
| RMSE: | 0.0121 | 0.0165 | 0.0087 | 0.0173 | 0.0086 | 0.0083 | |
| R2: | 0.8709 | 0.7617 | 0.9333 | 0.7367 | 0.9354 | 0.9395 | |
| avg_ratio | MAE: | 0.0099 | 0.0122 | 0.0046 | 0.0124 | 0.0047 | 0.0044 |
| RMSE: | 0.0124 | 0.0154 | 0.0081 | 0.0156 | 0.0080 | 0.0078 | |
| R2: | 0.7562 | 0.6278 | 0.8969 | 0.6160 | 0.8981 | 0.9042 | |
| avg_feret | MAE: | 0.4821 | 0.4723 | 0.2075 | 0.6265 | 0.2094 | 0.1956 |
| RMSE: | 0.6528 | 0.6132 | 0.3992 | 0.8254 | 0.3682 | 0.3543 | |
| R2: | 0.9359 | 0.9434 | 0.9760 | 0.8975 | 0.9796 | 0.9811 | |
| avg_area | MAE: | 15.1655 | 11.7210 | 5.1240 | 16.6422 | 5.1750 | 4.8583 |
| RMSE: | 20.9219 | 15.9116 | 9.8292 | 22.1228 | 9.2016 | 8.9570 | |
| R2: | 0.9185 | 0.9529 | 0.9820 | 0.9089 | 0.9842 | 0.9851 | |
| avg_perimeter | MAE: | 1.6143 | 1.4848 | 0.6786 | 2.0360 | 0.6677 | 0.6305 |
| RMSE: | 2.1658 | 1.9395 | 1.3183 | 2.6715 | 1.1948 | 1.1554 | |
| R2: | 0.9291 | 0.9431 | 0.9737 | 0.8921 | 0.9784 | 0.9798 | |
| avg_distance | MAE: | 1.0661 | 0.9509 | 0.4268 | 1.2218 | 0.4446 | 0.4142 |
| RMSE: | 1.4201 | 1.2371 | 0.7917 | 1.5800 | 0.7923 | 0.7559 | |
| R2: | 0.8390 | 0.8778 | 0.9500 | 0.8007 | 0.9499 | 0.9544 |
| Model | Evaluation Metrics | |||
|---|---|---|---|---|
| MAE | RMSE | R2 | ||
| GFs-SVR | Training set | 0.0106 | 0.0136 | 0.9764 |
| Test set | 0.0133 | 0.0173 | 0.9613 | |
| GFs-MLP | Training set | 0.0187 | 0.0238 | 0.9271 |
| Test set | 0.0192 | 0.0245 | 0.9223 | |
| GFs-RF | Training set | 0.0030 | 0.0051 | 0.9966 |
| Test set | 0.0081 | 0.0137 | 0.9756 | |
| GFs-GBR | Training set | 0.0257 | 0.0328 | 0.8622 |
| Test set | 0.0262 | 0.0334 | 0.8554 | |
| GFs-XGBoost | Training set | 0.0019 | 0.0027 | 0.9991 |
| Test set | 0.0063 | 0.0104 | 0.9861 | |
| GFs-CatBoost | Training set | 0.0015 | 0.0021 | 0.9995 |
| Test set | 0.0058 | 0.0098 | 0.9876 | |
| CatBoost | Training set | 0.0038 | 0.0054 | 0.9963 |
| Test set | 0.0147 | 0.0258 | 0.9131 | |
| Parameter Name | Value |
|---|---|
| n_estimators | 2000 |
| learning_rate | 0.1 |
| max_depth | 9 |
| l2_leaf_reg | 3 |
| early_stopping_rounds | 30 |
| loss_function | RMSE |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Liu, Y.; He, Y.; Pan, Z.; Li, Z. A Hybrid Estimation Model for Graphite Nodularity of Ductile Cast Iron Based on Multi-Source Feature Extraction. Modelling 2025, 6, 126. https://doi.org/10.3390/modelling6040126
Yang Y, Liu Y, He Y, Pan Z, Li Z. A Hybrid Estimation Model for Graphite Nodularity of Ductile Cast Iron Based on Multi-Source Feature Extraction. Modelling. 2025; 6(4):126. https://doi.org/10.3390/modelling6040126
Chicago/Turabian StyleYang, Yongjian, Yanhui Liu, Yuqian He, Zengren Pan, and Zhiwei Li. 2025. "A Hybrid Estimation Model for Graphite Nodularity of Ductile Cast Iron Based on Multi-Source Feature Extraction" Modelling 6, no. 4: 126. https://doi.org/10.3390/modelling6040126
APA StyleYang, Y., Liu, Y., He, Y., Pan, Z., & Li, Z. (2025). A Hybrid Estimation Model for Graphite Nodularity of Ductile Cast Iron Based on Multi-Source Feature Extraction. Modelling, 6(4), 126. https://doi.org/10.3390/modelling6040126






