Abstract
Beta regression models are a class of models used frequently to model response variables in the interval . Although there are articles in which these models are used to model clustered and longitudinal data, the prediction of random effects is limited, and residual analysis has not been implemented. In this paper, a random intercept beta regression model is proposed for the complete analysis of this type of data structure. We proposed some types of residuals and formulate a methodology to obtain the best prediction of random effects. This model is developed through the parameterisation of beta distribution in terms of the mean and dispersion parameters. A log-likelihood function is approximated by the Gauss–Hermite quadrature to numerically integrate the distribution of random intercepts. A simulation study is used to investigate the performance of the estimation process and the sampling distributions of the residuals.
1. Introduction
The class of models known as beta regression models is used to model variables that assume values in the interval , e.g., rates, proportions, or percentages, as this type of data appears so frequently that these models have received the attention of many researchers. Paolino [1], Kieschnick and McCullough [2], and Smithson and Verkuilen [3] proposed a beta regression model with applications for political science, market shares, and psychology. Ferrari and Cribari-Neto [4] defined a parameterisation of the beta distribution in terms of the mean and precision parameter and proposed a beta regression model with a regression structure for the mean.
Extensions of the regression model proposed by Ferrari and Cribari-Neto [4] have been developed. Venezuela [5] developed a generalised estimating equation to analyse longitudinal data by considering marginal beta regression models. Simas et al. [6] proposed a regression structure for the precision parameter and nonlinear regression structure for the mean. Ferrari and Pinheiro [7] considered regression structure for the precision parameter and performed small-sample inference for beta regression models.
Cribari-Neto and Souza [8] performed testing inference in beta regression models based on a second parameterisation of the beta distribution that considers the mean and dispersion parameters. Rigby and Stasinopoulos [9] incorporated this parameterisation into the framework of generalised additive models for location, scale, and shape (GAMLSS).
Some more recent theoretical works include those by Karlsson [10], Abonazel and Dawoud [11], and Algamal [12] in which different estimators are proposed to address the problem of multicollinearity in the regression model. In applied publications, the work of Mullen [13] illustrates the use of these models in solar radiation predictions; the work of Douma [14] highlights the use of this type of models in ecology and evolution; the work of Geissinger [15] emphasises their application in the natural sciences; the work of Abonazel [16] shows a comparative study in medical science; and the work of Cribari-Neto [17] shows a beta regression analysis of COVID-19 mortality in Brazil.
A mixed beta regression model provides a class of models for the analysis of clustered and longitudinal data for beta-distributed responses. Early contributions of this class of models include a logit random intercept beta regression model implemented by Rigby and Stasinopoulos [9] on the R gamlss package, a logit random intercept beta regression model via Template Model Builder (TBM) implemented by Brooks et al. [18] on the R glmmTMB package, and a mixed beta regression model with logit and log link functions, a special case of which is the finite mixture model proposed by Verkuilen and Smithson [19].
The main goal of this article is to propose a random intercept beta regression model using a parameterisation scheme defined in terms of the mean and dispersion parameters by considering different link functions and utilising an estimation method different from the GAMLSS model. In this model, the parameters related to fixed and random effects are estimated jointly using the maximum likelihood method. The advantages of using random intercept beta regression model instead of the usual beta regression model are that by introducing random effects into the mean, we describe the heterogeneity of the means between clusters, and by introducing random effects into the dispersion, we can describe the dispersions between clusters. According to Lee, Nelder, and Pawitan (2006) [20], introducing random effects in the dispersion can describe abrupt changes among repeated measures.
Also, with the proposed model, we can analyse hierarchical datasets, such as clustered data, repeated measurements, and longitudinal data. We also develop predictions of random effects and propose residuals for the proposed model. An application is provided with the longitudinal data from a prospective ophthalmology study described in the work of Meyers et al. [21], in which the percentage of gas left in the eye of each patient was recorded on different follow-up days.
The rest of this paper unfolds as follows. In Section 2, we define the random intercept beta regression model and present the associated log-likelihood function. Further, we obtain closed-form expressions for the score function and observed information matrix. In the third section, we define the mean, variance, and covariance of the marginal distribution of beta random variables and use them to build the marginal residual. In Section 4, we describe randomised quantiles and conditional and marginal residuals to detect outlying observations and standardised random effect estimates to detect outlying clusters. The prediction of random effects used to build the proposed residuals is presented in Section 5. The results of the simulations regarding the performance of the estimation method and the residuals are presented in Section 6. In Section 7, we analyse a dataset with the proposed model. Finally, concluding remarks are presented in Section 8. Some technical details are collected in the Supplementary Material.
2. Random Intercept Beta Regression Model
In this section, we present two different parameterisations of the beta distribution, the random intercept model, the likelihood inference, and the estimation procedure.
2.1. Beta Distribution
Suppose Y is a response variable that follows a beta distribution. Ferrari and Cribari-Neto [4] proposed a parameterisation of its density indexed by the mean and precision parameter . The parameterisation is given by
where , , and . The mean and variance of Y are given, respectively, by and .
Alternatively, the beta distribution can be parameterised in terms of the mean and the dispersion parameter .
with , , and . In this parameterisation, the mean of Y is , and the variance of Y is .
2.2. Random Intercept Model
Without loss of generality, we assume that , where a and b are known scalars, . If the response variable is constrained to the interval , we model instead of y.
Let , , be the observed repeated measurements on the i-th clusters, and let , , be the corresponding times on which the measurements are taken on each cluster. In the beta random intercept model, it is assumed that the conditional distribution of given follows a beta distribution with a density given by Equation (2). Given , the repeated measurements, are independent. We will assume the following model:
where and contain values of explanatory variables, possibly defined in terms of . The vectors and are fixed parameters that do not depend on the time. The random intercepts and are shared among measurements within the same cluster. The link functions and are strictly monotonic and twice differentiable. The same or different link function may be used for the mean and the dispersion parameter, e.g., logit, probit, clog-log, log-log, or cauchit. For a discussion of these link functions, see McCullagh and Nelder [22].
The random intercepts and are independent and identically distributed normal random variables.
where and are the standard deviations of random intercepts. Larger estimates of these parameters, and , imply greater differences between the groups. In the particular case where , the mean of the response variable can be modelled without a random intercept.
2.3. Likelihood Inference
Let denote the probability density function of . Let and denote the probability density functions of and , respectively. The parameter vector is . The marginal distribution of is given by
and the likelihood function of given the observed data is
Unlike a Gaussian linear model, the marginal distribution (5) and the likelihood function (6) do not have closed-form expressions. The main difficulty of likelihood inference for a random intercept beta regression model is the evaluation of intractable integrals in likelihood function (6). Common approaches include Monte Carlo integration, EM algorithms, and approximation methods (see Wu [23]). In this work, we use multivariate Gauss–Hermite quadrature to approximate the integrals. Thus, the likelihood function is
and the log-likelihood function can be written as
where and denote the numbers of quadrature points, and are the quadrature points, and and are the corresponding quadrature weights. For more details on multivariate Gauss–Hermite quadrature, see Fahrmeir and Tutz [24].
2.4. Estimating Procedure
The maximum likelihood estimators (MLEs) of are obtained as the solutions of the nonlinear system , where denotes the p-dimensional gradient of , with . The score function is , where the vectors and and the quantities and are defined in the Supplementary Material.
The maximum likelihood estimators do not have closed forms and must be computed by numerically maximising the log-likelihood function (7) using a nonlinear optimisation algorithm, e.g., Newton’s method or a quasi-Newton algorithm. As initial values for and , we suggest and , the estimates from the beta regression model without random intercepts, i.e.,
These models can be fitted in R, for example, using the packages gamlss or betareg, developed by Rigby and Stasinopoulos [9] and Cribari-Neto and Zeileis [25], respectively. For the parameters and , the standard deviations of random intercepts, we suggest starting with initial values of 0, which corresponds to the usual beta regression model.
To obtain the covariance matrix of , the observed information matrix is required, which can be written as
where the elements of are defined in the Supplementary Material.
Under the usual regularity conditions for maximum likelihood estimation, the MLEs of are such that , where denotes convergence in distribution.
3. Moments
The moments of the marginal distribution of in model (3) are given by
where the expectations involving and are taken with respect to the distributions of the random intercepts and . Note that the results depend on the link functions used for and . To obtain these moments, the required integrals must be solved using numerical integration methods.
4. Prediction of Random Effects
In practice, we are usually primarily interested in estimating the fixed-effect parameters, but it is often useful to obtain predictions of the random effects and as well. Because the random effects reflect between-cluster variability, they are particularly useful for detecting unusual response profiles or groups of clusters whose profiles evolve differently over time. Moreover, estimates of the random effects are needed whenever cluster-specific predictions are of interest (Fitzmaurice et al. [26]). We propose using an empirical Bayes method to obtain the best predictor (BP) of the random intercepts, which takes the following form:
where and .
5. Residual Analysis
Authors such as Hilden-Minton [27], Verbeke and Lesaffre [28], Pinheiro and Bates [29], and Nobre and Singer [30] have presented different types of residuals that accommodate the additional sources of variability present in linear mixed models. To study departures from these assumptions, outlying observations, and clusters, we adopt three types of residuals that account for the extra variability in the proposed model: randomised quantile residuals (see Dunn and Smyth [31]), standardised conditional residuals and standardised marginal residuals. In addition, we define standardised random effect estimates for and to assess the distribution of random effects and to study the presence of outlying clusters.
To assess the overall adequacy of the random intercept beta regression model for the data, we proposed the randomised quantile residual, which is given by
where denotes the cumulative distribution function of the standard normal distribution, and denotes the cumulative distribution function of .
To study outlying observations, we consider the standardised conditional and marginal residuals. The standardised conditional residual is defined as
where and , with and ; and are the maximum likelihood estimators of and ; and and denote the best predictors (BPs) of and , respectively.
The standardised marginal residual is given by
where and .
Thus, when the logit link function is used for and , the mean and the variance are given by
where and . Replacing , and , we obtain , and , as well as and . Note that to calculate these estimates, multivariate Gauss–Hermite quadrature is used to approximate the integrals in parameter estimation and random intercept prediction.
To study outlying clusters and assess the random effect distribution, we consider the standardised random effect estimates for and , defined as
with , where and are the BPs of and , and and are the maximum likelihood estimates of and .
Atkinson [32] and Kutner et al. [33] suggested the use of probability plots with simulated half-normal envelopes as diagnostic tools. Such plots are useful for identifying outliers and examining the adequacy of the fitted model, even when the residual distribution is unknown. Half-normal plots with a simulated envelope can be produced as follows:
- Fit the beta random intercept model and generate a sample of n independent observations, treating the fitted model as the true model.
- Fit the beta random intercept model to the generated sample and compute the ordered absolute residuals.
- Repeat steps (1) and (2) k times.
- For each of the n positions, collect the k order statistics and compute their average, minimum, and maximum values.
- Plot these values together with the ordered residuals of the original sample against the half-normal scores , where i is the ith order statistic, , and n is the sample size.
The minimum and maximum values of the k-order statistics define the envelope. Observations with absolute residuals outside the simulated limits warrant further investigation. Moreover, if a considerable proportion of points falls outside the envelope, there is evidence against the adequacy of the fitted model.
6. Simulation Study
The purpose of this simulation study is twofold. First, we study the behaviour of the estimates of , and as the number of clusters, cluster size, and the standard deviations of the random intercepts in and for clustered and longitudinal data. Second, we investigate the sampling distribution of the residuals for identifying outlying observations and clusters.
The data were generated according to the following random intercept beta regression model:
where , , is the logit function, and and are parameter vectors. The covariates are generated following simulation studies with longitudinal data, such as those by Park and Wu [34], Guoyou and Zhongyi [35], and Fu and Wang [36]. The covariate is generated from the uniform distribution, , with a different value for each pair . The design time points are taken between 0 and 1 as , taking the same values for each cluster. Both parameter vectors are identical , and are independent of the random intercepts, which are generated as and .
We examined all combinations of five clusters, N, ; four cluster sizes, , ; and three standard deviations of the random effects, , . In total, there were 60 combinations, and we simulated 10,000 datasets for each of them. For the Gauss–Hermite quadrature method, quadrature points were used to obtain the estimates and predictions of the random intercepts. All analyses were conducted in R [37]; the R glmmML package proposed by Broström and Holmberg [38] was used to calculate the points and weights needed for Gauss–Hermite quadrature, and the R Stats function nlminb [37] was used to maximise the log-likelihood function (7).
To study the maximum likelihood estimates of , we used the root multivariate mean squared error (RMSE) for , following Wissel [39], which is defined as
To analyse the convergence of the optimiser used in the estimation process, we computed the convergence rate (CR), defined as
where “final iterations” corresponds to the number of iterations required to complete 10,000 simulations. If the convergence rate equals one, this indicates that 10,000 iterations were sufficient. If it is less than one, more than 10,000 iterations were needed to complete the simulation study. Additional iterations occur when the algorithm does not converge because the simulated values of y are very close to zero or one due to large variances in the random effects.
Table 1 presents the RMSE across 10,000 simulated datasets for and . The RMSE decreases as the cluster size increases for fixed and , indicating improved estimation with larger within-cluster information. For example, with , , and , the RMSE values are for , and 12, respectively. RMSE also decreases with a larger number of clusters , holding and fixed. For instance, with , , and , the RMSE values are for , and 150. Conversely, RMSE increases with higher for given fixed values of , , and , reflecting reduced estimation accuracy under greater random-intercept variability. For example, with , , and , the RMSE values are for . Exceptions arise for and with and , and for and with . A similar pattern is observed for : RMSE increases as rises for fixed , N, and . For instance, with , , and , the RMSE values are for and .

Table 1.
RMSE of when and .
Table 2 presents the convergence rate (CR) over 10,000 simulated datasets for and .

Table 2.
CR when and .
To study the sampling distributions of the proposed residuals, we used the maximum likelihood estimates and the best predictors (BPs) of the random intercepts for and , computed in each replication of the study, to obtain the residuals and , as well as the standardised random effect estimates and . In addition, estimates of the mean and variance of the marginal distribution of were used to compute the residual defined in expression (11).
Figure 1 presents normal probability plots for the randomised quantile , standardised conditional , and standardised marginal residual for , , , and . Each panel includes the three residuals. The plots show that the randomised quantile residuals follow an approximately normal distribution, while the conditional and marginal residuals exhibit symmetry with heavier tails, consistent with Student’s t distribution. Similar results were obtained for and 12.
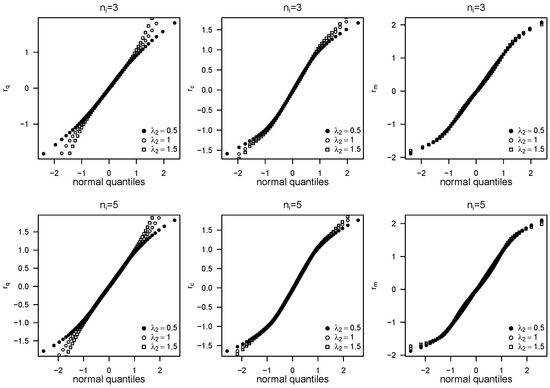
Figure 1.
Normal probability plots for randomised quantile (column 1), conditional (column 2), and marginal (column 3) residuals with , , , and .
Figure 2 displays normal probability plots for the standardised random effect estimates and , with and . Both distributions are well approximated by the normal law. Similar plots were generated for , , and , and comparable results (not shown) were also obtained for and .
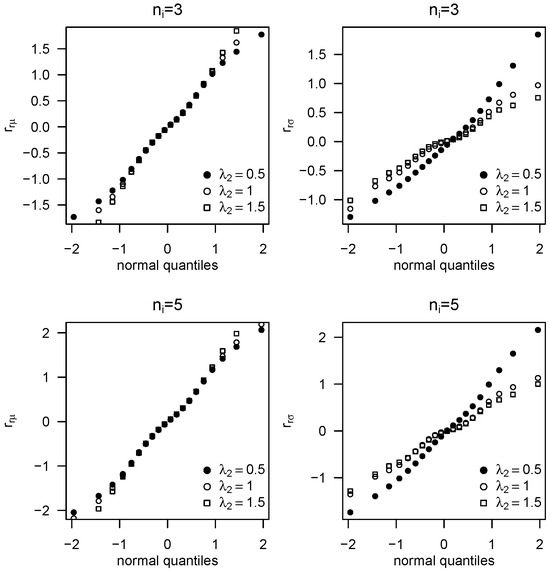
Figure 2.
Normal probability plots for standardised random effect estimates for and with , , , and .
7. Application
In this section, we analyse data from a prospective ophthalmology study reported by Meyers et al. [21], with emphasis on heterogeneous mean and dispersion. Previous analyses of these data have examined homogeneous and heterogeneous dispersion using simplex regression models [40,41]. In the study, intraocular gas was used in complex retinal surgeries to provide an internal tamponade for retinal breaks. The concentration levels of administered were 25%, 20%, and 15%. The primary objective was to assess whether the concentration of injected gas affected its decay rate. The sample comprised 29 patients, each followed-up with between 3 and 15 times over a 3-month period. Let denote the proportion of remaining gas volume relative to the initial injected volume for patient i at time j on follow-up day . Since the response variable lies in , the beta regression model is an appropriate choice.
As the initial specification, we adopted the quadratic model proposed in [40]:
with , where and . Here, denotes the time covariate (days after surgery) and represents the standardised gas concentration, coded as , or .
The standard beta regression model was first fitted to the data, after which nonsignificant variables were removed. The final specification for and was
Subsequently, a random-intercept beta regression model for was fitted, using the same linear predictors as in (14). The resulting specification for and was
Finally, a random-intercept beta regression model for both and was fitted, using the same linear predictors as in (14). The specification for and was
Table 3 summarises the parameter estimates and standard errors for the beta regression model (BRM), the beta regression model via TBM (TBMBRM), and the mixed beta regression model (MBRM). The Akaike information criterion (AIC) values were , , and for BRM, TBMBRM, and MBRM, respectively, leading to the selection of the MBRM as the best-fitting model. The results indicate that gas concentration is statistically significant, showing that higher concentrations are associated with slower decay of gas volume. Moreover, was greater than , suggesting greater variability in the random intercept of the mean.
Figure 3 presents the half-normal probability plot with a simulated envelope for the randomised quantile, standardised conditional, and standardised marginal residuals of the random-intercept beta regression model. As no observations fall outside the simulated envelope, we conclude that the beta regression model with random intercepts provides an adequate fit to the data.
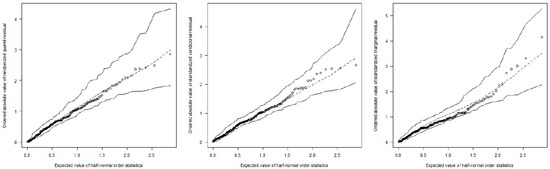
Figure 3.
Half-normal probability plot with simulated envelope for randomised quantile, standardised conditional, and standardised marginal residuals.
8. Conclusions
In this paper, we proposed a random-intercept beta regression model for the analysis of clustered and longitudinal data expressed as proportions, rates, or percentages. The model accommodates heterogeneity and heteroscedasticity across clusters by incorporating random effects in both the mean and dispersion structures. Maximum likelihood estimation was carried out using Gauss–Hermite quadrature to approximate the integrals of the log-likelihood, allowing simultaneous estimation of parameters and hyperparameters and straightforward prediction of random effects. We also introduced new residuals to evaluate model adequacy and detect potential outliers at both the observation and cluster levels. Simulation studies confirmed the effectiveness of the methodology, and its application to a real dataset demonstrated its practical usefulness.
Supplementary Materials
The following supporting information can be downloaded at https://github.com/fhernanb/Paper_Modeling_Interval_Data (accessed on 9 October 2025).
Author Contributions
Conceptualisation, O.U.-M. and V.G.; methodology, O.U.-M. and V.G.; software, O.U.-M. and F.H.-B.; validation, O.U.-M., F.H.-B. and V.G.; formal analysis, O.U.-M. and V.G.; investigation, O.U.-M.; resources, V.G.; data curation, O.U.-M. and F.H.-B.; writing—original draft preparation, O.U.-M.; writing—review and editing, O.U.-M., F.H.-B. and V.G.; supervision, V.G.; project administration, V.G.; funding acquisition, V.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior—Brazil (CAPES) and by the Conselho Nacional de Desenvolvimento Científico e Tecnológico—Brazil (CNPq).
Data Availability Statement
Dataset is available on request from the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Paolino, P. Maximum Likelihood Estimation of Models with Beta-Distributed Dependent Variables. Political Anal. 2001, 9, 325–346. [Google Scholar] [CrossRef]
- Kieschnick, R.; McCullough, B. Regression analysis of variates observed on (0, 1): Percentages, proportions and fractions. Stat. Model. 2003, 3, 193–213. [Google Scholar] [CrossRef]
- Smithson, M.; Verkuilen, J. A Better Lemon Squeezer? Maximum-Likelihood Regression with Beta-Distributed Dependent Variables. Psychol. Methods 2006, 11, 54–71. [Google Scholar] [CrossRef] [PubMed]
- Ferrari, S.; Cribari-Neto, F. Beta regression for modeling rates and proportions. J. Appl. Stat. 2004, 31, 799–815. [Google Scholar] [CrossRef]
- Venezuela, M. Equação de Estimação Generalizada e Influência Local para Modelos de Regressão Beta com Medidas Repetidas. Ph.D. Thesis, Instituto de Matemática e Estatística, Universidade de São Paulo, São Paulo, Brasil, 2008. [Google Scholar][Green Version]
- Simas, A.; Barreto-Souza, W.; Rocha, A. Improved estimators for a general class of beta regression models. Comput. Stat. Data Anal. 2010, 54, 348–366. [Google Scholar] [CrossRef]
- Ferrari, S.; Pinheiro, E. Improved likelihood inference in beta regression. J. Stat. Comput. Simul. 2011, 81, 431–443. [Google Scholar] [CrossRef]
- Cribari-Neto, F.; Souza, T. Testing inference in variable dispersion beta regressions. J. Stat. Comput. Simul. 2012, 82, 1827–1843. [Google Scholar] [CrossRef]
- Rigby, R.; Stasinopoulos, D. Generalized additive models for location, scale and shape. Appl. Stat. 2005, 54, 507–554. [Google Scholar] [CrossRef]
- Karlsson, P.; Månsson, K.; Kibria, B.G. A Liu estimator for the beta regression model and its application to chemical data. J. Chemom. 2020, 34, e3300. [Google Scholar] [CrossRef]
- Abonazel, M.R.; Dawoud, I.; Awwad, F.A.; Lukman, A.F. Dawoud–Kibria estimator for beta regression model: Simulation and application. Front. Appl. Math. Stat. 2022, 8, 775068. [Google Scholar] [CrossRef]
- Algamal, Z.Y.; Abonazel, M.R. Developing a Liu-type estimator in beta regression model. Concurr. Comput. Pract. Exp. 2022, 34, e6685. [Google Scholar] [CrossRef]
- Mullen, R.; Marshall, L.; McGlynn, B. A beta regression model for improved solar radiation predictions. J. Appl. Meteorol. Climatol. 2013, 52, 1923–1938. [Google Scholar] [CrossRef]
- Douma, J.C.; Weedon, J.T. Analysing continuous proportions in ecology and evolution: A practical introduction to beta and Dirichlet regression. Methods Ecol. Evol. 2019, 10, 1412–1430. [Google Scholar] [CrossRef]
- Geissinger, E.; Khoo, C.; Richmond, I.; Faulkner, S.; Schneider, D. A case for beta regression in the natural sciences. Ecosphere 2022, 13. [Google Scholar] [CrossRef]
- Abonazel, M.R.; Said, H.A.; Tag-Eldin, E.; Abdel-Rahman, S.; Khattab, I.G. Using beta regression modeling in medical sciences: A comparative study. Commun. Math. Biol. Neurosci. 2023, 2023, 18. [Google Scholar] [CrossRef]
- Cribari-Neto, F. A beta regression analysis of COVID-19 mortality in Brazil. Infect. Dis. Model. 2023, 8, 309–317. [Google Scholar] [CrossRef] [PubMed]
- Brooks, M.E.; Kristensen, K.; van Benthem, K.J.; Magnusson, A.; Berg, C.W.; Nielsen, A.; Skaug, H.J.; Maechler, M.; Bolker, B.M. glmmTMB Balances Speed and Flexibility Among Packages for Zero-inflated Generalized Linear Mixed Modeling. R J. 2017, 9, 378–400. [Google Scholar] [CrossRef]
- Verkuilen, J.; Smithson, M. Mixed and Mixture Regression Models for Continuous Bounded Responses Using the Beta Distribution. J. Educ. Behav. Stat. 2012, 37, 82–113. [Google Scholar] [CrossRef]
- Lee, Y.; Nelder, J.; Pawitan, Y. Generalized Linear Models with Random Effects: Unified Analysis via H-Likelihood; Chapman and Hall/CRC: Orange, CA, USA, 2017. [Google Scholar]
- Meyers, S.; Ambler, J.; Tan, M.; Werner, J.; Huang, S. Variation of perfluorproane disappearance after vitrectomy. Retina 1992, 12, 359–363. [Google Scholar] [CrossRef]
- McCullagh, P.; Nelder, J. Generalized Linear Models, 2nd ed.; Chapman and Hall: London, UK, 1989. [Google Scholar]
- Wu, L. Mixed Effects Models for Complex Data; Chapman & Hall/CRC: Boca Raton, FL, USA, 2010. [Google Scholar]
- Fahrmeir, L.; Tutz, G. Multivariate Statistical Modelling Based on Generalized Linear Models, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Cribari-Neto, F.; Zeileis, A. Beta Regression in R. J. Stat. Softw. 2010, 34, 1–24. [Google Scholar] [CrossRef]
- Fitzmaurice, G.; Davidian, M.; Verbeke, G.; Molenberghs, G. Longitudinal Data Analysis, 2nd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2009. [Google Scholar]
- Hilden-Minton, J. Multilevel Diagnostics for Mixed and Hierarchical Linear Models. Ph.D. Thesis, University of California, Los Angeles, CA, USA, 1995. [Google Scholar]
- Verbeke, G.; Lesaffre, E. A linear mixed-effects model with heterogeneity in the random-effects population. J. Am. Stat. Assoc. 1996, 91, 217–221. [Google Scholar] [CrossRef]
- Pinheiro, J.; Bates, D. Mixed-Effects Models in S ans S-PLUS; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Nobre, J.; Singer, J. Residual Analysis for Linear Mixed Models. Biom. J. 2007, 49, 863–875. [Google Scholar] [CrossRef]
- Dunn, P.; Smyth, G. Randomized Quantile Residuals. J. Comput. Graph. Stat. 1996, 5, 236–244. [Google Scholar] [CrossRef]
- Atkinson, A. Plots, Transformations and Regression: An Introduction to Graphical Methods of Diagnostic Regression Analysis; Oxford University Press: New York, NY, USA, 1985. [Google Scholar]
- Kutner, M.; Nachtsheim, C.; Neter, J.; Li, W. Applied Linear Statistical Models, 5th ed.; McGraw-Hill: New York, NY, USA, 2005. [Google Scholar]
- Park, J.G.; Wu, H. Backfitting and local likelihood methods for nonparametric mixed-effects models with longitudinal data. J. Stat. Plan. Inference 2006, 136, 3760–3782. [Google Scholar] [CrossRef]
- Guoyou, Q.; Zhongyi, Z. Robust estimation in partial linear mixed model for longitudinal data. Acta Math. Sci. 2008, 28, 333–347. [Google Scholar] [CrossRef]
- Fu, L.; Wang, Y.G. Quantile regression for longitudinal data with a working correlation model. Comput. Stat. Data Anal. 2012, 56, 2526–2538. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2025; ISBN 3-900051-07-0. [Google Scholar]
- Broström, G.; Holmberg, H. glmmML: Generalized Linear Models with Clustering; R Package Version 0.82-1; R Core Team: Vienna, Austria, 2011; Available online: https://CRAN.R-project.org/package=glmmML (accessed on 20 September 2024).
- Wissel, J. A New Biased Estimator for Multivariate Regression Models with Highly Collinear Variables. Ph.D. Thesis, Institut für Mathematik, Universität Würzburg, Würzburg, Germany, 2009. [Google Scholar]
- Song, P.X.K.; Tan, M. Marginal models for longitudinal continuous proportional data. Biometrics 2000, 56, 496–502. [Google Scholar] [CrossRef]
- Song, P.; Qiu, Z.; Tan, M. Modelling Heterogeneous Dispersion in Marginal Models for Longitudinal Proportional Data. Biom. J. 2004, 46, 540–553. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).