Abstract
This research delves into the design, modeling, and finite element impact analysis of the segmented sandwich composite armor system subjected to impact loading, considering different parameters such as materials to be used, armor height, and armor design configuration. Initial studies were performed to select the ideal model that will provide the best impact resistance at the least weight and with minimal fabrication requirements. Material type, thickness, and overall model configuration were defined during the initial model development period. Once the final design was defined, finite element analysis was performed using 2017 ABAQUS software to observe the performance of the model and to validate the efficiency of the chosen armor. Based on the results from the material selection and thickness validation, the optimal design with the best impact resistance was noted as 1.2 mm thick rectangular segmented silicon carbide tiles, serving as the top layer that covers the three-level gradient core composed of a titanium metal honeycomb frame filled with silicon carbide inserts, and finally a 2 mm thick glass epoxy composite layer made from four laminas in a 0/45/90/-45-degree configuration serving as the last layer of the armor.
1. Introduction
Composite armors consist of various material layers usually made from metals, composite, ceramics, and other materials closely bonded together [1]. Composite armor has spearheaded a vast innovation within the industry, and although there have been some remarkable milestones, the advancement in ballistic technology requires the need for armor systems with more extraordinary mechanical and impact performance, reduced weight, and better formability, capable of resisting high threats. There has been an increased interest in human and equipment protection against fast-moving penetrating projectiles [2]. This topic of interest has pioneered the study of advanced sandwich-type composite armors, which are composed of a cocktail of functional materials, consisting of ceramics, metals, and composites, purposefully selected and combined for their impactor tip erosion functionality, energy dissipation properties, light-weight nature, high stiffness, ductility, and higher protective advantage over the conventional protective bulletproof vest, which is usually made from a single layer of fabric, mostly aramid. The aim of this research is to understand the design of current sandwich armors and use the findings to create a sandwich composite armor with better qualities. Since higher and continuous impact resistance are the focus of armor manufacturers, segmented armors are a great way to improve current armor designs. This research is focused on creating a segmented sandwich armor with a gradient core mid-section. The gradient core design is to ensure that the light-weight armor system is still capable of higher ballistic resistance.
The advancement of additive powder-based technology has made it possible to create more complex composites and new structural configurations using 3D printing [3]. An impact test was conducted on a hybrid composite material with a core composed of a Ti6Al4V lattice filled with AlSi10Mg. It was observed that the core’s nature minimized delamination and reduced layer separation issues. Composite materials with high specific energy absorption characteristics, such as high strength, rupture strain, and low density, are considered ideal based on experimental testing. The research concludes that future trends for the development of lighter armor involving nanofillers, ceramic–composite hybrids, and 3D composites are promising and can offer further lighter armor solutions. Kiran et al. [4] confirmed, through testing and comparing the individual response of composite armors in different configurations, that ceramics are stronger than metals under heavy compressive loads near the impact location. The lower density of ceramics makes them attractive alternatives to metallic armor.
Zhong-Nan et al. [5] concluded, based on investigations of the ballistic behavior of multilayer composites against projectiles, that any composite armor tested near the ballistic limit suffers multiple failure modes. Metallic face sheets primarily failed in a ductile hole enlargement mode, and the ceramic layer tended to be fragmented with radial and spall cracks. The study observed that placing the ceramic layer in front of the front face sheet is beneficial for reducing the residual velocity of the projectile and improving the energy absorption of the armor. Back support with high rigidity and a high loading rate maximized the performance of the ceramic layer. In Mainak’s research [6], high altitude versatile armor (HAVA) made from diglycidyl ether of bisphenol A (DGEBA) epoxy carbon fiber with a filament diameter of 7 mm and a hardener composed of diethyltoluenediamine (DETDA) used as the matrix were sandwiched between two layers of polymer-infused aerogel. The aerogel exhibited a high strength-to-volume ratio and mechanical toughness similar to that of Kevlar. They found that aerogel’s ductile and malleable properties, combined with its lightweight nature, make it ideal for providing protection in impact-resistant applications.
A study on the impact of ceramic balls on composite target plates [7] found that increasing the thickness of a ceramic panel and the strength of the metal back plate leads to an increase in the stress applied to the micro units of the ceramic ball and a more severe fracturing of the ceramic ball under the same impact velocity. With an increase in the impact speed, damage to the interface is more likely to occur, decreasing the chance of the ceramic ball piercing the metal back plate. To gain a better understanding of a projectile’s behavior on impact, Saurabh et al. [8] conducted extensive studies on the failure mechanisms of metals, ceramics, and composites. The ballistic performance of Al2O3/Al 5083 and AlN/Al bi-layer composite armor, subjected to a 7.62 AP projectile, was analyzed in ANSYS using the Johnson–Cook model for the bullet and the Johnson–Holmquist material model for the armor. They found that 200 °C tempered armor steel exhibited superior ballistic properties and heat treatment improved the strength and hardness by 30% and the ballistic efficiency by 21%.
In a study [9], researchers found that although alumina has interesting properties, its low fracture toughness limits its ballistic resistance. By tweaking the microstructure of alumina, properties such as fracture toughness can be improved. Alumina was noted as being capable of withstanding six rounds of NATO ammunition impact, while B4C and SiC became obsolete after two ballistic shots. Having an initial layer (Ti-3% Al-2.5%V alloy, carbon fiber/epoxy pre-preg, E-glass/epoxy pre-preg, and glass fiber tape) on the front face of the alumina armor tile improved its ballistic efficiency by 20% and increased its areal density by 2.5%. Farias-Aguilar et al. [10] conducted studies on the mechanical properties of fiberglass by varying the glass fiber content from 10 to 30%. Varying the thickness between 4 mm and 20 mm of the glass fiber-reinforced polymer (GRP) and aramid composite and subjecting them to ballistic impact revealed that at 20 mm thickness, both materials showed the same impact penetration resistance. Kevlar composite sandwich panels adequately resist the penetration of a 9 mm caliber projectile by dissipating the kinetic energy through fiber reorientation around the impact cavity, causing severe microcracking and permanent deformation. Junbo Yan et al. [11] found from a study on the response of auxetic honeycomb sandwich panels that it possesses superior hit resistance compared to foam core and hexagonal honeycomb sandwich armor. Impact tests also showed that the auxetic core resists impact by compressive deformation, which contributed to the creation of several minor cracks. Sumelka et al. [12] dealt with a numerical simulation of the dynamic failure of an aluminum plate under air blast loading. Constitutive modelling based on fractional viscoplasticity was used in their study. They used an applied fractional differential operator that was implemented as a user material in the engineering finite element computation code ABAQUS. The finite element simulations in the fractional viscoplasticity framework were successfully applied to study the deformation process of an aluminum plate under air blast loading. The finite element results were compared with those from experiments, and acceptable agreement was obtained. Many combinations of different composite layups and impact velocities were created to analyze residual velocity and energy absorption capability. Another simulation research was presented to find the ballistic impact limit [13]. A rigid projectile was utilized with only the Hashin damage model applied to the target plate.
Zhao et al. [14] worked on mosaic alumina and mosaic alumina enhanced by aluminum honeycomb. The enhanced version had better performance compared to the pure alumina version. The honeycomb-enhanced mosaic armor confined the ceramic tile and its fragments, which contribute to ballistic resistance. Furthermore, this structure could improve multi-hit ballistic resistance when compared with monolithic and mosaic alumina. The aluminum honeycomb localized the damaged region and kept the bonding between the adjacent tiles and backing plate. Another study showed that fiber-reinforced composite should not stand alone in ballistic armor [15]. Instead, high-hardness bulletproof materials like ceramics should be placed in front of the composite layer to enhance ballistic resistance. The geometry of mosaic ceramics had significant influence on ballistic behavior. Different geometries in cylindrical, hexagonal, or square shape were made and tested to generate different residual velocities. Wu et al. [16] developed a composite structure that was made from ultrahigh molecular weight polyethylene (UHMWPE) fabric and ceramics layer mounted on the back using epoxy resin. A ratio thickness of silicon carbide with a thickness of 8.190 mm and Dyneema of 6.96 mm can withstand ballistic impact up to National Institute of Justice (NIJ) ballistic protection level IV.
Based on the above literature review, the shortcomings of various armor systems indicate that there is room for the improvement in current armor design. The segmented sandwich composite armor system has the advantage of allowing for localized damage without affecting the overall armor system and was highlighted as the armor design of interest. The maximum energy absorption, without compromising on the weight of the armor, makes it favorable for numerous applications. To modify the chosen segment sandwich composite armor, a three-layer gradient metal lattice in a ceramic matrix core was incorporated into the armor design, which is shown to allow for more significant layer interaction and higher impact resistance.
2. Model Development
Hardness and ductility are amongst the properties essential for good ballistic resistance. This section details the steps that were taken to create the segmented sandwich composite armor system. Steps such as part creation, assigning material properties to the parts, defining the boundary conditions, and assigning a load (velocity) value to the impactor that will be contacting the armor; creating the interaction between the various layers and parts; ensuring mesh convergence; and, finally, running a simulation to confirm the maximum energy absorption potential, as well as the ballistic limit of the armor and the residual velocity of the bullet, are detailed in the sections below.
2.1. Modeling of Armor
The non-destructive analysis utilizes the Lagrangian numerical approach in 2017 ABAQUS software to simulate the behavior of a physical system, dividing its elements into small components with defined properties, assigned boundary conditions, and loads, resulting in realistic behavior predictions. For this research, sandwich armor consisting of a gradient core made of metal filled with ceramic inserts, a segmented ceramic face, and a uniform composite backing plate is studied using the finite element method. The subsections below provide more details on the parameters used to model the different parts of the chosen system.
2.1.1. Ceramic Face
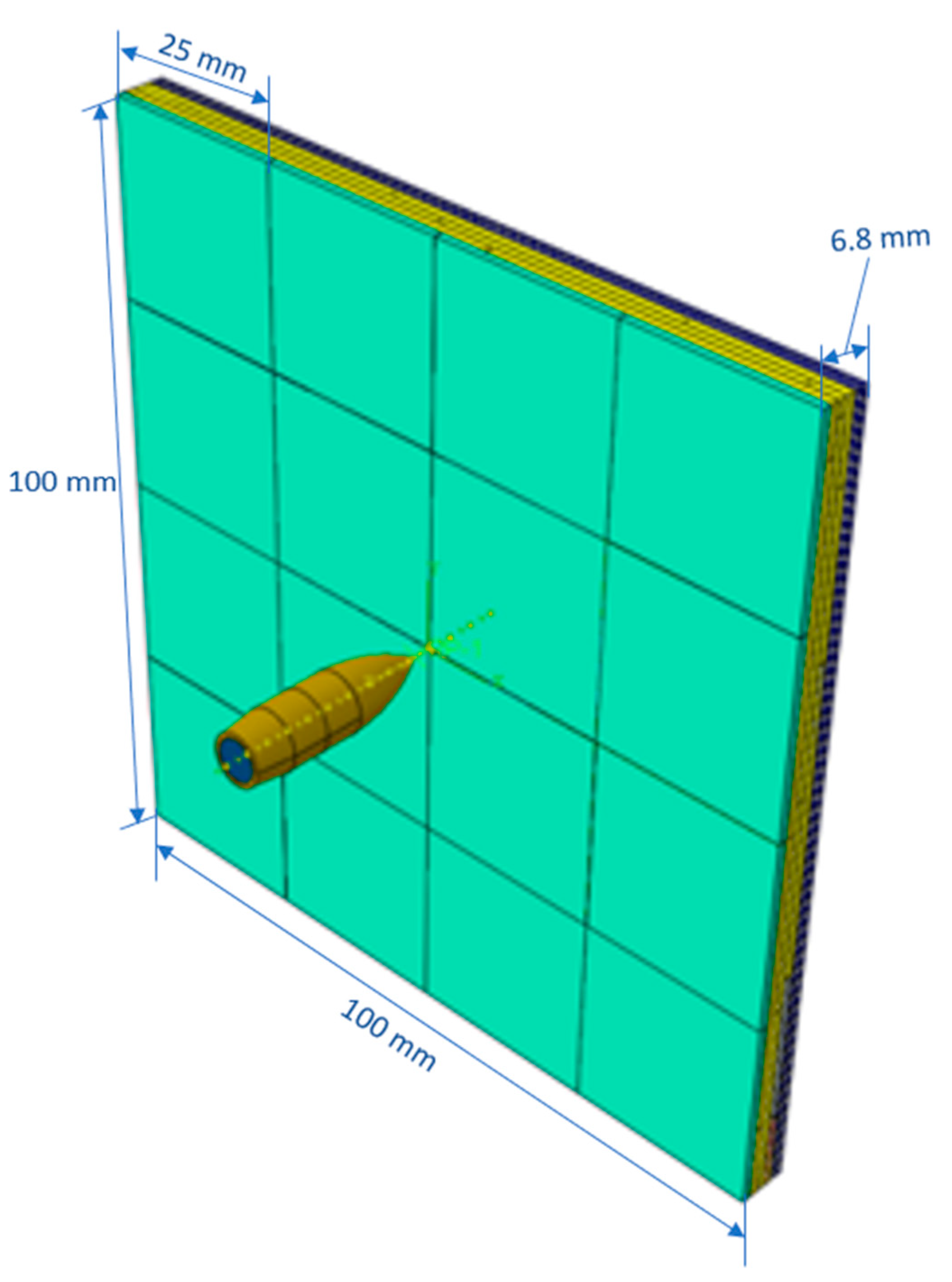
The initial impact layer of the armor is modeled in a segmented ceramic tile arrangement, with unit dimensions of 25 mm by 25 mm pieced together using the assembling and tie interaction features to create an assembled piece of 100 mm by 100 mm. The armor system incorporates the ceramic layer due to its exceptional hardness, which resists penetration from high-velocity impacts; excellent abrasion resistance; and the ability to absorb and disperse energy upon impact. The ceramic layer of the armor reduces the force transmitted to the wearer. The ceramic layer also offers multi-hit capability, ensuring the armor system withstands repeated impacts without significant effectiveness reduction, providing specific protection against threats like armor-piercing projectiles.
2.1.2. Gradient Honeycomb Core Frame and Inserts
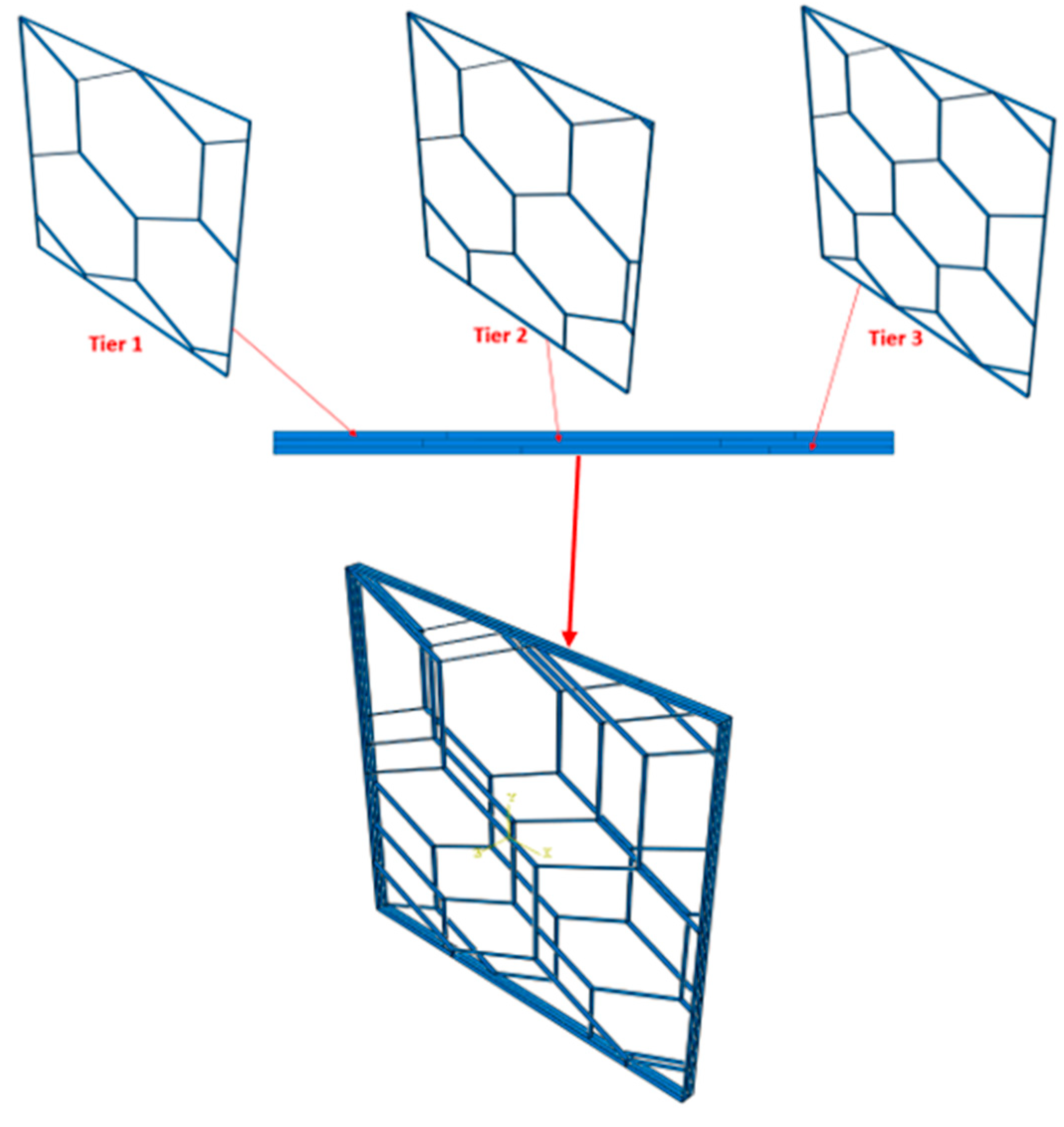
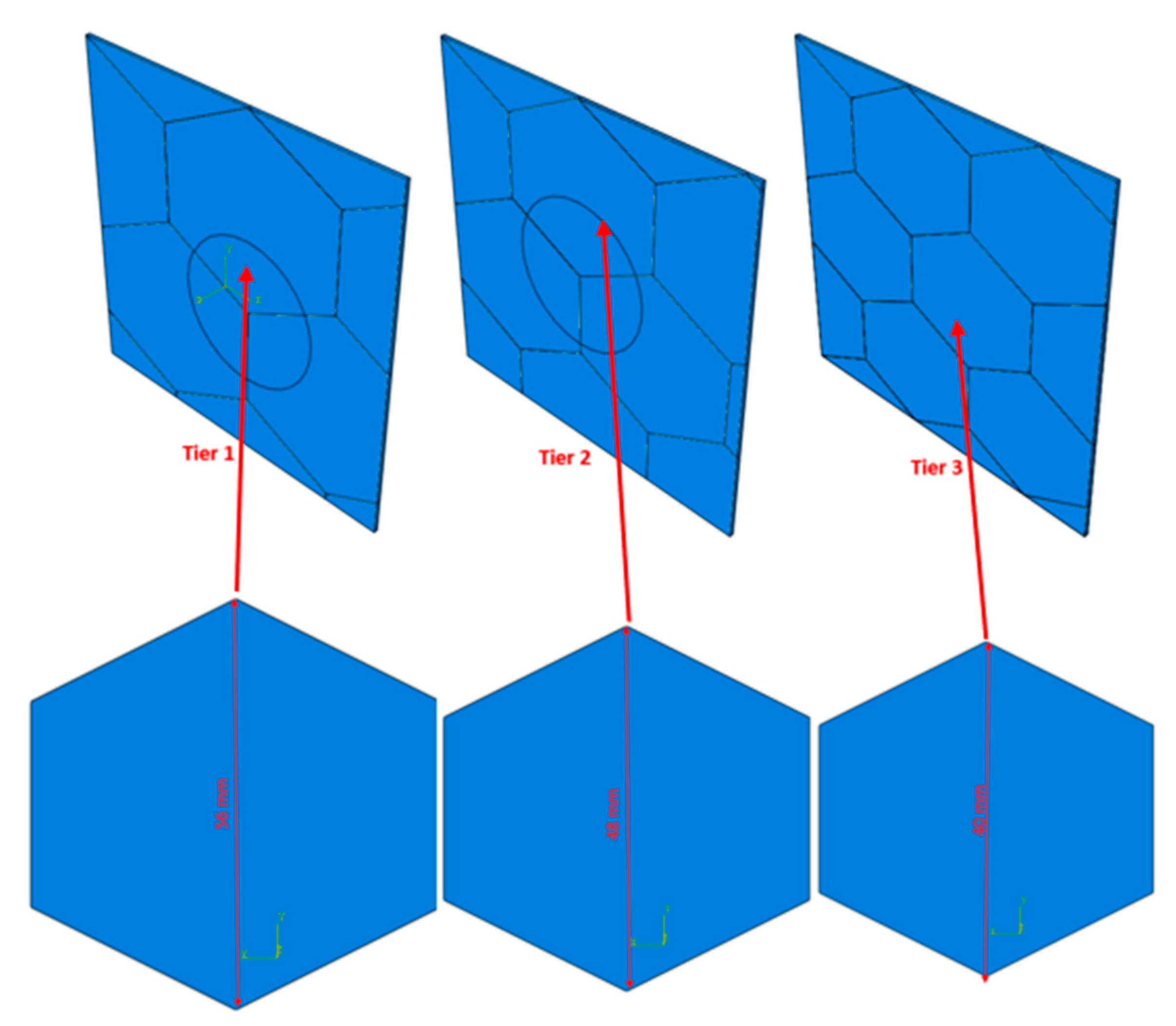
The gradient core frame of the sandwich armor is a 3.6 mm high metal honeycomb core made from three levels of 1.2 mm high varying-sized vertical hexagonal cavities. In the initial honeycomb core layer, the honeycomb cells boast a width of 56 mm, followed by a reduction to 48 mm in the subsequent layer, and a further reduction to 40 mm in the final honeycomb layer. The cavities of the gradient core are filled with their respectively sized ceramic inserts bonded to the frame using epoxy, thus ensuring good impact resistance, and hardness at a reduced density. Figure 1 and Figure 2 show the design of the gradient honeycomb core. The honeycomb core layer in the armor system offers a remarkable strength-to-weight ratio, effective energy absorption upon impact, and structural integrity, contributing to the rigidity and stiffness of the armor, multi-impact resistance, and customizable design for optimized protection against various threats.
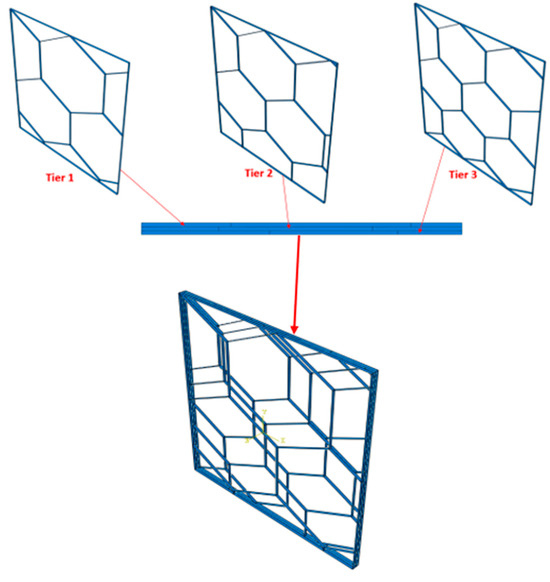
Figure 1.
Gradient core metal frame.
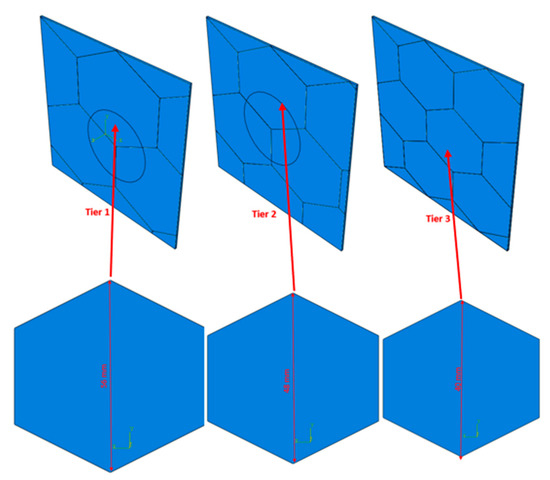
Figure 2.
Metal core with ceramic inserts.
2.1.3. Composite Face
The final layer of the armor is the composite face, which is modeled in a uniform 100 mm by 100 mm singular unit made from 4 laminas in a 0/45/90/-45-degree configuration, with the property of glass epoxy. The uniform, non-segmented nature of the final layer is to ensure better damage dispersion than a segmented layer. The composite layer in the armor system brings a host of advantages, offering a tailored approach to protection through the combination of different materials with specialized properties. This results in a high strength-to-weight ratio, ensuring effective protection. The flexibility and durability of composite materials strike a balance, allowing for the armor to withstand deformation while maintaining structural integrity. With corrosion resistance and potential cost-effectiveness, the composite layer stands as a versatile and efficient solution in the realm of armor design.
2.1.4. NATO Ball Bullet
A 7.83 mm diameter NATO ball bullet made of a steel core encased in a brass jacket, with a total length of 28.6 mm and a predefined velocity type field, was modeled in ABAQUS CAE as a deformable solid structure.
2.1.5. Assembly
The various parts of the sandwich armor shall be pieced together in the assembly space with a 2 mm gap kept between the tip of the bullet (reference point) and the central point of the front-facing layer of the armor system. Figure 3 shows the whole assembly of the segmented sandwich composite armor system.
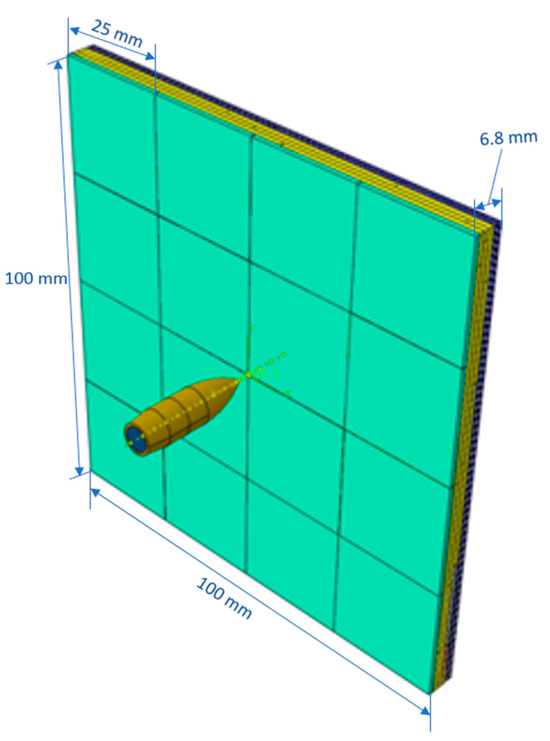
Figure 3.
Segment sandwich composite armor model.
2.2. Mesh
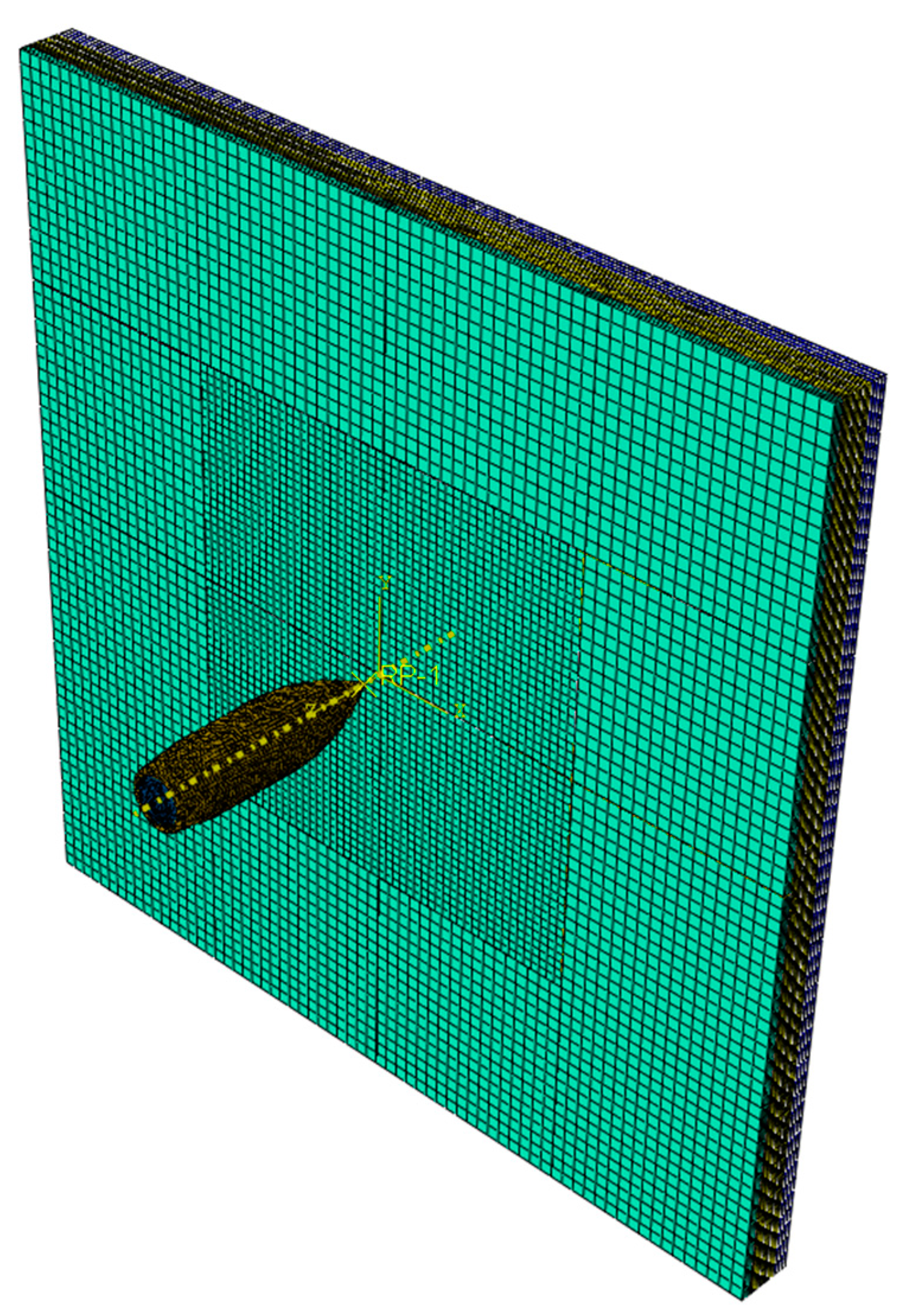
To obtain an accurate result, proper meshing techniques such as partitioning and creating a dense mesh around the impact region are required. For the segmented gradient core sandwich armor model, the central part of the model where the bullet is positioned to impact was partitioned and assigned denser meshing to provide a good result at a reduced time. For the gradient core part of the armor system, a tetrahedral mesh with a global size of 1.5 mm was applied. Similar to the front and backing plates, the central part of the gradient metal core was partitioned and assigned a mesh size of 1.3 mm. For the ceramic core inserts, the central inserts were partitioned and assigned an increased number of meshes. A global size of 1.5 mm and a hexahedral element were used for the non-partitioned inserts, with the central inserts being assigned a seed size of 1.3 mm for all levels. Due to the ogive nature of the bullet, and to prevent excessive distortion, the bullet is partitioned into various sections and meshed separately. A global seed of 0.9 mm is assigned to the bullet with a gradual mesh size decrease to 0.4 mm as it approaches the apex of the bullet. All sections of the bullet were assigned a hexahedral element. The complete isometric view of the dermal-inspired gradient core armor assembly mesh is illustrated in Figure 4.
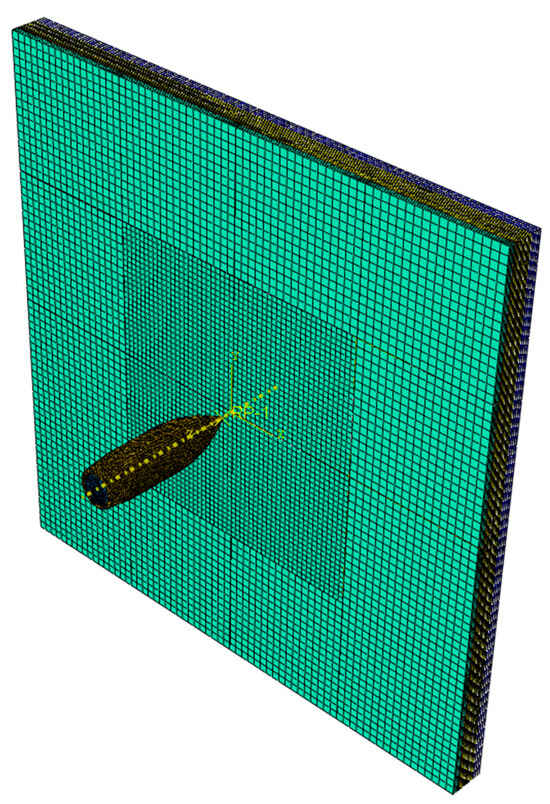
Figure 4.
Isometric view of mesh assembly.
Mesh Convergence
To verify mesh convergence, varying global seed sizes (3 mm, 2 mm, and 1.5 mm) were run at an initial velocity of 750 m/s using a discrete rigid bullet. The kinetic energy at the end of the analysis period was used to verify mesh convergence. With a reduction in mesh size from 1.5 mm to 1.3 mm, there was a minor kinetic energy increment of less than 5%, which implies model mesh convergence. The change in results between the two mesh sizes was less than 3.23%. The assigned mesh was applied to the model to perform the final analysis at various velocities.
2.3. Material Properties
The ceramic plate and inserts were modeled based on the properties of either alumina, silicon carbide, or boron carbide and observed the Johnson–Holmquist 2 (JH-2) damage model, which describes the strength and the gradual behavior of accumulated damage in a material. For the gradient metal core, the material under study was either titanium, aluminum, or armor steel and observed the high strain rate loading behavior under the Johnson–Cook material damage model. The composite layer of the armor was assigned glass epoxy material properties and reacted to impact under Hashin damage criteria. Hardened steel, with high fatigue, toughness, and torsional strength, served as the material for the bullet. The mechanical properties of boron carbide [17], silicon carbide [18], alumina [18], aluminum [19], titanium [19,20], hardened steel 4340 [21,22], and armor steel [23] were used in the model.
2.4. Interactions
2.4.1. Multipoint Constraint
A multipoint (tie-type) constraint was created between the different contacting surfaces to ensure a good relationship, like that of an epoxy adhesive bond, between the surfaces in a real-world scenario; this is to ensure good resistance to shear and tensile stresses and minimize delamination of the various parts of the armor when ballistic impact occurs. For the interaction between the ceramic layer and the armor core, a ceramic surface was chosen as the master layer, and the armor core surface was chosen as the slave surface. Similarly, the metal surface interacting with the armor core was elected as the master surface, with the armor core elected as the slave surface. For the different levels of the armor core layer, the bottom part of level 1 in contact with the top part of level 2 served as the slave surface, with the top part of level 2 serving as the master surface. Similarly, the top part of level 3 in contact with the bottom part of level 2 served as the slave surface, with the bottom part of level 2 serving as the master serve. For the interaction between the core metal cavity and the ceramic inserts, the ceramic inserts served as the slave, with the cavities acting as the master surface.
2.4.2. Contact Interaction
A general contact (explicit) interaction was created at the initial step of the simulation, with a penalty tangential behavior having a friction coefficient of 0.1 chosen for the global property assignment. The friction coefficient of 0.1 was used between the metal and ceramic surface [24]. In addition to the tangential behavior, normal behavior with a hard contact pressure–overclosure relationship and a default constraint enforcement method was applied to the model [24]. Pressure–overclosure signifies the amount of contact pressure in the normal direction that is created for penetration to occur. To obtain a more refined interaction between the bullet and the armor system, a surface-to-surface interaction was created, with the surface of the armor serving as the master surface and the central node of the armor’s ceramic plate serving as the slave.
2.5. Boundary Conditions
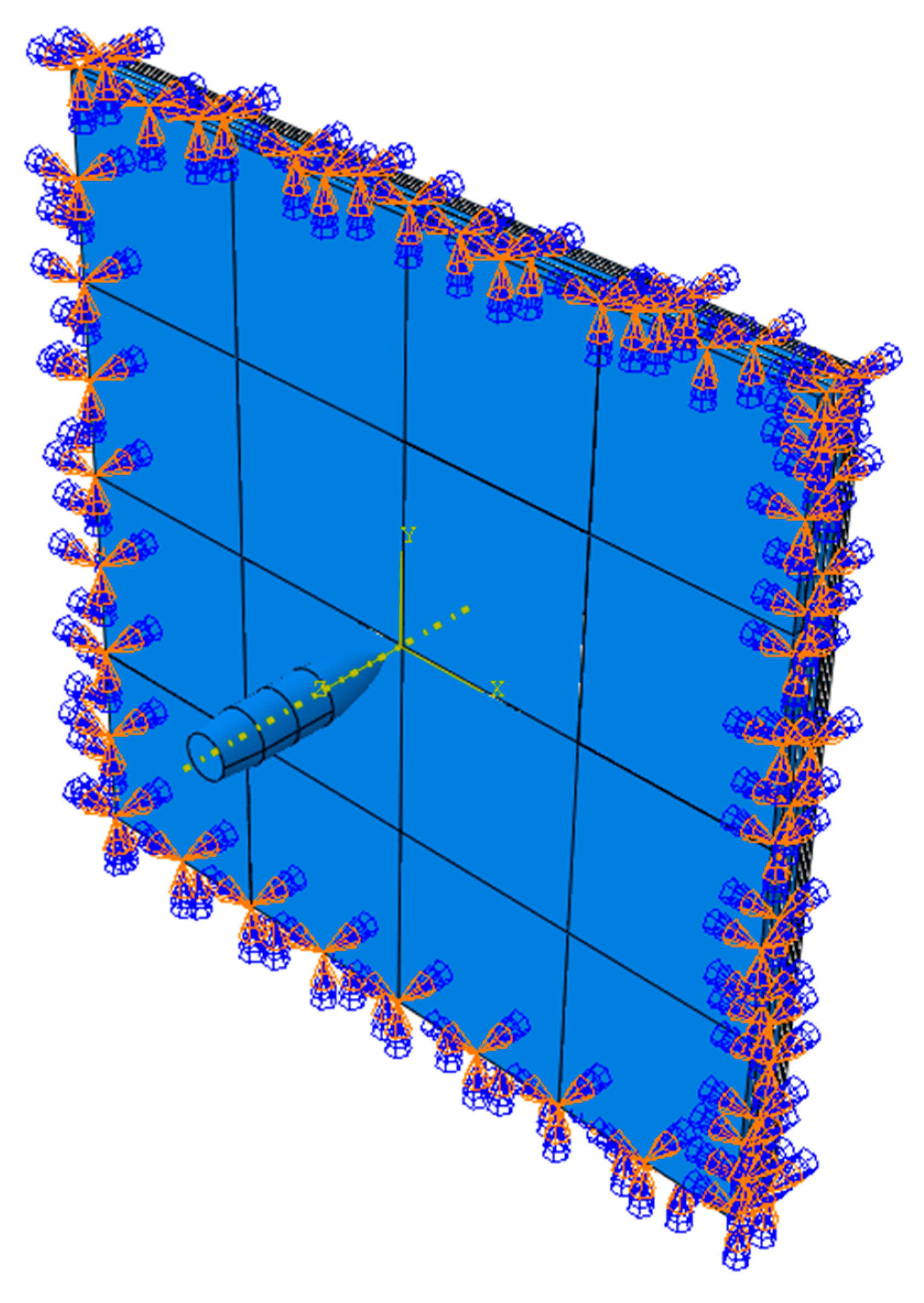
The entire outer region of the armor was fixed in all the translational and rotational degrees of freedom and is shown in Figure 5.
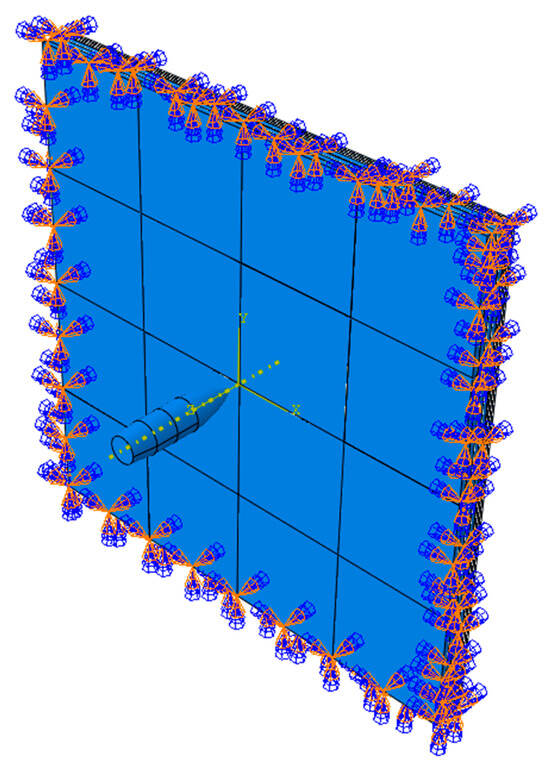
Figure 5.
Armor boundary condition.
2.6. Load
Toward the armor, a predefined velocity value was assigned to the bullet at the initial step of the simulation. To verify the true capability of the chosen armor, varying bullet velocity simulations were conducted.
2.7. Mechanism of Failure
The understanding of how different materials react to impact is essential to the finite element analysis of an armor system since it influences the behavior of the different materials and their interconnected reaction during deformation. This section discusses the fracture and failure mechanisms for the different material types used for the dermal-inspired gradient core sandwich armor.
2.7.1. Mechanism of Failure for Ceramics
Ceramics are classified under brittle materials since they have low tensile strength and high compressive strength. When a brittle material is impacted by a load, microfractures occur, leading to continuous degradation of the material. The Johnson–Holmquist 2 (JH-2) model [25], which assumes that the strength equation is a function of pressure, is deemed an ideal failure model when considering deformation and continuous degradation and was used for the modeling of the ceramic components of the armor system.
For the Johnson–Holmquist 2 model, strength is defined using stress (), as stated in the two equations below:
where is the intact equivalent stress, D is the damage variable, and is the fractured equivalent stress. The stress at the Hugoniot elastic limit () is calculated as follows:
For the above equation, is the pressure at the Hugoniot elastic limit. Below is the strain rate in the case of undamaged and totally damaged material states as per the Johnson–Holmquist 2 definition:
where A, B, C, M, and N are parameters of the material under consideration, with the normalized pressure () being calculated as follows:
and the normalized maximum tensile hydrostatic pressure () stated as the following:
Just like the Johnson–Cook model, the Johnson–Holmquist 2 model also assumes that damage increases along with plastic strain as per the equations below:
The pressure and volume relationship for ceramics is given by the interactive equation below, where , , and are material constants.
At material failure, a pressure increment is introduced, which results in the following pressure calculation:
Below is an illustration of the volumetric strain and pressure relation.
2.7.2. Mechanism of Failure for Metals
Due to the ductile behavior of metals, they deform when impacted by tensile load, following the description of the stress–strain plot. Within the elastic limit, the deformed metal will un-deform back to its initial condition after the impact. However, within the plastic region, a deformed metal will remain permanently deformed. Below is an illustration of the ductile material stress–strain plot.
To mimic the fracture behavior due to the sudden impact experienced by the metal components of the armor system in ABAQUS CAE, the Johnson–Cook plasticity deformation model is used to model the high strain rate deformation [26].
In the Johnson–Cook failure model, the equivalent stress () is defined as below:
where A, B, C, m, and n are material constants, which are the yield stress of the material, strain hardening constant, strengthening coefficient of strain rate, strain hardening coefficient, and thermal softening coefficient. is the applied equivalent plastic strain, and
is the equivalent strain rate, with a reference strain rate of . In the Johnson–Cook model, is calculated as follows:
with being the reference temperature in question and being the material’s melting point.
2.7.3. Mechanism of Failure for Composite
For composite material failure, there is a mixture of damage initiation and evolution in the laminas following Hashin’s damage criteria, where damage initiation is referred to as the moment where the breakdown of the lamina’s stiffness is observed, and damage evolution refers to the behavior of the lamina after the initiation damage has occurred. Overall, the Hashin’s damage criteria incorporate the collective damage mechanism data response of the fiber and matrix tension and compression during impact [27]. Fiber tension on the progressive curve is defined as follows:
where is greater than 0. On the other side of the spectrum, fiber compression on the progressive curve is defined below:
where is less than 0. The matrix’s progressive damage behavior is based on the following two equations:
where is greater than or equal to 0 for matrix tension.
where is less than 0 for matrix compression.
The above symbols are defined below:
- = effective stress tensor.
- = longitudinal tensile strength.
- = longitudinal compressive strength.
- = transverse tensile strength.
- = transverse compressive strength.
- = longitudinal shear strength.
- = transverse shear strength.
The post-damage initiation characteristics of a composite material, known as damage evolution, depict the degradation rate of stiffness post-damage initiation point. The damage evolution characteristic of a composite is based on a scalar point of approach:
For the equation, D represents the combination of all active damage mechanisms, and the total loss of load bearing capability of the composite is observed when the variable D is equal to one.
2.8. Model Validation
The segmented sandwich armor is made up of a tiled ceramic layer, three-level gradient core, and a composite backing face. Titanium armor with silicon carbide inserts—which are similar to the materials used in the segmented sandwich armor—was used for model validation. The selection of titanium and silicon carbide for the armor’s design is due to a multifaceted set of advantages. Combining the extreme hardness and durability of silicon carbide with the strength and toughness inherent in titanium results in armor that excels in hardness and toughness, effectively safeguarding against diverse ballistic threats. Titanium’s lightweight nature contributes to overall weight reduction, crucial for enhancing wearer comfort and mobility in personal protection applications. The synergistic interplay of silicon carbide’s hardness and titanium’s toughness endows the armor with a unique multi-hit capability, pivotal in scenarios with the potential for repeated attacks. Additionally, silicon carbide’s excellent abrasion resistance ensures the armor’s resilience against wear and tear, particularly vital for deployments in challenging environments. The ductility of titanium, facilitating energy absorption through deformation, complements silicon carbide’s attributes, enhancing the overall energy absorption capacity. Furthermore, both titanium and silicon carbide contribute to corrosion resistance, fortifying the armor’s durability and longevity, particularly in demanding environmental conditions. In crafting armor systems, these distinctive properties are strategically leveraged to strike a balance that effectively addresses diverse threats while considering factors such as weight, durability, and multi-hit capability. The experimental analysis of the penetration resistance of ceramic–metal hybrid structures by Chao et al. [28] studied the penetration resistance ability of a target armor by launching a projectile at the armor using a ballistic rifle and studying the armor’s response to impact. To better understand the armor’s impact behavior, an ABAQUS CAE model following the same part dimensions, material properties, and assembly was fashioned after a real-life model, and the impact was analyzed at the respective test velocities. This model serves as a validation of the results attained from the experimental test.
In Chao et al.’s [28] model, a 100 mm × 120 mm × 19 mm titanium frame with five equally sized and spaced 16 mm × 10 mm 100 mm silicon carbide prism inserts adhesively bonded to the same dimension cavities made inside the metal block. The target armor was impact analyzed with a 52 mm ogive nose steel bullet with a diameter of 10.8 mm, shot at initial velocities of 835 m/s, 855 m/s, and 940 m/s.
To validate the experimental and simulated results, the bullet’s residual velocity, backplane deformation, kinetic energy, and residual length were compared to understand their similarity and deviations at the 3 different velocity profiles. Results from Chao et al.’s [28] experiment showed an impactor’s residual velocity of 0 m/s, 0 m/s, and 394 m/s from 835 m/s, 855 m/s, and 940 m/s, respectively. For the ABAQUS CAE model, the residual velocities for the 835 m/s, 855 m/s, and 940 m/s test samples were 0 m/s, 0 m/s, and 373 m/s at the end of the simulation period. The residual length of the 52 mm projectile for the 835 m/s, 855 m/s, and 940 m/s test samples in Chao et al.’s [28] experiment resulted in projectile residual lengths of 25 mm, 24 mm, and 22 mm, respectively; however, in the ABAQUS CAE model, the resulting residual lengths were 24.04 mm, 23.96 mm, and 22.66 mm. Chao et al.’s [28] experiment saw a back plane deformation of 14 mm, 15 mm, and 10 mm, whilst the ABAQUS CAE model observed a back plane deformation of 9.17 mm, 10.71 mm, and 8.18 mm for the 835 m/s, 855 m/s, and 940 m/s test samples. Finally for the residual kinetic energy, the experimental and ABAQUS CAE models had similar behavior, with the 835 m/s and 855 m/s test samples having a zero residual kinetic energy and the 940 m/s test samples having 1250 J and 1210 J for Chao et al.’s [20] experiment and the ABAQUS CAE model, respectively. Table 1 shows the validation summary, which compares the experimental and numerical results.

Table 1.
Validation summary. Comparison of experimental and numerical results.
In both models, the response of the armor to impact was similar, with minor variation between the experimental and simulation model. For both the experimental and simulation model, partial perforation was observed at 835 m/s and 855 m/s initial velocity, with full penetration occurring at 940 m/s initial velocity. The similarity in the results and minor deviation between the ABAQUS CAE model and the Chao et al. [28] experiment attest to the fact that ABAQUS CAE can be used to validate a real-world experiment.
3. Results and Discussions
To study the parametric behavior of the segmented sandwich composite armor system, various simulations were carried out to understand the main effects of the system and to determine the optimal armor design.
3.1. Ceramic and Metal Material Selection Results
To determine the specific metal and ceramic materials for the armor system, a plate was modeled with material properties from the proposed list of ceramics (silicon carbide, boron carbide, and alumina) and metals (armor steel, titanium, and aluminum). Simulations were then created, subjecting the single-layer plate to a deformable steel bullet with velocities of 600 m/s and 950 m/s to better understand their behavior and aid in selecting the best option for use.
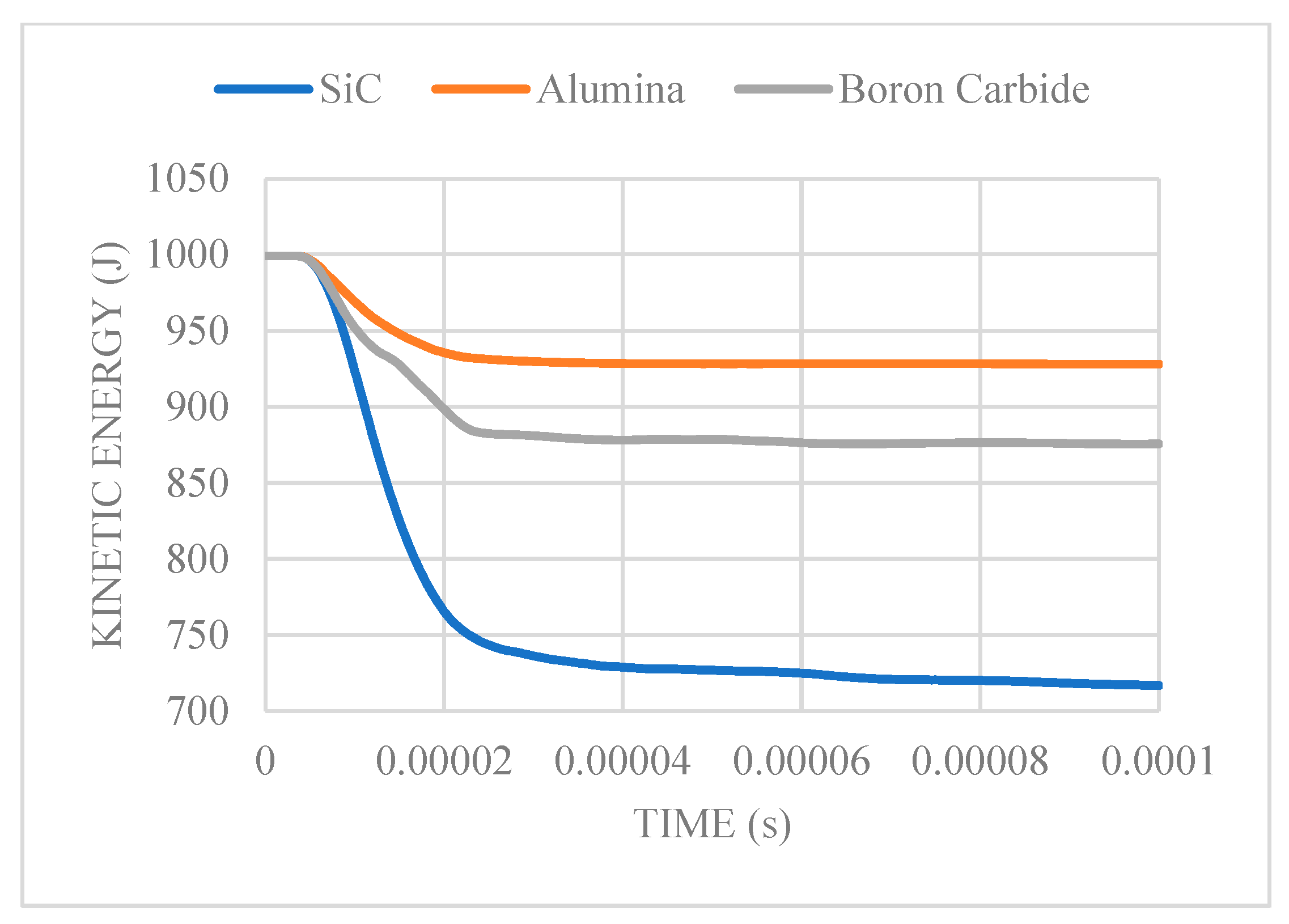
Using the kinetic energy criterion, silicon carbide exhibited considerably lower kinetic energy after impact. At an initial bullet velocity of 600 m/s, the bullet penetrates the silicon carbide plate, causing excessive fragmentation in the silicon carbide plate. Among the various ceramic materials, bullet deformation is greatest with silicon carbide.
Figure 6 illustrates the kinetic energy plot for the various ceramic materials. From the kinetic energy plot, the superior capabilities of silicon carbide over boron carbide and alumina in impeding the movement of the bullet can be deduced. At 20 microseconds (penetration moment), there is an approximately 25% drop in the kinetic energy of silicon carbide, with boron carbide dropping by 10%, and alumina having the smallest kinetic energy drop at 7.1%.
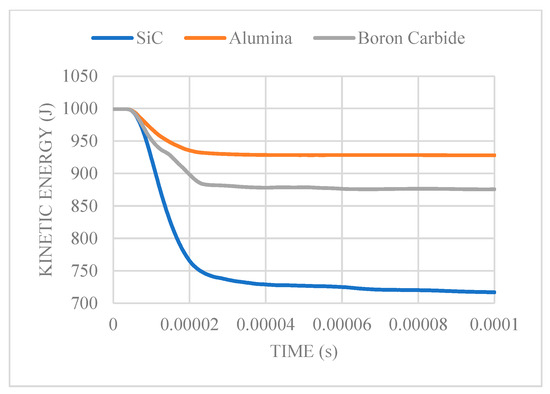
Figure 6.
Kinetic energy vs. time plot at an initial velocity of 600 m/s.
A summary of the results from the various ceramic impact analyses at varying velocities is tabulated in Table 2.

Table 2.
Ceramic plate performances at varying impact velocities.
From the summary table above, it is observed that the variation between the initial and residual kinetic energy is wider at 600 m/s. At 900 m/s, the variation reduces in terms of the percentage drop. Using kinetic energy, silicon carbide was identified as the superior material for use, followed by boron carbide, with alumina being the least preferred for use based on the simulation results.
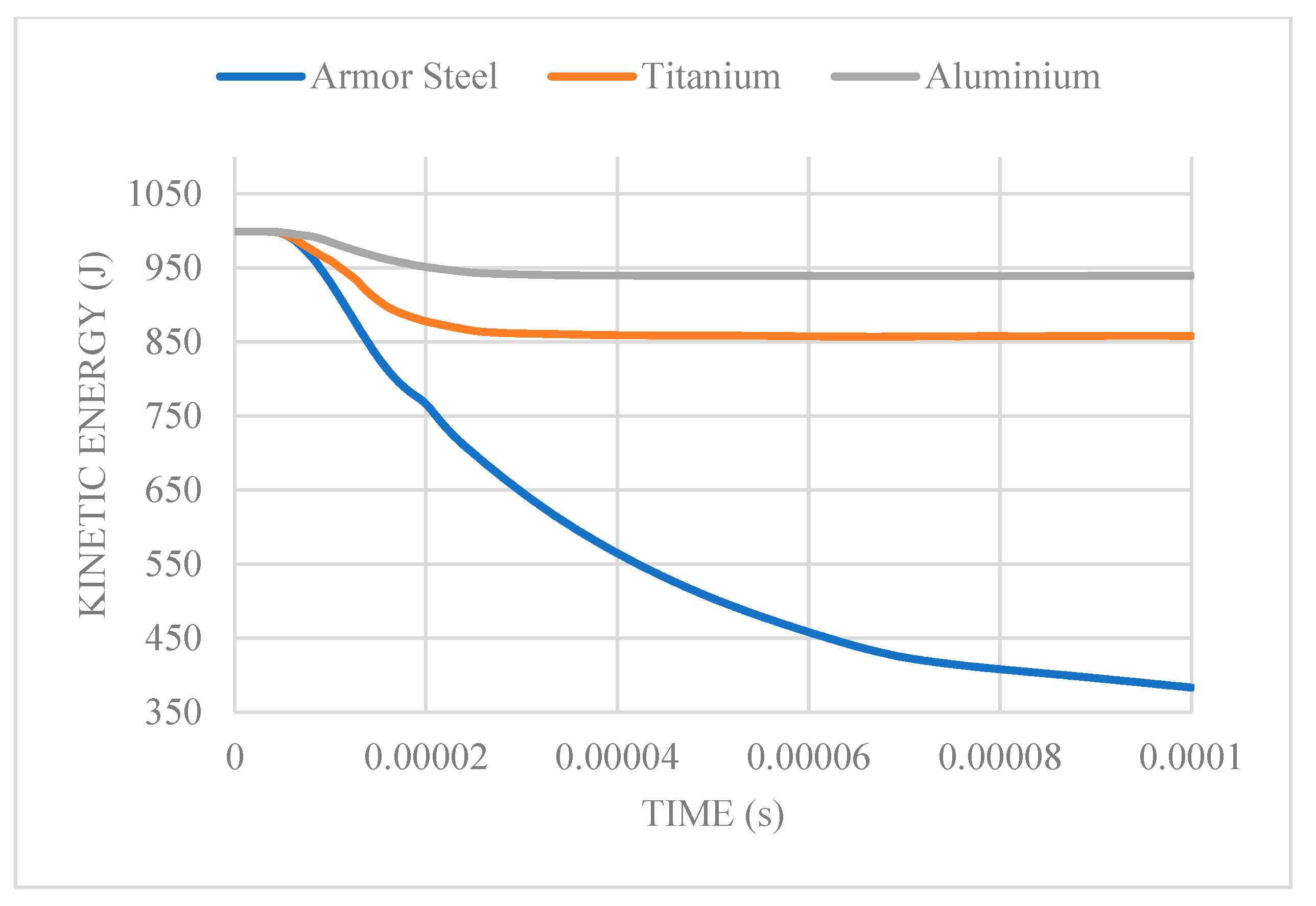
The kinetic plot for the various metal materials at a 600 m/s bullet velocity in Figure 7 shows that armor steel had the greatest regression, exhibiting a 61.6% drop from the initial kinetic energy value. Aluminum had the least regression, experiencing a 6% drop, with titanium having a regression of 14.1%. After the penetration period, kinetic energy regression stabilized linearly for titanium and aluminum, while with armor steel, continuous regression was noted over the simulation period.
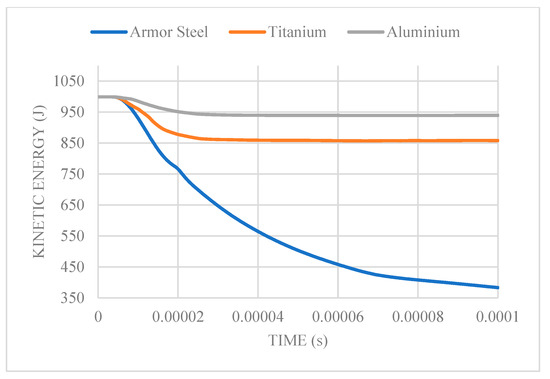
Figure 7.
Kinetic energy vs. time plot at an impact velocity of 600 m/s.
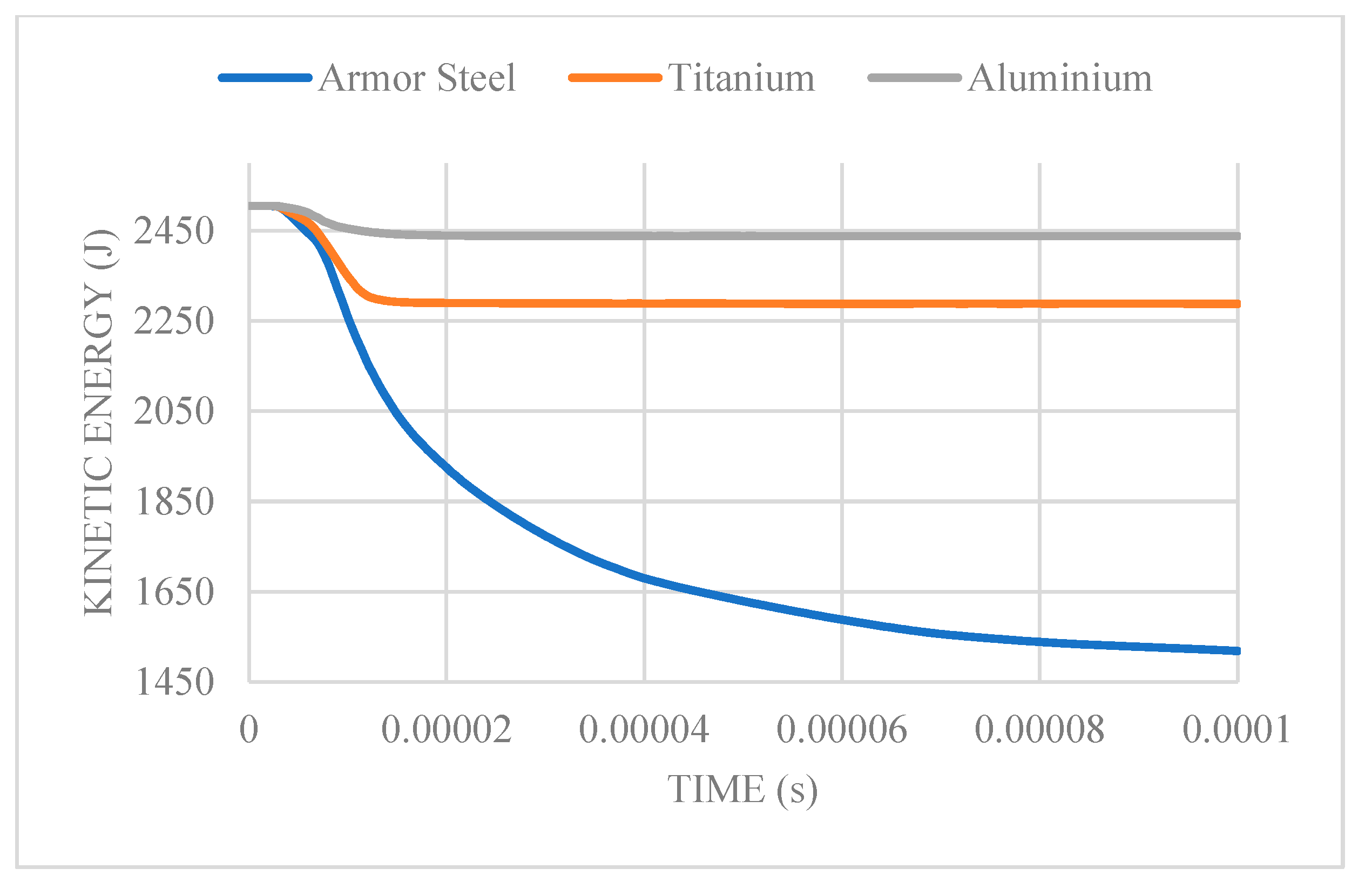
The kinetic plot for the various metal materials at a 950 m/s bullet velocity mirrors that of the plot for kinetic energy for the different metal materials at a 600 m/s bullet velocity. Figure 8 allows for us to deduce that armor steel exhibited the greatest regression, showing a 39.4% drop from the initial kinetic energy value. Aluminum had the least regression, observing a 2.68% drop, with titanium having a regression of 8.7%. After the penetration period, kinetic energy regression stabilizes linearly for titanium and aluminum, while armor steel exhibits continuous regression over the simulation period.
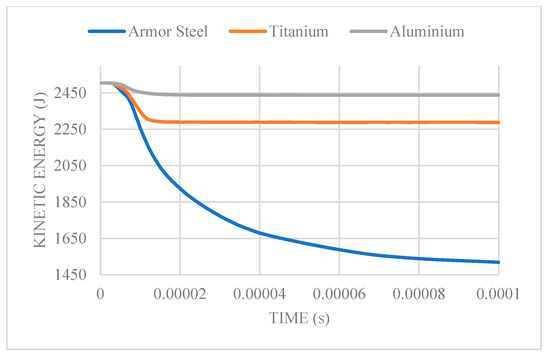
Figure 8.
Kinetic energy vs. time plot at an impact velocity of 950 m/s.
A summary of the results from the various metal impact analyses at varying velocities is tabulated in Table 3

Table 3.
Metal plate performances at a varying impact velocities.
From the summary table above, armor steel proves to be considerably more advantageous for bullet resistance than titanium or aluminum. It is noteworthy that the variation between the initial and residual kinetic energy and velocity decreases with an increase in initial velocity. Despite its approximately 40 percent higher density than the other metals, armor steel is identified as the superior material for use based on the validation criteria.
Upon initial validation results, the proposed plan is to create an armor system with a segmented ceramic front face and ceramic inserts. This configuration allows for localized replacement and reuse after impact, ensuring that only the damaged part of the armor system is replaced, if necessary, ultimately reducing the maintenance/repair cost of the armor. Based on the validation and engineering reasoning, silicon carbide will serve as the ceramic material for use in the armor, with titanium serving as the metal for the armor system. Although armor steel has superior properties to titanium, it is substituted for titanium, mainly due to its approximately 40 percent density difference and the fact there are more data available in the literature for authentication of the design’s behavior.
To determine the ideal shape for a unit ceramic tile, ease of manufacturing in terms of ceramic shape cutting, assembly process, and binding complexity are used as the selection criteria. Based on quantitative engineering reasoning, quadrilateral-shaped tiles are deemed the best for use.
3.2. Ceramic Thickness Selection Results
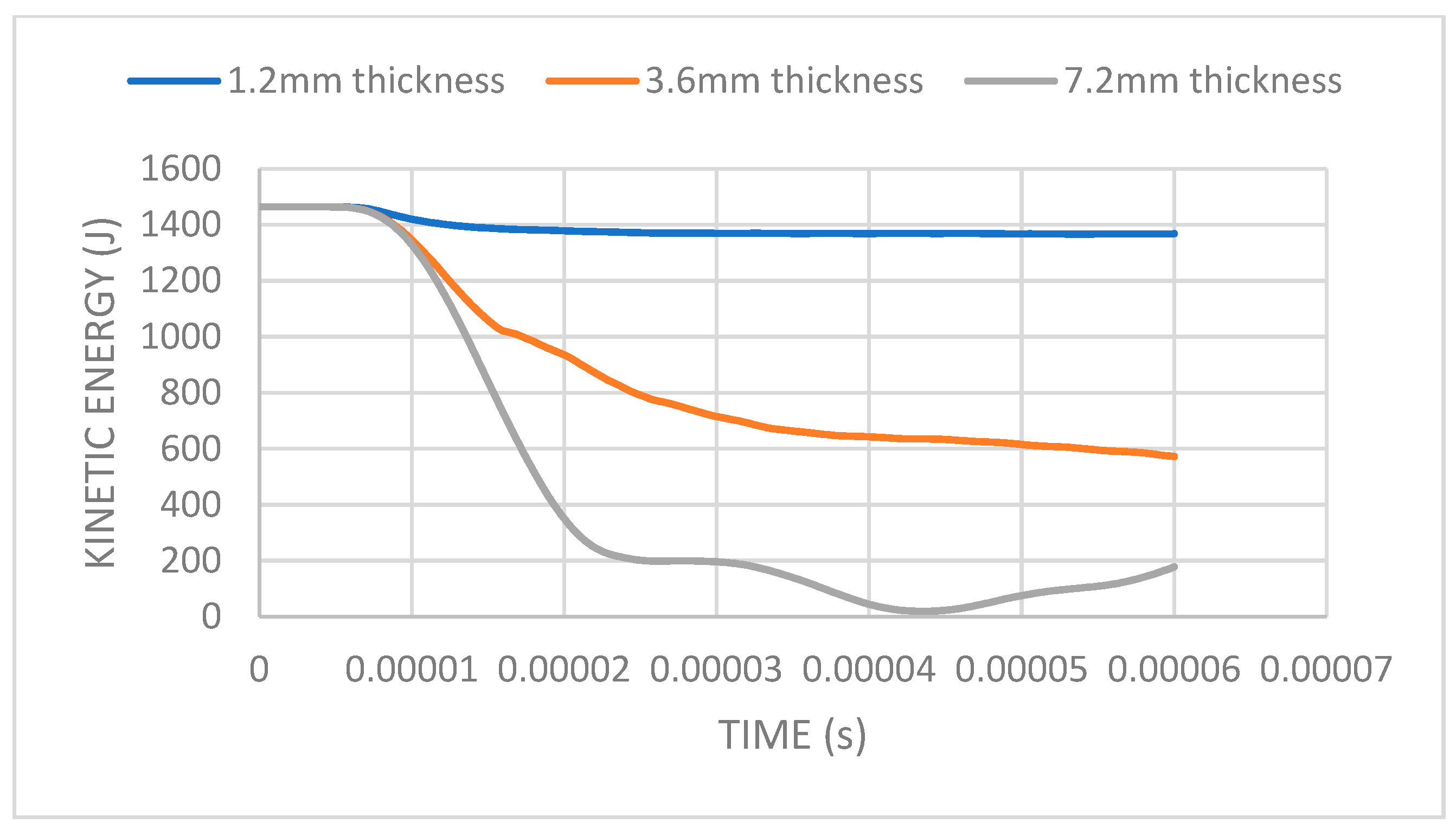
Since the initial ceramic layer of an armor plays an influential part in the impactor tip breaking and the drastic deceleration of the bullet, and ultimately minimizes impact damage, an extensive analysis was carried out to determine the ideal thickness of the ceramic layer that compliments the rest of the armor system. By performing simulation analysis on 1.2 mm, 3.6 mm, and 7.2 mm thick segmented ceramic plates at 600 m/s and 950 ms initial velocity, main effects analysis was used determine the ideal ceramic thickness for the final design using kinetic energy as the determining parameter.
As indicated in Figure 9, at 600 m/s initial bullet velocity, there is a transferable behavior between the thickness of the ceramic layer and the corresponding residual kinetic energy. By tripling the thickness of the ceramic from 1.2 mm to 3.6 mm, the impact resistance capability of the armor is only improved by 58% with the additional thickness increment to 7.2 mm improving the residual kinetic energy by 79%, highlighting that an improvement in thickness does not contribute to an equal improvement in the ballistic capabilities of the armor.
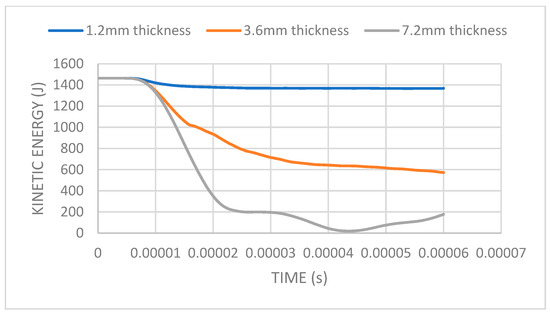
Figure 9.
Ceramic thickness selection using kinetic energy at an impact velocity of 600 m/s.
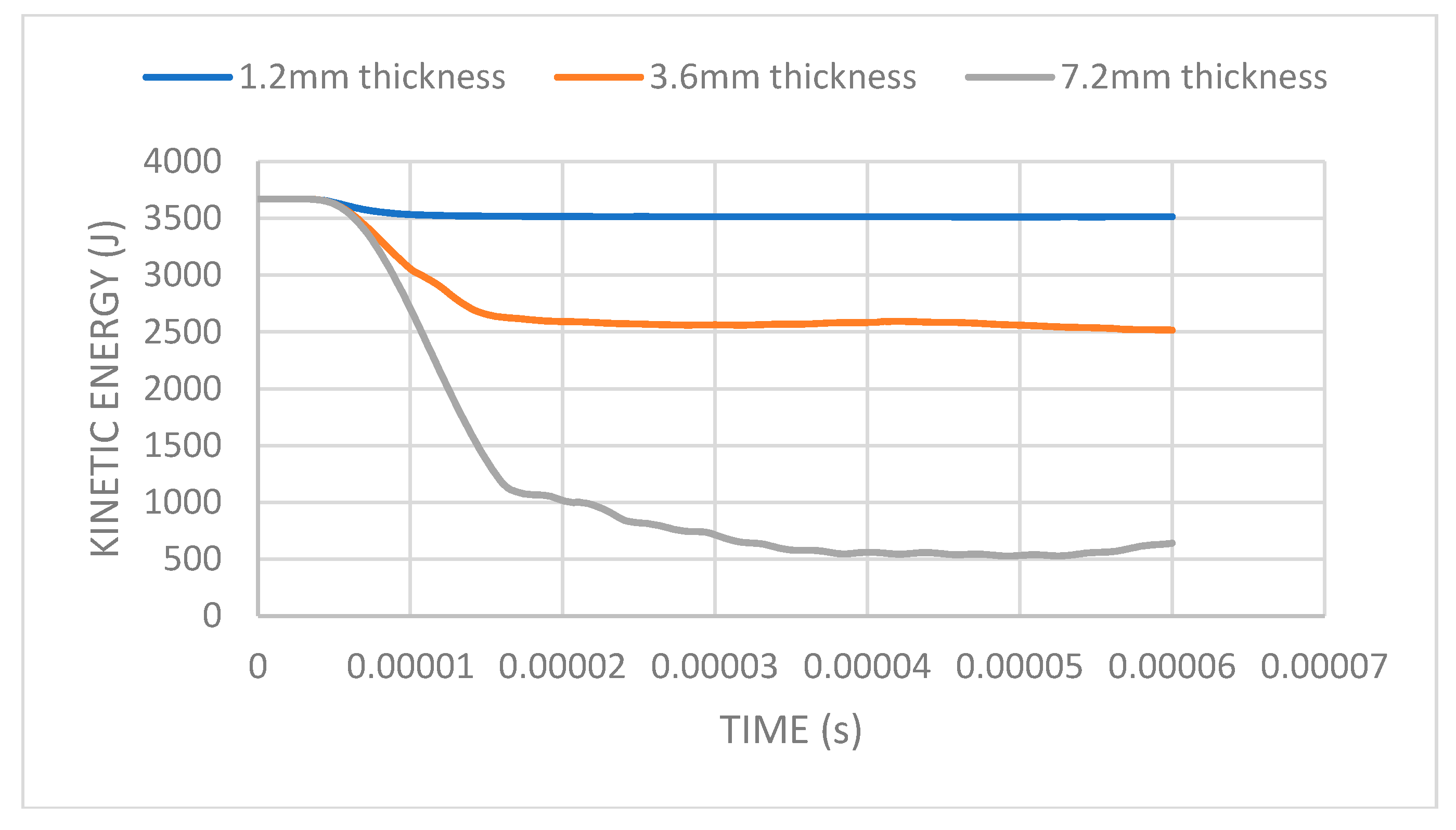
Similar to the pattern observed at 600 m/s initial bullet velocity, Figure 10, which illustrates the kinetic energy behavior at 950 m/s initial bullet velocity, mimics the same transferable behavior between the thickness of the ceramic layer and the corresponding residual kinetic energy. By tripling the thickness of the ceramic from 1.2 mm to 3.6 mm, the impact resistance capability of the armor is only improved by 28.4%, with the additional thickness increment to 7.2 mm improving the residual kinetic energy by 75%, again indicating that an improvement in thickness does not contribute to an equal improvement in the ballistic capabilities of the armor.
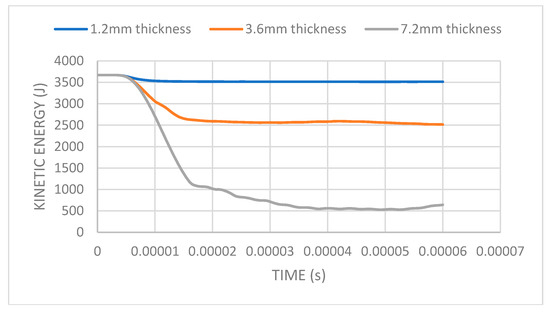
Figure 10.
Ceramic thickness selection using kinetic energy at an impact velocity of 950 m/s.
Based on the deduction made from kinetic plots analysis, which concludes that an increment in the thickness does not translate to the same increment in ballistic resistance, it is ideal to use the 1.2 mm thick ceramic tile for the ceramic layer in the final design of the armor, ensuring optimal armor design with reduced weight due to the increased thickness.
3.3. Ballistic Simulation of Final Model
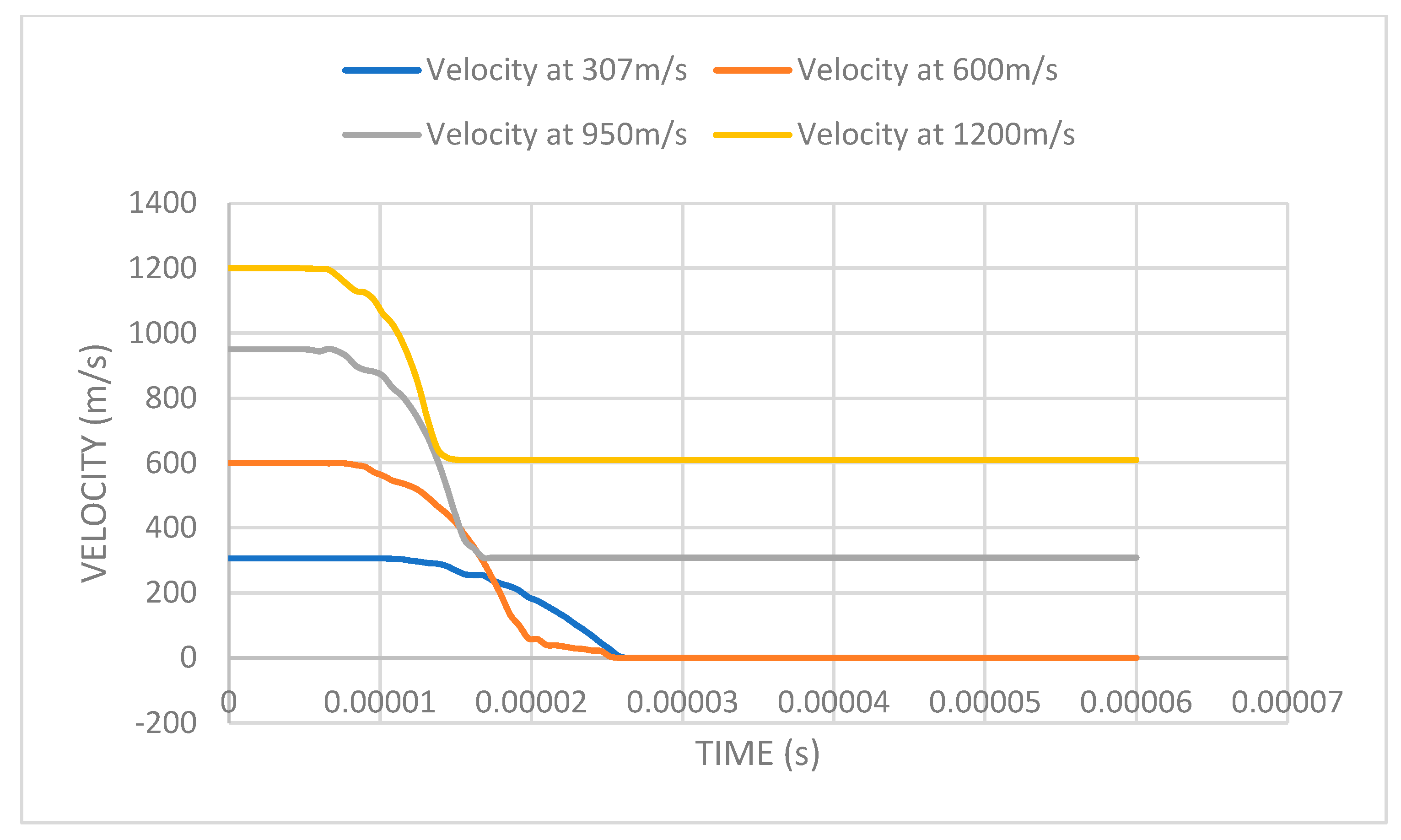
The chosen design of the segmented gradient core sandwich composite armor is composed of a 1.2 mm thick silicon carbide front face in a segmented rectangular tile arrangement and a 2 mm uniform glass epoxy composite in a 0/45/90/-45 0.5 mm lamina configuration serving as the backing face. Sandwiched between the front face and the backing face is a 3.6 mm high metal-reinforced ceramic composite core constructed from three levels of gradually reducing sizes of hexagonal metal frame filled with ceramics. To determine the behavior and better understand the response to impact of the armor system, simulations were created, subjecting the armor to impact from an impactor travelling at 307 m/s, 600 m/s, 950 m/s, and 1200 m/s velocities. Considering the deformation at the various velocities, it is observed that the bullet has a gradual velocity decrease as it travels towards the armor until it impacts the armor. The impact causes a significant velocity decrease and initiates minor bullet deformation, which in turn slow down the bullet further. In tandem, the adhesive (tie constraint) that bonds the different layers together slowly decays, causing weakness within the entire armor. This results in sectional delamination of the composite layer around the impact region mainly due to the ceramic fragments from the damaged armor core hitting the composite layer. At lower impact velocity (307 m/s and 600 m/s), although there was damage within the armor system, penetration did not occur; however, at higher velocity profiles, full penetration was observed within the armor.
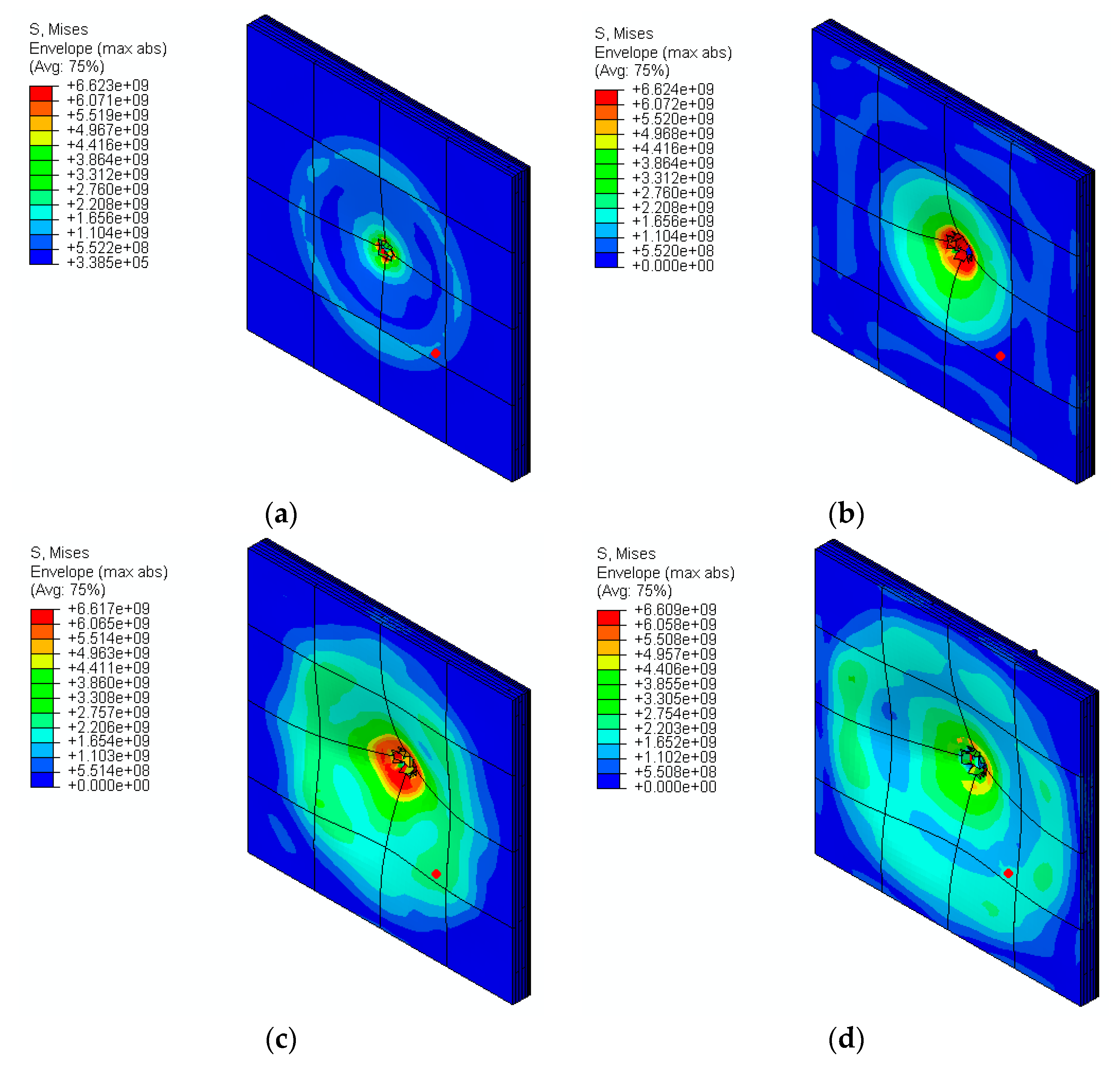
By studying the residual velocity of the bullet, bullet deformation, and damage dissipation energy of the model, the behavior of the armor at the different velocities can be quantified. For residual velocity plots, bullet repulsion velocity (ricochet action) is considered negligible in this study, to better evaluate penetration resistance. The plots below provide a graphical representation of the armor’s performance at the different velocities. von Mises stress plots at step times of 10 μs, 15 μs, 20 μs, and 25 μs are shown in Figure 11a–d, respectively. As time increases, the bullet penetration and von Mises stress distribution areas increase.
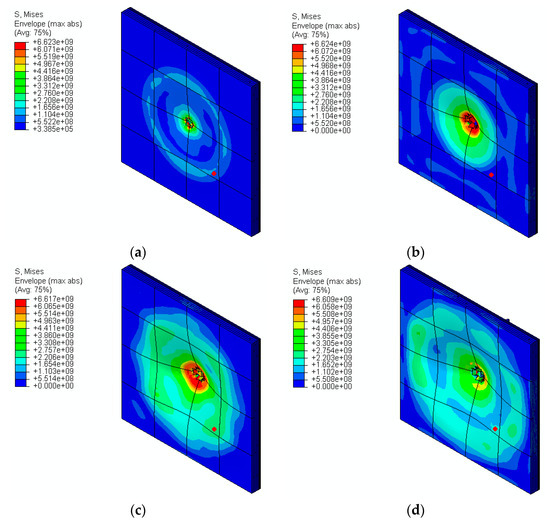
Figure 11.
von Mises stress (Pa) at time instances (a) 10 μs, (b) 15 μs, (c) 20 μs, and (d) 25 μs at an impact velocity of 950 m/s.
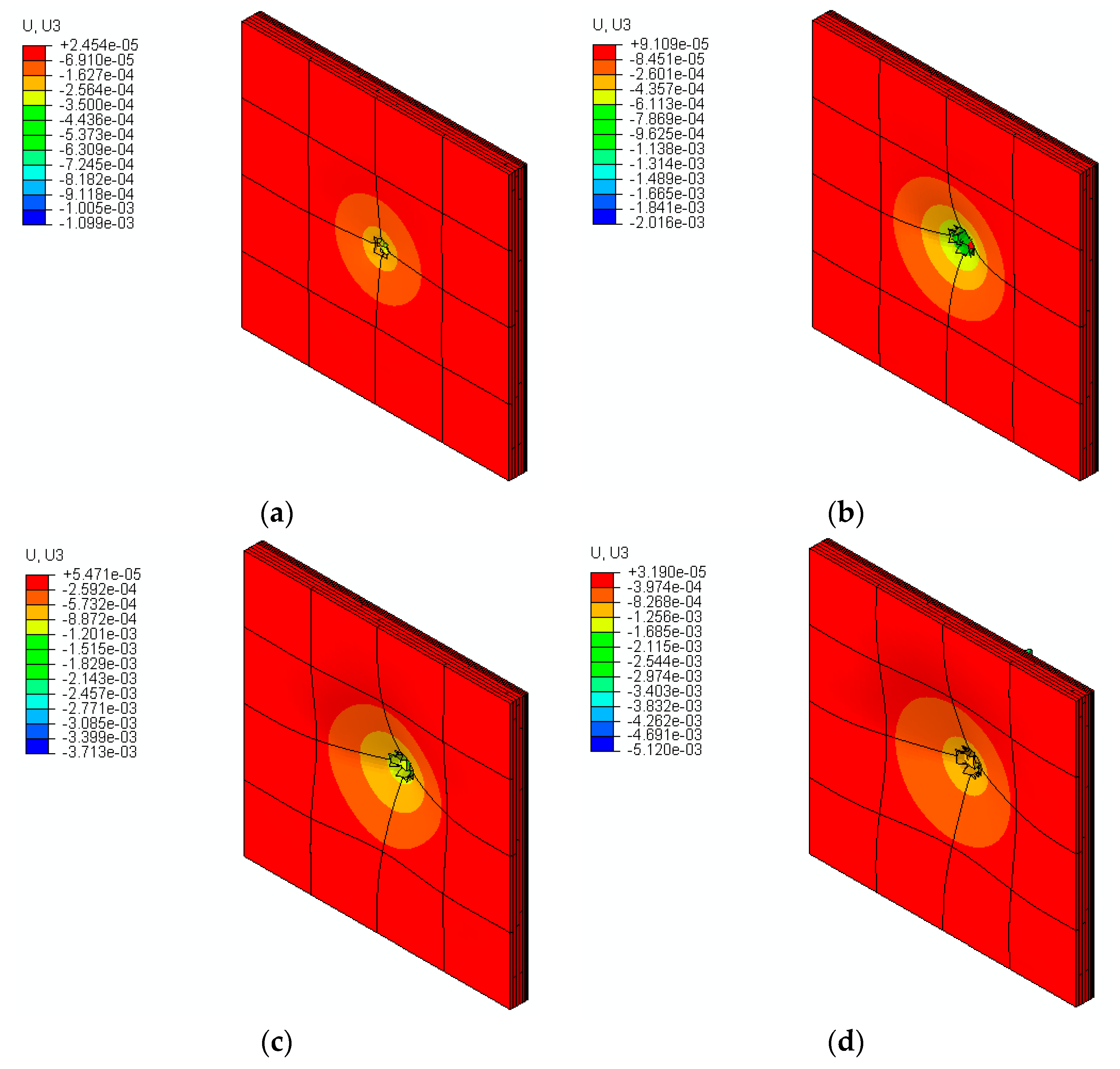
Out-of-plane displacement plots at step times of 10 μs, 15 μs, 20 μs, and 25 μs are shown in Figure 12a–d, respectively. As time increases, the bullet impact, armor penetration, and out-of-plane displacement increase (negative displacement is bullet penetration direction). The maximum displacement is found at the center of the armor.
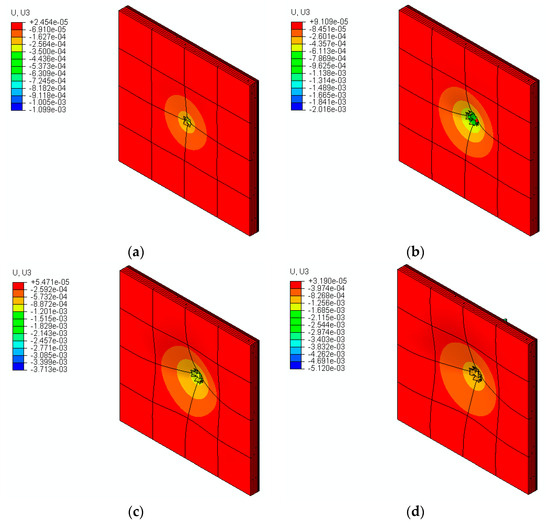
Figure 12.
Out-of-plane displacement (m) at time instances (a) 10 μs, (b) 15 μs, (c) 20 μs, (d) and 25 μs at an impact velocity of 950 m/s.
From the velocity plots shown in Figure 13, it is observed that bullet deceleration for the non-penetration simulations occurs earlier with an increase in initial velocity profile; this is due to the fact that the increase in velocity is directly proportional to the rate of deformation of the bullet, leading to an accelerated velocity drop due to the bullet tip deformation effect. For velocity simulation where penetration occurs, the higher deceleration rate plateaus and maintains the post-penetration velocity.
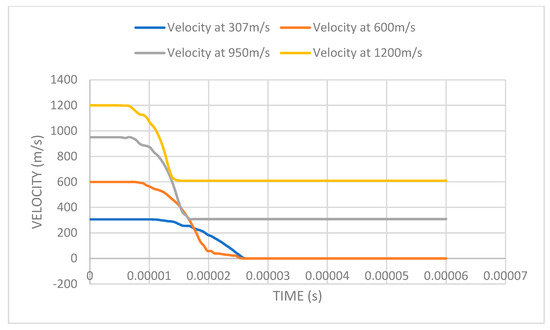
Figure 13.
Velocity vs. time plot for dermal-inspired armor.
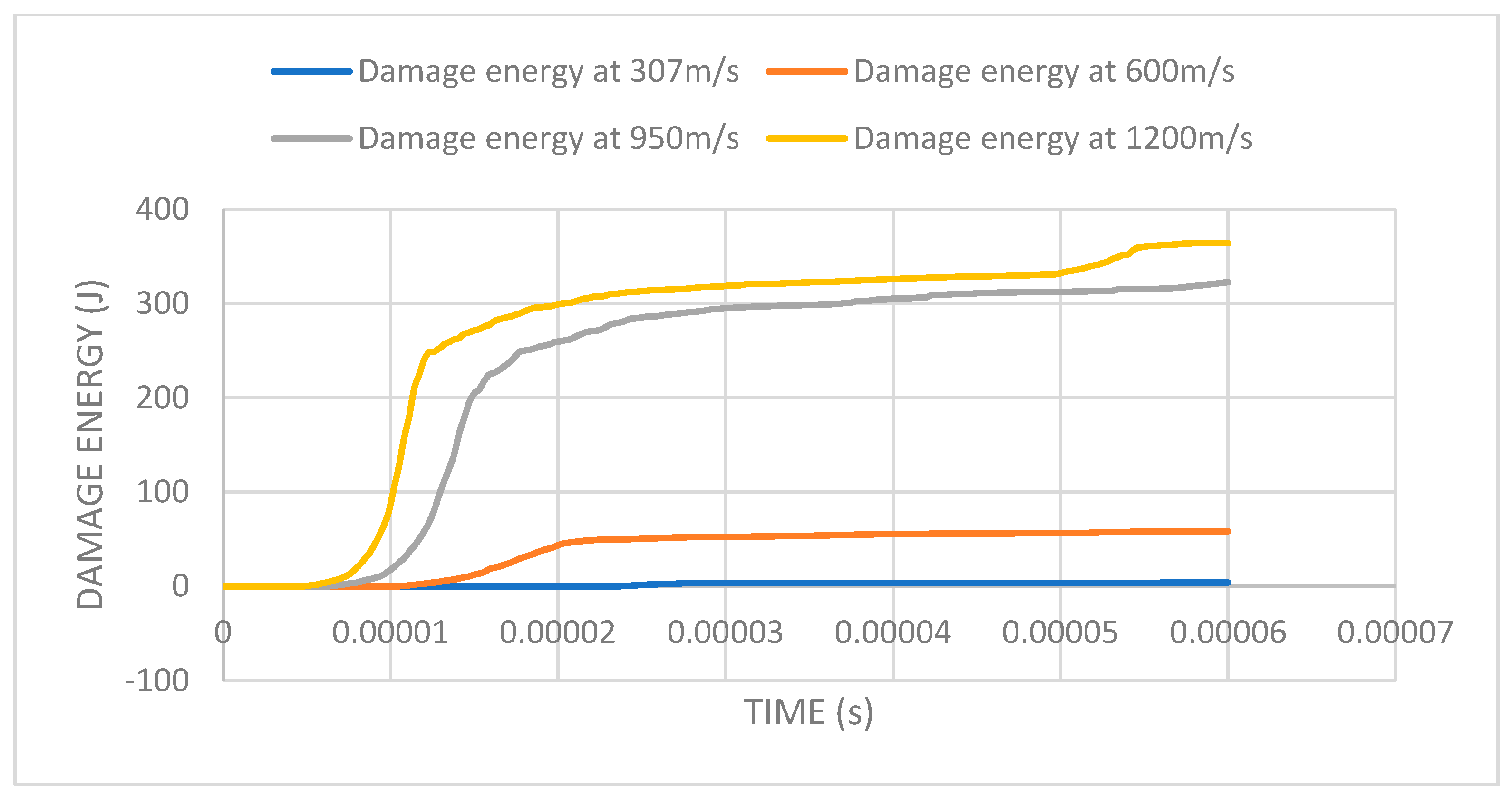
The damage energy dissipation plot shown in Figure 14 considers the overall unrecoverable energy lost when fracture or breakdown occurs. From the plot, the damage dissipation energy is noted to increase with an increase in velocity. Using the 60-microsecond duration, negligible damage energy dissipation of 3.87 joules occurs at 307 m/s bullet velocity, with the armor experiencing a 94% slightly elevated damage energy dissipation at 600 m/s bullet velocity. Bullet velocities of 950 m/s and 1200 m/s introduce significantly more damage dissipation energy to the armor system, with the residual damage energy dissipation being noted, respectively, as 322.715 joules and 364.478 joules. Figure 13 shows the damage dissipation energy over the duration of the simulation, giving insight into the correlation between armor damage and impactor velocity.
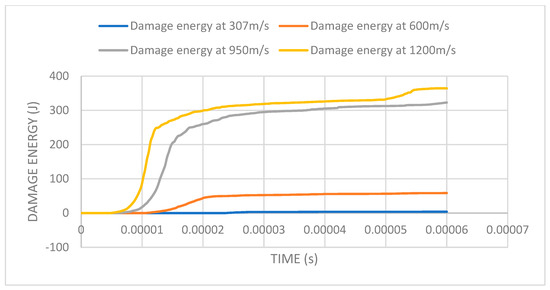
Figure 14.
Damage dissipation energy vs. time plot of armor system.
A summary of the final model’s analysis is tabulated in Table 4.

Table 4.
Summary table for chosen model.
From the summary table above, the segment gradient core sandwich composite armor design is sufficient for low- to mid-level ballistic resistance, having the ability to prevent bullet penetration at a simulated velocity profile of 600 m/s. Although penetration occurred at 950 m/s and 1200 m/s bullet velocity, damage is noted to be mostly focused on the impact region, with no back face deformation in the armor system due to the fact the ceramic portions fragment when failure occurs. Further explanation of the armor’s performance is detailed in the Conclusions section.
4. Conclusions
This study aimed to investigate the impact of ceramic and metal components, along with their configurations, on ballistic resistance. The findings revealed that silicon carbide exhibited superior impact resistance capabilities. Armor steel demonstrated exceptional properties in both low and high ballistic impact analyses, albeit with the observation of excessive petalling during impacts, potentially causing secondary damage to the underlying surface. Consequently, titanium is recommended for future works pertaining to personnel and equipment protection. The analysis of the chosen front face indicated that increasing the thickness of the ceramic layer did not proportionally enhance the armor’s impact resistance. The damage localized on the impact area in all ballistic impact tests, primarily due to the metal-reinforced ceramic core’s nature and the segmented front face. This design facilitated superior damage dispersion by delamination through adhesive disbanding and sacrificing the ceramic segment via fragmentation at the failure location. The ceramic front face, coupled with the metal-reinforced ceramic core, ensured bullet tip deformation, significantly reducing bullet velocity and penetration power while maintaining minimal armor weight. Although effective for low- and mid-level impact loading, the armor system may prove inadequate for continuous ballistic impact without part replacement, given its sacrificial nature to resist impact. Despite its effectiveness, the armor system presents notable limitations and disadvantages concerning energy dissipation. Challenges include potential core compression under high-velocity impacts, influencing the armor’s ability to dissipate energy effectively. Temperature sensitivity, moisture absorption affecting core properties, and difficulties in tailoring stiffness and flexibility parameters pose additional challenges. Repairing compromised core materials is challenging, affecting the armor’s long-term viability. Awareness of these limitations is crucial for optimizing the armor system for applications where effective energy dissipation is a critical requirement.
Author Contributions
Writing—original draft preparation, P.A.; review, editing and supervision, S.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Army Research Office (ARO), grant award number W911NF-18-1-0478.
Data Availability Statement
The data presented in this study are available on request from the corresponding author due to privacy reason.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Pengcheng, H.; Yuansheng, C.; Pan, Z.; Jun, L.; Haifu, Y.; Jianyong, C. A Metal/UHMWPE/SiC Multi-Layered Composite Armor Against Ballistic Impact of Flat-Nosed Projectile. Ceram. Int. 2021, 47, 22497–22513. [Google Scholar]
- Hare, P. What Is Composite Ballistic. Coventive Composites. 2019. Available online: https://coventivecomposites.com/explainers/what-is-composite-ballistic-armour/ (accessed on 29 November 2021).
- Ramin, R.; Maksim, A.; Miha, B. Lightweight 3D Printed Ti6Al4V-AlSi10Mg Hybrid Composite for Impact Resistance and armor Piercing Shielding. J. Mater. Res. Technol. 2020, 6, 13842–13854. [Google Scholar]
- Kiran, A.; Niranjan, K. Composite Armour—A Review. J. Indian Inst. Sci. 2015, 95, 297–313. [Google Scholar]
- Zhao, Z.N.; Han, B.; Zhang, R.; Zhang, Q.; Zhang, Q.C.; Ni, C.Y.; Lu, T.J. Enhancement of UHMWPE Encapsulation on the Ballistic Performance of Bi-Layer Mosaic Armors. Compos. Part B 2021, 221, 109023–109024. [Google Scholar] [CrossRef]
- Mainak, G. Construction and Simulation of a Novel High Altitude Versatile Armor Comprising of X-Aerogel and Carbon Fiber Composite with Ansys 2020 R2. Mater. Today Proc. 2021, 44, 3045–3049. [Google Scholar]
- Wang, W.Z.; Chen, Z.G.; Feng, S.S.; Zhao, T.Y. Experimental Study on Ceramic Balls Impact Composite Armor. Def. Technol. 2021, 16, 408–416. [Google Scholar] [CrossRef]
- Saurabh, B.; Supreet, T.; Prathamesh, S.; Pawar, J. Finite Element Analysis of Armor Steel and Aluminium Alloy under the Impact of 7.62 mm Projectile. Mater. Today Proc. 2021, 44, 4086–4091. [Google Scholar]
- Saravanan, V.; Muthumanickam, M.; Ragavendran, V.; Jeyanthinath, M.; Vishnukanthan, V. Technical Review: Improvement of Mechanical Properties and Suitability Towards Armor Applications–Alumina Composites. Ceram. Int. 2021, 47, 23693–23701. [Google Scholar]
- Farias-Aguilar, J.; Ramırez-Moreno, M.; Gonzalez-Garcıa, D.; Tellez-Jurado, L.; Balmori-Ramırez, H. Evaluation of the Ballistic Protection Level of (Glass-Fiber Reinforced Polyamide 6)-Aramid Fabric Sandwich Composite Panels. J. Mater. Res. Technol. 2021, 17, 1606–1614. [Google Scholar] [CrossRef]
- Junbo, Y.; Yan, L.; Zichen, Y.; Fan, B.; Zhenqing, S.; Peng, S.; Fenglei, H. Ballistic characteristics of 3D-printed auxetic honeycomb sandwich panel using CFRP face sheet. Int. J. Impact Eng. 2022, 164, 104186. [Google Scholar]
- Sumelka, W.; Nowak, M.; Nassr, A.; Al-Rifaie, H.; Malendowski, M.; Gajewski, T.; Peksa, P.; Studzinski, R.; Sielicki, P. Dynamic failure of the aluminium plate under air-blast loading in the framework of the fractional viscoplasticity model—Theory and validation. Int. J. Impact Eng. 2021, 158, 104024. [Google Scholar] [CrossRef]
- Connor, N. What Is Titanium–Chemical Properties of Titanium–Symbol Ti. Nuclear-Power. 2020. Available online: https://www.nuclear-power.com/Titanium-properties/ (accessed on 16 November 2021).
- Xie, W.; Yang, F.; Meng, S.; Scarpa, F.; Wang, L. Perforation of needle-punched carbon-carbon composites during high-temperature and high-velocity ballistic impacts. Compos. Struct. 2020, 245, 112224. [Google Scholar] [CrossRef]
- Zhao, Z.N.; Han, B.; Li, F.H.; Zhang, R.; Su, P.B.; Yang, M.; Zhang, Q.; Zhang, Q.C.; Lu, T.J. Enhanced bi-layer mosaic armor: Experiments and simulation. Ceram. Int. 2020, 46, 23854–23866. [Google Scholar] [CrossRef]
- Hu, D.; Zhang, Y.; Shen, Z.; Cai, Q. Investigation on the ballistic behavior of mosaic SiC/UHMWPE composite armor systems. Ceram. Int. 2017, 43, 10368–10376. [Google Scholar] [CrossRef]
- Wu, K.K.; Chen, Y.L.; Yeh, J.N.; Chen, W.L.; Lin, C.S. Ballistic impact performance of SiC Ceramic-Dyneema fibre composite materials. Adv. Mater. Sci. Eng. 2020, 2020, 9457489. [Google Scholar] [CrossRef]
- Parmar, S. Impact Analysis of a X-Core Filled Ceramic Composite Armor System. Master’s Thesis, Texas A&M University, Kingsville, TX, USA, 2021. [Google Scholar]
- Guo, G.; Alam, S.; Peel, L. An Investigation of the effect of Kevlar-29 Composite Cover Layer on the Penetration Behavior of a Ceramic Armor System Against 7.62 mm APM2 Projectiles. Int. J. Impact Eng. 2021, 157, 104000. [Google Scholar] [CrossRef]
- Guo, G.; Alam, S.; Peel, L. Numerical Analysis of Ceramic Mosaic Armor Subjected to Ballistic Impact. Int. J. Compos. Mater. 2021, 11, 5–12. [Google Scholar]
- Banerjee, A.; Dhar, S.; Acharyya, S.; Datta, D.; Nayak, N. Determination of Johnson Cook Material and Failure Model Constants and Numerical Modelling of Charpy Impact Test of Armour Steel. Mater. Sci. Eng. A 2015, 640, 200–209. [Google Scholar] [CrossRef]
- Alam, S.; Shakar, S. Ballistic Performance of Sandwich Composite Armor System. ASME Int. Mech. Eng. Congr. Expo. 2020, 84607, V012T12A012. [Google Scholar]
- Tondolo, F.; Leone, M.; Fantilli, A.; Aiello, M. Bond Mechanisms Between Steel Bars and Lightweight Rubberized Concrete from Waste Tyres. Proc. Italian Concrete Days 2018 2020, 3, 421–431. [Google Scholar]
- Wang, J.X.; Yin, Y.; Lou, C. Johnson-Holmquist-II (JH-2) Constitutive Model for Rock Materials: Parameter Determination and Application in Tunnel Smooth Blasting. Appl. Sci. 2018, 8, 1675–1678. [Google Scholar] [CrossRef]
- Johnson, G.R.; Holmquist, T.J. An improved computational constitutive model for brittle materials. AIP Conf. Proc. 1994, 309, 981–984. [Google Scholar]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Hashin, Z. Fatigue failure criteria for unidirectional fibre composites. J. Appl. Mech. 1981, 48, 846–852. [Google Scholar] [CrossRef]
- Chao, T.; Qitian, S.; Xuanyi, A.; Ping, Y.; Yongxiang, D. Influences of Ceramic Constraint on Protection Performances of Ceramic-Metal Hybrid Structures under Impact Loads. Int. J. Mech. Sci. 2019, 159, 81–90. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).