Ratcheting Response of Heat-Treated Notched 1045 Steel Samples Undergoing Asymmetric Uniaxial Loading Cycles
Abstract
1. Introduction
2. Hardening Rule Frameworks
2.1. The Ahmadzadeh–Varvani Hardening Rule
2.2. The Chaboche Hardening Rule
2.3. Stress and Strain at Notch Root
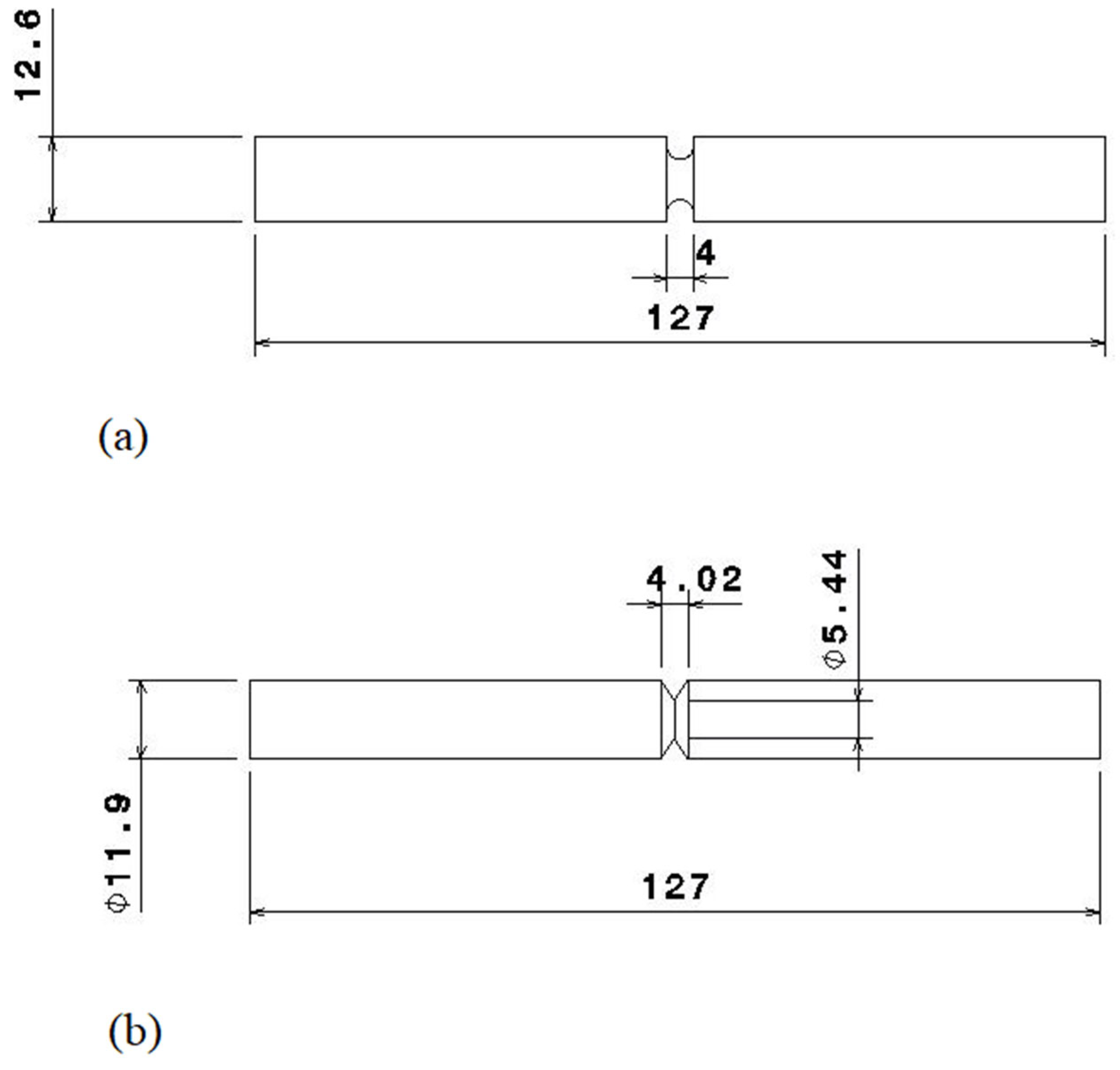
3. Materials and Testing Conditions
4. Finite Element Analysis
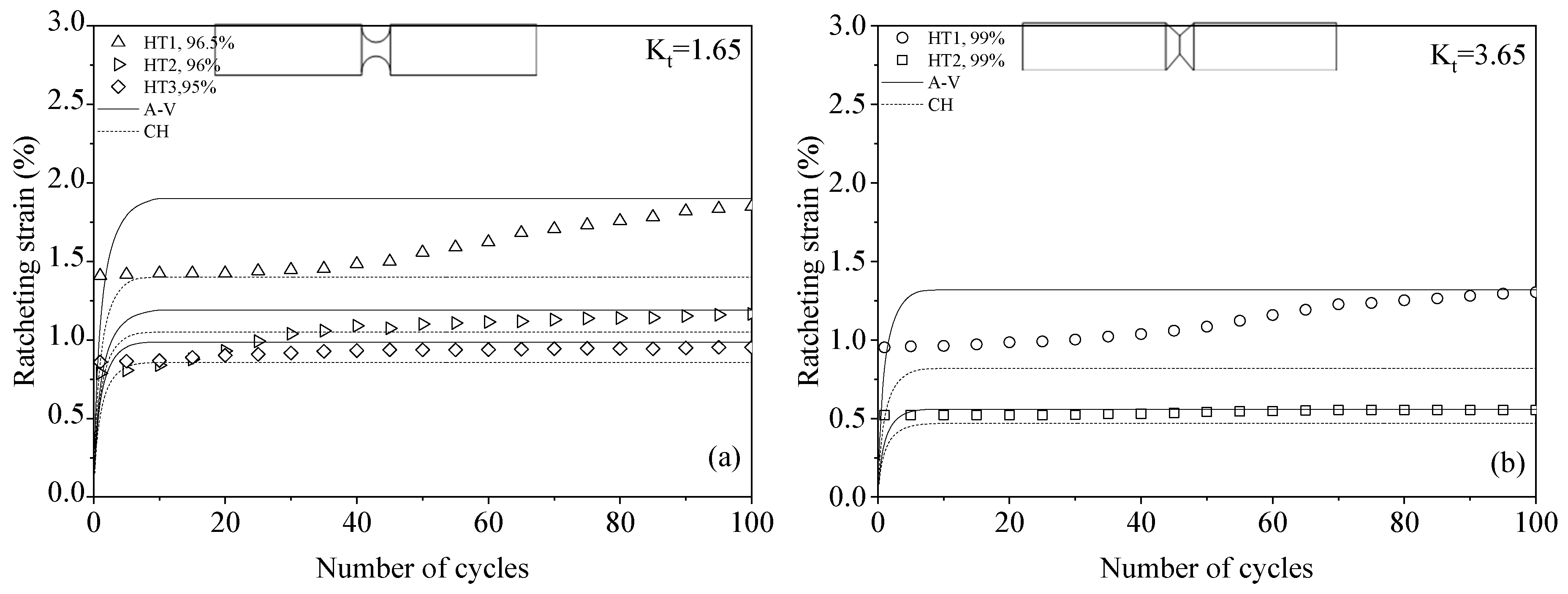
5. Results and Discussion
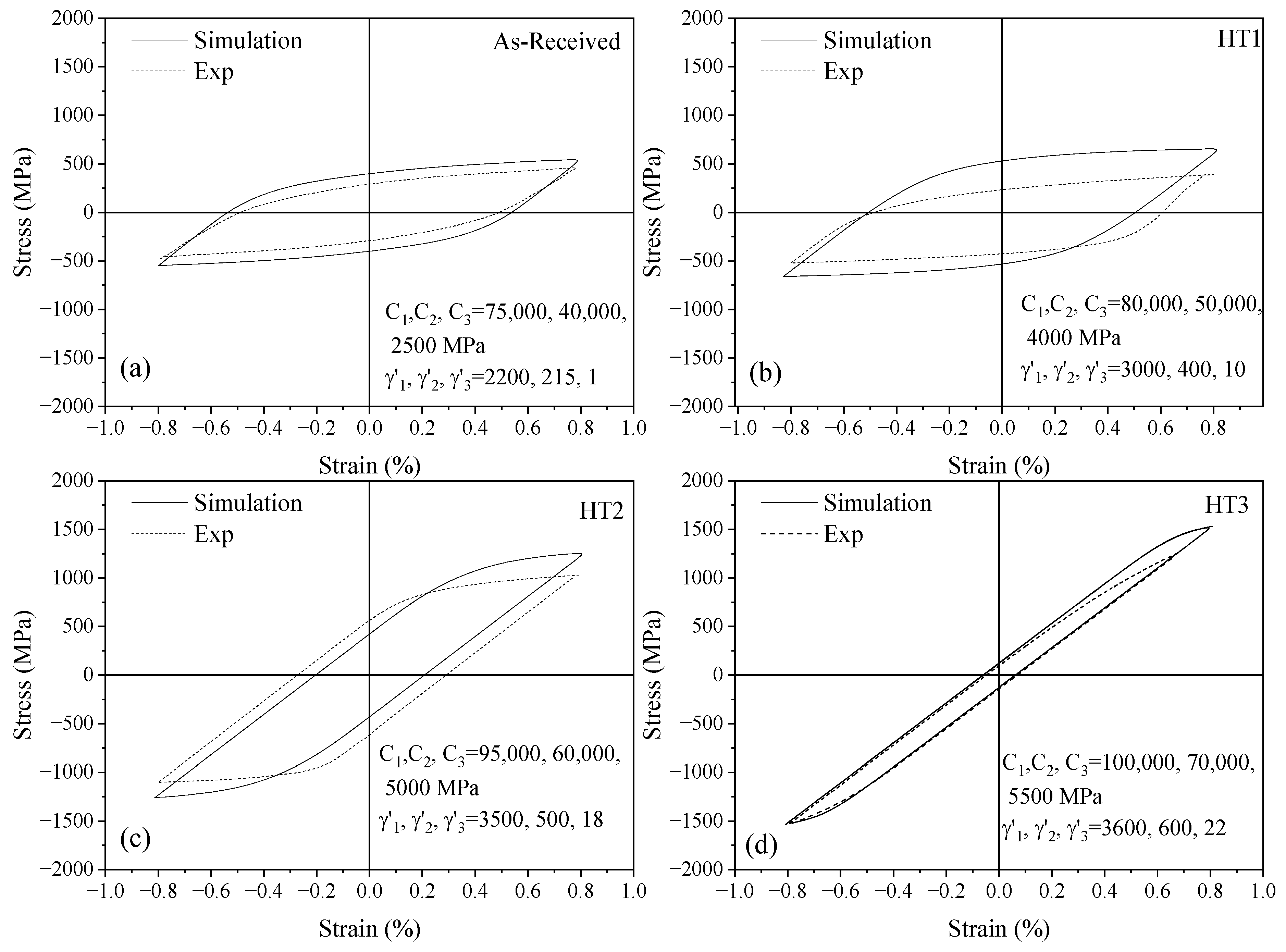
5.1. The A–V Hardening Rule Coefficients
5.2. The CH Hardening Rule Coefficients
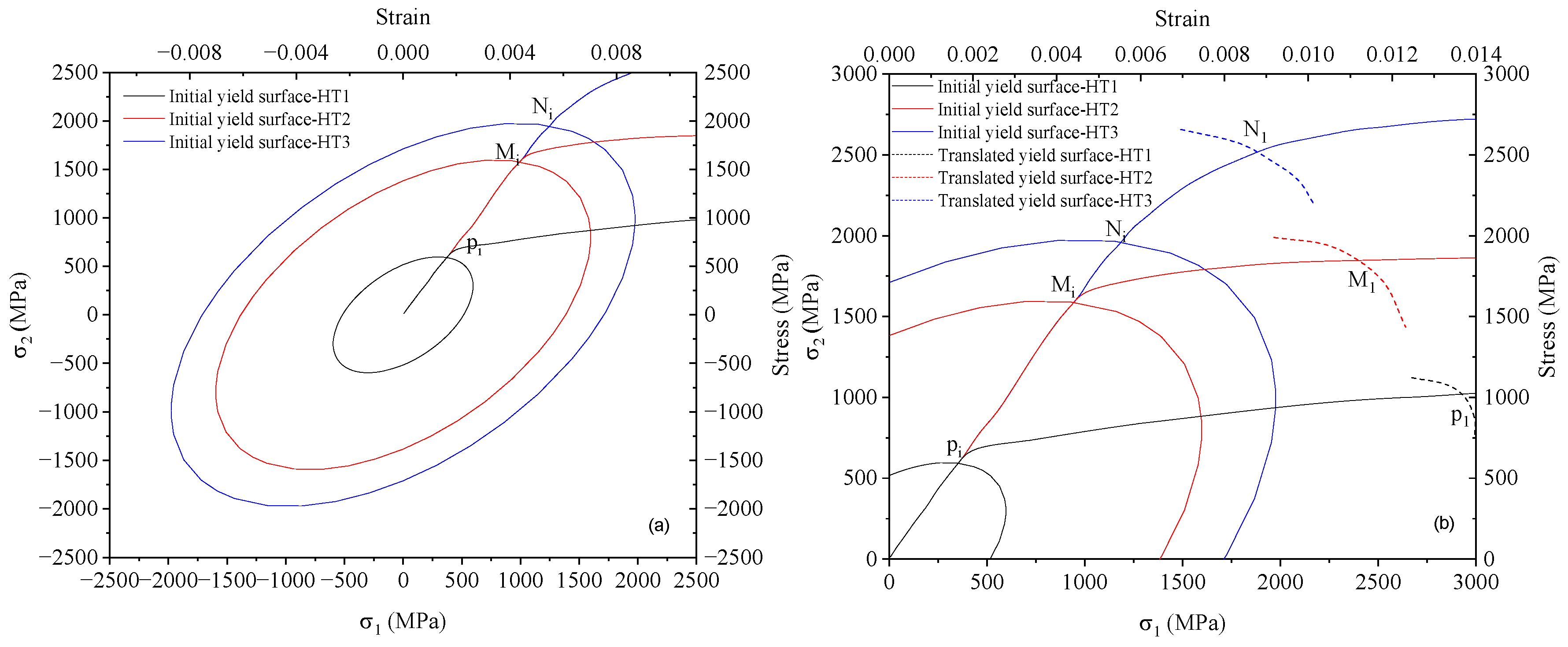
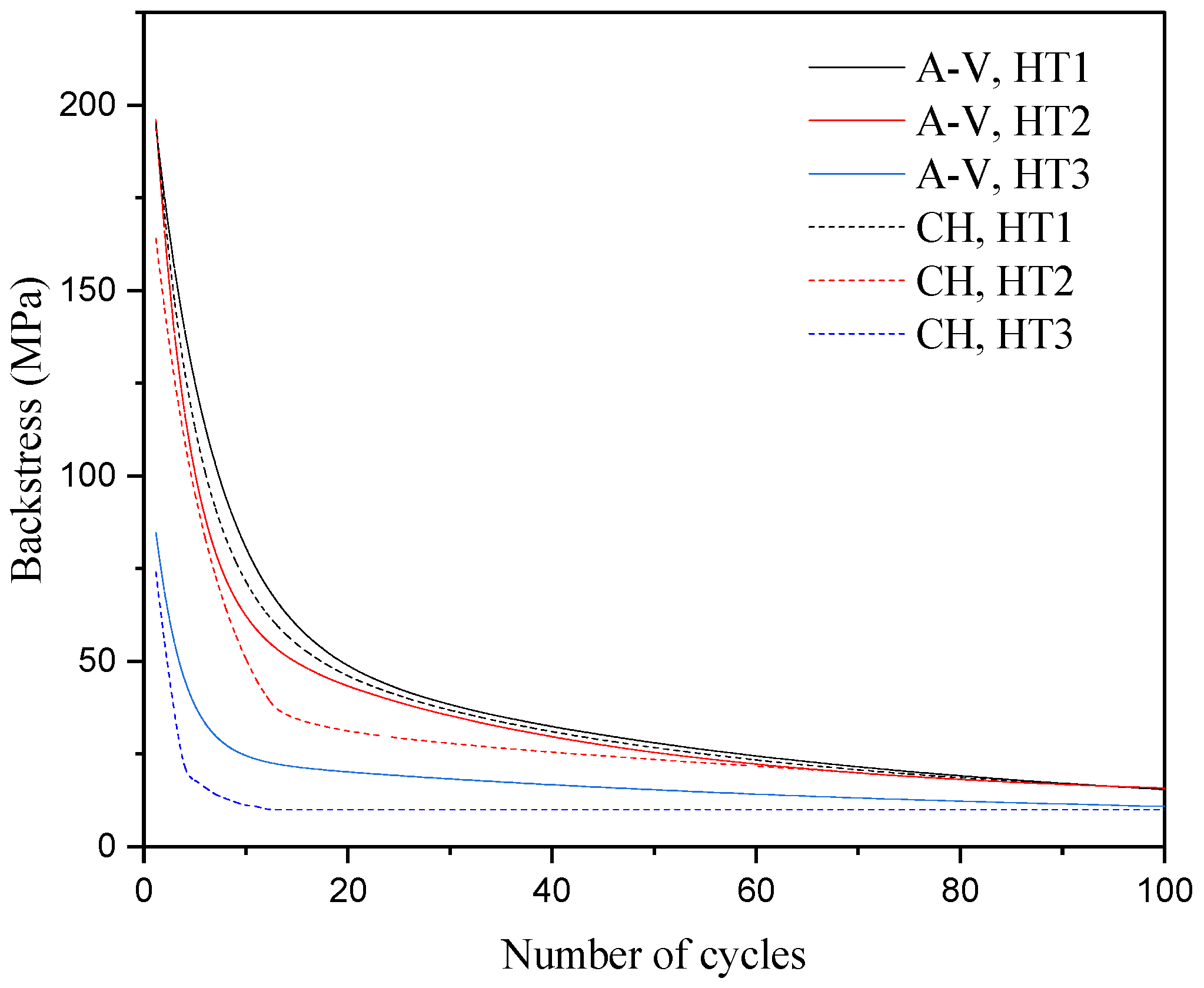
5.3. Backstress Increments and Yield Surface Translation
5.4. Predicted Local Ratcheting
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Total strain increment tensor | |
| Elastic strain increment tensor | |
| Plastic strain increment tensor | |
| E | Modulus of elasticity |
| Plastic modulus | |
| Backstress tensor | |
| Stress tensor | |
| Unit tensor | |
| Poisson’s ratio | |
| G | Shear modulus |
| Deviatoric stress tensor | |
| Yield strength | |
| D | Circular notch diameter |
| Coefficients of the A-V model | |
| , | Chaboche materials coefficients |
| Stress concentration factor | |
| Internal variable of the A-V model tensor | |
| Ramberg-Osgood coefficients | |
| S,e | Nominal stress and strain |
| R | Stress ratio |
| , | Stress and strain concentration factors |
| Uniaxial local stress and strain at the notch root |
References
- Wang, C.H.; Rose, L.R.F. Transient and steady-state deformation at notch root under cyclic loading. Mech. Mater. 1998, 30, 229–241. [Google Scholar] [CrossRef]
- Hu, W.; Wang, C.H.; Barter, S. Analysis of Cyclic Mean Stress Relaxation and Strain Ratchetting Behavior of Aluminum 7050; Aeronautical and Maritime Research Lab Melbourne (Australia): Melbourne, Australia, 1999. [Google Scholar]
- Rahman, S.M.; Hassan, T. Advanced cyclic plasticity models in simulating ratcheting responses of straight and elbow piping components, and notched plates. In Proceedings of the ASME Pressure Vessels and Piping Conference, Denver, CO, USA, 17–21 July 2005; pp. 421–427. [Google Scholar]
- Chaboche, J. On some modifications of kinematic hardening to improve the description of ratcheting effects. Int. J. Plast. 1991, 7, 661–678. [Google Scholar] [CrossRef]
- Ohno, N.; Wang, J.D. Kinematic hardening rules with critical state of dynamic recovery, part I: Formulations and basic features for ratcheting behavior. Int. J. Plast. 1993, 9, 375–390. [Google Scholar] [CrossRef]
- Ohno, N.; Abdel Karim, M. Uniaxial ratcheting of 316FR steel at room temperature—Part II: Constitutive modeling and simulation. ASME J. Appl. Mech. 2000, 122, 35–41. [Google Scholar]
- Firat, M. A notch strain calculation of a notched specimen under axial-torsion loadings. Mater. Des. 2011, 32, 3876–3882. [Google Scholar] [CrossRef]
- Neuber, H. Theory of stress concentration for shear-strained prismatical bodies with arbitrary nonlinear stress-strain law. J. Appl. Mech. 1961, 28, 544–550. [Google Scholar] [CrossRef]
- Barkey, M.E. Calculation of Notch Strains under Multiaxial Nominal Loading. Ph.D. Thesis, Department of Theoretical and Applied Mechanics, University of Illinois at Urbana-Champaign, Illinois City, IL, USA, 1993. [Google Scholar]
- Liu, C.; Shi, S.; Cai, Y.; Chen, X. Ratcheting behavior of pressurized-bending elbow pipe after thermal aging. Int. J. Press. Vessel. Pip. 2019, 169, 160–169. [Google Scholar] [CrossRef]
- Chen, X.; Jiao, R.; Kim, K.S. On the Ohno-Wang kinematic hardening rules for multiaxial ratcheting modeling of medium carbon steel. Int. J. Plast. 2005, 21, 161–184. [Google Scholar] [CrossRef]
- Kolasangiani, K.; Farhangdoost, K.; Shariati, M.; Varvani-Farahani, A. Ratcheting assessment of notched steel samples subjected to asymmetric loading cycles through coupled kinematic hardening-Neuber rules. Int. J. Mech. Sci. 2018, 144, 24–32. [Google Scholar] [CrossRef]
- Shekarian, A.; Varvani-Farahani, A. Ratcheting prediction at the notch root of steel samples over asymmetric loading cycles. J. Eng. Mater. Technol. Trans. 2020, 142, 1–23. [Google Scholar] [CrossRef]
- Shekarian, A.; Varvani-Farahani, A. Concurrent ratcheting and stress relaxation at the notch root of steel samples undergoing asymmetric tensile loading cycles. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 1402–1413. [Google Scholar] [CrossRef]
- Shekarian, A.; Varvani-Farahani, A. Ratcheting behavior of notched stainless-steel samples subjected to asymmetric loading cycles. J. Iron Steel Res. Int. 2021, 28, 86–97. [Google Scholar] [CrossRef]
- Shekarian, A.; Varvani-Farahani, A. Ratcheting response of SS316 steel samples with different notch shapes under various loading spectra. J. Mater. Eng. Perform. 2021, 30, 3524–3535. [Google Scholar] [CrossRef]
- Armstrong, P.J.; Frederick, C.O. A Mathematical Representation of the Multiaxial Bauschinger Effect, CEGB Rep. RD/B/N, 731; Berkeley Nuclear Laboratories: Berkeley, CA, USA, 1966. [Google Scholar]
- Ahmadzadeh, G.R.; Varvani-Farahani, A. Ratcheting assessment of materials based on the modified Armstrong–Frederick hardening rule at various uniaxial stress levels. Fatigue Fract. Eng. Mater. Struct. 2013, 36, 1232–1245. [Google Scholar] [CrossRef]
- Hatami, F.; Varvani-Farahani, A. Accumulation of plastic strain at notch root of steel specimens undergoing asymmetric fatigue cycles: Analysis and simulation. Materials 2023, 16, 2153. [Google Scholar] [CrossRef] [PubMed]
- Weiyuan, N.; Shanglei, Y.; Jin, J.; Jianying, B.; Yangshenglan, L. Fatigue property of Al-5Zn-2Mg aluminum alloy welding joints used in high-speed trains. Rare Met. Mater. Eng. 2016, 45, 2774–2778. [Google Scholar] [CrossRef]
- Duan, C.; Yang, S.; Gu, J.; Xiong, Q.; Wang, Y. Microstructure and ratcheting behavior of 6061 aluminum alloy laser-MIG hybrid welding joint. Mater. Res. Express 2019, 6, 086534. [Google Scholar] [CrossRef]
- Wang, H.; Jing, H.; Zhao, L.; Han, Y.; Lv, X.; Xu, L. Uniaxial ratcheting behaviour of 304L stainless steel and ER308L weld joints. Mater. Sci. Eng. 2017, 708, 21–42. [Google Scholar] [CrossRef]
- Gioielli, P.; Buitrago, J.; Kan, W.; Weir, M.; Chell, G.; Hudak, S.J., Jr. Calibration of Flaw Extension Model Under Ratcheting Fatigue. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Honolulu, HW, USA, 31 May–5 June 2009; pp. 267–277. [Google Scholar]
- Schmiedt, A.; Manka, M.; Tillmann, W.; Walther, F. Local quasi-static and cyclic deformation behaviour of brazed AISI 304L/BAu-4 joints characterised by digital image correlation. Weld. World 2019, 63, 501–509. [Google Scholar] [CrossRef]
- Chakherlou, T.N.; Vogwell, J. A novel method of cold expansion which creates near-uniform compressive tangential residual stress around a fastener hole. Fatigue Fract. Eng. Mater. Struct. 2004, 27, 343–351. [Google Scholar] [CrossRef]
- Chakherlou, T.N.; Aghdam, A.B. An experimental investigation on the effect of short time exposure to elevated temperature on fatigue life of cold expanded fastener holes. Mater. Design 2008, 29, 1504–1511. [Google Scholar] [CrossRef]
- Chakherlou, T.N.; Mirzajanzadeh, M.; Saeedi, K.H. Fatigue crack growth and life prediction of a single interference fitted holed plate. Fatigue Fract. Eng. Mater. Struct 2010, 33, 633–644. [Google Scholar] [CrossRef]
- Chakherlou, T.N.; AJRI, M. Strain ratcheting and stress relaxation around interference-fitted single-holed plates under cyclic loading: Experimental and numerical investigations. Fatigue Fract. Engng. Mater. Struct. 2012, 36, 327–339. [Google Scholar] [CrossRef]
- Tripathy, S.; Mondal, A.K.; Dutta, K. Effect of pre-strain on ratcheting behavior of A668 Class D steel. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Rourkela, India, 12–13 December 2016; p. 012037. [Google Scholar]
- Hatami, F.; Varvani-Farahani, A. Local Ratcheting at the Notch Region of Non-Press-Fitted and Press-Fitted Al 7075-T6 Samples Undergoing Asymmetric Stress Cycles. Metals 2023, 13, 1549. [Google Scholar] [CrossRef]
- Kreethi, R.; Verma, P.; Dutta, K. Influence of heat treatment on ratcheting fatigue behavior and post ratcheting tensile properties of commercial aluminum. Trans. Indian Inst. Met. 2015, 68, 229–237. [Google Scholar] [CrossRef]
- Kreethi, R.; Mondal, A.K.; Dutta, K. Ratcheting fatigue behaviour of 42CrMo4 steel under different heat treatment conditions. Mater. Sci. Eng. 2017, A 679, 66–74. [Google Scholar] [CrossRef]
- Azadi, M.; Basiri, A.; Dadashi, A.; Winter, G.; Seisenbacher, B.; Gruen, F. Effect of nano-clay addition and heat-treatment on tensile and stress-controlled low-cycle fatigue behaviors of aluminum-silicon alloy: Effect of nano-clay addition and heat-treatment. Frat. Ed Integrità Strutt. 2021, 15, 373–397. [Google Scholar] [CrossRef]
- Xu, X.; Wang, Z.; Gao, G.; Zhang, X.; Kang, G.; Kan, Q. The effect of microstructure evolution on the ratchetting-fatigue interaction of carbide-free bainite rail steels under different heat-treatment conditions. Int. J. Fatigue 2022, 160, 106872. [Google Scholar] [CrossRef]
- Pals, T.G.; Stephens, R.I. The influence of high R ratio on mild and sharp notched and unnotched fatigue behavior of 1045 steel with three different heat treatments. Int. J. Fatigue 2004, 26, 651–661. [Google Scholar] [CrossRef]
- Karadag, M.; Stephens, R.I. The influence of high R ratio on unnotched fatigue behavior of 1045 steel with three different heat treatments. Int. J. Fatigue 2003, 25, 191–200. [Google Scholar] [CrossRef]
- Vantiger, T.R.; Stephens, R.I.; Karadag, M. The influence of high R ratio on notched fatigue behaviour of 1045 steel with three different heat treatments. Int. J. Fatigue 2002, 24, 1275–1284. [Google Scholar] [CrossRef]
- Varvani-Farahani, A. A comparative study in descriptions of coupled kinematic hardening rules and ratcheting assessment over asymmetric stress cycles. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 882–893. [Google Scholar] [CrossRef]
- Rezaiee-Pajand, M.; Sinaie, S. On the calibration of the Chaboche hardening model and a modified hardening rule for uniaxial ratcheting prediction. Int. J. Solids Struct. 2009, 46, 3009–3017. [Google Scholar] [CrossRef]
- Abaqus Inc. ABAQUS User’s Manual. Version 6.13; Hibbitt, Karlsson & Sorensen, Incorporated: Pennsylvania, LA, USA, 2016. [Google Scholar]
- Kolasangiani, K. Analysis of Local and Global Ratcheting Behavior of AISI 1045 Steel Specimens with Cutout. Ph.D. Thesis, Department of Mechanical Engineering, Ferdowsi University of Mashhad, Razavi Khorasan, Iran, 2018. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hatami, F.; Varvani-Farahani, A. Ratcheting Response of Heat-Treated Notched 1045 Steel Samples Undergoing Asymmetric Uniaxial Loading Cycles. Appl. Mech. 2024, 5, 362-375. https://doi.org/10.3390/applmech5020021
Hatami F, Varvani-Farahani A. Ratcheting Response of Heat-Treated Notched 1045 Steel Samples Undergoing Asymmetric Uniaxial Loading Cycles. Applied Mechanics. 2024; 5(2):362-375. https://doi.org/10.3390/applmech5020021
Chicago/Turabian StyleHatami, Faezeh, and Ahmad Varvani-Farahani. 2024. "Ratcheting Response of Heat-Treated Notched 1045 Steel Samples Undergoing Asymmetric Uniaxial Loading Cycles" Applied Mechanics 5, no. 2: 362-375. https://doi.org/10.3390/applmech5020021
APA StyleHatami, F., & Varvani-Farahani, A. (2024). Ratcheting Response of Heat-Treated Notched 1045 Steel Samples Undergoing Asymmetric Uniaxial Loading Cycles. Applied Mechanics, 5(2), 362-375. https://doi.org/10.3390/applmech5020021




