Intelligent Structure Identification and Robust Control Implementation

Abstract

This study outlines a comprehensive strategy for designing and implementing robust controllers tailored for intelligent structures. This study presents a robust control-based structural identification technique that uses the input/output data of the system to construct a state-space mode and frequency domain. To reduce vibrations, a robust controller is created using the control Simulink model. The identification and robust control of smart structures using Simulink involve a combination of system identification techniques and control design within the MATLAB Simulink environment. The key challenge is dealing with uncertainties and variations in system dynamics. Robust control methods have been employed to suppress the vibrations during dynamic disturbances. These methods are important for mechanical systems operating under stochastic loading conditions.

1. Introduction

This study represents an innovation in intelligent structural control. The problem in this study was the suppression of oscillations caused by the dynamic vibrations. Smart materials such as piezoelectric materials are used to achieve vibration damping. In this work, control methods are applied to constructions that were originally modeled with finite elements, and the discovery of advanced control techniques greatly increases the accounting requirements of the auditor, while an appropriate selection of control weights is made to achieve complete suppression of oscillations. Innovation is the application of robust control to suppress structural oscillations, which is a problem that has not yet been solved. This study applies robust control to smart structures [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]. One of the main problems in engineering is the damping of structural oscillations, which can be caused by winds or earthquakes [5,6,7,8,16]. The application of the theory of control mentioned in the reports is a problem that still concerns engineers, and an attempt is being made to introduce it into structures stressed by dynamic loads, such as airplane wings, bridges, and tall buildings [5,6,7,8,9,10,11,12,13,14,15].

This process is crucial for understanding the responses of structures to various loads and environmental conditions. Robust control focuses on ensuring that a system remains stable and performs effectively despite uncertainties or variations in its parameters or environment. In structural engineering, this may involve Active Control Systems [5,7,8,9,16,17]. These include active mass dampers and tunable vibration absorbers that can adapt to changing conditions to mitigate undesirable vibrations [5,8,9,10,11,12,13,14,15,18].

Smart structures, also known as intelligent or adaptive structures, are designed to sense changes in their environment and respond in a controlled and effective manner [1,2,3]. This entails combining sensors, actuators, and control systems to improve the performance and functionality of structures [4,19,20,21]. Smart structures often exhibit nonlinear behavior, parameter variations, and external disturbances [21,22,23,24,25,26]. Piezoelectric materials play a crucial role as sensors and actuators in smart structures. When mechanical stress is exerted on a piezoelectric material, it produces an electric charge that can be used for sensing. Conversely, when an electric field is applied, these materials undergo deformation, leading to their use as actuators for precise control and adjustment of smart structures [27,28,29,30]. The capability of piezoelectric materials to convert mechanical and electrical energy has been harnessed for diverse engineering applications. In this study, robust control for the reduction in structural oscillations was applied. Smart materials, mainly piezoelectric materials, are used to control the oscillations.

Our research offers a more specialized method for implementing robust control in the field of smart structures using MATLAB Simulink v. 5.0.2 (MathWorks, Natick, MA, USA). A detailed dynamic model of the smart structure in Simulink was developed by considering factors such as the piezoelectric actuators, sensors, and structural dynamics. H-infinity control is selected as the robust control strategy. The “H-infinity Loop Shaping” and “H-infinity Synthesis” blocks were utilized in Simulink to design controllers that optimize performance while considering uncertainties. These controllers were designed to effectively reject external disturbances [4,19,20,21]. Disturbance rejection techniques include feedforward control and disturbance observers. Adaptive control techniques were implemented in cases where the smart structure exhibited time-varying behavior or uncertainties that changed over time. Simulink provides adaptive control blocks for this purpose. Where applicable, real-time implementation using Simulink Real-Time for hardware-in-the-loop (HIL) testing was considered by exploiting Simulink’s extensive toolbox and simulation capabilities [31,32].

The use of smart materials to reduce structural oscillations has attracted the attention of several researchers. If the smart structure exhibits time-varying behavior or unknown changes over time, adaptive control strategies can be applied. Controllers that successfully resist external interference were also created. Disturbance rejection strategies such as disturbance observers or feedforward control were used. Adaptive control blocks are available in Simulink for this purpose. Several simulations of closed-loop systems with varying uncertainties and disturbances have been conducted [33,34,35]. The resilience and performance characteristics of the system were analyzed using Simulink. Combining smart structures with μ analysis allows the optimization of materials and design for enhanced functionality and efficiency. By understanding how materials behave at the microscale, we can make informed decisions regarding their composition, structure, and fabrication techniques [5,6,36,37]. This, in turn, contributes to the development of structures that are not only intelligent in their response to external stimuli but also finely tuned at the micro level for optimal performance [5,8,9,10,11,12,13,14,15,18]. Intelligent structure identification and robust control implementation represent cutting-edge approaches in engineering and offer significant benefits in terms of the safety, reliability, and performance of structures [5,6,7,8,9,10,11,12,13,14,15,18]. Continued advancements in technology and engineering are likely to expand their applications and effectiveness in the coming years.

2. Methods

The dynamics of a structure with piezoelectric patches can be described using equations of motion that incorporate electromechanical coupling introduced by the piezoelectric effect [6,7,8]. Piezoelectric materials possess a distinctive capability to convert mechanical energy into electrical energy, and conversely, electrical energy into mechanical energy [1,2,3,10,15]. When used as patches on structures, they can act as sensors or actuators owing to their bidirectional energy conversion properties. The dynamic equation of motion for a structure with piezoelectric patches generally combines the mechanical and electrical behaviors into a unified framework [7,8,9,10,16,17]. A piezoelectric patch attached to a mechanical structure (such as a beam, plate, or shell) can be modeled using the principles of piezoelectricity and structural dynamics. The mechanical vibration of the structure induces strain in the piezoelectric material, which generates an electric field (and hence, a voltage) across the material owing to the direct piezoelectric effect [10,15]. Conversely, when an external electric field is applied across a piezoelectric material, strain is induced in the material, thereby altering the vibration of the structure owing to the converse piezoelectric effect [10,11,13,14]. Sensors, actuators, and control systems are frequently integrated to enable intelligent structures to respond to changing environmental conditions [6,7,8,9,10,11,12,15]. Dynamic equations governing intelligent structures can be intricate and contingent on the particular assembly and components employed. In the subsequent section, the performance of an eight-element cantilever smart structure equipped with four pairs of symmetrically linked piezoelectric patches on the top and bottom surfaces of each beam element is discussed [19,20,24,25,26,27]. Equation (1) is a dynamic equation of mechanics, as mentioned in [15]. This equation is second-order, and, with a proper transformation, is converted into a different first-order equation. The equation is in the state-space domain. The smart system was a smart cantilever beam with piezoelectric patches. The disturbances are the dynamic force fm(t) and electric force fe(t) [10,11,12,13,14,15]. The following section presents a list of dimensions of each intelligent structure component. The dynamic characterization of the system can be understood using the following equation:

The dynamical equation without the electrical force of the Pzt is [7,8,9,10,15]:

$$M\ddot{q}\left(t\right)+D\dot{q}+Kq\left(t\right)=fm\left(t\right)$$

The dynamical equation with the electrical force of the pzt patches [7,8,9,10,15] is:

$$M\ddot{q}\left(t\right)+D\dot{q}+Kq\left(t\right)=fm\left(t\right)+fe\left(t\right)$$

(1)

The independent q(t) variable was defined using the finite element method, with two degrees of freedom for each node. The rotations ψi and transverse deflections wi are independent variables q(t) in this context.

$$q(t)=\left[\begin{array}{c}{w}_1\\ {\psi }_1\\ ⋮\\ w_n\\ {\psi }_n\end{array}\right]$$

(2)

In Framework (1), K represents the overall stiffness matrix, fe represents the comprehensive force vector derived from electromechanical coupling effects, and fm is the total external mechanical force vector. These elements are generally adjusted using a feedback control mechanism that leverages sensor data to alter the behavior of a structure dynamically. The primary objective is to augment the response or effectiveness of the structure under various conditions. The symbols D and M denote the matrices for viscous damping and overall mass, respectively, with ψi indicating rotation and transverse deflection. The analysis employed n to signify the aggregate count of the finite elements. Both the vectors w and fm are directed upward. The rotations ψi and transverse deflections wi are independent variables q(t) in this context. Allow (in a customary way) a transition to state-space control representation.

$$x(t)=\left[\begin{array}{c}q\left(t\right)\\ \dot{q}\left(t\right)\end{array}\right]$$

(3)

Furthermore, fe(t) can be described as Bu(t) by formulating it as F_e^∗u, where F_e^∗ with dimensions 2n × n symbolizes the unit piezoelectric force attributed to the corresponding actuator, as referenced in [36,37], where u denotes the actuator voltage as discussed in [5,6,7,8]. Finally, d(t) = fm(t) is identified as a disturbance vector.

$$\begin{gathered} \dot{x}(t)=\left[\begin{array}{cc}{0}_{2n\times 2n}& I_{2n\times 2n}\\ -M^{-1}K& -M^{-1}K\end{array}\right]x(t)+\left[\begin{array}{c}{0}_{2n\times n}\\ M^{-1}{F}_e^{\ast }\end{array}\right]u(t)+\left[\begin{array}{c}{0}_{2n\times 2n}\\ M^{-1}\end{array}\right]d(t) \\ =Ax(t)+Bu(t)+Gd(t) \\ =Ax(t)+\left[\begin{array}{cc}B& G\end{array}\right]\left[\begin{array}{c}u(t)\\ d(t)\end{array}\right] \\ =Ax(t)+B\tilde{u}(t) \end{gathered}$$

(4)

In this formulation, d represents a 2n × 1 vector (where n is the number of nodes), and u is at most an n × 1 vector (although it could be smaller). The units used are Newtons (N), seconds (s), radians (rad), and meters (m). Through a more thorough examination of stability in the frequency domain, our approach maintains stability in the time domain.

y(t) = [x₁(t) x₃(t) … x_n−1(t)]^T = C x(t)

(5)

This state-space representation encapsulates the first-order dynamics of the smart structure, wherein the state vector x(t) encompasses both displacement and velocity. The dynamic equation of motion of intelligent construction is second-order, whereas, with appropriate transformation, it is modified into a differential equation of first order. We consider the response of the smart structure in the space-state domain with and without control. There were two degrees of freedom at each node, and we obtained the results for displacements, rotations, velocity, angular velocity, acceleration, and angular acceleration. The displacement and rotation results were also presented. We employed the following approach to handle the uncertainty in the M and K matrices.

K = K₀(I + k_pI_2n×2nδ_K)
M = M₀(I + m_pI_2n×2nδ_M)

(6)

Furthermore, since D = 0.0005(K + M), a suitable form for D is,

D = 0.0005[K₀(I + k_pI_2n×2nδ_K) + M₀(I + m_pI_2n×2nδ_M)]
where D₀ = 0.0005K₀ + 0.0005M₀
Then, D = D₀ + 0.0005[K₀k_pI_2n×2nδ_K + M₀m_pI_2n×2nδ_M]

(7)

D denotes the damping matrix associated with the structure, where damping is considered a minor fraction of both the mass and stiffness matrices. Using the experimental apparatus, this fraction was determined to be 0.0005 for both the mass and stiffness matrices, as noted in [16]. The lower the damping value, the more challenging it is to halt the vibrations of the structure, as indicated in [17]. However, it is generally understood that

D = α K + β M

The structural damping matrix, denoted as D, can be understood as a linear combination of the mass and stiffness matrices, a concept referred to as Rayleigh damping. Under this paradigm, the coefficients α and β were determined by examining the first and second normal modes of vibration, with both values set to 0.0005. Thus, D can be formulated similarly to K (stiffness matrix) and M (mass matrix), as follows:

D = D₀ (I + d_pI_2n×2nδ_D)

(8)

We introduced uncertainty as the proportional deviation of the relevant matrices. This approach to incorporating uncertainty is particularly effective in our context because the length can be measured with high precision. The likelihood of uncertainty arises more from specific terms than from the core matrices. The following assumptions were made in this case.

$$║\mathbf{\Delta }{║}_{\infty }\stackrel{\mathrm{def}}{=}{‖\left[\begin{array}{cc}{{\rm I}}_{n\times n}{\delta }_{{\rm K}}& 0_{n\times n}\\ 0_{n\times n}& {{\rm I}}_{n\times n}{\delta }_{{\rm M}}\end{array}\right]‖}_{\mathrm{\infty }}<1$$

(9)

Therefore, m_p and k_p were employed to scale the proportionality value with nominal values denoted by subscripts of zero.

(It is urged that for matrix A_n×m, the norm is determined via ║A║_∞ = $\underset{1\le j\le m}{\mathrm{m}\mathrm{a}\mathrm{x}}\sum _{j=1}^n\left|a_{ij}\right|$.)

Taking these specifications into consideration, Equation (4) changes to

$$\begin{gathered} M_0\left(I+m_p{I}_{2n\times 2n}{\delta }_{{\rm M}}\ddot{q}\left(t\right)\right)+K_0\left(I+k_p{I}_{2n\times 2n}{\delta }_{K}q\left(t\right)\right)+[D+0.0005\left[K_0{k}_p{I}_{2\times 2}{\delta }_K+{M_{0}m}_p{I}_{2\times 2}{\delta }_{{\rm M}}\right]\dot{q}\left(t\right)+f_m\left(t\right)+f_e(t) \\ \Rightarrow M_0\ddot{q}\left(t\right)+D_0\dot{q}\left(t\right)+K_{0}q\left(t\right)=-\left[M_0{m}_p{I}_{2n\times 2n}{\delta }_{{\rm M}}\ddot{q}\left(t\right)+0.0005\left[K_0{k}_p{I}_{2\times 2}{\delta }_K+{M_{0}m}_p{I}_{2\times 2}{\delta }_{{\rm M}}\right]\dot{q}\left(t\right)+{K_{0}k}_p{I}_{2n\times 2n}{\delta }_{K}q\left(t\right)\right]+f_m\left(t\right)+f_e\left(t\right) \\ \Rightarrow M_0\ddot{q}(t)+D_0\dot{q}(t)+K_{0}q(t)=\tilde{D}{q}_u(t)+f_m(t)+f_e(t) \end{gathered}$$

(10)

where

$$\begin{gathered} q_u(t)=\left[\begin{array}{c}\ddot{q}\left(t\right)\\ \dot{q}\left(t\right)\\ q\left(t\right)\end{array}\right] \\ \tilde{D}=-\left[\begin{array}{cc}{M}_0{m}_p& K_0{k}_p\end{array}\right]\begin{array}{c}\end{array}\left[\begin{array}{cc}{I}_{2n\times 2n}{\delta }_{{\rm M}}& 0_{2n\times 2n}\\ 0_{2n\times 2n}& I_{2n\times 2n}{\delta }_{{\rm K}}\end{array}\right]\begin{array}{c}\end{array}\left[\begin{array}{ccc}{I}_{2n\times 2n}& 0.0005I_{2n\times 2n}& 0_{2n\times 2n}\\ 0_{2n\times 2n}& 0.0005I_{2n\times 2n}& I_{2n\times 2n}\end{array}\right]= \\ =G_1\cdot \mathsf{\Delta }\cdot G_2 \end{gathered}$$

(11)

$$G_1=-\left[\begin{array}{cc}{M}_0{m}_p& K_0{k}_p\end{array}\right], G_2=\left[\begin{array}{ccc}{I}_{2n\times 2n}& 0.0005I_{2n\times 2n}& 0_{2n\times 2n}\\ 0_{2n\times 2n}& 0.0005I_{2n\times 2n}& I_{2n\times 2n}\end{array}\right]$$

When Equation (7) is expressed in the state-space form, it yields the following representation:

$$\begin{gathered} \dot{x}(t)=\left[\begin{array}{cc}{0}_{2n\times 2n}& I_{2n\times 2n}\\ -M^{-1}K& -M^{-1}D\end{array}\right]x(t)+\left[\begin{array}{c}{0}_{2n\times n}\\ M^{-1}{f}_e^{\ast }\end{array}\right]u(t)+\left[\begin{array}{c}{0}_{2n\times 2n}\\ M^{-1}\end{array}\right]d(t)+\left[\begin{array}{c}{0}_{2n\times 6n}\\ M^{-1}{G}_1\cdot \mathsf{\Delta }\cdot G_2\end{array}\right]q_u(t) \\ =Ax\left(t\right)+{\rm B}u\left(t\right)+Gd\left(t\right)+G_u{G}_2{q}_u\left(t\right) \end{gathered}$$

(12)

Equations (11) and (12) are the dynamic equations of motion of the structure in which the mass and stiffness of the structure are inserted, which are modeled using the finite element method. This relationship is in the space state domain, and we can obtain the dynamic response of the construction, that is, how the structure oscillates with and without control. The initial conditions of construction change can be considered by changing the mass and stiffness registers using K_p and m_p. This implies that the structure can be damaged and the initial conditions can be changed. In other words, the modeling uncertainty of the initial construction conditions was introduced. For example, on a bridge, when there is wind damage or an earthquake, the distribution of mass and stiffness changes.

In this approach, the uncertainty of the original matrices is treated as an additional uncertainty parameter. These equations capture the concept of incorporating active and flexible controls into smart structures in order to respond to dynamic loads or changing situations. The hard part is coming up with efficient control algorithms and systems that react as best they can to the external forces and the status of the structure.

Robust Synthesis: μ-Controller

A popular approach in control system design for analyzing and addressing uncertainty in dynamic systems is μ analysis, which is sometimes called mu-analysis. This is particularly beneficial for understanding the impact of uncertainties on the stability and robustness of the control systems.

In the field of robust control, μ analysis involves the evaluation of the stability and performance of a system under uncertain conditions. The structured singular value (μ) serves as a measure of robust control to quantify the extent of uncertainty that a system can withstand while remaining stable.

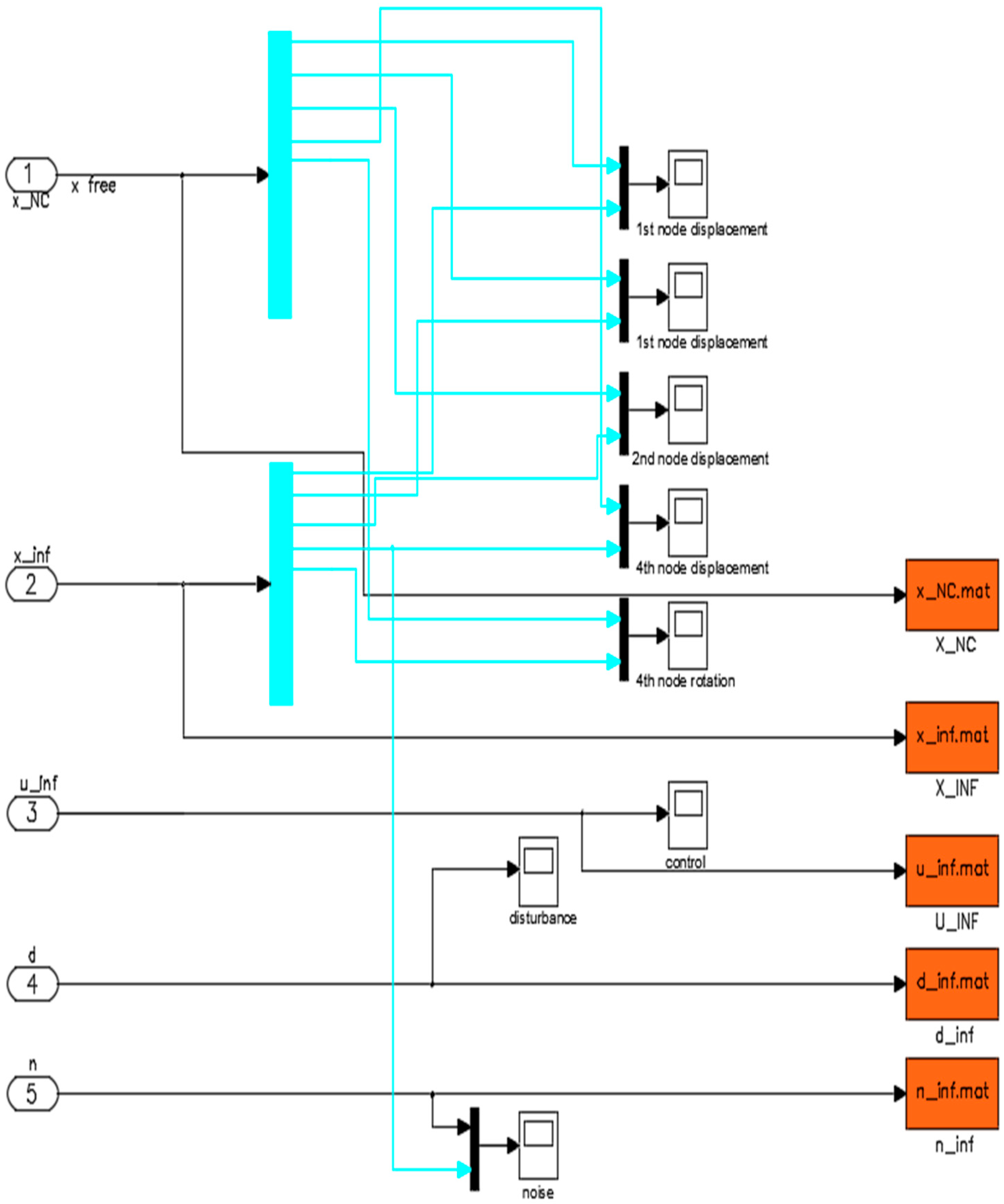
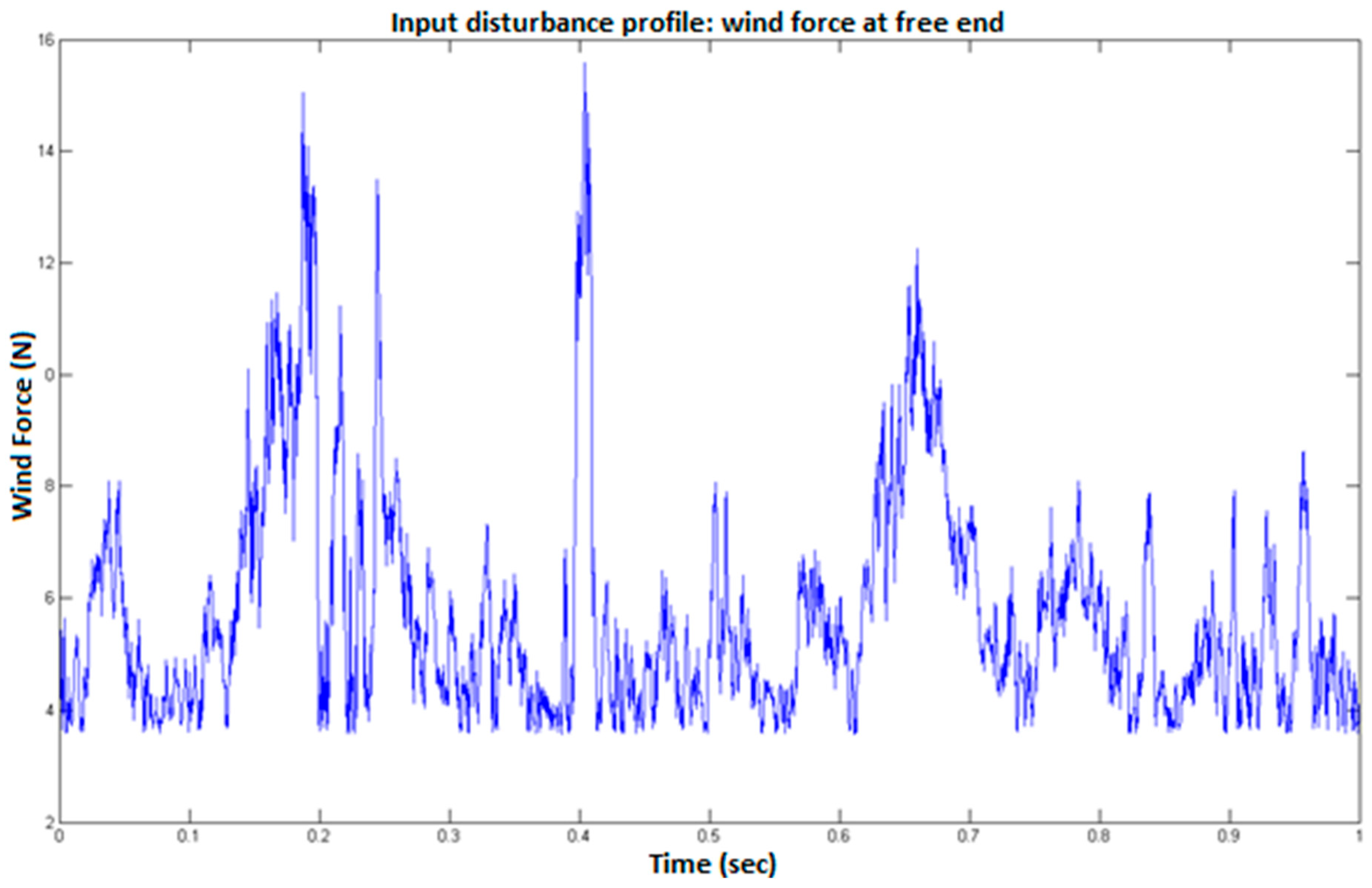
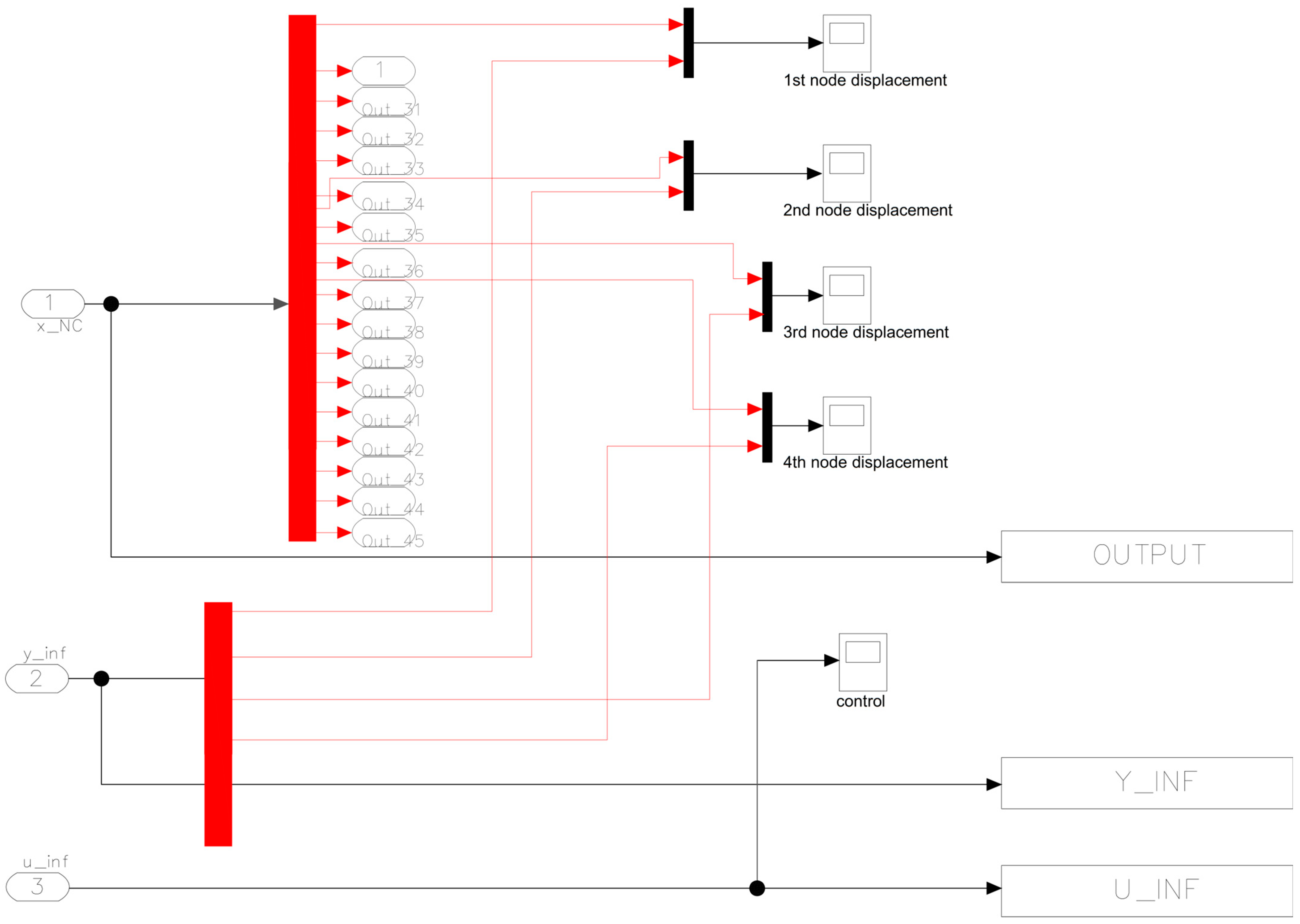
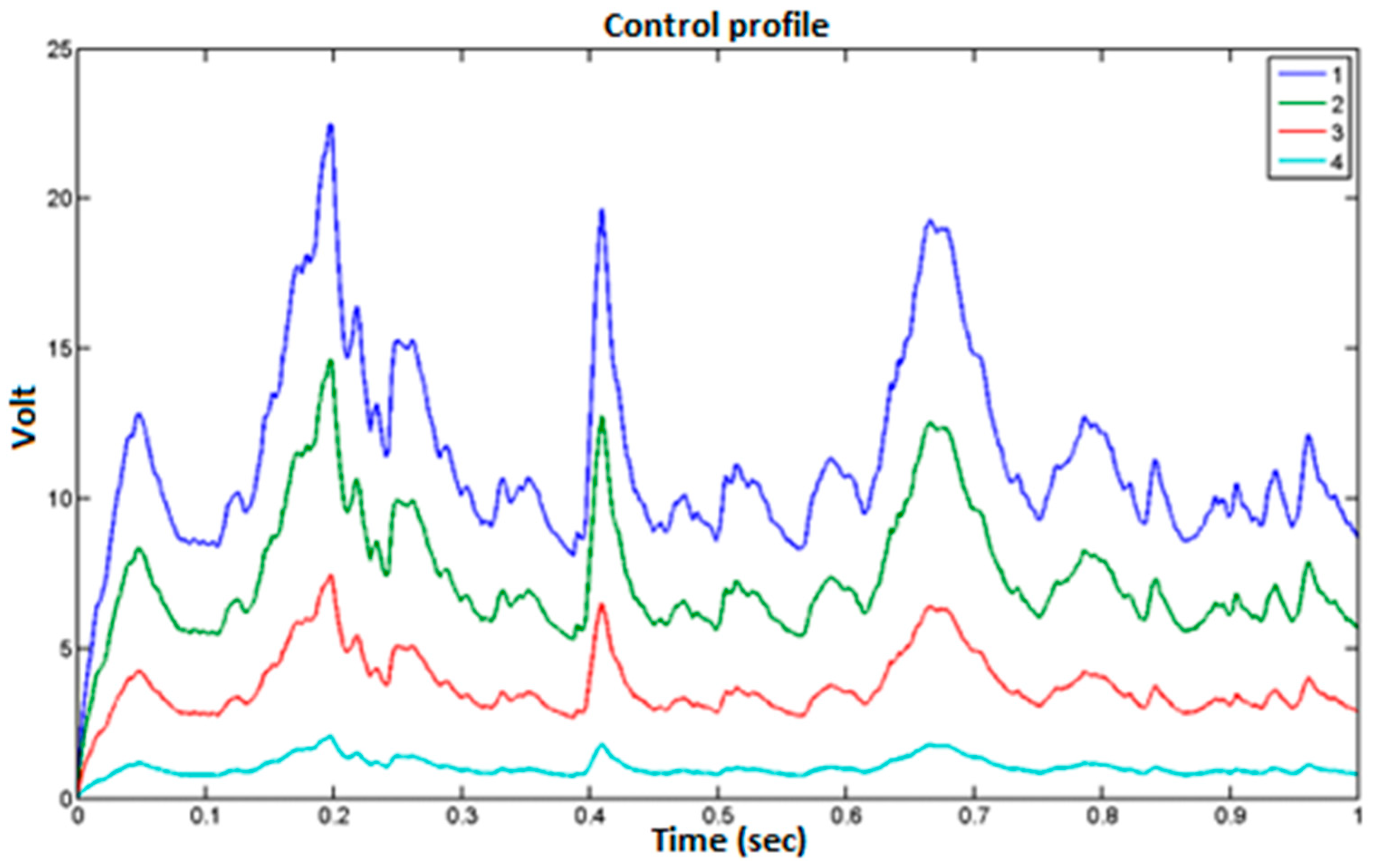
We analyzed our smart structures using a μ analysis. The purpose of μ analysis is to define a performance measure, represented by μ, and to evaluate system performance in the face of uncertainty. The same restrictions involving the constants m_p and k_p enclose this uncertainty [20,24,30,31,36]. The outcome of each simulation was based on MATLAB Simulink (Figure 1) and the noise was represented as ±2% of the disturbance in each case. The results concern the rotation and displacement of smart beam nodes. Figure 1 shows the displacements of the nodes that have piezoelectric actuators. Each node has two displacements one vertical displacement and one rotational. The outputs are the vertical displacement and the rotation. The outputs are the results of the displacements with and without control and the voltages of the actuators. In addition, measurement noise as a percentage of the measurements is taken into account.

The μ synthesis is a robust control technique used to design controllers for systems with uncertainties. It aims to maximize the system performance while ensuring stability in the presence of uncertainties. The “μ” denotes the maximum singular value of the transfer function from uncertainty to performance [11,12,13,14].

Here, a step-by-step guide on how to apply μ synthesis in a Simulink environment is provided.

System Modeling Simulink was used to create a comprehensive dynamic model of the system that included all its essential components and dynamics.

Modeling Uncertainty: The uncertainty of the system is determined and represented. Examples include variations in the parameters, external disturbances, and other sources of uncertainty.

Transfer Function Representation: Simulink’s transfer function blocks were used to represent uncertainty. Each block represents a dynamic fluctuation or unknown parameter.

μ Sensitivity Analysis: Examine how uncertainties impact the sensitivity of the system using Simulink’s “μ Sensitivity Analysis” tool.

μ Synthesis Tool: To start the μ synthesis process, Simulink’s μ Synthesis Tool is used, if required. The user was guided by the design process using this tool.

Controller design: Controllers are created using μ synthesis findings as a guide. Simulink offers blocks to represent controllers created using this method.

A closed-loop simulation simulator was used to simulate the closed-loop system and assess the performance of the planned controller under various conditions, including uncertainties.

Analysis and Tuning: To attain the intended performance, the simulation results were analyzed, and the controller parameters were adjusted as needed.

Validation: The resilience of the developed controller is examined by subjecting it to various uncertainties and disturbances. To confirm its validity, the planned resilience of the controller is tested against a range of uncertainties and disturbances.

Reporting and Documentation: Keep track of controller design, simulation outcomes, and μ synthesis procedure. A Simulink Report Generator was used to create the reports.

Systems with complicated uncertainties and fluctuating operating conditions significantly benefit from μ synthesis. This makes it possible to create resilient controllers that can continue to operate and remain stable, despite these uncertainties. The Simulink toolbox offers a suitable environment for developing and testing controllers built using the μ synthesis approach [10,34,35,36,37].

In Figure 1, we present a block diagram in Simulink for our intelligent structure problem. The inputs were the mechanical disturbance and noise, and the outputs were the control force u and displacements of the four Pzt patches of the smart beam. The noise was represented as ±2% of the disturbance in each case. The outputs of each node were displacement and rotation.

It should be noted that Simulink was not used exclusively but was combined with finite element analysis, programming in MATLAB, and subroutines in Simulink, which are good for better simulation of the problem. Advanced intelligent control techniques were used, and all calculations were performed with high accuracy. This problem has been addressed by many researchers [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15], but the results presented below are much improved compared to other publications [5,8,9,10,11,12,13,14,15,18].

3. Results

This section investigates an eight-element cantilever smart structure (as depicted in Figure 2 and Figure 3) featuring four pairs of piezoelectric patches that are symmetrically bonded to both the top and bottom surfaces of each beam element. Several sections of the building were subjected to the measurements listed in

Table 1. Parameters of the smart beam.

Parameters	Values
L, for beam length	1.20 m
W, for beam width	0.003 m
Wp, pzt width	0.003 m
h, for beam thickness	0.096 m
hp, piezoelectric thickness	0.0002 m
ρ, for beam density	1700 kg/m3
E, for Young’s modulus of the beam	1.7 × 1011 N/m2
Ep, Young’s modulus of pzt
6.3 × 1010 N/m2
bs, ba, for Pzt thickness	0.002 m
d31 the piezoelectric constant	240 × 10−12 m/V

.

The function f_m(t) in Equation (1) was derived from the wind velocity data shown in Figure 4.

$$f_m(t)=\frac{1}{2}\rho C_u{V}^2(t)$$

(13)

where V = velocity, ρ = density and C_u = 1.5.

3.1. Controller Synthesis

The solutions to the analytical problems and methods for evaluating controller performance are addressed in the aforementioned sections. It is feasible to calculate a controller that delivers a specific performance by using a structured singular value [14,15,18]. This is the so-called (D, G − K) iteration [24,25,26] in which finding a μ-optimal controller Κ_s such that μ(Φ_u(F(jω), Κ_s(jω)) ≤ β, $\forall$ω, is transformed into the problem of finding transfer function matrices D(ω)$ϵ\forall \mathsf{\Delta }$ and G(ω)ϵΓ, such that:

$$\underset{\omega }{sup\overline{\sigma }}\left[\left(\frac{D\left(\omega \right)\left(F_u\left(F\left(j\omega \right),{\rm K}\left(j\omega \right)\right)D^{-1}\right(\omega )}{\gamma }-jG(\omega )\right){\left({\rm I}+G^2(\omega )\right)}^{-\frac{1}{2}}\right]\le 1,\begin{array}{c}\forall \omega \end{array}$$

(14)

Unfortunately, this method does not guarantee the discovery of the local maxima. However, for complex perturbations, an alternative method called D-K iteration (also implemented in MATLAB Simulink, Mathworks, Natick, MA, USA) [28,29,32] is available, often providing favorable results through a combination of μ analysis and Hinf synthesis. The initial value represents the upper bound of μ in terms of the scaled singular value [14,18,19,36,38].

$$\mu (N)\le \underset{D\in D}{min}\overline{\sigma }(DN{D}^{-1})$$

(15)

The goal was to determine a controller that reduces the peak frequency of the upper limit.

$$\underset{K}{min}\left(\underset{D\in D}{min}{‖DN\left(K\right)D^{-1}‖}_{\infty }\right)$$

(16)

By alternately minimizing ${‖DN\left(K\right)D^{-1}‖}_{\infty }$ with respect to either K_s or D (while maintaining the other constant) [18,24,25,26,36,39].

The term D-K iteration specifically denotes a method that combines μ analysis and Hinf synthesis. This approach focuses on obtaining a controller that reduces to the minimum peak of the upper limit across frequencies. This is achieved by iteratively minimizing either the controller (K_s) or the transfer function matrices (D) while keeping the other constant [18,24,25,26,36,39].

Figure 5 shows a Simulink block diagram of the intelligent structure problem. The measurements pertain to the four nodes of the beam, and modeling of the intelligent structure was conducted through Finite Element Analysis (part 2 methodology). Control Voltages, the rotations with and without control, and outputs include displacements with and without control, as shown in Figure 6, Figure 7, and Figure 8, respectively. Figure 6 shows the voltages utilized and obtained in Figure 5 (output diagram) for the four measured nodes of the smart structure. These voltages were maintained below 500 Volts, adhering to PZT limits.

In Figure 7, the rotations (output diagram) of the four measured nodes of the intelligent beam with and without control are presented. The uncontrolled rotations are depicted in blue, representing the turns in the open loop, whereas the rotations in green represent the closed loop with the application of the μ synthesis. A noteworthy decrease in the number of revolutions was nearly zero.

In Figure 8, the displacements (output diagram) of the four measured nodes of the smart beam are illustrated with and without control. The uncontrolled displacements are shown in green, indicating the displacements in the open loop, whereas the displacements in red indicate the closed loop with μ analysis applied. The substantial reduction in the number of revolutions was nearly zero. Equation (15) is then used in Figure 9, considering the modeling uncertainty. Various values of the mass and stiffness matrices were derived from this connection.

K = K₀(I + k_pI2n × 2nδK)

M = M₀(I + m_pI2n × 2nδM)

The initial matrices M₀ and K₀ were used with varying values of m_p and k_p, respectively. Figure 9a (upper part) shows the displacements at the free end of the smart structure with control (μ analysis) for different mass (M) and stiffness (K) matrix values. In Figure 9b (middle), the displacements at the free end of the smart structure are presented with (blue line) and without control considering the different prices of the M and K matrices. Figure 9c (lower part) shows the control voltages for the free end of the smart structure with control (μ analysis) for various mass (M) and stiffness (K) matrix prices. The blue line is in the top and middle figure is the displacement of the free end of the beam using the intelligent Hinfinity controller. In the lower figure the blue line is the piezoelectric actuator voltages for the free end of the beam.

These results are noteworthy because the oscillations were significantly reduced by varying the values of mass and stiffness parameters. The oscillation of the smart beam approaches zero, which is a crucial outcome in mechanical construction owing to the damping of the oscillations. This vibration reduction is vital in engineering applications such as aerospace, automotive, and civil engineering, as it not only enhances performance but also mitigates the risk of structural failures associated with varying mass and stiffness values. All simulations were conducted using MATLAB and Simulink v. 5.0.2 software. The combination of Simulink, Modal Identification, and μ analysis proved to be a potent approach for addressing and optimizing the performance of smart structures by reducing vibrations.

3.2. The Structured Singular Value (μ)

The structured singular value μ measures the smallest amount of uncertainty that can destabilize a system. It considers the specific structure of the uncertainty (e.g., real, complex, or diagonal) that affects the system. Unlike other measures of system robustness such as the singular value, μ considers the interaction between different uncertainties and provides a more accurate measure of the robustness of the system.

Complexity: The μ synthesis process can be mathematically complex and computationally intensive, particularly for high-dimensional systems with large-uncertainty models.

Modeling uncertainties: Accurate modeling of uncertainties in a system is crucial for the success of μ synthesis. Overestimating or underestimating these uncertainties can lead to overly conservative and inadequate control design.

Despite these challenges, μ synthesis remains a powerful tool for designing robust controllers for complex and uncertain systems, offering a level of performance and stability assurance that is difficult to achieve by using other methods.

The limits of μ in the frequency domain are shown in Figure 10. This corresponds to a deviation of approximately 90% from the nominal values of the stiffness and mass matrices M and K, respectively. As observed, the system maintains robust and stable performance because the upper limits of both values remain below one across all relevant frequencies.

4. Discussion

Variations in the parameters, nonlinear behavior, and sensitivity to external perturbations are typical characteristics of smart structures. Piezoelectric materials are essential for these structures because they can act as both sensors and actuators. When mechanical stress is applied to piezoelectric materials, an electric charge is produced, which can be used for sensing. However, when an electric field is applied, these materials undergo deformation, which makes them suitable actuators for smart structures for accurate control and adaptation. The specific results of vibration reduction in intelligent structures using robust control may differ depending on the control mechanisms employed, the system dynamics, and the applications. Some typical results and advantages are offered by strong control strategies for vibration reduction. Robust control strategies attempt to promote system stability. Consequently, the smart structure exhibited better dynamic behavior and was less susceptible to instability. Robust controllers are designed to function effectively in a variety of working environments, including variations in the load and structural factors. This flexibility guarantees efficient vibration attenuation in various situations. Ensuring robust control reduces the effects of the errors and uncertainties in the model. This is particularly important for smart structures, where precise modeling of control and structural aspects may be difficult. Sturdy controllers can react quickly to system changes, enabling prompt vibration mitigation modifications. This is significant for dynamic systems, in which the conditions may change quickly. Robust control techniques can reject external disturbances that may cause smart structures to vibrate. Consequently, the system becomes more robust and continues to function, even when external factors are present. By accurately and consistently suppressing the vibrations, it can be ensured that the smart structure performs within predetermined bounds. This is essential for applications that require an accurate vibration control. Uncertainties and complex dynamics are common in smart structures. Robust control offers a dependable and flexible vibration-reduction solution by adjusting the parameter uncertainty. μ analysis measures the worst-case performance loss caused by uncertainty to evaluate the resilience of a control system. It is crucial to remember that real outcomes rely on the particular effective control approach used, that is, the standard of robust control techniques for reducing vibrations in smart structures.

Smart structures also referred to as intelligent or adaptive structures, are designed to detect and respond to environmental changes in a controlled and efficient manner. This involves the integration of sensors, actuators, and control systems to improve the overall performance and capability of structures. It is known that the system parameters of intelligent structures constantly change for various reasons. Under altered circumstances, ordinary controllers are ineffective and cannot ensure the reliability of closed-loop systems. However, robust control-theory-based controllers not only preserve the highest performance but also the closed-loop stability of the perturbed system with wide variations in system parameters. The relative superiority of these controllers is discussed based on a few time-domain features of the closed-loop system, which cannot be represented by the frequency-domain findings alone. Specific examples of multi-objective robust control challenges include strong stabilization, which necessitates an inherently stable controller, and simultaneous stabilization, which entails designing a single controller to stabilize multiple plants. Moreover, many current approaches or heuristics for addressing these challenges often lead to excessively high-order controllers. The results underscore the significance of the proposed model and techniques, and the control behavior of the beam aligns with the predictions.

In conclusion, we use μ analysis, also known as structured singular value analysis, which focuses on analyzing and designing controllers for systems with structured uncertainty (such as parameter variations within known bounds). Deals with uncertainties can be described using known structures or bounds. The system robustness is evaluated by computing the μ value, which represents the worst-case gain of the uncertainty in the output. Mathematical techniques, such as singular value decomposition and optimization algorithms, are involved. Compared to other works and other controllers [13,15,17,18,36], our work considers modeling uncertainties and fully suppresses oscillations even with varying mass stiffness dampers. The structural oscillations are fully damped. In works dealing with the same subject, complete suppression of oscillations was not achieved in references [8,9,13,15,18,36]. The use of the H∞ control did not achieve complete rejection of the oscillations. H∞ control minimizes [9,13,15,17,36] the sensitivity to disturbances, whereas μ-analysis evaluates robustness using the μ-value, representing the worst-case gain. The μ analysis can be more complex owing to its mathematical techniques and the explicit consideration of structured uncertainties. Both methods find applications in industries where robust control is crucial, but the choice between them depends on the nature of the uncertainties and the desired trade-offs between performance and robustness.

In summary, H-infinity (H∞), analysis, and μ analysis are powerful tools for designing robust controllers, with H∞ [13,15,17] focusing on general robustness and disturbance rejection, while μ analysis specializes in handling structured uncertainties and explicitly evaluating robustness using the μ value. In our work, we achieved complete rejection of the structural oscillations, even for the uncertainty plan in the initial smart model. The results are remarkable and different from those of previous studies [6,8,9,15,17,21]. This study investigated the benefits of intelligent control in smart systems. It uses μ analysis and synthesis techniques in state-space and frequency simulations in comparison with other studies in that we have state-space [8,9,15] or frequency [6,9,13] simulations. The advantages of this approach include leveraging the measurement noise, achieving full oscillation suppression, decreasing the controller complexity, and introducing white noise as a disturbance input.

5. Conclusions

This paper presented advanced control techniques for suppressing oscillations caused by dynamic loads. Intelligent control was used, whereas a robust μ controller was used to dampen oscillations. We evaluated the robustness and usefulness of the system after performing system analysis. Disturbance rejection in smart structures with piezoelectric materials is a critical aspect, and this study investigated the advantages of resilient control in intelligent systems by implementing μ analysis in state-space simulations and frequency analyses. This study presents a thorough approach to the design and implementation of robust controllers, specifically for intelligent structures. This paper proposes a robust control-based structural identification method that builds a state-space mode and frequency domain using the input and output data of the system. Using this control model, a reliable controller was developed to reduce the vibrations. Managing the uncertainties and fluctuations in system dynamics is the main difficulty. Techniques for controlling vibrations have been used to dampen them during dynamic disturbances. These techniques are crucial to the functioning of mechanical systems under stochastic loading conditions. In this work, complete suppression of oscillations is achieved, which has not been achieved in other publications [5,8,9,10,11,12,13,14,15,18], and very good results are presented in both the state-space and frequency domains. The oscillations were suppressed, even after introducing uncertainty into the simulation model. It should be noted that Simulink was not used exclusively but was combined with finite element analysis, programming in MATLAB, and subroutines in Simulink, which are good for better simulation of the problem. Advanced intelligent control techniques were used, and all calculations were performed with high accuracy. This problem has been addressed by many researchers [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15], but the results presented below are significantly improved compared with other publications [5,8,9,10,11,12,13,14,15,18].

The benefits of this work are as follows: To obtain the desired outcomes, programming was performed in MATLAB by leveraging the measurement noise from the beam’s state; our approach achieves complete suppression of oscillations while reducing the controller’s order. White noise was introduced as the disturbance input and its magnitude was set as a percentage of the disturbances. We created reliable controllers capable of managing uncertainty. We achieved disturbance rejection, particularly in smart structures with piezoelectric materials. This study explores the advantages of resilient control in intelligent systems by implementing μ analysis and synthesis in state-space simulations. The benefits of this work include utilizing measurement noise, achieving complete oscillation suppression, reducing the controller order, and introducing white noise as a disturbance input.

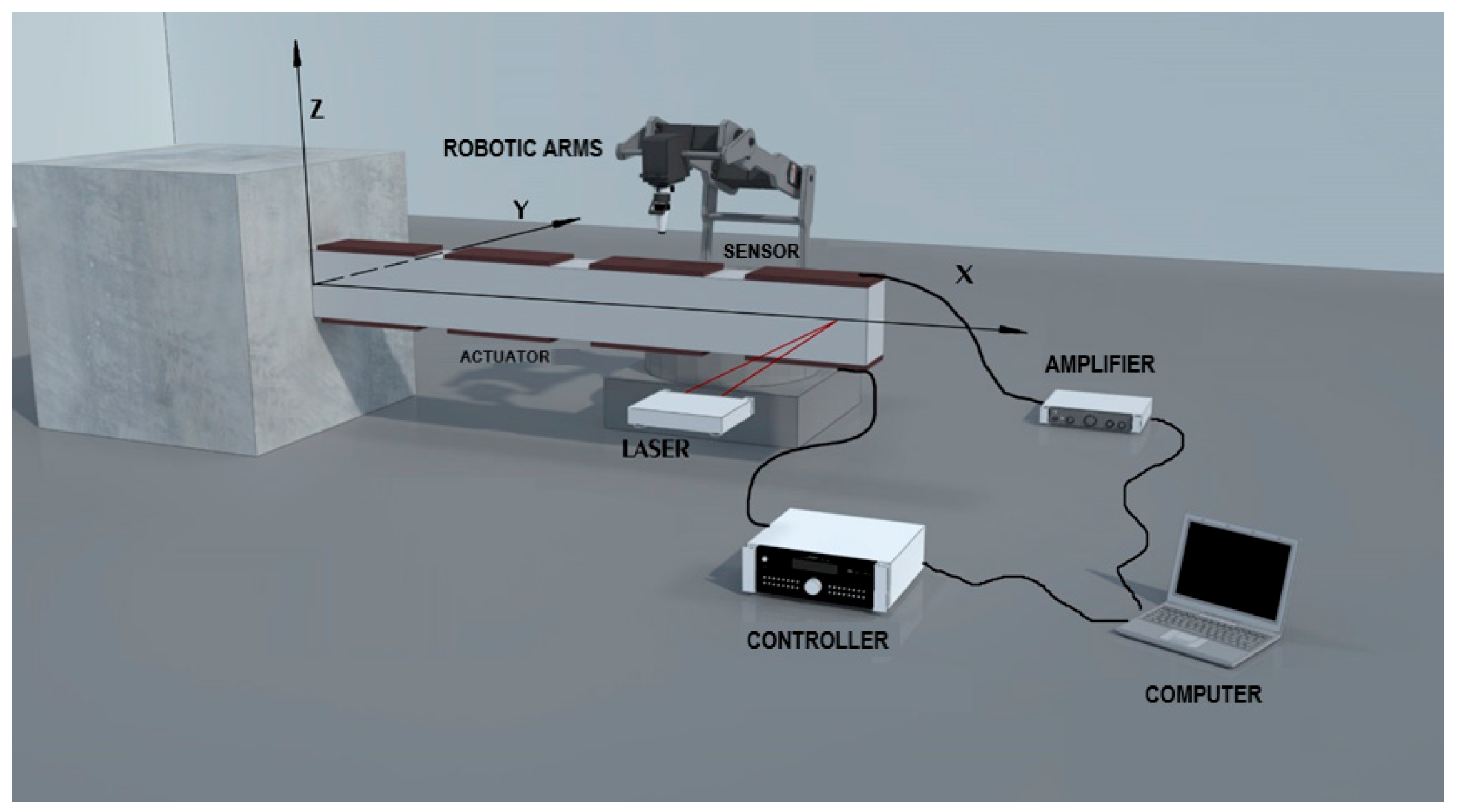
Programming involves obtaining desired outcomes, such as creating reliable controllers capable of handling uncertainty. The objective of robust control techniques is to maintain the system stability and peak efficiency, even when the parameters change. Future research will focus on applying these control mechanisms to actual intelligent structures in experimental contexts and utilizing artificial intelligence to mitigate vibrations and noise in structures.