Abstract
The ongoing digital transformation is bringing a pervasive diffusion of ultra-broadband, fixed-mobile connectivity, the deployment of cloud-native Fifth Generation (5G) infrastructures, edge and fog computing and a wide adoption of artificial intelligence. This transformation will have far-reaching techno-economic impacts on our society and industry. Nevertheless, this transformation is still laying its foundation in electronics and the impending end of Moore’s law. Therefore, looking at the future, a rethinking of the ways of doing computations and communications has already started. An extended adoption of quantum technologies is one possible direction of innovation. As a matter of fact, a first quantum revolution, started decades ago, has already brought quantum technologies into our daily lives. Indeed, today, a second revolution seems to be underway, exploiting advancements in the ability to detect and manipulate single quantum objects (e.g., photons, electrons, atoms and molecules). Among the different technological approaches, topological photonics is a rapidly growing field of innovation. Drawing inspiration from the discovery of the quantum Hall effect and topological insulators in condensed matter, recent advances in topological photonics hold a promising opportunity for optical networking and quantum computing applications.
1. Introduction
Today, we are experiencing a profound digital transformation of society and industry. Technologies such as software-defined networking (SDN) and network function virtualization (NFV) offer the opportunity to design and deploy 5G infrastructures, showing unprecedented flexibility and programmability. SDN concerns the separation of network control functions from network forwarding ones, while NFV seeks to abstract (i.e., virtualize) networking functions from the hardware on which they are executed.
These technologies are enabling a deeper integration of network infrastructures with cloud computing platforms, which seek to deliver on-demand information technology (IT) services (e.g., on a pay-as-you-go basis). This trend is also true for edge and fog computing, which represent the evolution of cloud computing in the direction of deploying and using information technology (IT) resources closer and closer to the end users.
As a matter of fact, an orchestrated use of cloud, edge and fog computing and networking virtual resources allows for the composition and delivery of a continuum of network capabilities, functions and services for multiple digital applications.
At the same time, the future sustainability of said infrastructures will have to face several techno-economic challenges, such as the transmission and processing of enormous quantities of data with ultra-low latencies, automation of management, orchestration and control processes, fulfilment of the strict requirements of resilience, security and privacy and the optimization of energy consumption.
These challenges will become more and more complex to be tamed in the future, as this transformation is still laying its foundation in electronics and the impending end of Moore’s law. Therefore, a rethinking of the ways of doing computations and communications has already started. In this scenario, a more profound adoption of quantum technologies is one possible evolutionary direction.
As a matter of fact, a first quantum revolution, started decades ago, has already brought quantum technologies into our everyday lives. Chips for computers and smartphones, systems for medical imaging (e.g., nuclear magnetic resonance and positron emission tomography), LEDs and lasers are all devices and systems whose functioning is based on quantum mechanics principles.
Today, a second revolution seems to be underway, exploiting advancements in the ability to detect and manipulate single quantum objects (e.g., photons, electrons, atoms and molecules). We are witnessing, in fact, an impressive growth of interests, with several investments from public and private organizations worldwide also targeting new applications. In particular, there are three quantum phenomena, well known and tested in physics, that a second revolution pretends to engineer and control.
These phenomena are superposition, entanglement and measurement, and are defined as follows:
- Superposition concerns the property of quantum objects to stay in a linear combination of multiple states until they are observed;
- Entanglement is defined as the possibility that two or more quantum objects stay intrinsically linked in an intertwined composite state, regardless of how far apart the objects are from one another. Recently, hyperentanglement has been discovered, defined as the entanglement in multiple degrees of freedom (DOFs) of a quantum system, such as the polarization, spatial mode, orbital angular momentum, time-bin and frequency DOFs of photons;
- Measurement regards the collapse and disruption of a quantum state from a coherent, probabilistic superposition state into a discrete one.
It is expected that within 10 years, quantum technologies will become mature enough to control and exploit these three phenomena, generating an impact over many markets, ranging from telecommunications and Information and Communication Technologies (ICT) to medicine, finance, transportation and so on. International innovation activities and standardization bodies are aligned in identifying four main application areas: communications, computing, simulations and sensing and metrology.
The area of quantum communications includes two main subdomains: (1) so-called quantum-safe communications and (2) the teleporting of quantum information (e.g., quantum Internet). The former subdomain is about quantum-safe communications, which leverage systems such as quantum key distribution (QKD) and quantum random number generators (QRNGs). Today, these systems have high technology readiness levels (TRLs) of around 7–9. The latter, the teleporting of qubits, has a rather low TRL of around 2–3, as it is still in research and innovation labs.
Quantum computers leverage on the above-mentioned three quantum principles to operate faster than classical computers in solving complex optimization and combinatorial problems (processing time reduced from exponential to polynomial time). Today, trapped ions and superconducting qubits seem to be the quantum computing technologies which better satisfy the five required criteria for quantum computing, formerly defined by Di Vincenzo:
- A scalable physical system with well characterized qubits;
- The ability to initialize the state of the qubits to a simple fiducial state;
- Long, relevant decoherence times;
- A universal set of quantum gates;
- A qubit-specific measurement capability.
Other approaches are gaining momentum, such as impurity spins in solids, neutral Rydberg atoms and topological photonics. In fact, this is a rapidly growing field of innovation.
The application area of quantum simulations concerns all those applications where well-controlled quantum systems are used to simulate the behavior of other systems, which are less accessible and more complex for a direct simulation (TRL is about 6–8). Quantum sensing and metrology includes those applications where the high sensitivities of quantum systems can be exploited to measure physical properties and timing with more precision (e.g., magnetic and heat sensors, gravimeters, GPS-free navigators and clocks, with TRLs of about 5–8).
Overall, while some quantum applications are already commercially available today (e.g., QKD, QRNG, quantum annealers, quantum simulations, atomic clocks and some quantum sensors), the current use of the second wave of quantum technologies is still relatively limited. This is due to both technical limitations and tradeoffs between technical performance and costs. While further progress is still needed, innovation achievements are accelerating, and the international community is recognizing the disruptive potential of this second quantum revolution.
In particular, in view of these advancements, a future scenario pursuing a profound integration of optical communications and quantum optical computing would offer several techno-economic advantages, in terms of efficiency, performance and savings. In this regard, this paper aims at highlighting that topological photonics could be the technology playing this integrative role.
In particular, the main contributions of this paper include the following:
- A brief description of a vision aiming at the integration of optical communications and quantum optical computing;
- A description of some key concepts and definitions on topological photonics, with a focus on the adoption of orbital angular momentum (OAM) for optical communications, networking and quantum optical computing;
- An overview of the state-of-the-art future challenges and applications.
2. Quantum Communications and Quantum Optical Computing
As mentioned earlier, the term quantum communications refers to communications with quantum security (e.g., QKD and QRNG) and by the teleporting of qubits (e.g., quantum Internet).
Quantum Internet has been defined as a global network exploiting some principles of quantum physics for transmitting, networking, processing and storing qubits.
Some key characteristics of the quantum Internet have been recently overviewed by an Internet Engineering Task Force (IETF) draft [1]. Specifically, the quantum Internet is expected to teleport quantum information without actually sending any qubits through the quantum channel [2,3]. Quantum teleportation requires two communication links: a classical link for transmitting the pair of classical bits and a quantum link for entanglement generation and distribution. The integration of classical and quantum resources is crucial for a quantum Internet [4] and for any telecommunications infrastructure exploiting quantum technologies (e.g., QKD and quantum cloud computing).
Today, the development and exploitation of the quantum Internet still has several open challenges. For instance, while in the classical Internet bits can be duplicated within a node or among the different nodes of a network, this is not valid anymore for the quantum Internet. This is due to the so-called no-cloning theorem, which forbids any possibility of duplicating an unknown qubit.
This means that when a qubit (for example, encoded within an inner state of a photon) is transmitted to a remote node via a fiber link, attenuation or noise can degenerate it in a way that the associated quantum information cannot be recovered via a measuring process or duplication.
In other words, it is not possible to count on optical amplification, as used in standard optical networks (ONs), by multiplying the number of photons. Nevertheless, ONs are still considered to be the optimal medium for quantum communication, even if the maximum communication distance is severely limited by optical losses in optical fibers. Much progress is being made. Already in 2006, entanglement-based quantum communication reached 144 km [5].
Quantum repeaters are believed to be the most promising way to overcome the distance limit. Current technological paradigms for a quantum repeater consist of three basic approaches: entanglement swapping [6,7], entanglement purification [8,9] and quantum memory [10,11,12].
Recently, significant progress has been made both theoretically [13,14,15] and experimentally [16,17,18]. However, some technological obstacles still remain in building practical quantum repeaters, thus reducing the levels of performance.
In this regard of quantum communications, a quantum optical network (QON) extends the current model of ONs based on wavelength division multiplexing (WDM) nodes, add-drop multiplexers and optical cross-connects (which are used for multiplexing, demultiplexing, extracting and routing different channels of light into an optical network).
QONs are aimed at transporting, elaborating and storing quantum information encoded in photonic qubits. As a matter of fact, photon generation and detection technologies have enormously improved the quality of optical quantum states and efficiency in handling them. Integrated circuits evolved from a basic demonstration of beam splitting to massively multimode reconfigurable optical circuits, and the number of photons that can be simultaneously used is growing [19,20]. There are already several field trials with commercial QKD pieces of equipment integrated in current telecommunications infrastructures. For example, quantum cryptographic keys are generated and transported in terms of single-photon qubits over a quantum link, in parallel to a traditional transmission link.
As mentioned, it is also possible to use photon qubits to perform quantum computation tasks. There are, in fact, remarkable advancements in the silicon photonic route to quantum optical computing.
A description of the state of the art of quantum optical computing is outside the scope of this paper, but it is highlighted that only computing systems using photonic qubits show some key advantages. For instance, they do not require the cooling which is needed when using superconducting qubits, and they show lower energy consumption and less sensitivity to de-coherence. Moreover, this paper aims at addressing the opportunity offered by a simpler and broader integration of quantum optical networks with optical quantum computing. This would lead to the development of quantum optical infrastructures (Figure 1). In particular, the term infrastructure as a service (IaaS) indicates all those (digital and quantum) physical nodes, systems and links used for offering communications, networking, storage and computing services. A platform as a service (PaaS) provides developers with a complete software environment for the development and deployment of higher levels of services, from simple apps to articulated infrastructure-based services.
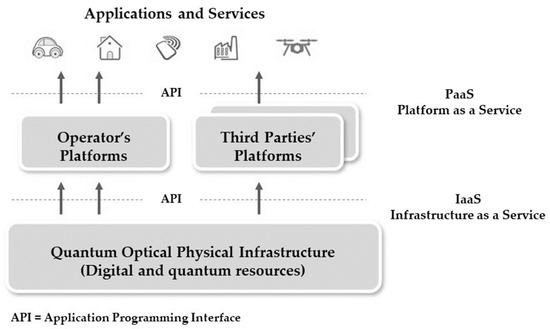
Figure 1.
Infrastructure integrating quantum optical networks and optical quantum computing.
Nevertheless, said integration is challenging, and it should be pursued at least at these three levels:
- Infrastructure architectural integration;
- ○
- Management, control and orchestration (abstractions and interfaces) of digital and quantum resources and services;
- Optics integration;
- ○
- Integrated photonic components and sub-system systems;
- Channels integration;
- ○
- Quantum optical vs. classical optical links.
Among the different optical technologies, topological photonics is gaining rapidly growing attention, thus holding a promising opportunity for applications in optical networking and optical quantum computing.
The next section will provide some definitions and basic concepts on topology and topological photonics.
3. Topological Photonics and OAM
3.1. Basic Concetps on Topology
In mathematics, topology is concerned with the properties of a geometric object that are preserved under continuous deformations, such as stretching, twisting, crumpling and bending, but not tearing or gluing. The classical example is the topological equivalence between a donut and a coffee cup [21]. Different topologies can be characterized by integers called topological invariants.
Systems having the same topological invariant are topologically equivalent, showing the same topological phase. A topological phase transition is a process during which the topological invariant changes. A topological quantum number (also called topological charge) is any quantity assuming only one of a discrete set of values due to topological considerations. A topological quantum number is sometimes called a winding number. This idea will be useful when discussing the encoding of quantum information in topological photons.
In general, the concept of topology has been widely adopted in physics and, more recently, for describing quantum effects and the properties of topological materials [22].
The concept of topological order, in fact, emerged in physics following the discovery of the Fractional Quantum Hall (FQH) effect in 1982 [23,24]. The FQH effect occurs in two-dimensional electron systems in a strong magnetic field. The Hall conductance of 2D electrons precisely shows values at the fractional level. It becomes a property of a collective state in which electrons bind magnetic flux lines and create quasiparticles, called anyons.
In particular, the FQH effect shows two specific phenomena: (1) fractionalization, where anyon excitations carry fractional quantum numbers and even fractional statistics, and (2) topological degeneracy, where the number of degenerate ground states responds non-trivially to the changing of the topology of the underlying manifold. These properties are essential components in the development of topological quantum computing, for example, based on anyons.
Anyons are quasiparticles whose existence has been proposed since the late 1970s, and they were officially named by Frank Wilczek in early 1980s. Anyons emerge in 2D materials and braid in significantly different ways than fermions and bosons. If a fermion or a boson were dragged around another one, the action would not produce any record. Anyons alter wave functions, so they would create a record. Specifically, this involves inserting a phase into the wave function. Due to this property, anyons can be used to encode and process quantum information. Remarkably, their topological behavior provides resilience against decoherence and robustness to local perturbations.
The idea of encoding quantum information in topologies began with a proposal [25] about the use of the collective state of interacting spins on a surface. For instance, topological qubits could be coded not just with FQH states [26] and Majorana zero modes [27,28], but also with photons. This possible use of photons is not surprising. In fact, the photonic analogue of the FQH effect in photonic crystals has been described in [29], where the periodic variation of optical materials mold photons the same way as solids modulating electrons. The idea was confirmed by Wang et al., who provided realistic material designs [30] and experimental observations [31].
As the discovery of topological insulators has inspired the topological properties of interfacial electrons transported without dissipation, similarly, the exploitation of topological photonics (e.g., with photonic crystals, coupled resonators, metamaterials and quasicrystals) will allow the creation and manipulation of states of light with innovative properties.
An overview is provided in the next section, starting from some key characteristics of photons that allow the encoding quantum information in topological photonic qubits.
3.2. Topological Photonic: Vortex and Qubits
It is known that each mode of the electromagnetic (EM) field can be considered as an individual quantum degree of freedom. For example, depending on the transmission mode, the axis of oscillation in electromagnetic transmission may have different orientations to the direction of transmission.
In a transverse electric (TE) mode, the electrical field is transverse to the direction of propagation while the magnetic field is normal to it. In a transverse magnetic (TM) mode, the magnetic field is transverse to the direction of propagation while the electrical field is normal to it. In a transverse electric and magnetic (TEM) mode, both the electrical field and the magnetic field (always perpendicular to one another in free space) are transverse to the direction of travel.
Different sets of modes open the possibility of considering the same quantum state from different perspectives; a given state can be entangled in one basis and factorized in another one. Therefore, it is possible, using the techniques of nonlinear optics, to tailor quantum fields not only in choosing the modes that participate, but also optimizing their spatial-temporal shapes.
Moreover, an EM beam can carry spin angular momentum (SAM) as well as orbital angular momentum (OAM). In general, SAM is associated with circular polarization while OAM, generally arising in conjunction with the spatial variations of the EM field, is present in optical vortices and vortex-like configurations (Figure 2).
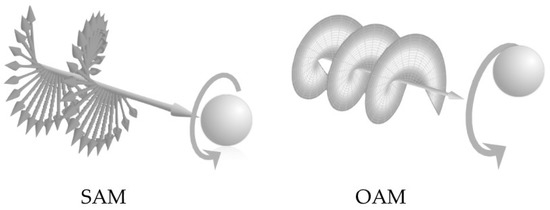
Figure 2.
Spin angular momentum (SAM) and orbital angular momentum (OAM).
More specifically, the SAM is related to the helicity of an EM beam. For a single photon, it assumes two values S = ± (h/2π). In fact, polarization enables only two photon spin states. OAM is related to the spatial helicoidal shape of the wave front. The orbital terms are generated by the gradient of the phase. For a single photon, it assumes the value L = l (h/2π), with l = 0 for a plane wave and l ≠ 0 for a helicoidal wave front.
OAM is a property associated with optical vortices and vortex-like configurations [32]. In fact, in 1992, Allen et al. [33] reported that OAM can be carried by an EM vortex beam. Imagine a beam whose amplitude presents a spatial structure showing a ring-like doughnut profile and phase-front twists in a helical fashion as it propagates. The number of 2π phase changes in the azimuthal direction is the OAM. Beams with different OAM values can be orthogonal to each other.
Such beams can be seen as a subset of the Laguerre-Gaussian modes which has two modal indices: (1) l represents the number of 2π phase shifts in the azimuthal direction and the size of the rings grown with l, and (2) p + 1 represents the number of concentric amplitude rings [34].
As a simple example, the generation of light beams carrying OAM can be achieved through the insertion in the optical path of a phase-modifying device (e.g., a spiral plate or holograms) which imprints vorticity on the phase distribution of the incident beam. Also, Pancharatnam-Berry optical elements (PBOEs), acting on the geometric phase, have proven to be useful for the manipulation of light beams.
The orthogonality of OAM modes (Figure 3) is very important, as it allows multiple independent optical beams to be multiplexed, transmitted and demultiplexed, all with minimal inherent crosstalk.
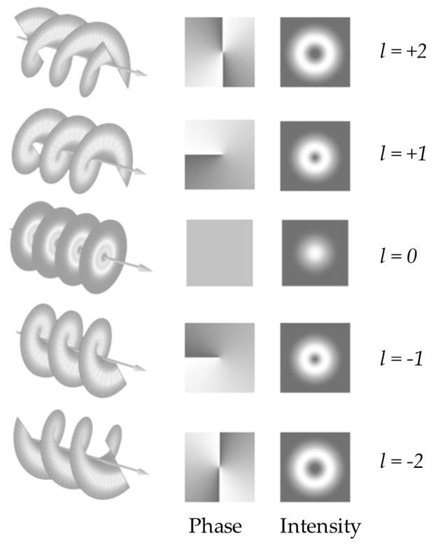
Figure 3.
Orthogonality of orbital angular momentum (OAM) modes.
This is called mode division multiplexing (MDM), which is a subset of space division multiplexing [35,36,37,38]. In an ON, MDM could complement WDM, such that each of many wavelengths can contain many orthogonal structured beams. This could dramatically increase data capacity [39]. For instance, [40] provides an overview of OAM-multiplexed communications.
Moreover, innovative implementations of QKD protocols have been developed and demonstrated [41], both in discrete variable (DV-QKD) and continuous variable (CV-QKD) scenarios [42]. Efforts have been focused, for example, on the design and realization of polarization-sensitive OAM (de)multiplexers, in order to exploit high-dimensional QKDs [43].
In general, the development and exploitation of MDM technology would benefit greatly from advances in devices and subsystems with desirable features, such as low insertion loss, high amplifier gain, uniform performance for different modes, high modal purity, low modal coupling and intermodal crosstalk, high efficiency for mode conversion, high dynamic range, small size, large wavelength range, and the accommodation of high numbers of modes. This a main focus of ON innovation today.
It would also be possible to individually route, switch or drop optical channels in the spatial domain by taking advantage of the beam structure and orthogonality among different OAM modes. This functionality might extend the adoption of OAM beyond static point-to-point links. Remarkable progress is being made in this direction, making MDM based on OAM one of the most promising technologies for the future evolution of ONs.
In the previous section, it has been mentioned that topological quantum numbers are sometimes called winding numbers. The states of the Laguerre-Gauss (LG) mode functions can be seen to depend on the winding number associated with the angle about the propagation axis (i.e., the OAM) [44]. The radially symmetric Airy beams, which exhibit abrupt autofocusing, have also been demonstrated to be capable of carrying OAM in the optical domain. Since its first observation in optics, the Airy beam has been a subject of great interest for its self-acceleration, self-healing and non-diffractive properties during optical manipulation and propagation.
Although most studies of OAM concentrate on the optical domain, there is also great interest in exploring the potential applications of OAM in the millimeter wave and THz domains [45].
The infinite number of orthogonal states of OAM places no limit on the number of bits that can be carried by a single photon. In fact, the ability to create states with different OAMs and superpositions of these OAMs allows the realization of qubits, in an N-dimensional space, with single photons. This is valuable for the development of both analog processing with light and for quantum optical computing. We are reminded that analog computing can be used for making mathematical operations (such as spatial differentiation, integration or convolution) directly using the profile of an impinging EM wave as it propagates through metamaterials. For instance, two typical approaches are subwavelength structured meta-screens combined with graded-index waveguides and multilayered slabs designed to achieve a desired spatial Green’s function.
It was proven in [46] that a single photon with quantum data encoded in its OAM could be manipulated with simple optical elements to provide any desired quantum computation. In addition, it has been shown how building any quantum unitary operator based on beam splitters, phase shifters, holograms and any extraction gate based on quantum interrogation. In 2001, Zeilinger’s group [47] already used OAM in various applications, such as OAM-entangled photon pairs and the use of optical vortices or twisted photons.
It was addressed in [48] how a purely photonic implementation of quantum computing by providing a short overview on how building a large-scale, silicon-photonic quantum computer has been reduced to the creation of good sources of three-photon entangled states.
4. Quantum Materials
There is evidence of a trend showing that interest in topological photonics is growing quite rapidly. A key question remains as to how fast this field may develop over the next 5–10 years.
As mentioned earlier, development and exploitation of this technology would greatly benefit from advances in devices and subsystems (e.g., processors, transmitters, (de)multiplexers and receivers).
Surely, this will very much depend on the advances in quantum materials. It is expected that, in the future, there will be significant advances in the development of new topological mirrors, phases and invariants [49]. Moreover, in the long term, topological photonics can evolve towards other bosonic systems like surface plasmons, excitons [50], exciton polaritons [51], phonons [52] and magnons [53]. This evolution will mainly depend on the availability of innovation quantum materials, and it will surely have far-reaching techno-economic implications.
The 2020 Quantum Materials Roadmap review [54] provides a remarkable overview, including references to the use of artificial intelligence methods.
It should also be mentioned that advances in silicon photonics are creating optical components and elements with high levels of integration. In comparison with plasmonic metamaterials, for example, the advantages also stand in low-cost and well-established nanofabrication techniques. Moreover, silicon nanostructures show simpler integration with existing photonic architectures and compatibility with complementary metal–oxide semiconductors (CMOSs) [55,56].
5. Conclusions and Outlook
A first quantum revolution has already brought quantum technologies into our everyday lives for decades. Chips for computers and smartphones, systems for medical imaging, LEDs and lasers are all based on technologies exploiting quantum mechanics principles. Now, a second revolution seems to be underway, leveraging on the three quantum principles of superposition, (hyper)entanglement and measurement. It is safe to predict that a second wave of quantum technologies could potentially have a major impact in many markets, ranging from telecommunications and ICT to medicine, finance and transportation. Significant investments are being made worldwide across public and private organizations.
Today, quantum security is quite mature for commercialization and implementation in actual networks. Of course, quantum repeaters will be required for both long-distance QKD and distributed quantum computing. Concerning quantum computing, one roadblock is mitigating random fluctuations and noise that could occasionally flip or randomize the state of the qubits during processing.
In general, among the different technological approaches, topological photonics is a rapidly growing field of innovation. Since the discovery of the quantum Hall effect and topological insulators in condensed matter, progressive advances in topological photonics hold great promise for optical networking and quantum computing applications. As a matter of fact, a future scenario pursuing deeper and deeper integration of optical communications and quantum optical computing would offer several techno-economic advantages.
In this regard, this paper aims at highlighting that topological photonics using OAM could be the technology playing this role. For instance, it would be possible to use OAM not only for optical quantum computing, but also for routing, switching and dropping photonic channels in the spatial domain. The common element is taking advantage of the beam structure and orthogonality among different OAM photonic modes.
The development and exploitation of this technology would greatly benefit from advances in the devices and subsystems (e.g., processors, transmitters, (de)multiplexers and receivers) based on quantum materials. Applications would be far-reaching and cover a range of applications, from super-dense coding to teleportation in quantum communications and quantum optical computation.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
References
- Kozlowski, W.; Wehner, S.; Meter, R.V.; Rijsman, B.; Cacciapuoti, A.S.; Caleffi, M. Architectural Principles for a Quantum Internet. In Internet-Draft Draft-Irtf-Qirg-Principles-03; Internet Engineering Task Force: Fremont, CA, USA, 2020. [Google Scholar]
- Cacciapuoti, A.S.; Caleffi, M.; Van Meter, R.; Hanzo, L. When entanglement meets classical communications: Quantum teleportation for the quantum Internet. IEEE Trans. Commun. 2020, 6, 3808–3833. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1973, 70, 1895. [Google Scholar] [CrossRef] [PubMed]
- Cacciapuoti, A.S.; Caleffi, M.; Tafuri, F.; Cataliotti, F.S.; Gherardini, S.; Bianchi, G. Quantum internet: Networking challenges in distributed quantum computing. IEEE Netw. 2019, 34, 137–143. [Google Scholar] [CrossRef]
- Ursin, R.; Tiefenbacher, F.; Schmitt-Manderbach, T.; Weier, H.; Scheidl, T.; Lindenthal, M.; Blauensteiner, B.; Jennewein, T.; Perdigues, J.; Ömer, B.; et al. Entanglement-based quantum communication over 144 km. Nat. Phys. 2007, 3, 481–486. [Google Scholar] [CrossRef]
- Żukowski, M.; Zeilinger, A.; Horne, M.A.; Ekert, A.K. Event-ready-detectors Bell experiment via entanglement swapping. Phys. Rev. Lett. 1993, 71, 4287–4290. [Google Scholar] [CrossRef]
- Pan, J.-W.; Bouwmeester, D.; Weinfurter, H.; Zeilinger, A. Experimental entanglement swapping: Entangling photons that never interacted. Phys. Rev. Lett. 1998, 80, 3891–3894. [Google Scholar] [CrossRef]
- Pan, J.-W.; Simon, C.; Brukner, Č.; Zeilinger, A. Entanglement purification for quantum communication. Nature 2001, 410, 1067–1070. [Google Scholar] [CrossRef]
- Pan, J.-W.; Gasparoni, S.; Ursin, R.; Weihs, G.; Zeilinger, A. Experimental entanglement purification of arbitrary unknown states. Nature 2003, 423, 417–422. [Google Scholar] [CrossRef]
- Chou, C.W.; Laurat, J.; Deng, H.; Choi, K.S.; De Riedmatten, H.; Felinto, D.; Kimble, H.J. Functional quantum nodes for entanglement distribution over scalable quantum networks. Science 2007, 316, 1316–1320. [Google Scholar] [CrossRef]
- Moehring, D.L.; Maunz, P.; Olmschenk, S.; Younge, K.C.; Matsukevich, D.N.; Duan, L.M.; Monroe, C. Entanglement of single-atom quantum bits at a distance. Nature 2007, 449, 68–71. [Google Scholar] [CrossRef]
- Yuan, Z.S.; Chen, Y.A.; Zhao, B.; Chen, S.; Schmiedmayer, J.; Pan, J.W. Experimental demonstration of a BDCZ quantum repeater node. Nature 2008, 454, 1098–1101. [Google Scholar] [CrossRef]
- Zwerger, M.; Dür, W.; Briegel, H.J. Measurement-based quantum repeaters. Phys. Rev. A 2012, 85, 062326. [Google Scholar] [CrossRef]
- Munro, W.; Stephens, A.; Devitt, S.; Harrison, K.; Nemoto, K. Quantum communication without the necessity of quantum memories. Nat. Photonics 2012, 6, 777–781. [Google Scholar] [CrossRef]
- Muralidharan, S.; Kim, J.; Lütkenhaus, N.; Lukin, M.D.; Jiang, L. Ultrafast and fault-tolerant quantum communication across long distances. Phys. Rev. Lett. 2014, 112, 250501. [Google Scholar] [CrossRef]
- Chen, L.K.; Yong, H.L.; Xu, P.; Yao, X.C.; Xiang, T.; Li, Z.D.; Liu, C.; Lu, H.; Liu, N.L.; Yang, T.; et al. Experimental nested purification for a linear optical quantum repeater. Nat. Photonics 2017, 11, 695–699. [Google Scholar] [CrossRef]
- Xu, P.; Yong, H.L.; Chen, L.K.; Liu, C.; Xiang, T.; Yao, X.C.; Lu, H.; Li, Z.D.; Liu, N.L.; Li, L.; et al. Two-hierarchy entanglement swapping for a linear optical quantum repeater. Phys. Rev. Lett. 2017, 119, 170502. [Google Scholar] [CrossRef]
- Kalb, N.; Reiserer, A.A.; Humphreys, P.C.; Bakermans, J.J.; Kamerling, S.J.; Nickerson, N.H.; Benjamin, S.C.; Twitchen, D.J.; Markham, M.; Hanson, R. Entanglement distillation between solid-state quantum network nodes. Science 2017, 356, 928–932. [Google Scholar] [CrossRef]
- Zhong, H.S.; Li, Y.; Li, W.; Peng, L.C.; Su, Z.E.; Hu, Y.; Ding, X.; Zhang, W.; Li, H.; Zhang, L.; et al. 12-photon entanglement and scalable scattershot boson sampling with optimal entangled-photon pairs from parametric down-conversion. Phys. Rev. Lett. 2018, 121, 250505. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Paesani, S.; Ding, Y.; Santagati, R.; Skrzypczyk, P.; Salavrakos, A.; Tura, J.; Augusiak, R.; Mančinska, L.; Bonneau, D.; et al. Multidimensional quantum entanglement with large-scale integrated optics. Science 2018, 360, 285–291. [Google Scholar] [CrossRef]
- Asorey, M. Space, matter and topology. Nat. Phys. 2016, 12, 616–618. [Google Scholar] [CrossRef][Green Version]
- Castelvecchi, D. The strange topology that is reshaping physics. Nat. News 2017, 547, 272. [Google Scholar] [CrossRef]
- Tsui, D.C.; Stormer, H.L.; Gossard, A.C. Two-dimensional magnetotransport in the extreme quantum limit. Phys. Rev. Lett. 1982, 48, 1559. [Google Scholar] [CrossRef]
- Laughlin, R.B. Anomalous quantum Hall effect: An incompressible quantum fluid with fractionally charged excitations. Phys. Rev. Lett. 1983, 50, 1395. [Google Scholar] [CrossRef]
- Kitaev, A.Y. Fault-tolerant quantum computation by anyons. Ann. Phys. 2003, 303, 2–30. [Google Scholar] [CrossRef]
- Stern, A.; Lindner, N.H. Topological quantum computation—From basic concepts to first experiments. Science 2013, 339, 1179–1184. [Google Scholar] [CrossRef]
- Kouwenhoven, L. Majorana Qubits. In Proceedings of the 2018 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 1–5 December 2018. [Google Scholar]
- Franz, M.; Pikulin, D.I. Quantized, finally. Nat. Phys. 2018, 14, 334–336. [Google Scholar] [CrossRef]
- Meade, R.D.; Winn, J.N.; Joannopoulos, J.D. Photonic Crystals: Molding the Flow of Light; Princeton University Press: Princeton, NJ, USA, 1995. [Google Scholar]
- Wang, Z.; Chong, Y.D.; Joannopoulos, J.D.; Soljačić, M. Reflection-free one-way edge modes in a gyromagnetic photonic crystal. Phys. Rev. Lett. 2008, 100, 013905. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Chong, Y.; Joannopoulos, J.D.; Soljačić, M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature 2009, 461, 772–775. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, X.; Xie, Z.; Min, C.; Fu, X.; Liu, Q.; Gong, M.; Yuan, X. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light Sci. Appl. 2019, 8, 1–29. [Google Scholar] [CrossRef]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185. [Google Scholar] [CrossRef]
- Yao, A.M.; Padgett, M.J. Orbital angular momentum: Origins, behavior and applications. Adv. Opt. Photonics 2011, 3, 161–204. [Google Scholar] [CrossRef]
- Bozinovic, N.; Yue, Y.; Ren, Y.; Tur, M.; Kristensen, P.; Huang, H.; Willner, A.E.; Ramachandran, S. Terabit-scale orbital angular momentum mode division multiplexing in fibers. Science 2013, 340, 1545–1548. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Yang, J.Y.; Fazal, I.M.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.; Yue, Y.; Dolinar, S.; Tur, M.; et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 2012, 6, 488–496. [Google Scholar] [CrossRef]
- Pang, K.; Song, H.; Zhao, Z.; Zhang, R.; Song, H.; Xie, G.; Li, L.; Liu, C.; Du, J.; Molisch, A.F.; et al. 400-Gbit/s QPSK free-space optical communication link based on four-fold multiplexing of Hermite-Gaussian or Laguerre-Gaussian modes by varying both modal indices. Opt. Lett. 2018, 43, 3889–3892. [Google Scholar] [CrossRef]
- Willner, A.E.; Huang, H.; Yan, Y.; Ren, Y.; Ahmed, N.; Xie, G.; Bao, C.; Li, L.; Cao, Y.; Zhao, Z.; et al. Optical communications using orbital angular momentum beams. Adv. Opt. Photonics 2015, 7, 66–106. [Google Scholar] [CrossRef]
- Huang, H.; Xie, G.; Yan, Y.; Ahmed, N.; Ren, Y.; Yue, Y.; Rogawski, D.; Willner, M.J.; Erkmen, B.I.; Birnbaum, K.M.; et al. 100 Tbit/s free-space data link enabled by three-dimensional multiplexing of orbital angular momentum, polarization, and wavelength. Opt. Lett. 2014, 39, 197–200. [Google Scholar] [CrossRef] [PubMed]
- Willner, A.E. Communication with a twist. IEEE Spectr. 2016, 53, 34–39. [Google Scholar] [CrossRef]
- Bouchard, F.; Heshami, K.; England, D.; Fickler, R.; Boyd, R.W.; Englert, B.-G.; Sanchez-Soto, L.L.; Karimi, E. Experimental investigation of high-dimensional quantum key distribution protocols with twisted photons. Quantum 2018, 2, 111. [Google Scholar] [CrossRef]
- Qu, Z.; Djordjevic, I.B. High-speed free-space optical continuous variable quantum key distribution enabled by three-dimensional multiplexing. Opt. Express 2017, 25, 7919–7928. [Google Scholar] [CrossRef]
- Larocque, H.; Gagnon-Bischoff, J.; Mortimer, D.; Zhang, Y.; Bouchard, F.; Upham, J.; Grillo, V.; Boyd, R.W.; Karimi, E. Generalized optical angular momentum sorter and its application to high-dimensional quantum cryptography. Opt. Express 2017, 25, 19832–19843. [Google Scholar] [CrossRef]
- Jaeger, G.; Simon, D.S.; Sergienko, A.V. Topological qubits as carriers of quantum information in optics. Appl. Sci. 2019, 9, 575. [Google Scholar] [CrossRef]
- Liu, C.; Liu, J.; Niu, L.; Wei, X.; Wang, K.; Yang, Z. Terahertz circular Airy vortex beams. Sci. Rep. 2017, 7, 1–8. [Google Scholar] [CrossRef]
- García-Escartín, J.C.; Chamorro-Posada, P. Universal quantum computation with the orbital angular momentum of a single photon. J. Opt. 2011, 13, 064022. [Google Scholar] [CrossRef]
- Mair, A.; Vaziri, A.; Weihs, G.; Zeilinger, A. Entanglement of the orbital angular momentum states of photons. Nature 2001, 412, 313–316. [Google Scholar] [CrossRef] [PubMed]
- Rudolph, T. Why I am optimistic about the silicon-photonic route to quantum computing. APL Photonics 2017, 2, 030901. [Google Scholar] [CrossRef]
- Schnyder, A.P.; Ryu, S.; Furusaki, A.; Ludwig, A.W. Classification of topological insulators and superconductors in three spatial dimensions. Phys. Rev. B 2008, 78, 195125. [Google Scholar] [CrossRef]
- Yuen-Zhou, J.; Saikin, S.K.; Yao, N.Y.; Aspuru-Guzik, A. Topologically protected excitons in porphyrin thin films. Nat. Mater. 2014, 13, 1026–1032. [Google Scholar] [CrossRef] [PubMed]
- Karzig, T.; Bardyn, C.E.; Lindner, N.; Refael, G. Topological polaritons from quantum wells in photonic waveguides or microcavities. arXiv 2014, arXiv:1406.4156. [Google Scholar]
- Prodan, E.; Prodan, C. Topological phonon modes and their role in dynamic instability of microtubules. Phys. Rev. Lett. 2009, 103, 248101. [Google Scholar] [CrossRef]
- Shindou, R.; Matsumoto, R.; Murakami, S.; Ohe, J.I. Topological chiral magnonic edge mode in a magnonic crystal. Phys. Rev. B 2013, 87, 174427. [Google Scholar] [CrossRef]
- Giustino, F.; Bibes, M.; Lee, J.H.; Trier, F.; Valentí, R.; Winter, S.M.; Son, Y.W.; Taillefer, L.; Heil, C.; Figueroa, A.I. The 2020 Quantum Materials Roadmap. J. Phys. Mater. 2020. [Google Scholar] [CrossRef]
- Capasso, F. The future and promise of flat optics: A personal perspective. Nanophotonics 2018, 7, 953–957. [Google Scholar] [CrossRef]
- Staude, I.; Schilling, J. Metamaterial-inspired silicon nanophotonics. Nat. Photonics 2017, 11, 274–284. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).