Higher-Order Information Measures from Cumulative Densities in Continuous Variable Quantum Systems

Abstract

A definition of three-variable cumulative residual entropy is introduced, and then used to obtain expressions for higher order or triple-wise correlation measures, that are based on cumulative residual densities. These information measures are calculated in continuous variable quantum systems comprised of three oscillators, and their behaviour compared to the analogous measures from Shannon information theory. There is an overall consistency in the behaviour of the newly introduced measures as compared to the Shannon ones. There are, however, differences in interpretation, in the case of three uncoupled oscillators, where the correlation is due to wave function symmetry. In interacting systems, the cumulative based measures are shown in order to detect salient features, which are also present in the Shannon based ones.

1. Introduction

One interpretation of quantum mechanics is that of a statistical theory, thus analysis of the information obtained from the underlying densities of quantum systems is essential in understanding quantum phenomena. Important tools for interpreting this behaviour have evolved from consideration of position and momentum densities. A key theme in this regard is the measure of the uncertainty that is inherent in any probability distribution. A related concept for distributions with two or more variables is the quantification of the statistical correlation that exists between variables. One way to achieve these goals is with Shannon information theory [1,2], where the central quantity is an information entropy.

The original definition of Shannon entropy is in terms of N discrete random variables

$$S=-\sum _{i=1}^N{p}_{i}ln{p}_i,$$

(1)

where ${\displaystyle \sum _{i=1}^N}{p}_i=1$ and $p_i$ is the probability of the ith event. This entropy has properties, such as being bounded and positive-definite $(S\ge 0)$, since $0\le p_i\le 1$. The interpretation of the entropy is that of a measure of uncertainty in a random variable. When these variables represent particles, as in quantum mechanics, the entropy can be interpreted as a measure that is related to the localization or (de)localization of particles. Smaller entropic values are indicative of a more localized distribution, while larger values imply a more delocalized one.

The differential Shannon entropy

$$S_x=-{\int }_{-\infty }^{\infty }\rho \left(x\right)ln\rho \left(x\right)\mathrm{d}x,$$

(2)

should be used when examining the probability densities with continuous variables. The density, $\rho \left(x\right)$, is normalized, $\underset{-\infty }{\overset{\infty }{\int }}\rho \left(x\right)\mathrm{d}x=1$, over the region $[-\infty ,\infty ]$. However, $\rho \left(x\right)$ is not necessarily bounded as in the discrete case, which can lead to negative values of the entropy. Furthermore, there has been discussion as to the dimensional consistency, in particular when the density inside the logarithmic argument contains units [3,4,5,6]. Nevertheless, the use of Shannon and related entropies has seen widespread application in the study of a variety of different quantum systems [5,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43]. This popularity is perhaps due to the formulation of the Heisenberg uncertainty principle in terms of D-dimensional entropic uncertainty relationships [44,45]

$$S_T^D=S_x^D+S_p^D\ge D(1+ln\pi ).$$

(3)

$S_x^1$ is given in Equation (2) by taking $\rho \left(x\right)$ as the position space density of quantum systems, while $S_p^1$ is obtained by substituting $\rho \left(x\right)$ with the corresponding momentum space density. This uncertainty relation has provided the motivation for the examination and discussion of Shannon entropies in both position and momentum representations.

One approach to overcome the difficulties that are presented by differential entropy is to examine cumulative probability densities, instead of the parent density, $\rho \left(x\right)$. These densities are bounded by unity, are positive-definite, and are dimensionless. The survival (cumulative residual), $s{u}_x\left(a\right)$ and cumulative $c{u}_x\left(a\right)$ densities, are defined in terms of the parent density as

$$s{u}_x\left(a\right)=P(x>a)={\int }_a^{\infty }\rho \left(x\right)\mathrm{d}x=1-c{u}_x\left(a\right)\mathrm{with}c{u}_x\left(a\right)=P(x\le a)={\int }_{-\infty }^a\rho \left(x\right)\mathrm{d}x.$$

(4)

In particular, one can define an entropy for the $s{u}_x\left(a\right)$ density by

$${ϵ}_a=-{\int }_{-\infty }^{\infty }s{u}_x\left(a\right)lns{u}_x\left(a\right)\mathrm{d}a.$$

(5)

This definition is referred to as the cumulative residual entropy (CRE) [46]. Entropic definitions for the $c{u}_x\left(a\right)$ density have also been considered [46]. The question to be asked is, if the interpretations obtained from ${ϵ}_a$ and $S_x$ are consistent in nature, when applied to continuous variable quantum systems. The behaviours of $S_x$ and ${ϵ}_a$ have been compared and contrasted in some representative continuous variable quantum systems, where differences have been observed [47].

2. Two-Variable Information Measures

2.1. Entropies from Two-Variable Distributions

The definitions that were encountered in the previous section can also be applied to two-variable distributions. Such distributions are encountered when one considers two-particle (variable) quantum systems. The pair differential Shannon entropy is defined in terms of the joint or two-variable probability distribution $\Gamma (x_1,x_2)$, as

$$S_{\Gamma }=-{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }\Gamma (x_1,x_2)ln\Gamma (x_1,x_2)\mathrm{d}{x}_1\mathrm{d}{x}_2.$$

(6)

The pair and one-variable Shannon entropies are related through

$$S_{\Gamma }=S_x+S(x_2\left|x_1\right),$$

(7)

where the second term is a conditional entropy or conditional expected value

$$E[S\left(x_2\left|x_1\right)\right]=S(x_2\left|x_1\right)=-{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }\Gamma (x_1,x_2)ln\left[\frac{\Gamma (x_1,x_2)}{\rho \left(x_1\right)}\right]\mathrm{d}{x}_1\mathrm{d}{x}_2,$$

(8)

and $\rho \left(x_1\right)={\int }_{-\infty }^{\infty }\Gamma (x_1,x_2)\mathrm{d}{x}_2$. Note that, for indistinguishable quantum systems, $\rho \left(x_1\right)=\rho \left(x_2\right)=\rho \left(x\right)$, in the notation used.

A joint cumulative probability distribution can be defined in terms of the parent two-variable distribution as

$$\begin{array}{c}\hfill c{u}_x(a,b)=P(x_1\le a,x_2\le b)={\int }_{-\infty }^a{\int }_{-\infty }^b\Gamma (x_1,x_2)\mathrm{d}{x}_1\mathrm{d}{x}_2,\end{array}$$

(9)

while the joint survival (cumulative residual) density is

$$\begin{array}{c}\hfill s{u}_x(a,b)=P(x_1>a,x_2>b)={\int }_a^{\infty }{\int }_b^{\infty }\Gamma (x_1,x_2)\mathrm{d}{x}_1\mathrm{d}{x}_2.\end{array}$$

(10)

It is possible to use the cumulative residual density to establish a pair cumulative residual entropy, analogous to the pair entropy, as

$$\begin{array}{c}\hfill {ϵ}_{ab}=-{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }s{u}_x(a,b)lns{u}_x(a,b)\mathrm{d}a\mathrm{d}b.\end{array}$$

(11)

However, there is difficulty in applying this definition, since the preceding integral diverges in the case of infinite support. On the other hand, it is convergent in the case of finite support.

To obtain a suitable definition of the pair cumulative residual entropy, one can consider the joint cumulative residual entropy ($JCRE$) [46], which is expressed in an analogous manner to Equation (7), as

$$JCRE={ϵ}_a+E[ϵ\left(b\left|x_1\right)\right].$$

(12)

The last term,

$$E[ϵ\left(b\left|x_1\right)\right]=-{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }P(x_1,x_2>b)ln\left[\frac{P(x_1,x_2>b)}{\rho \left(x_1\right)}\right]\mathrm{d}b\mathrm{d}{x}_1,$$

(13)

is the expected value of

$$ϵ(b\left|x_1\right)=-{\int }_{-\infty }^{\infty }\frac{P(x_1,x_2>b)}{\rho \left(x_1\right)}ln\left[\frac{P(x_1,x_2>b)}{\rho \left(x_1\right)}\right]\mathrm{d}b,$$

(14)

where

$$\begin{array}{cc}\hfill P(x_1,x_2>b)=& {\int }_b^{\infty }\Gamma (x_1,x_2)\mathrm{d}{x}_2.\hfill \end{array}$$

(15)

In the above, note that $E[ϵ\left(b\left|x_1\right)\right]=E[ϵ\left(a\left|x_2\right)\right]$, in quantum systems with indistinguishable particles. The behaviours of $S_{\Gamma }$ and $JCRE$ have been compared and contrasted in two-particle quantum systems [47].

2.2. Pairwise Statistical Correlation Measures

Another fundamental quantity in information theory is the Mutual Information (MI). It quantifies the pairwise correlation between two variables [2], and it is defined as

$$\begin{array}{cc}\hfill I_x& ={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }\Gamma (x_1,x_2)ln\left[\frac{\Gamma (x_1,x_2)}{\rho \left(x_1\right)\rho \left(x_2\right)}\right]\mathrm{d}{x}_1\mathrm{d}{x}_2\ge 0,\hfill \\ \hfill & =S_x-S\left(x_1\right|x_2),\hfill \end{array}$$

(16)

where the last term is the expectation, $E[S\left(x_1\left|x_2\right)\right]=S\left(x_1\right|x_2)$. Measures of pairwise statistical correlation have been used in order to interpret the types and strength of interparticle correlations present in quantum systems [48]. The idea here is that the statistical correlation measures can be used to examine how particle interaction is encoded into the densities and wave functions of quantum systems.

Measures, such as the correlation energy [49], are employed in quantum chemistry to gauge the correlation effects in approximate wave functions. The correlation coefficient has also been used to quantify and examine correlation in quantum systems [50,51]. It is defined in terms of the covariance as

$${\tau }_x=\frac{Cov(x_1,x_2)}{{\sigma }_{x_1}{\sigma }_{x_2}}=\frac{\langle x_1{x}_2\rangle -\langle x_1\rangle \langle x_2\rangle }{\sqrt{\langle x_1^2\rangle -{\langle x_1\rangle }^2}\sqrt{\langle x_2^2\rangle -{\langle x_2\rangle }^2}}.$$

(17)

The expectation values are

$$\langle x_1{x}_2\rangle ={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{x}_1{x}_2\Gamma (x_1,x_2)\mathrm{d}{x}_1\mathrm{d}{x}_2,$$

(18)

$$\langle x_1\rangle =\langle x_2\rangle =\langle x\rangle ={\int }_{-\infty }^{\infty }x\rho \left(x\right)\mathrm{d}x,$$

(19)

$$\langle x_1^2\rangle =\langle x_2^2\rangle =\langle x^2\rangle ={\int }_{-\infty }^{\infty }{x}^2\rho \left(x\right)\mathrm{d}x,$$

(20)

for indistinguishable quantum systems. ${\tau }_x$ is known to be sensitive to linear correlations. MI, on the other hand, is a more general measure of correlation, which is capable of detecting non-linear dependencies. However, the correlation coefficient is bounded by $-1<{\tau }_x<1$; thus, it is able to detect differences between positive and negative correlations. That is, when the variables move in the same or opposite directions. The behaviours and properties of MI and the correlation coefficient have been examined in two-particle quantum systems [48].

The second expression that is given in Equation (16) can be used to establish an analogous definition of MI in terms of cumulative entropies, which is called the cross cumulative residual entropy ($CCRE$) [46,52,53],

$$CCRE={ϵ}_a-E[ϵ\left(b\left|x_1\right)\right].$$

(21)

$CCRE$ and $MI$ have been compared in two-particle quantum systems [47]. The questions to be addressed are the following: are the behaviours and interpretations obtained from the cumulative-based measures, consistent with the Shannon-based ones, when addressing continuous variable systems? Are there systems that present inconsistencies in the interpretations that arise from the two sets of measures? These two-variable cumulative measures, along with three-variable ones that will be presented in subsequent sections, have not been examined in three-particle (variable) quantum systems. Two-variable measures in this case depend on the properties of the reduced two-variable (particle) densities.

3. Three-Variable Information Measures

3.1. Entropies from Three-Variable Distributions

The focus of this work is the study of the information quantities in three-variable (particle) quantum systems. The Shannon differential entropy for the three-variable case is defined in terms of the wave function, as

$$S_{\Psi }=-{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{|\Psi (x_1,x_2,x_3)|}^{2}ln\left[{|\Psi (x_1,x_2,x_3)|}^2\right]\mathrm{d}{x}_1\mathrm{d}{x}_2\mathrm{d}{x}_3.$$

(22)

In such systems, the two-variable density is a reduced one and it is defined as

$$\Gamma (x_1,x_2)={\int }_{-\infty }^{\infty }{|\Psi (x_1,x_2,x_3)|}^2\mathrm{d}{x}_3,$$

(23)

where the integration can be carried out over any of the three variables due to indistinguishability.

A chain relation similar to Equation (7) exists for the three-variable entropy [2] as

$$S_{\Psi }=S_x+S(x_2\left|x_1\right)+S(x_3\left|x_1{x}_2\right)=S_{\Gamma }+S(x_3\left|x_1{x}_2\right),$$

(24)

where the last term is a conditional expected value

$$E[S\left(x_3\left|x_1{x}_2\right)\right]=S(x_3\left|x_1{x}_2\right)=-{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{|\Psi (x_1,x_2,x_3)|}^{2}ln\left[\frac{{|\Psi (x_1,x_2,x_3)|}^2}{\Gamma (x_1,x_2)}\right]\mathrm{d}{x}_1\mathrm{d}{x}_2\mathrm{d}{x}_3.$$

(25)

Equation (24) above can be used in order to obtain an analogous expression for the three-variable cumulative residual entropy $TCRE$

$$TCRE={ϵ}_a+E[ϵ\left(b\left|x_1\right)\right]+E[ϵ\left(c\left|x_1{x}_2\right)\right]=JCRE+E[ϵ\left(c\left|x_1{x}_2\right)\right],$$

(26)

where

$$ϵ(c\left|x_1{x}_2\right)=-{\int }_{-\infty }^{\infty }\frac{P(x_1,x_2,x_3>c)}{\Gamma (x_1,x_2)}ln\left[\frac{P(x_1,x_2,x_3>c)}{\Gamma (x_1,x_2)}\right]\mathrm{d}c,$$

(27)

and

$$E[ϵ\left(c\left|x_1{x}_2\right)\right]=-{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }P(x_1,x_2,x_3>c)ln\left[\frac{P(x_1,x_2,x_3>c)}{\Gamma (x_1,x_2)}\right]\mathrm{d}{x}_1\mathrm{d}{x}_2\mathrm{d}c,$$

(28)

with

$$P(x_1,x_2,x_3>c)={\int }_c^{\infty }{|\Psi (x_1,x_2,x_3)|}^2\mathrm{d}{x}_3.$$

(29)

We emphasise that this definition of $TCRE$ has not, to our knowledge, been presented before, nor has it been studied in continuous variable quantum systems.

3.2. Triple-Wise Statistical Correlation Measures

The concept of pairwise statistical correlation is a standard one, which has been applied in many fields of science. On the other hand, the quantification and examination of triple-wise correlations are not nearly so well-established. These higher-order correlations represent the interactions among the three particles (variables) as a group, and go beyond the pairwise interactions. There is current interest in quantifying higher-order or triple-wise correlations in various disciplines, which range from the neurosciences [54,55,56], to applications in big data analysis [57]. One of the goals of this work is to examine these higher-order correlations in continuous variable systems, and to extend the definitions of higher-order correlations to the consideration of cumulative densities. Higher-order measures have been examined in systems with discrete distributions [58,59], but little has been done to extend these studies to continuous variable systems [60,61].

The interaction information [2,58,59,60,61,62,63] takes into account the correlation or interaction among the three variables and it is expressed as

$$\begin{array}{cc}\hfill I_x^3& ={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{|\Psi (x_1,x_2,x_3)|}^{2}ln\left[\frac{{|\Psi (x_1,x_2,x_3)|}^2\rho \left(x_1\right)\rho \left(x_2\right)\rho \left(x_3\right)}{\Gamma (x_1,x_2)\Gamma (x_1,x_3)\Gamma (x_2,x_3)}\right]\mathrm{d}{x}_1\mathrm{d}{x}_2\mathrm{d}{x}_3,\hfill \\ \hfill & =3S_{\Gamma }-3S_x-S_{\Psi }=(S_{\Gamma }+S_x-S_{\Psi })-2I_x.\hfill \end{array}$$

(30)

The last equality or grouping is meant to express $I_x^3$ as a difference between two positive terms. The second one is referred to as the redundancy because it contains information about the pairwise correlation ($2I_x$). The first term has the information regarding how the three variables are correlated as a group. This term is called the synergy. $I_x^3$ is positive when the synergic first term dominates, while it is negative when the redundancy, or twice the pair correlation, is larger than the synergic term.

One can obtain an expression for higher-order or triple-wise correlation, based on cumulative densities ($TCCRE$), by substituting the expressions for $S_{\Psi }$ and $S_{\Gamma }$ from Equations (7) and (24), into Equation (30), to yield

$$\begin{array}{cc}\hfill TCCRE& =2E[ϵ\left(b\left|x_1\right)\right]-{ϵ}_a-E[ϵ\left(c\left|x_1{x}_2\right)\right],\hfill \\ \hfill & =(JCRE+CRE-TCRE)-2CCRE.\hfill \end{array}$$

(31)

Another triple-wise information measure that can be formulated is the total correlation [64,65]

$$\begin{array}{cc}\hfill I_3^x& ={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{|\Psi (x_1,x_2,x_3)|}^{2}ln\left[\frac{{|\Psi (x_1,x_2,x_3)|}^2}{\rho \left(x_1\right)\rho \left(x_2\right)\rho \left(x_3\right)}\right]\mathrm{d}{x}_1\mathrm{d}{x}_2\mathrm{d}{x}_3,\hfill \\ \hfill & =3S_x-S_{\Psi }.\hfill \end{array}$$

(32)

Taking the difference, $(I_3^x-I_x^3)$, yields $3I_x$, which shows that the correlations that are included in $I_3^x$, which are not present in $I_x^3$, are pairwise ones.

Thus, the corresponding total cumulative correlation $TcCCRE$ in terms of cumulative densities is defined as

$$TcCCRE=3CRE-TCRE.$$

(33)

$TCCRE$ and $TcCCRE$ have not been previously discussed in the literature.

It is also possible to extend the concept of the correlation coefficient in order to consider triple-wise correlations, by using moments of the distribution to define the correlation in terms of joint cumulants. The second joint cumulant is the covariance or numerator of the correlation coefficient. The third joint cumulant of interest here is

$$\begin{array}{cc}\hfill \kappa \left(x_1{x}_2{x}_3\right)& =\langle x_1{x}_2{x}_3\rangle -\langle x_1{x}_2\rangle \langle x_3\rangle -\langle x_1{x}_3\rangle \langle x_2\rangle -\langle x_2{x}_3\rangle \langle x_1\rangle +2\langle x_1\rangle \langle x_2\rangle \langle x_3\rangle ,\hfill \\ \hfill & =\left[\langle x_1{x}_2{x}_3\rangle -\langle x_2{x}_3\rangle \langle x_1\rangle \right]-Cov(x_1,x_2)\langle x_3\rangle -Cov(x_1,x_3)\langle x_2\rangle ,\hfill \end{array}$$

(34)

where

$$\langle x_1{x}_2{x}_3\rangle ={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{x}_1{x}_2{x}_3{|\Psi (x_1,x_2,x_3)|}^2\mathrm{d}{x}_1\mathrm{d}{x}_2\mathrm{d}{x}_3.$$

(35)

One can highlight the similarities between the cumulant and higher-order Shannon measures by considering the indistinguishable case,

$$\begin{array}{cc}\hfill \kappa \left(x_1{x}_2{x}_3\right)& =\langle x_1{x}_2{x}_3\rangle -3\langle x_1{x}_2\rangle \langle x\rangle +2{\langle x\rangle }^3,\hfill \\ \hfill & =\left[\langle x_1{x}_2{x}_3\rangle -\langle x_1{x}_2\rangle \langle x\rangle \right]-2Cov(x_1,x_2)\langle x\rangle .\hfill \end{array}$$

(36)

This last expression is similar in nature to the last equality for $I_x^3$ in Equation (30), where there is a subtraction of the pair correlation, through the $2I_x$ term. Taking the difference between $\langle x_1{x}_2{x}_3\rangle -{\langle x\rangle }^3$, and $\kappa (x_1,x_2,x_3)$ from the previous equation yields $3Cov(x_1,x_2)\langle x\rangle$. This expression, which quantifies the pair correlation, resembles the $3I_x$ term, is obtained from the $(I_3^x-I_x^3)$ difference.

The goal of this work is to compare and contrast the behaviour of the measures thta are based on the cumulative densities, with their counterpart measures from Shannon theory. Special emphasis is placed on the higher-order measures, since the definitions for $TCRE$, $TcCCRE$, and $TCCRE$ introduced here are new ones. Furthermore, the one- and two-variable cumulative measures have not been examined in three-particle systems. That is, when the parent densities are ones that have been reduced by integration. Pertinent results from both position and momentum space are presented. The cumulative based measures have not been previously studied in momentum space. All of the measures in momentum space are easily obtained by replacing $\Psi (x_1,x_2,x_3)$ with $\Phi (p_1,p_2,p_3)$, $\Gamma (x_1,x_2)$ with $\Pi (p_1,p_2)$, and $\rho \left(x\right)$ with $\pi \left(p\right)$, in the corresponding position space expressions. These measures are not explicitly given for the sake of brevity.

Three-particle uncoupled and coupled oscillator systems, whose wave functions are analytically representable, are used in this study. In the coupled scenario, we examine the effects of the presence of an attractive or repulsive pair potential on the information measures. In the uncoupled case, the effects of indistinguishability on the information measures are explored. The next section presents the uncoupled and coupled wave functions.

4. Three Uncoupled and Coupled Oscillators

Non-interacting oscillator wave functions are orbital products of the harmonic oscillator wave function

$${\varphi }_n\left(x\right)=\sqrt{\frac{{\omega }^{1/2}}{2^{n}n!{\pi }^{1/2}}}{e}^{-\omega x^2/2}{H}_n\left(\sqrt{\omega }x\right),$$

(37)

where we consider (anti)symmetrized determinantal products to build symmetric and antisymmetric wave functions

$$\Psi (x_1,x_2,x_3)=\frac{1}{\sqrt{6}}\left|{\varphi }_{n_1}\left(x_1\right){\varphi }_{n_2}\left(x_2\right){\varphi }_{n_3}\left(x_3\right)\right|.$$

(38)

The momentum space representation of the orbitals is

$${\tilde{\varphi }}_n\left(p\right)=\sqrt{\frac{1}{2^{n}n!{\left(\omega \pi \right)}^{1/2}}}{e}^{-p^2/2\omega }{H}_n\left(\frac{p}{\sqrt{\omega }}\right),$$

(39)

with wave functions

$$\Phi (p_1,p_2,p_3)=\frac{1}{\sqrt{6}}\left|{\tilde{\varphi }}_{n_1}\left(p_1\right){\tilde{\varphi }}_{n_2}\left(p_2\right){\tilde{\varphi }}_{n_3}\left(p_3\right)\right|.$$

(40)

The Hamiltonian for the three interacting oscillators is

$$H=-\frac{1}{2}\left(\frac{{\partial }^2}{\partial x_1^2}+\frac{{\partial }^2}{\partial x_2^2}+\frac{{\partial }^2}{\partial x_3^2}\right)+\frac{1}{2}{\omega }^2(x_1^2+x_2^2+x_3^2)+\frac{1}{2}{\lambda }^2[{(x_1-x_2)}^2+{(x_1-x_3)}^2+{(x_2-x_3)}^2].$$

(41)

We use units of $\hslash =m=1$. $\omega$ can be identified with the natural frequency of the oscillators, while $\lambda$ controls the strength of the two-particle interactions. The positive sign corresponds to attractive potentials while the negative sign to repulsive ones.

The eigenfunctions for three interacting harmonic oscillators are written as a product of three harmonic oscillator eigenfunctions in Jacobi coordinates [66,67]

$${\Psi }_{n_R{n}_{r_1}{n}_{r_2}}(R,r_1,r_2)={\psi }_{n_R}\left(R\right){\psi }_{n_{r_1}}\left(r_1\right){\psi }_{n_{r_2}}\left(r_2\right)=|n_R{n}_{r_1}{n}_{r_2}\rangle ,$$

(42)

where

$${\psi }_{n_R}\left(R\right)={\left(\frac{{{\alpha }_1}^{\frac{1}{4}}}{2^{n_R}{n}_R!{\pi }^{\frac{1}{2}}}\right)}^{\frac{1}{2}}{e}^{-\frac{1}{2}\sqrt{{\alpha }_1}{R}^2}{H}_{n_R}\left({\alpha }_1^{\frac{1}{4}}R\right),$$

(43)

$${\psi }_{n_{r_1}}\left(r_1\right)={\left(\frac{{{\alpha }_2}^{\frac{1}{4}}}{2^{n_{r_1}}{n}_{r_1}!{\pi }^{\frac{1}{2}}}\right)}^{\frac{1}{2}}{e}^{-\frac{1}{2}\sqrt{{\alpha }_2}{r}_1^2}{H}_{n_{r_1}}\left({\alpha }_2^{\frac{1}{4}}{r}_1\right),$$

(44)

$${\psi }_{n_{r_2}}\left(r_2\right)={\left(\frac{{{\alpha }_3}^{\frac{1}{4}}}{2^{n_{r_2}}{n}_{r_2}!{\pi }^{\frac{1}{2}}}\right)}^{\frac{1}{2}}{e}^{-\frac{1}{2}\sqrt{{\alpha }_3}{r}_2^2}{H}_{n_{r_2}}\left({\alpha }_3^{\frac{1}{4}}{r}_2\right).$$

(45)

The cyclic permutation of Jacobi coordinates $(R,r_1,r_2)$

$$R=R^{\prime }=R^{\prime \prime }=\frac{1}{\sqrt{3}}(x_1+x_2+x_3),$$

(46)

$$r_1=\frac{1}{\sqrt{6}}(-2x_1+x_2+x_3),r_1^{\prime }=\frac{1}{\sqrt{6}}(x_1-2x_2+x_3),r_1^{\prime \prime }=\frac{1}{\sqrt{6}}(x_1+x_2-2x_3),$$

(47)

$$r_2=\frac{1}{\sqrt{2}}(x_2-x_3),r_2^{\prime }=\frac{1}{\sqrt{2}}(x_3-x_1),r_2^{\prime \prime }=\frac{1}{\sqrt{2}}(x_1-x_2),$$

(48)

allows for quantum numbers to be defined as $n_R=n_{R^{\prime }}=n_{R^{\prime \prime }}$ for the center-of-mass coordinates R, and $n_{r_1}=n_{r_1^{\prime }}=n_{r_1^{\prime \prime }}$ and $n_{r_2}=n_{r_2^{\prime }}=n_{r_2^{\prime \prime }}$, for the relative coordinates $r_1$ and $r_2$.

The wave function in momentum space can be obtained by either applying the Fourier transform or solving the Hamiltonian in the momentum representation. These procedures lead to wave functions that are analogous to Equations (42)–(45), by making the substitutions $R\to Q$, $r_1\to q_1$ and $r_2\to q_2$. Q, $q_1$ and $q_2$ are defined similarly to Equations (46)–(48), by substituting $x_i\to p_i$ and ${\alpha }_j\to 1/{\alpha }_j$.

On the other hand, antisymmetric wave functions for interacting harmonic oscillators with spin included are obtained [67]

$$\begin{array}{c}\hfill N\left[\left(|n_{R^{\prime \prime }}{n}_{r_1^{\prime \prime }}{n}_{r_2^{\prime \prime }}\rangle |++-\rangle +|n_{R^{\prime }}{n}_{r_1^{\prime }}{n}_{r_2^{\prime }}\rangle |+-+\rangle +|n_R{n}_{r_1}{n}_{r_2}\rangle |-++\rangle \right)\right],\end{array}$$

(49)

for odd values of $n_{r_2}$. Through this procedure we obtain the spin-traced density function in position space as

$$\begin{array}{c}\hfill N^2\left[|n_R{n}_{r_1}{n}_{r_2}\rangle \langle n_R{n}_{r_1}{n}_{r_2}|+|n_{R^{\prime }}{n}_{r_1^{\prime }}{n}_{r_2^{\prime }}\rangle \langle n_{R^{\prime }}{n}_{r_1^{\prime }}{n}_{r_2^{\prime }}|+|n_{R^{\prime \prime }}{n}_{r_1^{\prime \prime }}{n}_{r_2^{\prime \prime }}\rangle \langle n_{R^{\prime \prime }}{n}_{r_1^{\prime \prime }}{n}_{r_2^{\prime \prime }}|\right].\end{array}$$

(50)

5. Results

The presentation of the results is divided into subsections for the uncoupled and coupled oscillators. The behaviours of the information measures in the uncoupled oscillators are examined as a function of the $\omega$ frequency. We then turn our attention to the coupled oscillators, and how the measures vary with the coupling strength $\lambda$, in the presence of an attractive or repulsive pair potential. The principal goal of this discussion is the comparison of the Shannon and cumulative density measures in different environments. 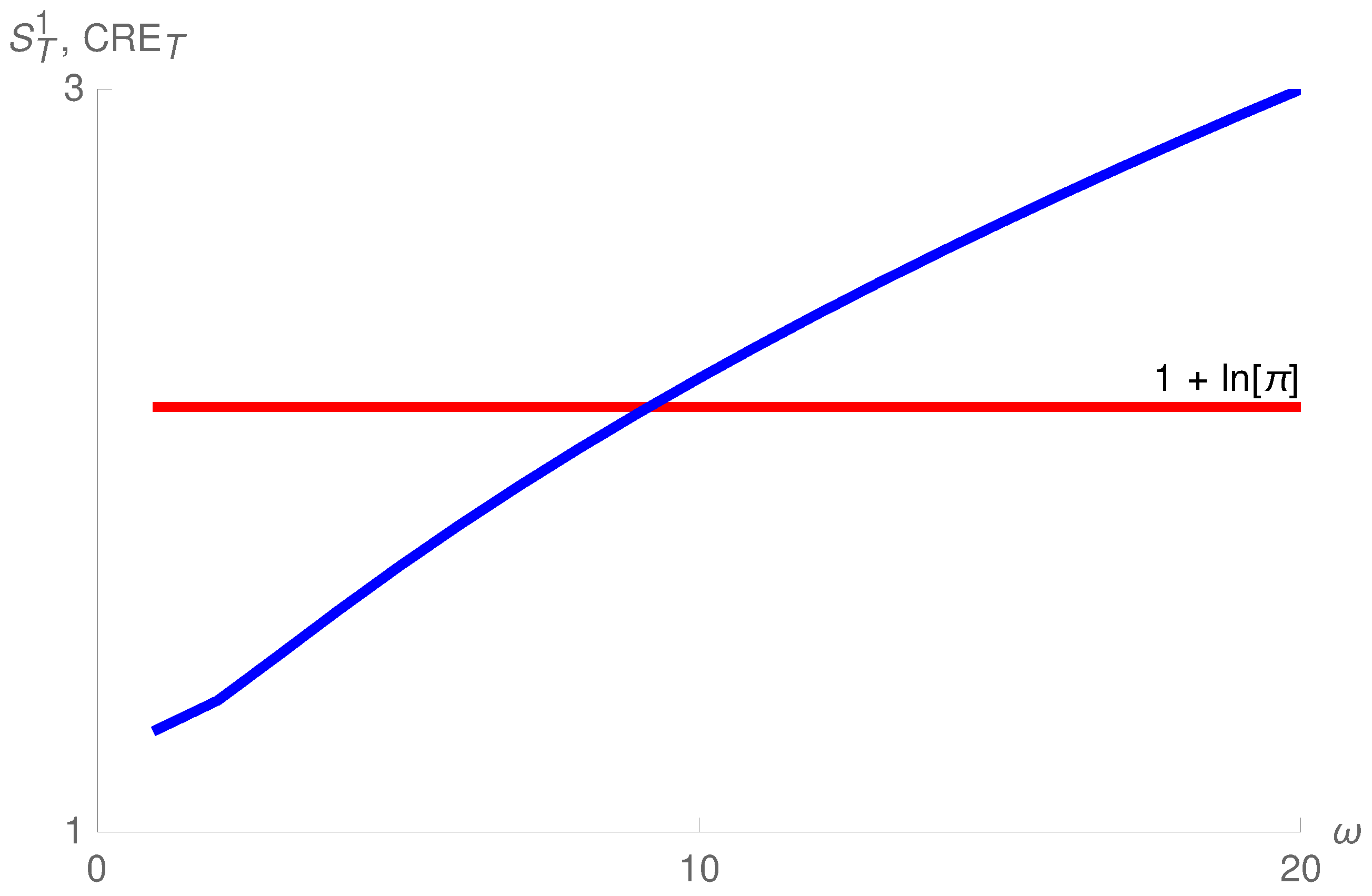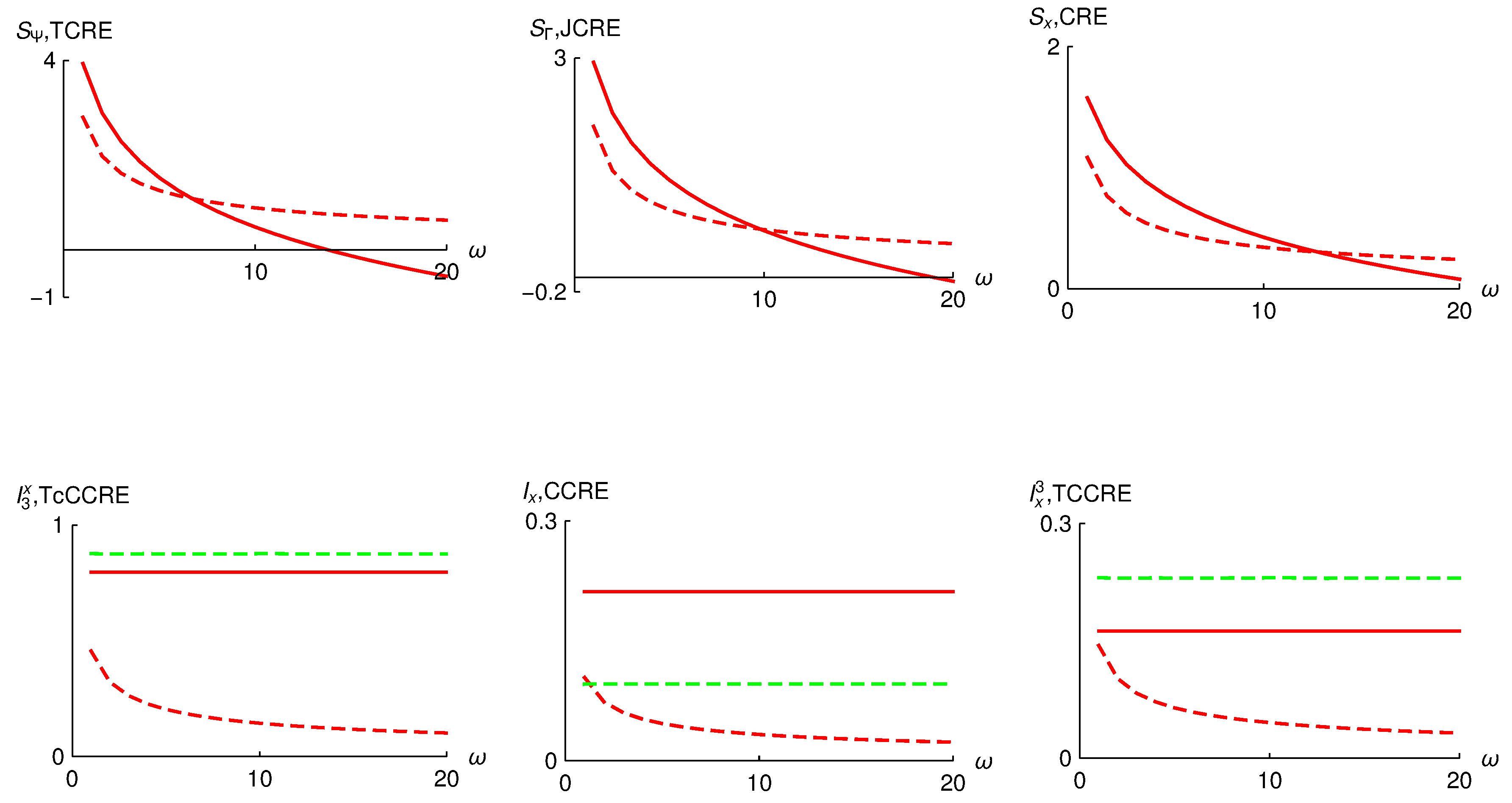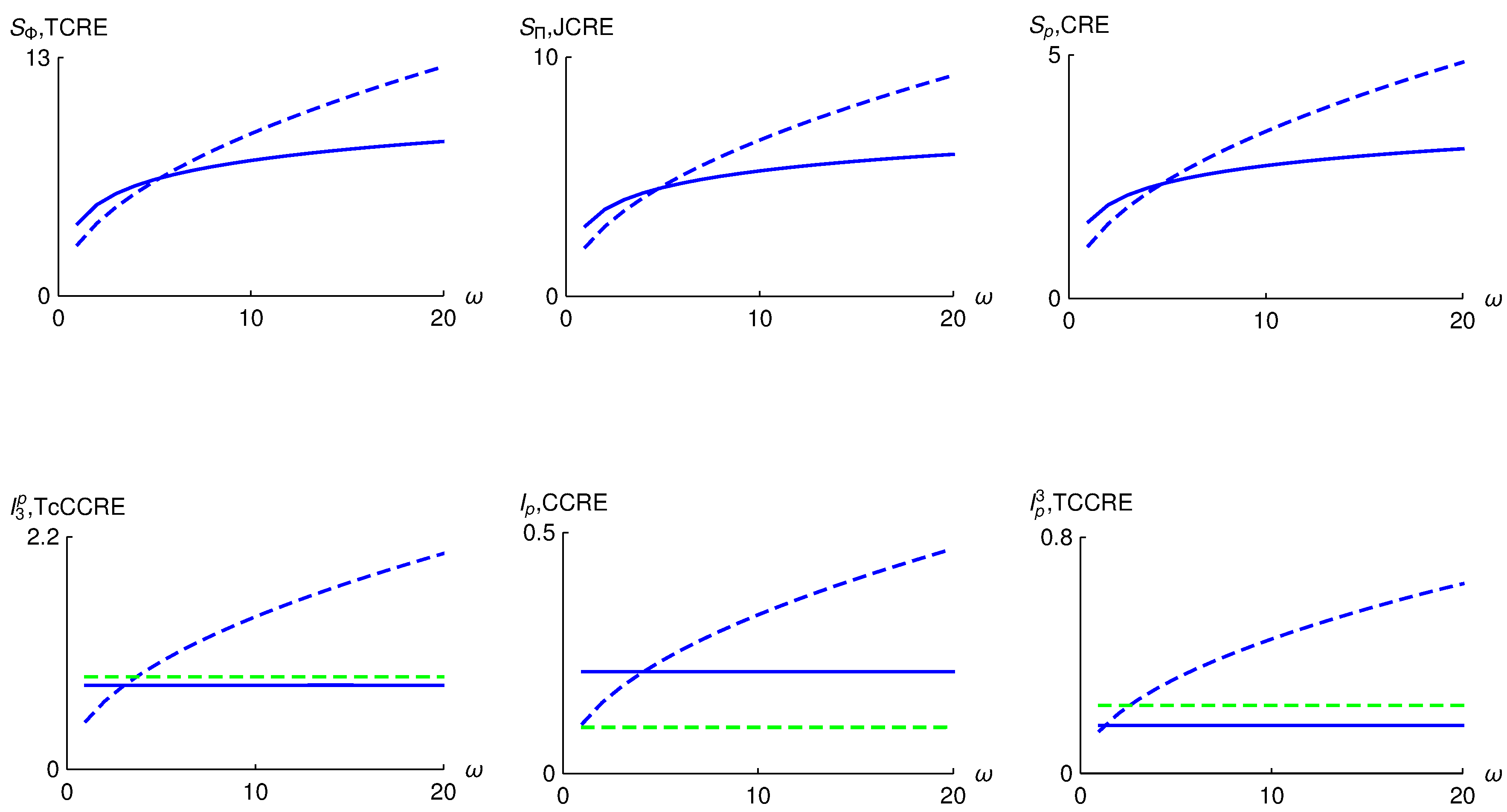Appendix A presents a discussion of the entropic sums for these systems.

5.1. Uncoupled Oscillators

Figure 1 presents the behaviour of the Shannon and cumulative entropies as a function of $\omega$. All of the entropies decrease with $\omega$, thus the cumulative and Shannon entropies are consistent in their interpretation. That is, the underlying densities localize with increasing $\omega$. Note that $S_{\Psi }$ and $S_{\Gamma }$ become negative-valued at larger values of $\omega$. However, $TCRE$ and $JCRE$ remain positive, illustrating the property of the cumulative survival densities to be bounded between zero and one, which provides positive-valued entropies.

The second row of Figure 1 shows the Shannon and cumulative correlation measures. The two sets of measures exhibit a major difference in their behaviours. The Shannon measures are constant with $\omega$. The interpretations from these measures are that both the pair and higher-order statistical correlations, due to the symmetry of the wave function, are constant with $\omega$. On the other hand, the cumulative based measures all decay with $\omega$. Thus, the magnitude of the correlations decrease with $\omega$. The interpretations that were obtained from the two distinct viewpoints are not consistent. The correlation coefficient is constant with $\omega$ and negative-valued. Hence, the behaviours of $I_x$ and ${\tau }_x$ are consistent.

A constant behaviour as a function of $\omega$ can be recovered from the cumulative measures, if one rescales the quantities. These curves are presented in Figure 1. $CCRE/CRE$, $TcCCRE/CCRE$ and $TCCRE/CCRE$, are constant for all values of $\omega$. This result illustrates that the one-, two-, and three-variable cumulative entropies possess the same $\omega$-dependence. Rescaling thus allows one to recapture an interpretation which is consistent with the Shannon measures. That is, the pairwise and higher-order correlations are constant in these uncoupled systems.

Figure 2 presents the measures in momentum space. The Shannon and cumulative entropies now all increase with $\omega$, and are consistent in their behaviour. That is, the momentum space densities delocalize with increasing $\omega$. The Shannon based correlation measures are all constant, as in position space, while the cumulative based measures now increase with $\omega$. Thus, the inconsistencies in the interpretations that were obtained from the Shannon and cumulative based measures are also present in momentum space. Furthermore, the interpretation from the cumulative measures is that the magnitude of the correlation increases with $\omega$, in momentum space, while it decreases in position space. The correlation coefficient here is constant with $\omega$ and positive-valued. Hence, $I_x$ and ${\tau }_p$ are consistent in their behaviour. As in position space, rescaling the cumulative measures yields a constant behaviour, which is consistent with the Shannon measures. The same types of results were also observed for the corresponding symmetric state wave function and are not presented.

5.2. Interacting Oscillators: Symmetric Wave Function

We now turn our attention to the interacting system $|000\rangle$ with attractive pair potential, in position space and $\omega =1.0$. Figure 3 shows the behaviours of the entropic measures as a function of coupling strength $\lambda$.

The Shannon and cumulative entropies decrease with increasing $\lambda$ and are consistent in their behaviour, although the exhibited functional forms are different. $TCRE$ retains its positivity at larger $\lambda$, while $S_{\Psi }$ is negative-valued.

The left column of Figure 4 presents plots of the one-variable reduced parent and survival densities in position space. One can appreciate the differences between the two forms of densities. One can also observe how the increase in intensity of the attractive pair potential leads to a localization of both densities around the origin. This localization is captured by decreasing entropies in Figure 3. There is another difference between the parent and survival densities. While the parent densities are analytically representable, there are no closed form expressions for the survival densities in these systems. These survival densities are calculated by the numerical integration of the parent densities.

The magnitudes of the Shannon and cumulative correlation measures in Figure 5, increase with $\lambda$, and are consistent in their behaviour. Thus, pairwise and higher-order statistical correlations increase with the strength of the pair potential. This consistency among the behaviours of the Shannon and cumulative measures is distinct from the non-interacting case presented in Figure 1. Hence, the interpretation that was obtained from the two sets of measures is now consistent, when interaction is included. Rescaling the cumulant measures results in curves that have a similar behaviour to the unscaled curves. Thus we do not pursue this further in these cases. Note also that both $I_x^3$ and $TCCRE$ are increasingly negative-valued with $\lambda$. The interpretation here from both measures is that the dominant higher-order interactions are redundant in nature. All of the correlation measures go to zero as the coupling is turned off ($\lambda \to 0$).

The top row of Figure 6 shows the behaviour of the Shannon and cumulative measures for the $|000\rangle$ state in momentum space. One can observe that the Shannon and cumulative entropies increase with $\lambda$. Both sets of measures are consistent in their interpretations. That is, the underlying densities delocalize with an increasing intensity of the attractive potential. The delocalization of the one-variable densities in momentum space, as $\lambda$ increases, can be seen from the group of plots in the right hand column of Figure 4.

The bottom row of Figure 6 illustrates that the respective Shannon and cumulative correlation measures have a consistent behaviour in momentum space, since all measures increase with $\lambda$. All of the measures are zero with no coupling. This consistency in behaviour is different from the previously examined case of non-interacting oscillators, as presented in Figure 2. The results for the state with a repulsive potential are not presented. All Shannon and cumulative measures in these systems were observed to display consistent behaviour.

5.3. Interacting Oscillators: Antisymmetric Wave Function

The results for the interacting $|001\rangle$ state with attractive potential in position space, and repulsive one in momentum space, are presented in this section. These examples were chosen since the Shannon measures present interesting behaviour [60]. We will focus our attention here on the statistical correlation measures. All Shannon and cumulative entropies for this state, with attractive and repulsive potentials and, in position and momentum space, exhibit a consistent behaviour as in the previous figures. These plots are not presented.

Figure 7 gives the behaviour of the correlation measures for the attractive potential in position space. There are minima present that are features of this state [60]. The minima indicate that correlation actually decreases with increasing $\lambda$, before it begins to increase at larger coupling strength. It is significant that the minimum in $I_3^x$ at smaller $\lambda$, is also captured by $TcCCRE$. The corresponding minimum in $I_x$ also appears in $CCRE$. However, note that the locations of the minima in the Shannon measures are slightly different from the cumulative-based ones. This is especially true for the $I_x$, $CCRE$ pair.

The synergic behaviour, when the dominant interactions occur as a group, is picked up by both $I_x^3$ and $TCCRE$ (positive valued), at smaller values of $\lambda$. The transition from synergic to redundant dominance (positive to negative) in $I_x^3$ is also caught by $TCCRE$. Thus, the interpretations that were obtained from the Shannon and cumulative-based measures are consistent. The correlation measures here do not go to zero as the interaction is turned off. This is due to the wave function symmetry. That is, the wave function when $\lambda$ is zero, is not a separable one.

The presence of the minima in $I_x$ and $CCRE$ can be investigated by examining ${\tau }_x$. This is presented in Figure 8. The location of the minima in $I_x$ and $CCRE$, correspond to the regions of $\lambda$ where ${\tau }_x$ changes sign. This value of $\lambda$ is where the reduced pair density transitions from being negatively correlated to positively correlated. ${\tau }_x$ is zero-valued at this point since $\langle x_1{x}_2\rangle$ is also zero-valued. This point is also characterised by the transition of $\langle x_1{x}_2\rangle$ from negative to positive values. On the other hand, $I_x$ and $CCRE$ cannot be negative, by construction. Thus, these measures detect this transition with the presence of a minimum.

One could also consider comparing the behaviour of $I_x^3$ and $TCCRE$ with $\kappa \left(x_1{x}_2{x}_3\right)$. However, $\kappa (x_1,x_2,x_3)$ is zero for all values of $\lambda$ in these systems and, thus, is unable to capture the effects of higher-order or triple-wise correlation. This value of zero does not result from a cancellation of the terms in Equation (36), but rather that both the one- and three-variable expectation values are zero-valued. This occurs in both position and momentum space.

The corresponding plot for the $|001\rangle$ state, with a repulsive potential, in momentum space, is presented in Figure 9. As in position space, all of the measures have non zero values with no coupling. There are also minima in $I_3^p$ and $TcCCRE$, and in $I_p$ and $CCRE$, but now at larger values of $\lambda$. Both $I_p^3$ and $TCCRE$ exhibit a transition from positive to negative values, at larger $\lambda$. Thus, the behaviours of the Shannon and cumulative measures are similar, and consistent, in momentum space. The point here is that $TcCCRE$ and $CCRE$ are able to detect the minima that are present in $I_3^p$ and $I_p$. The higher-order measure, $TCCRE$, detects the positive to negative transition, which is present in $I_p^3$ at larger $\lambda$.

Figure 8 shows the behaviour of ${\tau }_p$, which can be compared to $I_p$ and $CCRE$ in Figure 9. ${\tau }_p$ transits from negative to positive values, in the region of $\lambda$, where $I_p$ and $CCRE$ exhibit minima. Both ${\tau }_x$ and ${\tau }_p$ approach unity (perfect correlation), in the limit of large $\lambda$.

6. Conclusions

An expression for three-variable entropy, which is based on cumulative residual densities, is introduced, and it is used to construct higher-order (triple-wise) correlation measures. The cumulative based measures are compared to the corresponding Shannon ones in continuous variable quantum systems. These systems consist of three coupled and uncoupled oscillators, with attractive and repulsive pair potentials, in position and in momentum space. The results show that the behaviours of the one-, two-, and the newly introduced three-variable cumulative entropies, are consistent with those obtained from the Shannon entropies, in all studied systems. However, the Shannon correlation (mutual information) measures are constant as a function of oscillator frequency in the uncoupled systems, while the cumulative based measures decrease in position space, and increase in momentum space, as a function of the frequency. Rescaling the cumulative based measures leads to a constant behaviour, which is consistent with the interpretation that was obtained from the Shannon ones. On the other hand, the presence of an attractive or repulsive pair potential in the coupled systems yields that both the Shannon and cumulative correlation measures are consistent in their interpretations, when examined as a function of coupling strength. This is particularly relevant in the discussion of the newly introduced higher-order cumulative measures. The results also give credence to the interpretations that were obtained from the Shannon ones. The cumulative-based measures detect the presence of minima, which are also present in the Shannon measures. These minima occur in the regions of coupling strength where the correlation coefficient changes its sign.