Simulation and Optimization Experiment of Brush-Belt-Type High-Speed Seed Dispersal Device for Maize Based on Discrete Element Method and Multi-Body Dynamics

Abstract

Under the condition of high-speed maize seeding, the collision between the seeds and the restraint seeding guide device, as well as the excessively high seeding speed, will lead to a sharp increase in the coefficient of variation in the seed spacing during seeding. To address these problems, this study designed a brush-belt-type seed-guiding device incorporating an auxiliary seed-receiving mechanism (ASRM). The aim of this device is to improve the stability of the brush tube in receiving seeds through the ASRM and to stabilize the seed spacing during seeding under the constraint of the brush belt and the seeding tube. Finally, the seeding speed is balanced by adjusting the rotational speed of the brush belt to achieve zero-speed seeding. A multi-body dynamics model of the seeding machine and a discrete element model of the soil were constructed. The seeding process of the device was simulated and analyzed using the discrete element method and multi-body dynamics (DEM-MBD) coupling simulation method. The seeding height and seeding angle were used as experimental factors, and a two-factor five-level orthogonal simulation experiment was conducted. The qualified rate of seed spacing, the re-seeding rate, and the missed seeding rate were used as experimental indicators. The results show that the optimal operating parameters of this device are as follows: seeding height of 46.8 mm, seeding angle of 25.5°, qualified coefficient of seed spacing of 96.03%, missed seeding rate of 1.76%, and re-seeding rate of 3.48%. Under the optimal working parameters of the device, speed performance verification tests were conducted. The research results show that when the operating speed is 12–16 km h⁻¹, the qualified rate of grain spacing is not less than 94.3%, the re-seeding rate does not exceed 3.92%, the missed seeding rate does not exceed 3.19%, and the damage rate does not exceed 0.19%. This study can provide a reference for the design and optimization of high-speed maize seeding devices.

1. Introduction

Maize ranks first in both cultivation area and total output among the three major grain crops in China. According to information from the National Bureau of Statistics of China, China’s maize cultivation area ranks second in the world. However, in 2023, the average yield of maize in China was approximately 6.10 Mg ha⁻¹, while the maize yield in the United States during the same period reached 11.10 Mg ha⁻¹. There is still a significant gap in maize yield between China and developed countries. With the increase in the speed of maize sowing under large-scale operations, the collision and bouncing of seeds and seeding components during planting have increased, resulting in a sharp decline in the stability of sowing volume and the uniformity of row spacing and plant spacing [1,2]. This leads to fierce competition among adjacent maize seedlings and a decrease in harvest efficiency, which restricts the increase in maize yield.

In order to solve the problem of seed collision damage and poor seeding accuracy in the process of high-speed seed introduction, Amazone (Germany) and Ferguson (UK) designed an airflow-assisted seed guide device by introducing positive airflow into the tube [3]. Based on the Venturi principle, Liu Rui analyzed the mechanism of airflow-assisted seed delivery and zero-speed seed delivery and designed and determined the key structural parameters of the airflow seed-guiding device and the curve of the seed-guiding device [4]. The air-assisted seed-guiding device enables the seeds to quickly pass through the seed-guiding tube, which reduces collision with the tube wall. However, the seed casting speed is too high, making it difficult to balance under the acceleration of the air flow. Precision Planting, Inc., United States, has designed a Speed Tube-type conveyor belt seed guide device with a seed device [5]. Chen Xuegeng designed a belt seed guide device integrating transmission and a seed-throwing mechanism under the condition of comprehensive seed plate speed and seeder walking speed [6]. Liu Quanwei proposed a seed delivery method with accurate seed acceptance, stable seed delivery, and precise seed delivery and designed a synchronous belt seed delivery mechanism [7]. John Deere, United States, designed a brush-belt seed guide device by adjusting the speed of the brush belt to control the initial speed of the seed landing level, which can achieve zero-speed seeding [8].

Wei Maikang analyzed different tube structures of seed-guiding devices, taking into account factors such as the angle of seed entry, machine vibration, and the inclination angle of the seed-guiding tube [9]. He derived an “optimal straight line + fastest descent curve” optimal guiding curve for seed-guiding tubes. Based on the principle of secondary seeding, he designed an active brush-wheel-type seed-guiding mechanism. By configuring an active brush wheel during the seed transportation stage in the U-shaped groove seed-guiding tube and using a stepper motor to adjust the rotational speed of the brush wheel in real time, the brush wheel can regulate the speed and trajectory of the seeds after entering the seed-guiding tube. Yi Shujuan, based on the belt seed-guiding device, aimed to address the stability issue during the transition of corn seeds from the seed discharge tray to the seed cavity of the guiding belt by designing a belt seed-guiding device with a rotating clamping auxiliary seeding structure [10]. At the seed discharge port of the seed discharger, a main and auxiliary indexing wheel were configured. During sowing, the main and auxiliary indexing wheels use the rotating clamping method to actively remove the seeds adsorbed on the seed tray and then transport and discharge them to the seed cavity of the indexing synchronous belt. Although the instantaneous speed of the seeds under the brush wheel’s brushing effect can reach the designed ideal state, the complexity of the working environment makes it difficult for the seed landing trajectory to perfectly conform to the designed seed-guiding curve. Moreover, this seed-guiding device does not consider the speed balance problem when seeds are projected under high-speed operation conditions.

In this paper, we design a brush-belt-type seed-guiding device with an auxiliary seed-receiving mechanism based on relevant studies, such as the stable seed conveying distance achieved by belt seeding devices, the seed conveying speed regulated by the brush wheel, and the improved seeding stability achieved by the auxiliary seeding devices, combined with the physical characteristics of soil and maize seeds. The ASRM uses finger opening and closing to form a seed cavity to guide the single seed to fall into the brush tube in sequence and realize smooth migration and zero-speed seed throwing under the excitation of the brush. The discrete element model of maize seeds and soil was established using the ADAMS-EDEM coupling simulation analysis method. The interaction relationship between seeds and soil in the process of seed throwing was analyzed, and the key parameters of seed throwing height and angle of the seed-throwing device were determined.

2. Materials and Methods

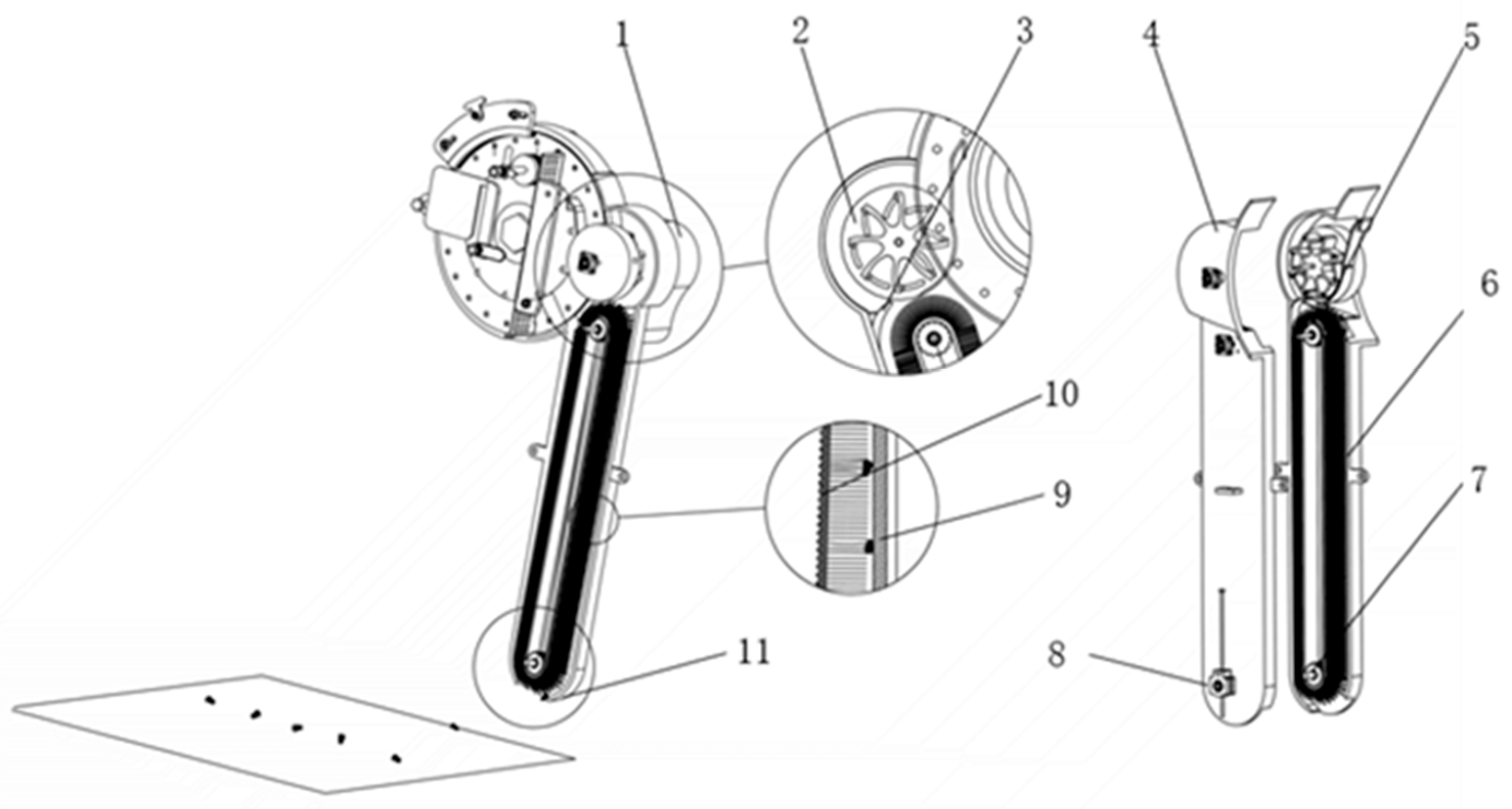
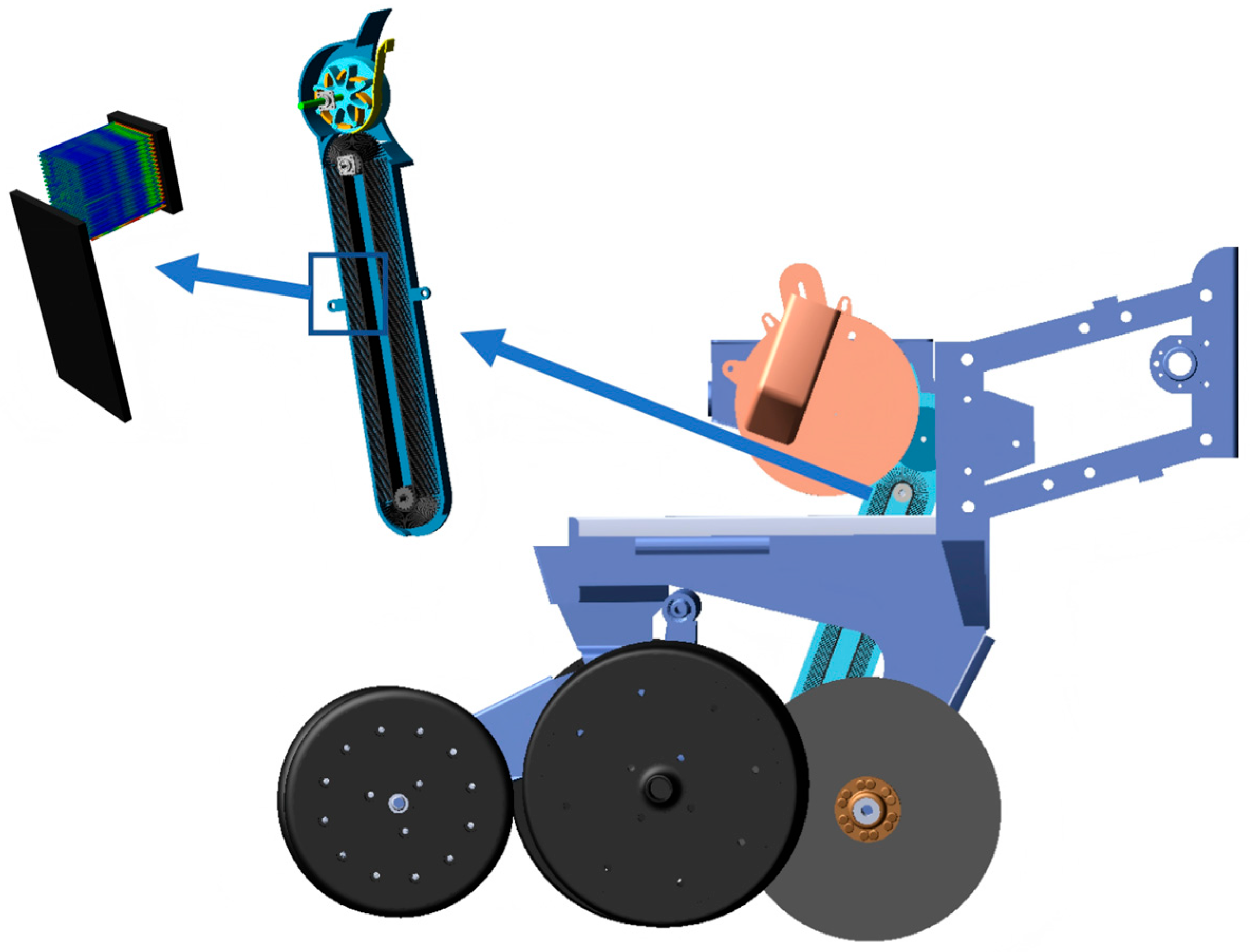
As shown in Figure 1, the seed-guiding device is installed at the seed discharge port of the seed metering device. The seed plate and the auxiliary seed-receiving mechanism are driven by the seeder motor and the ASRM motor to rotate at a fixed speed ratio. When the grain is separated from the position of the seed plate, it is closed under the action of its own gravity; therefore, the seed falls into the rotary seed cavity when it moves through the air suction area and is then discharged into the brush belt under the action of the ASRM. Under the rotational excitation of the brush belt, the seeds migrate to the bottom of the seeding tube and are placed into the seed furrow.

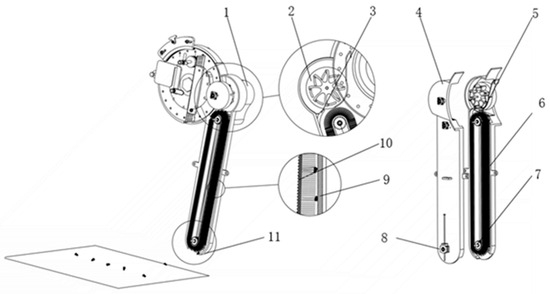
Figure 1. Schematic diagram of the structure of the brush-belt-type high-speed maize seed-guiding device with ASRM. 1—motor gearbox; 2—auxiliary seed-receiving mechanism; 3—guide plate; 4—rear housing; 5—driving pulley; 6—front housing; 7—passive pulley; 8—tensioning device; 9—rubber spacer; 10—brush belt; 11—curved seed board.

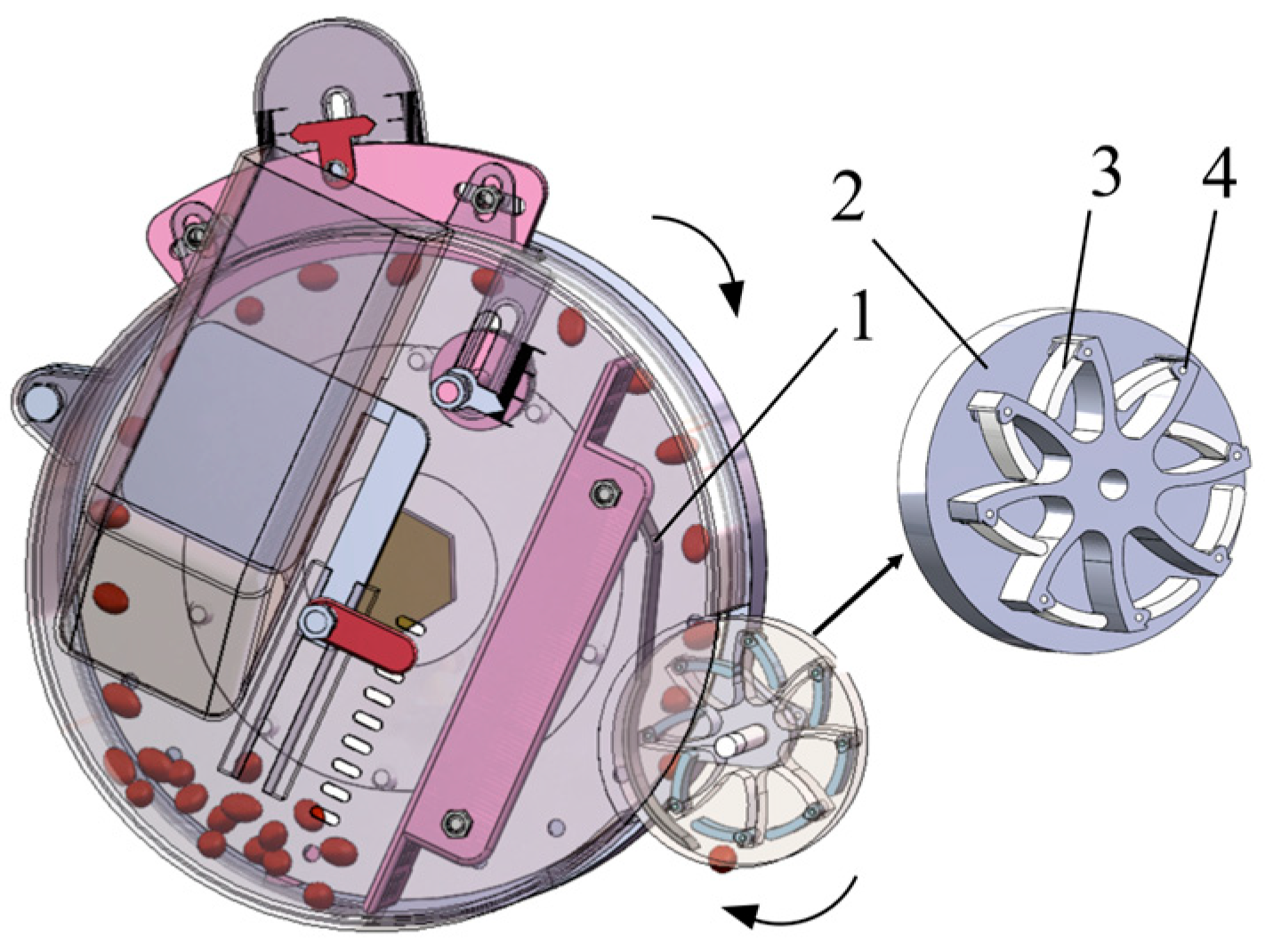
In order to improve the accuracy and stability of the brush tube in the seed, a seed-receiving auxiliary device with a rotary guide method was designed. The direction of seed migration is guided by the way the finger opens and closes to form a single seed-loading seed cavity during the rotation of the guide wheel, and the seed protection plate is used to accurately place the seed into the migration trajectory of the brush tube during sowing so as to improve the stability and accuracy of the seed migrating from the seeding plate to the brush tube. The ASRM is mainly composed of the main body of the guide wheel, the finger, the finger shaft, the seed plate, and so on. The maximum circumference diameter of the main body of the design guide wheel is 90 mm. The number of sowing fingers is 8, which are evenly distributed along the circumference of the control wheel. The main body of the dial finger and the guide wheel are connected by the sowing finger shaft. The interference fit between the dial finger shaft and the hole on the guide wheel ensures that the dial finger shaft rotates with the guide wheel. The clearance fit between the dial finger shaft hole and the dial finger shaft ensures that the dial finger rotates with the guide wheel under the action of gravity and relies on its own gravity to achieve opening and closing. The structure and installation position of the ASRM are shown in Figure 2.

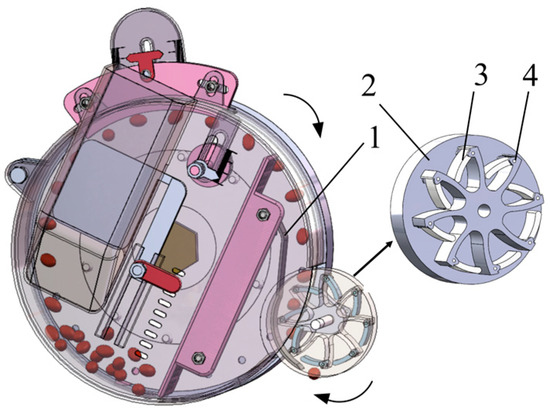
Figure 2. Structure and principle diagram of the rotary steering device. 1—protection for the seed device; 2—guide wheel body; 3—shift finger; 4—the axis of the finger.

In order to avoid collision between the seed and the tube wall of the seed guide and prevent damage to the seed coat caused by the vibration of the seeder and other reasons, the brush belt is used to constrain the full degree of freedom of the seed after leaving the seed metering device, and the seed is forced to remain in an orderly state.

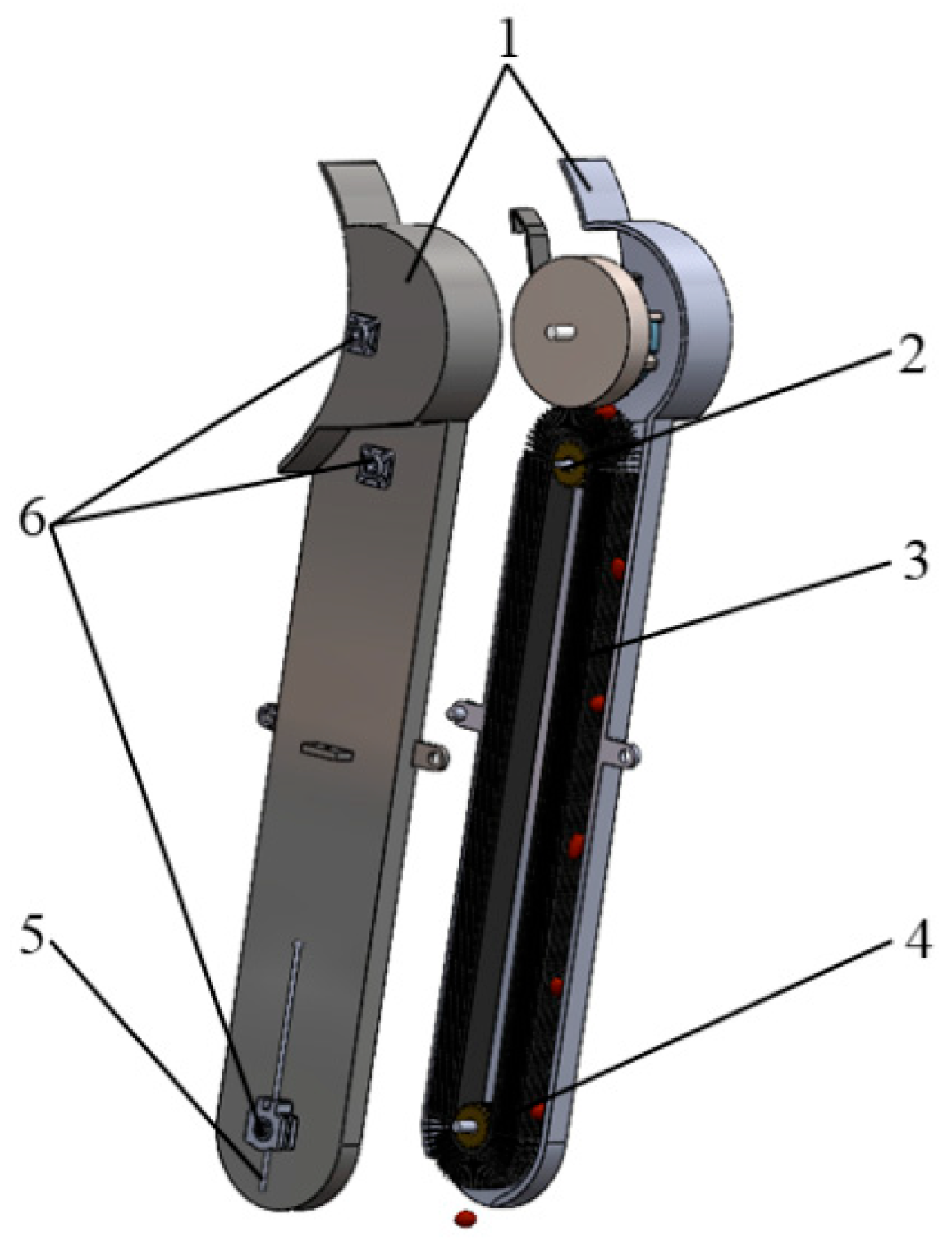
The seed-guiding device is mainly composed of the shell of the seed-guiding device, the active pulley, the brush belt, the passive pulley, the tensioning device, and the bearing seat of each transmission shaft. Seed shear damage occurs under the action of the high-speed movement of the brush and the tube wall of the seed guide. To prevent this, the brush belt is specially planted with a soft nylon wire brush. According to the size limit of the seeding monomer, the given brush length range is 20–40mm. The rotational speed of the active pulley is reversely designed for the purpose of “zero-speed seeding”. The seeding angle and the rotational speed of the pulley are adjusted according to the working speed of the unit. The “zero-speed seeding” in the horizontal direction is realized using the offset between the horizontal sub-speed and the forward speed of the unit when the seeds are thrown out. At the same time, the influence of the sub-speed and the throwing height of the seeds in the vertical direction of the ground on the seed bounce in the seed furrow is observed according to the experiment, and the rotational speed of the pulley and the seeding angle are then adjusted by feedback. The structure of the brush tape is shown in Figure 3.

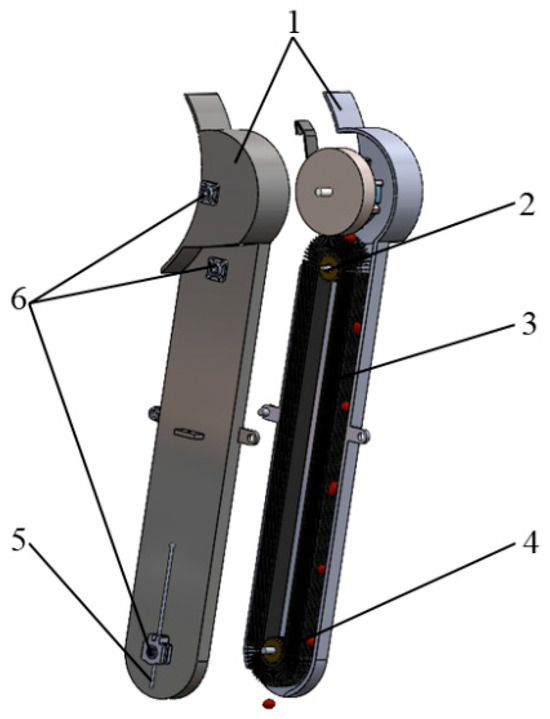
Figure 3. Brush-belt-type seed pipe structure diagram. 1—seed guide device shell; 2—active pulley; 3—brush belt; 4—passive pulley; 5—tensioning device; 6—bearing seat.

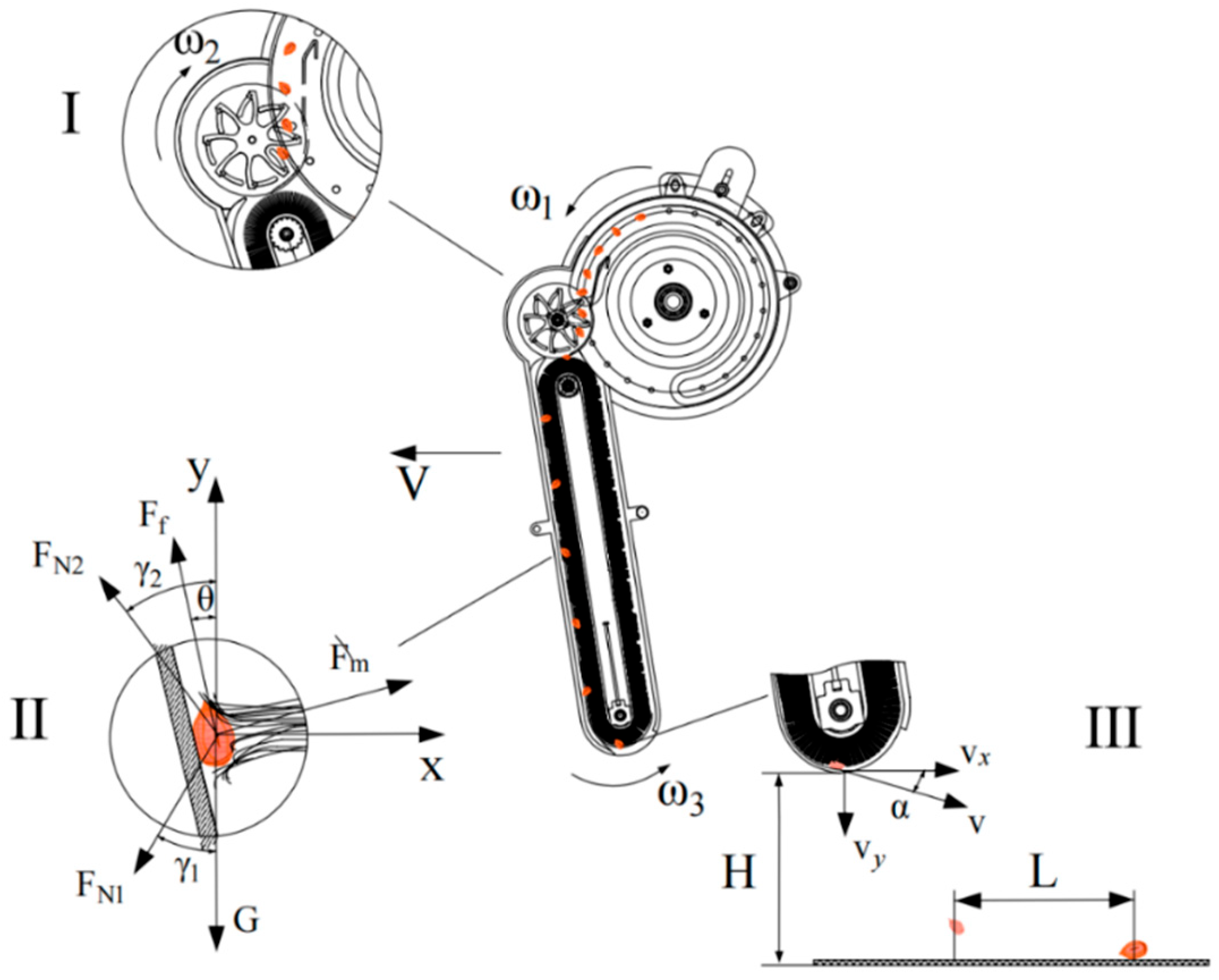
According to the state of seed movement, the process of seed introduction with the brush tape can be divided into three parts: seeding I, seeding II, and seeding III, as shown in Figure 4.

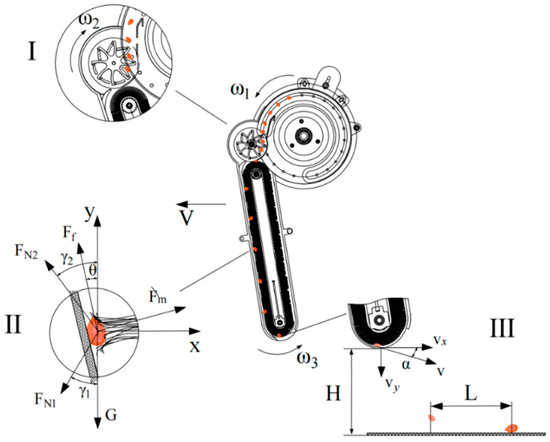
Figure 4. Structure and schematic diagram of the seed-guiding device. I—guide wheel assists the seed-receiving stage; II—brush-belt seed conveyor stage; III—brush-belt casting seed stage. The meaning of the letters in the figure follows the equations below.

The speed of the unit is $\mathrm{V}$; the speed of seed throwing is $\mathrm{v}$; the speeds of the seed plate, ASRM, and brush pulley are ${\mathsf{\omega }}_1$, ${\mathsf{\omega }}_2$, and ${\mathsf{\omega }}_3$; the theoretical grain spacing is $\mathrm{L}$; and the height of seed throwing is $\mathrm{H}$. Because the brush-belt guide is a fully constrained state for seed movement, the speed $\mathrm{v}$ of the seed in the brush tube is the same and is completely determined by the speed of the brush pulley and the length of the brush. According to classical rotational dynamics, the relationship is obtained by Equation (1):

$$\mathrm{v}=\left({\mathrm{R}}_3+\mathrm{s}\right){\mathsf{\omega }}_3$$

(1)

where v—the speed of seed throwing (m s⁻¹); R₃—belt wheel diameter (m); s—the length of the brush hairs (m); and ω₃—belt wheel speed (rad s⁻¹).

For this device, the seeding angle α is the angle between the initial velocity direction of the seed and the horizontal direction. The zero-speed seeding technology refers to the instantaneous relative ground velocity of the seed falling into the seedbed being close to zero. The horizontal velocity of the seed is offset by the forward velocity of the unit. The relationship is obtained by Equation (2):

$${\mathrm{v}}_{\mathrm{x}}=-\mathrm{V}$$

(2)

where v_x—the horizontal velocity of seed throwing (m s⁻¹), and V—unit forward speed (m s⁻¹).

At this time, the speed requirements in the horizontal ground direction of zero-speed seeding are met, and the speed parameters of each part of the device can be reversely designed based on this condition. The pulley speed can be obtained by Equation (3):

$${\mathsf{\omega }}_3=-{\displaystyle \frac{\mathrm{V}}{\left({\mathrm{R}}_3+\mathrm{s}\right)\cos \mathsf{\alpha }}}$$

(3)

where α—seeding angle (°).

Assuming that the interval length of the seed on the brush belt is k, the time interval between the two seeds thrown by the seed guide device is obtained by Equation (4):

$$\mathrm{t}={\displaystyle \frac{\mathrm{L}}{\mathrm{V}}}={\displaystyle \frac{\mathrm{k}}{\mathrm{v}}}$$

(4)

where t—the time interval between two seeds thrown by the seed-guiding device (s); L—the theoretical grain spacing (m); and k—the interval length of the seed on the brush belt (m).

The relationship between k and guide wheel speed ω2 is given by Equation (5):

$$\mathrm{k}=\mathrm{v}{\displaystyle \frac{2\mathsf{\pi }}{{\mathrm{n}}_2{\mathsf{\omega }}_2}}$$

(5)

where ω₂—rotating speed of steering control wheel (rad s⁻¹), and n₂—the number of guiding wheel cavity.

The speed of the ASRM can be calculated by Equation (6):

$${\mathsf{\omega }}_2={\displaystyle \frac{2\mathsf{\pi }}{{\mathrm{n}}_2}}{\displaystyle \frac{\mathrm{V}}{\mathrm{L}}}$$

(6)

The ASRM in the seeding process is directly connected to the seeding plate hole of the air-suction seed metering device, thus replacing the cam pressure relief seed unloading structure of the original seed metering device. In order to ensure that the seeds in the hole of the seed plate will enter the brush tube through the seed-receiving device in an orderly manner, each hole should have a corresponding guiding wheel seed cavity to complete the seed transmission. Therefore, the relationship between the speed of the seed metering device, ω₁ and the speed of the ASRM, ω₂ satisfies Equation (7):

$${\displaystyle \frac{2\mathsf{\pi }}{{\mathrm{n}}_1{\mathsf{\omega }}_1}}={\displaystyle \frac{2\mathsf{\pi }}{{\mathrm{n}}_2{\mathsf{\omega }}_2}}$$

(7)

where n₁—the number of seeding plate holes (constants), and ω₁—rotation speed of the seed metering device (rad s⁻¹).

The rotational speed of the seed plate can be calculated by Equation (8):

$${\mathsf{\omega }}_1={\displaystyle \frac{2\mathsf{\pi }\mathrm{V}}{{\mathrm{n}}_1\mathrm{L}}}$$

(8)

According to Equation (8), when the forward speed of the unit and the theoretical grain distance are given, the horizontal speed of the seed is offset by the forward speed of the unit in the condition of zero-speed seeding, and the rotational speed of the active pulley and the auxiliary guiding wheel in the brush-belt seed guide device can be determined. The rotational speed of the seed metering device that matches the rotational speed of the guiding wheel is also determined. Due to the vibration of the unit and the instability of the motor speed in the actual working environment, as well as the influence of different seed heights and seed incident speeds, the interaction between seed and seed furrow soil is more complex. Therefore, it is necessary to test the seed height and incident speed according to the characteristics of the soil and observe the influence on the seed bounce phenomenon.

Under the ideal state of stable migration of seeds in the brush tube, the seeds move downward at a uniform speed along the inner wall of the shell of the seed guide device under the excitation of the brush, and the seeds do not move relative to the brush. Because the force of the brush on the seed is greatly affected by the shape of the seed falling into the brush tube and the size of the seed, and the bending degree of the brush is more complicated, in the force analysis, only the brush hair directly in contact with the seed is divided into two parts: the pressure on the top of the seed and the support force on the bottom of the seed. The force analysis diagram is shown in the second part of Figure 4, and according to classical mechanics, Equation (9) can be derived as follows:

$$\left\{\begin{array}{l}{\mathrm{F}}_{\mathrm{N}2}{\cos \mathsf{\gamma }}_2{+\mathrm{F}}_{\mathrm{f}}\cos \mathsf{\theta }+{\mathrm{F}}_{\mathrm{m}}\sin \mathsf{\theta }={\mathrm{F}}_{\mathrm{N}1}{\cos \mathsf{\gamma }}_1+\mathrm{G}\\ {\mathrm{F}}_{\mathrm{N}2}{\sin \mathsf{\gamma }}_2{+\mathrm{F}}_{\mathrm{f}}\sin \mathsf{\theta }+{\mathrm{F}}_{\mathrm{N}1}{\sin \mathsf{\gamma }}_1{=\mathrm{F}}_{\mathrm{m}}\cos \mathsf{\theta }\end{array}\right.$$

(9)

where F_N2—pressure of top bristles on seeds (N); F_N1—supporting force of bottom bristles on seeds (N); ${\mathsf{\gamma }}_2$—angle between F_N2 and y-axis directions (°); ${\mathsf{\gamma }}_1$—angle between F_N1 and y-axis directions (°); Fm—the support force of the inner wall of the brush tube to the seed (N); F_f—the friction force of the inner wall of the brush tube to the seed (N); G—seeds subject to their own gravity (N); and ${\mathsf{\mu }}_2$—dynamic friction coefficient between seeds and inner wall of brush house (constants).

In order to ensure that the maize seeds can be stably transported to the seed opening under the action of the brush belt and the tube wall during the seed introduction process, and to prevent the slip and damage of the seeds caused by the too-small or too-large force of the brush on the seeds, the multi-body dynamics simulation software Adams 2020 was used to establish the kinematics model of the seeding monomer and the brush belt. The discrete element simulation software EDEM 2021.2 was used to establish the discrete element model of maize seeds and ridges. The relationship between seeds and brushes during seed transportation was simulated by coupling the simulation. At the same time, based on the actual measured physical parameters of soil, a seed furrow model was established to explore the interaction law between the seeds and soil under different seeding speeds and heights of the seed guide device and to determine the optimal parameter combination [11].

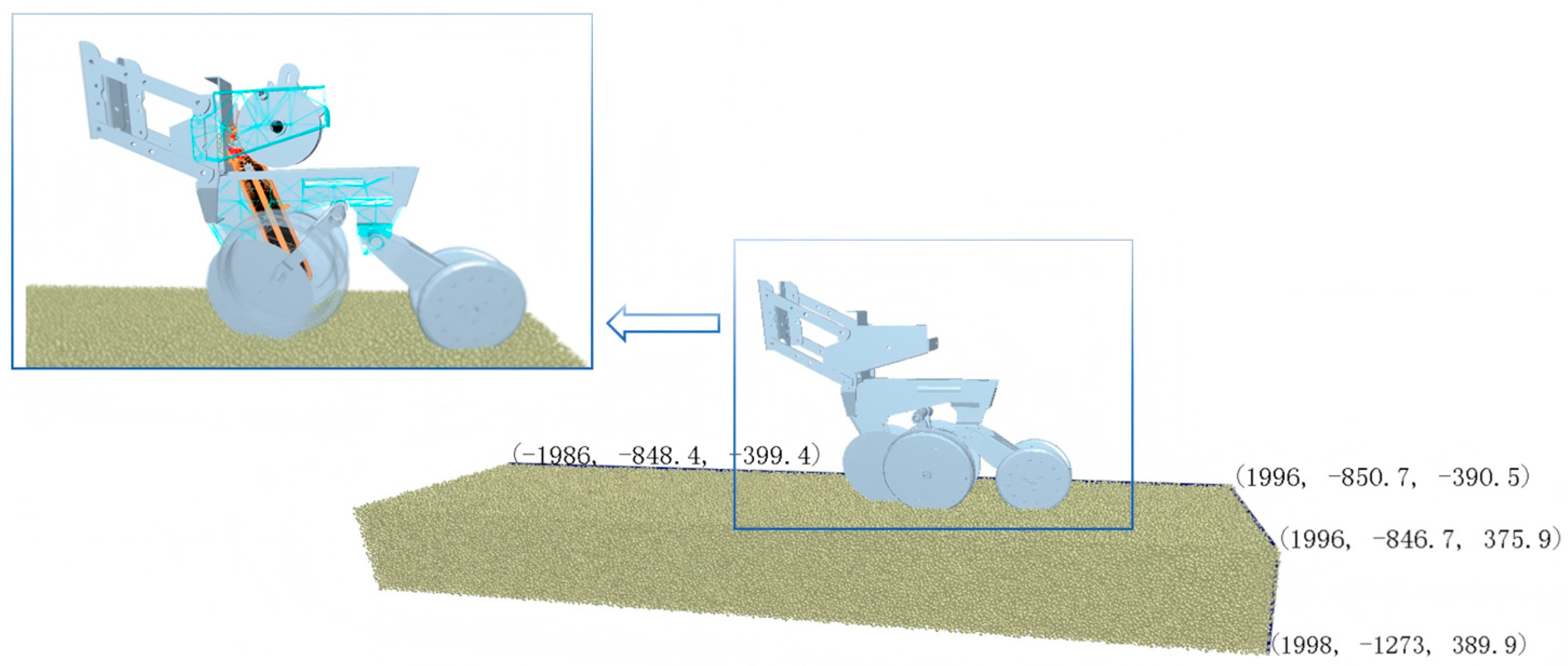
According to the characteristics of the soil working environment and simulation timeliness during the maize planting period in the land, the EDEM model of maize ridge and furrow was established according to the measured soil particle size distribution and mass fraction in the land and the soil intrinsic parameters obtained from the reference literature. The simulated diameter was five times the measured soil particle arithmetic average particle size. Hertz–Mindlin (no slip) was selected as the contact model between soil particles. The calculation amount was small, and the calculation speed was fast. The size of the soil trough was about (length × width × height) 4000 × 800 × 400 mm. The total number of soil particles generated by the simulated soil furrow was 873,000, as shown in Figure 5. Maize seeds were modeled based on the actual measured average triaxial size of maize seeds. Hertz–Mindlin with the bonding contact model was selected as the particle contact model, which expresses the broken process of maize when the shear force is too large [12]. The mass fraction is shown in Table 1. In EDEM, the seed particles were confined within a fixed simulation domain defined by the geometry of the brush-belt channel and the auxiliary seed-receiving cavity. The inlet boundary was treated as a particle factory with a constant generation rate, while the outlet boundary allowed particles to exit freely under gravity. Contact interactions between seeds and device surfaces were governed by a Hertz–Mindlin contact model. Gravity was applied as a global field in the negative z-direction. All external walls were modeled as rigid bodies to constrain particle motion within the working region. Contact forces between seeds imported from EDEM and the device components were computed through a normal contact stiffness model combined with a Coulomb friction formulation [13]. No external displacement constraints were applied except those necessary to maintain the assembly’s mechanical integrity.

Figure 5. Maize ridge-furrow model of soil in EDEM software.

Table 1. Simulated particle size and mass fraction of soil.

Actual Particle Size/mm	Simulated Particle Diameter/mm	Percentage of Quality/%
0~0.25	0.625	5.00
0.25~0.50	1.875	7.96
0.5~1.0	3.250	10.26
1.0~2.0	7.500	24.91
2.0~3.0	12.500	23.18
≥3.0	15.000	28.69

The specific contact parameters of soil, seed, inner wall of seed tube, brush, and double disc opener are shown in Table 2.

Table 2. Simulation parameter table.

Argument	Materials
	Seed	Inner Wall of Seed Tube	Brush Belt	Soil
Poisson’s ratio of maize grain	0.36	0.38	0.32	0.32
Shear modulus of maize grain/MPa	0.837	3.11	0.84	1.2
Density/(g·cm−3)	1.04	1.13	1.12	2.27
Coefficient of restitution (with maize grains)	0.501	0.519	0.01	0.358
Coefficient of static friction (with maize grains)	0.213	0.441	0.45	0.546
Coefficient of rolling friction (with maize grains)	0.035	0.126	0.5	0.15

In order to save simulation time and improve the accuracy of the simulation calculation, the seeding monomer was simplified, the seed fertilizer box and the transmission system were deleted, and only the key structure of the ditching and covering soil and the seed-guiding device was retained; the same quality was added in Adams [14]. The three-dimensional model of the seeding monomer was established by SolidWorks (https://www.solidworks.com/), and the assembly interference was checked. It was saved as STEP format and imported into the Adams pre-processing module [15,16,17]. In order to simulate the working conditions of trenching and seeding in the actual operation of the device, a moving pair was defined between the single profiling four-bar linkage structure and the ground, and a uniform linear motion was set up in the same direction as the forward direction of the machine. The model included several center rotation pairs: one between the depth-limiting wheel and the depth-limiting arm, one between the depth-limiting arm and the seeding monomer frame, one between the pressing wheel and the seeding monomer frame, one between the pressing wheel and the pressing main frame, and one between the trenching disc and the trenching disc shaft. The seed metering device, the brush-belt guide device, and the single frame were set as fixed pairs [18]. The coupling model in Adams software is shown in Figure 6.

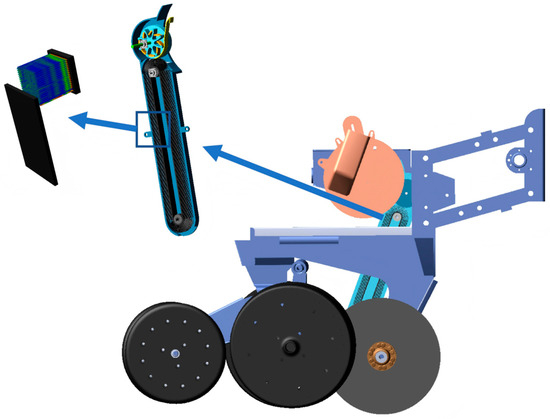
Figure 6. Simulation model of seeding monomer in Adams software.

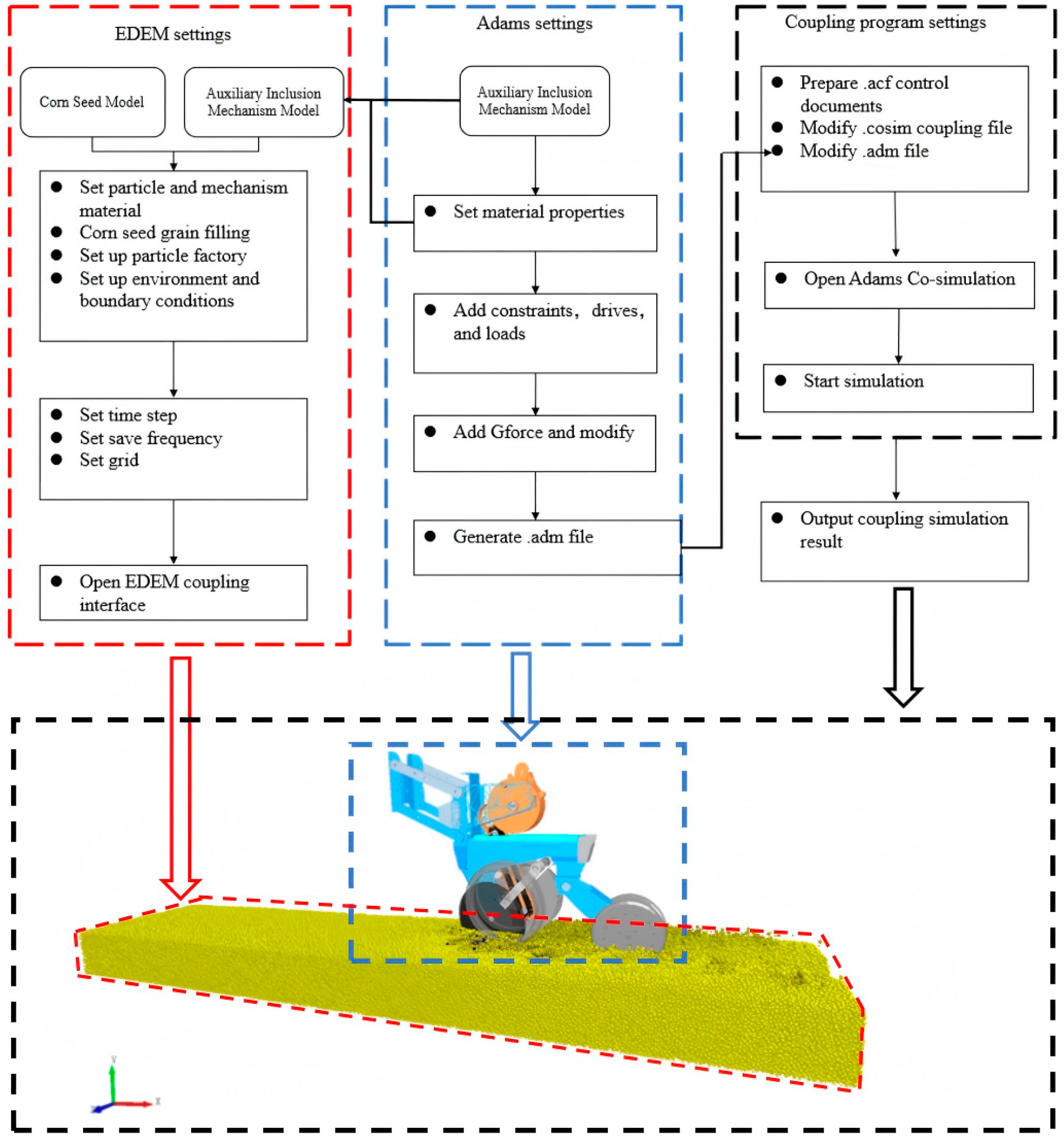
In order to carry out the coupling simulation of the soil–seeding interaction mechanism, the Adams co-simulation module is used to call the cosim file for the coupling simulation. The maize seed particle parameters and particle factory were set in EDEM. The coupling components of EDEM and Adams are configured in the intermediate coupling file, cosim file. The running time of the simulation is controlled to be 5 s by modifying the command of the ACF file. The EDEM and Adams software are set to be integer times the simulation time step, and the environmental variables are configured in the ADM file. When the ditching device is operating in the soil, EDEM and Adams, respectively, transmit the soil particle information and dynamic signals in a two-way interactive way [19,20,21]. The coupling simulation process and principle are shown in Figure 7.

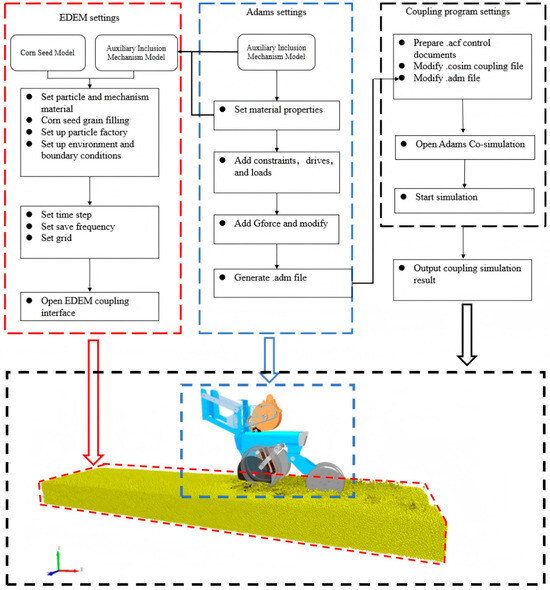
Figure 7. Coupling simulation model.

3. Results and Discussion

Compared with the ordinary seed guide tube or the positive-pressure air-flow-assisted seed guide tube, the brush-belt seed guide device designed in this paper is accurate and controllable for the seed delivery speed. By adjusting the inclination angle of the seed guide device and the speed of the brush pulley, the horizontal speed of the seed delivery and the forward speed of the unit are offset. At this time, the main influencing factors of the seed bounce amplitude are the initial speed of the seed perpendicular to the ground and the seeding height. At the same time, when the forward speed of the machine is determined, the speed of the brush pulley is determined, and the initial speed of the seed vertical to the ground can be calculated by the throwing angle and the forward speed of the unit. In order to explore the influence of seeding height on seed bounce amplitude, determine the optimal range of seeding height, and keep other parameters such as seeding angle and working speed unchanged, the seeding height was divided into three levels—20, 50, and 70 mm—according to previous experience. The seeding effect and seed bounce information are shown in Figure 8 and Figure 9.

Figure 8. Simulation of the sowing effect under different seeding heights: (A) when the seeding height is 70 mm; (B) when the seeding height is 50 mm; (C) when the seeding height is 20 mm.

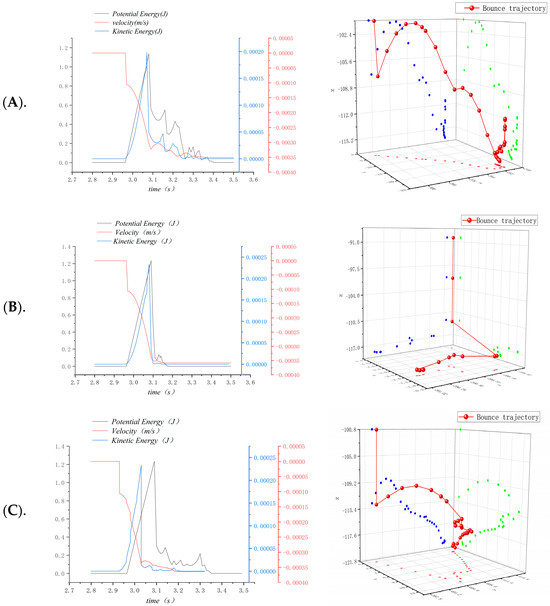
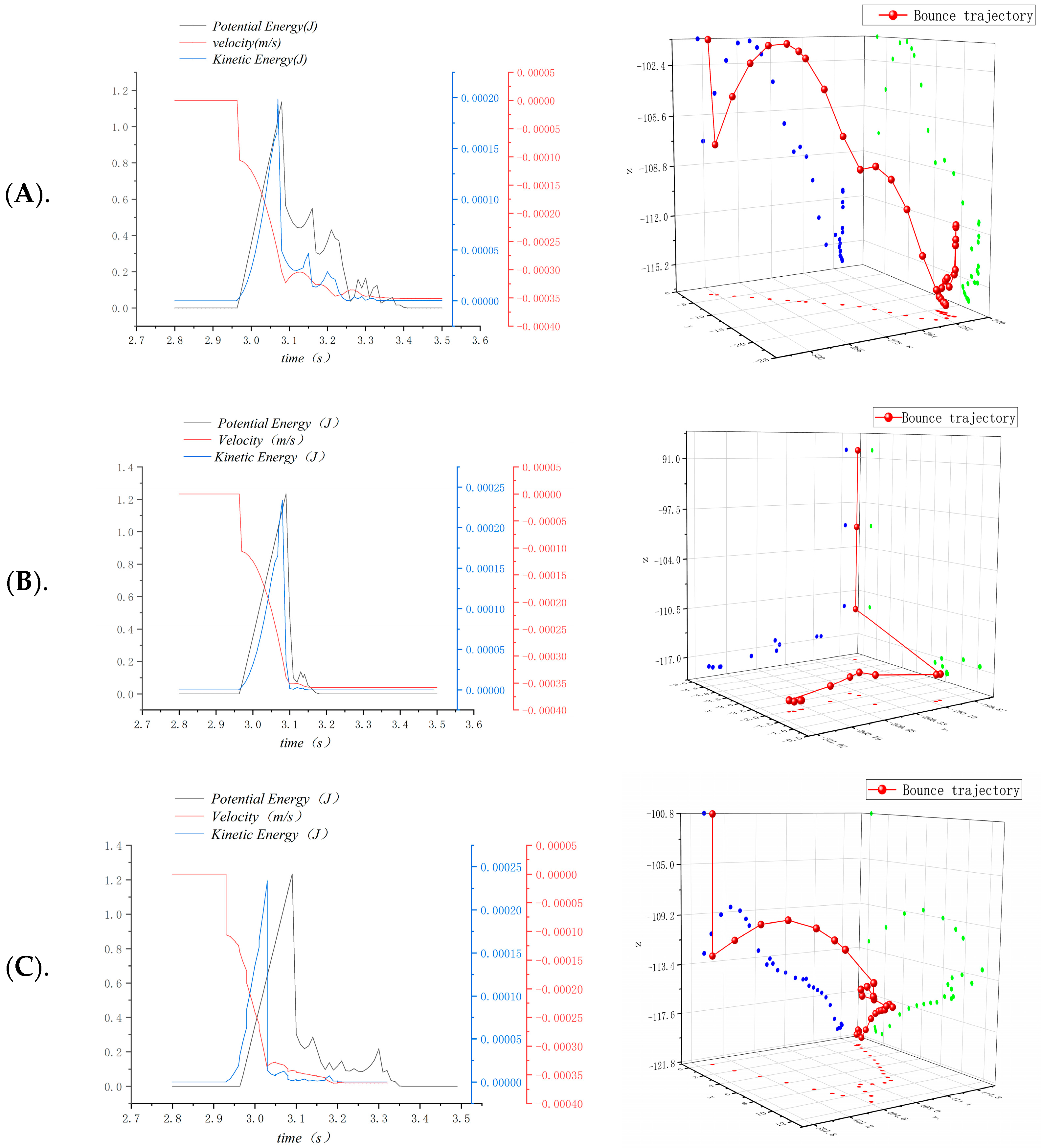
Figure 9. Seeding trajectory and grain movement information map at the same position under different seeding heights: (A) when the seeding height is 70 mm; (B) when the seeding height is 50 mm; (C) when the seeding height is 20 mm.

The qualified rate of seed spacing increased first and then decreased with the decrease in seeding height, as shown in Figure 8. The reason can be derived from the seed bouncing trajectory in Figure 9: within 0.1 s of seed dropping, the increasing trend of seed kinetic energy and velocity is the same as the decreasing trend of gravitational potential energy. When the dropping height is 70 mm, the instantaneous kinetic energy of the soil particles at the bottom of the seed ditch is larger, which causes the bouncing amplitude to be larger than the other two dropping heights. When the seeding height is 20 mm, due to the high-speed operation of the unit, the seeds enter the seed furrow but do not come into contact with the soil at the bottom of the seed furrow and collide with the soil on both sides of the seed furrow, resulting in ectopic seeds. Based on the above analysis, 40~60 mm was taken as the best seeding height range.

According to the single-factor test and design parameters, when the seeding height is 40~60 mm and the seeding angle is 10~20°, the uniformity of seed spacing is better. The coding table of test factors is shown in Table 3. During the test, the number of grains measured in each test should not be less than 100 grains. The test scheme and results are shown in Table 4.

Table 3. Test factor code table.

Encoding	Experimental Factor
	Seed Dropping Height (X1) H/mm	Seed Dropping Angle (X2) α/(°)
−1.41	43	11.5
−1	45	12.5
0	50	15
1	55	17.5
1.414	57	18.5

Table 4. Experimental scheme and results.

Experimental Factor			Acceptance Index (Y1/%)	Replay Index (Y2/%)	Leakage Index (Y3/%)
Serial Number	X1	X2
1	0	0	95.4	2.4	3.1
2	0	1.414	92.6	2.2	7.8
3	1	−1	95.3	5.4	1.5
4	−1.414	0	90.7	2.3	7.1
5	−1	1	88.6	2.6	9.2
6	−1	−1	94.2	2.8	4.1
7	0	−1.414	95.6	3.5	1.1
8	1.414	0	95.8	4.3	0.2
9	0	0	96.5	3.3	3.6
10	0	0	95.3	2.6	2.8
11	1	1	96.4	2.9	5.2
12	0	0	94.4	3.1	3.2
13	0	0	94.8	2.7	2.5

According to the requirements for the seeding effect of corn seeders in “Corn No-tillage Seeding Machine Operating Quality NY/T 1628-2008”, the test indicators are the qualified rate of seed spacing Y₁, the re-sowing rate Y₂, and the missed seeding rate Y₃. During the test, it was ensured that the number of seeds measured for each test plot was not less than 1000.

$$\left\{\begin{array}{l}{\mathrm{Y}}_1={\displaystyle \frac{Q_1}{Q_0}}\times 100\%\\ {\mathrm{Y}}_2={\displaystyle \frac{Q_2}{Q_0}}\times 100\%\\ {\mathrm{Y}}_3={\displaystyle \frac{Q_3}{Q_0}}\times 100\%\end{array}\right.$$

(10)

In Equation (10), Y₁ represents the qualified rate of particle spacing, expressed as a percentage; Q₁ denotes the number of qualified particle spacings; Q₀ represents the total number of measured particle spacings; Y₂ indicates the omission rate, expressed as a percentage; Q₂ signifies the number of omitted particle spacings; Y₃ stands for the repetition rate, expressed as a percentage; and Q₃ indicates the number of repeated particle spacings.

Using Design-Expert 13.0 software to analyze the variance of the test results of the table, the quadratic regression model values of the qualified index of grain spacing (Y₁), the replay index (Y₂), and the missing index (Y₃) were obtained as shown in Equation (11).

$$\left\{\begin{array}{l}{\mathrm{Y}}_1=57.76+2{.50\mathrm{X}}_1-4{.24\mathrm{X}}_2+0{.13\mathrm{X}}_1{\mathrm{X}}_2-0.04{{\mathrm{X}}_1}^2-0.09{{\mathrm{X}}_2}^2\\ {\mathrm{Y}}_2=3.08+0{.72\mathrm{X}}_1-0{.57\mathrm{X}}_2-0{.58\mathrm{X}}_1{\mathrm{X}}_2\\ {\mathrm{Y}}_3=3.04-2{.04\mathrm{X}}_1+2{.28\mathrm{X}}_2-0{.35\mathrm{X}}_1{\mathrm{X}}_2+0.54{{\mathrm{X}}_1}^2+0.94{{\mathrm{X}}_2}^2\end{array}\right.$$

(11)

As shown in Table 5, the regression model values of the particle spacing qualification rate (Y₁), the omission rate (Y₂), and the repetition rate (Y₃) are all less than 0.01, and the residual sum of squares values are all greater than 0.05. This indicates that the regression models of these three indicators are extremely significant, and there is no significant misfit problem. The model has a high degree of fit and can effectively explain the variation pattern of the response variable.

Table 5. ANOVA table.

Source	Qualified Spacing Rate (Y1/%)					Multiple Seeding Rate (Y2/%)					Missed Seeding Rate (Y3/%)
	Sum of Squares	Degree of Freedom	Mean Aquare	F	p	Sum of Squares	Degree of Freedom	Mean Aquare	F	p	Sum of Squares	Degree of Freedom	Mean Aquare	F	p
Model	62.13	5	12.43	30.23	0.0001	8.00	3	2.67	14.47	0.0009	83.11	5	16.62	30.61	0.0001
X1	32.45	1	32.45	78.95	0.0001	4.10	1	4.10	22.27	0.0011	33.45	1	33.45	61.6	0.0001
X2	9.55	1	9.55	23.24	0.0019	2.57	1	2.57	13.98	0.0046	41.75	1	41.75	76.89	0.0001
X1X2	11.22	1	11.22	27.30	0.0012	1.32	1	1.32	7.18	0.00252	0.4900	1	0.4900	0.9052	0.3738
X12	7.34	1	7.34	17.87	0.0039	-	-	-	-	-	2.05	1	2.05	3.77	0.0933
X22	2.53	1	2.53	6.14	0.0423	-	-	-	-	-	6.18	1	6.18	11.38	0.0119
Residual	2.88	7	0.41			1.66	9	0.1842	-		3.80	7	0.5430	-	-
Lack of Fit	0.37	3	0.12	0.1963	0.8939	1.11	5	0.2220	1.62	0.3303	3.11	3	1.04	5.99	0.0582
Pure Error	2.51	4	0.63	-	-	0.55	4	0.1370	-	-	0.6920	4	0.1730	-	-
Cor Total	65	12	-	-	-	9.66	12	-	-	-	86.91	12	-	-	-

Note: p < 0.01 indicates a highly significant effect; 0.01 ≤ p < 0.05 indicates a significant effect. When the F-value is significantly greater than 1, it indicates statistical significance, suggesting that the observed effects are not merely due to random chance or noise but reflect genuine systematic differences or model explanatory power.

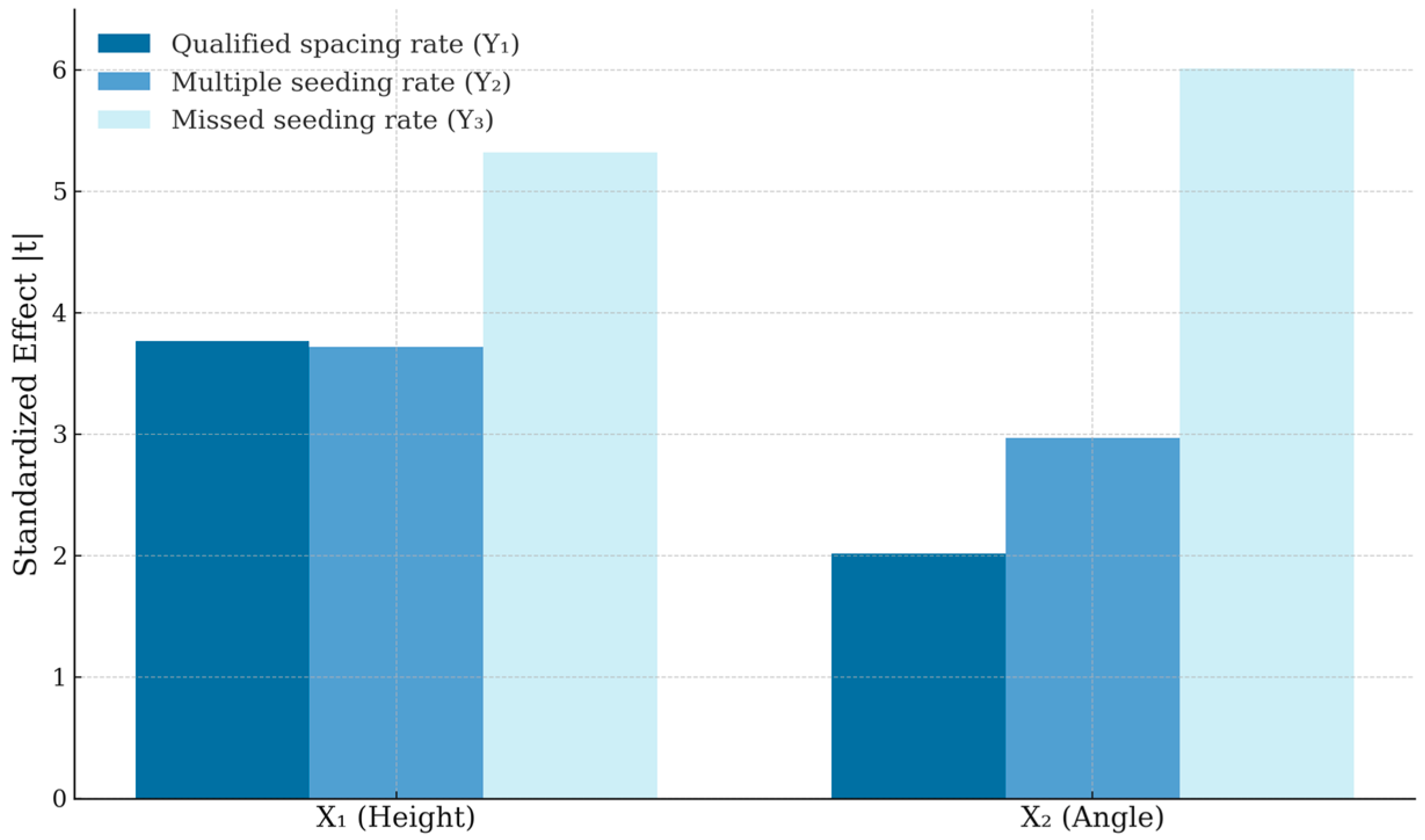
The Pareto chart illustrating the influence of experimental factors on experimental indicators is shown in Figure 10, from which it can be seen that both factor X₁ (height) and factor X₂ (angle) exert marked standardized effects on all three responses, with the missed seeding rate (Y₃) exhibiting the highest sensitivity to changes in these factors, followed by the qualified spacing rate (Y₁) and the multiple seeding rate (Y₂).

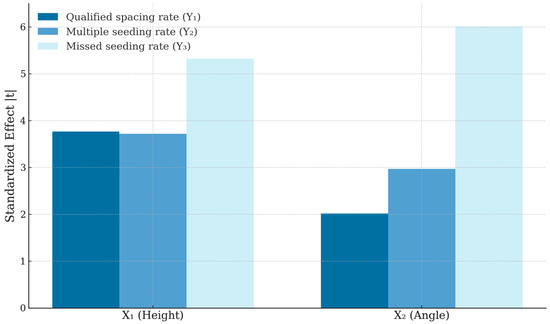
Figure 10. Combined Pareto chart of standardized effects for the experimental responses.

In order to obtain the best level combination of test factors, that is, the best working parameter combination of seeding height and seeding angle, the test was optimized. The mathematical model of parameter optimization was established. Combined with the boundary conditions of the test factors, the three regression equations of the qualified index of the grain spacing, the replay rate, and the leakage rate, shown in Equation (11), were analyzed. The optimization model of the nonlinear programming is shown in Equation (12):

$$\left\{\begin{array}{l}{\mathrm{maxY}}_1\left(\mathrm{H},\mathsf{\alpha }\right)\\ {\mathrm{minY}}_2\left(\mathrm{H},\mathsf{\alpha }\right)\\ {\mathrm{minY}}_3\left(\mathrm{H},\mathsf{\alpha }\right)\\ \mathrm{s}.\mathrm{t}\left\{\begin{array}{l}40 \mathrm{mm}\le \mathrm{H}\le 60\mathrm{mm}\\ 10 \mathrm{deg}\le \mathsf{\alpha }\le 20\mathrm{deg}\end{array}\right.\end{array}\right.$$

(12)

Through the optimization solution, it can be concluded that when the seeding height is 46.8 mm and the seeding angle is 15.5°, the seeding performance is the best. At this time, the corresponding qualified coefficient of grain spacing is 96.03%, the missed seeding rate is 1.76%, and the replay rate is 3.48%.

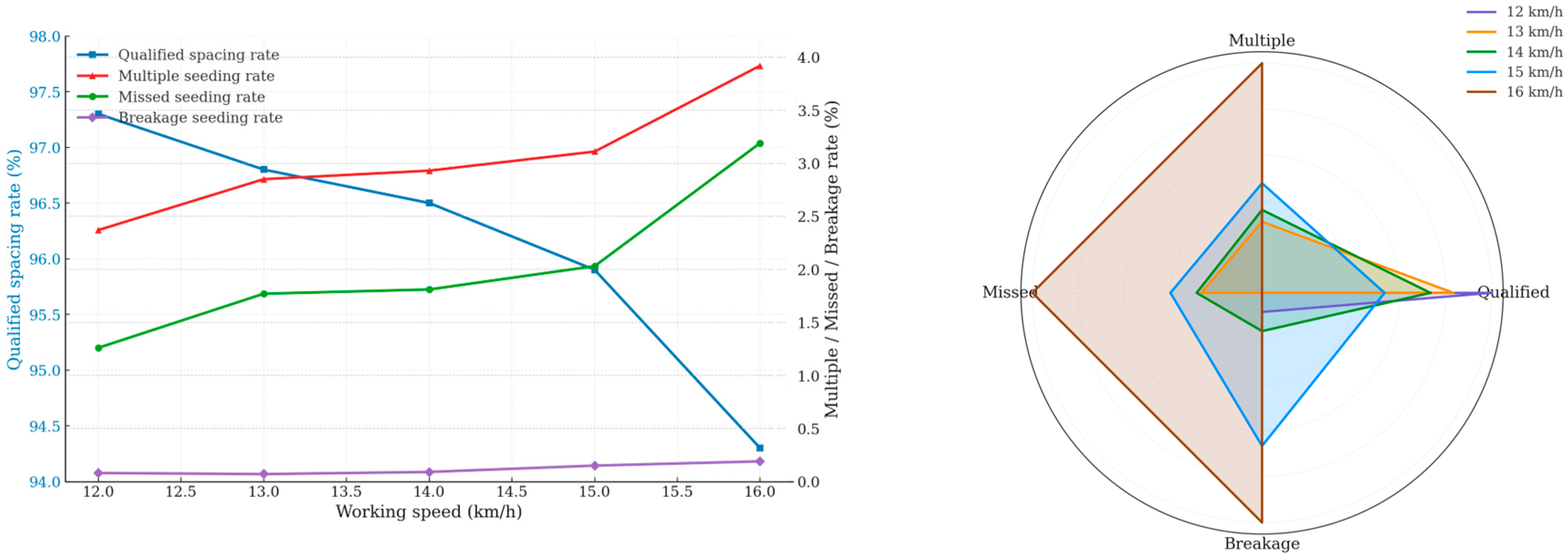
Under the optimal parameters of the brush tube obtained from the parameter optimization test, the simulation tests with working speeds of 12, 13, 14, 15, and 16 km·h⁻¹ were carried out. The test setup process is shown in Figure 11, and the test results are shown in Figure 12.

Figure 11. Bench test.

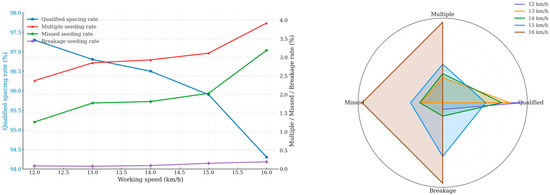
Figure 12. Test results at different operating speeds.

It can be seen from Figure 12 that when the operation speed is within 12~16 km h⁻¹, the qualified rate of grain spacing is not less than 94.3%, the re-seeding rate is not higher than 3.92%, the missed seeding rate is not higher than 3.19%, and the damage rate is not higher than 0.19%. The seed-guiding device designed in this paper meets the needs of high-speed operation well.

4. Conclusions

1. In the process of high-speed sowing of maize, the grain bounces and collides inside the under-constrained seed-guiding device, which causes grain damage, and the seeding accuracy cannot meet the requirements of seed spacing. A brush-belt high-speed seed-guiding device was designed in this study. The working principle of the seed guide device was expounded. According to the requirements of the zero-speed seeding process, the rotational speed relationship of the main components of the device was reversely designed.

2. Through DEM-MBD coupling simulation technology, a maize ridge and furrow model was established. The relationship between the seeding height of the seeding device and the qualified rate of the seed spacing was determined. The optimal seeding height was determined to be 40~60 mm, and the two-factor five-level rotation orthogonal combination test was combined with the seeding angle to obtain the optimal working parameters. The seeding height was 46.8 mm, and the seeding angle was 15.5°. The simulation test results under the optimal parameters were as follows: the qualified coefficient of the seed spacing was 96.03%, the missed seeding rate was 1.76%, and the re-seeding rate was 3.48%.

3. It was verified that when the working speed of the seeder is within 12~16 km h⁻¹, the qualified rate of the seed spacing is not less than 94.3%, the replay rate is not higher than 3.92%, the missed seeding rate is not higher than 3.19%, and the breakage rate is not higher than 0.19%. The device meets the requirements of high-speed maize sowing and can provide a reference for the design and optimization of a high-speed maize sowing device.