A Joint Transformer–XGBoost Model for Satellite Fire Detection in Yunnan
Abstract
1. Introduction
2. Study Area and Data
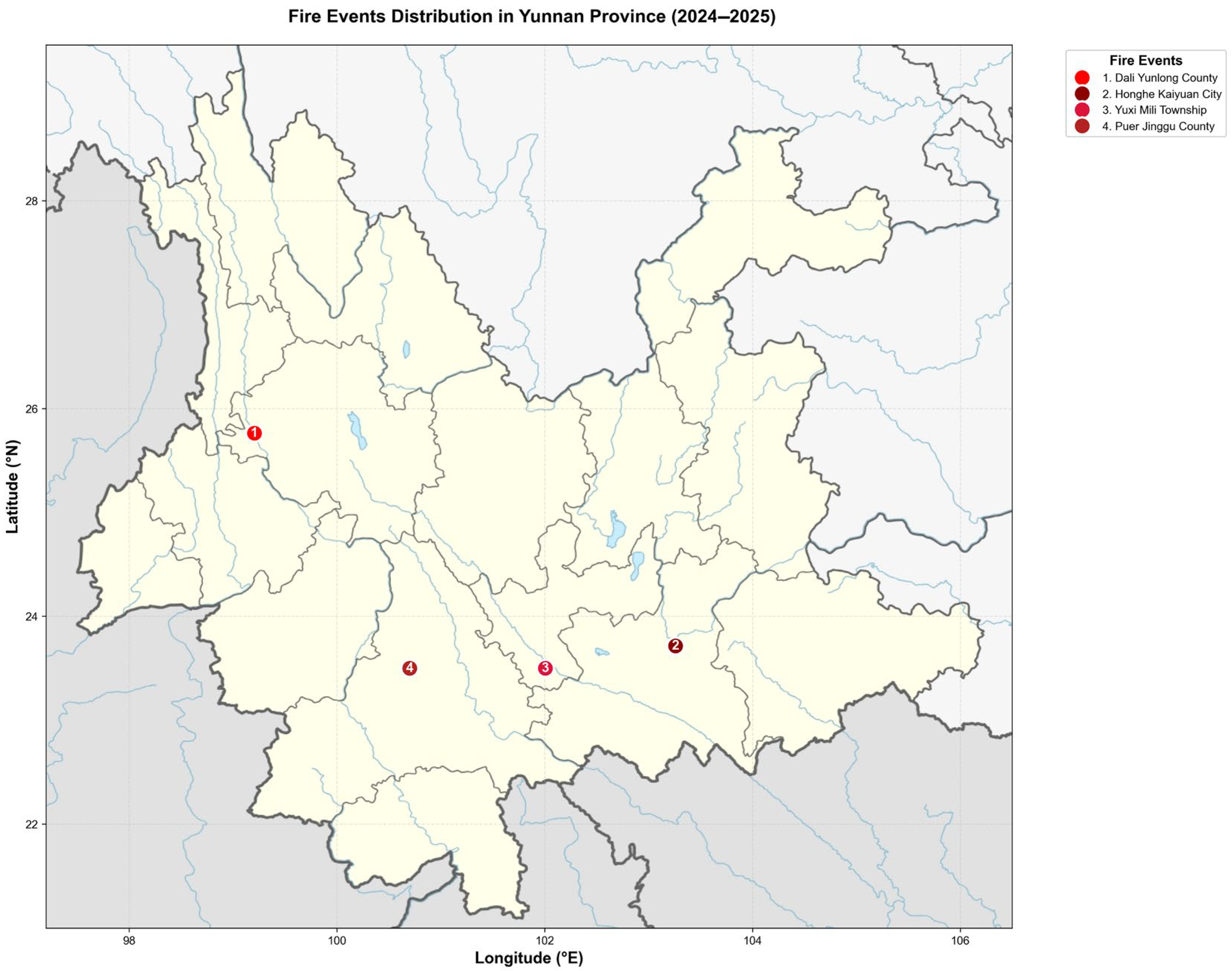
2.1. Study Area
2.2. Data Sources
2.2.1. Himawari-8/9
2.2.2. Fire Point Reference Product
3. Fire Point Detection Framework Based on Transformer and XGBoost
3.1. Overall Framework Design
3.2. Deep Feature Extraction Based on Transformer
3.2.1. Multidimensional Feature Engineering
- A. Thermal anomaly characteristics (“heat” signal)
- Spectral Differences ();
- 2.
- Robust Temporal Difference ();
- 3.
- Spatial Variance ();
- B. Reflectance Feature (“Smoke and Traces” Signal)
- 4.
- Normalized Difference Fire Index ();
- 5.
- Smoke Extinction Index ();
- 6.
- Shortwave Infrared Anomaly (SWIR Anomaly, );
- C. Advanced Interaction and Validation Features (“Confirmation” Signals)
- 7.
- Multiplicative Thermal-Reflectance Index ();
- 8.
- Temporal Consistency Score ();
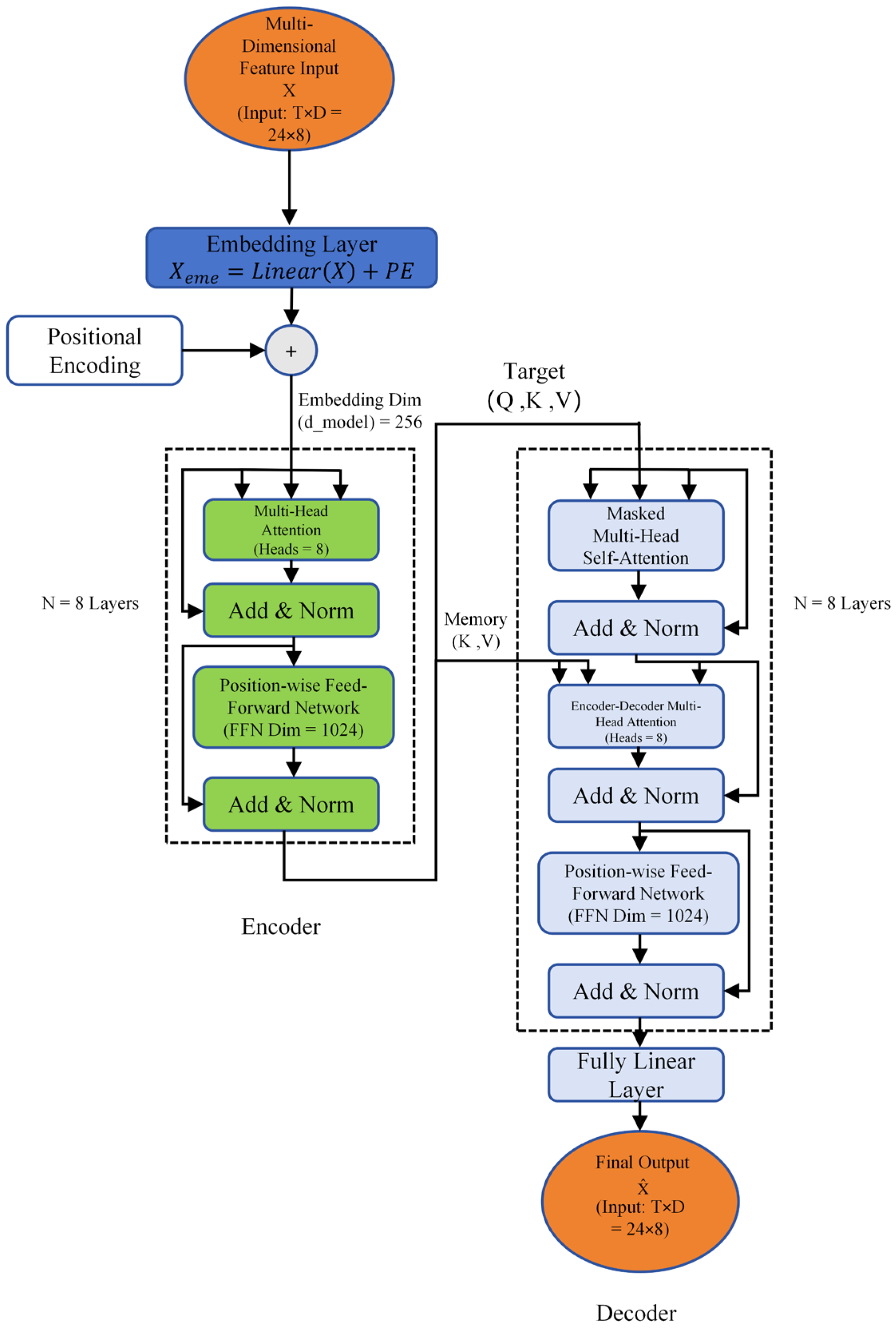
3.2.2. Transformer Autoencoder Model
- Input Embedding and Positional Encoding;
- 2.
- Encoder;
- 3.
- Decoder;
- 4.
- Differential Feature Extraction;
- (1)
- Global Reconstruction Error Features;
- (2)
- Time-Dimension Error Features;
- Mean Error ();
- Standard Deviation of Error ();
- Skewness of the Reconstruction Error ();
- Kurtosis of the Reconstruction Error ();
- (3)
- Latent Space Features;
3.3. Semi-Supervised Hotspot Detection Based on XGBoost
3.3.1. Design Concept
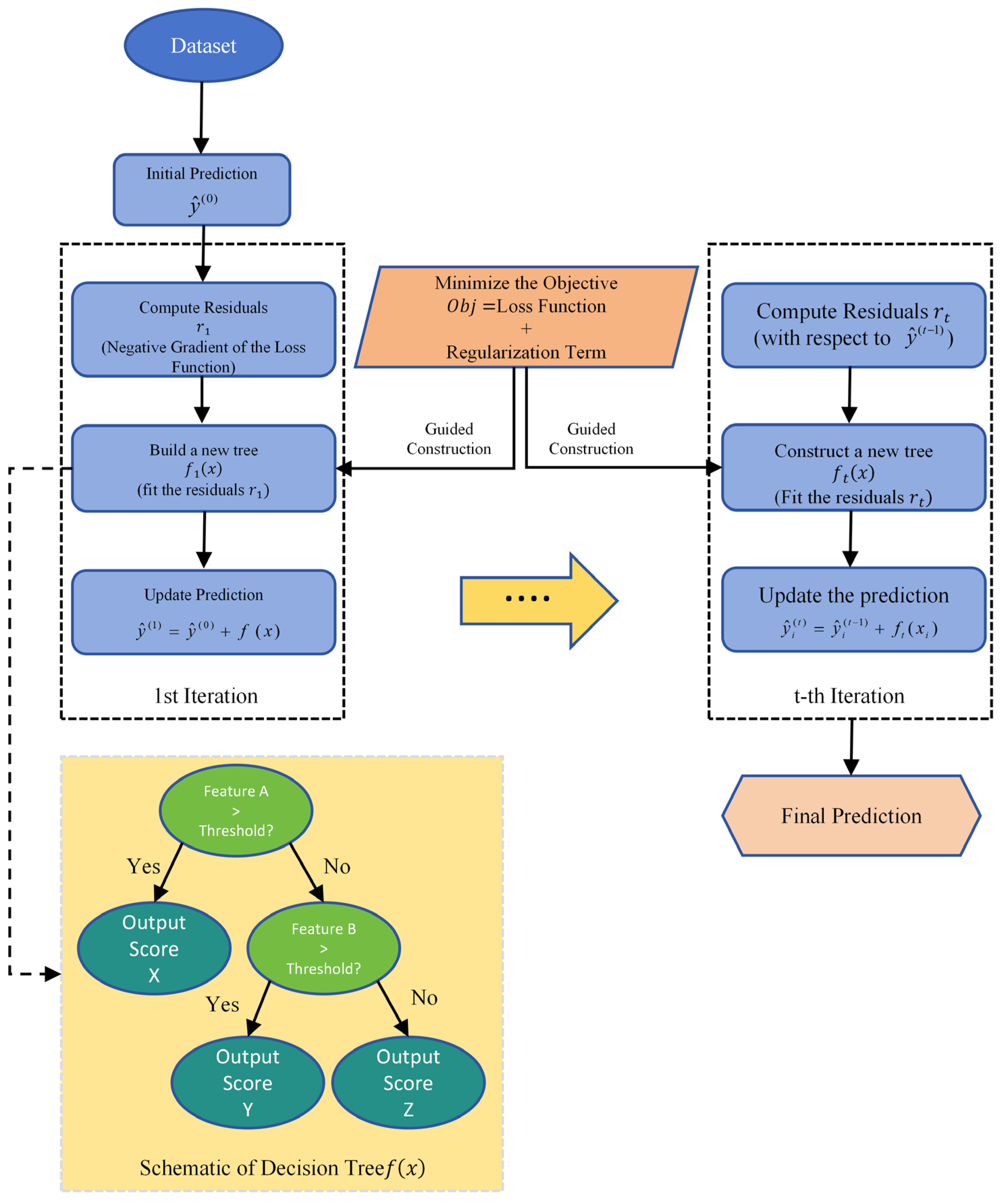
3.3.2. XGBoost Model
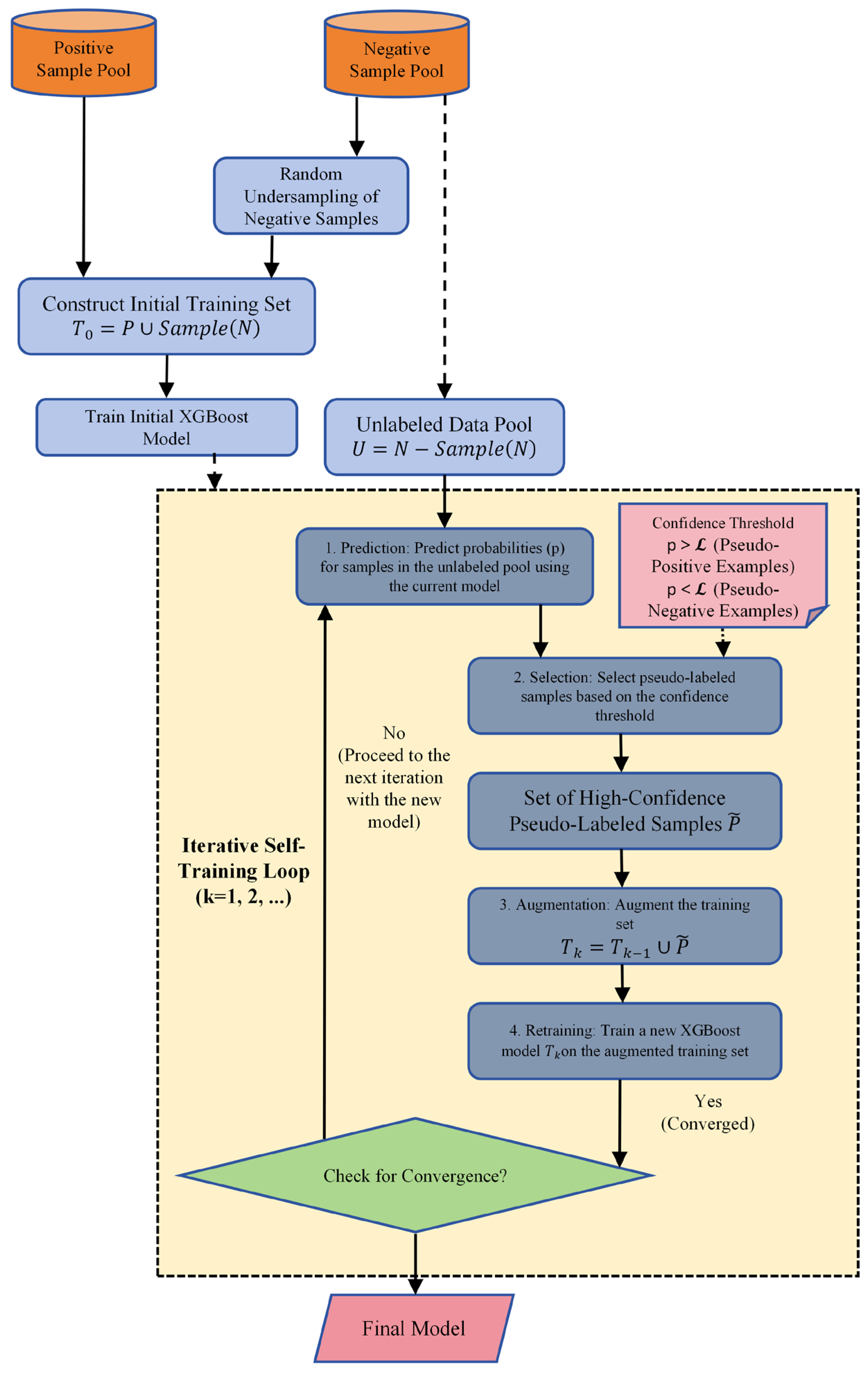
3.3.3. Iterative Pseudo-Label Self-Training
- 1.
- Training set construction;
- 2.
- Training and handling imbalance;
- 3.
- Iterative enhancement loop;
- (1)
- Predict;
- (2)
- Filter;
- Filtering pseudo-positive samples ()
- Filtering pseudo-negative samples ()
- (3)
- Augmentation;
- (4)
- Retrain;
- 4.
- Convergence and Final Optimization
4. Experimental Results and Analysis
4.1. Experimental Setup
- 1.
- Precision;
- 2.
- Recall;
- 9.
- Score;
4.2. Experimental Environment
4.2.1. Environment Configuration
4.2.2. Hyperparameter Settings for the Model
4.3. Experimental Results
4.3.1. Case Analysis
4.3.2. Quantitative Performance Comparison
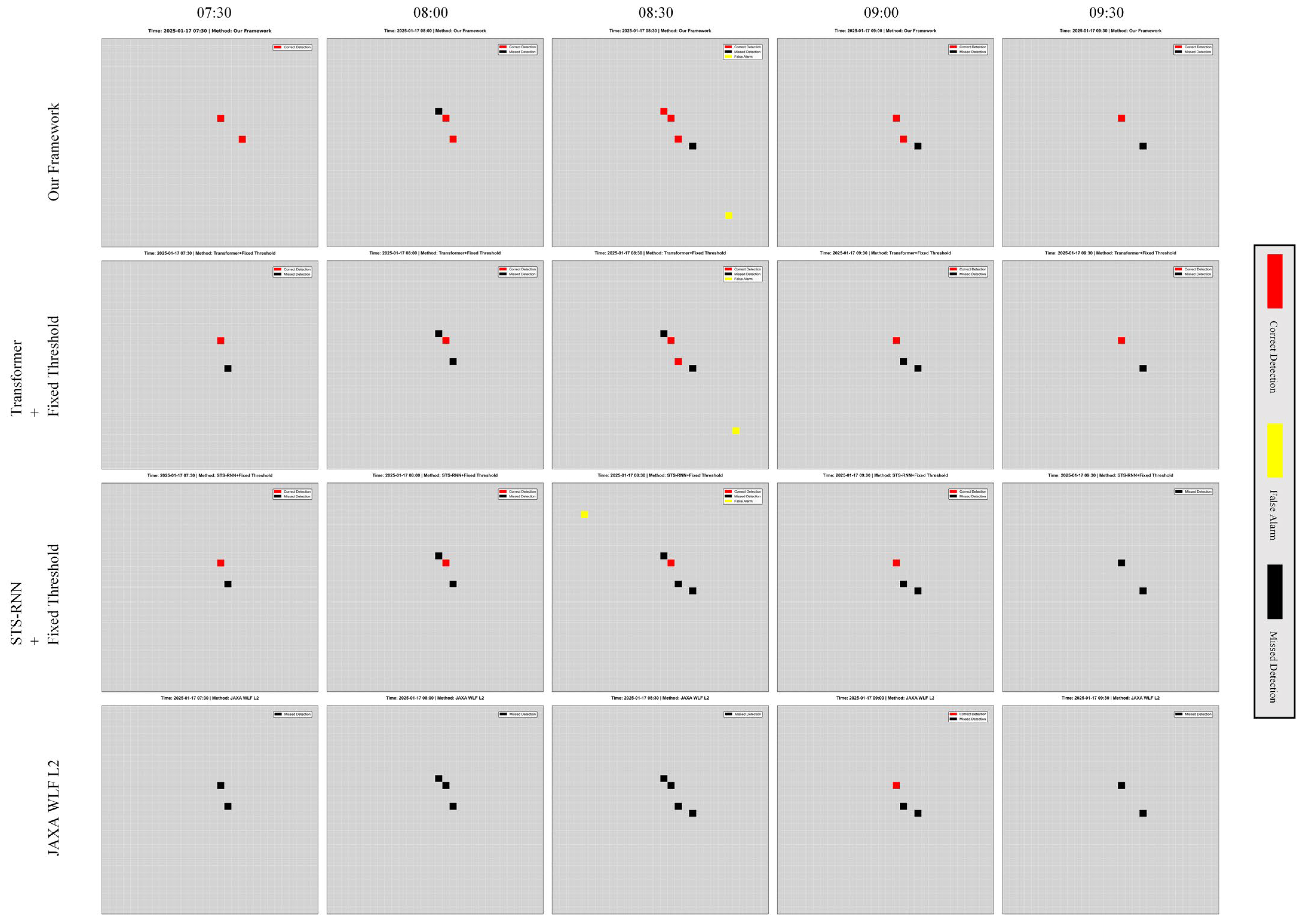
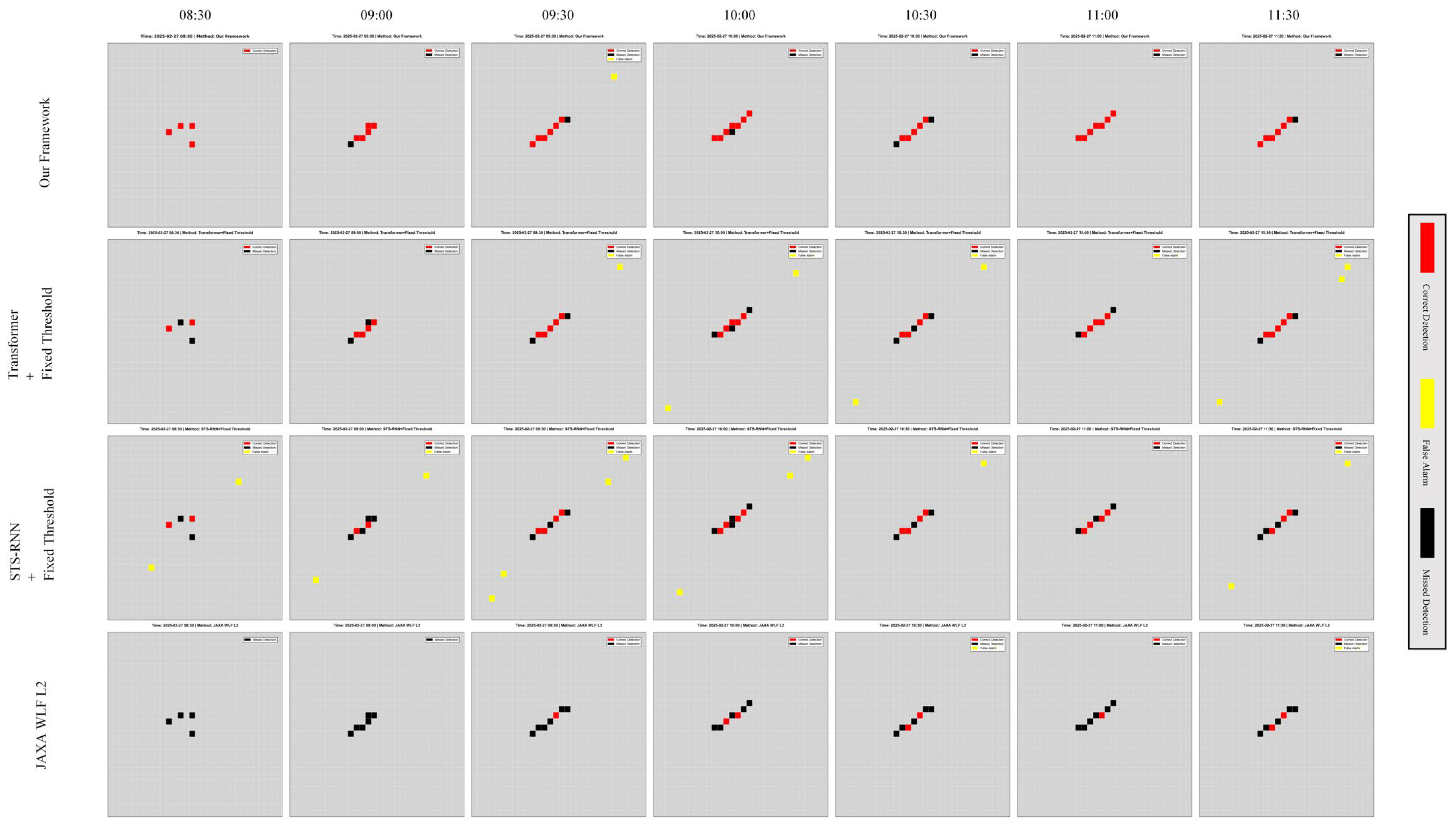
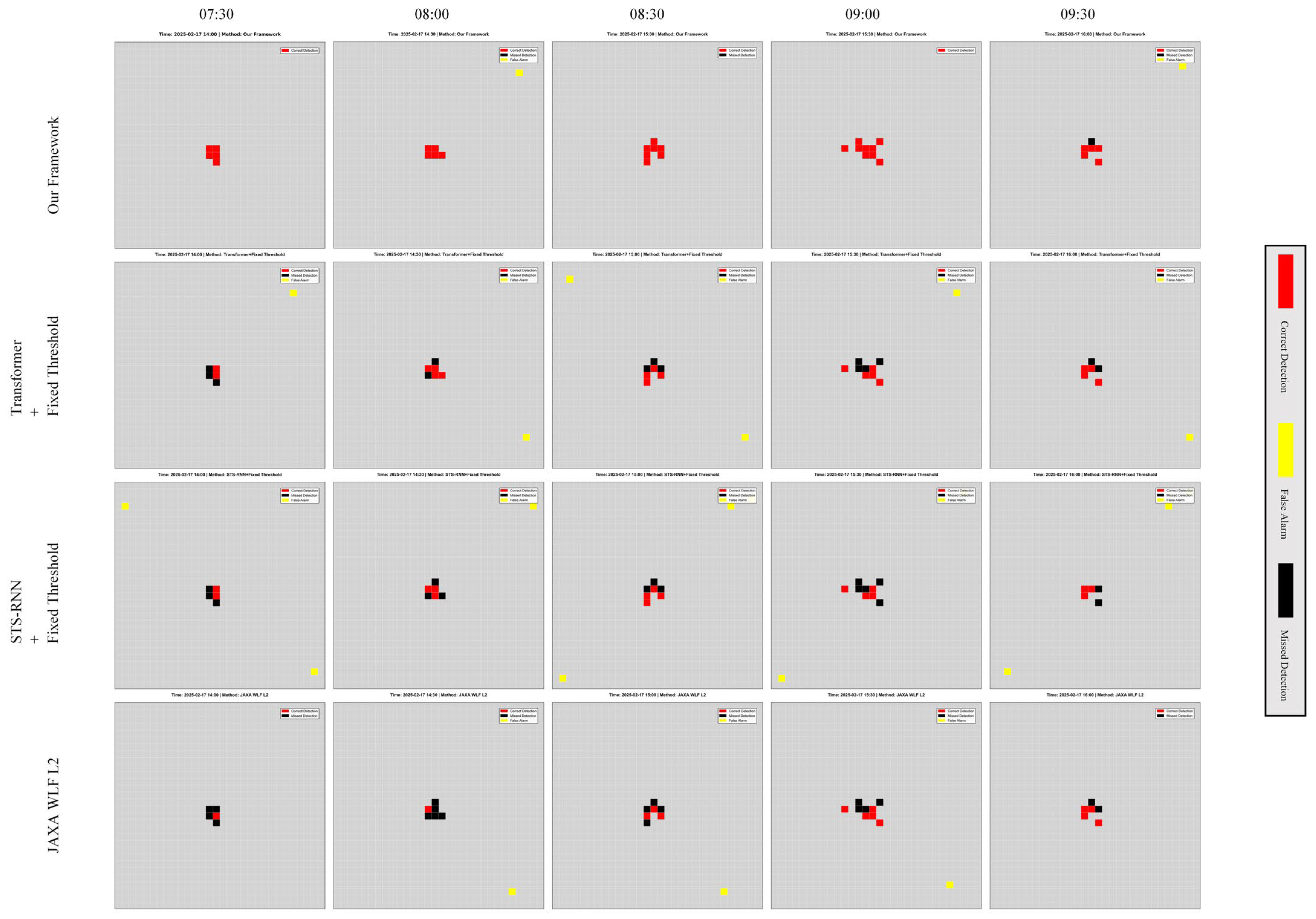
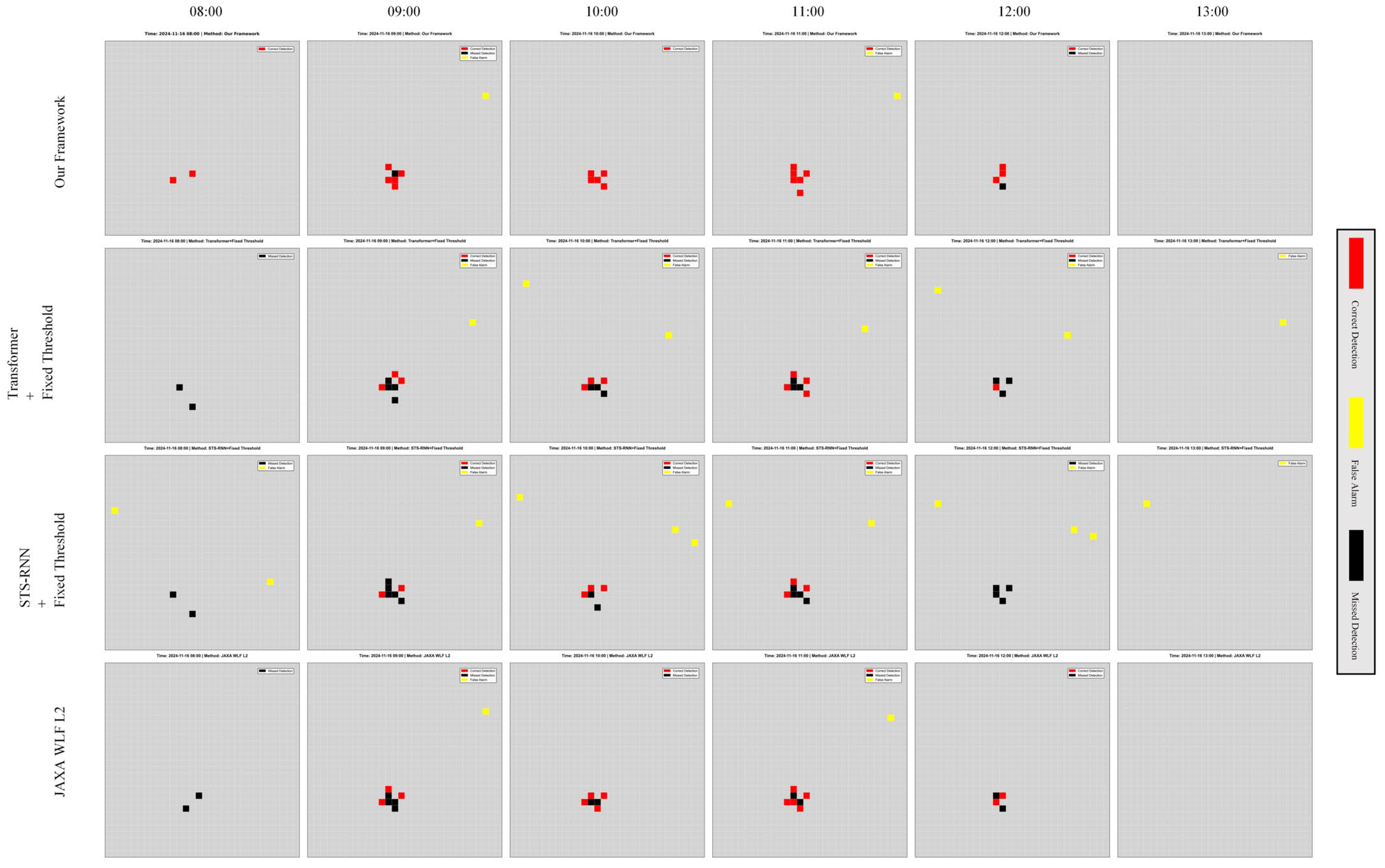
4.3.3. Qualitative Results Visualization
- Legend:
- Red: correctly detected fire points (True Positive, TP);
- Black: missed true fire points (False Negative, FN);
- Yellow: false alarms (False Positive, FP).
4.3.4. Error Analysis
- 1.
- Analysis of False Negatives (FN);
- 2.
- Analysis of False Positives (FP);
4.4. Computational Performance and Near-Real-Time Feasibility
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AHI | Advanced Himawari Imager |
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| MCD14ML | MODIS 1 km Active Fire |
| JAXA WLF L2 | JAXA WLF L2 Product |
| SD | Spectral Differences |
| rTD | Robust Temporal Difference |
| SV | Spatial Variance |
| TBB | Brightness Temperature |
| MIR | Mid-Infrared |
| TIR | Thermal Infrared |
| SWIR | Shortwave Infrared |
| NDFI | Normalized Difference Fire Index |
| SEI | Smoke Extinction Index |
| SA | Shortwave Infrared Anomaly |
| MTRI | Multiplicative Thermal-Reflectance Index |
| TCS | Temporal Consistency Score |
| Transformer | Transformer (self-attention network) |
| XGBoost | eXtreme Gradient Boosting |
| RNN | Recurrent Neural Network |
| GRU | Gated Recurrent Unit |
| LSTM | Long Short-Term Memory |
| CNN | Convolutional Neural Network |
| MSE | Mean Squared Error |
| MAE | Mean Absolute Error |
| TP | True Positive |
| FP | False Positive |
| FN | False Negative |
| P | Positive |
| RN | Reliable Negative |
| U | Unlabelled |
References
- Jang, E.; Kang, Y.; Im, J.; Lee, D.-W.; Yoon, J.; Kim, S.-K. Detection and Monitoring of Forest Fires Using Himawari-8 Geostationary Satellite Data in South Korea. Remote Sens. 2019, 11, 271. [Google Scholar] [CrossRef]
- Maeda, N.; Tonooka, H. Early Stage Forest Fire Detection from Himawari-8 AHI Images Using a Modified MOD14 Algorithm Combined with Machine Learning. Sensors 2023, 23, 210. [Google Scholar] [CrossRef]
- Moreno-Ruiz, J.A.; García-Lázaro, J.R.; Arbelo, M.; Cantón-Garbín, M. MODIS sensor capability to burned area mapping-assessment of performance and improvements provided by the latest standard products in boreal regions. Sensors 2020, 20, 5423. [Google Scholar] [CrossRef] [PubMed]
- Ban, Y.; Zhang, P.; Nascetti, A.; Bevington, A.; Wulder, M.A. Near Real-Time Wildfire Progression Monitoring with Sentinel-1 SAR Time Series and Deep Learning. Sci. Rep. 2020, 10, 1322. [Google Scholar] [CrossRef] [PubMed]
- Hong, Z.; Tang, Z.; Pan, H.; Zhang, Y.; Zheng, Z.; Zhou, R.; Ma, Z.; Zhang, Y.; Han, Y.; Wang, J.; et al. Active Fire Detection Using a Novel Convolutional Neural Network Based on Himawari-8 Satellite Images. Front. Environ. Sci. 2022, 10, 794028. [Google Scholar] [CrossRef]
- Zhang, D.; Huang, C.; Gu, J.; Hou, J.; Zhang, Y.; Han, W.; Dou, P.; Feng, Y. Real-Time Wildfire Detection Algorithm Based on VIIRS Fire Product and Himawari-8 Data. Remote Sens. 2023, 15, 1541. [Google Scholar] [CrossRef]
- Hong, D.; Yokoya, N.; Xia, G.S.; Chanussot, J.; Zhu, X.X. X-ModalNet: A semi-supervised deep cross-modal network for classification of remote sensing data. ISPRS J. Photogramm. Remote Sens. 2020, 167, 12–23. [Google Scholar] [CrossRef]
- Wang, S.; Chen, W.; Xie, S.M.; Azzari, G.; Lobell, D.B. Weakly Supervised Deep Learning for Segmentation of Remote Sensing Imagery. Remote Sens. 2020, 12, 207. [Google Scholar] [CrossRef]
- Moghim, S.; Mehrabi, M. Wildfire assessment using machine learning algorithms in different regions. Fire Ecol. 2024, 20, 104. [Google Scholar] [CrossRef]
- Wickramasinghe, C.; Wallace, L.; Reinke, K.; Jones, S. Intercomparison of Himawari-8 AHI-FSA with MODIS and VIIRS active fire products. Int. J. Digit. Earth 2020, 13, 457–473. [Google Scholar] [CrossRef]
- Giglio, L.; Schroeder, W.; Justice, C.O. The collection 6 MODIS active fire detection algorithm and fire products. Remote Sens. Environ. 2016, 178, 31–41. [Google Scholar] [CrossRef]
- Giglio, L.; Boschetti, L.; Roy, D.P.; Humber, M.L.; Justice, C.O. The Collection 6 MODIS burned area mapping algorithm and product. Remote Sens. Environ. 2018, 217, 72–85. [Google Scholar] [CrossRef]
- Windrim, L.; Ramakrishnan, R.; Melkumyan, A.; Murphy, R.J.; Chlingaryan, A. Unsupervised feature-learning for hyperspectral data with autoencoders. Remote Sens. 2019, 11, 864. [Google Scholar] [CrossRef]
- Shenoy, J.; Zhang, X.D.; Tao, B.; Mehrotra, S.; Yang, R.; Zhao, H.; Vasisht, D. Self-Supervised Learning across the Spectrum. Remote Sens. 2024, 16, 3470. [Google Scholar] [CrossRef]
- Zhou, W.; Shao, Z.; Diao, C.; Cheng, Q. High-resolution remote-sensing imagery retrieval using sparse features by auto-encoder. Remote Sens. Lett. 2015, 6, 775–783. [Google Scholar] [CrossRef]
- Ghaderpour, E.; Vujadinovic, T. Change Detection within Remotely Sensed Satellite Image Time Series via Spectral Analysis. Remote Sens. 2020, 12, 4001. [Google Scholar] [CrossRef]
- Hanson, G.; Schmidt, C.C.; Lindstrom, S.J.; Lovellette, A.M.; Wood, C.; Weidner, S. Multispectral Satellite Imagery Products for Fire Weather Applications. J. Atmos. Ocean. Technol. 2023, 40, 881–899. [Google Scholar]
- Gentilucci, M.; Younes, H.; Hadji, R.; Casagli, N.; Pambianchi, G. Influence of land surface temperatures, precipitation, total water storage anomaly and fraction of absorbed photosynthetically active radiation anomaly, obtained from MODIS, IMERG and GRACE satellite products on wildfires in eastern Central Italy. Int. J. Remote Sens. 2025, 46, 5465–5499. [Google Scholar]
- Yuan, Y.; Lin, L. Self-supervised pretraining of transformers for satellite image time series classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 474–487. [Google Scholar] [CrossRef]
- Yang, J.; Wan, H.; Shang, Z. Enhanced hybrid CNN and transformer network for remote sensing image change detection. Sci. Rep. 2025, 15, 10161. [Google Scholar] [CrossRef]
- Wang, R.; Ma, L.; He, G.; Johnson, B.A.; Yan, Z.; Chang, M.; Liang, Y. Transformers for Remote Sensing: A Systematic Review and Analysis. Sensors 2024, 24, 3495. [Google Scholar] [CrossRef]
- Haque, A.; Soliman, H. A Transformer-Based Autoencoder with Isolation Forest and XGBoost for Malfunction and Intrusion Detection in Wireless Sensor Networks for Forest Fire Prediction. Future Internet 2025, 17, 164. [Google Scholar] [CrossRef]
- Zhang, H.; Eziz, A.; Xiao, J.; Tao, S.; Wang, S.; Tang, Z.; Zhu, J.; Fang, J. High-Resolution Vegetation Mapping Using eXtreme Gradient Boosting Based on Extensive Features. Remote Sens. 2019, 11, 1505. [Google Scholar] [CrossRef]
- Shadrin, D.; Illarionova, S.; Gubanov, F.; Evteeva, K.; Mironenko, M.; Levchunets, I.; Belousov, R.; Burnaev, E. Wildfire spreading prediction using multimodal data and deep neural network approach. Sci. Rep. 2024, 14, 2606. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, Z.; Zhang, L.; Cai, W. A semi-supervised boundary segmentation network for remote sensing images. Sci. Rep. 2025, 15, 2007. [Google Scholar] [CrossRef]


| Data Category | Dataset Name | Technical Specifications |
|---|---|---|
| Geostationary satellite imagery | Himawari-8/9 | Spatial Resolution: 0.5–2 km Temporal Resolution: 10 min |
| Fire Point Reference Product | China Southern Power Grid Yunnan Electric Power Research Institute verifies fire point records | — |
| JAXA WLF L2 Product | Spatial resolution: 2 km; Temporal resolution: 10 min | |
| MODIS 1 km Active Fire (MCD14ML) | Spatial resolution: 1 km; Time resolution: 1–2 days global coverage |
| Band Number | Center Wavelength (µm) | Bandwidth (nm/µm) | Spatial Resolution (km) | Signal-to-Noise Ratio (SNR) or Noise Equivalent Temperature Difference (NEΔT) |
|---|---|---|---|---|
| 3 | 0.64 | 30 nm | 0.5 | SNR ≤ 300 @ 100% albedo |
| 6 | 2.26 | 20 nm | 2.0 | SNR ≤ 300 @ 100% albedo |
| 7 | 3.90 | 0.22 µm | 2.0 | NEΔT ≤ 0.16 K @ 300 K |
| 14 | 11.20 | 0.20 µm | 2.0 | NEΔT ≤ 0.10 K @ 300 K |
| Case | Metric | Our Model | Transformer + Fixed Threshold | RNN + Fixed Threshold | JAXA WLF L2 |
|---|---|---|---|---|---|
| Case 1 (Prescribed Burn) | Precision (Macro/Micro) | 0.9500/ 0.909 | 0.9333/ 0.8571 | 0.7000/ 0.8000 | 0.2000/ 1.0000 |
| Recall (Macro/Micro) | 0.7167/ 0.7143 | 0.4333/ 0.4286 | 0.2833/ 0.2857 | 0.0667/ 0.0714 | |
| F1-Score (Macro/Micro) | 0.8033/ 0.8000 | 0.5810/ 0.5714 | 0.4000/ 0.4211 | 0.1000/ 0.1333 | |
| Case 2 (Grassland Wildfire) | Precision (Macro/Micro) | 0.9796/ 0.9762 | 0.7976/ 0.7500 | 0.6388/ 0.6216 | 0.6190/ 0.8000 |
| Recall (Macro/Micro) | 0.8302/ 0.8200 | 0.5955/ 0.6000 | 0.4606/ 0.4600 | 0.1531/ 0.1702 | |
| F1-Score (Macro/Micro) | 0.8963/ 0.8913 | 0.6748/ 0.6667 | 0.5278/ 0.5287 | 0.2377/ 0.2807 | |
| Case 3 (Agroforestry Wildfire) | Precision (Macro/Micro) | 0.9464/ 0.9459 | 0.7533/ 0.7600 | 0.5976/ 0.5926 | 0.8167/ 0.8333 |
| Recall (Macro/Micro) | 0.9020/ 0.8974 | 0.5022/ 0.5000 | 0.4350/ 0.4324 | 0.3594/ 0.3947 | |
| F1-Score (Macro/Micro) | 0.9228/ 0.9211 | 0.5990/ 0.6032 | 0.5013/ 0.5000 | 0.4845/ 0.5357 | |
| Case 4 (Mountain Forest Wildfire) | Precision (Macro/Micro) | 0.9464/ 0.9235 | 0.4800/ 0.6111 | 0.3533/ 0.4000 | 0.7167/ 0.8750 |
| Recall (Macro/Micro) | 0.9214/ 0.9230 | 0.3500/ 0.4231 | 0.2629/ 0.3200 | 0.4619/ 0.5385 | |
| F1-Score (Macro/Micro) | 0.9295/ 0.9228 | 0.4015/ 0.5000 | 0.2891/ 0.3556 | 0.5563/ 0.6667 | |
| Average (Macro/Micro) | Precision (Macro/Micro) | 0.9556/ 0.9386 | 0.7410/ 0.7445 | 0.5674/ 0.6036 | 0.5881/ 0.8771 |
| Recall (Macro/Micro) | 0.8426/ 0.8387 | 0.4702/ 0.4879 | 0.3599/ 0.3745 | 0.2603/ 0.2937 | |
| F1-Score (Macro/Micro) | 0.8880/ 0.8839 | 0.5645/ 0.5853 | 0.4295/ 0.4514 | 0.3489/ 0.4041 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, L.; Wang, Y.; Li, C.; Zhu, W.; Yu, H.; Tian, H. A Joint Transformer–XGBoost Model for Satellite Fire Detection in Yunnan. Fire 2025, 8, 376. https://doi.org/10.3390/fire8100376
Dong L, Wang Y, Li C, Zhu W, Yu H, Tian H. A Joint Transformer–XGBoost Model for Satellite Fire Detection in Yunnan. Fire. 2025; 8(10):376. https://doi.org/10.3390/fire8100376
Chicago/Turabian StyleDong, Luping, Yifan Wang, Chunyan Li, Wenjie Zhu, Haixin Yu, and Hai Tian. 2025. "A Joint Transformer–XGBoost Model for Satellite Fire Detection in Yunnan" Fire 8, no. 10: 376. https://doi.org/10.3390/fire8100376
APA StyleDong, L., Wang, Y., Li, C., Zhu, W., Yu, H., & Tian, H. (2025). A Joint Transformer–XGBoost Model for Satellite Fire Detection in Yunnan. Fire, 8(10), 376. https://doi.org/10.3390/fire8100376








