Scenario-Based Wildfire Boundary-Threat Indexing at the Wildland–Urban Interface Using Dynamic Fire Simulations
Abstract
1. Introduction
2. Literature Review
2.1. The Data-Driven Statistical Paradigm: Mapping Fire Likelihood
2.2. The Process-Based Paradigm: Modeling Fire Behavior
2.3. The Analytical Gap: Systematic Assessment
2.4. WUI-BTI: Filling the Analytical Gap
3. Methodology
3.1. Domain Definitions
3.1.1. Simulation Domain and Environmental Parameters
3.1.2. Urban Influence Zone and Community Boundaries
3.1.3. Ignition Block Definition
3.1.4. Fire Progression Tracking
3.2. WUI-BTI Fire Impact Metrics
3.2.1. Boundary Breach Detection and Timing ()
3.2.2. Breach Size ()
3.2.3. Minimum Approach Distance ()
3.2.4. Fire Impact WUI-BTI Index
3.3. Benchmarking Metrics: Parsimony and Boundary Concentration
3.4. Operational Workflow and Profile
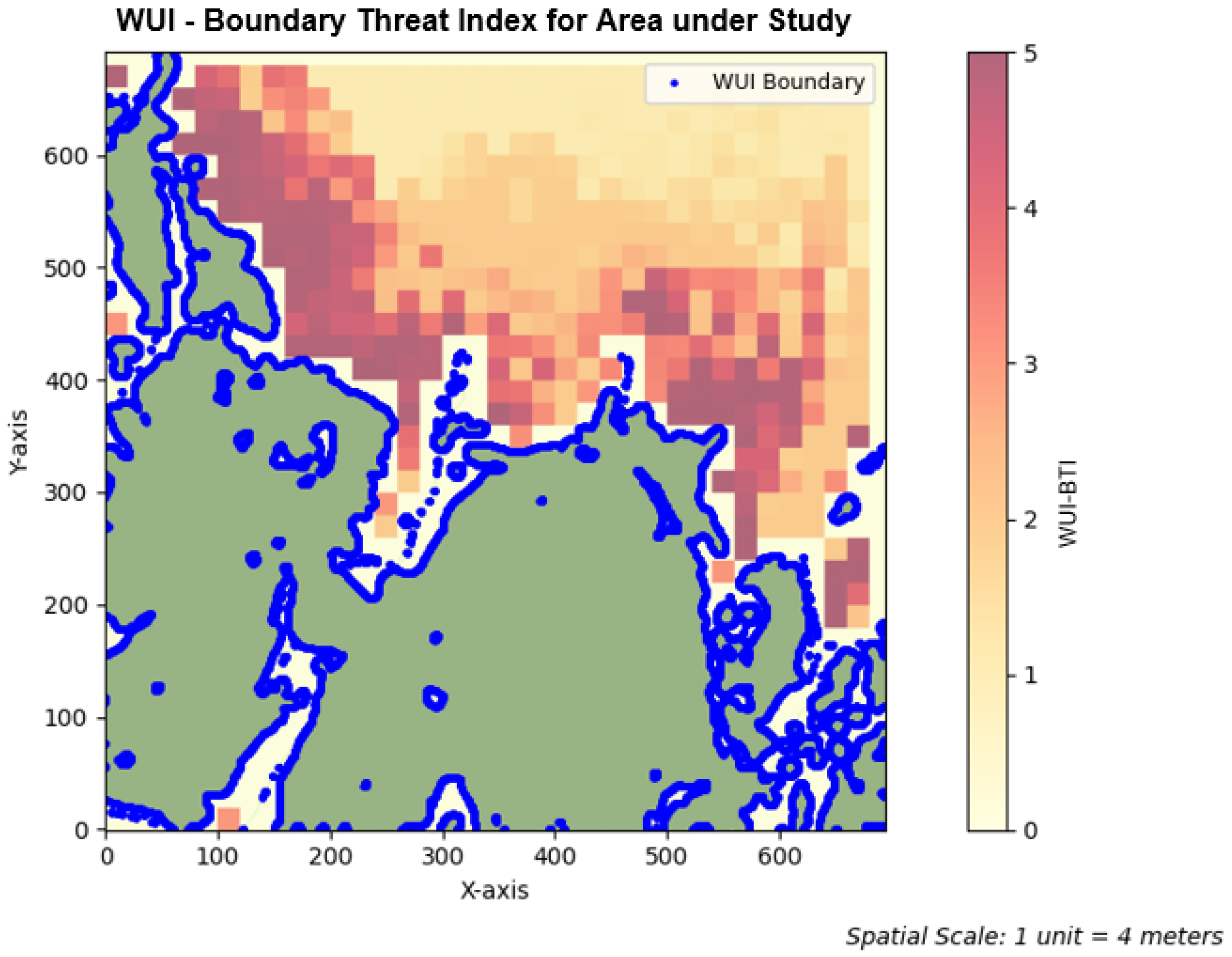
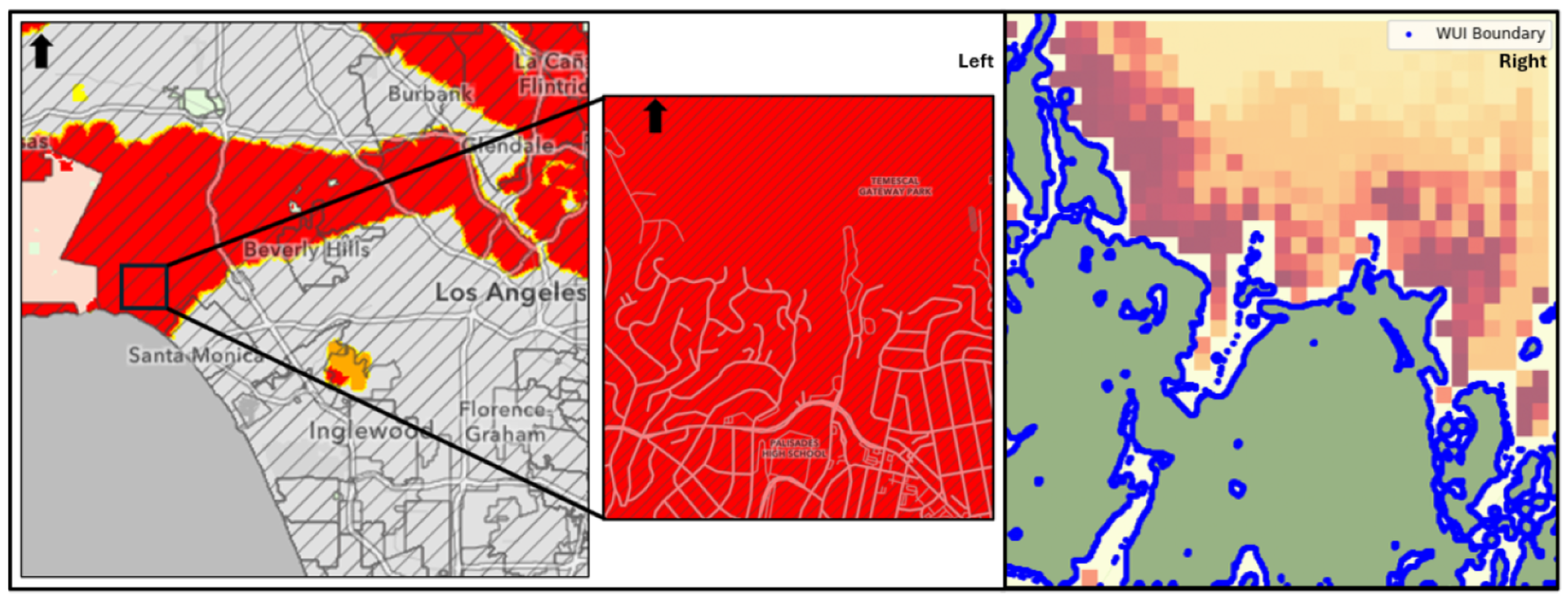
4. Case Study
5. Results and Discussion
6. Conclusions
- Prioritize mitigation: Treat top-ranked FAS as candidates for fuel reduction, access improvements, and boundary hardening.
- Pre-position resources: Stage crews and equipment along boundary segments adjacent to high-threat blocks under forecast winds.
- Refine evacuation planning: Use high-threat approach sectors to set trigger points and route contingencies.
- Monitor and adapt: Recompute WUI-BTI seasonally or when fuels/weather regimes shift; track how the top-k list changes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| WUI-BTI | Wildland Urban Interface Boundary Threat Index |
| FAS | Fire Amplification Site |
Appendix A. Simulation Setup and Inputs
| Category | Symbol/Value | Description |
|---|---|---|
| Study area & discretization | ||
| Domain size | Grid dimensions of simulation domain G | |
| Spatial resolution | Cell size used for discretization of G | |
| WUI delineation | Urban set U, wildland , and community boundary | |
| Ignition design | ||
| Ignition blocks | Number of square ignition blocks covering | |
| Block size | cells per side | physical dimensions per block |
| Environmental forcing (standardized Santa Ana scenario) | ||
| Wind direction | Fixed throughout simulation horizon | |
| Wind speed | Fixed magnitude | |
| Air temperature | Fixed ambient temperature | |
| Relative humidity | Fixed RH | |
| Fuel & terrain inputs (from LANDFIRE) | ||
| Fuel density | [kg m−2] | Surface fuel load per cell |
| Fuel height/depth | [m] | Representative fuel depth per cell |
| Fuel moisture | [%] | Fuel moisture content per cell |
| Topography | elevation [m] | Digital elevation model over G |
| Simulation control | ||
| Duration & step | Total horizon and time step | |
| Time steps | Number of saved output times | |
| Outputs & WUI-BTI metrics | ||
| Time to breach | [s] | First time the fire reaches (if breached) |
| Breach size | [m] | Length of breached boundary segment |
| Min Approach | [m] | Closest distance to when no breach |
| Modeling engine | ||
| Wildfire model | QUIC–FIRE | Coupled QUIC–URB wind + FIRE–CA spread; probabilistic cellular automata |
| Framework stance | Simulator–agnostic | WUI-BTI is model–agnostic; QUIC–FIRE used here for efficiency/fidelity |
References
- Pandey, P.; Huidobro, G.; Lopes, L.F.; Ganteaume, A.; Ascoli, D.; Colaco, C.; Xanthopoulos, G.; Giannaros, T.M.; Gazzard, R.; Boustras, G.; et al. A global outlook on increasing wildfire risk: Current policy situation and future pathways. Trees For. People 2023, 14, 100431. [Google Scholar] [CrossRef]
- Link, E.D.; Maranghides, A. Burnover events identified during the 2018 Camp Fire. Int. J. Wildland Fire 2023, 32, 989–997. [Google Scholar] [CrossRef]
- Radeloff, V.C.; Mockrin, M.H.; Helmers, D.; Carlson, A.; Hawbaker, T.J.; Martinuzzi, S.; Schug, F.; Alexandre, P.M.; Kramer, H.A.; Pidgeon, A.M. Rising wildfire risk to houses in the United States, especially in grasslands and shrublands. Science 2023, 382, 702–707. [Google Scholar] [CrossRef] [PubMed]
- O’Mara, T.; Sánchez Meador, A.; Colavito, M.; Waltz, A.; Barton, E. Navigating the evolving landscape of wildfire management: A systematic review of decision support tools. Trees For. People 2024, 16, 100575. [Google Scholar] [CrossRef]
- Martell, D.L. A Review of Recent Forest and Wildland Fire Management Decision Support Systems Research. Curr. For. Rep. 2015, 1, 128–137. [Google Scholar] [CrossRef]
- Zacharakis, I.; Tsihrintzis, V.A. Environmental forest fire danger rating systems and indices around the globe: A review. Land 2023, 12, 194. [Google Scholar] [CrossRef]
- Zacharakis, I.; Tsihrintzis, V.A. Integrated wildfire danger models and factors: A review. Sci. Total Environ. 2023, 899, 165704. [Google Scholar] [CrossRef]
- Dunn, C.J.; Calkin, D.E.; Thompson, M.P. Towards enhanced risk management: Planning, decision making and monitoring of US wildfire response. Int. J. Wildland Fire 2017, 26, 551–556. [Google Scholar] [CrossRef]
- Thompson, M.P.; Calkin, D.E. Uncertainty and risk in wildland fire management: A review. J. Environ. Manag. 2011, 92, 1895–1909. [Google Scholar] [CrossRef]
- Parisien, M.A.; Snetsinger, S.; Greenberg, J.A.; Nelson, C.R.; Schoennage, T.; Dobrowski, S.Z.; Moritz, M.A. Spatial variability in wildfire probability across the western United States. Int. J. Wildland Fire 2012, 21, 313–327. [Google Scholar] [CrossRef]
- Parisien, M.A.; Walker, G.R.; Little, J.M.; Simpson, B.N.; Wang, X.; Perrakis, D.D.B. Considerations for modeling burn probability across landscapes with steep environmental gradients: An example from the Columbia Mountains, Canada. Nat. Hazards 2013, 66, 439–462. [Google Scholar] [CrossRef]
- Jaffe, M.R.; Scott, J.H.; Callahan, M.N.; Dillon, G.K.; Karau, E.C.; Lazarz, M.T. Wildfire Risk to Communities: Spatial Datasets of Wildfire Risk for Populated Areas in the United States; Forest Service Research Data Archive: Fort Collins, CO, USA, 2024. [Google Scholar] [CrossRef]
- Dillon, G.K.; Lazarz, M.T.; Karau, E.C.; Story, S.J.; Pohl, K.A. Community Wildfire Risk Reduction Zones for the United States; Forest Service Research Data Archive: Fort Collins, CO, USA, 2024. [Google Scholar] [CrossRef]
- Radeloff, V.C.; Hammer, R.B.; Stewart, S.I.; Fried, J.S.; Holcomb, S.S.; McKeefry, J.E. The wildland-urban interface in the United States. Ecol. Appl. 2005, 15, 799–805. [Google Scholar] [CrossRef]
- Xu, Z.; Li, J.; Cheng, S.; Rui, X.; Zhao, Y.; Xu, L. Wildfire Risk Prediction: A Review. arXiv 2024, arXiv:2405.01607. [Google Scholar] [CrossRef]
- Oliveira, S.; Rocha, J.; Sá, A. Wildfire risk modeling. Curr. Opin. Environ. Sci. Health 2021, 23, 100274. [Google Scholar] [CrossRef]
- Preisler, H.K.; Brillinger, D.R.; Burgan, R.E.; Benoit, J.W. Probability based models for estimation of wildfire risk. Int. J. Wildland Fire 2004, 13, 133–142. [Google Scholar] [CrossRef]
- Massada, A.B.; Syphard, A.D.; Stewart, S.I.; Radeloff, V.C. Wildfire ignition-distribution modelling: A comparative study in the Huron–Manistee National Forest, Michigan, USA. Int. J. Wildland Fire 2013, 22, 174–183. [Google Scholar] [CrossRef]
- Chuvieco, E.; Yebra, M.; Martino, S.; Thonicke, K.; Gómez-Giménez, M.; San-Miguel, J.; Oom, D.; Velea, R.; Mouillot, F.; Molina, J.R.; et al. Towards an Integrated Approach to Wildfire Risk Assessment: When, Where, What and How May the Landscapes Burn. Fire 2023, 6, 215. [Google Scholar] [CrossRef]
- Van Wagner, C.E. Development and Structure of the Canadian Forest Fire Weather Index System; Forestry Technical Report 35; Canadian Forest Service, Petawawa National Forestry Institute: Chalk River, ON, Canada, 1987; 37p. [Google Scholar]
- Deeming, J.E.; Burgan, R.E.; Cohen, J.D. The National Fire-Danger Rating System, 1978; Technical Report 39; Intermountain Forest and Range Experiment Station, Forest Service, U.S. Department of Agriculture: Ogden, UT, USA, 1977. [Google Scholar]
- Sharples, J.J. A note on fire weather indices. Int. J. Wildland Fire 2022, 31, 728–734. [Google Scholar] [CrossRef]
- Jain, P.; Coogan, S.C.; Subramanian, S.G.; Crowley, M.; Taylor, S.; Flannigan, M.D. A review of machine learning applications in wildfire science and management. Environ. Rev. 2020, 28, 478–505. [Google Scholar] [CrossRef]
- Dorph, A.; Marshall, E.; Parkins, K.A.; Penman, T.D. Modelling ignition probability for human- and lightning-caused wildfires in Victoria, Australia. Nat. Hazards Earth Syst. Sci. 2022, 22, 3487–3499. [Google Scholar] [CrossRef]
- Muhs, J.W.; Parvania, M.; Nguyen, H.T.; Palmer, J.A. Characterizing Probability of Wildfire Ignition Caused by Power Distribution Lines. IEEE Trans. Power Deliv. 2021, 36, 3681–3688. [Google Scholar] [CrossRef]
- Schreck, J.; Petzke, W.; Jiménez, P.; Brummet, T.; Knievel, J.; James, E.; Kosović, B.; Gagne, D. Machine Learning and VIIRS Satellite Retrievals for Skillful Fuel Moisture Content Monitoring in Wildfire Management. Remote Sens. 2023, 15, 3372. [Google Scholar] [CrossRef]
- Klimas, K.B.; Yocom, L.L.; Murphy, B.P.; Hudak, A.T.; Herynk, J.A.; Abatzoglou, J. A machine learning model to predict wildfire burn severity for pre-fire risk assessments, Utah, USA. Fire Ecol. 2025, 21, 8. [Google Scholar] [CrossRef]
- Sampson, R.N.; Atkinson, R.D.; Lewis, J.W. Mapping Wildfire Hazards and Risks; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Rodríguez-Martínez, A.; Vitoriano, B. Probability-Based Wildfire Risk Measure for Decision-Making. Mathematics 2020, 8, 557. [Google Scholar] [CrossRef]
- Tedim, F.; Samora-Arvela, A.; Aranha, J.; Coimbra, C.; Correia, F.; Pinto, D.M. Bridging knowledge gaps on the role of spatial planning in wildfire risk reduction: Insights from Portugal. Int. J. Wildland Fire 2023, 32, 403–416. [Google Scholar] [CrossRef]
- Bergonse, R.; Oliveira, S.; Santos, P.; Zêzere, J. Wildfire Risk Levels at the Local Scale: Assessing the Relative Influence of Hazard, Exposure, and Social Vulnerability. Fire 2022, 5, 166. [Google Scholar] [CrossRef]
- Ellis, T.M.; Bowman, D.M.J.S.; Jain, P.; Flannigan, M.D.; Williamson, G.J. Global increase in wildfire risk due to climate-driven declines in fuel moisture. Glob. Change Biol. 2022, 28, 1544–1559. [Google Scholar] [CrossRef]
- Mitchell, H.; Gwynne, S.; Ronchi, E.; Kalogeropoulos, N.; Rein, G. Integrating wildfire spread and evacuation times to design safe triggers: Application to two rural communities using PERIL model. Saf. Sci. 2023, 157, 105914. [Google Scholar] [CrossRef]
- Ager, A.A.; Day, M.A.; Palaiologou, P.; Houtman, R.M.; Ringo, C.; Evers, C.R. Cross-Boundary Wildfire and Community Exposure: A Framework and Application in the Western U.S.; Technical Report RMRS-GTR-392; U.S. Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2019. [CrossRef]
- Bakhshaii, A.; Johnson, E.A. A review of a new generation of wildfire–atmosphere modeling. Can. J. For. Res. 2019, 49, 565–574. [Google Scholar] [CrossRef]
- Albini, F.A. Estimating Wildfire Behavior and Effects; General Technical Report INT-30; USDA Forest Service, Intermountain Forest and Range Experiment Station: Ogden, UT, USA, 1976.
- Van Wagner, C. Calculations on forest fire spread by flame radiation; Departmental Publication 1185; Government of Canada, Department of Forestry and Rural Development, Petawawa Forest Experiment Station: Chalk River, ON, USA, 1967. [Google Scholar]
- Sullivan, A.L. Wildland surface fire spread modelling, 1990–2007. 1: Physical and quasi-physical models. Int. J. Wildland Fire 2009, 18, 349–368. [Google Scholar] [CrossRef]
- Sullivan, A.L. Wildland surface fire spread modelling, 1990–2007. 3: Simulation and mathematical analogue models. Int. J. Wildland Fire 2009, 18, 387–403. [Google Scholar] [CrossRef]
- Sullivan, A.L. Wildland surface fire spread modelling, 1990–2007. 2: Empirical and quasi-empirical models. Int. J. Wildland Fire 2009, 18, 369–386. [Google Scholar] [CrossRef]
- Perry, G.L. Current approaches to modelling the spread of wildland fire: A review. Prog. Phys. Geogr. Earth Environ. 1998, 22, 222–245. [Google Scholar] [CrossRef]
- Ager, A.; Finney, M. Application of wildfire simulation models for risk analysis. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 19–24 April 2009; p. 5489. [Google Scholar]
- Finney, M. FARSITE: Fire Area Simulator-Model Development and Evaluation; Research Paper RMRS-RP-4, Revised 2004; U.S. Department of Agriculture, Forest Service, Rocky Mountain Research Station: Ogden, UT, USA, 1998.
- Patton, E.; Coen, J. WRF-Fire: A coupled atmosphere–fire module for WRF. In Proceedings of the The 5th WRF/14th MM5 Users’ Workshop, Boulder, CO, USA, 22–25 June 2004; pp. 221–223. [Google Scholar]
- Coen, J.L.; Douglas, C.C. Computational Modeling of Large Wildfires: A Roadmap. In Proceedings of the 2010 Ninth International Symposium on Distributed Computing and Applications to Business, Engineering and Science, Hong Kong, China, 10–12 August 2010; pp. 113–117. [Google Scholar] [CrossRef]
- Beverly, J.L.; McLoughlin, N.; Chapman, E. A simple metric of landscape fire exposure. Landsc. Ecol. 2021, 36, 785–801. [Google Scholar] [CrossRef]
- Elhami-Khorasani, N.; Ebrahimian, H.; Buja, L.; Cutter, S.L.; Kosovic, B.; Lareau, N.; Meacham, B.J.; Rowell, E.; Taciroglu, E.; Thompson, M.P.; et al. Conceptualizing a probabilistic risk and loss assessment framework for wildfires. Nat. Hazards 2022, 114, 1153–1169. [Google Scholar] [CrossRef]
- Scott, J.H.; Thompson, M.P.; Calkin, D.E. A Wildfire Risk Assessment Framework for Land and Resource Management; Technical Report RMRS-GTR-315; US Department of Agriculture, Forest Service, Rocky Mountain Research Station: Ogden, UT, USA, 2013; 83p.
- Linn, R.; Goodrick, S.; Brambilla, S.; Brown, M.; Middleton, R.; O’Brien, J.; Hiers, J. QUIC-fire: A fast-running simulation tool for prescribed fire planning. Environ. Model. Softw. 2020, 125, 104616. [Google Scholar] [CrossRef]
- Matey, Y.; de Callafon, R.; Altintas, I. Optimizing Prescribed Burn Risk Management: A Computational and Economic Modeling Approach Using QUIC FIRE Simulations. In Proceedings of the Computational Science— ICCS 2024: 24th International Conference, Malaga, Spain, 2–4 July 2024; Franco, L., de Mulatier, C., Paszynski, M., Krzhizhanovskaya, V.V., Dongarra, J.J., Sloot, P.M.A., Eds.; Springer: Cham, Switzerland, 2024; pp. 266–280. [Google Scholar]
- Bar Massada, A.; Radeloff, V.C.; Stewart, S.I.; Hawbaker, T.J. Wildfire risk in the wildland–urban interface: A simulation study in northwestern Wisconsin. For. Ecol. Manag. 2009, 258, 1990–1999. [Google Scholar] [CrossRef]
- Korená Hillayová, M.; Holécy, J.; Korený, L.; Škvarenina, J. Reducing the negative impact of wildfire disasters through multi-scenario risk analysis of land investment. Prog. Disaster Sci. 2024, 23, 100359. [Google Scholar] [CrossRef]
- Alcasena, F.J.; Salis, M.; Ager, A.A.; Castell, R.; Vega-García, C. Assessing Wildland Fire Risk Transmission to Communities in Northern Spain. Forests 2017, 8, 30. [Google Scholar] [CrossRef]
- CAL FIRE. Fire Hazard Severity Zones. 2023. Available online: https://osfm.fire.ca.gov/what-we-do/community-wildfire-preparedness-and-mitigation/fire-hazard-severity-zones (accessed on 22 July 2025).
- Microsoft. USBuildingFootprints. 2024. Available online: https://github.com/Microsoft/USBuildingFootprints (accessed on 22 May 2025).
- Suzuki, S.; Abe, K. Topological Structural Analysis of Digitized Binary Images by Border Following. Comput. Vision Graph. Image Process. 1985, 30, 32–46. [Google Scholar] [CrossRef]
- Shimrat, M. Algorithm 112: Position of point relative to polygon. Commun. ACM 1962, 5, 434. [Google Scholar] [CrossRef]
- LANDFIRE Program. Existing Vegetation Type Layer, LANDFIRE 2.0.0; U.S. Department of the Interior, Geological Survey, and U.S. Department of Agriculture. 2020. Available online: http://www.landfire.gov/viewer (accessed on 18 April 2025).
- Dye, A.W.; Kim, J.B.; Riley, K.L. Spatial heterogeneity of winds during Santa Ana and non-Santa Ana wildfires in Southern California with implications for fire risk modeling. Heliyon 2020, 6, e04159. [Google Scholar] [CrossRef]
- Miller, N.L.; Schlegel, N.J. Climate change projected fire weather sensitivity: California Santa Ana wind occurrence. Geophys. Res. Lett. 2006, 33, L15711. [Google Scholar] [CrossRef]
- Gallagher, M.R.; Cope, Z.; Giron, D.R.; Skowronski, N.S.; Raynor, T.; Gerber, T.; Linn, R.R.; Hiers, J.K. Reconstruction of the Spring Hill Wildfire and Exploration of Alternate Management Scenarios Using QUIC-Fire. Fire 2021, 4, 72. [Google Scholar] [CrossRef]
- Tymstra, C.; Bryce, R.; Wotton, B.; Taylor, S.; Armitage, O. Development and Structure of Prometheus: The Canadian Wildland Fire Growth Simulation Model; Information Report NOR-X-417; Natural Resources Canada, Canadian Forest Service, Northern Forestry Centre: Edmonton, AB, Canada, 2010. [Google Scholar]
- Papadopoulos, G.; Pavlidou, F. A Comparative Review on Wildfire Simulators. IEEE Syst. J. 2011, 5, 233–243. [Google Scholar] [CrossRef]
- Linn, R.; Harlow, F. FIRETEC: A Transport Description of Wildfire Behavior; Los Alamos National Lab.: Los Alamos, MN, USA, 1997. [CrossRef]
- Coen, J.; Cameron, M.; Michalakes, J.; Patton, E.; Riggan, P.; Yedinak, K. WRF-Fire: Coupled Weather–Wildland Fire Modeling with the Weather Research and Forecasting Model. J. Appl. Meteorol. Climatol. 2013, 52, 16–38. [Google Scholar] [CrossRef]
- Pardyjak, E.; Brown, M. QUIC-URB v. 1.1: Theory and User’s Guide; Los Alamos National Laboratory: Los Alamos, NM, USA, 2003.
- Singh, B.; Hansen, B.; Brown, M.; Pardyjak, E. Evaluation of the QUIC-URB fast response urban wind model for a cubical building array and wide building street canyon. Environ. Fluid Mech. 2008, 8, 281–312. [Google Scholar] [CrossRef]
- Achtemeier, G. Field validation of a free-agent cellular automata model of fire spread with fire–atmosphere coupling. Int. J. Wildland Fire 2012, 22, 148–156. [Google Scholar] [CrossRef]
- Achtemeier, G.; Goodrick, S.; Liu, Y. Modeling multiple-core updraft plume rise for an aerial ignition prescribed burn by coupling Daysmoke with a cellular automata fire model. Atmosphere 2012, 3, 352–376. [Google Scholar] [CrossRef]
- National Wildfire Coordinating Group (NWCG) Fuels Management Committee. Fire Line Production Rate Tables; 2014; Originally published in *Wildland Fire Incident Management Field Guide, PMS 210* (2014; discontinued 2021). Available online: https://www.nwcg.gov/committee/fuels-management-committee (accessed on 23 July 2025).
- International Association of Fire Fighters (IAFF). Summary Sheet: NFPA 1710 Standard. 2021. Available online: https://www.iaff.org/wp-content/uploads/Departments/Fire_EMS_Department/30541_Summary_Sheet_NFPA_1710_standard.pdf (accessed on 23 July 2025).
- Eggleston, J. Using Initial Fire Attack Evolutions to Evaluate a Fire Fighting Team’s Effectiveness; Technical Report; National Fire Academy: Franklin, VA, USA, 1999.
- Rahn, M. Initial Attack Effectiveness: Wildfire Staffing Study. In California Wildfire Staffing Study; Technical Report Wildfire Research Report No. 2; San Diego State University: San Diego, CA, USA, 2010; Available online: https://www.iaff.org/wp-content/uploads/2019/05/Initial-Attack-Effectiveness-Study.pdf (accessed on 23 July 2025).
- Jeremy, F.; Paul, M. Efficient Initial Attacks: Analysis of Capacity and Funding Provides Insights to Wildfire Protection Planning; Science Findings 164; Department of Agriculture, Forest Service, Pacific Northwest Research Station: Portland, OR, USA, 2014; 6p.
- Syphard, A.D.; Brennan, T.J.; Keeley, J.E. The role of defensible space for residential structure protection during wildfires. Int. J. Wildland Fire 2014, 23, 1165–1175. [Google Scholar] [CrossRef]
- Wadhwani, R.; Sutherland, D.; Moinuddin, K. Simulated transport of short-range embers in an idealised bushfire. In Proceedings of the 6th International Fire Behavior and Fuels Conference, Sydney, Australia, 29 April–3 May 2019. [Google Scholar]

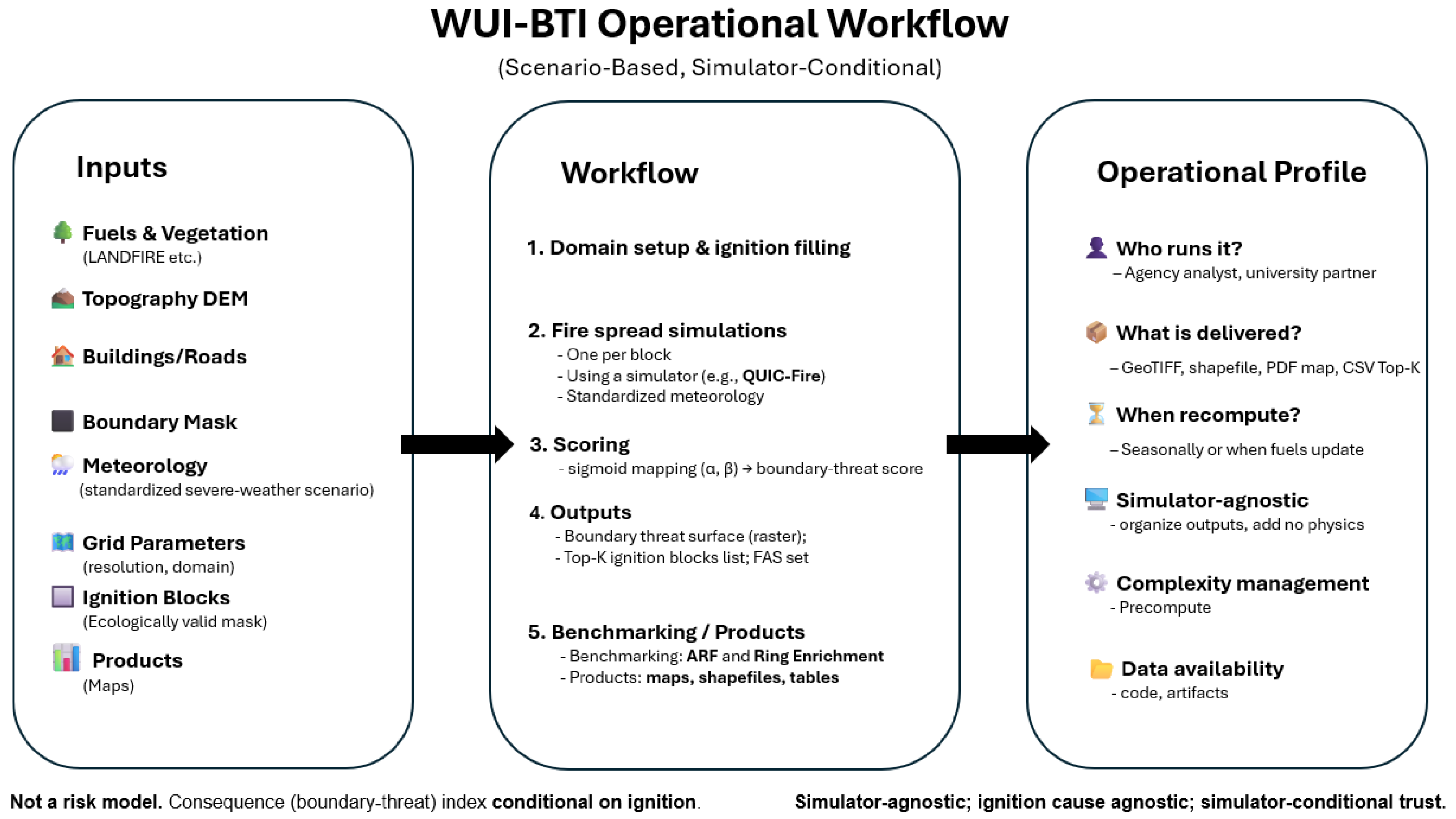
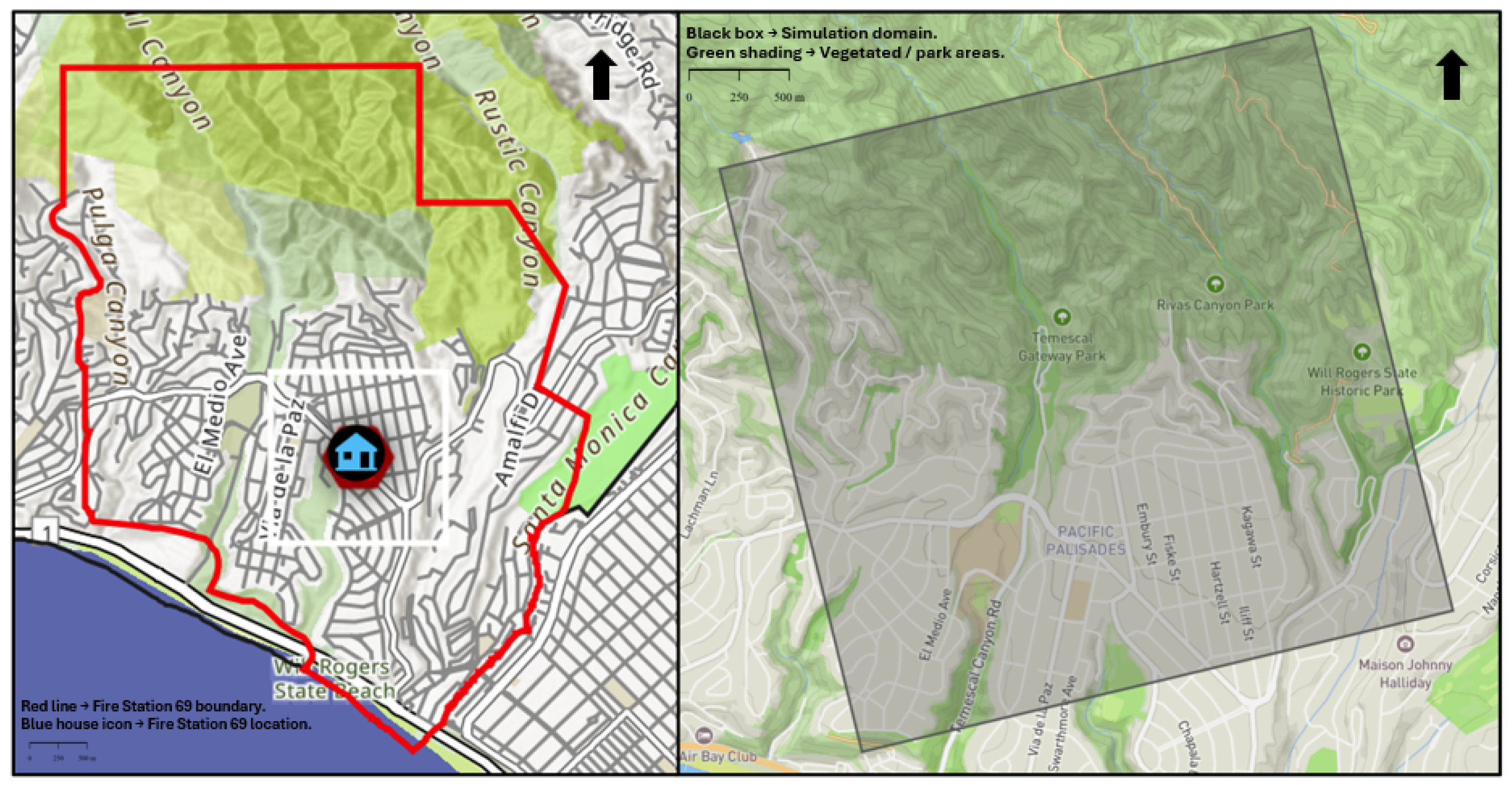

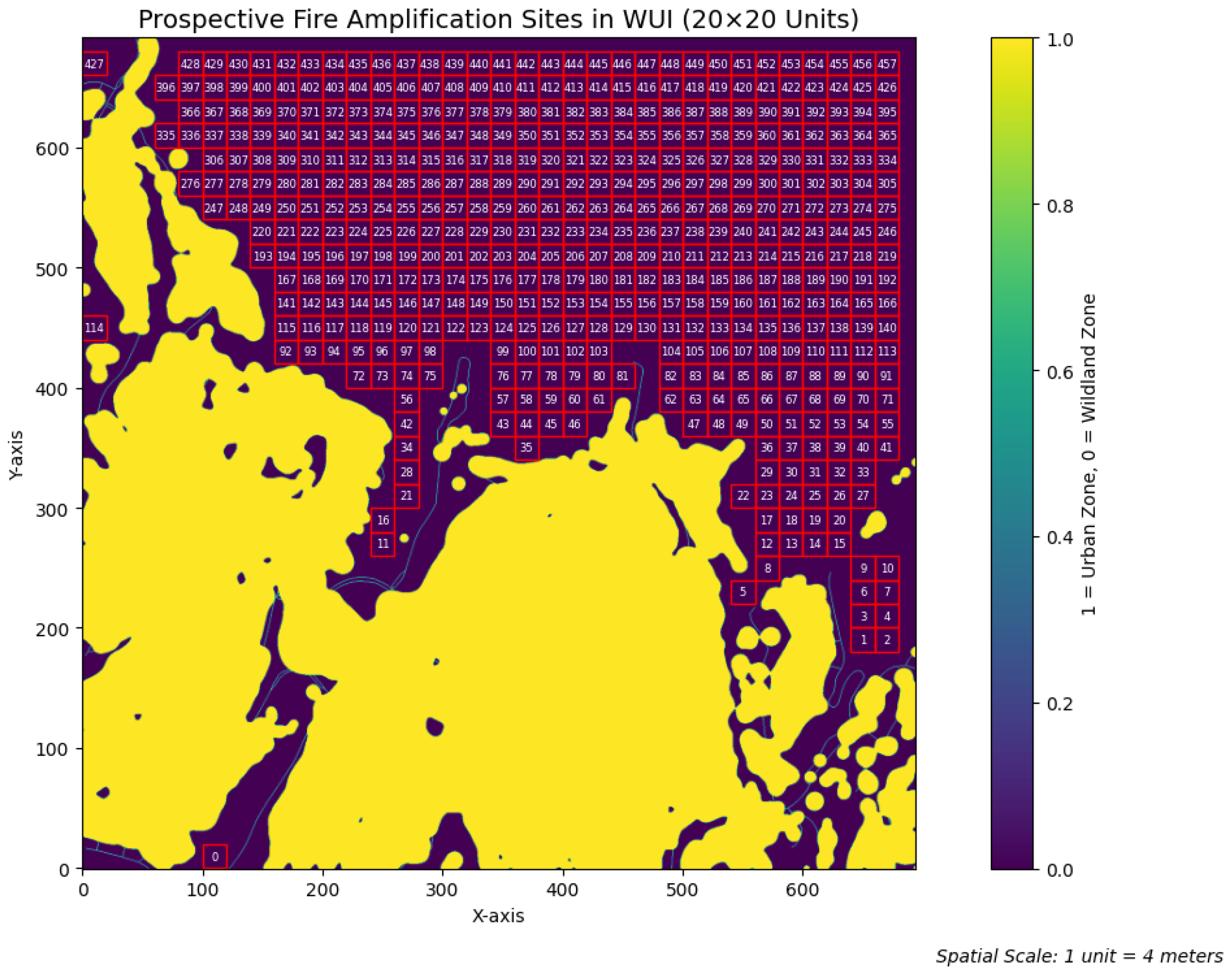
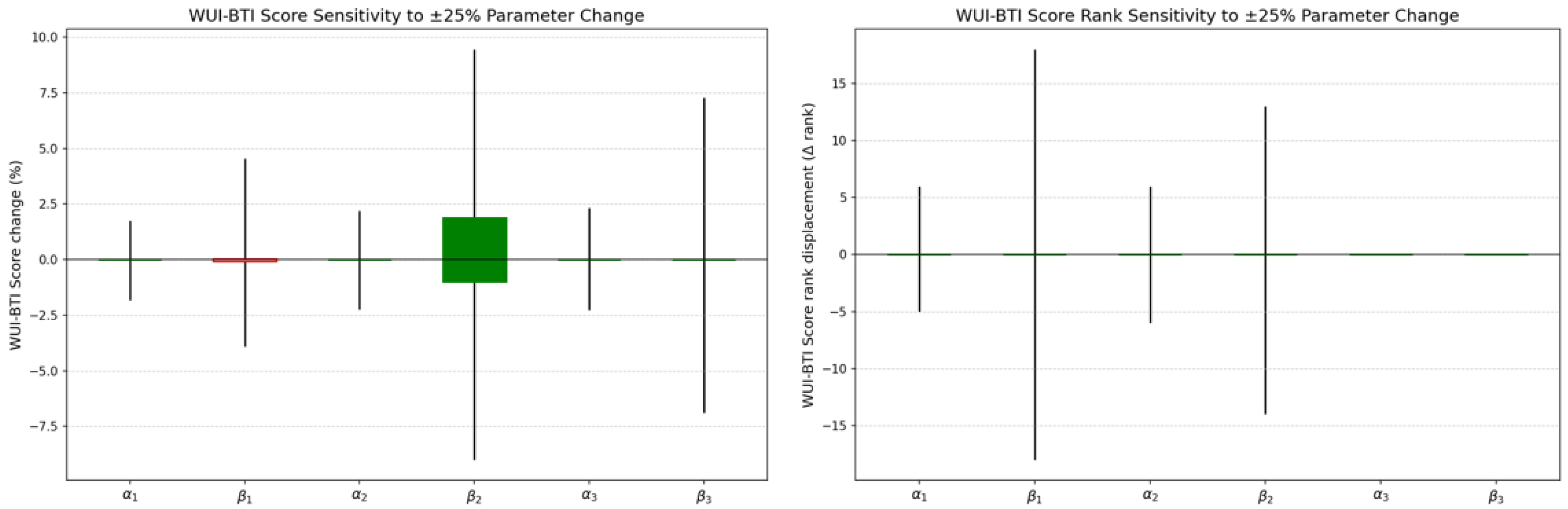
| Item | Content | Format/Notes |
|---|---|---|
| Fuels/vegetation | LANDFIRE or equivalent | Raster (GeoTIFF) |
| Topography | DEM | Raster (GeoTIFF) |
| Built environment | Buildings/roads mask | Vector/raster (SHP/GeoTIFF) |
| Boundary | Community polygon U | Vector (SHP/GeoPackage) |
| Meteorology | Standardized severe-weather | Config (YAML/JSON) |
| Grid setup | Resolution r, domain G | Config + CRS |
| Ignition blocks | Ecological validity mask | Raster (GeoTIFF) |
| Boundary-threat surface | Ranked output | Raster (GeoTIFF) |
| Top-k blocks | Prioritized ignition list | CSV (block ID, score, metrics) |
| FAS set | High-threat blocks | Vector (SHP)/CSV |
| Benchmarking | ARF, ring enrichment | Table (PDF/CSV) |
| Parameter | Meaning | Suggested Value |
|---|---|---|
| Steepness for breach size influence | 0.02 | |
| Midpoint for breach size (in meters) | 200 | |
| Steepness for breach timing influence | 0.005 | |
| Midpoint for breach timing (in seconds) | 900 | |
| Steepness for minimum approach distance influence | 0.02 | |
| Midpoint for (in meters) | 250 |
| Block ID | Scenario | (s) | (m) | (m) | WUI-BTI |
|---|---|---|---|---|---|
| Breach | 60 | 2192 | – | 4.97 | |
| No Breach | – | – | 48 | 1.98 | |
| Breach | 960 | 104 | – | 2.61 | |
| No Breach | – | – | 263 | 1.001 | |
| Breach | 180 | 128 | – | 3.35 |
| Area of (km2) | 0.4183 | 0.8366 | 1.0457 |
| ARF (×) | 10.00 | 5.00 | 4.00 |
| Median dist. (m) | 117.6 | 164.9 | 169.7 |
| EF 0–250 m | 1.860 | 1.520 | 1.433 |
| EF 250–500 m | 0.357 | 1.282 | 1.425 |
| EF 500–750 m | 0.000 | 0.016 | 0.141 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matey, Y.; de Callafon, R.; Altintas, I. Scenario-Based Wildfire Boundary-Threat Indexing at the Wildland–Urban Interface Using Dynamic Fire Simulations. Fire 2025, 8, 377. https://doi.org/10.3390/fire8100377
Matey Y, de Callafon R, Altintas I. Scenario-Based Wildfire Boundary-Threat Indexing at the Wildland–Urban Interface Using Dynamic Fire Simulations. Fire. 2025; 8(10):377. https://doi.org/10.3390/fire8100377
Chicago/Turabian StyleMatey, Yeshvant, Raymond de Callafon, and Ilkay Altintas. 2025. "Scenario-Based Wildfire Boundary-Threat Indexing at the Wildland–Urban Interface Using Dynamic Fire Simulations" Fire 8, no. 10: 377. https://doi.org/10.3390/fire8100377
APA StyleMatey, Y., de Callafon, R., & Altintas, I. (2025). Scenario-Based Wildfire Boundary-Threat Indexing at the Wildland–Urban Interface Using Dynamic Fire Simulations. Fire, 8(10), 377. https://doi.org/10.3390/fire8100377






