A Tutorial on the One-Dimensional Theory of Electron-Beam Space-Charge Effect and Steady-State Virtual Cathode
Abstract
1. Introduction
2. Space-Charge Limited Current in an Acceleration Gap
2.1. Non-Relativistic Space Charge Limited Current
2.2. Relativistic Space Charge Limited Current
3. Electron Beam Injection into a Drifting Space
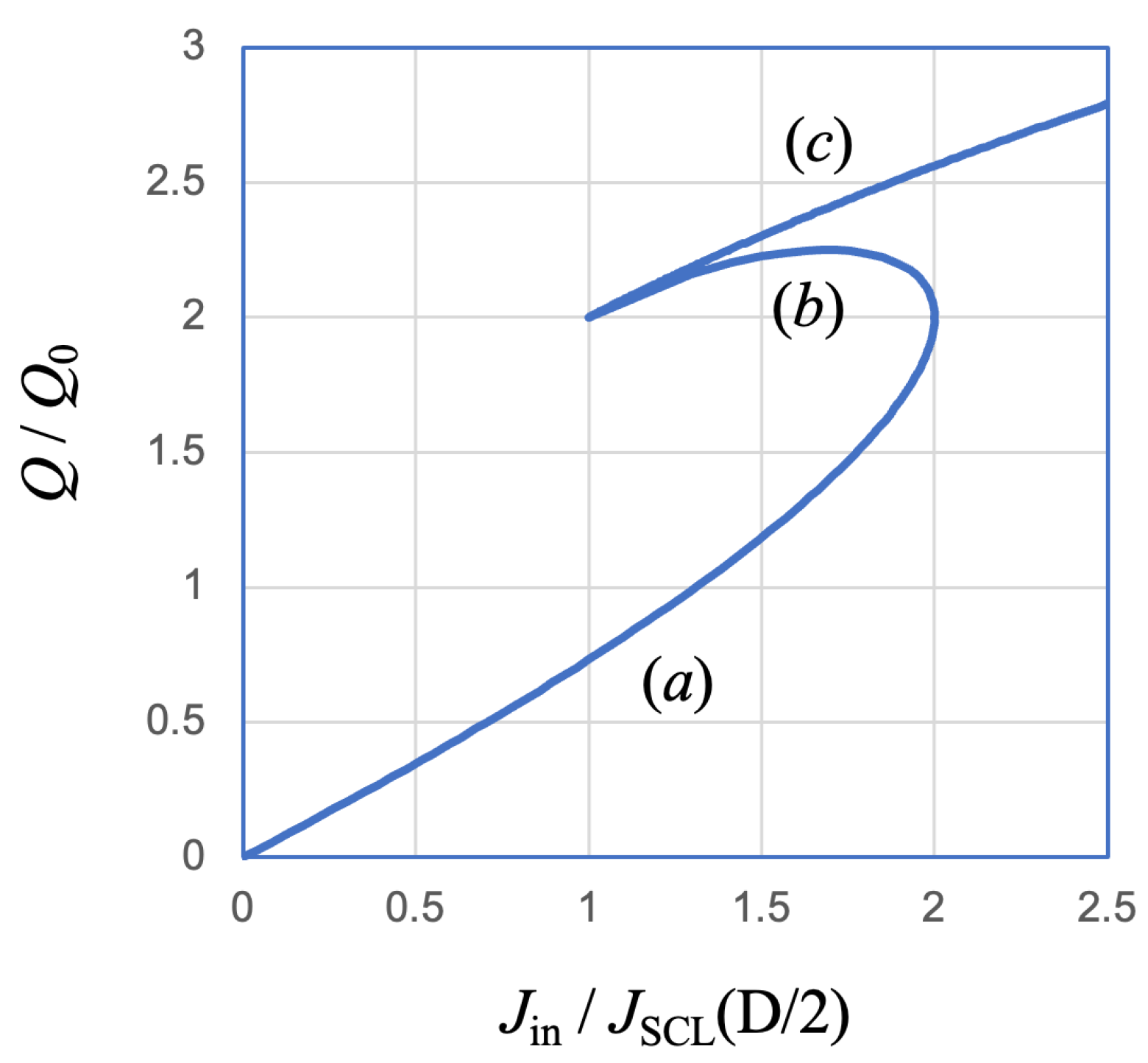
3.1. When Beam Current Density Is Relatively Low
3.2. When Beam Current Density Is Higher Than the Limiting Value
3.3. Stable State and Unstable State
4. An Acceleration Gap and a Drifting Space
4.1. When the Drifting Space Is Relatively Narrow
4.2. When the Drifting Space Is Wider Than the Critical Limit
5. Summary
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, P.; Valfells, A.; Ang, L.K.; Luginsland, J.W.; Lau, Y.Y. 100 years of the physics of diodes. Appl. Phys. Rev. 2017, 4, 011304. [Google Scholar] [CrossRef]
- Harris, J.R.; O’Shea, P.G. Gridded Electron Guns and Modulation of Intense Beams. IEEE Trans. Electron Devices 2006, 53, 2824–2829. [Google Scholar] [CrossRef]
- Siman-Tov, M.; Leopold, J.G.; Krasik, Y.E. Self-oscillations in an over-injected electron diode–Experiment and analysis. Phys. Plasmas 2019, 26, 033113. [Google Scholar] [CrossRef]
- Humphries, S., Jr. Chapter 5 Introduction to Beam-Generated Forces. In Charged Particle Beams; John Wiley and Sons: Hoboken, NJ, USA, 1990. [Google Scholar]
- Miller, R.B. Chapter 3 Propagation of Intense Beams in Vacuum. In An Introduction to the Physics of Intense Charged Particle Beams; Plenum Press: New York, NY, USA, 1982. [Google Scholar]
- Sullivan, D.J.; Walsh, J.E.; Coutsias, E.A. Chapter 13 Virtual Cathode Oscillator–(Vircator) Theory. In High-Power Microwave Sources; Granatstein, V.L., Alexeff, I.A., Eds.; Artech House: Boston, MA, USA; London, UK, 1987. [Google Scholar]
- Benford, J.; Swegle, J.A.; Schamiloglu, E. Chapter 10 Vircators. In High Power Microwaves, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Valfells, A.; Feldman, D.W.; Virgo, M.; O’Shea, P.G. Effects of pulse-length and emitter area on virtual cathode formation in electron guns. Phys. Plasmas 2002, 9, 2377–2382. [Google Scholar] [CrossRef]
- Child, C.D. Discharge from Hot CaO. J. Phys. Rev. Ser. I 1911, 32, 492–511. [Google Scholar] [CrossRef]
- Lungmuir, I. The Effect of Space Charge and Initial Velocities on the Potential Distribution and Thermionic Current between Parallel Plane Electrodes. Phys. Rev. 1923, 21, 419–435. [Google Scholar] [CrossRef]
- Fay, C.E.; Samuel, A.L.; Shockley, W. On the Theory of Space Charge Between Parallel Plane Electrodes. Bell Syst. Tech. J. 1938, 17, 705–717. [Google Scholar] [CrossRef]
- Strutt, M.J.; van der Ziel, A. On Electronic Space-Charge with Homogeneous Initial Electron Velocity between Plane Electrodes. Physica 1938, 5, 705–717. [Google Scholar] [CrossRef]
- Jaffe, G. On the Currents Carried by Elections of Uniform Initial Velocity. Phys. Rev. 1944, 65, 91–98. [Google Scholar] [CrossRef]
- Bull, C.S.; Birdsall, C.K. Space-Charge Effects in Beam Tetrodes and Other Valves. J. Inst. Electr. Eng.-Part III 1948, 95, 17–24. [Google Scholar]
- Page, L.; Adams, N.I. Diode Space Charge for Any Initial Velocity and Current. Phys. Rev. 1949, 76, 381–388. [Google Scholar] [CrossRef]
- Klemperer, O. Chapter 8 Electron Optics and Space Charge. In Electron Optics, 2nd ed.; Cambridge University Press: London, UK; New York, NY, USA, 1953. [Google Scholar]
- Birdsall, C.K.; Bridges, W.B. Space-Charge Instabilities in Electron Diodes and Plasma Converters. J. Appl. Phys. 1961, 32, 2611–2618. [Google Scholar] [CrossRef]
- Bridges, W.B.; Birdsall, C.K. Space-Charge Instabilities in Electron Diodes, II. J. Appl. Phys. 1963, 34, 2946–2955. [Google Scholar] [CrossRef]
- Birdsall, C.K.; Bridges, W.B. Chapter 3 Stability of Flow; Nonlinear Solution of Multiparticle Model. In Electron Dynamics of Diode Regions; Academic Press: New York, NY, USA, 1966. [Google Scholar]
- Bridges, W.B.; Frey, J.I.; Birdsall, C.K. Limiting Stable Currents in Bounded Electron and Ion Streams. IEEE Trans. Electron Devices 1965, 12, 264–272. [Google Scholar] [CrossRef]
- Jory, H.R.; Trivelpiece, A.W. Exact Relativistic Solution for the One-Dimensional Diode. J. Appl. Phys. 1969, 40, 3924–3926. [Google Scholar] [CrossRef]
- Prono, D.S.; Creedon, J.M.; Smith, I.; Bergstrom, N. Multiple reflections of electrons and the possibility of intense positive-ion flow in high v/γ diodes. J. Appl. Phys. 1975, 46, 3310–3319. [Google Scholar] [CrossRef]
- Miller, P.A.; Halbleib, J.A.; Poukey, J.W. Inverse ion diode experiment. J. Appl. Phys. 1981, 52, 593–598. [Google Scholar] [CrossRef]
- Neumann, J.G.; Harris, J.R.; O’Shea, P.G. Production of photoemission-modulated beams in a thermionic electron gun. Rev. Sci. Instrum. 2005, 76, 033303. [Google Scholar] [CrossRef]
- González, G.; González, F.J. A novel approach to the Child-Langmuir law. Rev. Mex. Fís. E. 2017, 63, 83–86. [Google Scholar]
- Leopold, J.G.; Siman-Tov, M.; Goldman, A.; Krasik, Y.E. Over-injection and self-oscillations in an electron vacuum diode. Phys. Plasmas 2017, 24, 073136. [Google Scholar] [CrossRef]
- Mahaffey, R.A.; Sprangle, P.; Golden, J.; Kapetanakos, C.A. High-Power Microwave from a Nonisochronic Reflecting Electron System. Phys. Rev. Lett. 1977, 39, 843–846. [Google Scholar] [CrossRef]
- Kwan, T.J.T. High-Efficiency, Magnetized, Virtual-Cathode Microwave Generator. Phys. Rev. Lett. 1986, 57, 1895–1898. [Google Scholar] [CrossRef] [PubMed]
- Benford, J.; Price, D.; Sze, H.; Bromley, D. Interaction of a Vircator Microwave Generator with an Enclosing Resonant Cavity. J. Appl. Phys. 1987, 61, 2098–2100. [Google Scholar] [CrossRef]
- Jiang, W.; Masugata, K.; Yatsui, K. Mechanism of Microwave Generation by Virtual Cathode Oscillation. Phys. Plasmas 1995, 2, 982–986. [Google Scholar] [CrossRef]
- Jiang, W.; Woolverton, K.; Dickens, J.; Kristiansen, M. High Power Microwave Generation by a Coaxial Virtual Cathode Oscillator. IEEE Trans. Plasma Sci. 1999, 27, 1538–1542. [Google Scholar] [CrossRef]
- Jiang, W.; Kristiansen, M. Theory of the Virtual Cathode Oscillator. Phys. Plasmas 2001, 8, 3781–3787. [Google Scholar] [CrossRef]
- Selemir, V.D.; Dubinov, A.E.; Voronin, V.V.; Zhdanov, V.S. Key Ideas and Main Milestones of Research and Development of Microwave Generators With Virtual Cathode in RFNC-VNIIEF. IEEE Trans. Plasma Sci. 2020, 48, 1860–1867. [Google Scholar] [CrossRef]













Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, W. A Tutorial on the One-Dimensional Theory of Electron-Beam Space-Charge Effect and Steady-State Virtual Cathode. Plasma 2024, 7, 29-48. https://doi.org/10.3390/plasma7010003
Jiang W. A Tutorial on the One-Dimensional Theory of Electron-Beam Space-Charge Effect and Steady-State Virtual Cathode. Plasma. 2024; 7(1):29-48. https://doi.org/10.3390/plasma7010003
Chicago/Turabian StyleJiang, Weihua. 2024. "A Tutorial on the One-Dimensional Theory of Electron-Beam Space-Charge Effect and Steady-State Virtual Cathode" Plasma 7, no. 1: 29-48. https://doi.org/10.3390/plasma7010003
APA StyleJiang, W. (2024). A Tutorial on the One-Dimensional Theory of Electron-Beam Space-Charge Effect and Steady-State Virtual Cathode. Plasma, 7(1), 29-48. https://doi.org/10.3390/plasma7010003






