Abstract
Despite significant interest in their functional properties, the mechanical behavior of high-entropy oxides (HEOs) is not well studied, particularly at elevated temperatures. Bulk (Co,Cu,Mg,Ni,Zn)O (transition metal (TM)-HEO) samples were deformed under compression at applied stresses and temperatures ranging from 5 to 31 MPa and 600 to 850 °C, respectively. All of the deformation conditions result in creep stress exponents of n < 3, indicating that TM-HEO exhibits superplastic deformation. A transition from structural to solution-precipitation-based superplasticity is observed during deformation above 650 °C. Additionally, TM-HEO exhibits shear-thickening behavior when deformed at stresses above 9 MPa. The formation and behavior of a Cu-rich tenorite secondary phase during deformation is identified as a key factor underpinning the deformation mechanisms. The microstructure and phase state of TM-HEO before deformation also influenced the behavior, with finer grain sizes and increasing concentrations of Cu-rich tenorite, resulting in the increased prevalence of solution-precipitation deformation. While complex, the results of this study indicate that TM-HEO deforms through known superplastic deformation mechanisms. Superplasticity is a highly efficient manufacturing method and could prove to be a valuable strategy for forming HEO ceramics into complex geometries.
1. Introduction
Since their discovery in 2016, high-entropy oxides (HEOs) have been intensely researched due to their wide range of properties and behaviors [1]. HEOs typically contain five or more oxide components and form a single-phase solid-solution crystal structure after processing. The large number of elements in HEOs, and their ability to form stable solid solutions, have greatly expanded the compositional design space available to material engineers. As such, HEOs are being studied for a wide range of applications. For example, HEOs have garnered particular attention in battery [2,3] and catalysis applications [4].
Some HEOs have been found to exhibit a reversible phase transformation. For example, the transition metal HEO (Cu, Co, Mg, Ni, Zn)O (referred to here as TM-HEO) segregates a Cu-rich tenorite phase and a Co-rich spinel phase during its transformation [5,6]. This transformation occurs during heat treatment within the temperature window of 650–850 °C. Above 850 °C, TM-HEO returns to its single-phase state consisting of a rocksalt crystal structure. In our previous study, we observed that this phase transformation was sensitive to microstructure, with smaller grain sizes leading to greater amounts of secondary phase forming [6]. We also observed that the phase transformation in nanocrystalline TM-HEO (grain sizes < 100 nm) initiated at temperatures 200 °C lower than their coarse-grain counterparts. Additionally, we have found that the Cu-rich tenorite phase forms ubiquitously in the grain boundaries of TM-HEO [5].
Compared to their functional properties, the mechanical properties of HEOs are not well studied. Through simulations, Pitike et al. found that TM-HEO should exhibit greater ductility compared to other conventional ceramics [7]. Our group confirmed the existence of this ductility by experimentally demonstrating that TM-HEO exhibits significant dislocation activity during deformation at room temperature [8]. While dislocations form readily in coarse-grain TM-HEO, this is not the case in nanocrystalline TM-HEO. We observed that nanocrystalline TM-HEO forms few dislocations and fails primarily through intergranular fracture [8]. This intergranular fracture contributes to TM-HEO exhibiting inverse Hall–Petch behavior at fine grain sizes [9].
Ceramics are known to exhibit a variety of mechanical behaviors at elevated temperatures. A small subset of ceramics has the capacity for superplastic deformation, where the ceramic exhibits substantial plastic deformation without strain localization [10]. Superplasticity represents a potentially revolutionary avenue for fabricating ceramics with complex geometries. Previous studies have demonstrated that ceramics with superplastic behavior can be successfully formed into net-shaped parts. For example, Zhou et al. were able to forge sharp channels into Al2O3-containing carbon nanotubes [11]. Luo et al. successfully formed SiAlON into functional gears [12]. In both scenarios, the superplastically formed parts had smooth surfaces and were defect-free.
In our previous study, we demonstrated that TM-HEO could be formed into net shapes at 800 °C and pressures as low as 70 kPa [13]. Our investigation found that TM-HEO exhibited superplastic deformation facilitated through a solution-precipitation mechanism. Most interestingly, we observed that TM-HEO exhibited shear-thickening-based deformation, which is rare in inorganic solids. However, our previous study only explored a narrow set of deformation conditions, with many details underpinning the deformation behavior of TM-HEO still being unknown. In the present study, we perform compressive deformation experiments on TM-HEO under a wide range of stress and temperature values. We find that TM-HEO exhibits transitions in deformation mechanisms, which are triggered by both stress and temperature. Additionally, we find that some of these deformation mechanisms are sensitive to microstructure. Our findings provide additional insight into the underlying deformation mechanisms operative in TM-HEO, which could facilitate the efficient manufacturing of these important materials.
2. Materials and Methods
2.1. Synthesis and Processing
TM-HEO samples were prepared using solid-state synthesis followed by powder consolidation using sintering. Samples were prepared with a range of grain sizes (coarse, fine, and nanocrystalline) as well as phase states (single-phase and multi-phase). First, the five binary oxide nanopowders of CoO (50 nm, 99.7 wt% purity), CuO (25–55 nm, 99.95%), MgO (50 nm, 99.95%), NiO (18 nm, 99.98%), and ZnO (18 nm, 99.95%) (US Research Nanomaterials, Houston, TX, USA) were blended in equimolar amounts using a mortar and pestle. This blended powder was then planetary ball milled using a Pulverisette 7 planetary ball mill (Fritsch, Idar-Oberstein, Germany) for 3 h at 300 rpm. The powders were suspended in isopropanol and milled using Si3N4 media. The powder was then heat-treated in a furnace at 900 °C for 20 min to complete the solid-state reaction and form TM-HEO. This TM-HEO powder was once again milled in the PBM for 12 h in order to refine the particle size. More details about our powder synthesis and processing procedures can be found in our previous work [6].
These powders were consolidated into cylindrical samples that were approximately 14 mm in diameter and 2 mm in height. Different sintering routes were used to achieve the different desired microstructures. For the coarse-grain samples (CG, target grain size of ~20 μm), the powder was conventionally sintered at 1100 °C for 12 h. For the fine-grain samples (FG, target grain size of ~1 μm), the powders were consolidated using spark plasma sintering (SPS) at 900 °C for 10 min with a heating rate of 200 °C/min. For the nanocrystalline samples (NC, target grain size of ~100 nm), the powder was consolidated using SPS at 700 °C for 10 min with a heating rate of 200 °C/min.
After consolidation, the as-sintered TM-HEO samples were polished down to 1 µm diamond suspension. Density measurements were performed on the polished samples using the Archimedes method at room temperature. Each sample was measured five times in deionized water. The measurements were performed using an AG204 balance (Mettler Toledo, Greifensee, Switzerland) with an accuracy and repeatability of 0.1 mg. All processing routes yielded samples that were fully dense (≥98% ± 1% dense according to Archimedes measurements). Guided by our previous work [6], some of the samples were heat-treated at 700 °C for 12 h to form multi-phase microstructures. These multi-phase samples (-MP) were compared to the as-sintered single-phase (-SP) samples. Heat treatment of the nanocrystalline samples resulted in significant grain growth, and as such, multi-phase nanocrystalline samples were not investigated in this study. The sample labels used in this study, as well as the sample characteristics, are summarized in Table 1.

Table 1.
TM-ESO samples for high-temperature compression tests.
2.2. High-Temperature Compression Experiments
To carry out high-temperature compression experiments, a custom-built high-temperature mechanical testing system was constructed inside an Instron load frame. Custom compression rods were machined out of Inconel 718. A clamshell furnace was used to heat the samples, and the compression rods and Instron load frame were kept cool through two water-cooled adapters that attached to the compression rods. The samples were compressed between Si3N4 platens. These platens were coated in boron nitride lubricant spray before each experiment. The sample–platen assembly was held in place using an Inconel die. A through-hole was drilled into the Inconel die and was used to hold a thermocouple. This thermocouple was positioned to touch the bottom platen and was set ~1 mm away from the sample. Before deformation, the as-fabricated TM-HEO samples were polished down to 1 µm diamond suspension. The cylindrical TM-HEO samples were approximately 14 mm in diameter and 2 mm in height.
Single-phase and multi-phase samples were each compressed at stress values of 5, 9, 13, 20, and 31 MPa and at deformation temperatures ranging from 600 °C to 850 °C in 50 °C increments (with the exception of sample NC-SP, which was deformed at temperatures up to 700 °C to avoid grain growth at elevated temperatures). The samples were first heated to the desired temperature under no load and then allowed to equilibrate at temperature for several minutes. Once the temperature stabilized, a uniaxial pressure was applied to the samples at a rate of 0.5 MPa/min. During preliminary testing, it was found that a steady-state strain rate was achieved after ~5 min at pressure. Based on this short time to achieve steady-state conditions, the samples were held at each pressure for 10 min. All data reported here are based on these 10 min holds at pressure. The samples were deformed continuously with increasing stress values to generate a strain–time curve for each compression experiment. These strain–time curves were then used to calculate the steady-state strain rate at each applied stress. The total experiment time at each temperature was ~2 h. The validity of our high-temperature compression apparatus and testing methods was verified by performing deformation experiments on N-BK7 glass (Schott, Mainz, Germany). These cylindrical glass samples were tested under the same conditions used to test our TM-HEO samples. The deformation behavior of the glass cylinders closely resembles studies presented in the literature [14,15].
2.3. Characterization
X-ray diffraction (XRD) and Rietveld refinement were used to determine if a phase transformation occurred during high-temperature deformation, and how much secondary phase formed during the high-temperature deformation experiments. XRD was performed with a SmartLab X-ray Diffractometer (Rigaku, Tokyo, Japan) with a 2θ range of 30° to 80°. Rietveld refinement was performed on the acquired XRD data using the Maud software (v2.9995) [16] to estimate the relative atomic fraction of the primary rocksalt phase and the secondary Cu-rich tenorite for each test condition.
Scanning electron microscopy (SEM) was used to observe the fracture surfaces of the samples to understand how deformation affected the grain morphology. The fracture surfaces were imaged with a Magellan 400 XHR SEM (FEI, Hillsboro, OR, USA), using an accelerating voltage of 5 kV and a current of 50 pA. The average grain size was calculated from the fracture surface micrographs by measuring the diameter of >300 grains with the FIJI/ImageJ software (v2.9.0) [17]. It is important to note that the various phases observed in TM-HEO are all multi-cation oxides [18]. Consequently, the phases have similar composite Z- numbers, making back-scatter electron microscopy unsuitable for detecting phase contrast in TM-HEO. Energy-dispersive X-ray spectroscopy (EDS) mapping was used to observe the morphology of the secondary phases in the fine-grain TM-ESO before and after high-temperature deformation. Samples were prepared for EDS analysis by polishing down to 1 μm diamond suspensions. The polished samples were mounted onto SEM stubs with colloidal silver paste (Ted Pella Inc., Redding, CA, USA) and sputter-coated with 3 nm of iridium. EDS was performed in a GAIA SEM-FIB microscope (Tescan, Brno, Czech Republic) using a silicon drift detector with an area of 150 mm2 (Oxford Instruments, Abingdon, UK).
3. Results
3.1. Microstructure and Phase State
The microstructure and phase state of the as-sintered samples were controlled through sintering conditions. All as-sintered samples exhibit equiaxed grain structures and full density. As listed in Table 1, the as-sintered single-phase coarse-grain, fine-grain, and nanocrystalline samples (labeled as CG-SP, FG-SP, and NC-SP, respectively) exhibit average grain sizes of 22 ± 10 µm, 1.1 ± 0.3 µm, and 90 ± 60 nm, respectively. Representative fracture surface micrographs are presented in Figure 1. It is important to note that voids visible in the fracture surface micrographs for sample NC-SP are not pores, but are instead caused by bulk material being dislodged during fracture surface preparation. The microstructure–processing relationship observed here is consistent with our previous study [6].

Figure 1.
Fracture surface micrographs of the single-phase fine-grain (FG-SP) and nanocrystalline (NC-SP) samples, both before deformation (as-sintered) and after deformation at 700 °C.
As observed in previous studies [5,6,18], the three as-fabricated samples exhibit the expected single-phase primary rocksalt crystal structure for TM-HEO, and the heat-treated samples exhibit the primary rocksalt phase as well as the Cu-rich tenorite and Co-rich spinel secondary phases. The phase state for samples FG-SP and FG-MP before and after deformation are presented in Figure 2 and Figure 3. We note that the concentration of the Cu-rich tenorite secondary phase is higher than that of the Co-rich spinel secondary phase. Cu-rich tenorite secondary phase is observed in the grain boundaries, whereas the Co-rich spinel secondary phase is only observed in the grain interior [5,18]. Because all of the deformation mechanisms discussed in this study involve deformation facilitated through grain boundary diffusion or related mechanisms, we focus on the Cu-rich tenorite secondary phase and neglect the Co-rich spinel secondary phase in our analysis. Future research should investigate the role of this Co-rich spinel secondary phase on high-temperature deformation by modifying the composition of the TM-HEO such that the Cu-rich tenorite secondary phase formation is suppressed [19].
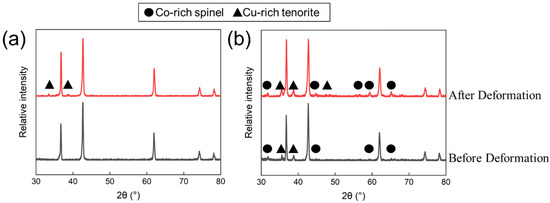
Figure 2.
XRD patterns for the fine-grain (a) single-phase (FG-SP) and (b) multi-phase (FG-MP) samples before and after deformation. Secondary phase peaks are denoted with triangles (Cu-rich tenorite secondary phase) and circles (Co-rich spinel secondary phase).

Figure 3.
Secondary electron (SE) and Cu elemental maps for the fine-grain single-phase (FG-SP) and multi-phase (FG-MP) samples before and after deformation.
3.2. Deformation
Our as-fabricated samples were compressed at applied stresses in the range of 5 to 31 MPa while exposed to temperatures of 600 to 850 °C. These conditions resulted in measurable deformation, which we used to analyze the deformation behavior in TM-HEO. It is important to note that nanocrystalline TM-HEO exhibits significant grain growth when deformed at temperatures above 700 °C. Such grain growth could convolute the identification of the deformation mechanisms in nanocrystalline TM-HEO. Consequently, sample NC-SP was only deformed at 600, 650, and 700 °C. The strain rate was calculated at each applied stress and temperature condition. We observe that the role of stress on strain rate in TM-HEO is dependent on both applied pressure and temperature. For further analysis, we apply the standard Norton power-law creep model [20], which defines the strain rate due to creep as
where A is a constant and n is the stress exponent. Qualitatively, n provides crucial insight into the mechanisms underpinning high-temperature deformation in materials by describing the role of applied stress on strain rate [20].
The role of applied stress on strain rate for samples FG-SP and FG-MP deformed at 600 °C can be seen in Figure 4a. Strain rate increases with increasing stress for both samples. When deformed at 600 °C, both samples exhibit a transition at ~9 MPa, where the role of stress on strain rate changes. This sensitivity to applied stress can be quantified using n from Equation (1). At stresses ≤ 9 MPa, the strain rate is highly sensitive to applied stress, with samples FG-SP and FG-MP having values of n = 2.1 ± 0.3 and 1.4 ± 0.2, respectively. Conversely, at stresses ≥ 13 MPa, the strain rate becomes mostly insensitive to pressure, with both samples exhibiting a stress exponent of n = 0.6 ± 0.1. We note that this transition from stress-sensitive to stress-insensitive was observed in all samples deformed at 600 °C. At stresses ≤ 9 MPa, all samples had values of n = 1 to 2.5, while at stresses ≥ 13 MPa, all samples had values of n = 0.5 to 0.7.
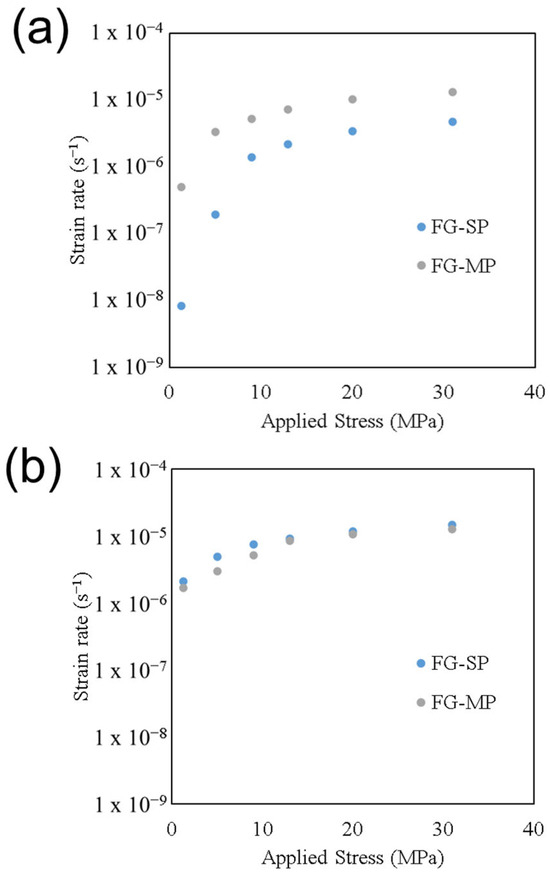
Figure 4.
The role of applied stress on deformation strain rate for the fine-grain single-phase (FG-SP) and multi-phase (FG-MP) samples deformed at (a) 600 °C and (b) 850 °C.
The role of applied stress on strain rate for samples FG-SP and FG-MP deformed at 850 °C can be seen in Figure 4b. Similarly to the deformation at 600 °C, a transition in stress sensitivity is observed between 9 and 13 MPa. The samples deformed at 850 °C exhibit lower overall stress exponents compared to those deformed at 600 °C. At stresses ≤ 9 MPa, the stress exponents are n = 0.4 ± 0.2 for sample FG-SP and n = 0.3 ± 0.1 for sample FG-MP. At stresses ≥ 13 MPa, the stress exponents are n = 0.3 ± 0.1 for sample FG-SP and n = 0.2 ± 0.1 for sample FG-MP. While a decrease in n is observed at stresses ≥ 13 MPa, all of the stress exponent values observed at 850 °C are n < 0.4, making TM-HEO mostly insensitive to stress at this deformation temperature.
We observe that all samples in this study exhibit a transition in stress sensitivity between 5 and 13 MPa regardless of the deformation temperature. The role of temperature on n for every material deformed in this study is shown in Figure 5. For clarity, we divide our analysis into two datasets: stress exponents acquired below the transition (≤9 MPa, Figure 5a) and stress exponents acquired above the transition (≥9 MPa, Figure 5b). The value of n generally decreases with increasing temperature. Below 9 MPa, the stress exponent ranges from n = 1.1 to 2.5 at 600 °C and decreases with increasing temperature, ranging from n = 0.3 to 0.4 at 850 °C. The stress exponent values generally decrease with increasing temperature at stresses > 13 MPa, ranging from n = 0.5 to 0.7 at 600 °C and decreasing to n = 0.2 to 0.3 at 850 °C. Overall, the observed stress exponents vary from n = 0.2 to 2.5 depending on deformation pressure and temperature.
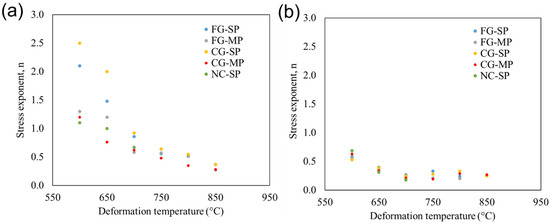
Figure 5.
Role of deformation temperature on stress exponent, n, for deformation (a) below the stress transition (≤9 MPa) and (b) above the stress transition (≥9 MPa).
High-temperature deformation in ceramics is often compensated through diffusion-based mechanisms, making the strain rate highly sensitive to temperature. These diffusion-based deformation mechanisms follow an Arrhenius law, with strain rate having the form of
where T is the temperature during deformation, R is the gas constant, and Q is the activation energy for deformation. The activation energy represents the role of temperature on strain rate. Qualitatively, Q can be used to identify the mechanisms that are contributing to the high-temperature deformation.
The role of temperature on strain rate for samples FG-SP and FG-MP deformed at 9 MPa are shown in the Arrhenius plot in Figure 6a. The strain rate increases with increasing temperature for both samples. Both samples exhibit a transition in temperature dependance at distinct temperatures. This temperature dependance can be quantified using Q from Equation (2). At temperatures ≤ 650 °C, sample FG-SP has a value of Q = 250 ± 70 kJ/mol. At temperatures ≥ 650 °C the activation energy decreases to Q = 95 ± 10 kJ/mol, indicating that there is a significant decrease in temperature sensitivity at higher temperatures. Sample FG-MP has a value of Q = 240 ± 45 kJ/mol at temperatures ≤ 700 °C and Q = 60 ± 5 kJ/mol at temperatures ≥ 700 °C. The role of temperature on strain rate for samples FG-SP and FG-MP deformed at 31 MPa are shown in the Arrhenius plot in Figure 6b. The transition in temperature dependance is much more subtle compared to that observed for the deformation at 9 MPa. Additionally, both samples FG-SP and FG-MP exhibit similar temperature sensitivities under these deformation conditions. At temperatures ≤ 650 °C, both samples have activation energies of Q = ~100 ± 10 kJ/mol. At temperatures ≥ 650 °C their activation energies decrease to Q = ~40 ± 5 kJ/mol.
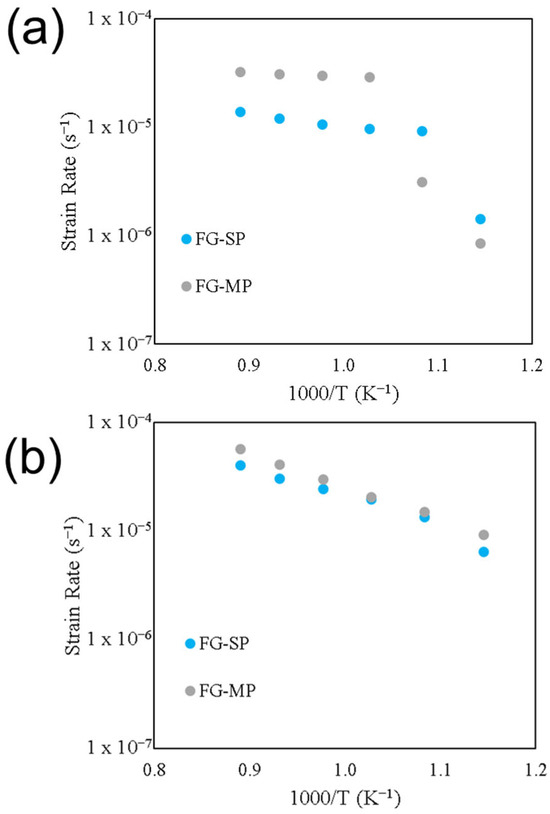
Figure 6.
The role of temperature on the deformation strain rate for the fine-grain single-phase (FG-SP) and multi-phase (FG-MP) samples deformed at (a) 9 MPa and (b) 31 MPa.
We observe that most of the samples in this study exhibit a transition in temperature sensitivity between 650 and 700 °C. The nanocrystalline samples (NC-SP) were not deformed above 700 °C, and thus their temperature transition was not explored in this study. For most samples, this transition is characterized by a higher activation energy below the transition compared to activation energy values above the transition. We observe that the activation energy associated with deformation is highly dependent on applied stress. The role of stress on activation energy can be seen in Figure 7. Deforming TM-HEO at 5 MPa and at temperatures below the temperature transition (Figure 7a) results in activation energies of Q > 150 kJ/mol. The activation energy decreases with increasing pressure, reaching values as low as Q = 50 kJ/mol at 31 MPa. In contrast, deformations above the transition temperature (Figure 7b) are lower, having values of Q = 80 to 150 kJ/mol at 5 MPa and Q = 20 to 50 kJ/mol at 31 MPa.
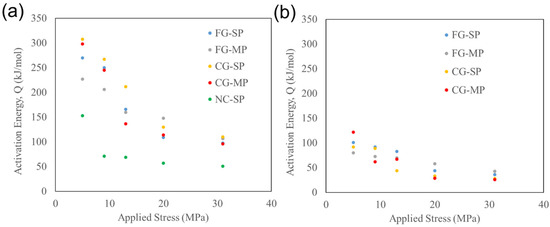
Figure 7.
Role of applied stress on activation energy, Q, for deformation (a) below the transition temperature (≤700 °C) and (b) above the transition temperature (≥700 °C).
3.3. Post-Deformation Microstructure Characterization
The post-deformation microstructure for samples FG-SP and NC-SP can be seen in the fracture surface micrographs in Figure 1. The average grain size in sample FG-SP does not increase during deformation, and the grains retain their equiaxed morphology after deformation. The microstructures of the FG and CG samples look similar before and after deformation, indicating that the deformation process does not meaningfully alter the microstructure. In contrast, the average grain size for sample NC-SP grows from 90 ± 60 nm to 260 ± 140 nm during deformation at 700 °C, as observed in Figure 1. Similarly to the fine-grain samples, the microstructure of sample NC-SP after deformation is also equiaxed. It is also important to note that there is no sign of cavitation or fracture in the microstructure after deformation.
Our previous studies have shown that TM-HEO forms a Cu-rich tenorite secondary phase when heat-treated between 650 and 850 °C [6]. Additionally, our previous study on superplastic deformation in TM-HEO demonstrated that the Cu-rich tenorite phase forms during deformation and influences its mechanical behavior [13]. In the current study, our TM-HEO samples are deformed within the temperature range for Cu-rich tenorite formation. As such, we expect the Cu-rich tenorite secondary phase to form during deformation and play a significant role in the deformation process. XRD patterns for samples FG-SP and FG-MP after deformation at 700 °C are shown in Figure 2. After deformation, sample FG-SP has peaks corresponding to the Cu-rich tenorite phase, indicating that this secondary phase formed during deformation. For sample FG-MP, the intensity of the secondary phase peaks is greater after deformation compared to before deformation, indicating the formation of additional secondary phase during high-temperature deformation. EDS elemental maps for Cu confirm the increased concentration of Cu-rich tenorite secondary phase after high-temperature deformation (Figure 3).
4. Discussion
Our compression experiments indicate that TM-HEO exhibits time-dependent deformation when deformed at elevated temperatures. Time-dependent deformation is common in inorganic solids at elevated temperatures. The two most important categories of time-dependent deformation are creep and superplasticity, both of which have a variety of potential mechanisms. The stress exponent, n (Equation (1)), is an important parameter for identifying deformation mechanisms. For example, creep mechanisms typically have values of n > 3, while superplasticity has values of n < 3. All of the stress exponents observed in this study are n < 3, indicating superplastic deformation. In addition to our deformation behavior, our post-deformation microstructures further support deformation through superplasticity. All of the samples in this study exhibit equiaxed microstructures with no signs of cavitation after deformation, which is a defining feature of superplasticity. We will therefore limit our discussion of deformation in TM-HEO to only superplastic deformation mechanisms.
4.1. Deformation Mechanisms
There are multiple mechanisms that can contribute to superplastic deformation. These mechanisms are defined based on how the grain boundary sliding is accommodated. Each mechanism is characterized by a stress exponent. For example, structural superplasticity, the most common form of superplasticity in ceramics, is characterized by a stress exponent of n = ~2. Structural superplasticity involves grain boundary sliding accommodated by grain boundary diffusion. The strain rate due to structural superplasticity in ionic solids can be estimated by [21]
where Deff is the relevant diffusion coefficient (often the grain boundary diffusion coefficient), d is the grain size, and E is the modulus of elasticity. While the room-temperature elastic modulus of TM-HEO is known (~125 GPa) [9,19], the temperature dependance of the elastic modulus is not known. However, the elastic behavior of MgO, one of the constituents of TM-HEO, has been well studied [22,23]. The room temperature modulus of TM-HEO is known to be lower than MgO [7]. However, TM-HEO and MgO possess similar crystal structures and bonding behavior, and we propose that their mechanical properties will scale similarly with temperature. For our estimations of structural superplasticity (Equation (3)), we assume that the elastic modulus of TM-HEO exhibits the same temperature sensitivity as MgO, leading to an estimated modulus on the order of 10 GPa for TM-HEO under the deformation temperatures used in this study.
As a diffusion-driven process, proper estimation of Deff is important for the accurate estimation of strain rate values due to structural superplasticity. However, the diffusion behavior in TM-HEO is not well studied. Previous work by Grzesik et al. measured the diffusion coefficient of TM-HEO during oxidation and reduction reactions [24]. However, their measured values (8 × 10−8 cm2/s at 700 °C) are very high for a complex oxide, which the authors attribute to the diffusion of oxygen and oxygen defects. Using their diffusion coefficients in Equation (3) results in strain rates more than five orders of magnitude greater than our measured strain rate values. In our previous study, we calculated the diffusion coefficient for the growth of the Cu-rich tenorite secondary phase, finding that it was on the order of Deff = 1 × 10−12 cm2/s at 700 °C [18]. This diffusion coefficient closely resembles the cation diffusion coefficients in CoO (10−11 cm2/s at 700 °C) and MgO (10−14 cm2/s at 700 °C) rocksalt oxides [25,26], indicating that the growth of the Cu-rich tenorite secondary phase in TM-HEO is controlled by cation diffusion. We use this cation-based diffusion coefficient for Deff in our calculations for the following reasons. First, structural superplasticity is rate-limited by the slow-moving element (in this case the cations) along their fastest path [20]. Second, the fastest diffusion path for structural superplasticity is along the grain boundaries, which are known to contain Cu-rich phases in TM-HEO [5].
The results of Equation (3) at 600 and 850 °C, using our previously calculated diffusion coefficients, are shown in Figure 8a and Figure 8b, respectively. The experimentally measured strain rates for sample FG-SP are denoted with filled circles. Our estimated structural superplasticity strain rates closely match the experimental strain rate at 600 °C, indicating that structural superplasticity is likely the dominant deformation mechanism under these conditions. Conversely, our estimated structural superplasticity strain rates overestimate the experimental strain rates at 850 °C, indicating that the dominant deformation mechanism changes at elevated temperatures. As mentioned above, our estimated strain rates due to structural superplasticity use our previously calculated diffusion coefficients, as opposed to the much higher values measured by Grzesik et al. [24]. The close match to our experimentally measured strain rates indicates that structural superplasticity in TM-HEO is dominated by cation diffusion. Such an observation is consistent with observations that structural superplasticity is controlled by the diffusion of the slowest element along its fastest path [19].
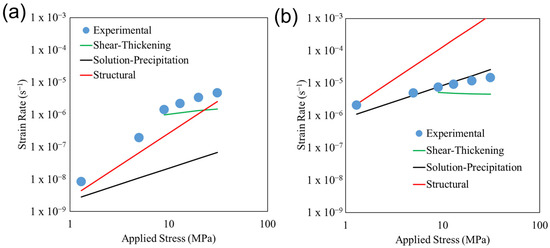
Figure 8.
Role of applied stress on the deformation strain rate for the fine-grain single-phase sample (FG-SP) after deformation at (a) 600 °C and (b) 850 °C. The experimentally determined strain rates (circles) are compared to the strain rates calculated on the basis of the various proposed models (solid lines).
While less common than structural superplasticity, ceramics with stress exponents n ≈ 1 have also been observed. This linear dependance on stress, referred to as Newtonian flow, occurs due to grain boundary sliding accommodated by the action of a secondary phase [27]. The most well-studied Newtonian flow superplastic ceramic is Si3N4, which forms an amorphous (glassy) secondary phase in the grain boundary due to the incorporation of sintering aids [28]. This amorphous phase facilitates grain boundary sliding due to a solution-precipitation mechanism. The solution-precipitation mechanism in Si3N4 operates as follows. Grain boundaries under compression dissolve solute from the Si3N4 phase into the amorphous phase. This solute diffuses through the amorphous phase along the grain boundaries toward grain boundaries under tension. The solute then redeposits back into the Si3N4 phase.
Our previous studies demonstrate that TM-HEO forms a Cu-rich tenorite secondary phase when heat-treated in the temperature range of 600–850 °C [5,6,18]. While the Cu-rich tenorite secondary phase forms throughout the microstructure, it forms most readily in the grain boundaries, leading to an interconnected secondary phase network. While the Cu-rich tenorite secondary phase does not form as a liquid or amorphous phase, we still hypothesize that its presence is influencing the superplastic deformation in TM-HEO. In our previous study, we identified that deformation of TM-HEO at 800 °C occurs through a solution-precipitation method facilitated by the Cu-rich tenorite secondary phase [13].
The strain rate due to the solution-precipitation mechanism can be estimated using [29]
where k is Boltzmann’s constant. The term kt is a rate constant representing the rate of exchange of atoms between the primary phase (rocksalt in TM-HEO) and the secondary phase (Cu-rich tenorite in TM-HEO). For this study, we use the kinetic constant for the coarsening of the Cu-rich tenorite secondary phase determined in our previous study [18]. These kinetic constants were calculated from experimentally measured particle-coarsening data. Our use of these kinetic constants in our calculations is justified since the coarsening of the Cu-rich tenorite phase is based on the diffusion between the Cu-rich tenorite phase and the primary rocksalt TM-HEO phase. We hypothesize that a solution-precipitation-based deformation process could be facilitated through the Cu-rich tenorite phase located in the grain boundaries of TM-HEO. The estimated strain rate derived from Equation (4) is shown in Figure 8. The solution-precipitation model underestimates our experimental strain rates during deformation at 600 °C, indicating that the deformation is not driven by a solution-precipitation mechanism under these conditions. Conversely, the solution-precipitation model closely matches our experimental strain rates during deformation at 850 °C, indicating that the deformation is dominated by the solution-precipitation mechanism at this temperature.
Stress exponent values of n < 1 indicate shear-thickening behavior, where deformation is inhibited by particle–particle friction. Greater applied stresses will result in greater particle–particle friction, and thus, a resistance to deformation. While shear-thickening behavior is common in liquids and slurries, it is comparatively uncommon in bulk ceramic materials. Shear-thickening behavior with a stress exponent of n = 0.5 has been observed in SiAlON [30,31]. The shear-thickening effect occurs in SiAlON due to the applied stress resulting in the amorphous phase being compressed and the thickness of the phase decreasing. This reduction in the thickness of the amorphous phase increases the probability of contact between the SiAlON grains, and in turn, leading to increased friction during deformation. In our previous study, we identified that TM-HEO exhibits shear-thickening behavior during deformation at 800 °C [13].
A defining characteristic of shear-thickening behavior is the observation of a transition stress, σc, above which the shear-thickening behavior becomes active. Previous researchers have observed that shear-thickening behavior occurs in SiAlON at stresses > 20 MPa [30]. At stresses < 20 MPa, SiAlON exhibits Newtonian flow (n = 1). It is important to note that shear-thickening behavior is not an accommodation mechanism for superplastic deformation on its own. Instead, shear-thickening effects modify the stress dependance of existing deformation mechanisms. For example, SiAlON deforms through a solution-precipitation mechanism, even when the applied stress is higher than the transition stress.
The strain rate associated with shear-thickening deformation can be estimated using [28]
where η is the apparent viscosity and σc is the transition stress. The apparent viscosity can be estimated using , which results in values on the order of 1 × 1014 to 1 × 1012 Pa·s. We observe that the transition in the stress exponent (and thus deformation mechanism) occurs between 5 and 13 MPa regardless of the deformation temperature (Figure 4). While we do not know the exact value of transition stress, for our calculations, we assume a value of σc = 9 MPa (halfway between 5 and 13 MPa). We note that selecting a different transition stress value between 5 and 13 MPa does not meaningfully alter our results and interpretation of the data. Using Equation (5), we calculate the strain rate due to shear-thickening at deformation stresses ≥ 9 MPa (Figure 8). Our estimated strain rates closely match our measured strain rates, indicating that shear-thickening is influencing the high-temperature deformation behavior at pressures > σc.
While the stress exponent, n, reflects the stress dependance of the strain rate, it also provides insight into the operative deformation mechanisms. Changes in n imply that the deformation mechanism is changing. For most inorganic solids, n increases with increasing pressure and increasing temperature [20]. For example, in many superplastic alloys, n will increase with increasing temperature due to a transition from structural superplasticity to power-law creep [32]. In contrast, n values for shear-thickening in Si3N4 are not sensitive to temperature, indicating that the shear-thickening mechanism is stable across a range of temperatures [30]. TM-HEO exhibits the opposite behavior, with n decreasing with increasing deformation temperature (Figure 5).
We observe a change in the activation energy associated with deformation at approximately 650 to 700 °C (Figure 6). We refer to this temperature as the “transition temperature”. Based on our comparison to existing superplasticity models (Figure 8), we determine that TM-HEO deforms through structural superplasticity below the transition temperature and solution-precipitation above the transition temperature. However, the results in Figure 5 show a gradual decline in n with increasing temperature, and not a discrete transition. As temperature increases, the deformation mechanism gradually transitions from structural superplasticity deformation to solution-precipitation. Similar transition behavior with temperature has been observed in Si3N4 ceramics [33]. The extent of our observed decrease in n with temperature is dependent on the applied stress. The decline in n is most pronounced when TM-HEO is deformed below the stress transition (Figure 5a). Above the stress transition, n decreases with increasing deformation temperature up to 700 °C. The values for n do not change significantly above 700 °C. This more muted decrease above the stress transition is due to the influence of the shear-thickening behavior. Above the stress transition, the high-temperature deformation behavior in TM-HEO is dictated by the shear-thickening behavior, which is mostly insensitive to temperature.
As a diffusion-driven process, superplastic deformation in ceramics is often highly sensitive to temperature, with higher temperatures leading to greater strain rates (Equation (2)). As expected, increasing deformation temperature leads to increasing strain rates during the deformation of TM-HEO (Figure 4). Unexpectedly, however, our TM-HEO samples exhibit a transition in temperature sensitivity (activation energy) above 650 to 700 °C. We observe this transition in all samples except for sample NC-SP. At temperatures below this transition, the deformation in TM-HEO is highly sensitive to temperature. Above the temperature transition, the deformation becomes comparatively insensitive to temperature.
The samples with as-fabricated grain sizes of 1.1 μm (FG-SP and FG-MP) and 22 μm (CG-SP and CG-MP) exhibit activation energy values of 230 to 310 kJ/mol when deformed below the transition temperature at 5 MPa. These activation energy values fall within the range of activation energies associated with diffusion in rocksalt-structured MgO, indicating that the high-temperature deformation is compensated by cation diffusion in the rocksalt structure. As described above, we hypothesize that TM-HEO exhibits structural superplasticity when deformed below the stress and temperature transitions. Our measured activation energies further support our conclusion that structural superplasticity is operative under these conditions.
The samples with as-fabricated grain sizes of 1.1 μm (FG-SP and FG-MP) and 22 μm (CG-SP and CG-MP) exhibit activation energy values of 80 to 120 kJ/mol when deformed above the transition temperature at 5 MPa. These activation energy values fall within the range of activation energies associated with diffusion in copper oxides [34,35]. Our TM-HEO samples form a Cu-rich tenorite secondary phase when exposed to temperatures between 650 and 850 °C [6]. Additionally, the Cu-rich tenorite secondary phase forms most readily in the grain boundaries. Our measured strain rates closely resemble those expected from a solution-precipitation mechanism (Figure 8). From our measured activation energies, we propose that above the transition temperature, TM-HEO deforms though a solution-precipitation mechanism involving the Cu-rich tenorite secondary phase at the grain boundaries. This secondary phase then acts as a solvent during high-temperature deformation, dissolving, transporting, and reprecipitating the TM-HEO phase.
Activation energy decreases with increasing pressure for all of the samples measured in this study. Below the transition temperature, the activation energy is as low as Q = 50 kJ/mol. Above the transition temperature the activation energy is as low as Q = 20 kJ/mol at 31 MPa. Such low activation energies are not commonly observed during superplastic deformation of ceramics, and do not correspond to any relevant diffusion scenario. However, low activation energies for deformation are commonly observed in shear-thickening slurries, such as melts containing slag (~40 kJ/mol) [36] and polymer slurries with high solid loading (40–70 kJ/mol) [37]. In shear-thickening slurries, these low activation energies are interpreted as the deformation being insensitive to temperature. The flow of these slurries is restricted by friction between the solid particles, which, even at elevated temperatures, dominates the rheological behavior.
We hypothesize that the deformation in TM-HEO exhibits shear-thickening behavior above the transition stress. Our observation of low activation energies above the transition stress further supports this argument. The transition to shear-thickening behavior would be expected to be discrete in materials with uniform grain size and morphology, occurring at a specific value of stress where particle–particle friction initiates. However, real materials will have a distribution of grain sizes and morphologies and, therefore, the influence of shear-thickening will occur gradually as stress increases. We propose that the decrease in activation energy with increasing pressure occurs due to the shear-thickening behavior becoming more important as the pressure increases.
4.2. Role of Microstructure on Deformation
Structural superplastic deformation is known to be highly dependent on microstructure. The role of grain size on superplastic deformation has been well studied, with smaller grain sizes leading to increased strain rates. For example, Wakai found that decreasing the grain size of yttria stabilized zirconia from 2.6 μm to 0.5 μm and increased the strain rate by one order of magnitude during deformation at 10 MPa [38]. Various researchers demonstrated strain rates on the order of 10−2 s−1 in fine-grain ceramics [39]. For example, Kim et al. achieved strain rates on the order of 10−1 s−1 in a ceramic composite consisting of tetragonal zirconium oxide, magnesium aluminate spinel, and alumina, all with grain sizes < 300 nm [40]. Additionally, reducing the grain size can reduce the temperature required for superplastic formation. For example, CaF2 and TiO2 with grain sizes on the order of <10 nm were found to deform at temperatures as low as 80 °C and 180 °C, respectively [41].
In contrast to structural superplasticity, solution-precipitation deformation is less sensitive to grain size. For example, Xu et al. performed superplastic deformation experiments on Si3N4 with grain sizes as small as 70 nm [42]. They observed strain rates on the order of 10−4 s−1, compared to 10−6 s−1 observed in Si3N4 having grain sizes of 1 μm [28]. While not intensely studied, grain size is thought to have little-to-no influence on shear-thickening behavior [30]. It is important to note that shear-thickening does not directly accommodate superplastic deformation on its own. Shear-thickening only modulates the stress dependance of the operative deformation mechanism, usually solution-precipitation-based deformation. Thus, any observed influence of grain size on deformation in shear-thickening materials is the result of the underlying accommodation mechanism, and not the role of shear-thickening directly. For example, Wananuruksawong et al. found that finer grain sizes increased the observed strain rates in SiAlON due to solution-precipitation deformation but did not directly modify the shear-thickening behavior [43].
However, changes in grain size can also lead to changes in the deformation mechanisms, such as the transition from creep to superplastic deformation mechanisms with decreasing grain size in many metals [19]. Such changes in the mechanism with changes in grain size occur in both engineering materials as well as geological materials [44]. We observe a decrease in n value with decreasing grain size during high-temperature deformation of TM-HEO below the transition stress and transition temperature (Figure 5). While the change in n between sample CG-SP (22 ± 10 µm grain size) and sample FG-SP (1.1 ± 0.3 µm grain size) is relatively small (n = 2.5 to 2.1), there is a substantial decrease in n for sample NC-SP (n = 1.1), implying a change in the high-temperature deformation mechanism.
While superplastic deformation is highly sensitive to grain size, the activation energies for deformation are often not strongly influenced by grain size. Superplasticity in ceramics is facilitated through one or more diffusion mechanisms, making the activation energy a reflection of the rate-limiting diffusion mechanism. As such, changes in grain size would not be expected to influence activation energy unless there was a change in the mechanism. While there is little difference in activation energies between sample FG-SP (Q = 240 to 270 kJ/mol) and sample CG-SP (Q = 270 to 310 kJ/mol), the activation energy for deformation in sample NC-SP (70–150 kJ/mol) is significantly lower at all applied stresses. The observed decrease in activation energy in sample NC-SP indicates the emerging influence of another deformation mechanism. We do not observe a grain size dependance in activation energy during deformation above the transition temperature.
The presence of secondary phases is known to influence superplastic behavior. The most common example of this is the use of Zener-pinning particles, which limit grain growth and extend the duration of superplastic formation [20]. In ceramics such as ZrO2 and Si3N4, the presence of an amorphous phase in the grain boundary is known to enhance superplastic deformation [28,45]. In TM-HEO, we attribute the solution-precipitation and shear-thickening-based superplastic behavior to the presence of the Cu-rich tenorite secondary phase, which forms during heating. As a result, it would be expected that the amount of Cu-rich tenorite secondary phase in TM-HEO would directly influence the high-temperature deformation mechanisms. During deformation at 600 to 650 °C (below the stress transition), samples FG-SP and CG-SP exhibit higher stress exponents of n ≥ 1.5 compared to their multi-phase counterparts, which exhibit stress exponents of n = 0.7 to 1.2 (Figure 5). From this comparison, it might be expected that the single-phase samples deform through a structural superplasticity mechanism below the stress and temperature transition, while the multi-phase samples deform through a solution-precipitation mechanism. However, under these conditions, there is little difference between the activation energies of the four samples (Figure 7), indicating that the phase state is not changing the dominant deformation mechanism. We hypothesize that both structural and solution-precipitation superplastic deformation mechanisms are operative in the multi-phase samples under these conditions.
In our previous study, we observed that smaller grain sizes lead to increased secondary phase formation and enhanced transformation kinetics in TM-HEO, with nanocrystalline samples exhibiting transformation temperatures 200 °C lower compared to their coarse-grain counterparts [6,18]. We attributed this increase in transformation kinetics to the higher concentration of grain boundaries in the nanocrystalline samples, with the Cu-rich tenorite secondary phase forming most readily on the grain boundaries. We would, therefore, expect significantly more Cu-rich tenorite secondary phase to form during deformation in sample NC-SP compared to in the samples with larger grain sizes. For samples FG-SP and CG-SP, the observed deformation behavior fits well with a structural superplasticity model. However, the significantly lower activation energy and stress exponent (Figure 5 and Figure 7) in sample NC-SP indicates the emerging influence of another deformation mechanism with a lower activation energy. We propose that nanocrystalline TM-HEO deforms through the solution-precipitation mechanism instead of through a structural superplasticity mechanism.
The solution-precipitation mechanism requires a secondary phase in the grain boundaries. The high grain boundary concentration, and thus high Cu-rich tenorite concentration, will result in the deformation in nanocrystalline TM-HEO being predominantly facilitated by solution-precipitation through the Cu-rich tenorite grain boundary secondary phase. While the nanocrystalline grain size results in a transition to a new deformation mechanism, it does not alter the shear-thickening transition also observed in the samples with larger grain sizes. The deformation behavior of the nanocrystalline sample is significant in that it demonstrates that the role of as-fabricated grain size on deformation mechanisms in TM-HEO is not straightforward. Instead, there is an interplay between grain size, phase transformation, and deformation behavior that needs to be further investigated.
4.3. Deformation Mechanism Map
In our previous study, we demonstrated that superplastic deformation was a viable method of forming TM-HEO into net-shaped parts [13]. The present study provides insight into the mechanisms underpinning that superplastic deformation. While complex, TM-HEO deforms through known superplasticity mechanisms. As a result, the high-temperature deformation of TM-HEO can be modeled and predicted using existing equations. Combining Equations (1) and (2) results in the full temperature-dependent Norton model:
where B is a constant and A ≠ B. Our experimental high-temperature deformation results show that both n and Q are stress- and temperature-dependent. Additionally, the dependance of these values changes depending on the stress and temperature regime used during deformation, and the resulting operative deformation mechanisms.
Using Equation (6), we calculate the expected strain rates during the deformation of TM-HEO. Lines of constant strain rate (strain rate contours) are presented in the form of an experimentally derived Ashby deformation mechanism map, as seen in Figure 9 [32]. It is important to note that Ashby deformation mechanism maps are commonly prepared using the equations associated with the deformation model (such as Equations (3)–(5) in this study). However, TM-HEO exhibits superplastic deformation modified by shear-thickening behavior. It is currently unknown how to calculate the combined effects of superplastic deformation and shear-thickening. As a result, our deformation mechanism map is prepared by applying regression analysis to the experimental data. The solid red lines in Figure 9 denote the estimated transition stress and transition temperature values used in this study. We note that the transition stress and transition temperature values are not calculated but are instead estimated based on experimental observations. The gray box in Figure 9 denotes the stress and temperature values investigated experimentally in this study. All data outside the gray box are extrapolated based on the experimental data. To our knowledge, this is the first report of such a deformation mechanism map for a high-entropy ceramic.
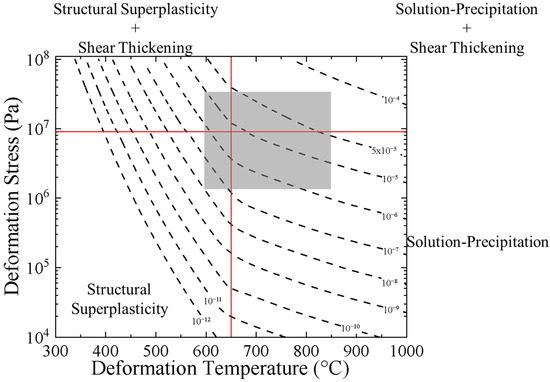
Figure 9.
Experimentally derived Ashby deformation mechanism map for the fine-grain single-phase sample (FG-SP). Dashed lines correspond to lines of constant strain rate (strain rate contours). Solid red lines denote the estimated transition stress and transition temperature used in this study, which are used to divide the deformation diagrams into quadrants based on the predominant deformation mechanisms. The gray box denotes the stress and temperature values investigated in this study. All data outside the gray box are extrapolated based on the experimental data.
Our experimentally derived Ashby deformation mechanism map can be used to estimate the deformation conditions required to form TM-HEO at specific strain rates. Additionally, a qualitative examination of the map can provide some insight on how the high-temperature deformation in TM-HEO differs from other materials. In particular, the relative positioning of the strain rate contours differs compared to other materials. The strain rate contours in TM-HEO become further spread apart from one another as the temperature and pressure increase (the upper-right quadrant of the map), indicating that higher stress and temperature are required to increase strain rate. Most metals exhibit the opposite behavior. The strain rate contours in metals group closer together as temperature and stress increase due to the transition to power-law creep and the activation of dynamic recrystallization [32].
In contrast to metals, ceramics often have highly complex deformation mechanism maps due to their limited dislocation plasticity and more complex diffusion. However, similar to TM-HEO, many ceramics exhibit strain rate contours that spread apart as stress and temperature increase [46]. This increasing spread in strain rate contours in ceramics is often attributed to changes in defect chemistry with temperature. In MgO, for example, increasing temperature leads to a transition in the dominant defects [47]. As a result, the diffusion of oxygen becomes rate-limiting at high temperatures, decreasing the temperature sensitivity of creep in MgO. We can rule out a similar defect-induced transition in TM-HEO for two reasons. First, in contrast to MgO, TM-HEO has been shown to predominantly form oxygen vacancies as its primary defect throughout the temperature range used in this study [24]. Second, the activation energies we observe above the transition temperature are much lower than the activation energy for any known diffusion mechanism in a rocksalt oxide [25,26].
5. Conclusions
Bulk TM-HEO samples were prepared with variable grain sizes and as-fabricated phase states. These TM-HEO samples were deformed in compression under an applied stress of 5 to 31 MPa and temperatures ranging from 600 to 850 °C. Under all deformation conditions, these TM-HEO samples exhibited stress exponents of n < 3, indicating that the deformation occurred through superplasticity. Notably, the mechanism facilitating the superplastic deformation varied based on the temperature and stress. At stresses ≤ 9 MPa and temperatures ≤ 650 °C, the values of the stress exponent (n = 1 to 2.5) and activation energy (230 to 310 kJ/mol) indicate that the deformation proceeds through a structural superplastic deformation mechanism. A transition to a solution-precipitation mechanism is observed for deformation at temperatures > 650 °C. We attribute this transition to the observed formation of the Cu-rich tenorite secondary phase during deformation. The deformation in TM-HEO exhibits shear-thickening behavior at applied stress values > 9 MPa. The as-fabricated microstructure influences the deformation behavior, with smaller grain sizes and greater quantities of secondary phase leading to an increased prevalence of solution-precipitation deformation. From our current understanding of the deformation mechanisms, we are able to construct a deformation mechanism map for TM-HEO, the first of its kind for a high-entropy ceramic. Our mechanism map allows for the deformation behavior of TM-HEO to be predicted across a wide range of deformation conditions. Additional variables should be investigated in future research, including chemical compositions beyond the equimolar composition, a wider range of grain sizes, pressures, and temperatures, and alternative sample geometries, to further elucidate and confirm these deformation mechanisms.
Author Contributions
Conceptualization, J.M.S. and A.D.D.; methodology, S.E.-A. and A.D.D.; formal analysis, S.E.-A. and A.D.D.; investigation, S.E.-A., S.C. and A.D.D.; writing—original draft preparation, S.E.-A. and A.D.D.; writing—review and editing, J.M.S. and A.D.D.; supervision, J.M.S. and A.D.D.; project administration, J.M.S. and A.D.D.; funding acquisition, J.M.S. All authors have read and agreed to the published version of the manuscript.
Funding
The authors acknowledge support from the National Science Foundation (NSF) awards CMMI-2029966 and CMMI-2414950. S.E.-A. is thankful for support from NSF award DGE-1839285, the ARCS Foundation, and the University of California, Irvine (UC Irvine) Provost Ph.D. Fellowship. The use of instrumentation and facilities at the University of California, Irvine Materials Research Institute (IMRI), which is partially supported by NSF DMR-2011967, is also acknowledged.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Rost, C.M.; Sachet, E.; Borman, T.; Moballegh, A.; Dickey, E.C.; Hou, D.; Jones, J.L.; Curtarolo, S.; Maria, J.-P. Entropy-Stabilized Oxides. Nat. Commun. 2015, 6, 8485. [Google Scholar] [CrossRef] [PubMed]
- Sarkar, A.; Wang, Q.; Schiele, A.; Chellali, M.R.; Bhattacharya, S.S.; Wang, D.; Brezesinski, T.; Hahn, H.; Velasco, L.; Breitung, B. High-Entropy Oxides: Fundamental Aspects and Electrochemical Properties. Adv. Mater. 2019, 31, 1806236. [Google Scholar] [CrossRef] [PubMed]
- Sarkar, A.; Velasco, L.; Wang, D.; Wang, Q.; Talasila, G.; de Biasi, L.; Kübel, C.; Brezesinski, T.; Bhattacharya, S.S.; Hahn, H.; et al. High Entropy Oxides for Reversible Energy Storage. Nat. Commun. 2018, 9, 3400. [Google Scholar] [CrossRef] [PubMed]
- Albedwawi, S.H.; AlJaberi, A.; Haidemenopoulos, G.N.; Polychronopoulou, K. High Entropy Oxides-Exploring a Paradigm of Promising Catalysts: A Review. Mater. Des. 2021, 202, 109534. [Google Scholar] [CrossRef]
- Dupuy, A.D.; Schoenung, J.M. Morphological Evolution in Nanostructured Secondary Phases in Entropy Stabilized Oxides. Mater. Charact. 2022, 193, 112301. [Google Scholar] [CrossRef]
- Dupuy, A.D.; Wang, X.; Schoenung, J.M. Entropic Phase Transformation in Nanocrystalline High Entropy Oxides. Mater. Res. Lett. 2019, 7, 60–67. [Google Scholar] [CrossRef]
- Pitike, K.C.; Marquez-Rossy, A.E.; Flores-Betancourt, A.; Chen, D.X.; Santosh, K.; Cooper, V.R.; Lara-Curzio, E. On the Elastic Anisotropy of the Entropy-Stabilized Oxide (Mg, Co, Ni, Cu, Zn)O Compound. J. Appl. Phys. 2020, 128, 015101. [Google Scholar] [CrossRef]
- Wang, X.; Cortez, J.; Dupuy, A.D.; Schoenung, J.M.; Bowman, W.J. High Entropy Oxide (Co,Cu,Mg,Ni,Zn)O Exhibits Grain Size Dependent Room Temperature Deformation. Mater. Res. Lett. 2023, 11, 196–204. [Google Scholar] [CrossRef]
- Cortez, J.; Dupuy, A.D.; Vahidi, H.; Donaldson, O.K.; Bowman, W.J.; Rupert, T.J.; Schoenung, J.M. Grain Size Dependent Indentation Response of Single-Phase (CoCuMgNiZn)O High Entropy Oxides. J. Eur. Ceram. Soc. 2024, 44, 116673. [Google Scholar] [CrossRef]
- Maehara, Y.; Langdon, T.G. Superplasticity in Ceramics. J. Mater. Sci. 1990, 25, 2275–2286. [Google Scholar] [CrossRef]
- Zhou, X.; Li, L.; Shen, L.; Zhou, J.; Zhang, J.; Mukherjee, A.K.; Xiang, C.; Tang, H.; Huang, Q. Superplastic Behavior of Alumina Composites Mediated by Carbon Nanotubes. Nanomicro Lett. 2013, 5, 174–181. [Google Scholar] [CrossRef]
- Luo, J.; Xi, C.; Gu, Y.; Zhang, L.; Zhang, C.; Xue, Y.; Liu, R. Superplastic Forging for Sialon-Based Nanocomposite at Ultralow Temperature in the Electric Field. Sci. Rep. 2019, 9, 2452. [Google Scholar] [CrossRef]
- Dupuy, A.D.; Schoenung, J.M. Low-Temperature Superplastic Forming of High-Entropy Oxides. Adv. Eng. Mater. 2025, e202500769. [Google Scholar] [CrossRef]
- Ding, L.; Thieme, M.; Demouchy, S.; Kunisch, C.; Kaus, B.J.P. Effect of Pressure and Temperature on Viscosity of a Borosilicate Glass. J. Am. Ceram. Soc. 2018, 101, 3936–3946. [Google Scholar] [CrossRef]
- Ding, L.; Qu, C.; Yang, Y.; Wilkinson, C.J.; Lee, K.; DeCeanne, A.V.; Doss, K.; Mauro, J.C. Dilatometric Fragility and Prediction of the Viscosity Curve of Glass-forming Liquids. J. Am. Ceram. Soc. 2020, 103, 4248–4255. [Google Scholar] [CrossRef]
- Lutterotti, L.; Bortolotti, M.; Ischia, G.; Lonardelli, I.; Wenk, H.-R. Rietveld Texture Analysis from Diffraction Images. Z. Krist. Suppl. 2007, 26, 125–130. [Google Scholar] [CrossRef]
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Preibisch, S.; Rueden, C.; Saalfeld, S.; Schmid, B.; et al. Fiji: An Open-Source Platform for Biological-Image Analysis. Nat. Methods 2012, 9, 676–682. [Google Scholar] [CrossRef] [PubMed]
- Dupuy, A.D.; Chellali, M.R.; Hahn, H.; Schoenung, J.M. Nucleation and Growth Behavior of Multicomponent Secondary Phases in Entropy-Stabilized Oxides. J. Mater. Res. 2023, 38, 198–214. [Google Scholar] [CrossRef]
- El-Azab, S.A.; Norman, J.E.; Gomez, L.; Dupuy, A.D.; Schoenung, J.M. Dislocation-Mediated Room-Temperature Mechanical Behavior of Multiphase Entropy Stabilized Oxides. Acta Mater. 2024, 281, 120428. [Google Scholar] [CrossRef]
- Padmanabhan, K.A.; Balasivanandha Prabu, S.; Mulyukov, R.R.; Nazarov, A.; Imayev, R.M.; Chowdhury, S.G. Superplasticity; Engineering Materials; Springer: Berlin/Heidelberg, Germany, 2018; ISBN 978-3-642-31956-3. [Google Scholar]
- Wakai, F.; Kato, H. Superplasticity of TZP/Al2O3 Composite. Adv. Ceram. Matter 1988, 3, 71–76. [Google Scholar] [CrossRef]
- Rijal, A.; Cobden, L.; Trampert, J.; Marquardt, H.; Jackson, J.M. Shear Properties of MgO Inferred Using Neural Networks. Eur. J. Miner. 2023, 35, 45–58. [Google Scholar] [CrossRef]
- Soga, N.; Anderson, O.L. High-Temperature Elastic Properties of Polycrystalline MgO and Al2O3. J. Am. Ceram. Soc. 1966, 49, 355–359. [Google Scholar] [CrossRef]
- Grzesik, Z.; Smoła, G.; Stygar, M.; Dąbrowa, J.; Zajusz, M.; Mroczka, K.; Danielewski, M. Defect Structure and Transport Properties in (Co,Cu,Mg,Ni,Zn)O High Entropy Oxide. J. Eur. Ceram. Soc. 2019, 39, 4292–4298. [Google Scholar] [CrossRef]
- Mrowec, S.; Grzesik, Z. The Influence of Chromium on the Defect Structure and Their Mobility in Nonstoichiometric Cobaltous Oxide. J. Phys. Chem. Solids 2003, 64, 1387–1394. [Google Scholar] [CrossRef]
- Wuensch, B.J.; Vasilos, T. Diffusion of Transition Metal Ions in Single-Crystal MgO. J. Chem. Phys. 1962, 36, 2917–2922. [Google Scholar] [CrossRef]
- de Arellano-López, A.R.; Meléndez-Martínez, J.J.; Cruse, T.A.; Koritala, R.E.; Routbort, J.L.; Goretta, K.C. Compressive Creep of Mullite Containing Y2O3. Acta Mater. 2002, 50, 4325–4338. [Google Scholar] [CrossRef]
- Melendez-Martinez, J.J.; Dominguez-Rodriguez, A. Creep of Silicon Nitride. Prog. Mater. Sci. 2004, 49, 19–107. [Google Scholar] [CrossRef]
- Raj, R.; Chyung, C.K. Solution-Precipitation Creep in Glass Ceramics. Acta Met. 1981, 29, 159–166. [Google Scholar] [CrossRef]
- Chen, I.; Hwang, S. Shear Thickening Creep in Superplastic Silicon Nitride. J. Am. Ceram. Soc. 1992, 75, 1073–1079. [Google Scholar] [CrossRef]
- Chen, C.; Chuang, T. Improved Analysis for Flexural Creep with Application to Sialon Ceramics. J. Am. Ceram. Soc. 1990, 73, 2366–2373. [Google Scholar] [CrossRef]
- Ashby, M.F. A First Report on Deformation-Mechanism Maps. Acta Met. 1972, 20, 887–897. [Google Scholar] [CrossRef]
- Santos, C.; Strecker, K.; Barboza, M.J.R.; Piorino Neto, F.; Silva, O.M.M.; Silva, C.R.M. Compressive Creep Behavior of Hot-Pressed Si3N4 Ceramics Using Alumina and a Rare Earth Solid Solution as Additives. Int. J. Refract. Met. Hard Mater. 2005, 23, 183–192. [Google Scholar] [CrossRef]
- Rebane, J.A.; Yakovlev, N.V.; Chicherin, D.S.; d Tretyakov, Y.; Leonyuk, L.I.; Yakunin, V.G. An Experimental Study of Copper Self-Diffusion in CuO, Y2Cu2O5 and YBa2Cu3O7−x by Secondary Neutral Mass Spectrometry. J. Mater. Chem. 1997, 7, 2085–2089. [Google Scholar] [CrossRef]
- Freer, R. Self-Diffusion and Impurity Diffusion in Oxides. J. Mater. Sci. 1980, 15, 803–824. [Google Scholar] [CrossRef]
- Mehdizadeh, H.; Najafi Kani, E. Rheology and Apparent Activation Energy of Alkali Activated Phosphorous Slag. Constr. Build. Mater. 2018, 171, 197–204. [Google Scholar] [CrossRef]
- Laun, H.M.; Bung, R.; Schmidt, F. Rheology of Extremely Shear Thickening Polymer Dispersions a) (Passively Viscosity Switching Fluids). J. Rheol. 1991, 35, 999–1034. [Google Scholar] [CrossRef]
- Wakai, F.; Nagono, T. The Role of Interface-Controlled Diffusion Creep on Superplasticity of Yttria-Stabilized Tetragonal ZrO2 Polycrystals. J. Mater. Sci. Lett. 1988, 7, 607–609. [Google Scholar] [CrossRef]
- Hiraga, K.; Kim, B.-N.; Morita, K.; Yoshida, H.; Suzuki, T.S.; Sakka, Y. High-Strain-Rate Superplasticity in Oxide Ceramics. Sci. Technol. Adv. Mater. 2007, 8, 578–587. [Google Scholar] [CrossRef]
- Kim, B.-N.; Hiraga, K.; Morita, K.; Sakka, Y. A High-Strain-Rate Superplastic Ceramic. Nature 2001, 413, 288–291. [Google Scholar] [CrossRef] [PubMed]
- Karch, J.; Birringer, R.; Gleiter, H. Ceramics Ductile at Low Temperature. Nature 1987, 330, 556–558. [Google Scholar] [CrossRef]
- Xu, X.; Nishimura, T.; Hirosaki, N.; Xie, R.-J.; Yamamoto, Y.; Tanaka, H. Superplastic Deformation of Nano-Sized Silicon Nitride Ceramics. Acta Mater. 2006, 54, 255–262. [Google Scholar] [CrossRef]
- Wananuruksawong, R.; Shinoda, Y.; Akatsu, T.; Wakai, F. High-Strain-Rate Superplasticity in Nanocrystalline Silicon Nitride Ceramics under Compression. Scr. Mater. 2015, 103, 22–25. [Google Scholar] [CrossRef]
- Hansen, L.N.; Zimmerman, M.E.; Kohlstedt, D.L. Grain Boundary Sliding in San Carlos Olivine: Flow Law Parameters and Crystallographic-Preferred Orientation. J. Geophys. Res. 2011, 116, B08201. [Google Scholar] [CrossRef]
- Langdon, T.G. Transitions in Creep Behavior. Mater. Trans. JIM 1996, 37, 359–362. [Google Scholar] [CrossRef]
- Frost, H.J.; Ashby, M.F. Deformation-Mechanism Maps: The Plasticity and Creep of Metals and Ceramics; Franklin Book Company: Dallas, TX, USA, 1995. [Google Scholar]
- Chiang, Y.-M.; Birnie, D.P.; Kingery, W.D. Physical Ceramics: Principles for Ceramic Science and Engineering; Wiley: Hoboken, NJ, USA, 1996. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).