Experimental and Numerical Validation of an Extended FFR Model for Out-of-Plane Vibrations in Discontinuous Flexible Structures
Abstract
1. Introduction
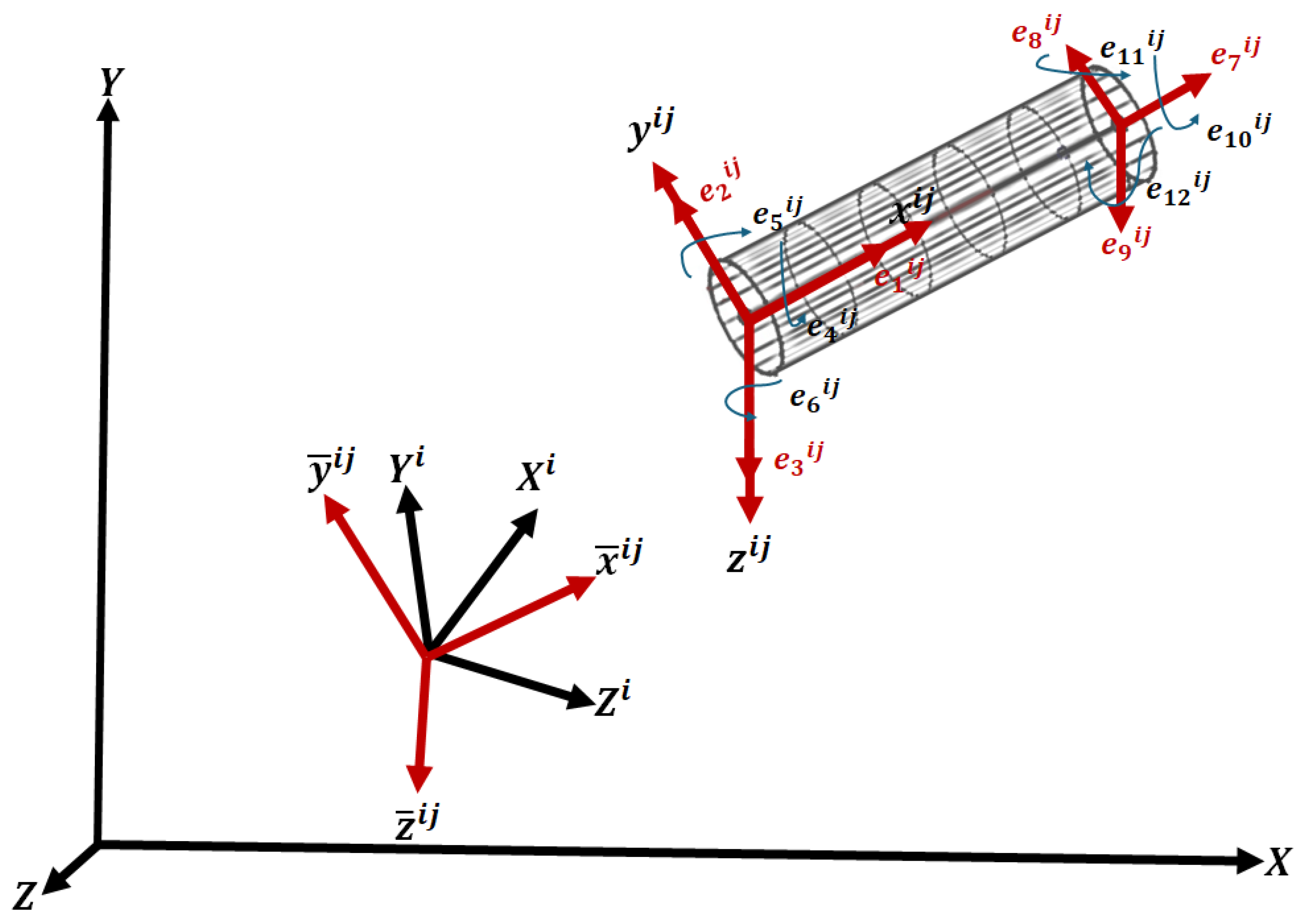
2. Floating Frame of Reference Formulation
Slope Discontinuity
3. Experimental Study
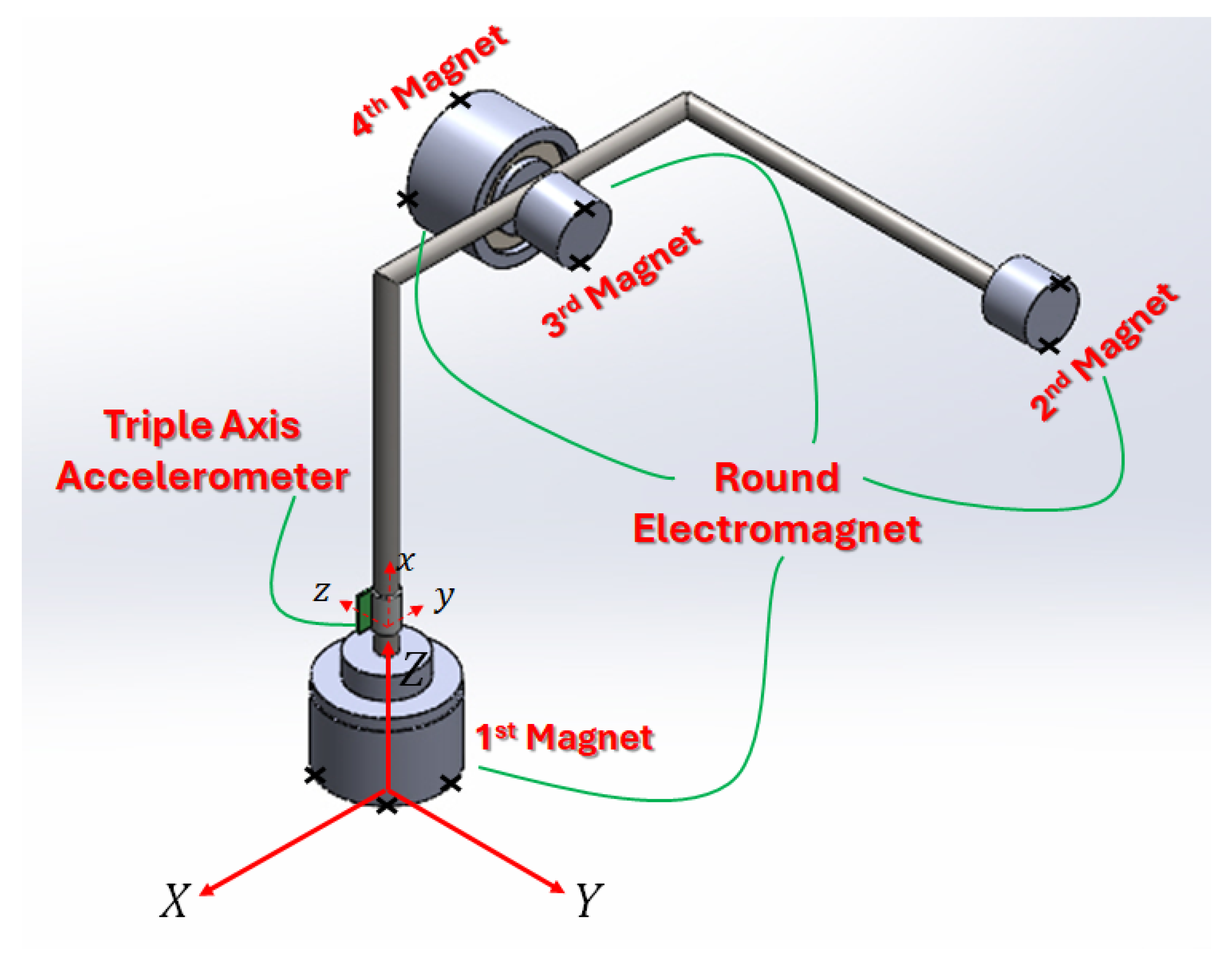
3.1. Experimental Validation
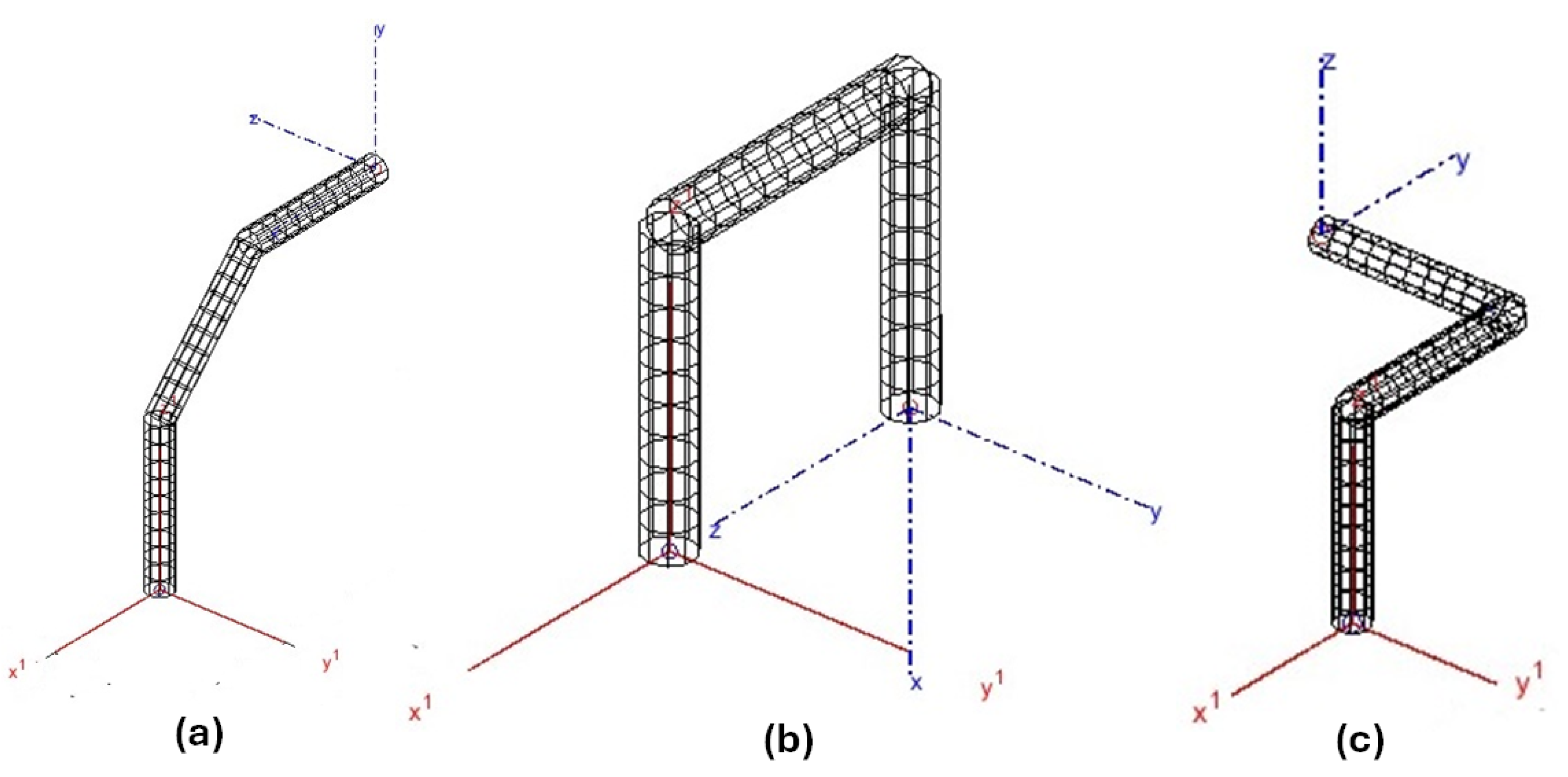
3.2. Finite Element Verification of Modal Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
Abbreviations
| ANCF | Absolute Nodal Coordinate Formulation |
| FEA | Finite Element Analysis |
| FFT | Fast Fourier Transform |
| FFR | Floating Frame of Reference |
| FMBSs | Flexible MultiBody Systems |
| FXF | Free-Fixed-Free |
| XFF | Fixed-Free-Free |
| XFX | Fixed-Free-Fixed |
| Symbols | |
| Transformation matrix | |
| The connectivity matrix | |
| The linear-transformation matrix | |
| The modified connectivity matrix | |
| The rotation matrix | |
| Overall stiffness matrix with slope discontinuities | |
| Overall stiffness matrix | |
| The length of the element | |
| Overall mass matrix with slope discontinuities | |
| Overall mass matrix | |
| An arbitrary point | |
| The position of the origin of the body-fixed coordinate system, which corresponds to the floating frame | |
| The shape matrix | |
| (,0) | The position of point in its undeformed state |
| (,f) | The elastic deformation of the element |
| The position of the point in relation to the body-fixed coordinate system | |
| () | The unconstrained vector of nodal coordinates for body i |
| Position vector | |
| Natural Frequency |
References
- Shabana, A.A. Flexible multibody dynamics: Review of past and recent developments. Multibody Syst. Dyn. 1997, 1, 189–222. [Google Scholar] [CrossRef]
- Shabana, A.A. Theory of Vibration: An Introduction, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- Shabana, A.A. Dynamics of Multibody Systems, 4th ed.; Cambridge University Press: Cambridge UK, 2013. [Google Scholar] [CrossRef]
- Géradin, M.; Cardona, A. Flexible Multibody Dynamics: A Finite Element Approach; John Wiley and Sons: Hoboken NJ, USA, 2001; Volume 4. [Google Scholar]
- Wasfy, T.; Noor, A. Computational strategies for flexible multibody systems. Appl. Mech. Rev. 2003, 56, 553–613. [Google Scholar] [CrossRef]
- Zienkiewicz, O.; Taylor, R.; Zhu, J. The Finite Element Method: Its Basis and Fundamentals. In The Finite Element Method: Its Basis and Fundamentals, 7th ed.; Butterworth-Heinemann: Oxford, UK, 2013; p. i. [Google Scholar] [CrossRef]
- Sugiyama, H.; Shabana, A.A.; Omar, M.A.; Loh, W.Y. Development of nonlinear elastic leaf spring model for multibody vehicle systems. Comput. Methods Appl. Mech. Eng. 2006, 195, 6925–6941. [Google Scholar] [CrossRef]
- Shabana, A.A. Definition of ANCF Finite Elements. J. Comput. Nonlinear Dyn. 2015, 10, 054506. [Google Scholar] [CrossRef]
- Nada, A.; Bishiri, A. Floating Frame of Reference formulation for modeling flexible multi-body systems in premise operational conditions. J. Vib. Control 2019, 25, 2706–2720. [Google Scholar] [CrossRef]
- Nada, A.; Hussein, B.; Megahed, S.; Shabana, A. Floating Frame of Reference and Absolute Nodal Coordinate Formulations in the Large Deformation Analysis of Robotic Manipulators: A Comparative Experimental and Numerical Study. In Proceedings of the ASME 2009 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference (IDETC/CIE 2009), San Diego, CA, USA, 30 August–2 September 2009. [Google Scholar] [CrossRef]
- Nowakowski, C.; Fehr, J.; Fischer, M.; Eberhard, P. Model Order Reduction in Elastic Multibody Systems using the Floating Frame of Reference Formulation. IFAC Proc. Vol. 2012, 45, 40–48. [Google Scholar] [CrossRef]
- Korkealaakso, P.; Mikkola, A.; Rantalainen, T.; Rouvinen, A. Description of joint constraints in the floating frame of reference formulation. Proc. Inst. Mech. Eng. Part K J.-Multi-Body Dyn. 2009, 223, 133–145. [Google Scholar] [CrossRef]
- Schilder, J.P. A New Floating Frame of Reference Formulation for Flexible Multibody Dynamics; University of Twente: Enschede, The Netherlands, 2017. [Google Scholar]
- De Ponti, J.M.; Colombi, A.; Ardito, R.; Braghin, F.; Corigliano, A.; Craster, R.V. Graded elastic metasurface for enhanced energy harvesting. New J. Phys. 2020, 22, 013013. [Google Scholar] [CrossRef]
- Huang, S.; Dong, G.; Zhou, M. Low-Frequency Broadband Piezoelectric Vibration Energy Harvester Based on Double L-shaped Beam Structures. J. Vib. Eng. Technol. 2022, 10, 3179–3189. [Google Scholar] [CrossRef]
- Wang, W.; Chen, J.; Zivkovic, A.S.; Xie, H. A Fourier Transform Spectrometer Based on an Electrothermal MEMS Mirror with Improved Linear Scan Range. Sensors 2016, 16, 1611. [Google Scholar] [CrossRef]
- Ahmed, R.; Mir, F.; Banerjee, S. A review on energy harvesting approaches for renewable energies from ambient vibrations and acoustic waves using piezoelectricity. Smart Mater. Struct. 2017, 26, 085031. [Google Scholar] [CrossRef]
- Bishiri, A.; Nada, A. Modal Analysis and Experimental Validation of Continuum Multibody Models with Slope Discontinuity and Restricted Deformations. J. Vib. Eng. Technol. 2025, 13, 235. [Google Scholar] [CrossRef]
- Heo, S.; Koo, W. Dynamic Response Analysis of a Wavestar-Type Wave Energy Converter Using Augmented Formulation in Korean Nearshore Areas. Processes 2021, 9, 1721. [Google Scholar] [CrossRef]
- Kim, D.; Bae, Y.H. Multibody Analysis of Wave Energy Converters and a Floating Platform in the Time Domain. J. Mar. Sci. Eng. 2024, 12, 265. [Google Scholar] [CrossRef]
- Li, Y.; Ren, N.; Li, X.; Ou, J. Hydrodynamic Analysis of a Novel Modular Floating Structure System Integrated with Floating Artificial Reefs and Wave Energy Converters. J. Mar. Sci. Eng. 2022, 10, 1091. [Google Scholar] [CrossRef]
- Sui, S.; Cao, L.; Gao, Y.; Huo, Z.; Chen, Q. Numerical Simulation Study on Hydrodynamic Characteristics of Offshore Floating Photovoltaics. J. Mar. Sci. Eng. 2025, 13, 142. [Google Scholar] [CrossRef]
- Ling, H.; Ying, L.; Bin, Y.; Yueqin, Z. Dynamic modeling and simulation of flexible beam finite rotation with ANCF method and FFR method. Mechanics 2018, 24, 715–724. [Google Scholar] [CrossRef]
- Slimak, T.; Zwölfer, A.; Todorov, B.; Rixen, D. A machine learning approach to simulate flexible body dynamics. Multibody Syst. Dyn. 2025, 64, 515–541. [Google Scholar] [CrossRef]
- Angeli, A.; Desmet, W.; Naets, F. Deep learning for model order reduction of multibody systems to minimal coordinates. Comput. Methods Appl. Mech. Eng. 2021, 373, 113517. [Google Scholar] [CrossRef]
- Moaveni, S. Finite Element Analysis: Theory and Application with Ansys; Pearson Education Limited: New York, NY, USA, 2015. [Google Scholar]
- Wittenburg, J. Dynamics of Multibody Systems; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Wallrapp, O. Standardization of Flexible Body Modeling in Multibody System Codes, Part I: Definition of Standard Input Data*. Mech. Struct. Mach. 1994, 22, 283–304. [Google Scholar] [CrossRef]
- Flores, P.; Ambrosio, J.; Claro, J.C.; Lankarani, H.M. Kinematics and dynamics of multibody systems with imperfect joints: Modeling and numerical simulation. Multibody Syst. Dyn. 2008, 20, 105–134. [Google Scholar] [CrossRef]
- Bauchau, O.A.; Craig, J.I. Structural Analysis: With Applications to Aerospace Structures; Springer: Dordrecht, The Netherlands, 2009. [Google Scholar] [CrossRef]
- Gere, W.; James, M.; Weaver, J. Analysis of Framed Structures; University Series in Civil Engineering and Applied Mechanics; Van Nostrand: Princeton, NJ, USA, 1965; p. xi + 475. [Google Scholar]
- Cook, R.D.; Malkus, D.S.; Plesha, M.E.; Witt, R.J. Concepts and Applications of Finite Element Analysis; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Nada, A.; Bayoumi, M. Development of a constraint stabilization method of multibody systems based on fuzzy logic control. Multibody Syst. Dyn. 2024, 61, 233–265. [Google Scholar] [CrossRef]



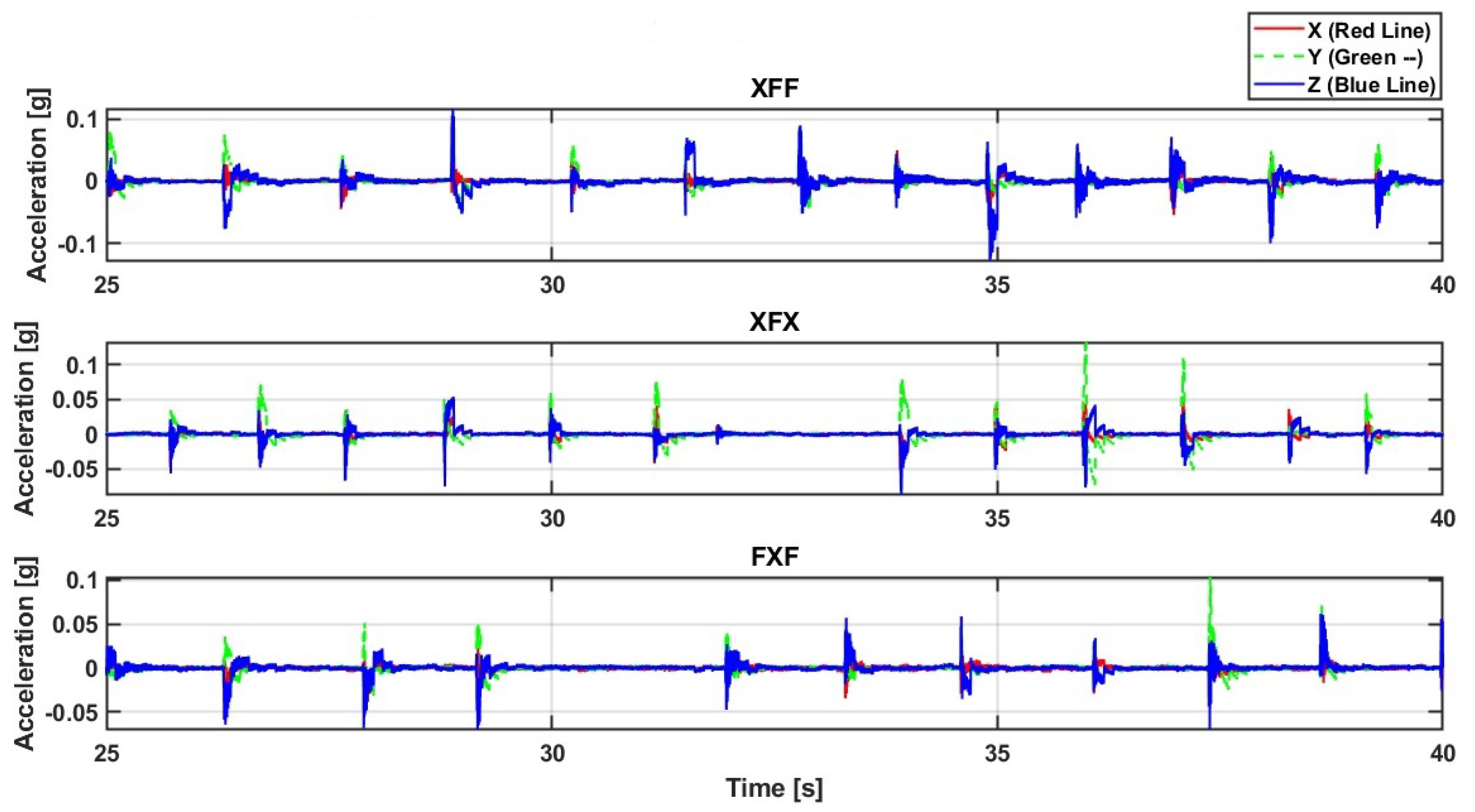
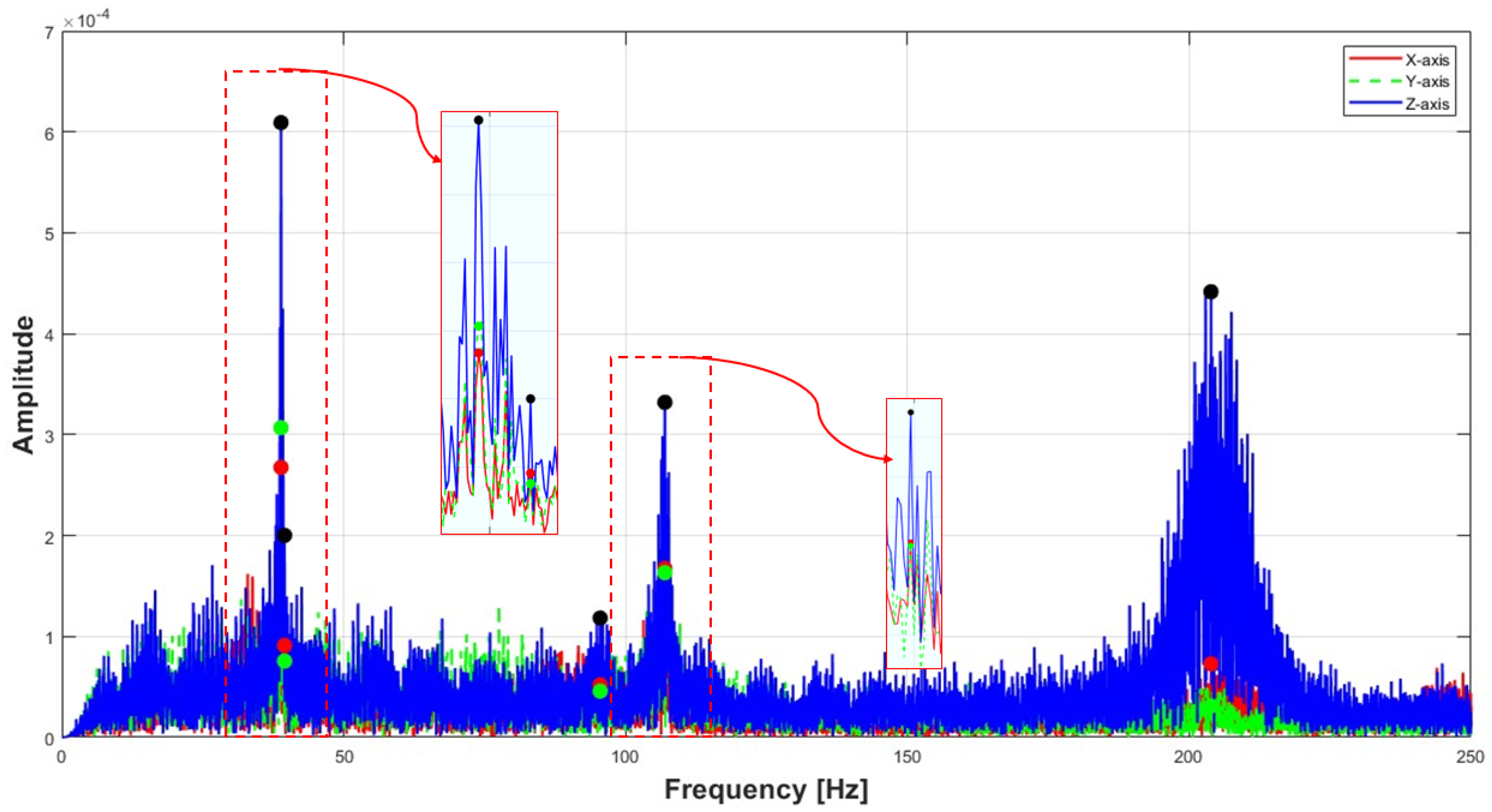
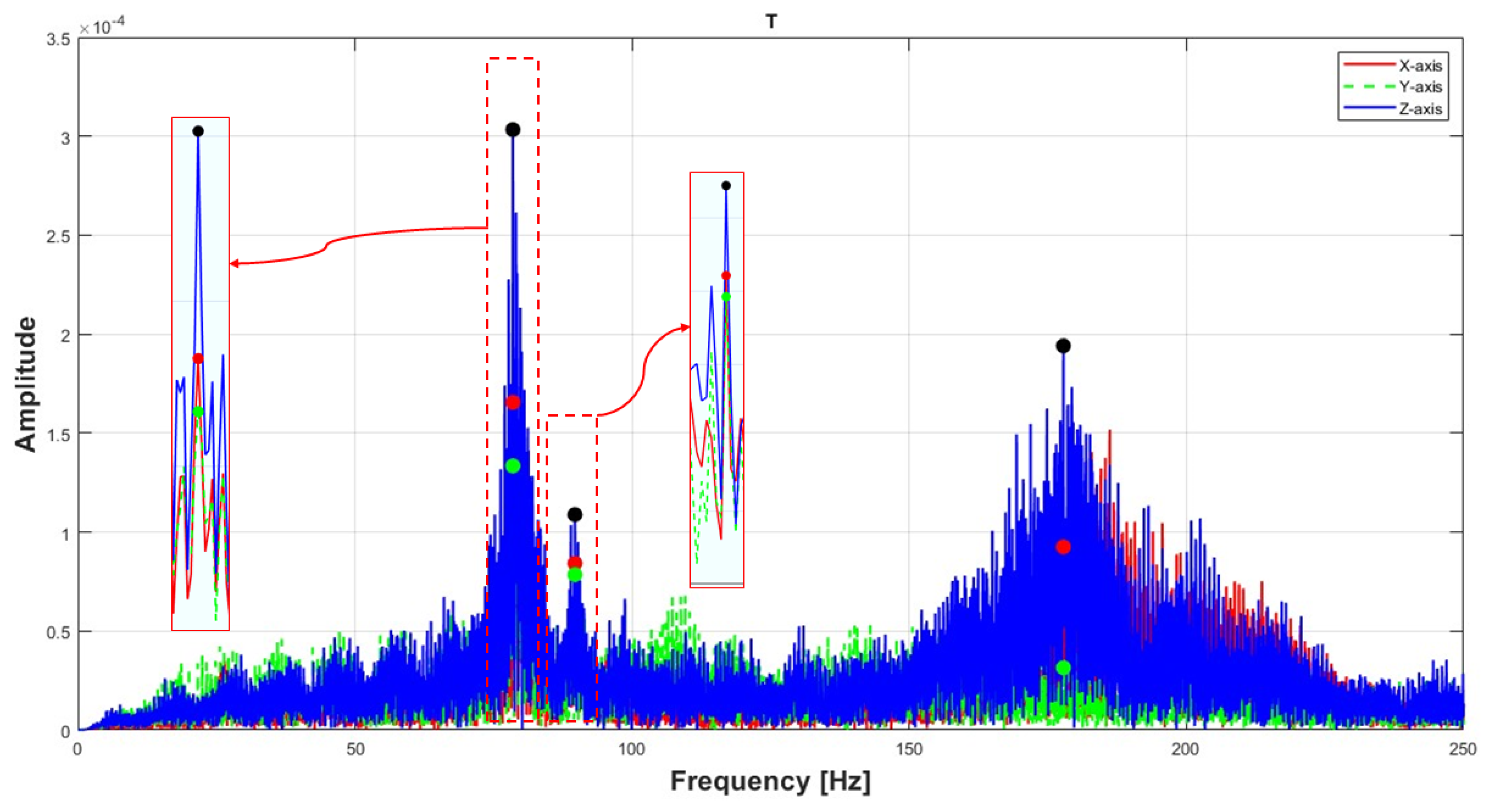
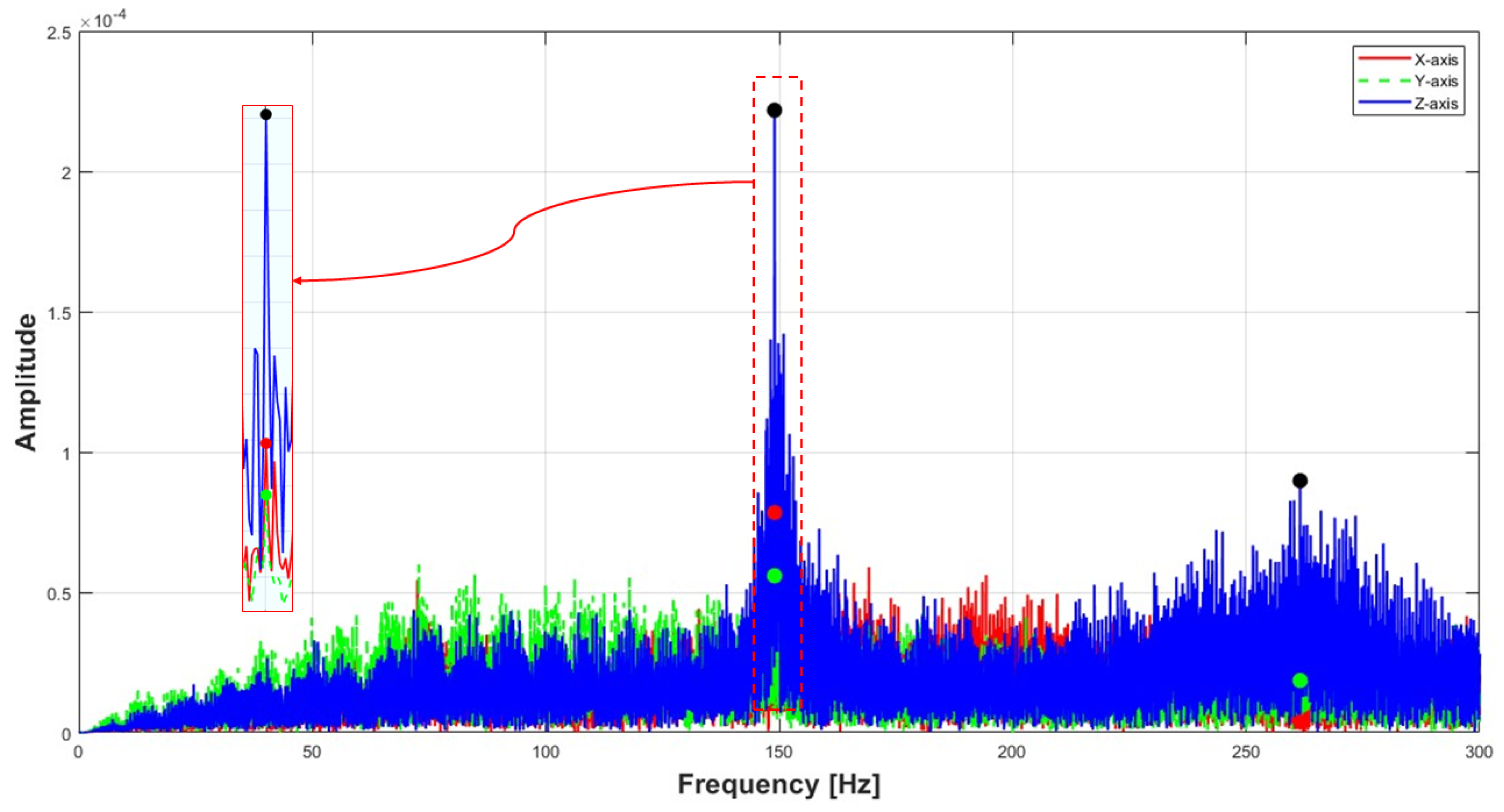
| Natural Frequency | XFF | XFX | FXF |
|---|---|---|---|
| 38.76 | 148.17 | 77.62 | |
| 45.68 | 270.67 | 89.32 | |
| 95.71 | … | 211.57 | |
| 115.89 | … | ||
| 219.24 | … |
| Natural Frequency | XFF | XFX | FXF |
|---|---|---|---|
| 36.49 | 146.91 | 74.29 | |
| 40.31 | 250.78 | 79.59 | |
| 99.79 | … | 218.97 | |
| 108.97 | … | ||
| 205.96 | … |
| Mode | Boundary Condition | FFR (Hz) | Experiment (Hz) | ANSYS (Hz) |
|---|---|---|---|---|
| XFF | 38.76 | 38.87 | 36.49 | |
| 45.68 | 39.50 | 40.31 | ||
| 95.71 | 95.50 | 99.79 | ||
| 115.89 | 106.97 | 108.97 | ||
| 219.24 | 203.87 | 205.96 | ||
| FXF | 77.62 | 78.49 | 74.29 | |
| 89.32 | 89.68 | 79.59 | ||
| 211.57 | 177.81 | 218.97 | ||
| XFX | 148.17 | 149.01 | 146.91 | |
| 270.67 | 261.56 | 250.78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Institute of Knowledge Innovation and Invention. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koda, S.M.; Matsubara, M.; Fath El-Bab, A.M.R.; Nada, A.A. Experimental and Numerical Validation of an Extended FFR Model for Out-of-Plane Vibrations in Discontinuous Flexible Structures. Appl. Syst. Innov. 2025, 8, 118. https://doi.org/10.3390/asi8050118
Koda SM, Matsubara M, Fath El-Bab AMR, Nada AA. Experimental and Numerical Validation of an Extended FFR Model for Out-of-Plane Vibrations in Discontinuous Flexible Structures. Applied System Innovation. 2025; 8(5):118. https://doi.org/10.3390/asi8050118
Chicago/Turabian StyleKoda, Sherif M., Masami Matsubara, Ahmed M. R. Fath El-Bab, and Ayman A. Nada. 2025. "Experimental and Numerical Validation of an Extended FFR Model for Out-of-Plane Vibrations in Discontinuous Flexible Structures" Applied System Innovation 8, no. 5: 118. https://doi.org/10.3390/asi8050118
APA StyleKoda, S. M., Matsubara, M., Fath El-Bab, A. M. R., & Nada, A. A. (2025). Experimental and Numerical Validation of an Extended FFR Model for Out-of-Plane Vibrations in Discontinuous Flexible Structures. Applied System Innovation, 8(5), 118. https://doi.org/10.3390/asi8050118






