Existence, Uniqueness, and Stability of Weighted Fuzzy Fractional Volterra–Fredholm Integro-Differential Equation
Abstract
1. Introduction
- A new class of fuzzy fractional Volterra–Fredholm integro-differential equations (FWFVFIDEs) is introduced using weighted fractional calculus in the Caputo sense.
- Existence and uniqueness results are established using Banach’s and Krasnoselskii’s fixed-point theorems under weighted Lipschitz conditions.
- Stability results in the Ulam–Hyers and Ulam–Hyers–Rassias senses are derived, ensuring robustness under perturbations.
- A modified Adomian decomposition method (MADM) is presented to construct the solution in the form of a recursive series.
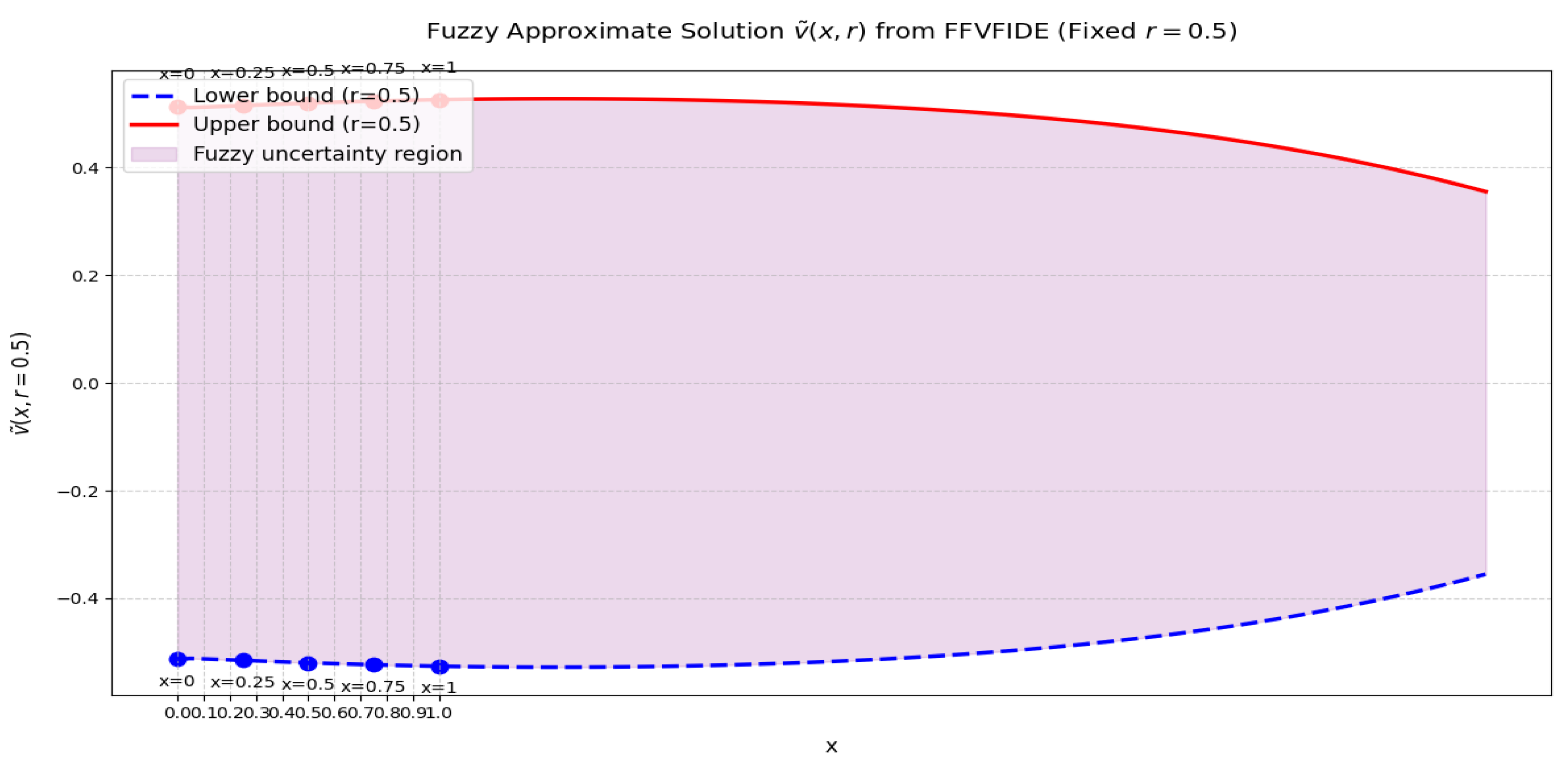
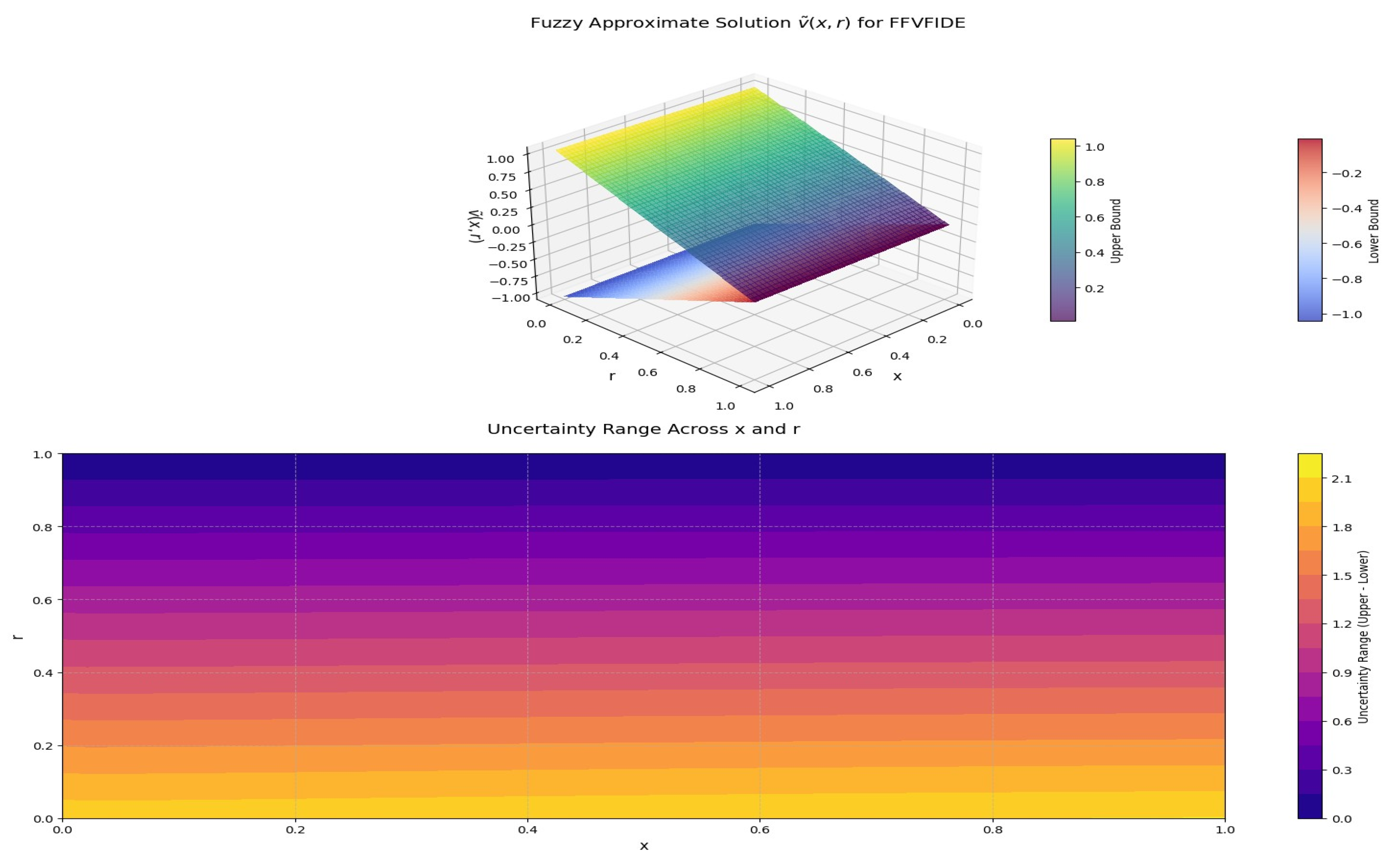
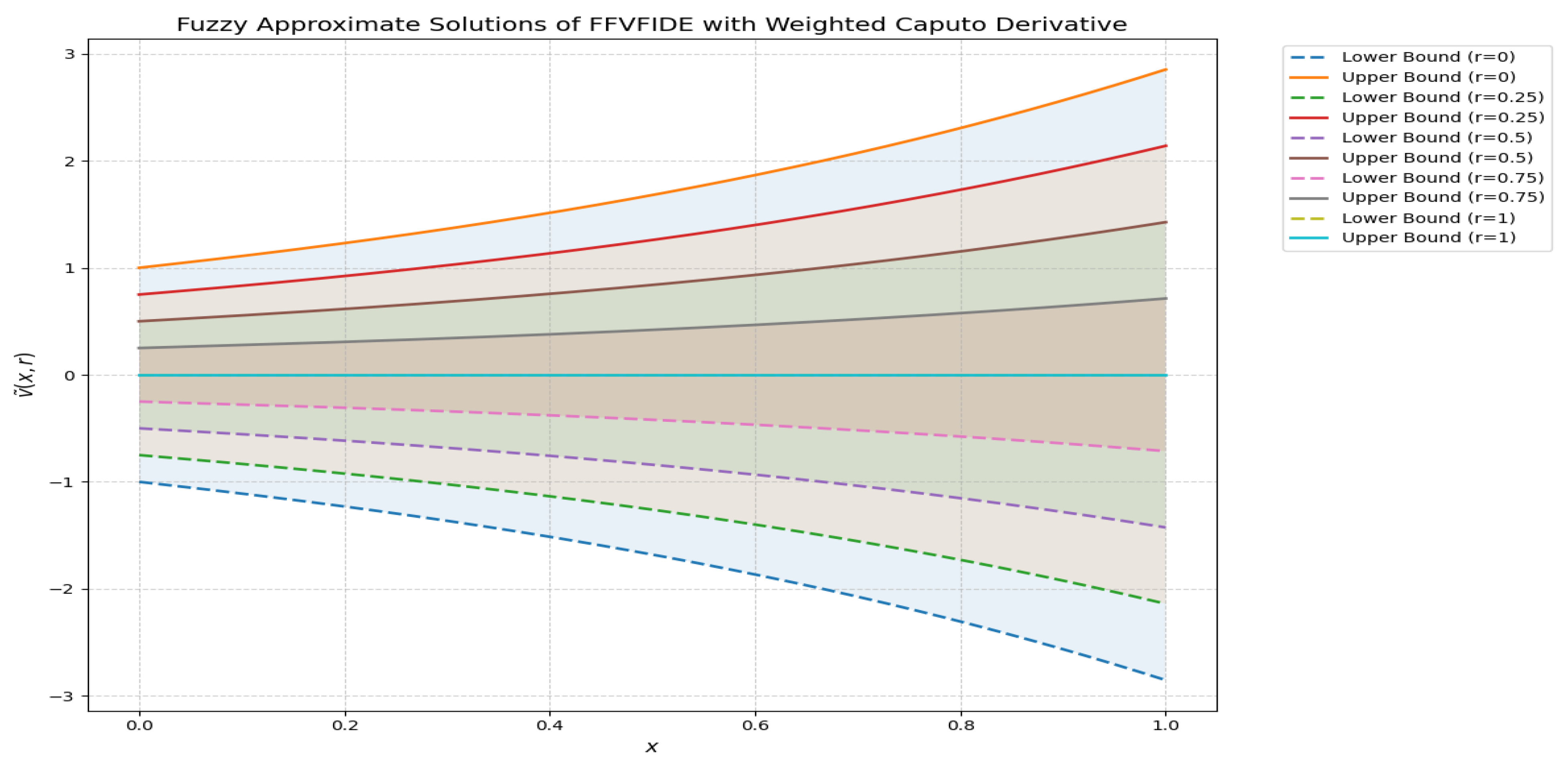
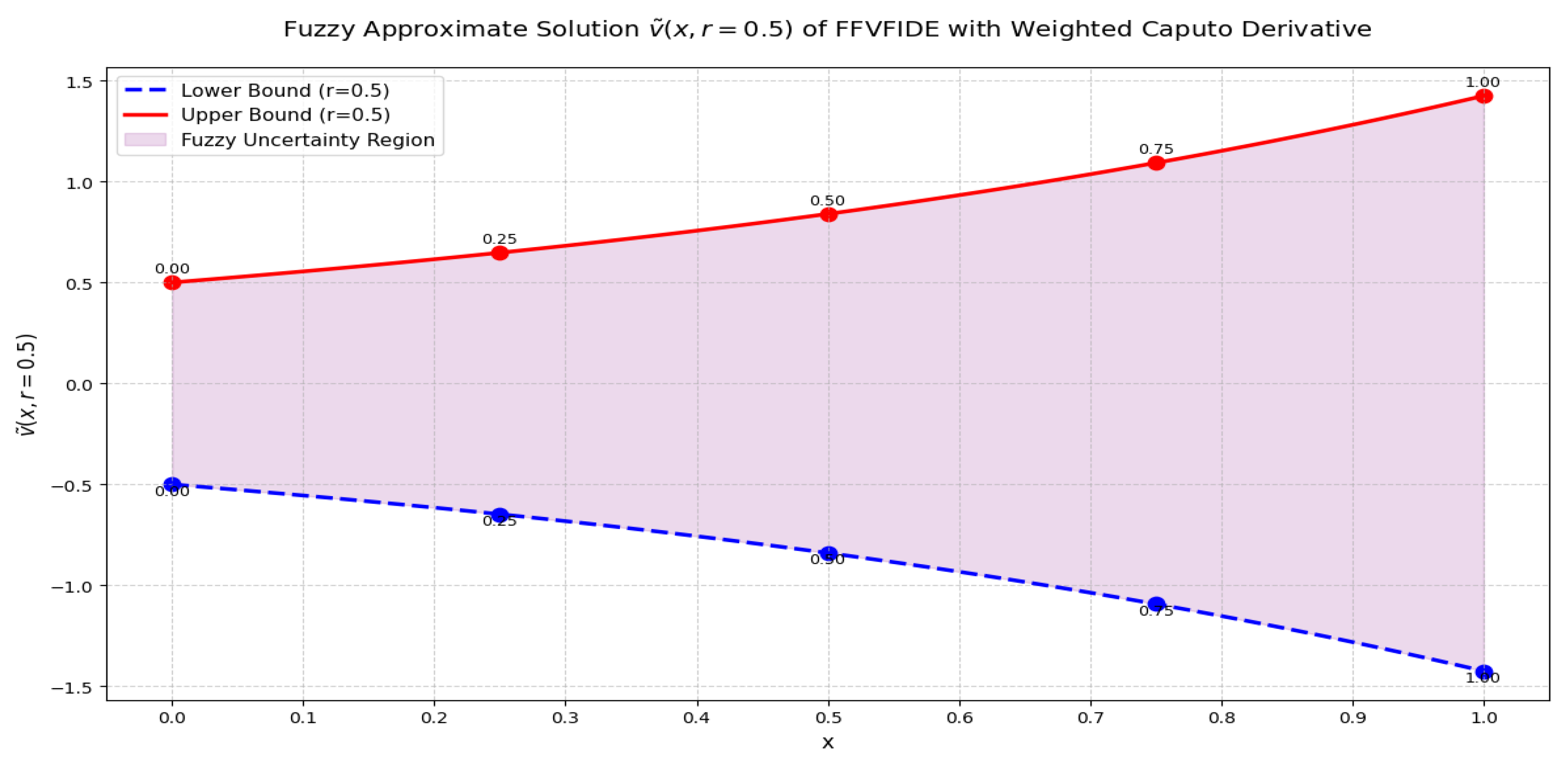
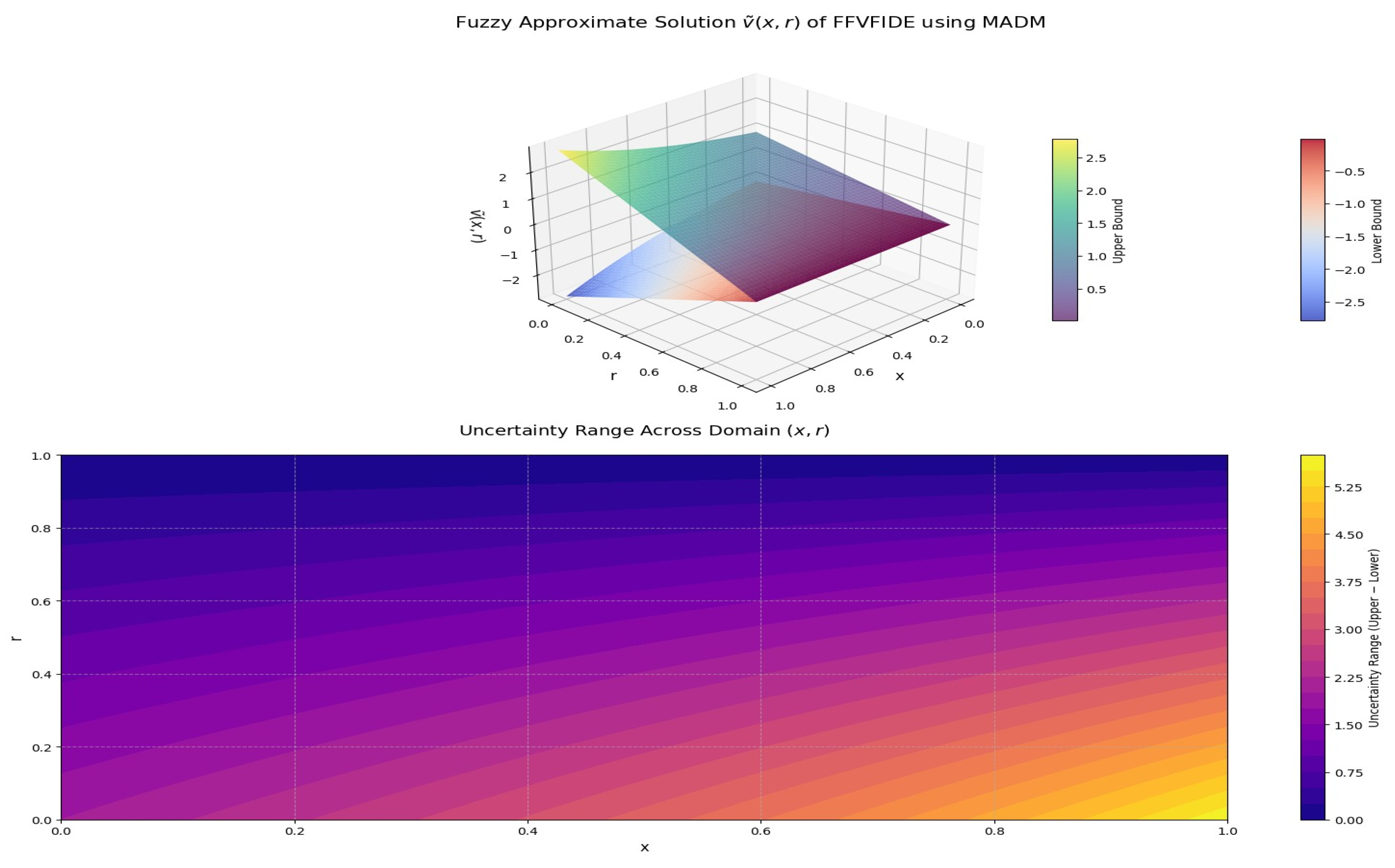
- A numerical example, along with graphical interpretation, is provided to illustrate the effectiveness and applicability of the proposed method.

2. Preliminaries
- The lower-bound function () is defined on the interval of and is bounded, left-continuous, and monotonically increasing.
- The upper-bound function () is also defined on and is bounded, left-continuous, and monotonically decreasing.
- For all , it holds that .
- 1.
- , ;
- 2.
- ;
- 3.
- ;
- 4.
- , λ is scalar;
- 5.
- .
- 1.
- For all , the sum of ;
- 2.
- is a contraction mapping;
- 3.
- is continuous and compact.
3. Existence and Uniqueness
4. Stability
5. Modified Adomian Decomposition Method
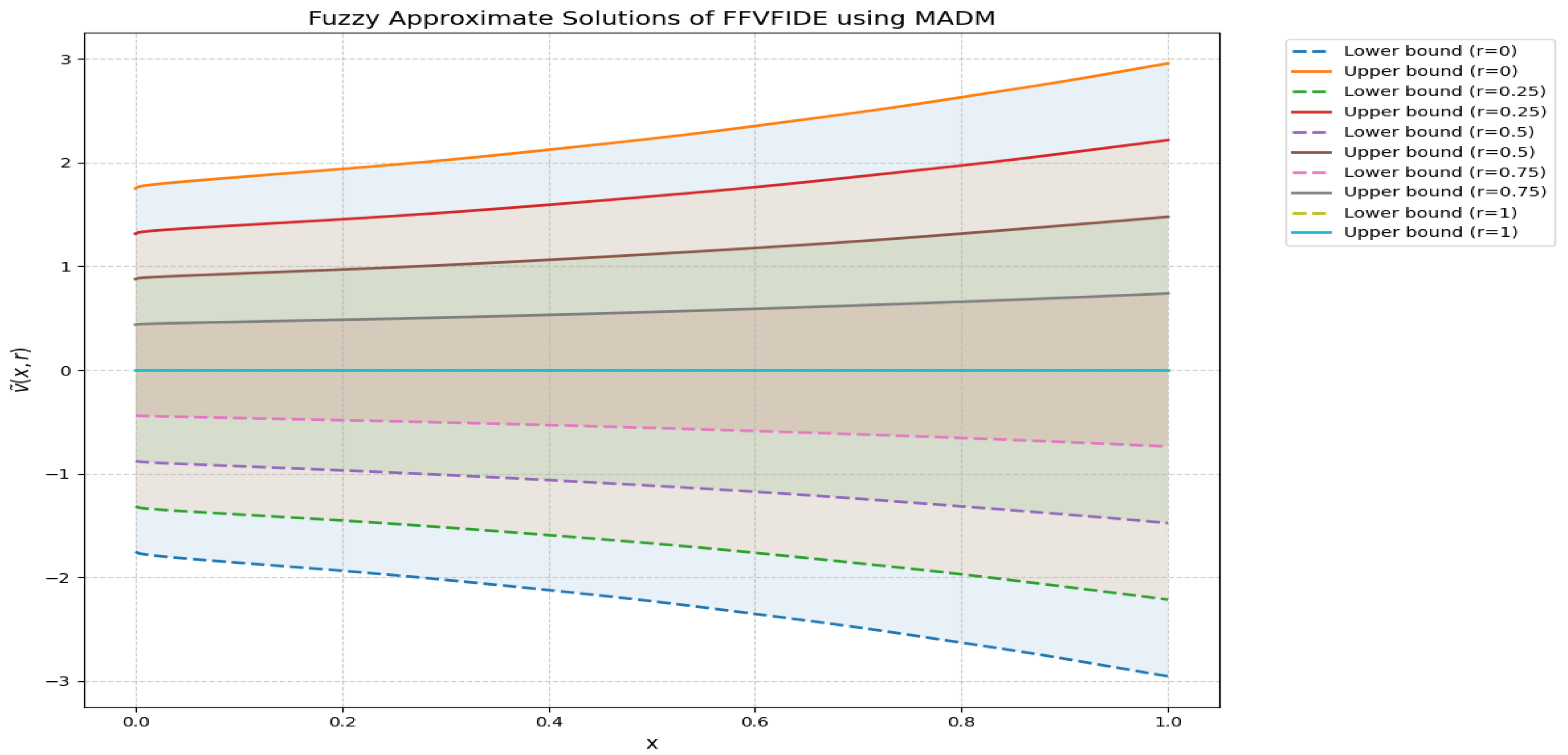
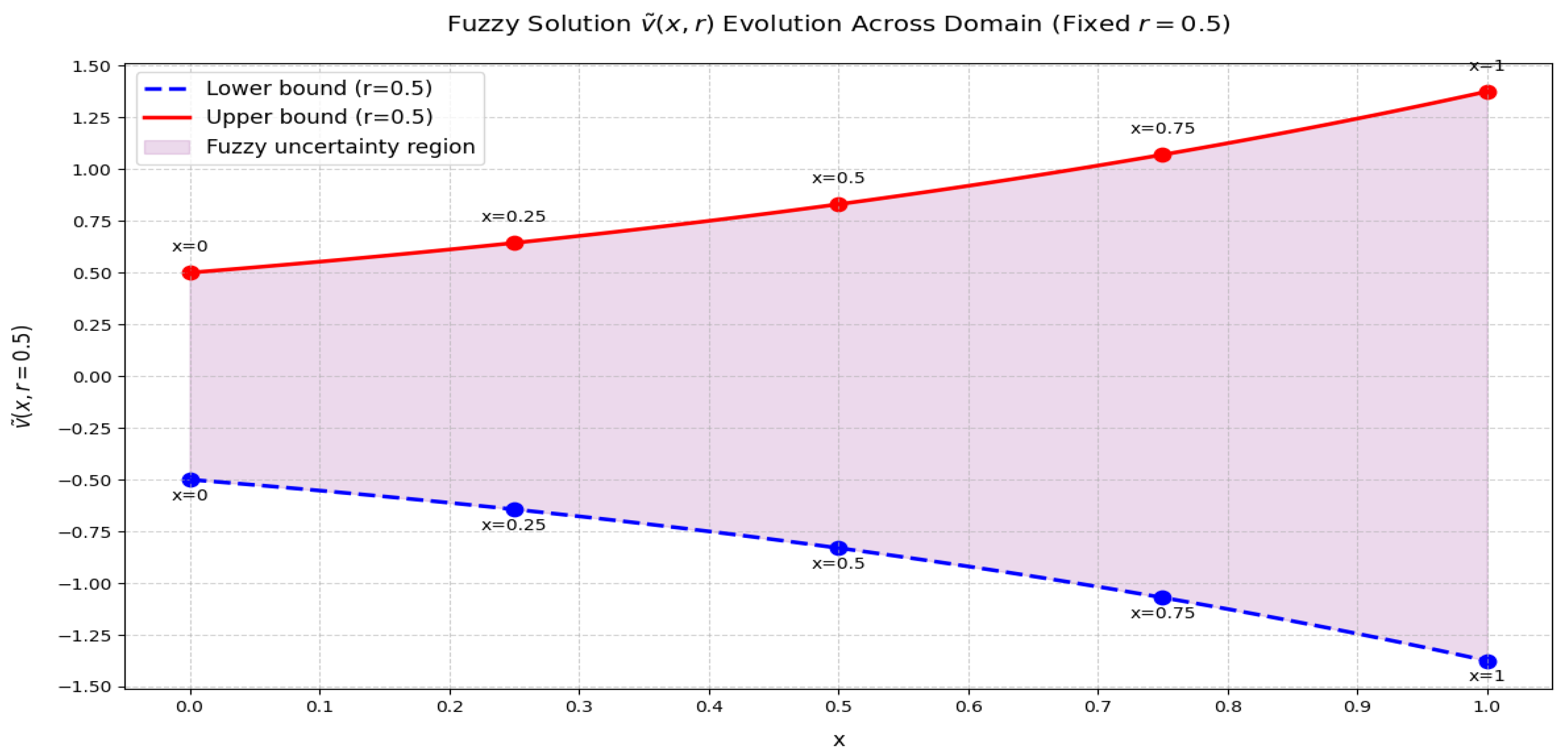
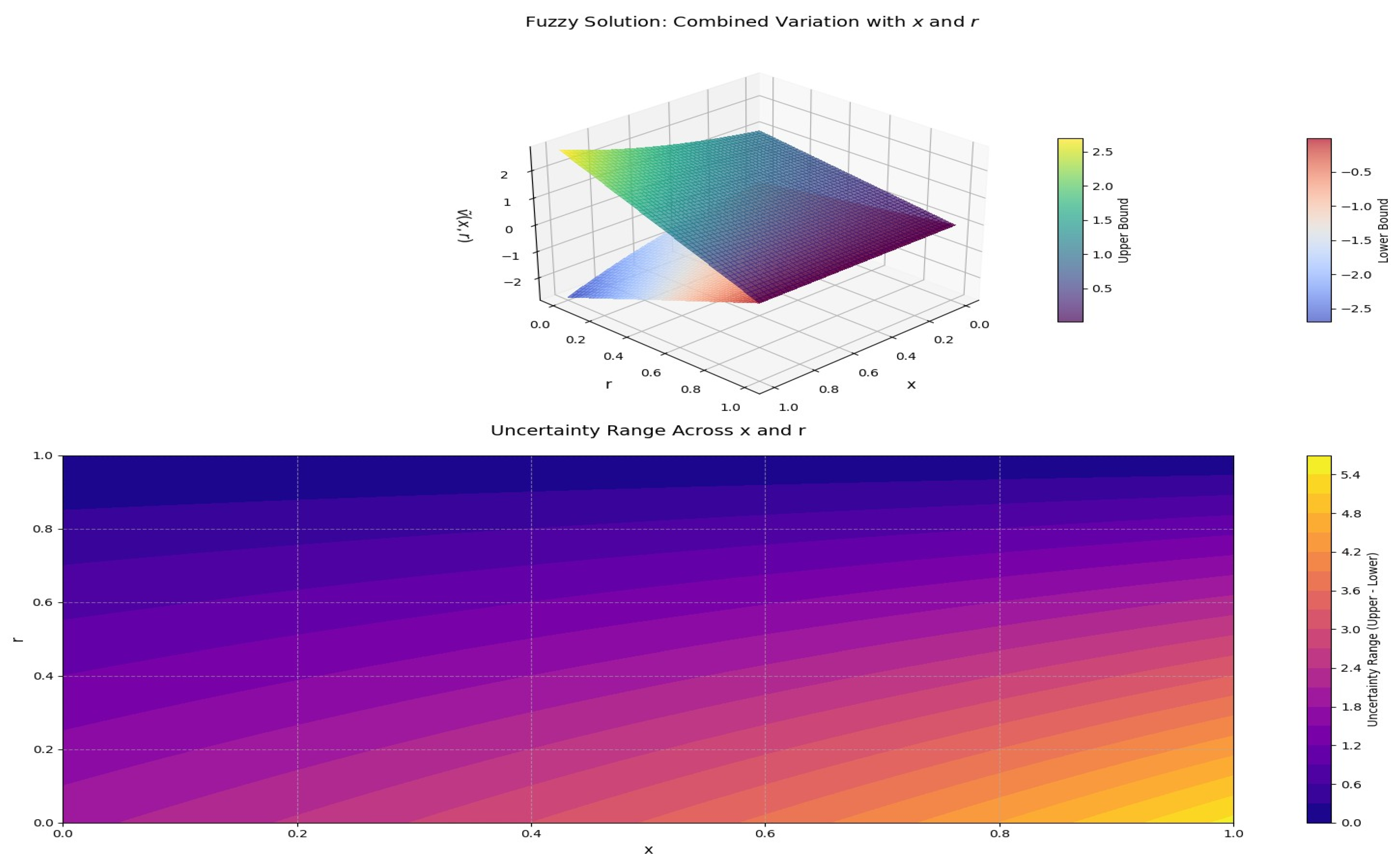
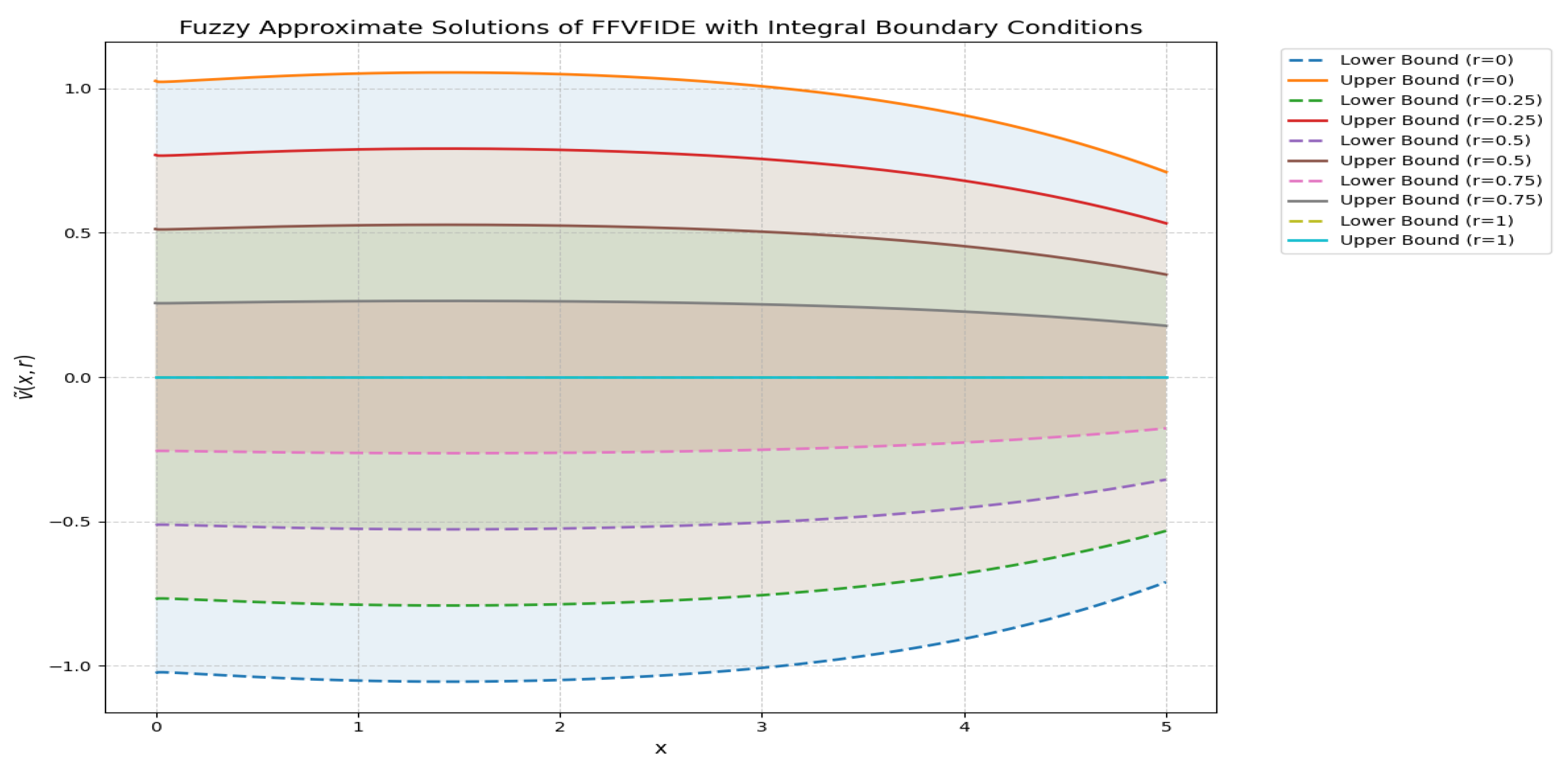
Numerical Examples
6. Conclusions and Future Research
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kilbas, A. Theory and applications of fractional differential equations. N.-Holl. Math. Stud. 2006, 204. [Google Scholar] [CrossRef]
- Fernandez, A.; Uçar, S.; Özdemir, N. Solving a well-posed fractional initial value problem by a complex approach. Fixed Point Theory Algorithms Sci. Eng. 2021, 2021, 11. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Dubois, D.J. Fuzzy Sets and Systems: Theory and Applications; Academic Press: Cambridge, MA, USA, 1980. [Google Scholar]
- Alaroud, M.; Al-Smadi, M.; Rozita Ahmad, R.; Salma Din, U.K. An analytical numerical method for solving fuzzy fractional Volterra integro-differential equations. Symmetry 2019, 11, 205. [Google Scholar] [CrossRef]
- Allahviranloo, T. Fuzzy fractional differential operators and equations. In Studies in Fuzziness and Soft Computing; Springer: Berlin/Heidelberg, Germany, 2021; Volume 397. [Google Scholar]
- Chakraverty, S.; Tapaswini, S.; Behera, D. Fuzzy Differential Equations and Applications for Engineers and Scientists; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Kumar, S.; Nieto, J.J.; Ahmad, B. Chebyshev spectral method for solving fuzzy fractional Fredholm–Volterra integro-differential equation. Math. Comput. Simul. 2022, 192, 501–513. [Google Scholar] [CrossRef]
- Shabestari, M.R.M.; Ezzati, R.; Allahviranloo, T. Numerical solution of fuzzy fractional integro-differential equation via two-dimensional Legendre wavelet method. J. Intell. Fuzzy Syst. 2018, 34, 2453–2465. [Google Scholar] [CrossRef]
- Ahmad, N.; Ullah, A.; Ullah, A.; Ahmad, S.; Shah, K.; Ahmad, I. On analysis of the fuzzy fractional order Volterra-Fredholm integro-differential equation. Alex. Eng. J. 2021, 60, 1827–1838. [Google Scholar] [CrossRef]
- Phung, N.N.; Ta, B.Q.; Ho, V. Ulam-Hyers stability and Ulam-Hyers-Rassias stability for fuzzy integrodifferential equation. Complexity 2019, 201, 275979. [Google Scholar]
- Hamoud, A.A.; Osman, M. Existence, uniqueness and stability results for fractional nonlinear Volterra-Fredholm integro-differential equations. TWMS J. Appl. Eng. Math. 2023, 13, 491–506. [Google Scholar] [CrossRef]
- Awad, Y.A.R.; Kaddoura, I.H. On the Ulam-Hyers-Rassias stability for a boundary value problem of implicit?-Caputo fractional integro-differential equation. TWMS J. Appl. Eng. Math. 2024, 14, 79–93. [Google Scholar]
- Fernandez, A.; Fahad, H.M. Weighted fractional calculus: A general class of operators. Fractal Fract. 2022, 6, 208. [Google Scholar] [CrossRef]
- Agrawal, O.P. Some generalized fractional calculus operators and their applications in integral equations. Fract. Calc. Appl. Anal. 2012, 15, 700–711. [Google Scholar] [CrossRef]
- Abdo, M.S.; Abdeljawad, T.; Ali, S.M.; Shah, K.; Jarad, F. Existence of positive solutions for weighted fractional order differential equations. Chaos Solitons Fractals 2020, 141, 110341. [Google Scholar] [CrossRef]
- Pengyan, W.; Yongzhong, W. Positive solutions for a weighted fractional system. Acta Math. Sci. 2018, 38, 935–949. [Google Scholar] [CrossRef]
- Makogin, V.; Mishura, Y. Fractional integrals, derivatives and integral equations with weighted Takagi-Landsberg functions. arXiv 2020, arXiv:2003.13285. [Google Scholar] [CrossRef]
- Ezzati, R.; Zabihi, S. Fuzzy fractional calculus: A comprehensive overview with a focus on weighted Caputo-type generalized Hukuhara differentiability and analytical solutions for fuzzy fractional differential equations. Iran. J. Fuzzy Syst. 2024, 21, 19–34. [Google Scholar]
- Kasimala, N.R.; Chakraverty, S. Fuzzy Fractional Order Volterra-Fredholm Integro-Differential Equations Using MADM. Res. Sq. 2022. preprint. [Google Scholar]
- Savla, S.; Sharmila, R. Solving Linear and Nonlinear Fuzzy Fractional Volterra-Fredholm Integro Differential Equations Using Shehu Adomian Decomposition Method. Indian J. Sci. Technol. 2024, 17, 1222–1230. [Google Scholar] [CrossRef]
- Ghazouani, A.E.; Elomari, M.; Melliani, S. Existence, uniqueness, and UH-stability results for nonlinear fuzzy fractional Volterra–Fredholm integro-differential equations. J. Nonlinear Complex Data Sci. 2025, 25, 457–477. [Google Scholar] [CrossRef]
- Wazwaz, A.M.; El-Sayed, S.M. A new modification of the Adomian decomposition method for linear and nonlinear operators. Appl. Math. Comput. 2001, 122, 393–405. [Google Scholar] [CrossRef]
- Conejero, J.A.; Garibo-i Orts, Ò.; Lizama, C. A new paradigm in the logistic and similar maps: Time stepping schemes. Rev. Real Acad. Cienc. Exactas Físicas Y Nat. Ser. A Mat. 2024, 118, 75. [Google Scholar] [CrossRef]

| Stability Type | Perturbation Bound | Stability Estimate |
|---|---|---|
| Ulam–Hyers Stability (UHS) | Constant perturbation | where b is a constant |
| Generalized Ulam–Hyers Stability (GUHS) | Perturbation and | with continuous and positive |
| Ulam–Hyers–Rassias Stability (UHRS) | Mixed perturbation and | , combining constant and variable components |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbas, S.; Abro, A.A.; Daniyal, S.M.; Abdallah, H.A.; Ahmad, S.; Ateya, A.A.; Zahid, N.B. Existence, Uniqueness, and Stability of Weighted Fuzzy Fractional Volterra–Fredholm Integro-Differential Equation. Fractal Fract. 2025, 9, 540. https://doi.org/10.3390/fractalfract9080540
Abbas S, Abro AA, Daniyal SM, Abdallah HA, Ahmad S, Ateya AA, Zahid NB. Existence, Uniqueness, and Stability of Weighted Fuzzy Fractional Volterra–Fredholm Integro-Differential Equation. Fractal and Fractional. 2025; 9(8):540. https://doi.org/10.3390/fractalfract9080540
Chicago/Turabian StyleAbbas, Sahar, Abdul Ahad Abro, Syed Muhammad Daniyal, Hanaa A. Abdallah, Sadique Ahmad, Abdelhamied Ashraf Ateya, and Noman Bin Zahid. 2025. "Existence, Uniqueness, and Stability of Weighted Fuzzy Fractional Volterra–Fredholm Integro-Differential Equation" Fractal and Fractional 9, no. 8: 540. https://doi.org/10.3390/fractalfract9080540
APA StyleAbbas, S., Abro, A. A., Daniyal, S. M., Abdallah, H. A., Ahmad, S., Ateya, A. A., & Zahid, N. B. (2025). Existence, Uniqueness, and Stability of Weighted Fuzzy Fractional Volterra–Fredholm Integro-Differential Equation. Fractal and Fractional, 9(8), 540. https://doi.org/10.3390/fractalfract9080540









